小型月面跳跃机器人设计及运动建模

doi:10.16183/j.cnki.jsjtu.2023.646

小型月面跳跃机器人设计及运动建模

严赫¹, 朱星月¹, 侯张俪¹, 王卫军², 张执南^,¹

1.上海交通大学机械与动力工程学院, 上海 200240

2.上海宇航系统工程研究所, 上海 201109

Design and Motion Modeling of a Small-Scale Lunar Jumping Robot

YAN He¹, ZHU Xingyue¹, HOU Zhangli¹, WANG Weijun², ZHANG Zhinan^,¹

1. School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Shanghai Institute of Aerospace System Engineering, Shanghai 201109, China

通讯作者: 张执南,教授,博士生导师,电话(Tel.):021-34208037;E-mail:zhinanz@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-12-26 修回日期: 2024-02-17 接受日期: 2024-03-7

基金资助:

中国航天科技集团有限公司第八研究院产学研合作基金(USCAST2022-15)

Received: 2023-12-26 Revised: 2024-02-17 Accepted: 2024-03-7

作者简介 About authors

严赫(2000—),现为华为技术有限公司软件开发工程师,从事摩擦-动力学建模与分析研究.

摘要

跳跃是月面探测机器人的一种可行的运动方式.由于缺乏与月壤特性的耦合研究,跳跃机器人在月面探测中尚未有成熟应用.针对月面探测器5 kPa的承载指标要求,开展机器人与月面的耦合研究,提出跳跃机器人新型储能腿构型,实现起跳时初速度大小与方向可变的低承载跳跃;优化储能元件参数,实现机器人的近恒力起跳,并在动力学仿真环境中完成验证.为实现机器人在月球表面的精确跳跃目标,建立考虑阻尼特性的月壤力学特性模型,基于离散元仿真环境测定了模型的关键力学参数,进而构建月壤表面机器人跳跃动力学模型,并通过离散元-动力学耦合仿真验证了模型的精确性.基于所建立的动力学模型,实现了两种运动规划算法,验证了模型的应用可能性.

关键词： 月面探测; 跳跃机器人; 月壤力学特性; 动力学模型; 离散元仿真

Abstract

Jumping is a viable form of locomotion for lunar surface exploration. However, due to the limited research on the coupling between jumping robots and the lunar surface, applying jumping robots for lunar surface detection remains challenging. Aiming at the load index of 5 kPa for the lunar surface detector, a new energy storage leg configuration of a jumping robot was proposed to realize low load jump with variable initial velocity and direction during take-off. The parameters of energy storage element were optimized to realize near-constant force take-off of the robot, which was validated in a dynamic simulation environment. To enable accurate jumps on the surface of the moon, a lunar soil mechanical property model considering damping characteristics was proposed, a discrete element simulation environment was built to determine the mechanical parameters, with a jumping dynamics model of the lunar surface robot established to verify the model accuracy through discrete element dynamics coupling simulation. Based on this dynamic model, two motion planning algorithms are implemented, confirming the application of the model.

Keywords： lunar surface detection; jumping robot; mechanical properties of lunar soil; dynamic model; discrete element simulation

PDF (10631KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

严赫, 朱星月, 侯张俪, 王卫军, 张执南. 小型月面跳跃机器人设计及运动建模[J]. 上海交通大学学报, 2025, 59(8): 1169-1180 doi:10.16183/j.cnki.jsjtu.2023.646

YAN He, ZHU Xingyue, HOU Zhangli, WANG Weijun, ZHANG Zhinan. Design and Motion Modeling of a Small-Scale Lunar Jumping Robot[J]. Journal of Shanghai Jiaotong University, 2025, 59(8): 1169-1180 doi:10.16183/j.cnki.jsjtu.2023.646

月表地形十分复杂,包括撞击坑、月球高地、月海和风化层等,这些地形上还分布着大量直径 0.01~1 m的月岩、月坑等障碍物^[1].常规轮式月球车无法完全适应月表复杂地形.月球的重力加速度是地球的1/6,大气密度为地球的1/1 012,接近真空状态^[2].基于月面的特殊特性,同等条件下跳跃机器人在月球表面可实现更高、更远和更可控的跳跃,跳跃机器人在月面复杂地形的探测中具有巨大的应用前景.

目前,国内外学者针对月面跳跃机器人开展了一定研究.例如,李贺等^[3]设计了一种通过气缸储能进行跳跃的月面移动机器人,从能量角度评估了机器人的跳跃能力,但没有通过试验验证月壤上的跳跃能力.Yoshikawa等^[4]设计了一种通过弹簧储能进行跳跃的月面探测机器人,该跳跃机器人在地球重力下的模拟月壤上的跳跃距离为0.2~1.0 m,该研究虽然验证了机器人构型的可行性,但由于缺乏月壤对跳跃影响的研究,无法让机器人实现可控的精确跳跃,从而难以直接应用到月面探测任务中.而在主要从硬地起跳的小型跳跃机器人领域,重点是通过仿生设计与参数优化来达到跳跃性能的目标,如跳蚤^[5]、蝉^[6]、夜猴^[7]、弹尾虫^[8]等仿生跳跃形式.然而,该类机器人在松软地貌起跳研究多以试验为主,如麻省理工学院(MIT)猎豹机器人在软硬地面跳跃进行了实验数据测试^[9],但微观机制上的颗粒介质力的定律并未研究透彻,因此在松软地貌上实现精准跳跃具有挑战性.

基于上述分析,探明跳跃过程中月壤力学特性对机器人的影响是实现月面上可控精确跳跃的基础.目前月面机器人与月壤力学特性相关的研究以轮-壤相互作用为主,我国学者已对月球车在月面行驶过程中车轮所受月壤的正向受力^[10]与侧向受力^[11]进行了较为充分的研究.而经典轮-壤接触模型中所考虑的杰西剪切理论与Bekker承压模型^[12]为准静态模型,能否直接应用于跳跃这一短暂动态过程有待进一步研究.

目前,研究月壤力学特性的方法主要有两种:① 模拟月壤试分析法.张宇等^[13-14]针对不同孔隙比的CAS-1型模拟月壤进行三轴实验,得到剪切特性曲线与承载特性曲线,并定性描述了模拟月壤阻尼比的变化规律.黄晗等^[15]对不同密实度的JLU5型模拟月壤进行贯入阻力力学实验,得到模拟月壤的贯入特性曲线.王康等^[16]对CE5型模拟月壤进行触月压痕试验,通过偏最小支持向量机(LSSVM)由实验结果预测模拟月壤力学状态.田野等^[17]基于应力波反射法,借助霍普金森压杆试验装置,研究了模拟月壤受冲击特性.② 离散元仿真分析法.邹猛等^[18]采用颗粒流软件PFC 3D,设计离散元模拟三轴试验,测定了离散元月壤的剪切特性曲线与承载特性曲线.林呈祥等^[19]采用颗粒流软件PFC 2D研究了不同颗粒形状对离散元月壤抗剪特性的影响.黄晗等^[15]采用颗粒流软件EDEM,设计了离散元模拟圆锥贯入试验,研究了离散元月壤密实度与圆锥指数梯度的关系.林云成等^[20]采用PFC 2D,设计了足垫冲击离散元月壤的仿真试验,得到了冲击过程离散元月壤的动态变化情况.实际上,基于模拟月壤的方法难以模拟月面低重力环境,而基于离散元的方法难以模拟真实月壤颗粒的微观形态.由于跳跃过程受重力影响显著,离散元方法更加适合研究跳跃中的月壤力学特性.虽然,针对月壤力学特性种类的研究众多,但明确哪些特性在跳跃过程中起主导作用是实现月面可控跳跃的关键问题之一.

本文设计了一种新型跳跃机器人,针对机器人可控精确跳跃目标,建立机器人在月壤上跳跃的动力学模型.该动力学模型的核心是基于跳跃相关月壤力学特性,建立月壤-机器人作用机理的理论表达式.基于动力学模型设计了具有月面探测应用价值的跳跃运动规划算法,验证了动力学模型的可行性.

1 跳跃机器人结构设计

1.1 总体构型

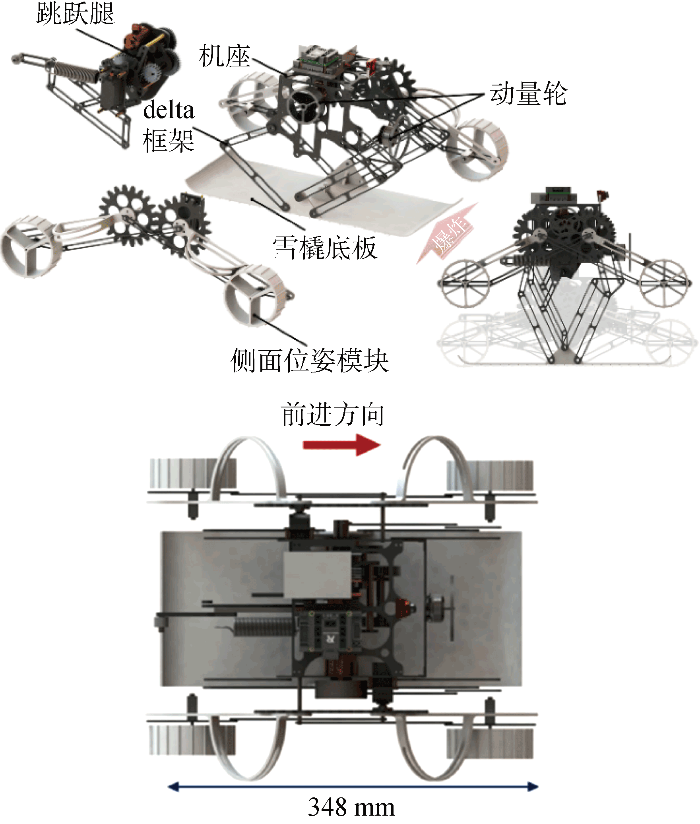
以月壤5 kPa的承载压强需求为基础指标,考虑机器人在月壤上跳跃时的下陷与滑移现象,设计一款以大面积雪橇底板式跳跃腿为核心的跳跃机器人构型,可实现起跳时月面受力较小、起跳角与起跳初速度可调的月面跳跃运动.采用雪橇板设计的主要原因在于该种方案能够将机器人起跳过程中和月壤的相互作用过程中产生的作用力进行简化,由于雪撬板底部布有平行式栅栏,所以起跳过程中雪撬板与月壤颗粒间的相互作用主要为横向滑移力和法向承载力.如图1所示,机器人由机座、雪橇底板、跳跃腿、delta框架、侧面位姿模块和动量轮6部分构成.其中,雪橇底板底部带有梳齿结构,可减少起跳时机器人的滑移量;delta框架为被动平面二自由度结构,确保机座与雪撬板平行;侧面位姿模块由主动舵机带动双平行四边形结构,底部连杆固连主动车轮,可实现侧面主动车轮的升降.机器人总质量约为1.8 kg.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 机器人总构型示意图

Fig.1 Schematic diagram of robot configuration

机器人在起跳前通过机座与跳跃腿间的伺服电动机改变起跳角度,控制侧面位姿模块的升降使得身体的滚转角能够自适应月壤平面的倾斜度,配合主动控制腿部伸缩带动身体升降初步踩平月壤,使得雪橇底板与月面基本贴合,跳跃腿储能释放实现跳跃;在空中通过动量轮实现滚转角与俯仰角的稳定控制,使得跳跃腿与月面的夹角达到指定的落地角度;在落地时通过跳跃腿的主动伺服电动机进行腿部的落地缓冲;需要转向时,在月面上通过侧面位姿模块的主动轮差速运动进行水平转向.

1.2 跳跃腿构型

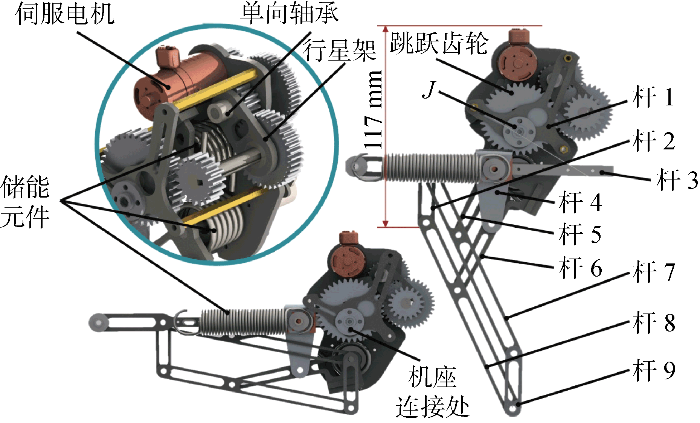
跳跃腿与机座的伺服电动机相连,腿部由主动释放装置与直线跳跃腿两部分构成,其结构如图2所示.图中:J关节为释放装置中跳跃齿轮与跳跃腿固连处.通过机座处伺服电动机与跳跃腿的串联实现起跳角的变化,即当舵机旋转一定角度时,跳跃腿会相对基座旋转一定的初始起跳角度.主动释放装置由伺服电动机和三组齿轮对构成,用于调整起跳初速度.压缩腿储能时,伺服电动机逆时针旋转,此时单向轴承正常转动,行星架所带动的齿轮组与最终跳跃部分的齿轮啮合,腿部实现压缩储能;腿部跳跃时,伺服电动机反转,此时由于单向轴承反向无法转动,行星架与该处的旋转轴等效固连,行星架逆时针旋转,齿轮脱离啮合,储能释放实现跳跃.通过在不同的储能条件下释放,可实现不同的起跳初速度调制.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 跳跃腿结构示意图

Fig.2 Schematic diagram of jumping leg structure

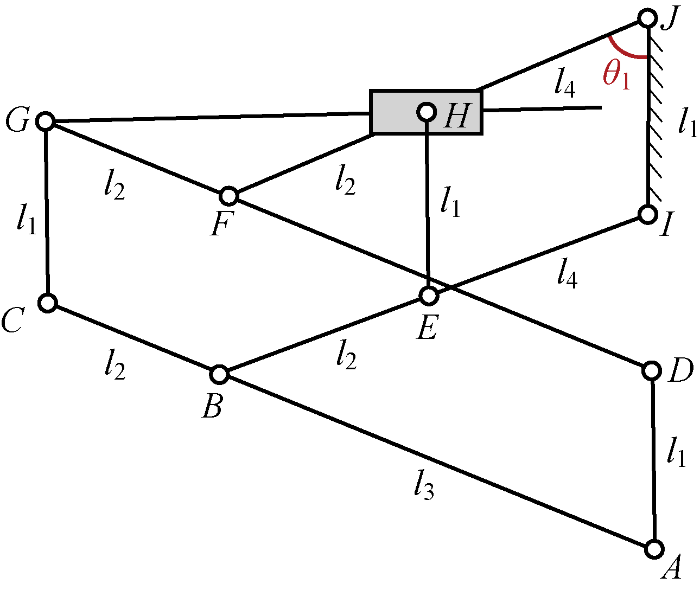
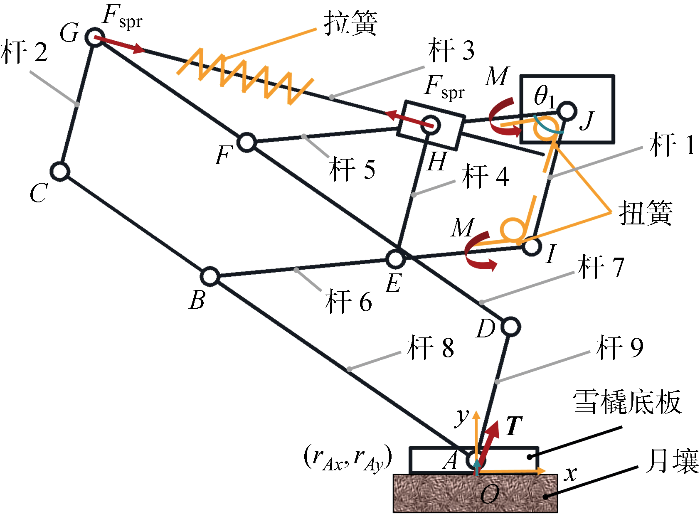
直线跳跃腿的核心设计目标是实现高伸缩比的稳定直线运动,同时实现月面近恒力的起跳.传统的单弹簧导轨滑块跳跃设计由于不同腿长下刚度发生线性变化,无法实现动力学的月面受力优化;同时纯连杆设计多为近似直线运动,且在运动时部分关节受力较大,仅适用于质量较轻的跳跃机器人.本直线跳跃腿设计将导轨滑块与直线连杆相结合,创新提出一款平面九连杆跳跃腿机构,如图3所示.图中:A~I关节为机构连接副;l₁~l₄为连杆各部分尺寸;θ₁为跳跃腿主动角.该机构通过双平行四边形构型约束实现稳定的直线运动,并且具有高伸缩比的潜力.其中,连接副由转动副与移动副构成,移动副在机械实现上选择采用微型滑轨滑块装置.为保证直线运动轨迹的实现,l₄需满足l₄=l₃-l₂.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 直线跳跃腿机构简图

Fig.3 Schematic diagram of straightline jumping leg mechanism

运动学设计上高伸缩比的主要原因是,起跳时月面承载的压强需要尽可能小,而在相同情况下跳跃腿在起跳过程中运动距离越大,则跳到相同高度所需的月面平均受力越小,故对月面储能跳跃而言,高伸缩比能有效降低起跳过程中月面的平均压强,从而提升机器人起跳过程的稳定性.本机构的设计优势在于若不考虑机械限制,理论腿长变化范围最大可达2l₃;最大伸缩比可达2l₃/l₁.最终机器人的机械实现中伸缩比为2.63.

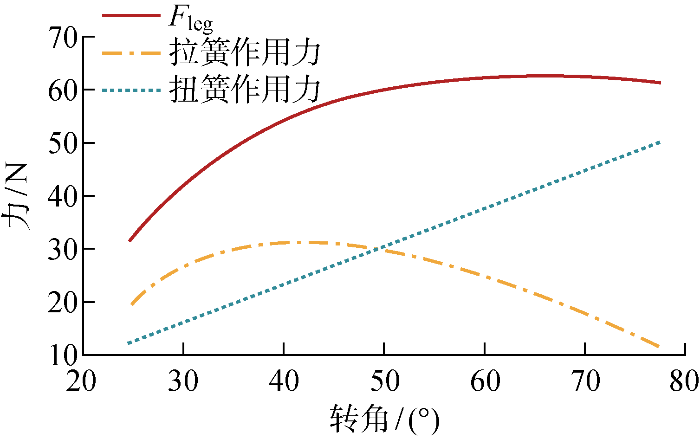
动力学设计上月面近恒力起跳的主要原因是,当起跳时月面平均压强一定时,起跳动态过程的月面峰值受力也需要尽可能小.对九杆直线跳跃腿机构采用静力学分析,若设置储能点为I、J关节处扭簧,G、H导轨处拉簧,在初步优化参数下腿上下两端的承载力F_leg与扭簧、拉簧作用力的变化关系如图4所示,其中承载力是扭簧和拉簧两者产生的作用力的合力.可以得到,拉簧作用力与扭簧作用力随θ₁的增大变化趋势相反,故本直线跳跃腿具有起跳时月面受力接近恒力的优化空间.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 F_leg与扭簧拉簧作用力的关系图

Fig.4 Relationship between F_leg and the force of the torsion springs and tension springs

1.3 月面起跳过程机器人多体动力学

机器人硬地起跳与月壤起跳最大的区别在于起跳过程中月壤自身的变形使得机器人跳跃底板产生运动,且月壤所能提供的支持力与月壤自身的变形状态有关.目前已有研究中从机器人本体出发的跳跃动力学模型构建主要采用能量守恒的方式,然而该方式并不适用于本研究的月壤起跳,因为机器人在月壤上起跳时,月壤的支持力由于月表的下陷变形对机器人本体做功,使得起跳过程中机器人能量并不守恒,所以基于能量守恒的方式建立机器人跳跃动力学仅适用于硬地起跳研究.

本推导过程将月壤的力学特性分解为竖直方向的承载作用力与水平方向的剪切作用力,作用点假设为雪橇底板底部中心点,从而将月壤抽象为可以计算分析的力学模型.将月壤力学模型与储能跳跃腿作为整体进行多体动力学分析,如图5所示,其中坐标xOy表示世界的定坐标轴,位于初始状态下雪撬板底部与月壤的接触处.图中:F_spr为储能拉簧所产生的力;M为储能扭簧所产生的力矩;T为月壤对底板的作用力;r_Ax与r_Ay分别为点A关于世界坐标系xOy的x和y坐标.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 月面起跳动力学模型示意图

Fig.5 Schematic diagram of the lunar take-off dynamic model

考虑到机器人本体跳跃腿的复杂性,选择基于拉格朗日方程的分析力学进行跳跃动力学模型的构建.在本动力学模型中,若起跳角给定,则跳跃腿具有跳跃过程的一个自由度;雪橇底板相对于月面会产生水平和竖直方向两个方向的位移,具有两个自由度.故定义广义坐标q为

(1)q=

$\left(\begin{array}{l}{\theta }_{1}\\ {r}_{Ax}\\ {r}_{Ay}\end{array}\right)$

随后对该模型建立运动学分析,得到各个关节与质心的位置、速度、角速度与广义坐标中各参数及其导数θ₁,${\stackrel{·}{\theta }}_{1}$,r_Ax,${\stackrel{·}{r}}_{Ax}$,r_Ay,${\stackrel{·}{r}}_{Ay}$的关系,从而得到各个构件的速度雅可比矩阵J_i,J_i满足:

(2)$\left(\begin{array}{l}{v}_{ix}\\ {v}_{iy}\\ {w}_{i}\end{array}\right)$=J_i$\left(\begin{array}{l}{\stackrel{·}{\theta }}_{1}\\ {\stackrel{·}{r}}_{Ax}\\ {\stackrel{·}{r}}_{Ay}\end{array}\right)$, i=1, 2, …, 9

式中:i表示构件标号;v_ix与v_iy分别表示i构件此时相对世界坐标系xOy中x和y方向的质心速度;w_i表示i构件此时的角速度.

每个构件的广义惯量满足:

(3)Ø_i=

$\left[\begin{array}{ll}{m}_{i}I& 0\\ 0& {I}_{i}\end{array}\right]$

式中:m_i为i构件的质量;I_i为i构件在动力学模型平面的惯量;I为二维单位矩阵.

每个构件所受到的广义力可表示为

(4)

${\hat{\mathrm{F}}}_{\mathrm{i}}$

$\left[\begin{array}{l}{F}_{i}\\ {\mathrm{M}}_{\mathrm{i}}\end{array}\right]$

式中:F_i与M_i分别表示i构件所受的外力与外力矩,方向参照式(1)中的广义坐标.

对整个系统来讲,广义力可分为T、F_spr、M、各个构件自身的重力G_i.其中T的具体表达式与月壤力学特性有关.

最后建立系统的微分方程:

(5)

$\stackrel{~}{Ø}\ddot{\mathrm{q}}$

$\frac{\mathrm{d}\stackrel{~}{Ø}}{\mathrm{d}t}\stackrel{·}{q}$

$\frac{1}{2}\frac{\partial }{\partial q}\left({\stackrel{·}{q}}^{\mathrm{T}}\stackrel{~}{Ø}\stackrel{·}{q}\right)$

$\stackrel{~}{F}$

式中:$\stackrel{~}{Ø}$为系统广义惯量;$\stackrel{~}{F}$为系统广义力,

(6)

$\left.\begin{array}{l}\stackrel{~}{Ø}=\stackrel{9}{\sum _{i=1}}{{J}^{\mathrm{T}}}_{i}{Ø}_{i}{J}_{i}\\ \stackrel{~}{F}=\stackrel{9}{\sum _{i=1}}{{J}^{\mathrm{T}}}_{i}\mathrm{ }{\stackrel{~}{F}}_{i}\end{array}\right\}$

对本动力学模型进行数值求解,即可精准计算得到机器人月面起跳过程中的相关参数.

2 月壤与机器人相互作用机理

2.1 离散元模型构建

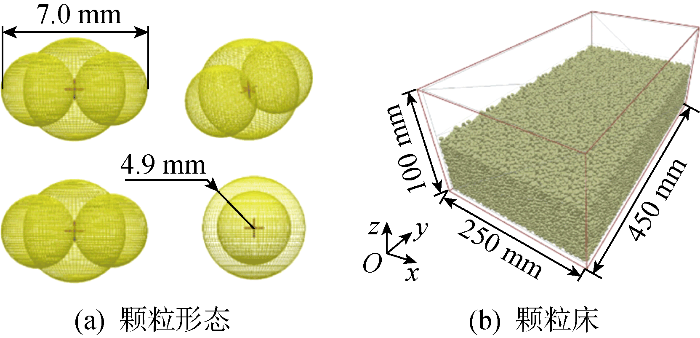
1.3 节中对月壤力学模型进行了抽象,下面将基于离散元仿真环境进一步研究跳跃过程中月壤动力学特性.如图6所示,采用颗粒流软件EDEM构建与跳跃机器人尺寸相匹配的离散元颗粒及颗粒床.离散元颗粒基于三球模型,参考真实月壤颗粒的延性参数^[11]构建,受限于计算机算力,颗粒的最大直径设置为7.0 mm.颗粒床是基于长、宽、高分别为50、50、100 mm的自由堆积颗粒块,密集排列构建而成.受限于计算机算力和存储空间,离散元软件无法将颗粒床做得足够大,从而使剪切变形模量k接近真实月壤,所以目前构建的在接下来用于跳跃实验的颗粒床,在剪切变形模量方面与真实月壤有较大差距.颗粒床越大,仿真效果与实际越接近,但考虑到仿真算力限制,将颗粒床尺寸设置为如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 离散元模型

Fig.6 Discrete element model

为保证离散元颗粒床接近月球表面真实月壤,离散元环境的重力加速度设定为1.623 m/s²,与月面相同^[1],同时颗粒床的力学特性要接近月面月壤.标定颗粒床力学特性可以基于松软地面轮-壤接触模型的剪切特性曲线^[12].该特性曲线可表示为

(7)$\tau=\tau_{\max }\left(1-\mathrm{e}^{-\frac{j}{k}}\right)$

(8)$\tau_{\max }=c+\sigma \tan \theta$

式中:τ,τ_max分别为切应力和最大抗剪强度;j为地面剪切位移;c为内聚力;σ为作用在地面上的正应力;θ为内摩擦角.

测量离散元颗粒床的剪切特性参数并与月面月壤的对应参数^[21]进行比较,通过离散元月壤剪切特性仿真实验拟合内摩擦角和内聚力,迭代修正离散元颗粒参数,最终得到的颗粒床剪切特性参数如表1所示,其中用于标定的真实月壤特性参考郑永春等^[22]基于美国苏联探月工程实验数据总结的就位月壤机械性质.

表1 颗粒床与真实月壤剪切参数比较

Tab.1 Comparison of shear parameters of granular bed and real lunar soil

材质	k/mm	c/Pa	θ/(°)
离散元颗粒床	2.912	189.4	26.89
真实月壤	无	260~1 800	25~40

新窗口打开| 下载CSV

颗粒床的内聚力小于真实月壤,主要是受限于离散元颗粒形态与月壤颗粒形态的差异,包括颗粒形态与颗粒直径等相关参数.

2.2 跳跃过程月壤力学特性拓展

建立机器人在月面运动的接触模型时,一般采用的经典月壤力学特性模型.除了式(7)和式(8)所示的剪切特性模型,还有Bekker等^[12]提出的月壤承压特性模型,其表达式为

(9)σ=$\left(\frac{{k}_{1}}{b}+{k}_{2}\right)$zⁿ=Kzⁿ

式中:b为矩形压板的宽度;k₁为地面的黏聚模量;k₂为地面的摩擦模量;K为土壤变形模量;z为压板沉降量;n为土壤变形指数.

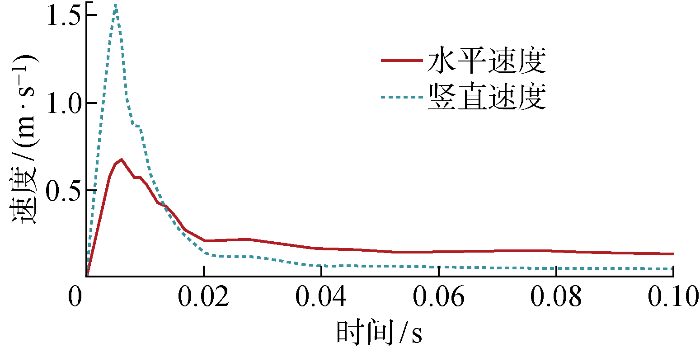
经典的月壤力学特性模型是准静态模型,适用于轮式机器人、蛇形机器人等运动平稳的机器人构型.通过在离散元环境中仿真压板在颗粒床上倾斜承压,可以大致模拟跳跃机器人触月底板在起跳时的运动情况,触月底板的运动速度如图7所示,跳跃底板长宽与所设计的机器人保持一致,为300 mm×150 mm.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 触月底板起跳过程速度曲线

Fig.7 Speed curves of the bottom plate in the take-off process

在非常短暂(0.1 s内)的起跳过程中,触月底板的运动速度变化明显,且速度量级超过几乎所有月面机器人的平均速度,因此机器人接触月壤的跳跃过程是一个高度动态的过程,需要在经典月壤力学特性模型的基础上引入阻尼的影响.参照Bekker承压模型的形式,可以引入如下两个动态力学特性模型,分别描述单位接触面积上的剪切阻尼和承载阻尼,其表达式分别为

(10)$\varepsilon_{\mathrm{h}}=A_{\mathrm{h}} \sigma^{m_{\mathrm{h}}}$

(11)$\varepsilon_{\mathrm{v}}=A_{\mathrm{v}} z^{m_{\mathrm{v}}}$

式中:ε_h为剪切过程中的阻尼强度系数,即单位面积上的剪切阻尼系数;A_h为剪切过程中的阻尼强度模量;m_h为剪切过程中的阻尼变形指数;ε_v为承载过程中的阻尼强度系数,即单位面积上的承载阻尼系数;A_v为承载过程中的阻尼强度模量;m_v为承载过程中的阻尼变形指数.

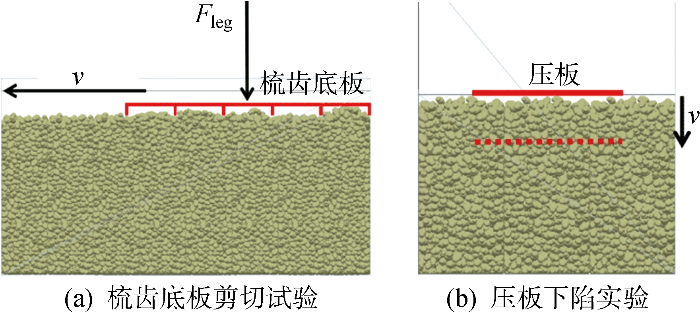
为了验证所提出动态力学特性模型的合理性,可以设计如图8所示的离散元仿真实验进行验证.测量仿真中梳齿底板(或压板)不同运动速度v下的受力变化,可以得到受力随运动速度的变化率,即剪切阻尼(或承载阻尼).

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 离散元仿真实验示意图

Fig.8 Schematic diagram of discrete element simulation experiment

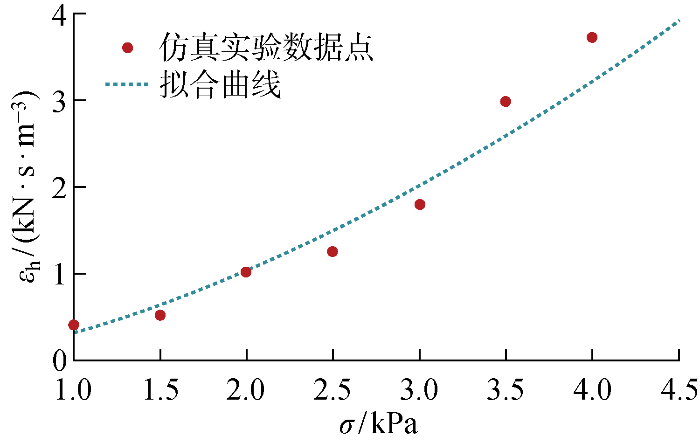
对梳齿底板施加不同正压力,可以测得对应的剪切阻尼,转换成σ与ε_h的映射关系后,通过式(10)进行拟合,得到图9所示的结果.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 剪切仿真实验拟合结果

Fig.9 Fitting results of shear simulation experiments

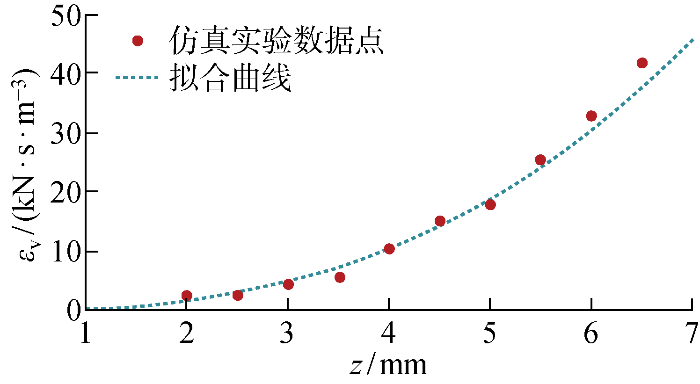
对压板设置不同的z,可以测得对应的承压阻尼,转换成z与ε_v的映射关系后,通过式(11)进行拟合,得到图10所示的结果.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 承载仿真实验拟合结果

Fig.10 Fitting results of bearing simulation experiments

剪切仿真实验结果的拟合度R²=0.957 8,承载仿真实验结果的拟合度R²=0.970 9.

通过仿真实验测得的离散元月壤动态力学特性参数与准静态的经典力学特性参数汇总于表2中.

表2 离散元月壤力学特性参数汇总

Tab.2 Mechanical properties of discrete elemental lunar soil

参数	取值
k/mm	2.912
c/Pa	189.4
θ/(°)	26.89
K/[MN·m^-(2+ⁿ⁾]	599.7
n	2.513 4
A_h/[{N}^{1+m_h}·s·{m}^{-(3+m_h)}]	4.615 2×10^-3
m_h	1.622 5
A_v/[GN·s·{m}^{-(3+m_v)}]	23.353
m_v	2.648 9

新窗口打开| 下载CSV

2.3 跳跃过程底板-月壤接触模型

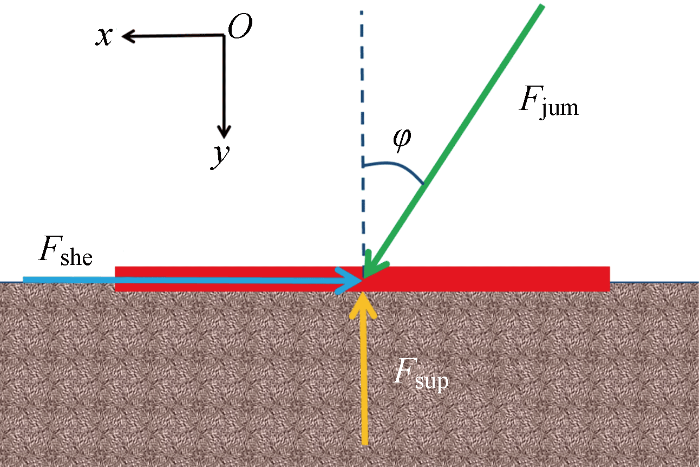
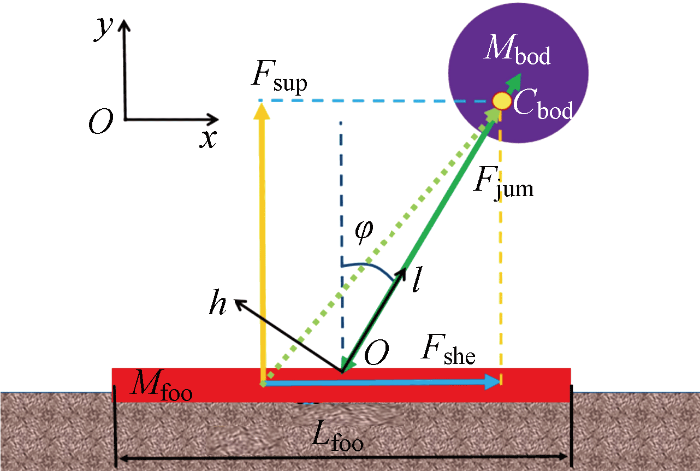
基于离散元月壤力学特性参数可以建立跳跃过程机器人的底板与月壤的接触模型.模型示意图如图11所示.图中:F_jum表示跳跃底板受到机械的相互作用外力的总和,在跳跃机器人中就是跳跃时对底板的作用力;φ表示F_jum与跳跃底板平面法线的夹角;F_she表示跳跃底板受到的月壤的水平剪切力,F_sup表示跳跃底板受到的月壤的竖直承载力,F_she、F_sup即T的水平、竖直分量;x和y分别表示底板的水平位移和竖直位移.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 底板-月壤接触模型

Fig.11 Contact model of the bottom plate and lunar soil

联立式(7)和式(8)可得

(12)$F_{\mathrm{sup}}=S_{0}\left(K y^{n}+A_{\mathrm{v}} y^{m_{\mathrm{v}}} \dot{y}\right)$

式中:S₀为跳跃底板的底面积.

联立式(7)~(9)和式(12)可得

(13)$\begin{aligned}F_{\text {she }}= & S_{0}\left[c+\left(K y^{n}+A_{\mathrm{v}} y^{m_{\mathrm{v}}} \dot{y}\right) \tan \theta\right]\left(1-\mathrm{e}^{\frac{-|x|}{k}}\right)+ \\& S_{0} A_{\mathrm{h}}\left(K y^{n}+A_{\mathrm{v}} y^{m_{\mathrm{v}}} \dot{y}\right)^{m_{\mathrm{h}}} \dot{x}\end{aligned}$

与月壤接触过程中底板的动力学方程为

(14)

$\left.\begin{array}{l}{M}_{\mathrm{f}\mathrm{o}\mathrm{o}}\ddot{y}={F}_{\mathrm{j}\mathrm{u}\mathrm{m}}cos\phi -{F}_{\mathrm{s}\mathrm{u}\mathrm{p}}\\ {M}_{\mathrm{f}\mathrm{o}\mathrm{o}}\ddot{x}={F}_{\mathrm{j}\mathrm{u}\mathrm{m}}sin\phi -{F}_{\mathrm{s}\mathrm{h}\mathrm{e}}\end{array}\right\}$

式中:M_foo为底板质量.

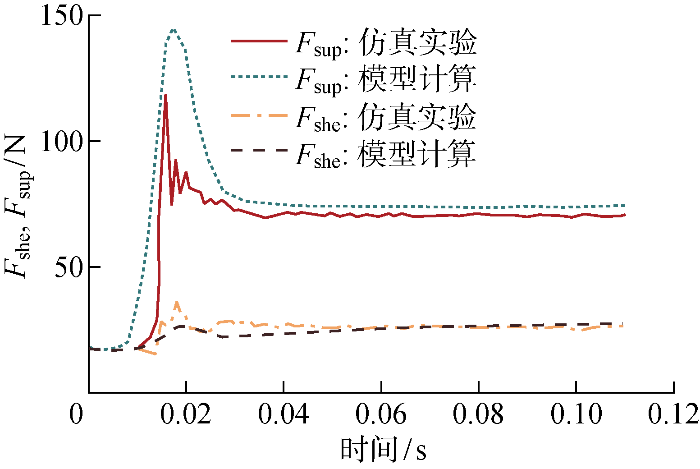
将式(12)和式(13)代入式(14),得到的动力学方程即底板-月壤接触模型.由式(12)和式(13)的表达式不难发现,底板-月壤接触模型是非线性的,可以通过龙格-库塔法求解数值解.为了便于体现模型的效果,F_jum设置为恒定 62 N(接近机器人起跳过程的平均受力),φ设置为10°,重力忽略不计,初始边界条件均为0.底板-月壤接触模型受力的计算结果与离散元仿真实验的测定结果如图12所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 模型计算结果与仿真比较

Fig.12 Comparison of the model calculation results and simulation results

从结果来看,F_she的模型计算结果比较接近仿真结果;F_sup的模型计算结果相对于仿真结果偏大,主要原因可能是底板-月壤接触模型中没有考虑水平剪切运动对于竖直承载能力的减益影响,这一点有待未来进一步的研究.

3 月面跳跃过程机器人动力学模型

3.1 模型建立

前述内容通过研究月壤与机器人相互作用机理,得到机器人起跳过程中月壤对跳跃底板的作用力特性.在此基础上,可以建立机器人在月面跳跃过程中统一的动力学方程.为了便于讨论,首先建立双质量的月面跳跃机器人模型进行方法性验证,在此基础上建立整机的月面跳跃动力学模型.

如图13所示,在忽略机器人跳跃腿质量的情况下,可以将跳跃机器人简化为由质量M_bod的主体和质量M_foo的底板构成的二体相互作用模型.图中:C_bod为机器人质心;L_foo为底板长度.由于底板-月壤接触模型不能描述底板巨大面积上的作用力分布,因此机器人系统所受外力的等效作用点未知.类比硬地跳跃的情况,假设T指向C_bod.基于此假设可以确定外力等效作用点,也意味着机器人系统无外力矩.为了便于推导动力学模型,基于跳跃腿伸长方向建立lOh坐标系,并且在质心系中讨论机器人主体和底板的运动.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 抽象机器人的动力学模型

Fig.13 Dynamic model of the abstract robot

底板和主体的世界系坐标分别记为(x_f, y_f)和(x_b, y_b);机器人质心的世界系坐标为(l_c, l_c);底板和主体在质心系中的坐标分别记为(l_cf, h_cf)和(l_cb, h_cf).月壤作用于底板的承载力F_sup与剪切力F_she与底板的世界系坐标系直接相关,因此底板位置和速度需要进行如下坐标转换:

(15)

$\left.\begin{array}{l}{x}_{\mathrm{f}}=({l}_{\mathrm{c}}+{l}_{\mathrm{c}\mathrm{f}})\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\phi }-{h}_{\mathrm{c}}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\phi }\\ {y}_{\mathrm{f}}=({l}_{\mathrm{c}}+{l}_{\mathrm{c}\mathrm{f}})\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\phi }+{h}_{\mathrm{c}}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\phi }\\ {\stackrel{·}{x}}_{\mathrm{f}}=({\stackrel{·}{l}}_{\mathrm{c}}+{\stackrel{·}{l}}_{\mathrm{c}\mathrm{f}})sin\phi -{\stackrel{·}{h}}_{\mathrm{c}}cos\phi \\ {\stackrel{·}{y}}_{\mathrm{f}}=({\stackrel{·}{l}}_{\mathrm{c}}+{\stackrel{·}{l}}_{\mathrm{c}\mathrm{f}})cos\phi +{\stackrel{·}{h}}_{\mathrm{c}}sin\phi \end{array}\right\}$

由式(12)和式(13),月壤作用于底板的平均承载应力σ_sup与平均切应力σ_she的表达式为

(16)$\sigma_{\text {sup }}=K\left(-y_{\mathrm{f}}\right)^{n}+A_{\mathrm{v}}\left(-y_{\mathrm{f}}\right)^{m_{\mathrm{v}}}\left(-\dot{y}_{\mathrm{f}}\right)$

(17)$\begin{aligned}\sigma_{\text {she }}= & \left(c+\sigma_{\text {sup }} \tan \theta\right)\left(1-\mathrm{e}^{\frac{-\left|x_{\mathrm{f}}\right|}{k}}\right)+ \\& A_{\mathrm{h}} \sigma_{\text {sup }}^{m_{\mathrm{h}}}\left(-\dot{x}_{\mathrm{f}}\right)\end{aligned}$

底板沿跳跃腿方向的动力学方程为

(18)M_foo${\ddot{l}}_{\mathrm{c}\mathrm{f}}$=$\frac{{M}_{\mathrm{b}\mathrm{o}\mathrm{d}}}{{M}_{\mathrm{s}\mathrm{u}\mathrm{m}}}$S₀(σ_supcos φ+σ_shesin φ)-F_jum

式中:机器人总质量M_sum=M_foo+M_bod.

主体沿跳跃腿方向的动力学方程为

(19)M_bod

${\ddot{l}}_{\mathrm{c}\mathrm{b}}$

=-M_foo

${\ddot{l}}_{\mathrm{c}\mathrm{f}}$

世界系质心沿跳跃腿方向的动力学方程为

(20)M_sum${\ddot{l}}_{\mathrm{c}}$=S₀(σ_supcos φ+σ_shesin φ)-M_sumg_luncos φ

式中:g_lun为月球表面的重力加速度.

底板垂直跳跃腿方向的动力学方程为

(21)M_foo${\ddot{h}}_{\mathrm{c}\mathrm{f}}$=0

主体垂直跳跃腿方向的动力学方程为

(22)M_bod${\ddot{h}}_{\mathrm{c}\mathrm{b}}$=0

世界系质心垂直跳跃腿方向的动力学方程为

(23)$\begin{aligned}M_{\mathrm{sum}} \ddot{h}_{\mathrm{c}}= & S_{0}\left(\sigma_{\mathrm{sup}} \sin \varphi-\sigma_{\mathrm{she}} \cos \varphi\right)- \\& M_{\mathrm{sum}} g_{\mathrm{lun}} \sin \varphi\end{aligned}$

联立式(15)~(23)得到的微分方程组可以化为一阶非线性方程组,通过隆格-库塔法可以求解给定边界条件的数值解.求数值解时,M_bod取1.86 kg,M_foo取0.14 kg,g_lun取1.623 m/s².

3.2 抽象化机器人的动力学模型验证

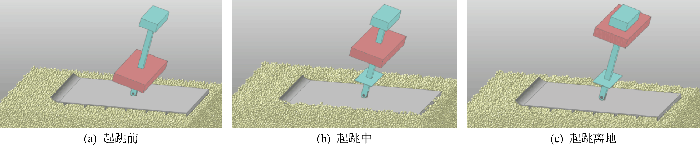
为验证基于底板-月壤接触模型的机器人月面跳跃动力学模型在描述机器人跳跃过程中的适用性,采用离散元软件EDEM与动力学软件RecurDyn,进行耦合仿真验证.耦合仿真模拟抽象化机器人以59 N的作用力进行不同角度的恒力起跳.仿真时间0.09 s,时间步数900.

以17° 起跳角起跳为例,耦合仿真过程如图14所示.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 抽象机器人耦合仿真起跳过程

Fig.14 Coupling simulation of the robot take-off process

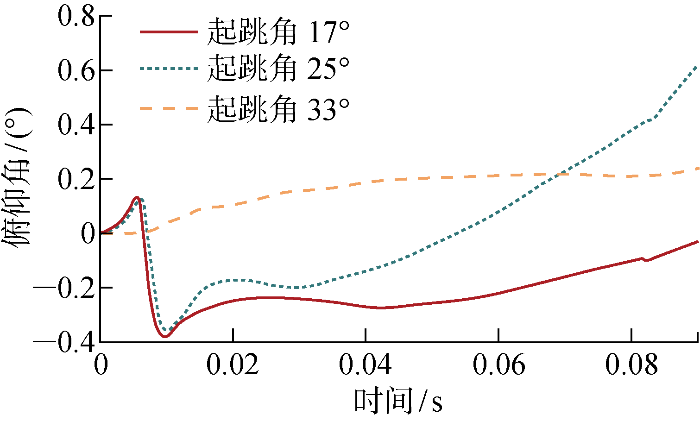
跳跃机器人运动性能的主要指标是跳远距离和跳跃高度.在月球表面接近真空的环境下,这两项指标在机器人离开地面后就可以确定.月球的低重力环境下,机器人起跳过程离地前的质心位移量远小于离地后的质心位移量.因此跳远距离和跳跃高度主要由离地瞬间机器人质心的速度v_z决定.图15为机器人质心在17°、25°和33° 的起跳角下水平速度和竖直速度随跳跃腿作用距离L的关系曲线比较.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 起跳过程动力学模型计算结果与耦合仿真结果比较

Fig.15 Comparison between the calculation results and the coupled simulation results of the dynamic model in the take-off process

从图15中的比较结果来看,理论模型计算的质心水平速度分量与耦合仿真的契合度较好,但是竖直分量的契合度较差.随着起跳角度的增加,理论模型计算的质心竖直速度分量的偏差相应增加.这是因为随着起跳角度的增加,起跳过程的水平剪切运动更加明显,由于目前的底板-月壤接触模型未考虑月壤水平剪切对竖直承载的影响,所以偏差越来越大.

耦合仿真中不同起跳角度下机器人的俯仰转角随时间的变化如图16所示.可以看出,起跳过程机器人俯仰角变化很小,因此动力学模型中外力指向质心的基本假设近似成立.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 起跳过程机器人俯仰角变化曲线

Fig.16 Variation of the robot pitch angle in the take-off process

3.3 机器人完整结构月面起跳动力学结果分析

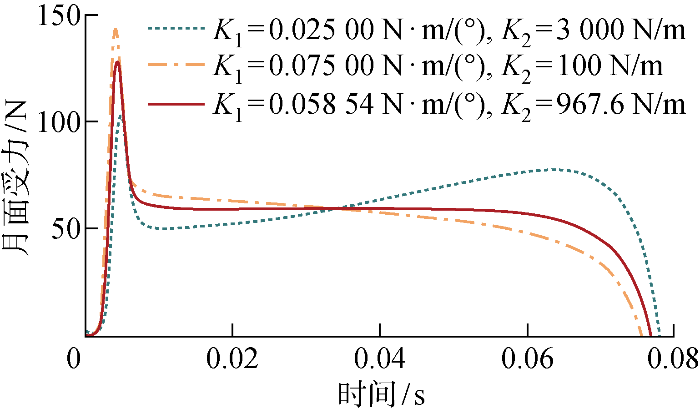
利用抽象机器人动力学模型的仿真结果验证底板-月壤接触模型后,将接触模型中F_she、F_sup的表达式代入1.3节所推导的机器人多体动力学模型中并进行起跳过程的数值求解,可得到不同储能刚度方案下的机器人完整结构以最大初速度竖直起跳过程中月面受力随起跳时间的变化情况,如图17所示.图中:K₁表示扭簧刚度,K₂表示拉簧刚度.通过优化调整储能元件刚度和变化范围,最终选定储能刚度方案为K₁=0.058 54 N·m/(°)与K₂=967.60 N/m,如图17中红实线所示,该储能方案综合考虑了详细结构设计时的实际储能元件选型与杆件强度需求,实现起跳过程中月面受力近似恒力.

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 储能方案优化过程示意图

Fig.17 Optimization process of the energy storage solution

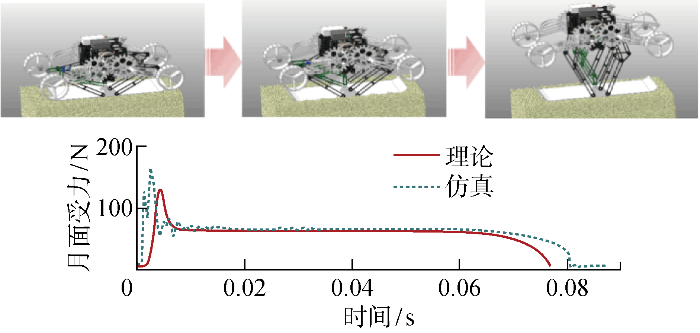
机器人完整结构的动力学模型结果通过联合仿真环境进行验证,验证过程与结果如图18所示.可以看到在离散元联合仿真环境中,起跳过程中的月面受力曲线与理论解总体变化趋势一致,但仍存在一定偏差,主要表现为:受力仿真解最开始表现为两个峰值,而非理论解所呈现的单个峰值.这是因为实际起跳时存在雪橇底板底部针形肋板插入月壤的过程,所以第1个峰为肋板下陷的瞬间受力,第2个峰为雪撬板本体的下陷瞬间受力.此外,仿真环境中的起跳时间偏长导致最终产生瞬间碰撞限位起跳,引起起跳时间点比自然起跳时间点偏前,可能是由于仿真环境的各项参数设置(如各部件质量、质心等)与理论解仍存在差异.

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 机器人月面起跳动力学理论与仿真结果对比图

Fig.18 Comparison of theoretical results and simulation results of the robot’s lunar take-off dynamics

4 跳跃机器人运动规划算法设计

跳跃机器人在月球表面运动时需要在空中不碰到障碍物的前提下精确跳跃到点,这意味着机器人离地时需要具备精确的初速度;同时为了降低机器人落地后的受损风险,需要进行主动缓冲.为了满足这两项基本要求,本文设计了对应的运动规划算法.

4.1 精确跳跃到点的运动规划算法

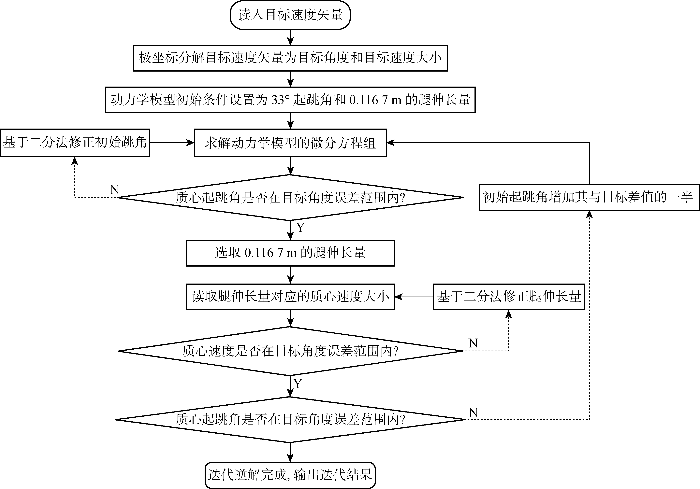
机器人精确跳跃到点的运动规划,本质上是从给定的离地速度逆解出起跳角度与跳跃腿作用距离.月面跳跃过程的机器人动力学模型没有解析解,因此需要采用二分法逼近求得近似数值解.具体的算法逻辑框图如图19所示.

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 精确跳跃到点的运动规划算法逻辑框图

Fig.19 Flow chart of the motion planning algorithm for accurate jumping to the point

该算法逆解结果中质心速度矢量的大小偏差±2 mm/s,角度偏差 ±0.005°,在此情形下,采用个人电脑(CPU intel i7-10750H 2.6 GHz)的运算时间控制在0.005 s内.如果优化正解过程(非解方程的方法),运算时间可能更短.这说明3.1小节得到的动力学模型具有实际应用潜力.

4.2 落地主动缓冲的运动规划算法

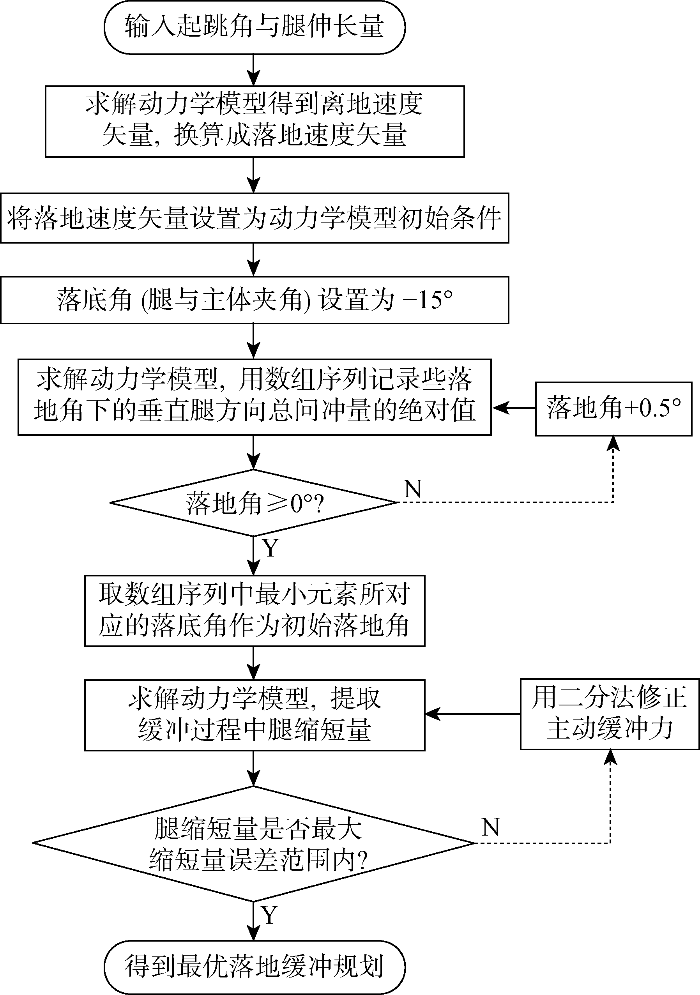
主动缓冲算法的设计目标是为了尽可能降低落地过程中底板接触地面后跳跃机器人所受的外力.沿跳跃腿方向的受力可以通过减小主动缓冲力实现,但是缓冲力的下限受跳跃腿行程范围限制;垂直跳跃腿方向的受力可以通过跳跃腿的角度实现.主动缓冲力和跳跃腿角度的取值通过二分法逼近.具体算法逻辑框图如图20所示.

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 落地主动缓冲的运动规划算法逻辑框图

Fig.20 Flow chart of the motion planning algorithm for active buffering on the ground

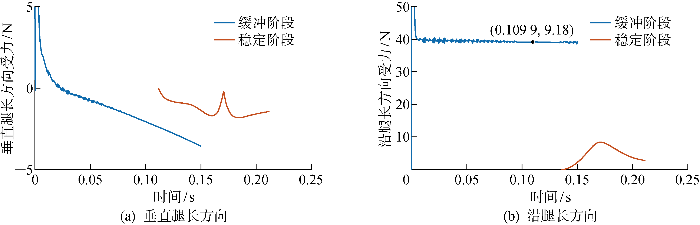
机器人采用此算法进行主动缓冲的全过程如图21所示,缓冲阶段在稳定阶段开始时就结束了.缓冲阶段指采用主动缓冲算法通过控制跳跃电机的力矩来进行落地时的缓冲过程,在机器人在月壤上停止下陷时结束.随后是稳定阶段,在这一过程中机器人不进行主动缓冲,机器人作为一个单一刚体在月壤上运动.由图21可见,以33° 起跳角为例,垂直跳跃腿方向的理论受力小于5 N,沿腿方向的理论受力稳定小于40 N,合力小于起跳力平均值的70%,满足所设计机器人的结构强度要求.该算法基于个人电脑的运算时间占机器人离地后滞空时间的40%以下,初步验证了其可行性.

图21

新窗口打开| 下载原图ZIP| 生成PPT

图21 跳跃机器人最优缓冲规划的落地过程中外力作用结果

Fig.21 Results of external forces during active buffering of jumping robots

5 结论

(1) 基于月球表面低重力环境及月壤特性设计了一款月面跳跃机器人.该机器人的跳跃机构是一种拉簧与扭簧复合的多连杆储能释放结构.该结构具有较高的伸缩比,并且能够实现接近恒力的释放过程.

(2) 针对月面跳跃过程高度动态的特点,拓展了传统月面机器人分析所采用的月壤力学特性理论,提出考虑月壤相互作用中阻尼影响的底板-月壤接触模型.该接触模型应用在跳跃动力学中与离散元-动力学耦合仿真的结果在水平方向上契合度较好,竖直方向上的偏差来源于水平剪切对沉降的耦合影响.该影响的具体规律有待进一步研究.

(3) 基于机器人月壤表面跳跃动力学模型设计了起跳过程的精确跳跃到点运动规划算法与落地过程的主动缓冲运动规划算法,并验证了其可行性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

肖福根, 庞贺伟.

月球地质形貌及其环境概述

[J]. 航天器环境工程, 2003(2): 5-14.

[本文引用: 2]

XIAO

Fugen

, PANG

Hewei

An overview of lunar geological features and their environment

[J]. Spacecraft Environmental Engineering, 2003(2): 5-14.

[本文引用: 2]

[2]

叶培建, 肖福根.

月球探测工程中的月球环境问题

[J]. 航天器环境工程, 2006(1): 1-11.