近年来,机器人产业迅速发展. 2019年全球机器人市场规模超过200亿美元[1 ] ,使得机器人技术倍受世界关注,各国将机器人作为重点发展领域之一,如中国制造2025、美国的工业互联网、德国的工业4.0等. 传统的机器人主要应用于工业生产环境,但随着机器人智能化水平提升,人们越来越希望机器人能融入生活. 这就要求机器人具有更高的智能,能通过自主学习技能来完成更复杂的任务. 因此,提升机器人技能学习的能力具有重要实际意义.
示教学习是一种简化机器人技能学习的有效方法[2 ] ,一般包含演示、学习和复现3个阶段. 演示阶段主要指人与机器人之间的动作传递过程,已有视觉示教、动觉示教和遥操作示教等成熟的方法. 学习阶段的主要问题在于如何对技能进行建模,常见的方法有动态系统(Dynamic System,DS)[3 ] 、高斯混合模型(Gaussian Mixture Model,GMM)[4 ] 和隐马尔科夫模型 [5 ] . 其中,由非线性DS发展而来的动态运动原语(Dynamic Movement Primitive,DMP)[6 ] 受到国内外学者的关注. Meier等[7 ] 将DMP重构成一个带有控制输入的线性动态系统概率模型,并将感知测量单元耦合到系统中使其可在线获取反馈信息,根据似然估计结果对任务成败作出预判. Gašpar等[8 ] 提出弧长参数化的动态原语模型,将空间信息与时间信息分开表示用于解决示教中存在较大运动速度差异的问题. Li等[9 ] 提出一种基于DMP的分层控制策略,该策略考虑运动建模和动态控制器的性能. 然而DMP建模精度受高斯基个数影响,而且单次示教数据往往存在噪声,导致DMP从单次示教中往往无法得到需要的动作模型. 因此研究如何让DMP从多轨迹中提取主要特征建模动作,并在更少的高斯基下提高建模精度非常有必要.
示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务.
为改善示教学习的效果,本文提出一种基于DMP和自适应神经网络控制的机器人技能学习方法. 主要创新点包括:① 将RBFNN引入DMP的非线性函数拟合中,改善高斯基函数的分布,提出一种RBF-DMP方法,从而提升DMP的建模能力; ② 为克服传统DMP只能从单条示教轨迹建模动作的局限性,将GMM和高斯混合回归(Gaussic Minture Regression, GMR)引入DMP的强迫项拟合,从多示教轨迹中建模动作,减少示教不确定性带来的动作建模误差; ③ 设计基于自适应神经网络的控制器来控制机械臂复现示教动作,并对闭环系统的稳定性进行分析.
1 基于动态运动原语的动作建模
1.1 动态运动基元
DMP模型[6 ] 由以下弹簧-阻尼系统和非线性强迫项函数组成:
(1) τ s z · = α z [ β z ( g - y ) - z ] + f ( x )
(2) τ s y · = z
(3) τ s x · = - α x x
式中: y ∈ R n z ∈ R n τ s τ s α z β z α x β z = α z / 4
(4) f ( x ) = ∑ i = 1 N g Ψ i ( x ) w i ∑ i = 1 N g Ψ i ( x ) x ( g - y 0 )
(5) Ψ i ( x ) = e x p 1 2 σ i 2 ( x - c i ) 2
式中: Ψ i ( x ) c i σ i w i y 0 N g w i c i
DMP拟合动作的过程即拟合非线性函数f(x),假设给定一组一维演示轨迹并编码成时间的序列{ θ t , θ · t , θ ¨ t t = 1 , 2 , … , T } θ t θ · t θ ¨ t
(6) f ^ ( x ) = τ s 2 θ ¨ t - α z β z ( g - θ t ) + α z τ s θ · t
权重项wi 可以通过局部线性回归(Locally Weighted Regression,LWR)求解下式获得:
(7) m i n ∑ ( f ^ ( x ) - f ( x ) ) 2
1.2 基于RBFNN的RBF-DMP
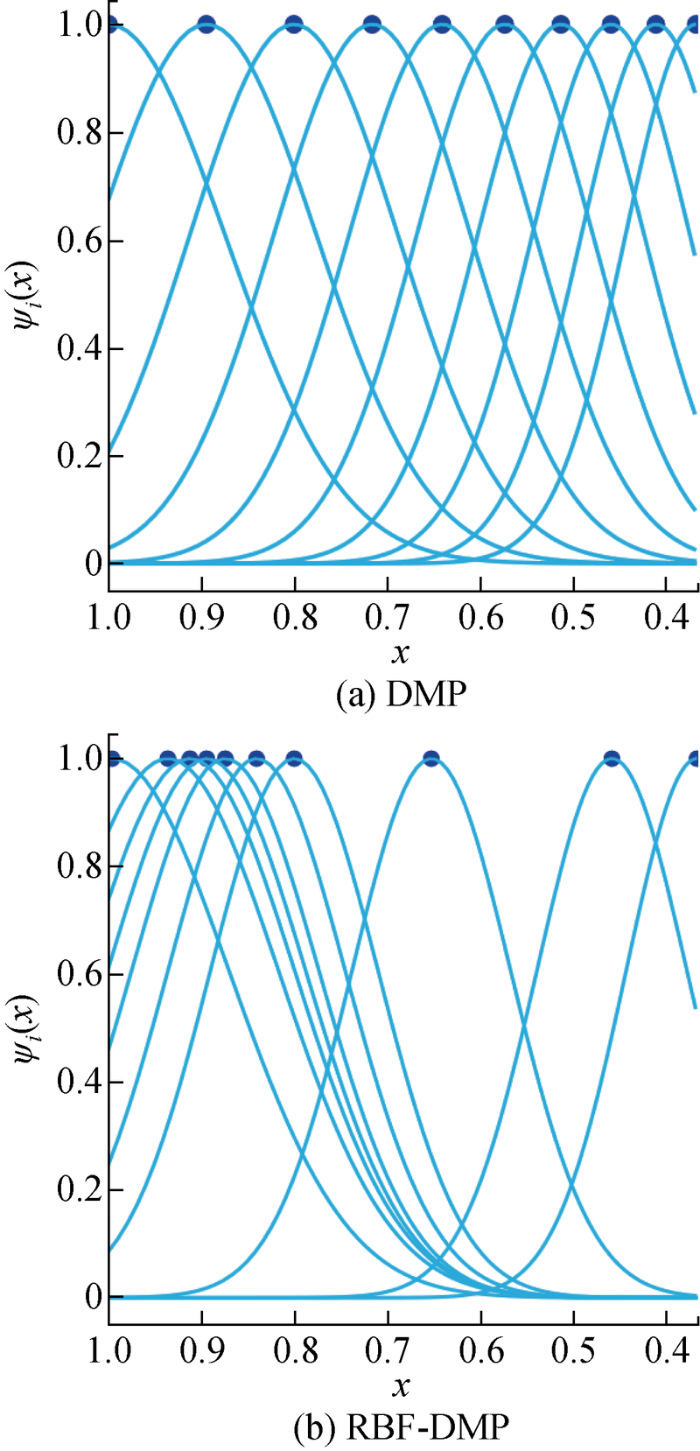
上述DMP在式(3)的x 轨迹上等时间间隔选取c i [ 5 ] 图1 (a)所示,再通过LWR求解式(7)获取权重wi . 然而对于不同动作,应采用不同高斯基分布方式,从而提高建模精度,如图1 (b)所示.
图1
图1
DMP和RBF-DMP拟合同一技能得到的高斯基中心位ci 的分布
Fig.1
Distribution of center position ci of Gaussian base obtained by DMP and RBF-DMP fitting the same action
为此,将RBFNN引入DMP中,提出RBF-DMP方法. 该方法以梯度下降的方式学习权重w i 和 高 斯 基 中 心 位 置 c i , [20 ] 定义如下:
(8) F ( x ) = W T S ( x )
(9) s i ( x ) = exp − ( x − c i ) T ( x − c i ) σ i 2 i = 1 , 2 , . . . , N g
(10) W = [ w 1 w 2 … w N g ] T
(11) W = a r g m i n W ^ ∈ R N g ( s u p x ∈ Ω x | f ( x ) - W ^ T S ( x ) | )
即在输入空间x ∈ Ω x 中 最 小 化 误 差 值 , W ^ 为 W x ( g - y 0 )
(12) F ( x ) = f ^ ( x ) x ( g - y 0 ) = ∑ i = 1 N g Ψ i ( x ) w i ∑ i = 1 N g Ψ i ( x )
由采样轨迹得出的强迫项$\text{\hat{f}}$和相位系统式(3)的输出x可计算一组函数值$ F\left( \lambda \right)\left| \lambda \right.=1,2,\ldots,T $.将其用于训练神经网络,DMP的强迫项即可写成下式:
(13) f ( x ) = F ( x ) x ( g - y 0 )
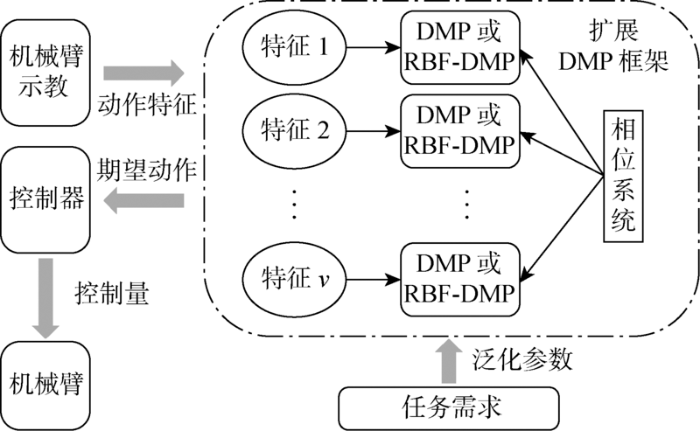
该方法相比DMP需要更大的计算量,但在相同的高斯基个数下具有更高的建模精度. 为将DMP和RBF-DMP两者的优势相结合,提出如图2 所示的扩展框架,其通过式(3)将DMP和RBF-DMP结合到一起,并统一到同一相位系统以便于泛化.
图2
图2
结合DMP和RBF-DMP的DMP扩展框架
Fig.2
DMP extension framework combining DMP and RBF-DMP
1.3 基于GMM和GMR的改进DMP
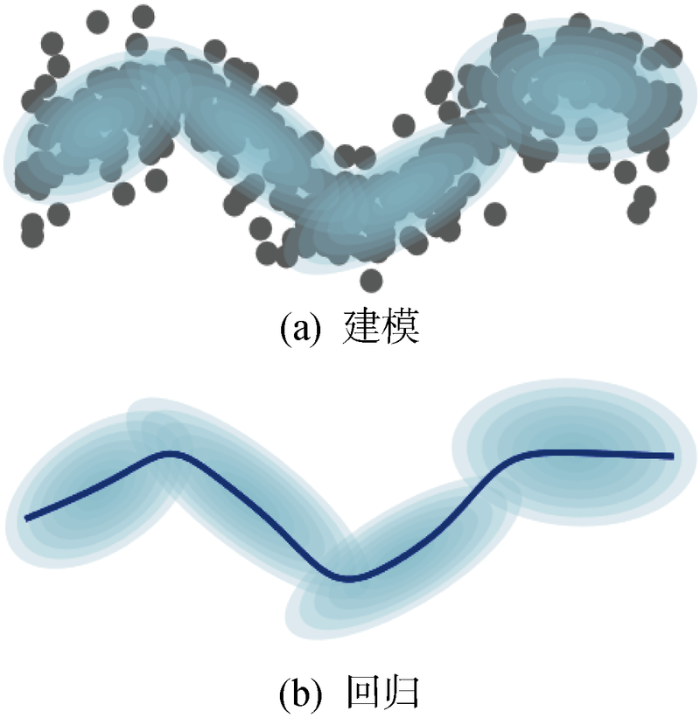
DMP从单次示教轨迹中建模动作[6 ] ,但单次示教数据往往存在噪声和误差. 通常希望能通过多次示教,从多条轨迹中获得主要的动作特征以消除这些干扰. 鉴于GMM和GMR的统计特性,将二者引入到DMP中,利用GMM对多组强迫项进行建模,然后通过GMR去估计真实的强迫函数,如图3 所示.
图3
图3
使用GMM和GMR对DMP的强迫项进行建模和回归
Fig.3
Modeling and regression of DMP forcing terms by GMM and GMR
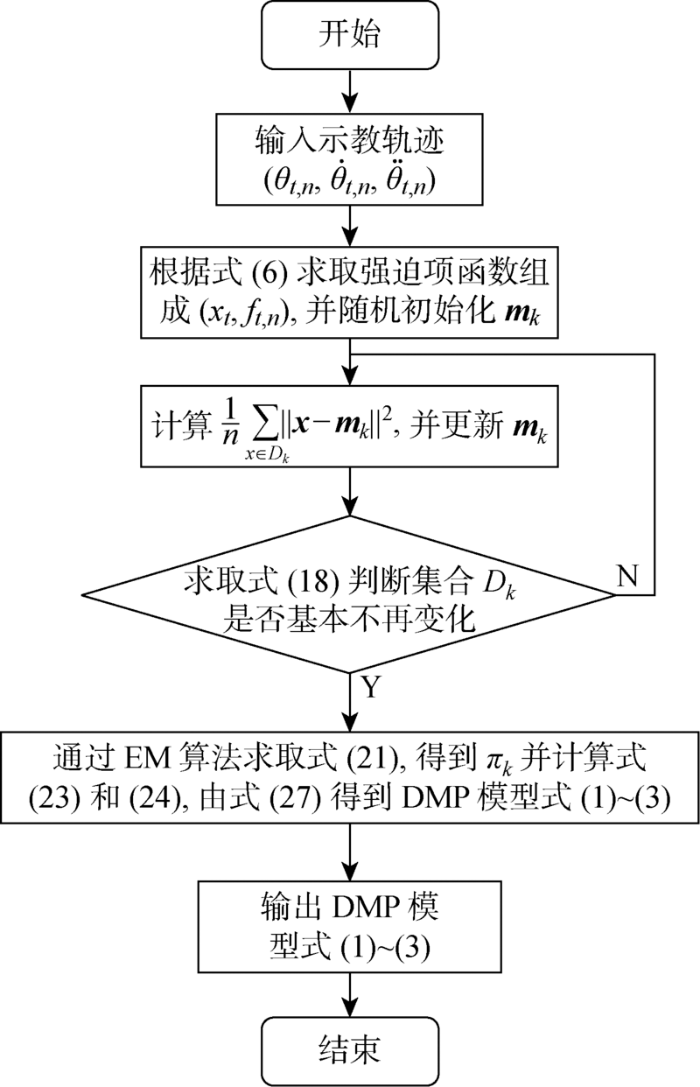
改进DMP算法流程如图4 所示.先将N d { ( θ t , p , θ · t , p , θ ¨ t , p ) t = 1 , 2 , … , T ; p = 1 , 2 , … , N d } { ( x t , f t , p ) t = 1 , 2 , … , T ; p = 1 , 2 , … , N d } . 为了对这组数据集进行建模,定义如下GMM联合概率密度函数:
(14) p ( x , f ) = ∑ k = 1 K α k N ( x , f ; μ k , Σ k )
(15) ∑ k = 1 K α k = 1
(16) μ k = μ x , k μ f , k , Σ k = Σ x , k Σ x f , k Σ f x , k Σ f , k
(17) N ( x , f ; μ k , Σ k ) = e x p - 1 2 ( [ x f ] T - μ k ) T Σ k - 1 ( [ x f ] T - μ k ) 2 π ( Σ k )
式中: K 为高斯分布的数目;α k ≥ 0 μ k ∈ R 2 × 1 Σ k ∈ R 2 × 2 α k μ k Σ k
图4
图4
改进DMP算法流程图
Fig.4
Flow chart of improved DMP algorithm
由于期望最大 (Expectation-Maximum, EM)算法求解GMM模型参数需要获取1组适当的初始参数, 所以先对数据进行K均值聚类,即最小化以下函数来把数据集分成K个子集合D = { D 1 , D 2 , … , D K } .
(18) D ^ = a r g m i n D ∑ k = 1 K ∑ x ∈ D k x - m k 2
式中: x = [ x t f t , n ] T m k D k α k μ k Σ k .
(19) α k = D k ∑ i = 1 K D i
(20) μ k = m k , Σ k = Σ x 1 Σ x 1 x 2 Σ x 2 x 1 Σ x 2 x ∈ D k
然后用EM算法估计GMM参数得到强迫项函数的模型,即通过最大化以下对数似然函数求取
(21) π k = ( α k , μ k , Σ k ) : π ^ k = a r g m a x π k l n ( p ( x , f π k ) )
(22) p ( x , f ) = ∑ k = 1 K α k N ( f ; η ^ k , σ ^ k 2 ) N ( x ; μ x , k , Σ x , k )
(23) η ^ k ( x ) = μ f , k + Σ f x , k ( Σ x , k ) - 1 ( x - μ x , k )
(24) σ ^ k 2 = Σ f , k - Σ f x , k ( Σ x , k ) - 1 Σ x f , k
(25) p ( x ) = ∫ p ( x , f ) d x = ∑ k = 1 K α k N ( x ; μ x , k , Σ x , k )
(26) p ( f ∣ x ) = ∑ k = 1 K β k ( x ) N ( f ; η ^ k , σ ^ k 2 )
式中:β k ( x ) = α k N ( x ; μ x , k , Σ x , k ) ∑ k = 1 K α k N ( x ; μ x , k , Σ x , k ) .
(27) f ^ ( x ) = E ( f | x ) = ∑ k = 1 K β k ( x ) η ^ k ( x )
2 自适应神经网络控制器
2.1 控制器的设计
为设计控制律使机械臂跟踪期望的轨迹q d q · d q ¨ d q d < c q , q · d < c q · , q ¨ d < c q ¨ c q , c q · , c q ¨ ∈ R + . 反馈增益矩阵Kp 和Kd 是正定的,Kd 最小特征值要大于正实数β ∈ R + σ m i n ( K d ) > β .
考虑如下具有外部负载力矩的n 杆刚性机械臂动力学模型:
(28) τ = H ( q ) q ¨ + C ( q , q · ) q · + G ( q ) + τ p
式中: q ∈ R n τ ∈ R n τ p H ( q ) ∈ R n × n C ( q , q · ) ∈ R n × n G ( q ) ∈ R n [21 ] ,即
(2) H · ( q )-2C (q , q · ) ∈Rn × n H ( q ) H (q )-H (q' )||≤L q - q ' L ≥0,q ,q' ∈Rn .
(3) 矩阵C (q , q · ) 是q 上有界且关于q · q , q · p · n cc ∈R+ ,||C (q , q · ) ||≤cc q · C (q , q · ) p · C (q , p · ) q · .
为加速控制器神经网络的收敛速度,将辨识参数作为训练网络参数的初始值,动力学模型的辨识参数表示为
(29) τ m = H m ( q ) q ¨ + C m ( q , q · ) q · + G m ( q )
式中:H m ,C m ,G m 为动力学模型的估计参数. 设计如下控制律,即
(30) τ c = H ^ ( q ) q ¨ d + C ^ ( q , q · ) q · d + G ^ ( q ) + τ d m p - K d e · - K p e
式中:τ dmp 为RBF-DMP对τ p 的建模结果,其建模误差表示为ε dmp =τ p -τ dmp ,e =q -q d 是轨迹跟踪误差,H ^ ( q ),C ^ ( q , q · ) ,G ^ ( q )由机械臂模型参数H m ,C m ,G m 和RBFNN拟合结果组成,即
(31) H ^ ( q ) = H m ( q ) + W ^ H T S H ( q ) C ^ ( q , q · ) = C m ( q , q · ) + W ^ C T S C ( q , q · ) G ^ ( q ) = G m ( q ) + W ^ G T S G ( q )
式中:W ^ H R n N g × n W ^ C R 2 n N g × n W ^ G R n N g × n
W H = W H i , j , W C = W C i , j W G = d i a g ( W G i )
其中: W H i , j ∈ R N g W C i , j ∈ R 2 N g W G i ∈ R N g H i , j ( θ ) ∈ R C i , j ( θ ) ∈ R G i ( θ ) ∈ R S H ( θ ) S C ( θ , θ · ) S G ( θ )
S H ( θ ) = d i a g ( S θ , … , S θ ) S C ( θ , θ · ) = d i a g S θ S θ · , … , S θ S θ · S G ( θ ) = S T θ … S T θ T
其中:S H ∈ R n N g × n S C ∈ R 2 n N g × n S G ∈ R n N g S θ = [ s 1 ( θ ) s 2 ( θ ) … s N g ( θ ) ] T ∈ R l S θ · = [ s 1 ( θ · ) s 2 ( θ · ) … s N g ( θ · ) ] T .
将式(30)代入机械臂的动力学方程式(28)中可得:
(32) H ( q ) q ¨ + C ( q , q · ) q · + G ( q ) + τ p = H ^ ( q ) q ¨ d + C ^ ( q , q · ) q · d + G ^ ( q ) + τ d m p - K d e · - K p e
(33) H ( q ) = H m ( q ) + W H T S H ( q ) + ε H C ( q , q · ) = C m ( q , q · ) + W C T S C ( q , q · ) + ε C G ( q ) = G m ( q ) + W G T S G ( q ) + ε G
式中:ε H = H ( q ) - H ^ ( q ) , ε C = C ( q , q · ) - C ^ ( q , q · ) , ε G = G ( q ) - G ^ ( q )
(34) e ¨ = - H ( q ) - 1 ( W ~ H T S H ( q ) q ¨ d + W ~ C T S C ( q , q · ) q · d + W ~ G T S G ( q ) + C ( q , q · ) e · + K p e + K d e · + ε d m p + ε H q ¨ d + ε C q · d + ε G )
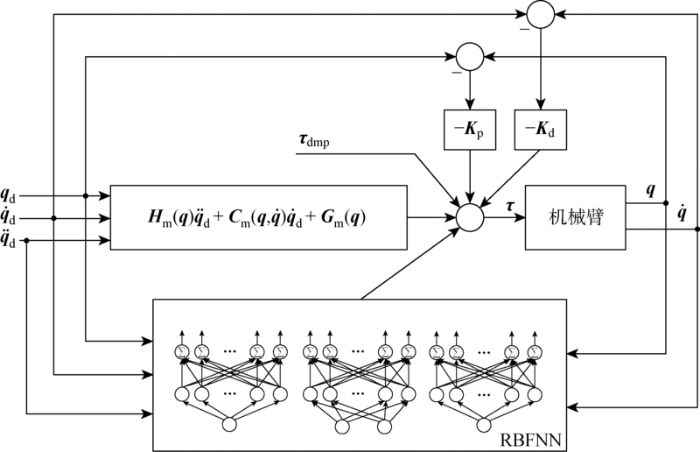
式中:W ~ H WH -W ^ H W ~ C WC -W ^ C W ~ G WG -W ^ G 图5 所示.
图5
图5
闭环控制系统框图
Fig.5
Block diagram of closed-loop control system
2.2 系统稳定性分析
机械臂进行技能复现的过程中,系统的稳定性尤为重要,其保证了机械臂和操作者的安全. 以下将给出技能复现过程机械臂控制系统的稳定性分析结果.
定理1 考虑机械臂动力学模型式(28),在给定的有界q d 和q · d
(35) V = V 1 + V 2
V 1 = 1 2 e · T H e · + 1 2 e T K p e V 2 = 1 2 t r ( W ~ H T Γ H - 1 W ~ H ) + 1 2 t r ( W ~ C T Γ C - 1 W ~ C ) + 1 2 t r ( W ~ G T Γ G - 1 W ~ G )
其中:Γ H - 1 Γ C - 1 Γ G - 1 V 1 求导可得
(36) V · 1 = e · T H e ¨ + 1 2 e · T H · e · + e · T K p e
令ε dmp +εH q ¨ d εC q · d εG =ε r ,将式(34)代入式(36)可得:
(37) V · 1 = e · T ( W ~ H T S H ( q ) q ¨ d + W ~ C T S C ( q , q · ) q · d + W ~ G T S G ( q ) + ε r - C ( q , q · ) e · - K p e - K d e · ) + e · T K p e + e · T [ 1 2 ( H · - 2 C ( q , q · ) ) + C ( q , q · ) ] e ·
由属性(2)可知H · -2 C 是一个反对称矩阵,从而可将式(37)转化为
(38) V · 1 = e · T ε r - e · T K d e · + e · T W ~ H T S H ( q ) q ¨ d + e · T W ~ C T S C ( q , q · ) q · d + e · T W ~ G T S G ( q )
(39) V · 2 = t r ( W ~ H T Γ H - 1 W ~ · H ) + t r ( W ~ C T Γ C - 1 W ~ · C ) + t r ( W ~ G T Γ G - 1 W ~ · G )
根据式(36),并结合W ~ · H W · H - W ^ · H W ~ · C W · C - W ^ · C W ~ · G W · G - W ^ · G
(40) V · = - e · T ε r - e · T K d e · + t r W ~ H T ( S H q ¨ d e · T + Γ H - 1 W ^ · H ) + t r W ~ C T ( S C q · d e · T + Γ C - 1 W ^ · C ) + t r W ~ G T ( S G e · T + Γ G - 1 W ^ · G )
(41) W ^ · H = - Γ H ( S H q ¨ d e · T + ρ H W ^ H ) W ^ · C = - Γ C ( S C q · d e · T + ρ C W ^ C ) W ^ · G = - Γ G ( S G e · T + ρ G W ^ G )
式中:ρH , ρG , ρC 为设置的学习率,将式(41)代入式(40)可得:
(42) V · = - e · T ε r - e · T K d e · + t r ρ H W ~ H T W ^ · H + t r ρ C W ~ C T W ^ · C + t r ρ G W ~ G T W ^ · G
根据杨氏不等式和tr(W ~ ( • ) T W ^ ( • ) ) ≤-1 2 W ~ ( • ) F 2 1 2 W ( • ) F 2
(43) V ˙ ≤ − ( K d − 1 2 ) e ˙ 2 + ω ˜ − ρ H 2 W ˜ H F 2 − ρ c 2 W ˜ c F 2 − ρ G 2 W ˜ G F 2
式中:成立的条件为ω ˜ = ρ H 2 W ˜ H F 2 + ρ c 2 W ˜ c F 2 + ρ G 2 W ˜ G F 2 + 1 2 K F 2 KF 为ε r Kd 的最小值,因此使得V ˙ ≤ 0
ζ = K d − 1 2 e ˙ 2 + ρ H 2 W ˜ H F 2 + ρ c 2 W ˜ c F 2 + ρ G 2 W ˜ G F 2 , ζ ≥ ω ˜
(44) Ω = e ˙ , W H , W c , W G | ζ / ω ˜ ≤ 1
3 实验结果及分析
3.1 RBF-DMP算法的性能分析
提供DMP和RBF-DMP在人类手写数据库即LASA数据集上的仿真结果,并通过建模精度对比RBF-DMP和DMP的性能优劣.
为对比二者性能,设置DMP和RBF-DMP参数αz =βz /4=25,τ s =1,αx =1,且二者强迫项部分都采用50个高斯基. 将30类手写轨迹视为一个动作包含的30个特征,用DMP和RBF-DMP对其进行建模并复现.图6 给出3组动作的示教轨迹和相应的DMP、RBF-DMP复现轨迹,可以看出RBF-DMP的复现效果普遍好于DMP.而且在相同高斯基个数下DMP和RBF-DMP的强迫项存在以下关系:
∑ i = 1 N g Ψ i ( x ) w i ∑ i = 1 N g Ψ i ( x ) = ∑ i = 1 N g Ψ i ( x ) ∑ j = 1 N g Ψ j ( x ) w i = ∑ i = 1 N g S i ( x ) w i
图6
图6
DMP和RBF-DMP在LASA数据集上的复现结果
Fig.6
Repeatable results of DMP and RBF-DMP on LASA dataset
可知RBF-DMP通过改善高斯基函数分布来提升建模精度.
为定量分析RBF-DMP相比于DMP在建模精度方面的优越性,通过均方误差(Mean Squared Error,MSE)描述动作建模误差,其计算公式如下:
M S E = 1 L ∑ l = 1 L 1 M ∑ m = 1 M ( y ^ ( m ) - y ( m ) ) 2
其中: y ^ ( m ) y (m )分别为复现和示教轨迹;M 为当前示教轨迹点的个数;L 为示教的次数.MSE可以反映示教和复现的一致性.
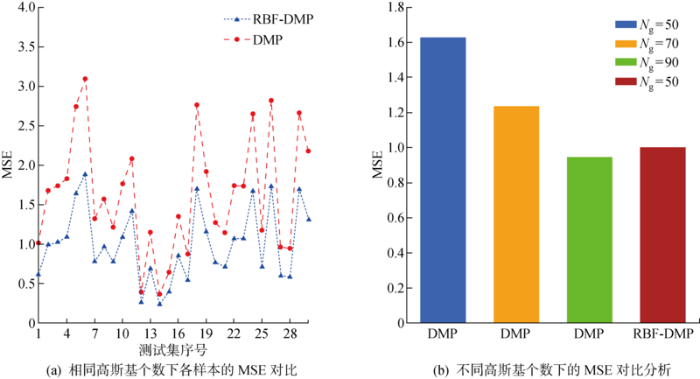
分别计算DMP和RBF-DMP复现轨迹与演示轨迹之间的MSE,如图7(a) 所示,其横坐标与图6 中的演示轨迹类相对应. 再分别增加DMP的高斯基个数至70和90个,同时计算MSE得到图7(b) . 结合图6 和图7(a) 可以看出,对于不同复杂度的轨迹,RBF-DMP在较为复杂的轨迹上能大幅提升建模精度,而对于较为简单的轨迹其建模精度与DMP相近. 从图7(b) 中还可以看出RBF-DMP能在更少的高斯基下达到更好的建模效果,从而减少所需的高斯基个数,降低模型复杂度.
图7
图7
DMP和RBF-DMP在LASA数据集上MSE分析
Fig.7
MSE analysis of DMP and RBF-DMP on LASA datasets
表1 给出DMP和RBF-DMP两种方法在50个高斯基的情况下,对LASA数据集中所有演示轨迹进行建模所花费的时间,从表中可以看出RBF-DMP在耗时上长于DMP. 结合图7(a) 的曲线,为了在提升建模精度的同时减少建模时间的增长,提出图2 中的扩展框架,可以对动作中不同复杂度的特征采用不同的建模方法. 为体现这一框架的优越性,对LASA数据集中的不同类轨迹按照轨迹拐点个数进行分类,将拐点数大于2的示教轨迹作为复杂动作特征,而其余的作为常规特征. 然后利用扩展框架将DMP和RBF-DMP相结合,对LASA数据集进行建模和复现,最后计算出总MSE和总建模时间即拓展框架,可以看出其在少量增加总建模时间的情况下,大幅减少总MSE.
3.2 机械臂实验
为验证本文提出的机器人技能学习方法的有效性,在七自由度的机械臂Franka Emika Panda上进行实验验证.
示教人员将机械臂末端拖动至桌子上的物块点,然后将物块夹取并搬运到指定的位置, 如图8 所示,其中物块的质量为1.03 kg. 通过4次演示,采集4组各个关节的运动轨迹用于技能学习, 在演示过程中加入少量的误操作与抖动,为便于表示,将从基座到末端的7个关节依次命名为J1-J7.
图8
图8
物块搬运的演示过程
Fig.8
Demonstration of block handling process
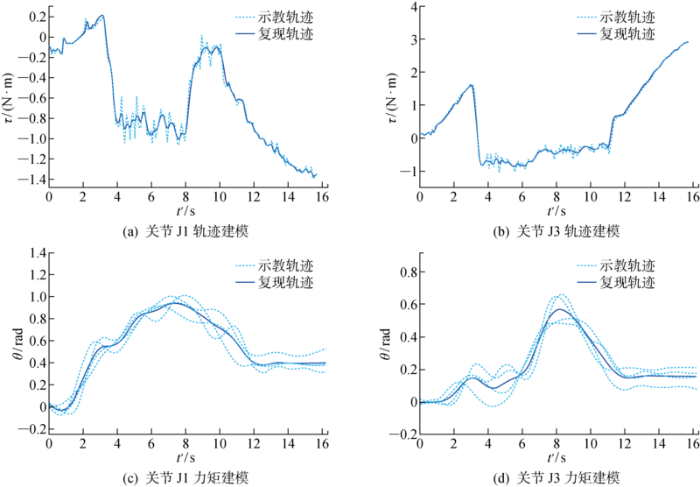
然后用改进的DMP对演示轨迹进行学习,其参数αz =βz /4=25,τ s =1,αx =1,用得到的模型生成复现动作,结果如图9(a) 和9(b) 所示.由于关节数较多,只展示J1和J3的效果,其中虚线为多次拖动演示得到的数据,实线为复现数据. 可以看出该方法能从多次示教中提取出主要的动作特征,消除不必要的演示干扰. 与此同时,对于较为复杂的负载力矩数据,采用RBF-DMP对其建模,其结果如图9(c) 和9(d) 所示. 最后通过扩展框架将二者统一到同一相位系统中,便于泛化. 图中:t '为实验时间点,τ 为力矩,θ 为关节角度.
图9
图9
基于改进DMP和RBF-DMP的动作特征建模
Fig.9
Motion feature modeling based on improved DMP and RBF-DMP
改进DMP从多次示教中学习技能,但多次示教中,物块放置的目标位置会存在误差,将导致学习到的动作在复现时,放置位置产生偏移. 另外,通过示教学习到的动作应当能用于处理一类近似的任务,而不是单一任务.
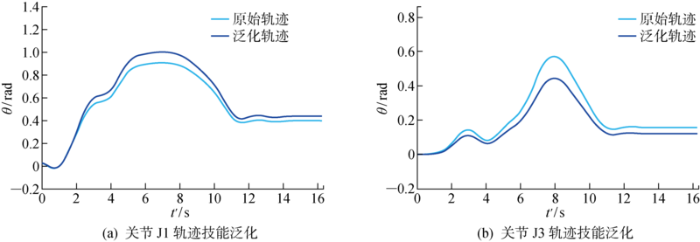
为解决这两类问题,需对学习到的技能进行泛化,通过相机测量物块放置的目标坐标,然后通过Track-IK工具包求逆解,得到新的期望关节位置g' ,然后调节式(1)和式(4)中的g ,使得模型收敛到新的目标点g' ,其泛化结果如图10 .
图10
图10
动作泛化
Fig.10
Action generalization
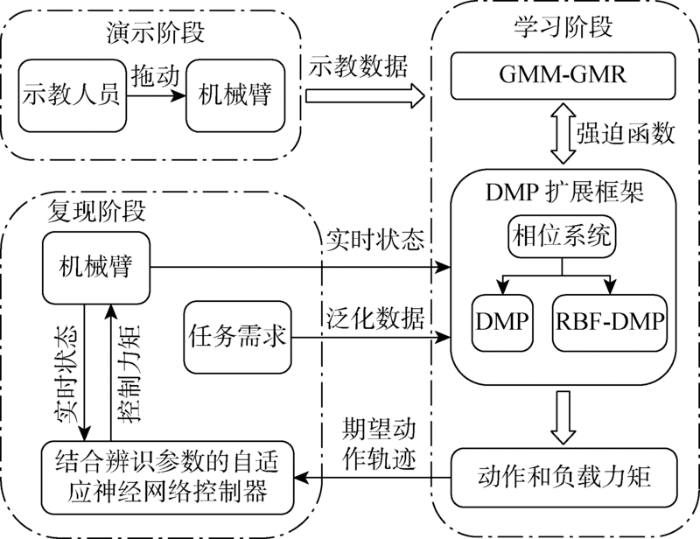
为验证所提出自适应神经网络控制器的有效性. 利用如图11 所示的机械人技能学习系统复现从演示中学习得到的搬运技能.
图11
图11
机器人技能学习系统
Fig.11
Robot skill learning system
首先对自适应神经网络控制器参数进行设置:在每个输入维度上选取3个径向基网络节点,其节点的中心位置在关节位置和速度的可执行范围内均匀分布. 对于H (θ ),G (θ )的补偿,设置网络节点数N g =37 =2 187 个;同理,对C (θ , θ · ) 选取2N g 个网络节点,并设置初始权重参数 W ^ H W ^ C W ^ G K p =diag(50, 50, 40, 40, 35, 35, 30),K d =diag(5, 5, 5, 5, 3, 3, 3). 对于机械臂的模型辨识参数,Panda机械臂具有动力学参数求取功能,可以估计出当前机械臂自身的动力学参数,但受外部因素影响而并不准确,因此将这些参数作为H m ,C m ,G m . 然后通过DMP动作模型生成轨迹序列和力矩量. 最后结合上述自适应网络控制器数据,并根据式(28)~(29)即可得控制量,控制机械臂复现演示动作,如图12 所示.
图12
图12
机械臂复现并泛化技能
Fig.12
Reproduction and generalization skills of mechanical arm
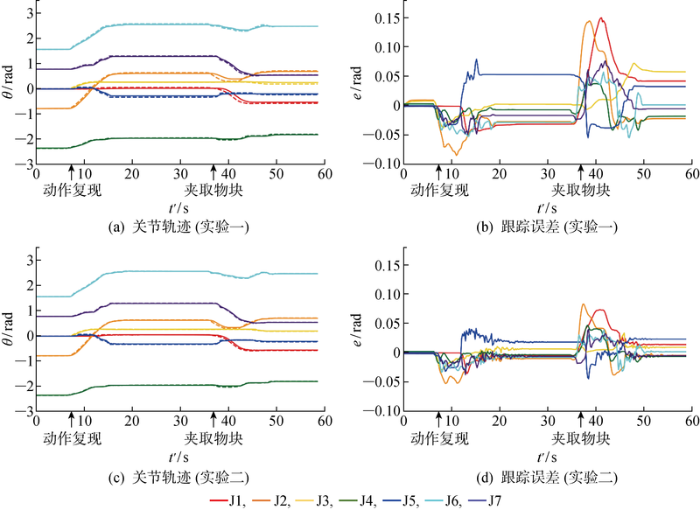
通过两组对比实验对本文设计的控制器的有效性进行检验. 第1组实验采用比例微分控制,不启用自适应神经网络和外部负载力矩补偿. 第2组实验使用本文提出的自适应神经网络控制器. 两次实验的期望关节轨迹(虚线)和实际关节轨迹(实线)如图13 (a)和13(c)所示,对应的关节轨迹误差如图13 (b)和13(d)所示. 可以看出,实验二中机械臂各个关节的轨迹跟踪精度明显好于实验一的结果,这是由于实验一中机械臂动力学参数不够准确以及外部负载的影响,而实验二通过自适应神经网络和外部负载力矩对其分别进行补偿,使得轨迹跟踪误差减少到[-0.05 rad, 0.05 rad].
图13
图13
机械臂的期望关节轨迹和实际关节轨迹 以及跟踪误差曲线
Fig.13
Desired and actual joint trajectories and tracking error curves of manipulator
4 结语
提出一种基于DMP和自适应神经网络控制的机器人技能学习方法,主要就动作建模和动作复现两部分进行改善. 动作建模方面,首先引入RBFNN到DMP的强迫项拟合中提出RBF-DMP,再通过GMM-GMR建模和回归多组轨迹得到的强迫项函数,使改进后的DMP能从多轨迹中建模动作. 在动作复现方面,设计自适应神经网络控制器用于补偿机械臂动力学模型中的误差,使得机械臂能够更准确地复现建模的动作. 最后在LASA数据集上验证RBF-DMP算法的优越性,并在Franka Panda机械臂上验证所提出的机器人技能学习方法,实验结果显示该方法能有效提升机器人动作建模和复现的精度. 未来将研究如何更便捷地学习和生成动作,使得该方法可以更灵活地应用于技能学习.
参考文献
View Option
[1]
马良 , 徐晓兰 , 丁汉 , 等 . 2019年中国机器人产业发展报告
[R]. 北京: 中国电子学会 , 2019 .
[本文引用: 1]
MA Liang XU Xiaolan DING Han , et al China robot industry development report 2019
[R]. Beijing: China Electronics Association , 2019 .
[本文引用: 1]
[2]
EWERTON M MAEDA G KOLLEGGER G , et al Incremental imitation learning of context-dependent motor skills
[C]// 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids) Cancun, Mexico : IEEE , 2016 : 351 -358 .
[本文引用: 1]
[3]
BROCK O KHATIB O . Elastic strips: A framework for integrated planning and execution
[C]// Experimental Robotics VI London : Springer , 2000 : 329 -338 .
[本文引用: 1]
[4]
ZHANG H W LENG Y Q . Motor skills learning and generalization with adapted curvilinear Gaussian mixture model
[J]. Journal of Intelligent & Robotic Systems 2019 , 96 (3/4 ): 457 -475 .
[本文引用: 1]
[5]
CHANG G T KULIĆ D . Motion learning from observation using affinity propagation clustering
[C]// 2013 IEEE RO-MAN Gyeongju, Korea (South) : IEEE , 2013 : 662 -667 .
[本文引用: 1]
[6]
IJSPEERT A J NAKANISHI J HOFFMANN H , et al Dynamical movement primitives: Learning attractor models for motor behaviors
[J]. Neural Computation 2013 , 25 (2 ): 328 -373 .
DOI:10.1162/NECO_a_00393
PMID:23148415
[本文引用: 3]
Nonlinear dynamical systems have been used in many disciplines to model complex behaviors, including biological motor control, robotics, perception, economics, traffic prediction, and neuroscience. While often the unexpected emergent behavior of nonlinear systems is the focus of investigations, it is of equal importance to create goal-directed behavior (e.g., stable locomotion from a system of coupled oscillators under perceptual guidance). Modeling goal-directed behavior with nonlinear systems is, however, rather difficult due to the parameter sensitivity of these systems, their complex phase transitions in response to subtle parameter changes, and the difficulty of analyzing and predicting their long-term behavior; intuition and time-consuming parameter tuning play a major role. This letter presents and reviews dynamical movement primitives, a line of research for modeling attractor behaviors of autonomous nonlinear dynamical systems with the help of statistical learning techniques. The essence of our approach is to start with a simple dynamical system, such as a set of linear differential equations, and transform those into a weakly nonlinear system with prescribed attractor dynamics by means of a learnable autonomous forcing term. Both point attractors and limit cycle attractors of almost arbitrary complexity can be generated. We explain the design principle of our approach and evaluate its properties in several example applications in motor control and robotics.
[7]
MEIER F SCHAAL S . A probabilistic representation for dynamic movement primitives
[EB/OL]. (2016 -12 -18 ) [2021 -06 -05 ]. https://arxiv.org/abs/1612.05932.
URL
[本文引用: 1]
[8]
GAŠPAR T NEMEC B MORIMOTO J , et al Skill learning and action recognition by arc-length dynamic movement primitives
[J]. Robotics & Autonomous Systems 2018 , 100 : 225 -235 .
[本文引用: 1]
[9]
LI J J LI Z J LI X D , et al Skill learning strategy based on dynamic motion primitives for human-robot cooperative manipulation
[J]. IEEE Transactions on Cognitive & Developmental Systems 2021 , 13 (1 ): 105 -117 .
[本文引用: 1]
[10]
YANG C G JIANG Y M LI Z J , et al Neural control of bimanual robots with guaranteed global stability and motion precision
[J]. IEEE Transactions on Industrial Informatics 2017 , 13 (3 ): 1162 -1171 .
DOI:10.1109/TII.2016.2612646
URL
[本文引用: 1]
[12]
YANG C G JIANG Y M NA J , et al Finite-time convergence adaptive fuzzy control for dual-arm robot with unknown kinematics and dynamics
[J]. IEEE Transactions on Fuzzy Systems 2019 , 27 (3 ): 574 -588 .
DOI:10.1109/TFUZZ.91
URL
[本文引用: 1]
[13]
ZHANG S DONG Y T OUYANG Y C , et al Adaptive neural control for robotic manipulators with output constraints and uncertainties
[J]. IEEE Transactions on Neural Networks & Learning Systems 2018 , 29 (11 ): 5554 -5564 .
[本文引用: 1]
[14]
ZHANG Y Y CHEN S Y LI S , et al Adaptive projection neural network for kinematic control of redundant manipulators with unknown physical parameters
[J]. IEEE Transactions on Industrial Electronics 2018 , 65 (6 ): 4909 -4920 .
DOI:10.1109/TIE.41
URL
[本文引用: 1]
[15]
XU Z H LI S ZHOU X F , et al Dynamic neural networks based kinematic control for redundant manipulators with model uncertainties
[J]. Neurocomputing 2019 , 329 : 255 -266 .
DOI:10.1016/j.neucom.2018.11.001
URL
[本文引用: 1]
[16]
MAO Z Y ZHAO F L . Structure optimization of a vibration suppression device for underwater moored platforms using CFD and neural network
[J]. Complexity 2017 , 2017 : 5392539.
[本文引用: 1]
[17]
YIN X C CHEN Q J . Learning nonlinear dynamical system for movement primitives
[C]// 2014 IEEE International Conference on Systems , Man , and Cybernetics San Diego, USA : IEEE , 2014 : 3761 -3766 .
[本文引用: 1]
[18]
YANG C G CHEN C Z HE W , et al Robot learning system based on adaptive neural control and dynamic movement primitives
[J]. IEEE Transactions on Neural Networks & Learning Systems 2019 , 30 (3 ): 777 -787 .
[本文引用: 1]
[19]
YANG C G WANG X Y CHENG L , et al Neural-learning-based telerobot control with guaranteed performance
[J]. IEEE Transactions on Cybernetics 2017 , 47 (10 ): 3148 -3159 .
DOI:10.1109/TCYB.2016.2573837
PMID:28113610
[本文引用: 1]
In this paper, a neural networks (NNs) enhanced telerobot control system is designed and tested on a Baxter robot. Guaranteed performance of the telerobot control system is achieved at both kinematic and dynamic levels. At kinematic level, automatic collision avoidance is achieved by the control design at the kinematic level exploiting the joint space redundancy, thus the human operator would be able to only concentrate on motion of robot's end-effector without concern on possible collision. A posture restoration scheme is also integrated based on a simulated parallel system to enable the manipulator restore back to the natural posture in the absence of obstacles. At dynamic level, adaptive control using radial basis function NNs is developed to compensate for the effect caused by the internal and external uncertainties, e.g., unknown payload. Both the steady state and the transient performance are guaranteed to satisfy a prescribed performance requirement. Comparative experiments have been performed to test the effectiveness and to demonstrate the guaranteed performance of the proposed methods.
[20]
YANG C G WANG X J LI Z J , et al Teleoperation control based on combination of wave variable and neural networks
[J]. IEEE Transactions on Systems , Man , & Cybernetics: Systems 2017 , 47 (8 ): 2125 -2136 .
[本文引用: 1]
[21]
GHORBEL F SRINIVASAN B SPONG M . On the positive definiteness and uniform boundedness of the inertia matrix of robot manipulators
[C]// Proceedings of 32nd IEEE Conference on Decision and Control San Antonio, USA : IEEE , 1993 : 1103 -1108 .
[本文引用: 1]
2019年中国机器人产业发展报告
1
2019
... 近年来,机器人产业迅速发展. 2019年全球机器人市场规模超过200亿美元[1 ] ,使得机器人技术倍受世界关注,各国将机器人作为重点发展领域之一,如中国制造2025、美国的工业互联网、德国的工业4.0等. 传统的机器人主要应用于工业生产环境,但随着机器人智能化水平提升,人们越来越希望机器人能融入生活. 这就要求机器人具有更高的智能,能通过自主学习技能来完成更复杂的任务. 因此,提升机器人技能学习的能力具有重要实际意义. ...
2019年中国机器人产业发展报告
1
2019
... 近年来,机器人产业迅速发展. 2019年全球机器人市场规模超过200亿美元[1 ] ,使得机器人技术倍受世界关注,各国将机器人作为重点发展领域之一,如中国制造2025、美国的工业互联网、德国的工业4.0等. 传统的机器人主要应用于工业生产环境,但随着机器人智能化水平提升,人们越来越希望机器人能融入生活. 这就要求机器人具有更高的智能,能通过自主学习技能来完成更复杂的任务. 因此,提升机器人技能学习的能力具有重要实际意义. ...
Incremental imitation learning of context-dependent motor skills
1
2016
... 示教学习是一种简化机器人技能学习的有效方法[2 ] ,一般包含演示、学习和复现3个阶段. 演示阶段主要指人与机器人之间的动作传递过程,已有视觉示教、动觉示教和遥操作示教等成熟的方法. 学习阶段的主要问题在于如何对技能进行建模,常见的方法有动态系统(Dynamic System,DS)[3 ] 、高斯混合模型(Gaussian Mixture Model,GMM)[4 ] 和隐马尔科夫模型 [5 ] . 其中,由非线性DS发展而来的动态运动原语(Dynamic Movement Primitive,DMP)[6 ] 受到国内外学者的关注. Meier等[7 ] 将DMP重构成一个带有控制输入的线性动态系统概率模型,并将感知测量单元耦合到系统中使其可在线获取反馈信息,根据似然估计结果对任务成败作出预判. Gašpar等[8 ] 提出弧长参数化的动态原语模型,将空间信息与时间信息分开表示用于解决示教中存在较大运动速度差异的问题. Li等[9 ] 提出一种基于DMP的分层控制策略,该策略考虑运动建模和动态控制器的性能. 然而DMP建模精度受高斯基个数影响,而且单次示教数据往往存在噪声,导致DMP从单次示教中往往无法得到需要的动作模型. 因此研究如何让DMP从多轨迹中提取主要特征建模动作,并在更少的高斯基下提高建模精度非常有必要. ...
Elastic strips: A framework for integrated planning and execution
1
2000
... 示教学习是一种简化机器人技能学习的有效方法[2 ] ,一般包含演示、学习和复现3个阶段. 演示阶段主要指人与机器人之间的动作传递过程,已有视觉示教、动觉示教和遥操作示教等成熟的方法. 学习阶段的主要问题在于如何对技能进行建模,常见的方法有动态系统(Dynamic System,DS)[3 ] 、高斯混合模型(Gaussian Mixture Model,GMM)[4 ] 和隐马尔科夫模型 [5 ] . 其中,由非线性DS发展而来的动态运动原语(Dynamic Movement Primitive,DMP)[6 ] 受到国内外学者的关注. Meier等[7 ] 将DMP重构成一个带有控制输入的线性动态系统概率模型,并将感知测量单元耦合到系统中使其可在线获取反馈信息,根据似然估计结果对任务成败作出预判. Gašpar等[8 ] 提出弧长参数化的动态原语模型,将空间信息与时间信息分开表示用于解决示教中存在较大运动速度差异的问题. Li等[9 ] 提出一种基于DMP的分层控制策略,该策略考虑运动建模和动态控制器的性能. 然而DMP建模精度受高斯基个数影响,而且单次示教数据往往存在噪声,导致DMP从单次示教中往往无法得到需要的动作模型. 因此研究如何让DMP从多轨迹中提取主要特征建模动作,并在更少的高斯基下提高建模精度非常有必要. ...
Motor skills learning and generalization with adapted curvilinear Gaussian mixture model
1
2019
... 示教学习是一种简化机器人技能学习的有效方法[2 ] ,一般包含演示、学习和复现3个阶段. 演示阶段主要指人与机器人之间的动作传递过程,已有视觉示教、动觉示教和遥操作示教等成熟的方法. 学习阶段的主要问题在于如何对技能进行建模,常见的方法有动态系统(Dynamic System,DS)[3 ] 、高斯混合模型(Gaussian Mixture Model,GMM)[4 ] 和隐马尔科夫模型 [5 ] . 其中,由非线性DS发展而来的动态运动原语(Dynamic Movement Primitive,DMP)[6 ] 受到国内外学者的关注. Meier等[7 ] 将DMP重构成一个带有控制输入的线性动态系统概率模型,并将感知测量单元耦合到系统中使其可在线获取反馈信息,根据似然估计结果对任务成败作出预判. Gašpar等[8 ] 提出弧长参数化的动态原语模型,将空间信息与时间信息分开表示用于解决示教中存在较大运动速度差异的问题. Li等[9 ] 提出一种基于DMP的分层控制策略,该策略考虑运动建模和动态控制器的性能. 然而DMP建模精度受高斯基个数影响,而且单次示教数据往往存在噪声,导致DMP从单次示教中往往无法得到需要的动作模型. 因此研究如何让DMP从多轨迹中提取主要特征建模动作,并在更少的高斯基下提高建模精度非常有必要. ...
Motion learning from observation using affinity propagation clustering
1
2013
... 示教学习是一种简化机器人技能学习的有效方法[2 ] ,一般包含演示、学习和复现3个阶段. 演示阶段主要指人与机器人之间的动作传递过程,已有视觉示教、动觉示教和遥操作示教等成熟的方法. 学习阶段的主要问题在于如何对技能进行建模,常见的方法有动态系统(Dynamic System,DS)[3 ] 、高斯混合模型(Gaussian Mixture Model,GMM)[4 ] 和隐马尔科夫模型 [5 ] . 其中,由非线性DS发展而来的动态运动原语(Dynamic Movement Primitive,DMP)[6 ] 受到国内外学者的关注. Meier等[7 ] 将DMP重构成一个带有控制输入的线性动态系统概率模型,并将感知测量单元耦合到系统中使其可在线获取反馈信息,根据似然估计结果对任务成败作出预判. Gašpar等[8 ] 提出弧长参数化的动态原语模型,将空间信息与时间信息分开表示用于解决示教中存在较大运动速度差异的问题. Li等[9 ] 提出一种基于DMP的分层控制策略,该策略考虑运动建模和动态控制器的性能. 然而DMP建模精度受高斯基个数影响,而且单次示教数据往往存在噪声,导致DMP从单次示教中往往无法得到需要的动作模型. 因此研究如何让DMP从多轨迹中提取主要特征建模动作,并在更少的高斯基下提高建模精度非常有必要. ...
Dynamical movement primitives: Learning attractor models for motor behaviors
3
2013
... 示教学习是一种简化机器人技能学习的有效方法[2 ] ,一般包含演示、学习和复现3个阶段. 演示阶段主要指人与机器人之间的动作传递过程,已有视觉示教、动觉示教和遥操作示教等成熟的方法. 学习阶段的主要问题在于如何对技能进行建模,常见的方法有动态系统(Dynamic System,DS)[3 ] 、高斯混合模型(Gaussian Mixture Model,GMM)[4 ] 和隐马尔科夫模型 [5 ] . 其中,由非线性DS发展而来的动态运动原语(Dynamic Movement Primitive,DMP)[6 ] 受到国内外学者的关注. Meier等[7 ] 将DMP重构成一个带有控制输入的线性动态系统概率模型,并将感知测量单元耦合到系统中使其可在线获取反馈信息,根据似然估计结果对任务成败作出预判. Gašpar等[8 ] 提出弧长参数化的动态原语模型,将空间信息与时间信息分开表示用于解决示教中存在较大运动速度差异的问题. Li等[9 ] 提出一种基于DMP的分层控制策略,该策略考虑运动建模和动态控制器的性能. 然而DMP建模精度受高斯基个数影响,而且单次示教数据往往存在噪声,导致DMP从单次示教中往往无法得到需要的动作模型. 因此研究如何让DMP从多轨迹中提取主要特征建模动作,并在更少的高斯基下提高建模精度非常有必要. ...
... DMP模型[6 ] 由以下弹簧-阻尼系统和非线性强迫项函数组成: ...
... DMP从单次示教轨迹中建模动作[6 ] ,但单次示教数据往往存在噪声和误差. 通常希望能通过多次示教,从多条轨迹中获得主要的动作特征以消除这些干扰. 鉴于GMM和GMR的统计特性,将二者引入到DMP中,利用GMM对多组强迫项进行建模,然后通过GMR去估计真实的强迫函数,如图3 所示. ...
A probabilistic representation for dynamic movement primitives
1
2021
... 示教学习是一种简化机器人技能学习的有效方法[2 ] ,一般包含演示、学习和复现3个阶段. 演示阶段主要指人与机器人之间的动作传递过程,已有视觉示教、动觉示教和遥操作示教等成熟的方法. 学习阶段的主要问题在于如何对技能进行建模,常见的方法有动态系统(Dynamic System,DS)[3 ] 、高斯混合模型(Gaussian Mixture Model,GMM)[4 ] 和隐马尔科夫模型 [5 ] . 其中,由非线性DS发展而来的动态运动原语(Dynamic Movement Primitive,DMP)[6 ] 受到国内外学者的关注. Meier等[7 ] 将DMP重构成一个带有控制输入的线性动态系统概率模型,并将感知测量单元耦合到系统中使其可在线获取反馈信息,根据似然估计结果对任务成败作出预判. Gašpar等[8 ] 提出弧长参数化的动态原语模型,将空间信息与时间信息分开表示用于解决示教中存在较大运动速度差异的问题. Li等[9 ] 提出一种基于DMP的分层控制策略,该策略考虑运动建模和动态控制器的性能. 然而DMP建模精度受高斯基个数影响,而且单次示教数据往往存在噪声,导致DMP从单次示教中往往无法得到需要的动作模型. 因此研究如何让DMP从多轨迹中提取主要特征建模动作,并在更少的高斯基下提高建模精度非常有必要. ...
Skill learning and action recognition by arc-length dynamic movement primitives
1
2018
... 示教学习是一种简化机器人技能学习的有效方法[2 ] ,一般包含演示、学习和复现3个阶段. 演示阶段主要指人与机器人之间的动作传递过程,已有视觉示教、动觉示教和遥操作示教等成熟的方法. 学习阶段的主要问题在于如何对技能进行建模,常见的方法有动态系统(Dynamic System,DS)[3 ] 、高斯混合模型(Gaussian Mixture Model,GMM)[4 ] 和隐马尔科夫模型 [5 ] . 其中,由非线性DS发展而来的动态运动原语(Dynamic Movement Primitive,DMP)[6 ] 受到国内外学者的关注. Meier等[7 ] 将DMP重构成一个带有控制输入的线性动态系统概率模型,并将感知测量单元耦合到系统中使其可在线获取反馈信息,根据似然估计结果对任务成败作出预判. Gašpar等[8 ] 提出弧长参数化的动态原语模型,将空间信息与时间信息分开表示用于解决示教中存在较大运动速度差异的问题. Li等[9 ] 提出一种基于DMP的分层控制策略,该策略考虑运动建模和动态控制器的性能. 然而DMP建模精度受高斯基个数影响,而且单次示教数据往往存在噪声,导致DMP从单次示教中往往无法得到需要的动作模型. 因此研究如何让DMP从多轨迹中提取主要特征建模动作,并在更少的高斯基下提高建模精度非常有必要. ...
Skill learning strategy based on dynamic motion primitives for human-robot cooperative manipulation
1
2021
... 示教学习是一种简化机器人技能学习的有效方法[2 ] ,一般包含演示、学习和复现3个阶段. 演示阶段主要指人与机器人之间的动作传递过程,已有视觉示教、动觉示教和遥操作示教等成熟的方法. 学习阶段的主要问题在于如何对技能进行建模,常见的方法有动态系统(Dynamic System,DS)[3 ] 、高斯混合模型(Gaussian Mixture Model,GMM)[4 ] 和隐马尔科夫模型 [5 ] . 其中,由非线性DS发展而来的动态运动原语(Dynamic Movement Primitive,DMP)[6 ] 受到国内外学者的关注. Meier等[7 ] 将DMP重构成一个带有控制输入的线性动态系统概率模型,并将感知测量单元耦合到系统中使其可在线获取反馈信息,根据似然估计结果对任务成败作出预判. Gašpar等[8 ] 提出弧长参数化的动态原语模型,将空间信息与时间信息分开表示用于解决示教中存在较大运动速度差异的问题. Li等[9 ] 提出一种基于DMP的分层控制策略,该策略考虑运动建模和动态控制器的性能. 然而DMP建模精度受高斯基个数影响,而且单次示教数据往往存在噪声,导致DMP从单次示教中往往无法得到需要的动作模型. 因此研究如何让DMP从多轨迹中提取主要特征建模动作,并在更少的高斯基下提高建模精度非常有必要. ...
Neural control of bimanual robots with guaranteed global stability and motion precision
1
2017
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Stable model-based control with Gaussian process regression for robot manipulators
1
2017
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Finite-time convergence adaptive fuzzy control for dual-arm robot with unknown kinematics and dynamics
1
2019
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Adaptive neural control for robotic manipulators with output constraints and uncertainties
1
2018
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Adaptive projection neural network for kinematic control of redundant manipulators with unknown physical parameters
1
2018
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Dynamic neural networks based kinematic control for redundant manipulators with model uncertainties
1
2019
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Structure optimization of a vibration suppression device for underwater moored platforms using CFD and neural network
1
2017
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Learning nonlinear dynamical system for movement primitives
1
2014
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Robot learning system based on adaptive neural control and dynamic movement primitives
1
2019
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Neural-learning-based telerobot control with guaranteed performance
1
2017
... 示教学习效果不仅取决于技能建模效果,还取决于技能复现中的轨迹跟踪精度. 然而机械臂的轨迹跟踪精度通常受机械臂自身动力学模型精度和外部负载力矩的影响[10 ⇓ -12 ] ,比如机械臂动力学模型中未辨识部分和搬运物体时受到的外部负载力矩.对于机械臂动力学模型的误差,通常利用神经网络逼近动力学模型中的非线性特性和辨识误差来补偿[13 ⇓ -15 ] . 文献[16 ]使用反向传播神经网络(BackPropagation Neural Network,BPNN)逼近减震装置模型中的未知非线性部分,用于控制器的设计;而文献[17 ]将径向基神经网络(Radial Basis Function Neural Network, RBFNN)用于逼近机械臂的动力学模型未辨识部分,与BPNN相比,RBFNN具有收敛到最优解、训练相对较快的优势,但因机械臂动力学参数完全由神经网络拟合,所以依旧会导致收敛过程较长. 对于机械臂外部负载力矩,文献[18 -19 ]通过RBFNN网络补偿外部负载力矩,使机械臂能更好地完成任务. ...
Teleoperation control based on combination of wave variable and neural networks
1
2017
... 为此,将RBFNN引入DMP中,提出RBF-DMP方法. 该方法以梯度下降的方式学习权重 w i 和 高 斯 基 中 心 位 置 c i , [20 ] 定义如下: ...
On the positive definiteness and uniform boundedness of the inertia matrix of robot manipulators
1
1993
... 式中: q ∈ R n τ ∈ R n τ p H ( q ) ∈ R n × n C ( q , q · ) ∈ R n × n G ( q ) ∈ R n [21 ] ,即 ...