复杂环境下基于改进Informed RRT*的无人机路径规划算法

doi:10.16183/j.cnki.jsjtu.2022.442

复杂环境下基于改进Informed RRT^*的无人机路径规划算法

刘文倩¹, 单梁^,¹, 张伟龙¹, 刘成林², 马强¹

1.南京理工大学自动化学院,南京 210094

2.江南大学轻工过程先进控制教育部重点实验室,江苏无锡 214122

Unmanned Aerial Vehicle Path Planning Algorithm Based on Improved Informed RRT^* in Complex Environment

LIU Wenqian¹, SHAN Liang^,¹, ZHANG Weilong¹, LIU Chenglin², MA Qiang¹

1. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China

2. Key Laboratory of Advanced Process Control of Light Industry of the Ministry of Education, Jiangnan University, Wuxi 214122, Jiangsu, China

通讯作者: 单梁,副教授;E-mail:shanliang@njust.edu.cn.

责任编辑: 王历历

收稿日期: 2022-11-4 修回日期: 2022-12-12 接受日期: 2022-12-21

基金资助:

国家自然科学基金资助项目(61973139)
江苏省自然科学基金面上项目(BK20191286)
中央高校基本科研业务费专项资金资助项目(30920021139)

Received: 2022-11-4 Revised: 2022-12-12 Accepted: 2022-12-21

作者简介 About authors

刘文倩(2000-),硕士生,从事无人机路径规划与控制算法研究.

摘要

针对无人机在复杂环境中进行路径规划时,快速搜索随机树(RRT)算法易出现规划时间长、路径冗余、狭窄空间中易陷入局部约束导致规划失败的问题,提出一种改进的Informed RRT^*算法.首先,引入人工势场法使采样点按照势场下降的方式向目标点移动,以提高RRT树扩展的目的性和方向性.然后,考虑随机树在扩展过程中全局环境的复杂度,引入自适应步长调整策略以增加随机树在无障碍环境下的扩展速度,并在随机树扩展的过程中加入相关约束条件以确保生成路径的可行性.在找到第一条可达路径后,采用变化的椭圆或椭球采样域限制采样点选取和自适应步长的扩展范围,加快算法收敛到渐进最优的速度.最后,在复杂二维和三维环境下进行传统算法和改进算法的对比实验,仿真分析表明:改进算法可以在很少的迭代次数下找到更优的初始路径,更快地锁定椭圆或椭球采样域,从而给路径优化留出更多时间,算法规划效果更好.

关键词： 路径规划; Informed RRT^*; 人工势场法; 自适应步长; 椭圆采样域

Abstract

To address the problems of long planning time, redundant planning path, and even planning failure caused by local constraints in narrow spaces in the rapid exploring random trees (RRT) algorithm when unmanned aerial vehicle is planning a path in a complex environment, an improved Informed RRT^* algorithm is proposed. First, the artificial potential field (APF) method is used to make the sampling points move to the target point in the way of potential field descending, which improves the purpose and directionality of RRT tree expansion. Considering the complexity of the global environment during tree expansion, an adaptive step size is introduced to accelerate the expansion speed of the RRT tree in an unobstructed environment. Then, relevant constraints are added in the process of random tree expansion to ensure the feasibility of the generated paths. After the first reachable path is found, variable elliptic or ellipsoidal sampling domain is used to limit the selection of sampling points and the expansion range of adaptive step size, so as to accelerate the convergence of the algorithm to the asymptotic optimization. Finally, the original algorithm and the improved algorithm are compared in two-dimensional and three-dimensional complex environment. The simulation results show that the improved algorithm can find a better reachable path with a small number of iterations, lock the elliptic or ellipsoidal sampling domain faster and leave more time for path optimization. The improved algorithm performs better in path planning.

Keywords： path planning; Informed RRT^* (IRRT^*); artificial potential field (APF) method; adaptive step size; elliptic sampling domain

PDF (11075KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘文倩, 单梁, 张伟龙, 刘成林, 马强. 复杂环境下基于改进Informed RRT^*的无人机路径规划算法[J]. 上海交通大学学报, 2024, 58(4): 511-524 doi:10.16183/j.cnki.jsjtu.2022.442

LIU Wenqian, SHAN Liang, ZHANG Weilong, LIU Chenglin, MA Qiang. Unmanned Aerial Vehicle Path Planning Algorithm Based on Improved Informed RRT^* in Complex Environment[J]. Journal of Shanghai Jiaotong University, 2024, 58(4): 511-524 doi:10.16183/j.cnki.jsjtu.2022.442

随着机器人技术的发展,各种各样以无人系统技术为基础的智能设备如无人机、无人车等,被广泛应用于轨道交通、物流运输、巡查勘探、应急救灾等多个领域^[1].特别是在新冠疫情中大量人员居家隔离的情况下,无人机在进行防疫物资配送、喷洒消毒中发挥了重要作用.为完成物资配送任务,无人机须在有大量复杂障碍物的环境中完成路径规划.在喷洒消毒的过程中,无人机保持在固定高度飞行,进行路径规划时可以将三维路径规划问题降至二维以简化问题的复杂度^[2].此外由于无人机续航时间受限制,如何为无人机在二维和三维环境中以更快的速度规划出一条长度更短、轨迹更优的路径依旧是当前研究的热门方向.无人机路径规划根据对环境信息的把握程度可分为基于先验完全信息的全局路径规划和基于传感器信息的局部路径规划^[3].

常见的全局路径规划^[4]算法分为基于搜索的路径规划如Dijkstra和A^*算法、基于概率的路径规划如概率路图(Probabilistic Roadmap, PRM)和快速扩展随机树(Rapidly-Exploring Random Trees, RRT)算法,以及基于智能算法(神经网络、遗传算法、蚁群算法)的路径规划.文献[5]中采用改进的A^*算法对低空物流无人机进行路径规划.文献[6]中采用改进的PRM算法解决带有多角度的多无人机路径规划能耗问题.文献[7]中采用改进的蚁群算法对三维环境下无人机的路径规划问题进行研究.文献[8]中采用改进的RRT算法对电力杆塔巡检无人机进行路径规划.文献[9]中采用改进的RRT^*算法为无人机生成初始离散路径点并采用凸优化方法进行航迹平滑.

上述无人机全局路径规划算法中基于搜索的算法在进行路径规划时需要建立栅格地图,而在三维环境下构建栅格地图十分复杂;基于智能算法的路径规划具有智能算法泛化性差、参数选择困难的缺点;RRT算法无需构建栅格地图,更适合高维度环境下的路径规划^[10],且该算法有概率完备性和计算量小的优点.然而该算法也有致命的缺点:采样的随机性使得算法每次规划出的路径不一致,无法得到最优路径,路径规划速度缓慢.针对该问题,众多学者对该算法展开研究与改进.

为了提高随机树扩展的目的性,文献[11]中在RRT算法的基础上引入启发式扩展的思想,使两棵树不断地向对方交替扩展,这种带有启发式的扩展方法使得树的生长更加贪婪和明确.为了得到一条渐进最优路径,文献[12]中提出RRT^*算法,通过增加重选父节点和重新布线的过程使得规划出的路径接近渐进最优.文献[13]中提出的kino-dynamic RRT^*算法,在文献[12]的基础上改变新节点的扩展函数使得规划出的路径更符合无人机的运动学约束.文献[14]中提出的Informed RRT^*(IRRT^*)算法在文献[12]的基础上引入椭圆采样域限制采样空间,从而减少采样点选取的随机性.文献[15]中提出一种基于RRT^*的离线规划算法,通过连接区域、目标偏差有界采样和路径优化3种策略来提高随机树扩展的速度.文献[16]中在随机树扩展的过程中引入蚁群优化算法,为无人机规划出一条渐进最优的路径.文献[17]中将双向人工势场(Artificial Potential Field, APF)法与双向有偏采样思想相结合,提出BPIB-RRT^*算法,用于三维环境中无人机路径规划.文献[18]中针对IRRT^*算法易出现降级为RRT^*算法的问题,在IRRT^*算法的基础上通过增加A^*算法预规划路径的方式来缩小椭圆采样域的范围.文献[19]中在IRRT^*新节点扩展时改进其steer函数,通过计算最近临近点所受到吸引力和斥力的合力,决定生成新节点的扩展方向.

基于以上分析可知,大量算法从采样方式、扩展方式、采样域的限制以及启发式扩展这几个方面对RRT算法进行了改进.本文所提算法则在IRRT^*算法的基础上引入APF法指引随机采样点向目标点生成,使得随机树的扩展更具有目的性和方向性;接着引入自适应步长调整策略加速随机树在无障碍环境下的扩展速度;再在新节点扩展时计算其偏航角和俯仰角,判断是否满足约束条件以确保规划路径的可行性;其次,在找到第一条可达路径后,采用变化的椭圆或椭球采样域对采样点的选取以及自适应步长的扩展范围进行限制,以加快算法收敛到渐进最优的速度;最终在二维和三维复杂环境下进行仿真对比实验以验证所提算法的有效性.

1 问题定义

1.1 路径规划问题定义

给出无人机路径规划中所需的相关概念和相关定义.令X⊆Rⁿ为规划问题的状态空间^[20],X_obs⊆X为碰撞空间,X_free=X\X_obs为自由空间,x_start∈X_free为初始状态,x_goal∈X_free为期望的最终状态,σ: [0,1]→X_free为路径的序列状态且是所有重要路径的合集,Σ为所有可行路径的集合.

最优路径规划^[21]问题则是对路径σ^*的搜索,最优路径使得在自由空间X_free中规划从初始点x_start到目标点x_goal时的成本函数c: Σ→R^*最小,表示如下:

${{\sigma }^{*}}=\underset{\sigma \in \Sigma }{\mathop{\text{arg }\!\!~\!\!\text{ min}}}\,\{c(\sigma )|\sigma (0)={{x}_{start}},\sigma (1)={{x}_{goal}},\forall s\in [0,1],\sigma (s)\in {{X}_{free}}\}$

(1)

RRT路径规划算法由于其概率完备性总会找到一条从起始点到目标点的可行路径,但由于树生长的随机性,规划出的路径不一定是最优路径.RRT^*算法增加了重选父节点和重布线的过程.重选父节点使新生成的路径成本尽可能小,重布线使得生成新节点后的随机树减少冗余通路,进而减少路径成本,从而找到一条渐进最优路径.

1.2 椭圆形子集直接采样

超椭球中均匀分布的样本x_ell~u(X_ell)可以通过n维单位球中均匀分布的样本x_ball~u(X_ball)变换生成^[14],即

${{x}_{ell}}=L{{x}_{ball}}+{{x}_{cen}}$

(2)

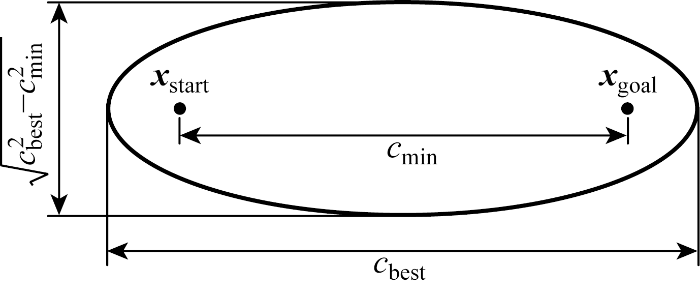
式中:x_cen=(x_start+x_goal)/2,是超椭球体两个焦点x_start和x_goal的中心,如图1所示.图中:c_min为x_start和x_goal的距离,c_best为找到的最短路径长度,X_ball为n维单位球,可以表示为X_ball={x_a∈X | ‖x_a‖₂≤1},x_a为状态空间X中任一变量.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 椭圆形子集采样域

Fig.1 Elliptic subset sampling domain

变换L可以通过超椭球体的Cholesky分解来计算,即

$L{{L}^{T}}=S$

(3)

式中:S∈Rⁿ^×ⁿ,且满足下式,

${{({{x}_{a}}-{{x}_{cen}})}^{T}}S({{x}_{a}}-{{x}_{cen}})=1$

(4)

式中:S的特征向量对应于超椭球横轴{a_i},即c_best,S的特征值对应于超椭球半径平方{ $r_{i}^{2}$ },即 $c_{b e s t}^{2}$ - $c_{m i n}^{2}$ ,变换L使得超椭球X_ell中的样本x_ell均匀分布.对超椭球体,变换L可根据横轴和半径计算,与横轴对齐的矩阵是对角矩阵,即

$S=\text{diag}\left( \frac{c_{\text{best}}^{2}}{4},\frac{c_{\text{best}}^{2}-c_{\text{min}}^{2}}{4}, ~ \ldots,\frac{c_{\text{best}}^{2}-c_{\text{min}}^{2}}{4} \right)$

(5)

对式(5)进行分解计算得到变换L如下:

$L=\text{diag}\left( \frac{{{c}_{\text{best}}}}{2},\frac{\sqrt{c_{\text{best}}^{2}-c_{\text{min}}^{2}}}{2},\text{ }\ldots,\frac{\sqrt{c_{\text{best}}^{2}-c_{\text{min}}^{2}}}{2} \right)$

(6)

综上,得到从n维单位球中均匀分布的样本转换到超椭球中均匀分布的样本所需变换矩阵L.然后给出从椭球坐标系到世界坐标系的旋转矩阵C,即

$C=U\text{diag}\left( 1, ~ 1, ~ \ldots, ~ 1,\text{det}\left( U \right)\text{det}\left( V \right) \right){{V}^{T}}$

(7)

式中:det(U)和det(V)分别为矩阵U和V的行列式,U和V为矩阵M通过奇异值分解得到的酉矩阵,即

$U\sum{{{V}^{T}}}\equiv M$

(8)

式中:M为世界坐标系下超椭球体横轴a₁与单位矩阵l₁第一列的外积;Σ为M经奇异值分解后对角线上的元素为M奇异值的矩阵,即

$M={{a}_{1}}\times {{l}_{1}}$

(9)

${{a}_{1}}=({{x}_{goal}}-{{x}_{start}})/{{\left( {{x}_{\text{goal}}}-{{x}_{\text{start}}} \right)}_{2}}$

(10)

通过变换L、旋转C和平移运算,最终得到世界坐标系下超椭球采样域中均匀分布的样本x_f~u(X_f)如下:

${{x}_{f}}=CL{{x}_{ball}}+{{x}_{cen}}$

(11)

对无人机的三维路径规划和二维路径规划均进行研究,在二维平面中,采样空间为椭圆;在三维路径规划问题中,采样空间为椭球.根据以上分析,以三维为例,可通过n维单位球中均匀分布的样本得到世界坐标系下超椭球中均匀分布样本的算法如下.

1.3 无人机路径规划约束条件

针对规划出的新节点无人机能否执行的问题,进行最大转弯角与最大爬升角的约束分析.最大转弯角对水平面内运动进行限制,约束无人机从当前路径点到下一路径点只能改变一定范围内的偏航角,其本质上是限制最小转弯半径^[22].最大爬升角对无人机的升降运动进行限制,约束无人机从当前路径爬升至下一路径点时只能改变一定范围内的俯仰角.假设无人机运动飞行时的相邻两路径点坐标为p_i(x_i, y_i, z_i)和p_i₊₁(x_i₊₁, y_i₊₁, z_i₊₁),进行如下讨论.

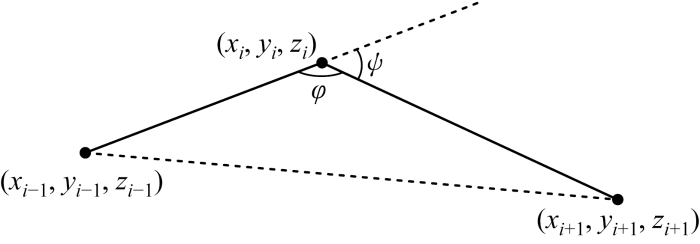
(1) 当高度不变即z_i_-1= z_i= z_i₊₁(该情况主要用于二维平面)时,相邻两段路径的偏航角ψ如图2所示,其中φ为ψ的补角.偏航角ψ应满足约束0≤ψ≤ψ_max,其中ψ_max为最大偏航角,根据余弦定理计算:

$\begin{matrix} & \psi =-\text{arccos}(\cos \varphi )= \\ & -\text{arccos}\left( \frac{{{({{x}_{i}}-{{x}_{i-1}})}^{2}}+{{({{y}_{i}}-{{y}_{i-1}})}^{2}}+{{({{x}_{i+1}}-{{x}_{i}})}^{2}}+{{({{y}_{i+1}}-{{y}_{i}})}^{2}}-{{({{x}_{i+1}}-{{x}_{i-1}})}^{2}}-{{({{y}_{i+1}}-{{y}_{i-1}})}^{2}}}{2\sqrt{{{({{x}_{i}}-{{x}_{i-1}})}^{2}}+{{({{y}_{i}}-{{y}_{i-1}})}^{2}}}\sqrt{{{({{x}_{i+1}}-{{x}_{i}})}^{2}}+{{({{y}_{i+1}}-{{y}_{i}})}^{2}}}} \right)= \\ & \text{arccos}\left( \frac{\left( {{x}_{i}}-{{x}_{i-1}} \right)\left( {{x}_{i+1}}-{{x}_{i}} \right)+\left( {{y}_{i}}-{{y}_{i-1}} \right)\left( {{y}_{i+1}}-{{y}_{i}} \right)}{\sqrt{{{({{x}_{i}}-{{x}_{i-1}})}^{2}}+{{({{y}_{i}}-{{y}_{i-1}})}^{2}}}\sqrt{{{({{x}_{i+1}}-{{x}_{i}})}^{2}}+{{({{y}_{i+1}}-{{y}_{i}})}^{2}}}} \right) \\ \end{matrix}$

(12)

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 相邻两段路径偏航角示意图

Fig.2 Schematic diagram of yaw angle of two adjacent paths

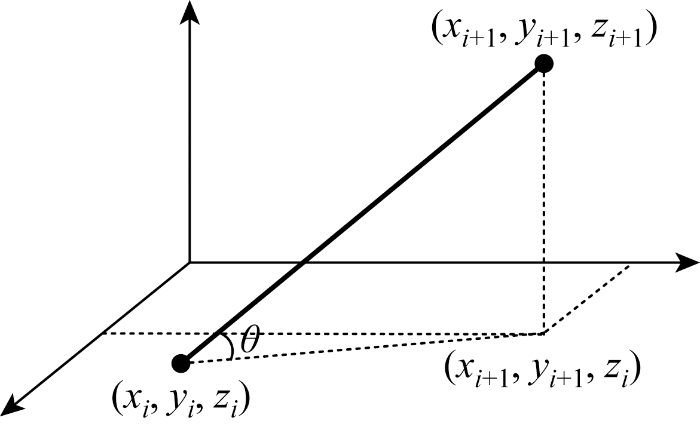
(2) 若z_i≠ z_i₊₁,该情况主要用于三维空间,此时无人机完成爬升操作,俯仰角如图3中θ所示,应满足0≤θ≤θ_max,其中θ_max为最大俯仰角,计算可得:

$θ = a r c t a n (\frac{|z_{i + 1} - z_{i}|}{\sqrt{(x_{i + 1} - x_{i})^{2} + (y_{i + 1} - y_{i})^{2}}})$

(13)

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 俯仰角示意图

Fig.3 Schematic diagram of pitch angle

2 基于自适应步长的 APF-IRRT^*算法

2.1 IRRT^*算法分析

IRRT^*算法^[14]是所提基于自适应步长的APF-Informed RRT^*(AAPF-IRRT^*)算法的基础.IRRT^* 算法在RRT^*算法的基础上进行采样域限制,找到第一条可达路径后,路径优化过程在以起始点和目标点作为焦点,路径长度作为长轴长的椭圆域内进行采样.当路径向最优路径逐渐逼近时,采样域也逐渐减小,路径优化速度加快,其过程如图4所示.当迭代次数k为116时,找到第一条路径c_best=904.5.以起点和终点为焦点,c_best为长轴长的椭圆域中进行采样,在找到比c_best路径短的路径后,缩小椭圆域,进行椭圆域的更新如图4(b)所示.当没有障碍物时,随着迭代次数的增加,路径会达到最优路径即起始点和目标点的直线距离,如图4(c)所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 IRRT^*采样过程

Fig.4 Sampling process of IRRT^*

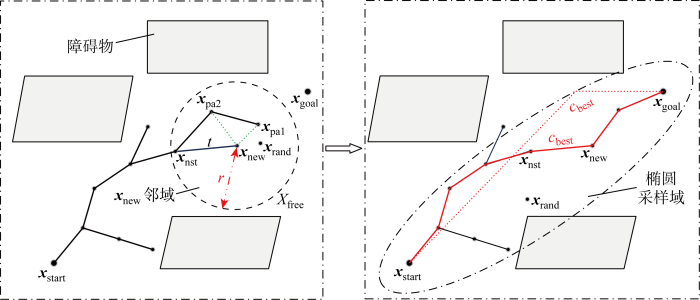
IRRT^*算法的基本思想如下:将起始点x_start作为随机树的根节点,在自由空间X_free中按照椭圆子集采样的形式随机生成一个采样点x_rand,遍历随机树找到距离x_rand最近的节点x_nst,沿x_nst与x_rand之间的连线方向上拓展一个随机树的生长步长t得到x_new,若x_new与x_nst之间没有障碍物,则将x_new加入随机树中.重新在随机树中找到x_new邻域r圆周内的所有点,对x_new重新选择父节点并进行重新布线,具体过程如图5所示,图中x_pa1和x_pa2为父节点.当找到一条从起始点到终点的路径(红色实线)后,采样域变为以起点和终点为椭圆焦点、路径长度c_best为长轴长(红色虚线)的椭圆内.随着路径长度c_best的不断缩短,采样域也在减小,采样速度增加.算法流程如算法二所示.算法中X_soln表示找到到的可行路径x_soln的集合,IRRT^*算法需要在每次找到可行路径后重新计算最短的路径长度c_best并以c_best来更新椭圆域,T为搜索树的集合.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 IRRT^*树生长过程示意图

Fig.5 Growth process of IRRT^* tree

2.2 自适应步长的APF-IRRT^*算法

2.2.1 APF-IRRT^*算法

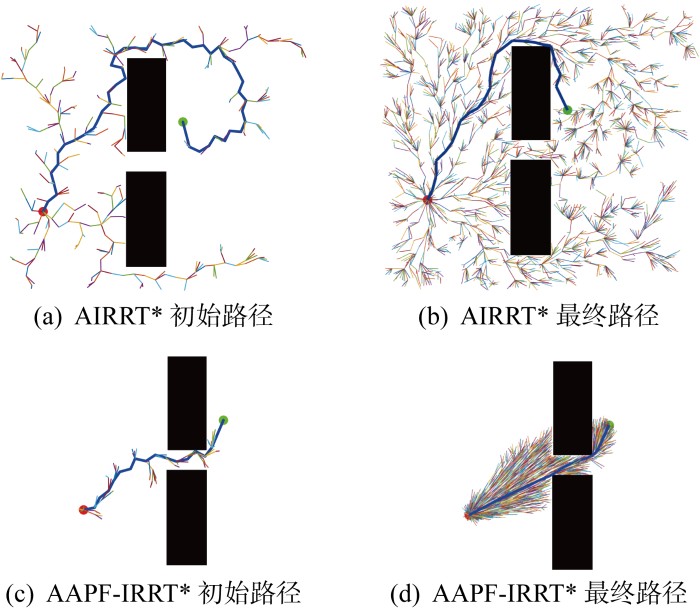
IRRT^*算法虽然增加了椭圆域对采样范围进行限制,但首先需要找到第一条可执行路径,而由于采样的随机性,找到第一条路径所需要的时间往往很长;且规划出的第一条路径较为冗余,椭圆采样域不会在很大程度上得到限制,算法达不到理想的收敛速度.其次,在狭窄空间中进行路径规划时,算法需要进行大量采样,甚至有可能陷入局部约束,收敛速度缓慢,效率大幅下降,如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 狭窄通道陷入局部约束

Fig.6 Narrow passage trapped in local constraint

为了解决以上算法中存在的问题,提出一种基于APF法^[23]的IRRT^*(APF-IRRT^*)路径规划算法.APF法使用梯度下降^[24]的规划方法最小化人工势能.目标点x_goal对无人机x产生吸引势能U_att,障碍物对无人机产生排斥势能U_rep,合势能U=U_att+U_rep,无人机朝着目标点吸引而障碍物排斥的合力方向F前进,F即合势能的负梯度F=-▽U.无人机受到的吸引力势能如下:

$U_{a t t} = \{\begin{array}{l} K_{a} d^{2} (x, x_{g o a l}), & d (x, x_{g o a l}) > d_{g}^{*} \\ K_{a} [d_{g}^{*} d (x, x_{g o a l}) - (d_{g}^{*})^{2}], & d (x, x_{g o a l}) \leq d_{g}^{*} \end{array}$

(14)

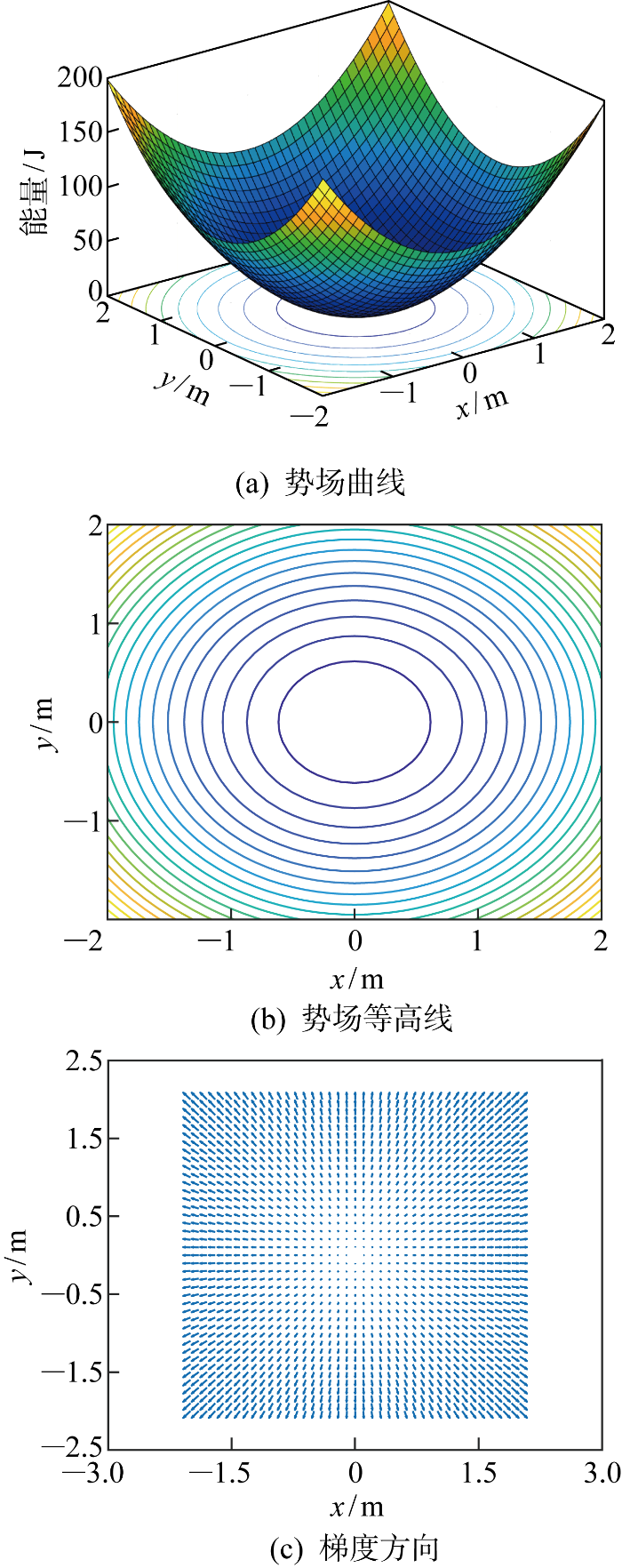
式中:K_a为吸引力势场的比例因子,用来调节吸引势能的大小;参数 $d_{g}^{*}$ 为定义的无人机与目标点的临界范围.吸引势能随着无人机与目标点之间的距离而改变,当距离函数d(x, x_goal)> $d_{g}^{*}$ 时,吸引力势能呈二次方变化.为了防止无人机在接近目标点时因吸引力太大而超出目标区域,当d(x, x_goal)≤ $d_{g}^{*}$ 时,吸引势能降低呈一次变化.吸引力是吸引势能的负梯度,即

$F_{a t t} = \{\begin{array}{l} - 2 K_{a} d (x, x_{g o a l}), & d (x, x_{g o a l}) > d_{g}^{*} \\ - 2 d_{g}^{*} K_{a} \frac{x - x_{g o a l}}{d (x, x_{g o a l})}, & d (x, x_{g o a l}) \leq d_{g}^{*} \end{array}$

(15)

吸引力势能的三维曲线图、势场等高线以及梯度方向图分别如图7(a)~7(c)所示.由图可见吸引力总是沿着势场梯度下降的方向,即当吸引力为0时,就会到达目标点.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 吸引力势场

Fig.7 Attractive potential field

由障碍物x_obs⊆X产生的排斥势能如下:

$U_{r e p} = \{\begin{array}{l} \frac{1}{2} K_{r} {(\frac{1}{d_{m i n}} - \frac{1}{D_{o b s}})}^{2}, & d_{m i n} \leq D_{o b s} \\ 0, & d_{m i n} > D_{o b s} \end{array}$

(16)

${{d}_{\min }}=\underset{x'\in {{\text{X}}_{obs}}}{\mathop{\text{min}}}\,d(x,x')$

(17)

式中:K_r为排斥力势场比例因子;式(17)用来计算机器人到障碍物的最近距离d_min,当d_min大于界定值D_obs时,排斥力为0,机器人距离障碍物很远,机器人快速向目标点移动.排斥力为排斥势能的负梯度,为

$F_{r e p} = \{\begin{array}{l} K_{r} (\frac{1}{D_{o b s}} - \frac{1}{d_{m i n}}) \frac{1}{d_{m i n}^{2}} \frac{\partial d_{m i n}}{\partial x}, & d_{m i n} \leq D_{o b s} \\ 0, & d_{m i n} > D_{o b s} \end{array}$

(18)

APF-IRRT^*算法采用APF法指引采样点的生成,具体如下:首先得到随机采样点x_rand, 利用式(14)和式(15)计算该点和目标点之间的势场力F_att;接着利用势场力指引随机采样点,使得随机采样点在势场减小的方向上以步长η移动;随着采样点越来越接近目标点,引力势场为0.算法三描述了APF法指引采样点向目标点方向靠近的算法流程.F_att←APF(x_goal, x_prand)计算目标点和随机采样点之间的吸引力,其中x_prand为经过APF指引的采样点,然后利用公式x_prand←x_prand+η $(\frac{F_{a t t}}{|F_{a t t}|})$ 使得随机采样点向目标点以步长η移动.在伪代码中,d_min>D_obs && x_prand≠x_goal为随机采样点向目标点的移动条件,当采样点未扩展到目标点且离障碍物的最近距离d_min>D_obs时,采样点向势场减小方向以一定的步长η移动.

图8描述了在无障碍环境中采用很少的迭代次数就能够找到一条接近于渐进最优路径,图中蓝点表示x_rand,红点表示x_prand.由于APF的指引,采样点直接为目标点,树以一定的步长一直向目标点扩展,可以得到渐进最优路径.当找到的第一条路径长度较短时,之后椭圆域的限制也会更小,能够加快迭代速度.且由于只用到引力场,不会出现合力为0的情况,采样点不易陷入局部最优,因此APF-IRRT^* 不会产生APF容易陷入死区的问题.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 APF指引采样点生成

Fig.8 Generation of APF guiding sampling points

2.2.2 自适应步长策略设计

考虑到树扩展过程中全局环境的复杂度,一般设置较小扩展步长.在无障碍空间或者障碍物比较少的环境下,以较小步长t由x_nst向APF指引点x_prand方向扩展,会使得扩展次数较多,从而采样次数增多,树的扩展速度下降,特别是在高维空间中,多次采样会造成树的扩展速度更低.为解决该问题,加快APF-IRRT^*的扩展速度,引入自适应步长调节策略,使得树在无障碍环境下以倍数k_s扩展直到达到步长上限t_max.为了兼顾路径的平滑度,k_s∈[2,3]较为合适^[25].其中t的取值根据能通过最小障碍物狭窄缝隙的最小步长确定,在无障碍环境下自适应步长的扩展如图9所示.因为采用自适应步长进行扩展,可以看出只需要很少次数的采样就可以到达目标点.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 无障碍环境下自适应步长扩展

Fig.9 Adaptive step size expansion in obstacle free environment

自适应步长调节策略具体为:首先判断最近临近点x_nst和APF指引点x_prand能否以步长t正常扩展,如果可以且尚未达到步长上限t_max,则以倍数k_s扩展步长t,并以扩展后的步长生成新节点x_new.从图9可以看出,若不进行步长的扩展以t固定步长进行随机树的生长,那么采样次数必将大于4,即图中当前的采样次数.这种扩展步长的做法一定程度上减小了采样次数,增加了随机树的扩展速度.自适应步长的扩展算法如算法四所示.新节点扩展过程中需要注意,为了使得路径满足最大偏航角和俯仰角的要求,在算法中对x_new重选父节点x_pa后,利用式(12)~(13)计算偏航角和俯仰角判断其是否满足最大偏航角和最大俯仰角的约束条件,若满足则将x_new加入树中,若不满足,则舍弃x_new进行重新采样.

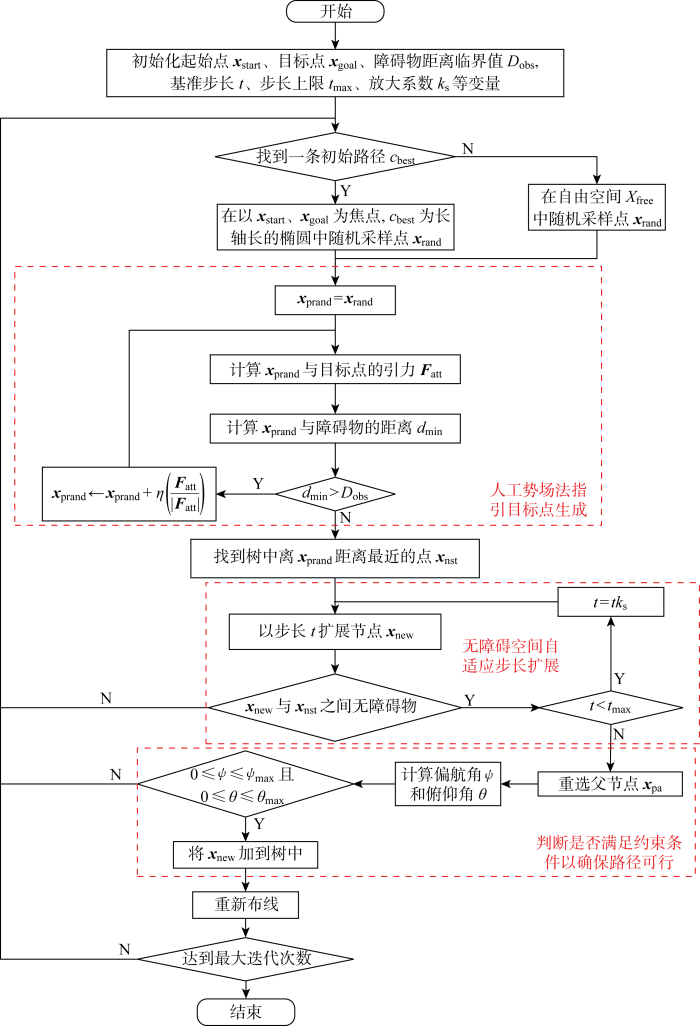
结合APF-IRRT^*算法和自适应步扩展策略,得到AAPF-IRRT^*路径规划算法整体流程如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 基于自适应步长的APF-IRRT^*路径规划算法流程图

Fig.10 Flow chart of APF-IRRT^* path planning algorithm based on adaptive step size

3 仿真验证与分析

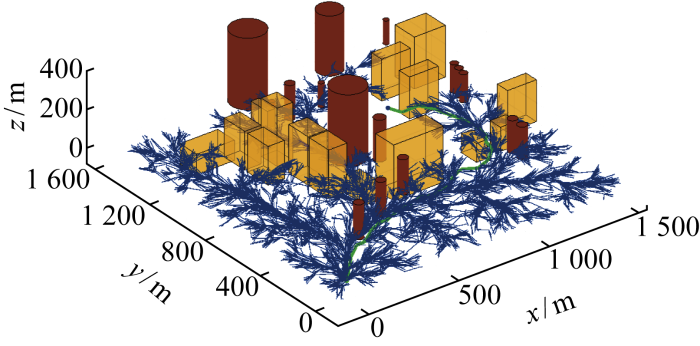
实验仿真采用AMD R7-5800H Windows 11和MATLAB R2020b环境,将无人机作为质点,设无人机轴距为0.5 m,偏航角和俯仰角约束范围为:0≤ψ≤ψ_max=π/2,0≤θ≤θ_max=π/2.首先对环境地图进行0.5 m的膨胀以确保无人机的安全运行,环境地图均经过膨胀处理.首先构造二维复杂环境,进行二维环境下的算法验证;接着构建三维复杂环境,用于验证三维环境中改进算法的有效性.

3.1 APF-IRRT^*算法

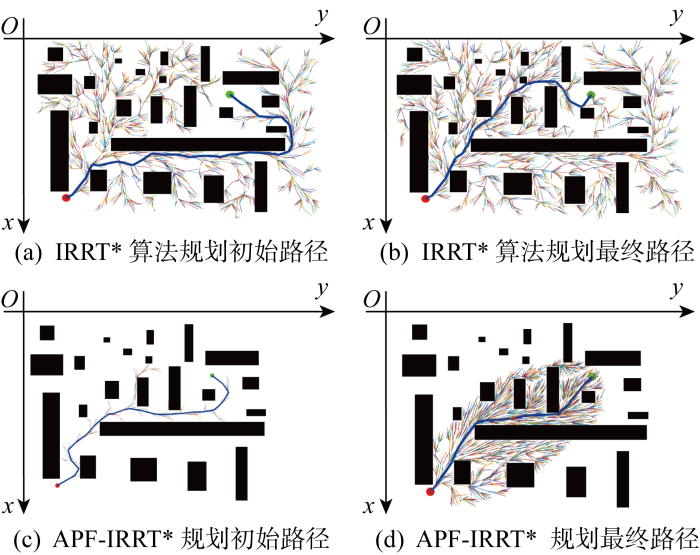
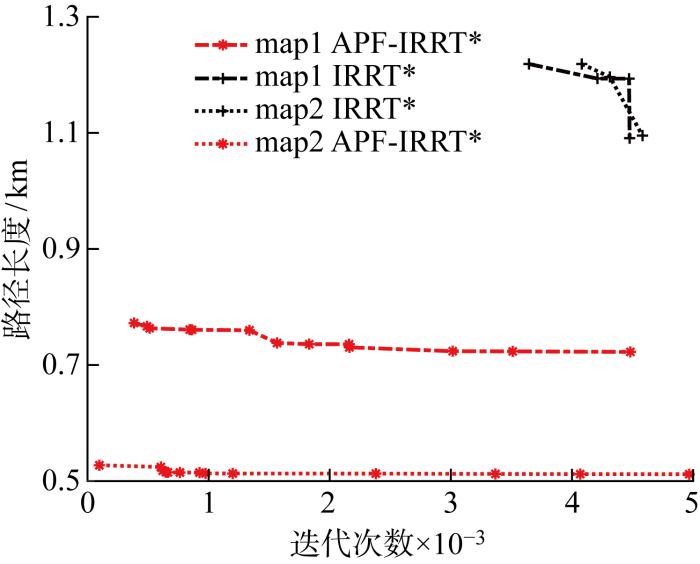
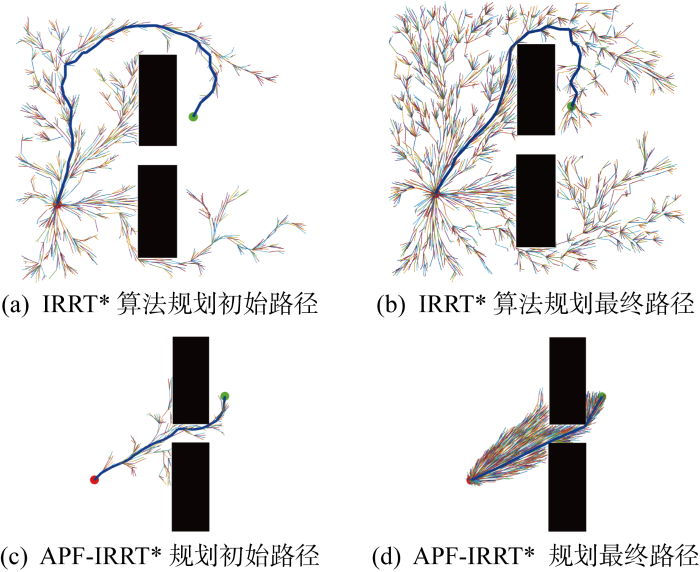
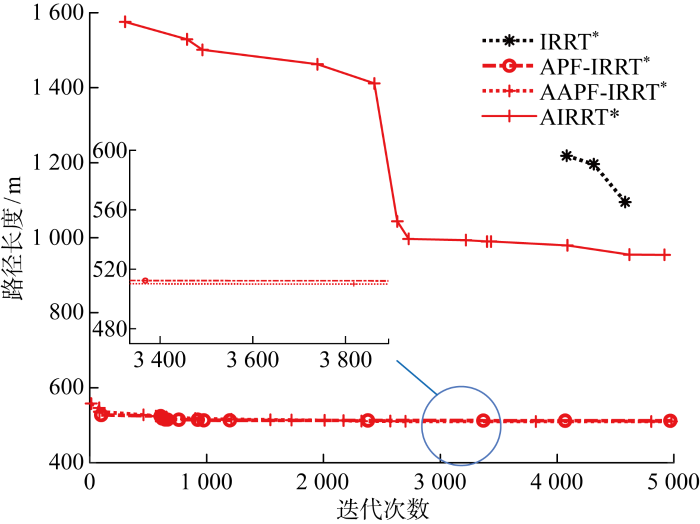
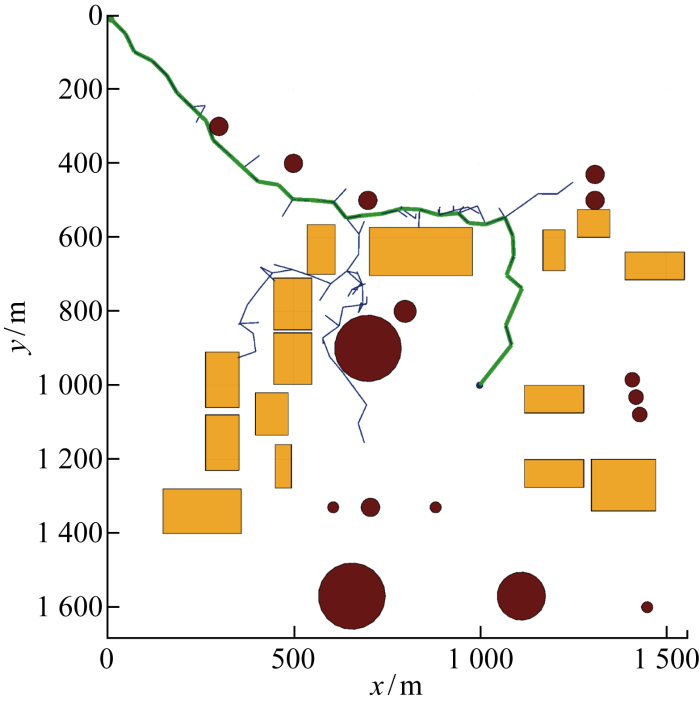
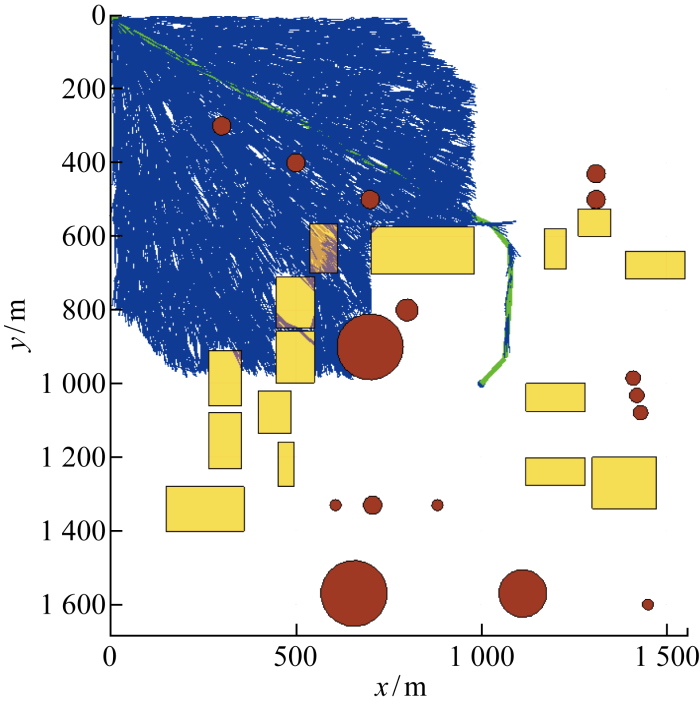
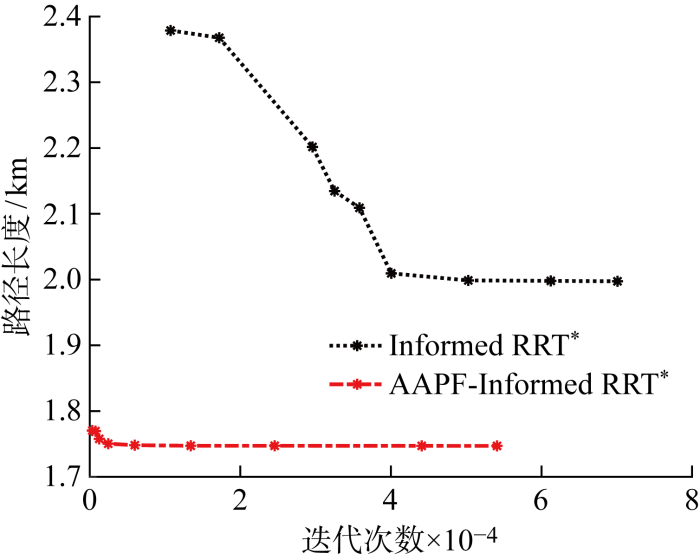
二维仿真地图中选取的地图尺寸为960 m×682 m,起始点和终止点分别为(114, 604),(650, 220),黑色区域为障碍物.IRRT^*算法^[14]的固定步长t=10,改进算法中D_obs=0.1,引力势场比例因子K_a=0.062 5.图11采用地图map1,对比图11(a)和11(b)可以看出,APF-IRRT^*路径规划算法不是在整个X_free中随机采样,而是通过APF的吸引朝目标点x_goal方向扩展,直到在障碍物前0.1 m停止扩展;对比图11(c)和11(d)可以看到,改进后的算法由于规划出的初始路径较短,采样域可以迅速限制在更小椭圆域中,加速树的收敛速度.从图12中APF-IRRT^*算法与传统算法路径长度的收敛曲线中可以看出,改进后算法的路径长度较短,能在更少迭代次数下收敛到渐进最优路径.尤其是在狭窄通道map2中,改进后的算法在向终点扩展的过程中更有目标性,速度更快,如图13所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 IRRT^*和APF-IRRT^*算法对比

Fig.11 Comparison of IRRT^* and APF-IRRT^* algorithms

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 APF-IRRT^*与传统算法路径长度收敛曲线

Fig.12 Path length convergence curves of APF-IRRT^* and original algorithm

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 狭窄通道中IRRT^*算法和APF-IRRT^*算法对比

Fig.13 Comparison of IRRT^* and APF-IRRT^* algorithm in a narrow channel

3.2 自适应步长的APF-IRRT^*算法

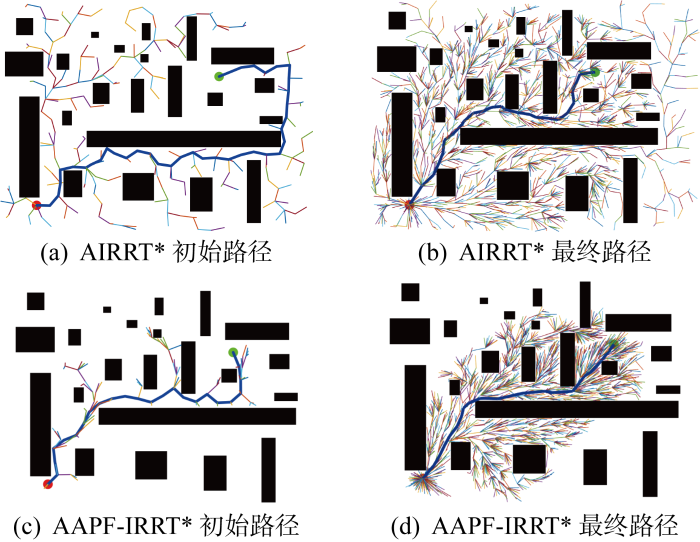
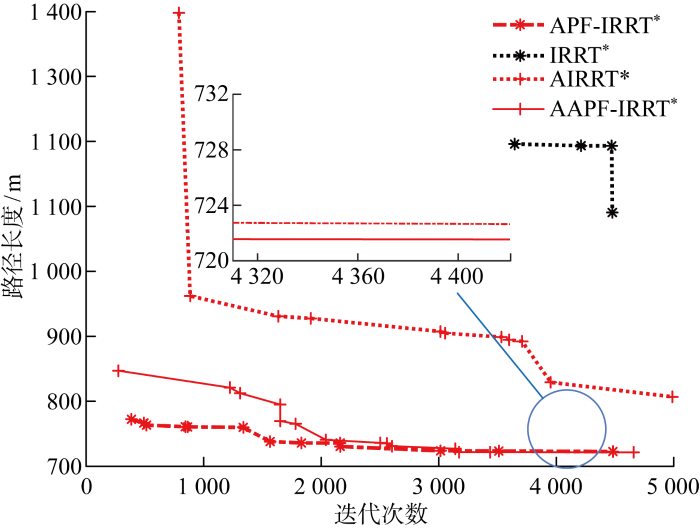
在map1和map2两张环境地图上进行自适应步长的IRRT^*(AIRRT^*)、AAPF-IRRT^*与原算法IRRT^*的对比仿真实验.自适应步长策略调节倍数k_s=2.图14为在地图map1中AIRRT^*随机树和AAPF-IRRT^*随机树的扩展过程.从图15中改进算法和原算法路径长度的比较可以看出,增加自适应步长调整策略的AIRRT^*算法能够在更少迭代次数下找到第一条路径,从而更快锁定椭圆采样域,而AAPF-IRRT^*算法因为有APF法向目标点的采样指引,能够在最短迭代次数下找到初始路径,从而给路径优化至渐进最优提供更多时间,路径质量更好.增加了APF法的指引和自适应步长的扩展,改进算法在狭窄且有大量无障碍空间下的规划速度更快、路径效果更好(见图16),map2下的路径迭代曲线如图17所示.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 map1算法对比

Fig.14 Comparison of algorithm in map1

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 map1改进算法和原算法路径长度收敛曲线

Fig.15 Path length convergence curves of improved map1 algorithm and original algorithm

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 map2算法对比

Fig.16 Comparison of algorithm in map2

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 map2改进算法和原算法路径长度收敛曲线

Fig.17 Path length convergence curves of improved map2 algorithm and original algorithm

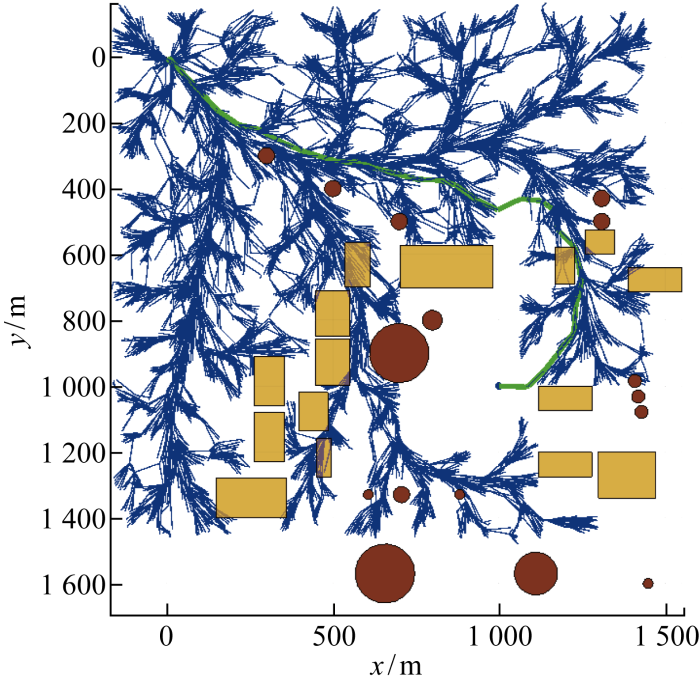
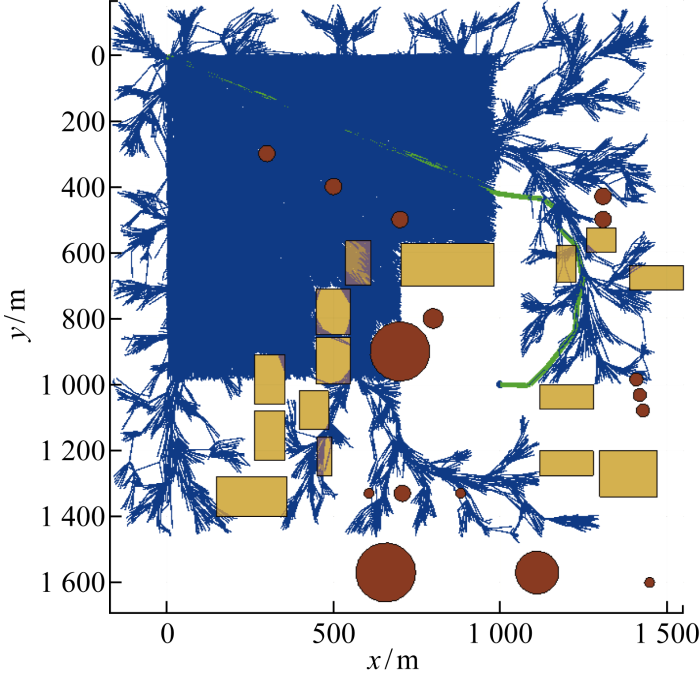
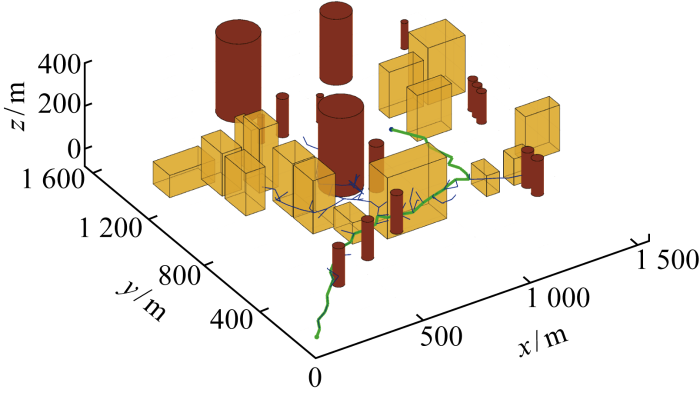
3.3 三维环境下自适应步长的APF-IRRT^*算法

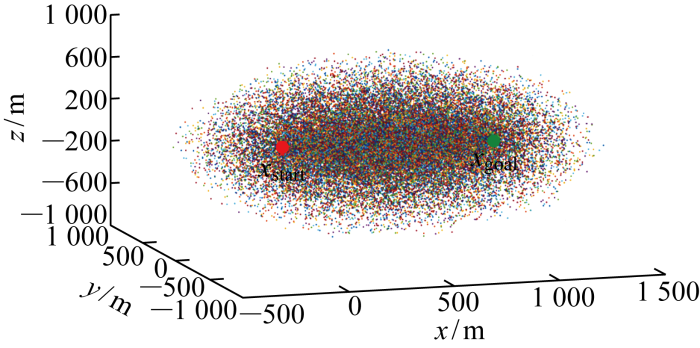
节3.1和3.2在复杂二维环境中进行改进算法的验证,适用于二维飞行任务的无人机路径规划.本节在三维复杂环境中对改进后的AAPF-IRRT^*与传统算法IRRT^*进行仿真对比.与二维空间不同的是,三维空间下IRRT^*算法找到一条可达路径c_best后,在以x_start和x_goal为焦点,c_best为长轴长的椭球域内采样,随着c_best路径长度的优化,椭球采样域越来越小,如图18所示.

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 椭球采样域

Fig.18 Ellipsoidal sampling domain

图19~21分别是三维环境下IRRT^*规划出的初始路径正视图、二维俯视图以及规划出的最终路径二维俯视图.

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 三维环境下IRRT^*初始路径正视图

Fig.19 Front view of the first path planned by IRRT^* in 3D environment

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 三维环境下IRRT^*初始路径二维俯视图

Fig.20 2D top view of the first path planned by IRRT^* in 3D environment

图21

新窗口打开| 下载原图ZIP| 生成PPT

图21 三维环境下IRRT^*最终路径二维俯视图

Fig.21 2D top view of the final path planned by IRRT^* in 3D environment

图22~24分别是三维环境下改进后AAPF-IRRT^*规划出的初始路径正视图、二维俯视图以及最终路径二维俯视图.对比可发现,三维环境下,改进后算法由于有APF法的指引和自适应步长扩展树的生长,只需要很少迭代次数就可以找到一条路径长度更短的可达路径.

图22

新窗口打开| 下载原图ZIP| 生成PPT

图22 三维环境下改进后算法初始路径正视图

Fig.22 Front view of the first path planned by improved algorithm in 3D environment

图23

新窗口打开| 下载原图ZIP| 生成PPT

图23 三维环境下改进后算法初始路径二维俯视图

Fig.23 2D top view of the first path planned by improved algorithm in 3D environment

图24

新窗口打开| 下载原图ZIP| 生成PPT

图24 三维环境下改进后算法最终路径二维俯视图

Fig.24 2D top view of the final path planned by the improved algorithm in 3D environment

从图25三维环境下改进算法和原算法路径长度收敛曲线中可以看出,在三维环境下改进后算法能够在很大程度上节省采样时间,得到一条更短、更优的路径.

图25

新窗口打开| 下载原图ZIP| 生成PPT

图25 三维环境下改进算法和原算法路径长度收敛曲线

Fig.25 Path length convergence curves of improved and original algorithms in 3D environment

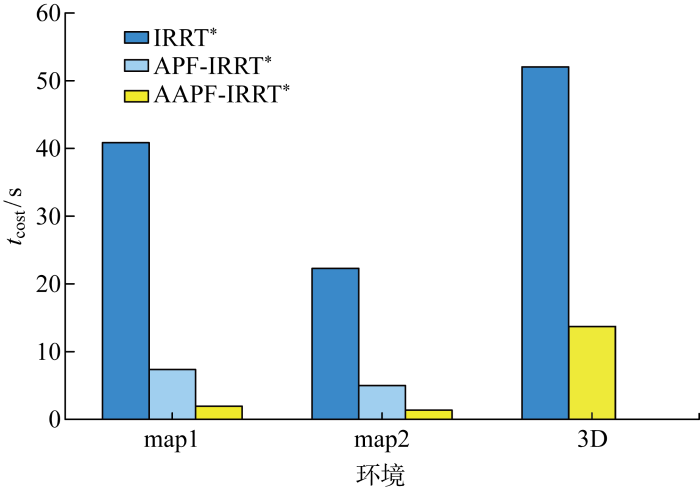
最后,对仿真中各个算法找到初始路径的程序运行耗时进行计算说明.由于随机树扩展具有随机性,所以对每个算法进行10次实验,计算其找到第一条可达路径时所消耗的时间t_cost,并计算平均时间,结果如表1所示.

表1 不同地图环境下原始算法与改进算法找到初始路径所耗费时间

Tab.1 Time consumed by original algorithm and improved algorithm in finding initial path in different map environments

环境	算法	t_cost/s
环境	算法	实验1	实验2		实验3		实验4		实验5		实验6
map1	IRRT^*	21.60287	15.5735		75.43213		11.9442		58.0835		9.934
map1	APF-IRRT^*	11.1223	10.4460		8.0520		5.6783		4.0484		7.4060
map1	AAPF-IRRT^*	1.3111	3.9898		1.5462		2.8812		1.2479		1.0312
map2	IRRT^*	8.1384	9.9257		14.1959		34.3551		46.8274		15.7147
map2	APF-IRRT^*	3.9932	4.4203		7.0841		4.1881		3.8764		5.9439
map2	AAPF-IRRT^*	0.8612	0.8457		1.4761		2.0935		1.3418		1.5886
3D	IRRT^*	20.2574	32.2878		20.6133		20.4921		91.9290		91.6779
3D	AAPF-IRRT^*	14.6385	17.2127		16.4404		14.7832		11.1154		12.0652
环境	算法	t_cost/s
环境	算法	实验7		实验8		实验9		实验10		平均
map1	IRRT^*	83.1127		12.6667		51.1817		69.0751		40.8606
map1	APF-IRRT^*	7.5079		5.7140		5.2071		8.3225		7.35045
map1	AAPF-IRRT^*	2.9592		2.2278		0.8121		1.4574		1.9464
map2	IRRT^*	10.4236		8.9757		64.0088		10.4278		22.2993
map2	APF-IRRT^*	4.7732		4.4239		7.1845		3.9987		4.9886
map2	AAPF-IRRT^*	1.5822		1.2133		1.7045		0.9273		1.3634
3D	IRRT^*	20.6224		24.5895		29.4656		168.4688		52.0403
3D	AAPF-IRRT^*	16.6168		10.1393		13.0260		11.1180		13.7156

新窗口打开| 下载CSV

为更清楚地展示各个环境下算法的运行效率,将其平均时间作如图26柱状图形式的展示.从表1和图26中可以看到,IRRT^*算法由于其随机性,找到初始路径的时间差别很大,有的甚至需要上百秒才能找到初始路径;而加入APF法指引后的算法更加有目的性,算法运行时间比较稳定,几乎在同一数量级,再者增加了自适应步长扩展后树的扩展速度更快,使得找到初始路径的时间更短.

图26

新窗口打开| 下载原图ZIP| 生成PPT

图26 不同环境下原始算法与改进算法t_cost对比

Fig.26 Comparison of t_cost between original algorithm and improved algorithm in different environments

4 结语

针对无人机在复杂环境中进行路径规划时,快速搜索随机树算法易出现规划时间长、路径冗余、在狭窄空间易陷入局部约束而导致规划失败的问题,提出APF法指引随机采样点朝目标点生成和在无障碍环境下自适应步长加速树的扩展速度这两点改进方法,并最终提出AAPF-IRRT^*路径规划算法.二维和三维复杂环境下的仿真分析均表明,所提算法由于APF法指引随机采样点向目标点生成,使得树的扩展更具有目的性;而自适应步长则加快树在无障碍空间向目标点的扩展速度.分析结果发现,所提算法可以在很少的采样次数下找到一条更优初始路径,更快锁定更小椭圆采样域,从而使得最终规划的路径效果更好.

所提算法可以很好地改善RRT树扩展的随机性和生成路径的冗余性,尤其能更好地提升三维空间中路径规划的速度和效果.未来将结合无人机的运动学特性对所生成路径进行进一步的平滑,使其更符合无人机运动.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

杨旭, 王锐, 张涛.

面向无人机集群路径规划的智能优化算法综述

[J]. 控制理论与应用, 2020, 37(11): 2291-2302.

[本文引用: 1]

YANG

, WANG

Rui

, ZHANG

Tao

Review of unmanned aerial vehicle swarm path planning based on intelligent optimization

[J]. Control Theory & Applications, 2020, 37(11): 2291-2302.

[本文引用: 1]

[2]

徐伟华, 聊士超, 张根瑞, 等.

改进Theta^*算法的物流无人机城域三维路径规划

[J]. 计算机工程与应用, 2023, 59(17): 334-340.

DOI:10.3778/j.issn.1002-8331.2205-0428 [本文引用: 2]

针对物流无人机城域配送路径规划问题，使用改进栅格法进行环境建模，设计路径安全代价函数提高路径安全性。为了解决Theta*算法在城市区域规划时路径海拔变化较大的问题，同时为减少路径节点数，提高路径平滑性，在算法实际代价函数中引入海拔变化代价及姿态调整代价；在算法搜索路径节点过程中，通过提出视线存在预设策略减少多余检查过程，提高算法搜索效率。与A*算法及Theta*算法对比验证了改进Theta*算法适用性。设计对照实验确定了目标函数权重及估价函数权重最优取值。在随机不同环境及真实环境下进行仿真，结果表明：相比于传统算法，改进Theta*算法规划路径的海拔变化、路径点数、规划时间及路径总代价均有较明显减少，证明了改进策略的有效性，在城域无人机路径规划方面有一定应用价值。

Weihua

, LIAO

Shichao

, ZHANG

Genrui

, et al.

3D path planning of logistics UAV based on improved Theta^* algorithm in metropolitan area

[J]. Computer Engineering & Applications, 2023, 59(17): 334-340.

[本文引用: 2]

[3]

王琼, 刘美万, 任伟建, 等.

无人机航迹规划常用算法综述

[J]. 吉林大学学报(信息科学版), 2019, 37(1): 58-67.

[本文引用: 2]

WANG

Qiong

, LIU

Meiwan

, REN

Weijian

, et al.

Overview of common algorithms for UAV path planning

[J]. Journal of Jilin University(Information Science Edition), 2019, 37(1): 58-67.

[本文引用: 2]

[4]

张伟龙, 单梁, 常路, 等.

基于改进DWA的多无人水面艇分布式避碰算法

[J]. 控制与决策, 2023, 38(4):951-962.

[本文引用: 1]

ZHANG

Weilong

, SHAN

Liang

, CHANG

, et al.

Distributed collision avoidance algorithm for multiple unmanned surface vessels based on improved DWA

[J]. Control & Decision, 2023, 38(4):951-962.

[本文引用: 1]

[5]

刘光才, 马寅松, 齐福强, 等.

基于改进A^*-人工势场法的城市物流无人机路径规划

[J]. 飞行力学, 2022, 40(6): 16-23.

[本文引用: 1]

LIU

Guangcai

, MA

Yinsong

, QI

Fuqiang

, et al.

Flight path planning for urban logistics UAV based on improved A^*-artificial potential field method algorithm

[J]. Flight Dynamics, 2022, 40(6): 16-23.

[本文引用: 1]

[6]

W M

, WANG

, ZOU

A W

, et al.

Path planning for UAV based on improved PRM

[J]. Energies, 2022, 15(19): 7267.

DOI:10.3390/en15197267 URL [本文引用: 1]

In this paper, an improved probabilistic roadmap (IPRM) algorithm is proposed to solve the energy consumption problem of multi-unmanned aerial vehicle (UAV) path planning with an angle. Firstly, in order to simulate the real terrain environment, a mathematical model was established; secondly, an energy consumption model was established; then, the sampling space of the probabilistic roadmap (PRM) algorithm was optimized to make the obtained path more explicit and improve the utilization rate in space and time; then, the sampling third-order B-spline curve method was used to curve the rotation angle to make the path smoother and the distance shorter. Finally, the results of the improved genetic algorithm (IGA), PRM algorithm and IPRM algorithm were compared through a simulation. The data analysis shows that the IGA has significant advantages over other algorithms in some aspects, and can be well applied to the path planning of UAVs.

[7]

孔维立, 王峰, 周平华, 等.

改进蚁群算法的无人机三维路径规划

[J]. 电光与控制, 2023, 30(3): 63.

[本文引用: 1]

KONG

Weili

, WANG

Feng

, ZHOU

Pinghua

, et al.

Three dimensional path planning of UAV based on improved ant colony algorithm

[J]. Electronics Optics & Control, 2023, 30(3): 63.

[本文引用: 1]

[8]

罗隆福, 李冬, 钟杭.

基于改进RRT的无人机电力杆塔巡检路径规划

[J]. 湖南大学学报(自然科学版), 2018, 45(10): 80-86.

[本文引用: 1]

LUO

Longfu

, LI

Dong

, ZHONG

Hang

Path planning of unmanned aircraft inspection for electric towers based on advanced RRT algorithm

[J]. Journal of Hunan University(Natural Sciences), 2018, 45(10): 80-86.

[本文引用: 1]

[9]

黄宇昊, 韩超, 赵明辉, 等.

考虑安全飞行通道约束的无人机飞行轨迹多目标优化策略

[J]. 上海交通大学学报, 2022, 56(8): 1024-1033.

DOI:10.16183/j.cnki.jsjtu.2021.154 [本文引用: 1]

针对无人机在复杂环境下难以规划出兼顾平滑性和安全性等指标的时域连续轨迹问题,基于安全飞行通道提出了一种多目标轨迹规划算法.在基于快速拓展随机树(RRT)改进的RRT<sup>*</sup>算法生成的初始离散路径点基础上,建立以凸多面体集合表示的安全飞行通道;根据轨迹在安全飞行通道内部的约束建立安全项目标函数,结合飞行平滑性、动力学特性、飞行时间等性能指标,建立加权多目标优化函数;采用基于梯度下降的凸优化算法,对离散路径点的位置、速度、加速度及轨迹的时间分配进行优化,生成分段多项式表示的时域连续轨迹.基于煤矿井下等复杂环境对算法的有效性及相关性能进行试验及对比验证,结果表明:相比现有算法,本文算法在综合性能上有一定的提升.

HUANG

Yuhao

, HAN

Chao

, ZHAO

Minghui

, et al.

Multi-objective optimization strategy of trajectory planning for unmanned aerial vehicles considering constraints of safe flight corridors

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(8): 1024-1033.

[本文引用: 1]

[10]

魏武, 韩进, 李艳杰, 等.

基于双树Quick-RRT算法的移动机器人路径规划

[J]. 华南理工大学学报(自然科学版), 2021, 49(7): 51-58.

DOI:10.12141/j.issn.1000-565X.200769 [本文引用: 1]

最优快速拓展随机树 ( RRT* ) 是一种渐进最优的移动机器人路径规划方法，Quick-RRT* 缩短了 RRT* 的初始路径长度，提高了路径收敛速度。为进一步提高 QuickRRT*的收敛速度，文中提出了一种双树 Quick-RRT* 算法。首先，基于 Quick-RRT* 算法在起点和终点分别生成一棵随机树，起点树和终点树轮流生长，两棵树的连接采用贪婪法; 然后，对提出的算法的概率完备性和渐进最优性进行理论分析，证明了算法的概率完备性和渐进最优性; 最后，基于 Matlab 平台，在 3 种环境下采用双树 Quick-RRT*与 RRT* 、Quick-RRT* 和双向 RRT* 算法进行了对比仿真实验。结果表明，文中改进的算法不仅可以在更短的时间内找到初始路径和次优路径，而且初始路径更短。

WEI

, HAN

Jin

, LI

Yanjie

, et al.

Path planning of mobile robots based on dual-tree quick-RRT Algorithm

[J]. Journal of South China University of Technology (Natural Science Edition), 2021, 49(7): 51-58.

[本文引用: 1]

[11]

刘文倩, 单梁, 王志强, 等.

机械臂的位姿分离求逆和改进RRT-connect算法研究

[J/OL]. 控制工程. https://doi.org/10.14107/j.cnki.kzgc.20210234.

URL [本文引用: 1]

LIU

Wenqian

, SHAN

Liang

, WANG

Zhiqiang

, et al.

Research on inverse kinematics analysis based on position and attitude separation and improved path planning algorithm of manipulator

[J/OL]. Control Engineering of China. https://doi.org/10.14107/j.cnki.kzgc.20210234.

URL [本文引用: 1]

[12]

KARAMAN

, FRAZZOLI

Sampling-based algorithms for optimal motion planning

[J]. The International Journal of Robotics Research, 2011, 30(7): 846-894.

DOI:10.1177/0278364911406761 URL [本文引用: 3]

During the last decade, sampling-based path planning algorithms, such as probabilistic roadmaps (PRM) and rapidly exploring random trees (RRT), have been shown to work well in practice and possess theoretical guarantees such as probabilistic completeness. However, little effort has been devoted to the formal analysis of the quality of the solution returned by such algorithms, e.g. as a function of the number of samples. The purpose of this paper is to fill this gap, by rigorously analyzing the asymptotic behavior of the cost of the solution returned by stochastic sampling-based algorithms as the number of samples increases. A number of negative results are provided, characterizing existing algorithms, e.g. showing that, under mild technical conditions, the cost of the solution returned by broadly used sampling-based algorithms converges almost surely to a non-optimal value. The main contribution of the paper is the introduction of new algorithms, namely, PRM* and RRT*, which are provably asymptotically optimal, i.e. such that the cost of the returned solution converges almost surely to the optimum. Moreover, it is shown that the computational complexity of the new algorithms is within a constant factor of that of their probabilistically complete (but not asymptotically optimal) counterparts. The analysis in this paper hinges on novel connections between stochastic sampling-based path planning algorithms and the theory of random geometric graphs.

[13]

WEBB

D J

, BERG

J V D

. Kinodynamic RRT^*: Optimal motion planning for systems with linear differential constraints[DB/OL]. (2012-05-23) [2022-10-11]. https://arxiv.org/abs/1205.5088 .

URL [本文引用: 1]

[14]

GAMMELL

J D

, SRINIVASA

S S

, BARFOOT

T D

Informed RRT^*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic

[C]// 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems. Chicago, USA: IEEE, 2014: 2997-3004.

[本文引用: 4]

[15]

NOREEN

, KHAN

, RYU

, et al.

Optimal path planning in cluttered environment using RRT^*-AB

[J]. Intelligent Service Robotics, 2018, 11(1): 41-52.

DOI:10.1007/s11370-017-0236-7 URL [本文引用: 1]

[16]

YANG

, FANG

, GAO

, et al.

Obstacle avoidance path planning for UAV based on improved RRT algorithm

[J]. Discrete Dynamics in Nature & Society, 2022, 2022: 1-9.

[本文引用: 1]

[17]

X J

, XU

, ZHEN

, et al.

Biased sampling potentially guided intelligent bidirectional RRT algorithm for UAV path planning in 3D environment

[J]. Mathematical Problems in Engineering, 2019, 2019: 1-12.

[本文引用: 1]

[18]

施英杰

. 基于改进蚁群算法及改进informed-RRT^*算法的机器人路径规划研究[D]. 长春: 吉林大学, 2022.

[本文引用: 1]

SHI

Yingjie

. Research on robot path planning based on improved ant colony algorithm and improved informed-RRT^* algorithm[D]. Changchun: Jilin University, 2022.

[本文引用: 1]

[19]

D H

, WEI

L S

, WANG

G L

, et al.

APF-IRRT^*: An improved informed rapidly-exploring random trees-star algorithm by introducing artificial potential field method for mobile robot path planning

[J]. Applied Sciences, 2022, 12(21): 10905.

DOI:10.3390/app122110905 URL [本文引用: 1]

An Informed RRT* (IRRT*) algorithm is one of the optimized versions of a Rapidly-exploring Random Trees (RRT) algorithm which finds near-optimal solutions faster than RRT and RRT* algorithms by restricting the search area to an ellipsoidal subset of the state space. However, IRRT* algorithm has the disadvantage of randomness of sampling and a non-real time process, which has a negative impact on the convergence rate and search efficiency in path planning applications. In this paper, we report a hybrid algorithm by combining the Artificial Potential Field Method (APF) with an IRRT* algorithm for mobile robot path planning. By introducing the virtual force field of APF into the search tree expansion stage of the IRRT* algorithm, the guidance of the algorithm increases, which greatly improves the convergence rate and search efficiency of the IRRT* algorithm. The proposed algorithm was validated in simulations and proven to be superior to some other RRT-based algorithms in search time and path length. It also was performed in a real robotic platform, which shows that the proposed algorithm can be well executed in real scenarios.

[20]

杨俊成, 李淑霞, 蔡增玉.

路径规划算法的研究与发展

[J]. 控制工程, 2017, 24(7): 1473-1480.

[本文引用: 1]

YANG

Juncheng

, LI

Shuxia

, CAI

Zengyu

Research and development of path planning algorithm

[J]. Control Engineering of China, 2017, 24(7): 1473-1480.

[本文引用: 1]

[21]

ZHONG

X Y

, TIAN

, HU

H S

, et al.

Hybrid path planning based on safe A^* algorithm and adaptive window approach for mobile robot in large-scale dynamic environment

[J]. Journal of Intelligent & Robotic Systems, 2020, 99(1): 65-77.

[本文引用: 1]

[22]

张启钱, 许卫卫, 张洪海, 等.

复杂低空物流无人机路径规划

[J]. 北京航空航天大学学报, 2020, 46(7): 1275-1286.

[本文引用: 1]

ZHANG

Qiqian

, XU

Weiwei

, ZHANG

Honghai

, et al.

Path planning for logistics UAV in complex low-altitude airspace

[J]. Journal of Beijing University of Aeronautics & Astronautics, 2020, 46(7): 1275-1286.

[本文引用: 1]

[23]

李东方, 李科伟, 邓宏彬, 等.

基于人工势场与IB-LBM的机器蛇水中2D避障控制算法

[J]. 机器人, 2018, 40(3): 346-359.

DOI:10.13973/j.cnki.robot.170421 [本文引用: 1]

为了提高多冗余度、多自由度机器蛇水下环境运动适应能力，提出了基于人工势场与IB-LBM （immersed boundary method-lattice Boltzmann method）相结合的机器蛇水中2D智能避障算法.首先，采用格子Boltzmann方法描述2D水中障碍模型、构造统一形式.然后，运用浸入边界法，结合现有的蛇形曲线运动方程，在计入人工势场法引力和斥力作用的情况下，推导得到机器蛇2D水中避障模型.之后，通过改变障碍影响距离、机器蛇摆动振幅、摆动频率、障碍点斥力增益系数、雷诺数以及目标点引力增益系数等重要参数，研究机器蛇在不同情况下的避障效率和避障安全性.最后，通过多次仿真求取各项参数的最优值.仿真结果表明，在各项参数都最优时，该算法能使机器蛇快速、安全、有效地避开水下复杂环境中的静态障碍而到达目标点.该方法不仅能够充分研究机器蛇在水中的流固耦合特性，获得实时避障效果，而且能够利用已知的环境信息生成最优路径.

Dongfang

, LI

Kewei

, DENG

Hongbin

, et al.

The 2D aquatic obstacle avoidance control algorithm of the snake-like robot based on artificial potential field and IB-LBM

[J]. Robot, 2018, 40(3): 346-359.

DOI:10.13973/j.cnki.robot.170421 [本文引用: 1]

To improve the underwater adaptability of the multi-DOF (degree of freedom) snake-like robot with high redundancy,a 2D aquatic intelligent obstacle avoidance algorithm based on artificial potential field and IB-IBM (immersed boundary method-lattice Boltzmann method) is proposed.Firstly,the lattice Boltzmann method is used to describe 2D aquatic obstacle model and construct the unified form.Then,by applying immersed boundary method and combining the existing snake curve motion equation,the 2D aquatic obstacle avoidance model is deduced under the attraction and repulsion action of artificial potential field.Afterwards,the obstacle avoidance efficiency and safety of the snake-like robot are studied under different conditions,including changing obstacle distances,swing amplitude and swing frequency of the snake-like robot, the repulsive gains of obstacle points,the Reynolds number,the attractive gains of target points as well as other important parameters.Finally,the optimal values of every parameter are obtained by several simulations.The simulation results prove that the algorithm enables the snake-like robot to avoid the static obstacles in complex underwater environment and reach its destination swiftly,safely and efficiently when the parameters are optimal.The method can not only fully study the fluid structure coupling characteristics of the underwater snake-like robot and achieve the real-time obstacle avoidance effect,but also generate the optimal path by using the known environmental information.

[24]

ZHOU

H B

, ZHOU

, YU

, et al.

Trajectory optimization of pickup manipulator in obstacle environment based on improved artificial potential field method

[J]. Applied Sciences, 2020, 10(3): 935.

DOI:10.3390/app10030935 URL [本文引用: 1]

In order to realize the technique of quick picking and obstacle avoidance, this work proposes a trajectory optimization method for the pickup manipulator under the obstacle condition. The proposed method is based on the improved artificial potential field method and the cosine adaptive genetic algorithm. Firstly, the Denavit–Hartenberg (D-H) method is used to carry out the kinematics modeling of the pickup manipulator. Taking into account the motion constraints, the cosine adaptive genetic algorithm is utilized to complete the time-optimal trajectory planning. Then, for the collision problem in the obstacle environment, the artificial potential field method is used to establish the attraction, repulsion, and resultant potential field functions. By improving the repulsion potential field function and increasing the sub-target point, obstacle avoidance planning of the improved artificial potential field method is completed. Finally, combined with the improved artificial potential field method and cosine adaptive genetic algorithm, the movement simulation analysis of the five-Degree-of-Freedom pickup manipulator is carried out. The trajectory optimization under the obstacle environment is realized, and the picking efficiency is improved.

[25]

臧强, 张国林, 靳雨桐, 等.

一种基于动态步长的AAPF-RRT^*移动机器人路径规划新算法

[J]. 中国科技论文, 2021, 16(11): 1227-1233.

[本文引用: 1]

ZANG

Qiang

, ZHANG

Guolin

, JIN

Yutong

, et al.

A novel path planning method of mobile robot based on AAPF-RRT^* with dynamic step

[J]. China Sciencepaper, 2021, 16(11): 1227-1233.

[本文引用: 1]

面向无人机集群路径规划的智能优化算法综述

2020

... 随着机器人技术的发展,各种各样以无人系统技术为基础的智能设备如无人机、无人车等,被广泛应用于轨道交通、物流运输、巡查勘探、应急救灾等多个领域^[1].特别是在新冠疫情中大量人员居家隔离的情况下,无人机在进行防疫物资配送、喷洒消毒中发挥了重要作用.为完成物资配送任务,无人机须在有大量复杂障碍物的环境中完成路径规划.在喷洒消毒的过程中,无人机保持在固定高度飞行,进行路径规划时可以将三维路径规划问题降至二维以简化问题的复杂度^[2].此外由于无人机续航时间受限制,如何为无人机在二维和三维环境中以更快的速度规划出一条长度更短、轨迹更优的路径依旧是当前研究的热门方向.无人机路径规划根据对环境信息的把握程度可分为基于先验完全信息的全局路径规划和基于传感器信息的局部路径规划^[3]. ...

Review of unmanned aerial vehicle swarm path planning based on intelligent optimization

2020

改进Theta^*算法的物流无人机城域三维路径规划

2023

... 考虑到树扩展过程中全局环境的复杂度,一般设置较小扩展步长.在无障碍空间或者障碍物比较少的环境下,以较小步长t由x_nst向APF指引点x_prand方向扩展,会使得扩展次数较多,从而采样次数增多,树的扩展速度下降,特别是在高维空间中,多次采样会造成树的扩展速度更低.为解决该问题,加快APF-IRRT^*的扩展速度,引入自适应步长调节策略,使得树在无障碍环境下以倍数k_s扩展直到达到步长上限t_max.为了兼顾路径的平滑度,k_s∈[2,3]较为合适^[25].其中t的取值根据能通过最小障碍物狭窄缝隙的最小步长确定,在无障碍环境下自适应步长的扩展如图9所示.因为采用自适应步长进行扩展,可以看出只需要很少次数的采样就可以到达目标点. ...

3D path planning of logistics UAV based on improved Theta^* algorithm in metropolitan area

2023

无人机航迹规划常用算法综述

2019

Overview of common algorithms for UAV path planning

2019

基于改进DWA的多无人水面艇分布式避碰算法

2023

... 常见的全局路径规划^[4]算法分为基于搜索的路径规划如Dijkstra和A^*算法、基于概率的路径规划如概率路图(Probabilistic Roadmap, PRM)和快速扩展随机树(Rapidly-Exploring Random Trees, RRT)算法,以及基于智能算法(神经网络、遗传算法、蚁群算法)的路径规划.文献[5]中采用改进的A^*算法对低空物流无人机进行路径规划.文献[6]中采用改进的PRM算法解决带有多角度的多无人机路径规划能耗问题.文献[7]中采用改进的蚁群算法对三维环境下无人机的路径规划问题进行研究.文献[8]中采用改进的RRT算法对电力杆塔巡检无人机进行路径规划.文献[9]中采用改进的RRT^*算法为无人机生成初始离散路径点并采用凸优化方法进行航迹平滑. ...

Distributed collision avoidance algorithm for multiple unmanned surface vessels based on improved DWA

2023

基于改进A^*-人工势场法的城市物流无人机路径规划

2022

Flight path planning for urban logistics UAV based on improved A^*-artificial potential field method algorithm

2022

Path planning for UAV based on improved PRM

2022

改进蚁群算法的无人机三维路径规划

2023

Three dimensional path planning of UAV based on improved ant colony algorithm

2023

基于改进RRT的无人机电力杆塔巡检路径规划

2018

Path planning of unmanned aircraft inspection for electric towers based on advanced RRT algorithm

2018

考虑安全飞行通道约束的无人机飞行轨迹多目标优化策略

2022

Multi-objective optimization strategy of trajectory planning for unmanned aerial vehicles considering constraints of safe flight corridors

2022

基于双树Quick-RRT算法的移动机器人路径规划

2021

... 上述无人机全局路径规划算法中基于搜索的算法在进行路径规划时需要建立栅格地图,而在三维环境下构建栅格地图十分复杂;基于智能算法的路径规划具有智能算法泛化性差、参数选择困难的缺点;RRT算法无需构建栅格地图,更适合高维度环境下的路径规划^[10],且该算法有概率完备性和计算量小的优点.然而该算法也有致命的缺点:采样的随机性使得算法每次规划出的路径不一致,无法得到最优路径,路径规划速度缓慢.针对该问题,众多学者对该算法展开研究与改进. ...

Path planning of mobile robots based on dual-tree quick-RRT Algorithm

2021

机械臂的位姿分离求逆和改进RRT-connect算法研究

... 为了提高随机树扩展的目的性,文献[11]中在RRT算法的基础上引入启发式扩展的思想,使两棵树不断地向对方交替扩展,这种带有启发式的扩展方法使得树的生长更加贪婪和明确.为了得到一条渐进最优路径,文献[12]中提出RRT^*算法,通过增加重选父节点和重新布线的过程使得规划出的路径接近渐进最优.文献[13]中提出的kino-dynamic RRT^*算法,在文献[12]的基础上改变新节点的扩展函数使得规划出的路径更符合无人机的运动学约束.文献[14]中提出的Informed RRT^*(IRRT^*)算法在文献[12]的基础上引入椭圆采样域限制采样空间,从而减少采样点选取的随机性.文献[15]中提出一种基于RRT^*的离线规划算法,通过连接区域、目标偏差有界采样和路径优化3种策略来提高随机树扩展的速度.文献[16]中在随机树扩展的过程中引入蚁群优化算法,为无人机规划出一条渐进最优的路径.文献[17]中将双向人工势场(Artificial Potential Field, APF)法与双向有偏采样思想相结合,提出BPIB-RRT^*算法,用于三维环境中无人机路径规划.文献[18]中针对IRRT^*算法易出现降级为RRT^*算法的问题,在IRRT^*算法的基础上通过增加A^*算法预规划路径的方式来缩小椭圆采样域的范围.文献[19]中在IRRT^*新节点扩展时改进其steer函数,通过计算最近临近点所受到吸引力和斥力的合力,决定生成新节点的扩展方向. ...

Research on inverse kinematics analysis based on position and attitude separation and improved path planning algorithm of manipulator

Sampling-based algorithms for optimal motion planning

2011

... 算法,在文献[12]的基础上改变新节点的扩展函数使得规划出的路径更符合无人机的运动学约束.文献[14]中提出的Informed RRT^*(IRRT^*)算法在文献[12]的基础上引入椭圆采样域限制采样空间,从而减少采样点选取的随机性.文献[15]中提出一种基于RRT^*的离线规划算法,通过连接区域、目标偏差有界采样和路径优化3种策略来提高随机树扩展的速度.文献[16]中在随机树扩展的过程中引入蚁群优化算法,为无人机规划出一条渐进最优的路径.文献[17]中将双向人工势场(Artificial Potential Field, APF)法与双向有偏采样思想相结合,提出BPIB-RRT^*算法,用于三维环境中无人机路径规划.文献[18]中针对IRRT^*算法易出现降级为RRT^*算法的问题,在IRRT^*算法的基础上通过增加A^*算法预规划路径的方式来缩小椭圆采样域的范围.文献[19]中在IRRT^*新节点扩展时改进其steer函数,通过计算最近临近点所受到吸引力和斥力的合力,决定生成新节点的扩展方向. ...

... )算法在文献[12]的基础上引入椭圆采样域限制采样空间,从而减少采样点选取的随机性.文献[15]中提出一种基于RRT^*的离线规划算法,通过连接区域、目标偏差有界采样和路径优化3种策略来提高随机树扩展的速度.文献[16]中在随机树扩展的过程中引入蚁群优化算法,为无人机规划出一条渐进最优的路径.文献[17]中将双向人工势场(Artificial Potential Field, APF)法与双向有偏采样思想相结合,提出BPIB-RRT^*算法,用于三维环境中无人机路径规划.文献[18]中针对IRRT^*算法易出现降级为RRT^*算法的问题,在IRRT^*算法的基础上通过增加A^*算法预规划路径的方式来缩小椭圆采样域的范围.文献[19]中在IRRT^*新节点扩展时改进其steer函数,通过计算最近临近点所受到吸引力和斥力的合力,决定生成新节点的扩展方向. ...

2022

Informed RRT^*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic

2014

... 超椭球中均匀分布的样本x_ell~u(X_ell)可以通过n维单位球中均匀分布的样本x_ball~u(X_ball)变换生成^[14],即 ...

... IRRT^*算法^[14]是所提基于自适应步长的APF-Informed RRT^*(AAPF-IRRT^*)算法的基础.IRRT^* 算法在RRT^*算法的基础上进行采样域限制,找到第一条可达路径后,路径优化过程在以起始点和目标点作为焦点,路径长度作为长轴长的椭圆域内进行采样.当路径向最优路径逐渐逼近时,采样域也逐渐减小,路径优化速度加快,其过程如图4所示.当迭代次数k为116时,找到第一条路径c_best=904.5.以起点和终点为焦点,c_best为长轴长的椭圆域中进行采样,在找到比c_best路径短的路径后,缩小椭圆域,进行椭圆域的更新如图4(b)所示.当没有障碍物时,随着迭代次数的增加,路径会达到最优路径即起始点和目标点的直线距离,如图4(c)所示. ...

... 二维仿真地图中选取的地图尺寸为960 m×682 m,起始点和终止点分别为(114, 604),(650, 220),黑色区域为障碍物.IRRT^*算法^[14]的固定步长t=10,改进算法中D_obs=0.1,引力势场比例因子K_a=0.062 5.图11采用地图map1,对比图11(a)和11(b)可以看出,APF-IRRT^*路径规划算法不是在整个X_free中随机采样,而是通过APF的吸引朝目标点x_goal方向扩展,直到在障碍物前0.1 m停止扩展;对比图11(c)和11(d)可以看到,改进后的算法由于规划出的初始路径较短,采样域可以迅速限制在更小椭圆域中,加速树的收敛速度.从图12中APF-IRRT^*算法与传统算法路径长度的收敛曲线中可以看出,改进后算法的路径长度较短,能在更少迭代次数下收敛到渐进最优路径.尤其是在狭窄通道map2中,改进后的算法在向终点扩展的过程中更有目标性,速度更快,如图13所示. ...

Optimal path planning in cluttered environment using RRT^*-AB

2018

Obstacle avoidance path planning for UAV based on improved RRT algorithm

2022

Biased sampling potentially guided intelligent bidirectional RRT algorithm for UAV path planning in 3D environment

2019

2022

APF-IRRT^*: An improved informed rapidly-exploring random trees-star algorithm by introducing artificial potential field method for mobile robot path planning

2022

路径规划算法的研究与发展

2017

... 给出无人机路径规划中所需的相关概念和相关定义.令X⊆Rⁿ为规划问题的状态空间^[20],X_obs⊆X为碰撞空间,X_free=X\X_obs为自由空间,x_start∈X_free为初始状态,x_goal∈X_free为期望的最终状态,σ: [0,1]→X_free为路径的序列状态且是所有重要路径的合集,Σ为所有可行路径的集合. ...

Research and development of path planning algorithm

2017

Hybrid path planning based on safe A^* algorithm and adaptive window approach for mobile robot in large-scale dynamic environment

2020

... 最优路径规划^[21]问题则是对路径σ^*的搜索,最优路径使得在自由空间X_free中规划从初始点x_start到目标点x_goal时的成本函数c: Σ→R^*最小,表示如下: ...

复杂低空物流无人机路径规划

2020

... 针对规划出的新节点无人机能否执行的问题,进行最大转弯角与最大爬升角的约束分析.最大转弯角对水平面内运动进行限制,约束无人机从当前路径点到下一路径点只能改变一定范围内的偏航角,其本质上是限制最小转弯半径^[22].最大爬升角对无人机的升降运动进行限制,约束无人机从当前路径爬升至下一路径点时只能改变一定范围内的俯仰角.假设无人机运动飞行时的相邻两路径点坐标为p_i(x_i, y_i, z_i)和p_i₊₁(x_i₊₁, y_i₊₁, z_i₊₁),进行如下讨论. ...

Path planning for logistics UAV in complex low-altitude airspace

2020

基于人工势场与IB-LBM的机器蛇水中2D避障控制算法

2018

... 为了解决以上算法中存在的问题,提出一种基于APF法^[23]的IRRT^*(APF-IRRT^*)路径规划算法.APF法使用梯度下降^[24]的规划方法最小化人工势能.目标点x_goal对无人机x产生吸引势能U_att,障碍物对无人机产生排斥势能U_rep,合势能U=U_att+U_rep,无人机朝着目标点吸引而障碍物排斥的合力方向F前进,F即合势能的负梯度F=-▽U.无人机受到的吸引力势能如下: ...

The 2D aquatic obstacle avoidance control algorithm of the snake-like robot based on artificial potential field and IB-LBM

2018

Trajectory optimization of pickup manipulator in obstacle environment based on improved artificial potential field method

2020

一种基于动态步长的AAPF-RRT^*移动机器人路径规划新算法

2021

A novel path planning method of mobile robot based on AAPF-RRT^* with dynamic step

2021

〈

〉