自适应动态周期下的移动水声网络自定位算法

doi:10.16183/j.cnki.jsjtu.2021.193

自适应动态周期下的移动水声网络自定位算法

高婧洁^,¹, 王威¹, 申晓红²

1.长安大学信息工程学院,西安 710064

2.西北工业大学航海学院,西安 710072

A Self-Localization Algorithm with Adaptive and Dynamic Observation Period for Mobile Underwater Acoustic Networks

GAO Jingjie^,¹, WANG Wei¹, SHEN Xiaohong²

1. School of Information Engineering, Chang’an University, Xi’an 710064, China

2. School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China

责任编辑: 王一凡

收稿日期: 2021-06-8

基金资助:

国家自然科学基金(61901057)
国家自然科学基金(61871059)

Received: 2021-06-8

作者简介 About authors

高婧洁(1988-),女,陕西省西安市人,讲师,主要从事水声网络通信与定位研究;E-mail:gaojingj@chd.edu.cn.

摘要

针对移动水声网络中定位精度与通信开销之间的矛盾,提出一种自适应动态周期下的移动水声网络自定位算法.该算法根据系统状态估计与观测采样之间的残差,设计自适应的动态周期选择机制和非均匀的动态更新网络定位周期,进而实现非均匀动态周期下的移动水声网络高精度预测定位.该算法无需大量通信观测即可实现移动节点位置的实时跟踪,达到了定位精度与通信开销间的平衡.仿真结果表明,所提算法既保证了网络的定位估计精度,又减小了冗余定位通信开销,实现了有限通信开销下的高精度定位,更适用于精度要求高且通信带宽有限的水下环境中.

关键词： 移动水声网络; 自定位; 自适应动态周期

Abstract

In order to resolve the conflicts between the communication traffic and the localization accuracy, a self-localization algorithm with adaptive and dynamic observation period for mobile underwater acoustic networks (MUANs) was proposed to improve the localization performance. First, an adaptive and dynamic observation period selection scheme was designed, which could generate a non-uniform observation period vector according to the residual change. Then, based on the non-uniform observation period vector, a self-localization algorithm was proposed, which could precisely predict the trajectory of each mobile node in the network. The simulation results show that the proposed algorithm, which could balance the tradeoff between the localization accuracy and the communication cost, is more suitable for the underwater environment.

Keywords： mobile underwater acoustic networks (MUANs); self-localization; adaptive and dynamic observation period

PDF (1288KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

高婧洁, 王威, 申晓红. 自适应动态周期下的移动水声网络自定位算法[J]. 上海交通大学学报, 2022, 56(12): 1658-1665 doi:10.16183/j.cnki.jsjtu.2021.193

GAO Jingjie, WANG Wei, SHEN Xiaohong. A Self-Localization Algorithm with Adaptive and Dynamic Observation Period for Mobile Underwater Acoustic Networks[J]. Journal of Shanghai Jiaotong University, 2022, 56(12): 1658-1665 doi:10.16183/j.cnki.jsjtu.2021.193

随着水下自主航行器(AUV)研究的进展,由AUV协调运作组成的移动水声网络(MUANs)逐渐成为研究的热点.相较于传统的水声网络,移动水声网络具有更广的探测范围和更高的智能性以及更强的机动性,被广泛地应用于各种水下工程、海洋环境监测、水下数据采集及海洋军事等领域,受到越来越多国家与学者的关注^[1⇓-3].

移动水声网络在实现环境数据采集、处理及分析时,网络内各节点的位置信息是不可或缺的先验信息之一,因此针对移动水声网络自定位技术的研究成为了网络研究的基础.目前常见的网络自定位算法分为基于测距的定位算法与基于非测距的定位算法.其中基于非测距的定位算法无需测量节点间的距离信息,仅依据网络间的通信连通度即可实现节点的位置估计,因此该类算法计算开销小、硬件成本低,但网络的定位精度也较低,仅能应用于对精度要求不高的定位环境中^[4].基于测距的定位算法主要利用到达时间(TOA)、到达时间差(TDOA)和到达角度(DOA)等观测信息进行节点位置估计^[5].基于二阶时间差(STDOA)定位算法可用于解决信号周期以及时间同步未知情况下的水声定位问题^[6-7].基于测距的定位算法精度较高,但对于移动水声网络,网络拓扑的实时变化对定位精度的影响较大,因此需要开展变化拓扑下的网络定位算法研究.针对移动水声网络的自定位算法主要包括考虑运动模式的自定位算法(MASL)和基于最大后验概率的定位算法(MAP)等,该类算法需要预知网络拓扑变化先验信息.利用惯导系统(INS)也可直接估计移动节点动态位置,但该方法存在较大的误差累积.目前常使用基于滤波的移动水声网络自定位算法,该类算法根据网络节点的运动模型与观测模型实现节点位置的实时预测更新^[8⇓-10].然而滤波算法为了提高定位精度需要引入大量的观测信息,使得算法的通信开销较大;若降低定位通信开销则直接影响了网络的定位精度,因此存在网络定位精度与通信开销间的矛盾.

本文针对移动水声网络自定位精度与通信开销之间的矛盾,提出了一种自适应动态周期下的移动水声网络自定位算法.该算法可根据系统状态估计与观测采样之间的残差,自适应的动态更新网络定位周期,实现非均匀周期下的移动节点预测定位,保证定位精度的同时降低了通信开销,平衡了通信开销与定位精度之间的矛盾,更适用于精度要求高且通信带宽有限的水下网络环境.

1 移动水声网络自定位系统模型

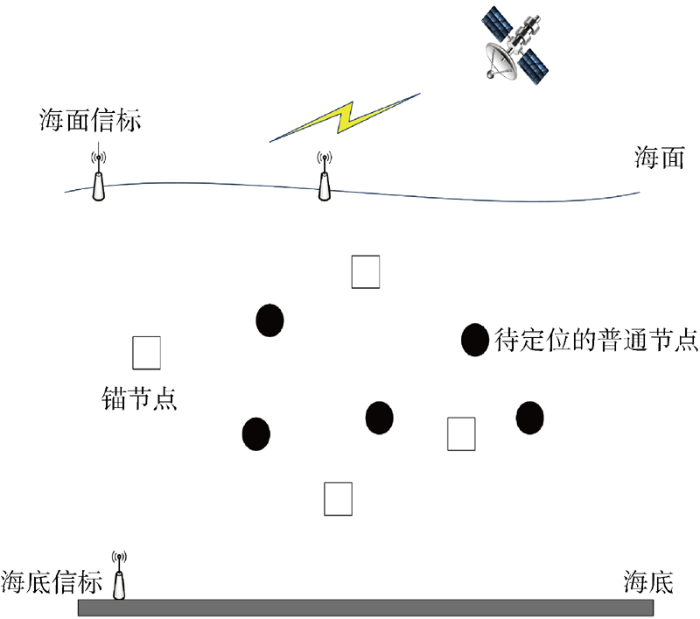
移动水声网络自定位系统通常采用协同定位方式实现全网的拓扑位置发现.网络自定位系统中的节点类型主要由两部分组成:锚节点与待定位的普通节点.

(1) 锚节点位置坐标已知,且具有更强的通信能力与更广的传输范围.锚节点可通过与预先布置在海底或海面的信标通信,或通过浮出水面与全球定位系统(GPS)直接通信来获取其自身的位置信息,从而辅助待定位的普通节点实现位置估计.

(2) 待定位的普通节点位置信息未知,需要通过与锚节点进行信息交互,从而实现其位置信息的预测与更新.

根据上述分析,移动水声网络自定位系统的模型结构如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 移动水声网络自定位系统模型

Fig.1 Self-localization system model for MUANs

2 自适应动态周期下的移动水声网络自定位算法

为了解决移动水声网络通信开销和定位精度之间的矛盾,提出一种自适应动态周期下的移动水声网络自定位算法,实现定位精度与通信开销之间的平衡.

2.1 移动水声网络节点的初始位置估计

假设移动水声网络由M个位置信息已知的锚节点与N个待定位的普通节点组成,其中k时刻下锚节点的位置坐标可表示为 $[x_{i}^{k} y_{i}^{k} z_{i}^{k}]^{T}, 1 \leq i \leq M;$ k时刻下普通节点的位置坐标可表示为 $[x_{j}^{k} y_{j}^{k} z_{j}^{k}]^{T}, M + 1 \leq j \leq M + N .$ 假设普通节点j在初始时刻与M个锚节点间的距离分别为 $d_{j 1}, d_{j 2}, \dots, d_{j M},$ 则采用最小二乘法可得节点j的初始位置估计,即

(1)

\begin{matrix} [x_{j}^{0} y_{j}^{0} z_{j}^{0}]^{T} = (a^{T} {a)}^{- 1} a^{T} b \end{matrix}

式中:

\begin{array}{l} \begin{matrix} a = [\begin{array}{l} 2 (x_{1}^{0} - x_{M}^{0}) & 2 (y_{1}^{0} - y_{M}^{0}) & 2 (z_{1}^{0} - z_{M}^{0}) \\ ︙ & ︙ & ︙ \\ 2 (x_{M - 1}^{0} - x_{M}^{0}) & 2 (y_{M - 1}^{0} - y_{M}^{0}) & 2 (z_{M - 1}^{0} - z_{M}^{0}) \end{array}] \end{matrix} \\ b = [\begin{array}{l} (x_{1}^{0})^{2} - (x_{M}^{0})^{2} + (y_{1}^{0})^{2} - (y_{M}^{0})^{2} + (z_{1}^{0})^{2} - (z_{M}^{0})^{2} + d_{j M}^{2} - d_{j 1}^{2} \\ ︙ \\ (x_{M - 1}^{0})^{2} - (x_{M}^{0})^{2} + (y_{M - 1}^{0})^{2} - (y_{M}^{0})^{2} + (z_{M - 1}^{0})^{2} - (z_{M}^{0})^{2} + d_{j M}^{2} - d_{j (M - 1)}^{2} \end{array}] \end{array}

2.2 自适应动态周期下的移动节点定位预测算法

假设移动水声网络中任意普通节点均可与M个锚节点进行定位通信,则k-1时刻普通节点j与M个锚节点的联合定位周期可表示为 $T_{j}^{k - 1} = [T_{1, j}^{k - 1} T_{2, j}^{k - 1} \dots T_{M, j}^{k - 1}]$ ,其中 $T_{i, j}^{k - 1} 表示普通节点 j 与锚节点 i$ 间的定位通信周期.

根据定位周期 $T_{j}^{k - 1}$ 将节点的运动模型表示为

(2)

X_{j}^{k} = F_{j}^{k - 1} X_{j}^{k - 1} + W_{j}^{k}

(3)

\begin{array}{l} X_{j}^{k} = \\ {[\begin{array}{l} x_{j}^{k} & {\overset{\cdot}{x}}_{j}^{k} & {\ddot{x}}_{j}^{k} & y_{j}^{k} & {\overset{\cdot}{y}}_{j}^{k} & {\ddot{y}}_{j}^{k} & z_{j}^{k} & {\overset{\cdot}{z}}_{j}^{k} & {\ddot{z}}_{j}^{k} \end{array}]}^{T} \end{array}

(4)

F_{j}^{k - 1} = (\begin{array}{l} 1 & T_{j}^{k - 1} & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & T_{j}^{k - 1} & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & T_{j}^{k - 1} \\ 0 & 0 & 0 & 0 & 0 & 1 \end{array})

式中: $X_{j}^{k}$ 表示在k时刻普通节点j的系统状态向量; $W_{j}^{k}$ 表示k时刻普通节点j的系统过程噪声,且 $E [W_{j}^{k} (W_{j}^{k})^{T}] = Q_{j}^{k} .$

采用距离观测模型,则k时刻下普通节点j与锚节点之间的观测距离可表示为

(5)

Z_{j}^{k} = h^{k} (X_{j}^{k}) = {[\begin{array}{l} Z_{1, j}^{k} & Z_{2, j}^{k} & \dots & Z_{M, j}^{k} \end{array}]}^{T}

(6)

\begin{array}{l} Z_{i, j}^{k} = \sqrt{(x_{i}^{k} - x_{j}^{k})^{2} + (y_{i}^{k} - y_{j}^{k})^{2} + (z_{i}^{k} - z_{j}^{k})^{2}} + \\ μ_{i, j}^{k} \end{array}

式中: $μ_{i, j}^{k} 表示距离观测误差, 且 E [μ_{i, j}^{k} (μ_{i, j}^{k})^{T}] = R_{i, j}^{k} .$

由于系统观测的非线性特征,本文基于扩展卡尔曼滤波实现移动水声网络节点的位置预测与更新.

状态预测:

(7)

\begin{matrix} \begin{array}{l} X_{j}^{k | k - 1} = F_{j}^{k - 1} X_{j}^{k - 1} \\ P_{j}^{k | k - 1} = F_{j}^{k} P_{j}^{k - 1} (F_{j}^{k})^{T} + Q_{j}^{k} \end{array}\} \end{matrix}

式中: $X_{j}^{k | k - 1} 为状态预测矩阵; P_{j}^{k | k - 1}$ 为协方差预测矩阵.

状态更新:

(8)

\begin{array}{l} Z_{j}^{k | k - 1} = h (X_{j}^{k | k - 1}) \\ K_{j}^{k} = P_{j}^{k | k - 1} (H_{j}^{k})^{T} (H_{j}^{k} P_{j}^{k | k - 1} (H_{j}^{k})^{T} + R_{j}^{k})^{T} \\ X_{j}^{k} = X_{j}^{k | k - 1} + K_{j}^{k} (Z_{j}^{k} - Z_{j}^{k | k - 1}) \\ P_{j}^{k} = P_{j}^{k | k - 1} - K_{j}^{k} H_{j}^{k} P_{j}^{k | k - 1} \end{array}\}

式中: $H_{j}^{k} = {\frac{\partial h}{\partial x}|}_{X_{j}^{k | k - 1}}; Z_{j}^{k | k - 1}$ 为观测矩阵; $K_{j}^{k}$ 为k时刻的滤波增益; $X_{j}^{k}$ 为k时刻的状态更新矩阵; $P_{j}^{k} 为 k$ 时刻的协方差更新矩阵.

根据式(7)~(8)可得定位系统残差 $ε_{j}^{k},$ 即在k时刻普通节点j的观测值 $Z_{j}^{k}$ 与预测值 $Z_{j}^{k | k - 1}$ 之间的差值:

(9)

\begin{matrix} ε_{j}^{k} = [\begin{array}{l} ε_{1, j}^{k} & ε_{2, j}^{k} & \dots & ε_{M, j}^{k} \end{array}] = Z_{j}^{k} - Z_{j}^{k | k - 1} \end{matrix}

2.2.1 自适应动态周期选择机制

根据式(9)所得的定位系统残差 $ε_{j}^{k},$ 设计一种自适应动态周期选择机制,该机制通过引入周期因子ω来描述定位周期在不同时刻的变化情况,进而实现定位周期的动态选择.

假设在k时刻普通节点j与锚节点i间的周期因子为 $ω_{i, j}^{k},$ 设计关于周期因子 $ω_{i, j}^{k}$ 的动态周期因子函数.动态周期因子的选择原则为:若系统残差较大,则周期因子选取较小的值,以提高定位精度;若系统残差较小,则周期因子选取较大的值,以降低通信开销.基于此,以双正切函数为基础,设计动态周期因子函数,将系统残差与周期因子相结合.通过引入周期因子参数q与α来控制动态周期因子的变化范围与变化趋势,以满足定位系统的需求.动态周期因子函数为

(10)

\begin{array}{l} \begin{matrix} ω_{i, j}^{k} = 1 + \frac{q α}{α - 1 + e x p |ε_{i, j}^{k}|} \end{matrix} \\ 1 \leq i \leq M, M + 1 \leq j \leq M + N \end{array}

q与α应根据不同系统关于定位精度与通信开销的要求进行相应设置.为了保证周期因子仅在系统残差较大时变化率较大,参数q与α的选择需要满足 $α ≫ q,$ 以达到系统要求.

假设系统定位周期的基本单位为t₀,则依据式(10),将所得的动态周期因子函数与定位周期相关联,得到自适应动态周期选择机制:

(11)

\begin{matrix} T_{i, j}^{k + 1} = \{\begin{array}{l} t_{0}, & k = 0 \\ [ω_{i, j}^{k}] t_{0}, & k \neq 0 \end{array} \end{matrix}

式中:[·]表示取整.

综上,本文所设计的自适应动态周期选择机制为

(1) 设置基本周期单元 $t_{0}$ 以及周期因子参数q与α.

(2)初始时刻周期为 $T_{i, j}^{1} = t_{0}, 1 \leq i \leq M, M + 1 \leq j \leq M + N .$

(3)计算系统残差 $ε_{i, j}^{k} .$

(4)计算动态周期因子 $ω_{i, j}^{k} = 1 + \frac{q α}{α - 1 + e x p |ε_{i, j}^{k}|} .$

(5)获得任意时刻下的动态周期变量 $T_{i, j}^{k + 1} = [ω_{i, j}^{k}] t_{0} .$

2.2.2 基于非均匀周期的移动节点预测定位

根据所设计的自适应动态周期选择机制,可以得到网内任意普通节点j在n次观测采样下的非均匀周期变量:

(12)

\begin{array}{l} T_{j} = [\begin{array}{l} T_{j}^{1} & T_{j}^{2} & \dots & T_{j}^{k} & T_{j}^{k + 1} & \dots & T_{j}^{n - 1} & T_{j}^{n} \end{array}] \end{array}

式中:

T_{j}^{k} = [\begin{array}{l} T_{1, j}^{k} & T_{2, j}^{k} & \dots & T_{M, j}^{k} \end{array}], 1 \leq k \leq n .

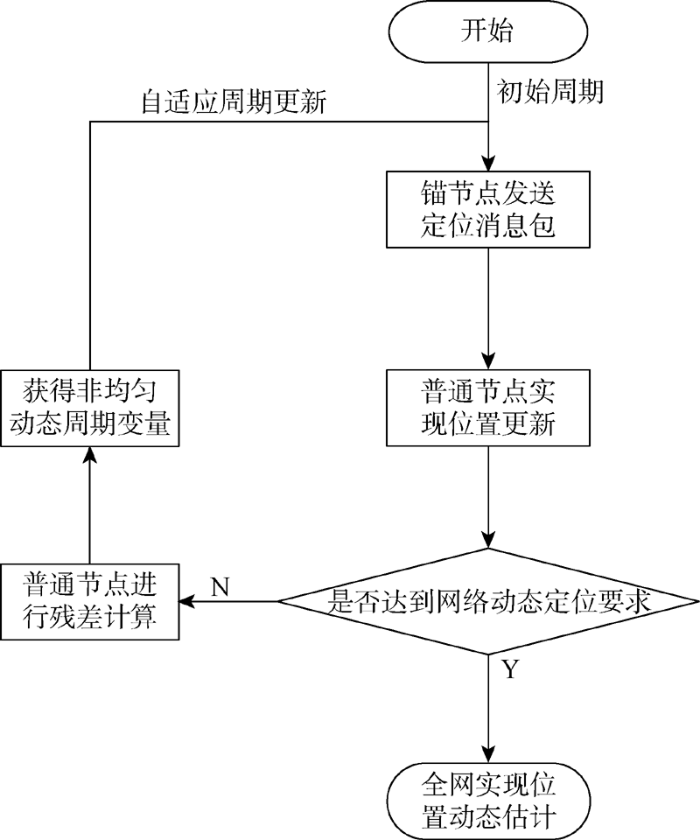
根据该非均匀周期变量 $T_{j},$ 利用式(7)~(8),实现非均匀周期下的移动节点预测定位,进而得到自适应动态周期下的移动水声网络自定位结果.

本文提出的自适应动态周期下的移动水声网络自定位算法可根据系统状态估计与观测采样之间的残差,自适应的更新观测周期,在动态非均匀观测周期下实现网络高精度定位,平衡了定位精度与通信开销间的矛盾.图2表示了所提移动水声网络自定位算法的流程图.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 移动水声网络自定位算法的流程图

Fig.2 Flow diagram of proposed self-localization algorithm for MUANs

3 仿真性能分析

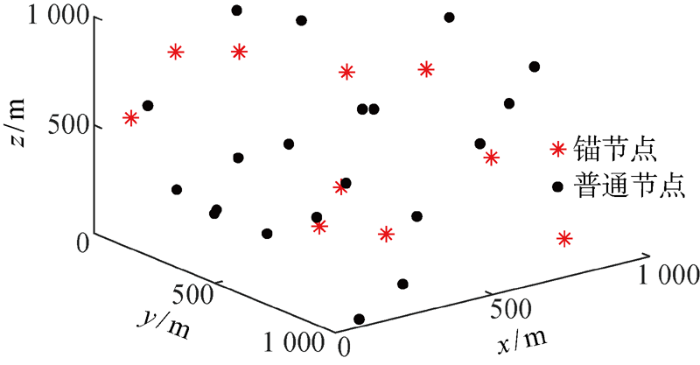
在一定水域内随机布放M=10个锚节点和N=20个普通节点,组成三维的移动水声网络,其中锚节点位置已知.仿真网络的初始拓扑结构如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 网络初始分布的拓扑结构图

Fig.3 Initial topology of MUANs

3.1 周期因子函数的参数选择

讨论与分析当系统选择不同参数α和q时,定位系统残差(ε)与周期因子(ω)之间的关系,并据此为周期因子函数选择合适的参数α和q来保证定位精度与通信开销间的平衡.

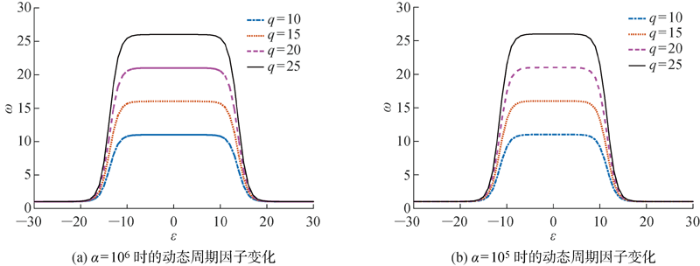
(1) 固定参数α,比较不同q值对周期因子ω的影响.

若参数α分别固定为 $α = 10^{6} 和 α = 10^{5}$ 保持不变,参数q分别为10、15、20和25时,定位系统残差ε与周期因子ω之间的关系如图4所示.由图4可得,若参数α保持不变,增大参数q可以显著提高相同定位系统残差下的周期因子值,而周期因子的大小将直接影响定位周期的扩展倍数,并改变非均匀周期的跨度.因此在相同参数α下,可以通过选择不同的参数q来获得相同定位残差下不同跨度的非均匀周期变量.若参数q较大,则非均匀周期变量的周期跨度会增大,大跨度的非均匀周期可有效减小定位所需的通信开销,但同时也会使得定位精度存在一定程度的降低;若参数q较小,则非均匀周期变量的跨度也相应减小,小跨度的非均匀周期可以提高定位精度,但同时引入了大量的通信开销.因此可以通过改变非均匀周期变量的扩展跨度,平衡非均匀周期对定位精度与通信开销的影响.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 参数α不变,选取不同q值下的动态周期因子函数变化曲线

Fig.4 Changing curves of proposed dynamic function for periodic factor at a fixed α and different q values

(2) 固定参数q,比较不同α值对周期因子ω的影响.

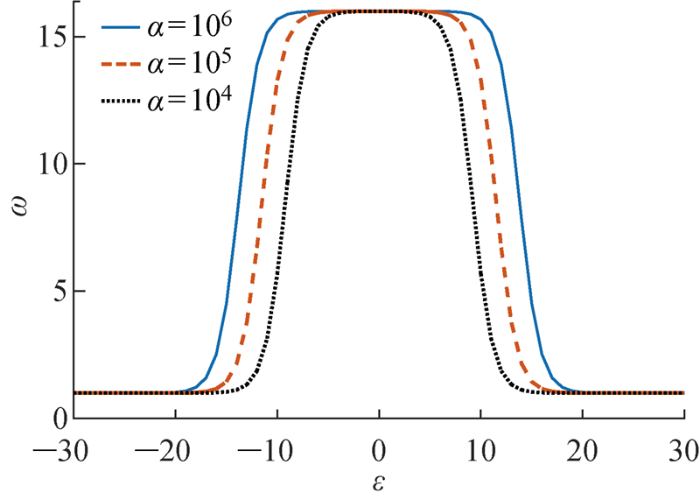
若 $q 值固定为 15, 而 α 分别取 α = 10^{4}, 10^{5}, 10^{6}$ 时,定位系统残差ε与周期因子ω之间的关系如图5所示.由图5可得,若保持q值不变,随着参数α的增加,周期因子的最大值基本不变,但周期因子函数会发生不同程度的展宽;并且参数α越大,周期因子函数最大斜率所对应的系统残差也越大.因此在相同参数q下,可以通过选择参数α来改变不同残差下定位系统的周期因子变化率.若α值较大,则系统在较大残差时的周期因子变化率更大,使得定位通信开销有所减小,但同时也降低了定位精度;若α值较小,则系统在较小残差时的周期因子变化率更大,使得定位精度有所提高,但也增大了定位通信开销.因此需要选择适当的α值来调节周期因子在不同系统残差下的变化幅度,从而平衡非均匀周期对定位精度与通信开销的影响.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 参数q=15不变,选取不同α值下的动态周期因子函数变化曲线

Fig.5 Changing curves of proposed dynamic function for periodic factor at q=15 and different α values

根据上述分析可知,在实际应用中,需要根据定位系统的需求对α和q值进行综合考虑,选择合适的α和q值,获得适当的动态周期因子扩展跨度与变化率,保证网络定位精度与通信开销间的平衡.在本文中,分别选取为 $α = 10^{6}, q = 15 .$

3.2 定位精度分析

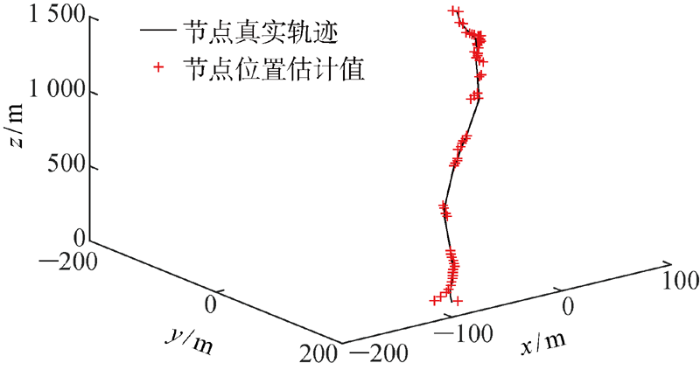
网内任一普通节点在一定时间间隔内的移动轨迹与其实时定位结果如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 网内任一普通节点在一定时间间隔内的移动轨迹与定位估计结果

Fig.6 Trajectory and estimation results of one mobile node in the network within a certain time

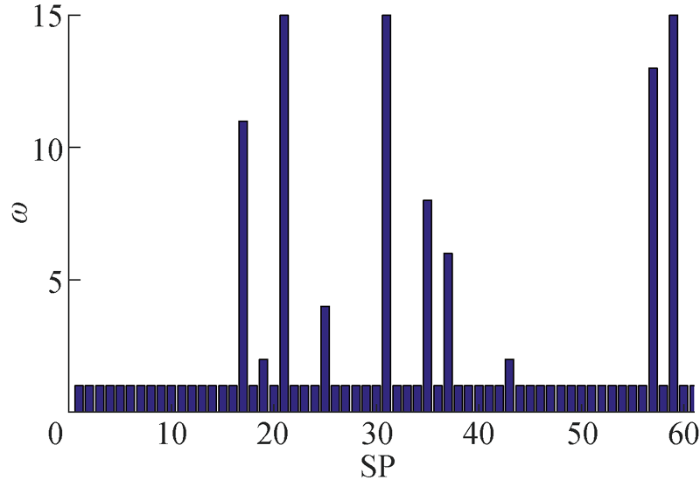
各采样点处的动态周期因子变化结果如图7所示.根据各采样点(SP)处的动态周期因子ω,可以获得移动节点的非均匀定位周期变量.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 各采样点处的动态周期因子变化

Fig.7 Variation of dynamic periodic factor at each sampling point

以网络节点在k时刻的定位状态估计协方差来表示系统定位精度的统计分析,其中节点j在k时刻的定位状态估计协方差为

(13)

\begin{array}{l} P_{j}^{k} = E {[{\overset{⌒}{X}}_{j}^{k} - X_{j}^{k}] [{\overset{⌒}{X}}_{j}^{k} - X_{j}^{k}]^{T}} = \\ (I - K_{j}^{k} H_{j}^{k}) P_{j}^{k | k - 1} = \\ (I - K_{j}^{k} H_{j}^{k}) (F_{j}^{k} P_{j}^{k - 1} (F_{j}^{k})^{T} + Q_{j}^{k}) \end{array}

式中: ${\overset{⌒}{X}}_{j}^{k}$ 为普通节点j的在k时刻的位置估计值;X_j^k 为普通节点j的在k时刻的位置真值; $K_{j}^{k}, H_{j}^{k}, F_{j}^{k}, Q_{j}^{k}$ 可根据式(7)~(8)的滤波算法得到.

由式(13)及式(7)~(8)可知,网络节点在k时刻的定位状态估计协方差不仅与上一时刻估计误差有关,还与定位周期的选择、观测噪声和过程噪声的分布有关.在噪声分布一定的情况下,由于所提算法可根据系统状态自适应的动态更新定位周期,因此可在有限的通信开销下保证一定的定位精度.

将本文提出的自适应动态周期下的移动水声网络自定位预测算法与现有的滤波定位算法相比较.由于现有滤波定位算法均是基于固定采样周期进行的,即周期因子在定位过程中保持不变,因此分别选择固定的周期因子ω=1和ω=5进行滤波定位.网络分布仍由10个锚节点与20个普通节点组成,1 000 次蒙特卡洛实验后的统计结果如图8~10所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

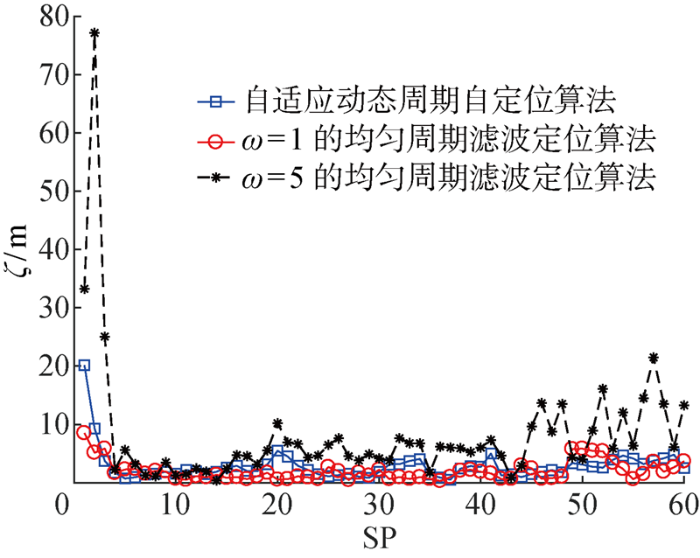
图8 不同采样点下的位置估计偏差比较

Fig.8 Comparison of position estimates at different sampling points

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同测距误差方差下的位置估计偏差比较

Fig.9 Comparison of position estimates at different range error variances

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同锚节点密度下的位置估计偏差比较

Fig.10 Comparison of position estimates at different anchor node densities

当测距误差方差为3,不同采样点下各方法的位置估计偏差 $(ζ)$ 比较如图8所示.由图8可得,本文提出算法的定位误差与最小周期ω=1时的滤波定位算法误差相差不大,且明显小于ω=5时的滤波定位算法.

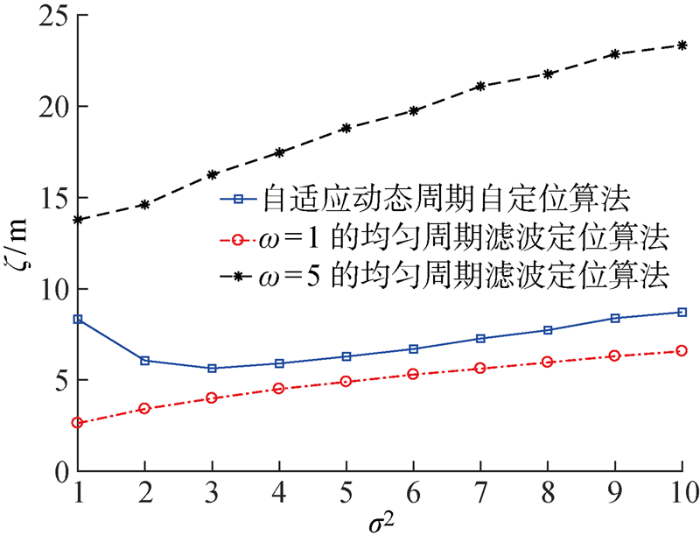
若网络结构保持不变,而测距误差方差由1增加至10,则不同测距误差方差(σ²)下的位置估计偏差比较如图9所示.

由图9可得,随着测距误差的增加,现有滤波定位算法的位置估计误差也随之增加.但本文提出的自适应动态周期定位算法在测距误差方差较小时,随着测距误差的增加,位置估计误差有一定程度下降.这是由于当测距误差方差较小时,定位周期选择的跨度会较大;而周期选择的跨度越大,相应周期下的误差累积越大.因此当测距误差较小时,周期选择的变化对定位精度的影响更大,从而导致位置估计误差曲线有一定程度的下降.但总体比较,本文提出算法误差略大于最小周期ω=1时的滤波定位算法,但远小于ω=5时的滤波定位算法.

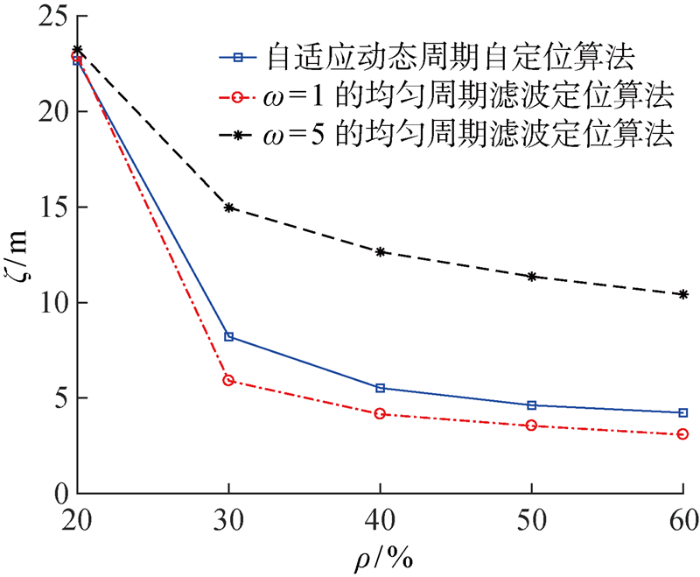
若保持网络节点总数不变,改变网络中的锚节点密度,分析锚节点密度对网络定位精度的影响.锚节点密度定义为

(14)

\begin{matrix} ρ = \frac{M}{M + N} \end{matrix}

仿真实验假设网络中节点总数为30,锚节点密度由20%增加至60%,则锚节点密度与位置估计误差间的关系如图10所示.由图10可得,随着锚节点密度的增加,定位系统内可使用的有效观测越多,因此基于上述各算法的网络位置估计误差均有显著的降低.但相同条件下,本文提出算法误差仍然略大于最小周期ω=1时的滤波定位算法,且远小于ω=5时的滤波定位算法.

通过图8~10的仿真比较可得,在定位精度方面,本文提出的算法接近最小周期ω=1时的滤波定位算法,且远小于ω=5时的滤波定位算法,满足一定的网络定位精度要求.

3.3 通信开销分析

针对所提出的自适应动态周期下的移动水声网络自定位算法进行通信开销分析.通信开销根据定位算法流程和定位过程中的消息报文数据大小来进行统计分析.因此首先根据算法的实现过程,设计网络定位的消息报文格式如图11~13所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 定位消息报文格式

Fig.11 Message format for localization procedure

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 定位消息报文

Fig.12 Message for localization

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 周期消息报文

Fig.13 Message for localization period

图11中,发送端ID为消息发送节点的ID (容量为lb(M+N),M+N为网络中节点总数);消息类型分为定位消息报文与周期消息报文(1 bit),两种不同类型消息对应的数据报文格式分别如下.

(1) 定位消息报文.图12中:时间戳表示发送消息的时刻(28 bit);位置表示消息发送节点的位置信息(30 bit).

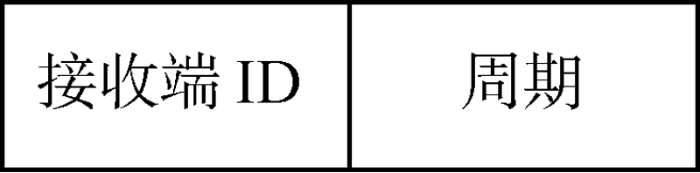
(2) 周期消息报文.图13中:接收端ID为消息接收节点的ID(容量为lb M);周期表示动态周期变量的周期因子ω(容量为lb ω).

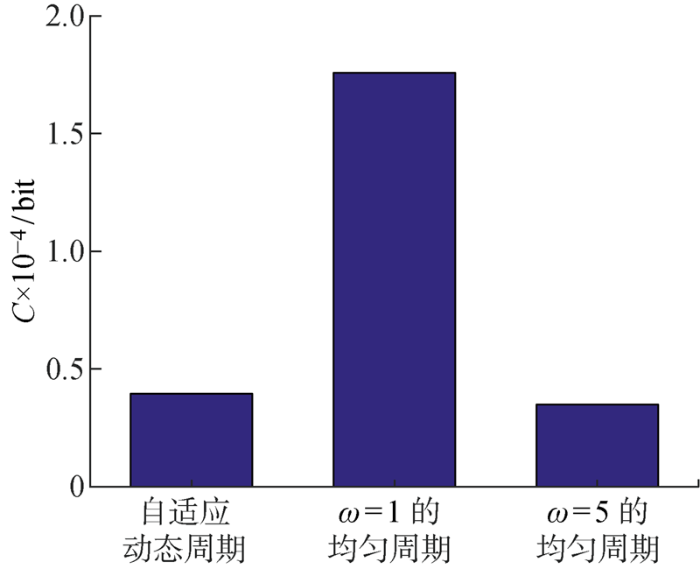
所提定位系统按照设计的消息报文格式和定位流程发送定位所需数据,实现节点间的通信交互,并基于此完成网络的定位过程,获得通信开销统计量(C).将该通信开销与固定采样周期下滤波定位算法的通信开销相比较,结果如图14所示.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 通信开销比较

Fig.14 Comparison of communication traffic

由图14可知,所提算法在通信开销方面明显小于最小周期ω=1时的滤波定位算法,且与ω=5时的滤波定位算法接近,充分体现了该算法在保证定位精度的同时其通信开销方面的优势.

3.4 综合性能比较

由于移动水声网络定位系统需要在保证定位精度的同时降低通信开销,以平衡通信开销与定位精度之间的矛盾.所以将定位精度与通信开销两大性能参数进行综合比较,反映不同算法的综合性能.

将综合定位性能δ表示为归一化位置估计误差与归一化通信开销之和,以统一不同性能指标间的差异,即

(15)

\begin{matrix} δ = \frac{ζ_{l}}{m a x E} + \frac{c_{l}}{m a x C} \end{matrix}

式中: $ζ_{l} 和 c_{l} 分别表示第 l$ 种算法的位置估计误差和通信开销;max E和max C分别表示所有算法联合组成的位置估计误差向量和通信开销向量的最大值.

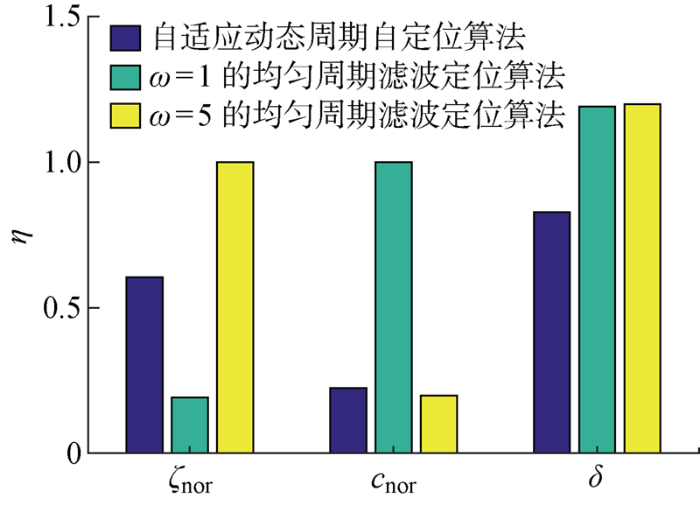
综合定位性能的比较结果如图15所示,图中η表示性能指数,ζ_nor和c_nor分别表示各算法的归一化位置估计误差与归一化通信开销性能结果.由图15可得,与前文分析一致,由于所提算法采用自适应的动态周期进行预测定位,可在满足较高定位精度的同时适当减小定位信息交互频率,降低通信开销,有效平衡了网络自定位所需通信开销与网络自定位精度之间的矛盾,具有更优的综合定位性能评价,更适用于通信开销有限且精度要求高的水声网络环境中.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 定位性能综合比较

Fig.15 Comprehensive comparison of positioning performance

4 结语

针对移动水声网络自定位中通信开销和定位精度之间的矛盾,提出一种自适应动态周期下的移动水声网络自定位算法.该算法首先根据系统状态估计与观测采样之间的残差变化,设计自适应的动态周期选择机制,获得非均匀的定位周期变量.在此基础上,提出基于非均匀定位周期的移动节点定位预测算法,实现了非均匀观测下的节点位置实时跟踪,达到了定位精度与通信开销间的平衡.通过性能仿真实验可得,所提算法既保证了移动水声网络的定位估计精度,又减小了冗余通信开销,实现了有限通信开销下的高精度网络定位,更适用于精度要求高且通信带宽有限的水下环境中.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

冯艺璇, 肖东, 陈岩, 等.

无精准同步的小规模水声网络节点相对自定位

[J]. 声学学报, 2020, 45(4): 486-496.

[本文引用: 1]

FENG

Yixuan

, XIAO

Dong

, CHEN

Yan

, et al.

Relative self-positioning method for small-scale underwater acoustic network nodes without precise synchronization

[J]. ACTA ACUSTICA, 2020, 45(4): 486-496.

[本文引用: 1]

[2]

方国灿.

水声传感网络中水下移动节点的分布式定位方法研究[D]. 杭州: 浙江大学, 2019.

[本文引用: 1]

FANG

Guocan

Distributed positioning method of mobile nodes in underwater acoustic networks[D]. Hangzhou: Zhejiang University, 2019.

[本文引用: 1]

[3]

TOKY

, SINGH

R P

, DAS

Localization schemes for underwater acoustic sensor networks—A review

[J]. Ad Hoc Networks, 2020, 37: 1-18.

DOI:10.1016/j.adhoc.2015.10.001 URL [本文引用: 1]

[4]

SAEED

, CELIK

, Al

NAFFOURI T Y

, et al.

Underwater optical wireless communications, networking, and localization: A survey

[J]. Ad Hoc Networks, 2018: 32-41.

[本文引用: 1]

[5]

JIA

, HO

K C

, WANG

Localization of a moving object with sensors in motion by time delays and doppler shifts

[J]. IEEE Transactions on Signal Processing, 2020, 68: 5824-5841.

DOI:10.1109/TSP.2020.3023972 URL [本文引用: 1]

[6]

SUN

, QIN

, HAO

Underwater acoustic localization of the black box based on generalized second-order time difference of arrival (GSTDOA)

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 99: 1-11.

[本文引用: 1]

[7]

SUN

, ZHANG

, ZHENG

Underwater Acoustical localization of the black box utilizing single autonomous underwater vehicle based on the second-order time difference of arrival

[J]. IEEE Journal of Oceanic Engineering, 2020, 45(4): 1268-1279.

DOI:10.1109/JOE.2019.2950954 URL [本文引用: 1]

[8]

CHOI

, SHIN

, YI

Information source localization with protector diffusion in networks

[J]. Journal of Communications and Networks, 2019, 21(2): 136-147.

DOI:10.1109/JCN.2019.000020 [本文引用: 1]

Recently, the problem of detecting the information source in a network has been much studied, where it has been shown that the detection probability cannot be beyond 31% even for regular trees if the number of infected nodes is sufficiently large. In this paper, we study the impact of an anti-information spreading on the original information source detection. We first show a negative result: the anti-information diffusion does not increase the detection probability under Maximum-Likelihood-Estimator (MLE) when the number of infected nodes are sufficiently large by passive diffusion that the anti-information starts to be spread by a special node, called the protector, after is reached by the original information. We next consider the case when the distance between the information source and the protector follows a certain type of distribution, but its parameter is hidden. Then, we propose the following learning algorithm: a) learn the distance distribution parameters under MLE, and b) detect the information source under Maximum-A-Posterior-Estimator (MAPE) based on the learnt parameters. We provide an analytic characterization of the source detection probability for regular trees under the proposed algorithm, where MAPE outperforms MLE by up to 50% for 3-regular trees and by up to 63% when the degree of the regular tree becomes large. We demonstrate our theoretical findings through numerical results, and further present the simulation results for general topologies (e.g., Facebook and US power grid networks) even without knowledge of the distance distribution, showing that under a simple protector placement algorithm, MAPE produces the detection probability much larger than that by MLE.

[9]

HUANG

, ZHANG

, XU

, et al.

A new adaptive extended Kalman filter for cooperative localization

[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 353-368.

DOI:10.1109/TAES.2017.2756763 URL [本文引用: 1]

[10]

SOARES

, GOME

, FERRERIA

, et al.

LocDyn: Robust distributed localization for mobile underwater networks

[J]. IEEE Journal of Oceanic Engineering, 2017, 42(4): 1063-1074.

DOI:10.1109/JOE.2017.2736951 URL [本文引用: 1]

无精准同步的小规模水声网络节点相对自定位

2020

... 随着水下自主航行器(AUV)研究的进展,由AUV协调运作组成的移动水声网络(MUANs)逐渐成为研究的热点.相较于传统的水声网络,移动水声网络具有更广的探测范围和更高的智能性以及更强的机动性,被广泛地应用于各种水下工程、海洋环境监测、水下数据采集及海洋军事等领域,受到越来越多国家与学者的关注^[1⇓-3]. ...

无精准同步的小规模水声网络节点相对自定位

2020

2019

Localization schemes for underwater acoustic sensor networks—A review

2020

Underwater optical wireless communications, networking, and localization: A survey

2018

... 移动水声网络在实现环境数据采集、处理及分析时,网络内各节点的位置信息是不可或缺的先验信息之一,因此针对移动水声网络自定位技术的研究成为了网络研究的基础.目前常见的网络自定位算法分为基于测距的定位算法与基于非测距的定位算法.其中基于非测距的定位算法无需测量节点间的距离信息,仅依据网络间的通信连通度即可实现节点的位置估计,因此该类算法计算开销小、硬件成本低,但网络的定位精度也较低,仅能应用于对精度要求不高的定位环境中^[4].基于测距的定位算法主要利用到达时间(TOA)、到达时间差(TDOA)和到达角度(DOA)等观测信息进行节点位置估计^[5].基于二阶时间差(STDOA)定位算法可用于解决信号周期以及时间同步未知情况下的水声定位问题^[6-7].基于测距的定位算法精度较高,但对于移动水声网络,网络拓扑的实时变化对定位精度的影响较大,因此需要开展变化拓扑下的网络定位算法研究.针对移动水声网络的自定位算法主要包括考虑运动模式的自定位算法(MASL)和基于最大后验概率的定位算法(MAP)等,该类算法需要预知网络拓扑变化先验信息.利用惯导系统(INS)也可直接估计移动节点动态位置,但该方法存在较大的误差累积.目前常使用基于滤波的移动水声网络自定位算法,该类算法根据网络节点的运动模型与观测模型实现节点位置的实时预测更新^[8⇓-10].然而滤波算法为了提高定位精度需要引入大量的观测信息,使得算法的通信开销较大;若降低定位通信开销则直接影响了网络的定位精度,因此存在网络定位精度与通信开销间的矛盾. ...

Localization of a moving object with sensors in motion by time delays and doppler shifts

2020

Underwater acoustic localization of the black box based on generalized second-order time difference of arrival (GSTDOA)

2020

Underwater Acoustical localization of the black box utilizing single autonomous underwater vehicle based on the second-order time difference of arrival

2020

Information source localization with protector diffusion in networks

2019

A new adaptive extended Kalman filter for cooperative localization

2018

LocDyn: Robust distributed localization for mobile underwater networks

2017

〈

〉