仿人表情机器人的下颌机构设计与运动

doi:10.16183/j.cnki.jsjtu.2022.469

仿人表情机器人的下颌机构设计与运动

赵威, 袁绍珂, 李忆楠, 费燕琼^,

上海交通大学机器人研究所,上海 200240

Design and Motion Analysis of Bionic Jaw Mechanism for Humanoid Expression Robot

ZHAO Wei, YUAN Shaoke, LI Yinan, FEI Yanqiong^,

Research Institute of Robotics, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 费燕琼,教授,电话(Tel.):021-34201458; E-mail:fyq@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-11-21 修回日期: 2023-01-12 接受日期: 2023-03-3

基金资助:

国家重点研发项目(2022YFB4703202)
深圳自由探索类基础研究项目(2021Szvup078)
转化医学国家重大科技基础设施(上海)开放课题(TMSK-2021-110)

Received: 2022-11-21 Revised: 2023-01-12 Accepted: 2023-03-3

作者简介 About authors

赵威(1996-),硕士生,从事仿人表情机器人研究.

摘要

针对目前仿人表情机器人口部运动模式单一的问题,基于人类下颌的解剖学运动机理,设计了一种新颖的多自由度仿生下颌机构.建立了仿生下颌机构的逆向运动学模型,分析了其运动模式,实现了仿生下颌机构在空间中的多自由度运动.对多自由度仿生下颌机构进行了多刚体仿真,并通过实验验证了其可行性.仿真和实验结果表明,基于逆向运动学模型,该机构可以模拟人类下颌的张合、前推、偏移3种基本运动模式,以及咀嚼、咬唇等口部复杂运动模式,弥补了现有仿人表情机器人口部运动模式受限的问题.

关键词： 仿生下颌; 仿生机器人; 表情机器人; 机构设计; 逆运动学分析

Abstract

In order to solve the current problem of a single oral motion mode for the humanoid expression robot, a novel multi degree of freedom (DOF) bionic jaw mechanism was designed based on the anatomical motion mechanism of the human jaw. The inverse kinematics model of the mechanism was established, and the motion mode of the mechanism was analyzed to realize the multi DOF motion of the bionic jaw mechanism in space. A multi rigid body simulation of the bionic jaw mechanism was conducted, whose feasibility was verified by the experiments. The simulation and experimental results demonstrate that, based on the inverse kinematics model, the mechanism designed is able to simulate the three basic motion modes of human jaw, including open-close movement, protrusion movement, and side shifting movement, as well as the complex oral motion modes including chewing and lip biting. Therefore, the proposed mechanism can compensate for the limits of oral movement patterns of the existing humanoid robots.

Keywords： bionic jaw; bionic robot; expression robot; mechanism design; inverse kinematic analysis

PDF (26383KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

赵威, 袁绍珂, 李忆楠, 费燕琼. 仿人表情机器人的下颌机构设计与运动[J]. 上海交通大学学报, 2024, 58(8): 1231-1239 doi:10.16183/j.cnki.jsjtu.2022.469

ZHAO Wei, YUAN Shaoke, LI Yinan, FEI Yanqiong. Design and Motion Analysis of Bionic Jaw Mechanism for Humanoid Expression Robot[J]. Journal of Shanghai Jiaotong University, 2024, 58(8): 1231-1239 doi:10.16183/j.cnki.jsjtu.2022.469

在服务型人机交互任务中,目前仿人表情机器人面临的口部运动自由度不足、运动模式单一等问题限制了机器人的口部运动灵活性,使其难以实现逼真的面部表情动作.因此需要开发与人类口部结构相似并能够模拟人类口部运动模式的仿人表情机器人机构,从而提升机器人口部运动的灵活性,改善交互体验.当前的仿人表情机器人口部机构可按照驱动方式不同分为刚性驱动型、柔性驱动型和刚柔耦合驱动型.Wu等^[1]基于连杆滑块机构实现了对仿人表情机器人下颌张合自由度和3个唇部自由度的驱动.Faraj等^[2]基于线牵引和舵机直驱的方式,以低成本的方式实现了对EVA机器人4个唇部自由度和1个下颌张合自由度的驱动.Ishihara等^[3]则通过线牵引和同步带传动方式,实现了对Affetto机器人3个唇部和下颌自由度的驱动.Toan等^[4]基于7自由度连杆设计了机器人唇部驱动机构,可实现多模式的复杂唇部形状,一定程度上提升了机器人口部运动的灵活性,但无法与下颌机构联动.Madumal等^[5]采用舵机直驱的方法设计了3自由度的口部驱动机构,可分别实现上下唇和下颌的单自由度驱动,并能够实现一定程度的口型模拟.Yang等^[6]以平面滑台机构为启发设计了3自由度的机器人下颌驱动机构,可实现下颌张合和平面内滑动,提升了下颌运动的灵活性.Liu等^[7]以形状记忆合金(SMA)和离子聚合物金属复合材料(IPMC)作为混合人工肌肉,实现了对仿人表情机器人1个下颌自由度和4个唇部自由度的驱动,提供了一种全柔性口部驱动方案.

由上述研究现状可知,当前仿人表情机器人在提升唇部驱动自由度的同时,对与下颌运动相关的口部驱动方案研究不足,导致机器人难以实现与下颌运动相关的面部动作,存在口部动作僵硬、运动模式单一的问题,从而无法获得更好的人机交互体验.针对这些不足,本文以人类下颌运动机制为启发,基于空间连杆机构,提出了一种新颖的多自由度仿生下颌机构,该机构依靠舵机驱动,可模拟人类下颌的张合、前推、偏移3种基本运动模式,并能够实现以咀嚼和咬唇为代表的口部复杂运动模式,提升了仿人表情机器人的口部动作灵活性.

1 下颌运动与仿人表情

人类的面部表情动作主要由面部肌肉和面部活动器官的耦合运动形成^[8],下颌骨作为人类面部唯一的活动骨骼,对于口部表情动作的形成至关重要.下颌运动可视为下颌骨与上颌颞骨之间的相对运动,具体表现为一系列复杂的三维转动和滑动.人类下颌骨的运动通过咀嚼肌驱动下颌头与颞骨下颌窝之间形成的颞下颌关节(TMJ)来实现.人类下颌骨运动参考轴及运动参考平面如图1所示,3种基本运动模式如图2所示.水平轴、矢状轴和冠状轴交汇于下颌骨TMJ,通过咀嚼肌群的驱动,可实现如图2(a)的下颌骨沿TMJ矢状轴的前推运动、如图2(b)的绕TMJ冠状轴的偏移运动,以及如图2(c)的绕TMJ水平轴的张合运动,此为人类下颌骨的3种基本运动模式,其中前推运动和偏移运动在水平面内实现,具有3个自由度,而张合运动在矢状面内实现,具有1个自由度,3种基本运动模式可以彼此复合实现如咀嚼等更复杂的下颌运动模式^[9-10].

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 人类下颌骨运动参考轴及运动参考平面

Fig.1 Reference axes and motion reference planes of human jaw movement

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 人类下颌骨的3种基本运动模式

Fig.2 Three basic motion patterns of human jaw

仿生下颌的运动与仿人表情间的联系可以用面部动作编码系统(Facial Action Coding System, FACS)来描述.FACS是由美国心理学家 Ekman 等^[11]于 1971年提出的面部表情描述方法,描述了面部肌肉、活动器官动作与面部表情之间的映射关系.FACS 根据人类面部肌肉与开心、愤怒、伤心、恐惧、厌恶和惊讶6种基本表情之间的对应关系,将人脸划分为 46 个相互独立而又相互联系的运动单元(Action Unit, AU).对比无表情的中性人脸特征,基本表情的人脸特征有独特的肌肉运动规律^[12],并且可以采用 FACS 来量化表示.下颌的3种运动模式对应了3种不同运动单元的动作,表1体现了下颌运动与运动单元的映射关系.

表1 下颌运动与运动单元映射关系表

Tab.1 Mapping relationship between mandibular movement and action unit

运动单元	下颌运动	对应肌肉
AU26	下颌下降	咬肌、颞肌、翼状肌
AU29	下颌外推	翼状肌
AU30	下颌侧移	翼状肌、咬肌、颞肌

新窗口打开| 下载CSV

人类的表情形成是由多条肌肉共同参与协调运动的结果^[13],FACS理论表明下颌通过3种基本动作参与到面部表情的形成过程,其中最主要的下颌张合运动在6种基本表情中直接参与到了恐惧、惊讶、愤怒表情的形成中.同时人类的基本表情引申出许多程度较弱的变种情绪^[14],为了扩大仿生下颌应用的表情范围,本研究同样将此类表情纳入研究.人们通常通过抿嘴来传递模棱两可信息^[15],或通过下颌前伸来表达更高程度的愤怒^[16],上述两种表情需要下颌前推来实现;人们显露蔑视或轻视表情时,往往会将嘴巴向一侧抬起,需要下颌偏移来实现^[17].在个体高度紧张的情况下可能会出现咬嘴唇的动作^[18],通过下颌基本动作的耦合可以对此实现模拟.因此仿人表情机器人下颌的张合、前推、偏移3种基本运动模式对于逼真表情形成具有重要作用,本文以FACS中AU26、AU29、AU30,3个运动单元及其对应的运动模式为启发进行多自由度仿生下颌的设计.

2 机械设计

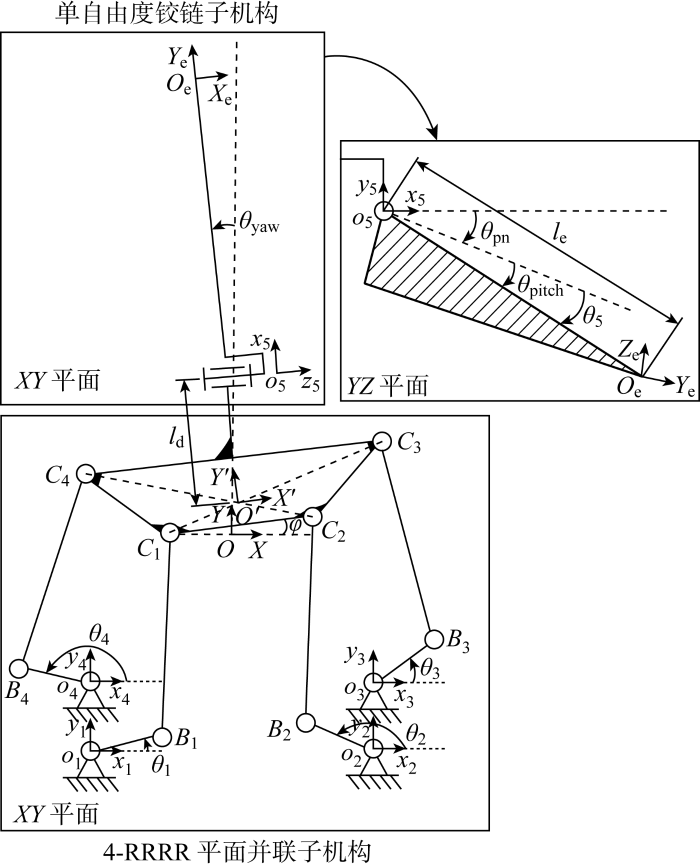
为复现人类下颌的3种基本运动模式及其复合运动,基于空间连杆设计了一种新颖的多自由度仿生下颌机构,如图3所示.该机构共有5个驱动自由度,由一个4-RRRR平面并联子机构和一个单自由度平面铰链子机构正交组成.其中单自由度铰链子机构用于实现仿生下颌骨在矢状面内的张合运动模式,如图3(a)所示,单自由度铰链子机构的两台总线舵机同轴逆向同步旋转,形成如图3(b)中的旋转运动R5,驱动仿生下颌骨进行张合运动模式.4-RRRR平面并联子机构用于实现仿生下颌骨在水平面内的前推和偏移运动模式,如图3(a)所示,该机构的4台数字舵机带动各自摇臂旋转,形成如图3(b)中的旋转运动R1~R4,通过中间连杆将运动传递至动平台,实现动平台在水平面内的位置和姿态控制.其中图3(b)中第4台舵机的旋转运动R4为冗余自由度,用于保证机构运动的驱动力和平稳性.下颌机构的基本尺寸遵循人类模特的下颌及头骨约束尺寸设计,同时受到仿人表情机器人内部其他驱动模块、相关电路布线等空间约束的影响,对其进行了紧凑性设计.此外下颌机构中连杆长度和铰链位置通过蒙特卡洛法确定其工作空间进行优化设计得到.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 多自由度仿生下颌机构

Fig.3 Mechanism of multi-DOF bionic jaw

多自由度仿生下颌机构运动效果如图4所示.机器人的尺寸根据人类女性下颌尺寸确定,如图4(a)所示, 仿生下颌机构以单自由度铰链子机构的转轴D为旋转中心,可在矢状面内产生 0°~45° 范围内的张合角度θ_pitch,所实现的开口度高于正常人类的3.7 cm;可在水平面内沿y轴方向产生 -2~12 mm 范围内的纵向位移Δy,高于正常人类下颌前伸范围的10 mm;可在水平面内沿旋转中心R产生 0°~20°范围内的偏移转角θ_yaw,高于正常人类的15°^[18],所设计多自由仿生下颌可覆盖人类下颌的运动范围,具备模拟人类各种表情的运动能力.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 多自由度仿生下颌机构运动效果

Fig.4 Movements of multi-DOF bionic jaw mechanism

3 运动分析

3.1 逆向运动学分析

图5所示为多自由度仿生下颌机构运动简图.4-RRRR平面并联子机构由摇臂o_iB_i、中间连杆B_iC_i和动平台C₁C₂C₃C₄组成,其中关节o_i为主动关节,摇臂o_iB_i杆长为l,中间连杆B_iC_i杆长为h.单自由度铰链子机构通过主动关节o₅将末端执行器o₅O_e铰接于4-RRRR平面并联子机构的动平台C₁C₂C₃C₄上.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 多自由度仿生下颌机构运动简图

Fig.5 Motion diagram of multi-DOF bionic jaw mechanism

设末端工具坐标系X_eO_eY_e相对于世界坐标系XOY的RPY姿态向量R_jaw和位置向量P_jaw分别如下:

R_jaw=[

$\begin{array}{l} 0 ° & θ_{p i t c h} & θ_{y a w} \end{array}$ ]

(1)

P_jaw=[

$\begin{array}{l} x_{e} & y_{e} & z_{e} \end{array}$ ]

(2)

θ_pitch与z_e存在依赖关系:

θ_pitch=arcsin

$(\frac{z_{e}}{l_{e}})$ -θ_pn

(3)

式中:l_e为连杆o₅O_e的长度;θ_pn表示初始时刻连杆o₅O_e与XY平面之间的夹角.

设动坐标系X'O'Y'相对于世界坐标系XOY的位姿矩阵为q=[ $\begin{array}{l} x & y & φ \end{array}$ ]^T,由几何关系可得,系X'O'Y'的位姿矩阵q与末端工具坐标系X_eO_eY_e的位姿向量的关系如下:

q=[

$\begin{array}{l} x & y & φ \end{array}$ ]^T=

$(\begin{array}{l} x_{e} - l_{e} c o s (θ_{p i t c h} + θ_{p n}) s i n θ_{y a w} \\ y_{e} - [l_{d} + l_{e} c o s (θ_{p i t c h} + θ_{p n})] c o s θ_{y a w} \\ θ_{y a w} \end{array})$

(4)

式中:l_d表示关节o₅与动坐标系X'O'Y'原点O'在XY平面内的投影距离;x、y、φ分别为动坐标系X'O'Y'在世界坐标系XOY中的坐标与转角.

在参考坐标系XOY中,由几何法可得封闭矢量方程:

OO'=Oo_i+o_iB_i+B_iC_i+C_iO', i=1~4

(5)

式(5)写为以下标量方程:

k_i₁sin θ_i+k_i₂cos θ_i+k_i₃=0, i=1~4

(6)

利用三角万能公式求解式(6)可得图4中4个主动关节o₁~o₄的驱动角度θ₁~θ₄:

θ_i=2arctan

$\frac{- k_{i 1} \pm \sqrt{k_{i 1}^{2} + k_{i 2}^{2} - k_{i 3}^{2}}}{k_{i 3} - k_{i 2}}$

i=1~4

(7)

$\begin{array}{l} k_{i 1} = - 2 l_{i 1} [y + l_{i 3} s i n (ϕ_{i} + φ) - l_{i 4} s i n α_{i}] \\ k_{i 2} = - 2 l_{i 1} [x + l_{i 3} c o s (ϕ_{i} + φ) - l_{i 4} c o s α_{i}] \\ k_{i 3} = [y + l_{i 3} s i n (ϕ_{i} + φ) - l_{i 4} s i n α_{i}]^{2} + \\ [x + l_{i 3} c o s (ϕ_{i} + φ) - l_{i 4} c o s α_{i}]^{2} + \\ l_{i 1}^{2} - l_{i 2}^{2} \end{array}\}$

(8)

式中:l_i₁、l_i₂分别表示图5中摇臂o_iB_i、中间连杆B_iC_i的长度;l_i₃、l_i₄分别表示向量Oo_i和C_iO'的长度;ϕ_i'、α_i分别表示向量和在世界坐标系XOY中的角度.

因此,可得仿生下颌机构5个主动关节o₁~o₅的驱动角度向量θ_drive:

θ_drive=[

$\begin{array}{l} θ_{1} & θ_{2} & θ_{3} & θ_{4} & θ_{5} \end{array}$ ]^T=

$[\begin{array}{l} 2 a r c t a n \frac{- k_{11} \pm \sqrt{k_{11}^{2} + k_{12}^{2} - k_{13}^{2}}}{k_{13} - k_{12}} \\ 2 a r c t a n \frac{- k_{21} \pm \sqrt{k_{21}^{2} + k_{22}^{2} - k_{23}^{2}}}{k_{23} - k_{22}} \\ 2 a r c t a n \frac{- k_{31} \pm \sqrt{k_{31}^{2} + k_{32}^{2} - k_{33}^{2}}}{k_{33} - k_{32}} \\ 2 a r c t a n \frac{- k_{41} \pm \sqrt{k_{41}^{2} + k_{42}^{2} - k_{43}^{2}}}{k_{43} - k_{42}} \\ θ_{p i t c h} \end{array}]$

(9)

3.2 运动模式分析

多自由度仿生下颌机构依靠其4-RRRR平面并联子机构可实现对下颌末端的水平前推以及水平面内的旋转偏移,同时依靠单自由度铰链子机构可实现下颌末端在矢状面内的张合.多自由度仿生下颌机构运动模式如图6所示.图6(a)为机构在静止状态下的构型,对应人类下颌的静止闭合状态.依靠机构逆向运动学模型驱动如图6(b)所示的关节θ₁~θ₄联合动作,可使机构动平台产生y轴的轴向位移Δy,进而带动单自由度铰链子机构整体前移,实现下颌的前推运动模式.同理,在指定如图6(c)的偏移旋转中心R后,可依靠机构逆向运动学模型驱动关节θ₁~θ₄联合动作,使机构动平台和单自由度铰链子机构整体以R为中心旋转偏移转角θ_yaw,同时使下颌末端产生x、y轴向位移Δx和Δy,实现下颌的偏移运动模式.如图6(d)所示,单自由度铰链子机构在动平台的运动基础上,通过关节θ₅旋转可实现在矢状面内的俯仰转角θ_pitch,并使下颌末端产生y、z轴向的叠加位移Δy和Δz,实现下颌的张合运动模式.基于上述3种运动模式,该多自由度仿生下颌机构能够实现对人类下颌运动的逼真模拟.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 多自由度仿生下颌机构运动模式

Fig.6 Motion pattern of multi-DOF bionic jaw mechanism

4 实验与结果

4.1 基本运动模式实验

图4(b)展示了多自由度仿生下颌机构样机进行张合、前推、偏移3种基本运动时的运动效果.提取得到样机的实际下颌运动轨迹与MATLAB仿真轨迹对比如图7所示.由图7可以看出,仿生下颌机构对张合、前推、偏移运动时的下颌运动趋势有较好的跟踪效果,其中对于张合、前推、偏移运动进行20次实验得到的平均轨迹跟踪误差分别为0.5、0.6和0.9 mm,轨迹跟踪精度较好.如图7(a)所示,对于前推运动和偏移运动,最大轨迹跟踪误差发生在初始时刻和终止时刻,分析其主要原因为起动加速度下机构振动较大以及运动过程中由于机构装配产生的累计误差,但对下颌整体轨迹跟踪效果的影响较小.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 多自由度仿生下颌机构基本运动模式轨迹跟踪曲线

Fig.7 Trajectory tracking of basic motion mode of multi-DOF bionic jaw mechanism

4.2 复杂运动模式实验

多自由度仿生下颌机构除可进行张合、前推、偏移3种基本运动模式外,还可以在其工作空间内实现更加复杂的复合运动模式.咀嚼运动是人类下颌最重要、最复杂的复合运动之一,根据已有的人类咀嚼运动轨迹测量数据^[19],将咀嚼运动轨迹近似拟合为如图8所示的二次曲面上的封闭空间曲线.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 咀嚼运动空间拟合轨迹

Fig.8 Spatial fitting trajectory of chewing motion

实验采用多自由度仿生下颌机构复现如图8所示的咀嚼运动轨迹,得到了如图9所示的XZ、YZ平面内对周期为T的咀嚼运动的实现效果.图中:t为运动时间.同时为分析运动频率对多自由度仿生下颌机构轨迹跟踪精度的影响,测试了其在运动频率f=1,2,3 Hz下对咀嚼运动轨迹的跟踪曲线, 如图10所示.结果表明,在1 Hz运动频率下,多自由度仿生下颌机构在XZ、YZ投影平面内对咀嚼运动轨迹的最大跟踪误差分别为0.5和 0.6 mm,跟踪效果较好.当运动频率上升至2 Hz时,机构在XZ、YZ投影平面内的最大跟踪误差分别为0.8和0.85 mm,对咀嚼轨迹的跟踪效果变差,在轨迹最低点附近的偏离尤为明显.当运动频率上升至3 Hz时,多自由度仿生下颌机构对咀嚼运动轨迹的跟踪精度进一步下降,在XZ、YZ投影平面内的最大跟踪误差分别上升至1.6和1.55 mm,约为1 Hz运动频率下跟踪误差的3倍.由此证明随着运动频率升高,多自由度仿生下颌机构的空间轨迹跟踪精度随之下降,分析其原因如图11所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 多自由度仿生下颌机构咀嚼运动效果

Fig.9 Effect of chewing motion of multi-DOF bionic jaw mechanism

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同运动频率下多自由度仿生下颌结构咀嚼运动轨迹

Fig.10 Chewing trajectory of structure of multi-DOF bionic jaw at different motion frequencies

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同频率咀嚼运动下多自由度仿生下颌机构最高舵机转矩仿真结果

Fig.11 Simulation results of the highest steering gear torque of multi-DOF bionic jaw mechanism at different frequencies of chewing motion

图11显示了MATLAB多刚体仿真下,多自由度仿生下颌机构在不同运动频率下的最高舵机转矩曲线,即每一时刻机构中所有6台舵机的峰值转矩.可见随着运动频率的升高,最高舵机转矩峰值逐渐逼近舵机极限转矩,此时运动频率过快则舵机转矩无法完全克服部件惯性力和摩擦力作用,从而无法提供足够的驱动力,最终导致机构对咀嚼轨迹的跟踪精度下降.因此,在使用多自由度仿生下颌机构跟踪空间轨迹时不宜选择过高的运动频率.

此外,在与仿人表情机器人的柔性面部皮肤耦合运动时,多自由度仿生下颌机构还可以实现多种唇部动作,如图12所示.如图12(a)所示,当机构耦合机器人口部皮肤动作时可通过偏移运动模式实现侧向咬唇的表情动作,即产生x轴方向的侧向位移Δx.同时,多自由度仿生下颌机构还能够通过附加下颌运动的方式增强仿人表情机器人进行基本面部表情时的动作幅度和动作细节.图12(b)为附加下颌前推运动模式后得到增强的愤怒表情效果,即产生了y轴方向的前推位移Δy,在增加了下颌前推运动后的愤怒表情被认为更具有攻击性^[20].

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 多自由度仿生下颌机构与口部皮肤的耦合运动效果

Fig.12 Coupling motion of multi-DOF bionic jaw and oral skin

5 结语

本文针对目前仿人表情机器人口部动作僵硬、运动模式单一的问题,设计了一种新颖的多自由度仿生下颌机构,并对其进行了逆向运动学建模和运动模式分析.通过仿真和实验证明了该机构能够模拟人类下颌的张合、前推、偏移基本运动模式,同时能够实现以咀嚼运动为代表的复杂运动模式,提升了仿人表情机器人的口部运动灵活性,为仿人表情机器人的口部驱动机构设计提供了一种新的思路.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

, LIN

, CAO

, et al.

Head design and optimization of an emotionally interactive robot for the treatment of autism

[C]// Proceedings of the 2019 4th International Conference on Automation, Control and Robotics Engineering. Shenzhen, China: Association for Computing Machinery, 2019: 1-10.