上述文献基于几何曲线法生成泊车路径,对场景的适用性较差,部分参数需要结合实际场景调参,因此近些年来更多的研究关注于基于图搜索的方法.文献[7]提出混合A*算法,该方法将车辆的运动学约束融入到图搜索中,可在各类复杂环境内搜索出泊车路径.自混合A*算法提出以来,有许多工作在此基础上进行改进.文献[13]改进了奖惩函数的设计,解决了规划结果频繁变换行驶方向的问题.文献[14]改进节点拓展方式,能够在直道偏多的场景里起到加速搜索的作用.文献[15]用螺旋线代替圆弧作为运动基元,很大程度上解决了规划结果曲率不连续平滑性差的问题.文献[16]在原算法的曲线平滑基础上分析了问题并做了修正,解决了曲线坍缩,优化前后曲线起始处朝向不一致等问题.文献[17]基于混合A*算法生成初始路径,再结合数值优化的方式,生成平滑无碰撞的轨迹,所得到的轨迹质量较好.然而上述方法对泊车场景规划结果的实时性和安全性关注较少,在路径平滑方面也未考虑曲率的最大约束,并且未进行速度规划.文献[17]虽然通过数值方法解决了路径平滑中曲率约束以及速度规划的问题,但由于提出的优化问题较为复杂、计算量大、耗时较长,所以实时性方面无法满足要求.
针对现有方法的不足,本文提出一种面向泊车场景的智能车辆轨迹规划方法,采用路径搜索与轨迹生成两阶段完成泊车轨迹规划.在路径搜索阶段,改进混合A*算法的解析扩展,加快算法收敛,同时引入风险评估函数,极大限度保证路径的安全性.在轨迹生成阶段,采用横纵向解耦的方式分别完成路径平滑以及速度规划,路径平滑主要以离散点的二阶差分作为优化目标,结合车辆曲率约束实现,速度规划考虑车辆运动约束即速度及加速度等约束后,定义为二次规划问题进行解决.本文工作可在泊车场景下,为智能车辆提供一种实时、平滑、可靠的轨迹规划方法.
1 混合A*算法
混合A*算法是一种基于图搜索的运动规划算法,在传统A*算法基础上改进而来,解决了传统A*算法规划结果无法满足车辆非完整性约束的问题,适用于半结构化环境下智能车辆的路径规划.与A*算法相似,混合A*算法将搜索空间离散成栅格化的形式,并建立Open表和Closed表维护节点搜索信息,每搜索一步都利用评估函数
1.1 节点扩展
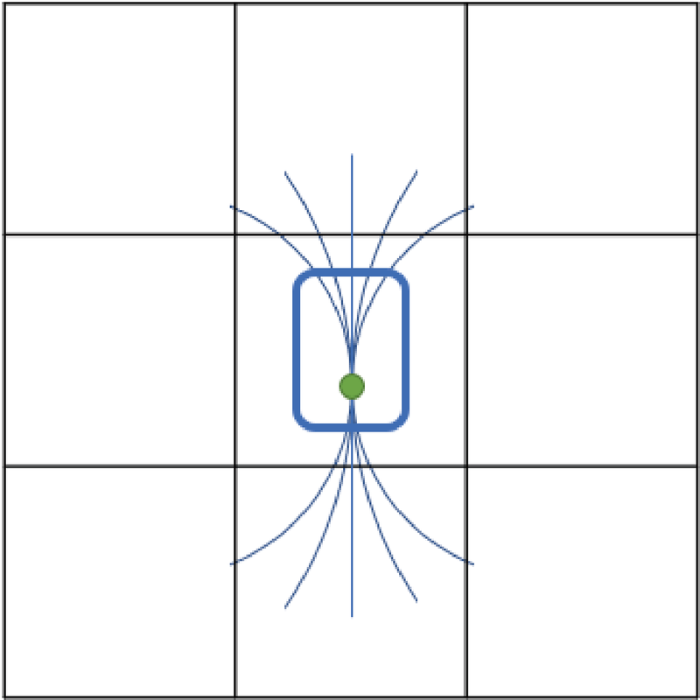
传统A*算法采用二维平面栅格化的方式将搜索空间离散化,然后在该空间中进行搜索扩展,通常以直线段作为扩展方式. 而混合A*算法采用额外引入车辆航向角进行三维搜索空间的离散化,扩展方式根据扩展距离以及前轮转角生成相应的运动基元,使路径曲率不超过车辆可行驶的最大曲率,保证路径满足车辆的运动学约束.混合A*算法节点扩展示意图如图1所示.
图1
1.2 启发函数
对于启发式算法,启发函数的设计至关重要,在复杂环境下,如果以欧氏距离或者曼哈顿距离作为启发值,由于未考虑障碍物导致搜索效率不高.混合A*算法定义两种启发值,并取两者中最大值为节点启发值.
首先考虑障碍物的约束,而不考虑车辆运动约束来计算启发值,其考虑的是允许全向运动情况下节点坐标
其次考虑车辆运动约束,而不考虑障碍物的启发值计算,其考虑的是无视障碍情况下节点n(x, y, φ)到终点nend(xend, yend, φend)满足非完整约束情况下的最短路径,通常可以通过计算Reeds-Shepp曲线得到,简记为h2(n, nend).
最终,该节点的启发值可表示为
2 基于改进混合A*算法的路径搜索
传统混合A*算法虽然解决了A*算法无法满足车辆非完整性约束的问题,然而在实际应用中仍然存在诸多问题,例如规划时间长、路径平滑性差、安全性与求解效率难以平衡等缺陷.针对上述问题本文通过优化解析扩展,引入风险评估函数,进一步提升算法搜索效率同时保障搜索路径的安全性.
2.1 解析扩展
在进行节点扩展的过程中,无法精确地扩展至终点,因此在靠近终点时,需要考虑构造曲线等解析扩展的方式完成节点与终点的连接.传统混合A*算法通过构造Reeds-Shepp曲线,进一步进行碰撞检测,若不存在碰撞情况则完成连接.然而在狭窄泊车场景中,该曲线构造连接方式大多难以通过碰撞检测,即使在空旷场景下不会出现该问题,多数Reeds-Shepp曲线会存在1~2个行进方向档位切换点,这并不是合理的驾驶行为.
为解决上述问题,本文尝试在节点坐标n(x, y, φ)与终点坐标nend(xend, yend, φend)之间采用一段曲率小于车辆可行驶的最大曲率的圆弧衔接直线实现.具体解析以终点为原点的笛卡尔坐标系下展开,记连接终点的直线段长为l0,衔接的圆弧长为l1,如图2所示.其中:红色箭头为终点位姿;绿色箭头为连接的节点位姿.
图2
记以终点为原点的笛卡尔坐标系下节点
经过变换后可以根据n'(x', y', φ')求得l0,l1和κ的表达式:
式中:κmax为路径允许的最大曲率.
相比于Reeds-Shepp曲线,该种构造方式更加符合人类驾驶行为,更加适用于泊车场景,能够使得算法容易通过终点连接的碰撞检测,从而加快算法收敛.
2.2 风险评估函数
多数情况下由混合A*算法搜索得到的路径比较靠近障碍物,解决这个问题的一种方式是进行膨胀处理和更严格的碰撞检测,但在狭窄环境下这样的处理可能会导致无法搜索出可行解.
为了在最大保证安全限度的同时保证可解性,对节点扩展的优先级设计进行优化.原算法对于节点n(x,y,φ)将(n,f(n))放入优先级队列,根据评估函数值f(n)最小的节点进行扩展.本文对于(n,f(n))进行扩展为(n,f(n),d(n))放入优先级队列,d(n)为风险评估函数,可表示为
式中:do为节点距离最近障碍物的距离值;dmax为安全距离.
优先级方面优先考虑d(n)最小,在d(n)相近时考虑f(n)最小的节点进行扩展.这样设计保证规划过程能与障碍物保持安全距离,同时当面临狭窄区域时不会阻碍规划.
3 基于二次规划的轨迹生成
由于运动基元根据前轮偏角进行离散采样得到,所以通过上述方法得到的初始路径仍然存在路径曲率不连续的问题,需要进行相应的路径后处理来生成轨迹.
3.1 路径平滑
在泊车场景中,搜索路径存在档位切换的情况,需要对路径按照行进方向进行分段平滑处理,每段路径的平滑处理如下.
在初始路径上等距采样m个路径点,记为
式中:ω1,ω2均为优化目标的权重系数;第1项优化目标使得离散点一阶差分尽可能相近同时路段长度尽可能短;第2项优化目标使得路径平滑性增强.
考虑优化过程中起始点和终止点的位置以及朝向均不变,可以得出等式约束:
考虑优化过程中避免与障碍物发生碰撞,需要限定离散路径点坐标,具体数值可由初始路径点距离最近障碍物的距离值作为参考确定,该不等式约束可表示为
式中:
考虑车辆行驶的运动学性质,路径曲率存在一个最大曲率的限制,假定离散点一阶差分近似相等,构建曲率约束如下:
其中:R为pi点对应的曲率半径.
式(8)两边同时平方,展开得到:
综上,路径平滑问题可以建模成以式(5)为优化目标,式(6)~(7)和(9)为约束的二次规划问题.约束项式(9)为非线性约束,导致原问题难以求解,对此可以采用序列二次规划的方式进行求解,按照当前迭代点将原问题处理成凸二次规划问题,不断求解迭代直至收敛.
3.2 速度规划
在进行速度规划时,对于存在档位切换的路径同样进行分段处理的方式,在档位切换处,车辆处于静止状态.对正向行驶的速度规划问题予以阐述,反向行驶的速度规划问题可以类推之.考虑限定时间tk内车辆行驶路径长度为s的路径,起始点的车辆处于静止状态.
在时域
式中:
为了使得车辆能够尽可能快地行驶目标距离,需要建立优化目标
式中:
定义状态量
根据式(12),状态量Sz以及控制量uz的约束可表示为
将式(10)以状态量Sz以及控制量uz表示,可以得到:
由于车辆在起始点处于静止状态,所以可以得到
4 实验结果与分析
通过设计仿真和实车试验,验证本文所提方法的有效性和实用性.实验软件环境为Ubuntu 16.04,并基于机器人操作系统(ROS)进行C++算法开发,所使用的计算平台CPU型号为i7-10510U,内存大小为8 GB.
4.1 仿真实验
4.1.1 路径搜索
路径搜索实验所涉及算法的参数如表1所示.
表1 路径搜索算法相关参数
Tab.1
| 参数 | 取值 |
|---|---|
| 位置离散分辨率/m | 0.5 |
| 角度离散分辨率/(°) | 7.5 |
| 前轮转角离散数 | 5.0 |
| 步长/m | 0.8 |
图3
表2 路径搜索实验数据
Tab.2
| 算法 | 路径 长度/m | 拓展节点 | 档位切换 | 搜索 时间/ms |
|---|---|---|---|---|
| 文献[15]算法 | 13.5 | 1769 | 3 | 84 |
| 本文算法 | 13.7 | 478 | 3 | 18 |
4.1.2 路径平滑
路径平滑实验所涉及算法的参数如表3所示.
表3 路径平滑算法相关参数
Tab.3
| 参数 | 取值 |
|---|---|
| 离散状态点数 | 50 |
| 一阶差分权重 | 1 |
| 最大曲率 | 5 |
| 二阶差分权重 | 1000 |
图4
图5
式中:spa为路径总长度;w为将路径离散化后点的个数;κj为各个离散点处对应的曲率.
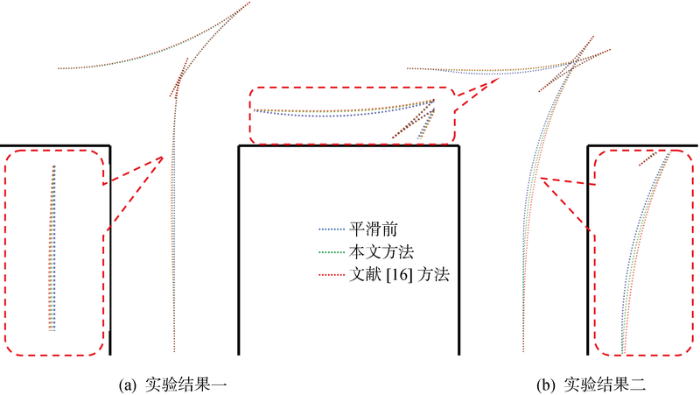
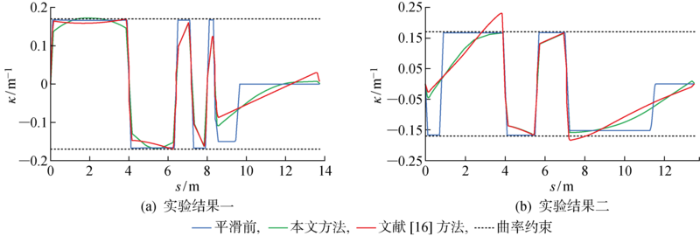
路径处理前后平滑性指标Jκ如表5所示.
表5
路径平滑前后平滑性指标
Tab.5
| 实验组 | 平滑前的Jκ | 本文方法的Jκ | 文献[16]的Jκ |
|---|---|---|---|
| 实验一 | 0.01707 | 0.01383 | 0.01372 |
| 实验二 | 0.02042 | 0.01434 | 0.01545 |
4.1.3 速度规划
在路径平滑后进行速度规划,关于速度规划中二次规划问题的各参数如表6所示.
表6 速度规划算法相关参数
Tab.6
| 参数 | 取值 |
|---|---|
| 离散状态点数 | 24 |
| 最大速度/(m·s-1) | 1.0 |
| 最大加速度/(m·s-2) | 1.0 |
| 最大加加速度/(m·s-3) | 0.5 |
| 距离权重 | 10000 |
| 加速度权重 | 10 |
| 加加速度权重 | 10 |
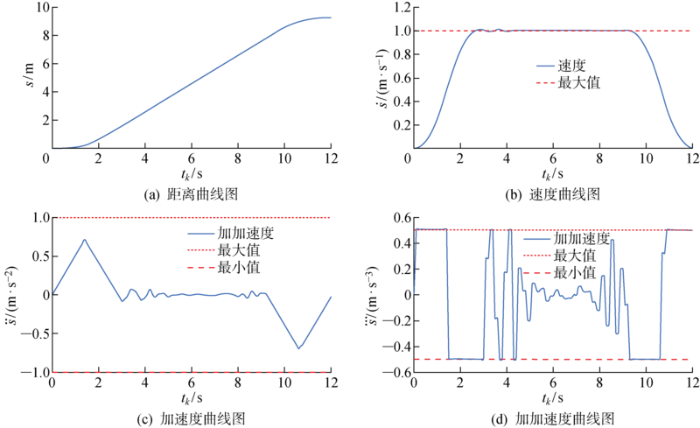
以一段路径为例:路径长度s为9.25 m,限定时间tk取12 s,规划耗时为6 ms.规划结果如图6所示.
图6
4.2 实车试验
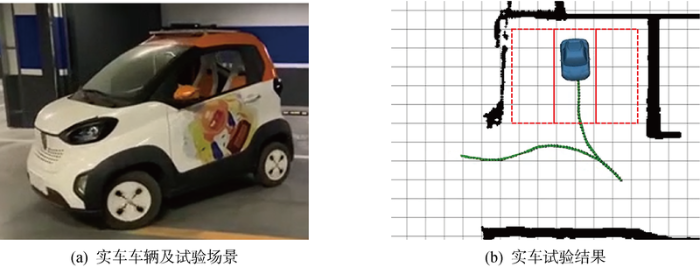
为进一步验证本文方法的实用性,本文在实际的泊车场景开展实车验证,如图7所示.首先搭建实车平台,以Kinect V2作为主传感器获取环境信息,完成场景下感知以及定位工作并进行规划控制,并利用机器人操作系统平台上的可视化工具Rviz实现实验结果的可视化.
图7
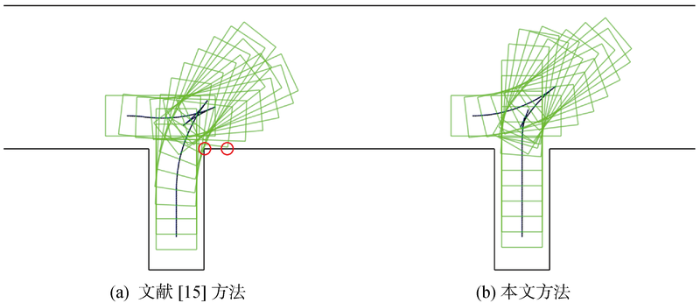
在该环境下,文献[15]所述方法的搜索节点为 1324 个,总耗时为76 ms,而本文方法搜索节点数为218个,初始路径搜索以及轨迹生成总耗时为 54 ms.可以看出,虽然本文方法相较于文献[15]增添了路径平滑和速度规划等轨迹生成的工作,但得益于本文方法在路径搜索方面的改进,并不会影响规划结果的实时性.规划结果经控制执行后,文献[15]所述方法实验结果在终止处有0.143 m的横向误差,1.537° 的角度误差,本文方法实验结果在终止处有0.078 m的横向误差,0.946° 的角度误差.可以得到,本文方法所述的路径平滑和速度规划这些轨迹生成的工作提升了规划结果的可行性,对车辆控制更加友好,进一步验证了方法的实用性.
5 结语
本文提出了一种面向泊车场景智能车辆轨迹规划方法,该方法包括初始路径搜索以及轨迹生成两个步骤.在基于混合A*算法实现的初始路径搜索中,本文优化解析扩展,加快算法收敛,同时引入风险评估函数,保证路径的安全性.在基于二次规划的轨迹生成中,本文分别将离散点路径平滑以及速度规划建立为二次规划问题进行求解.最后,设计仿真实验进行验证,验证本文方法的有效性,并通过实车实验说明可行性.结果表明,本文方法提升了路径搜索实时性与安全性,路径平滑与速度规划都具备良好的平滑性.下一步工作将致力于研究动态环境下车辆泊车轨迹规划的问题.
参考文献
基于地面快速鲁棒特征的智能车全局定位方法
[J].
Global localization for intelligent vehicles using ground SURF
[J].
Optimal trajectory generation for dynamic street scenarios in a Frenét Frame
[C]//
Autonomous driving: Cognitive construction and situation understanding
[J].
A two-level path planning method for on-road autonomous driving
[C]//
Curvature continuous path generation for autonomous vehicle using B-spline curves
[J].DOI:10.1016/j.cad.2009.12.007 URL [本文引用: 1]
Differentially constrained mobile robot motion planning in state lattices
[J].DOI:10.1002/rob.v26:3 URL [本文引用: 1]
Path planning for autonomous vehicles in unknown semi-structured environments
[J].
DOI:10.1177/0278364909359210
URL
[本文引用: 2]

We describe a practical path-planning algorithm for an autonomous vehicle operating in an unknown semi-structured (or unstructured) environment, where obstacles are detected online by the robot’s sensors. This work was motivated by and experimentally validated in the 2007 DARPA Urban Challenge, where robotic vehicles had to autonomously navigate parking lots. The core of our approach to path planning consists of two phases. The first phase uses a variant of A* search (applied to the 3D kinematic state space of the vehicle) to obtain a kinematically feasible trajectory. The second phase then improves the quality of the solution via numeric non-linear optimization, leading to a local (and frequently global) optimum. Further, we extend our algorithm to use prior topological knowledge of the environment to guide path planning, leading to faster search and final trajectories better suited to the structure of the environment. We present experimental results from the DARPA Urban Challenge, where our robot demonstrated near-flawless performance in complex general path-planning tasks such as navigating parking lots and executing U-turns on blocked roads. We also present results on autonomous navigation of real parking lots. In those latter tasks, which are significantly more complex than the ones in the DARPA Urban Challenge, the time of a full replanning cycle of our planner is in the range of 50—300 ms.
Motion planning for urban driving using RRT
[C]//
The future of parking: A survey on automated valet parking with an outlook on high density parking
[C]//
一种基于环视相机的自动泊车方法
[J].
Automatic parking based on bird’s eye view cameras
[J].
Path planning for autonomous car parking
[C]//
A trajectory planning method based on forward path generation and backward tracking algorithm for Automatic Parking Systems
[C]//
一种基于改进混合A*的智能车路径规划算法
[J].
Hybrid A* algorithm-based path planning for intelligent vehicle
[J].
一种基于等步长分层拓展的混合A*路径规划方法
[J].
A hybrid-A* path planning method based on equal step hierarchical expansion
[J].
Hybrid A*-based curvature continuous path planning in complex dynamic environments
[C]//
Enhanced path smoothing based on conjugate gradient descent for firefighting robots in petrochemical complexes
[J].DOI:10.1080/01691864.2019.1632221 URL [本文引用: 7]
Autonomous parking using optimization-based collision avoidance
[C]//