极板受到压力的变化而产生挠度偏移,从而产生电容的变化,其输出电容与压力之间的关系存在较大的非线性.非线性误差一方面是由于在“位移-电容”的关系转换中,电容值与两极板的距离成反比例关系;另一方面是由于在“压力-位移”的关系转换中,极板在大挠度情况下,板的刚度随着挠度的增加而增加,挠度值不再与压力成正比[5].对于前者,采用差动结构的电容式传感器可以大大降低其非线性误差;对于后者,可对极板施加预张力,使其力学变形特性发生改变,挠度的非线性行为可以得到显著改善.
对于板的大挠度问题,通常使用von Kármán理论方程作为其控制方程,这是一个典型且极具挑战的非线性问题.长期以来,研究学者对大挠度方程的求解进行了大量研究,也取得了丰硕成果.Way于1934年首次采用级数解法给出大挠度理论与线性理论的差别.Vincent和钱伟长分别于1931年和1947年采用摄动法,分别以载荷和中心位移作为摄动参数求解了均布载荷作用下圆板的大挠度问题.近些年,陆续涌现出一些新的解析方法,不断提升求解的效率和精度,如同伦摄动法(HPM)[6]、小波数值法和同伦分析法(HAM)[7-8],其中HAM最具灵活性和一般性.然而以上对圆板大挠度的求解都没有研究横向载荷在与初始平面张力联合作用下的挠度非线性情况.
在研究圆薄板变形理论中,不可避免会涉及到板行为向膜行为的过渡问题,当板内的薄膜应力对板的平衡起绝对作用时,板的抗弯刚度可以忽略不计,进而用薄膜理论代替板的大挠度理论,von Kármán方程的求解难度得到降低.在此条件下,文献[9]推广了Hencky薄膜变换,得到圆薄膜在初始拉应力或压应力下的封闭解.求解虽然相对方便,但忽略了弯矩的影响,与von Kármán方程的解存在一定误差,并且当弯曲应力与薄膜应力相比越大时,误差也越大.
在圆薄板受预张力下的线性理论研究基础上,推导出圆薄板受预张力下的非线性控制方程.使用HAM对控制方程进行求解,分析并讨论圆薄板在预张力和均布横向载荷作用下的变形特性以及中心挠度与压力的非线性偏差,给出测量膜片的预张力和厚度对差压式电容传感器输出特性的影响.
1 圆薄板变形的控制方程与边界条件
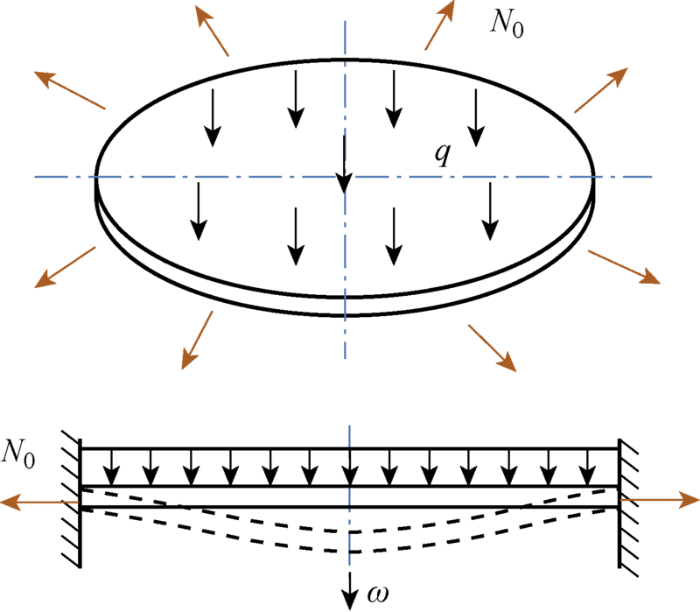
考虑图1所示半径为a、厚度为h的圆形夹支薄板受到单位长度的预张力N0与均布横向载荷q的联合作用,设薄板内任一点距离薄板圆心为r处的径向位移(加预张力后)为u,横向挠度为ω, 以及径向应变为εt,切向应变为εt,则大挠度板的应变可表示为
式中:
图1
图1
受预张力与均布横向载荷作用下的夹支圆薄板示意图
Fig.1
Diagram of clamped circular thin plate subjected to pretension and uniform lateral load
根据弹性理论可得到:
式中:Nr和Nt分别为单位长度的径向和切向薄膜张力;
基于小转角的假设,通过对薄板内任一点r处的静力及力矩平衡分析,得到平衡方程为
式中:
结合式(2)~(5)即可得到von Kármán圆板大挠度控制方程:
当r=a时,边界条件为
当r=0时,dω/dr和Nr 均为有限值.由于
当圆板为小挠度即挠度相对于板厚为小量时,增加的薄膜张力
文献[5]应用贝塞尔函数给出了式(10)的解为
式中:
在小挠度的情况下,由式(11)可以看出各点的挠度
2 圆薄板变形分析与求解
引入以下无量纲参数:
其中: y为半径的无量纲量;W为挠度的无量纲量;
当y=0和y=1时,对应的边界条件分别为
式中:
为了方便求解,需进一步将微分方程转化成积分方程,使用解微分方程常见的格林函数法[15],得到等价的积分方程为
式中: y和ξ为格林函数K(y,ξ)和G(y,ξ)的变量,0≤y,ξ≤1.函数表示为
HAM[16]是取得该方程近似解析解的一种有效方法.在已知Q和S0的情况下,构造如下零阶变形方程:
式中: p为嵌入变量;c为收敛控制参数;
关于变量
其中:
如果以上级数在p=1时收敛,则可以得到级数解:
将零阶变形方程中p的同幂次项进行合并,得到n阶变形方程:
由此,可以把式(19)和(20)的部分和作为式(15)和(16)的近似解析解:
并且,可以将多项式函数作为解表达式的基函数,选择符合边界条件式(14)的初始近似解:
为提高求解效率,采用文献[16]中的迭代技术,将m阶的同伦近似解作为新的初始近似解进行M次迭代运算.借助MATLAB软件中的多项式系列函数进行迭代运算,可以获得良好的求解速度.另外收敛控制参数c的最优值选取主要依据控制方程式(15)和(16)的最小化平方余量残差:
表1为一部分不同
表1
部分不同
Tab.1
| S0 | Q | m | M | c | Emin | 计算时间/s |
|---|---|---|---|---|---|---|
| [0, 40] | [0, 400] | 2 | 110 | -0.1 | (0, 10-20) | 0.07 |
| [0, 150] | [0, 1 000] | 2 | 300 | -0.04 | (0, 10-20) | 0.11 |
| [0, 700] | [0, 4 200] | 4 | 700 | -0.01 | (0, 10-20) | 0.35 |
| [0, 1 500] | [0, 19 000] | 10 | 5000 | -0.001 | (0, 10-20) | 8.00 |
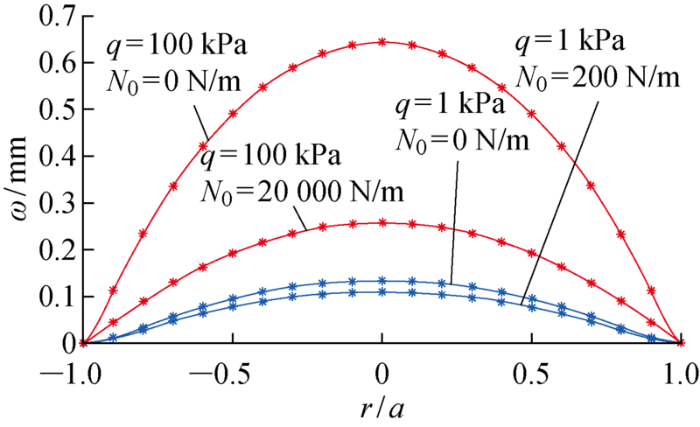
FEM通常可以提供高精度的数值解,使用ANSYS有限元软件对计算数据做进一步对比验证.选择SHELL181单元构建圆薄板的实体模型,板的半径a=15 mm,板厚h=0.04 mm.SHELL181采用Reissner-Mindlin理论, 考虑了板横向剪切变形的影响, 从薄板到厚板都具有很强的适用性.使用HAM和FEM计算了有预张力和无预张力的解析解和数值解,圆板直径方向上的挠度曲线如图2所示,其中,实线表示HAM解,星号表示FEM解,可以看出HAM的挠度曲线与FEM的挠度曲线吻合度非常高.另外表2展示了当a=15 mm,h=0.04 mm时,在载荷 q=100,10,1 kPa下的6组FEM和HAM的中心挠度数据对比,显示最大的中心挠度结果偏差仅为0.38%.表中:ω0为中心挠度;结果偏差为FEM和HAM求解的挠度与FEM求解的挠度之比.由此对于夹支圆薄板的挠度变形问题,通过与FEM数值解的对比,验证了文中大挠度理论方程及近似解析解的有效性.
图2
图2
圆板直径方向上的FEM解与HAM解的挠度曲线对比图
Fig.2
Comparison of deflection curves between FEM and HAM solution in diameter direction of circular plate
表2 FEA解和HAM解的中心挠度对比
Tab.2
| q/kPa | N0/ (N·m-1) | ω0/mm | 结果 偏差/% | |
|---|---|---|---|---|
| FEM | HAM | |||
| 100 | 20 000 | 0.257 76 | 0.257 60 | 0.06 |
| 100 | 0 | 0.644 18 | 0.642 88 | 0.20 |
| 10 | 2 000 | 0.192 92 | 0.192 45 | 0.24 |
| 10 | 0 | 0.295 53 | 0.295 38 | 0.05 |
| 1 | 200 | 0.109 05 | 0.108 64 | 0.38 |
| 1 | 0 | 0.132 99 | 0.132 96 | 0.02 |
3 挠度的非线性分析
由计算可知,预张力可以使挠度增长变慢并在一定范围内趋于线性,此时得到的简化线性解式(11)计算误差较小.随着压力q的增大,简化线性解的误差也越大,以中心挠度分析其非线性特性.
对解式(11)无量纲化为
式中:
相应的中心挠度为
考虑中心挠度的线性偏差为
由式(24)和(25)可得:
令
将式(27)带入式(15)可得:
使用HAM求解式(28)和(16),即可得到不同δ值下的解析解.
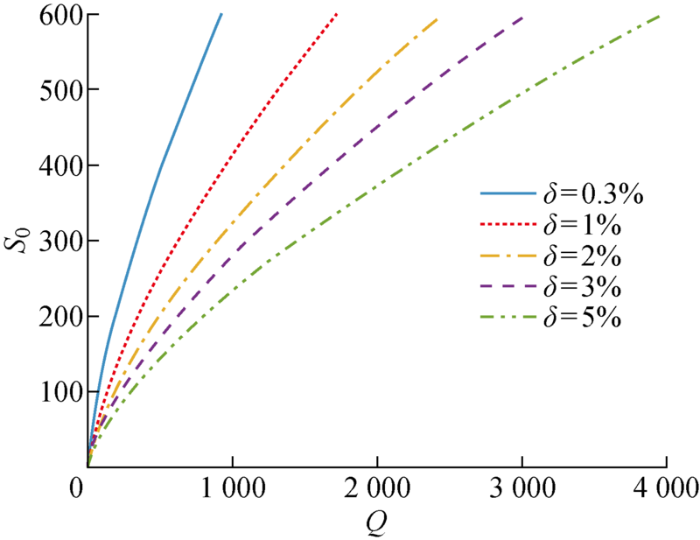
在δ=0.3%,1%,2%,3%,5%时,S0与Q的对应关系如图3所示,其中关系曲线与横坐标分别相交于Q=0.519 2,0.903 6,1.289 9,1.594 9,2.097 9 的点上,表示为在无预张力作用下,达到相应线性偏差的无量纲压力值.各曲线的左边区域表明von Kármán方程求解得到的中心挠度线性偏差小于对应的值,同时也表明使用简化方程求解的挠度值具有相对可靠的精度.
图3
图3
不同中心挠度线性偏差下的S0与Q的关系
Fig.3
S0 versus Q at different center deflection linear deviations
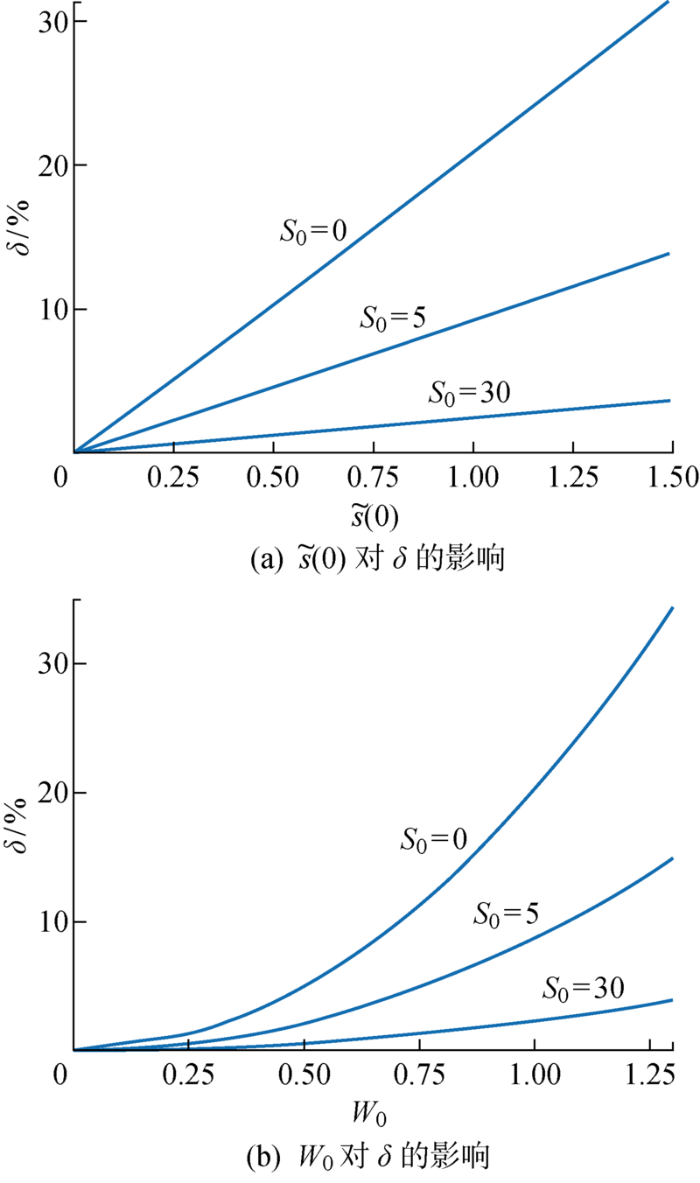
板抵抗外力变形的能力由弯曲内力和薄膜张力提供,而薄膜张力是由于板的绷紧拉伸变形而产生的平行于板中面的内力,由初始薄膜力和因挠曲变形而增加的薄膜力组成.在小挠度的情况下,增加的薄膜力可以忽略,弯矩、横向载荷以及初始薄膜力形成力学平衡,得到简化方程式(10),此时挠度值与压力成线性关系.当挠度随压力继续增大,增加的薄膜力随着板的进一步拉伸也逐渐增大, 此时由弯矩、初始薄膜力和增加的薄膜力共同抵抗横向载荷,形成大挠度控制方程组,其中式(8)表明增加的薄膜力
图4
图4
不同S0下中心挠度线性偏差的变化
Fig.4
Variation of linear deviation of central deflection at different S0 values
4 差压式电容传感器输出特性分析
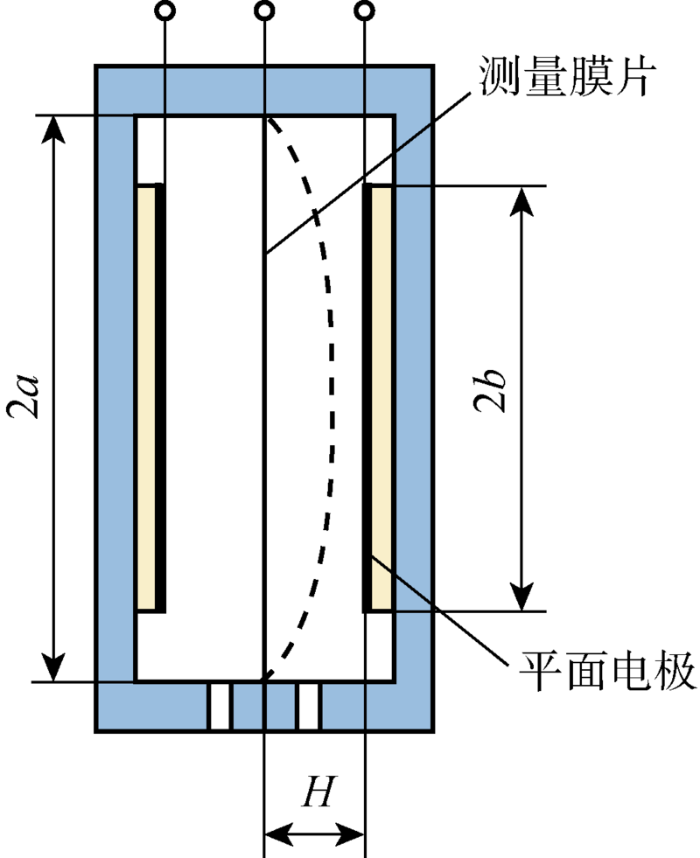
为研究板的变形特性对电容式压力传感器输出特性的影响,利用差压式传感器的实例进行分析.图5所示传感器的固定电极结构为圆形平面电极,作为传感器中心电极的测量膜片半径为a=15 mm,膜片的厚度为h,固定电极平行于中心电极,其半径为b=10.5 mm,固定电极与中心电极的距离为 H=0.1 mm.
图5
图5
差压式电容传感器结构示意图
Fig.5
Structure diagram of differential pressure capacitance sensor
考虑差动结构中低压腔电极间的电容为C1,高压腔电极间的电容为C2,无压力时初始电容C0=C1=C2,真空介电常数为ε0,电介质的介电常数为εr,本文电介质按干燥空气进行计算且假设恒定,εr=1.000 53.则电容的计算公式分别为
在差动电容结构中,将低压端和高压端电容的对比变化值
表3
500 Pa量程在不同膜厚和不同挠度线性偏差下的
Tab.3
| h/ mm | qmax/ Pa | Qmax | δ= 5% | δ= 1% | |||
|---|---|---|---|---|---|---|---|
| S0 | N0/ (N·m-1) | S0 | N0/ (N·m-1) | ||||
| 0.02 | 500 | 1 372.32 | 289 | 489.3 | 514.6 | 871.3 | |
| 0.03 | 500 | 271.08 | 93.3 | 533.1 | 168.5 | 962.9 | |
| 0.04 | 500 | 85.77 | 40.6 | 549.9 | 74.9 | 1 014.5 | |
| 0.05 | 500 | 35.13 | 20.5 | 542.3 | 39.1 | 1 034.4 | |
图6
图6
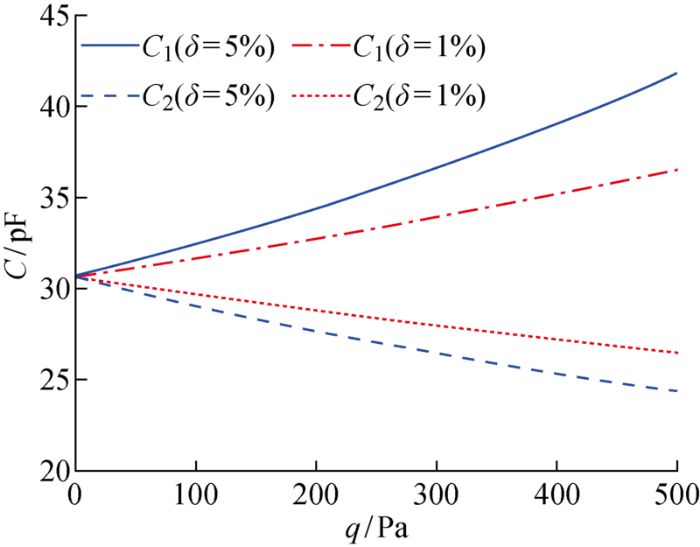
不同挠度线性偏差下低压端和高压端压力-电容特性曲线(h=0.05 mm)
Fig.6
Pressure-capacitance characteristic curves of low and high pressure parts at different deflection linear deviations (h=0.05 mm)
利用得到图6的相同方法,除了可以得到其他膜厚下的压力-电容特性曲线,也可以得到压力与输出量
表4 不同膜厚和不同挠度线性偏差下的灵敏度和输出非线性误差
Tab.4
| h/mm | δ= 5% | δ= 1% | |||||
|---|---|---|---|---|---|---|---|
| 低压端 灵敏度/(pF·Pa-1) | 高压端 灵敏度/(pF·Pa-1) | 非线性 误差/% | 低压端 灵敏度/(pF·Pa-1) | 高压端 灵敏度/(pF·Pa-1) | 非线性 误差/% | ||
| 0.02 | 0.039 4 | -0.016 8 | 0.86 | 0.018 3 | -0.011 3 | 0.15 | |
| 0.03 | 0.030 8 | -0.015 0 | 0.94 | 0.015 1 | -0.010 0 | 0.17 | |
| 0.04 | 0.025 8 | -0.013 7 | 0.95 | 0.013 2 | -0.009 1 | 0.18 | |
| 0.05 | 0.022 4 | -0.012 6 | 0.94 | 0.011 7 | -0.008 4 | 0.18 | |
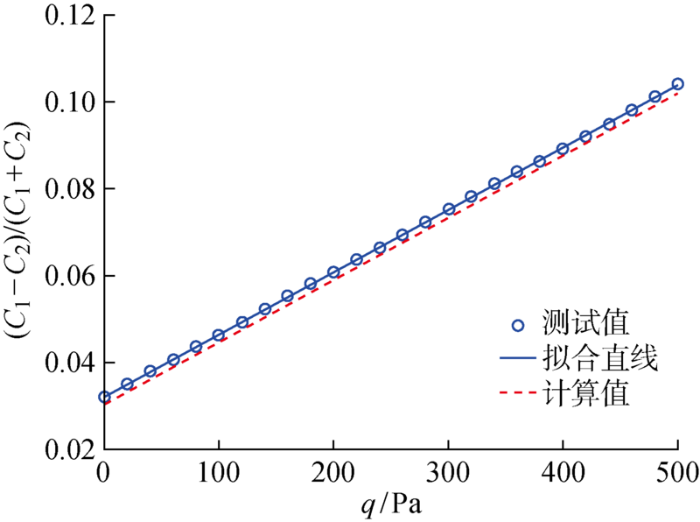
5 测试结果
图7
表5 传感器实际结构参数
Tab.5
| 传感器参数 | 数值 | 传感器参数 | 数值 |
|---|---|---|---|
| a/mm | 15 | H1/mm | 0.32 |
| h/mm | 0.02 | H2/mm | 0.34 |
| b/mm | 10.5 | N0/(N·m-1) | 840 |
图8
6 结论
本文研究了夹支圆板在预张力和均布横向载荷联合作用下的挠曲变形问题,参照von Kármán方程推导了相关公式,应用HAM并借助计算机程序求解出了近似解析解,同时对比FEM的数值解,验证了理论公式及求解方法的有效性.此外,通过对简化线性解和精确非线性解的对比分析,发现新增薄膜张力是造成板挠度非线性变化的主要因素.并得到了不同中心挠度线性偏差下的预张力和横向均布载荷的关系:预张力越大,横向均布载荷越小,板挠度的线性偏差越小.
研究板挠度的非线性特性对掌握电容式压力传感器的输出特性具有重要的现实意义.利用板挠度的非线性理论结果,可以指导差压式电容传感器测量膜片的参数设计,并以一种差压式电容传感器的结构为例,按照中心挠度线性偏差δ在5%和1%的情况下,计算传感器的非线性误差.结果表明:δ=5%时的非线性误差是δ=1%时的5倍左右,预张力可以显著降低传感器输出的非线性误差,至于预张力增加而带来的灵敏度降低的问题,可以通过减小膜片的厚度来弥补.最后,结合差压式电容传感器的性能测试,验证了本文对膜片预张力和非线性进行计算分析的合理性和正确性.
参考文献
Fabrication of single capacitive type differential pressure sensor for differential flow meter
[J].DOI:10.6117/kmeps.2017.24.1.051 URL [本文引用: 1]
Differential pressure transmitter with unified electronics unit
[J].DOI:10.1109/JSEN.7361 URL [本文引用: 1]
基于电容式传感器的非接触式液位测量系统
[J].
Non-contact liquid level measurement system based on capacitive sensor
[J].
Development of a system for measuring head differential pressure and density of working fluid at high pressures
[J].DOI:10.1016/j.measurement.2018.08.065 URL [本文引用: 1]
Application of the homotopy perturbation method for the large deflection problem of a circular plate
[J].DOI:10.1016/j.apm.2014.09.001 URL [本文引用: 1]
Analytic solutions of von Kármán plate under arbitrary uniform pressure—Equations in differential form
[J].DOI:10.1111/sapm.2017.138.issue-4 URL [本文引用: 1]
Analytic approximations of von Kármán plate under arbitrary uniform pressure—Equations in integral form
[J].
Large deflection analysis of axially symmetric deformation of prestressed circular membranes under uniform lateral loads
[J].
DOI:10.3390/sym12081343
URL
[本文引用: 1]

In this study, the problem of axisymmetric deformation of peripherally fixed and uniformly laterally loaded circular membranes with arbitrary initial stress is solved analytically. This problem could be called the generalized Föppl–Hencky membrane problem as the case where the initial stress in the membrane is equal to zero is the well-known Föppl–Hencky membrane problem. The problem can be mathematically modeled only in terms of radial coordinate owing to its axial symmetry, and in the present work, it is reformulated by considering an arbitrary initial stress (tensile, compressive, or zero) and by simultaneously improving the out-of-plane equilibrium equation and geometric equation, while the formulation was previously considered to fail to improve the geometric equation. The power-series method is used to solve the reformulated boundary value problem, and a new and more refined analytic solution of the problem is presented. This solution is actually observed to be able to regress into the well-known Hencky solution of zero initial stress, allowing the considered initial stress to be zero. Moreover, the numerical example conducted shows that the obtained power-series solutions for stress and deflection converge very well, and have higher computational accuracy in comparison with the existing solutions.
Large deflection of clamped circular plate and accuracy of its approximate analytical solutions
[J].
基于微机电系统的水下灵巧手触觉力测量传感器
[J].
Tactile force sensor of underwater dexterous hand based on micro electromechanical system
[J].
圆薄板轴对称弯曲问题的基本方程讨论
[J].
Discussions on the fundamental equations for axisymmetric thin circular plates
[J].
Pressurized axisymmetric membrane deforming into a prescribed shape
[J].DOI:10.1016/j.ijsolstr.2020.04.021 URL [本文引用: 1]
Determination of large deflections for elastic circular plate
[J].
DOI:10.1680/jencm.17.00019
URL
[本文引用: 1]

Elastic large deflections of a clamped circular plate subjected to uniform normal pressure are governed by a system of ordinary nonlinear differential equations of the fifth order. The solution of the system must satisfy the given boundary conditions at the centre and the edge of the plate. An analytical solution of this boundary-value problem is not feasible. The numerical solution of the problem using the shooting method is reported in this paper. Integration of differential equations is carried out by the Runge–Kutta method. The method of embedded polygons is used to find initial values of deflections at the edge of the plate. The idea of the method is to construct a sequence of embedded polygons in Euclidean phase space that converge to a single point that maps the desired solution. Polygon vertices are determined under the assumption that each of the boundary conditions is a function of only one of the unknowns in the set of initial conditions. On the basis of this algorithm, a computer program has been developed. Numerical examples illustrate the capabilities of the program. The results of solving examples are presented in the form of graphs of distributions of deflections and stresses in the plate.
格林公式在微分方程中的应用
[J].
Application of Green’s formula in differential equations
[J].DOI:10.12677/AAM.2018.79137 URL [本文引用: 1]