深海钻井立管系统遭遇极端环境或特殊状况时需要将底部的下部海洋立管总成(LMRP)系统与防喷器组(BOP)进行紧急解脱,解脱后立管系统在张紧器预存过提力作用下加速向上运动,称之为反冲运动[1 ] .立管反冲是一个极其危险的过程,反冲过高会导致立管系统撞击钻台,导致伸缩节、分流器等顶部设备损坏;反冲过低会导致底部触底,从而引发立管系统弯曲或折断[2 ] .随着当前油气勘探向深水和超深水进军,所面临的环境与操作风险越发严峻,发生紧急解脱的概率也越来越高.2020年10月墨西哥湾某钻井船遭遇飓风Zeta,解脱后立管系统剧烈反冲,与船体多次碰撞,LMRP多次触碰海底,造成张紧器、伸缩节、立管、LMRP等多部位严重损坏.因此,开展深海钻井立管系统紧急解脱反冲及控制研究对保障安全钻探具有重要意义.
众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲.
综上所述,如何在仅有名义立管系统模型的基础上,构建可自适应系统参数不确定性的立管反冲控制方法,从而有效进行反冲控制是目前亟需解决的难题.依据反冲动力学名义模型与闭环系统稳定性根分布特征,构建考虑模型不确定性的立管反冲控制方程,采用径向基(RBF)神经网络逼近系统模型不确定性并选取稳定的自适应律,最终建立考虑系统模型不确定性的深海钻井立管系统实时自适应反冲控制策略,该方法解决了工程中立管系统无精确力学参数时的反冲控制难题.
1 立管系统反冲控制动力学模型
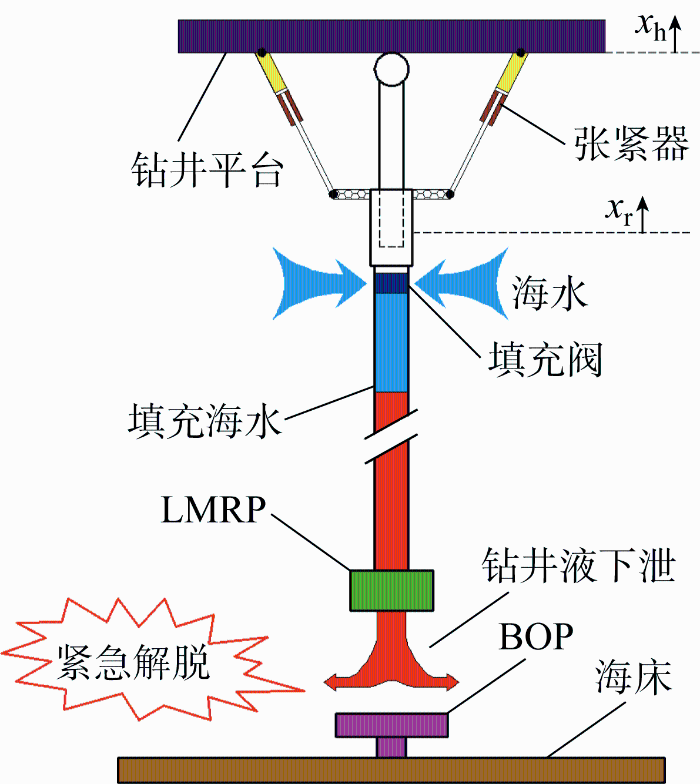
深海钻井立管系统紧急解脱及反冲重点关注其轴向动力响应,需同时防止底部碰撞海底与顶部达到张紧器冲程极限、冲击钻台.立管反冲最危险的是轴向的响应且反冲控制只能通过反冲控制阀调控,立管系统顶部横向无其他作动器,因此波流等横向环境载荷在反冲动力学分析与控制中通常不考虑[16 ] .平台升沉响应幅值算子(RAO)受波浪参数影响,从而影响立管轴向反冲响应.立管紧急脱离及反冲示意图如图1 所示,其中x h 为平台升沉,x r 为立管系统轴向位移.解脱后,立管系统在张紧器作用下加速向上反冲,同时为降低立管压溃等失效风险,将内部钻井液释放入海水,并从填充阀填充密度较轻的海水,整个反冲过程为下泄钻井液与立管系统耦合的过程.
图1
图1
立管紧急脱离及反冲示意图
Fig.1
Schematic diagram of riser emergency disconnection and recoil
对立管反冲进行动力学建模,立管系统本质上是一个无限维度的连续弹性体,常规立管动力学分析中,多采用有限元方法或集中质量法.Wang等[17 ] 证明了立管有限元段数对反冲轴向位移影响有限,且立管系统解脱后的振动频率主要受张紧器等效刚度影响.因此,直接假设立管系统为一刚性体,该假设与立管反冲位移测量一致,平台上反冲过程中通常只能测量顶部位移,底部反冲位移不易测量,可通过立管系统的形变量进行反演.
采用六缸直接作用式张紧器,单个液压缸的原理图如图2 所示.张紧器及控制系统由低压氮气瓶、液压缸、反冲控制阀、蓄能器、卸荷回路、高压空气瓶(APV)等结构组成.紧急解脱反冲时,调控反冲控制阀阀口开度是控制反冲的唯一途径.
图2
图2
张紧器原理图
Fig.2
Schematic diagram of tensioner system
假设张紧器气液变化过程为绝热过程,考虑张紧器内部的阻尼效应及阀口损失,直接给出张紧器经泰勒展开式近似之后的等效方程式为
$ \begin{array}{l}F_{\mathrm{t}}=N_{\mathrm{t}}\left[\left(p_{\mathrm{h}, 0} A_{\mathrm{r}}-p_{\mathrm{l}, 0} A_{\mathrm{p}}\right)-\right. \\\left.\quad\left(\frac{n p_{\mathrm{h}, 0} A_{\mathrm{r}}^{2}}{V_{\mathrm{h}, 0}}+\frac{n p_{1,0} A_{\mathrm{p}}^{2}}{V_{1,0}}\right) x_{\mathrm{p}}-C_{\mathrm{T}} \dot{x}_{\mathrm{p}}-\zeta \frac{\rho_{\mathrm{o}}\dot{x}_{\mathrm{p}}^{3} A_{\mathrm{r}}^{3}}{2\left|\dot{x}_{\mathrm{p}}\right| \lambda^{2} A^{2}}\right]\end{array}$
(1) F 0 = N t ( p h , 0 A r - p l , 0 A p ) K t = N t n p h , 0 A r 2 V h , 0 + n p l , 0 A p 2 V l , 0 C t = N t C T , u = N t ζ ρ o x · p 3 A r 3 2 x · p λ 2 A 2
式中:F t 为张紧器系统提供的顶张力;N t = 6,表示张紧器系统共有6个液压缸;p h,0 为初始高压压力;A r 为有杆腔截面积;p l,0 为初始低压压力;A p 为无杆腔截面积;n 为气体常数;V h,0 为初始高压气体体积;V l,0 为初始低压气体体积;x p = x r -x h ,为活塞杆相对于液压缸的位移;ζ 为压损系数;ρ o 为液压油密度;A 为反冲控制阀阀口最大通流截面积;λ 为阀口开度,取0~1;F 0 为张紧器系统初始等效顶张力;K t 为张紧器系统实际等效刚度;C T 和C t 分别为单个张紧器和张紧器系统的等效阻尼系数;u 为阀口的压力损耗,也是反冲控制的输入量;某深水钻井平台张紧器各液压缸轴向夹角小于6°,最大夹角不超过10°,因此忽略张紧器轴向夹角.张紧器液压油流动具有方向性,且反冲控制阀的阀口开度在0~1范围内变化,因此立管反冲控制属于被动调控的受限控制,只是按照最佳调控趋势进行的控制.
根据牛顿第二定律和式(1),给出立管系统的等效力学平衡方程,以矩阵的形式表示:
(2) $\begin{array}{c}\boldsymbol{M} \ddot{x}_{\mathrm{r}}+C_{\mathrm{t}} \dot{x}_{\mathrm{r}}+K_{\mathrm{t}} x_{\mathrm{r}}=-u+F_{0}+K_{\mathrm{t}} x_{\mathrm{h}}+ \\C_{\mathrm{t}} \dot{x}_{\mathrm{h}}-\boldsymbol{M} g+F_{\mathrm{b}}-F_{\mathrm{f}}-F_{\mathrm{w}}\end{array}$
式中:M F b 为立管所受海水浮力;F f 为钻井液下泄摩擦力;F w 为立管反冲过程中的轴向水动力阻尼力;F f 和F w 默认方向为x r 负方向;g 为重力加速度.令d =F 0 +K t x h +C t x · h - M gF b -F f -F w ,d 视为干扰项.对单一单元的F w 求解采用下式:
(3) $F_{\mathrm{w}}=\frac{1}{2} \rho_{\mathrm{w}} D_{\mathrm{h}} \pi C_{\mathrm{w}} \dot{x}_{\mathrm{r}}\left|\dot{x}_{\mathrm{r}}\right| L$
式中:ρ w 为海水密度;D h 为立管水动力外径;C w 为立管外部的无量纲轴向水动力阻尼系数[5 ] ;L 为立管长度.
钻井液下泄采用整体液柱模型(WFCM)进行表征.WFCM更便于与立管运动耦合,且具有较高精度[18 -19 ] ,通过迭代求解可以求得钻井液下泄对管壁的摩擦力:
(4) $\begin{array}{l}-\rho_{\mathrm{w}} g A_{\mathrm{e}} L_{\mathrm{w}}-\rho_{\mathrm{m}} g A_{\mathrm{e}}\left(L-L_{\mathrm{w}}\right)+ \\\quad 2 f_{\mathrm{w}} \frac{A_{\mathrm{e}}}{D_{\mathrm{e}}} \rho_{\mathrm{w}} v^{2} L_{\mathrm{w}}+2 f_{\mathrm{m}} \frac{A_{\mathrm{e}}}{D_{\mathrm{e}}} \rho_{\mathrm{m}} v^{2}\left(L-L_{\mathrm{w}}\right)+ \\\quad \rho_{\mathrm{w}} \mathrm{~g} A_{\mathrm{e}} L+\frac{1}{2} \rho_{\mathrm{m}} A_{\mathrm{e}} v^{2}= \\\quad\left[\rho_{\mathrm{w}} A_{\mathrm{e}} L_{\mathrm{w}}+\rho_{\mathrm{m}} A_{\mathrm{e}}\left(L-L_{\mathrm{w}}\right)\right] a\end{array}$
式中:ρ m 为钻井液密度;A e 为立管内截面积;L w 为立管内填充海水长度;v 为钻井液下泄速度;a 为钻井液下泄加速度;D e 为立管内径;f w 和f m 分别为海水与钻井液的摩阻系数.
(5) x 0 =0
立管紧急解脱后最终会达到一个平衡态,将其平衡态作为反冲控制的期望.期望位置x d 、期望速度 x · d x ¨ d x d 可以是动态变化形状也可是静态位置,但需大于0,以避免反冲触底.x · d x ¨ d
(6) $x_{\mathrm{d}}=\frac{F_{0}-M g+F_{\mathrm{b}}}{K_{\mathrm{t}}}+x_{\mathrm{h}}, \quad \dot{x}_{\mathrm{d}}=0, \quad \ddot{x}_{\mathrm{d}}=0$
实际与期望之间的位移e 、速度误差e · e ¨
(7) $e=x_{\mathrm{r}}-x_{\mathrm{d}}, \quad \dot{e}=\dot{x}_{\mathrm{r}}-\dot{x}_{\mathrm{d}}, \quad \ddot{e}=\ddot{x}_{\mathrm{r}}-\ddot{x}_{\mathrm{d}}$
2 立管系统不确定性表征与自适应控制器
2.1 基于RBF神经网络的立管不确定性逼近
对控制输入u d =0,且不存在建模不确定部分时,控制器可为
(8) $\boldsymbol{u}=-\boldsymbol{M}\left(\ddot{x}_{\mathrm{d}}-k_{\mathrm{d}} \dot{e}-k_{\mathrm{p}} e\right)-C_{\mathrm{t}} \dot{x}_{\mathrm{r}}-K_{\mathrm{t}} x_{\mathrm{r}}$
将式(8)代入式(2),根据闭环系统稳定性根分布特征,选取常数k d 与k p ,使
(9) $\ddot{e}+k_{\mathrm{d}} \dot{e}+k_{\mathrm{p}} e=0$
式中:k d 等同于PID的微分系数;k p 等同于比例系数.满足式(9)即满足控制系统的拉氏方程的解为负值,则所有根部位于复平面的左半开部分,系统渐进稳定.
假设名义模型分别为已知量M 0 、K t0 、C t0 ,与式(8)相似,直接以名义模型代替实际模型作为反冲控制计算量,则针对名义模型的通过阀口调节得到的控制输入为
(10) $\boldsymbol{u}=-\boldsymbol{M}_{0}\left(\ddot{x}_{\mathrm{d}}-k_{\mathrm{d}} \dot{e}-k_{\mathrm{p}} e\right)-C_{\mathrm{t} 0} \dot{x}_{\mathrm{r}}-K_{\mathrm{t} 0} x_{\mathrm{r}}$
(11) $\left.\begin{array}{l}\Delta \boldsymbol{M}=\boldsymbol{M}_{0}-\boldsymbol{M}, \quad \Delta C_{\mathrm{t}}=C_{\mathrm{t} 0}-C_{\mathrm{t}} \\\Delta K_{\mathrm{t}}=K_{\mathrm{t} 0}-K_{\mathrm{t}}\end{array}\right\}$
将式(10)和式(11)代入式(2),得到稳态控制方程关系式[20 ] :
(12) $\begin{array}{l}\ddot{e}+k_{\mathrm{d}} \dot{e}+k_{\mathrm{p}} e= \\\quad \boldsymbol{M}_{0}^{-1}\left(\Delta \boldsymbol{M} \ddot{x}_{\mathrm{r}}+\Delta C_{\mathrm{t}} \dot{x}_{\mathrm{r}}+\Delta K_{\mathrm{t}} x_{\mathrm{r}}+d\right)\end{array}$
式(12)表示动力学模型的不确定部分会导致控制性能的下降,需要对不确定部分进行逼近和补偿,等式右边代表控制模型整体不确定部分,令
(13) $f=\boldsymbol{M}_{0}^{-1}\left(\Delta \boldsymbol{M} \ddot{x}_{\mathrm{r}}+\Delta C_{\mathrm{t}} \dot{x}_{\mathrm{r}}+\Delta K_{\mathrm{t}} x_{\mathrm{r}}+d\right)$
(14) $\begin{aligned}\dot{\boldsymbol{E}} & =\boldsymbol{A} \boldsymbol{E}+\boldsymbol{B} \boldsymbol{f}, \quad \boldsymbol{E}=\left[\begin{array}{ll}e & \dot{e}\end{array}\right]^{\mathrm{T}} \\\boldsymbol{A} & =\left[\begin{array}{cc}0 & \boldsymbol{I} \\-k_{\mathrm{p}} & -k_{\mathrm{d}}\end{array}\right], \quad \boldsymbol{B}=\left[\begin{array}{ll}0 & \boldsymbol{I}\end{array}\right]^{\mathrm{T}}\end{aligned}$
若不确定部分f
(15) $\begin{aligned}\boldsymbol{u}= & -\boldsymbol{M}_{0}\left(\ddot{x}_{\mathrm{d}}-k_{\mathrm{d}} \dot{e}-k_{\mathrm{p}} e\right)- \\& C_{\mathrm{t} 0} \dot{x}_{\mathrm{r}}-K_{\mathrm{t} 0} x_{\mathrm{r}}+\boldsymbol{M}_{0} f\end{aligned}$
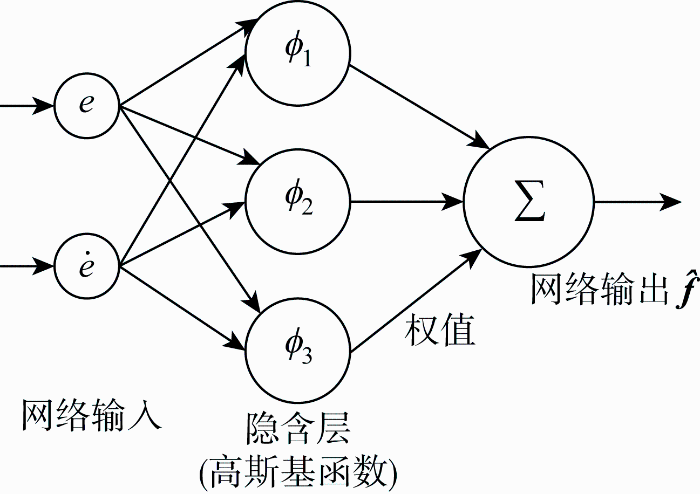
模型不确定部分f 是难以测量的,采用RBF神经网络对不确定部分进行逼近[21 ] .RBF神经网络是在控制领域最常用的一种神经网络,采用高斯基函数,是单隐层的3层前馈神经网络,如图3 所示.理论上RBF神经网络可以对任何未知非线性函数进行任意精度范围的逼近,属于局部逼近的神经网络,其独特的结构类型可大大加快学习速度并避免局部极小问题,适合实时控制的要求.
图3
图3
RBF神经网络结构
Fig.3
Structure of RBF neural network
RBF神经网络输入为误差状态E f
(16) $\left.\begin{array}{l}\phi_{i}=\exp \left(-\left\|\boldsymbol{E}-\boldsymbol{c}_{i}\right\|^{2} / b_{i}^{2}\right), \quad i=1,2, \cdots, s \\\hat{\boldsymbol{f}}=\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{\varphi}(\boldsymbol{E}), \quad \boldsymbol{\varphi}=\left[\begin{array}{llll}\phi_{1} & \phi_{2} & \cdots & \phi_{s}\end{array}\right]\end{array}\right\}$
式中:c i i 个隐层神经元的中心点向量值;bi 为隐含层神经元i 的高斯基函数宽度;φ θ s 为隐含层结点数;$\hat{f}$为神经网络对不确定部分的估计输出. 假设估计输出$\hat{f}$连续有界,存在极小正值ε 0 ,使理想的估计输出$\hat{\boldsymbol{f}}\left(\boldsymbol{E}, \boldsymbol{\theta}^{*}\right)$满足[22 ]
(17) $\left.\begin{array}{l}\max \left\|\hat{\boldsymbol{f}}\left(\boldsymbol{E}, \boldsymbol{\theta}^{*}\right)-\boldsymbol{f}(\boldsymbol{E})\right\| \leqslant \varepsilon_{0} \\\boldsymbol{\theta}^{*}=\arg \min _{\theta \in \beta\left(M_{\theta}\right)}\left\{\sup _{E \in \beta\left(M_{E}\right)}\|\boldsymbol{f}(\boldsymbol{E})-\hat{\boldsymbol{f}}(\boldsymbol{E}, \boldsymbol{\theta})\|\right\}\end{array}\right\}$
式中:$\boldsymbol{\theta}^{*}$为n 阶方阵,是$\boldsymbol{f}(\boldsymbol{E}) $的最佳逼近权值;$\boldsymbol{f}(\boldsymbol{E})$即为式(13)的$\boldsymbol{f} $,与误差$\boldsymbol{E} $有关.
取$\left\|\boldsymbol{\theta}^{*}\right\|_{\mathrm{F}} \leqslant \boldsymbol{\theta}_{\text {max }}$为有界函数,则控制系统关于误差的状态方程为
(18) $\left.\begin{array}{rl}\dot{\boldsymbol{E}} & =\boldsymbol{A} \boldsymbol{E}+\boldsymbol{B}\left(\hat{\boldsymbol{f}}\left(\boldsymbol{E}, \boldsymbol{\theta}^{*}\right)+\boldsymbol{\eta}\right) \\\boldsymbol{\eta} & =\boldsymbol{f}(\boldsymbol{E})-\hat{\boldsymbol{f}}\left(\boldsymbol{E}, \boldsymbol{\theta}^{*}\right)\end{array}\right\}$
式中:$\boldsymbol{\eta}$为神经网络理想逼近误差,误差有界为$ \boldsymbol{\eta}_{0}, \boldsymbol{\eta}_{0}=\sup \|\boldsymbol{f}(\boldsymbol{E})-\hat{\boldsymbol{f}}(\boldsymbol{E}, \boldsymbol{\theta})\| $.神经网络最佳估计 $ \hat{\boldsymbol{f}}(\boldsymbol{E}, \boldsymbol{\theta})=\boldsymbol{\theta}{ }^{\mathrm{T}} \boldsymbol{\varphi}(\boldsymbol{E})$,则
(19) $\dot{\boldsymbol{E}}=\boldsymbol{A} \boldsymbol{E}+\boldsymbol{B}\left(\boldsymbol{\theta}^{* \mathrm{~T}} \boldsymbol{\varphi}(\boldsymbol{E})+\boldsymbol{\eta}\right)$
2.2 自适应控制器设计
根据式(15)修正的控制器,结合RBF神经网络对不确定部分的估计输出,设计控制输入为
(20) $\left.\begin{array}{c}\boldsymbol{u}=-\boldsymbol{M}_{0}\left(\ddot{x}_{\mathrm{d}}-k_{\mathrm{d}} \dot{e}-k_{\mathrm{p}} e\right)- \\C_{\mathrm{t} 0} \dot{x}_{\mathrm{r}}-K_{\mathrm{t} 0} x_{\mathrm{r}}+\boldsymbol{M}_{0} \hat{\boldsymbol{f}} \\\hat{\boldsymbol{f}}=\hat{\boldsymbol{\theta}}^{\mathrm{T}} \boldsymbol{\varphi}(\boldsymbol{E})\end{array}\right\}$
式中:$\hat{\boldsymbol{\theta}}$为$\boldsymbol{\theta}^*$的估计值.将式(20)代入方程(2)中,结合式(11)和(12),可得
(21) $\begin{aligned}\ddot{e}+k_\mathrm{d}\dot{e}+k_\mathrm{p}e+\hat{f}(E,\boldsymbol{\theta}) & = \\\boldsymbol{M}_0^{-1}\left(\Delta\boldsymbol{M}\ddot{x}_\mathrm{r}+\Delta C_\mathrm{t}\dot{x}_\mathrm{r}+\Delta K_\mathrm{t}x_\mathrm{r}+d\right)\end{aligned}$
(22) $\dot{\boldsymbol{E}}=\boldsymbol{A} \boldsymbol{E}+\boldsymbol{B}(\boldsymbol{f}(\boldsymbol{E})-\hat{\boldsymbol{f}}(\boldsymbol{E}, \boldsymbol{\theta}))$
令$\widetilde{\boldsymbol{\theta}}=\boldsymbol{\theta}^*-\hat{\boldsymbol{\theta}}$,得到
(23) $\boldsymbol{f}(\boldsymbol{E})-\hat{\boldsymbol{f}}(\boldsymbol{E}, \boldsymbol{\theta})=\boldsymbol{\eta}+\widetilde{\boldsymbol{\theta}}^{\mathrm{T}} \boldsymbol{\varphi}(\boldsymbol{E})$
任取$\gamma>0$,定义满足非负的Lyapunov函数为
(24) $V=\frac{1}{2} \boldsymbol{E}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{E}+\frac{1}{2 \gamma}\|\widetilde{\boldsymbol{\theta}}\|_{\mathrm{F}}^{2}$
(25) $\boldsymbol{P A}+\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P}=-Q$
(26) $\begin{aligned}\dot{V}= & \frac{1}{2}\left[\boldsymbol{E}^{\mathrm{T}} \boldsymbol{P} \dot{\boldsymbol{E}}+\dot{\boldsymbol{E}}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{E}\right]+\frac{1}{\gamma} \operatorname{tr}\left(\dot{\tilde{\boldsymbol{\theta}}}^{\mathrm{T}} \widetilde{\boldsymbol{\theta}}\right)= \\& -\frac{1}{2} \boldsymbol{E}^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{E}+\frac{1}{\gamma} \operatorname{tr}\left(\gamma \boldsymbol{B}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{E} \boldsymbol{\varphi}^{\mathrm{T}}(\boldsymbol{E}) \widetilde{\boldsymbol{\theta}}+\right. \\& \left.\dot{\boldsymbol{\theta}}^{\mathrm{T}} \widetilde{\boldsymbol{\theta}}\right)+\boldsymbol{\eta}^{\mathrm{T}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{E}\end{aligned}$
结合式(25),选取关于神经网络权值的自适应律[23 ] 为
(27) $\dot{\hat{\boldsymbol{\theta}}}=\gamma \boldsymbol{\varphi} \boldsymbol{E}^{\mathrm{T}} \boldsymbol{P B}-k_{1} \gamma\|\boldsymbol{E}\| \hat{\boldsymbol{\theta}}$
当满足以下条件之一时,V ·
(28) $\left.\begin{array}{l}\|\boldsymbol{E}\| \geqslant \frac{2}{\lambda_{\min }(\boldsymbol{Q})}\left(\boldsymbol{\eta}_{0} \lambda_{\max }(\boldsymbol{P})+\frac{k_{1}}{4} \theta_{\max }^{2}\right) \\\|\widetilde{\boldsymbol{\theta}}\|_{\mathrm{F}} \geqslant \frac{\theta_{\max }}{2}+\sqrt{\frac{1}{k_{1}}\left(\boldsymbol{\eta}_{0} \lambda_{\max }(\boldsymbol{P})+\frac{k_{1}}{4} \theta_{\max }^{2}\right)}\end{array}\right\}$
可根据P Q
3 立管反冲及控制响应分析
3.1 基本数据
基于所建立的立管系统反冲控制方法,在MATLAB/Simulink中开发反冲控制仿真模型.以文献[11 ]中某 1 km 水深级的简化深水钻井立管系统为例,进行解脱反冲响应与控制分析,立管系统各名义计算参数与张紧器液压缸参数如表1 和表2 所示.为充分发挥控制作用,设定控制时间为解脱后的前 50 s,解脱开始时刻阀口全开,50 s 后按照阀口设定调控速率增大直至全开.
$\begin{array}{l}c=\left[\begin{array}{rrrrrrr}-12 & -8 & -4 & 0 & 4 & 8 & 12 ; -5 & -3 & -1 & 0 & 1 & 3 & 5\end{array}\right] \\b=8.0 \times \operatorname{ones}(7,1), \quad k_{\mathrm{p}}=0.05 \\k_{\mathrm{d}}=0.1, \quad \gamma=50, \quad k_{1}=0.01\end{array}$
PID控制器的参数设置为k p =0.05,k i = 0,k d =0.1.
3.2 反冲控制响应分析
基于所提控制方法,开展有无控制作用的立管反冲响应分析,建立常规的PID控制模型,对比验证所提RBF自适应控制模型的优越性.根据深水钻井实际情况,明确反冲控制分析中不确定的参数为张紧器等效刚度与等效阻尼、反冲过程中钻井液下泄对钻井立管的摩擦力与立管运动过程中的外部轴向水动力载荷、钻井立管在海水中所受的海水浮力.确定参数为阀口开度、阀口调控速率、阀口压力损耗系数、张紧器高压气体压力与体积及低压气体压力与体积.分别探究系统各参数均精确和系统参数存在不确定情况下的反冲控制效果,以说明无论立管系统参数是否确定,本反冲控制方法均适用.
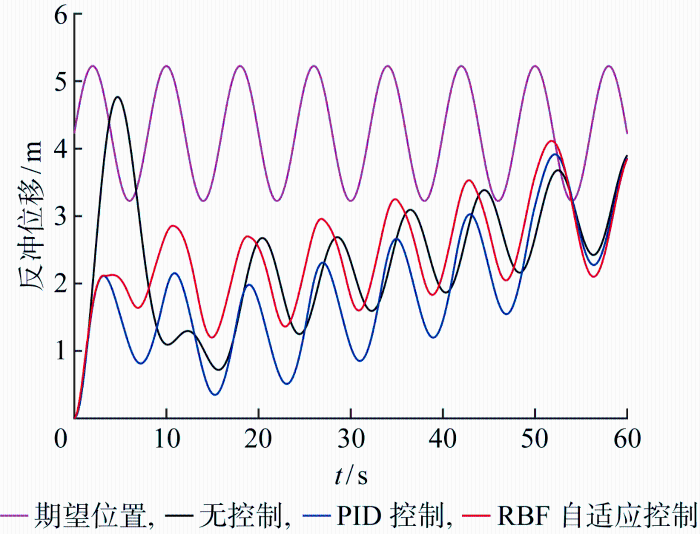
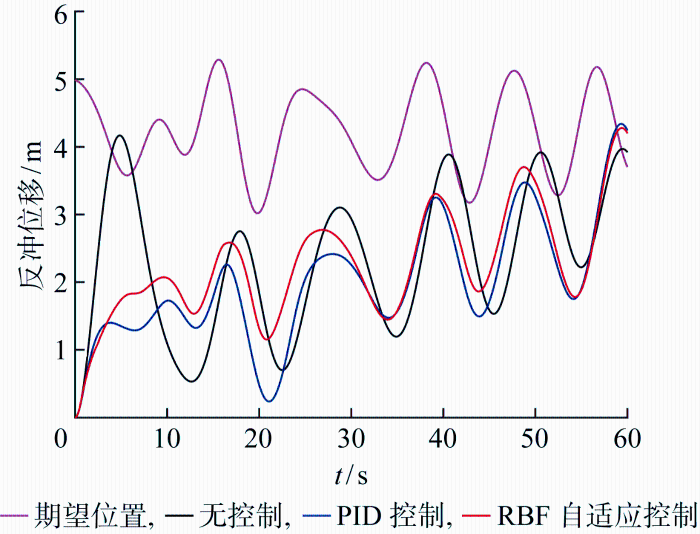
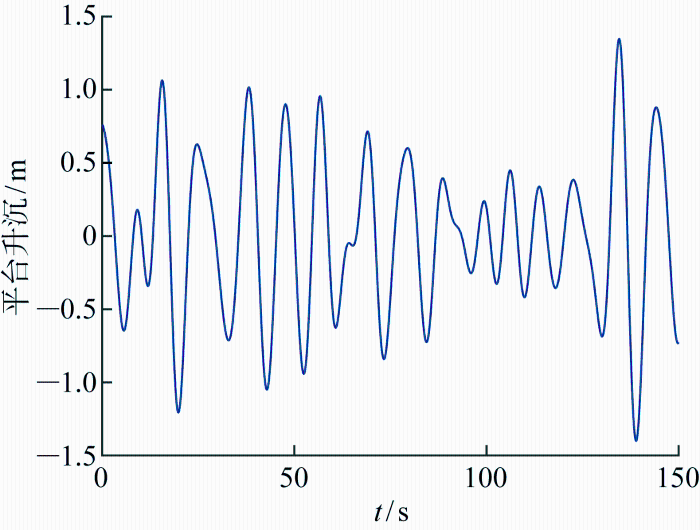
(1) 系统参数确定的反冲控制.假设立管反冲动力学各参数均精确,不考虑系统不确定性,反冲控制阀阀口可任意无差别瞬时调节到指定位置,阀口最大关闭度设置为0.10.分别探究了平台规则升沉和随机升沉作用下的反冲响应及控制,如图4 和图5 所示.其中平台规则升沉假设周期为8 s、幅值为 1 m,随机升沉曲线如图6 所示.
图4
图4
规则升沉作用的反冲及控制响应
Fig.4
Recoil and control response to regular heave
图5
图5
不规则升沉作用的反冲及控制响应
Fig.5
Recoil and control response to irregular heave
图6
图6
随机升沉时程曲线
Fig.6
Irregular heave
图4 与图5 中红色曲线为基于RBF自适应控制,蓝色曲线为基于PID控制.由图可知,无论是规则升沉作用还是随机升沉作用,采用RBF自适应控制与采用PID控制都能在反冲前期对反冲响应起到很好的调控,有效降低反冲前期的振荡幅值.由图4 可知,在规则升沉下,无控制、PID控制、RBF自适应控制3种工况解脱后5 s左右的反冲最高点分别为 4.73、2.02、2.06 m;而15.7 s左右的反冲最低点分别为0.72、0.35、1.20 m.由图5 可知,在不规则升沉下,该3种工况解脱后5 s左右的反冲最高点分别为4.15、1.45、1.82 m;而反冲最低点分别为0.53、0.25、1.15 m.因此,相较于PID控制,RBF自适应控制得到的反冲响应稍高,调控之后反冲振荡更平稳,在避免触底方面效果更佳.结合期望位置曲线,RBF自适应控制比PID控制更接近于期望位置;而PID控制虽然在降低反冲位移方面表现较优,但却增加了触底风险,其反冲振荡平稳度比RBF自适应控制差.
实际作业中,反冲控制阀不可能直接从开启状态跳转至近似闭合状态,反冲控制阀具有一定的调控速率与极限阀口开度,以保障张紧器及反冲控制系统平稳运行,这也是现有的反冲控制文献中所没有考虑的.在控制过程中当超过反冲控制阀的极限阀口开度时,按照极限阀口开度计算;当理想调控阀口的变化速率大于实际阀口变化速率时,按照上一时刻阀口开度与阀口调节速率朝有利阀口输出的方向调控.
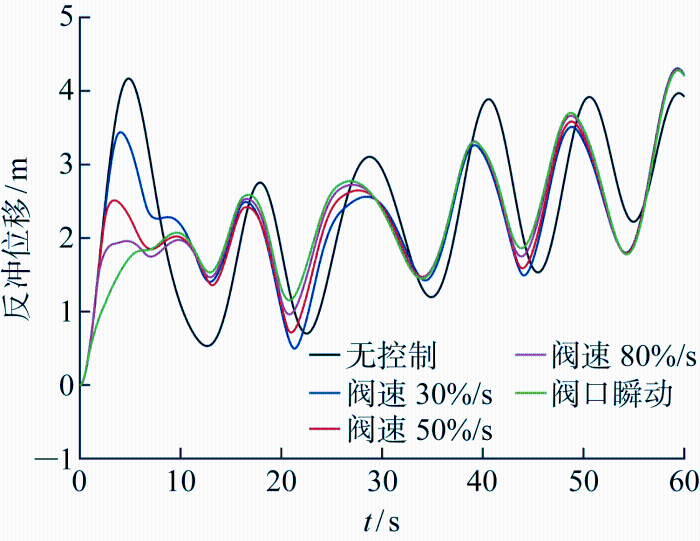
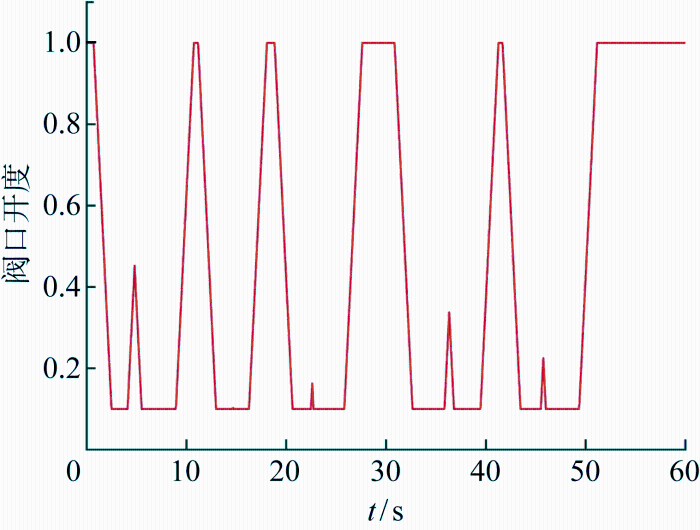
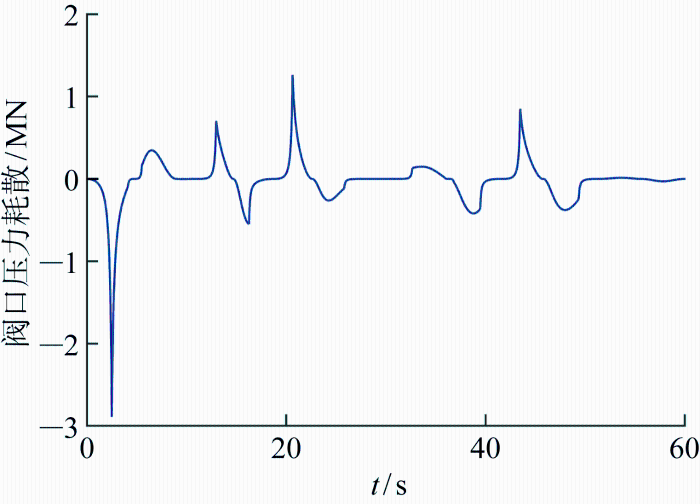
采用RBF自适应控制,进一步探究在不规则升沉作用下,不同阀口开度速率对反冲响应及反冲控制的影响.假设阀口调节速率分别为瞬时、80%/s、50%/s和30%/s,不同阀口作动速率时的反冲控制效果如图7 所示.在第一个反冲振荡周期内,阀口作动速率分别为30%/s、50%/s、80%/s以及阀口瞬动时,在第一个反冲振荡周期内,经控制之后的反冲最高位移相比于无控制分别下降17.5%、39.8%、53.0%、53.4%;且在21 s左右的反冲振荡最低点分别为0.49、0.71、0.96、1.15 m.因此,阀口响应越迅速控制效果越好,工程中应尽可能选择响应迅速的控制阀.如图8 和图9 所示,对应阀口作动速率50% /s时进行反冲控制的阀口变化历程以及阀口压力损耗,阀口变化较为平缓,且控制输入整体上变化较为平稳,未引起张紧器内部压力瞬变.
图7
图7
阀口作动速率对反冲及控制的影响
Fig.7
Effect of valve actuation rate on recoil and control
图8
图8
50%/s调控速率的控制阀作动曲线
Fig.8
Operation curve at a control valve of 50%/s
图9
图9
50%/s调控速率的控制阀压力损耗
Fig.9
Controlled pressure dissipation force at a control valve of 50%/s
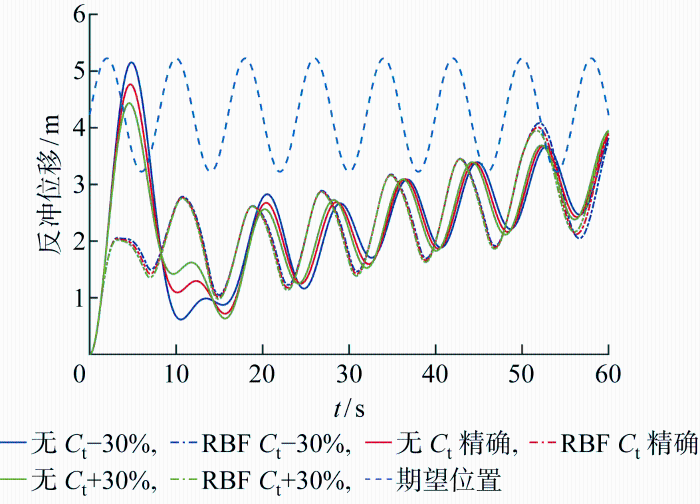
(2) 系统参数不确定的反冲控制.仍然假设反冲控制阀阀口的最大关闭度为0.1,阀口作动速率假设为80%/s,探究存在立管系统参数不确定时的反冲控制.
张紧器阻尼不确定对反冲响应及反冲控制的影响如图10 所示.图中,“无C t -30%”的“无”表示未施加控制,“C t -30%”表示张紧器实际阻尼比名义阻尼小30%;“RBF”表示施加RBF自适应控制.当无控制时,立管系统反冲提升量与张紧器阻尼大小呈负相关,高阻尼的张紧器系统有助于缓冲反冲响应.采用RBF自适应控制对不同张紧器阻尼的反冲都起到良好的控制作用,既降低了反冲最高位移,又增高了反冲最低位移;且能自适应一定范围内的张紧器阻尼的变化,使不同张紧器阻尼力的反冲在控制之后的位移曲线几乎一致.
图10
图10
张紧器阻尼不确定对反冲及控制的影响
Fig.10
Influence of tension damper uncertainty on recoil and control
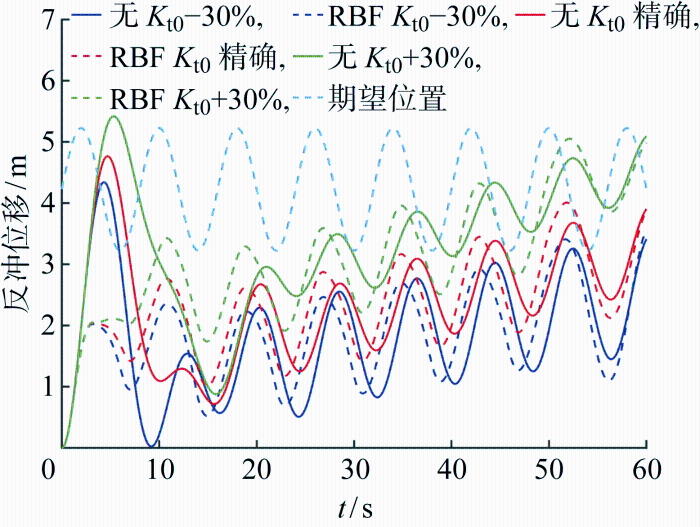
由于实际刚度无法测量,式(6)的期望位置仍然按照名义刚度设置.由图11 可知,刚度对反冲及控制都有较大影响,大的张紧器刚度会增大反冲位移,小的张紧器刚度会降低反冲振荡最低点.RBF自适应控制对张紧器刚度不确定性同样具有很好的自适应控制效果.
图11
图11
张紧器刚度不确定时的反冲及控制响应
Fig.11
Recoil and control response to uncertain tensioner stiffness
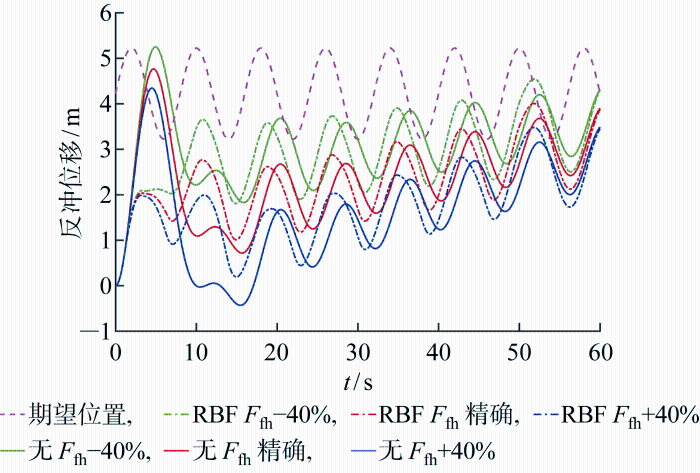
钻井液下泄摩擦力与外部水动力载荷(F fh )的不确定对反冲响应及控制效果影响显著,如图12 所示.RBF自适应控制有效降低了反冲位移,使反冲较为平缓地逐步趋近期望位置,且没有出现负位移.另外,虽然RBF自适应控制仍然在尽可能地朝不触底的趋势控制,但不触底的安全裕量仍然较小,反冲振荡最低点仅为0.19 m.主要是因为反冲振荡的决定性因素是张紧器提供的张紧力与立管系统其余各载荷之间的平衡,大的水动力载荷导致立管系统受力的实际平衡点下移.
图12
图12
水动力载荷不确定对反冲及控制的影响
Fig.12
Influence of hydrodynamic load uncertainty on recoil and control
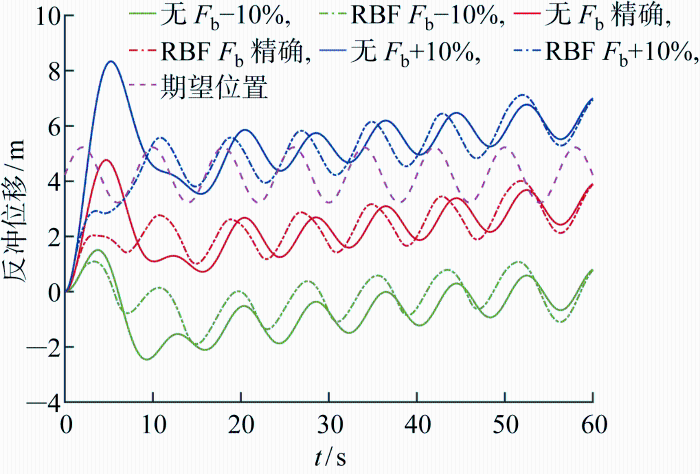
立管系统浮力(F b )是一个正方向非常大的力,稍不精确就会对反冲响应产生显著影响.决定反冲的仍然是立管张紧力与其余各力的平衡,由图13 所示RBF自适应控制在努力朝着名义的反冲期望位置发展,尽可能既降低反冲正位移,又提高反冲负位移.
图13
图13
浮力不确定时的反冲及控制响应
Fig.13
Recoil and control response to uncertain buoyancy
4 结论
基于名义反冲控制模型开发RBF自适应控制方法控制反冲,无论立管系统参数是否确定,均可实现有效的反冲控制,主要结论如下:
(1) 系统参数确定时,采用RBF自适应控制既可有效控制反冲正向位移,又可进一步降低触底风险,比常规PID控制的反冲振荡更平稳,且响应速率快的反冲控制阀阀口对反冲控制效果更佳.
(2) 张紧器阻尼与刚度、水动力载荷及立管系统浮力载荷的不确定性对反冲响应影响较大,但RBF自适应控仍可有效减小反冲正位移且提高反冲负位移,提升反冲振荡平稳度,具有较好的自适应能力.
RBF神经网络参数及闭环系统稳定性参数会对控制性能造成一定影响.后续须针对这些参数的选取进行优化研究,提供自动调整控制参数与最优化参数搜索方法,以便于工程应用.
参考文献
View Option
[1]
NIE Z Y CHANG Y J LIU X Q et al A DBN-GO approach for success probability prediction of drilling riser emergency disconnect in deepwater
[J]. Ocean Engineering 2019 , 180 : 49 -59 .
[本文引用: 1]
[2]
CHANG Y J CHEN G M WU X F et al Failure probability analysis for emergency disconnect of deepwater drilling riser using Bayesian network
[J]. Journal of Loss Prevention in the Process Industries 2018 , 51 : 42 -53 .
[本文引用: 1]
[3]
王坤鹏 , 薛鸿祥 , 唐文勇 . 全耦合深海平台系统中液压张紧器的数值模拟
[J]. 上海交通大学学报 2012 , 46 (10 ): 1652 -1657 .
[本文引用: 1]
基于利用ABAQUS开发的平台/系泊索/立管全耦合分析程序,研究应用于深海平台系统与顶端张紧式立管连接的液压张紧器的数值模型.对数值模拟液压张紧器中的刚度非线性效应、摩擦效应以及平台、张紧器和顶端张紧式立管的耦合连接方式进行了研究,提出了非线性液压张紧器模型.通过张紧器线性和非线性模型结果的比较,得到了非线性效应对立管和平台响应的影响,对提高顶端张紧式立管极限强度和疲劳寿命的预报精度有一定的帮助作用.
WANG Kunpeng XUE Hongxiang TANG Wen-yong Numerical simulation of hydraulic tensioner in fully coupled deep-sea platform system
[J]. Journal of Shanghai Jiao Tong University 2012 , 46 (10 ): 1652 -1657 .
[本文引用: 1]
[4]
齐娟娟 . 悬挂状态下钻井隔水管的结构动力学及涡激振动研究 [D]. 上海 : 上海交通大学 , 2015 .
[本文引用: 1]
QI Juanjuan A Study on structure dynamics and vortex shedding vibration of drilling risers under hang off mode [D]. Shanghai : Shanghai Jiao Tong University , 2015 .
[本文引用: 1]
[5]
MENG S CHE C D ZHANG W J Discharging flow effect on the recoil response of a deep-water drilling riser after an emergency disconnect
[J]. Ocean Engineering 2018 , 151 : 199 -205 .
[本文引用: 2]
[6]
MENG S CHEN Y CHE C D Coupling effects of a deep-water drilling riser and the platform and the discharging fluid column in an emergency disconnect scenario
[J]. China Ocean Engineering 2020 , 34 (1 ): 21 -29 .
[本文引用: 1]
[7]
WANG Y B GAO D L Influence of the damping matrix and mud discharge on the recoil response of deepwater drilling riser after emergency disconnection
[J]. Ocean Engineering 2021 , 222 : 108591 .
[本文引用: 1]
[8]
WANG X L LIU X Q LIU Z W et al Dynamic recoil response of tensioner and riser coupled in an emergency disconnection scenario
[J]. Ocean Engineering 2022 , 247 : 110730 .
[本文引用: 1]
[9]
田秀娟 . 深水钻井隔水管张紧系统反冲控制研究 [D]. 青岛 : 中国石油大学(华东) , 2013 .
[本文引用: 1]
TIAN Xiujuan Study on recoil control of riser tensioning system in deepwater drilling [D]. Qingdao : China University of Petroleum , 2013 .
[本文引用: 1]
[10]
何新霞 , 张方芬 , 田秀娟 , 等 . 深水钻井隔水管反冲控制系统建模与仿真
[J]. 石油机械 2016 , 44 (3 ): 63 -67 .
[本文引用: 1]
HE Xinxia ZHANG Fangfen TIAN Xiujuan et al Modeling and simulation for recoil control system of deepwater drilling riser
[J]. China Petroleum Machinery 2016 , 44 (3 ): 63 -67 .
[本文引用: 1]
[11]
LIU X Q LIU Z W WANG X L et al Recoil control of deepwater drilling riser system based on optimal control theory
[J]. Ocean Engineering 2021 , 220 : 108473 .
[本文引用: 2]
[12]
LIU X Q LIU Z W WANG X L et al An intelligent recoil controller for riser system based on fuzzy control theory
[J]. International Journal of Naval Architecture and Ocean Engineering 2022 , 14 : 100439 .
[本文引用: 1]
[13]
李欢 , 李鹏 , 范松 , 等 . 基于AMESim的隔水管张紧器抗反冲控制研究
[J]. 石油机械 2019 , 47 (9 ): 84 -89 .
[本文引用: 1]
LI Huan LI Peng FAN Song et al AMESim-based research on anti-recoil control of riser tensioner
[J]. China Petroleum Machinery 2019 , 47 (9 ): 84 -89 .
[本文引用: 1]
[14]
SUN Y T ZHAO Y D ZHANG B L et al Recoil control of deepwater-drilling riser with optimal guaranteed cost H∞ control
[J]. Applied Sciences 2022 , 12 (8 ): 3945.
[本文引用: 1]
[15]
ZHAO Y D SUN Y T ZHANG B L et al Recoil control of deepwater drilling riser systems via optimal control with feedforward mechanisms
[J]. Ocean Engineering 2022 , 257 : 111690 .
[本文引用: 1]
[16]
American Petroleum Institute . Design, selection, operation, and maintenance of marine drilling riser systems: API RP 16Q [S]. Washington, USA : API , 2017 .
[本文引用: 1]
[17]
WANG X L LIU X Q ZHANG N et al Improved recoil dynamic analysis of the deepwater riser system after emergency disconnection
[J]. Applied Ocean Research 2021 , 113 : 102719 .
[本文引用: 1]
[18]
LI C W FAN H H WANG Z M et al Two methods for simulating mud discharge after emergency disconnection of a drilling riser
[J]. Journal of Natural Gas Science and Engineering 2016 , 28 : 142 -152 .
[本文引用: 1]
[19]
WANG X L LIU X Q ZHANG S Y et al Study on mud discharge after emergency disconnection of deepwater drilling risers
[J]. Journal of Petroleum Science and Engineering 2020 , 190 : 107105 .
[本文引用: 1]
[20]
YANG Y HUANG D Q DONG X C Enhanced neural network control of lower limb rehabilitation exoskeleton by add-on repetitive learning
[J]. Neurocomputing 2019 , 323 : 256 -264 .
[本文引用: 1]
[21]
JI N LIU J K YANG H J Sliding mode control based on RBF neural network for a class of under-actuated systems with unknown sensor and actuator faults
[J]. International Journal of Systems Science 2020 , 51 (16 ): 3539 -3549 .
[本文引用: 1]
[22]
HUO X X GE T WANG X Y Horizontal path-following control for deep-sea work-class ROVs based on a fuzzy logic system
[J]. Ships and Offshore Structures 2018 , 13 (6 ): 637 -648 .
[本文引用: 1]
[23]
LIU J K Radial basis function (RBF) neural network control for mechanical systems [M]. Beijing : Tsinghua & Springer Press , 2013 : 133 -159 .
[本文引用: 1]
A DBN-GO approach for success probability prediction of drilling riser emergency disconnect in deepwater
1
2019
... 深海钻井立管系统遭遇极端环境或特殊状况时需要将底部的下部海洋立管总成(LMRP)系统与防喷器组(BOP)进行紧急解脱,解脱后立管系统在张紧器预存过提力作用下加速向上运动,称之为反冲运动[1 ] .立管反冲是一个极其危险的过程,反冲过高会导致立管系统撞击钻台,导致伸缩节、分流器等顶部设备损坏;反冲过低会导致底部触底,从而引发立管系统弯曲或折断[2 ] .随着当前油气勘探向深水和超深水进军,所面临的环境与操作风险越发严峻,发生紧急解脱的概率也越来越高.2020年10月墨西哥湾某钻井船遭遇飓风Zeta,解脱后立管系统剧烈反冲,与船体多次碰撞,LMRP多次触碰海底,造成张紧器、伸缩节、立管、LMRP等多部位严重损坏.因此,开展深海钻井立管系统紧急解脱反冲及控制研究对保障安全钻探具有重要意义. ...
Failure probability analysis for emergency disconnect of deepwater drilling riser using Bayesian network
1
2018
... 深海钻井立管系统遭遇极端环境或特殊状况时需要将底部的下部海洋立管总成(LMRP)系统与防喷器组(BOP)进行紧急解脱,解脱后立管系统在张紧器预存过提力作用下加速向上运动,称之为反冲运动[1 ] .立管反冲是一个极其危险的过程,反冲过高会导致立管系统撞击钻台,导致伸缩节、分流器等顶部设备损坏;反冲过低会导致底部触底,从而引发立管系统弯曲或折断[2 ] .随着当前油气勘探向深水和超深水进军,所面临的环境与操作风险越发严峻,发生紧急解脱的概率也越来越高.2020年10月墨西哥湾某钻井船遭遇飓风Zeta,解脱后立管系统剧烈反冲,与船体多次碰撞,LMRP多次触碰海底,造成张紧器、伸缩节、立管、LMRP等多部位严重损坏.因此,开展深海钻井立管系统紧急解脱反冲及控制研究对保障安全钻探具有重要意义. ...
全耦合深海平台系统中液压张紧器的数值模拟
1
2012
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
Numerical simulation of hydraulic tensioner in fully coupled deep-sea platform system
1
2012
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
1
2015
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
1
2015
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
Discharging flow effect on the recoil response of a deep-water drilling riser after an emergency disconnect
2
2018
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
... 式中:ρ w 为海水密度;D h 为立管水动力外径;C w 为立管外部的无量纲轴向水动力阻尼系数[5 ] ;L 为立管长度. ...
Coupling effects of a deep-water drilling riser and the platform and the discharging fluid column in an emergency disconnect scenario
1
2020
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
Influence of the damping matrix and mud discharge on the recoil response of deepwater drilling riser after emergency disconnection
1
2021
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
Dynamic recoil response of tensioner and riser coupled in an emergency disconnection scenario
1
2022
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
1
2013
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
1
2013
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
深水钻井隔水管反冲控制系统建模与仿真
1
2016
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
Modeling and simulation for recoil control system of deepwater drilling riser
1
2016
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
Recoil control of deepwater drilling riser system based on optimal control theory
2
2021
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
... 基于所建立的立管系统反冲控制方法,在MATLAB/Simulink中开发反冲控制仿真模型.以文献[11 ]中某 1 km 水深级的简化深水钻井立管系统为例,进行解脱反冲响应与控制分析,立管系统各名义计算参数与张紧器液压缸参数如表1 和表2 所示.为充分发挥控制作用,设定控制时间为解脱后的前 50 s,解脱开始时刻阀口全开,50 s 后按照阀口设定调控速率增大直至全开. ...
An intelligent recoil controller for riser system based on fuzzy control theory
1
2022
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
基于AMESim的隔水管张紧器抗反冲控制研究
1
2019
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
AMESim-based research on anti-recoil control of riser tensioner
1
2019
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
Recoil control of deepwater-drilling riser with optimal guaranteed cost H∞ control
1
2022
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
Recoil control of deepwater drilling riser systems via optimal control with feedforward mechanisms
1
2022
... 众多学者从不同角度、采用不同方法对立管动力学分析[3 -4 ] 及反冲问题[5 ⇓ ⇓ -8 ] 开展了研究,对立管反冲动力学的研究为进一步开展紧急解脱反冲控制奠定了基础.田秀娟[9 ] 、何新霞等[10 ] 较早开展了立管反冲控制研究,开发了基于模糊比例-积分-微分(PID)的反冲控制系统;Liu等[11 -12 ] 先后提出基于线性二次型调节器(LQR)控制和基于模糊理论的反冲控制策略;李欢等[13 ] 采用AMESim对张紧器反冲控制系统进行搭建与基于位置控制的研究;Sun等[14 ] 、Zhao等[15 ] 同样基于状态空间表达式引入最优保成本与基于前馈优化的控制方法进行反冲控制.以上研究均基于准确的立管反冲力学模型开展,在张紧器、立管受力等方面做了部分简化,但在实际工程中,张紧器刚度和阻尼很难准确获取,且下泄钻井液对立管内壁的摩擦力、反冲过程中海水对立管外部的水动力载荷、立管系统所受海水浮力等都难以测量,即使钻井平台上配有反冲控制装置,有时也仍无法有效控制反冲. ...
1
2017
... 深海钻井立管系统紧急解脱及反冲重点关注其轴向动力响应,需同时防止底部碰撞海底与顶部达到张紧器冲程极限、冲击钻台.立管反冲最危险的是轴向的响应且反冲控制只能通过反冲控制阀调控,立管系统顶部横向无其他作动器,因此波流等横向环境载荷在反冲动力学分析与控制中通常不考虑[16 ] .平台升沉响应幅值算子(RAO)受波浪参数影响,从而影响立管轴向反冲响应.立管紧急脱离及反冲示意图如图1 所示,其中x h 为平台升沉,x r 为立管系统轴向位移.解脱后,立管系统在张紧器作用下加速向上反冲,同时为降低立管压溃等失效风险,将内部钻井液释放入海水,并从填充阀填充密度较轻的海水,整个反冲过程为下泄钻井液与立管系统耦合的过程. ...
Improved recoil dynamic analysis of the deepwater riser system after emergency disconnection
1
2021
... 对立管反冲进行动力学建模,立管系统本质上是一个无限维度的连续弹性体,常规立管动力学分析中,多采用有限元方法或集中质量法.Wang等[17 ] 证明了立管有限元段数对反冲轴向位移影响有限,且立管系统解脱后的振动频率主要受张紧器等效刚度影响.因此,直接假设立管系统为一刚性体,该假设与立管反冲位移测量一致,平台上反冲过程中通常只能测量顶部位移,底部反冲位移不易测量,可通过立管系统的形变量进行反演. ...
Two methods for simulating mud discharge after emergency disconnection of a drilling riser
1
2016
... 钻井液下泄采用整体液柱模型(WFCM)进行表征.WFCM更便于与立管运动耦合,且具有较高精度[18 -19 ] ,通过迭代求解可以求得钻井液下泄对管壁的摩擦力: ...
Study on mud discharge after emergency disconnection of deepwater drilling risers
1
2020
... 钻井液下泄采用整体液柱模型(WFCM)进行表征.WFCM更便于与立管运动耦合,且具有较高精度[18 -19 ] ,通过迭代求解可以求得钻井液下泄对管壁的摩擦力: ...
Enhanced neural network control of lower limb rehabilitation exoskeleton by add-on repetitive learning
1
2019
... 将式(10)和式(11)代入式(2),得到稳态控制方程关系式[20 ] : ...
Sliding mode control based on RBF neural network for a class of under-actuated systems with unknown sensor and actuator faults
1
2020
... 模型不确定部分f 是难以测量的,采用RBF神经网络对不确定部分进行逼近[21 ] .RBF神经网络是在控制领域最常用的一种神经网络,采用高斯基函数,是单隐层的3层前馈神经网络,如图3 所示.理论上RBF神经网络可以对任何未知非线性函数进行任意精度范围的逼近,属于局部逼近的神经网络,其独特的结构类型可大大加快学习速度并避免局部极小问题,适合实时控制的要求. ...
Horizontal path-following control for deep-sea work-class ROVs based on a fuzzy logic system
1
2018
... 式中:c i i 个隐层神经元的中心点向量值;bi 为隐含层神经元i 的高斯基函数宽度;φ θ s 为隐含层结点数;$\hat{f}$为神经网络对不确定部分的估计输出. 假设估计输出$\hat{f}$连续有界,存在极小正值ε 0 ,使理想的估计输出$\hat{\boldsymbol{f}}\left(\boldsymbol{E}, \boldsymbol{\theta}^{*}\right)$满足[22 ] ...
1
2013
... 结合式(25),选取关于神经网络权值的自适应律[23 ] 为 ...