海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业.
日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态.
尝试提出基于模型预测控制(Model Predictive Control, MPC)深海钻井再入井控制系统.首先基于哈密顿原理推导悬挂立管横向运动模型.然后结合立管模态时域响应模型与井口目标位置设计优化函数及约束项,构建非线性扰动观测器以实现对洋流力模型误差以及洋流速度扰动补偿.最后引入动力定位系统开展仿真测试,与传统PID控制再入井作业比较.
1 硬悬挂立管横向运动数学模型
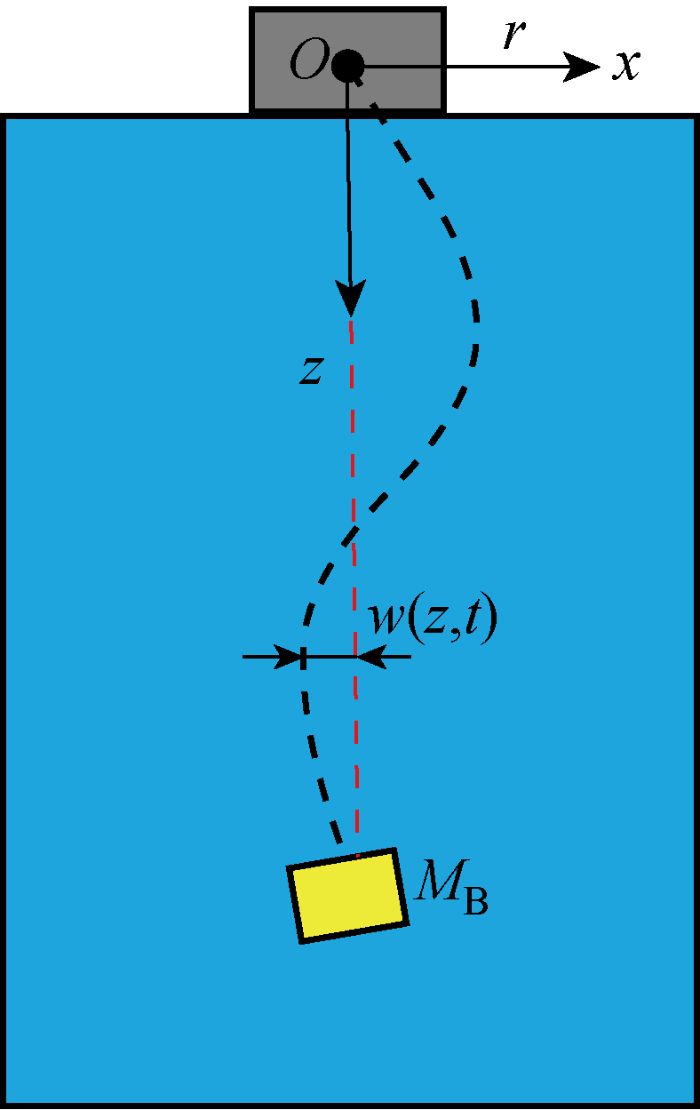
根据立管顶端连接方式,悬挂撤离分为硬悬挂与软悬挂模式.硬悬挂时立管和母船固定连接.软悬挂时,张紧器系统仍起作用,液压装置的液压杆部件通过张力环与立管连接.两种模式各有优势,不能盲目采用软悬挂或硬悬挂模式,应当结合实际情况选择合适模式[21 ] .本研究设定为硬悬挂模式,图1 为深海钻井立管硬悬挂模式示意图,立管顶端固定在母船,立管底端自由且附带一个点质量M B ,即立管的底端总成(Lower Marine Riser Package, LMRP).采用二维欧拉坐标系Oxz ,其中坐标原点O 建立在母船的初始位置,x 为母船横向运动正方向,z 为重力加速度方向.r (t )为母船横向位移,t 为时间. 不考虑母船垂荡和横摇以及立管涡激振动效应等,立管横向运动是由母船运动r (t )和横向形变w (z , t )叠加而成的,因此立管横向位移y (z , t )=r (t )+w (z , t ),这里以y B (t )标记立管底端总成的位移.
图1
图1
深海钻井立管硬悬挂模式示意图
Fig.1
A hard hang-off deep-water marine riser
(1) ∫ t 1 t 2
式中:K 和V 分别为系统动能和势能;W 为非保守力所做的虚功. K 包括钻井船的动能K 1 与悬挂立管(含LMRP)的动能K 2 :
(2) K 1 = 1 2 M r · 2
(3) K 2 = 1 2 ∫ 0 l B ](w · r · 2 dz
式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为
(4) V g =- ∫ 0 l μ + δ ( z - l ) M B g
(5) V e = 1 2 ∫ 0 l v ' + 1 2 w ' 2 2
(6) V t = 1 2 ∫ 0 l l ~ 2 dz
式中:μ =(ρ p -ρ o )Ag 代表立管单位长度湿重,ρ p 、ρ o 分别为立管及立管外部流体的密度,A 为立管的横截面积,g 为重力加速度;E 为弹性模量;v 为立管的轴向形变量;为方便计算可设定l ~ l +M B g μ . 采用莫里森经验公式,海洋流体力所做的虚功变分为
(7) $\begin{aligned} \delta W_1 & ={ }_0^l Q \delta(r+w) \mathrm{d} z= \\ & { }_0^l\left[-m_{\mathrm{a}}(\ddot{r}+\ddot{w})-\zeta_{\mathrm{d}}\left|v_{\text {rel }}\right| v_{\text {rel }}\right] \delta(r+w) \mathrm{d} z\end{aligned}$
式中:Q 为流体阻力;附加质量m a =ρ o A o C a ,ρ o 为外流密度,A o 为外径横截面面积,附加质量系数C a =1;阻尼系数ζ d =1 2 ρ o d o C d ,d o 为立管外径,曳力系数 C d =1.2;v rel =r · w · - v c 为立管与海流的相对速度,v c 为洋流速度.同时,母船推力f 所做的虚功为
(8) δW 2 =f δr
利用变分法可求出船舶横向运动、立管横向运动和轴向形变方程,其中立管横向运动方程为
(9) $\begin{array}{l}{\left[m+m_{\mathrm{a}}+\delta_{\mathrm{D}}(z-l) M_{\mathrm{B}}\right](\ddot{r}+\ddot{w})+} \\\quad \zeta_{\mathrm{d}}\left|v_{\text {rel }}\right| v_{\mathrm{rel}}-\left(P_{\mathrm{e}} w^{\prime}\right)^{\prime}+ \\\quad E A\left[v^{\prime \prime} w^{\prime}+\left(v^{\prime}+\frac{3}{2} w^{\prime 2}\right) w^{\prime \prime}\right]=0\end{array}$
式中:δD 为狄拉克函数;P e =μ (l -z )+M B g. 本研究只考虑横向运动,因此含v (z , t )项舍去. 定义一阶小量w'~σ ,得:w' 2 ~σ 2 , 只保留一阶小量情况下,横向运动方程最后简化为
(10) $\begin{array}{l}\left(m+m_{\mathrm{a}}\right)(\ddot{r}+\ddot{w})+\zeta_{\mathrm{d}}\left|v_{\text {rel }}\right| v_{\text {rel }}+ \\\mu\left[(z-\widetilde{l}) w^{\prime \prime}+w^{\prime}\right]+ \\\quad \delta_{\mathrm{D}}(z-l) M_{\mathrm{B}}(\ddot{r}+\ddot{w})=0\end{array}$
(11) $w(z, t)=\varphi_{i=1}(z) q_{i}(t)=\boldsymbol{\varphi}^{\mathrm{T}}(z) \boldsymbol{q}(t)$
式中:N 为模态函数的数量;qi (t )为时间坐标且定义q (t )=[q 1 ( t ) … q N ( t ) T . 模态函数φi (z )可以采用相同边界条件下缆索系统(顶端固定,底端自由且附带一个点质量)的固有振型函数且定义φ T (z )=[φ 1 ( z ) … φ N ( z ) . 最后得到悬挂立管横向结构动力方程为
(12) $\begin{array}{l}\left[\begin{array}{ll}\boldsymbol{M}_{1} & \boldsymbol{M}_{2}\end{array}\right]\left|\begin{array}{l}\ddot{r} \\\ddot{\boldsymbol{q}}\end{array}\right|+\left[\begin{array}{ll}\boldsymbol{D}_{1} & \boldsymbol{D}_{2}\end{array}\right]\left[\begin{array}{l}\dot{r} \\\dot{\boldsymbol{q}}\end{array}\right]+\boldsymbol{K} \boldsymbol{q}=\boldsymbol{f}_{\mathrm{c}}\\\boldsymbol{M}_{1}={ }_{0}^{l}\left(m+m_{\mathrm{a}}\right) \boldsymbol{\varphi}(z) \mathrm{d} z+M_{\mathrm{B}} \boldsymbol{\varphi}(l) \\\boldsymbol{M}_{2}={ }_{0}^{l}\left(m+m_{\mathrm{a}}\right) \boldsymbol{\varphi}(z) \boldsymbol{\varphi}^{\mathrm{T}}(z) \mathrm{d} z+M_{\mathrm{B}} \boldsymbol{\varphi}(l) \boldsymbol{\varphi}^{\mathrm{T}}(l) \\\boldsymbol{D}_{1}={ }_{0}^{l} \zeta_{\mathrm{d}}\left|v_{\mathrm{rel}}\right| \boldsymbol{\varphi}(z) \mathrm{d} z \\\boldsymbol{D}_{2}={ }_{0}^{l} \zeta_{\mathrm{d}}\left|v_{\mathrm{rel}}\right| \boldsymbol{\varphi}(z) \boldsymbol{\varphi}^{\mathrm{T}}(z) \mathrm{d} z \\\boldsymbol{K}=-\mu_{0}^{l} z \boldsymbol{\varphi}^{\prime}(z) \boldsymbol{\varphi}^{\prime \mathrm{T}}(z) \mathrm{d} z+\mu \tilde{l}_{0}^{l} \boldsymbol{\varphi}^{\prime}(z) \boldsymbol{\varphi}^{\prime \mathrm{T}}(z) \mathrm{d} z \\\boldsymbol{f}_{\mathrm{c}}={0}^{l} \boldsymbol{\varphi}(z) \zeta_{\mathrm{d}}\left|v_{\mathrm{rel}}\right| v_{\mathrm{c}} \mathrm{d} z\end{array}$
式中:M 1 和M 2 为质量矩阵;D 1 和D 2 为阻尼矩阵;K 为刚度矩阵;f c 为流体力.
引入日本九州大学Kajiwara实验模型参数[7 ] 进行仿真计算,预测的立管底端防喷器位置y d 响应曲线如图2 所示,与试验数据拟合较好,从而完成模型验证.
图2
图2
立管底端防喷器仿真结果与试验数据对比
Fig.2
Comparison of predicted time trace of LMRP displacement and experimental data
2 控制系统设计
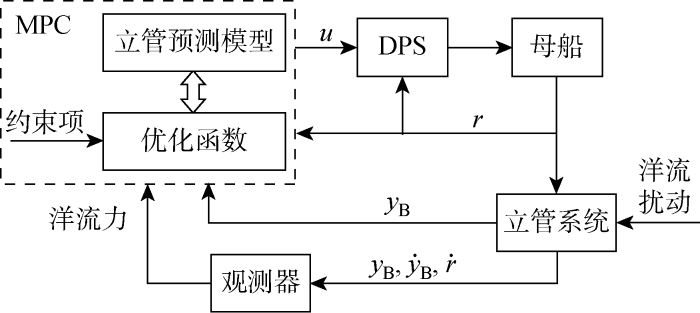
图3 所示为基于MPC的立管再入井控制系统原理图.MPC控制器在接收到实船以及立管底端位置信息后,求解下一时刻的最优船速u 作为控制指令输入至动力定位系统,从而控制母船及立管的运动轨迹,并记录实船及立管的底端位置作为新的MPC输入.同时在系统中引入观测器对立管受到的洋流扰动进行逼近,以此来提升立管动态响应预测的精度.
图3
图3
基于 MPC的海洋立管再入井作业控制系统原理图
Fig.3
Proposed control system of marine drilling riser in reentry based on MPC
2.1 立管动态响应预测模型
(13) $\begin{aligned}\ddot{r}+\boldsymbol{M}_{1}^{-1} \boldsymbol{M}_{2} \ddot{\boldsymbol{q}}+\boldsymbol{M}_{1}^{-1} \boldsymbol{D}_{1} \dot{\boldsymbol{r}}+ \\\quad \boldsymbol{M}_{1}^{-1} \boldsymbol{D}_{2} \dot{\boldsymbol{q}}+\boldsymbol{M}_{1}^{-1} \boldsymbol{K} \boldsymbol{q}=\boldsymbol{M}_{1}^{-1} \boldsymbol{f}_{\mathrm{c}}\end{aligned}$
(14) $\begin{aligned}\ddot{\boldsymbol{\xi}}+ & \boldsymbol{M}_{1}^{-1} \boldsymbol{D}_{2} \boldsymbol{M}_{2}^{-1} \boldsymbol{M}_{1} \dot{\boldsymbol{\xi}}+\boldsymbol{M}_{1}^{-1} \boldsymbol{K} \boldsymbol{M}_{2}^{-1} \boldsymbol{M}_{1} \boldsymbol{\xi}= \\& \boldsymbol{M}_{1}^{-1} \boldsymbol{f}_{\mathrm{c}}+\boldsymbol{M}_{1}^{-1} \boldsymbol{K} \boldsymbol{M}_{2}^{-1} \boldsymbol{M}_{1} r+ \\& \left(\boldsymbol{M}_{1}^{-1} \boldsymbol{D}_{2} \boldsymbol{M}_{2}^{-1} \boldsymbol{M}_{1}-\boldsymbol{M}_{1}^{-1} \boldsymbol{D}_{1}\right) \dot{r}\end{aligned}$
状态变量设定为X =r ξ · ξ T r 和立管底端总成的位置y B 作为输出量Y =r y B r · u ,得到系统状态空间方程和输出方程为
(15) X · 0 0 0 A 1 A 2 A 3 0 1 0 1 B 1 0 0 M 1 - 1 f c 0
(16) $\begin{aligned}\boldsymbol{Y}= & \boldsymbol{C} \boldsymbol{X}= \\& {\left[\begin{array}{ccc}1 & 0 & 0 \\1-\boldsymbol{\varphi}(l) \boldsymbol{M}_{2}^{-1} \boldsymbol{M}_{1} & 0 & \boldsymbol{\varphi}(l) \boldsymbol{M}_{2}^{-1} \boldsymbol{M}_{1}\end{array}\right] \boldsymbol{X} }\end{aligned}$
式中:A 1 =M 1 - 1 K M 2 - 1 M 1 ;A 2 =-M 1 - 1 D 2 M 2 - 1 A 3 =-M 1 - 1 K M 2 - 1 M 1 ;B 1 =M 1 - 1 D 2 M 2 - 1 M 1 -M 1 - 1 D 1 ;C 为输出矩阵. 设定步长为T ,任意第k 时间步,已知X (k )和u (k )作为初值,利用欧拉法可对未来H 步即k +1~k +H 步(H 为设定的预测时域步数)状态变量X 进行预报,
(17) X ( k + 1 ) = X ( k ) + T X · ( k ) ︙ X ( k + H ) = X ( k ) + T ∑ i = k k + H - 1 X · ( i )
2.2 优化函数
在欧拉坐标系Oxz 下,设井口坐标(y d , l ),且悬挂立管初始时刻未发生形变时r (0)=0,y (z , 0)=0. 设定控制输出目标为Y d =y d y d k 步构建优化函数
(18) $\begin{array}{l} \min \sum_{i=1}^{H}\left(\boldsymbol{Y}(k+i)-\boldsymbol{Y}_{\mathrm{d}}\right)^{\mathrm{T}} \boldsymbol{Q}\left(\boldsymbol{Y}(k+i)-\boldsymbol{Y}_{\mathrm{d}}\right)+ \\\sum_{i=0}^{H-1} R \Delta u(k+i)^{2} \\\text { s. t. } u \in\left[u_{\min }, u_{\max }\right], \quad \Delta u \in\left[\Delta u_{\min }, \Delta u_{\max }\right]\end{array}$
式中:Q 、R 为设定权重;引入输入增量Δu 的二次型寻求母船及LMRP到达指定位置,同时母船在再入井作业过程中尽量保持较小速度增量.引入输入指令u 及其增量Δu 的约束u min 、u max 、Δu min 、Δu max 将母船速度和加速度限制在一定范围内.由于立管预测模型中含有洋流力非线性项,需采用序列二次规划方法对非线性规划问题进行求解,在线求得预测时域内控制输入序列.采用的MPC优化函数结构符合稳定性标准,稳定性证明如下.
(19) $X_{\mathrm{a}}(k+1)=\boldsymbol{f}\left(X_{\mathrm{a}}(k), u_{\mathrm{a}}(k)\right)$
(20) $\begin{array}{l}V_{\mathrm{a}}(k)= \\\quad \min \sum_{i=1}^{H} l_{\text {cost }}\left(X_{\mathrm{a}}(k+i), u_{\mathrm{a}}(k+i-1)\right) \\\text { s. t. } X_{\mathrm{a}} \in X_{\lim }, \quad u_{\mathrm{a}} \in U_{\lim }\end{array}$
式中:l cost (X a , u a )≥0,且当且仅当X a =0,u a =0时l cost =0.U lim 和X lim 均为包含原点的非空集合.引入终端约束,
(21) X a (k +H )=0
假设X a =0,u a =0为系统的一个平衡点,并假设每个周期的优化问题都有可行解且能求解得到全局最优解,可认定系统在X a =0,u a =0处稳定.
证明 利用Lyapunov稳定性进行证明,将V a (k )作为Lyapunov函数.由于l cost (X a , u a )≥0,可得V a (k )≥0,仅需证明V a (k )≥V a (k +1),假设模型是无偏的,即预测状态与实际状态一致,得:
(22) $\begin{array}{l}V_{\mathrm{a}}(k+1)= \\\quad \min \sum_{i=1}^{H} l_{\text {cost }}\left(X_{\mathrm{a}}(k+i+1), u_{\mathrm{a}}(k+i)\right)= \\\quad \min \left(\sum_{i=1}^{H} l_{\text {cost }}\left(X_{\mathrm{a}}(k+i), u_{\mathrm{a}}(k+i+1)\right)-\right. \\\left.\quad l_{\text {cost }}\left(X_{\mathrm{a}}(k+1), u_{\mathrm{a}}(k)\right)\right)+ \\\quad \min l_{\text {cost }}\left(X_{\mathrm{a}}(k+1+H), u_{\mathrm{a}}(k+H)\right) \leqslant \\\quad-l_{\text {cost }}\left(X_{\mathrm{a}}(k+1), u_{\mathrm{a}}(k)\right)+V_{\mathrm{a}}(k)+ \\\quad \min l_{\text {cost }}\left(X_{\mathrm{a}}(k+1+H), u_{\mathrm{a}}(k+H)\right)\end{array}$
由于-l cost (X (k +1), u (k ))≤0,且引入终端约束,min l cost (X (k +1+H ), u (k +H ))=0. 可得V a (k )≥V a (k +1),证毕.
2.3 扰动观测器
海洋流体力中引入未知扰动d 实时修正,修正后的f c 为
(23) f c =f c0 +d
这里定义f c0 =∫ 0 l ζ d v r e l φ (z )v c dz. 设计一款非线性扰动观测器测得d ^ d 进行逼近,设误差e =d -d ^ d · 3×1 ,则 e · d ^ · . 令
(24) e · d ^ · M 1 - 1 d ^
L 为设计的观测器函数,为使误差e 收敛到0,需保证L M 1 - 1 L =(M 1 - 1 ) T ,得
(25) $$\begin{aligned} \dot{\hat{\boldsymbol{d}}}= & \boldsymbol{L}|| \begin{array}{ccc}0 & 0 & 0 \\ \boldsymbol{A}_1 & \boldsymbol{A}_2 & \boldsymbol{A}_3 \\ 0 & 1 & 0\end{array}|\boldsymbol{X}+| \begin{array}{c}1 \\ \boldsymbol{B}_1 \\ 0\end{array}|u+| \begin{array}{c}0 \\ \boldsymbol{M}_1^{-1} \boldsymbol{f}_{\mathrm{c} 0} \\ 0\end{array}||- \\ & \boldsymbol{L} \boldsymbol{M}_1^{-1} \hat{\boldsymbol{d}}\end{aligned}$$
由于状态变量X · p (X )=∫ 0 t L X · t =LX , h =d ^ - p (X )得
(26) $\begin{aligned}\dot{\boldsymbol{h}}= & -\boldsymbol{L}|| \begin{array}{ccc}0 & 0 & 0 \\\boldsymbol{A}_{1} & \boldsymbol{A}_{2} & \boldsymbol{A}_{3} \\0 & 1 & 0\end{array}|\boldsymbol{X}+| \begin{array}{c}1 \\\boldsymbol{B}_{1} \\0\end{array}|u+| \begin{array}{c}0 \\\boldsymbol{M}_{1}^{-1} \boldsymbol{f}_{\mathrm{c} 0} \\0\end{array}||- \\& \boldsymbol{L} \boldsymbol{M}_{1}^{-1}(\boldsymbol{h}+p(\boldsymbol{X})) \\\hat{\boldsymbol{d}}= & \boldsymbol{h}+p(\boldsymbol{X})\end{aligned}$
(27) d ^
求解式(26)和(27)可得d ^ d 的实时预测.
2.4 动力定位系统及推进器
根据文献[22 ],母船采用Abkowitz低频运动模型,在船舶较低航速情况下可对船舶受到的水动力进行简化.在再入井过程中由于船速较低(本研究设定船速范围[-1, 1] m/s),可以忽略二阶速度项.在不考虑船舶艏向角影响下,母船一维横向低频运动可近似表示为
(28) (M - M r · r ¨ r (r · c0 )=τ+ω
式中:M 为母船的质量;M r · Mr 为船舶水动力位置导数;v c0 为水平面洋流流速;τ 为推力;ω 为零均值白噪声. 令u =r · - v c0 ,可构建动力定位系统的控制方程:
(29) $\begin{aligned}\dot{u}= & -\left(M-M_{\dot{r}}\right)^{-1} M_{r} u+\left(M-M_{\dot{r}}\right)^{-1} \tau+ \\& \left(M-M_{\dot{r}}\right)^{-1} \omega\end{aligned}$
钻井船一般采用一对全回转导管推进器或吊舱推进器作为主推,可以提供全方向360°的推力,以及一对仅提供横向推力的侧推器.本研究中推进器仅提供船舶纵荡方向的推力,因此仅考虑了单一推进器提供定向推力.引入一阶延时模型用于模拟推进器的动力特性[23 ] ,
(30) τ · thr (τ-τn )
式中:τ n 为DPS发出的推力指令;这里只考虑纵荡方向,因此定义A thr =1 T 0 T 0 为等效时间常数.
(1) 设任意第k 时间步(k =1, 2, …),已知立管底端总成位置及母船位置即Y (kT )=r ( k T ) y B ( k T ) ( 在k =1时,取Y (T )=02×1 ).
(2) 利用式(14)计算得状态变量X ^ ( kT )作为X (kT )迭代计算的初值.
(3) 初始化控制输入指令的序列 u 0 =u ( k T ) u ( k T + T ) … u ( k T + H T - T ) T H ×1 .
(4) 利用式(14)可求得状态变量X 预估值X ^ X ^ ( k T ) X ^ ( k T + T ) … X ^ ( k T + H T - T ) T . 代入式(15)可求得输出变量Y 预估值Y ^ Y ^ ( k T ) Y ^ ( k T + T ) … Y ^ ( k T + H T - T ) T .
(5) 将u 0 和Y ^ u 0 .
(6) 重复(4)和(5),最终求得最优控制序列u 0 * . 将u 0 * u (kT )发送给DPS系统并操纵母船并利用立管横向响应模型可求得第k +1步Y (kT +T ),然后转入(1)开展下一时间步计算.
3 仿真分析
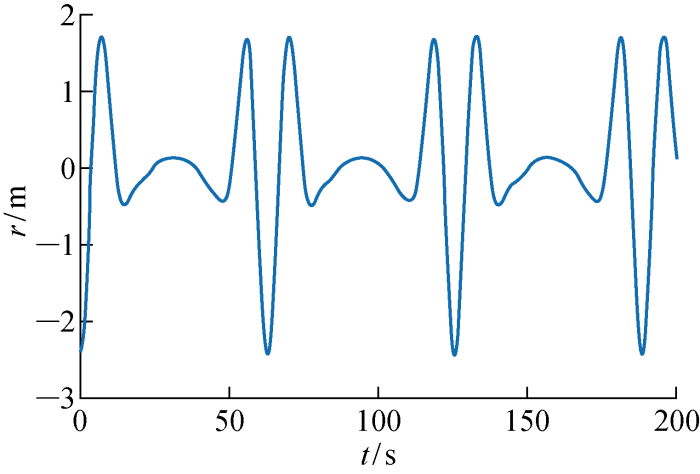
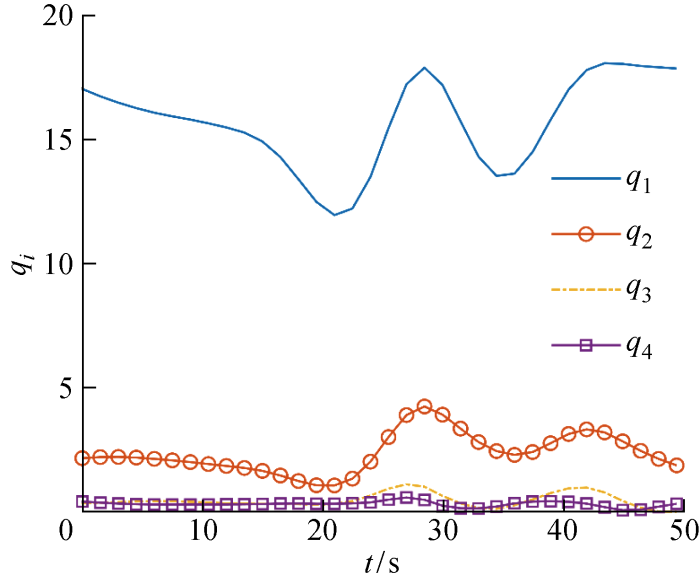
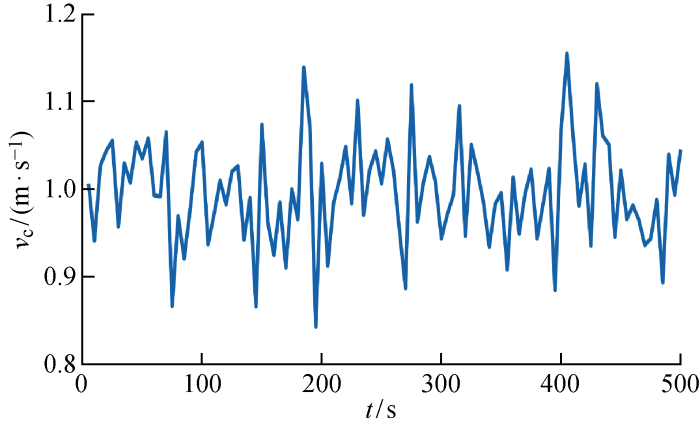
选用某深海钻井立管系统,立管总长 1 500 m,立管内径和外径分别为0.44 m和 0.5 m,立管密度为 7 900 kg/m3 ,底端总成净重为100 t.母船净重为 4 200 t,船舶水动力系数 M r · Mr =-1 260 000.引入东海地区六级海况,三一平均波高 ζ - ω / 3 r )如图4 所示.悬挂立管受到母船纵荡和v c =1 m/s均匀洋流作用下的模态响应时间坐标曲线如图5 所示,发现立管的第1阶模态始终占据主导,第2阶已被激发,3阶及以上模态分量可以忽略,因此选用模态数N =3是足够的.
图4
图4
波浪谱下船舶纵荡响应
Fig.4
Vessel surge motion in wave spectrum
图5
图5
悬挂立管前4阶模态时间坐标响应曲线
Fig.5
Time traces of first four modal coordinates
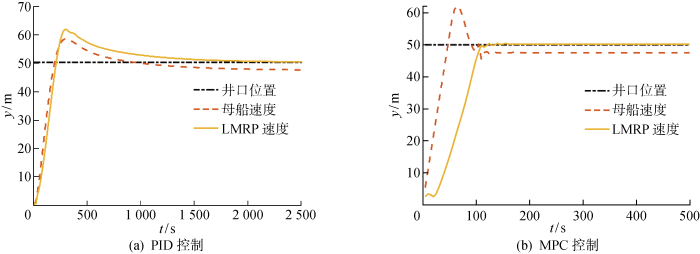
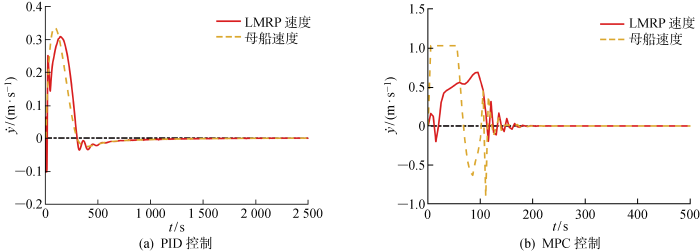
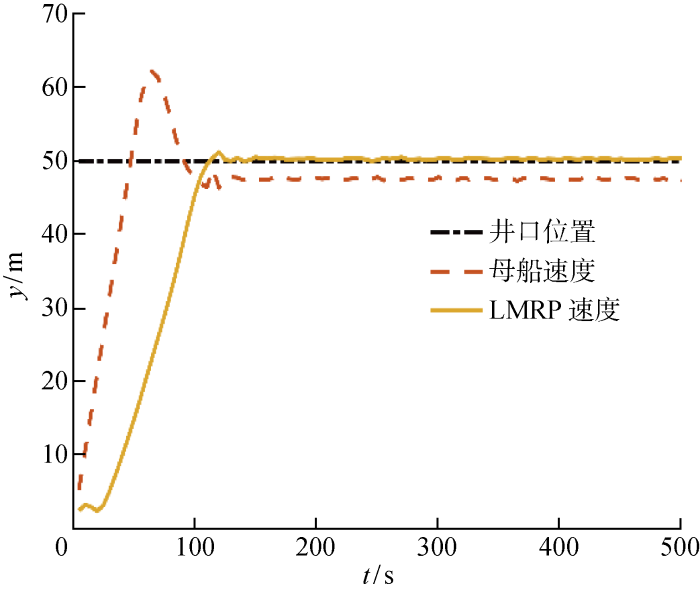
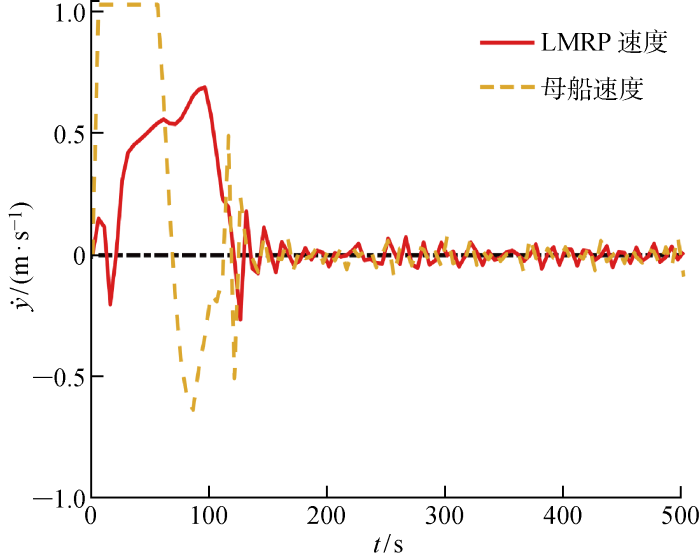
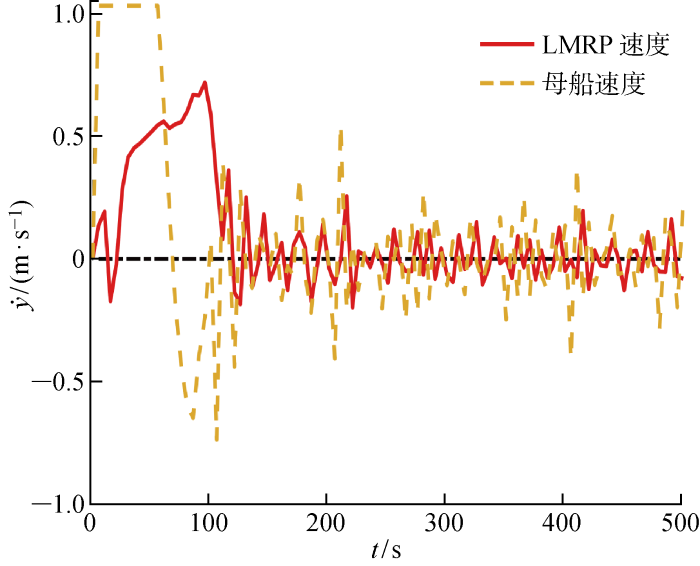
设定仿真时间步长T =5 s,预测时域步数H =20,并保持控制时域与预测时域相同.设推进器2 s延迟即A thr =3 s-1 ,权重Q =1 0 0 10 R =1,指令约束为-1 m/s<u <1 m/s和-5 m/s<Δu <5 m/s,y d =50 m即井口坐标(50, 1 500) m,外部均匀洋流且流速为1.0 m/s.采用MATLAB自编程与传统PID再入井系统进行比较.图6 为母船与LMRP位置在两种再入井系统作用下的位移(y )响应曲线.PID控制作用下母船和LMRP几乎同时在t ≈200 s时越过井口位置进而产生超调,在t ≈2 000 s 时,LMRP到达井口位置并保持稳定,从而完成再入井作业.MPC控制作用下,母船能够快速做出响应,悬挂立管也随之快速运动,尽管母船出现较大超调量且在井口上方发生往返运动,在t ≈150 s时LMRP到达井口位置并保持稳定.需说明的是,LMRP在t ≈120 s 出现波动,但其超调量一直较小,满足工程要求.图7 为母船与LMRP位置在两种再入井控制系统作用下的速度(y · ) 响应曲线.在PID控制下,LMRP初始阶段受到洋流力作用产生一定波动.MPC控制下,母船快速响应且在t =0~200 s 出现明显波动,因MPC有母船速度和加速度限制,母船速度始终维持在-1~1 m/s.LMRP相较于母船具有一定延迟,但也能随母船快速动作,且在t ≈200 s 实现了速度稳定.
图6
图6
母船及立管底端总成位置响应曲线
Fig.6
Time traces of mother vessel and LMRP
图7
图7
母船及立管底端总成速度响应曲线
Fig.7
Time traces of mother vessel velocity and LMRP velocity
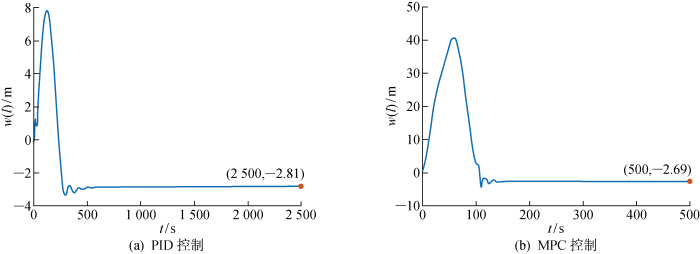
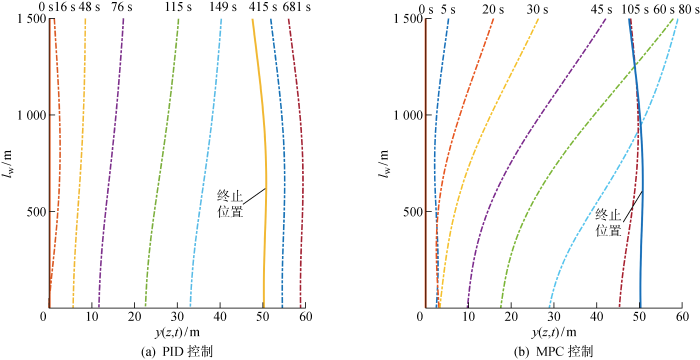
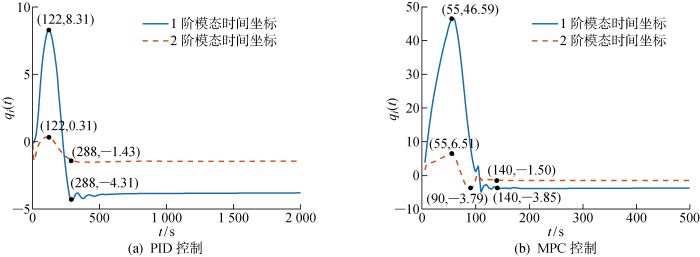
再入井作业过程中悬挂立管的第一阶模态通常占主导,一般通过立管的顶端和LMRP横向偏移来探讨悬挂立管弯曲程度.图8 为两种再入井系统作用下,立管顶端与LMRP横向偏移时间曲线.PID控制下,立管顶端和LMRP水平距离始终保持较小值,最高不超过8 m. MPC控制下,在t ≈60 s时立管顶端和底端距离最高达到40 m,这是由于母船的快速响应和立管因长径比增加致使柔性显著增强造成的.图9 为悬挂立管在再入井过程形变响应曲线.图中:l w 为立管与井口的垂直距离.PID控制下,悬挂立管始终保持较小形变.MPC控制下,悬挂立管展现丰富动态响应特征.为深入分析,悬挂立管前两阶模态时间坐标响应如图10 所示.PID控制作用下,第1阶模态始终占主导作用.在t =122 s时第1阶和第2阶模态时间坐标同时达到了最高值,再入井过程中悬挂立管形变量较小.在MPC控制作用下, 第2阶模态影响明显增加,在母船和立管回调过程中可能占主导(见t =90 s).这是因为当母船越过钻井口后,需通过DPS对母船实施反方向操纵,而立管由于运动延迟尚未到达井口,激发了悬挂立管第2阶模态.
图8
图8
立管顶端与底端总成之间的横向偏移
Fig.8
Offset of the top-end to the LMRP of riser
图9
图9
再入井过程悬挂立管形变曲线
Fig.9
Deformation curves of hang-off riser in reentry
图10
图10
悬挂立管前两阶模态时间坐标响应曲线
Fig.10
Time traces of first two modal coordinates
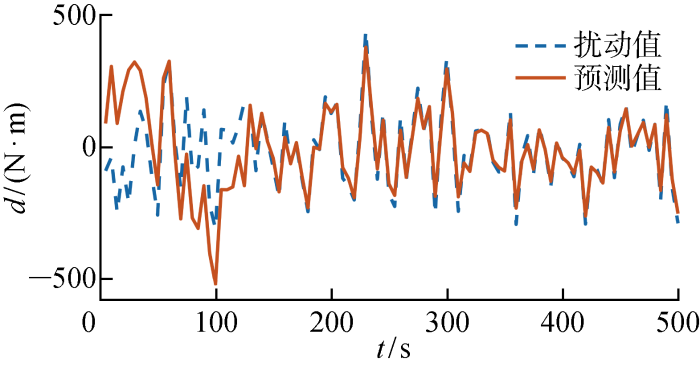
分析MPC立管再入系统对洋流力附加模型误差的补偿作用.首先利用wgn函数产生随机高斯白噪声序列,乘以5作为f c 的扰动d ,如式(23)所示.施加的扰动和非线性扰动观测器测定的扰动数据如图11 所示.受初值及收敛速度影响,t ≈150 s 后预测数值与实际扰动数据具有较好贴合度.为防止收敛前的扰动值不能准确预测,可提前启动观测器,然后进行仿真计算.母船与LMRP位置和速度响应曲线分别如图12 和图13 所示.在扰动影响下,母船和LMRP的响应过程有一定振荡,但依然能很快地完成再入井作业 (LMRP 在t ≈120 s到达井口并保持稳定),说明非线性扰动观测器对于扰动具有较好补偿作用.
图11
图11
洋流力附加扰动时间历程曲线
Fig.11
Time trace of added disturbances in hydrodynamic force term
图12
图12
洋流力扰动下母船及LMRP位置响应曲线
Fig.12
Time traces of mother vessel and LMRP under the current resistance disturbance
图13
图13
洋流力扰动下母船及LMRP速度响应曲线
Fig.13
Velocities of mother vessel and LMRP under the current resistance disturbance
分析MPC立管再入系统对洋流速度扰动的补偿作用.利用wgn函数产生0.1 m/s 左右的随机高斯白噪声序列作为均匀流速扰动d c ,即v c =1.0 m/s+d c ,洋流速度时间曲线如图14 所示.母船与LMRP位置和速度的响应曲线分别如图15 和图16 所示.扰动作用下,母船和立管的响应过程有一定振荡,但依然能很快地完成再入井作业.底端总成到底钻井口目标位置后,母船仍有一定速度对扰动流速进行动态补偿,保证LMRP始终维持较低速度,有益于安全稳定实现立管再入井作业,从而证明MPC作用下的立管再入系统对于洋流速度扰动具有良好鲁棒性.需指出的是,洋流流速变化导致预测模型中相对速度等参数发生变化,观测器对模型中参数摄动补偿效果有限,仍然需要选择温和海况进行再入井作业.
图14
图14
洋流速度时间历程曲线
Fig.14
Time trace of incoming uniform current
图15
图15
流速扰动下母船及LMRP位置响应曲线
Fig.15
Time traces of mother vessel and LMRP under the flow rate disturbance
图16
图16
流速扰动下母船及LMRP速度响应曲线
Fig.16
Velocities of mother vessel and LMRP under the flow rate disturbance
4 结语
当前海洋钻井工程逐步迈入深海区,恶劣的海洋气候和复杂的海洋环境使钻井立管系统发生脱离(立管底端总成和防喷器断开)的几率大幅增加.如果天气预报成功,可以有时间回收立管并驶离.若不能及时预报则必须进行紧急脱离.天气转好后,则需要将底端总成和防喷器重新连接,称为再入井作业.由于深海区天气与海况复杂多变,确认海洋环境适合时需要尽快完成再入井作业.但是悬挂立管系统因长径比的大幅增加,立管的柔性显著增强,这对在母船激励和复杂海况下(即使海况温和)安全快速完成再入井作业提出新的严峻挑战.
基于修正哈密顿原理建立底端含集中质量(底端总成)的柔性悬挂立管系统仿真模型,结合立管动态响应预测模型及井口位置设计优化函数和约束,构建非线性扰动观测器实现对洋流力的模型误差和洋流速度的扰动补偿,尝试提出一种基于MPC的深海钻井立管再入井控制系统.仿真发现:相比于传统钻井立管再入井作业PID控制,在MPC控制系统作用下,母船和悬挂立管可快速做出响应,立管系统能够安全稳定地实现再入井作业,能较好地处理洋流力模型误差问题,且在洋流速度扰动下具有良好鲁棒性.
本研究属于寻找海洋立管快速再入井策略初步探索,有许多不足之处.例如,只考虑了立管横向(母船纵荡)运动;当洋流泄涡频率接近系统固有频率时,立管可能发生涡激振动.下一步将开展横向和纵向耦合动态响应分析及二维再入控制系统研究,此时需要分析推进器布置及推力分配问题.同时为防止立管形变较大产生破坏,可在优化函数中引入悬挂立管最大形变约束,这些将在后续工作中逐步完成.
参考文献
View Option
[1]
MURAI M YAMAMOTO M An experimental analysis of the internal flow effect on marine risers
[C]// Proceedings of the Internal Conference on Marine Technology Dhaka, Bangladesh : MARTEC , 2010 : 159 -165 .
[本文引用: 1]
[2]
王宗义 , 肖坤 , 庞永杰 , 等 . 船舶动力定位的数学模型和滤波方法
[J]. 哈尔滨工程大学学报 2002 , (4 ): 24 -28 .
[本文引用: 1]
WANG Zongyi XIAO Kun PANG Yongjie et al Mathematical models and filtering methods for dynamic ship positioning
[J]. Journal of Harbin Engineering University 2002 (4 ): 24 -28 .
[本文引用: 1]
[3]
SUZUKI H YOSHIDA K SHIDA S et al Active control of riser deformation and vessel motion for automatic entry/reentry system
[C]// Proceedings of 4th International Offshore and Polar Engineering Conference Osaka, Japan : ISOPE , 1994 : 216 -223 .
[本文引用: 4]
[4]
SUZUKI H TAO Q WATANABE K Learning tracking controllers under unknown disturbances for the installation of rigid and flexible structures
[J]. Journal of Marine Science & Technology 1999 , 4 (4 ): 187 -199 .
[本文引用: 4]
[5]
TAKAYUKI I KAZUHISA O KAJIWARA H et al On vibration control of flexible pipe in ocean drilling system
[C]// Proceedings of the Sixteenth International Offshore and Polar Engineering Conference San Francisco, USA : ISOPE , 2006 : 26 -30 .
[本文引用: 4]
[6]
KOTERAYAMA W NAKAMURA M KAJIWARA H et al Development of a training simulator for dynamic reentry operations of a riser pipe hanged off
[C]// Proceedings of the Eighteenth International Offshore and Polar Engineering Conference Vancouver, Canada : ISOPE , 2008 : 67 -70 .
[本文引用: 4]
[7]
KOTERAYAMA W KARJIWARA H NAKAMURA M et al Model experiments of reentry control based on riser pipe dynamics
[C]// The Eighth ISOPE Pacific/Asia Offshore Mechanics Symposium Bangkok, Thailand : ISOPE , 2008 : 8 -12 .
[本文引用: 5]
[8]
KARJIWARA H NORIDOMI K Reentry control system design for a riser pipe experimental model under steady current
[C]2009 ICCAS-SICE Fukuoka, Japan : IEEE , 2009 : 3896 -3901 .
[本文引用: 4]
[9]
HU Y L YAO B H ZHENG Z et al Research on marine riser in different installations stages of subsea production tree
[C]// Shanghai, China China : IEEE , 2016 : 920 -922 .
[本文引用: 2]
[10]
WANG S W XU X S YAO B H et al A finite difference approximation for dynamic calculation of vertical free hanging slender riser in re-entry application
[J]. China Ocean Engineering 2012 , 26 (4 ): 637 -652 .
DOI:10.1007/s13344-012-0048-7
URL
[本文引用: 3]
[11]
王盛炜 , 徐雪松 , 姚宝恒 , 等 . 针对立管重入井过程中等路径段加速度的改进型蚁群优化算法
[J]. 上海交通大学学报 , 2013 , 47 (10 ): 1585 -1590 .
[本文引用: 3]
WANG Shengwei XU Xuesong YAO Baoheng et al Improved ant colony optimization for accelerations of equal-length paths of riser re-entry
[J]. Journal of Shanghai Jiao Tong University 2013 , 47 (10 ): 1585 -1590 .
[本文引用: 3]
[13]
TRIANTAFYLLOU M S Cable mechanics for moored floating systems
[C]// Proceedings of the Seventh International Conference on the Behavior of Offshore Structures Massachusetts, USA : Pergamon , 1994 : 57 -79 .
[本文引用: 1]
[15]
HU Y L CAO J J YAO B H et al Dynamic behaviors of a marine riser with variable length during the installation of a subsea production tree
[J]. Journal of Marine Science and Technology 2017 , 23 (3 ): 1 -11 .
DOI:10.1007/s00773-017-0462-x
URL
[本文引用: 1]
[16]
胡永利 . 深海钻井立管重入井作业运动特性及其优化研究 [D]. 上海 : 上海交通大学 , 2018 .
[本文引用: 1]
HU Yongli Study of properties and optimization of deep-sea drilling riser in reentry [D]. Shanghai : Shanghai Jiao Tong University , 2018 .
[本文引用: 1]
[17]
HU Y L YAO B H LIAN L Analysis of drilling riser in re-entry operation under complex currents
[J]. Journal of Ship Mechanics 2019 , 23 (12 ): 1528 -1540 .
[本文引用: 1]
[18]
YAMAMOTO M MOROOKA C K UENO S Dynamic behavior of a semi-submersible platform coupled with drilling riser during re-entry operation in ultra-deep water
[C]// Proceedings of the ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering San Diego, California, USA : ASME , 2007 : 239 -248 .
[本文引用: 1]
[19]
YAMAMOTO M An automatic approaching control for the petroleum well re-entry operation in ultra-deep water
[C]// Proceedings of the 8th IFAC International Conference on Maneuvering and Control of Marine Craft Guarujá, Brazil : IFAC , 2009 : 388 -393 ,
[本文引用: 1]
[20]
YAMAMOTO M MOROOKA C K Feedback control system for blow-out preventer positioning
[J]. Applied Ocean Research 2019 , 82 : 362 -369 .
DOI:10.1016/j.apor.2018.11.013
[本文引用: 1]
During the drilling of ultra-deep-water subsea petroleum wells, a blow-out preventer (BOP), a piece of safety equipment, must be assembled on the wellhead. The BOP is suspended using the drilling riser during the wellhead approach operation, and the riser's top end is connected to the floating platform rig. This article presents a feedback control system for the automatic approach of the BOP to the wellhead. Compared to state-of-the-art controls, ours does not require ancillary thrusters installed alongside the riser nor inclination sensors atop of the drilling riser. Additionally, our proposed control embeds a closed-loop dynamic positioning system, thus retaining the characteristics of the original control system and adding an extra closed-loop. This eases implementation of the BOP approach control to an existing platform. To calculate the optimal gains for the BOP controller, we assume a linear system for the riser, including only the pendulum-shape. The simulation is carried out using nonlinear models for both riser and floating platform. We assume an International Towing Tank Conference standard semi-submersible platform, coupled with a 3000-m free-hanging vertical riser for the time-domain simulation. The results show the BOP tracking to be a step-shaped input signal under current and wave loads. A discussion of the performance of feedback control under different environmental loads is also included.
[21]
毛良杰 , 付燈煌 , 曾松 . 正常连接与悬挂撤离工况下深水钻井隔水管动力特性与安全分析
[J]. 船舶力学 2022 , 26 (2 ): 250 -263 .
[本文引用: 1]
MAO Liangjie FU Denghuang ZENG Song Dynamic characteristics and safety analysis of deep water drilling riser under normal connected condition and hang-off evacuation condition
[J]. Journal of Ship Mechanics 2022 , 26 (2 ): 250 -263 .
[本文引用: 1]
[22]
FOSSEN T I Guidance and control of ocean vehicles
[M]. Chichester , England : John Wiley & Sons , 1994 .
[本文引用: 1]
[23]
SØRENSEN A J SAGATUN S I FOSSEN T I Design of a dynamic positioning system using model-based control
[J]. Control Engineering Practice 1996 , 4 (3 ): 359 -368 .
DOI:10.1016/0967-0661(96)00013-5
URL
[本文引用: 1]
An experimental analysis of the internal flow effect on marine risers
1
2010
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
船舶动力定位的数学模型和滤波方法
1
2002
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
船舶动力定位的数学模型和滤波方法
1
2002
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
Active control of riser deformation and vessel motion for automatic entry/reentry system
4
1994
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... [3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ].当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
Learning tracking controllers under unknown disturbances for the installation of rigid and flexible structures
4
1999
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... ⇓ ⇓ ⇓ ⇓ ⇓ -9 ].当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
On vibration control of flexible pipe in ocean drilling system
4
2006
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... ⇓ ⇓ ⇓ ⇓ -9 ].当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
Development of a training simulator for dynamic reentry operations of a riser pipe hanged off
4
2008
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... ⇓ ⇓ ⇓ -9 ].当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
Model experiments of reentry control based on riser pipe dynamics
5
2008
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... ⇓ ⇓ -9 ].当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
... 引入日本九州大学Kajiwara实验模型参数[7 ] 进行仿真计算,预测的立管底端防喷器位置y d 响应曲线如图2 所示,与试验数据拟合较好,从而完成模型验证. ...
Reentry control system design for a riser pipe experimental model under steady current
4
2009
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... ⇓ -9 ].当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
Research on marine riser in different installations stages of subsea production tree
2
2016
... 海洋资源开发一般分为两步,首先是立管钻井和完井作业,然后是生产和输送作业.因此从功能用途上区分,海洋立管可以分为钻井立管和生产立管两大类[1 ] .海洋立管是海洋工程中典型的超细长结构物,是连接顶端平台和水下井口的唯一通道,是整个油气系统最为薄弱的环节.钻井作业时一旦遭遇台风或其他恶劣海况,为避免环境载荷超过作业极限必须将底端总成与防喷器断开,然后撤离至安全海域.等到海洋环境改善需将悬挂立管底端总成与防喷器重新连接,此过程称为再入井作业.由于锚链对于深海作业不适用,深海钻井船和钻井平台需采用动力定位系统(Dynamic Position System, DPS)来对船体位置进行校正[2 ⇓ ⇓ ⇓ ⇓ ⇓ -8 ] .传统的再入井策略是借助水下机器人(Remotely Operated Vehicle, ROV)观察底端总成位置,然后通过比例-积分-微分(PID)控制系统发送指令给DPS,通过控制顶端母船的位置来实现立管再入井作业.由于悬挂立管系统承受母船激励及海洋力作用,其复杂动态响应使再入井作业繁琐耗时[3 ⇓ ⇓ ⇓ ⇓ ⇓ -9 ] .当前海洋开发工程步入深海区,频繁遭遇恶劣天气使钻井立管系统发生断开概率大幅提升.海况转好后必须快速完成立管再入井作业以适应多变的天气和海洋环境.立管由于长径比的大幅增加导致柔性显著增强.在母船及海洋环境力的激励下,悬挂立管在快速再入井过程中必然展现新的响应特性,给工程师们带来新的严峻挑战.当母船到达井口上方时,立管底端总成可能还未达到井口.当母船继续平移时,立管底端总成则会很容易错过钻井口.因此,需要重新优化设计再入井控制系统,以辅助操作员快速安全地完成再入井作业. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
A finite difference approximation for dynamic calculation of vertical free hanging slender riser in re-entry application
3
2012
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... [10 ⇓ -12 ]提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
针对立管重入井过程中等路径段加速度的改进型蚁群优化算法
3
2013
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... ⇓ -12 ]提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
针对立管重入井过程中等路径段加速度的改进型蚁群优化算法
3
2013
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... ⇓ -12 ]提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
Movement optimization of freely-hanging deepwater risers in reentry
3
2016
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... -12 ]提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
... 式中:M 为钻井船质量;m 为立管单位长度质量;l 为立管长度.由于深海立管长径比很大,柔性很强,可采用缆绳模型进行计算[3 ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ -12 ] ,所以没有弯曲应变能.立管系统势能V 包括重力势能V g 、拉伸应变势能V e 与横向应变势能V t ,经过推导其表达式为 ...
Cable mechanics for moored floating systems
1
1994
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
A finite differences formulation for the linear and nonlinear dynamics of 2D catenary risers
1
2008
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
Dynamic behaviors of a marine riser with variable length during the installation of a subsea production tree
1
2017
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
1
2018
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
1
2018
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
Analysis of drilling riser in re-entry operation under complex currents
1
2019
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
Dynamic behavior of a semi-submersible platform coupled with drilling riser during re-entry operation in ultra-deep water
1
2007
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
An automatic approaching control for the petroleum well re-entry operation in ultra-deep water
1
2009
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
Feedback control system for blow-out preventer positioning
1
2019
... 日本海洋科学技术中心在研发“地球”号钻探船再入井装置中,东京大学Suzuki等[3 -4 ] 基于哈密顿原理推导了母船与悬臂立管耦合非线性水动力方程,然后基于小变形理论进行线性化,基于最优控制理论提出了一种主动控制方法,通过在立管中段和底端添加推进器来实现对立管再入井运动控制,但在深海钻井立管上安装推进器在工程实施过程中难度较大.九州大学Takayuki 等[5 ⇓ ⇓ -8 ] 基于缆索模型,通过立管动态响应特性和模态分析,将立管底端位置以及顶端偏移角作为反馈信号,采用线性变参数(Linear Parameter Varying, LPV)和线性二次型积分(Linear Quadratic with Integral action, LQI)控制策略规划母船路径规划,通过控制母船速度完成再入控制系统设计,并研发了一款再入井作业模拟器用以培训船员,但具体设计未对外公开.Wang等[10 ⇓ -12 ] 基于Triantafyllou[13 ] 水下缆索模型以及Chatjigeorgiou[14 ] 悬链线立管模型建立了离散化悬挂立管横向运动模型,采用有限差分逼近(Finite Difference Approximation,FDA)进行了仿真分析,并通过改进蚁群算法对再入井运动策略进行规划,目前该成果还不能直接应用于实际工程,同时只考虑了母船单一激励. Hu等[15 ⇓ -17 ] 基于缆索模型采用有限元法开展了深海钻井立管在多重复合激励下的重入井下放阶段非线性运动特性仿真分析,对Wang等[10 ⇓ -12 ] 提出的蚁群算法进行针对性改进,并优化设计了母船速度和加速度等参数以抑制立管底端偏移和振荡,但未能结合再入控制系统进行研究.Yamamoto等[18 ⇓ -20 ] 基于有限元法建立了悬挂立管在二阶波浪力及涡激振动效应作用下横向运动模型,并基于线性二次型调节器(Linear Quadratic Regulator,LQR)策略设计了再入井作业控制系统,但该研究只考虑悬臂立管一阶模态响应.快速再入井过程中,大长径比柔性悬挂立管在母船激励和沿轴向复杂海洋流体力作用下可能会激发更高阶模态. ...
正常连接与悬挂撤离工况下深水钻井隔水管动力特性与安全分析
1
2022
... 根据立管顶端连接方式,悬挂撤离分为硬悬挂与软悬挂模式.硬悬挂时立管和母船固定连接.软悬挂时,张紧器系统仍起作用,液压装置的液压杆部件通过张力环与立管连接.两种模式各有优势,不能盲目采用软悬挂或硬悬挂模式,应当结合实际情况选择合适模式[21 ] .本研究设定为硬悬挂模式,图1 为深海钻井立管硬悬挂模式示意图,立管顶端固定在母船,立管底端自由且附带一个点质量M B ,即立管的底端总成(Lower Marine Riser Package, LMRP).采用二维欧拉坐标系Oxz ,其中坐标原点O 建立在母船的初始位置,x 为母船横向运动正方向,z 为重力加速度方向.r (t )为母船横向位移,t 为时间. 不考虑母船垂荡和横摇以及立管涡激振动效应等,立管横向运动是由母船运动r (t )和横向形变w (z , t )叠加而成的,因此立管横向位移y (z , t )=r (t )+w (z , t ),这里以y B (t )标记立管底端总成的位移. ...
正常连接与悬挂撤离工况下深水钻井隔水管动力特性与安全分析
1
2022
... 根据立管顶端连接方式,悬挂撤离分为硬悬挂与软悬挂模式.硬悬挂时立管和母船固定连接.软悬挂时,张紧器系统仍起作用,液压装置的液压杆部件通过张力环与立管连接.两种模式各有优势,不能盲目采用软悬挂或硬悬挂模式,应当结合实际情况选择合适模式[21 ] .本研究设定为硬悬挂模式,图1 为深海钻井立管硬悬挂模式示意图,立管顶端固定在母船,立管底端自由且附带一个点质量M B ,即立管的底端总成(Lower Marine Riser Package, LMRP).采用二维欧拉坐标系Oxz ,其中坐标原点O 建立在母船的初始位置,x 为母船横向运动正方向,z 为重力加速度方向.r (t )为母船横向位移,t 为时间. 不考虑母船垂荡和横摇以及立管涡激振动效应等,立管横向运动是由母船运动r (t )和横向形变w (z , t )叠加而成的,因此立管横向位移y (z , t )=r (t )+w (z , t ),这里以y B (t )标记立管底端总成的位移. ...
Guidance and control of ocean vehicles
1
1994
... 根据文献[22 ],母船采用Abkowitz低频运动模型,在船舶较低航速情况下可对船舶受到的水动力进行简化.在再入井过程中由于船速较低(本研究设定船速范围[-1, 1] m/s),可以忽略二阶速度项.在不考虑船舶艏向角影响下,母船一维横向低频运动可近似表示为 ...
Design of a dynamic positioning system using model-based control
1
1996
... 钻井船一般采用一对全回转导管推进器或吊舱推进器作为主推,可以提供全方向360°的推力,以及一对仅提供横向推力的侧推器.本研究中推进器仅提供船舶纵荡方向的推力,因此仅考虑了单一推进器提供定向推力.引入一阶延时模型用于模拟推进器的动力特性[23 ] , ...