基于自适应黏菌算法优化的无人机三维路径规划

doi:10.16183/j.cnki.jsjtu.2022.191

基于自适应黏菌算法优化的无人机三维路径规划

黄鹤^a^,^b, 高永博^a, 茹锋^a^,^b, 杨澜^,^c, 王会峰^b

a.长安大学电子与控制工程学院, 西安 710064

b.长安大学西安市智慧高速公路信息融合与控制重点实验室, 西安 710064

c.长安大学信息工程学院,西安 710064

3D Path Planning of UAV Based on Adaptive Slime Mould Algorithm Optimization

HUANG He^a^,^b, GAO Yongbo^a, RU Feng^a^,^b, YANG Lan^,^c, WANG Huifeng^b

a. School of Electronic and Control Engineering, Chang’an University, Xi’an 710064, China

b. Xi’an Key Laboratory of Intelligent Expressway Information Fusion and Control, Chang’an University, Xi’an 710064

c. School of Information Engineering, Chang’an University, Xi’an 710064, China

通讯作者: 杨澜,高级工程师;E-mail:lanyang@chd.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-06-1 修回日期: 2022-09-1 接受日期: 2022-10-17

基金资助:

国家重点研发计划项目(2021YFB2501200)
国家自然基金面上项目(52172324)
国家自然基金面上项目(52172379)
陕西省重点研发计划项目(2021SF-483)
陕西省自然科学基础研究计划项目(2021JM-184)
西安市智慧高速公路信息融合与控制重点实验室(长安大学)开放基金项目(300102321502)
中央高校基本科研业务费资助项目(300102240203)

Received: 2022-06-1 Revised: 2022-09-1 Accepted: 2022-10-17

作者简介 About authors

黄鹤(1979-),教授,博士生导师,研究方向为无人系统测控、信息融合等.

摘要

针对无人机在三维路径规划时存在搜素范围和寻优性能不足等问题,以及现有黏菌算法(SMA)寻优精度不足, 易陷入局部最优的缺陷,提出了一种基于自适应黏菌算法(GSMA)优化的无人机三维路径规划方法.首先,根据无人机经过的实际环境,建立三维地形、威胁源和无人机自身约束条件;其次,针对搜素范围不足的问题,设计改进的Logistic混沌映射增加种群的多样性并扩大搜索范围,提升了SMA的全局搜索能力;然后,设计一种非线性自适应惯性权重因子,将线性收敛方式改进为非线性收敛,利用权重值更新黏菌位置,提高了收敛速度;最后,在算法后期中设计自适应柯西变异,增大了黏菌的搜索空间,寻优精度也得到了提高.实验结果表明,GSMA相比于灰狼优化(GWO)算法、SMA和海鸥算法(SOA)3种算法,路径更短且更平滑,收敛速度更快,寻优精度更高,同时能耗更低,进一步提升了无人机的路径规划能力.

关键词： 无人机; 路径规划; 黏菌算法; 混沌映射; 自适应柯西变异; 自适应权重

Abstract

Aimed at the problems of insufficient search range and optimization performance in 3D path planning of unmanned aerial vehicles (UAVs), and the lack of optimization accuracy of the existing slime mould algorithm (SMA), which is easy to fall into local optimization, a 3D path planning method for UAV based on adaptive slime mould algorithm optimization is proposed. First, according to the actual environment that the UAV passes through, the 3D terrain, the threat source and the constraints of the AUV were established. Next, for the problem of insufficient search range, an improved Logistic chaotic map is designed to increase the diversity of the population and expand the search range, which improves the global search ability of SMA. Then, a nonlinear adaptive inertia weight factor is designed to change the linear convergence method into nonlinear convergence, and the weight value is used to update the position of the slime mould, which improves the convergence speed. Finally, in the later stage of the algorithm, the adaptive cauchy mutation is designed, which increases the search space of the slime mould and improves the optimization accuracy. The experimental results show that GSMA has a shorter and smoother path, a faster convergence, a higher optimization accuracy, and a lower energy consumption compared with the gray wolf optimizer (GWO) algorithm, the SMA, and the seagull algorithm (SOA), which further improves the path planning capability of the UAV.

Keywords： unmanned aerial vehicle (UAV); path planning; slime mould algorithm (SMA); chaos mapping; adaptive Cauchy variation; adaptive weights

PDF (4295KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄鹤, 高永博, 茹锋, 杨澜, 王会峰. 基于自适应黏菌算法优化的无人机三维路径规划[J]. 上海交通大学学报, 2023, 57(10): 1282-1291 doi:10.16183/j.cnki.jsjtu.2022.191

HUANG He, GAO Yongbo, RU Feng, YANG Lan, WANG Huifeng. 3D Path Planning of UAV Based on Adaptive Slime Mould Algorithm Optimization[J]. Journal of Shanghai Jiaotong University, 2023, 57(10): 1282-1291 doi:10.16183/j.cnki.jsjtu.2022.191

无人机具有生存能力强和机动性能优越的特点,被应用于民生和国防等诸多领域^[1-2].设计高效合理的无人机路径规划方案,可以保证无人机在执行任务时有效躲避各种威胁区域,顺利到达目的地.近年来许多国内外学者对无人机的路径规划方法进行了大量的研究,对此提出了一些路径规划算法,主要可以分为两大类:① 传统算法,如人工势场法^[3]和A^*算法^[4]等;② 智能算法,如粒子群算法^[5]、灰狼算法^[6]和蝠鲼觅食算法^[7]等.采用群体智能优化算法解决无人机路径规划的问题是目前的研究热点,相比于传统算法,智能算法具有寻优速度快、稳定性强的优点.在此基础上,王翼虎等^[8] 利用改进粒子群优化算法解决无人机路径规划的问题,生成一条航程较短的飞行路径,收敛速度更快,但收敛精确度不高.黄书召等^[9]为无人机成功通过威胁区域提出了一种改进遗传算法的无人机三维路径规划,提升了搜索性能,但威胁区域考虑得比较单一,实际应用效果并不理想.吴坤等^[10]利用贪婪优化策略改进鲸鱼算法,通过扩大搜索路径提升全局寻优能力,收敛速度较慢.上述研究算法虽然实现了无人机的路径规划,但算法的收敛速度和寻优精度有限.2020年,Li等^[11]根据黏菌在觅食过程探索路径的行为提出了黏菌算法(Slime Mould Algorithm,SMA),特点是寻优速度快、算法简单、模型易修改,适合应用在无人机路径规划中,但SMA自身存在寻优精度不高和容易陷入局部最优的缺点,仍需进一步改进.因此,本文提出了一种基于改进的自适应黏菌算法(GSMA),保证了寻优速度和寻优精度,又避免陷入局部最优,应用在无人机中能够提高其路径搜索能力.

1 无人机三维路径规划建模

在无人机三维路径规划的过程中,根据任务、威胁源情况和地形等实际因素,构建了三维地形和威胁源约束.将这些威胁源结合自身约束条件建模,等效出三维环境下总的地形约束.

1.1 地形约束

地形环境是无人机路径规划首先要考虑的问题,不同的地貌环境对无人机的威胁不同.三维地形可大致分为山地、丘陵和平原,其中山地条件中的山峰对无人机的正常飞行影响最大,当然也不能忽略海拔的影响.山峰建模坐标Z(x, y)如下所示:

(1)Z(x,y)=h

e^{{(- \frac{(x - x_{0})^{2}}{λ_{1}} - \frac{(y - y_{0})^{2}}{λ_{2}})}^{2}}

式中:坐标(x, y)和(x₀, y₀)分别表示三维地形下山峰在地平面上和中心点的位置;h表示山峰的高度;λ₁、λ₂表示山峰的倾斜度.无人机路径规划过程中的地形威胁代价函数表示如下:

(2)f_Z_j=

\{\begin{array}{l} K_{Z}, & h_{j} - Z_{j} < 0 \\ K'_{Z}, & 0 \leq h_{j} - Z_{j} < 0.1 \\ 0, & h_{j} - Z_{j} \geq 0.1 \end{array}

式中:K_Z和K'_Z为地形威胁系数;h_j、Z_j和f_Z_j分别为无人机第j个航迹点的海拔高度、地形高度以及对应的威胁代价.无人机航迹点j的高度代价表示如下:

(3)f_H_j=h_j

要充分保证无人机的飞行安全,在路径规划中除了要考虑地形约束的影响,还需要考虑飞行的边界和最高距离.实验中,假设无人机的飞行范围表示为(X_min, Y_min)=(0, 0) km和(X_max, Y_max)=(100, 100) km,探索路径过程中的最高飞行高度为Z_max=5 km.

1.2 威胁模型约束

无人机在飞行过程中的威胁主要来自雷达、电磁威胁和导弹截击等,建模如下.

(1) 雷达威胁.

雷达主要通过电磁波探测飞行物的距离和速度信息,对无人机的安全通过威胁很大.雷达侦测飞行物的方程可以简化为圆锥形探测模型,描述如下:

(4)P₀=(X_M-X₀)²+(Y_M-Y₀)²=

{(\frac{h_{0} - Z_{M}}{h_{0}})}^{2} r_{0}^{2}

, Z_M-Z₀<h

式中:(X₀, Y₀, Z₀)表示雷达中心地面坐标;(X_M, Y_M, Z_M)表示雷达威胁区最大位置坐标;h₀代表雷达威胁源的高度;r₀为圆锥模型底面半径.

(2) 电磁威胁.

电磁威胁是无人机路径规划的又一主要威胁.一般情况下,可以用半球形等价电磁威胁区域.电磁威胁函数模型P_C可表示为

(5)P_C=

\{\begin{array}{l} X = R s i n α c o s β \\ Y = R s i n α c o s β \\ Z = R c o s α \end{array}

, Z>0

式中:X、Y、Z分别指三维平面的X轴、Y轴和Z轴;R代表电磁威胁半球形的区域半径;α和β分别为三维平面上Z轴正向与电磁威胁半径的夹角以及威胁半径在水平面上与X轴正向夹角.

(3) 导弹威胁.

敌方导弹威胁到无人机的正常工作,飞行过程中必须躲避.导弹威胁区域P_d1、攻击距离P_d2和威胁总代价P_D模型表示如下:

(6)P_d₁=

\{\begin{array}{l} \frac{1}{2} k_{d} {(\frac{1}{r_{d}} - \frac{1}{r_{c}})}^{2}, & r_{d} \in (0, r_{c}) \\ 0, & r_{d} \geq r_{c} \end{array}

(7)P_d₂=

\frac{1}{2}

k_g

r_{g}^{2}

(8)P_D=P_d₁+P_d₂

式中:k_d和k_g分别表示导弹击中无人机的概率和导弹的加速度参数;r_d代表航迹点到导弹威胁中心的距离;r_c表示导弹影响范围半径;r_g表示无人机和目标之间的直线距离.

(4) 禁飞区威胁.

无人机在飞行过程中还会受到恶劣天气和复杂环境的影响,被称为禁飞区.禁飞区的代价表示为

(9)P_F=K_F

式中:K_F为禁飞区的威胁代价.

将威胁源等效为地形模型,假设距离威胁源中心越近,威胁代价越大,地形越高,反之则越低.因此,可以将威胁源等效为

(10)Q_jp=

\{\begin{array}{l} 0, R \geq R_{m a x, p} \\ K_{t h r} \sqrt{R_{m a x, p}^{2} - [(x - x_{p})^{2} + (y - y_{p})^{2}]}, \end{array}

其他式中:K_thr为威胁源修正系数;R_max,_p表示第p个威胁源的最大半径;第p个威胁源中心的水平坐标为(x_p, y_p).禁飞区的威胁区域的代价f_jp表示如下:

(11)f_jp=

\{\begin{array}{l} P_{0}, P_{C}, P_{D}, P_{F}, & r_{j, p} \leq R_{m a x, p} \\ 0, & 其 他 \end{array}

式中:r_j,p为航迹点j到威胁源中心p的距离.

无人机在进行执行任务的同时与地形威胁山源保持安全距离,避免产生碰撞,同时规避雷达、电磁和导弹威胁,保障无人机飞行安全.

1.3 无人机自身约束

无人机抽象为一个质点模型,无需考虑自身的质量和形状.在路径规划的过程中,无人机不仅受到外部条件威胁,也受限于自身约束条件,如自身转弯角度α₀、向上爬升角度β₀和燃油消耗(用飞行航程表示).设最大转弯角度α_max、向上最大爬升角度β_max,这些自身物理约束条件可以表示为

(12)J_h=

\{\begin{array}{l} 0, & α_{0} \leq α_{m a x} \\ Q_{h}, & α_{0} > α_{m a x} \end{array}

(13)J_v=

\{\begin{array}{l} 0, & β_{0} \leq β_{m a x} \\ Q_{v}, & β_{0} > β_{m a x} \end{array}

(14)J_L_j=

\{\begin{array}{l} l_{j}, & j > 1 \\ 0, & j = 1 \end{array}

式中:Q_h和Q_v分别为无人机的转弯角和爬升角系数;J_h和J_v分别为转弯角度和向上爬升角度的代价函数;J_L_j为航迹点j对应的航程;l_j为无人机的飞行航程.综合上述所有的代价函数,无人机航迹点总约束代价表示为

(15)f_Jj=J_h+J_v+J_L_j

1.4 航迹代价函数

将上述地形约束、高程代价、威胁模型约束及无人机自身物理约束的代价加权综合起来,得到无人机总的代价函数,用F(R_j)表示为

(16)F(R_j)=

\overset{d}{\sum_{j = 1}}

(ω₁f_Z_j+ω₂f_H_j+ω₃

\overset{σ}{\sum_{j = 1}}

f_jp+ω₄f_Jj)

式中:d为航迹点数目;σ威胁源总数;ω₁、ω₂、ω₃、ω₄为各约束代价的权重.

2 改进的黏菌觅食算法

2.1 黏菌算法

黏菌是一种真核生物,SMA模拟了黏菌在捕食过程中的行为变化,利用黏菌的觅食过程进行路径规划.

2.1.1 黏菌觅食位置的更新

黏菌在觅食过程中,空气中食物的浓度越大,黏菌自身细胞质流动越快,进而觅食成功.黏菌觅食的过程可用函数表达式表示,位置更新公式如下:

(17)X_new=r(B_U-B_L)+B_L, r<c

(18)X_new=

\{\begin{array}{l} X_{b} (t) + V_{b} (W X_{A} (t) - X_{B} (t)), & r < p \\ V_{c} X (t), & r \geq p \end{array}

(19)a=(arctan h)

(- \frac{t}{T_{m a x}} + 1)

(20)p=tanh(S(i)-D_F)

式(17)和(18)表示黏菌觅食的过程,B_U和B_L规定了黏菌搜索食物范围的上下边界;c为常量,文中取0.03;r的取值范围是在0至1区间内的随机值;V_b参数在-a到a区间内取值;V_c参数在觅食过程中线性减少至0;t表示黏菌的迭代次数;X_b代表食物浓度最高的位置;X为黏菌的位置;X_A和X_B代表黏菌的两个任意位置;W为黏菌自身的质量;T_max表示最大迭代次数.黏菌位置X可以随着其获得的最优位置的变化而更新,同时黏菌位置也可以根据V_b、V_c和W参数的微调而更新^[12].式(20)中的S(i)为黏菌的适应度,i表示种群的位置,而D_F为黏菌的最佳适应度.此外,黏菌质量参数W在不同食物浓度的函数表达式表示如下:

(21)W(S_r)=

\{\begin{array}{l} 1 + r l g (\frac{b_{F} - S (i)}{b_{F} - w_{F}} + 1), & N / 2 \\ 1 - r l g (\frac{b_{F} - S (i)}{b_{F} - w_{F}} + 1), & 其 他 \end{array}

(22)S_r=sort(S)

式中:N/2表示前一半黏菌的数量;b_F和w_F分别为在迭代过程中的最优适应度和最差适应度;sort表示对种群的适应度进行升序排列;S_r表示呈递增型的适应度序列.

2.1.2 算法流程

SMA流程如下.

步骤1 初始化种群,设定参数.

步骤2 计算种群适应度值并排序.

步骤3 利用式(17)和(18)更新黏菌种群位置.

步骤4 计算种群适应度值,并更新最优位置,计算当前最优位置.

步骤5 判断是否满足最优条件,若满足则输出最优结果,否则执行步骤2~5直至满足最优.

2.2 基于改进的SMA的无人机三维路径规划

2.2.1 航迹编码

无人机飞行过程中的任一条路径被随机的一只黏菌所定义,而飞行路径由许多个航迹点连接而成的线组成,并且每个航迹点均具有三维空间属性(x, y, z).路径规划过程中,要确定航迹点数,然后将z方向的坐标固定不变,即将三维等效为二维问题解决,则只需要对x和y方向坐标进行寻优.

2.2.2 改进的Logistic映射

由于SMA存在过度依赖种群初始位置的问题,以随机方式初始种群易使得种群分布不均匀,影响算法的求解精度.混沌运动具有遍历性和不重复性等特点,适合用来生成种群的初始位置^[12].大多群体智能优化算法初始种群映射方式使用的是Tent映射和Logistic映射,Tent映射在0~2的取值范围内存在着小周期现象、容易陷入不动点的问题,而传统Logistic映射对初始值条件要求严格,使得初始化黏菌种群的分布不均且多样性不足.据此,设计一种改进的Logistic混沌映射,以增加种群的多样性和均匀分布.具体表达如下:

(23)x_temp=mod(a/x_n+λx_n(1-x_n),b)

(24)x_n+1=

\{\begin{array}{l} x_{t e m p} - 1, & x_{t e m p} > 1 \\ x_{t e m p}, & x_{t e m p} \leq 1 \end{array}

式中:mod为取模函数;x_temp为中间变量;mod(a/x_n, b)的取值范围为[0, 1);λ为常数,文中取0.3;b为(0, 1)中的随机数,文中设定b=0.7;最后输出序列x_n的范围是(0, 1].式(23)将不会出现不定值,且在a不同取值下仍具有较好的随机均匀性.

2.2.3 非线性自适应权重因子

权重因子是SMA的核心参数,设计自适应权重因子可以用于改善算法的搜索能力^[13]. SMA中参数是线性变化的,搜索能力较差且搜素范围局受到限制,寻优能力较弱.为解决这个问题,设计了一种非线性自适应权重因子w,黏菌位置更新公式如下:

(25)X_new=

\{\begin{array}{l} w X_{b} (t) + V_{b} (W X_{A} (t) - X_{B} (t)), & r < p \\ V_{c} X (t), & r \geq p \end{array}

(26)w=w_min+(w_max-w_min)arctan

(\frac{π t}{2 T_{m a x}})

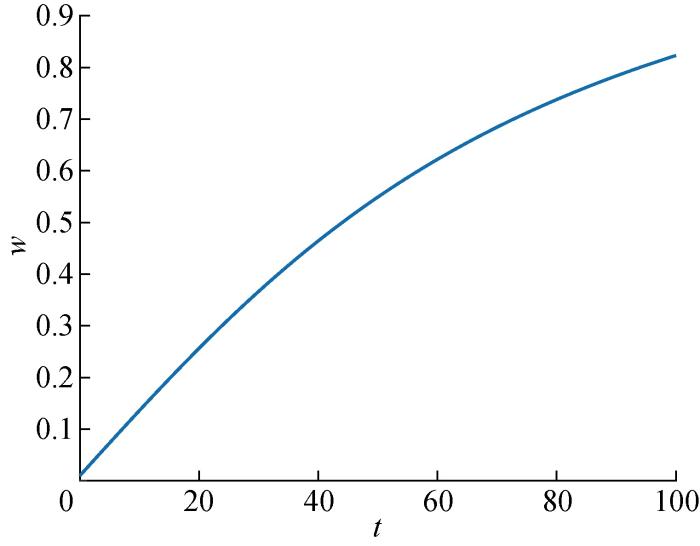
式中:w_max和w_min分别为惯性权重因子的最大值和最小值,本文经过大量实验取值为w_max=0.82,w_min=0.01.自适应权重因子w系数变化如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 w系数变化图

Fig.1 Variation plot of w coefficient

在迭代前期的权重因子w快速增大,扩大种群的搜索范围,w在迭代后期增速放缓,有利于黏菌觅食过程中跳出局部最优,提高了算法的精度,有益于寻找到更合适的位置^[14].自适应权重变化是指黏菌觅食过程中,黏菌位置会根据黏菌的迭代次数的变化而更新.GSMA设计的非线性自适应惯性权重因子,增强了搜索能力,同时避免了陷入局部最优.

2.2.4 自适应柯西变异策略

由于地形情况较为复杂,在黏菌觅食过程中,对最优位置进行柯西变异^[15],可以提高迭代后期的搜素能力.柯西分布的特点是中间的峰值比较小而两边范围比较广,这样可以使黏菌在当前范围产生更大的扰动.针对路径规划过程中出现陷入局部最优和搜索能力较弱的情况,标准柯西变异处理后优化效果有限,因此提出了一种自适应柯西变异策略,公式如下:

(27)F(γ;t)=

\frac{1}{π}

arctan γ+

\frac{1}{2}

(28)γ=exp

(- \frac{θ t}{T_{m a x}}) (1 - \frac{r}{r_{m a x}})

式中:θ为常数,在文中取10;r_max为黏菌个体之间的最大距离;F(γ;t)为柯西变异累计分布函数.自适应柯西变异在黏菌群体迭代过程中可以获得较多的最优值,保证平滑收敛至最优,增强GSMA的全局搜素能力,减少了黏菌最优值的动荡并提高了其寻优速度.自适应柯西变异下的黏菌位置更新如下所示:

(29)X_bnew=X_new+F(γ;t)

式中:X_new为上一代的黏菌最优位置;X_bnew为经过自适应柯西变异更新后黏菌新的位置.

2.2.5 改进的黏菌算法收敛性分析

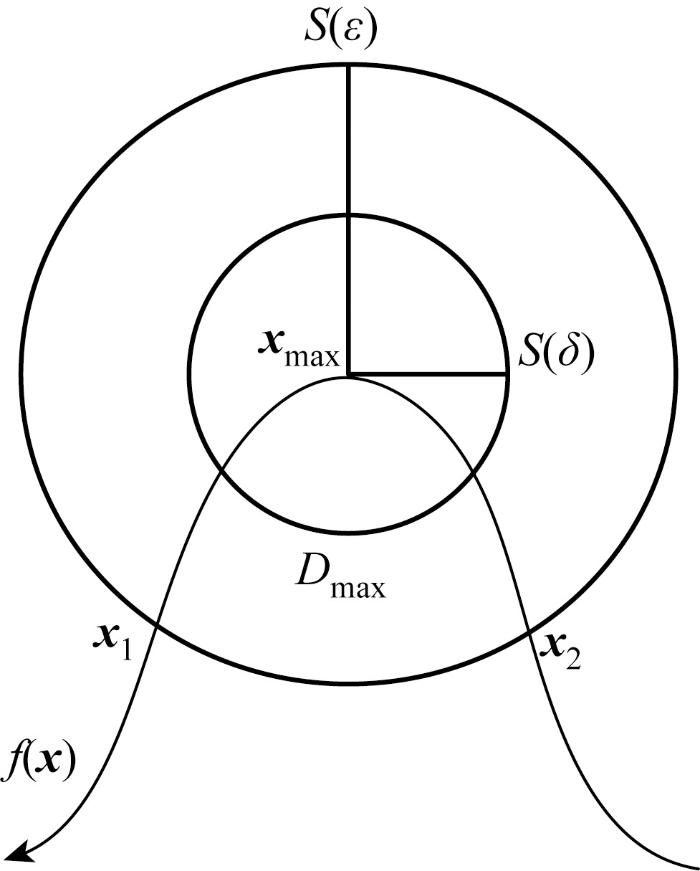
欲将GSMA应用到路径规划中,需验证GSMA的收敛性.设GSMA的初始解在圆心为x_max、半径为δ的圆S(δ)内,可以表示为 $‖x_{0} - x_{m a x}‖$ ≤δ,圆S(ε)与函数f(x)相交于x₁、x₂,最优区域宽度为D_max.经过改进后的式(25)可知,此时算法进行局部寻得最优值,种群个体会逐渐逼近最优值x_max,在局部优值区域D_max来分析算法的收敛性.GSMA的收敛过程如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 GSMA收敛过程

Fig.2 Convergence process of GSMA

当解位于D_max区域时,算法的解个体会向着最优值x_max靠近,即方程的解x(t;x₀, t₀) 就会向着x_max靠近,此时解的过程表达式为

(30)δ≤min{f(x_max)-f(x₁), f(x_max)-f(x₂)}≤ε

当t→∞时,解x(t;x₀, t₀)总是位于圆S(ε)内,GSMA的平衡状态x_max在李雅普诺夫意义下是稳定的.对于任意实数ε>0,存在满足式(30)的任意实数δ,使得满足 $‖x_{0} - x_{m a x}‖$ ≤δ的任意x₀出发的运动,方程的解始终都在圆S(δ)内,即解满足:

(31)

‖x (t; x_{0}, t_{0}) - x_{m a x}‖

≤δ≤ε

因此,圆S(δ)的半径δ与初始状态t₀无关,所以GSMA的平衡状态x_max是一致稳定的,即

(32)$\begin{array}{r}\lim_{x \to \infty} \left\|\boldsymbol{x}\left(t ; \boldsymbol{x}_{0}, t_{0}\right)-(0,0,0)\right\|= \\\lim_{x \to \infty} \left\|\boldsymbol{x}\left(t ; \boldsymbol{x}_{0}, t_{0}\right)-\boldsymbol{x}_{\max }\right\|=0\end{array}$

综上所述,GSMA可以收敛到全局最优值.

2.2.6 GSMA流程

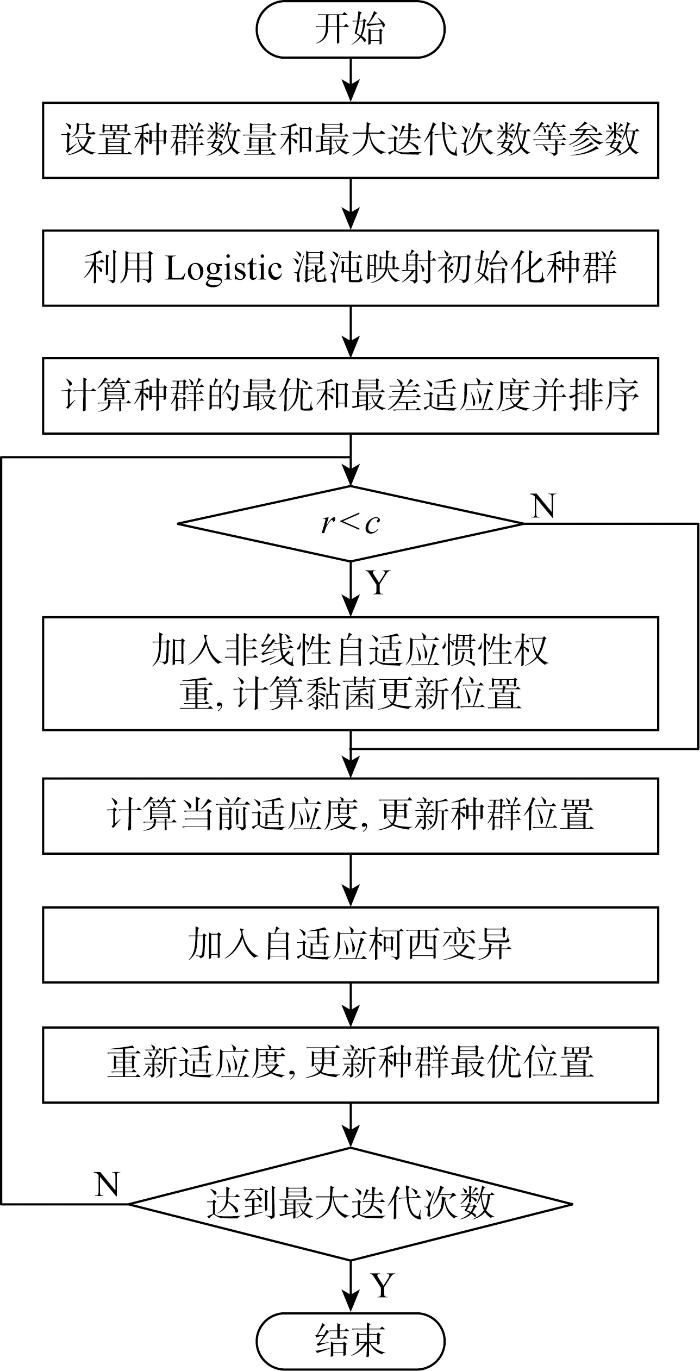
GSMA流程如图3所示,具体流程如下.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 算法流程图

Fig.3 Flow chart of algorithm

步骤1 设置种群数量、最大迭代次数和相关参数.

步骤2 利用改进Logistic混沌映射初始化种群,计算种群的最优和最差适应度并排序.

步骤3 判断随机数r<c.如果满足,则黏菌靠近食物,同时在其过程中加入非线性自适应权重因子,如果不满足则执行步骤5.

步骤4 计算适应度值,更新最优位置.

步骤5 根据每次适应度的不同进行排序.

步骤6 对当前位置进行自适应柯西变异,计算适应度值,更新最优位置.

步骤7 是否到达最大迭代数,满足则输出最优值,不满足则重复上述步骤直至满足条件.

3 GSMA对比实验

3.1 测试函数

利用不同的测试函数对算法性能优劣进行比较,在不同复杂度的情况下验证GSMA寻优能力的强弱.测试函数具体描述如下所示.

(1) Rosenbrock函数.

(33)f₁(x)=

\overset{n - 1}{\sum_{i = 1}}

[100(x_i+1-x_i)²]+(x_i-1)²

式中:Rosenbrock函数搜索范围为[-30, 30],维度为30,全局最优值为0.

(2) Schwefel函数.

(34)f₂(x)=-

\overset{n}{\sum_{i = 1}}

(x_isin

\sqrt{| x_{i} |}

)

式中:Schwefel函数搜索范围为[-500, 500],维度为30,全局最优值为 12 569.5.

(3) Foxholes函数.

(35)f₃(x)=

{[\frac{1}{500} + \overset{25}{\sum_{j = 1}} \frac{1}{j + \overset{2}{\sum_{j = 1}} (x_{i} - a_{i j})^{6}}]}^{- 1}

式中:Foxholes函数搜索范围为[-65.536, 65.536],维度为2,全局最优值为0.998.

(4) Kowalik函数.

(36)f₄(x)=

\overset{11}{\sum_{i = 1}} {|a_{i} - \frac{x_{1} (b_{i}^{2} + b_{i} x_{2})}{b_{i}^{2} + b_{i} x_{3} + x_{4}}|}^{2}

式中:Kowalik函数搜索范围为[-5, 5],维度为4,全局最优值为0.000 3.

(5) Hartman 6函数.

(37)f₅(x)=-

\overset{4}{\sum_{i = 1}}

exp[-

\overset{6}{\sum_{j = 1}}

a_ij(x_j-p_ij)²]

式中:Hartman 6函数搜索范围为[0,1],维度为6,全局最优值为 -3.332.

(6) Shekel 10函数.

(38)f₆(x)=-

\overset{10}{\sum_{i = 1}}

|(x_i-a_i)(x_i-a_i)^T+c_i|^-1

式中:Shekel 10函数搜索范围为[-5, 5],维度为4,全局最优值为 -10.536 3.

3.2 实验验证

利用Rosenbrock、Schwefel、Foxholes、Kowalik、Hartman 6和Shekel 10共6种测试函数评估SMA、灰狼优化(Grey Wolf Optimizer, GWO)算法^[16]、海鸥算法^[17] (Seagull Optimization Algorithm, SOA)以及GSMA的性能.经过30次测试后,适应度F随着迭代次数t变化如图4所示.适应度的最优值F_best及均值F_avg如表1所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 各测试函数上的适应度变化曲线

Fig.4 Adaptability change curve of each test function

表1 4种算法在测试函数上的实验对比

Tab.1 Experimental comparison of test functions of four algorithms

测试函数	算法	F_best	F_avg
Rosenbrock	SMA	28.63	28.98
	GWO	28.17	28.34
	SOA	29.67	29.93
	GSMA	27.89	28.15
Schwefel	SMA	-1.22×10⁴	-1.31×10⁴
	GWO	-5.66×10³	-5.61×10³
	SOA	-5.66×10³	-5.66×10³
	GSMA	-1.26×10⁴	-1.32×10⁴
Foxholes	SMA	0.068	0.153 8
	GWO	2.699	2.981
	SOA	0.928	0.563
	GSMA	0.076	0.095
Kowalik	SMA	1.28×10^-3	1.71×10^-3
	GWO	2.04×10^-3	2.43×10^-3
	SOA	2.04×10^-3	2.12×10^-3
	GSMA	6.34×10^-4	6.97×10^-4
Hartman 6	SMA	-3.11	-3.19
	GWO	-3.17	-3.75
	SOA	-2.65	-2.82
	GSMA	-3.16	-3.27
Shekel 10	SMA	-3.75	-3.63
	GWO	-10.50	-10.46
	SOA	-4.87	-4.87
	GSMA	-10.56	-10.53

新窗口打开| 下载CSV

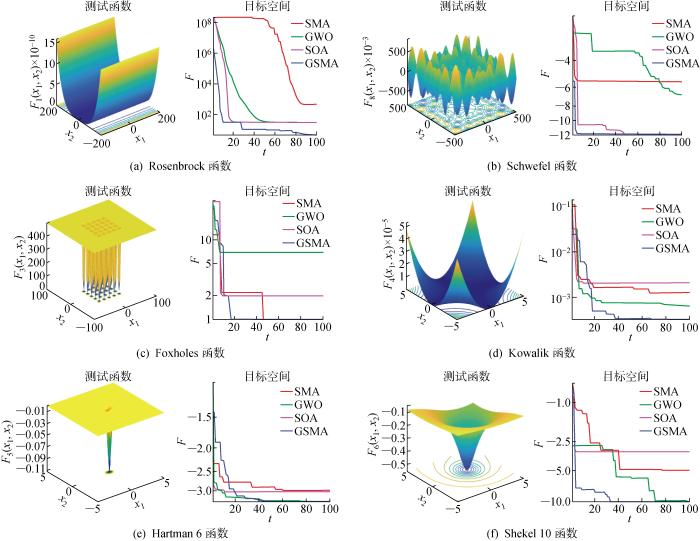
由图4和表1可知,针对Rosenbrock函数,SMA收敛速度弱于GWO、SOA和GSMA,迭代80次时收敛并陷入局部最优;而另外3种算法均寻得最优,其中GSMA的收敛速度和寻优精度均最优.针对Schwefel函数,SMA和GWO过早收敛,SOA的寻优速度不如GSMA.经过改进后的GSMA寻优能力更好,优于GWO和SMA.针对Foxholes函数,GSMA迭代不足10次已经收敛,而GWO和SOA则陷入了局部最优.针对Kowalik函数,GWO和SOA迭代10次已收敛并陷入局部最优,SMA迭代90次时陷入局部最优,而GSMA迭代60次寻得最优,且收敛速度和寻优精度均为最优.针对Hartman 6函数,GWO、SOA和SMA分别迭代60、60和80次寻得最优,SMA的寻优精度更高,GSMA收敛速度则更快且寻得最优.针对Shekel 10函数,SOA过早陷入局部最优,SMA寻优精度和速度较低,而GSMA和GWO寻优精度大致相同,但收敛速度明显高于GWO和SMA.综上所述,SMA改进后提升了寻优速度和精度,更易跳出局部最优.

4 无人机突防仿真测试及分析

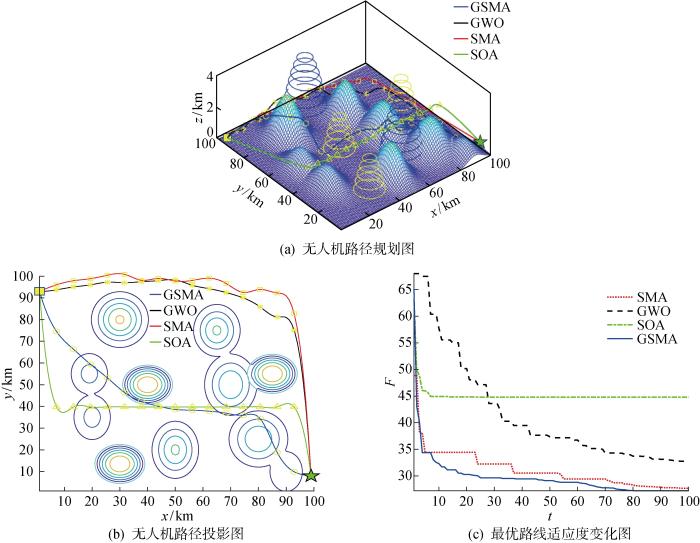
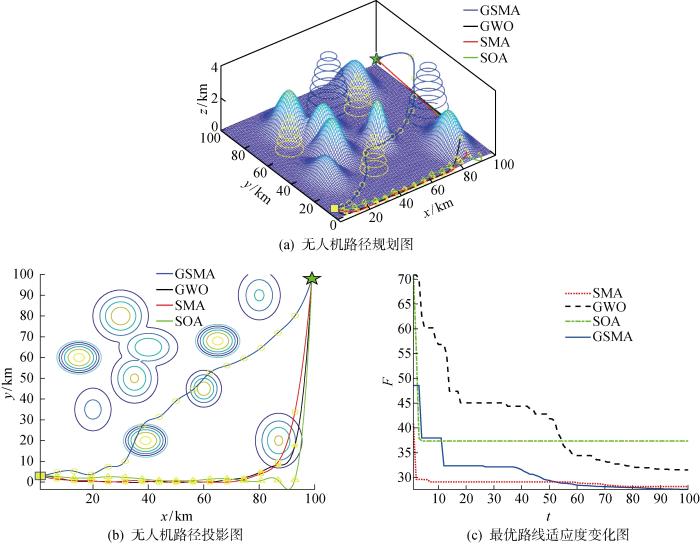
实验平台为Window10系统的计算机,CPU为AMD R5-5600H,频率为3.30 GHz、内存为16 GB,软件采用MATLAB 2021a.测试区域为100 km×100 km,高度为5 km,采用两种不同的仿真地形.在地形1中,无人机的起始与终止坐标分别为(1, 93, 0.2) km、(98, 8, 0.5) km,3座不同类型的雷达位置坐标分别为(32, 40, 0) km、(70, 58, 0) km、(40, 12, 0) km,侦测半径设定为9、11、14 km,电磁和导弹威胁半径分别为12、18 km.地形2的区域大小也为100 km×100 km,无人机的起始点和终点为(2, 3, 0.2) km、(99, 87, 0.5) km,3座不同类型的雷达位置坐标分别为(30, 40, 0) km、(69, 70, 0) km、(40, 11, 0) km,侦测半径设定为6、9、10 km,电磁和导弹威胁半径分别为10、16 km,飞行过程中的最大转弯角为60°.为提高无人机的生存和路径规划能力,两种地形山峰位置有所不同.仿真种群数量均为100,最大迭代次数也是100.建模的主要参数如表2所示,表中:v为飞行速度.两种地形中,无人机的三维路径的仿真结果如图5和图6所示,各算法仿真结果如表3和表4所示.

表2 主要建模参数

Tab.2 Main modeling parameters

参数	数值
v/(km·h^-1)	30~40
K_Z	100
K'_Z	100
K_F	100
k_d	0.6
k_g/(km·s^-2)	5
Q_h	10
Q_v	10
a_max	60
β_max	60
K_thr	R_max,_p/3
ω₁	0.23
ω₂	0.45
ω₃	0.2
ω₄	0.12
d	15

新窗口打开| 下载CSV

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 地形1仿真结果图

Fig.5 Simulation result of Terrain 1

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 地形2仿真结果图

Fig.6 Simulation result of Terrain 2

表3 地形1仿真结果统计

Tab.3 Statistics of Terrain 1 simulation results

算法	航程/km	最优适应度	转弯和爬升角代价	寻优成功率/%
SMA	166.23	30.86	100	76
GWO	159.38	34.09	70	79
SOA	162.17	36.72	120	82
GSMA	133.54	29.43	10	95

新窗口打开| 下载CSV

表4 地形2仿真结果统计

Tab.4 Statistics of Terrain 2 simulation results

算法	航程/km	最优适应度	转弯和爬升角代价	寻优成功率/%
SMA	165.43	27.06	100	85
GWO	163.85	34.37	80	78
SOA	171.65	37.78	90	75
GSMA	139.86	28.89	20	93

新窗口打开| 下载CSV

地形中黄色波为不同类型的雷达探测区域,蓝色波表示电磁和导弹威胁区域.为对于仿真地形1,由图5(a)和5(b)可以看出,在SOA结果中,无人机成功穿过了第1座山峰,但在第2座山峰处撞山且被敌方雷达侦测到,不能成功到达目的地;而GWO和SMA结果中,无人机虽然成功规避了山峰和雷达侦察,但没有绕开电磁威胁区域和导弹攻击区域,且路线过长,导致撞击山脉的概率增加,影响实用价值;相比之下,GSMA不仅成功规避了山脉和雷达侦测,而且选择了最优路线以更小的代价穿过地形.从表3可以看出,SMA、GWO、SOA以及GSMA的航程分别为166.23、159.38、162.17、133.54 km,最优适应度分别为30.86、34.09、36.72、29.43,GSMA的规划路径最短,转弯及爬升角代价最低,整体保持低空平稳飞行,航迹代价最低,优势明显.图5(c)的仿真结果表明,SOA和GWO在迭代次数为80时仍未寻得最优而陷入了局部最优,寻优性能相比于SMA较差,并不适合无人机的径规划;SMA的精度相对较低,迭代至90次陷入局部最优,且路径规划距离过长.

相比于地形1,图6中地形2的山峰更为密集,导弹和电磁覆盖威胁范围更广.从图6(a)和6(b)可以看出, SOA、GWO和SMA都规避了密集连片山脉,但经过了导弹威胁区域,降低了飞机的安全性且规划的路线过于漫长,实用性不高.GWO与山峰发生碰撞,未能安全到达目的地.而GSMA规避了雷达的侦测,选择最佳路线快速穿过地形2.相比之下,GSMA寻优精度和寻优速度都优于GWO及SMA,在迭代至80次时已经寻得最优.而此时GWO及SMA仍未收敛,SOA则迭代20次即陷入了局部最优.综上,GSMA能够更为有效地避开各种威胁地形,路径规划中的总代价也最小.

5 结语

提出了一种基于改进SMA的算法来解决无人机三维路径规划的问题.首先,建立相关的地形模型、各种威胁源和无人机约束模型,并建立代价函数.其次,采用混沌映射对种群初始化,用以增加种群的多样性和随机分布,扩大了其搜索范围更易获得最优;在SMA中引入了非线性自适应权重因子,加快算法的收敛速度,很好地弥补了SMA自身存在的缺陷;加入柯西变异,使得种群在前期跳出局部最优,提高收敛速度.实验结果表明,GSMA在无人机探索路径规划过程中,能够在最短航程的条件下快速穿过危险区域和规避障碍物,应用价值明显.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

EVDOKIMENKOV

V N

, KRASILSHCHIKOV

M N

, LYAPIN

N A

Guaranteeing UAV trajectory control when approaching a maneuvering air target

[J]. Journal of Computer and Systems Sciences International, 2018, 57(5): 789-800.

DOI:10.1134/S1064230718050040 [本文引用: 1]

[2]

GALYAEV

A A

, LYSENKO

P V

, YAKHNO

V P

2D optimal trajectory planning problem in threat environment for UUV with non-uniform radiation pattern

[J]. Sensors, 2021, 21(2): 396.

DOI:10.3390/s21020396 URL [本文引用: 1]

Path planning is necessary in many applications using unmanned underwater vehicles (UUVs). The main class of tasks is the planning of safe routes with minimal energy costs and/or minimal levels of emitted physical and information signals. Since the action planner is on board the UUV, the main focus is on methods and algorithms that allow it to build reference trajectories while minimizing the number of calculations. The study is devoted to the problem of the optimal route planning for a UUV with a non-uniform radiation pattern. The problem is stated in the form of two point variational problem for which necessary and sufficient optimality conditions are proved. Particular attention is paid to cases where optimality conditions are not met. These cases are directly related to found specific forms of a radiation pattern. Sufficient optimality conditions are extended on the class of two-link and multi-link motion paths. Software tools have been developed and computer simulations have been performed for various types of radiation patterns.

[3]

GUO

, LIU

, ZHANG

, et al.

3D path planning method for UAV based on improved artificial potential field

[J]. Journal of Northwestern Polytechnical University, 2020, 38(5): 977-986.

DOI:10.1051/jnwpu/20203850977 URL [本文引用: 1]

Path planning is the key technology for UAV to achieve autonomous flight. Considering the shortcomings of path planning based on the conventional potential field method, this paper proposes an improved optimization algorithm based on the artificial potential field method and extends it to three-dimensional space to better achieve flight constrained 3D online path planning for UAVs. The algorithm is improved and optimized aiming at the three problems of goal nonreachable with obstacle nearby (GNWON), easy to fall into local minimum, and path oscillation in traditional artificial potential field method. First, an improved potential field function with relative distance is used to solve the GNWON, and an optimized repulsive potential field calculation method based on different obstacles or threat models is proposed to optimize the planned path. Secondly, in order to make the drone jump out of the local minimum trap, a method of setting heuristic sub-target points is proposed. For local path oscillation, a method using memory sum force was proposed to improve the oscillation. The simulation results show that the improved optimization algorithm in this paper effectively makes up for the shortcomings of the traditional artificial potential field method, and the designed 3D online path planning algorithm for the UAV is practical and feasible.

[4]

MANDLOI

, ARYA

, VERMA

A K

Unmanned aerial vehicle path planning based on A^* algorithm and its variants in 3D environment

[J]. International Journal of Systems Assurance Engineering and Management, 2021(1): 1-11.