基于并联机构的多维隔振系统振动鲁棒最优半主动控制

doi:10.16183/j.cnki.jsjtu.2023.230

基于并联机构的多维隔振系统振动鲁棒最优半主动控制

高翔^,¹, 牛军川², 贺磊¹, 秦榛¹, 王忠龙¹

1.山东理工大学机械工程学院, 山东淄博 255000

2.山东大学机械工程学院, 济南 250061

Vibration Robust Optimal Semi-Active Control of Multi-Dimensional Vibration Isolator Based on Parallel Mechanism

GAO Xiang^,¹, NIU Junchuan², HE Lei¹, QIN Zhen¹, WANG Zhonglong¹

1. School of Mechanical Engineering, Shandong University of Technology, Zibo 255000, Shandong, China

2. School of Mechanical Engineering, Shandong University, Jinan 250061, China

责任编辑: 王一凡

收稿日期: 2023-06-7 修回日期: 2023-07-25 接受日期: 2023-09-11

基金资助:

国家自然科学基金(52075294)
山东省自然科学基金(ZR2021QE203)

Received: 2023-06-7 Revised: 2023-07-25 Accepted: 2023-09-11

作者简介 About authors

高翔(1989—),讲师,现主要从事机械系统动力学、振动与噪声控制研究.电话(Tel.):0533-2781723;E-mail:gaoxiang@sdut.edu.cn.

摘要

为隔离车载精密仪器所承受的多维振动,提出基于2-RPC/2-SPC并联机构和磁流变 (MR) 阻尼器的多维半主动隔振系统.通过几何关系和Lagrange方程分别建立多维隔振系统运动学和动力学模型,分别考虑质量、刚度和阻尼不确定因子,提出多维隔振系统鲁棒最优半主动控制策略,在随机路面激励下,研究多维隔振系统频域隔振能力和不确定因子变化对隔振性能的影响规律,与具有相同不确定因子的线性二次型调节器 (LQR) 半主动控制策略在阶跃激励下进行对比分析.研究表明:多维隔振系统可实现沿 x、 y、 z轴和绕y 轴的多维振动有效隔离;质量不确定因子变化对隔振性能影响最显著;存在不确定因素时,鲁棒最优半主动控制策略的隔振能力显著优于LQR半主动策略的隔振能力.

关键词： 并联机构; 多维隔振系统; 磁流变阻尼器; 半主动控制

Abstract

In order to isolate multi-dimensional vibration experienced by vehicle-mounted precise instrument, a novel multi-dimensional vibration isolator is proposed based on 2-RPC/2-SPC parallel mechanism and the magneto-rheological (MR) damper. The kinematic and dynamic models are established by geometric relation and the Lagrange approach respectively. The robust optimal semi-active control algorithm is obtained by deducing linear matrix inequality. The vibration isolation capability is addressed in time and frequency domain under stochastic road excitation with mass, stiffness, and damping coefficient uncertain factors respectively. Meanwhile, the relation between isolation performance and uncertain factors is explored. The isolation capability is compared with the linear quadratic regulator (LQR) semi-active control algorithm with the same uncertain factors under step excitation. The results demonstrate that the proposed isolator inhibit the vibration in the x, y, z axes and around the y axis significantly. The isolation performance is affected by mass uncertain factor most obviously. The robust optimal semi-active control algorithm is more effective than the LQR algorithm with uncertain factors.

Keywords： parallel mechanism; multi-dimensional vibration isolator; magneto-rheological (MR) damper; semi-active control

PDF (1969KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

高翔, 牛军川, 贺磊, 秦榛, 王忠龙. 基于并联机构的多维隔振系统振动鲁棒最优半主动控制[J]. 上海交通大学学报, 2025, 59(5): 648-656 doi:10.16183/j.cnki.jsjtu.2023.230

GAO Xiang, NIU Junchuan, HE Lei, QIN Zhen, WANG Zhonglong. Vibration Robust Optimal Semi-Active Control of Multi-Dimensional Vibration Isolator Based on Parallel Mechanism[J]. Journal of Shanghai Jiaotong University, 2025, 59(5): 648-656 doi:10.16183/j.cnki.jsjtu.2023.230

由于路面不平度和加减速、转弯等驾驶过程,车载精密仪器受到兼具移动和转动特征的多维振动激励.据统计,约有30%的车载精密仪器因多维振动损坏失效^[1].为实现多维振动有效控制,需引入与多维振动自由度数相匹配的隔振设备.浮筏、扭摆杆减振器等传统的多维隔振系统,虽在一定程度上实现了多自由度减振,但存在动力学特性不随外界激励变化而改变、隔振元件变形小、阻尼难以调节和配置等问题.

并联机构具有高刚度以及较高的运动精度和灵活度,以最少的主动关节实现多维运动输出,成为构建新型多维隔振系统的优势对象^[2-4].Wang等^[5]为降低立方Stewart隔振平台质量,提出一种新型双出杆磁流变阻尼器,建立并验证了多维隔振系统的动力学模型,研究表明,隔振系统能够实现6轴方向多维振动的有效衰减.Tang等^[6]通过Kane方法建立音圈电机驱动的Stewart隔振系统动力学模型,针对隔振系统线性和非线性部分,分别设计基于分散控制理论的线性控制器和基于改进鲁棒控制理论的非线性控制器,从而满足低频隔振的需求.Wei等^[7]基于螺旋理论获得一种新型4自由度并联机构用于救护车担架减振,研究了机构的奇异位姿,通过实验验证了隔振性能.Yang等^[8]通过伪刚体模型和虚功原理建立考虑连杆柔性的Stewart六轴隔振系统动力学模型,控制力由位姿反馈产生,能够实现6自由度多维振动的有效削弱.Zhao等^[9]提出一种3自由度多维隔振系统,采用滑模控制策略实时控制磁流变(MR)阻尼器的阻尼力输出,隔振系统能够实现水平、纵向和垂向多维振动的有效隔离.牛军川等^[10]建立基于变胞并联机构的多维隔振系统动力学方程,通过改变虎克副轴线的配置方式,实现了3自由度或4自由度多维振动的衰减.Li等^[11]提出一种5自由度并联隔振平台,建立隔振系统模糊最优半主动控制模型,通过实验验证了系统的隔振性能.张兵等^[12]提出液压冗余式主被动复合控制6自由度多维减振平台,采用模糊比例-积分-微分 (PID) 控制方法实现了多维振动抑制.Li等^[13]以隔振系统最小条件数为运动学优化目标,采用双四元数方法推导机构的齐次Jacobian矩阵并进行多目标优化,改善了多维隔振系统运动学指标.程明等^[14]以振动控制系统固有频率、静变形量为优化目标,通过多目标优化,提高了并联隔振系统的动力学性能.

上述研究表明了基于并联机构的多维隔振系统理论可行性.然而,诸如模型误差、未建模动态、被隔振物体的不同质量、弹簧和阻尼器的非线性特征等不确定因素引起的参数摄动量不可忽略,隔振系统在上述不确定因素影响下的振动抑制方法和隔振能力有待阐明.本文建立基于并联机构和磁流变阻尼器的多维隔振系统运动学和动力学模型,研究隔振系统在不确定因素影响下隔振能力的变化规律,提出兼具振动主动控制和被动控制优点且对不确定因素不敏感的鲁棒最优半主动控制策略,保证控制方法稳定并实现多维振动抑制.

1 多维隔振系统模型

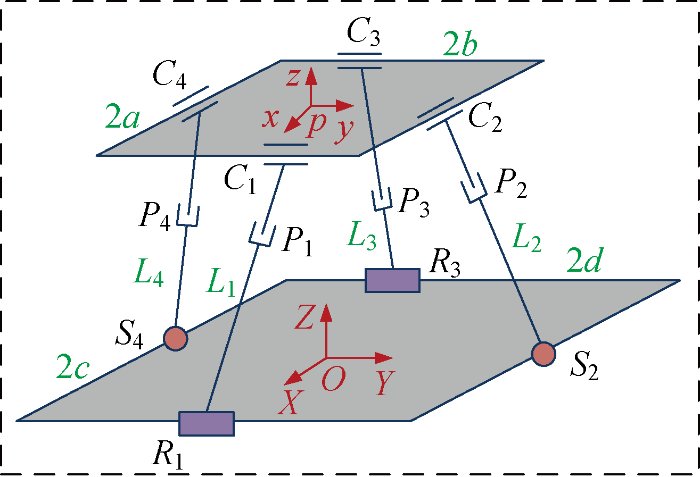
多维隔振系统的主体结构为2-RPC/2-SPC并联机构^[15],由动平台、定平台和4条支链构成,如图1所示.图中: L_i (i=1, 2, 3, 4)为4条支链;R为转动副; P为移动副; S为球面副; C 为圆柱副.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 2-RPC/2-SPC并联机构示意图

Fig.1 Schematic diagram of 2-RPC/2-SPC parallel mechanism

动平台和定平台均为矩形,长度分别为 2a×2b和2c×2d. 在动平台和定平台的形心处分别建立动坐标系p-xyz和静坐标系O-XYZ.从定平台到动平台,4条支链对称布置:支链 L₁和L₃分别由R、P和C组成;支链L₂和L₄分别由S、P和C 组成.选取移动副为主动关节,在移动副布置4组弹簧和磁流变阻尼器,即可构造多维半主动隔振系统.根据修正的G-K公式^[16],计算得到隔振系统自由度为4,分别为沿 x、 y、 z轴的平移运动和绕y 轴的旋转运动.

1.1 多维隔振系统运动学

在动和静坐标系中,点 C_i可分别表示为C_pi和C_Oi,那么C_Oi=T_yC_pi,T_y为绕y 轴的旋转变换矩阵,

(1)

T_{y} = [\begin{array}{l} c o s θ & 0 & s i n θ & x_{p} \\ 0 & 1 & 0 & y_{p} \\ - s i n θ & 0 & c o s θ & z_{p} \\ 0 & 0 & 0 & 1 \end{array}]

式中: ${[\begin{array}{l} x_{p} & y_{p} & z_{p} \end{array}]}^{T}$ 为动平台任意一点在动坐标系中的坐标;θ为绕y轴的转角.移动副的长度l_i (i=1, 2, 3, 4) 可通过图1并结合几何关系计算得到,

(2)

\begin{array}{l} l_{1}^{2} = (a c o s θ + x_{p} {- c)}^{2} + y_{p}^{2} + (- a s i n θ + z_{p})^{2} \\ l_{2}^{2} = x_{p}^{2} + (b + y_{p} {- d)}^{2} + z_{p}^{2} \\ l_{3}^{2} = (- a c o s θ + x_{p} {+ c)}^{2} + y_{p}^{2} + (a s i n θ + z_{p})^{2} \\ l_{4}^{2} = x_{p}^{2} + (- b + y_{p} {+ d)}^{2} + z_{p}^{2} \end{array}\}

那么根据并联机构的输入-输出关系,整理得到机构的Jacobian逆矩阵,

(3)

J^{- 1} = [\begin{array}{l} \frac{D_{5} - d + x_{p}}{\sqrt{D_{1}}} & \frac{y_{p}}{\sqrt{D_{1}}} & \frac{z_{p} - D_{6}}{\sqrt{D_{1}}} & \frac{D_{6} (d - x_{p}) - D_{5} z_{p}}{\sqrt{D_{1}}} \\ \frac{x_{p}}{\sqrt{D_{2}}} & \frac{a - c + y_{p}}{\sqrt{D_{2}}} & \frac{z_{p}}{\sqrt{D_{2}}} & 0 \\ \frac{- D_{5} + d + x_{p}}{\sqrt{D_{3}}} & \frac{y_{p}}{\sqrt{D_{3}}} & \frac{z_{p} + D_{6}}{\sqrt{D_{3}}} & \frac{D_{6} (d + x_{p}) + D_{5} z_{p}}{\sqrt{D_{3}}} \\ \frac{x_{p}}{\sqrt{D_{4}}} & \frac{- a + c + y_{p}}{\sqrt{D_{4}}} & \frac{z_{p}}{\sqrt{D_{4}}} & 0 \end{array}]

D₁=(bcos θ-d+x_p)²+(z_p-bsin θ)²+ $y_{p}^{2}$

D₂=(a-c+y_p)²+ $x_{p}^{2}$ + $z_{p}^{2}$

D₃=(-bcos θ+d+x_p)²+(z_p+bsin θ)²+ $y_{p}^{2}$

D₄=(-a+c+y_p)²+ $x_{p}^{2}$ + $z_{p}^{2}$

D₅=bcos θ

D₆=bsin θ

1.2 多维隔振系统动力学

磁流变阻尼器为多维隔振系统的作动器,提供的阻尼力^[17]为

(4)

\begin{array}{l} F_{e} = c_{e} \overset{\cdot}{x} + F_{M R} s g n (\overset{\cdot}{x}) \\ c_{e} = \frac{2 π r L η}{h} + \frac{6 L η A_{p}^{2}}{π r h^{3}} \\ F_{M R} = (2 π r L + \frac{3 L A_{p}}{h}) τ_{y} \end{array}\}

式中: $\overset{\cdot}{x}$ 为活塞速度;c_e为黏滞阻尼系数;F_e为阻尼力;F_MR为可控阻尼力;τ_y 为剪切屈服强度,可表示为多项式函数的形式^[18],

(5)τ_y=a₄B⁴+a₃B³+a₂B²+a₁B+a₀

式中:B为磁感应强度.式(4)和式(5)中的其他参数和数值^[19]如表1所示.

表1 磁流变阻尼器主要参数及取值^[19]

Tab.1 Parameters and values of MR damper^[19]

参数	取值
活塞有效面积,A_p/mm²	0.6
磁流变液黏度,η/(Pa·s)	0.15
阻尼通道长度,L/mm	25
阻尼器内外壳间隙,h/mm	1.5
阻尼器内壳外径,r/mm	1.2
拟合系数,a₄/(kPa·T^-3)	-1 090
拟合系数,a₃/(kPa·T^-2)	718.2
拟合系数,a₂/(kPa·T^-1)	11.4
拟合系数,a₁/kPa	0.271
拟合系数,a₀/(kPa·T^-4)	389.7

新窗口打开| 下载CSV

为便于求解,需对多维隔振系统的动力学建模过程进行适当合理的简化:定义动平台在平衡位置附近微幅振动,忽略重力势能;忽略各支链质量,仅考虑动平台质量.多维隔振系统的动力学模型可通过考虑阻尼耗散能的Lagrange方程推导得到,

(6)

M \ddot{X} + C_{e} \dot{X} + K X = Γ

式中: X= ${[\begin{array}{l} x_{p} & y_{p} & z_{p} & θ \end{array}]}^{T}$ 为隔振系统动平台的位姿向量;M=diag(m_p, m_p, m_p, I_y)为动平台惯量矩阵,m_p和I_y分别为动平台质量和绕y轴的转动惯量;K=Gdiag(k)G^T为刚度矩阵,k为弹簧刚度;C_e=Gdiag(c_e)G^T为阻尼矩阵;G=J^-T 为Jacobian力矩阵;Γ为广义力向量.

2 鲁棒最优半主动控制策略

多维隔振系统应用于车载精密仪器减振,由于路面不平度引起的随机激励可表示为白噪声的形式^[20]:

(7)

{\dot{x}}_{i} = - 2 π n_{0} v_{e} x_{i} + 2 π n_{1} w \sqrt{G_{q} v_{e}}

式中: x_i为路面激励幅值;G_q为路面不平度系数;v_e为车速;n₀和n₁分别为下截止频率和参考空间频率;w 为零均值的Gauss白噪声.实际工况下,路面随机振动经过悬架减振之后再输入到多维隔振系统.由于采用路面随机激励,在经过悬架减振之后其时域波形仍为随机信号,为简化分析过程,在此采用路面随机激励作为多维隔振系统的输入激励.

基于并联机构的多维隔振系统由不确定性引起的参数摄动量不可避免,在此,采用鲁棒最优半主动控制策略兼顾隔振系统振动控制效果和鲁棒性.定义 $Z = [\begin{array}{l} X & \dot{X} \end{array}]^{T}$ 为振动控制系统状态变量,考虑不确定因素的多维隔振系统状态空间方程可表示为

(8)

\begin{array}{l} \overset{\cdot}{Z} = (A + Δ A) Z + (B_{a} + Δ B_{a}) U_{R} + B {\ddot{x}}_{i} \\ Y = C_{1} Z \end{array}\}

式中:A和ΔA分别为系统矩阵的确定和不确定部分;B_a和ΔB_a分别表示控制矩阵的确定和不确定部分;B为输入矩阵;C₁为状态反馈矩阵;U_R为理想的鲁棒最优控制力向量; ${\ddot{x}}_{i}$ 表示随机路面加速度激励.系统矩阵、控制矩阵和输入矩阵可分别表示为

(9)

\begin{array}{l} A = [\begin{array}{l} 0 & I \\ - M^{- 1} K & - M^{- 1} C \end{array}] \\ B_{a} = [\begin{array}{l} 0 \\ M^{- 1} G \end{array}], B = [\begin{array}{l} 0 \\ G \end{array}] \end{array}\}

为求解理想鲁棒最优控制力向量,需确定式(8)中的不确定部分.不确定部分ΔA和ΔB通常可表示为范数有界的形式:

(10)

[\begin{array}{l} Δ A & Δ B \end{array}] = N F [\begin{array}{l} E_{1} & E_{2} \end{array}]

式中:N、 E₁和E₂为常数矩阵;F为不确定函数矩阵,且满足F^TF≤I,I为具有适当维数的单位矩阵.

线性二次型最优性能指标一般可表示为

(11)

λ = \int_{t}^{\infty} (Z^{T} Q Z + U_{R}^{T} R U_{R}) d t

式中: Q=diag(α_KK, α_MM)和R=β_RI分别为半正定和正定矩阵,α_K、 α_M和β_R 为权重系数.那么理想鲁棒最优控制力向量可表示为

(12)U_R=-G_KZ

式中:G_K为鲁棒最优控制增益.

为确定鲁棒最优控制增益,需保证多维隔振系统为鲁棒最优控制系统^[21],结合式(8)和式(11)可得,

(13)

\begin{array}{l} Q + G_{K}^{T} R G_{K} + P [A - B_{a} G_{K} + N F (E_{1} - E_{2} G_{K})] + \\ {[A - B_{a} G_{K} + N F (E_{1} - E_{2} G_{K})]}^{T} P + \\ γ^{- 2} P B B^{T} P + C_{1} C_{1}^{T} < 0 \end{array}

式中:γ为任意正数;P为具有对称元素的正定矩阵.

式(13)中存在难于求解的F,根据文献[22],定义具有适当维数的矩阵S, 可得如下关系:

(14)

\begin{array}{l} S = Q + G_{K}^{T} R G_{K} + P (A - B_{a} G_{K}) + \\ {(A - B_{a} G_{K})}^{T} P + γ^{- 2} P B B^{T} P + C_{1} C_{1}^{T} \end{array}

式(14)可推导变形为

(15)S+εPNN^TP+ε^-1(E₁-E₂G_K)^T(E₁-E₂G_K)<0

式中:ε为任意较小的正数.对式(15)应用Schur补引理^[23]可得:

(16)

[\begin{array}{l} L_{1} & (E_{1} - E_{2} G_{K})^{T} & I & G_{K}^{T} & C_{1}^{T} & P B^{T} \\ * & - ε I & 0 & 0 & 0 & 0 \\ * & * & - Q^{- 1} & 0 & 0 & 0 \\ * & * & * & - R^{- 1} & 0 & 0 \\ * & * & * & * & - I & 0 \\ * & * & * & * & * & - γ^{2} I \end{array}] < 0

式中: L₁=P(A-B_aG_K)+(A-B_aG_K)^TP+εPNN^TP; 符号“*”表示矩阵中的对称元素.

对式(16)分别左乘和右乘矩阵diag(P^-1, I, I, I, I, I),式(16)可转变为

(17)

[\begin{array}{l} L_{2} & (E_{1} X - E_{2} {W)}^{T} & P^{- 1} & W^{T} & P^{- 1} C_{1}^{T} & B \\ * & - ε I & 0 & 0 & 0 & 0 \\ * & * & - Q^{- 1} & 0 & 0 & 0 \\ * & * & * & - R^{- 1} & 0 & 0 \\ * & * & * & * & - I & 0 \\ * & * & * & * & * & - γ^{2} I \end{array}] < 0

式中: L₂=(AP^-1-B_aW)+(AP^-1-B_aW)^T+εNN^T;W=G_KP^-1.

定义系统的初始状态为X₀,线性二次型指标的期望值可表示为

(18)

\bar{λ} = E (λ) \leq t r (P)

式中:tr(*)为矩阵的迹.为保证存在不确定因素的多维隔振系统上限值最小,可得到如下线性矩阵不等式:

(19)

[\begin{array}{l} H & I \\ * & P^{- 1} \end{array}] > 0

式中:H>P>0.那么鲁棒最优控制增益可通过求解如下线性矩阵不等式 (LMI) 得到:

(20)

\underset{ε, W, P^{- 1}}{m i n} t r (H)

s . t . ε > 0, γ > 0

P^{- 1} > 0, H > 0

式(19),式(20)

多维隔振系统的实际阻尼力可通过计算理想阻尼力并结合限界Hrovat算法^[24]约束得到.限界Hrovat算法可表示为

(21)

F_{M R} = \{\begin{array}{l} F_{M R, m a x} s g n (\overset{\cdot}{x}), & u_{i} \overset{\cdot}{x} < 0 且 |u_{i}| > F_{M R, m a x} \\ |u_{i}| s g n (\overset{\cdot}{x}) - c_{e} \overset{\cdot}{x}, & u_{i} \overset{\cdot}{x} < 0 且 |u_{i}| < F_{M R, m a x} \\ F_{M R, m i n} s g n (\overset{\cdot}{x}), & u_{i} \overset{\cdot}{x} > 0 \end{array}

式中:F_MR_,_max和F_MR_,_min分别表示可控阻尼力的最大值和最小值;u_i(i=1, 2, 3, 4)为理想控制力.

3 算例分析

定义多维振动为沿x、 y、 z轴以及绕y轴的复合随机路面激励,那么振动控制系统的实际质量、刚度和阻尼系数可表示为

(22)

\begin{array}{l} m'_{p} = (1 + ω_{m}) m_{p} \\ k' = (1 + ω_{k}) k \\ c' = (1 + ω_{c}) c \end{array}\}

式中: ω_m、ω_k和ω_c分别表示质量、刚度和阻尼系数的不确定因子.在以下分析中,取ω_m=ω_k=ω_c=10%. 仿真分析所需主要参数和数值^[25]如表2所示.

表2 多维隔振系统主要参数及取值^[25]

Tab.2 Parameters and values of multi-dimensional vibration isolator^[25]

参数	取值
动平台质量,m_p/kg	25
动平台绕y轴转动惯量,I_y/(kg·m²)	0.67
弹簧刚度,k/(N·m^-1)	15 000
定平台边长,d/m	0.35
定平台边长,c/m	0.40
动平台边长,b/m	0.16
动平台边长,a/m	0.15
权重系数,α_K	70
权重系数,α_M	80
权重系数,β_M	6×10^-3
下截止频率,n₀/m^-1	0.012
参考空间频率,n₁/m^-1	0.1
路面不平度系数,G_q/m³	6.4×10^-5
车速,v_e/(m·s^-1)	16.7

新窗口打开| 下载CSV

为比较振动主动控制和振动半主动控制的隔振能力,均采用鲁棒最优半主动控制策略,振动半主动控制的实际阻尼力可由式(21)计算得到.结合式(7)、(8)、(12)和(20),以及表1和表2中的数据,采用Runge-Kuta方法求解得到存在质量、刚度和阻尼不确定因子时多维隔振系统的动平台时域速度输出.

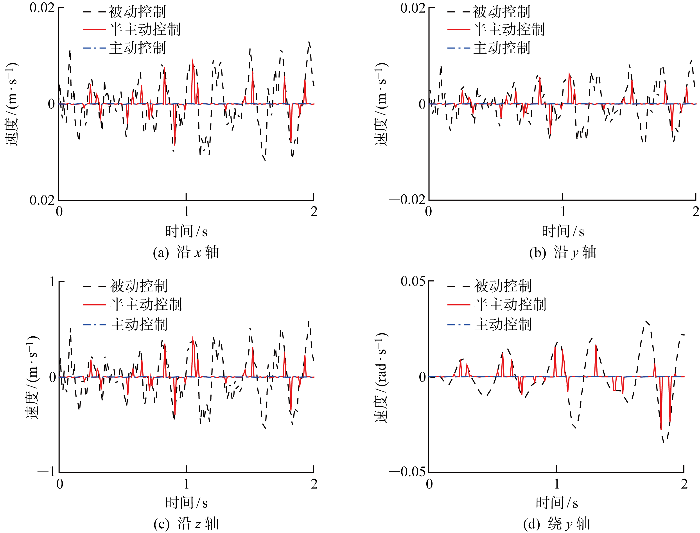
图2为存在不确定因子时多维隔振系统动平台各方向的时域速度输出.为衡量鲁棒最优半主动控制策略的隔振能力,同时给出具有相同不确定因子的鲁棒最优主动控制和被动控制的图像.由图2可得,振动主动控制具有最好的隔振效果,振动半主动控制的隔振能力介于振动主动控制和被动控制之间.由于限界Hrovat算法的约束,振动半主动控制图线在主动控制和被动控制之间不断切换.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 存在不确定因子时动平台各方向时域速度输出

Fig.2 Output velocity of moving platform in different directions with uncertain factors in time domain

为定量比较多维半主动隔振系统的隔振性能,选用动平台输出速度的均方根 (RMS) 值作为评价指标.表3为不同控制策略下动平台各方向速度输出的均方根值.与被动控制相比,振动半主动控制的均方根值在沿x、 y、 z轴方向和绕y轴方向分别降低了50.10%、 64.36%、 51.20%和68.57%,表明采用鲁棒最优半主动控制策略的多维隔振系统在不确定因素影响下各方向均表现出良好的隔振能力.

表3 不同控制策略的动平台输出速度均方根值

Tab.3 Velocity RMS values of different control algorithms

控制策略	沿x轴/ (m·s^-1)	沿y轴/ (m·s^-1)	沿z轴/ (m·s^-1)	绕y轴/ (rad·s^-1)
被动	5.01×10^-3	5.78×10^-3	2.09×10^-3	7.00×10^-3
半主动	2.50×10^-3	2.06×10^-3	1.02×10^-3	2.20×10^-3
主动	5.48×10^-5	8.84×10^-4	5.77×10^-4	2.11×10^-5

新窗口打开| 下载CSV

定义矩阵T= $[\begin{array}{l} 0_{4 \times 4} & I_{4 \times 4} \end{array}]$ ,将式(12)代入式(8)中,并取Fourier变换,可以得到动平台在鲁棒最优主动控制策略下的频域位移输出:

(23)

X_{a} (ω) = \frac{1}{j ω} T {[j ω I - (A + Δ A) + (B_{a} + Δ B_{a}) G_{K}]}^{- 1} B x_{i} (ω)

式中: x_i(ω)为随机路面位移激励的频域形式;ω 为激励的圆频率;j= $\sqrt{- 1}$ .当矩阵B_a和ΔB_a为零矩阵时,式(23)将变为被动控制的频域位移输出:

(24)

X_{p} (ω) = \frac{1}{j ω} T {[j ω I - (A + Δ A)]}^{- 1} B x_{i} (ω)

结合式(23)、式(24)以及限界Hrovat算法,可以得到鲁棒最优半主动控制策略下的动平台频域位移输出.

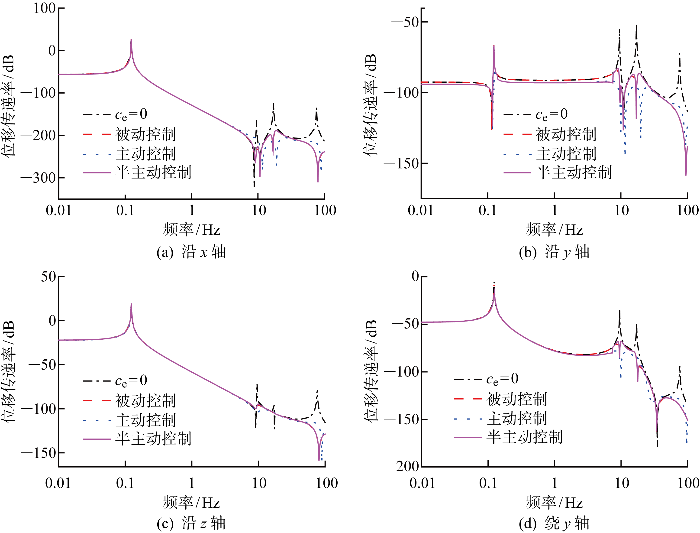
图3为存在不确定因子时动平台在各方向的频域位移输出.为比较振动半主动控制效果,同时给出了主动控制、被动控制和无阻尼控制的动平台位移输出频域解.结合表2中的数据,可以计算得到多维隔振系统的4阶固有频率分别为f₁=0.12 Hz, f₂=9.50 Hz, f₃=17.13 Hz, f₄=76.16 Hz,分别与无阻尼控制的4阶共振峰横坐标值对应相等.该现象表明,当不考虑黏滞阻尼系数时,隔振系统的4阶共振峰被完全激发,验证了理论分析的正确性.鲁棒最优半主动控制能够对共振峰实现有效削弱,其隔振效果接近振动主动控制.由于在仿真分析中引入了不确定量,求解线性矩阵不等式获得的鲁棒最优控制增益具有保守性且并非全局最优,所以振动主动控制和半主动控制对第1阶共振峰削弱能力有限,优势不显著.受到限界Hrovat算法约束,振动半主动控制在主动控制和被动控制之间不断切换.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 存在不确定因子时动平台各方向频域位移输出

Fig.3 Output displacement of moving platform in different directions with uncertain factors in frequency domain

为研究质量、刚度、阻尼不确定因子变化对多维隔振系统隔振能力的影响规律,选取多维隔振系统动平台输出速度的均方根值为隔振性能评价指标,定义质量、刚度和阻尼不确定因子的变化范围为±20%,求解得到隔振能力与不确定因子的关系.

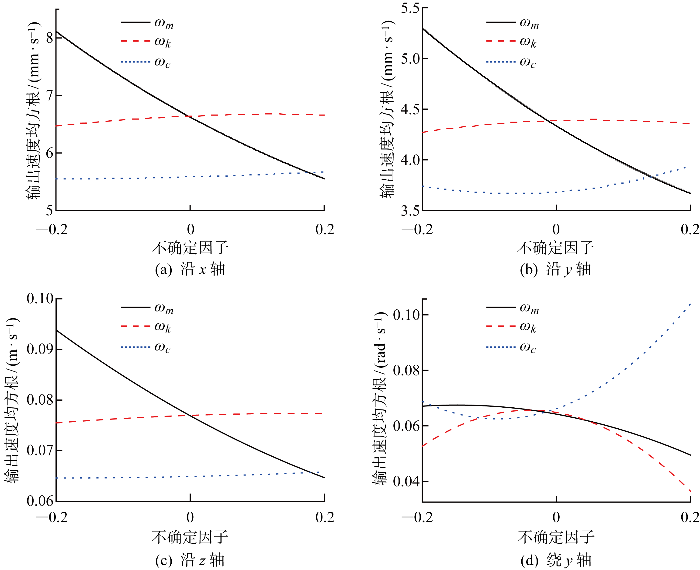
图4为存在不确定因子时动平台在各方向输出速度的均方根值,表明了隔振性能随质量、刚度和阻尼不确定因子的变化规律.各方向的隔振性能受质量不确定因子影响最显著且具有单调性,随着质量不确定因子的增大,隔振性能改善.隔振能力随刚度不确定因子的增大,先改善后逐渐恶化,在各方向上具有类似的变化趋势.隔振能力随阻尼不确定因子的增大表现出与刚度不确定因子相反的变化规律.随着刚度和阻尼不确定因子的逐渐增大,隔振性能在x、 y、 z轴方向较稳定,而绕y轴的隔振性能对上述变化最敏感.为保证良好的隔振效果,可在一定范围之内增大系统质量和刚度,上述结果可为多维隔振系统样机制作提供基础.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 存在不确定因子时动平台各方向的速度均方根值

Fig.4 RMS values of moving platform in different directions with uncertain factors

为阐明存在质量、刚度和阻尼不确定因子时多维隔振系统鲁棒最优半主动控制策略的有效性,与具有相同不确定因子的线性二次调节器 (LQR) 半主动控制策略在阶跃激励下进行了对比研究.

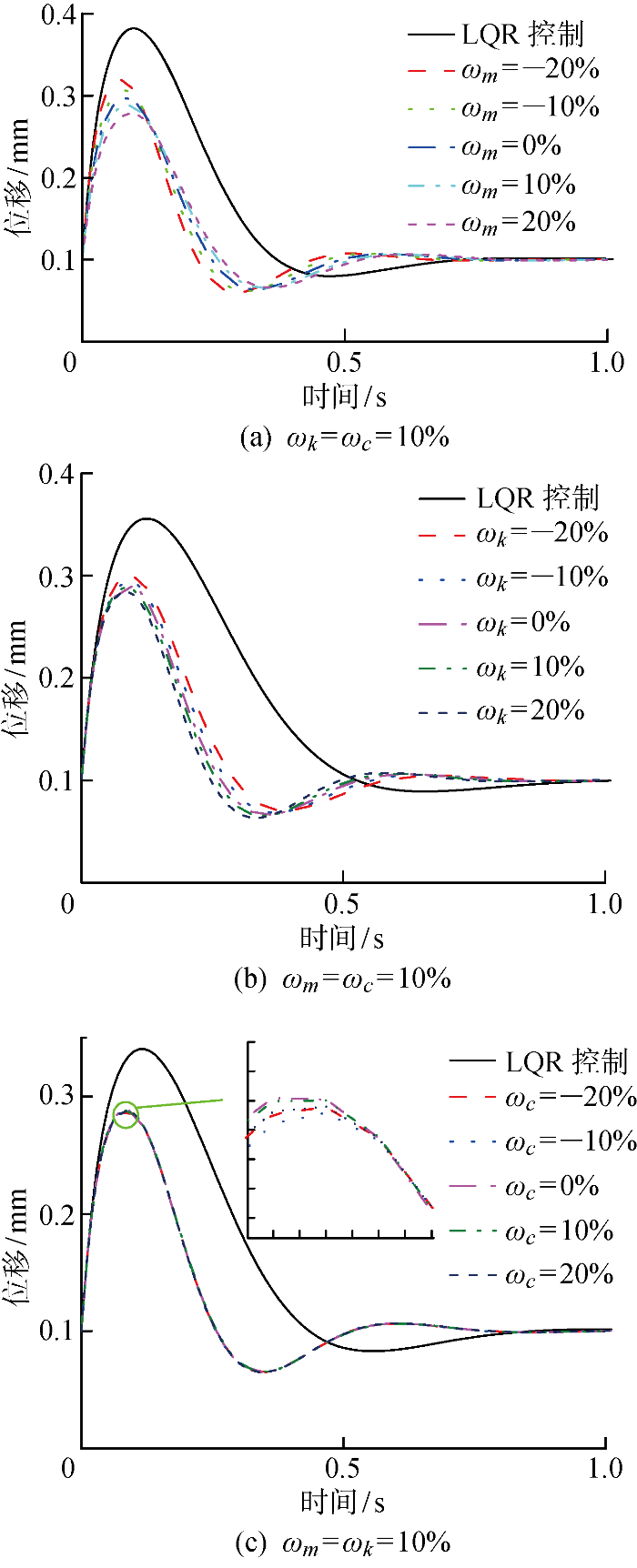
图5为考虑不同不确定因子时动平台在不同控制策略下的沿z向位移输出.依次固定质量、刚度和阻尼不确定因子中任意两个参数,研究另外一个不确定因子的变化对隔振能力的影响规律.在阶跃激励下,与LQR半主动策略相比,鲁棒最优半主动控制策略的超调量更小,上升的时间更短;随着质量不确定因子的增大,输出位移的幅值逐渐减小,该现象表明隔振能力有所改善;随着刚度不确定因子的增大,输出位移的幅值逐渐减小;随着阻尼不确定因子的增加,输出位移的幅值逐渐降低;质量和刚度不确定因子的变化对隔振能力影响显著.因限于篇幅,仅给出存在不确定因子时动平台的z向输出位移,研究表明,其余方向的输出位移变化规律具有类似的结论.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 动平台在不同不确定因子和控制策略下的z向位移

Fig.5 Displacement of moving platform in z direction with different uncertain factors and control strategies

4 结论

建立了基于2-RPC/2-SPC并联机构和磁流变阻尼器的多维隔振系统运动学和动力学模型,提出多维隔振系统鲁棒最优半主动控制策略,分别在时域和频域中研究存在质量、刚度和阻尼不确定因子的多维隔振系统隔振性能.研究结果表明:

(1) 当存在不确定因子时,采用鲁棒最优半主动控制策略的多维隔振系统能够实现沿x、 y、 z轴和绕y轴的多维振动有效衰减.

(2) 多维半主动隔振系统各方向的隔振能力受质量不确定因子影响最显著, 可在一定范围之内增大质量和系统刚度改善隔振效果.

(3) 在不确定因子影响下,采用鲁棒最优半主动控制策略的超调量和上升时间显著小于LQR半主动策略的超调量和上升时间,表明了存在不确定因子时鲁棒最优半主动控制策略的有效性和稳定性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

杜宁, 胡明勇, 毕勇, 等.

一种车载设备的低频水平减振方法

[J]. 振动与冲击, 2017, 36 (7): 184-190.