栅格地图路径规划旨在获取给定节点之间满足约束的最优或可行路径,在自动导引车等领域具有重要应用价值[1 ] .实际规划中,通常要综合考虑通行时间、路径的距离和弯折角度等,属于多目标路径规划问题[2 ] .各目标最优性互相冲突,无法获取所有目标均最优的路径,因此研究兼顾多方位代价的多目标求解算法具有一定的理论意义和实际应用价值.
栅格地图的多目标路径规划算法主要包含两类:基于权重分配的方法和基于帕累托前沿(Pareto front, PF)的方法.前者将各目标函数加权求和转换为单目标函数,最终返回一个解,其对于每个目标的质量取决于权重的分配[3 -4 ] ,但本质仍是单目标优化问题;后者并不进行多目标到单目标的转换,而是同时优化所有目标,最终返回PF,其包含的解互不支配[5 ] .相比前者,求解PF的多目标路径规划应用价值更大,结果更具有多样性和决策直观性.
基于PF的求解过程包含数学建模和算法应用两部分.将各目标函数量化为格元通行代价,构建基于代价向量的加权图是主流建模方法[6 ] .对于多目标路径规划算法,可以分为两大类:
(1) 基于图搜索的算法.以多目标A-Star算法(multi-objective A* , MOA* )[7 ] 为代表,于A-Star的基础上增加支配性比较,可以保留非支配解.NAMOA* (new approach MOA* )[8 ] 采用路径扩展方式替换节点扩展方式,提高MOA* 的求解效率.BOA* (bi-objective A* )[9 ] 从双目标图搜索问题出发,避免支配性重复比较,节约了时间成本.EMOA* (enhanced MOA* )算法[10 ] 综合BOA* 与快速支配检查方法,并利用平衡二叉搜索树提高支配性检查效率,进一步节约求解时间.另外,Hu等[11 ] 提出涟漪扩散算法(ripple spreading algorithm, RSA),并将其应用于多目标加权图的最短路径问题,可获取精确PF,且能够得到同一目标值下的不同解,这在多模式多目标路径规划[12 ] 问题上具有参考价值.基于搜索的算法优势在于求取完备非支配解,获得精确PF.但加权图多目标路径规划具备节点数目较大、层级划分明显和连通密度较低的特征,在地图范围扩张和节点跨度较大时,基于搜索的算法搜索状态呈指数级增长,时间成本耗费巨大.
(2) 基于群体智能的优化算法,主要包含多目标进化算法(multi-objective evolutionary algorithm, MOEA)及其衍生算法.虽然不能维持结果完备性与最优性,但求解框架简单,扩展性、迁移性和适应性较强.基于离散空间路径规划的进化算法框架[13 ] 、基于帕累托的非支配遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)[14 ] 和基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)[15 ] 在多目标路径规划问题上已具备成熟表现.在此基础上,许多研究考虑实际问题,针对初始化或选择策略进行了改进[16 18] .但上述方法并未关注求解效率,存在显著不足,突出体现在节点数量规模较大和目标数量较多时,求解的时间成本耗费较大、种群多样性欠缺以及PF质量不高.因此,研究具有大规模节点的加权图多目标路径规划(weighted graph multi-objective path planning with large-scale nodes, WGMOPP-LN)算法必要而迫切.
目前,多目标优化算法的研究趋向于关注大规模优化问题,旨在加快求解速度、提升PF质量和丰富种群多样性,以多目标粒子群优化(multi-objective particle swarm optimization, MOPSO)算法和MOEA为代表.MOPSO优化框架的原理简单,以个体和群体的状态转移向目标收敛.LMOCSO (large-scale multi-objective competitive swarm optimization)算法关注群体位置转移,融合竞争机制设计两阶段更新策略,大规模优化场景中的搜索效率得到提高[19 ] .此外,MOEA贡献了通用性更强的框架,有效的进化算子和环境选择策略通常是提高收敛速度和求解质量的关键.其中,基于分解的MOEA将原始问题分解为多个单目标问题,如参考向量引导多目标优化进化算法 (reference vector evolutionary algorithm, RVEA)将参考点转换为向量来分解原问题,并进行环境选择,维持了种群的多样性以提高PF质量[20 ] ;文献[21 ]中对NSGA-II进行变革提出NSGA-III,采用快速非支配排序,有助于解决目标数量较多的优化问题.而基于指标的MOEA,核心思想是在环境选择中基于解质量度量性能指标.针对算法对PF面形状敏感的问题,AR-MOEA (adaptative reference point MOEA)设计新的指标自适应调整参考点分布,于不同场景下有效保持种群多样性[22 ] .此外,文献[23 ]中提出AnD算法,设计基于角度和偏移密度估计的选择策略,以全新视角进行环境选择,算法结构简单、参数少,新策略兼顾多样性与收敛性,大规模问题下表现较好.
综上,现有基于加权图的多目标路径规划算法在节点和目标数目较多时,性能受影响明显.解决大规模问题需要综合考虑收敛性和多样性,以高效求解高质量PF集.上述LMOCSO和MOEA类算法可扩展至多目标路径规划场景,本文关注节点规模大、目标数目较多时的难点,针对多目标路径规划研究上述算法.此外,为解决上述算法求解效果不佳的问题,提出一种改进的多目标进化算法AD-MOEA (angle and shift-based density MOEA),保留NSGA-III 快速非支配排序,采用角度和偏移密度策略进行交叉个体选择和环境选择,综合考虑了算法求解效率、收敛性与多样性.在多个问题上进行了仿真实验,与上述算法以及主流多目标路径规划算法对比,取得更为优良的效果.主要贡献如下:①针对栅格地图的多目标路径规划问题提出基于代价向量加权图的完整建模流程;②改进连续空间中关注大规模决策变量问题的MOPSO和MOEA相关算法至路径规划场景,以解决WGMOPP-LN问题;③提出一种采取角度和偏移密度选择策略的改进多目标进化算法AD-MOEA.关注算法求解速度,以启发式初始化方法替代原框架下的随机初始化;关注算法的收敛性与多样性,基于角度和偏移密度策略进行交叉个体和环境选择,有利于避免盲目性,增强种群多样性.
1 栅格地图多目标路径规划建模
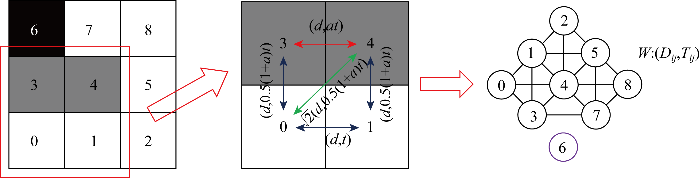
栅格划分是常规建图方法,考虑格元间具有不同的通行代价约束,构成多目标路径规划问题.将其建模为基于代价向量的多权重图最短路径模型,以优化时间和距离的双目标路径规划为例,选择图1 所示的3×3地图场景,建模过程如下.
图1
图1
多目标路径规划的加权图模型构建过程
Fig.1
Construction process of weighted graph model for multi-objective path planning
对栅格地图标号索引,设置通行性规则:黑色栅格表示障碍物不可通行,灰色栅格对通行时间有a (a >1)倍扩增,白色栅格表示正常通行.若设置栅格前、后、左、右的单位通行距离和时间分别为d 和t ,则8邻域相邻栅格间的通行代价如图1 所示.由此构建加权图模型,记为G=(V,E,W) ,其中$V=\left\{\mathrm{0,1},\dots,8\right\}$ $E=\left\{\left(\mathrm{0,1}\right),\left(\mathrm{0,3}\right),\dots,\left(\mathrm{7,8}\right)\right\}$ $W=\left\{{C}_{\mathrm{i}\mathrm{j}}^{1\times 2}|{C}_{\mathrm{i}\mathrm{j}}^{1\times 2}=\left({D}_{ij},{T}_{ij}\right),\left(i,j\right)\in E\right\}$ Dij 代表节点i 和j 间的通行距离代价,Tij 代表节点i 和j 间的通行时间代价.
设path(s , g )为s →g 一条可行路径的节点集合,满足条件:
(1) ${x}_{ij}=1, i,j\in \mathrm{p}\mathrm{a}\mathrm{t}\mathrm{h}(s,g)$
(2) ${x}_{ij}+{x}_{ji}=1, i,j\in \mathrm{p}\mathrm{a}\mathrm{t}\mathrm{h}(s,g)$
(3) ${\sum }_{j}{x}_{sj}+{\sum }_{j}{x}_{jg}=1, i,j\in \mathrm{p}\mathrm{a}\mathrm{t}\mathrm{h}(s,g)$
(4) ${x}_{ij}=\left\{\begin{array}{ll}1,& ({D}_{ij},{T}_{ij})\in E\\ 0,& \mathrm{其}\mathrm{他}\end{array}\right.$
多目标路径规划问题即归纳为基于加权图不断寻找可行路径极小化:
$\begin{array}{c}min\{{\sum }_{i}{\sum }_{j}{D}_{ij}{x}_{ij},{\sum }_{i}{\sum }_{j}{T}_{ij}{x}_{ij}\}\end{array}$
图模型中边权重的维度即为目标的数量,因此不同的优化目标只要量化为权重即可,模型可扩展性较强.
2 改进的多目标路径规划算法
2.1 多目标优化算法扩展
针对大规模优化问题的多目标优化算法研究集中在连续空间[19 23] ,改进上述算法应用至路径规划,以应对WGMOPP-LN问题.
LMOCSO算法[19 ] 涉及粒子位置与速度的状态更新,需要离散的编码方案且个体编码长度需要一致.但路径规划中个体包含节点数目并不总是一致,因此考虑到路径结果的完备性,统一的编码长度应为全部节点数目,不足编码长度时需要对中间节点进行重复扩维,如图2 所示.假设一张图具有10个节点,则编码长度为10,两条可行路径为0→1→3→5→9和0→1→7→3→2→9,节点数均小于10,需要进行循环补充,即逐次在各节点之间插入与前一个节点相同的值直至达到编码长度.初始个体生成采用随机初始化,每个个体由起点随机搜寻邻居节点直至到达终点,个体适应度计算通过加权图边集累加权重[13 ] .
图2
图2
统一长度编码方式
Fig.2
Encoding of unified length
由于可行路径的节点数目通常远小于节点总数,所以上述编码方式会造成编码重复和冗余.而多目标进化算法适合采用变长编码方案,每个个体代表一条可行路径,具有更好的通用性.基于成熟框架和变长编码方法[13 ] ,RVEA[20 ] 、NSGA-III[21 ] 以及AD-MOEA[22 ] 可扩展应用至路径规划场景.面对WGMOPP-LN问题时,上述算法能够有效节约时间成本,但PF质量仍显著不足,求解数量少,与精确PF面的近似程度低.
2.2 AD-MOEA简介
AD-MOEA完整流程如图3 所示.在种群构建层面,减少非必要随机性;在种群选择层面,关注非帕累托集合中个体趋向进一步收敛的能力.分别在初始化、个体选择、变异以及环境选择环节进行策略改进,综合考虑种群的收敛性与多样性,提高算法效率.AD-MOEA更适用于解决加权图多目标路径规划问题.
图3
图3
AD-MOEA流程图
Fig.3
Flow chart of AD-MOEA
2.2.1 启发式初始化
MOEA通常采用随机初始化,路径规划中,随机扩展邻居节点直至到达终点,虽然保持了种群初始化的多样性,但搜寻具有盲目性,节点数目较多时会严重影响速度.因此,提出一种关注目标权重的启发式初始化方案,平衡种群多样性与初始化速度.具体如下:对于n 目标$\left(n\ge 2\right)$ m 维种群$\left(m\gg n\right)$ n 个个体${p}_{1},{p}_{2},\dots,{p}_{n}$ pn+1 ~pm 由前n 个个体循环生成而来.生成规则如图4 所示,pn+i 由pq 生成,其中$q=\mathrm{m}\mathrm{o}\mathrm{d}\left(n+i,n\right)$ pq 按节点进行2(n-1) 个区间划分,其中vi,1 与vi,2 分别代表各区间左端、右端路径节点,各区间随机选择一个位置,对多个区间$1\to \mathrm{2,3}\to 4,\dots,2\left(n-1\right)-1\to 2\left(n-1\right)$ pq 所考虑目标外的n-1 个单目标最短路径,区间$2\to \mathrm{3,4}\to 5,\dots,2\left(n-2\right)\to 2\left(n-1\right)-1$ pq 原路径,最后拼接形成初始化个体pn+i .该初始化方法综合考虑了种群多样性和初始化速度.种群初始化后,计算适应度向量:
(5) $\begin{array}{c}F={\sum }_{i}{\sum }_{j}{C}_{\mathrm{i}\mathrm{j}}^{1\times \mathrm{n}}{x}_{ij}\end{array}$
图4
图4
新个体生成策略
Fig.4
New individual generation strategy
采用NSGA-III的快速非支配排序[21 ] 对当前种群进行帕累托次序标号,从低到高将当前种群进行划分,高次序集合任意个体总会被低次序集合个体支配,相同次序内个体互不支配.
2.2.2 个体选择策略
仅采用精英策略和锦标赛准则选择变异和交叉个体并不合理,非PF集合中的个体总会被舍弃,具有盲目性,容易陷入局部最优.双目标空间F1 和F2 (F1 代表第一维目标累加和,F2 代表第二维目标累加和) 个体分布如图5 所示,图中${\theta }_{1}~{\theta }_{3}$
图5
图5
双目标空间个体分布示意图
Fig.5
Individual distribution in bi-objective space
根据上述分析,设计个体选择的新策略以避免盲目性.首先,非PF集合中的个体有进一步收敛的空间,产生变异更具有意义,第v 代变异个体如下:
(6) $\begin{array}{c}{P}_{v}=\left\{\begin{array}{ll}\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{F}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}\left(P\right),& {p}_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}<{p}_{\mathrm{c}}\\ \mathrm{S}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{B}\mathrm{a}\mathrm{c}\mathrm{k}\left(P\right),& \mathrm{其}\mathrm{他}\end{array}\right.\end{array}$
式中:P 为当前种群;SelectFront(P )表示在PF中随机选择;SelectBack(P )表示在非PF集合中随机选择;p rand 为0~1随机数;p c 为选择概率.
其次,引入基于角度和偏移密度(shift-based density, SD)[23 ] 估计的策略来选择交叉个体.向量角度评判了两个个体的相似性,偏移密度用以衡量个体的收敛能力.交叉个体候选集总为非PF集合,以图5(b) 举例,A为非PF集合的个体,计算其与PF中各个体的向量夹角,选择最小值对应的前沿面个体B,即为与当前个体A最相似的个体.为保持种群多样性,交叉个体应从A和B中选择其一,选择标准为二者对于PF面个体的偏移密度,并取值小者,表明其更具备进一步收敛的能力,偏移密度策略具体如下所述.
设F 为当前PF,xi 为待计算SD个体,偏移操作将F 内个体向xi 进行平移.若F 内个体xl 某一维目标优于xi 对应目标时,将xl 相应目标值更改为xi 目标值,否则不变,描述如下:
(7) $\begin{array}{c}{{f}^{\mathrm{s}}}_{j}\left({x}_{l}\right)=\left\{\begin{array}{ll}{f}_{j}\left({x}_{i}\right),& {f}_{j}\left({x}_{l}\right)<{f}_{j}\left({x}_{i}\right)\\ {f}_{j}\left({x}_{l}\right),& \mathrm{其}\mathrm{他}\end{array}\right.\end{array}$
式中:${{f}^{\mathrm{s}}}_{j}\left({x}_{l}\right)$ fj (xl ) 的偏移目标值,构成n 维偏移目标${F}^{\mathrm{s}}\left({x}_{l}\right)=\left[{{f}^{\mathrm{s}}}_{1}\right({x}_{l}\left){{f}^{\mathrm{s}}}_{2}\right({x}_{l})\dots {{f}^{\mathrm{s}}}_{n}({x}_{l}\left)\right]$ .
(1) 基于xi 对F 内所有个体的目标向量进行偏移.
(2) 计算xi 目标向量与偏移目标向量的欧氏距离:
(8) $\begin{array}{l}d({x}_{i},{x}_{l})=\Vert {F}^{s}\left({x}_{l}\right)-F\left({x}_{i}\right)\Vert,\\ \begin{array}{c}{x}_{l}\in F\bigcap {x}_{l}\ne {x}_{i}\end{array}\end{array}$
(3) 按d(xi ,xl ) 升序排列,找到第k 个元素记为L(xk ) ,其中,$k=\sqrt{N}$ N 为F 内元素的数目.
(9) $\begin{array}{c}{\rho }^{\mathrm{S}\mathrm{D}}\left({x}_{i}\right)=\frac{1}{L\left({x}_{k}\right)+2}\end{array}$
(5) SD较大的个体代表个体进一步收敛能力不足,不选择.
2.2.3 变异策略
传统变异操作为对Pv 随机选择位置loc,丢弃loc后的节点并从loc随机搜寻邻居节点直至终点[13 ] ,节点规模大导致搜寻时间成本巨大.新的变异策略如图6 所示,vi 表示路径节点,随机选择位置loc,获取loc后第k' 个位置,将loc对应节点设为起点,loc+k' 对应节点设为终点,对起终点随机搜寻路径,并拼接原路径以生成变异个体.
图6
图6
变异策略
Fig.6
Mutation strategy
变异个体选择策略通常会选择帕累托次优个体,此变异操作期望提升次优个体的目标质量,且具备较快速度.变异子代与交叉个体执行交叉操作,采用模拟二项交叉[13 ] .交叉子代进行快速非支配排序并通过环境选择产生下一代种群.
2.2.4 环境选择策略
环境选择旨在保留收敛空间大、目标优良的个体,并维持种群多样性.采用2.2.2节所述的角度和偏移密度策略,评估非PF集合中的个体与PF中相似个体的收敛性,保留收敛性更好的个体进入下一轮循环.假设每轮个体数量固定为N, 若非PF集合内个体数目小于N, 则将所有个体按帕累托次序由低到高排列,依次补充未选择的个体至N ;若大于N ,则取前N 个个体.该策略维持了种群规模固定,且综合考虑了非PF集内个体的收敛性和种群多样性.
区别于文献[23 ]中对所有个体计算角度与偏移密度,本文个体和环境选择策略仅在非PF集合中进行计算,减少了时间与空间成本,又考虑了种群多样性与收敛性.
3 仿真实验及对比分析
构建随机加权图和Benchmark地图两类场景,在Windows系统下基于Python 3.9编程实现精确图搜索算法、LMOCSO和MOEA扩展算法以及AD-MOEA,根据求解时间、空间成本和求解质量指标验证AD-MOEA的有效性.
3.1 随机加权图场景
选择空白栅格地图构建加权图,以测试算法通用性.图7 展示随机加权图构建过程,以10×10空白栅格地图为例,不考虑障碍物等因素,构建双目标加权图模型,节点连通性基于栅格相邻关系,边的二维权重分量随机生成.
图7
图7
随机加权图建模流程
Fig.7
Modeling process of random weighted graph
根据上述规则,模拟生成4种随机加权图场景,具体参数如表1 所示.其中,节点数即为栅格数目,目标数为加权图的权重维度,可任意设置,节点数目和目标数量增加时精确解求解代价大.种群数量和迭代轮次为群体优化算法统一设置.
基于上述场景,设置起终点分别为第一个与最后一个节点,对比精确搜索算法NAMOA* [8 ] 、传统优化算法(NSGA-II[14 ] 和MOEA/D[15 ] )、扩展优化算法(NSGA-III[21 ] 、AR-MOEA[22 ] 、LMOCSO[19 ] )以及AD-MOEA的性能.表2 与表3 分别为运行10次的平均求解数目和平均时间,5 min未求解出结果则为超时(timeout).
空间成本可由算法执行时的运行内存占用率评估,表4 给出上述4种场景中各算法执行10次的平均内存占用率.对比可知,LMOCSO算法虽能有效节约时间,但所能获得的解数量较少,且占用空间成本较高.与精确搜索算法及其他优化算法相比,AD-MOEA能在不增加空间资源占用的前提下, 兼顾求解数量与时间成本,优势显著.
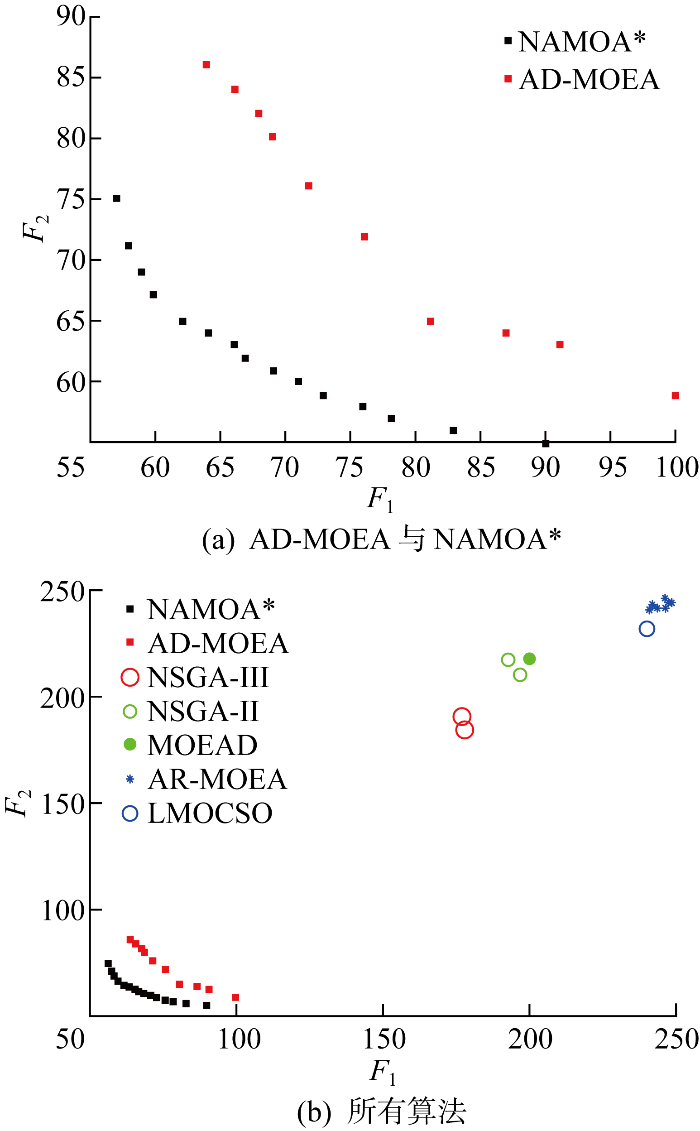
针对P3场景,图8 展示了上述算法求解的PF分布图.选择超体积(hypervolume,HV)与逆世代距离(inverted generational distance, IGD)作为评价指标以评估各优化算法PF的质量[23 ] .超体积指PF与参考点r 之间组成的超体积,如图9 所示,用于评价目标空间被近似PF覆盖的程度,衡量近似PF的支配性,选择r =(250, 250).
图8
图8
不同算法的PF面分布
Fig.8
Pareto front distribution of different algorithms
图9
图9
超体积示意图
Fig.9
Diagram of hypervolume
记精确帕累托前沿(PF* )集合元素数量为${N}_{\mathrm{P}{\mathrm{F}}^{\mathrm{*}}}$ y ,找到位于近似PF中与其相距最近的解xy ,计算欧氏距离d(y,xy ) 并取平均值,逆世代距离同时考虑了近似PF的多样性与收敛性,计算公式如下:
(10) $\begin{array}{c}{d}_{\mathrm{I}\mathrm{G}}=\frac{1}{{N}_{\mathrm{P}{\mathrm{F}}^{\mathrm{*}}}}\sum _{y\in \mathrm{P}{\mathrm{F}}^{\mathrm{*}}}d(y,{x}_{y})\end{array}$
基于图8 的PF分布图,表5 评估了上述算法求解PF的质量,以超体积和逆世代距离为指标进行评价,超体积越大、逆世代距离越小时,质量越好.
根据上述对比,AD-MOEA可以维持较低时间成本并有效提高求解质量,包括解的多样性、收敛性和近似精确PF的程度,加权图多目标最短路径问题中具有明显优势.
针对P1与P3场景,图10 给出AD-MOEA、NAMOA* 、NSGA-II与LMOCSO算法求解的多目标路径结果,可知AD-MOEA可获得更丰富、更接近最优解的路径.
图10
图10
P1与P3场景下4种算法的多目标路径
Fig.10
Multi-objective paths of four algorithms in Scenes P1 and P3
3.2 Benchmark地图场景
将AD-MOEA应用于Benchmark栅格地图场景的多目标路径规划,基准地图均为L×L 正方形栅格地图,具体尺寸参数及目标数量如表6 所示.
对3个场景应用改进算法AD-MOEA,表7 展示了运行10次的平均求解数目和平均时间,并以算法NAMOA* 求解数目为基准,图11 为求解路径的可视化结果.
图11
图11
AD-MOEA求解3种基准地图的MOPP结果
Fig.11
MOPP results of AD-MOEA for three benchmark maps
在Benchmark地图中,距离和时间作为优化目标,黑色区域表示不可通行,绿色区域增加通行时间,白色区域表示正常通行,加权图建模方式参照第1章.起点和终点相距较远时,AD-MOEA可维持较低时间成本而获得令人满意的解.进一步,地图不大时,AD-MOEA可获得更丰富的解,即相同目标对应的不同路径,这在多模式路径规划[12 ] 中具有重要意义.综合得到,AD-MOEA在随机加权图场景和Benchmark地图下均具有显著改进效果,求解速度快,结果质量较高.
4 结语
本文关注栅格地图多目标路径规划,基于代价向量的加权图进行建模,重点研究解决节点规模大、目标数量多、起终点跨度广的多目标路径规划算法.针对图搜索算法时间成本耗费巨大的问题,将连续空间解决大规模优化问题的LMOCSO和MOEA类算法改进并应用至路径规划场景,时间成本节约显著;针对传统MOEA与扩展算法求解帕累托前沿质量低的问题,提出改进算法AD-MOEA,关注时间与多样性,设计启发式初始化策略;关注非最优个体收敛性,基于角度和偏移密度估计策略进行交叉个体和环境选择,并改进变异策略,综合考虑了种群多样性和收敛性.最后,通过随机加权图和Benchmark地图对比实验,验证改进算法AD-MOEA求解效率高,在速度、结果多样性和收敛性方面均具有显著提升.
参考文献
View Option
[1]
裘柯钧 , 鲍中凯 , 陈璐 . 民用客机总装车间自动引导车任务分配及路径规划
[J]. 上海交通大学学报 2023 , 57 (1 ): 93 -102 .
DOI:10.16183/j.cnki.jsjtu.2021.223
[本文引用: 1]
为了实现自动引导车(AGV)在某民用客机总装车间的高效运作,提出AGV任务分配与路径规划两阶段求解方法,有效地解决了车间内AGV的多次往返配送调度问题.在任务分配阶段,提出基于行程的AGV任务分配模型,提高任务分配的效率;在路径规划阶段,采用时间窗算法,对AGV占用的地图资源进行时间窗的初始化、更新和排布,并针对由于避障和等待引起的物料送达时间无法满足的情况,设计了料包交换、优先级提前、预留时长放宽共3种递进的调整策略,实现AGV的无冲突路径规划.在数值实验中,两阶段方法应用于50、100、150个料包问题的平均求解时间分别为15.86、41.12、162.29 s,表明两阶段方法有效缓解了多行程AGV调度问题的复杂性,能在合理时间内实现民用客机总装车间AGV的调度优化,以适应民用客机年产量逐年快速递增的生产需求.
QIU Kejun BAO Zhongkai CHEN Lu . Task assignment and path planning for automatic guided vehicles in aircraft assembly workshop
[J]. Journal of Shanghai Jiao Tong University 2023 , 57 (1 ): 93 -102 .
[本文引用: 1]
[2]
ABED B M JASIM W M . Multi objective optimization algorithms for mobile robot path planning: A survey
[J]. International Journal of Online & Biomedical Engineering 2022 , 18 (15 ): 160 -177 .
[本文引用: 1]
[3]
OU Y Q FAN Y X ZHANG X L et al . Improved A* path planning method based on the grid map
[J]. Sensors 2022 , 22 (16 ): 6198 .
[本文引用: 1]
[4]
ZHANG D LUO R YIN Y B et al . Multi-objective path planning for mobile robot in nuclear accident environment based on improved ant colony optimization with modified A*
[J]. Nuclear Engineering and Technology 2023 , 55 (5 ): 1838 -1854 .
[本文引用: 1]
[5]
DUAN P SANG H Y LI J Q et al . Solving multi-objective path planning for service robot by a pareto-based optimization algorithm
[C]// 2018 Chinese Control and Decision Conference Shenyang, China : IEEE , 2018 : 3416 -3420
[本文引用: 1]
[6]
HOHMANN N BUJNY M ADAMY J et al . Hybrid evolutionary approach to multi-objective path planning for UAVs
[C]// 2021 IEEE Symposium Series on Computational Intelligence Orlando, USA : IEEE , 2021 : 9660187 .
[本文引用: 1]
[7]
STEWART B S WHITE C C . Multiobjective A*
[J]. Journal of the ACM 1991 , 38 (4 ): 775 -814 .
[本文引用: 1]
[8]
MANDOW L DE LA CRUZ J L P . Multiobjective A* search with consistent heuristics
[J]. Journal of the ACM 2008 , 57 (5 ): 1 -25 .
[本文引用: 2]
[9]
Ulloa C H Yeoh W Baier J et al . A simple and fast bi-objective search algorithm
[C]// Proceedings of the International Conference on Automated Planning and Scheduling Nancy, France : AAAI , 2020 , 30 : 143 -151 .
[本文引用: 1]
[10]
REN Z Q ZHAN R RATHINAM S et al . Enhanced multi-objective A* using balanced binary search trees
[C]// Proceedings of the International Symposium on Combinatorial Search Vienna, Austria : AAAI , 2022 : 162 -170 .
[本文引用: 1]
[11]
HU X B GU S H ZHANG C et al . Finding all Pareto optimal paths by simulating ripple relay race in multi-objective networks
[J]. Swarm and Evolutionary Computation 2021 , 64 : 100908 .
[本文引用: 1]
[12]
JIN B . Multi-objective A* algorithm for the multimodal multi-objective path planning optimization
[C]// 2021 IEEE Congress on Evolutionary Computation Kraków, Poland : IEEE , 2021 : 1704 -1711 .
[本文引用: 2]
[13]
AHN C W RAMAKRISHNA R S . A genetic algorithm for shortest path routing problem and the sizing of populations
[J]. IEEE Transactions on Evolutionary Computation 2002 , 6 (6 ): 566 -579 .
[本文引用: 5]
[14]
DEB K PRATAP A AGARWAL S et al . A fast and elitist multiobjective genetic algorithm: NSGA-II
[J]. IEEE Transactions on Evolutionary Computation 2002 , 6 (2 ): 182 -197 .
[本文引用: 2]
[15]
LI K FIALHO A KWONG S et al . Adaptive operator selection with bandits for a multiobjective evolutionary algorithm based on decomposition
[J]. IEEE Transactions on Evolutionary Computation 2014 , 18 (1 ): 114 -130 .
[本文引用: 2]
[16]
REN Q YAO Y YANG G et al . Multi-objective path planning for UAV in the urban environment based on CDNSGA-II
[C]// 2019 IEEE International Conference on Service-Oriented System Engineering San Francisco, USA : IEEE , 2019 : 350 -3505 .
[本文引用: 1]
[17]
YAO X Y LI W H PAN X G et al . Multimodal multi-objective evolutionary algorithm for multiple path planning
[J]. Computers & Industrial Engineering 2022 , 169 : 108145 .
[18]
ZHENG S H ZHENG C R LI W . Research on multi-objective shortest path based on genetic algorithm
[C]// 2022 2nd International Conference on Computer Science and Blockchain Wuhan, China : IEEE , 2022 : 127 -130 .
[本文引用: 1]
[19]
TIAN Y ZHENG X T ZHANG X Y et al . Efficient large-scale multiobjective optimization based on a competitive swarm optimizer
[J]. IEEE Transactions on Cybernetics 2020 , 50 (8 ): 3696 -3708 .
DOI:10.1109/TCYB.2019.2906383
PMID:30951490
[本文引用: 4]
There exist many multiobjective optimization problems (MOPs) containing a large number of decision variables in real-world applications, which are known as large-scale MOPs. Due to the ineffectiveness of existing operators in finding optimal solutions in a huge decision space, some decision variable division-based algorithms have been tailored for improving the search efficiency in solving large-scale MOPs. However, these algorithms will encounter difficulties when solving problems with complicated landscapes, as the decision variable division is likely to be inaccurate and time consuming. In this paper, we propose a competitive swarm optimizer (CSO)-based efficient search for solving large-scale MOPs. The proposed algorithm adopts a new particle updating strategy that suggests a two-stage strategy to update position, which can highly improve the search efficiency. The experimental results on large-scale benchmark MOPs and an application example demonstrate the superiority of the proposed algorithm over several state-of-the-art multiobjective evolutionary algorithms, including problem transformation-based algorithm, decision variable clustering-based algorithm, particle swarm optimization algorithm, and estimation of distribution algorithm.
[20]
CHENG R JIN Y C OLHOFER M et al . A reference vector guided evolutionary algorithm for many-objective optimization
[J]. IEEE Transactions on Evolutionary Computation 2016 , 20 (5 ): 773 -791 .
[本文引用: 2]
[21]
DEB K JAIN H . An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints
[J]. IEEE Transactions on Evolutionary Computation 2014 , 18 (4 ): 577 -601 .
[本文引用: 4]
[22]
TIAN Y CHENG R ZHANG X Y et al . An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility
[J]. IEEE Transactions on Evolutionary Computation 2018 , 22 (4 ): 609 -622 .
[本文引用: 3]
[23]
LIU Z Z WANG Y HUANG P Q . AnD: A many-objective evolutionary algorithm with angle-based selection and shift-based density estimation
[J]. Information Sciences 2020 , 509 : 400 -419 .
[本文引用: 5]
民用客机总装车间自动引导车任务分配及路径规划
1
2023
... 栅格地图路径规划旨在获取给定节点之间满足约束的最优或可行路径,在自动导引车等领域具有重要应用价值[1 ] .实际规划中,通常要综合考虑通行时间、路径的距离和弯折角度等,属于多目标路径规划问题[2 ] .各目标最优性互相冲突,无法获取所有目标均最优的路径,因此研究兼顾多方位代价的多目标求解算法具有一定的理论意义和实际应用价值. ...
Task assignment and path planning for automatic guided vehicles in aircraft assembly workshop
1
2023
... 栅格地图路径规划旨在获取给定节点之间满足约束的最优或可行路径,在自动导引车等领域具有重要应用价值[1 ] .实际规划中,通常要综合考虑通行时间、路径的距离和弯折角度等,属于多目标路径规划问题[2 ] .各目标最优性互相冲突,无法获取所有目标均最优的路径,因此研究兼顾多方位代价的多目标求解算法具有一定的理论意义和实际应用价值. ...
Multi objective optimization algorithms for mobile robot path planning: A survey
1
2022
... 栅格地图路径规划旨在获取给定节点之间满足约束的最优或可行路径,在自动导引车等领域具有重要应用价值[1 ] .实际规划中,通常要综合考虑通行时间、路径的距离和弯折角度等,属于多目标路径规划问题[2 ] .各目标最优性互相冲突,无法获取所有目标均最优的路径,因此研究兼顾多方位代价的多目标求解算法具有一定的理论意义和实际应用价值. ...
Improved A* path planning method based on the grid map
1
2022
... 栅格地图的多目标路径规划算法主要包含两类:基于权重分配的方法和基于帕累托前沿(Pareto front, PF)的方法.前者将各目标函数加权求和转换为单目标函数,最终返回一个解,其对于每个目标的质量取决于权重的分配[3 -4 ] ,但本质仍是单目标优化问题;后者并不进行多目标到单目标的转换,而是同时优化所有目标,最终返回PF,其包含的解互不支配[5 ] .相比前者,求解PF的多目标路径规划应用价值更大,结果更具有多样性和决策直观性. ...
Multi-objective path planning for mobile robot in nuclear accident environment based on improved ant colony optimization with modified A*
1
2023
... 栅格地图的多目标路径规划算法主要包含两类:基于权重分配的方法和基于帕累托前沿(Pareto front, PF)的方法.前者将各目标函数加权求和转换为单目标函数,最终返回一个解,其对于每个目标的质量取决于权重的分配[3 -4 ] ,但本质仍是单目标优化问题;后者并不进行多目标到单目标的转换,而是同时优化所有目标,最终返回PF,其包含的解互不支配[5 ] .相比前者,求解PF的多目标路径规划应用价值更大,结果更具有多样性和决策直观性. ...
Solving multi-objective path planning for service robot by a pareto-based optimization algorithm
1
2018
... 栅格地图的多目标路径规划算法主要包含两类:基于权重分配的方法和基于帕累托前沿(Pareto front, PF)的方法.前者将各目标函数加权求和转换为单目标函数,最终返回一个解,其对于每个目标的质量取决于权重的分配[3 -4 ] ,但本质仍是单目标优化问题;后者并不进行多目标到单目标的转换,而是同时优化所有目标,最终返回PF,其包含的解互不支配[5 ] .相比前者,求解PF的多目标路径规划应用价值更大,结果更具有多样性和决策直观性. ...
Hybrid evolutionary approach to multi-objective path planning for UAVs
1
2021
... 基于PF的求解过程包含数学建模和算法应用两部分.将各目标函数量化为格元通行代价,构建基于代价向量的加权图是主流建模方法[6 ] .对于多目标路径规划算法,可以分为两大类: ...
Multiobjective A*
1
1991
... (1) 基于图搜索的算法.以多目标A-Star算法(multi-objective A* , MOA* )[7 ] 为代表,于A-Star的基础上增加支配性比较,可以保留非支配解.NAMOA* (new approach MOA* )[8 ] 采用路径扩展方式替换节点扩展方式,提高MOA* 的求解效率.BOA* (bi-objective A* )[9 ] 从双目标图搜索问题出发,避免支配性重复比较,节约了时间成本.EMOA* (enhanced MOA* )算法[10 ] 综合BOA* 与快速支配检查方法,并利用平衡二叉搜索树提高支配性检查效率,进一步节约求解时间.另外,Hu等[11 ] 提出涟漪扩散算法(ripple spreading algorithm, RSA),并将其应用于多目标加权图的最短路径问题,可获取精确PF,且能够得到同一目标值下的不同解,这在多模式多目标路径规划[12 ] 问题上具有参考价值.基于搜索的算法优势在于求取完备非支配解,获得精确PF.但加权图多目标路径规划具备节点数目较大、层级划分明显和连通密度较低的特征,在地图范围扩张和节点跨度较大时,基于搜索的算法搜索状态呈指数级增长,时间成本耗费巨大. ...
Multiobjective A* search with consistent heuristics
2
2008
... (1) 基于图搜索的算法.以多目标A-Star算法(multi-objective A* , MOA* )[7 ] 为代表,于A-Star的基础上增加支配性比较,可以保留非支配解.NAMOA* (new approach MOA* )[8 ] 采用路径扩展方式替换节点扩展方式,提高MOA* 的求解效率.BOA* (bi-objective A* )[9 ] 从双目标图搜索问题出发,避免支配性重复比较,节约了时间成本.EMOA* (enhanced MOA* )算法[10 ] 综合BOA* 与快速支配检查方法,并利用平衡二叉搜索树提高支配性检查效率,进一步节约求解时间.另外,Hu等[11 ] 提出涟漪扩散算法(ripple spreading algorithm, RSA),并将其应用于多目标加权图的最短路径问题,可获取精确PF,且能够得到同一目标值下的不同解,这在多模式多目标路径规划[12 ] 问题上具有参考价值.基于搜索的算法优势在于求取完备非支配解,获得精确PF.但加权图多目标路径规划具备节点数目较大、层级划分明显和连通密度较低的特征,在地图范围扩张和节点跨度较大时,基于搜索的算法搜索状态呈指数级增长,时间成本耗费巨大. ...
... 基于上述场景,设置起终点分别为第一个与最后一个节点,对比精确搜索算法NAMOA* [8 ] 、传统优化算法(NSGA-II[14 ] 和MOEA/D[15 ] )、扩展优化算法(NSGA-III[21 ] 、AR-MOEA[22 ] 、LMOCSO[19 ] )以及AD-MOEA的性能.表2 与表3 分别为运行10次的平均求解数目和平均时间,5 min未求解出结果则为超时(timeout). ...
A simple and fast bi-objective search algorithm
1
2020
... (1) 基于图搜索的算法.以多目标A-Star算法(multi-objective A* , MOA* )[7 ] 为代表,于A-Star的基础上增加支配性比较,可以保留非支配解.NAMOA* (new approach MOA* )[8 ] 采用路径扩展方式替换节点扩展方式,提高MOA* 的求解效率.BOA* (bi-objective A* )[9 ] 从双目标图搜索问题出发,避免支配性重复比较,节约了时间成本.EMOA* (enhanced MOA* )算法[10 ] 综合BOA* 与快速支配检查方法,并利用平衡二叉搜索树提高支配性检查效率,进一步节约求解时间.另外,Hu等[11 ] 提出涟漪扩散算法(ripple spreading algorithm, RSA),并将其应用于多目标加权图的最短路径问题,可获取精确PF,且能够得到同一目标值下的不同解,这在多模式多目标路径规划[12 ] 问题上具有参考价值.基于搜索的算法优势在于求取完备非支配解,获得精确PF.但加权图多目标路径规划具备节点数目较大、层级划分明显和连通密度较低的特征,在地图范围扩张和节点跨度较大时,基于搜索的算法搜索状态呈指数级增长,时间成本耗费巨大. ...
Enhanced multi-objective A* using balanced binary search trees
1
2022
... (1) 基于图搜索的算法.以多目标A-Star算法(multi-objective A* , MOA* )[7 ] 为代表,于A-Star的基础上增加支配性比较,可以保留非支配解.NAMOA* (new approach MOA* )[8 ] 采用路径扩展方式替换节点扩展方式,提高MOA* 的求解效率.BOA* (bi-objective A* )[9 ] 从双目标图搜索问题出发,避免支配性重复比较,节约了时间成本.EMOA* (enhanced MOA* )算法[10 ] 综合BOA* 与快速支配检查方法,并利用平衡二叉搜索树提高支配性检查效率,进一步节约求解时间.另外,Hu等[11 ] 提出涟漪扩散算法(ripple spreading algorithm, RSA),并将其应用于多目标加权图的最短路径问题,可获取精确PF,且能够得到同一目标值下的不同解,这在多模式多目标路径规划[12 ] 问题上具有参考价值.基于搜索的算法优势在于求取完备非支配解,获得精确PF.但加权图多目标路径规划具备节点数目较大、层级划分明显和连通密度较低的特征,在地图范围扩张和节点跨度较大时,基于搜索的算法搜索状态呈指数级增长,时间成本耗费巨大. ...
Finding all Pareto optimal paths by simulating ripple relay race in multi-objective networks
1
2021
... (1) 基于图搜索的算法.以多目标A-Star算法(multi-objective A* , MOA* )[7 ] 为代表,于A-Star的基础上增加支配性比较,可以保留非支配解.NAMOA* (new approach MOA* )[8 ] 采用路径扩展方式替换节点扩展方式,提高MOA* 的求解效率.BOA* (bi-objective A* )[9 ] 从双目标图搜索问题出发,避免支配性重复比较,节约了时间成本.EMOA* (enhanced MOA* )算法[10 ] 综合BOA* 与快速支配检查方法,并利用平衡二叉搜索树提高支配性检查效率,进一步节约求解时间.另外,Hu等[11 ] 提出涟漪扩散算法(ripple spreading algorithm, RSA),并将其应用于多目标加权图的最短路径问题,可获取精确PF,且能够得到同一目标值下的不同解,这在多模式多目标路径规划[12 ] 问题上具有参考价值.基于搜索的算法优势在于求取完备非支配解,获得精确PF.但加权图多目标路径规划具备节点数目较大、层级划分明显和连通密度较低的特征,在地图范围扩张和节点跨度较大时,基于搜索的算法搜索状态呈指数级增长,时间成本耗费巨大. ...
Multi-objective A* algorithm for the multimodal multi-objective path planning optimization
2
2021
... (1) 基于图搜索的算法.以多目标A-Star算法(multi-objective A* , MOA* )[7 ] 为代表,于A-Star的基础上增加支配性比较,可以保留非支配解.NAMOA* (new approach MOA* )[8 ] 采用路径扩展方式替换节点扩展方式,提高MOA* 的求解效率.BOA* (bi-objective A* )[9 ] 从双目标图搜索问题出发,避免支配性重复比较,节约了时间成本.EMOA* (enhanced MOA* )算法[10 ] 综合BOA* 与快速支配检查方法,并利用平衡二叉搜索树提高支配性检查效率,进一步节约求解时间.另外,Hu等[11 ] 提出涟漪扩散算法(ripple spreading algorithm, RSA),并将其应用于多目标加权图的最短路径问题,可获取精确PF,且能够得到同一目标值下的不同解,这在多模式多目标路径规划[12 ] 问题上具有参考价值.基于搜索的算法优势在于求取完备非支配解,获得精确PF.但加权图多目标路径规划具备节点数目较大、层级划分明显和连通密度较低的特征,在地图范围扩张和节点跨度较大时,基于搜索的算法搜索状态呈指数级增长,时间成本耗费巨大. ...
... 在Benchmark地图中,距离和时间作为优化目标,黑色区域表示不可通行,绿色区域增加通行时间,白色区域表示正常通行,加权图建模方式参照第1章.起点和终点相距较远时,AD-MOEA可维持较低时间成本而获得令人满意的解.进一步,地图不大时,AD-MOEA可获得更丰富的解,即相同目标对应的不同路径,这在多模式路径规划[12 ] 中具有重要意义.综合得到,AD-MOEA在随机加权图场景和Benchmark地图下均具有显著改进效果,求解速度快,结果质量较高. ...
A genetic algorithm for shortest path routing problem and the sizing of populations
5
2002
... (2) 基于群体智能的优化算法,主要包含多目标进化算法(multi-objective evolutionary algorithm, MOEA)及其衍生算法.虽然不能维持结果完备性与最优性,但求解框架简单,扩展性、迁移性和适应性较强.基于离散空间路径规划的进化算法框架[13 ] 、基于帕累托的非支配遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)[14 ] 和基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)[15 ] 在多目标路径规划问题上已具备成熟表现.在此基础上,许多研究考虑实际问题,针对初始化或选择策略进行了改进[16 18 ] .但上述方法并未关注求解效率,存在显著不足,突出体现在节点数量规模较大和目标数量较多时,求解的时间成本耗费较大、种群多样性欠缺以及PF质量不高.因此,研究具有大规模节点的加权图多目标路径规划(weighted graph multi-objective path planning with large-scale nodes, WGMOPP-LN)算法必要而迫切. ...
... LMOCSO算法[19 ] 涉及粒子位置与速度的状态更新,需要离散的编码方案且个体编码长度需要一致.但路径规划中个体包含节点数目并不总是一致,因此考虑到路径结果的完备性,统一的编码长度应为全部节点数目,不足编码长度时需要对中间节点进行重复扩维,如图2 所示.假设一张图具有10个节点,则编码长度为10,两条可行路径为0→1→3→5→9和0→1→7→3→2→9,节点数均小于10,需要进行循环补充,即逐次在各节点之间插入与前一个节点相同的值直至达到编码长度.初始个体生成采用随机初始化,每个个体由起点随机搜寻邻居节点直至到达终点,个体适应度计算通过加权图边集累加权重[13 ] . ...
... 由于可行路径的节点数目通常远小于节点总数,所以上述编码方式会造成编码重复和冗余.而多目标进化算法适合采用变长编码方案,每个个体代表一条可行路径,具有更好的通用性.基于成熟框架和变长编码方法[13 ] ,RVEA[20 ] 、NSGA-III[21 ] 以及AD-MOEA[22 ] 可扩展应用至路径规划场景.面对WGMOPP-LN问题时,上述算法能够有效节约时间成本,但PF质量仍显著不足,求解数量少,与精确PF面的近似程度低. ...
... 传统变异操作为对Pv 随机选择位置loc,丢弃loc后的节点并从loc随机搜寻邻居节点直至终点[13 ] ,节点规模大导致搜寻时间成本巨大.新的变异策略如图6 所示,vi 表示路径节点,随机选择位置loc,获取loc后第k' 个位置,将loc对应节点设为起点,loc+k' 对应节点设为终点,对起终点随机搜寻路径,并拼接原路径以生成变异个体. ...
... 变异个体选择策略通常会选择帕累托次优个体,此变异操作期望提升次优个体的目标质量,且具备较快速度.变异子代与交叉个体执行交叉操作,采用模拟二项交叉[13 ] .交叉子代进行快速非支配排序并通过环境选择产生下一代种群. ...
A fast and elitist multiobjective genetic algorithm: NSGA-II
2
2002
... (2) 基于群体智能的优化算法,主要包含多目标进化算法(multi-objective evolutionary algorithm, MOEA)及其衍生算法.虽然不能维持结果完备性与最优性,但求解框架简单,扩展性、迁移性和适应性较强.基于离散空间路径规划的进化算法框架[13 ] 、基于帕累托的非支配遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)[14 ] 和基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)[15 ] 在多目标路径规划问题上已具备成熟表现.在此基础上,许多研究考虑实际问题,针对初始化或选择策略进行了改进[16 18 ] .但上述方法并未关注求解效率,存在显著不足,突出体现在节点数量规模较大和目标数量较多时,求解的时间成本耗费较大、种群多样性欠缺以及PF质量不高.因此,研究具有大规模节点的加权图多目标路径规划(weighted graph multi-objective path planning with large-scale nodes, WGMOPP-LN)算法必要而迫切. ...
... 基于上述场景,设置起终点分别为第一个与最后一个节点,对比精确搜索算法NAMOA* [8 ] 、传统优化算法(NSGA-II[14 ] 和MOEA/D[15 ] )、扩展优化算法(NSGA-III[21 ] 、AR-MOEA[22 ] 、LMOCSO[19 ] )以及AD-MOEA的性能.表2 与表3 分别为运行10次的平均求解数目和平均时间,5 min未求解出结果则为超时(timeout). ...
Adaptive operator selection with bandits for a multiobjective evolutionary algorithm based on decomposition
2
2014
... (2) 基于群体智能的优化算法,主要包含多目标进化算法(multi-objective evolutionary algorithm, MOEA)及其衍生算法.虽然不能维持结果完备性与最优性,但求解框架简单,扩展性、迁移性和适应性较强.基于离散空间路径规划的进化算法框架[13 ] 、基于帕累托的非支配遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)[14 ] 和基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)[15 ] 在多目标路径规划问题上已具备成熟表现.在此基础上,许多研究考虑实际问题,针对初始化或选择策略进行了改进[16 18 ] .但上述方法并未关注求解效率,存在显著不足,突出体现在节点数量规模较大和目标数量较多时,求解的时间成本耗费较大、种群多样性欠缺以及PF质量不高.因此,研究具有大规模节点的加权图多目标路径规划(weighted graph multi-objective path planning with large-scale nodes, WGMOPP-LN)算法必要而迫切. ...
... 基于上述场景,设置起终点分别为第一个与最后一个节点,对比精确搜索算法NAMOA* [8 ] 、传统优化算法(NSGA-II[14 ] 和MOEA/D[15 ] )、扩展优化算法(NSGA-III[21 ] 、AR-MOEA[22 ] 、LMOCSO[19 ] )以及AD-MOEA的性能.表2 与表3 分别为运行10次的平均求解数目和平均时间,5 min未求解出结果则为超时(timeout). ...
Multi-objective path planning for UAV in the urban environment based on CDNSGA-II
1
2019
... (2) 基于群体智能的优化算法,主要包含多目标进化算法(multi-objective evolutionary algorithm, MOEA)及其衍生算法.虽然不能维持结果完备性与最优性,但求解框架简单,扩展性、迁移性和适应性较强.基于离散空间路径规划的进化算法框架[13 ] 、基于帕累托的非支配遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)[14 ] 和基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)[15 ] 在多目标路径规划问题上已具备成熟表现.在此基础上,许多研究考虑实际问题,针对初始化或选择策略进行了改进[16 18 ] .但上述方法并未关注求解效率,存在显著不足,突出体现在节点数量规模较大和目标数量较多时,求解的时间成本耗费较大、种群多样性欠缺以及PF质量不高.因此,研究具有大规模节点的加权图多目标路径规划(weighted graph multi-objective path planning with large-scale nodes, WGMOPP-LN)算法必要而迫切. ...
Multimodal multi-objective evolutionary algorithm for multiple path planning
0
2022
Research on multi-objective shortest path based on genetic algorithm
1
2022
... (2) 基于群体智能的优化算法,主要包含多目标进化算法(multi-objective evolutionary algorithm, MOEA)及其衍生算法.虽然不能维持结果完备性与最优性,但求解框架简单,扩展性、迁移性和适应性较强.基于离散空间路径规划的进化算法框架[13 ] 、基于帕累托的非支配遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)[14 ] 和基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)[15 ] 在多目标路径规划问题上已具备成熟表现.在此基础上,许多研究考虑实际问题,针对初始化或选择策略进行了改进[16 18 ] .但上述方法并未关注求解效率,存在显著不足,突出体现在节点数量规模较大和目标数量较多时,求解的时间成本耗费较大、种群多样性欠缺以及PF质量不高.因此,研究具有大规模节点的加权图多目标路径规划(weighted graph multi-objective path planning with large-scale nodes, WGMOPP-LN)算法必要而迫切. ...
Efficient large-scale multiobjective optimization based on a competitive swarm optimizer
4
2020
... 目前,多目标优化算法的研究趋向于关注大规模优化问题,旨在加快求解速度、提升PF质量和丰富种群多样性,以多目标粒子群优化(multi-objective particle swarm optimization, MOPSO)算法和MOEA为代表.MOPSO优化框架的原理简单,以个体和群体的状态转移向目标收敛.LMOCSO (large-scale multi-objective competitive swarm optimization)算法关注群体位置转移,融合竞争机制设计两阶段更新策略,大规模优化场景中的搜索效率得到提高[19 ] .此外,MOEA贡献了通用性更强的框架,有效的进化算子和环境选择策略通常是提高收敛速度和求解质量的关键.其中,基于分解的MOEA将原始问题分解为多个单目标问题,如参考向量引导多目标优化进化算法 (reference vector evolutionary algorithm, RVEA)将参考点转换为向量来分解原问题,并进行环境选择,维持了种群的多样性以提高PF质量[20 ] ;文献[21 ]中对NSGA-II进行变革提出NSGA-III,采用快速非支配排序,有助于解决目标数量较多的优化问题.而基于指标的MOEA,核心思想是在环境选择中基于解质量度量性能指标.针对算法对PF面形状敏感的问题,AR-MOEA (adaptative reference point MOEA)设计新的指标自适应调整参考点分布,于不同场景下有效保持种群多样性[22 ] .此外,文献[23 ]中提出AnD算法,设计基于角度和偏移密度估计的选择策略,以全新视角进行环境选择,算法结构简单、参数少,新策略兼顾多样性与收敛性,大规模问题下表现较好. ...
... 针对大规模优化问题的多目标优化算法研究集中在连续空间[19 23 ] ,改进上述算法应用至路径规划,以应对WGMOPP-LN问题. ...
... LMOCSO算法[19 ] 涉及粒子位置与速度的状态更新,需要离散的编码方案且个体编码长度需要一致.但路径规划中个体包含节点数目并不总是一致,因此考虑到路径结果的完备性,统一的编码长度应为全部节点数目,不足编码长度时需要对中间节点进行重复扩维,如图2 所示.假设一张图具有10个节点,则编码长度为10,两条可行路径为0→1→3→5→9和0→1→7→3→2→9,节点数均小于10,需要进行循环补充,即逐次在各节点之间插入与前一个节点相同的值直至达到编码长度.初始个体生成采用随机初始化,每个个体由起点随机搜寻邻居节点直至到达终点,个体适应度计算通过加权图边集累加权重[13 ] . ...
... 基于上述场景,设置起终点分别为第一个与最后一个节点,对比精确搜索算法NAMOA* [8 ] 、传统优化算法(NSGA-II[14 ] 和MOEA/D[15 ] )、扩展优化算法(NSGA-III[21 ] 、AR-MOEA[22 ] 、LMOCSO[19 ] )以及AD-MOEA的性能.表2 与表3 分别为运行10次的平均求解数目和平均时间,5 min未求解出结果则为超时(timeout). ...
A reference vector guided evolutionary algorithm for many-objective optimization
2
2016
... 目前,多目标优化算法的研究趋向于关注大规模优化问题,旨在加快求解速度、提升PF质量和丰富种群多样性,以多目标粒子群优化(multi-objective particle swarm optimization, MOPSO)算法和MOEA为代表.MOPSO优化框架的原理简单,以个体和群体的状态转移向目标收敛.LMOCSO (large-scale multi-objective competitive swarm optimization)算法关注群体位置转移,融合竞争机制设计两阶段更新策略,大规模优化场景中的搜索效率得到提高[19 ] .此外,MOEA贡献了通用性更强的框架,有效的进化算子和环境选择策略通常是提高收敛速度和求解质量的关键.其中,基于分解的MOEA将原始问题分解为多个单目标问题,如参考向量引导多目标优化进化算法 (reference vector evolutionary algorithm, RVEA)将参考点转换为向量来分解原问题,并进行环境选择,维持了种群的多样性以提高PF质量[20 ] ;文献[21 ]中对NSGA-II进行变革提出NSGA-III,采用快速非支配排序,有助于解决目标数量较多的优化问题.而基于指标的MOEA,核心思想是在环境选择中基于解质量度量性能指标.针对算法对PF面形状敏感的问题,AR-MOEA (adaptative reference point MOEA)设计新的指标自适应调整参考点分布,于不同场景下有效保持种群多样性[22 ] .此外,文献[23 ]中提出AnD算法,设计基于角度和偏移密度估计的选择策略,以全新视角进行环境选择,算法结构简单、参数少,新策略兼顾多样性与收敛性,大规模问题下表现较好. ...
... 由于可行路径的节点数目通常远小于节点总数,所以上述编码方式会造成编码重复和冗余.而多目标进化算法适合采用变长编码方案,每个个体代表一条可行路径,具有更好的通用性.基于成熟框架和变长编码方法[13 ] ,RVEA[20 ] 、NSGA-III[21 ] 以及AD-MOEA[22 ] 可扩展应用至路径规划场景.面对WGMOPP-LN问题时,上述算法能够有效节约时间成本,但PF质量仍显著不足,求解数量少,与精确PF面的近似程度低. ...
An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints
4
2014
... 目前,多目标优化算法的研究趋向于关注大规模优化问题,旨在加快求解速度、提升PF质量和丰富种群多样性,以多目标粒子群优化(multi-objective particle swarm optimization, MOPSO)算法和MOEA为代表.MOPSO优化框架的原理简单,以个体和群体的状态转移向目标收敛.LMOCSO (large-scale multi-objective competitive swarm optimization)算法关注群体位置转移,融合竞争机制设计两阶段更新策略,大规模优化场景中的搜索效率得到提高[19 ] .此外,MOEA贡献了通用性更强的框架,有效的进化算子和环境选择策略通常是提高收敛速度和求解质量的关键.其中,基于分解的MOEA将原始问题分解为多个单目标问题,如参考向量引导多目标优化进化算法 (reference vector evolutionary algorithm, RVEA)将参考点转换为向量来分解原问题,并进行环境选择,维持了种群的多样性以提高PF质量[20 ] ;文献[21 ]中对NSGA-II进行变革提出NSGA-III,采用快速非支配排序,有助于解决目标数量较多的优化问题.而基于指标的MOEA,核心思想是在环境选择中基于解质量度量性能指标.针对算法对PF面形状敏感的问题,AR-MOEA (adaptative reference point MOEA)设计新的指标自适应调整参考点分布,于不同场景下有效保持种群多样性[22 ] .此外,文献[23 ]中提出AnD算法,设计基于角度和偏移密度估计的选择策略,以全新视角进行环境选择,算法结构简单、参数少,新策略兼顾多样性与收敛性,大规模问题下表现较好. ...
... 由于可行路径的节点数目通常远小于节点总数,所以上述编码方式会造成编码重复和冗余.而多目标进化算法适合采用变长编码方案,每个个体代表一条可行路径,具有更好的通用性.基于成熟框架和变长编码方法[13 ] ,RVEA[20 ] 、NSGA-III[21 ] 以及AD-MOEA[22 ] 可扩展应用至路径规划场景.面对WGMOPP-LN问题时,上述算法能够有效节约时间成本,但PF质量仍显著不足,求解数量少,与精确PF面的近似程度低. ...
... 采用NSGA-III的快速非支配排序[21 ] 对当前种群进行帕累托次序标号,从低到高将当前种群进行划分,高次序集合任意个体总会被低次序集合个体支配,相同次序内个体互不支配. ...
... 基于上述场景,设置起终点分别为第一个与最后一个节点,对比精确搜索算法NAMOA* [8 ] 、传统优化算法(NSGA-II[14 ] 和MOEA/D[15 ] )、扩展优化算法(NSGA-III[21 ] 、AR-MOEA[22 ] 、LMOCSO[19 ] )以及AD-MOEA的性能.表2 与表3 分别为运行10次的平均求解数目和平均时间,5 min未求解出结果则为超时(timeout). ...
An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility
3
2018
... 目前,多目标优化算法的研究趋向于关注大规模优化问题,旨在加快求解速度、提升PF质量和丰富种群多样性,以多目标粒子群优化(multi-objective particle swarm optimization, MOPSO)算法和MOEA为代表.MOPSO优化框架的原理简单,以个体和群体的状态转移向目标收敛.LMOCSO (large-scale multi-objective competitive swarm optimization)算法关注群体位置转移,融合竞争机制设计两阶段更新策略,大规模优化场景中的搜索效率得到提高[19 ] .此外,MOEA贡献了通用性更强的框架,有效的进化算子和环境选择策略通常是提高收敛速度和求解质量的关键.其中,基于分解的MOEA将原始问题分解为多个单目标问题,如参考向量引导多目标优化进化算法 (reference vector evolutionary algorithm, RVEA)将参考点转换为向量来分解原问题,并进行环境选择,维持了种群的多样性以提高PF质量[20 ] ;文献[21 ]中对NSGA-II进行变革提出NSGA-III,采用快速非支配排序,有助于解决目标数量较多的优化问题.而基于指标的MOEA,核心思想是在环境选择中基于解质量度量性能指标.针对算法对PF面形状敏感的问题,AR-MOEA (adaptative reference point MOEA)设计新的指标自适应调整参考点分布,于不同场景下有效保持种群多样性[22 ] .此外,文献[23 ]中提出AnD算法,设计基于角度和偏移密度估计的选择策略,以全新视角进行环境选择,算法结构简单、参数少,新策略兼顾多样性与收敛性,大规模问题下表现较好. ...
... 由于可行路径的节点数目通常远小于节点总数,所以上述编码方式会造成编码重复和冗余.而多目标进化算法适合采用变长编码方案,每个个体代表一条可行路径,具有更好的通用性.基于成熟框架和变长编码方法[13 ] ,RVEA[20 ] 、NSGA-III[21 ] 以及AD-MOEA[22 ] 可扩展应用至路径规划场景.面对WGMOPP-LN问题时,上述算法能够有效节约时间成本,但PF质量仍显著不足,求解数量少,与精确PF面的近似程度低. ...
... 基于上述场景,设置起终点分别为第一个与最后一个节点,对比精确搜索算法NAMOA* [8 ] 、传统优化算法(NSGA-II[14 ] 和MOEA/D[15 ] )、扩展优化算法(NSGA-III[21 ] 、AR-MOEA[22 ] 、LMOCSO[19 ] )以及AD-MOEA的性能.表2 与表3 分别为运行10次的平均求解数目和平均时间,5 min未求解出结果则为超时(timeout). ...
AnD: A many-objective evolutionary algorithm with angle-based selection and shift-based density estimation
5
2020
... 目前,多目标优化算法的研究趋向于关注大规模优化问题,旨在加快求解速度、提升PF质量和丰富种群多样性,以多目标粒子群优化(multi-objective particle swarm optimization, MOPSO)算法和MOEA为代表.MOPSO优化框架的原理简单,以个体和群体的状态转移向目标收敛.LMOCSO (large-scale multi-objective competitive swarm optimization)算法关注群体位置转移,融合竞争机制设计两阶段更新策略,大规模优化场景中的搜索效率得到提高[19 ] .此外,MOEA贡献了通用性更强的框架,有效的进化算子和环境选择策略通常是提高收敛速度和求解质量的关键.其中,基于分解的MOEA将原始问题分解为多个单目标问题,如参考向量引导多目标优化进化算法 (reference vector evolutionary algorithm, RVEA)将参考点转换为向量来分解原问题,并进行环境选择,维持了种群的多样性以提高PF质量[20 ] ;文献[21 ]中对NSGA-II进行变革提出NSGA-III,采用快速非支配排序,有助于解决目标数量较多的优化问题.而基于指标的MOEA,核心思想是在环境选择中基于解质量度量性能指标.针对算法对PF面形状敏感的问题,AR-MOEA (adaptative reference point MOEA)设计新的指标自适应调整参考点分布,于不同场景下有效保持种群多样性[22 ] .此外,文献[23 ]中提出AnD算法,设计基于角度和偏移密度估计的选择策略,以全新视角进行环境选择,算法结构简单、参数少,新策略兼顾多样性与收敛性,大规模问题下表现较好. ...
... 针对大规模优化问题的多目标优化算法研究集中在连续空间[19 23 ] ,改进上述算法应用至路径规划,以应对WGMOPP-LN问题. ...
... 其次,引入基于角度和偏移密度(shift-based density, SD)[23 ] 估计的策略来选择交叉个体.向量角度评判了两个个体的相似性,偏移密度用以衡量个体的收敛能力.交叉个体候选集总为非PF集合,以图5(b) 举例,A为非PF集合的个体,计算其与PF中各个体的向量夹角,选择最小值对应的前沿面个体B,即为与当前个体A最相似的个体.为保持种群多样性,交叉个体应从A和B中选择其一,选择标准为二者对于PF面个体的偏移密度,并取值小者,表明其更具备进一步收敛的能力,偏移密度策略具体如下所述. ...
... 区别于文献[23 ]中对所有个体计算角度与偏移密度,本文个体和环境选择策略仅在非PF集合中进行计算,减少了时间与空间成本,又考虑了种群多样性与收敛性. ...
... 针对P3场景,图8 展示了上述算法求解的PF分布图.选择超体积(hypervolume,HV)与逆世代距离(inverted generational distance, IGD)作为评价指标以评估各优化算法PF的质量[23 ] .超体积指PF与参考点r 之间组成的超体积,如图9 所示,用于评价目标空间被近似PF覆盖的程度,衡量近似PF的支配性,选择r =(250, 250). ...