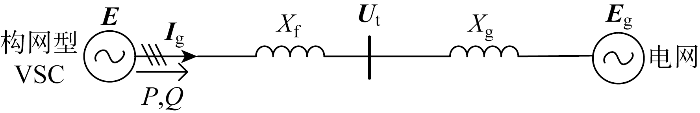构建以新能源为主体的新型电力系统既是我国电力系统转型升级的重要方向,也是实现“双碳”目标的关键途径[1 ] .在这一目标驱动下,风电、光伏等新能源发电迅速发展,并逐步取代同步机成为电力系统中的主要电源[2 ] .新能源成为主力电源后需要承担电网构建的责任与义务,这就要求新能源发电装备具有主动支撑电网的能力.而目前广泛应用的跟网型电压源型变换器(VSC)具有低惯量和弱阻尼的特点,给电力系统的安全稳定运行带来巨大挑战.因此,构网型控制技术成为近年研究热点.
不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注.
对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺.
关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性.
关于电压电流双环控制和直接电压控制VSC的对比研究同样集中在小扰动方面,如文献[23 ]中指出,相比电压电流双环控制结构,直接电压控制VSC提供更大耦合电抗,有利于提高VSC在强电网下的动态稳定性,但两者的暂态特性差异尚无对比研究.构网型VSC为系统提供主动支撑能力主要体现在类似同步机的惯量、阻尼特性,因此本文从等效惯量、等效阻尼角度对比两种控制方式VSC的暂态特性差异.
综上,现有研究针对两种控制结构的VSC在建模和大、小扰动稳定性分析方面做了大量工作,但对两者因控制结构不同产生的暂态特性的差异认识不清,对暂态特性差异的机理阐述不明.此外,关于暂态稳定问题的研究多依赖数值计算,在解析表达方面探索不足.
为了认识电压电流双环控制和直接电压控制构网型VSC暂态特性的差异,基于“功率激励-内电势响应”关系对两者进行暂态建模,从机电尺度等效惯量和等效阻尼角度对比两种控制的暂态特性.首先,简单介绍电压电流双环控制和直接电压控制构网型VSC结构;其次,建立两种控制方式VSC“功率激励-内电势响应”关系暂态模型,在此基础上对比内电势形成机制的异同;最后,简化得到两种控制机电尺度并网系统模型,基于此推导VSC等效惯量和等效阻尼的解析表达,并进行暂态特性对比分析和电磁暂态仿真验证.本文创新点在于:①基于“功率激励-内电势响应”统一视角对比两种构网型VSC内电势形成机制、等效惯量和阻尼的差异,弥补了现有研究对两者暂态特性对比不足的问题;②得到两种构网型VSC等效惯量和阻尼的解析表达,可为定量分析网络参数、功率水平等对系统暂态稳定的影响提供新思路.
1 构网型VSC控制结构
1.1 电压电流双环控制结构
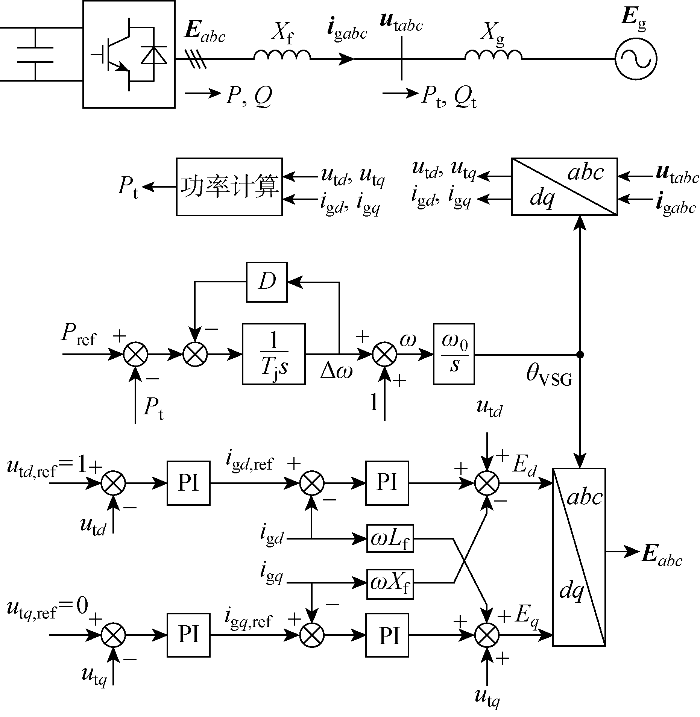
电压电流双环控制构网型VSC结构如图1 所示,控制结构主要包括虚拟同步控制、端电压控制、电流控制.VSG环节模拟同步机转子摇摆方程,其中T j 和D 分别表示惯量系数和阻尼系数. 电压外环级联电流内环生成变换器输出电压dq 轴分量Ed 、Eq . 图中:Eabc 、u t abc E g 、i g abc abc 静止坐标系下的变换器输出电压、端电压、电网电压、电网电流;X f 为滤波电抗;X g 为等效电网电抗;L f 为滤波电感;u t d u t q dq 分量;i g d i g q dq 分量;P 、Q 为变换器输出电压处的有功功率、无功功率;P t 、Q t 为端电压处的有功功率、无功功率;下标ref表示相应量的指令值;Δω 、ω 、θ VSG 分别为VSG输出角频率的偏差、输出角频率、输出相角;ω 0 为系统角频率基准值;1/s 为频域的积分运算;PI为比例积分器.
图1
图1
电压电流双环控制构网型VSC结构
Fig.1
Structure of VSC with voltage and current dual loop control
为维持VSC的稳定运行,不同控制环节的带宽按照一定原则设计,因而呈现不同时间尺度的控制动态[24 ] .VSG模拟同步发电机的运行特性,其控制动态呈现秒级机电时间尺度特征;电压环与电流环控制动态分别呈现百毫秒级的直流电压时间尺度特征和十毫秒级的交流电流时间尺度特征.因此,构网型VSC电压电流双环控制结构包含机电、直流电压、交流电流3个时间尺度的控制环路.
1.2 直接电压控制结构
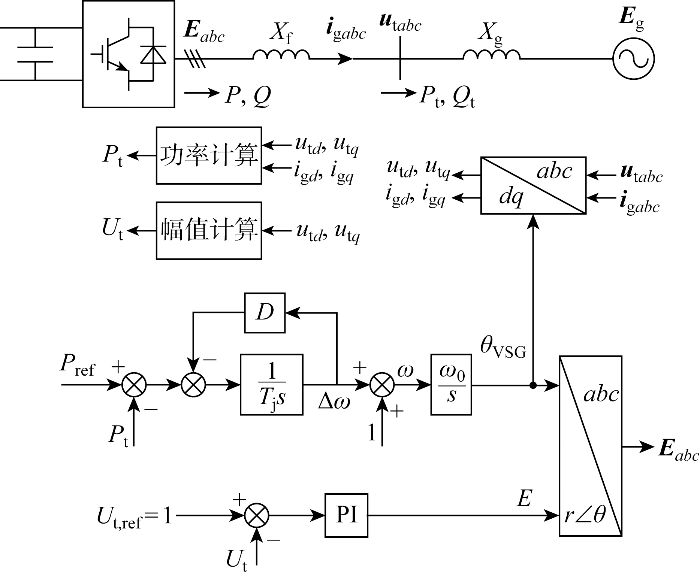
直接电压控制构网型VSC控制框图如图2 所示,主要包括虚拟同步控制、端电压控制,控制结构中无电流环.图中:r 、θ 为极坐标系下变量的幅值、相位.变换器输出电压幅值E 由控制端电压幅值U t 恒定的端电压控制直接生成,直接电压控制结构包含机电、直流电压两个时间尺度的控制环路.
图2
图2
直接电压控制构网型VSC结构
Fig.2
Structure of VSC with direct voltage control
电力系统暂态扰动根据是否引起电力电子装备硬件保护电路及暂态控制算法的切换分为浅度和深度扰动[24 ] .浅度扰动下两种构网型VSC保持常规控制结构运行;深度扰动下直接电压控制常采用模式切换方案切换至含电流环控制结构[21 -22 ] ,两者差异较小.因此,重点对比分析两种构网型VSC在浅度扰动下的差异.基于本文所研究的问题,作出如下假设[14 ] :I 假设有功功率指令值P ref 保持不变;II 忽略网侧滤波电感和网络电感的电流暂态以及系统中的电阻损耗;III 忽略直流电容电压的变化,认为直流电容电压恒定.
2 构网型VSC“激励-响应”关系暂态建模
根据戴维南等效定理,节点装备对外部网络均可等效成电压源(内电势E )串联阻抗(内电抗X )的形式.对于VSC,内电势定义为变换器输出电压矢量,内电抗为滤波电抗.对于新能源发电装备,有功和无功功率不平衡驱动装备中能量存储元件状态变化,相应控制器动作改变内电势幅值、角频率(以下简称频率),这反映了装备的暂态特性[24 ] .基于“有功和无功功率激励与内电势幅值和频率响应”关系(以下简称“激励-响应”关系)可对各装备特性进行物理化、统一化描述[14 ] ,文中内电势相位为内电势频率的积分.
应用“激励-响应”关系建模方法建立两种控制方式构网型VSC的暂态模型,对比分析两者内电势形成机制的差异,并对比电磁暂态仿真模型,验证了“激励-响应”关系模型的有效性.
2.1 电压电流双环控制暂态建模
由图1 可知,电压电流双环控制原始结构有多个输入信号,包括端电压处有功功率P t 、端电压u t dq i g dq .P 、无功功率Q 以及内电势幅值和相位表示.因为内电势与端电压之间仅存在滤波电抗,所以内电势处有功功率P 与端电压处有功功率P t 相等.
(1) 端电压u t d u t q
(1) P = E U t s i n ( θ V - θ t V ) / X f Q = E 2 / X f - E U t c o s ( θ V - θ t V ) / X f
式中:θ V 为VSG坐标系下内电势相位;θ t V
(2) U t = ( P X f ) 2 + ( E 2 - Q X f ) 2 / E θ t V = θ V - a r c t a n P X f E 2 - Q X f
(3) $ u_{\mathrm{t} d}=U_{\mathrm{t}} \cos \theta_{\mathrm{t}}^{\mathrm{V}}=f_{1}\left(P, Q, E, \theta^{\mathrm{V}}\right)$
(4) $ u_{\mathrm{t} q}=U_{\mathrm{t}} \sin \theta_{\mathrm{t}}^{\mathrm{V}}=f_{2}\left(P, Q, E, \theta^{\mathrm{V}}\right)$
(2) 电网电流i g d i g q . 根据电路关系,内电势处输出的有功、无功功率可由内电势幅值E 、电网电流幅值I g 及两者相位差表示为
(5) P = E I g c o s ( θ V - θ i V ) Q = E I g s i n ( θ V - θ i V )
(6) I g = P 2 + Q 2 / E θ i V = θ V - a r c t a n Q P
(7) $ i_{\mathrm{g} d}=I_{\mathrm{g}} \cos \theta_{\mathrm{i}}^{\mathrm{V}}=f_{3}\left(P, Q, E, \theta^{\mathrm{V}}\right)$
(8) $ i_{\mathrm{g} q}=I_{\mathrm{g}} \sin \theta_{\mathrm{i}}^{\mathrm{V}}=f_{4}\left(P, Q, E, \theta^{\mathrm{V}}\right)$
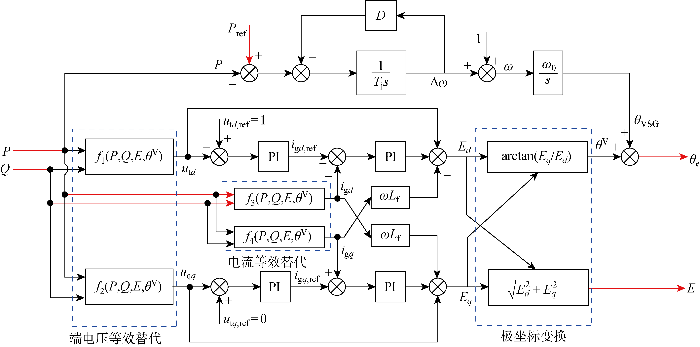
式(3)~(4)、(7)~(8)将端电压dq 轴分量、电网电流dq 轴分量统一为内电势处有功和无功功率、内电势幅值和相位.将以上各式代入电压电流双环控制原始框图,得到多时间尺度“激励-响应”关系模型,如图3 所示.图中:θ e 为静止坐标系下的内电势相位.
图3
图3
电压电流双环控制“激励-响应”模型
Fig.3
“Excitation-response” model of voltage and current dual loop control
2.2 直接电压控制暂态建模
对于图2 所示直接电压控制方式,除与内电势处有功功率P 和无功功率Q 直接相关的量外,原始结构中的输入量还包括端电压幅值U t .式(2)中U t 已表示为内电势处有功、无功功率和内电势幅值的函数,可进一步表示为
(9) $ \begin{aligned} U_{\mathrm{t}}= & \sqrt{\left(P X_{\mathrm{f}}\right)^{2}+\left(E^{2}-Q X_{\mathrm{f}}\right)^{2}} / E= \\ & g_{1}(P, Q, E) \end{aligned}$
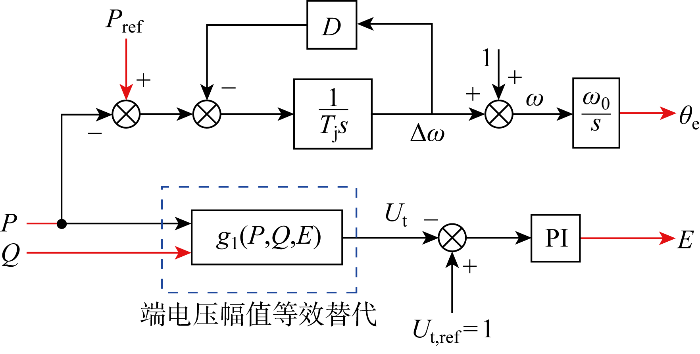
将式(9)代入图2 原始框图,得到直接电压控制多时间尺度“激励-响应”关系模型,如图4 所示.
图4
图4
直接电压控制激励-响应模型
Fig.4
“Excitation-response” model of direct voltage control
2.3 内电势形成机制对比
基于图3 和图4 所示的电压电流双环控制和直接电压控制“激励-响应”关系模型,从时间尺度特征、非线性特征、幅值和相位耦合特征对比电压电流双环控制VSC与直接电压控制VSC内电势形成机制的异同,如表1 所示.
2.4 模型验证
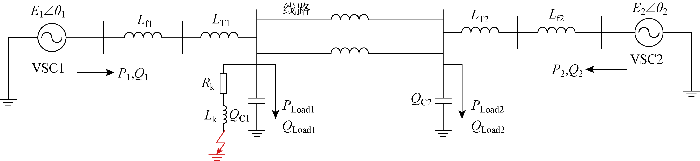
为验证以上“激励-响应”关系模型的有效性,分别建立采用两种控制方式的两VSC两区域系统电磁暂态仿真模型,系统结构如图5 所示.图中:E 1 、E 2 为VSC1、VSC2的内电势幅值;θ 1 、θ 2 为VSC1、VSC2的内电势相位;P 1 、P 2 为VSC1、VSC2的内电势处有功功率;Q 1 、Q 2 为VSC1、VSC2的内电势处无功功率.在线路三相接地故障扰动下对比电磁暂态模型和“激励-响应”关系模型的有功和无功功率以及内电势幅值和频率.在图中所示位置设置三相短路故障,230 kV/100 MV·A基准值下系统参数如表2 所示.
图5
图5
两构网型VSC两区域系统
Fig.5
Two grid-forming VSCs in a two-area system
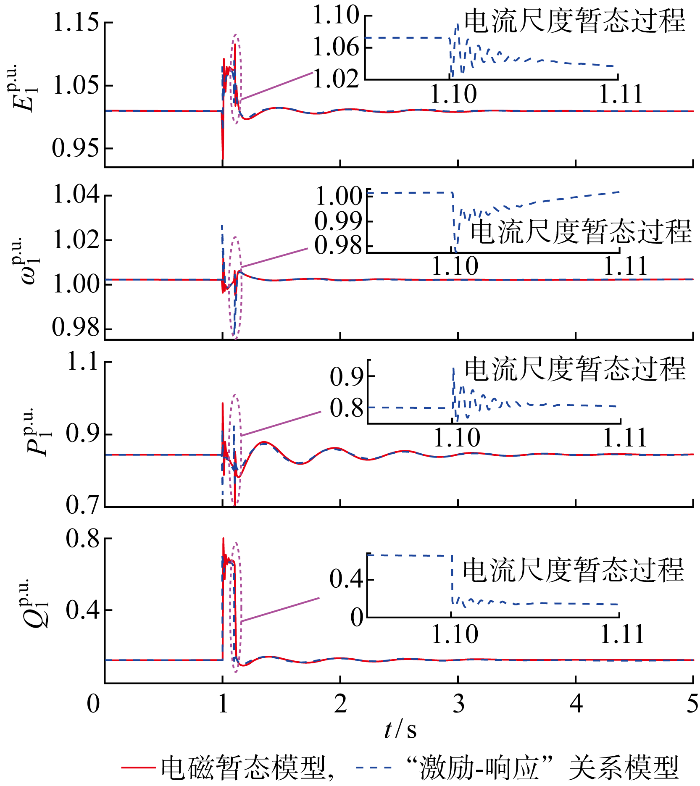
(1)电压电流双环控制模型验证.电压电流双环控制VSC控制参数如表3 所示,两机参数设置相同.1 s时设置故障,持续0.1 s后故障消失.以VSC1为例,电磁暂态模型和“激励-响应”关系模型的波形对比如图6 所示.图中:下标1表示VSC1的相应参数;记内电势频率为ω 1 .
图6
图6
电压电流双环控制模型验证
Fig.6
Model verification of voltage and current dual loop control
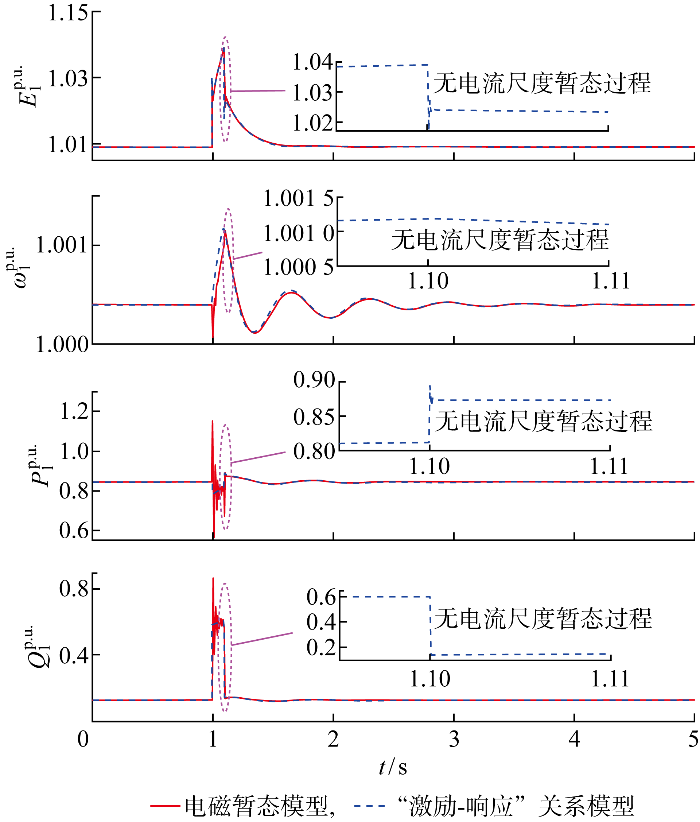
(2) 直接电压控制模型验证.直接电压控制VSC控制参数如表4 所示,两机参数设置相同.1 s时设置故障,持续0.1 s后故障消失.以VSC1为例,电磁暂态模型和激励响应模型的波形对比如图7 所示.
图7
图7
直接电压控制模型验证
Fig.7
Model verification of direct voltage control
由图6 和图7 可知,电压电流双环控制和直接电压控制“激励-响应”关系模型与电磁暂态模型的波形吻合很好.误差主要在于扰动施加的初始时段,这是由“激励-响应”关系模型不考虑网络中电感、电容的暂态过程导致.由图6 和图7 故障消失后“激励-响应”关系模型的波形放大图可知,由于电流环的存在,电压电流双环控制VSC内电势幅值和频率包含交流电流尺度暂态过程,而直接电压控制VSC内电势幅值仅呈现直流电压尺度暂态特征,内电势频率仅呈现机电尺度暂态特征.
3 不同控制方式机电尺度特性分析
电压电流双环控制VSC和直接电压控制VSC都通过VSG控制环节与电网实现同步,而VSG环节模拟同步机的转子摇摆,其控制动态呈现机电时间尺度特征.因此,本节重点关注机电时间尺度下两类构网型VSC的暂态特性并分析对比.在已建立的“激励-响应”关系模型基础上,忽略快尺度控制器的动态调节过程,简化得到机电尺度“激励-响应”关系模型,基于此解析得到两类控制方式VSC的等效惯量和等效阻尼,并分析对比和仿真验证.
3.1 电压电流双环控制VSC等效惯量和阻尼解析
构网型VSC并网系统如图8 所示,E 、U t 、E g 、I g 分别为内电势矢量、端电压矢量、电网电压矢量、电网电流矢量. 公共坐标系d轴与电网电压矢量E g 重合,下文中相位均为公共坐标系下的相位.
图8
图8
构网型VSC并网系统
Fig.8
Grid-forming VSC-connected power system
在研究机电时间尺度稳定问题时,通常认为直流电压尺度控制器和交流电流尺度控制器动作迅速,快尺度控制环节的动态调节过程可以忽略.对于电压电流双环控制方式,机电时间尺度下作出如下假设[14 ] :①忽略端电压控制器的动态调节过程,认为端电压理想跟踪其指令值,即u t d u t q
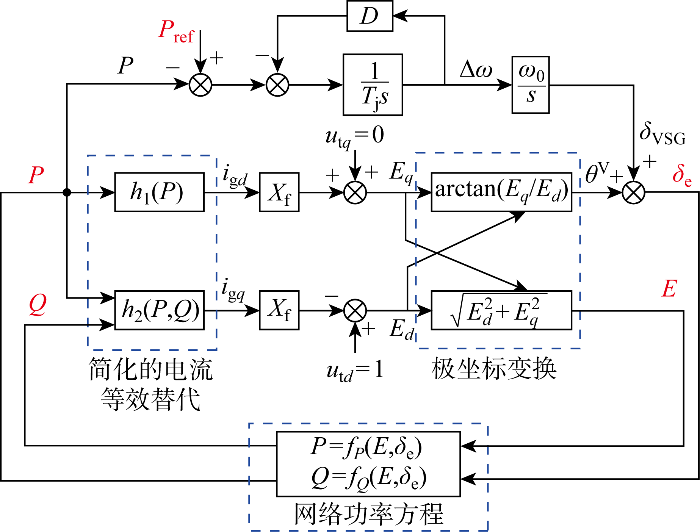
在上述假设条件下,基于图3 所示电压电流双环控制VSC“激励-响应”关系模型,得到并网系统机电尺度“激励-响应”关系模型,如图9 所示.图中:h 1 、h 2 分别为i g d i g q δ VSG 为VSG输出相位θ VSG 与公共坐标系d 轴相角差.
图9
图9
电压电流双环控制VSC并网系统机电尺度模型
Fig.9
Electromechanical scale model of VSC-connected system with voltage and current dual loop control
(10) P =fP (E ,δ e )=EE g sin δ e / (X f +X g )
(11) Q =fQ (E ,δ e )=(E 2 -EE g cos δ e )/ (X f +X g )
由图9 可知,机电尺度电压电流双环控制VSC虚拟同步环节二阶方程为
(12) $\left.\begin{array}{l} \Delta \dot{\omega}=\left(P_{\mathrm{ref}}-P-D \Delta \omega\right) / T_{\mathrm{j}} \\ \dot{\delta}_{\mathrm{VSG}}=\Delta \omega \omega_{0} \end{array}\right\}$
(13) $T_{\mathrm{j}} \ddot{\delta}_{\mathrm{VSG}}+D \dot{\delta} \dot{\mathrm{VSG}}^{+}+\omega_{0} P=\omega_{0} P_{\mathrm{ref}}$
式(13)描述了不平衡功率(P ref -P )驱动下VSG环节输出相位δ VSG 的运动.而设备与网络的接口为内电势,为了从“功率-内电势”统一视角刻画VSC的暂态特性,需要将式(13)中的δ VSG 替换为内电势相位δ e .
(14) Ut = X g X f + X g X f X f + X g g
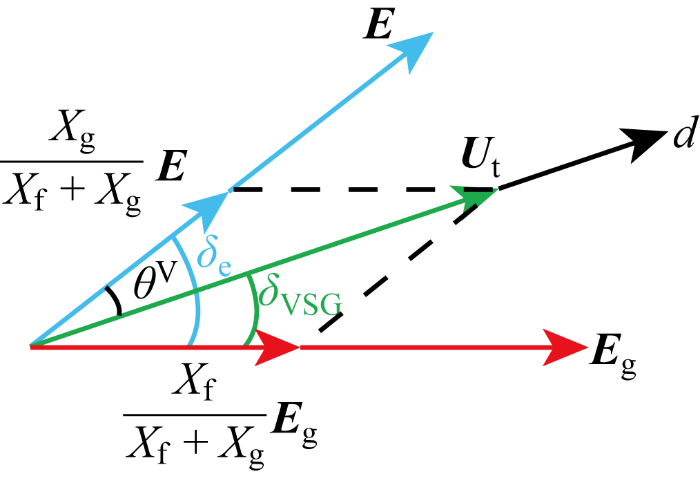
由于机电尺度下作假设①,所以端电压矢量U t 始终位于VSG坐标系d 轴上.电压矢量关系如图10 所示.根据电压三角形得到内电势相位δ e 与δ VSG 的关系为
(15) δVSG =δe -arcsin X f X g s i n δ e X f + X g
图10
图10
系统电压矢量关系
Fig.10
Relationship of system voltage vectors
(16) $\begin{aligned} E= & \sqrt{\left(\frac{X_{\mathrm{f}}}{X_{\mathrm{g}}}+1\right)^{2}-\left(\frac{X_{\mathrm{f}}}{X_{\mathrm{g}}} E_{\mathrm{g}} \sin \delta_{\mathrm{e}}\right)^{2}}- \\ & \frac{X_{\mathrm{f}}}{X_{\mathrm{g}}} E_{\mathrm{g}} \cos \delta_{\mathrm{e}} \end{aligned}$
联立式(10)、(13)、(15)、(16),得到电压电流双环控制VSC机电尺度内电势相位运动方程为
(17) $T_{\mathrm{j}}^{\prime} \ddot{\delta}_{\mathrm{e}}+D^{\prime} \dot{\delta_{\mathrm{e}}}+\omega_{0} P=\omega_{0} P_{\mathrm{ref}}$
(18) $\begin{array}{l} P= \\ \frac{\left(\sqrt{\left(X_{\mathrm{f}}+X_{\mathrm{g}}\right)^{2}-\left(X_{\mathrm{f}} E_{\mathrm{g}} \sin \delta_{\mathrm{e}}\right)^{2}}-X_{\mathrm{f}} E_{\mathrm{g}} \cos \delta_{\mathrm{e}}\right) E_{\mathrm{g}}}{X_{\mathrm{g}}\left(X_{\mathrm{f}}+X_{\mathrm{g}}\right)} \times \\ \sin \delta_{\mathrm{e}} \end{array}$
(19) T' j =T j f t (δ e )
(20) D'=Dft (δe )+Tj d f t ( δ e ) d t
(21) ft (δe )=1- c o s δ e X f + X g X f E g 2 - s i n 2 δ e
式(15)~(21)的详细推导过程见附录B.式(17)所示二阶方程刻画了电压电流双环控制VSC机电尺度下内电势相位的动态.与式(13)对照,T 'j 和D '分别定义为电压电流双环控制VSC的等效惯量和等效阻尼.
3.2 直接电压控制VSC等效惯量和阻尼解析
直接电压控制VSC机电尺度下忽略端电压控制器的动态调节过程,认为端电压幅值理想跟踪其指令值,即U t =1.式(9)中令U t =1,内电势幅值E 表示为P 、Q 的函数,即
(22) $\begin{aligned} E= & \frac{\sqrt{2}}{2} \sqrt{1+2 Q X_{\mathrm{f}}+\sqrt{1+4 Q X_{\mathrm{f}}-4 P^{2} X_{\mathrm{f}}}}= \\ & g_{\mathrm{E}}(P, Q) \end{aligned}$
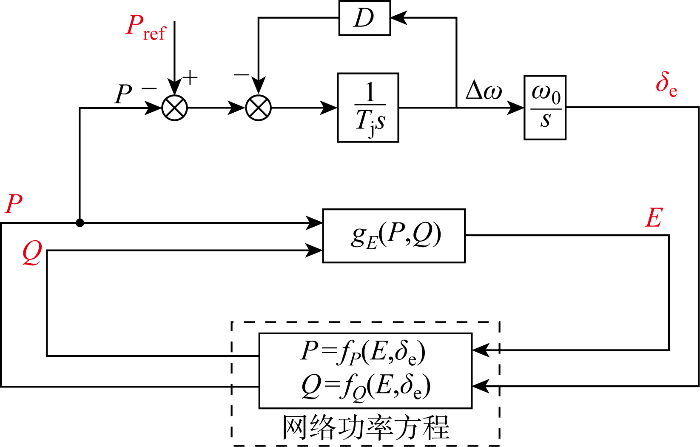
基于图4 直接电压控制VSC“激励-响应”关系模型和机电尺度简化条件,直接电压控制VSC并网系统机电尺度“激励-响应”关系模型如图11 所示.图中网络功率方程同式(10)和式(11).
图11
图11
直接电压控制VSC并网系统机电尺度模型
Fig.11
Electromechanical scale model of VSC-connected system with direct voltage control
由图11 可知,直接电压控制VSC内电势相位等于VSG输出相位.因此,直接电压控制VSC机电尺度内电势相位运动方程为
(23) $T_{\mathrm{j}} \ddot{\delta}_{\mathrm{e}}+D \dot{\delta}_{\mathrm{e}}+\omega_{0} P=\omega_{0} P_{\mathrm{ref}}$
式(16)所示的机电尺度内电势幅值和相位关系对两类控制方式均成立.因此,式(23)中有功功率P 的表达式同式(18).
式(23)所示二阶方程刻画了直接电压控制VSC内电势相位的机电尺度动态.T j 和D 分别定义为直接电压控制VSC的等效惯量和等效阻尼,数值上等于VSG控制环节设置的惯量系数和阻尼系数.
3.3 机电尺度暂态特性对比分析
电压电流双环控制和直接电压控制VSC机电尺度内电势相位运动方程分别如式(17)和式(23)所示.通过两式对比,两种控制方式VSC机电尺度的暂态特性由等效惯量和等效阻尼集中反映.其中,电压电流双环控制VSC等效惯量和等效阻尼除了与VSG控制参数相关外,还随系统运行点δ e 和网络参数X g 的变化而变化.下文着重分析电压电流双环控制VSC等效惯量和等效阻尼的特性.
电压电流双环控制VSC机电尺度等效惯量和等效阻尼分别如式(19)和式(20)所示.由于机电尺度动态过程内电势频率的变化量很小,等效阻尼中第二项的数量级为1,相比数量级为10倍的第一项Df t (δ e )可近似忽略,所以等效阻尼近似为
(24) D' ≈Df t (δ e )
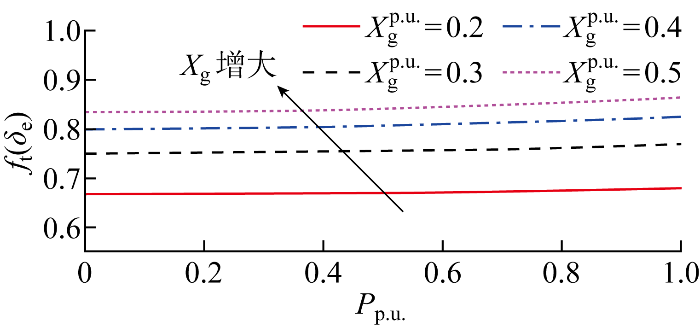
由式(19)和式(24)可知,当VSG控制参数确定时,等效惯量和等效阻尼由f t (δ e )决定.f t (δ e )与网络参数X g 和功率水平P 相关,P 影响δ e .由有功功率式(18)和式(21)可知,f t (δ e )随功率水平提高而增大,随网络电抗增大而增大,详细证明见附录C.不同X g 下f t (δ e )随功率水平的变化如图12 所示.
图12
图12
不同X g 下f t (δ e )随功率变化曲线
Fig.12
f t (δ e ) versus power at different X g values
直接电压控制和电压电流双环控制VSC机电尺度等效惯量和等效阻尼对比如下.
(1) 等效惯量和阻尼大小:直接电压控制VSC等效惯量和等效阻尼分别等于VSG环节设置的惯量系数和阻尼系数;由于在正常参数和功率范围内f t (δ e )<1,所以电压电流双环控制VSC的等效惯量和等效阻尼小于直接电压控制.
(2) 等效惯量和阻尼时变性:直接电压控制VSC等效惯量和等效阻尼为常数,不随系统运行点和网络参数的变化而变化;电压电流双环控制VSC等效惯量和等效阻尼在暂态过程中随输出有功功率的增加略有增大,随网络电抗的增大而显著增大.
3.4 机电尺度暂态特性仿真验证
3.4.1 单构网型VSC无穷大系统仿真验证
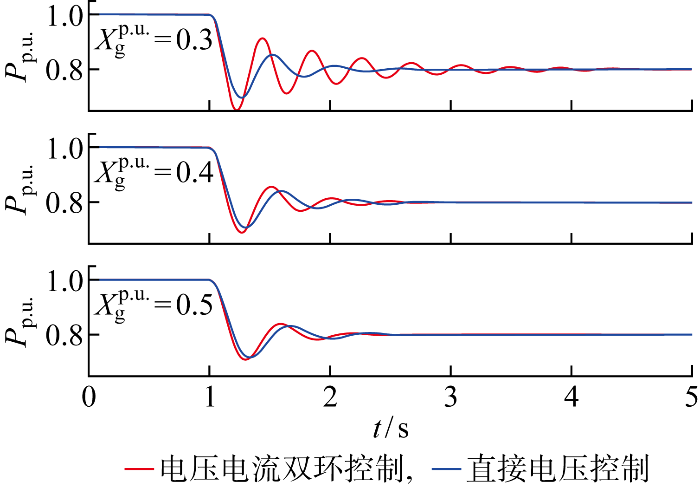
为验证两种控制VSC机电尺度等效惯量和等效阻尼,建立单构网型VSC无穷大系统电磁暂态模型.VSG阻尼系数D 设置为30,惯量系数T j 设置为5,网络电抗X g p . u . t =1 s 时功率指令标幺值由1变为0.8.不同X g 下电压电流双环控制和直接电压控制VSC内电势处有功功率如图13 所示.
图13
图13
不同X g 下内电势处有功功率
Fig.13
Active power at internal voltage at different X g values
由图13 扰动后有功功率的波形定性分析两种控制VSC的机电尺度特性.相同X g 下受到相同扰动后,电压电流双环控制VSC有功功率的振荡幅度和到达稳态所需时间大于直接电压控制,电压电流双环控制VSC等效阻尼更小.随着X g 增大,电压电流双环控制VSC等效阻尼与直接电压控制的差异减小.
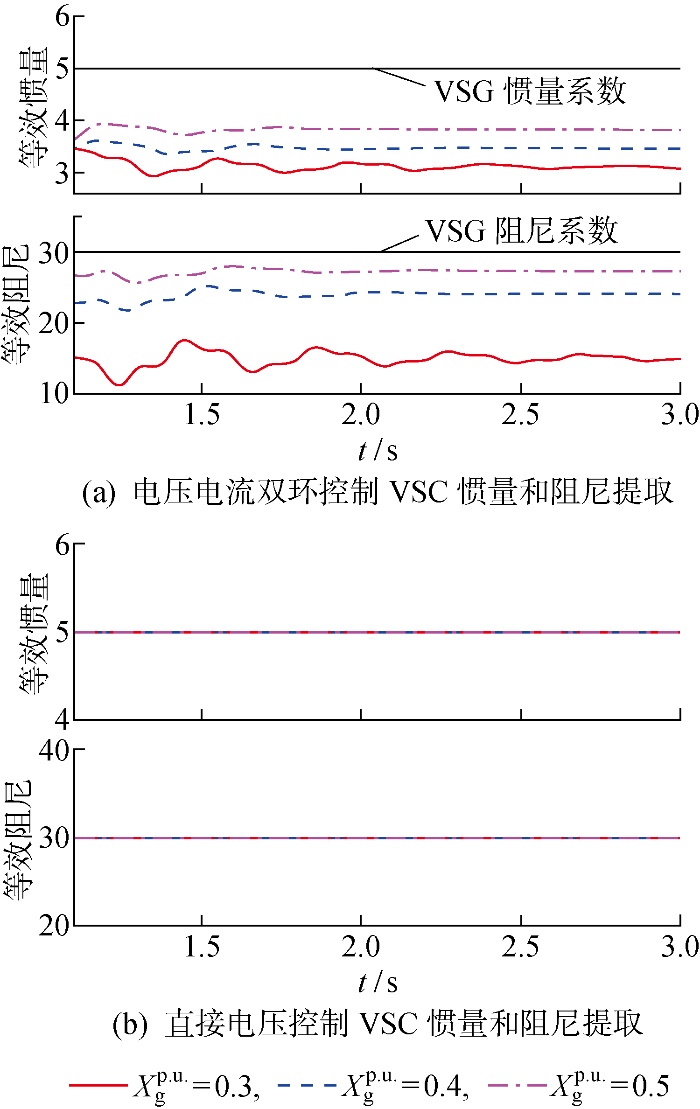
为进一步定量验证两种控制VSC机电尺度等效惯量和等效阻尼,基于电磁暂态仿真得到的P ref 、P 、$\dot{\delta}_{\mathrm{e}}$ $\ddot{\delta}_{\mathrm{e}}$ 图14 所示.由图14(a) 可知,在扰动发生0.1 s后的机电尺度暂态过程中,电压电流双环控制VSC的等效惯量和等效阻尼具有时变特征,随着网络电抗X g 的增大而增大,且均小于VSG设定的惯量系数和阻尼系数.而直接电压控制VSC的等效惯量和等效阻尼为常数,与VSG设定的惯量系数和阻尼系数相等,不随X g 的变化而变化.
图14
图14
等效惯量和阻尼提取
Fig.14
Extraction of equivalent inertia and damping
3.4.2 两构网型VSC两区域系统仿真验证
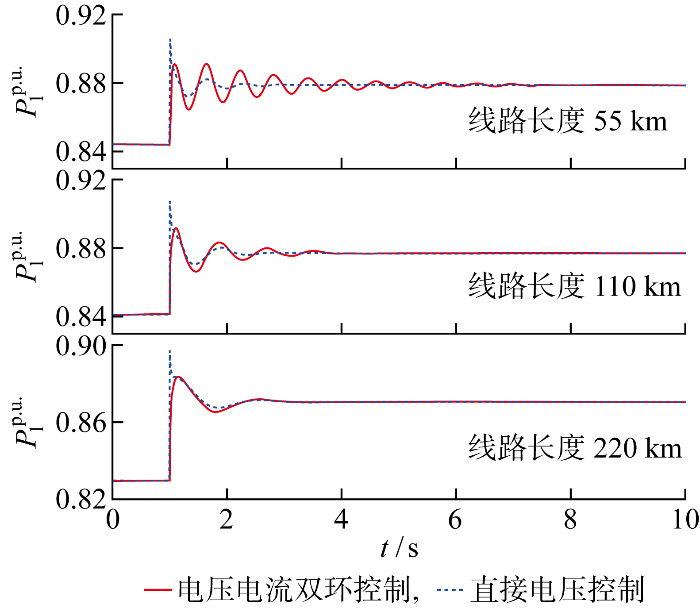
两机系统1 s时P Load1 增加100 MW,在线路长度分别为55、110、220 km下对比两种控制结构VSC1内电势处的有功功率,如图15 所示.相同线路长度下,电压电流双环控制VSC的阻尼小于直接电压控制,随着线路电抗的增大,两者差距减小.
图15
图15
两VSC系统不同线路长度下的内电势有功功率
Fig.15
Active power at internal voltage of two VSC systems at different line lengths
4 结论
以电压电流双环控制和直接电压控制VSC为研究对象,基于“功率激励-内电势响应”关系建立暂态模型,分析对比两种控制内电势形成机制的差异,得到机电尺度等效惯量和等效阻尼的解析表达,并对比分析其暂态特性.主要结论如下:
(1) 以有功功率和无功功率为输入,以内电势幅值和相位为输出,建立电压电流双环控制和直接电压控制VSC的暂态模型,该模型很好地描述了大扰动下VSC的暂态响应特性.
(2) 电压电流双环控制由于电流环的存在,内电势幅值和相位包含交流电流尺度暂态过程;直接电压控制内电势幅值和相位无交流电流尺度暂态过程.电压电流双环控制“激励-响应”关系模型中由于直角坐标-极坐标变换的存在,内电势相位与有功、无功功率输入呈现非线性关系,同时内电势幅值、相位存在耦合关系;而直接电压控制内电势相位由有功功率线性驱动,且与内电势幅值解耦.
(3) 直接电压控制VSC机电尺度等效惯量和阻尼为常数,等于VSG设置的惯量和阻尼系数;电压电流双环控制VSC机电尺度等效惯量和阻尼在暂态过程中随系统运行点而时变,随网络电抗的增大而显著增大,但始终小于直接电压控制.
附录见本刊网络版(xuebao.sjtu.edu.cn/article/2025/1006-2467/1006-2467-59-7-971.shtml)
参考文献
View Option
[1]
黄强 , 郭怿 , 江建华 , 等 . “双碳”目标下中国清洁电力发展路径
[J]. 上海交通大学学报 2021 , 55 (12 ): 1499 -1509 .
DOI:10.16183/j.cnki.jsjtu.2021.272
[本文引用: 1]
目前,第三次能源革命已经开始,为了减少碳排放,发达国家先后制定了清洁能源发展战略,并公布了放弃火电、核电的时间表.与此同时,中国也向世界作出承诺:2030年前碳排放达峰,2060年实现碳中和.因此,在“双碳”目标下,研究清洁电力发展路径具有重要意义.分析了中国水、风、光等清洁能源储量及其特征,预测了中长期电力需求,依据电力电量平衡原理,估算了2030和2050规划水平年电力系统结构组成,并分析了未来CO<sub>2</sub>排放趋势,提出了未来中国清洁电力的发展对策与建议.结果表明:预计2027年中国电力系统将实现“碳达峰”;2030年中国清洁电力发电量将超过总发电量的50%;2050年火电、核电将被水、风、光等清洁电力全部取代,电力行业将实现CO<sub>2</sub>的“零排放”,基本全面实现电力系统的绿色转型,以响应国家的“双碳”目标.
HUANG Qiang GUO Yi JIANG Jianhua et al Development pathway of China’s clean electricity under carbon peaking and carbon neutrality goals
[J]. Journal of Shanghai Jiao Tong University 2021 , 55 (12 ): 1499 -1509 .
[本文引用: 1]
[2]
张智刚 , 康重庆 . 碳中和目标下构建新型电力系统的挑战与展望
[J]. 中国电机工程学报 2022 , 42 (8 ): 2806 -2819 .
[本文引用: 1]
ZHANG Zhigang KANG Chongqing Challenges and prospects for constructing the new-type power system towards a carbon neutrality future
[J]. Proceedings of the CSEE 2022 , 42 (8 ): 2806 -2818 .
[本文引用: 1]
[3]
ROSSO R WANG X F LISERRE M et al Grid-forming converters: Control approaches, grid-synchronization, and future trends—A review
[J]. IEEE Open Journal of Industry Applications 2021 , 2 : 93 -109 .
[本文引用: 1]
[4]
ROSCOE A KNUEPPEL T DA SILVA R et al Response of a grid forming wind farm to system events, and the impact of external and internal damping
[J]. IET Renewable Power Generation 2020 , 14 (19 ): 3908 -3917 .
[本文引用: 1]
[5]
褚文从 , 刘静利 , 李永刚 , 等 . 考虑源端特性的虚拟同步直驱风机小信号建模与稳定性分析
[J]. 电力自动化设备 2022 , 42 (8 ): 3 -10 .
[本文引用: 2]
CHU Wencong LIU Jingli LI Yonggang et al Small-signal modeling and stability analysis of virtual synchronous PMSG considering source characteristics
[J]. Electric Power Automation Equipment 2022 , 42 (8 ): 3 -10 .
[本文引用: 2]
[6]
韩刚 , 蔡旭 . 虚拟同步发电机输出阻抗建模与弱电网适应性研究
[J]. 电力自动化设备 2017 , 37 (12 ): 116 -122 .
[本文引用: 1]
HAN Gang CAI Xu Output impedance modeling of virtual synchronous generator and its adaptability study in a weak grid
[J]. Electric Power Automation Equipment 2017 , 37 (12 ): 116 -122 .
[本文引用: 1]
[7]
马燕峰 , 郑力文 , 霍亚欣 , 等 . 虚拟同步发电机接入电力系统的阻尼转矩分析
[J]. 电力自动化设备 2020 , 40 (4 ): 166 -171 .
[本文引用: 2]
MA Yanfeng ZHENG Liwen HUO Yaxin et al Damping torque analysis of virtual synchronous generator connected to power system
[J]. Electric Power Automation Equipment 2020 , 40 (4 ): 166 -171 .
[本文引用: 2]
[8]
ALIPOOR J MIURA Y ISE T Power system stabilization using virtual synchronous generator with alternating moment of inertia
[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics 2015 , 3 (2 ): 451 -458 .
[本文引用: 1]
[9]
尚磊 , 胡家兵 , 袁小明 , 等 . 电网对称故障下虚拟同步发电机建模与改进控制
[J]. 中国电机工程学报 2017 , 37 (2 ): 403 -412 .
[本文引用: 3]
SHANG Lei HU Jiabing YUAN Xiaoming et al Modeling and improved control of virtual synchronous generators under symmetrical faults of grid
[J]. Proceedings of the CSEE 2017 , 37 (2 ): 403 -412 .
[本文引用: 3]
[10]
朱蜀 , 刘开培 , 秦亮 . 虚拟同步发电机的暂态稳定性分析
[J]. 电力系统自动化 2018 , 42 (9 ): 51 -58 .
[本文引用: 1]
ZHU Shu LIU Kaipei QIN Liang Transient stability analysis of virtual synchronous generator
[J]. Automation of Electric Power Systems 2018 , 42 (9 ): 51 -58 .
[本文引用: 1]
[11]
FU X K SUN J J HUANG M et al Large-signal stability of grid-forming and grid-following controls in voltage source converter: A comparative study
[J]. IEEE Transactions on Power Electronics 2021 , 36 (7 ): 7832 -7840 .
[本文引用: 1]
[12]
PAN D H WANG X F LIU F C et al Transient stability of voltage-source converters with grid-forming control: A design-oriented study
[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics 2020 , 8 (2 ): 1019 -1033 .
[本文引用: 2]
[13]
袁小明 , 程时杰 , 胡家兵 . 电力电子化电力系统多尺度电压功角动态稳定问题
[J]. 中国电机工程学报 2016 , 36 (19 ): 5145 -5154 .
[本文引用: 1]
YUAN Xiaoming CHENG Shijie HU Jiabing Multi-time scale voltage and power angle dynamics in power electronics dominated large power systems
[J]. Proceedings of the CSEE 2016 , 36 (19 ): 5145 -5154 .
[本文引用: 1]
[14]
唐王倩云 . 双馈型风机转子转速控制尺度暂态建模及其并网系统暂态稳定性分析 [D]. 武汉 : 华中科技大学 , 2020 .
[本文引用: 4]
TANG Wangqianyun Transient modeling of doubly fed induction generator-based wind turbine and transient stability analysis of its grid-connected power systems in rotor speed control timescale [D]. Wuhan : Huazhong University of Science and Technology , 2020 .
[本文引用: 4]
[15]
张巍 , 黄文 , 帅智康 , 等 . 虚拟调速器对VSG暂态功角稳定影响机理分析
[J]. 电力自动化设备 2022 , 42 (8 ): 55 -62 .
[本文引用: 1]
ZHANG Wei HUANG Wen SHUAI Zhikang et al Impact mechanism analysis of virtual governor on transient power angle stability of VSG
[J]. Electric Power Automation Equipment 2022 , 42 (8 ): 55 -62 .
[本文引用: 1]
[16]
XIANG Z M NI Q L LI Z H et al Transient stability analysis of grid-forming converter based on virtual synchronous generator
[C]// 2022 Asian Conference on Frontiers of Power and Energy. Chengdu China : IEEE , 2022 : 118 -124 .
[本文引用: 2]
[17]
王继磊 , 张兴 , 朱乔华 , 等 . 虚拟同步发电机暂态稳定性分析与控制策略
[J]. 电机与控制学报 2022 , 26 (12 ): 28 -37 .
[本文引用: 2]
WANG Jilei ZHANG Xing ZHU Qiaohua et al Transient stability analysis and control strategy of virtual synchronous generator
[J]. Electric Machines & Control 2022 , 26 (12 ): 28 -37 .
[本文引用: 2]
[18]
陈昕 , 张昌华 , 黄琦 , 等 . 与SG具有一致响应的VSG小信号建模和分析
[J]. 电力自动化设备 2017 , 37 (11 ): 78 -85 .
[本文引用: 1]
CHEN Xin ZHANG Changhua HUANG Qi et al Small signal modeling for virtual synchronous generator consistent with synchronous generator and analysis
[J]. Electric Power Automation Equipment 2017 , 37 (11 ): 78 -85 .
[本文引用: 1]
[19]
WU H RUAN X B YANG D S et al Small-signal modeling and parameters design for virtual synchronous generators
[J]. IEEE Transactions on Industrial Electronics 2016 , 63 (7 ): 4292 -4303 .
[本文引用: 1]
[20]
王硕 . 双馈风机虚拟同步并网控制基础理论与关键技术研究 [D]. 武汉 : 华中科技大学 , 2017 .
[本文引用: 2]
WANG Shuo Basic theory and key technology of virtual synchronous controlled DFIG-based wind turbine [D]. Wuhan : Huazhong University of Science and Technology , 2017 .
[本文引用: 2]
[21]
陈天一 , 陈来军 , 郑天文 , 等 . 基于模式平滑切换的虚拟同步发电机低电压穿越控制方法
[J]. 电网技术 2016 , 40 (7 ): 2134 -2140 .
[本文引用: 3]
CHEN Tianyi CHEN Laijun ZHENG Tianwen et al LVRT control method of virtual synchronous generator based on mode smooth switching
[J]. Power System Technology 2016 , 40 (7 ): 2134 -2140 .
[本文引用: 3]
[22]
SHI K SONG W T XU P F et al Low-voltage ride-through control strategy for a virtual synchronous generator based on smooth switching
[J]. IEEE Access 2017 , 6 : 2703 -2711 .
[本文引用: 3]
[23]
DU W CHEN Z SCHNEIDER K P et al A comparative study of two widely used grid-forming droop controls on microgrid small-signal stability
[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics 2019 , 8 (2 ): 963 -975 .
[本文引用: 1]
[24]
胡家兵 , 袁小明 , 程时杰 . 电力电子并网装备多尺度切换控制与电力电子化电力系统多尺度暂态问题
[J]. 中国电机工程学报 2019 , 39 (18 ): 5457 -5467 .
[本文引用: 3]
HU Jiabing YUAN Xiaoming CHENG Shijie Multi-time scale transients in power-electronized power systems considering multi-time scale switching control schemes of power electronics apparatus
[J]. Proceedings of the CSEE 2019 , 39 (18 ): 5457 -5467 .
[本文引用: 3]
“双碳”目标下中国清洁电力发展路径
1
2021
... 构建以新能源为主体的新型电力系统既是我国电力系统转型升级的重要方向,也是实现“双碳”目标的关键途径[1 ] .在这一目标驱动下,风电、光伏等新能源发电迅速发展,并逐步取代同步机成为电力系统中的主要电源[2 ] .新能源成为主力电源后需要承担电网构建的责任与义务,这就要求新能源发电装备具有主动支撑电网的能力.而目前广泛应用的跟网型电压源型变换器(VSC)具有低惯量和弱阻尼的特点,给电力系统的安全稳定运行带来巨大挑战.因此,构网型控制技术成为近年研究热点. ...
Development pathway of China’s clean electricity under carbon peaking and carbon neutrality goals
1
2021
... 构建以新能源为主体的新型电力系统既是我国电力系统转型升级的重要方向,也是实现“双碳”目标的关键途径[1 ] .在这一目标驱动下,风电、光伏等新能源发电迅速发展,并逐步取代同步机成为电力系统中的主要电源[2 ] .新能源成为主力电源后需要承担电网构建的责任与义务,这就要求新能源发电装备具有主动支撑电网的能力.而目前广泛应用的跟网型电压源型变换器(VSC)具有低惯量和弱阻尼的特点,给电力系统的安全稳定运行带来巨大挑战.因此,构网型控制技术成为近年研究热点. ...
碳中和目标下构建新型电力系统的挑战与展望
1
2022
... 构建以新能源为主体的新型电力系统既是我国电力系统转型升级的重要方向,也是实现“双碳”目标的关键途径[1 ] .在这一目标驱动下,风电、光伏等新能源发电迅速发展,并逐步取代同步机成为电力系统中的主要电源[2 ] .新能源成为主力电源后需要承担电网构建的责任与义务,这就要求新能源发电装备具有主动支撑电网的能力.而目前广泛应用的跟网型电压源型变换器(VSC)具有低惯量和弱阻尼的特点,给电力系统的安全稳定运行带来巨大挑战.因此,构网型控制技术成为近年研究热点. ...
Challenges and prospects for constructing the new-type power system towards a carbon neutrality future
1
2022
... 构建以新能源为主体的新型电力系统既是我国电力系统转型升级的重要方向,也是实现“双碳”目标的关键途径[1 ] .在这一目标驱动下,风电、光伏等新能源发电迅速发展,并逐步取代同步机成为电力系统中的主要电源[2 ] .新能源成为主力电源后需要承担电网构建的责任与义务,这就要求新能源发电装备具有主动支撑电网的能力.而目前广泛应用的跟网型电压源型变换器(VSC)具有低惯量和弱阻尼的特点,给电力系统的安全稳定运行带来巨大挑战.因此,构网型控制技术成为近年研究热点. ...
Grid-forming converters: Control approaches, grid-synchronization, and future trends—A review
1
2021
... 不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7 ] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注. ...
Response of a grid forming wind farm to system events, and the impact of external and internal damping
1
2020
... 不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7 ] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注. ...
考虑源端特性的虚拟同步直驱风机小信号建模与稳定性分析
2
2022
... 不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7 ] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注. ...
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Small-signal modeling and stability analysis of virtual synchronous PMSG considering source characteristics
2
2022
... 不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7 ] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注. ...
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
虚拟同步发电机输出阻抗建模与弱电网适应性研究
1
2017
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Output impedance modeling of virtual synchronous generator and its adaptability study in a weak grid
1
2017
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
虚拟同步发电机接入电力系统的阻尼转矩分析
2
2020
... 不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7 ] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注. ...
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Damping torque analysis of virtual synchronous generator connected to power system
2
2020
... 不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7 ] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注. ...
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Power system stabilization using virtual synchronous generator with alternating moment of inertia
1
2015
... 不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7 ] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注. ...
电网对称故障下虚拟同步发电机建模与改进控制
3
2017
... 不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7 ] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注. ...
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
Modeling and improved control of virtual synchronous generators under symmetrical faults of grid
3
2017
... 不同于锁相同步型VSC通过锁相环跟踪电网电压实现同步,构网型VSC通过构网同步环节主动构建与电网接口的VSC输出电压.目前,国内外已提出多种构网同步控制方式,包括虚拟同步控制、下垂控制、功率同步控制、虚拟振荡器控制等[3 ] .其中虚拟同步控制模拟同步机并网运行的惯量阻尼、调频调压等特性,成为主流的构网同步方式,并已在工程中示范应用[4 ] .以虚拟同步发电机(VSG)作为同步环节的构网型VSC控制结构分为两类:一类具有电压环级联电流环的结构,称为电压电流双环控制结构[5 7 ] ;另一类无电流内环,由VSG生成的相角和电压幅值直接进行矢量合成,称为直接电压控制结构[8 -9 ] .现有文献仅针对某种控制方式进行建模和稳定性分析,除故障电流限制外,两者控制结构差异对暂态特性的影响少有关注. ...
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
虚拟同步发电机的暂态稳定性分析
1
2018
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Transient stability analysis of virtual synchronous generator
1
2018
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Large-signal stability of grid-forming and grid-following controls in voltage source converter: A comparative study
1
2021
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Transient stability of voltage-source converters with grid-forming control: A design-oriented study
2
2020
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
... [12 ],分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
电力电子化电力系统多尺度电压功角动态稳定问题
1
2016
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Multi-time scale voltage and power angle dynamics in power electronics dominated large power systems
1
2016
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
4
2020
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
... 电力系统暂态扰动根据是否引起电力电子装备硬件保护电路及暂态控制算法的切换分为浅度和深度扰动[24 ] .浅度扰动下两种构网型VSC保持常规控制结构运行;深度扰动下直接电压控制常采用模式切换方案切换至含电流环控制结构[21 -22 ] ,两者差异较小.因此,重点对比分析两种构网型VSC在浅度扰动下的差异.基于本文所研究的问题,作出如下假设[14 ] :I 假设有功功率指令值P ref 保持不变;II 忽略网侧滤波电感和网络电感的电流暂态以及系统中的电阻损耗;III 忽略直流电容电压的变化,认为直流电容电压恒定. ...
... 根据戴维南等效定理,节点装备对外部网络均可等效成电压源(内电势E )串联阻抗(内电抗X )的形式.对于VSC,内电势定义为变换器输出电压矢量,内电抗为滤波电抗.对于新能源发电装备,有功和无功功率不平衡驱动装备中能量存储元件状态变化,相应控制器动作改变内电势幅值、角频率(以下简称频率),这反映了装备的暂态特性[24 ] .基于“有功和无功功率激励与内电势幅值和频率响应”关系(以下简称“激励-响应”关系)可对各装备特性进行物理化、统一化描述[14 ] ,文中内电势相位为内电势频率的积分. ...
... 在研究机电时间尺度稳定问题时,通常认为直流电压尺度控制器和交流电流尺度控制器动作迅速,快尺度控制环节的动态调节过程可以忽略.对于电压电流双环控制方式,机电时间尺度下作出如下假设[14 ] :①忽略端电压控制器的动态调节过程,认为端电压理想跟踪其指令值,即u t d u t q
4
2020
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
... 电力系统暂态扰动根据是否引起电力电子装备硬件保护电路及暂态控制算法的切换分为浅度和深度扰动[24 ] .浅度扰动下两种构网型VSC保持常规控制结构运行;深度扰动下直接电压控制常采用模式切换方案切换至含电流环控制结构[21 -22 ] ,两者差异较小.因此,重点对比分析两种构网型VSC在浅度扰动下的差异.基于本文所研究的问题,作出如下假设[14 ] :I 假设有功功率指令值P ref 保持不变;II 忽略网侧滤波电感和网络电感的电流暂态以及系统中的电阻损耗;III 忽略直流电容电压的变化,认为直流电容电压恒定. ...
... 根据戴维南等效定理,节点装备对外部网络均可等效成电压源(内电势E )串联阻抗(内电抗X )的形式.对于VSC,内电势定义为变换器输出电压矢量,内电抗为滤波电抗.对于新能源发电装备,有功和无功功率不平衡驱动装备中能量存储元件状态变化,相应控制器动作改变内电势幅值、角频率(以下简称频率),这反映了装备的暂态特性[24 ] .基于“有功和无功功率激励与内电势幅值和频率响应”关系(以下简称“激励-响应”关系)可对各装备特性进行物理化、统一化描述[14 ] ,文中内电势相位为内电势频率的积分. ...
... 在研究机电时间尺度稳定问题时,通常认为直流电压尺度控制器和交流电流尺度控制器动作迅速,快尺度控制环节的动态调节过程可以忽略.对于电压电流双环控制方式,机电时间尺度下作出如下假设[14 ] :①忽略端电压控制器的动态调节过程,认为端电压理想跟踪其指令值,即u t d u t q
虚拟调速器对VSG暂态功角稳定影响机理分析
1
2022
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Impact mechanism analysis of virtual governor on transient power angle stability of VSG
1
2022
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Transient stability analysis of grid-forming converter based on virtual synchronous generator
2
2022
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
... [16 -17 ].上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
虚拟同步发电机暂态稳定性分析与控制策略
2
2022
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
... -17 ].上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
Transient stability analysis and control strategy of virtual synchronous generator
2
2022
... 对于电压电流双环控制结构已有大量研究.在小扰动建模与稳定问题研究方面,已建立电压电流双环控制VSC的状态空间模型[5 ] 、阻抗模型[6 ] 、复转矩分析模型[7 ] ,并基于成熟的线性系统理论开展了小扰动稳定分析,但分析结论无法直接适用于暂态场景.在电压电流双环控制VSC暂态建模方面,文献[10 ]中建立电压电流双环控制VSC的高阶非线性微分代数方程,虽然能够精确描述系统暂态过程但无法揭示影响系统暂态稳定的物理机制.文献[11 -12 ]中在忽略电压环、电流环动态条件下建立用于揭示稳定机理的降阶模型,但仅适用于机电尺度,普适性不足.鉴于此,文献[13 ]中从电力系统基本目标和动态过程演化基本因果关系出发,提出基于“功率激励-内电势响应”关系的一般化建模方法,以理解装备响应物理过程及其在系统暂态行为中的作用机制.应用该方法建立了跟网型设备的暂态模型[14 ] ,但构网型VSC的暂态模型尚未建立.在电压电流双环控制VSC暂态稳定性分析方面,针对电压电流双环控制VSC并网系统,现有研究大多基于系统降阶模型,应用相平面法、等面积法等判断受扰后系统的稳定性[12 ] ,分析VSC主要控制参数[15 ] 、电压跌落程度[16 ] 、有功出力水平[17 ] 等对暂态稳定性的影响,并提出提高暂态稳定性的控制策略和参数优化方法[16 -17 ] .上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
... -17 ].上述研究重点针对VSG模拟同步机特性引发的功角稳定问题,在电压电流双环控制VSC本身物理特性认识方面尚有欠缺. ...
与SG具有一致响应的VSG小信号建模和分析
1
2017
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
Small signal modeling for virtual synchronous generator consistent with synchronous generator and analysis
1
2017
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
Small-signal modeling and parameters design for virtual synchronous generators
1
2016
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
2
2017
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
2
2017
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
基于模式平滑切换的虚拟同步发电机低电压穿越控制方法
3
2016
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... 电力系统暂态扰动根据是否引起电力电子装备硬件保护电路及暂态控制算法的切换分为浅度和深度扰动[24 ] .浅度扰动下两种构网型VSC保持常规控制结构运行;深度扰动下直接电压控制常采用模式切换方案切换至含电流环控制结构[21 -22 ] ,两者差异较小.因此,重点对比分析两种构网型VSC在浅度扰动下的差异.基于本文所研究的问题,作出如下假设[14 ] :I 假设有功功率指令值P ref 保持不变;II 忽略网侧滤波电感和网络电感的电流暂态以及系统中的电阻损耗;III 忽略直流电容电压的变化,认为直流电容电压恒定. ...
LVRT control method of virtual synchronous generator based on mode smooth switching
3
2016
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... 电力系统暂态扰动根据是否引起电力电子装备硬件保护电路及暂态控制算法的切换分为浅度和深度扰动[24 ] .浅度扰动下两种构网型VSC保持常规控制结构运行;深度扰动下直接电压控制常采用模式切换方案切换至含电流环控制结构[21 -22 ] ,两者差异较小.因此,重点对比分析两种构网型VSC在浅度扰动下的差异.基于本文所研究的问题,作出如下假设[14 ] :I 假设有功功率指令值P ref 保持不变;II 忽略网侧滤波电感和网络电感的电流暂态以及系统中的电阻损耗;III 忽略直流电容电压的变化,认为直流电容电压恒定. ...
Low-voltage ride-through control strategy for a virtual synchronous generator based on smooth switching
3
2017
... 关于直接电压控制建模和分析的研究大多集中在小扰动方面.文献[18 ]中建立VSG单机无穷大系统小信号模型,求取和分析系统特征根分布及其参与因子,研究参数变化对系统小扰动稳定性的影响.文献[19 ]中建立工频平均小信号模型,分析有功环和无功环的解耦条件,提出一种简单的VSG控制参数设计方法.关于直接电压控制暂态建模和分析的研究较少,现有文献重点针对故障电流限制问题提出虚拟电阻[9 ,20 ] 和模式切换[21 -22 ] 两种方案.对于虚拟电阻的研究,文献[9 ]中提出虚拟电阻和相量限流技术,有效限制了电网对称故障下的短路电流;文献[20 ]中分析了虚拟电阻对双馈风力发电机转子暂态电流及定子自由磁链衰减特性的影响,并提出暂态电流抑制方法.文献[21 -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... -22 ]中提出基于模式平滑切换的低电压穿越控制方法,故障期间切换至含电流环控制结构,实现故障限流和无功支撑.但上述文献重点关注电流限幅和故障穿越,未研究直接电压控制VSC的暂态特性. ...
... 电力系统暂态扰动根据是否引起电力电子装备硬件保护电路及暂态控制算法的切换分为浅度和深度扰动[24 ] .浅度扰动下两种构网型VSC保持常规控制结构运行;深度扰动下直接电压控制常采用模式切换方案切换至含电流环控制结构[21 -22 ] ,两者差异较小.因此,重点对比分析两种构网型VSC在浅度扰动下的差异.基于本文所研究的问题,作出如下假设[14 ] :I 假设有功功率指令值P ref 保持不变;II 忽略网侧滤波电感和网络电感的电流暂态以及系统中的电阻损耗;III 忽略直流电容电压的变化,认为直流电容电压恒定. ...
A comparative study of two widely used grid-forming droop controls on microgrid small-signal stability
1
2019
... 关于电压电流双环控制和直接电压控制VSC的对比研究同样集中在小扰动方面,如文献[23 ]中指出,相比电压电流双环控制结构,直接电压控制VSC提供更大耦合电抗,有利于提高VSC在强电网下的动态稳定性,但两者的暂态特性差异尚无对比研究.构网型VSC为系统提供主动支撑能力主要体现在类似同步机的惯量、阻尼特性,因此本文从等效惯量、等效阻尼角度对比两种控制方式VSC的暂态特性差异. ...
电力电子并网装备多尺度切换控制与电力电子化电力系统多尺度暂态问题
3
2019
... 为维持VSC的稳定运行,不同控制环节的带宽按照一定原则设计,因而呈现不同时间尺度的控制动态[24 ] .VSG模拟同步发电机的运行特性,其控制动态呈现秒级机电时间尺度特征;电压环与电流环控制动态分别呈现百毫秒级的直流电压时间尺度特征和十毫秒级的交流电流时间尺度特征.因此,构网型VSC电压电流双环控制结构包含机电、直流电压、交流电流3个时间尺度的控制环路. ...
... 电力系统暂态扰动根据是否引起电力电子装备硬件保护电路及暂态控制算法的切换分为浅度和深度扰动[24 ] .浅度扰动下两种构网型VSC保持常规控制结构运行;深度扰动下直接电压控制常采用模式切换方案切换至含电流环控制结构[21 -22 ] ,两者差异较小.因此,重点对比分析两种构网型VSC在浅度扰动下的差异.基于本文所研究的问题,作出如下假设[14 ] :I 假设有功功率指令值P ref 保持不变;II 忽略网侧滤波电感和网络电感的电流暂态以及系统中的电阻损耗;III 忽略直流电容电压的变化,认为直流电容电压恒定. ...
... 根据戴维南等效定理,节点装备对外部网络均可等效成电压源(内电势E )串联阻抗(内电抗X )的形式.对于VSC,内电势定义为变换器输出电压矢量,内电抗为滤波电抗.对于新能源发电装备,有功和无功功率不平衡驱动装备中能量存储元件状态变化,相应控制器动作改变内电势幅值、角频率(以下简称频率),这反映了装备的暂态特性[24 ] .基于“有功和无功功率激励与内电势幅值和频率响应”关系(以下简称“激励-响应”关系)可对各装备特性进行物理化、统一化描述[14 ] ,文中内电势相位为内电势频率的积分. ...
Multi-time scale transients in power-electronized power systems considering multi-time scale switching control schemes of power electronics apparatus
3
2019
... 为维持VSC的稳定运行,不同控制环节的带宽按照一定原则设计,因而呈现不同时间尺度的控制动态[24 ] .VSG模拟同步发电机的运行特性,其控制动态呈现秒级机电时间尺度特征;电压环与电流环控制动态分别呈现百毫秒级的直流电压时间尺度特征和十毫秒级的交流电流时间尺度特征.因此,构网型VSC电压电流双环控制结构包含机电、直流电压、交流电流3个时间尺度的控制环路. ...
... 电力系统暂态扰动根据是否引起电力电子装备硬件保护电路及暂态控制算法的切换分为浅度和深度扰动[24 ] .浅度扰动下两种构网型VSC保持常规控制结构运行;深度扰动下直接电压控制常采用模式切换方案切换至含电流环控制结构[21 -22 ] ,两者差异较小.因此,重点对比分析两种构网型VSC在浅度扰动下的差异.基于本文所研究的问题,作出如下假设[14 ] :I 假设有功功率指令值P ref 保持不变;II 忽略网侧滤波电感和网络电感的电流暂态以及系统中的电阻损耗;III 忽略直流电容电压的变化,认为直流电容电压恒定. ...
... 根据戴维南等效定理,节点装备对外部网络均可等效成电压源(内电势E )串联阻抗(内电抗X )的形式.对于VSC,内电势定义为变换器输出电压矢量,内电抗为滤波电抗.对于新能源发电装备,有功和无功功率不平衡驱动装备中能量存储元件状态变化,相应控制器动作改变内电势幅值、角频率(以下简称频率),这反映了装备的暂态特性[24 ] .基于“有功和无功功率激励与内电势幅值和频率响应”关系(以下简称“激励-响应”关系)可对各装备特性进行物理化、统一化描述[14 ] ,文中内电势相位为内电势频率的积分. ...