基于CEEMDAN-GSA-LSTM和SVR的光伏功率短期区间预测

doi:10.16183/j.cnki.jsjtu.2022.511

基于CEEMDAN-GSA-LSTM和SVR的光伏功率短期区间预测

李芬^,¹, 孙凌¹, 王亚维², 屈爱芳³, 梅念⁴, 赵晋斌¹

1.上海电力大学电气工程学院, 上海 200090

2.中国船舶集团有限公司第七二二研究所低频电磁通信技术实验室,武汉 430205

3.上海师范大学数理学院,上海 200234

4.国网经济技术研究院有限公司,北京 102209

Short-Term Interval Forecasting of Photovoltaic Power Based on CEEMDAN-GSA-LSTM and SVR

LI Fen^,¹, SUN Ling¹, WANG Yawei², QU Aifang³, MEI Nian⁴, ZHAO Jinbin¹

1. College of Electric Power Engineering, Shanghai University of Electric Power, Shanghai 200090, China

2. Laboratory of Low Frequency Electromagnetic Communication Technology, the 722 Research Institute, CSSC, Wuhan 430205, China

3. Mathematics and Science College, Shanghai Normal University, Shanghai 200234, China

4. State Grid Economic and Technological Research Institute Co., Ltd., Beijing 102209, China

责任编辑: 王历历

收稿日期: 2022-12-9 修回日期: 2023-03-14 接受日期: 2023-05-9

基金资助:

国家自然科学基金面上项目(52177184)
上海绿色能源并网工程技术研究中心(13DZ2251900)

Received: 2022-12-9 Revised: 2023-03-14 Accepted: 2023-05-9

作者简介 About authors

李芬(1984-),博士,副教授,主要研究方向为新能源开发利用与电力变换技术;E-mail:lifen2012@shiep.edu.cn.

摘要

针对光伏输出功率存在间歇性和波动性的问题,提出一种光伏功率短期区间预测模型.首先,该模型采用自适应噪声完备集合经验模态分解将历史光伏出力数据分解为不同的分量并按照其与赤纬角、时角等时序特征量的相关性定义为时序分量和随机分量.其次,分别使用经过引力搜索算法优化的长短期记忆神经网络和支持向量回归模型对时序分量和随机分量进行预测.再次,叠加时序分量和随机分量的预测结果得到点预测结果.然后,对误差进行Johnson变换及正态分布建模后得到光伏功率区间预测结果.最后,利用算例验证该模型的有效性.结果表明:在不同天气情况下,上述模型比现有预测模型精度更高,具有较好的鲁棒性,能够基于预测值提供较为精准的置信区间.

关键词： 光伏功率预测; 区间预测; 自适应噪声完备集合经验模态分解; 引力搜索算法; 长短期记忆; 支持向量回归; Johnson变换

Abstract

Aimed at the intermittency and fluctuation of photovoltaic output power, a short-term interval prediction model of photovoltaic power is proposed. First, the model uses the complete ensemble empirical mode decomposition of adaptive noise (CEEMDAN) to decompose the historical photovoltaic output data into different components and define them as time-series components and random components according to their correlation with time-series features such as declination and time angles. Then, the long short-term memory (LSTM) neural network and the support vector regression (SVR) model optimized by the gravitational search algorithm (GSA) are used to predict the time series components and the random components respectively, and the prediction results of the time series components and the random components are superimposed to obtain the point prediction result. After the error is subjected to Johnson transformation and normal distribution modeling, the photovoltaic power interval prediction result is obtained. Finally, the effectiveness of the method is verified by an example. The comparison of the proposed model with other existing prediction models under different weather conditions suggests that the proposed model has a higher accuracy and a better robustness, which can provide precise confidence intervals based on point prediction values.

Keywords： photovoltaic power prediction; interval prediction; complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN); gravitational search algorithm (GSA); long short-term memory (LSTM); support vector regression (SVR); Johnson transformation

PDF (2987KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李芬, 孙凌, 王亚维, 屈爱芳, 梅念, 赵晋斌. 基于CEEMDAN-GSA-LSTM和SVR的光伏功率短期区间预测[J]. 上海交通大学学报, 2024, 58(6): 806-818 doi:10.16183/j.cnki.jsjtu.2022.511

LI Fen, SUN Ling, WANG Yawei, QU Aifang, MEI Nian, ZHAO Jinbin. Short-Term Interval Forecasting of Photovoltaic Power Based on CEEMDAN-GSA-LSTM and SVR[J]. Journal of Shanghai Jiaotong University, 2024, 58(6): 806-818 doi:10.16183/j.cnki.jsjtu.2022.511

在“双碳”目标下,我国能源转型节奏越来越快,光伏发电进入新发展阶段^[1].光伏功率预测作为源网荷储一体化和多能互补发展的关键技术之一,对进一步规范和完善光伏电站消纳统计工作有重大意义,可以为电力系统的调度、运行及新能源消纳提供更为完善的数据支撑.

针对光伏功率与关键气象环境因素随时间变化的本质特征,文献[2]中提出利用经验模态分解(Empirical Mode Decomposition,EMD)产生不同尺度的环境数据序列,运用主成分分析方法对输入模型参数降维,最后采用长短期记忆(Long Short-Term Memory,LSTM)网络构建整体模型.实验结果表明,LSTM模型在光伏预测领域相较于反向传播神经网络(Back Propagation, BP)和极端梯度提升(Extreme Gradient Boosting,XGboost)具有更好的适应性.然而,太阳辐射在具有时序性的同时,也潜在很强的随机性,这导致光伏输出功率具有间歇性和波动性的特点^[3⇓-5],如果遇到气象条件不佳如环境因素波动较大的转折天气或恶劣天气,则上述模型的性能将大大降低.文献[6]中提出一种基于XGBoost 的实时校正光伏预测模型,它将基准预测值及其与实测值的实时动态误差作为实时层XGBoost 模型输入实时叠加,以实时误差修正的方法对XGboost算法进行优化.实验结果表明,经过实时误差修正的XGboost算法在超短期预测尺度上性能优于LSTM,有利于解决光伏输出功率在较短时间段内的随机波动问题.然而,这种实时误差修正的方法仅在超短期尺度下效果较好,在短期或中长期的尺度下进行实时修正会导致模型复杂度提高,因此必须额外考虑气象环境因素的时序特征.文献[7]中针对高维特征量提出一种基于卷积神经网络(Convolutional Neural Network,CNN)、LSTM的光伏功率预测模型,将高维特征量形成矩阵输入卷积层,优化了计算速度,在传统深度学习模型上提升了预测精度.但是,在特征量维度不高的情况下,该模型池化层中会丢失大量时序和随机性信息,影响预测效果.

针对光伏输出功率存在间歇性和波动性的特点,概率区间预测可以提供预测值的波动区间,在一定的置信水平下给出输出功率的上下界值^[8-9].文献[10]中提出一种基于互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition, CEEMD)和深度信念网络(Deep Belief Network, DBN)的光伏功率预测方法,对不同天气条件下的CEEMD-DBN预测结果进行核密度估计(Kernel Density Estimation, KDE),最后得到预测区间.该方法解决EMD分解带来的模态混叠问题的同时消除了辅助白噪声.但是,该模型也并未兼顾气象环境因素的时序特征,预测过程有待改善.

针对以上问题,在充分兼顾环境因素的时序性与随机性的基础上,本文提出一种基于自适应噪声完备集合经验模态分解(Complete Ensemble Empi~rical Mode Decomposition with Adaptive Noise,CEEMDAN)和引力搜索算法(Gravitational Search Algorithm,GSA)优化后的LSTM网络及支持向量回归(Support Vector Regression, SVR)的光伏功率短期区间预测模型.首先,利用CEEMDAN将历史出力数据分解为不同分量并按照其与赤纬角、时角等时序特征量的相关性定义为时序分量和随机分量.其次,分别使用经过GSA优化的LSTM和SVR模型对时序分量和随机分量进行预测.再次,叠加时序分量和随机分量的预测结果得到点预测结果.然后,对误差进行Johnson变换及正态分布建模后得到光伏功率区间预测结果.算例验证结果表明:与实时修正的XGboost算法、CNN-LSTM网络以及EMD-GSA-LSTM、EMD-GSA-SVR相比,所提模型在点预测环节中精度更高,鲁棒性较好,在区间预测环节中能够基于点预测值提供较为精准的置信区间.

1 模型理论基础

1.1 CEEMDAN算法

EMD是一种能将时间序列信号分解为数个本征模态函数(Intrinsic Mode Function, IMF)的信号分析方法,集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)在EMD的基础上加入高斯白噪声^[11],解决了EMD存在的模态混叠问题.CEEMDAN则在EEMD的基础上改进,在分解的每个阶段都加入特定自适应噪声,相较于EEMD提升了计算速度,得到更好的模态分解结果^[12].CEEMDAN算法的分解流程如下所示.

(1) 在信号x(n)中加入幅值为ε₀的高斯白噪声ω_i(n),即

(1)

\begin{matrix} x (n)' = x (n) + ε_{0} ω_{i} (n) \end{matrix}

式中:i为加入白噪声的次数.

(2) 定义E_j[·]为经过EMD分解后的第j个本征模态分量,对x(n)'进行i次EMD分解,其结果取平均值得到第一个本征模态分量H_IMF1(n),即

(2)

E_{1} [x (n)'] = H_{I M F 1}^{i} (n)

(3)

H_{I M F 1} (n) = \frac{1}{I'} \overset{I'}{\sum_{i = 1}} H_{I M F 1}^{i} (n)

(3) 计算去除H_IMF₁(n)后的残差R₁(n),即

(4)

\begin{matrix} R_{1} (n) = x (n)' - H_{I M F 1} (n) \end{matrix}

(4) 计算第二个本征模态分量H_IMF₂(n)及其残差R₂(n),即

(5)

H_{I M F 2} (n) = \frac{1}{I'} \overset{I'}{\sum_{i = 1}} E_{1} [R_{1} (n) + ε_{1} E_{1} [ω_{i} (n)]]

(6)

R_{2} (n) = R_{1} (n) - H_{I M F 2} (n)

(5) 对于其他阶段,重复以上步骤计算第k个本征模态分量和其残差,即

(7)

H_{I M F k} (n) = \frac{1}{I'} \overset{I'}{\sum_{i = 1}} E_{1} [R_{k - 1} (n) + ε_{k - 1} E_{k - 1} [ω_{i} (n)]]

(8)

R_{k} (n) = R_{k - 1} (n) - H_{I M F k} (n)

1.2 GSA算法

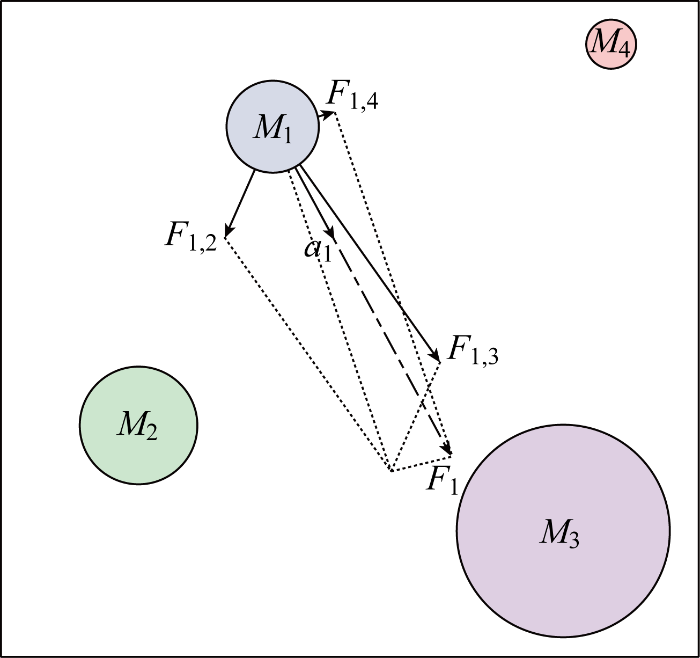
GSA算法是Rashedi等^[13]在2009年提出的一种优化算法.如图1所示,该算法通过模拟物体间的万有引力,让种群内所有物体都朝着质量更大的物体运动.F_{1, 2}、F_{1, 3}、F_{1, 4}分别为质量代理M₂、M₃、M₄对M₁的作用力,F₁为F_{1, 2}、F_{1, 3}、F_{1, 4}的合力,a₁为M₁在F₁方向的加速度.在GSA中,更大的质量代表更优的解,经过数次迭代后即可找到种群内的最优解.和常用的粒子群算法、蚂蚁群算法相比,GSA能够避免陷入局部最优解,在处理全局问题上能取得更好的效果^[14],具体方法如下.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 GSA质量代理运行示意图

Fig.1 Diagram of GSA agent operation

若D维种群内有N个质量代理,第K个质量代理的位置定义为

(9)

\begin{array}{l} \begin{matrix} X_{K} = (x_{K}^{1}, x_{K}^{2}, x_{K}^{3}, \dots, x_{K}^{D}), \end{matrix} \\ \begin{matrix} K = 1, 2, \dots, N \end{matrix} \end{array}

则t时刻质量代理b对质量代理a的作用力 $F_{a, b}^{D}$ 为

(10)

F_{a, b}^{D} (t) = G (t) \frac{M_{a} (t) M_{b} (t) (x_{b}^{D} (t) - x_{a}^{D} (t))}{R_{a b} (t) + δ}

式中:G(t)为随时间t递减的引力变量;R_ab(t)为a、b间的欧氏距离;M_a(t)、M_b(t)分别为质量代理a、b的惯性质量;δ为防止分母为0的变量.

(11)

R_{a b} (t) = {‖X_{a} (t), X_{b} (t)‖}_{2}

(12)

m_{a} (t) = \frac{B_{f i t}^{a} (t) - B_{w o r s t} (t)}{B_{b e s t} (t) - B_{w o r s t} (t)}

(13)

M_{a} (t) = \frac{m_{a} (t)}{\overset{N}{\sum_{K = 1}} m_{K} (t)}

式中: $B_{f i t}^{a}$ (t)为t时刻质量代理a的适应度.在最小值问题中,B_worst(t)为所有时刻中适应度最大值,B_best(t)为所有时刻中适应度最小值;最大值问题相反.

在t时刻,为了增加算法的随机特征引入[0,1]中的随机数τ_K,则质量代理a所受的在D维上的合力和其在D维上的加速度分别为

(14)

F_{a}^{D} (t) = \overset{N}{\sum_{i = K, K \neq a}} τ_{K} F_{a, b}^{D} (t)

(15)

a_{a}^{D} (t) = \frac{F_{a}^{D} (t)}{M_{a} (t)}

质量代理a在D维中下一时刻速度和位置分别为

(16)

\begin{matrix} v_{a}^{D} (t + 1) = τ_{K} v_{a}^{D} (t) + a_{a}^{D} (t) \end{matrix}

(17)

x_{a}^{D} (t + 1) = x_{a}^{D} (t) + v_{a}^{D} (t + 1)

1.3 LSTM神经网络

LSTM是基于循环神经网络(Recurrent Neural Network, RNN)诞生的一种神经网络,与RNN相比,LSTM解决了长序列训练过程中的梯度消失和梯度爆炸问题,更适用于光伏出力的预测^[15⇓-17].

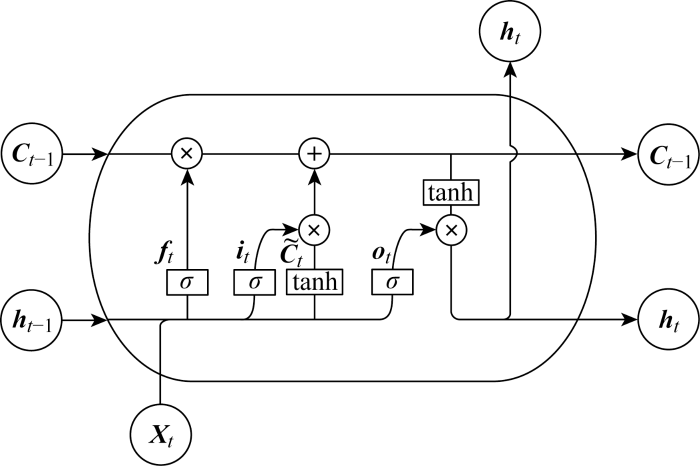
LSTM的一个神经元在t时刻有3个输入,包括细胞状态C_t_-1、隐层状态h_t_-1和输入向量X_t;两个输出为细胞状态C_t和隐层状态h_t.其中h_t_-1和X_t经过门控单元对C_t和h_t的输出造成影响,门控单元由遗忘门f_t、输入门i_t和输出门o_t构成.LSTM网络拓扑结构如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 LSTM拓扑结构图

Fig.2 Topology diagram of LSTM

W_f、W_i、W_o、W_c分别为遗忘门、输入门、输出门和输入单元状态权重矩阵;b_f、b_i、b_o、b_c分别为遗忘门、输入门、输出门和输入单元状态的偏置项;σ(·)为激活函数,一般为sigmoid函数;tanh(·)为双曲正切函数,则

(18)

\begin{matrix} \begin{array}{l} f_{t} = σ (W_{f} \cdot [h_{t - 1} x_{t}] + b_{f}) \\ i_{t} = σ (W_{i} \cdot [h_{t - 1} x_{t}] + b_{i}) \\ {\tilde{C}}_{t} = t a n h (W_{c} \cdot [h_{t - 1} x_{t}] + b_{c}) \\ C_{t} = f_{t} \times C_{t - 1} + i_{t} \times {\tilde{C}}_{t} \\ o_{t} = σ (W_{o} \cdot [h_{t - 1} x_{t}] + b_{o}) \\ h_{t} = o_{t} t a n h (C_{t}) \end{array}\} \end{matrix}

神经元作为LSTM的构成部分,它的数量对 $C_{t} 和 h_{t} 的迭代有很大影响 . 在学习过程中, 学习率 r_{L}$ 确定模型的学习速度,决定目标函数在何时收敛到最优解,因此在超参数优化环节中需要选取合适的LSTM神经元数量m和学习率r_L以达到更好的预测效果^[18].

1.4 SVR算法

SVR是基于支持向量机的一种回归算法,主要思想是寻找输入空间到输出空间的一个非线性映射Φ(x),将输入数据x映射到高维特征区间ψ中, 继而在高维空间内寻找到SVR函数^[19-20].

(19)

\begin{matrix} \begin{array}{l} f (x) = Φ (x) w + b \\ Φ (x) \in R^{D} \to ψ \\ w \in ψ \end{array}\} \end{matrix}

式中:w为权值向量;b为偏置项.可以通过最小化下列泛函数进行估计,

(20)

\begin{array}{l} R (w) = \frac{1}{2} {‖w‖}^{2} + C \overset{d}{\sum_{c = 1}} J^{θ} [y_{c}, f (x_{c})] \\ J^{θ} [y_{c}, f (x_{c})] = \\ \{\begin{array}{l} |y_{c} - f (x_{c})| - θ, & |y_{c} - f (x_{c})| \geq θ \\ 0, & |y_{c} - f (x_{c})| < θ \end{array} \end{array}\}

式中:C为惩罚参数;x_c、y_c分别为输入、输出变量的值;J^θ[y_c, f(x_c)]为θ不敏感函数,当SVR的输出与实际输出的绝对值小于设定的θ值时可以忽略不计,否则让损失函数的值为两者差的绝对值超过θ的部分.由式(20)可知,SVR可以表示为

(21)

\begin{matrix} \begin{array}{l} m i n [\frac{1}{2} {‖w‖}^{2} + C \overset{n}{\sum_{i = 1}} (ξ_{c}^{2} + {\hat{ξ}}_{c}^{2})] \\ \begin{array}{l} s . t . & (Φ (x_{c}) w + b) - y_{c} \leq θ + ξ_{c}, \\ c = 1, 2, \dots, d \\ y_{c} - (Φ (x_{c}) w + b) \leq θ + {\hat{ξ}}_{c}, \\ c = 1, 2, \dots, d \\ ξ_{c}, {\hat{ξ}}_{c} \geq 0, c = 1, 2, \dots, d \end{array} \end{array}\} \end{matrix}

为了让式(20)有解,式(21)中引入松弛变量ξ_c和 ${\hat{ξ}}_{c}$ ,通过拉格朗日乘子法可得:

(22)

\begin{matrix} w = \overset{n}{\sum_{c = 1}} (α_{c} - α_{c}^{*}) Φ (x_{c}) \end{matrix}

式中:α_c、 $α_{c}^{*}$ 为两个拉格朗日乘子.结合式(19)和式(22),f(x)可以表示为

(23)

\begin{matrix} \begin{array}{l} f (x) = \overset{n}{\sum_{c = 1}} (α_{c} - α_{c}^{*}) K (x_{c}, x) + b \\ K (x_{c}, x) = Φ (x_{c}) Φ (x) \end{array}\} \end{matrix}

式中: $K (x_{c}, x)$ 为核函数.由上式可见,SVR在计算 $f (x)$ 时,只需算出拉格朗日乘子和核函数,因此选择合适的核函数及其内部参数可以有效地提高SVR预测模型的精度^[21].

1.5 Johnson变换

Johnson变换是基于Johnson分布的一种数据变换方法,可以将非正态的样本通过一系列变换转换为正态分布的数据^[22-23].

Johnson变换从S_B、S_L、S_U 3个分布系列中选取最优函数对样本进行拟合,其形式为

(24)

\begin{matrix} Z = γ + δ g (\frac{X - ξ}{λ}) \end{matrix}

式中:γ、δ为形状参数;g(·)为变换函数;X为随机变量;ξ为位置参数;λ为尺度参数,如表1所示.

表1 Johnson变换的3种类型

Tab.1 Three types of Johnson transformation

分布系列	g(·)	约束条件
S_B	ln $\frac{X - ξ}{ξ + λ - X}$	ξ<X<ξ+λ,λ>0
S_L	ln $\frac{X - ξ}{λ}$	X>ξ,λ>0
S_U	arsinh $\frac{X - ξ}{λ}$	λ>0

新窗口打开| 下载CSV

2 模型结构

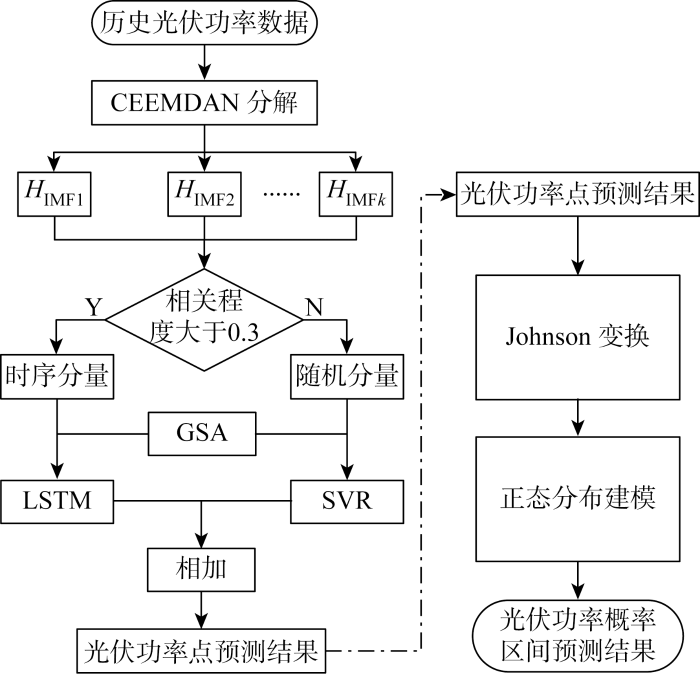
所提预测模型结构如图3所示,模型可以分成两个环节:点预测环节和区间预测环节.分别以这两个环节对模型整体结构进行阐述.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 CEEMDAN-GSA-LSTM和SVR区间预测模型结构示意图

Fig.3 Schematic diagram of interval prediction based on CEEMDAN-GSA-LSTM and SVR

2.1 点预测环节

点预测环节是模型的先行环节,如图3左半部分所示,主要目的是结合历史功率数据和多种地面辐射观测数据及常规气象要素观测数据,利用CEEMDAN-GSA-LSTM和SVR实现对未来3 d内光伏出力点的预测,流程如下:

(1) 针对历史光伏功率数据,选取合适的序列长度进行CEEMDAN分解,使得每次分解均能得到相同数量的H_IMF分量.

(2) 分析既有的地面辐射、气象要素观测数据及计算的天文数据,选取具有时序特征的数据作为时序特征量,其余特征量为随机特征量.计算各H_IMF分量与时序特征量的皮尔逊相关系数(ρ).根据经验,若两组数据之间的皮尔逊相关系数的绝对值大于0.3,则称这两组数据存在相关性^[24],因此将与时序特征量相关系数绝对值大于0.3的H_IMF分量定义为时序分量,其他分量定义为随机分量.

(3) 在时序分量和随机分量中各取一部分作训练,利用GSA对LSTM及SVR进行超参数优化.

(4) 使用经过GSA优化的LSTM和SVR模型对时序分量和随机分量进行预测,将所得结果相加即为点预测环节结果.

2.2 区间预测环节

区间预测环节是模型的后续环节,如图3右半部分所示,主要目的是结合点预测结果分析误差区间并利用Johnson变换进行正态分布建模,最终得到未来3 d内不同置信度下的光伏功率波动区间,流程如下.

(1) 计算点预测结果与真实值的误差,统计其分布情况.

(2) 按第1天、第2天和第3天将未来3 d内的预测误差分成3部分.

(3) 对3部分误差值进行Johnson变换,使变换后的误差符合正态分布.

(4) 结合正态分布的累计分布函数,经过Johnson逆变换,得到在不同置信度下的误差分布范围,从而得到光伏功率波动区间.

3 算例分析

3.1 数据来源及评价指标

算例中使用的地面辐射观测数据及常规气象要素观测数据均来自国家气象信息中心,同期历史光伏出力数据来自武汉某并网光伏电站,所有数据均经过高质量的数据清洗和归一化处理,剔除异常数据,可信度高.

算例中地面辐射观测数据及气象要素观测数据选取每日8:00—18:00的有效数据,每小时采样一次,每日共有11个采样点,共660个采样日,其中前600个采样日为训练集,后60个采样日为测试集,目标实现对未来3 d的功率数据预测.

算例中衡量点预测结果的评价指标采用归一化均方根误差和对称平均绝对百分比误差,分别记为e_N和e_S.衡量区间预测结果的评价指标选用预测区间平均宽度(Prediction Interval Normalized Average, PINAW)和预测区间覆盖率(Prediction Interval Coverage Probability, PICP),分别记为Q_PINAW和Q_PICP.表示为

(25)

\begin{matrix} \begin{array}{l} e_{N} = \frac{\sqrt{\frac{1}{N'} \overset{N'}{\sum_{s = 1}} (P_{f, s} - P_{o, s})^{2}}}{\frac{1}{N'} \overset{N'}{\sum_{s = 1}} P_{o, s}} \\ e_{S} = \frac{1}{N'} \overset{N'}{\sum_{s = 1}} \frac{| P_{o, s} - P_{f, s} |}{(| P_{o, s} | + | P_{f, s} |) / 2} \\ Q_{P I N A W} = \frac{1}{N'} \overset{N'}{\sum_{s = 1}} \frac{U_{s} - L_{s}}{y_{m a x} - y_{m i n}} \\ Q_{P I C P} = \frac{1}{N'} \overset{N'}{\sum_{s = 1}} κ_{s} \end{array}\} \end{matrix}

式中:P_f为预测值;P_o为实际值;L_s、U_s分别为第s个样本下、上边界值;y_max、y_min分别为目标值的最大值和最小值,可以保证Q_PINAW归一化在[0,1]内;κ_s为二进制变量,若实际功率包含于所构建的预测区间内,其值为1,否则为0.

3.2 时序分量和随机分量

在历史光伏出力数据中任意选取连续的5组数据进行CEEMDAN分解,每组数据均有77个采样点,结果均得到H_IMF1~H_IMF7共7组H_IMF分量.

算例中地面辐射、常规气象要素观测数据及经过计算的天文数据有气压、温度、相对湿度、过去1 h降水量、10 min内平均风速、10 min内平均能见度、总云量、赤纬角、时角、修正清晰度指数k'_T、大气层上界水平面总辐射I₀、水平面总辐射I、水平面直接辐射I_b、法向直射辐射I_on、日照百分率.其中,赤纬角是地球赤道平面与太阳和地球中心连线的夹角,它的变化反映出不同季节的变化.时角是天子午圈与天体的赤经圈在北极所成的球面角,增长速率为15°/h,它的变化反映出1 d内时间的变化.I₀指地球大气层外接收到的太阳辐射量,具有很强的时序特征^[25].修正清晰度指数 $k'_{T}$ 表示大气的透明程度,与太阳在天空中的位置密切相关^[26].因此,将赤纬角、时角、大气层上界水平面总辐射I₀、修正清晰度指数 $k'_{T}$ 定义为时序特征量,其他特征量定义为随机特征量.

分别计算每组光伏出力数据的7个H_IMF分量与其相对应的赤纬角、时角、 $I_{0} 、 k'_{T} 的皮尔逊相关系数 ρ,$ 将与时序特征量存在相关性的H_IMF分量定义为时序分量,其余分量定义为随机分量.

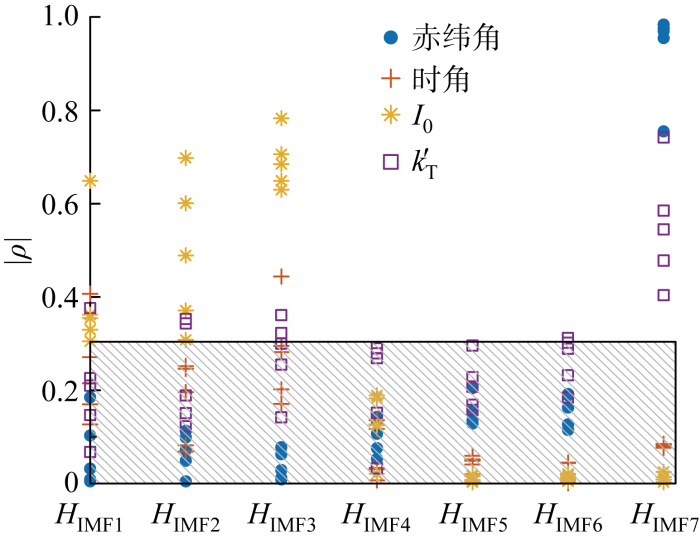
如图4所示,H_IMF4、H_IMF5、H_IMF6与4个时序特征量的相关系数绝对值均小于0.3,可以认为不存在相关性.因此,在算例中,将H_IMF1、H_IMF2、H_IMF3、H_IMF7定义为时序分量,将H_IMF4、H_IMF5、H_IMF6定义为随机分量.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 IMF分量与各时序特征量相关性示意图

Fig.4 Diagram of correlation between IMFs and time series characteristic quantities

3.3 基于GSA的超参数优化

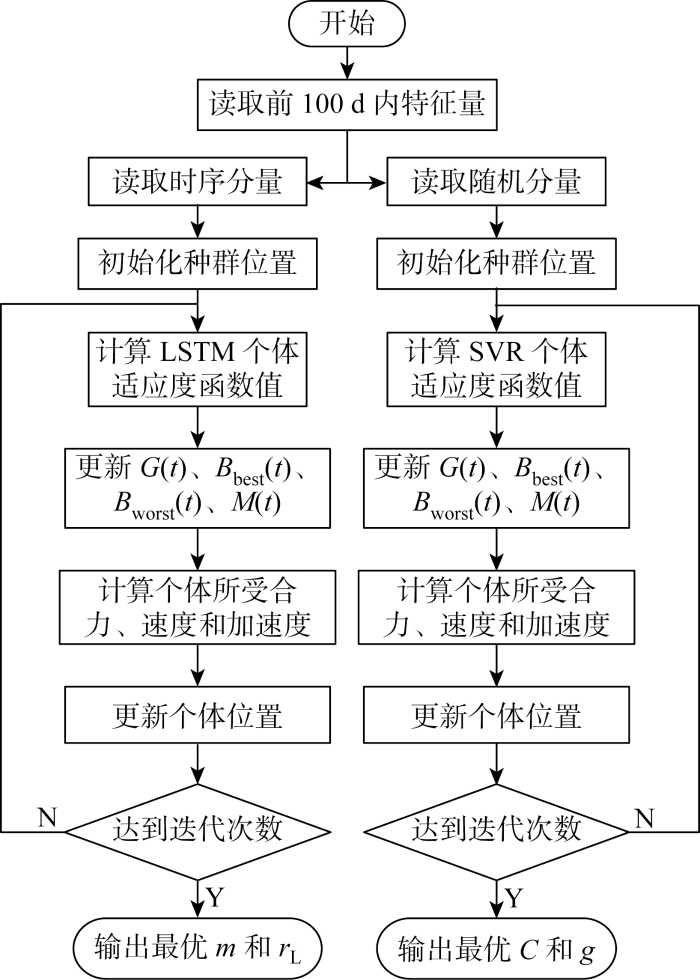
超参数设置对神经网络和机器学习的结果影响很大,针对不同气象环境特征,超参数应当相应作出调整.在算例中,对于LSTM中神经元个数 $m 、学习率 r_{L}$ 和SVR中的惩罚参数C、核函数参数g,选取前100 d内的特征量及其对应时序分量或随机分量训练,个体适应度选取为预测值与真实值的e_S,迭代次数取200,利用GSA算法进行优化,具体流程如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 GSA优化流程图

Fig.5 Flow chart of GSA optimization

LSTM网络模型由一个输入层、一个隐藏层和一个输出层构成.采用Adam算法作为网络求解器,激活函数使用tanh函数,为保证平稳收敛,学习率衰减率设置为0.8.SVR网络模型采用径向基函数作为核函数, 结果进行五折交叉验证.

经过迭代之后,LSTM个体最优适应度停留在13.6%,学习率最终保持在0.0013,神经元个数m最终稳定在8个;SVR个体最优适应度停留在11.9%;惩罚参数C最终保持在87,核函数参数g最终稳定在0.018.

3.4 点预测结论及算法适应性分析

选用前文中超参数对LSTM网络进行训练,实现对4个时序分量的预测.表2是预测结果和未经优化的LSTM网络、BP神经网络和SVR算法在3次不同天气情况中的预测性能对比.由表可见,在针对时序分量的预测环节中,LSTM相较于BP神经网络和SVR有更低的e_N和e_S,更具优势.对比GSA优化前后的LSTM预测评价指标, LSTM网络在经过GSA的优化后呈现出更好的性能,e_N平均降低11.7%,e_S平均降低16.2%.

表2 时序分量预测性能对比

Tab.2 Comparison of prediction performance of time series components

天气	分量	GSA-LSTM		LSTM		BP		SVR
天气	分量	e_S/%	e_N/%	e_S/%	e_N/%	e_S/%	e_N/%	e_S/%	e_N/%
晴天	H_IMF1	20.3	3.7	27.5	4.8	54.4	15.0	50.5	13.2
晴天	H_IMF2	21.4	3.5	26.3	5.2	52.3	14.3	49.4	14.5
晴天	H_IMF3	18.7	2.6	21.9	3.7	47.2	12.1	48.8	13.6
晴天	H_IMF7	18.2	2.1	19.9	3.6	48.1	9.9	41.0	10.3
转折	H_IMF1	47.0	10.1	59.5	14.7	94.4	44.2	89.2	42.7
转折	H_IMF2	39.2	9.7	60.3	15.6	94.6	43.1	87.6	42.0
转折	H_IMF3	35.4	6.4	52.0	12.3	88.7	38.5	88.7	36.3
转折	H_IMF7	29.1	5.5	52.3	13.3	83.3	40.3	82.1	36.9
阴雨	H_IMF1	45.5	13.2	70.6	44.0	110.5	55.5	100.3	57.2
阴雨	H_IMF2	40.3	12.1	65.5	42.5	103.2	52.4	97.0	51.4
阴雨	H_IMF3	41.2	10.1	71.3	35.4	99.9	43.6	92.3	40.2
阴雨	H_IMF7	38.9	7.8	62.2	32.1	101.2	44.2	90.1	41.1

新窗口打开| 下载CSV

同样选用前文中参数进行SVR建模,实现对3个随机分量的预测.表3是其预测结果和未经优化的SVR、BP神经网络和LSTM网络在3次预测中的性能对比.由表可见,在针对随机分量的预测环节中,SVR比BP神经网络和LSTM神经网络有更低的e_N和e_S,能够取得更好的效果.对比GSA优化前后的SVR预测评价指标,SVR算法在经过GSA的优化后呈现出更好的性能,e_N平均降低3.4%,e_S平均降低6.6%.

表3 随机分量预测性能对比

Tab.3 Comparison of prediction performance of random components

天气	分量	GSA-SVR		LSTM		BP		SVR
天气	分量	e_S/%	e_N/%	e_S/%	e_N/%	e_S/%	e_N/%	e_S/%	e_N/%
晴天	H_IMF4	25.7	7.1	39.0	10.5	42.3	10.0	36.2	9.2
晴天	H_IMF5	24.3	6.8	38.7	10.7	37.0	9.6	27.9	9.8
晴天	H_IMF6	22.4	5.6	32.2	8.8	31.1	8.4	30.2	8.0
转折	H_IMF4	60.0	17.5	75.4	34.7	86.3	35.4	67.8	22.3
转折	H_IMF5	57.1	20.3	69.7	32.8	83.3	34.9	62.4	24.6
转折	H_IMF6	50.9	15.4	75.2	30.9	75.1	31.6	55.3	18.7
阴雨	H_IMF4	62.4	20.5	87.3	42.4	99.9	45.4	69.4	22.9
阴雨	H_IMF5	56.2	19.6	89.0	40.0	97.1	41.0	64.4	27.1
阴雨	H_IMF6	54.8	18.7	83.5	34.9	89.0	35.7	59.9	21.0

新窗口打开| 下载CSV

将LSTM神经网络与SVR算法所得预测结果相加,即可得 CEEMDAN-GSA-LSTM和SVR模型点预测结果.表4是所提模型与EMD-GSA-LSTM模型、EMD-GSA-SVR模型、实时误差修正的XGboost模型和CNN-LSTM模型的预测效果对比.

表4 点预测结果性能对比

Tab.4 Comparison of point prediction performance

天气	CEEMDAN-GSA-LSTM 和SVR		EMD-GSA-LSTM		EMD-GSA-SVR		XGBoost-RC		CNN-LSTM
天气	e_S/%	e_N/%	e_S/%	e_N/%	e_S/%	e_N/%	e_S/%	e_N/%	e_S/%	e_N/%
晴天	22.8	3.7	29.6	5.0	38.6	9.1	30.1	4.5	24.2	9.1
转折	40.0	9.1	61.8	16.0	64.1	22.2	47.1	21.2	55.4	10.1
阴雨	48.5	14.6	78.4	40.3	63.0	26.2	54.7	32.5	50.7	19.6

新窗口打开| 下载CSV

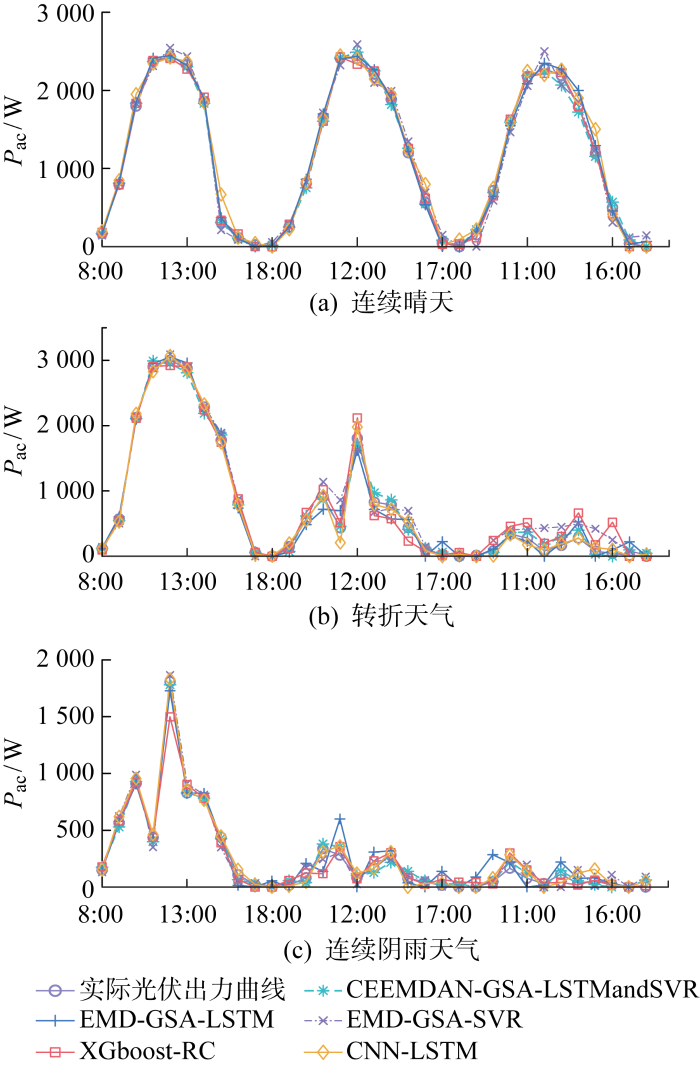
图6是表中几种预测模型的预测曲线与实际值的对比.图中:P_ac为交流功率.从表4和图6(a)中可以看出,在连续晴天、无气象条件突变的情况下,几种预测模型均具有良好的预测精度.相比较而言,所提模型e_N和e_S更小,预测效果更佳.结合图6(b)可以看出,在气象条件出现突变的转折天气情况下,光伏功率出力会发生较大波动,与连续晴天相比,各模型预测结果的e_N和e_S均有升高,预测精度均有下降.但在各预测模型中,所提模型的e_N和e_S保持最小,依然取得最好的预测效果.由图6(c)可以看出,在连续阴雨天气情况下,各模型的预测精度与晴天相比均大幅度降低,但所提模型的e_N和e_S相较而言保持最小,取得良好的预测效果.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 各模型点预测结果对比图

Fig.6 Comparison of prediction results of different models

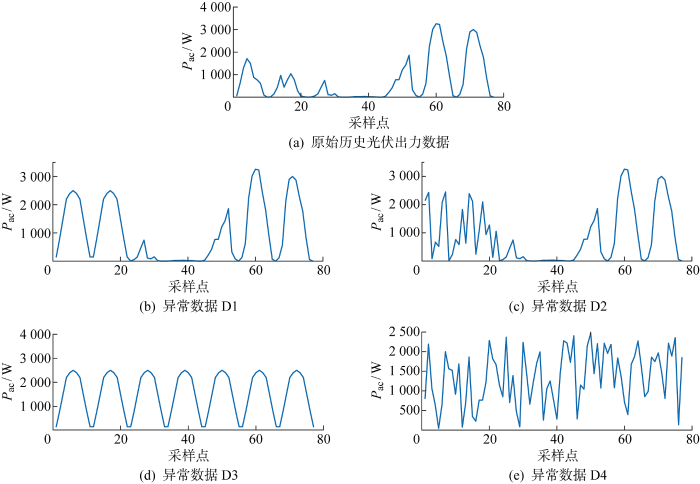
为了确保CEEMDAN-GSA-LSTM和SVR点预测模型具有良好的鲁棒性,设计一种算法适应性实验,在历史光伏出力数据出现异常错误的情况下验证算法准确性.为了模拟最恶劣的情况,沿用上文中连续阴雨天气下的情况进行试验,将77个历史光伏出力数据中的某些数据替换为异常数据后,再重新测试,实验所使用的历史光伏出力数据如图7所示,其中异常数据D1、D2是将第1~22个历史光伏出力数据替换为时序性数据和随机性数据的数据集合,异常数据D3、D4是将1~77个历史光伏处理数据全部替换为时序性数据和随机性数据的数据集合.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 五组光伏出力数据

Fig.7 Output data of five sets of PV

表5是在地面辐射、常规气象要素观测数据及经过计算的天文数据不变的情况下,仅改变原始历史数据时得到的适应性分析结果对比.可以看出,当原始数据出现异常错误时,各模型的预测精度都将下降,当原始数据完全不能对应时,预测精度达到最差.当出现各种类型的异常值错误时,与单独的LSTM和SVR相比,所提使用LSTM预测时序分量、使用SVR预测随机分量的方法预测精度更高,适应性更好.

表5 适应性分析结果对比

Tab.5 Comparison of adaptive analysis results

数据组别	CEEMDAN-GSA-LSTM和SVR		EMD-GSA-LSTM		EMD-GSA-SVR
数据组别	e_S/%	e_N/%	e_S/%	e_N/%	e_S/%	e_N/%
原始历史数据	48.5	14.6	78.4	40.3	63.0	26.2
D1	72.3	36.5	94.4	48.4	85.8	39.2
D2	73.4	38.9	98.9	53.3	91.1	57.1
D3	203.5	250.4	200.4	287.5	241.1	329.9
D4	212.3	233.9	240.1	298.8	242.9	310.5

新窗口打开| 下载CSV

整体来看,在各种气象条件和数据条件下,CEEMDAN-GSA-LSTM和SVR均能保持较好的预测性能,整体模型表现出较高的鲁棒性.

3.5 区间预测及其结论分析

使用CEEMDAN-GSA-LSTM和SVR模型对测试集前40个采样日的光伏出力以滑动窗口模式进行点预测,计算每个时刻的预测值与实际光伏出力的绝对误差ε.在点预测中,3个采样日内的预测精度呈现出递减趋势,因此,在区间预测过程中按照时间先后分类预测可以达到更好的效果.

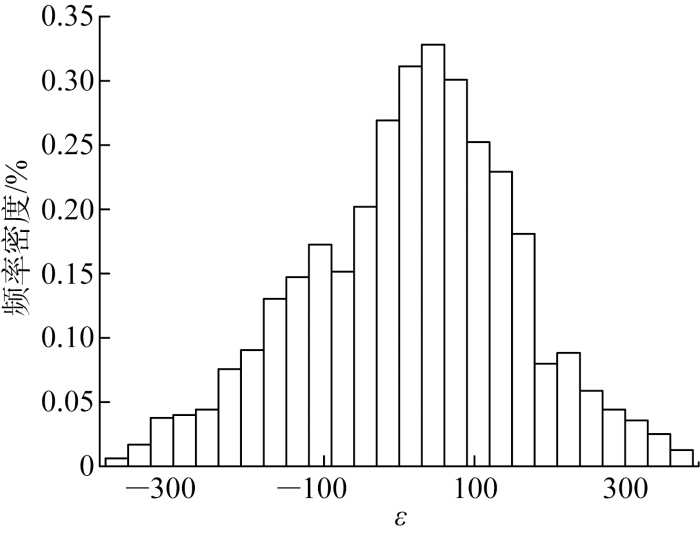
图8是40个采样日内共 1 254 个时刻的绝对误差的频率直方图,由图可见ε呈钟形分布,有一定的偏度特性.对ε进行Anderson-Darling正态性检验,得到P值小于0.05,不满足正态分布特征,正态分布不能有效地反映ε的整体分布情况.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 ε的频率直方图

Fig.8 Frequency histogram of ε

按第1、第2、第3个采样日将 1 254 个时刻的ε值分为3部分,每部分均有418个ε值,分别代表每次预测中第1~11,第12~22,第13~33个时刻的ε的集合,记为ε₁、ε₂、ε₃.

分别对ε₁、ε₂、ε₃作Anderson-Darling正态性检验,得到P值均小于0.05, 不满足正态分布特征,为了使其呈正态分布,对ε₁、ε₂、ε₃进行Johnson变换,得到ε'₁、ε'₂、ε'₃.

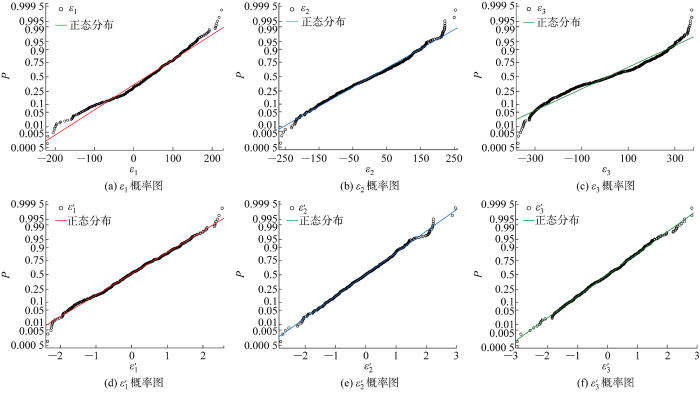
图9是ε₁、ε₂、ε₃进行Johnson变换前后的概率图,图中数据点越贴近正态分布的拟合曲线说明该数据越服从正态分布.由图可见,经过Johnson变换后,ε'₁、ε'₂、ε'₃更贴近曲线,对ε'₁、ε'₂、ε'₃进行正态性检验,结果中的P值均大于0.05,满足正态分布特征,可以认为符合正态分布.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 Johnson变换前后概率图对比

Fig.9 Comparison of probability graphs before and after Johnson transformation

利用正态分布分析ε'₁、ε'₂、ε'₃在不同置信水平下的置信区间,经过Johnson逆变换后得到对应的绝对误差范围,在点预测结果上叠加相应的绝对误差范围,得到区间预测结果.

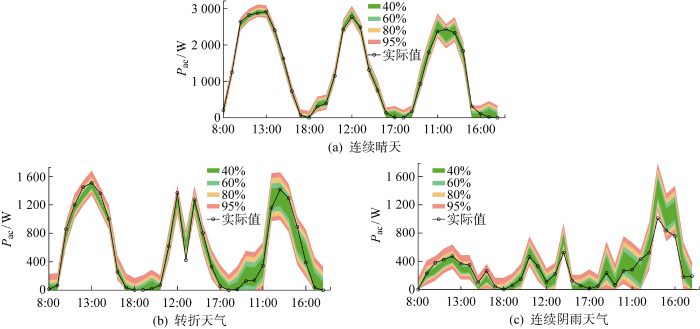
图10是所提区间预测方法在不同置信水平下的预测效果,表6是其对应的误差指标.由图10和表6可见,在不同天气条件下,预测对象基本能够落入95%置信水平所在区间内,当置信水平取40%时,连续阴雨天气下已经有超过50%的预测对象处于区间外.综合评价来看,在实际预测中,置信水平取80%~95%时,Q_PICP可以达到90%以上,能够取得较好效果.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 区间预测结果

Fig.10 Results of interval prediction

表6 不同置信水平下区间预测性能

Tab.6 Interval prediction performance at different confidence coefficients

置信水平/ %	晴天		转折		阴雨
置信水平/ %	Q_PICP	Q_PINAW	Q_PICP	Q_PINAW	Q_PICP	Q_PINAW
95	1.0000	0.1307	0.9697	0.2393	0.9394	0.2238
80	0.9394	0.0984	0.9394	0.1876	0.9091	0.1733
60	0.8485	0.0703	0.8182	0.1382	0.6970	0.1282
40	0.6364	0.0460	0.6364	0.0923	0.4848	0.0864

新窗口打开| 下载CSV

表7是所提区间预测方法和其他3种方法在95%置信水平不同天气条件下的预测结果.由表可见,在相同天气条件下,直接进行正态分布建模和logistic分布建模的方法与所提Johnson变换-正态分布建模的方法相比,Q_PINAW偏大,Q_PICP偏小.KDE作为当下较为流行的非参数估计方法,在3种天气条件下,Q_PICP均能达到93%以上,但它的Q_PINAW略大于所提区间预测方法,预测效果略劣于所提区间预测方法.

表7 区间预测结果性能对比

Tab.7 Comparison of interval prediction performance

天气	Johnson变换-正态分布		正态分布		logistic分布		KDE
天气	Q_PICP	Q_PINAW	Q_PICP	Q_PINAW	Q_PICP	Q_PINAW	Q_PICP	Q_PINAW
晴天	1.0000	0.1307	0.9697	0.2022	1.0000	0.2234	1.0000	0.1988
转折	0.9697	0.2393	0.9394	0.3375	0.9394	0.3257	0.9697	0.3028
阴雨	0.9394	0.2238	0.8788	0.3452	0.9091	0.3532	0.9394	0.2961

新窗口打开| 下载CSV

4 结论

为进一步完善光伏电站的消纳统计工作,针对光伏输出功率存在的间歇性和波动性问题,提出一种基于CEEMDAN-GSA-LSTM和SVR的光伏功率短期区间预测模型.经过算例分析,可以看出该模型具有以下优势:

(1) 兼顾气象环境因素的时序性和随机性,在各种天气下均能得到较好的预测结果.

(2) 本模型参数并非固定,可以根据当地气象环境数据进行本地化修正.

(3) 相比于其他模型,本模型点预测精度更高,预测效果有所提升.

(4) 给出较为精准的预测区间,解决了传统点预测难以量化光伏发电中不确定性的问题.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

国家发展改革会, 国家能源局.

关于促进新时代新能源高质量发展的实施方案

[EB/OL].(2022-05-30)[2022-05-30]. http://zfxxgk.nea.gov.cn/2022-05/30/c_1310608539.htm.

URL [本文引用: 1]

National Development and Reform Commission, National Energy Administration.

The implementation plan for promoting the high-quality development of new energy in a new era

[EB/OL].(2022-05-30)[2022-05-30]. http://zfxxgk.nea.gov.cn/2022-05/30/c_1310608539.htm.

URL [本文引用: 1]

[2]

张雲钦, 程起泽, 蒋文杰, 等.

基于EMD-PCA-LSTM的光伏功率预测模型

[J]. 太阳能学报, 2021, 42(9): 62-69.