自主垂直起降混合无人机能同时实现旋翼飞行器的灵活起降能力和大展弦比固定翼飞行器的长时续航优势,具有巨大军事和商业应用价值,成为一种有潜力的飞行器[1 ] .其解决了旋翼无人机的航程和飞行速度有限的问题,也摆脱了传统固定翼飞行器发射和着陆的繁琐,具有对起飞环境要求低、巡航时间长、应用范围广等优点,是当前无人机研究的热点[2 ] .变体飞行器可以调整其构型以适应不同类型的任务,可以始终保持优良的性能并有效完成复杂环境下的任务[3 -4 ] ,将变体飞行器技术应用到垂直起降上可以使飞行器灵活适应各种任务需求.
目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力.
关于垂直起降飞行器姿态稳定控制问题,国内外学者提出许多相关的控制方法,如比例积分微分(proportion integral differential, PID)控制[18 ] 、有限时间自适应控制[19 ] 、滑模控制[20 ] 、预测控制[21 ] 、最优控制[22 ] ,这些控制方法对于未知的非线性系统具有优势,但所针对的对象都是固定翼垂直起降飞行器,并未考虑结构变形对控制的影响,并且这些方法在非线性情况下会非常复杂.
本文提出一种垂直起降的折叠翼飞行器(folding wing aircraft,FWA)方案,通过折展机翼来解决旋翼垂直起飞阶段的风干扰问题,并在平飞时展开机翼,实现大展弦比飞行.首先,建立包含折叠变形的9自由度动力学模型,根据集中式变形条件下的气动特性给出零升迎角和失速迎角随变形的攻角边界.然后,对比分析折叠翼和固定翼在爬升段的飞行效率,并基于线性化模型分析姿态与结构耦合动力学的特点,分别设计串级PID实现折叠翼折展和姿态的控制.
1 基于拟拉格朗日的多体动力学建模
1.1 折叠翼飞行器构型
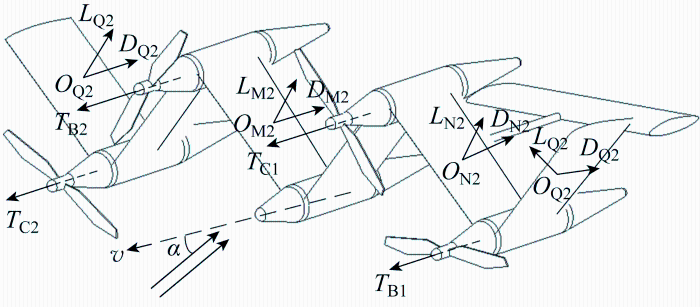
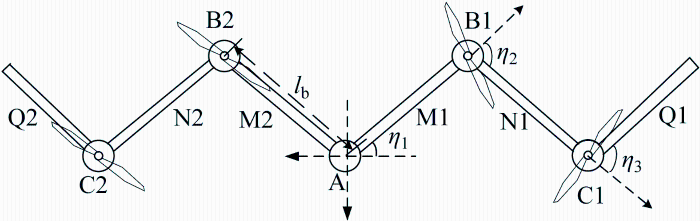
本文设计的FWA由5段机舱和6段单元翼串联组成,如图1 所示.图中:FWA左右两侧始终保持对称,中心机舱命名为A,由中心向外侧依次连接着单元翼M、N、Q和副舱B、C,其中左侧命名为M1,右侧命名为M2,以此类推.A的质心点相对于地面的飞行速度为v ,并称此处攻角为全局攻角α. 各单元翼分别受到气动力Lw 、Dw ,其中w 表示单元翼M、N、Q.4个机舱中各布置一旋翼,机舱受到螺旋桨推力Tb ,其中b 表示机舱B、C.单元翼M、N、Q分别受到安置于机舱A、B、C中的折展机构提供的折展力矩τi ,驱动单元翼绕机舱纵轴折展运动,其中 i =1,2,3,后侧安装有升降舵以提高纵向稳定性.与其他折叠翼飞行器相比,FWA单元翼的变形驱动机构由副翼变为折展机构,转向操纵可以通过非对称变形形成的向心力来实现,垂直起降阶段侧重于纵向机动,本文针对对称变形研究折叠翼的运动特性.
图1
图1
折叠翼的气动力分布
Fig.1
Aerodynamic distribution of FWA
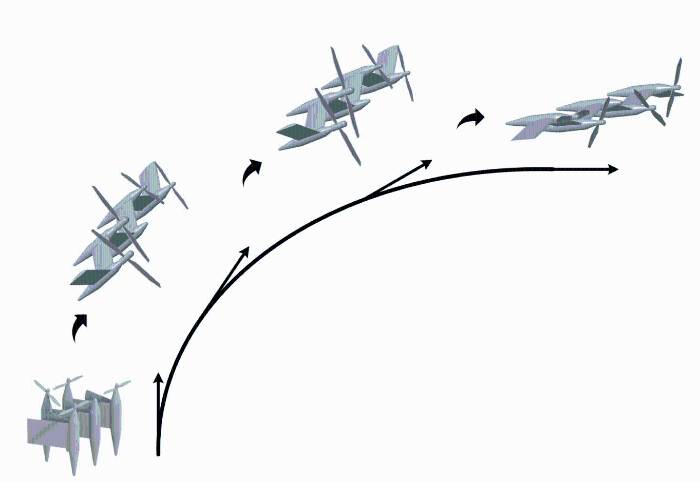
折叠翼倾转和机翼折叠过程如图2 所示.为了避免侧风干扰,在起降阶段收拢机翼并利用旋翼装置提供升力,随着姿态由垂直过渡到平飞,飞行速度逐渐增大,折展机构展开机翼,平衡重力的来源由旋翼过渡到翼面,从而实现大展弦比和长续航飞行.
图2
图2
爬升过程的倾转折叠示意图
Fig.2
Schematic of tilt-folding during climb
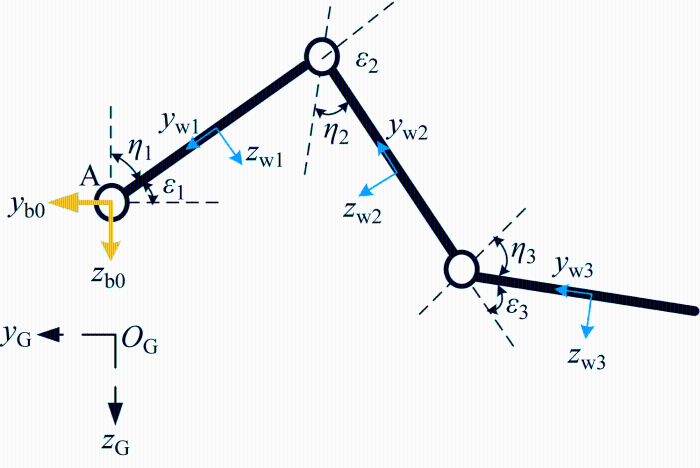
为便于对FWA进行运动描述和受力分析,引入固定于中心机舱上的全局坐标系和各单元翼上的局部坐标系,如图3 所示.全局坐标系O A x A y A z A 原点位于中心机舱A的质心, 局部坐标系Ow xw yw zw 原点选取为各单元翼的质心,惯性坐标系用O G x G y G z G 表示,除此之外还有全局气流坐标系O a x a y a z a 以及各单元翼的局部气流坐标系O a w xa w ya w za w .
图3
图3
局部坐标系及折叠角的定义
Fig.3
Definition of local coordinate system and folding angle
由于机舱具有对称性,机舱的转动惯量J b x y J b x z J b y z 表1 所示.
1.2 广义坐标和拟速度
中心舱串联各单元翼和副舱,表示系统的平移和旋转自由度的中心,为方便描述FWA位形选取广义坐标为
(1) $\boldsymbol{q}=\left[\begin{array}{lll}\boldsymbol{r}_{\mathrm{A}} & \boldsymbol{\theta}_{\mathrm{A}} & \boldsymbol{\eta}\end{array}\right]^{\mathrm{T}}$
式中:$\boldsymbol{r}_{\mathrm{A}}$为中心舱A质心在惯性坐标系下的位置矢量;$\boldsymbol{\theta}_{\mathrm{A}}$为中心舱A相对于地面惯性系的欧拉姿态角;$\boldsymbol{\eta}=\left[\begin{array}{lll}\eta_{1} & \eta_{2} & \eta_{3}\end{array}\right]^{\mathrm{T}} $为单元翼间的相对折展角,折展角的定义见图3 .
(2) $\boldsymbol{\omega}=\left[\begin{array}{lll}\boldsymbol{v}_{\mathrm{A}} & \boldsymbol{\omega}_{\mathrm{A}} & \boldsymbol{\omega}_{\eta}\end{array}\right]^{\mathrm{T}}$
式中:$v_{\mathrm{A}}$为中心舱质心在中心坐标系下的平移速度;$\omega_{\mathrm{A}}$为中心舱在中心坐标系下的转动角速度;$\boldsymbol{\omega}_{\eta}=\left[\begin{array}{lll}\omega_{1} & \omega_{2} & \omega_{3}\end{array}\right]^{\mathrm{T}} $为相应的折叠角速率,拟速度与广义速率的关系为
(3) $\left.\begin{array}{l}\boldsymbol{v}_{\mathrm{A}}=\boldsymbol{E}_{\mathrm{G}}^{\mathrm{A}} \dot{\boldsymbol{r}}_{\mathrm{A}} \\\boldsymbol{\omega}_{\mathrm{A}}=\boldsymbol{T}_{\omega} \dot{\boldsymbol{\theta}}_{\mathrm{A}} \\\boldsymbol{\omega}_{\eta}=\dot{\boldsymbol{\eta}}\end{array}\right\}$
式中:E G A Tω 为欧拉角速率和体轴角速度的转换矩阵.
1.3 多体串联运动学
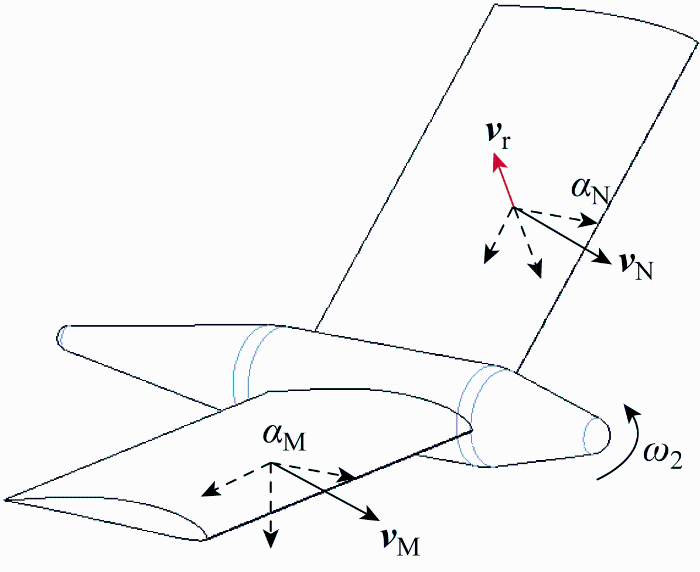
由于变形过程中各单元翼的速度和姿态均发生改变,单元翼局部攻角αw 因受折展运动而引起的附加相对速度v r 的影响,以单元翼M和N间的相对运动为例,如图4 所示.因此,在运动学建模中需要计算每个单元翼上的局部速度和局部攻角,各单元翼在局部体坐标系下的角速度和速度可以表示为
(4) $\left.\begin{array}{l}\boldsymbol{\omega}_{\mathrm{M}}=\boldsymbol{E}_{\mathrm{A}}^{\mathrm{M}} \boldsymbol{\omega}_{\mathrm{A}}+\left[\begin{array}{lll}\omega_{1} & 0 & 0\end{array}\right]^{\mathrm{T}} \\\boldsymbol{v}_{\mathrm{M}}=\boldsymbol{E}_{\mathrm{A}}^{\mathrm{M}} \boldsymbol{v}_{\mathrm{A}}+\boldsymbol{\omega}_{\mathrm{M}} \times \boldsymbol{r}_{\mathrm{AM}}^{\mathrm{M}}\end{array}\right\}$
(5) $\left.\begin{array}{l}\boldsymbol{v}_{\mathrm{B}}=\boldsymbol{E}_{\mathrm{A}}^{\mathrm{M}} \boldsymbol{v}_{\mathrm{A}}+\boldsymbol{\omega}_{\mathrm{M}} \times \boldsymbol{r}_{\mathrm{AB}}^{\mathrm{M}} \\\boldsymbol{\omega}_{\mathrm{N}}=\boldsymbol{E}_{\mathrm{M}}^{\mathrm{N}} \boldsymbol{\omega}_{\mathrm{M}}+\left[\begin{array}{lll}\boldsymbol{\omega}_{2} & 0 & 0\end{array}\right]^{\mathrm{T}} \\\boldsymbol{v}_{\mathrm{N}}=\boldsymbol{E}_{\mathrm{M}}^{\mathrm{N}} \boldsymbol{v}_{\mathrm{B}}+\boldsymbol{\omega}_{\mathrm{N}} \times \boldsymbol{r}_{\mathrm{BN}}^{\mathrm{N}}\end{array}\right\}$
(6) $\left.\begin{array}{l}\boldsymbol{v}_{\mathrm{C}}=\boldsymbol{E}_{\mathrm{M}}^{\mathrm{N}} \boldsymbol{v}_{\mathrm{B}}+\boldsymbol{\omega}_{\mathrm{N}} \times \boldsymbol{r}_{\mathrm{BC}}^{\mathrm{N}} \\\boldsymbol{\omega}_{\mathrm{Q}}=\boldsymbol{E}_{\mathrm{N}}^{\mathrm{Q}} \boldsymbol{\omega}_{\mathrm{N}}+\left[\begin{array}{ccc}\omega_{3} & 0 & 0\end{array}\right]^{\mathrm{T}} \\\boldsymbol{v}_{\mathrm{Q}}=\boldsymbol{E}_{\mathrm{N}}^{\mathrm{Q}} \boldsymbol{v}_{\mathrm{C}}+\boldsymbol{\omega}_{\mathrm{Q}} \times \boldsymbol{r}_{\mathrm{CQ}}^{\mathrm{Q}}\end{array}\right\}$
式中:r 为局部坐标系(上标字母)下从机舱(第1个下标字母)质心指向单元翼或另一机舱(第2个下标字母)质心的矢量;E 为坐标系(下标字母)到坐标系(上标字母)的坐标转换矩阵.
图4
图4
折叠过程单元翼的局部攻角
Fig.4
Local angle of attack of unit wing during folding
根据各单元翼的局部速度vw 可以计算出单元翼的气动力和力矩:
(7) $\left.\begin{array}{l}L_{w}=\rho\left|\boldsymbol{v}_{w}\right|^{2} S_{\mathrm{ref}} C_{L} / 2 \\D_{w}=\rho\left|\boldsymbol{v}_{w}\right|^{2} S_{\mathrm{ref}} C_{D} / 2 \\M_{w}=\rho\left|\boldsymbol{v}_{w}\right|{ }^{2} S_{\mathrm{ref}} C_{M} C_{\mathrm{ref}} / 2\end{array}\right\}$
式中:CL 、CD 、CM 分别为单元翼的升力、阻力、俯仰力矩系数;ρ 为空气密度;S ref 、c ref 分别为参考面积和参考弦长.
1.4 广义力和广义力矩
除重力外,FWA所受到的主动力还包括各单元翼的气动力和气动力矩、位于副舱的螺旋桨推力、每个单元翼受到折展机构的折展力矩以及中心舱受到的升降舵力矩.为了方便计算广义力和广义力矩,各单元翼和机舱所受合力在中心坐标系下可以表示为
(8) $\left.\begin{array}{l}\boldsymbol{F}_{\mathrm{A}}^{\mathrm{A}}=\boldsymbol{E}_{\mathrm{G}}^{\mathrm{A}} \boldsymbol{G}_{\mathrm{A}}^{\mathrm{E}} \\\boldsymbol{F}_{\mathrm{M}}^{\mathrm{A}}=\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{F}_{\mathrm{M}}^{\mathrm{M}}+\boldsymbol{E}_{\mathrm{G}}^{\mathrm{A}} \boldsymbol{G}_{\mathrm{M}}^{\mathrm{E}} \\\boldsymbol{F}_{\mathrm{B}}^{\mathrm{A}}=\boldsymbol{E}_{\mathrm{B}}^{\mathrm{A}} \boldsymbol{T}_{\mathrm{B}}^{\mathrm{B}}+\boldsymbol{E}_{\mathrm{G}}^{\mathrm{A}} \boldsymbol{G}_{\mathrm{B}}^{\mathrm{E}} \\\boldsymbol{F}_{\mathrm{N}}^{\mathrm{A}}=\boldsymbol{E}_{\mathrm{N}}^{\mathrm{A}} \boldsymbol{F}_{\mathrm{N}}^{\mathrm{N}}+\boldsymbol{E}_{\mathrm{G}}^{\mathrm{A}} \boldsymbol{G}_{\mathrm{N}}^{\mathrm{E}} \\\boldsymbol{F}_{\mathrm{C}}^{\mathrm{A}}=\boldsymbol{E}_{\mathrm{C}}^{\mathrm{T}} \boldsymbol{T}_{\mathrm{C}}^{\mathrm{C}}+\boldsymbol{E}_{\mathrm{G}}^{\mathrm{G}} \boldsymbol{G}_{\mathrm{C}}^{\mathrm{E}} \\\boldsymbol{F}_{\mathrm{Q}}^{\mathrm{A}}=\boldsymbol{E}_{\mathrm{Q}}^{\mathrm{A}} \boldsymbol{F}_{\mathrm{Q}}^{\mathrm{Q}}+\boldsymbol{E}_{\mathrm{G}}^{\mathrm{A}} \boldsymbol{G}_{\mathrm{Q}}^{\mathrm{E}}\end{array}\right\}$
式中:G w E G b E F w w w 在其局部体坐标系下的气动力;T b b b 在其局部坐标系下的螺旋桨推力.
广义坐标r A 对应的广义力Q r A
(9) $\boldsymbol{Q}_{r_{\mathrm{A}}}=\sum_{w} \boldsymbol{F}_{w}^{\mathrm{A}}+\sum_{b} \boldsymbol{F}_{b}^{\mathrm{A}}$
式中:∑ w ∑ b
广义坐标θ A 对应的广义力矩Q θ A
(10) $\begin{aligned}Q_{\theta_{\mathrm{A}}}= & \sum_{w}\left(\boldsymbol{E}_{w}^{\mathrm{A}} \boldsymbol{M}_{w}\right)+\boldsymbol{M}_{\mathrm{e}}+\left(\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{AM}}^{\mathrm{M}}\right) \times \boldsymbol{F}_{\mathrm{M}}^{\mathrm{A}}+ \\& \left(\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{AB}}^{\mathrm{M}}\right) \times \boldsymbol{F}_{\mathrm{B}}^{\mathrm{A}}+\left(\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{AB}}^{\mathrm{M}}+\boldsymbol{E}_{\mathrm{N}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{BN}}^{\mathrm{N}}\right) \times \boldsymbol{F}_{\mathrm{N}}^{\mathrm{A}}+ \\& \left(\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{AB}}^{\mathrm{M}}+\boldsymbol{E}_{\mathrm{N}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{BC}}^{\mathrm{N}}\right) \times \boldsymbol{F}_{\mathrm{C}}^{\mathrm{A}}+ \\& \left(\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{AB}}^{\mathrm{M}}+\boldsymbol{E}_{\mathrm{N}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{BC}}^{\mathrm{N}}+\boldsymbol{E}_{\mathrm{Q}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{CQ}}^{\mathrm{Q}}\right) \times \boldsymbol{F}_{\mathrm{Q}}^{\mathrm{A}}\end{aligned}$
式中:Mw 为单元翼w 的气动力矩;M e 为升降舵力矩.
广义力矩Qη 分别对应了各折叠角ηi ,因此定义Qη =Q η 1 Q η 2 Q η 3 T . 根据广义虚位移的任意性,给定折叠角ηi 虚位移δηi ,其中i =1,2,3,而其他折展角虚位移都为0. 各单元翼和机舱质心位置在中心坐标系下表示为r A w r A b ηi 广义力矩Q η i
(11) $Q_{\eta_{i}}=\frac{\sum_{w} \boldsymbol{F}_{w}^{\mathrm{A}} \delta \boldsymbol{r}_{w}^{\mathrm{A}}+\sum_{b} \boldsymbol{F}_{b}^{\mathrm{A}} \delta \boldsymbol{r}_{b}^{\mathrm{A}}+2 \tau_{i} \delta \eta_{i}}{\delta \eta_{i}}$
1.5 动力学方程
假设系统没有势能,拉格朗日量只包含动能,把重力当作外力来处理,拟拉格朗日方程公式[23 ⇓ -25 ] 可以表示为
(12) $\begin{array}{l}\frac{\mathrm{d}}{\mathrm{~d} t}\left(\frac{\partial T}{\partial \boldsymbol{v}_{\mathrm{A}}}\right)+\widetilde{\boldsymbol{\omega}}_{\mathrm{A}} \frac{\partial T}{\partial \boldsymbol{v}_{\mathrm{A}}}-\boldsymbol{E}_{\mathrm{G}}^{\mathrm{A}} \frac{\partial T}{\partial \boldsymbol{r}_{\mathrm{A}}}=\boldsymbol{Q}_{r_{\mathrm{A}}} \\\frac{\mathrm{~d}}{\mathrm{~d} t}\left(\frac{\partial T}{\partial \boldsymbol{\omega}_{\mathrm{A}}}\right)+\widetilde{\boldsymbol{v}}_{\mathrm{A}} \frac{\partial T}{\partial \boldsymbol{v}_{\mathrm{A}}}+\widetilde{\boldsymbol{\omega}}_{\mathrm{A}} \frac{\partial T}{\partial \boldsymbol{\omega}_{\mathrm{A}}}- \\\quad\left(\boldsymbol{T}_{\omega}^{-1}\right)^{\mathrm{T}} \frac{\partial T}{\partial \boldsymbol{\theta}_{\mathrm{A}}}=\boldsymbol{Q}_{\boldsymbol{\theta}_{\mathrm{A}}} \\\frac{\mathrm{~d}}{\mathrm{~d} t}\left(\frac{\partial T}{\partial \boldsymbol{\omega}_{\eta}}\right)-\frac{\partial T}{\partial \boldsymbol{\eta}}=\boldsymbol{Q}_{\boldsymbol{\eta}}\end{array}$
式中:上标~为对应向量的反对称矩阵;t 为时间;T 为系统总动能.
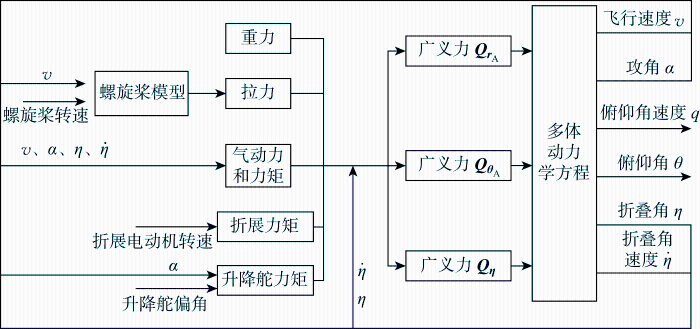
折叠翼多体动力学模型存在5个输入量,分别为3个折展力矩、升降舵偏角以及螺旋桨转速;输出量分别为飞行速度、全局攻角、俯仰角、俯仰角速度、折叠角和折叠角速度.多体动力学模型结构如图5 所示.
图5
图5
多体动力学模型仿真模块图
Fig.5
Module diagram for multi-body dynamics model simulation
对于任意数量单元翼串联的折叠翼建模,拟拉格朗日方程依然可以使用,选取各单元翼间的二面角作为广义坐标,根据多体串联运动学建立各单元翼的运动特性,并根据升力线理论建立各单元翼的气动力和力矩.根据虚位移原理,计算每个广义坐标所对应的广义力,将方程式(12)中的第3项扩展为多单元翼的形式,即可得到n 个单元翼串联的多体动力学模型:
(13) $\left.\begin{array}{c}\frac{\mathrm{d}}{\mathrm{~d} t}\left(\frac{\partial T}{\partial \omega_{1}}\right)-\frac{\partial T}{\partial \eta_{1}}=Q_{1} \\\vdots \\\frac{\mathrm{~d}}{\mathrm{~d} t}\left(\frac{\partial T}{\partial \omega_{n}}\right)-\frac{\partial T}{\partial \eta_{n}}=Q_{n}\end{array}\right\}$
2 折叠翼飞行器空气动力学特性
为了降低翼型运动的复杂性,将FWA的变形规划为对称变形下的集中式变形,如图6 所示.集中式变形所满足的条件如下:
(14) η 1 = η η 2 = - 2 η η 3 = 2 η η · 1 = η · η · 2 = - 2 η · η · 3 = 2 η ·
图6
图6
集中式变形的构型
Fig.6
Configurations of centralized deformation
2.1 多维复合力学机理建模
利用升力线法可以计算考虑动态折叠下的气动力.根据多体串联运动学计算各单元翼的气动力,可得FWA系统的气动力和气动力矩分别为
(15) $\begin{aligned}\boldsymbol{F}_{\mathrm{a}}= & \boldsymbol{E}_{\mathrm{A}}^{a} \sum_{w}\left(\boldsymbol{E}_{w}^{\mathrm{A}} \boldsymbol{F}_{w}^{w}\right) \end{aligned}$
(16) $\begin{aligned}\boldsymbol{M}_{\mathrm{a}}= & \boldsymbol{E}_{\mathrm{A}}^{a}\left[\sum_{w}\left(\boldsymbol{E}_{w}^{\mathrm{A}} \boldsymbol{M}_{w}\right)+\left(\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{AM}}^{\mathrm{M}}\right) \times\left(\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{F}_{\mathrm{M}}^{\mathrm{M}}\right)+\right. \\& \left(\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{AB}}^{\mathrm{M}}+\boldsymbol{E}_{\mathrm{N}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{BN}}^{\mathrm{N}}\right) \times\left(\boldsymbol{E}_{\mathrm{N}}^{\mathrm{A}} \boldsymbol{F}_{\mathrm{N}}^{\mathrm{N}}\right)+ \\& \left.\left(\boldsymbol{E}_{\mathrm{M}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{AB}}^{\mathrm{M}}+\boldsymbol{E}_{\mathrm{N}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{BC}}^{\mathrm{N}}+\boldsymbol{E}_{\mathrm{Q}}^{\mathrm{A}} \boldsymbol{r}_{\mathrm{CQ}}^{\mathrm{Q}}\right) \times\left(\boldsymbol{E}_{\mathrm{Q}}^{\mathrm{A}} \boldsymbol{F}_{\mathrm{Q}}^{\mathrm{Q}}\right)\right]\end{aligned}$
式中:E A a E A w w 到中心坐标系A的坐标变换;Mw 为单元翼w 所受气动力矩.
2.2 折叠翼的气动特性
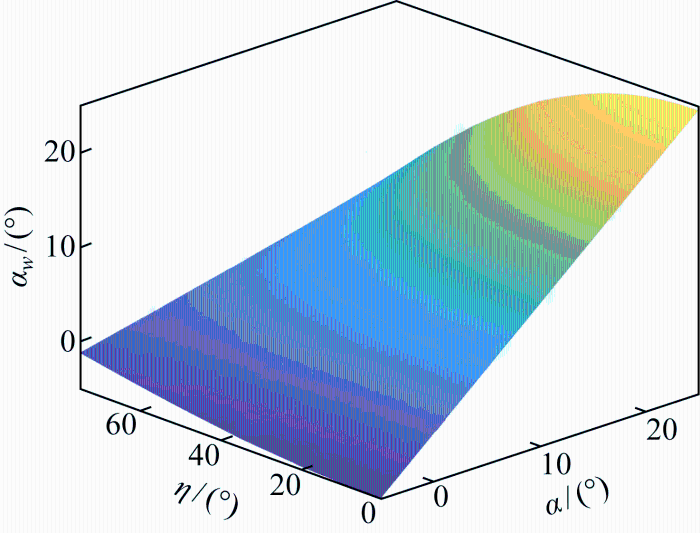
在无侧滑对称变形条件下,左右两侧机舱和单元翼对中心的侧向力和力矩相互抵消.在集中式静态变形下,单元翼的局部攻角的变化如图7 所示.单元翼的局部攻角在变形条件下小于全局攻角,因此,即使全局攻角为失速攻角也可以使飞行器处于良好的飞行性能下.
图7
图7
静态折叠下的局部攻角
Fig.7
Localized angle of attack in static folding
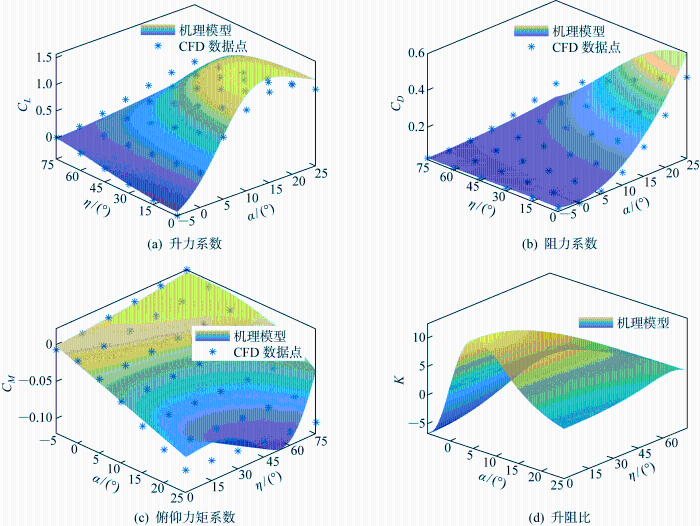
FWA的气动力和力矩如图8 所示,FWA的升力和阻力随着折叠角增大而减小,升阻比K 在小攻角范围内随着折叠角的增大而增大,在攻角α =6°时达到最大值.此外机翼收拢会使FWA产生正俯仰力矩,因此幅度过大的变形容易导致静不稳定.为了验证机理建模的准确性,利用Fluent软件获得FWA在集中式变形下的气动数据.假设变形响应足够快,变形产生的非定常气动力的影响可以忽略不计[26 ] ,计算流体力学软件CFD的计算验证了机理建模的合理性.
图8
图8
集中式变形下的气动力和力矩随迎角的变化
Fig.8
Aerodynamic forces and moments versus angle of approach in centralized deformation
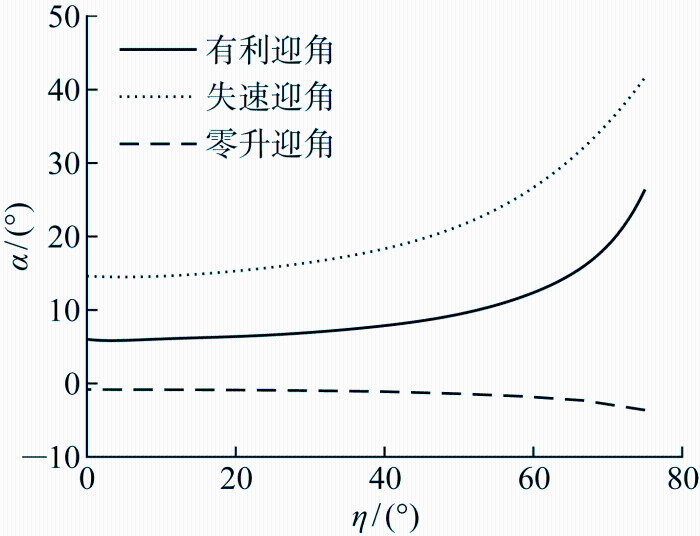
最大升力系数时的失速攻角随变形的变化如图9 所示,此边界为变形过程的迎角上限.随着折叠角增大,失速迎角会增大.不同折叠角下零升系数为迎角下限,超过此边界折叠翼的升力为负值.同时,也可以得到最大升阻比时的迎角随变形的有利迎角曲线,在小变形下有利迎角约为攻角上下限的中线位置,安全裕度较大.
图9
图9
折叠翼飞行攻角的限制随变形的变化
Fig.9
Limit of angle of attack of FWA flight versus deformation
3 飞行力学特性分析
为了验证FWA变构型策略的飞行效率,构建静态的固定翼六自由度动力学方程,在相同的爬升曲线下,对比固定翼策略和变构型策略两者的稳态配平曲线.
3.1 爬升性能分析
对于固定翼和FWA模型,纵向配平可以分别描述如下:对于固定翼模型,给定不同飞行速度v 和固定的折叠角η ,求解得到俯仰角θ ,并控制螺旋桨和升降舵,使得纵向运动速率v · α · q · θ · τi ,以保持折叠角速率η · η ·
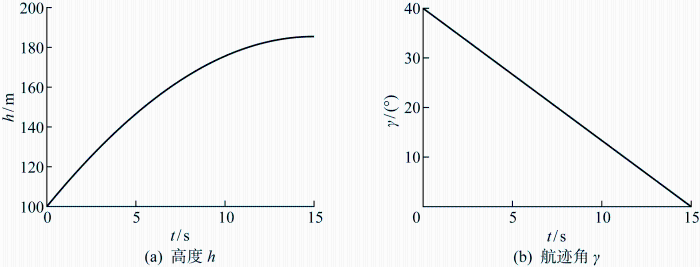
为验证变构型在爬升过程的飞行效率,给定爬升曲线如图10 所示,在折叠角η =55°的固定翼构型下,给定飞行器爬升飞行速度v =17 m/s.在变构型控制策略爬升中不再约束单元翼折叠角,飞行器在爬升过程中折叠角从55°收拢变化至5°展平状态.
图10
图10
爬升轨迹设计
Fig.10
Design of climbing trajectory
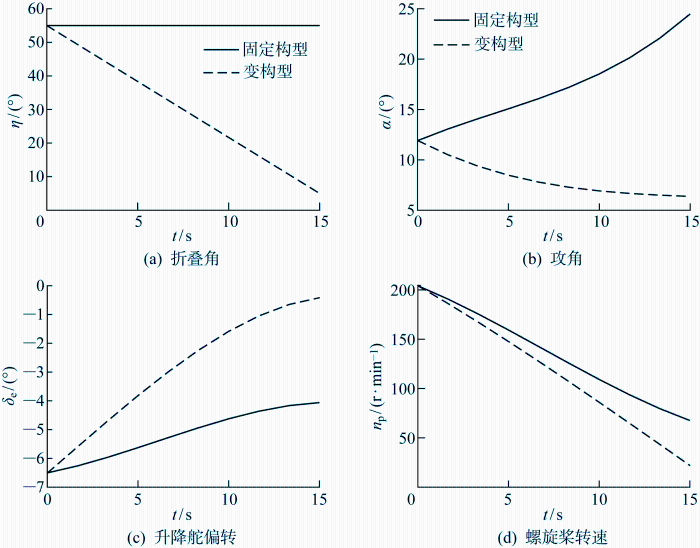
固定翼和变构型的稳态爬升过程如图11 所示,变构型控制策略可以避免大攻角,以安全裕度更大的小攻角飞行;同时螺旋桨转速(n p )显著减小,降低飞行能耗;升降舵舵面(δ e )偏转减小,提高了飞行操纵性.
图11
图11
固定构型和变构型的爬升性能分析
Fig.11
Climbing performance analysis of fixed and variable configurations
3.2 模态耦合特性分析
以定直平飞条件下的稳定构型作为分析对象,在配平点线性化得到状态矩阵,其特征值如表2 所示.除传统飞行模态外,FWA还存在一对由结构折叠状态量主导的折叠模态.翼尖对接飞行器具有固有的不稳定性[27 ] ,FWA也同样如此,其中一个折叠模态为发散状态,且折叠模态的时间常数很短,对飞行稳定性影响较大,因此需要增稳控制系统.
为了确定各模态的主导状态量,特征向量的灵敏度矩阵如表3 所示.折叠状态量只与纵向状态量耦合,而不与横向状态量耦合,这是因为机翼对称运动下侧向力和侧向力矩均为零.短周期模态、长周期模态中折叠状态量的比例较低,而折叠模态1中出现折叠角与攻角耦合的现象,折叠模态2为几乎完全由折叠状态量主导的发散模态,因此在姿态控制时需要考虑结构的影响.
3.3 开环仿真
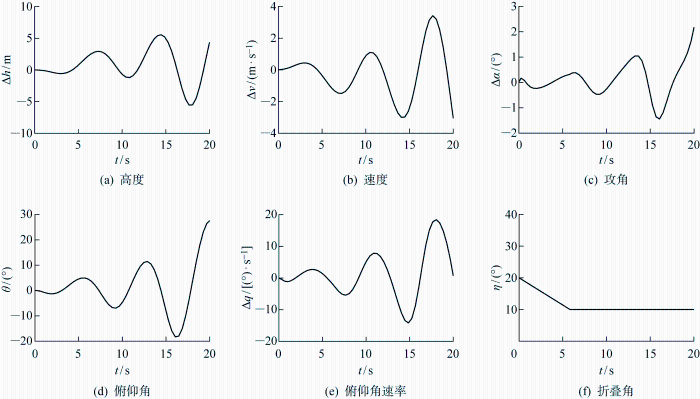
非线性动力学模型开环动力学仿真如图12 所示.初始条件为定直平飞,飞行速度为17 m/s,飞行攻角为7.19°,单元翼折叠角从20°匀速展开到10°,折展角的减小会产生正升力和正俯仰力矩,导致飞行高度增加和抬头动作,系统随着结构变形开始发散,结构变形与纵向运动的耦合主要表现在攻角和俯仰角速度上,响应分析与模态分析结果一致.
图12
图12
对称变形下的开环动力学仿真
Fig.12
Simulation of open-loop dynamics in symmetric deformation
4 飞行控制设计和闭环仿真
在平飞状态下,FWA的结构和姿态间存在弱耦合,因此针对姿态和结构可以分别设计增稳控制系统.
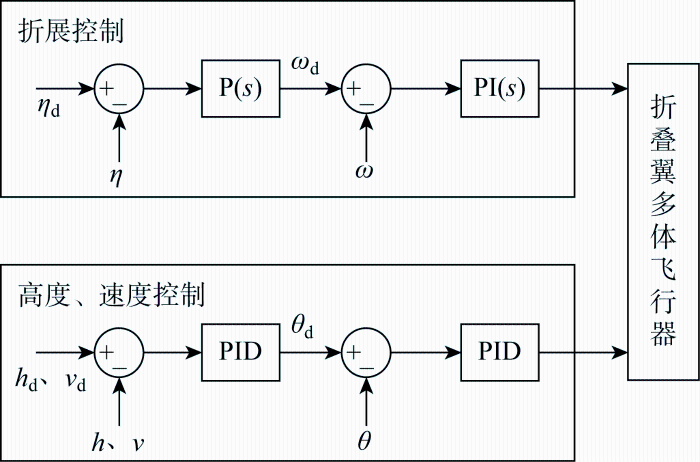
FWA的飞行动力学与传统的单架飞行器有所不同,但传统控制设计的基本原理依然可以使用,倾转过程中无人机的掉高问题需要考虑[28 ] ,整个飞行控制结构如图13 所示.采用串联式PID控制器,其中包括飞行器姿态高度控制器以及折展控制器,通过升降舵控制俯仰,螺旋桨控制飞行速度,折展机构控制折叠运动,其中P(s )为比例控制,PI(s )为比例积分控制,下标d表示预期指令.
图13
图13
控制结构图
Fig.13
Control structure
4.1 控制方案
针对结构和姿态分别设置控制通道,平飞折展机构用于单元翼折叠控制,控制律由内环和外环控制组成,外环控制用于折叠运动控制,内环用于折叠稳定.其公式表示如下:
(17) η · d = K P , η ( η d - η ) τ i = K P , η · ( η · d - η · ) + K I , η · ∫ ( η · d - η · ) d t
(18) $\begin{aligned}F_{\mathrm{T}}= & K_{\mathrm{P}, v}\left(v_{\mathrm{d}}-v\right)+K_{\mathrm{I}, v} \int\left(v_{\mathrm{d}}-v\right) \mathrm{d} t+ \\& K_{\mathrm{D}, v} \frac{\mathrm{~d}}{\mathrm{~d} t}\left(v_{\mathrm{d}}-v\right)\end{aligned}$
(19) θ d = K P , h ( h d - h ) + K I , h ∫ ( h d - h ) d t + K D , h d d t ( h d - h ) δ e = K P , θ ( θ d - θ ) + K I , θ ∫ ( θ d - θ ) d t + K D , θ d d t ( θ d - θ )
式中:K P, c K I, c K D, c c 表示各状态变量.
4.2 闭环仿真
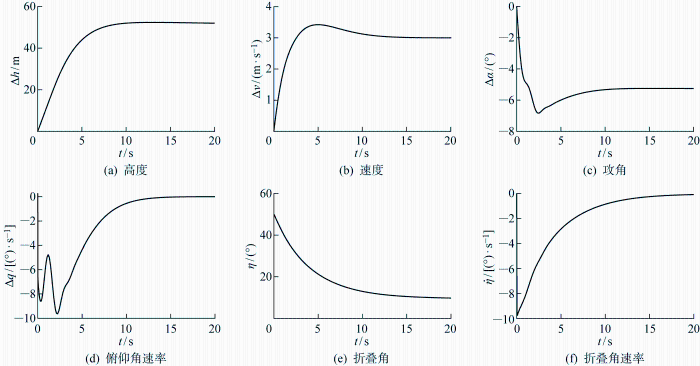
为了实现倾转折叠的飞行过渡过程,基于非线性多体动力学模型进行仿真,控制输入为螺旋桨转速、折展力矩和升降舵面.初始条件为匀速爬升的配平点,航迹角γ =30°,飞行速度v =17 m/s,攻角α =9.88°,折叠角η =50°,飞行高度h =100 m,目标是爬升到150 m,且折叠角展开到10°,飞行速度增大到20 m/s.相关状态量的闭环仿真结果如图14 所示,PID 控制器使折展角顺利展开,抑制了发散的折叠模态,同时也顺利完成了加速倾转的过程.
图14
图14
爬升过程倾转变形的闭环仿真
Fig.14
Closed-loop simulation of tilt-shift deformation during climb
5 结论
(1) 基于升力线理论分析静态变形下的气动和结构耦合特性,发现单元翼的局部攻角会在变形条件下小于折叠翼全局攻角,因此折叠翼可在大攻角范围内飞行,并给出折叠翼飞行攻角随变形的安全范围.此外,机翼收拢会使折叠翼产生正俯仰力矩,因此幅度过大的变形容易导致静不稳定.
(2) 基于拟拉格朗日方程建立考虑结构气动耦合效应的9自由度多体动力学模型,相比于传统的固定翼飞行器,折叠翼在倾转过程中可以避免大攻角失速,具有更好的飞行操纵性,并且能显著降低巡航段的飞行能耗.
(3) 对定直平飞时的配平点进行稳定性分析,折叠翼多出两个由折叠状态量主导的折叠模态,短周期模态、长周期模态中折叠状态量的耦合程度较低,而在折叠模态中出现折叠状态量与攻角耦合的现象,因此在姿态控制时需要考虑结构的影响.
(4) 基于串级PID控制器,设计爬升过程的姿态和结构变形稳定器,利用折叠角速度作为内环控制器,折叠角作为外环控制器的反馈量,实现折叠翼倾转过程中机翼展开和高度爬升.
基于上述结论,本设计方案适用于需要垂直起降和飞续航能力的应用场景中,如城市空中交通和应急救援.然而,还存在一定的局限性有待后续研究:①由于机翼受到旋翼的尾流干扰,所以在折叠翼悬停和垂直起飞时,旋翼-机翼、旋翼-旋翼间气动耦合效应可能会显著影响飞行性能,并降低飞行器的稳定性和载荷能力;②分布式变形以及非对称变形在特定条件下可以提升飞行器的性能,本文主要分析集中式变形的纵向特性,但尚未深入研究复杂的分布式变形和非对称变形研究,未来将进一步优化变形方式;③在飞行模式间的过渡阶段,飞行控制系统设计需要考虑结构和飞行强耦合性,本文仅分析了定直平飞下飞行与结构的耦合特性,但未涉及过渡模式下非稳态过程的耦合特性分析,将结构与姿态的相互影响引入飞行控制系统的设计中,可以有效提高模式转变过程的控制能力.
参考文献
View Option
[1]
REHAN M AKRAM F SHAHZAD A et al Vertical take-off and landing hybrid unmanned aerial vehicles: An overview
[J]. The Aeronautical Journal 2022 , 126 (1306 ): 2017 -2057 .
[本文引用: 1]
[2]
韦振鹏 , 刘峰 , 杨森 . 垂直起降固定翼无人机发展现状与技术要点
[J]. 飞机设计 2024 , 44 (1 ): 5 -13 .
[本文引用: 1]
WEI Zhenpeng LIU Feng YANG Sen Development and key technologies of vertical take-off and landing UAV with fixed wing
[J]. Aircraft Design 2024 , 44 (1 ): 5 -13 .
[本文引用: 1]
[3]
CHU L L LI Q GU F et al Design, modeling, and control of morphing aircraft: A review
[J]. Chinese Journal of Aeronautics 2022 , 35 (5 ): 220 -246 .
[本文引用: 1]
[4]
MISRA A JAYACHANDRAN S KENCHE S et al A review on vertical take-off and landing (VTOL) tilt-rotor and tilt wing unmanned aerial vehicles (UAVs)
[J]. Journal of Engineering 2022 , 2022 : 1803638 .
[本文引用: 1]
[5]
吴林峰 , 李春文 . 尾座式垂直起降无人机在时变侧风干扰下的轨迹跟踪控制
[J]. 清华大学学报(自然科学版) 2022 , 62 (1 ): 179 -188 .
[本文引用: 1]
WU Linfeng LI Chunwen Position tracking control for a tailsitter VTOL UAV experiencing time-varying crosswind disturbances
[J]. Journal of Tsinghua University (Science and Technology) 2022 , 62 (1 ): 179 -188 .
[本文引用: 1]
[6]
程宇轩 , 周洲 , 王科雷 . 分布式推进垂直起降固定翼的过渡走廊边界研究
[J]. 西北工业大学学报 2022 , 40 (6 ): 1195 -1203 .
[本文引用: 1]
CHENG Yuxuan ZHOU Zhou WANG Kelei Research on transition corridor boundary of distributed propulsion VTOL fixed wing
[J]. Journal of Northwestern Polytechnical University 2022 , 40 (6 ): 1195 -1203 .
[本文引用: 1]
[7]
吴瑷菁 . 垂起倾转旋翼无人机过渡模式控制系统设计 [D]. 哈尔滨 : 哈尔滨工业大学 , 2020 .
[本文引用: 1]
WU Aijing Control system design on transition stage of tilt rotor UAV [D]. Harb in:Harbin Institute of Technology, 2020 .
[本文引用: 1]
[8]
王鹏 , 陈浩岚 , 鲍存余 , 等 . 变形飞行器建模及控制方法研究综述
[J]. 宇航学报 2022 , 43 (7 ): 853 -865 .
[本文引用: 1]
WANG Peng CHEN Haolan BAO Cunyu et al Review on modeling and control methods of morphing vehicle
[J]. Journal of Astronautics 2022 , 43 (7 ): 853 -865 .
[本文引用: 1]
[9]
ZHU E T ZHOU Z LI H D Modal analysis and flight validation of compound multi-body aircraft
[J]. Aerospace 2023 , 10 (5 ): 442.
[本文引用: 1]
[10]
刘东旭 , 谢长川 , 洪冠新 . 翼尖铰接复合飞行器动力学特性研究
[J]. 北京航空航天大学学报 2021 , 47 (11 ): 2311 -2321 .
[本文引用: 1]
LIU Dongxu XIE Changchuan HONG Guanxin Dynamic characteristics of wingtip-jointed composite aircraft
[J]. Journal of Beijing University of Aeronautics & Astronautics 2021 , 47 (11 ): 2311 -2321 .
[本文引用: 1]
[11]
马仲航 , 张执南 . 多旋翼无人机遥操机械臂多功能仿真实验平台的设计与实现
[J]. 上海交通大学学报 2020 , 54 (6 ): 636 -642 .
[本文引用: 1]
MA Zhonghang ZHANG Zhinan Design and realization of a versatile simulation platform for telecontrol multi-rotor unmanned aerial vehicle with a robotic arm
[J]. Journal of Shanghai Jiao Tong University 2020 , 54 (6 ): 636 -642 .
[本文引用: 1]
[12]
NIU C YAN X T CHEN B Y Control-oriented modeling of a high-aspect-ratio flying wing with coupled flight dynamics
[J]. Chinese Journal of Aeronautics 2023 , 36 (4 ): 409 -422 .
[本文引用: 1]
[13]
GAO L JIN H Z ZHAO J et al Flight dynamics modeling and control of a novel catapult launched tandem-wing micro aerial vehicle with variable sweep
[J]. IEEE Access 2018 , 6 : 42294 -42308 .
[本文引用: 1]
[14]
GAO L ZHU Y H ZANG X Z et al Dynamic analysis and experiment of multiple variable sweep wings on a tandem-wing MAV
[J]. Drones 2023 , 7 (9 ): 552.
[本文引用: 1]
[15]
邹旭 , 刘贞报 , 赵闻 , 等 . 尾座式垂直起降无人机过渡轨迹优化方法研究
[J/OL]. 北京航空航天大学学报 https://doi.org/10.13700/j.bh.1001-5965.2023.0458 .
[本文引用: 1]
ZOU Xu LIU Zhen-bao ZHAO Wen et al Optimization method of transition trajectory for tail-sitter unmanned aerial vehicles
[J/OL]. Journal of Beijing University of Aeronautics & Astronautics https://doi.org/10.13700/j.bh.1001-5965.2023.0458 .
[本文引用: 1]
[16]
DAUD FILHO A C BELO E M A tilt-wing VTOL UAV configuration: Flight dynamics modelling and transition control simulation
[J]. The Aeronautical Journal 2024 , 128 (1319 ): 152 -177 .
[本文引用: 1]
[17]
PEDRO S TOMÁS D LOBO DO VALE J et al Design and performance quantification of VTOL systems for a canard aircraft
[J]. The Aeronautical Journal 2021 , 125 (1292 ): 1768 -1791 .
[本文引用: 1]
[18]
程子欢 , 裴海龙 . 涵道尾座式垂直起降飞行器全包线飞行控制
[J]. 控制理论与应用 2021 , 38 (11 ): 1863 -1873 .
[本文引用: 1]
CHENG Zihuan PEI Hailong A full envelope flight controller for ducted fan tail sitter vertical take-off and landing
[J]. Control Theory & Applications 2021 , 38 (11 ): 1863 -1873 .
[本文引用: 1]
[19]
DENG X F HUANG Y Q XU B Z et al Position and attitude tracking finite-time adaptive control for a VTOL aircraft using global fast terminal sliding mode control
[J]. Mathematics 2023 , 11 (12 ): 27 -32 .
[本文引用: 1]
[20]
夏济宇 , 周洲 , 王正平 , 等 . 基于NLESO的倾转动力无人机垂直起降模态轨迹跟踪控制
[J]. 西北工业大学学报 2023 , 41 (1 ): 1 -10 .
[本文引用: 1]
XIA Jiyu ZHOU Zhou WANG Zhengping et al Trajectory tracking control of tilt-propulsion UAV vertical take-off and landing mode based on NLESO
[J]. Journal of Northwestern Polytechnical University 2023 , 41 (1 ): 1 -10 .
[本文引用: 1]
[21]
曹煜琪 , 付皓然 , 高飞 , 等 . 基于MPCC的鸭翼尾座式垂直起降无人机轨迹跟踪控制算法
[J]. 航空学报 2023 , 44 (Sup.2) : 501 -511 .
[本文引用: 1]
CAO Yuqi FU Haoran GAO Fei et al Trajectory tracking control algorithm for canard-equipped tail-sitting vertical takeoff and landing UAV based on MPCC
[J]. Acta Aeronautica et Astronautica Sinica 2023 , 44 (Sup.2) : 501 -511 .
[本文引用: 1]
[22]
WEI Q L YANG Z S SU H Z et al Online adaptive dynamic programming for optimal self-learning control of VTOL aircraft systems with disturbances
[J]. IEEE Transactions on Automation Science & Engineering 2024 , 21 (1 ): 343 -352 .
[本文引用: 1]
[23]
MEIROVITCH L STEMPLE T Hybrid equations of motion for flexible multibody systems using quasicoordinates
[J]. Journal of Guidance , Control , & Dynamics 1995 , 18 (4 ): 678 -688 .
[本文引用: 1]
[24]
蒋国江 . 扑翼变形飞行器的动力学建模与飞行仿真 [D]. 长沙 : 国防科学技术大学 , 2015 .
[本文引用: 1]
JIANG Guojiang Dynamic modeling and flight simulation of flapping wing aerocraft [D]. Changsha : National University of Defense Technology , 2015 .
[本文引用: 1]
[25]
安朝 , 谢长川 , 孟杨 , 等 . 多体组合式无人机飞行力学稳定性分析及增稳控制研究
[J]. 工程力学 2021 , 38 (11 ): 248 -256 .
[本文引用: 1]
AN Chao XIE Changchuan MENG Yang et al Flight dynamics and stable control analyses of multi-body aircraft
[J]. Engineering Mechanics 2021 , 38 (11 ): 248 -256 .
[本文引用: 1]
[26]
杜万闪 , 周洲 , 拜昱 , 等 . 组合式飞行器多体动力学建模与飞行力学特性
[J]. 兵工学报 2023 , 44 (8 ): 2245 -2262 .
DOI:10.12382/bgxb.2022.0282
[本文引用: 1]
为精确、完整地描述组合式多体飞行器空间运动位形,基于拟坐标形式的Lagrange方程提出反映相对滚转运动的8自由度组合式三体飞行器动力学建模方法。采用计算流体力学方法建立考虑气动耦合效应的组合式飞行器系统气动力数据库。通过算例将所建模型与ADAMS软件的仿真结果进行对比,验证所建模型的准确性。在此基础上,进行配平方案及飞行力学特性研究,分析比较飞行器在不同配平状态的动力学特性,并基于串级PID控制方法进行增稳控制研究。研究结果表明:所建模型有效反映了组合式飞行器的相对运动;在给定配平方案及飞行工况后,该构型飞行器存在“对称下反”和“对称上反”两个配平状态,在两个状态下的相对滚转运动静稳定性显著不同;除了传统飞行力学模态,该构型飞行器还存在由相对滚转运动主导的4个新生运动模态,按运动特性可分为复合对称运动和复合反对称运动两类;针对在无控状态下该构型飞行器无法长期保持稳定飞行的问题,所提增稳控制方案合理有效,可以快速镇定发散的飞行力学系统;所提建模方法和增稳控制方案可为多体飞行器设计分析提供指导和参考。
DU Wanshan ZHOU Zhou BAI Yu et al Study on multibody dynamics modeling and flight dynamic characteristics of combined aircraft
[J]. Acta Armamentarii 2023 , 44 (8 ): 2245 -2262 .
DOI:10.12382/bgxb.2022.0282
[本文引用: 1]
To precisely and completely describe the location and shape of the combined multibody aircraft, a dynamic modeling method of the 8 DOF combined three-body aircraft reflecting relative rolling motion is proposed using Lagrange’s equations with quasi-coordinates. The aerodynamic database of the combined multibody aircraft system considering the aerodynamic coupling effect is established by the CFD method. The accuracy of the model is verified by comparing the model with ADAMS software through a numerical example. Based on this, the trim scheme and flight dynamic characteristics of the aircraft in different trim states are studied. The stability augmentation control is studied based on the cascade PID control method. The results show that the established model effectively reflects the relative motion of the combined aircraft. With the given trim scheme and flight condition, the aircraft of this configuration has two trim states of "symmetrical lower inverse" and "symmetrical upper inverse", and the static stability of relative rolling motion in the two states is quite different. In addition to the traditional flight mechanics mode, there are 4 new motion modes dominated by relative rolling motion, which can be divided into composite symmetric motion and composite antisymmetric motion according to the motion characteristics. To address the problem that the aircraft with this configuration cannot keep stable flight for a long time without control, the stability augmentation control scheme is reasonable and effective, which can quickly stabilize the divergent flight mechanics system. The proposed modeling method and stabilization control scheme can provide guidance and reference for the design and analysis of multibody aircrafts.
[27]
MENG Y AN C XIE C C et al Conceptual design and flight test of two wingtip-docked multi-body aircraft
[J]. Chinese Journal of Aeronautics 2022 , 35 (12 ): 144 -155 .
[本文引用: 1]
[28]
刘志豪 , 闵荣 , 方成 , 等 . 多飞行模式垂直起降无人机过渡飞行控制策略
[J]. 上海交通大学学报 2019 , 53 (10 ): 1173 -1181 .
[本文引用: 1]
LIU Zhihao MIN Rong FANG Cheng et al Transition flight control strategy of multiple flight mode vertical take-off and landing unmanned aerial vehicle
[J]. Journal of Shanghai Jiao Tong University 2019 , 53 (10 ): 1173 -1181 .
[本文引用: 1]
Vertical take-off and landing hybrid unmanned aerial vehicles: An overview
1
2022
... 自主垂直起降混合无人机能同时实现旋翼飞行器的灵活起降能力和大展弦比固定翼飞行器的长时续航优势,具有巨大军事和商业应用价值,成为一种有潜力的飞行器[1 ] .其解决了旋翼无人机的航程和飞行速度有限的问题,也摆脱了传统固定翼飞行器发射和着陆的繁琐,具有对起飞环境要求低、巡航时间长、应用范围广等优点,是当前无人机研究的热点[2 ] .变体飞行器可以调整其构型以适应不同类型的任务,可以始终保持优良的性能并有效完成复杂环境下的任务[3 -4 ] ,将变体飞行器技术应用到垂直起降上可以使飞行器灵活适应各种任务需求. ...
垂直起降固定翼无人机发展现状与技术要点
1
2024
... 自主垂直起降混合无人机能同时实现旋翼飞行器的灵活起降能力和大展弦比固定翼飞行器的长时续航优势,具有巨大军事和商业应用价值,成为一种有潜力的飞行器[1 ] .其解决了旋翼无人机的航程和飞行速度有限的问题,也摆脱了传统固定翼飞行器发射和着陆的繁琐,具有对起飞环境要求低、巡航时间长、应用范围广等优点,是当前无人机研究的热点[2 ] .变体飞行器可以调整其构型以适应不同类型的任务,可以始终保持优良的性能并有效完成复杂环境下的任务[3 -4 ] ,将变体飞行器技术应用到垂直起降上可以使飞行器灵活适应各种任务需求. ...
Development and key technologies of vertical take-off and landing UAV with fixed wing
1
2024
... 自主垂直起降混合无人机能同时实现旋翼飞行器的灵活起降能力和大展弦比固定翼飞行器的长时续航优势,具有巨大军事和商业应用价值,成为一种有潜力的飞行器[1 ] .其解决了旋翼无人机的航程和飞行速度有限的问题,也摆脱了传统固定翼飞行器发射和着陆的繁琐,具有对起飞环境要求低、巡航时间长、应用范围广等优点,是当前无人机研究的热点[2 ] .变体飞行器可以调整其构型以适应不同类型的任务,可以始终保持优良的性能并有效完成复杂环境下的任务[3 -4 ] ,将变体飞行器技术应用到垂直起降上可以使飞行器灵活适应各种任务需求. ...
Design, modeling, and control of morphing aircraft: A review
1
2022
... 自主垂直起降混合无人机能同时实现旋翼飞行器的灵活起降能力和大展弦比固定翼飞行器的长时续航优势,具有巨大军事和商业应用价值,成为一种有潜力的飞行器[1 ] .其解决了旋翼无人机的航程和飞行速度有限的问题,也摆脱了传统固定翼飞行器发射和着陆的繁琐,具有对起飞环境要求低、巡航时间长、应用范围广等优点,是当前无人机研究的热点[2 ] .变体飞行器可以调整其构型以适应不同类型的任务,可以始终保持优良的性能并有效完成复杂环境下的任务[3 -4 ] ,将变体飞行器技术应用到垂直起降上可以使飞行器灵活适应各种任务需求. ...
A review on vertical take-off and landing (VTOL) tilt-rotor and tilt wing unmanned aerial vehicles (UAVs)
1
2022
... 自主垂直起降混合无人机能同时实现旋翼飞行器的灵活起降能力和大展弦比固定翼飞行器的长时续航优势,具有巨大军事和商业应用价值,成为一种有潜力的飞行器[1 ] .其解决了旋翼无人机的航程和飞行速度有限的问题,也摆脱了传统固定翼飞行器发射和着陆的繁琐,具有对起飞环境要求低、巡航时间长、应用范围广等优点,是当前无人机研究的热点[2 ] .变体飞行器可以调整其构型以适应不同类型的任务,可以始终保持优良的性能并有效完成复杂环境下的任务[3 -4 ] ,将变体飞行器技术应用到垂直起降上可以使飞行器灵活适应各种任务需求. ...
尾座式垂直起降无人机在时变侧风干扰下的轨迹跟踪控制
1
2022
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Position tracking control for a tailsitter VTOL UAV experiencing time-varying crosswind disturbances
1
2022
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
分布式推进垂直起降固定翼的过渡走廊边界研究
1
2022
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Research on transition corridor boundary of distributed propulsion VTOL fixed wing
1
2022
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
1
2020
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
1
2020
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
变形飞行器建模及控制方法研究综述
1
2022
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Review on modeling and control methods of morphing vehicle
1
2022
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Modal analysis and flight validation of compound multi-body aircraft
1
2023
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
翼尖铰接复合飞行器动力学特性研究
1
2021
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Dynamic characteristics of wingtip-jointed composite aircraft
1
2021
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
多旋翼无人机遥操机械臂多功能仿真实验平台的设计与实现
1
2020
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Design and realization of a versatile simulation platform for telecontrol multi-rotor unmanned aerial vehicle with a robotic arm
1
2020
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Control-oriented modeling of a high-aspect-ratio flying wing with coupled flight dynamics
1
2023
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Flight dynamics modeling and control of a novel catapult launched tandem-wing micro aerial vehicle with variable sweep
1
2018
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Dynamic analysis and experiment of multiple variable sweep wings on a tandem-wing MAV
1
2023
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
尾座式垂直起降无人机过渡轨迹优化方法研究
1
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Optimization method of transition trajectory for tail-sitter unmanned aerial vehicles
1
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
A tilt-wing VTOL UAV configuration: Flight dynamics modelling and transition control simulation
1
2024
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
Design and performance quantification of VTOL systems for a canard aircraft
1
2021
... 目前,国内外学者针对垂直起降飞行器开展了一定研究.吴林峰等[5 ] 针对尾座式垂直起降无人机面临的时变侧风干扰问题,设计了一种基于新型姿态提取算法的轨迹跟踪控制方法,但并未考虑大展弦比飞行器受测风的影响.程宇轩等[6 ] 针对一种分布式推进垂直起降固定翼飞行器,基于机翼升力特性和动力单元需用功率的限制条件进行过渡走廊研究.吴瑷菁[7 ] 详述了垂起倾转旋翼机在旋翼模式、固定翼模式以及过渡模式下的飞行控制方案.当前关于变体飞行器的多体动力学建模方法主要分为牛顿欧拉法、拉格朗日法、凯恩法[8 ] .在翼尖铰接的变体组合式飞行器的研究中,Zhu等[9 ] 将三单元连接飞行器的模态区分为对称和非对称模态组,并解析推导出模态随构型的演化.刘东旭等[10 ] 以两单元铰接飞行器为研究对象,发现其多出2个分别由相对滚转角和相对滚转角速度主导的发散模态.马仲航等[11 ] 建立空中遥操机械臂整体动力学模型,实现对机器人系统的动力学精确描述和可视化仿真.Niu等[12 ] 对三体组合式复合飞行器进行模态灵敏度分析和输入输出配对,证明了在控制器设计中考虑结构动力学的必要性.Gao等[13 ] 利用可变后掠角代替传统的副翼,利用飞行试验[14 ] 验证副翼和升降舵进行姿态控制可行.传统的垂直起降飞行器多以尾坐式[15 ] 、倾转旋翼[16 ] 、鸭翼[17 ] 为主,飞行控制系统和机体结构设计与制造难度大,受测风等环境影响大.在垂直起飞时收拢机翼并依靠旋翼平衡重力,在巡航时展平并利用机翼升力平衡重力,将折叠翼变体方案与垂直起降结合的方案可以有效减少测风的影响,降低设计与制造难度,同时有效提高续航能力. ...
涵道尾座式垂直起降飞行器全包线飞行控制
1
2021
... 关于垂直起降飞行器姿态稳定控制问题,国内外学者提出许多相关的控制方法,如比例积分微分(proportion integral differential, PID)控制[18 ] 、有限时间自适应控制[19 ] 、滑模控制[20 ] 、预测控制[21 ] 、最优控制[22 ] ,这些控制方法对于未知的非线性系统具有优势,但所针对的对象都是固定翼垂直起降飞行器,并未考虑结构变形对控制的影响,并且这些方法在非线性情况下会非常复杂. ...
A full envelope flight controller for ducted fan tail sitter vertical take-off and landing
1
2021
... 关于垂直起降飞行器姿态稳定控制问题,国内外学者提出许多相关的控制方法,如比例积分微分(proportion integral differential, PID)控制[18 ] 、有限时间自适应控制[19 ] 、滑模控制[20 ] 、预测控制[21 ] 、最优控制[22 ] ,这些控制方法对于未知的非线性系统具有优势,但所针对的对象都是固定翼垂直起降飞行器,并未考虑结构变形对控制的影响,并且这些方法在非线性情况下会非常复杂. ...
Position and attitude tracking finite-time adaptive control for a VTOL aircraft using global fast terminal sliding mode control
1
2023
... 关于垂直起降飞行器姿态稳定控制问题,国内外学者提出许多相关的控制方法,如比例积分微分(proportion integral differential, PID)控制[18 ] 、有限时间自适应控制[19 ] 、滑模控制[20 ] 、预测控制[21 ] 、最优控制[22 ] ,这些控制方法对于未知的非线性系统具有优势,但所针对的对象都是固定翼垂直起降飞行器,并未考虑结构变形对控制的影响,并且这些方法在非线性情况下会非常复杂. ...
基于NLESO的倾转动力无人机垂直起降模态轨迹跟踪控制
1
2023
... 关于垂直起降飞行器姿态稳定控制问题,国内外学者提出许多相关的控制方法,如比例积分微分(proportion integral differential, PID)控制[18 ] 、有限时间自适应控制[19 ] 、滑模控制[20 ] 、预测控制[21 ] 、最优控制[22 ] ,这些控制方法对于未知的非线性系统具有优势,但所针对的对象都是固定翼垂直起降飞行器,并未考虑结构变形对控制的影响,并且这些方法在非线性情况下会非常复杂. ...
Trajectory tracking control of tilt-propulsion UAV vertical take-off and landing mode based on NLESO
1
2023
... 关于垂直起降飞行器姿态稳定控制问题,国内外学者提出许多相关的控制方法,如比例积分微分(proportion integral differential, PID)控制[18 ] 、有限时间自适应控制[19 ] 、滑模控制[20 ] 、预测控制[21 ] 、最优控制[22 ] ,这些控制方法对于未知的非线性系统具有优势,但所针对的对象都是固定翼垂直起降飞行器,并未考虑结构变形对控制的影响,并且这些方法在非线性情况下会非常复杂. ...
基于MPCC的鸭翼尾座式垂直起降无人机轨迹跟踪控制算法
1
2023
... 关于垂直起降飞行器姿态稳定控制问题,国内外学者提出许多相关的控制方法,如比例积分微分(proportion integral differential, PID)控制[18 ] 、有限时间自适应控制[19 ] 、滑模控制[20 ] 、预测控制[21 ] 、最优控制[22 ] ,这些控制方法对于未知的非线性系统具有优势,但所针对的对象都是固定翼垂直起降飞行器,并未考虑结构变形对控制的影响,并且这些方法在非线性情况下会非常复杂. ...
Trajectory tracking control algorithm for canard-equipped tail-sitting vertical takeoff and landing UAV based on MPCC
1
2023
... 关于垂直起降飞行器姿态稳定控制问题,国内外学者提出许多相关的控制方法,如比例积分微分(proportion integral differential, PID)控制[18 ] 、有限时间自适应控制[19 ] 、滑模控制[20 ] 、预测控制[21 ] 、最优控制[22 ] ,这些控制方法对于未知的非线性系统具有优势,但所针对的对象都是固定翼垂直起降飞行器,并未考虑结构变形对控制的影响,并且这些方法在非线性情况下会非常复杂. ...
Online adaptive dynamic programming for optimal self-learning control of VTOL aircraft systems with disturbances
1
2024
... 关于垂直起降飞行器姿态稳定控制问题,国内外学者提出许多相关的控制方法,如比例积分微分(proportion integral differential, PID)控制[18 ] 、有限时间自适应控制[19 ] 、滑模控制[20 ] 、预测控制[21 ] 、最优控制[22 ] ,这些控制方法对于未知的非线性系统具有优势,但所针对的对象都是固定翼垂直起降飞行器,并未考虑结构变形对控制的影响,并且这些方法在非线性情况下会非常复杂. ...
Hybrid equations of motion for flexible multibody systems using quasicoordinates
1
1995
... 假设系统没有势能,拉格朗日量只包含动能,把重力当作外力来处理,拟拉格朗日方程公式[23 ⇓ -25 ] 可以表示为 ...
1
2015
... 假设系统没有势能,拉格朗日量只包含动能,把重力当作外力来处理,拟拉格朗日方程公式[23 ⇓ -25 ] 可以表示为 ...
1
2015
... 假设系统没有势能,拉格朗日量只包含动能,把重力当作外力来处理,拟拉格朗日方程公式[23 ⇓ -25 ] 可以表示为 ...
多体组合式无人机飞行力学稳定性分析及增稳控制研究
1
2021
... 假设系统没有势能,拉格朗日量只包含动能,把重力当作外力来处理,拟拉格朗日方程公式[23 ⇓ -25 ] 可以表示为 ...
Flight dynamics and stable control analyses of multi-body aircraft
1
2021
... 假设系统没有势能,拉格朗日量只包含动能,把重力当作外力来处理,拟拉格朗日方程公式[23 ⇓ -25 ] 可以表示为 ...
组合式飞行器多体动力学建模与飞行力学特性
1
2023
... FWA的气动力和力矩如图8 所示,FWA的升力和阻力随着折叠角增大而减小,升阻比K 在小攻角范围内随着折叠角的增大而增大,在攻角α =6°时达到最大值.此外机翼收拢会使FWA产生正俯仰力矩,因此幅度过大的变形容易导致静不稳定.为了验证机理建模的准确性,利用Fluent软件获得FWA在集中式变形下的气动数据.假设变形响应足够快,变形产生的非定常气动力的影响可以忽略不计[26 ] ,计算流体力学软件CFD的计算验证了机理建模的合理性. ...
Study on multibody dynamics modeling and flight dynamic characteristics of combined aircraft
1
2023
... FWA的气动力和力矩如图8 所示,FWA的升力和阻力随着折叠角增大而减小,升阻比K 在小攻角范围内随着折叠角的增大而增大,在攻角α =6°时达到最大值.此外机翼收拢会使FWA产生正俯仰力矩,因此幅度过大的变形容易导致静不稳定.为了验证机理建模的准确性,利用Fluent软件获得FWA在集中式变形下的气动数据.假设变形响应足够快,变形产生的非定常气动力的影响可以忽略不计[26 ] ,计算流体力学软件CFD的计算验证了机理建模的合理性. ...
Conceptual design and flight test of two wingtip-docked multi-body aircraft
1
2022
... 以定直平飞条件下的稳定构型作为分析对象,在配平点线性化得到状态矩阵,其特征值如表2 所示.除传统飞行模态外,FWA还存在一对由结构折叠状态量主导的折叠模态.翼尖对接飞行器具有固有的不稳定性[27 ] ,FWA也同样如此,其中一个折叠模态为发散状态,且折叠模态的时间常数很短,对飞行稳定性影响较大,因此需要增稳控制系统. ...
多飞行模式垂直起降无人机过渡飞行控制策略
1
2019
... FWA的飞行动力学与传统的单架飞行器有所不同,但传统控制设计的基本原理依然可以使用,倾转过程中无人机的掉高问题需要考虑[28 ] ,整个飞行控制结构如图13 所示.采用串联式PID控制器,其中包括飞行器姿态高度控制器以及折展控制器,通过升降舵控制俯仰,螺旋桨控制飞行速度,折展机构控制折叠运动,其中P(s )为比例控制,PI(s )为比例积分控制,下标d表示预期指令. ...
Transition flight control strategy of multiple flight mode vertical take-off and landing unmanned aerial vehicle
1
2019
... FWA的飞行动力学与传统的单架飞行器有所不同,但传统控制设计的基本原理依然可以使用,倾转过程中无人机的掉高问题需要考虑[28 ] ,整个飞行控制结构如图13 所示.采用串联式PID控制器,其中包括飞行器姿态高度控制器以及折展控制器,通过升降舵控制俯仰,螺旋桨控制飞行速度,折展机构控制折叠运动,其中P(s )为比例控制,PI(s )为比例积分控制,下标d表示预期指令. ...