民用客机总装车间自动引导车任务分配及路径规划

doi:10.16183/j.cnki.jsjtu.2021.223

民用客机总装车间自动引导车任务分配及路径规划

裘柯钧, 鲍中凯, 陈璐^,

上海交通大学机械与动力工程学院,上海 200240

Task Assignment and Path Planning for Automatic Guided Vehicles in Aircraft Assembly Workshop

QIU Kejun, BAO Zhongkai, CHEN Lu^,

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 陈璐,副教授,博士生导师;E-mail:chenlu@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2021-06-5 修回日期: 2021-08-3

基金资助:

国家重点研发计划(2019YFB1705702)
国家自然科学基金资助项目(52175475)

Received: 2021-06-5 Revised: 2021-08-3

作者简介 About authors

裘柯钧(1999-),本科生,从事飞机总装生产物流配送相关研究.

摘要

为了实现自动引导车(AGV)在某民用客机总装车间的高效运作,提出AGV任务分配与路径规划两阶段求解方法,有效地解决了车间内AGV的多次往返配送调度问题.在任务分配阶段,提出基于行程的AGV任务分配模型,提高任务分配的效率;在路径规划阶段,采用时间窗算法,对AGV占用的地图资源进行时间窗的初始化、更新和排布,并针对由于避障和等待引起的物料送达时间无法满足的情况,设计了料包交换、优先级提前、预留时长放宽共3种递进的调整策略,实现AGV的无冲突路径规划.在数值实验中,两阶段方法应用于50、100、150个料包问题的平均求解时间分别为15.86、41.12、162.29 s,表明两阶段方法有效缓解了多行程AGV调度问题的复杂性,能在合理时间内实现民用客机总装车间AGV的调度优化,以适应民用客机年产量逐年快速递增的生产需求.

关键词： 自动引导车; 行程; 任务分配; 路径规划; 时间窗算法

Abstract

To realize efficient scheduling of automatic guided vehicles (AGV) in the aircraft final assembly workshop, a two-stage method of AGV task allocation and path planning is proposed which effectively solves the problem of multi-trip distribution scheduling of AGV in the workshop. In the task allocation stage, an AGV task allocation model based on the trip is established to improve task allocation efficiency. In the path planning stage, the time window algorithm is used to initialize, update, and arrange the time window of the resources occupied by the AGV. Considering that the latest delivery time constraints may be violated due to obstacle avoidance and waiting, three adjustment strategies are designed to realize the conflict-free path planning of AGV, including the package exchanging strategy, the priority exchanging strategy, and the reserved conflict duration relaxation strategy. In numerical experiments, the average solving time of the two-stage method applied to problems with the scale of 50, 100, and 150 is 15.86, 41.12, and 162.29 s, which indicates that the two-stage method effectively alleviates the complexity of the multi-trip AGV scheduling problem. The two-stage method can realize the scheduling of the AGV in aircraft assembly workshop within a reasonable time and adapt to the rapid increase in the annual production of aircraft.

Keywords： automatic guided vehicle (AGV); multi-trip; task allocation; path planning; time window algorithm

PDF (2561KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

裘柯钧, 鲍中凯, 陈璐. 民用客机总装车间自动引导车任务分配及路径规划[J]. 上海交通大学学报, 2023, 57(1): 93-102 doi:10.16183/j.cnki.jsjtu.2021.223

QIU Kejun, BAO Zhongkai, CHEN Lu. Task Assignment and Path Planning for Automatic Guided Vehicles in Aircraft Assembly Workshop[J]. Journal of Shanghai Jiaotong University, 2023, 57(1): 93-102 doi:10.16183/j.cnki.jsjtu.2021.223

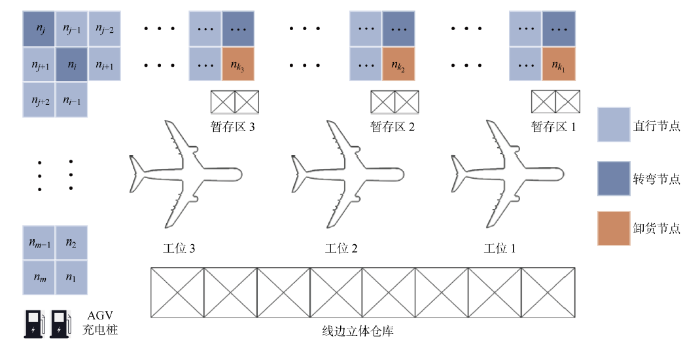
自动引导车(Automatic Guided Vehicle, AGV)是一种服务物流配送的智能化设备,凭借其高效、经济、灵活以及自动化水平高等优势,在某民用客机总装车间的物料配送中发挥着重要作用.该总装车间采用脉动式移动装配线生产模式,线边库采用立体仓库存储各装配大纲(Assembly Order, AO)的物料料包,车间内共有3个工位,分别完成功能系统的安装、功能系统的总装测试以及最终功能试验3大类作业.各工位边设置了工位暂存区,在AO工序开始前,车间内AGV将其料包提前从线边库配送至工位暂存区,供工人取用.

总装车间内AGV的调度优化是提高总装生产物流配送效率,满足生产计划正常有序进行的关键.对AGV的调度优化是指在生产计划的约束下,为多辆AGV分配配送任务,并规划每辆AGV的配送路径,同时避免AGV间碰撞、死锁等冲突现象发生.目标是在满足生产计划的前提下,最小化AGV的使用成本.AGV的调度优化问题得到了很多国内外学者的关注,目前已有研究大都集中在任务分配和路径规划两个方面.

针对AGV的任务分配问题,Hu等^[1]针对自动化集装箱码头中的联合车辆调度和存储分配问题建立了混合整数线性规划模型, 并设计了一种基于贪婪搜索的三阶段分解方法进行求解.Zou等^[2]以矩形制造车间为背景,建立AGV任务分配问题的混合整数规划模型,并设计了一种离散人工蜂群算法实现求解.夏扬坤等^[3]将AGV的配送问题定义为一个带软时间窗需求的车辆路径优化模型,并设计了具有自适应性的禁忌搜索算法(Tabu Search Algorithm, TSA)进行求解.Zou等^[4]针对AGV在多品种小批量生产制造车间取货送货的调度过程,构建了多目标混合整数线性规划模型,并提出一种多目标进化算法进行求解.

针对考虑实时路径及避撞的AGV路径规划问题,常用算法包括Dijkstra算法^[5-6]、A^*算法^[7-8]、遗传算法^[9-10]、人工势场法^[11-12]等.Xing等^[13]提出了一种改进TSA解决多个AGV同时工作时可能发生的冲突,以提高自动化仓库中AGV的拣货效率.曾庆成等^[14]针对自动化集装箱码头物流系统提出一种动态路径规划策略,建立AGV路径规划模型,并设计了基于动态路径规划策略的多种群蚁群算法进行求解.刘辉等^[15]将多智能体强化学习应用于AGV的路径规划问题,并提出了一种基于最大化累计回报频率的独立强化学习的方法.Murakami^[16]针对AGV在柔性制造系统中的无冲突路径规划问题,分别考虑AGV和物料流动,建立了时空网络模型,并将其转化为混合整数规划问题进行求解.

现有同时考虑AGV的任务分配与路径规划的研究中,基本都是通过简化其中一个问题的求解来实现的.如,杨雅洁等^[17]基于网格路径布局地图建立了混合整数规划模型对任务分配进行求解,通过在模型中加入AGV在路口避碰约束以实现无冲突路径规划.泰应鹏等^[18]则针对任务分配建立了混合整数规划模型,并通过对经过路径的时间窗的排布和更新解决碰撞冲突问题.Kelen等^[19]通过TSA算法实现任务分配的优化,接着基于Dijkstra算法的最短路径和时间窗方法实现AGV的路径规划.Hao等^[20]针对无人地下停车场中AGV系统的任务分配和路径规划问题,提出了一种基于混合遗传算法的AGV调度方法和一种基于时空图搜索算法的路径优化方法.Riazi等^[21]提出了一种基于改进Benders分解的方法,将AGV调度问题分解为任务分配和碰撞避免约束可行性检查两个阶段,但不适用于AGV数量较多的场景.

此外,现有文献都是假设AGV仅执行单次配送,鲜有文献考虑AGV在配送过程中执行多次往返配送(即配送站点及工位暂存区之间的往返配送)的问题,这是由于在AGV调度优化过程中考虑多次往返配送时,建模和求解过程变得非常复杂.为了解决民用客机总装车间物流配送过程中AGV的调度优化问题,本文提出任务分配与路径规划两阶段求解方法,同时针对AGV在车间内的多次往返配送现象,基于车间栅格化地图,设计了基于“行程”的AGV任务分配模型,进而采用时间窗算法对AGV实际配送中经过的栅格节点进行时间窗排布,并设计开发高效的启发式调整策略实现物料配送时间冲突消解.

1 总装车间地图建模

总装车间地图采用栅格表示法,通过离散化的栅格来近似连续的地图空间,进而达到简化描绘的目标^[22].在基于栅格的地图表示中,地图被划分为大小相等的栅格,每个栅格对应真实环境中的一个区域.在总装车间中,AGV的行驶道路已经提前规划好并栅格化,格点大小与AGV的尺寸一致,每个格点中心有一个二维码实现定位,如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 总装车间栅格化地图

Fig.1 Grid map of final assembly workshop

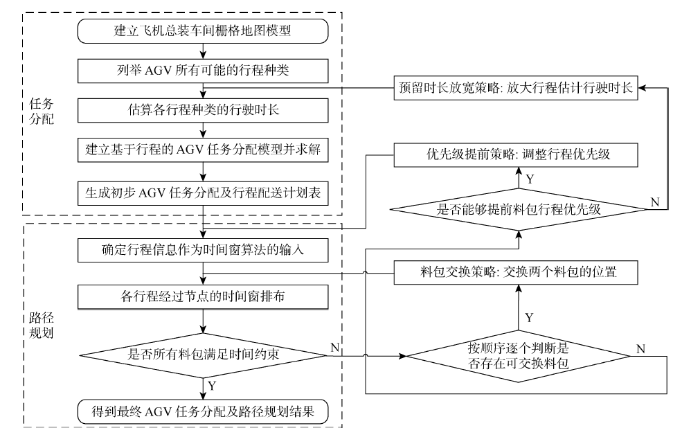
车间内包含两条AGV行驶道路,且均为单向行驶.根据行驶方向对各节点进行顺序编号,节点集合N={n₁, n₂, …, n_m},其中 $n_{k_{1}}$ , $n_{k_{2}}$ , $n_{k_{3}}$ 分别表示3个工位边的物料暂存区.AGV通过内侧道路行驶至目标工位暂存区配送AO料包,配送任务完成后通过外侧道路返回到AGV充电桩附近的停靠点.

基于栅格化地图模型,提出AGV任务分配与路径规划两阶段求解方法,流程图如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 两阶段求解方法流程图

Fig.2 Flow chart of two-stage method

2 基于行程的AGV任务分配模型

首先通过行程规划列举出车间内AGV所有可能的行程种类,在此基础上以最小化AGV的配送总成本为目标,建立基于行程的AGV任务分配混合整数规划模型.通过对AGV的行程规划,提前确定不同任务组合下的可能行程信息,能够简化物料送达时间约束的定义,进而降低决策变量维度,提高模型的求解效率.

2.1 行程规划

行程是指AGV从线边库出发,行驶至所有目标暂存区完成AO料包的配送,并最终回到AGV充电桩附近停靠点的整个回路.首先根据配送料包数量、行驶道路的特点、目标暂存区组合等对AGV行程进行分类,并估算每个行程的总行驶时长.假设工位暂存区数量为W,AGV的装载容量为Q,用J表示AGV所有可能的行程种类集合,则行程种类总数为 $|J|$ = $\overset{Q}{\sum_{u = 1}} C_{u + W - 1}^{W - 1}$ 式中:C表示排列组合符号.

一个行程种类信息可以用一个长度为W的向量α来表示,向量中第i个值表示送往暂存区i的AO料包数量,向量同时确定了AGV的所有目标暂存区,例如α_j=[0 Q … 0 0]表示该行程需要将Q个AO料包送往暂存区2.为了建立AGV配送的AO料包组合与行程的对应关系,首先为W个暂存区进行编号取值D=[D₁D₂ … D_W],第j种行程种类的编号取值通过以下公式计算得到:N_j=D $α_{j}^{T}$ 为了区分行程种类,需要设计D=[D₁D₂ … D_W]的取值,使得计算出的各个行程种类的编号取值各不相同,在任务分配模型时可以通过行程配送料包组合的不同,计算出编号取值N_j,得到该组合下的行程种类,实现料包组合与行程种类的一一对应.

2.2 AGV任务分配模型

模型参数及变量定义如下:I为AO料包集合;K为AGV车辆集合;R为每辆AGV实际配送的行程集合.第i(i∈I)个料包从线边库出发至目标工位暂存区的配送时长为T_i,最晚送达时间为L_i;第j(j∈J)种行程种类的AGV运行估计时长为C_j.AGV的单位投入成本和单位时间的运行成本分别定义为C_V和C_T.

模型决策变量包括:x_ikr (i∈I, k∈K, r∈R)为0-1变量,表示第i个料包是否由第k个AGV的第r次行程完成,是为1、否为0;w_jkr (j∈J, k∈K, r∈R)为0-1变量,表示第k辆AGV的第r次行程是否为第j种行程种类,是为1、否为0;c_kr (k∈K, r∈R)为连续型变量,表示第k辆AGV的第r次行程的运行时长;z_kr (k∈K, r∈R)为连续型变量,表示第k辆AGV的前r次行程的总运行时长;y_k (k∈K)为0-1变量,表示第k辆AGV是否被启用,是为1、否为0;t_i (i∈I)为连续型变量,表示第i个料包的实际送达时间.

建立AGV多行程任务分配模型如下:

(1)min C_V

\sum_{k \in K}

y_k+C_T

\sum_{k \in K} \sum_{r \in R}

c_kr

(2)s.t.

\sum_{k \in K} \sum_{r \in R}

x_ikr=1, ∀i∈I

(3)x_ikr≤y_k, ∀i∈I, ∀k∈K, ∀r∈R

(4)

\sum_{i \in I}

x_ikr≤Q, ∀k∈K, ∀r∈R

(5)

\sum_{i \in I}

x_ikrD_i=

\sum_{j \in J}

w_jkrN_j,∀k∈K, ∀r∈R

(6)

\sum_{j \in J}

w_jkr≤1, ∀k∈K, ∀r∈R

(7)c_kr=

\sum_{j \in J}

w_jkrC_j, ∀k∈K, ∀r∈R

(8)z_kr=

\overset{r}{\sum_{i = 1}}

c_kr, ∀k∈K

(9)t_i=

\sum_{r \in R} \sum_{k \in K}

z_k₍_r_-1)x_ikr+T_i, ∀i∈I

(10)t_i≤L_i, ∀i∈I

(11)

\sum_{i \in I}

x_ikr≤

\sum_{i \in I}

x_i₍_k_-1)_r,∀k∈K\{1}, ∀r∈R

(12)

\sum_{i \in I}

x_ikr≤

\sum_{i \in I}

x_ik₍_r_-1),∀k∈K, ∀r∈R\{1}

(13)x_ikr∈{0, 1}, ∀i∈I, ∀k∈K, ∀r∈R

(14)w_jkr∈{0, 1}, ∀j∈J, ∀k∈K, ∀r∈R

(15)y_k∈{0, 1}, ∀k∈K

(16)c_kr, z_kr∈R⁺, ∀k∈K, ∀r∈R

目标函数式(1)为最小化AGV投入和运行成本总和;式(2)保证每个AO料包有且仅由一辆AGV的一趟行程进行配送;式(3)保证AGV至少配送1个AO料包时就认为被启用;式(4)为AGV的装载容量约束;式(5)~(6)为AGV每趟行程中配送料包组合与行程种类的对应关系式;式(7)为计算AGV每趟行程的估计路径运行时长;式(8)~(9)为计算每个料包的实际送达时间;式(10)为每个料包的最晚送达时间约束;式(11)保证AGV的启用顺序为从k-1到k;式(12)保证配送行程的顺序从r-1到r;式(13)~(16)为决策变量的可行域.

3 基于时间窗算法的AGV路径规划

得到各AGV的任务分配结果和AGV每趟行程的具体信息后,通过时间窗算法来实现AGV在实际行驶过程中的无冲突路径规划.时间窗算法^[23]是建立在AGV外界环境无干扰假设下的一种预测式避障算法,即通过建立AGV的路径信息矩阵,预先安排AGV占用栅格地图中节点的顺序,避免行驶过程中的冲突和碰撞.

3.1 时间窗算法

3.1.1 行程信息的定义

总装车间栅格化地图中的每个栅格都可以用节点来表示,各节点的权重值定义为AGV通过该节点的运行时间与在该节点上的卸货时间之和:

(10)h_d=l_d/v_d+t_d

式中:l_d为节点n_d对应栅格的实际物理长度;v_d为AGV在节点n_d对应栅格上行驶的平均速度;t_d为在节点n_d对应栅格上的卸货时间,该时间仅在卸货节点存在.

以每辆AGV的每趟行程为单位,依次对每趟行程进行时间窗的排布.为了后续时间窗规划,对任务分配结果中所有AGV的所有行程进行重新编号,获得行程集合S,并通过一个列表M_s来表示每个行程的具体信息,转化为时间窗规划工作,作为时间窗算法的输入:

(18)M_s=[B I_s t_startk Y_rank]

式中:s为行程编号,s∈S;B为行程s对应的行程种类编号,B∈J;I_s为行程s的所有配送料包编号集合;t_start为行程s开始执行的时间;k为行程s对应的AGV编号;Y_rank为行程s的执行优先级,初始取值为行程s对应所有配送料包的剩余配送时间,定义为所有料包最晚送达时间和实际送达时间差值之和 $\sum_{i \in I_{s}}$ (L_i-t_i),取值越小则工作越紧迫,越需要优先排布时间窗.

3.1.2 栅格节点时间窗定义

M_s对应的行程s按照顺序经过的所有节点集合定义为N_s⊆{n₁, n₂, …, n_m},M_s在节点n_d∈N_s上的时间窗函数定义如下:

(19)T_w_,_sd=[q t_in,_d t_out,_d]

式中:q为节点n_d在节点集合N_s中的顺序编号;t_in,_d为车辆k进入节点n_d的时间;t_out,_d为车辆k离开节点n_d的时间.对于节点n_d的时间窗,满足下式:

(20)t_out,_d=t_in,_d+h_d

若节点n_d为起始节点,则进入起始节点的时间等于工作开始时间;若节点n_d不是起始节点,则进入节点的时间等于AGV离开路径中第q-1个节点的时间,即

(21)

t_{i n, d_{q}}^{q}

\{\begin{array}{l} t_{s t a r t}, & q = 0 \\ t_{o u t, d_{q - 1}}^{q - 1}, & q \geq 1 \end{array}

式中:d_q为AO料包q的目标暂存区对应的节点编号.

对于一个节点上的多个时间窗可用向量的形式表示为

(2)T_w_,_d=[T_w_{, 1}_d T_w_{, 2}_d … T_w_,_Pd]

式中:P为当前所有行程规划出的路径中经过节点n_d的总行程数.

若一条边上存在多个工作的时间窗,新加入工作时间窗中的进入时间必须满足:①进入该条边的时间必须大于AGV从上一条边的离开时间;②该条边的空闲时间窗的长度足够使车辆k在该时间内行驶离开该条边.假设在完成工作M_s之前,已经有s-1个工作安排,且该s-1个工作中有P个工作规划的行程是经过节点n_d的,为找出一个足够长的空余时间窗来安排新的工作,空余时间窗系数由下式确定:

(23)

C_K=arg $\underset{l}{m i n}$ {(t_in_,d)_l | (t_in_{, d})_l+1-

max {(t_out_{, d})_l, $t_{o u t, d_{q - 1}}^{q - 1}$ }≥h_d,

l=1, 2, …, P}

C_K确定后,节点n_d上的时间窗的进入时间如下:

(24)t_in_,d=max{(t_out_,d

)_{C_{K} - 1}

t_{o u t, d_{q - 1}}^{q - 1}

}

若节点n_d上的前P个时间窗排列紧密,无法在之前的空余时间窗排布出一个新的时间窗,则新的时间窗需要排在第P个时间窗之后,进入时间的对应函数为

(25) t_in_{, d}=(t_out_{, d})_P

时间窗规划完成后,得到的AO料包q的实际送达时间由下式给出:

(26)

t_{q}^{*}

t_{o u t, d_{q}})_{s_{q}}

式中:s_q为AO料包q对应的时间窗规划工作 $M_{s_{q}}$ 的编号.

3.1.3 时间窗算法步骤

时间窗算法具体的步骤如下.

步骤1 时间窗规划工作的定义.将AGV任务分配模型求解得到的所有AGV行程通过式(18)转化为时间窗规划工作.

步骤2 时间窗的初始化.根据工作对应的行程种类,找出行程经过的节点集合N_d⊆{n₁, n₂, …, n_m},根据式(19)~(21)为每个节点排布出理想的时间窗分布.

步骤3 时间窗的更新.在排布出理想情况下的节点时间窗后,再来检查不同行程之间是否包含相同的节点.若无相同节点,则结束时间窗规划;若存在相同节点,根据式(22)得到该节点的时间窗向量.

步骤4 时间窗的插入.根据式(23)计算出空余时间窗系数C_K,通过式(24)确定进入时间,并更新该工作在相同节点之后的所有节点的时间窗.

步骤5 实际送达时间计算.根据式(25)计算各个AO料包的实际送达时间.

3.2 基于启发式策略的冲突消解

时间窗算法在进行无冲突路径规划时,AO料包的实际送达时间会因冲突产生的等待而延迟,从而发生违反最晚送达时间的现象,对此设计了3种递进的调整策略以实现冲突的消解.

(1) 料包交换策略:对违背约束的料包,搜索具有相同目标暂存区的料包,通过交换两个料包的配送车辆编号及配送行程,实现料包实际送达时间的互换,若交换后两个料包的最晚送达时间约束都能满足,则进行互换.料包交换策略的具体步骤如下.

步骤1 检查时间窗算法路径规划结果,得到违背约束的料包集合I',以及集合中料包数量K_V,并令p=1.

步骤2 得到集合I'中第p个料包的目标暂存区,在所有料包集合I中搜索与之目标暂存区相同的料包集合I_p.

步骤3 遍历料包集合I_p,判断是否存在料包q满足:料包q的实际送达时间小于料包p的最晚送达时间,且料包p的实际送达时间小于料包q的最晚送达时间.若存在,则转至步骤4,否则,结束料包交换策略,并转至优先级提前策略.

步骤4 交换料包p和q的配送车次和行程轮次,并将第p个料包从集合I'中移除,判断集合I'是否为空集,若I'为空集,结束料包交换策略,调整完成;若I'非空,则令p=p+1,并转至步骤2.

(2) 优先级提前策略:若料包交换策略失效,则对违背约束的料包,找出料包所在行程,并将行程对应的时间窗规划工作优先级提前,重新进行时间窗规划,同时采用料包交换策略进行辅助调整.优先级提前策略的具体步骤如下.

步骤1 检查时间窗算法路径规划结果,得到违背约束的料包集合I'以及集合中料包数量K_V,若I'为空集,结束优先级提前策略,调整完成;若I'非空,则转步骤2.

步骤2 搜索得到集合I'中第1个料包所在的行程编号s_p.

步骤3 若s_p=1,结束优先级提前策略,转至预留时长放宽策略;若s_p≠1,则将行程s_p的优先级与行程s_p-1的优先级互换,重新通过时间窗算法排布行程集合P中的所有行程.

(3) 预留时长放宽策略:成倍放宽任务分配阶段行程的估计行驶时长,给AGV的冲突预留更多时间,重新求解任务分配模型,并运行时间窗算法进行路径规划,同时采用料包交换策略和优先级提前策略进行辅助调整.预留时长放宽策略的具体步骤如下.

步骤1 设置放宽倍数v=1.1.

步骤2 放宽任务分配阶段各个行程种类的估计行驶时长,令C_j=vC_j,并重新调用两阶段求解方法进行任务分配和路径规划.

步骤3 重新检查时间窗算法路径规划结果,得到违背约束的料包集合I'以及集合中料包数量K_V,若I'为空集,结束预留时长放宽策略,调整完成;若I'非空,通过料包交换策略和优先级提前策略进行调整,得到最终违背约束的料包集合I″,若I″为空集,结束预留时长放宽策略,调整完成,否则,令v=1.1v,转步骤2.

4 实例验证

4.1 算例描述

为验证本文方法的有效性,在Python 3.6.2中进行数值实验分析,并使用GUROBI 9.1求解器进行模型的求解.电脑配置为Intel Core TM i7-8550U CPU 1.80 GHz 以及16.0 GB内存的Windows操作系统.

某民用客机制造企业总装车间现场布局如图1所示.车间内共有3个工位暂存区,每辆AGV的配送料包数量上限为2个,计算得到所有行程种类,如表1所示.

表1 行程信息

Tab.1 Information of trips

行程编号	目标暂存区	配送料包数量	行驶时长/min	行程编号	目标暂存区	配送料包数量	行驶时长/min
1	暂存区3	1	6	6	暂存区1	2	10
2	暂存区3	2	6	7	暂存区3、暂存区2	2	8
3	暂存区2	1	8	8	暂存区3、暂存区1	2	10
4	暂存区2	2	8	9	暂存区2、暂存区1	2	10
5	暂存区1	1	10

新窗口打开| 下载CSV

根据物料需求计划,民用飞机一个架次的总装需要总计812个AO料包,部分料包的信息如表2所示,包括AO料包的编号、需求时间和需要送达的目标工位.

表2 部分AO料包的物料需求计划

Tab.2 Material requirement information for some AO

AO编号	需求时间/h	目标工位	AO编号	需求时间/h	目标工位
150C08RW6040	0	暂存区3	140C08ZF3401	8	暂存区2
150C08RW6030	0	暂存区3	140C08ZF3300	8	暂存区2
140C07BS0080	0	暂存区2	140C08ZF2500	8	暂存区2
140C05DA0030	0	暂存区2	140C08ZF2400	8	暂存区2
130C06KS0010	0	暂存区1	140C08ZF2100	8	暂存区2
130C01PJ0050	0	暂存区1	130C01RS0010	8	暂存区1
150C03RD0260	1	暂存区3	130C01KS0010	8	暂存区1
150C03JD0010	1	暂存区3	150C04SA0010	8.25	暂存区3
150C03DD0210	1	暂存区3	150C04AA0070	8.25	暂存区3
150C03DD0160	1	暂存区3	150C05SA0040	9	暂存区3

新窗口打开| 下载CSV

车间采取日配送的计划,即AGV提前1 d将下一工作日需要的所有AO料包从线边库配送至工位暂存区,每日所需配送AO料包数量如表3所示.

表3 每日所需配送料包数量

Tab.3 Number of packages required to be daily delivered

工作日编号	AO料包数量	工作日编号	AO料包数量
Day1	59	Day8	53
Day2	76	Day9	58
Day3	59	Day10	75
Day4	55	Day11	61
Day5	73	Day12	33
Day6	62	Day13	47
Day7	65	Day14	36

新窗口打开| 下载CSV

考虑到目前该型号民用客机的产量将逐年快速递增,每日所需配送的AO料包数量也会相应增加,因此本文设计了规模不等的算例,所包含的AO料包数量分别为50、100、150.各AO料包的最晚送达时间依据生产计划中各AO的开工时间生成.

4.2 求解结果分析

各规模算例的求解时长及使用的调整策略如表4所示.

表4 料包数为50、100、150的各算例求解时长和调整策略

Tab.4 Solution time and adjustment strategy of examples with 50, 100, and 150 packages

算例编号	料包数	求解时长/s	调整策略	算例编号	料包数	求解时长/s	调整策略
1	50	5.30	—	16	100	79.17	—
2	50	18.01	—	17	100	60.97	优先级提前
3	50	23.48	—	18	100	31.20	—
4	50	20.55	—	19	100	23.75	—
5	50	11.29	—	20	100	34.81	—
6	50	23.55	—	21	150	167.17	料包交换
7	50	14.72	—	22	150	197.26	料包交换
8	50	20.32	—	23	150	215.47	料包交换
9	50	14.70	—	24	150	122.01	料包交换
10	50	6.71	—	25	150	115.22	料包交换
11	100	24.29	—	26	150	163.90	—
12	100	57.54	—	27	150	113.82	料包交换
13	100	23.01	—	28	150	193.61	—
14	100	34.48	—	29	150	95.58	—
15	100	42.00	—	30	150	238.81	料包交换

新窗口打开| 下载CSV

由表中的数据分析可得:

(1) 料包数为50、100、150的算例平均求解时长分别为15.86、41.12、162.29 s,在最大规模即料包数为150时,平均求解时长达到162.29 s,在有限时间内得到了最优解,验证了模型的正确性.

(2) 随着料包数量的增加,在料包数为150的10个算例中出现了70%的算例需要通过料包交换策略进行调整.这表明,由于料包数量的增多,更容易出现料包的最晚送达时间违背约束的情况,也更需要相应调整策略.同时,由于AGV的数量较少,大部分料包的最晚送达时间约束比较宽松,只需前两种策略即可完成调整,未出现需要预留时长放宽策略进行调整的算例.

4.3 调整策略分析

以算例17为例,进一步分析冲突消解策略的应用.表5所示为该算例的最优AGV任务分配,表中元素为对应行程及AGV所配送的AO料包编号,配送AO料包编号按行程进行组合,并根据行程开始时间的先后进行排序.

表5 算例17的最优任务分配方案

Tab.5 Optimal task allocation solution of Example 17

行程编号	AGV编号
行程编号	AGV1	AGV2	AGV3	AGV4	AGV5
行程1	16, 37	24, 28	14, 29	30, 34	20, 23
行程2	52, 64	45, 61	15, 26	9, 18	66, 73
行程3	42, 47	41, 43	53, 59	31, 36	19, 90
行程4	55, 93	48, 57	50, 58	51, 62	21, 67
行程5	32, 35	46, 56	25, 79	54, 63	22, 68
行程6	11, 12	6, 39	13, 38	7, 17	1, 2
行程7	49, 65	8, 33	75, 76	27, 69	100, 74
行程8	77, 82	98, 99	10, 40	89, 96	4, 5
行程9	78, 88	70, 72	94, 95	91, 92	3, 84
行程10	85, 86	71, 83	80, 97	81, 87	44, 60

新窗口打开| 下载CSV

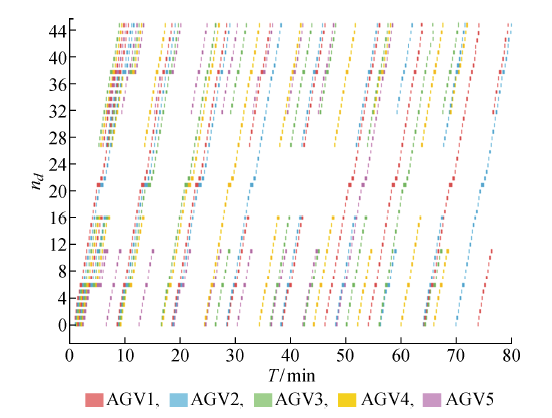
通过时间窗算法得到最优任务分配结果下各节点的时间窗如图3所示,横坐标为配送时间轴T,纵坐标为栅格地图中各个节点的编号n_d,不同颜色表示不同AGV的行程,每个色块的颜色表示对应的AGV,色块的纵坐标表示AGV经过的节点编号,色块的横向长度表示该颜色对应的AGV在该趟行程中占用该节点的时间窗长度.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 算例17的各节点时间窗规划结果

Fig.3 Time window planning results of Example 17

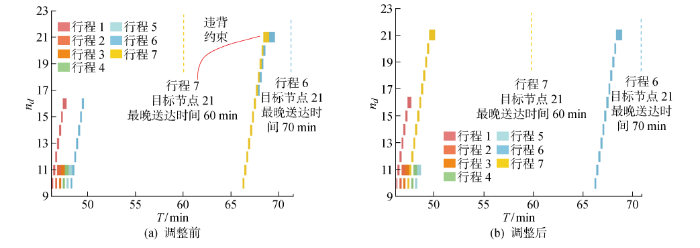
通过两阶段算法对算例17进行求解的过程中,第27个料包、第80个料包和第94个料包发生了实际送达时间违背最晚送达时间约束的情况.在尝试料包交换策略失败后,对这些料包采用了优先级提前策略进行了调整.图4所示为AGV4的第1~7个行程,以第7个行程中的第27个料包为例,将行程7的优先级提升至行程4之前,使第27个料包的送达时间从60.4 min缩短至50.4 min,满足了最晚送达时间为60 min的约束,并且重新检验料包送达时间信息,发现行程4、行程5、行程6所有料包的实际送达时间均小于最晚送达时间,通过优先级提前策略实现了冲突消解.实验表明,本方法实现了AGV高效的任务分配以及AGV间无冲突的路径规划.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 调整前后行程1~7在节点10~21的时间窗规划结果

Fig.4 Time window planning results of Trips 1—7 at Nodes 10—21 before and after adjustment

5 结语

本文研究了民用客机总装车间物流配送过程中的AGV多次往返配送问题.针对多次往返以及任务分配和路径规划协同决策等复杂问题特征,提出了一种AGV任务分配与路径规划的两阶段求解方法,分解任务分配和路径规划两个子问题:第1阶段提出“行程”的概念,通过行程规划对AGV行程进行分类,大大降低了建模的复杂度,在此基础上建立了基于“行程”的任务分配模型;第2阶段设计了以行程表为输入的时间窗算法与3种冲突消解策略.数值实验表明,该方法能在有限时间内找到AGV的最优调度方案,不仅能够有效解决当前产量下总装车间AGV多次往返配送问题,同时也能适应未来飞机产量快速提升的生产物流需求.

然而,本文假设AGV的装卸货均为固定时长,考虑AGV装卸货延迟随机性的动态优化问题有助于提高AGV调度方案的稳定性以及AGV的运行效率,将是AGV调度后续值得深入研究的问题.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

H T

, CHEN

X Z

, WANG

T S

, et al.

A three-stage decomposition method for the joint vehicle dispatching and storage allocation problem in automated container terminals

[J]. Computers & Industrial Engineering, 2019, 129: 90-101.

DOI:10.1016/j.cie.2019.01.023 URL [本文引用: 1]

[2]

ZOU

W Q

, PAN

Q K

, MENG

, et al.

An effective discrete artificial bee colony algorithm for multi-AGVs dispatching problem in a matrix manufacturing workshop

[J]. Expert Systems with Applications, 2020, 161: 113675.

DOI:10.1016/j.eswa.2020.113675 URL [本文引用: 1]

[3]

夏扬坤, 符卓, 谢九勇.

依订单拆分的多自动导引车物料配送路径规划

[J]. 计算机集成制造系统, 2017, 23(7): 1520-1528.