河口深槽可航宽度变化水域航行决策方法

doi:10.16183/j.cnki.jsjtu.2023.356

河口深槽可航宽度变化水域航行决策方法

贺益雄^a^,^b, 代永刚^a, 赵兴亚^a^,^b, 于德清^a, 黄立文^,^a^,^b

武汉理工大学 a. 航运学院；b.内河航运技术湖北省重点实验室,武汉 430063

Navigation Decision-Making Method in Estuary Deep Trough with Varying Width of Navigable Waters

HE Yixiong^a^,^b, DAI Yonggang^a, ZHAO Xingya^a^,^b, YU Deqing^a, HUANG Liwen^,^a^,^b

a. School of Navigation;b. Hubei Key Laboratory of Inland Shipping Technology, Wuhan University of Technology, Wuhan 430063, China

通讯作者: 黄立文,教授,博士生导师;E-mail:lwhuang@whut.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-07-31 修回日期: 2023-09-27 接受日期: 2023-11-8

基金资助:

国家自然科学基金面上项目(52071249)
国家自然科学基金面上项目(52271367)

Received: 2023-07-31 Revised: 2023-09-27 Accepted: 2023-11-8

作者简介 About authors

贺益雄(1976—),副教授,博士生导师,船长,从事智能航行研究.

摘要

为解决河口深槽可航宽度变化水域船舶航行决策挑战,以长江口北槽深水航道为例,围绕环境数字孪生、航行规则融入、船舶操纵性限制和特殊水域下避碰机理等关键科学问题开展研究.将环境构成要素分类、建模并实现环境数字孪生.归纳、量化解析航行规则要求并融入决策过程, 提出本船非线性操纵特性下的控制和过程预测方法.探究基于研究水域船舶行为特征的避碰机理,建立可行航向航速范围求取方法,提出多因素约束下能动态自适应系统剩余误差和目标船随机运动的航行决策方法.在预设场景下,本船在241、1 484、4 119 s 时,分别右转7°、右转2° 且将车令降到前进1、右转5° 且将车令降到前进1可安全通过.结果表明,提出的方法能在研究场景中精确进行航行决策,安全避让并及时跟踪航线.

关键词： 航行决策; 河口深槽水域; 避碰机理; 航向航速控制系统; 数字孪生环境

Abstract

To address the challenges of ship navigation decision-making in the water area where the navigable width of the estuary deep channel changes, taking the north channel deep waterway of the Yangtze River estuary as an example, research is conducted on the key scientific issues such as environmental digital twin, navigation rule integration, ship maneuverability limitation, and collision avoidance mechanism in special water area. First, the environmental components are classified, modeled, and implented into an environmental digital twin. Navigation requirements are summarized, quantitatively analyzed, and integrated into the decision-making process. A control and process prediction method for the nonlinear maneuvering characteristics of the own ship is proposed. Then, collision avoidance mechanism specific to the ship behavior characteristics of the research water area is explored. A method for obtaining the feasible heading and speed range is established, and a dynamic navigation decision-making method is proposed, which is capable of adapting to the system residual error and the random motion of the target ship under multiple constraints. In preset scenarios, the method proposed ensures all safe passage targets with adjustments of course 7° to starboard, course 2° to starboard with a telegraph order reduction to forward 1, course 5° to starboard with a telegraph order reduction to forward 1 at 241 s, 1 484 s, and 4 119 s respectively. The results show that the proposed method can accurately make navigation decisions, ensure collision avoidance, and perform route tracking in a timely manner.

Keywords： navigation decision; deep trough waters of estuary; collision avoidance mechanism; course speed control system; digital twin environment

PDF (5197KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

贺益雄, 代永刚, 赵兴亚, 于德清, 黄立文. 河口深槽可航宽度变化水域航行决策方法[J]. 上海交通大学学报, 2025, 59(4): 489-502 doi:10.16183/j.cnki.jsjtu.2023.356

HE Yixiong, DAI Yonggang, ZHAO Xingya, YU Deqing, HUANG Liwen. Navigation Decision-Making Method in Estuary Deep Trough with Varying Width of Navigable Waters[J]. Journal of Shanghai Jiaotong University, 2025, 59(4): 489-502 doi:10.16183/j.cnki.jsjtu.2023.356

水路运输的迅速发展增大了水上事故发生率,给船员的生命安全、经济和环境带来了极大风险^[1].调查表明,80%以上的水上事故由人为因素造成^[2].通航河流河口通常存在拦门沙,但有自然存在或疏浚深槽水道供大型船舶进出.河口深槽水道狭窄、障碍物较多、交通流复杂、船舶改向操纵严重受限,往往事故多发.在部分航道外存在可供船舶安全航行的水域,具有可航水域宽度可变的特征.在这些水域进行船舶辅助航行或自主航行决策(统称“航行决策”)研究,实现辅助航行乃至自主航行,能有效提高船舶在这些水域航行的自动、自主化水平,减少人为因素导致事故,是提高航行安全水平的有效途径^[3].

智能航行是智能船舶主要功能模块之一,航行决策是其基础,相关研究成果丰富.文献[4]中设计了开阔水域多船会遇局面下的动态智能航行决策方法.文献[5]中提出考虑避障半径的斥力场函数方法,进一步优化了水下自主航行器在复杂环境下的规划路径.文献[6]中提出一种基于驾驶实践的无人船智能避碰决策方法.文献[7]中研究了基于双延迟深度确定性策略梯度的船舶自主避碰方法.文献[8]中论述船舶拟人智能避碰决策的算法原理及其基础模型的构建方法,提出避碰算法合理性及完备性的测试方案.文献[9]中设计了一种基于操纵过程推演的自主避碰决策支持模型.文献[10]中考虑目标船的不确定性,提出了一种时变碰撞风险模型.文献[11]中利用模型预测控制算法和模糊数学理论构建避碰算法的评价函数,实现了船舶自主避碰.文献[12]中基于Coldwell船舶领域改进了多船避碰危险度评估模型.

现有航行决策研究大多集中于开阔水域,采取定速变向避让方法.在航道内单凭转向难以避让,需转向变速相结合.河口深槽水域航行规则多允许必要时利用航道外可航水域避让,因此可航宽度是变化的.此类水域航行决策研究缺乏,尚有以下关键科学问题亟待解决:① 按照航行决策的需要,建立包含各类要素的数字孪生环境模型;② 和航海实践一致,归纳、量化和融入《1972年国际海上避碰规则》、地方规则和良好船艺(合称“规则”)要求^[13];③ 为保证决策方案可执行性,建立基于船舶非线性操纵特性的航向航速控制和运动过程预测方法;④ 考虑河口深槽水道特殊环境和船舶行为,探究本船变速运动下速度矢量和避让效果之间的规律(避碰机理).本文围绕这4个关键科学问题,基于现有船舶按车钟挡位的分挡航速控制方法,提出了此类水域能动态自适应剩余误差和目标船机动的航行决策方法.

1 动态自适应航行决策框架构造方法

船舶智能航行需要完成环境态势感知、操纵方案决策和伺服机构执行3个步骤的循环过程.方案决策、态势感知和执行方法深度耦合:环境判断依赖于各种动静态物标和本船运动态势数据,可行方案基于环境判断和执行过程预演,执行过程依赖于船舶运动模型和航向航速控制方法的精度与可靠性.航行决策系统误差来源于感知误差(含风流、目标机动和本船态势数据误差)、本船运动模型和控制参数误差,可依靠提高传感器精度、选用合适船舶运动数学模型和优化控制器参数补偿系统误差,但误差无法完全消除,未消除的误差定义为剩余误差,可通过设计自适应系统进行补偿.

基于当前 $t_{0}$ 时刻信息,自适应系统将在固定时间间隔 $Δ t$ 内计算并执行决策方案,直到未来时间 $(t_{0} + Δ t)$ ; $Δ t$ 越长,误差越大.如果系统根据时间步长 $Δ t$ 之后的信息,循环、重新计算并执行新的决策方案,则从 $t_{0}$ 到 $(t_{0} + Δ t)$ 的误差将得到补偿.由于自 $t_{0}$ 时刻起,本船在 $Δ t$ 时段内是安全的,所以当 $Δ t$ 较短时, $(t_{0} + Δ t)$ 内的方案是可行的.由此,当 $k - 1$ 次更新可行方案时,从 $t_{0}$ 到 $(t_{0} + k Δ t)$ 方案均可行,k是正整数.实际的运行结果和上一次计算之间只有最后一步的误差.当然, $t_{0}$ 到 $(t_{0} + k Δ t)$ 的轨迹与 $t_{0}$ 时刻计算的轨迹会存在差异.每一步的误差越大,累计的差异就越大,但如前文所述,只要前一步计算的方案可行、 $Δ t$ 足够小,就可确保下一个时刻安全可行.但在快速变化的交通环境中, $Δ t$ 太大是不可接受的.

传统船舶一般使用分挡车钟控制螺旋桨转速.考虑对现有船舶辅助其航行决策或自主航行改造升级的需要,引入分挡控制螺旋桨转速的方法,结合风浪流下的可变速船舶操纵运动数学(MMG)模型和最优航向控制方法(PID方法)推演船舶操纵运动过程.

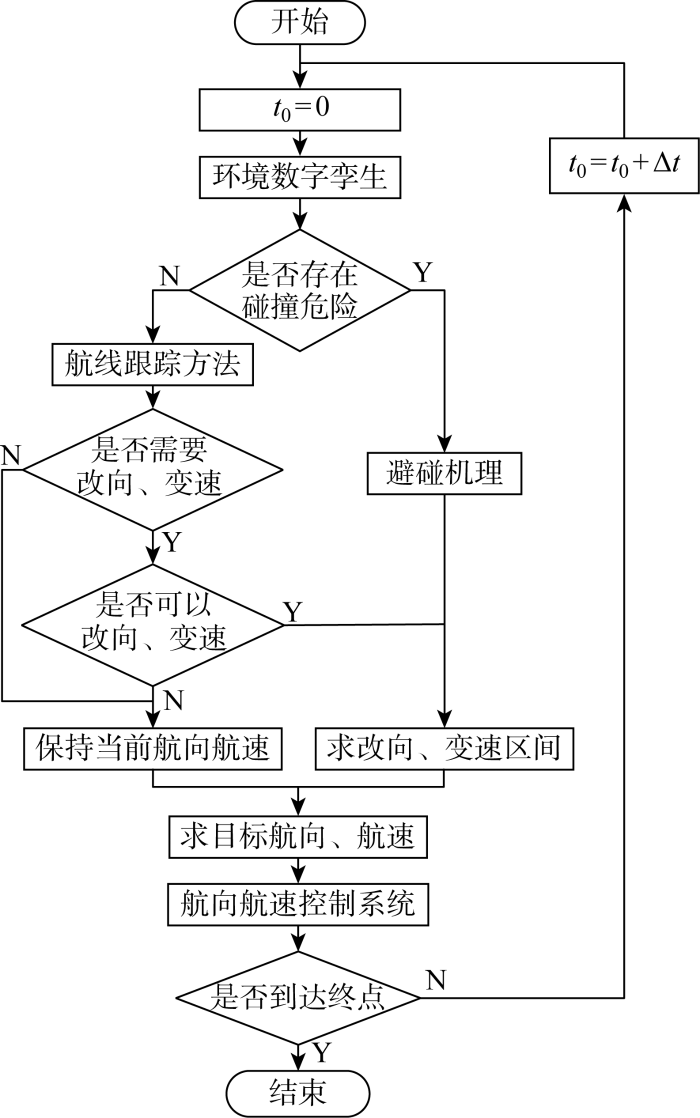
真实航行环境中,目标船可能会进行不协调避碰且极难预测.为自适应目标船本质上不可预测的机动操纵、自校正其他剩余误差,设计信息时序滚动输入、快速更新的自适应反馈校正计算框架,实现航行决策,流程如图1所示,主要步骤如下.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 航行决策流程

Fig.1 Navigation decision-making process

(1) 构建数字孪生环境.

(2) 输入本船、目标船信息.

(3) 基于特殊环境船位推算方法判断是否存在碰撞危险,存在则依靠约束条件下的避碰机理确定最优方案;不存在则根据航线跟踪方法计算改向角并推演船舶操纵运动过程,确定跟踪航线是否安全,是则开始航线跟踪,否则保持当前方案.

(4) 将(3)确定的方案输出作为航行辅助决策方案,自主航行时将其输入到航向航速控制系统中.

(5) 更新信息并重复(2)~(4).

上述方案采用时序滚动计算方法,快速更新输入信息,可补偿剩余误差对操纵方案的影响.同时,可避让不按避碰规则行动的目标船.只要信息采样频率满足奈奎斯特采样定理,当目标船发生不协调机动时,本船也会立即根据其动向调整航向,直到安全为止.

2 数字孪生环境模型和建立方法

2.1 坐标系与船舶领域

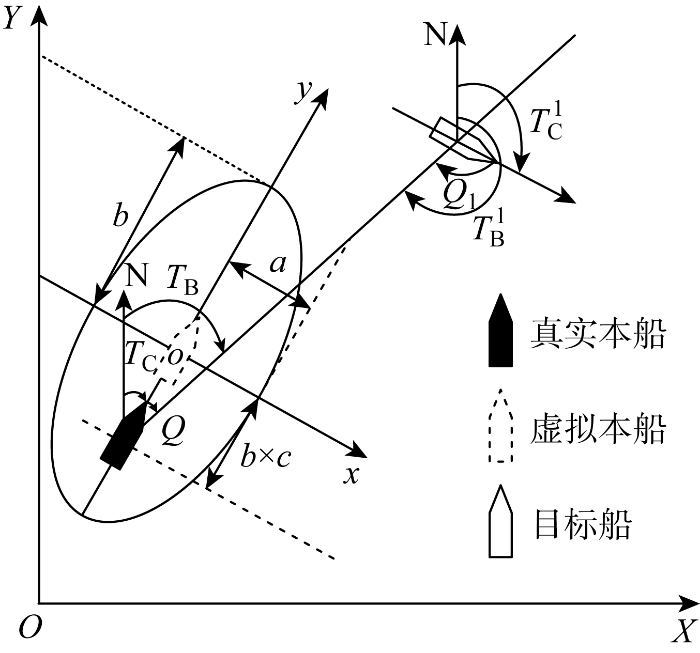
为方便导助航仪器中经纬度信息和直角坐标转换,建立以 $(λ_{0}, φ_{0})$ 为原点的大地坐标系XOY和本船重心为原点的随船坐标系 $x o y, X 、 Y 、 x$ 和y轴正向指向正东、北、右正横和船首,N表示正北方向,如图2所示.图中:T_C、 $T_{C}^{1}$ 分别为本船、目标船真航向; $T_{B} 、 Q$ 分别为目标船相对于本船的真方位、舷角; $T_{B}^{1} 、 Q_{1}$ 分别为本船相对于目标船的真方位、舷角; a、b、c分别为椭圆船舶领域的长半轴、短半轴、偏移系数.转换关系见文献[14].

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 坐标系与船舶领域

Fig.2 Coordinate system and ship domain

船舶领域为避免他船和静态物标进入的区域,用于衡量船舶间的安全性^[15].选取1艘7.6×10⁴ t级满载散货船“华洋理想”作为实验本船,适用船舶领域种类及参数、后续部分参数需要根据船舶特性、航行环境取值.但对于某一特定船舶、环境,可由最熟悉该船的船长确定,研究中由课题组几位有丰富航海经验也多次航行于北槽水道的船长(作者曾任“华洋理想”船长)确定.结合规则,采用如图2所示的椭圆船舶领域模型,取 $a = 1.2 L, b = 0.3 L, c = 0.3, L$ 为船长.

2.2 环境数字孪生方法

环境是受限水域航行决策的重要约束条件,根据决策需要感知并提取研究水域环境信息、实现环境数字孪生是正确判断航行态势的必要条件.构建针对某一类场景的数字孪生环境通用模型可以作为同类其他水域研究的基础模型.

数字孪生环境由动、静态环境2类要素构成.解构和提取动、静态环境各要素,构建其数学模型,由动、静态环境特征数据驱动这些模型实现数字孪生,建立满足该类水域船舶航行决策需要数字孪生环境的流程如下.

(1) 物标分类,按照各要素的速度、几何特征等将物标分类.

(2) 分类构建环境要素数学模型,构建各类动、静态环境要素数学表达式(模型).

(3) 数字孪生静态环境,针对具体水域环境,通过电子海图显示与信息系统开发静态信息提取工具,在海图中提取航行决策所需静态环境要素的数据信息,驱动流程(2)对应数学模型使各要素数字化,构建静态数字孪生环境.

(4) 数字孪生动态环境,通过船载设备获取研究水域一定范围内的动态数据并处理,将处理后的数据驱动对应动态要素模型,构建动态数字孪生环境.

(5) 组合流程(3)、(4)所构建的动、静态环境.

以河口深槽可航宽度变化水域为例,研究水域静态环境要素包括:通航分道、航道边界线、分隔带(线)、警戒区、推荐航向、航标、航道周围的锚地和浅滩等.动态环境要素包括本船、目标船、风流以及根据船舶吃水自适应调整的航道外边界线等.

对海图中影响船舶航行决策的相关环境信息提取、建模,将定线制以外的其他环境要素分为点状、圆形、条形、多边形物标模型,具体分类如表1所示.

表1 物标分类

Tab.1 Object classification

环境要素类型	要素模型	要素状态
钻井平台、岛屿	圆形	静态
浮标、明(暗)礁	点状	静态
浅滩、岸线	多边形	静态
常规机动船	普通机动船	动态
拖带船、拖网渔船	条形	动态
操限、失控船	圆形	动态
非机动船	点状	动态

新窗口打开| 下载CSV

某一河口深槽水道由M个分道通航制、N个警戒区、G个航标、W个不规则区域(航道附近锚地、浅滩)和D条航道外边界线构成.分道通航制数字模型包括:通航分道、航道边界线、分隔带(线)等.公式如下:

(1)

\begin{array}{l} F_{m} = \\ {L_{C N}^{m}, L_{S N}^{m}, L_{R N}^{m}, L_{S S}^{m}, L_{C S}^{m}, L_{R S}^{m}, T_{N}^{m}, T_{S}^{m}} \end{array}

式中: $F_{m}$ 表示第m个分道通航制; $L_{C N}^{m} 、 L_{C S}^{m}$ 表示北、南航道边界线; $L_{S N}^{m} 、 L_{S S}^{m}$ 表示北、南分隔带边界线; $L_{R N}^{m} 、 L_{R S}^{m}$ 表示北、南计划航线; $T_{N}^{m} 、 T_{S}^{m}$ 表示北、南通航分道.边界线和计划航线是由相等数量的n个点组成,通航分道由航道边界线和分隔带边界线构成,连接通航分道两条边界线点连线的中点构成计划航线,公式如下:

(2)

\begin{array}{l} T_{N}^{m} = {[L_{C N}^{m} L_{S N}^{m}]}^{T} \\ T_{S}^{m} = {[L_{C S}^{m} L_{S S}^{m}]}^{T} \end{array}\}

(3)

\begin{array}{l} \begin{array}{l} L_{C N}^{m} = (P_{C N}^{m 1}, P_{C N}^{m 2}, \dots, P_{C N}^{m n}) \\ L_{S N}^{m} = (P_{S N}^{m 1}, P_{S N}^{m 2}, \dots, P_{S N}^{m n}) \\ L_{R N}^{m} = (\frac{1}{2} (P_{C N}^{m 1} + P_{S N}^{m 1}), \dots, \frac{1}{2} (P_{C N}^{m n} + P_{S N}^{m n})) \end{array}\} \end{array}

(4)

\begin{array}{l} L_{C S}^{m} = (P_{C S}^{m 1}, P_{C S}^{m 2}, \dots, P_{C S}^{m n}) \\ L_{S S}^{m} = (P_{S S}^{m 1}, P_{S S}^{m 2}, \dots, P_{S S}^{m n}) \\ L_{R S}^{m} = (\frac{1}{2} (P_{C S}^{m 1} + P_{S S}^{m 1}), \dots, \frac{1}{2} (P_{C S}^{m n} + P_{S S}^{m n})) \end{array}\}

式中: $P_{C N}^{m n} 、 P_{S N}^{m n} 、 P_{C S}^{m n} 、 P_{S S}^{m n}$ 分别表示第m个分道通航制中航道北边界线、分隔带北边界线、航道南边界线、分隔带南边界线上的第n个点.

点状或圆形物标的数学模型公式如下:

(5)

\begin{array}{l} S_{i} = \\ (x_{i} + r_{1} c o s θ, y_{i} + r_{1} s i n θ), θ \in [0, 2 π) \end{array}

式中: $S_{i}$ 为第i个点状或圆形物标的面积; $(x_{i}, y_{i})$ 为第i个区域圆心; $r_{1}$ 为半径, $r_{1}$ 可根据具体环境适当调整; θ为参数.

条形、多边形和形状不一且不规则的其他物标可用多个点连线表示,公式如下:

(6)

\begin{matrix} A_{a} = [S_{a r e a} |\begin{array}{l} P_{1} & \dots \\ \dots & P_{j} \end{array}] \end{matrix}

式中: $A_{a}$ 为第a个不规则区域; $S_{a r e a}$ 为该不规则区域的面积; $P_{j}$ 为组成该区域的点,j为点的数量.

航道外边界线根据船舶吃水自适应调整,用长度不一的线段将其连成两条折线L_N、L_S,包含w、q个点,公式如下:

(7)

\begin{matrix} \begin{array}{l} L_{N} = (P_{N}^{1}, P_{N}^{2}, \dots, P_{N}^{w}) \\ L_{S} = (P_{S}^{1}, P_{S}^{2}, \dots, P_{S}^{q}) \end{array}\} \end{matrix}

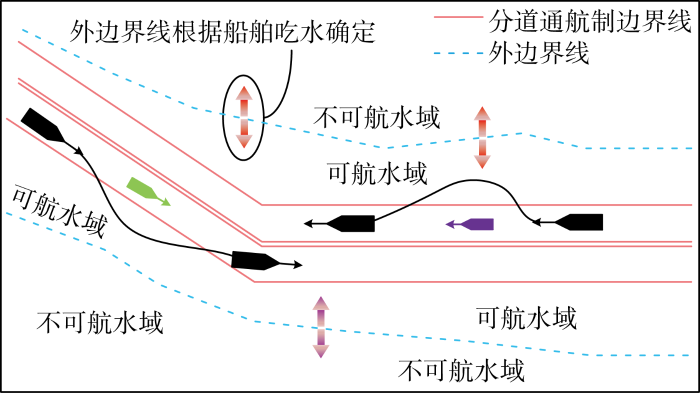
风流等动态环境要素影响船舶操纵性.在航海实践中,船舶进入深槽水道前,其吃水已确定.要进入深槽水道,必须确保航道水深(已考虑潮高)足够.为保证安全,通常只选择海图水深已满足安全要求的航道外水域作为可航水域.河口深槽水域航行规则允许必要时利用航道外可航水域进行避让.换言之,在正常航道内航行的船舶,如航道外水深允许,可驶出航道进行避让.因此,研究水域的可航宽度可根据吃水和航道外水深自适应变化,其动态特性主要体现在避碰决策时不同时刻能否驶出航道进行避让.可航宽度变化示意如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 可航宽度变化示意图

Fig.3 Variation of navigable width

3 航向航速控制与航线跟踪方法

求取的操纵方案为时序的车舵指令或航向航速指令,为判断方案是否可行,需推演该方案执行后的时序轨迹,因此需要建立船舶操纵运动模型、航向航速控制和航线跟踪方法.

3.1 船舶操纵运动模型

河口深槽水道航行决策暂时不考虑船舶的纵摇、横摇和垂荡,采用三自由度MMG模型,公式如下:

(8)

\begin{matrix} \begin{array}{l} (m_{s h i p} + m_{y}) \overset{\cdot}{v} + (m_{s h i p} + m_{x}) u r = \\ Y_{H} + Y_{P} + Y_{R} + Y_{w i n d} + Y_{w a v e} \\ (m_{s h i p} + m_{x}) \overset{\cdot}{u} - (m_{s h i p} + m_{y}) v r = \\ X_{H} + X_{P} + X_{R} + X_{w i n d} + X_{w a v e} \\ (I_{z z} + J_{z z}) \overset{\cdot}{r} = N_{H} + N_{R} + N_{P} + \\ N_{w i n d} + N_{w a v e} \end{array}\} \end{matrix}

式中: $m_{s h i p}$ 为船舶质量; $m_{x} 、 m_{y}$ 为船舶纵向、横向附加质量; u、v和r分别为x轴、y轴方向速度和转首角速度; $\overset{\cdot}{u} 、 \overset{\cdot}{v}$ 和 $\overset{\cdot}{r}$ 分别为x轴、y轴方向加速度和转首角加速度; $I_{z z} 、 J_{z z}$ 为首摇、附加转动惯量;X、Y和N分别为x轴、y轴方向合力和转首力矩;下标H、P和R分别表示船体、螺旋桨和舵;下标wind、wave表示风、浪干扰.

考虑到大型船舶操纵特性,该模型增加了推力随转速、航速变化的影响因子,考虑了风、流等外界干扰.模型参数计算及符号含义可参阅文献[16].可根据初始条件按龙格库塔方法求解任意时刻位置、航向等信息.

船舶匀速直线运动时,有效推力X_p如下:

(9)

\begin{matrix} X_{p} = (1 - t_{p 0}) F_{T} \end{matrix}

式中:F_T为螺旋桨推力;t_p0为推力减额系数,与船型、螺旋桨尺度、负荷有关.t_p0受船舶运动状态及螺旋桨负荷影响,

(10)$t_{\mathrm{p} 0}=\left\{\begin{array}{ll}0.04+\frac{\left(t_{\mathrm{p} 0}^{\prime}-0.04\right) u}{u_{0}}, & u \leqslant u_{0} \\t_{\mathrm{p} 0}^{\prime}, & u>u_{0}\end{array}\right.$

式中: $u_{0} 、 u$ 分别为额定、瞬时速度; $t'_{p 0}$ 为额定速度时的减额系数,受旋转和横向运动影响,

(11)$f=t_{\mathrm{p} 0}^{\prime}-t_{\mathrm{p} 0}$

(12)$\left.\begin{array}{l}f=k_{\mathrm{t}} \beta_{\mathrm{R}} \\k_{\mathrm{t}}=0.00023\left(\gamma_{\mathrm{A}} L / D_{\mathrm{p}}\right)-0.028 \\\gamma_{\mathrm{A}}=(B / d)\left[1.3\left(1-C_{\mathrm{b}}\right)-3.1 l_{\mathrm{cb}}\right] \\l_{\mathrm{cb}}=100 x_{\mathrm{c}} / L \\\beta_{\mathrm{R}}=\beta-l_{\mathrm{R}} r / v\end{array}\right\}$

式中:f为减额系数的影响函数; $β_{R}$ 和β分别为舵和船中心处漂角;B、d、 $D_{p}$ 和 $x_{c}$ 分别为船宽、吃水、螺旋桨直径和浮心纵向坐标;k_t、γ_A、C_b、l_cb和l_R分别为修正系数、船体整流系数、方形系数、浮心系数和漂角系数.

F_T求解公式如下:

(13)

\begin{matrix} F_{T} = ρ (N_{P})^{2} D_{p}^{2} K_{T} \end{matrix}

式中:K_T为螺旋桨推力系数;ρ为水密度;N_P为实时转速.

风流求解公式和其他参数计算见文献[17].

3.2 自适应最优航向控制方法

传统PID参数根据经验设置,无法随船舶和航速实时调整,引入最优控制理论,自适应调整PID参数.

传统PID参数可由二阶设计方法^[18-19]给出:

(14)

K_{p} = \frac{T ω_{n}^{2}}{K}

(15)

K_{i} = \frac{T ω_{n}^{3}}{10 K}

(16)

\begin{array}{l} K_{d} = \frac{2 T ξ ω_{n} - 1}{K} \end{array}

式中: $ω_{n} 、 ξ 分别为固有振荡频率和相对阻尼系数, 为保持系统性能, ξ 取值范围为 0.8 \leq ξ \leq 1; K 、 T$ 为船舶操纵性指数.

统筹考虑航向保持和节省燃油,选取性能优化函数:

(17)

\begin{matrix} J = 1 / [2 (E^{2} + λ δ^{2})] \end{matrix}

式中: E为航向偏差;λ为加权系数,其取值与风速大小相关;δ为舵角.为使式(17)的二次型性能优化函数值最小,根据线性二次型非定点输出理论可解得舵角的控制律^[20]:

(18)$\begin{array}{l}\delta=\left[\frac{1}{\sqrt{\lambda}} \frac{1}{K}\left(1-\sqrt{1+\frac{2 K T}{\lambda}}\right)\right]\left[\begin{array}{l}E \\E^{\prime}\end{array}\right]= \\\frac{1}{\sqrt{\lambda}} E+\frac{1}{K}\left(1-\sqrt{1+\frac{2 K T}{\lambda}}\right) E^{\prime}\end{array}$

式中:E'为航向偏差变化率.

则K_p、K_d的计算公式如下:

(19)

K_{p} = \frac{1}{\sqrt{λ}}

(20)

\begin{array}{l} K_{d} = \frac{1}{K} (1 - \sqrt{1 + \frac{2 K T}{λ}}) \end{array}

船舶航向控制是一个闭环控制系统,且该系统是二阶振荡和渐进稳定的,其固有振荡频率和相对阻尼系数计算公式如下:

(21)

\begin{matrix} \begin{array}{l} ω_{n} = \sqrt{\frac{K}{T \sqrt{λ}}} \\ ξ = \frac{1}{2} \sqrt{2 + \frac{\sqrt{λ}}{K T}} \end{array}\} \end{matrix}

将式(21)代入式(14)、(16),可得到K_p、K_d的计算公式与式(19)、(20)相同,代入式(15)得到K_i的计算公式如下:

(22)

\begin{matrix} K_{i} = \frac{1}{10} \sqrt{\frac{K}{T λ}} \end{matrix}

为求取K、T,将MMG拉普拉斯变化得:

(23)

\begin{array}{l} (m_{s h i p} + m_{x}) s u (s) = [X_{r} - \\ (m_{s h i p} + m_{y}) v_{0}] r (s) + X_{u} v (s) + X_{δ} δ (s) \\ (I_{z z} + J_{z z}) s r (s) = \\ N_{u} u (s) + N_{r} r (s) + N_{δ} δ (s) \end{array}\}

式中: s为拉普拉斯变换中的复变量;u(s)、v(s)、r(s)、δ(s)分别为u、v、r、δ的拉普拉斯变换; $X_{r} 、 X_{u} 、 X_{δ}$ 分别为与r、u相关的水动力系数、舵力系数; $N_{u} 、 N_{r} 、 N_{δ}$ 分别为与u、r、δ相关的首摇力矩系数; $v_{0}$ 为船舶漂移速度.

经过拉普拉斯逆换算,频域内转首角速度和横向速度对舵角的关系可转化为时域方程:

(24)

\begin{array}{l} T_{1} T_{2} \ddot{r} + (T_{1} + T_{2}) \overset{\cdot}{r} + r = K (δ + T_{3} \overset{\cdot}{δ}) \\ T_{1} T_{2} \ddot{u} + (T_{1} + T_{2}) \overset{\cdot}{u} + u = K_{u} (δ + T_{3 u} \overset{\cdot}{δ}) \end{array}\}

式中: $T_{1} 、 T_{2} 、 T_{3}$ 均为船舶操纵性指数;K_u为横向速度对舵角的增益系数;T_3u为时间常数.

(25)

\begin{array}{l} T_{1} T_{2} = \frac{(m_{s h i p} + m_{x}) (I_{z z} + J_{z z})}{C} \\ T_{1} + T_{2} = \frac{- (m_{s h i p} + m_{x}) N_{r} - (I_{z z} + J_{z z}) X_{u}}{C} \\ T_{3} = \frac{(m_{s h i p} + m_{x}) N_{δ}}{N_{u} X_{δ} - N_{δ} X_{u}} \\ K = \frac{N_{u} X_{δ} - N_{δ} X_{u}}{C} \\ C = X_{u} N_{r} - N_{u} [X_{r} - (m_{s h i p} + m_{y}) v_{0}] \\ T = T_{1} + T_{2} - T_{3} \end{array}\}

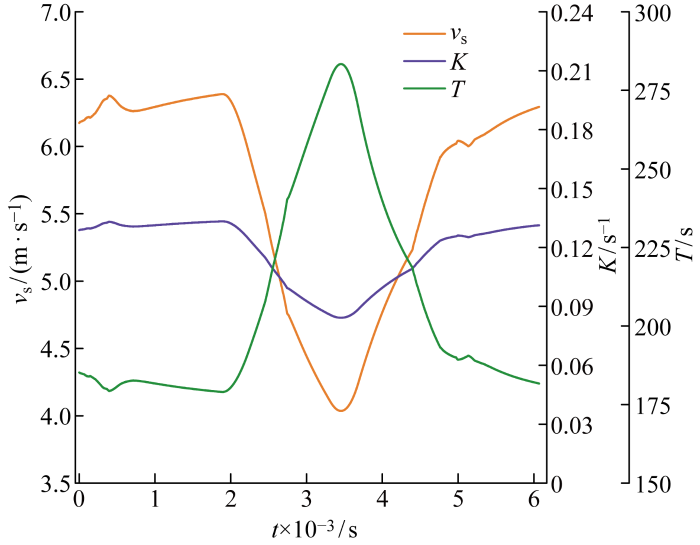
根据式(25)可通过水动力导数求出K、T值,水动力导数与航速相关,具体计算方法详见文献[21].K、T值是航速 $v_{s}$ 的函数,船舶航行时航速是变化的,K、T值也是时变的,因此,提出的航向控制方法可自适应不同船舶和航速.

以“华洋理想”轮为研究对象,取其在长江口北槽水道航行时的航速数据,可计算出随航速 $v_{s} 实时变化的 K 、 T$ 值,变化曲线如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 K、T值随v_s变化曲线

Fig.4 K and T versus v_s

已知控制系统模型方程,根据式(24)可得到系统特征方程:

(26)

T σ^{3} + (1 + K K_{d}) σ^{2} + K K_{i} σ + K K_{p} = 0

式中:σ为特征方程的根.

K、T值随航速变化曲线显示K>0,T>0.又因为λ>0,所以K_p>0,K_i>0,K_d>0,即特征方程的全部系数为正,并且劳斯表第1列元素均为正数.根据劳斯判据,该控制系统是稳定的.

综上,提出的航向控制方法基于最优控制策略,适用于不同船舶以航速为自变量的PID航向控制方法,可实现不同航速下的航向自适应最优控制.控制流程见文献[22].

3.3 分挡车钟航速控制方法

船舶变速通过改变主机转速来实现,在航海实践中,主机转速微小变化对避碰效果影响不大,使用分挡(一般10挡)车钟来发出转速指令.考虑长江北槽水道有航速限制,只需考虑进车.以“华洋理想”轮为例,如表2所示.表中:M/V表示机动船.

表2 “华洋理想”轮车钟转速表

Tab.2 Engine order telegraph of M/V “Huayang Dream”

车令	转速/ (r·min^-1)	匹配航速/kn	车令	转速/ (r·min^-1)	匹配航速/kn
海上速度	93	14	后退3	85	12
前进3	85	12	后退2	70	10.5
前进2	70	10.5	后退1	48	5
前进1	48	5	微速后退	35	3
微速前进	35	3	停车	0	0

新窗口打开| 下载CSV

若t₁时刻发出车令,完成变速时间为t₂,变速前、后螺旋桨转速分别为 $N_{P}^{1}$ 、 $N_{P}^{2}$ ,则t_m时刻螺旋桨转速公式如下:

(27)$N_{P}^{t}=\left\{\begin{array}{l}N_{P}^{1}, \quad t_{m} t_{1} \\N_{P}^{2}, \quad t_{m} t_{2} \\N_{P}^{1}+\left(t-t_{1}\right) k, \\t_{1} t_{m} t_{2} \text { 且 } N_{P}^{1} N_{P}^{2} \\N_{P}^{1}-\left(t-t_{1}\right) k, \\t_{1} t_{m} t_{2} \text { 且 } N_{P}^{1} N_{P}^{2}\end{array}\right.$

式中:k'为螺旋桨转速变化率,取0.25 r/s.

3.4 航线跟踪方法

航线跟踪是指结合本船避让行动,控制船舶沿计划航线行驶的行为,关键在于自动确定下一转向点和求取目标航向.

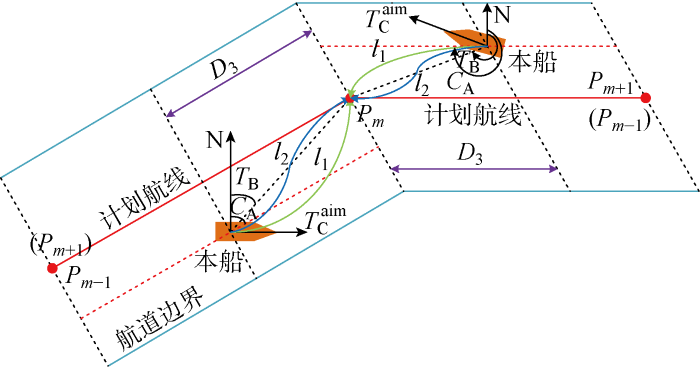
(1) 确定下一转向点.假设计划航线包含p个转向点,最近的记为 $P_{m}$ ,则 $P_{m - 1} 、 P_{m + 1}$ 为前、后相邻转向点,如图5所示.计算下一时刻与当前时刻本船到 $P_{m} 、 P_{m - 1}$ 点的距离差 $D_{1} 、 D_{2} . D_{1} D_{2} 0$ 时, $P_{m + 1}$ 点为下一转向点; $D_{1} D_{2} 0$ 时,若本船沿计划航线到 $P_{m}$ 的距离 $D_{3} 0.3 n m i l e, P_{m + 1}$ 点为下一转向点,否则 $P_{m}$ 为下一转向点.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 航线跟踪方法

Fig.5 Route tracking method

(2) 目标航向.为保证船舶能平滑地回到并沿计划航线行驶, 根据计划航向C_A和下一转向点相对本船的真方位T_B不断调整目标航向 $T_{C}^{a i m}$ :

(28)

\begin{matrix} T_{C}^{a i m} = τ (T_{B} - C_{A}) + C_{A} \end{matrix}

式中: τ为靠拢系数,τ值过大或过小都不利于跟踪航线.不断调整目标航向可得到如图5所示的航线跟踪路径.经多次实验,当 $τ = 1 、 τ = 1.5$ 时运动轨迹分别为 $l_{1} 、 l_{2}, l_{2}$ 更符合实践,因此取 $τ = 1.5 .$

4 航行决策方法

4.1 避碰机理

避碰机理是指船舶运动矢量和避碰效果之间的规律.通过探究符合船舶行为规律的研究水域避碰机理,计算可让清所有目标的操纵方案.

4.1.1 基于特殊环境船位推算方法的碰撞危险判断

为实时推算本船和目标船的船位,考虑到沿深槽水道航行船舶在航迹向和航道走向一致时,一般会继续沿航道航行,因此按照航道走向和对地速度推算船位;航迹向与航道走向有明显差别,或者是航道外船舶,按照当前航速矢量推算船位.判断操纵方案是否可行时,本船按照航向航速控制系统中的可变速MMG模型推算.顺、非顺交通流方向的目标船船位推算公式如下:

(29)$\left.\begin{array}{l}\left\{\begin{array}{l}x=x_{0}+v_{\mathrm{s}} t \sin T_{\mathrm{C}} \\y=y_{0}+v_{\mathrm{s}} t \cos T_{\mathrm{C}}\end{array} \quad t \in\left[0, t_{\mathrm{j}}\right)\right. \\\left\{\begin{array}{l}x=x_{1}+v_{\mathrm{s}}\left(t-t_{j}\right) \sin \alpha_{i+1} \\y=y_{1}+v_{\mathrm{s}}\left(t-t_{j}\right) \cos \alpha_{i+1}\end{array}\right\} \geqslant t_{\mathrm{j}}\end{array}\right\}$

(30)

\begin{array}{l} x = x_{0} + v_{s} t s i n T_{C} \\ y = y_{0} + v_{s} t c o s T_{C} \end{array}\}

式中: $(x_{0}, y_{0})$ 为船舶初始时刻位置; $T_{C}$ 为航向;α_(i+1) 表示船舶下一航段的交通流方向; $t_{j}$ 为船舶顺交通流方向航行时到达下一航段所需时间; $(x_{1}, y_{1})$ 为船舶到达下一航段时的船位.

可暂时不考虑距离太远和离进入本船船舶领域时间长的目标船,距离小于阈值D_d时才推算一定时长的船位.D_d暂取4 n mile.判断目标船是否进入本船船舶领域,若进入,保存该目标船信息及进入时刻t,判断公式^[23]如下:

(31)

\begin{array}{l} \frac{[(y - Y_{t}) c o s T_{C}^{t} + (x - X_{t}) s i n T_{C}^{t}]^{2}}{a^{2}} + \\ \frac{[(x - X_{t}) c o s T_{C}^{t} + (y - Y_{t}) s i n T_{C}^{t}]^{2}}{b^{2}} \leq 1 \end{array}

式中: $T_{C}^{t}$ 为t时刻本船航向; $(X_{t}, Y_{t})$ 为t时刻本船船舶领域中心位置.

本船与航标、浅滩、自适应的航道外边界线的碰撞危险也同理判断.将航道外约束边界线离散成若干个点,将航标视为静态点状障碍物.在本船运动过程中,若某一时刻有点进入本船船舶领域,则视为存在潜在碰撞危险(PCR).

4.1.2 碰撞危险度模型

碰撞危险度(CRI)是反映碰撞危险是否存在和采取避让措施紧迫程度的物理量.可分解为空间碰撞危险度(SCRI)和时间碰撞危险度(TCRI)^[24],公式如下:

(32)

\begin{matrix} u_{c} = u_{s} u_{t} \end{matrix}

式中:u_c、u_s、u_t分别为CRI、SCRI、TCRI的值.

定义研究水域碰撞危险形成条件为:存在PCR且到目标船进入本船船舶领域的时间t_i小于T_t,T_t取900 s.

(1) 空间碰撞危险度. SCRI表示两船是否存在PCR,公式如下:

(33)

\begin{array}{l} u_{s} = \\ \{\begin{array}{l} 1, \exists t \in [0, 1 800 s], (X_{t}^{k}, Y_{t}^{k}) \in D_{t} \\ 0, t \in [0, 1 800 s], (X_{t}^{k}, Y_{t}^{k}) \in D_{t} \end{array} \end{array}

式中: $(X_{t}^{k}, Y_{t}^{k})$ 表示第k艘目标船在t时刻的船位; $D_{t}$ 表示t时刻本船船舶领域内的点集.

(2) 时间碰撞危险度. TCRI是指两船存在碰撞危险时,目标船进入本船船舶领域、采取避让措施紧迫程度的物理量^[25].公式如下:

(34)$u_{\mathrm{t}}=\left\{\begin{array}{ll}1, & t_{\mathrm{i}} \leqslant 0 \\\left(1-t_{\mathrm{i}} / T_{t}\right)^{3.03}, & 0＜t_{\mathrm{i}}＜T_{t} \\0, & t_{\mathrm{i}} \geqslant T_{t}\end{array}\right.$

如存在PCR,按照上述模型,计算CRI,确定避让行动时机.

4.1.3 规则解析与融入

规则具有强制性,航行决策时须严格遵守,需要归纳、量化和融入规则,辨识两船会遇态势,融合避碰机理.

本船为长江口北槽水道中顺交通流方向行驶的机动船,规则要求应尽早避让特殊船舶(含操限船、失控船、非机动船、渔船和帆船等).根据河口深槽水域的特点,按照会遇局面确定两机动船的避让关系.为确定两船会遇局面,引入基于舷角比对的会遇局面辨识模型^[25].此外,规则规定河口深槽水域航行船舶航速不得超过15 kn,航道内平均航速应不低于10 kn,该条不免除或限制船长在任何时候采取安全航速的责任.

归纳、总结规则并融入航行决策的流程框图,如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 避让原则和方法

Fig.6 Principles and methods of avoidance

4.1.4 多约束下的可行避碰方案

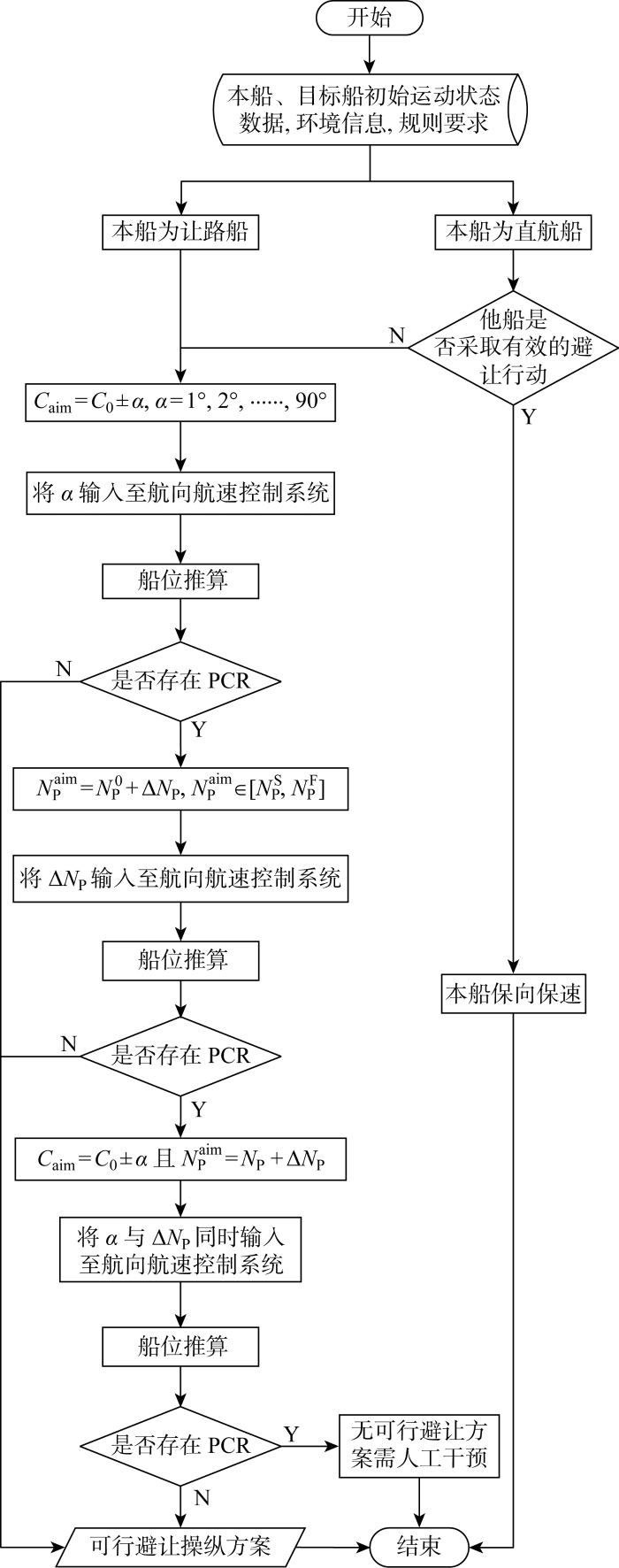
船舶可采取转向、变速和转向变速结合的避让方式.在航海实践中,转向最常用,转向无法有效避让时,采用变速或转向变速结合的方式.结合环境、规则和船舶操纵性等约束条件,求取可避让一定范围内所有目标的最优操纵方案,主要步骤如下,具体流程如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 可行避让方案求取

Fig.7 Derivation scheme of feasible avoidance plans

(1) 单凭转向的方案.根据规则,本船所有可行航向可表示为 $C_{a i m} = C_{0} \pm α$ ,其中 $C_{0}$ 为初始航向;α为改向角度, $α = 1 °, 2 °, \dots, 90 ° .$ 从较小改向角开始,依次验证所有改向角是否安全,能安全避让的最小改向角即为本船单凭转向的避让方案.若所有改向角都不可行,则采取变速避让.若本船船舶领域到达航道边界线,则航向更新为当前航段推荐航向,沿航道边界航行.

(2) 单凭变速的方案.根据主机性能,本船可达到的螺旋桨转速可表示为 $N_{P}^{a i m}$ = $N_{P}^{0}$ +ΔN_P, $N_{P}^{0}$ 、ΔN_P为本船的螺旋桨初始转速、转速改变量; $N_{P}^{a i m}$ ∈[ $N_{P}^{S}$ , $N_{P}^{F}$ ], $N_{P}^{S}$ 、 $N_{P}^{F}$ 为本船停车、全速前进时的螺旋桨转速.通过增加(减少)船舶的车令挡位,逐步验证所有可行的车令挡位是否安全,车令挡位改变较小的方案即为单凭变速的避让方案.若所有车令挡位都不可行,则转向变速结合.北槽水道航速受限,且停车和倒车速度过低导致船舶航向难以精确控制,因此仅考虑正车前进.

(3) 转向变速结合的方案.根据(1)和(2)中所列本船可行的航向C_aim和螺旋桨转速 $N_{P}^{a i m}$ ,从较小改向角加转速改变较小的挡位开始,依次验证所有可行的转向变速结合的避让方案是否安全.若所有结合的方案都不可行,则无可行避让方案,应立即人工干预.

为验证操纵方案是否安全,将所有改向角、车令挡位和本船船位输入至航向航速控制系统中,计算船舶操纵过程中的位置、航向和航速等信息.基于这些信息,进行船位推算,判断任意时刻目标船及其他碍航物(航道外边界、航标、浅滩等)是否将进入本船船舶领域.

找到可行避碰方案,本船开始避让.同时根据3.4节航线跟踪方法,求取目标航向.

4.2 航行决策方法

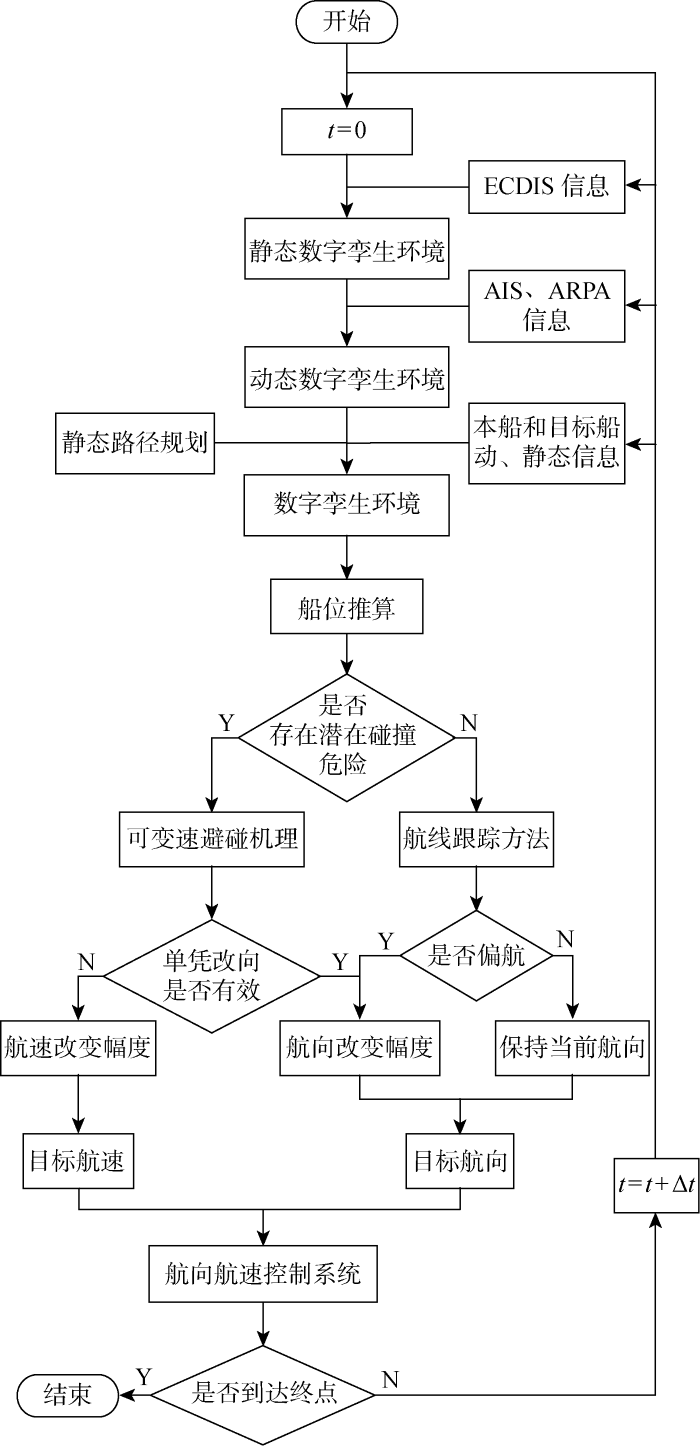
综上,在时变环境中,按固定步长获取实时信息,判断目标船运动状态,生成自适应目标船机动的航行决策方案,并循环执行.首先提取电子海图显示与信息系统(ECDIS)、卫星定位系统、自动识别系统(AIS)和自动雷达标绘辅助(ARPA)系统等助航仪器设备中的动静态环境信息,导入要素模型,构成数字孪生环境.其次推算一段时间的本船和目标船船位,计算碰撞危险度,识别最危险目标船;根据避碰机理求取航向、航速改变幅度.任意初始条件下的航行决策模型如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 航行决策模型

Fig.8 Navigation decision-making model

5 仿真实验与结果分析

5.1 数字孪生环境仿真

将河口深槽水域数字孪生环境通用模型应用到长江口北槽水道中, M=6,N=0,G=41,W=11,D=2. $F_{m} 、 S_{i} 、 A_{a} 、 L_{N} 、 L_{S}$ 均可用通用模型表示,其参数取值如下.当 $m = 1,3, 4,5, 6$ 时 $n = 4$ ,当 $m = 2$ 时 $n = 6; r_{1} = 15 m$ ;当 $a = 1,4, 5$ 时 $j = 5,$ 当 $a = 2,3, 6,7, 8,9, 10,11$ 时 $j = 6,7, 19,16,12,11,11,18;$ 航道外北、南边界线 $L_{N} 、 L_{S}$ ,对应参数 $w = 102, q = 110 .$ 如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 长江口北槽深水航道数字孪生

Fig.9 Digital twinning of deep water channel in the North Channel of the Yangtze River Estuary

5.2 仿真实验

风流以及根据船舶吃水和水深自适应调整的航道外边界线属于数字孪生环境中的动态环境要素,会直接影响船舶操纵性、轨迹跟踪精度和安全避碰决策.取2023年7月22日8:00长江口北槽水道实时风流数据:风向208°,风速6.1 m/s;流向215°,流速0.1 m/s;浪高0.4 m.结合水域海图水深,确定12.5 m等深线为根据吃水自适应调整的航道外边界线.

基于上述动态数据、风流下的MMG模型和自适应最优航向控制方法以及航行规则,设置两组实验验证船舶可变速航行决策方法的可行性,船舶参数如表3和4所示.实验1中所有目标船均不涉及变向变速,实验2中除目标船3外其余目标船保向保速, 目标船3为一艘从锚地出发驶往上行航道的小船,初始航向245°,航速2 kn,驶出锚地过程中逐渐加速,在t=2 007 s 时开始右转并加车,在t=2 140 s 时航向为285°,航速为6.5 kn.

表3 仿真实验1的初始数据

Tab.3 Initial data of simulation in Experiment 1

船舶类别	位置坐标/(°)	航向/(°)	航速/kn	船长/m
本船	(122.495, 31.104)	270	12	225
目标船1	(122.470, 31.104)	270	6	80
目标船2	(122.369, 31.118)	140	10	80
目标船3	(122.295, 31.110)	113	5	80
目标船4	(122.330, 31.094)	90	9	85
目标船5	(122.381, 31.101)	90	10	85

新窗口打开| 下载CSV

表4 仿真实验2的初始数据

Tab.4 Initial data of simulation in Experiment 2

船舶类别	位置坐标/(°)	航向/(°)	航速/kn	船长/m
本船	(122.122, 31.215)	300	12	225
目标船1	(122.110, 31.222)	305	6	80
目标船2	(122.044, 31.250)	205	5.4	85
目标船3	(121.018, 31.256)	245	2	50
目标船4	(121.978, 31.249)	102	9	85
目标船5	(122.053, 31.227)	108	8	85

新窗口打开| 下载CSV

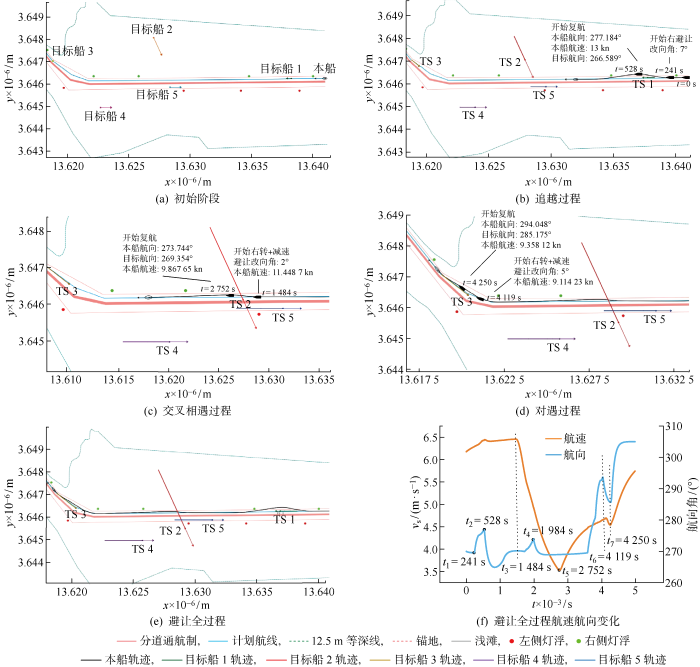
5.2.1 仿真实验1

根据表3的初始信息在Qt平台中进行模拟仿真, 如图10所示.图10(a)、10(e)、10(f)分别显示了仿真的开始阶段、全过程、避让过程中航向航速变化.图10(b)、10(c)、10(d)分别显示了追越、交叉相遇、对遇局面下的具体避让过程、避让时机和可行操纵区间.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 实验1仿真结果

Fig.10 Simulation results of Experiment 1

该场景下,操纵决策方案为:t=241 s时,本船航向右转7° 驶出通航分道追越目标船1,t=528 s时开始航线跟踪.t=1 484 s 时,本船开始减速(将车钟降到前进1)且航向右转2° 避让目标船2,t=1 984 s 时开始航线跟踪,t=2 752 s 车钟前进2.t=4 119 s 时,本船开始减速(车钟降到前进1)且航向右转5° 避让目标船3,t=4 250 s 时开始航线跟踪,同时车钟回到前进3.

5.2.2 仿真实验2

根据表4的初始信息在Qt平台中进行模拟仿真,如图11所示.考虑了目标船机动,图11(a)、11(e)、11(f)分别显示了仿真的开始阶段、全过程、避让过程中航向航速变化.图11(b)、11(c)分别显示了追越、交叉相遇局面下的具体避让过程、时机和可行操纵区间.图11(d)显示了目标船机动状态下的避让过程.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 实验2仿真结果

Fig.11 Simulation results of Experiment 2

该场景下,操纵决策方案为:t=37 s时,本船右转12° 驶出航道追越目标船1,t=332 s时开始航线跟踪.t=1 085 s 时,本船右转2° 避让目标船2同时车钟降到前进2,t=1 648 s 时开始航线跟踪,t=1 861 s 时将车钟回到前进3.t=2 140 s 时,本船开始右转8° 驶出通航分道追越目标船3同时持续加速,t=2 566 s 时开始航线跟踪.

5.3 结果分析

5.1节表明所提出的数字孪生环境模型适用于长江口北槽水道,能够较为全面地展示研究水域的相关静态环境信息.5.2节仿真实验1、2分别在未考虑、考虑了目标船机动的条件下,对所提出的多约束下的航行决策方案进行仿真,同时,两组实验在静态数字孪生环境的基础上,均考虑了风流等动态环境要素的约束,结果表明所提出的多约束下的航行决策方案能够安全避让所有目标.此外,避碰方案和过程涉及穷举法和重复计算验证,但基于环境、船舶操纵性、航行规则和良好船艺约束,在开始穷举验证前,筛除了不符合航海实践和海员通常做法的方案,缩小了穷举区间,降低了计算复杂度,利用C++编译器均可实现实时计算,计算时间约为0.1 s.

6 结语

针对河口深槽可航宽度变化水域的航行决策问题,考虑环境、规则和船舶操纵性等多因素约束,结合风流下的可变速MMG模型和自适应最优PID控制方法,提出了一种基于航向航速控制系统且能动态自适应系统剩余误差和目标船随机运动的可变速航行决策方法.该方法满足在此类水域安全航行的需求,实现操纵辅助决策和未来的自主航行决策,也能为后续其他类似水域航行决策实现提供理论基础.研究中尚未解决数字孪生动态环境的动态水深要素建模,变速避让范围未考虑极端情形下的“倒车”和“停车”,也未考虑变速与变向不同步时的耦合问题.后续研究可进一步完善动态水深影响下的全车钟变速、变速与变向不同步时的航行决策方法.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张英俊, 翟鹏宇.

海运船舶自主避碰技术研究进展与趋势

[J]. 大连海事大学学报, 2022, 48(3): 1-11.