Processing math: 46%
上海交通大学学报

上海交通大学学报, 2025, 59(1): 79-88 doi: 10.16183/j.cnki.jsjtu.2023.206

船舶海洋与建筑工程

基于网格归一化Astar算法的船舶管路布置

林焰1, 张乔宇,1, 楼建迪2

1.大连理工大学 船舶工程学院, 辽宁 大连 116024

2.宁波莱布尼茨信息技术有限公司, 浙江 宁波 315300

Ship Pipe Layout Based on Grid Normalized Astar Algorithm

LIN Yan1, ZHANG Qiaoyu,1, LOU Jiandi2

1. School of Naval Architecture and Ocean Engineering, Dalian University of Technology, Dalian 116024, Liaoning, China

2. Ningbo Leibniz Information Technology Co., Ltd., Ningbo 315300, Zhejiang, China

通讯作者: 张乔宇,博士生; E-mail:qiaoyuzhang@foxmail.com.

责任编辑: 王一凡

收稿日期: 2023-05-23   修回日期: 2023-07-17   接受日期: 2023-08-9  

基金资助: 国家重点实验室专项基金(S18315)

Received: 2023-05-23   Revised: 2023-07-17   Accepted: 2023-08-9  

作者简介 About authors

林焰(1963—),教授,博士生导师,从事船舶与海洋结构物数字化设计方法与软件开发研究.

摘要

为解决船舶管路布置方法中目前存在的依靠人工经验调节算法参数,权重系数的设置量级差距较大,以及求解布置方案单一的问题,提出一种网格归一化Astar (GNAstar)的布置方法.首先,采用包围盒和网格法建立数学模型.其次,通过分支管路拆分、网格标记值和父子网格搜索策略,使每一路径节点由不同目标的归一化权重值来共同决定,将传统Astar算法仅考虑长度的目标扩展成包括长度、弯头消耗和安装适用性的管路综合布置目标.最后,通过仿真案例将GNAstar算法与传统Astar算法进行对比分析,并以船舶机舱内不同管路系统为例,与文献中的蚁群算法和粒子群-Astar算法开展进一步比较.结果表明,GNAstar算法可获得有效的工程解,设计人员可通过设置不同目标的归一化权重系数来获得相应的布置方案.

关键词： 船舶管路; 布置优化; Astar算法; 网格归一化

Abstract

In order to solve the existing problems of relying on manual experience to adjust the algorithm parameters, large difference of weight coefficient, and single result in ship pipe layout, a grid normalized Astar (GNAstar) is proposed. First, the mathematical models are established using bounding box and the grid method. Then, each path node is determined by the normalized weight values of different targets using the branch pipes splitting method, grid marking values, and the parent-child grid search strategy. The cost objective of traditional Astar only considering path length is extended to the comprehensive layout objective of pipes including length, bend consumption, and installation suitability. Finally, the GNAstar proposed is compared with the traditional Astar in a simulation case, and different pipe systems in ship engine room are taken as cases to further compare with the ant colony algorithm and particle swarm-Astar. The results show that the GNAstar proposed can obtain effective engineering solutions, and designers can obtain the corresponding layout result by setting the normalized weight coefficients of different targets.

Keywords： ship pipe; layout optimization; Astar algorithm; grid normalization

PDF (12731KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

林焰, 张乔宇, 楼建迪. 基于网格归一化Astar算法的船舶管路布置[J]. 上海交通大学学报, 2025, 59(1): 79-88 doi:10.16183/j.cnki.jsjtu.2023.206

LIN Yan, ZHANG Qiaoyu, LOU Jiandi. Ship Pipe Layout Based on Grid Normalized Astar Algorithm[J]. Journal of Shanghai Jiaotong University, 2025, 59(1): 79-88 doi:10.16183/j.cnki.jsjtu.2023.206

管路布置是船舶详细设计工作的重要组成部分,由于布置空间内设备几何形状复杂,且需考虑避障、敷设成本和安装适用性等要求,设计人员手动布置耗时且容易出错.所以相关学者对自动布置方法开展研究,以提高船舶管路设计工作的质量与效率.通过归纳近些年国内外的相关研究,本文从数学模型和布置算法两个角度进行分析.

在数学模型方面,除了Kim等[1]以及Lin等[2]分别采用网络图和矢量线构建数学模型外,其余学者均基于网格模型对船舶管路布置方法进行设计,主要原因是虽然前两种模型相比网格模型可以减少搜索节点数量,从而降低数据存储空间,但其构建过程需要人工辅助,自动化水平较低;而网格模型不仅可根据管路尺寸自动构建,且支持大多数成熟的路径搜索算法,并且随着计算机硬件技术的发展,数据存储量已充分提高,因此该模型目前应用广泛.

另一方面,布置算法可分为确定式 (Dijkstra[1]、Astar[3]), 元启发式(遗传[4⇓⇓-7]、粒子群[8-9]、蚁群[10⇓⇓⇓⇓-15]) 和混合式[2,16⇓⇓ -19].确定式算法虽然求解效率较高,但目前只能获得单一固定解,且所考虑的约束条件形式较简单;元启发式算法虽然具有随机性,通过多次运行可获得多种布置方案,但难以保证其求解效率和质量;后来许多学者对结合不同算法优势的混合式算法开展研究,所考虑的布置约束也更贴合工程实际.

然而,上述研究尚存在如下有待解决的问题:① 元启发式和混合式算法的初始化过程需依赖人工经验设置多种优化参数,其求解质量受参数值影响较大;② 不同优化目标所对应的权重系数量级差距较大,在求解不同的船舶管路布置问题时需重新调节,鲁棒性较低;③ 不能根据设计师的不同实际需求获得相应的布置方案.由于Astar算法具有无需参数调节及求解效率高的特点,本文引入分支管路拆分、标记网格以及父子网格的搜索策略扩展了传统Astar算法的目标代价,提出一种网格归一化Astar (grid normalized Astar, GNAstar)的布置方法,并分别采用仿真案例和船舶机舱内不同的管路系统,与传统Astar算法以及考虑同样约束条件和布置目标的蚁群[10]和粒子群-Astar[17]文献算法进行布置结果比较,验证了GNAstar算法的有效性与鲁棒性,设计人员可设置归一化权重系数求解出满足不同设计需求的布置方案,进一步提升船舶管路布置工作的自动化水平和质量.

1 船舶管路布置数学模型

1.1 约束条件

通过对上述相关文献的调研,可将船舶管路布置工作需考虑的主要约束分为以下几类.

(1) 物理约束(physical constraints, P1~P4). P1为管路需连接指定的设备接口;P2为管路与设备之间无干涉;P3为不同管路之间无干涉;P4为管路应沿着舱室空间正交布置.

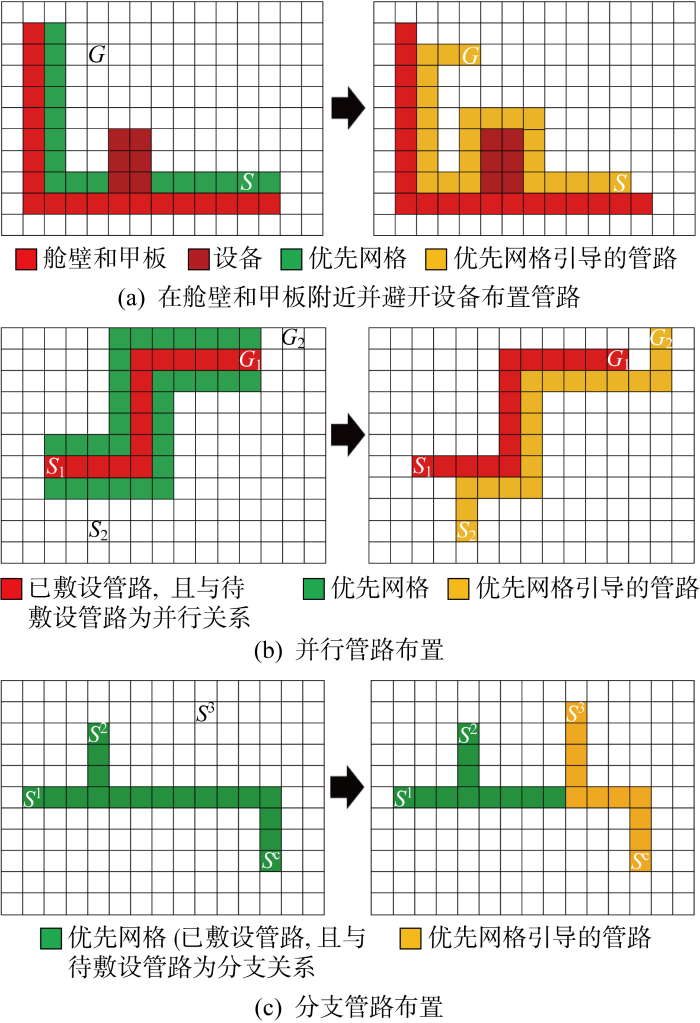
(2) 安装适用性约束(installation constraints, I1~I3). I1为管路应尽可能沿舱壁和甲板敷设;I2为并行管路应尽可能成束敷设;I3为分支管路应可能沿公共区域敷设.

(3) 经济约束(economic constraints, E1~E3). E1为管路长度应尽可能短;E2为弯头的消耗数量应尽可能少;E3为管路的安装适用性长度(符合 I1~I3约束的管路长度)应尽可能长.

(4) 顺序约束(sequence constraints, S1~S2). S1为优先布置重要设备之间的管路;S2为优先布置尺寸较大的管路.

其中,物理约束主要根据管路的接口坐标位置,从几何角度指出布置算法的路径搜索方向及障碍物坐标;安装适用性约束进一步指明管路的优先搜索区域,使管路的布置路径尽可能适合管路实际工程安装; 经济约束和顺序约束则分别确定出布置算法的目标代价和管路敷设顺序.通过以上分析,这些约束的具体表示形式如下:

包围盒,P2; 分支管路拆分,I3; 标记网格,P3、I1~I3; 归一化权重,E1~E3; 父子网格搜索,P1、P4、S1~S2.

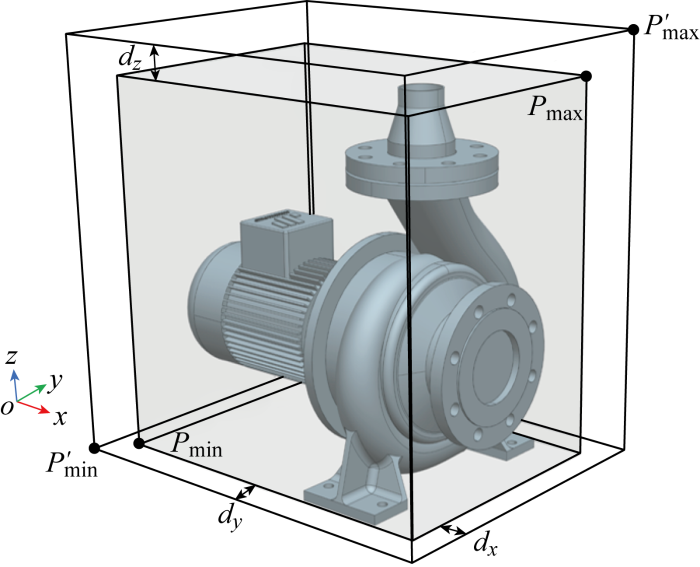
1.2 设备简化

为了提高避障检测效率,路径搜索领域的许多学者均有效地应用包围盒模型来表示障碍物[20-21].以图1所示的机舱水泵为例,只需确定对角线点P'min (x'min, y'min, z'min)和P'max (x'max, y'max, z'max),就可通过下式快速判断出布置空间内任意点(x, y, z)与此水泵的干涉关系:

x'min=xmin+dx,　y'min=ymin+dyz'min=zmin+dz,　x'max=xmax+dxy'max=ymax+dy,　z'max=zmax+dz{干涉,x'min≤x≤xmax, ymin≤y≤ymax,zmin≤z≤zmax不干涉,否则}
(1)

式中:(xmin,ymin,zmin)和(xmax,ymax,zmax)分别为水泵原有的包围盒对角顶点Pmin和Pmax的坐标;dx,dy,dz分别为水泵在3个方向上预留的操作维修距离.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   水泵包围盒示意图

Fig.1   Schematic diagram of bounding box of water pump


1.3 空间表示

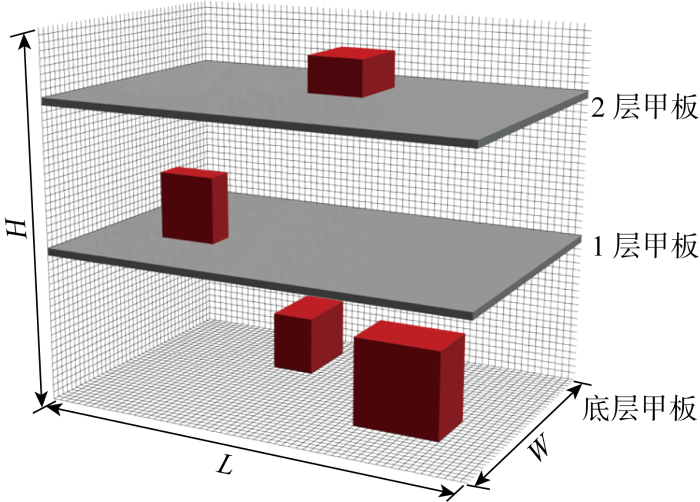
如图2所示,将尺寸为L×W×H的管道布置空间划分为若干三维网格单元,空间内的原始坐标与网格坐标的转换关系如下:

(gx,gy,gz)=(Math.floor(xo/g),Math.floor(yo/g),Math.floor(zo/g))
(2)

式中:(gx, gy, gz)为三维网格坐标;(xo, yo, zo)为三维原始坐标;Math. floor ()为向下取整函数;g为单元网格尺寸.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   空间网格示意图

Fig.2   Schematic diagram of space grid


为保证布置算法的求解质量与效率,将当前布置问题的最小管路直径作为单元网格尺寸, 其余尺寸管路则通过下式向外延伸对应数量的网格:

E=Math.ceil((D-g)/(2g))
(3)

式中:E为扩展网格的数量;Math.ceil()为向上取整函数;D为管路直径.

2 GNAstar算法

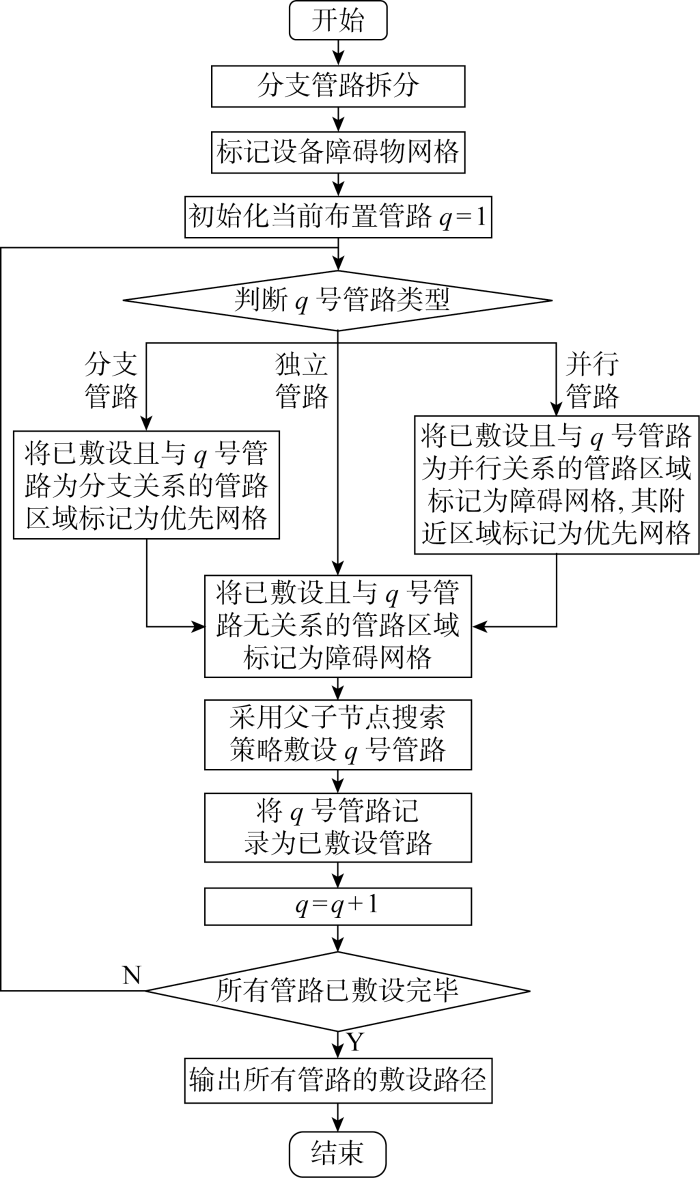
为实现船舶管路(包括多条独立、并行与分支管路)的综合布置,对GNAstar算法进行设计,整体流程如图3所示.图中:q为当前布置管路编号.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   GNAstar算法流程图

Fig.3   Flow chart of GNAstar algorithm


2.1 分支管路拆分

分支管路是一种具有多个接口的管路类型,将其拆分成多条单管路可以使分支管路与其他类型管路同时进行布置求解,具体过程如下.

输入 所有分支节点的网格坐标

N: 分支节点数量

输出 分支管路的共有起点网格坐标

1 for i=1 to N

2 设置 Gi 为空集

3 for j=1 to N

4 if i=j

5 j=j+1

6 else

7 以分支节点i 与j作为边界,将边界内的所有网格坐标添加到Gi集合中

8 j=j+1

9 删除Gi集合中的重复网格坐标

10 %end for

11 比较N个集合 (G1,G2, …,GN)中网格坐标的数量

12 选择包含网格坐标数量最多的集合Gk 所对应的分支节点k作为共有起点网格

13 %end for

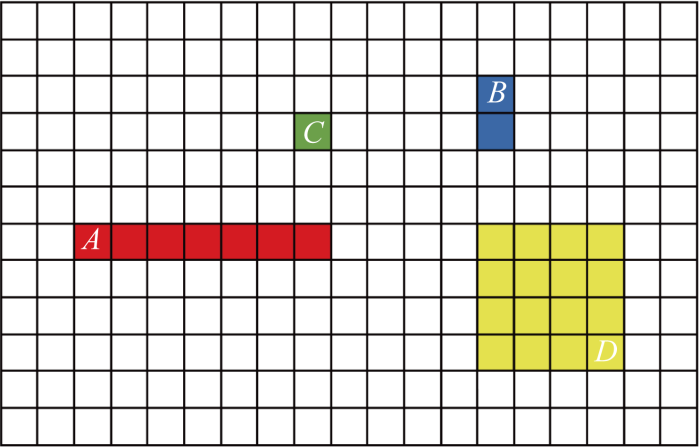
为直观地描述分支管路的拆分过程,以图4所示的4分支管路为例, GA,GB, GC, GD 4个节点集合分别包含7、2、1、16个网格坐标.因此,选择节点D作为该4分支管路的共有起点,并将其拆分为3个具有分支关系的独立管路,分别为D→A、D→B、D→C.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   分支管路拆分示例图

Fig.4   Sample diagram of branch pipe splitting


2.2 网格标记

网格标记示意图如图5所示.图中:S为管路起点;G为管路终点;S1和S2分别为2条并行管路的起点;G1和G2分别为2条并行管路的终点;S1, S2和S3分别为分支管路的3个分支点;Sc为分支管路的共有起点.所有网格标记为禁止网格、优先网格和一般网格,分别对应图5中的红色、绿色和白色网格区域.禁止网格主要包括设备、舱壁、甲板以及已敷设且没有分支关系的管路;优先网格主要是有利于管道安装的区域,包括舱壁与甲板附近(见图5(a))、并行管路附近(见图5(b))和分支管路的公共网格(见图5(c));一般网格主要是处上述网格外的可敷设管路区域.在3种网格的引导下,管路即可在满足约束条件的同时向着设计人员所期望的区域搜索布置方案.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   网格标记示意图

Fig.5   Schematic diagram of grid mark


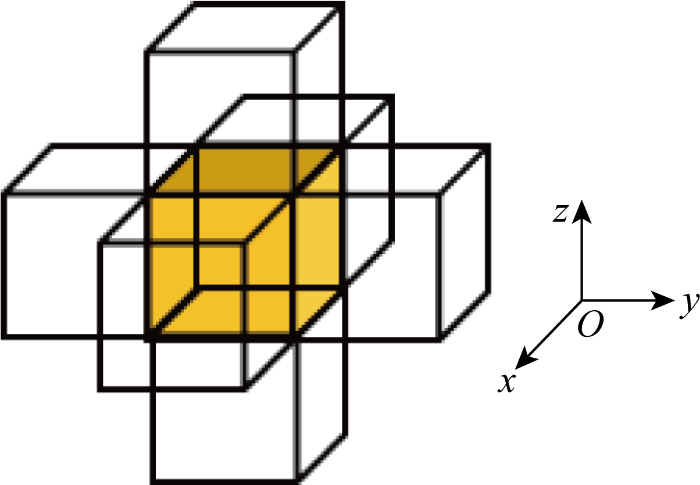
2.3 父子网格搜索

Astar是静态网络中搜索最短路径的确定式算法[22],基本思想是从起始点S开始,遍历到S代价最低的相邻网格,直至终点G为止.代价函数定义为

f(n)=g(n)+h(n)
(4)

式中:g(n)表示从起始点S到所遍历的任意点n的实际成本;h(n)表示从n点到终点G的启发式成本.目前仅考虑搜索长度的Astar算法已在物料搬运[23]、无人驾驶[24]等路径规划领域得到了广泛应用.然而船舶管路布置与一般路径搜索问题不同,除了考虑长度代价外,还需要关注弯头消耗数量、安装适用性的目标.因此本文引入了父子网格搜索策略,两种网格之间的关系如图6所示.在路径搜索过程中,每个网格对应6个方向的子网格,而只对应代价最低的父网格,扩展后的代价函数f'(n)为

f'(n)=g'(n)+h'(n)
(5)

g'(n)= {0,n是起点w1+gI(n),n'是起点w1+gB(n)+gI(n)+g'(n'),否则

gB(n)={w2,n, n', n″

gI(n)=-w3,n是优先网格0,n是一般网格

h'(n)=abs (xn-xG)+abs (yn-yG)+abs (zn-zG)

w1+w2+w3=1

式中:gB(n), gI(n)分别是弯头消耗与安装适用性长度;n'是网格n的父网格,n″是网格n'的父网格;(xn, yn, zn), (xG, yG, zG) 分别是网格n和终点G的坐标; abs( )是绝对值函数;w1, w2, w3分别是3个子目标的归一化权重.父子网格搜索过程如下.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   父(黄)子(白)网格

Fig.6   Grids of parent (yellow) and children (white)


输入 起点网格S, 终点网格G

输出 搜索的管路结果

1 将起点网格S添加到开放列表O中

2 while O≠⌀

3 在O中找到最小代价f'(n)所对应的网格n

4 从O中删除网格n,并将网格n添加到封闭列表C中

5 if 网格n是终点网格G

6 保存搜索的管路结果

7 % end while

8 else

9 生成网格n的6个子网格,并删除已在封闭列表C中的子网格

10 for 每个子网格ni ∉ C i∈(1, 2, 3, 4, 5, 6)

11 if ni∈O and f'(ni)>g'(ni) + h'(ni)

12 通过式(5)更新f'(ni)

13 else

14 通过式(5)计算f'(ni),将网格ni添加到O中

15 % end for

16 % end while

2.4 目标代价

针对不同管径和不同类型的管路,可通过下式计算出q号管路的长度代价fL,q,弯头消耗数量代价fB, q及安装适用性长度代价fI,q:

min fL,q=(Lq-Lcq)cqL,q为分支管路LqcqL,否则min fB,q=(Bq-Bcq)cqB,q为分支管路BqcqB,否则max fI,q=Lcq+L'q,q为分支管路Lpq+L'q,q为并行管路L'q,否则
(6)

式中:Lq,Bq分别表示q号管路的长度与弯头消耗数量;L'q表示q号管路沿舱壁或甲板布置的长度;cqL, cqB分别表示不同管径的q号管路敷设所消耗的单位长度成本和单个弯头成本;Lcq,Bcq分别表示该管路与其余分支公共部分的长度和弯头消耗数量;当q号管路为并行管路时,Lpq表示该管路与为其余管路的并行部分长度.

3 案例验证

3.1 仿真案例

为说明GNAstar算法相比传统Astar算法的性能提升,采用网格空间为50×50×30的仿真案例进行实验,包括6个设备(坐标范围如表1所示),以及一条4分支管路、两条并行管路和一条独立管路,全部管路的管径均为1个网格,并根据表2的编号顺序和接口坐标进行布置.两种算法的运行结果如图7和表3(L/B/I分别表示长度/弯头消耗数量/安装适用性长度)所示,其中GNAstar算法的权重设置为w1=0.3, w2=0.3, w3=0.4.

表1   设备网格坐标

Tab.1  Grid coordinate of facility

设备编号x范围y范围z范围
I(20, 29)(0, 3)(0, 26)
II(25, 27)(44, 49)(0, 8)
III(0, 8)(10, 15)(0, 10)
IV(0, 8)(30, 34)(0, 10)
V(20, 30)(20, 30)(0, 18)
VI(41, 49)(20, 28)(0, 20)

新窗口打开| 下载CSV


表2   管路接口网格坐标

Tab.2  Grid coordinate of pipe nozzle

管路编号类型连接设备接口坐标
1分支I(24, 2, 26)
II(26, 46, 8)
III(2, 12, 10)
IV(5, 32, 10)
2并行III(6, 12, 10)
VI(45, 23, 20)
3并行IV(6, 32, 10)
VI(45, 25, 20)
4独立I(29, 1, 20)
VI(45, 20, 16)

新窗口打开| 下载CSV


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   仿真案例布置效果

Fig.7   Layout effect of simulation case


表3   仿真案例计算结果

Tab.3  Calculation result of simulation case

qL/B/I
传统Astar算法GNAstar算法
1135/6/0137/6/30
260/3/2560/3/49
356/3/2556/3/49
439/4/039/2/20
总计289/16/50291/14/148

新窗口打开| 下载CSV


由图7和表3可知:对于1号分支管路, GNAstar算法的公共部分管路长度占此分支管路长度的22%, 而传统Astar算法的公共部分管路长度为0;对于2号和3号管路,相比于传统Astar算法,GNAstar算法的并行区域增加了24个网格长度;对于4号管路,GNAstar算法有53%长度的管路沿舱壁布置,而传统Astar算法的安装适用性长度为0.从整体上看,虽然在管路总长度方面,GNAstar算法略多于传统Astar算法,但在弯头消耗数量和安装适用性方面,GNAstar算法明显优于传统Astar算法,符合经济性指标.

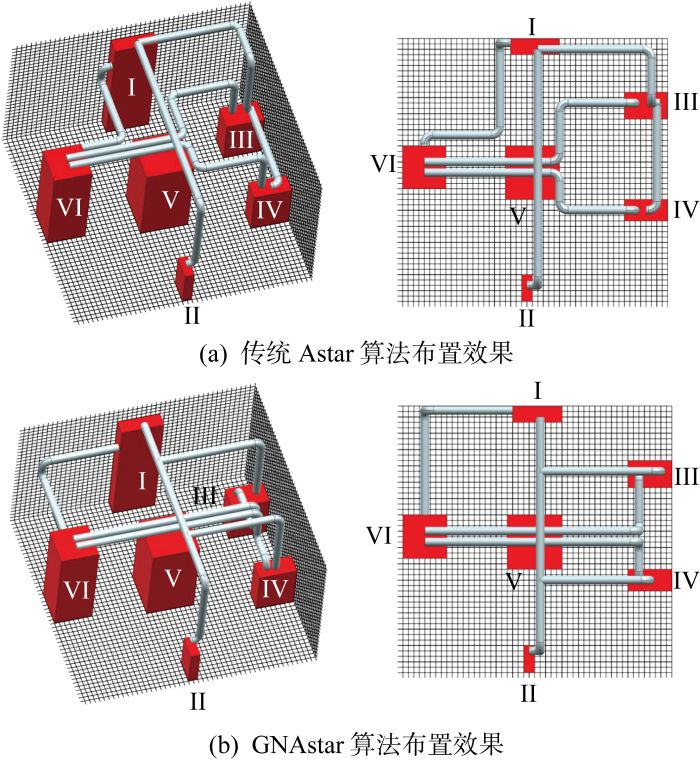
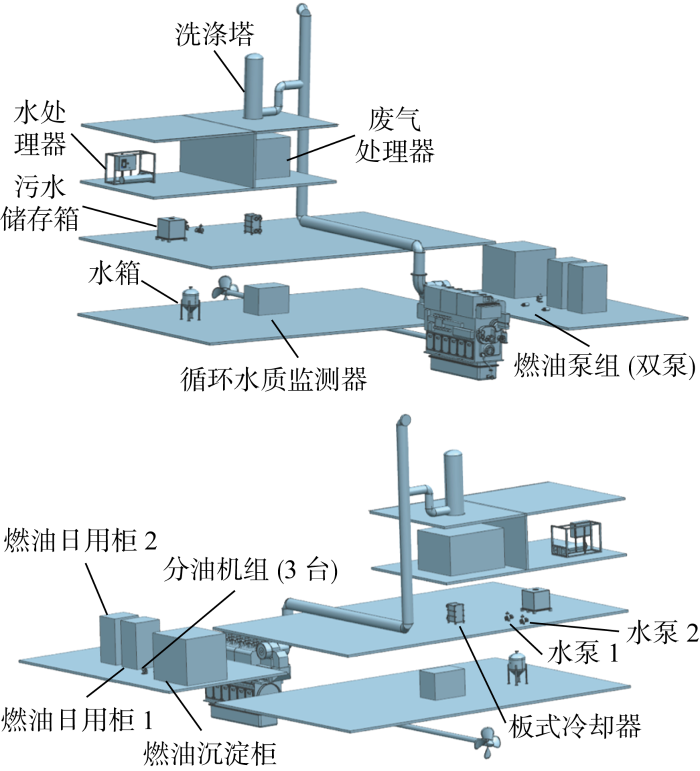
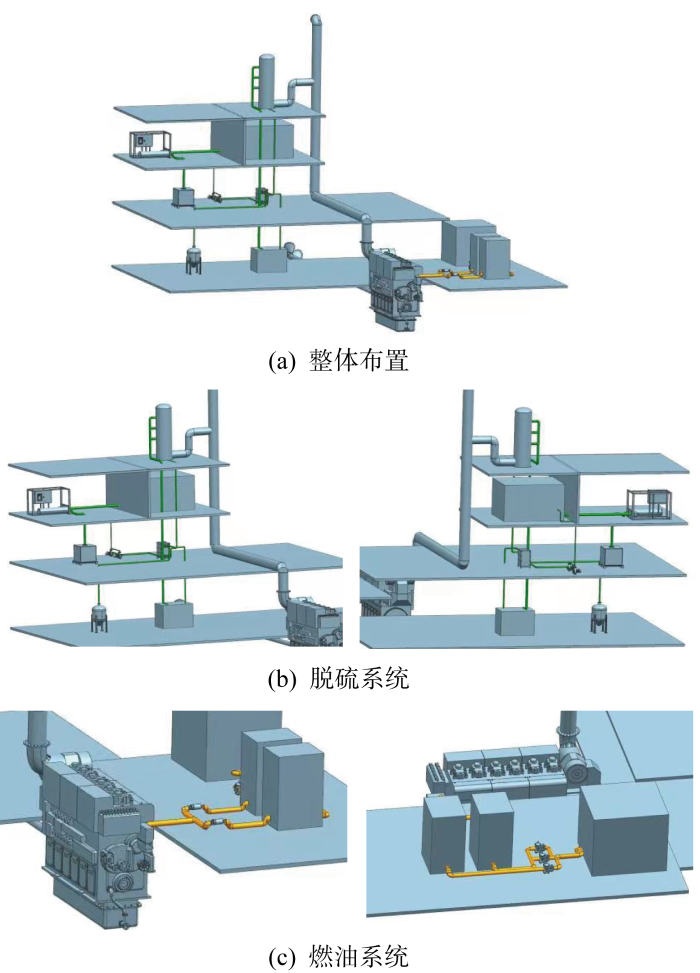
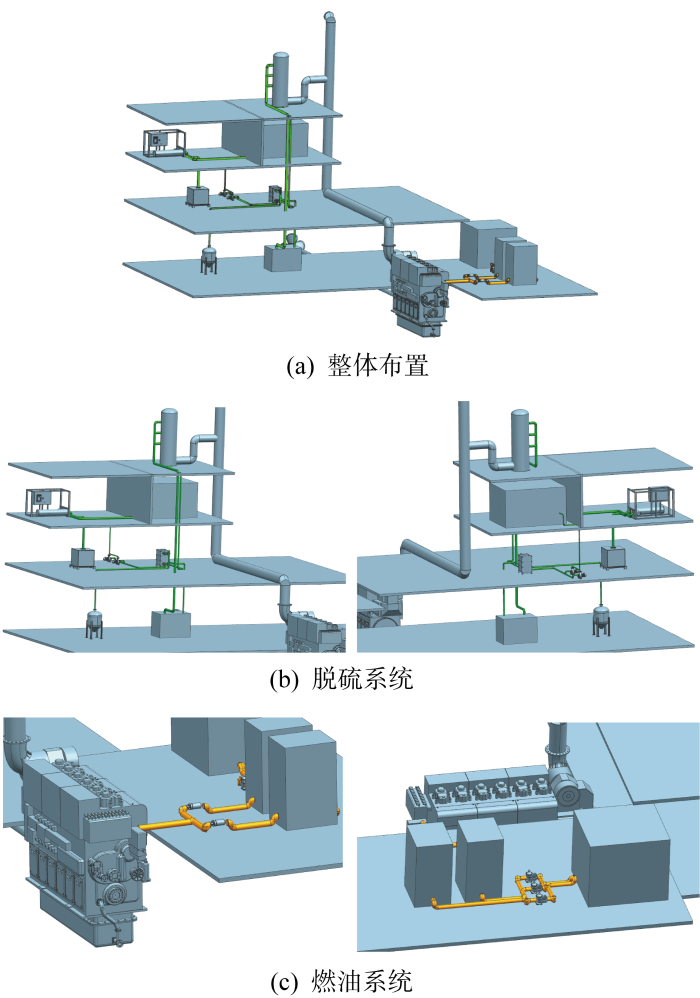
3.2 船舶机舱管路案例

为进一步验证GNAstar算法的有效性,以比例缩小的船舶机舱内(布置空间为 2 000 mm×4 000 mm×3 500 mm)脱硫和燃油管路系统为例,与考虑同样约束条件和优化目标的蚁群[10]、粒子群-Astar[17]文献算法进行布置效果比较.机舱内设备的整体分布情况如图8所示,管路类型、编号顺序、管径和所连设备等布置信息如表4所示,每种方法对于两种机舱管路系统的计算结果如表5所示.在实际的船舶管路布置工作中,设计师有时会根据任务需要,重点关注管路在优先区域的布置情况.因此除了考虑一般的布置工况外(w1=0.3, w2=0.3, w3=0.4,GNAstar-I),还对此类特殊需求的布置工况进行测试(w1=0.1, w2=0.2, w3=0.7,GNAstar-II), 两种工况下GNAstar算法所求解的管路布置效果分别如图9和10所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   机舱设备分布

Fig.8   Facility distribution in engine room


表4   机舱管路布置信息

Tab.4  Information of pipe layout in engine room

管道系统q类型连接设备坐标/mm直径/mm
脱硫系统1分支循环水质监测器洗涤塔(580, 3 220, 2 320)300
(610, 3 400, 3 180)
(610, 3 400, 3 130)
(610, 3 400, 3 080)
2并行水处理器(170, 3 420, 2 770)220
污水储存箱(220, 3 355, 2 600)
3并行水处理器(170, 3 460, 2 770)220
废气处理器(480, 3 300, 2 770)
4分支废气处理器(360, 3 570, 2 800)100
水泵1(440, 3 548, 2 557)
水泵2(440, 3 448, 2 557)
5分支板式冷却器(603, 3 297, 2 537)100
水泵1(448, 3 448, 2 537)
水泵2(448, 3 548, 2 537)
6并行板式冷却器(620, 3 297, 2 587)100
循环水质监测器(670, 3 220, 2 320)
7并行板式冷却器(600, 3 297, 2 587)100
水箱(245, 3 240, 2 300)
8独立洗涤塔(650, 3 400, 2 980)100
板式冷却器(620, 3 297, 2 537)
燃油系统1分支主机(1 030, 2 200, 2 320)600
燃油泵1(1 170, 2 270, 2 330)
燃油泵2(1 170, 2 130, 2 330)
2独立燃油日用柜1(1 330, 2 270, 2 330)600
燃油泵1(1 210, 2 270, 2 330)
3独立燃油日用柜2(1 330, 2 130, 2 330)600
燃油泵2(1 210, 2 130, 2 330)
4分支分油机1(1 385, 2 430, 2 320)480
分油机2(1 410, 2 430, 2 320)
燃油沉淀柜(1 400, 2 530, 2 330)
5并行燃油沉淀柜(1 400, 2 530, 2 330)480
分油机3(1 475, 2 430, 2 320)
6分支分油机1(1 370, 2 390, 2 320)480
分油机2(1 430, 2 390, 2 320)
燃油日用柜1(1 460, 2 265, 2 330)
7并行燃油日用柜2(1 460, 2 130, 2 330)480
分油机3(1 490, 2 390, 2 320)

新窗口打开| 下载CSV


表5   机舱管路计算结果

Tab.5  Pipe calculation result in engine room

管路系统qL/B/I
蚁群粒子群-AstarGNAstar-IGNAstar-II
脱硫系统11 490/4/8601 130/3/1 0401 130/3/1 0401 190/5/1 100
2278/4/101278/4/176278/4/101278/4/176
3470/2/0500/4/455500/3/180500/5/460
4494/2/0494/2/0494/4/67494/4/67
5700/3/356700/3/356700/3/356700/3/356
6638/4/364638/3/134616/3/443698/5/546
7432/4/329432/4/316445/4/345445/4/345
8464/4/434464/4/434464/4/434486/4/462
总计4 966/27/2 4444 636/27/2 9114 627/28/2 9664 791/34/3 512
燃油系统1286/4/117276/4/158276/4/158294/6/234
2120/0/0120/0/0148/4/100148/4/100
3120/0/0120/0/0148/4/100148/4/100
4200/4/85173/4/150173/4/150190/6/150
5310/4/85310/4/85310/4/270310/4/270
6321/3/117321/4/117298/5/270333/5/272
7190/4/85190/4/75202/5/164202/5/164
总计1 547/19/4891 510/20/5851 555/30/1 2121 625/34/1 290

新窗口打开| 下载CSV


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   GNAstar-I 布置效果

Fig.9   Layout effect of GNAstar-I


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   GNAstar-II 布置效果

Fig.10   Layout effect of GNAstar-II


通过比较不同算法的计算结果可知:蚁群与粒子群-Astar算法所求解两种管路系统中的弯头消耗数量均少于GNAstar算法,但两种算法均存在管路安装适用性低的问题(如脱硫系统的4号管路,燃油系统的2号和3号管路,其安装适用性长度均为0),不符合经济性要求,并且受其启发式参数和权重系数量级差距较大的影响,虽然所求解的燃油管路总长度略低于GNAstar算法,但脱硫管路的总长度较高,在求解不同的管路布置问题时需要调节有关参数和权重系数,鲁棒性较低;而GNAstar算法虽然在管路总长度和弯头消耗数量略高于前两种文献算法, 但两种管路系统中的每条管路均支持实际工程安装,满足经济性要求且鲁棒性较好.此外,GNAstar-I与GNAstar-II 两种布置结果与初始设定的权重目标比例均保持一致,相比于GNAstar-I,GNAstar-II 的布置方案虽然在管路总长度和弯头消耗数量方面略高,但可安装长度所占管路总长度的比例更高(如脱硫系统的1号、2号和3号管路,以及燃油系统的1号管路),设计师可根据实际需求便捷地调节GNAstar算法中不同目标的归一化权重系数,从而获得相应的布置方案.

4 结论

针对目前船舶管路布置方法中存在的依靠人工经验调节算法参数,权重系数的设置量级差距较大,以及无法根据实际需要获得不同布置方案的问题,本文在考虑多种实际约束的条件下通过包围盒和网格法建立数学模型,在此基础上对传统Astar算法进行改进,提出了一种船舶管路布置的GNAstar算法:

(1) 通过分支管路拆分、网格标记和父子网格搜索策略,将传统Astar算法仅考虑长度的目标扩展成包括长度、弯头消耗和安装适用性在内的管路综合设计目标,从而实现了不同目标所对应权重系数的归一化,不仅无需人工调节算法参数,且可同时求解包含分支、并行和独立管路在内的混合管路布置问题.

(2) 结合混合管路布置的仿真案例,将传统Astar算法与GNAstar算法进行对比,结果表明GNAstar算法可使管路尽可能沿分支管路公共部分、有利于并行管路成束以及舱壁等优先区域进行布置,所求解方案的经济性明显优于传统Astar算法.

(3) 以船舶机舱内脱硫与燃油管路系统为例,通过与文献中的蚁群和粒子群-Astar算法进行比较,验证了GNAstar算法可保证每条管路均符合经济性要求,鲁棒性较好,且设计人员可通过设置不同目标的归一化权重系数来获得相应的布置方案,为进一步提升船舶管路布置工作的自动化水平和质量提供了参考.

参考文献

KIM H, RUY W, JANG B S.

The development of a practical pipe auto-routing system in a shipbuilding CAD environment using network optimization

[J]. International Journal of Naval Architecture and Ocean Engineering, 2013, 5: 468-477.

[本文引用: 2]

LIN Y, BIAN X Y, DONG Z R.

A discrete hybrid algorithm based on Differential Evolution and Cuckoo Search for optimizing the layout of ship pipe route

[J]. Ocean Engineering, 2022, 261: 1-13.

[本文引用: 2]

BIAN X Y, LIN Y, DONG Z R.

Auto-routing methods for complex ship pipe route design

[J]. Journal of Ship Production and Design, 2022, 38(2): 100-114.

[本文引用: 1]

DONG Z, LIN Y.

Ship pipe routing method based on genetic algorithm and cooperative coevolution

[J]. Journal of Ship Production and Design, 2017, 33: 122-134.

[本文引用: 1]

董宗然, 楼偶俊, 管官.

基于改进遗传算法的船舶管路布局设计

[J]. 计算机工程与应用, 2020, 56(19): 252-260.

DOI:10.3778/j.issn.1002-8331.1906-0251      [本文引用: 1]

针对船舶管路布局设计中的路径规划问题提出一种改进型遗传算法求解方法。建立船舶管路布局设计问题的模型空间、约束条件和优化目标；提出一种基于连接点网格的定长编码方法，结合该编码方法设计了适合改进遗传算法应用的适应度函数和交叉、变异算子，定长编码可降低遗传算子设计复杂度和非法个体修补代价；提出在进化流程中嵌入以“去折弯”和“改模式”两种改善型变异方法构建的爬山操作，以提升算法收敛性和寻优能力。通过仿真实验验证所提算法具有可行性和先进性。

DONG Zongran, LOU Oujun, GUAN Guan.

Ship pipe route design based on improved genetic algorithm

[J]. Computer Engineering and Applications, 2020, 56(19): 252-260.

DOI:10.3778/j.issn.1002-8331.1906-0251      [本文引用: 1]

<p>In order to solve the Ship Pipe Route Design（SPRD） problem, an improved Genetic Algorithm（GA） optimization method is proposed. Firstly, the model space, constraint conditions and optimization objectives are established for the SPRD problem. Then a fixed-length encoding method based on connection-grids is proposed. Combined with this method, the fitness function and genetic operators such as crossover and mutation are designed for the improved GA. The fixed-length encoding simplifies the implementation of the genetic operators, and can reduce the cost of illegal individual repair. In addition, two improved mutation methods, i.e., &ldquo;bend-remove&rdquo; and &ldquo;mode-change&rdquo;, are embedded in the evolutionary process as the hill-climbing operator to improve the convergence and optimization abilities of the algorithm. Finally, a simulation experiment is conducted to verify the feasibility and advancement of the proposed algorithm.</p>

SUI H, NIU W.

Branch-pipe-routing approach for ships using improved genetic algorithm

[J]. Frontiers of Mechanical Engineering, 2016, 11(3): 316-323.

DOI:10.1007/s11465-016-0384-z      [本文引用: 1]

Branch-pipe routing plays fundamental and critical roles in ship-pipe design. The branch-pipe-routing problem is a complex combinatorial optimization problem and is thus difficult to solve when depending only on human experts. A modified genetic-algorithm-based approach is proposed in this paper to solve this problem. The simplified layout space is first divided into three-dimensional (3D) grids to build its mathematical model. Branch pipes in layout space are regarded as a combination of several two-point pipes, and the pipe route between two connection points is generated using an improved maze algorithm. The coding of branch pipes is then defined, and the genetic operators are devised, especially the complete crossover strategy that greatly accelerates the convergence speed. Finally, simulation tests demonstrate the performance of proposed method.

王运龙, 王晨, 韩洋, 等.

船舶管路智能布局优化设计

[J]. 上海交通大学学报, 2015, 49(4): 513-518.

[本文引用: 1]

WANG Yunlong, WANG Chen, HAN Yang, et al.

Intelligent layout optimization design of ship pipe

[J]. Journal of Shanghai Jiao Tong University, 2015, 49(4): 513-518.

[本文引用: 1]

DONG Z R, LIN Y.

A particle swarm optimization based approach for ship pipe route design

[J]. International Shipbuilding Progress, 2017, 63(1/2): 59-84.

[本文引用: 1]

林焰, 辛登月, 卞璇屹, 等.

改进自适应惯性权重粒子群算法及其在核动力管道布置中的应用

[J]. 中国舰船研究, 2023, 18(3): 1-12.

[本文引用: 1]

LIN Yan, XIN Dengyue, BIAN Xuanyi, et al.

Improved particle swarm algorithm with adaptive inertia weight and its application in nuclear power pipeline layout

[J]. Chinese Journal of Ship Research, 2023, 18(3): 1-12.

[本文引用: 1]

JIANG W Y, LIN Y, CHEN M, et al.

A co-evolutionary improved multi-ant colony optimization for ship multiple and branch pipe route design

[J]. Ocean Engineering, 2015, 102: 63-70.

[本文引用: 3]

DONG Z R, BIAN X Y, ZHAO S.

Ship pipe route design using improved multi-objective ant colony optimization

[J]. Ocean Engineering, 2022, 258(1): 1-14.

[本文引用: 1]

范小宁, 林焰, 纪卓尚.

多蚁群协进化的船舶多管路并行布局优化

[J]. 上海交通大学学报, 2009, 43(2): 193-197.

[本文引用: 1]

FAN Xiaoning, LIN Yan, JI Zhuoshang.

Multi ant colony cooperative coevolution for optimization of ship multi pipe parallel routing

[J]. Journal of Shanghai Jiao Tong University, 2009, 43(2): 193-197.

[本文引用: 1]

WU L, TIAN X, WANG H Y, et al.

Improved ant colony optimization algorithm and its application to solve pipe routing design

[J]. Assembly Automation, 2019, 39: 45-57.

[本文引用: 1]

WANG Y L, YU Y Y, LI K, et al.

A human-computer cooperation improved ant colony optimization for ship pipe route design

[J]. Ocean Engineering, 2018, 150: 12-20.

[本文引用: 1]

林焰, 金庭宇, 杨宇超.

舰船管路布置 PG-MACO 优化方法

[J]. 上海交通大学学报, 2024, 58(7): 1027-1035.

DOI:10.16183/j.cnki.jsjtu.2022.508      [本文引用: 1]

针对舰船管路设计效率低下的问题提出一种管路布置优化方法.综合考虑安全性、经济性、协调性和可操作性等工程背景建立优化数学模型,改进蚁群算法在处理混合管路布置工况下的缺陷,提出优化可行解搜索的空间状态转移策略,提升信息素启发效果并加速算法收敛的信息素扩散机制,面向混合管路布置工况设计多蚁群协同进化机制.基于二次开发技术实现本方法在第三方设计软件上的应用,采用核级一回路管道布置工程案例进行验证.结果表明信息素高斯扩散多蚁群优化(PG-MACO)算法的性能和布置效果优于传统蚁群算法,寻路效率提升58.38%,收敛代数缩短43.24%,布置结果中管路长度缩短33.88%,管路折弯次数减少41.67%,验证了本方法的有效性和工程实用性.

LIN Yan, JIN Tingyu, YANG Yuchao.

PG-MACO optimization method for ship pipeline layout

[J]. Journal of Shanghai Jiao Tong University, 2024, 58(7): 1027-1035.

[本文引用: 1]

JIANG W Y, LIN Y, CHEN M, et al.

An ant colony optimization-genetic algorithm approach for ship pipe route design

[J]. International Shipbuilding Progress, 2014, 61 (3/4): 163-183.

[本文引用: 1]

ASMARA A. Pipe routing framework for detailed ship design[D]. Delft, The Netherlands: Delft University of Technology, 2013.

[本文引用: 3]

DONG Z, BIAN X.

Ship pipe route design using improved A* algorithm and genetic algorithm

[J]. IEEE Access, 2020, 8: 153273-153296.

[本文引用: 1]

WANG Y, WEI H, ZHANG X, et al.

Optimal design of ship branch pipe route by a cooperative co-evolutionary improved particle swarm genetic algorithm

[J]. Marine Technology Society Journal, 2021, 55(5): 116-128.

[本文引用: 1]

XU J J, LIU Z F, YANG C B, et al.

A pseudo-distance algorithm for collision detection of manipulators using convex-plane-polygons-based representation

[J]. Robotics and Computer Integrated Manufacturing, 2020, 66: 1-19.

[本文引用: 1]

YI K C, WANG W P, LIU Y, et al.

Continuous collision detection for two moving elliptic disks

[J]. IEEE Transactions on Robotics, 2006, 2(22): 213-223.

[本文引用: 1]

HART P E, NILSSON N J, RAPHAEL B.

Correction to ‘A formal basis for the heuristic determination of minimum cost paths’

[J]. SIGART Newsletters, 1972, 37: 28-29.

[本文引用: 1]

MARIEM B, MARC Z, ROBERTA C A, et al.

3D facility layout problem

[J]. Journal of Intelligent Manufacturing, 2021, 32: 1065-1090.

[本文引用: 1]

李文博, 秦小林, 罗刚.

基于无障碍凸区域的无人机在线航迹规划

[J]. 系统科学与数学, 2021, 41(6), 1493-1506.

[本文引用: 1]

LI Wenbo, QIN Xiaolin, LUO Gang.

Online trajectory planning of UAV based on convex obstacle-free area

[J]. Journal of Systems Science and Mathematical Sciences, 2021, 41(6): 1493-1506.

DOI:10.12341/jssms20355      [本文引用: 1]

A method based on obstacle-free convex area is proposed to solve the problem of UAV (Unmanned Aerial Vehicle) online trajectory planning. Firstly, A* algorithm based on probabilistic roadmap (PRM) is used to plan a global path off-line. Then, the path planned above is used for local planning by IRIS-Astar algorithm proposed in this paper. The large convex obstacle-free area of the current position is calculated by IRIS (Iterative Regional Inflation By Semidefinite Programming) algorithm, which is used to find a global path point farthest from the current track point to be taken as the local target point. As the UAV travels towards the local target point, the large convex area of the current position is calculated in real time, at the same time, whether the local target point is in this area is judged. If it is, continue to travel towards the local target point; otherwise, the local target point is recalculated. Experimental results show that compared with traditional algorithms, the proposed method can effectively solve the collision avoidance problem of UAV and greatly reduce the energy consumption of UAV.

/

〈 〉