基于高斯过程回归和深度强化学习的水下扑翼推进性能寻优方法

doi:10.16183/j.cnki.jsjtu.2023.188

基于高斯过程回归和深度强化学习的水下扑翼推进性能寻优方法

杨映荷¹, 魏汉迪^,¹^,², 范迪夏³, 李昂³

1.上海交通大学海洋工程国家重点实验室,上海 200240

2.上海交通大学三亚崖州湾深海科技研究院,海南三亚 572024

3.西湖大学工学院,杭州 310024

Optimization Method of Underwater Flapping Foil Propulsion Performance Based on Gaussian Process Regression and Deep Reinforcement Learning

YANG Yinghe¹, WEI Handi^,¹^,², FAN Dixia³, LI Ang³

1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. SJTU Yazhou Bay Institute of Deepsea Sci-Tech, Sanya 572024, Hainan, China

3. School of Engineering, Westlake University, Hangzhou 310024, China

通讯作者: 魏汉迪,助理研究员;E-mail:weihandi@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-05-11 修回日期: 2023-06-14 接受日期: 2023-06-19

基金资助:

国家自然科学基金(42206192)
国家自然科学基金(52031006)
海南省自然科学基金项目(521QN275)
三亚崖州湾科技城科研项目(SKJC-2021-01-003)

Received: 2023-05-11 Revised: 2023-06-14 Accepted: 2023-06-19

作者简介 About authors

杨映荷(2001—),硕士生,主要研究方向为流体智能控制.

摘要

为了克服水下工作环境的复杂多变性,以及扑翼运动本身存在控制难度高、变量多、非线性特征显著等问题,提出一种直接探索环境并选取相应最优扑翼推进运动参数的寻优方法.采用拉丁超采样技术获取多维扑翼参数在实际水池中的数据样本,并基于该数据使用高斯过程回归(GPR)算法建立泛化工作环境的非参数模型.在不同推进性能需求下,采用深度强化学习(DRL)中的TD3算法并以奖励最大化为目标,训练得出连续区间内多参数动作最优组合解.实验结果表明,该GPR-TD3方法可以习得实验环境下扑翼推进的全定义域内最优解,包括最大速度和最大效率,并且该最优解可以在GPR中以二维形式直观验证其准确性.同时,针对任意给出的推进速度要求值,在290组真实样本前提下,新算法能够给出误差范围为0.23%~6.68%的推荐动作组合解,为真实应用提供参考.

关键词： 水下扑翼; 高斯过程回归; 深度强化学习; 推进性能寻优

Abstract

In order to overcome the complexity and variability of underwater working environments, as well as the difficulty of controlling the flapping motion due to the significant nonlinear characteristics and numerous variables involved, a direct exploration approach is proposed to search for the optimal flapping foil propulsion parameters in the environment. The Latin hypercube sampling technique is utilized to obtain the samples of multi-dimensional flapping parameters in actual water pool data, and a Gaussian process regression (GPR) machine learning model is established based on these samples to generalize the working environment. Under different propulsion performance requirements, the TD3 algorithm in deep reinforcement learning (DRL) is trained for maximizing rewards and obtaining the optimal combination of multiple parameter actions in continuous intervals. The experimental results demonstrate that the GPR-TD3 method is capable of learning the globally optimal solution for flapping propulsion in the experimental environment, including maximum speed and maximum efficiency. Furthermore, the accuracy of this optimal solution can be intuitively verified through a two-dimensional contour plot in the GPR. Meanwhile, with 290 sets of real samples provided for any given propulsion speed requirement, the agent can recommend a set of action combinations with an error range of 0.23% to 6.68%, which can provide reference for practical applications.

Keywords： underwater flapping foil; Gaussian process regression (GPR); deep reinforcement learning (DRL); propulsion performance optimization

PDF (6630KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨映荷, 魏汉迪, 范迪夏, 李昂. 基于高斯过程回归和深度强化学习的水下扑翼推进性能寻优方法[J]. 上海交通大学学报, 2025, 59(1): 70-78 doi:10.16183/j.cnki.jsjtu.2023.188

YANG Yinghe, WEI Handi, FAN Dixia, LI Ang. Optimization Method of Underwater Flapping Foil Propulsion Performance Based on Gaussian Process Regression and Deep Reinforcement Learning[J]. Journal of Shanghai Jiaotong University, 2025, 59(1): 70-78 doi:10.16183/j.cnki.jsjtu.2023.188

海洋航行物的动力推进一直是一项热门研究话题.考虑到操纵性、环保性、推进效率等因素,越来越多的水面航行物如各类船舶、自主水面航行器(ASV)和水下航行物如自主水下航行器(AUV)、水下滑翔机、无人潜航器等倾向于采用仿生扑翼推进手段^[1].

20世纪初至今,针对扑翼运动参数对水动力性能的影响是一个备受关注的研究方向^[2],目前集中在针对单一变量和离散变量的研究.其中,扑翼运动的拍动频率和振幅等参数设定对于推力、功率系数和推进效率等研究目标的优化至关重要^[3].已有研究表明,推力系数与振幅大小呈先增后减或单调递增趋势,推进效率的变化趋势则取决于推力系数与功率系数之间的相对增幅^[4⇓-6].此外,Amiralaei等^[7]的研究显示选取适当的扑翼运动参数可以有效提升扑翼推进性能,但是在单扑翼水动力性能与拍动频率、耦合运动相位差之间还未发现必然规律.因此,在连续运动区间内快速寻找单扑翼最佳水动力性能对应的耦合运动参数具有相当的应用价值和研究前景.

为了建立准确的扑翼运动模型并考虑到水下环境力的强非线性影响,本研究采用高斯过程回归(GPR)算法对扑翼推进运动进行非参数建模.与此同时,深度强化学习(DRL)可以通过水下扑翼与环境之间的实时交互以获取经验进行自主优化学习,具备着对多维参数进行自主特征提取、重构和优化的优势^[8].本文结合高斯过程回归和深度强化学习提出一种新的优化方法,能够在小样本基础上快速获取扑翼推进的非参数化模型,且该方法可对最佳推进性能以及特定推进性能需求下的扑翼运动参数进行优化结果选取.

1 扑翼推进问题

据Thakor等^[9]的研究显示,无论是针对水下扑翼还是空中扑翼,通常情况下扑翼运动研究所采用的扑翼正弦运动公式为

θ(t)=θ₀+Acos(2πf₀t)

(1)

式中:θ₀表示平均攻角;A表示攻角幅值;f₀为频率;t为时间.

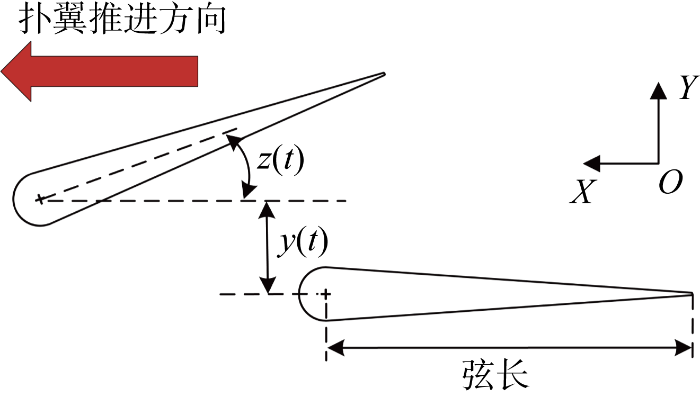
在典型公式基础上衍生出本文所使用的扑翼横荡(首摇)耦合运动时的对称正弦运动公式为

$\begin{array}{l} y = y_{0} s i n (2 π f t + ϕ) \\ z = z_{0} s i n (2 π f t) \end{array}\}$

(2)

式中:y₀表示横荡运动幅值;z₀表示首摇运动幅值;f为横荡(首摇)频率;ϕ为横荡(首摇)运动相位差.

在上述扑翼运动情况下,本文研究运动参数组合[ $\begin{array}{l} f & z_{0} & y_{0} & ϕ \end{array}$ ]相对推进性能参数的寻优问题.研究选取扑翼推进速度和扑翼推进效率作为扑翼推进性能参数指标.在扑翼推进运动问题中作为动作输入的参数、符号意义以及取值范围如表1所示.扑翼耦合运动下的推进模式如图1所示,扑翼弦长为190.66 mm,图中右侧扑翼示意扑翼初始位置,左侧扑翼示意任意时刻t后的扑翼位置.

表1 变量区间范围

Tab.1 Range of variable intervals

参数	下边界	上边界
横荡(首摇)频率,f/Hz	0.5	0.7
首摇运动幅值,z₀/(°)	25	55
横荡运动幅值,y₀/mm	20	65
运动相位差,ϕ/rad	0.52	5.76

新窗口打开| 下载CSV

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 扑翼耦合运动示意图

Fig.1 Illustration of flapping foil coupling motion

2 算法介绍

2.1 深度强化学习

该扑翼推进问题理论上能够直接使用深度强化学习方法进行研究,即通过深度强化学习算法与扑翼推进环境直接交互训练得出最优动作组合解.

深度强化学习是一种通过与环境实时交互观察后获取奖励以确定未来动作的学习算法.该算法使用人工神经网络(ANN)作为函数逼近器,以学习将状态映射为动作的关系.优化目标是最大化在某一场景实例中获得的累计奖励,累计奖励可表示为

R(τ)=

$\overset{T}{\sum_{t = 0}}$ γ^tr_t

(3)

式中:r_t为t时刻的奖励;γ∈[0,1]为折扣因子;T为总时间步.

强化学习核心概念简图如图2所示,t时刻学习算法接收到环境状态S_t并以此为基础选择出一个动作A_t,t+1时刻算法将接收到环境决定的奖励R_t并观测到新的环境状态值S_t₊₁,算法重复以上步骤直至任务结束.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 强化学习算法框架简图

Fig.2 Sketch of framework of reinforcement learning algorithm

然而,在扑翼推进问题中,单次扑翼推进实验生成一组样本,且在单次实验耗时较长的情况下,单工况实际所需实验总和至少数千组.因此,直接使用深度强化学习方法在实际应用中颇具难度且效率较低.

2.2 高斯过程回归

高斯过程回归是一种机器学习非参数建模手段,能够有效处理小样本数据下的非线性多维参数回归问题^[10].高斯回归可以为深度学习中的海量样本需求问题提供解决方法.高斯过程回归的算法本质是基于多元高斯过程和贝叶斯推理对非线性系统进行建模.假设一个具有任意有限数量样本的空间D={(X,y_i) $|i = 1, 2, \dots, n}$ ={X, Y_D}.其中:X=[x₁x₂ … x_n]^T为n维输入矩阵,x_i∈R^k为k维输入向量;y_i∈R为对应输出标量;Y_D为输出向量.回归过程将根据样本集学习输入X与输出Y_D的非线性映射关系,该回归模型表述为

y_noi=χ(x_*)+ε

(4)

式中:y_noi为考虑噪声后的观测值;χ为不考虑噪声的预测值;x_*为输入向量;ε为噪声,且ε~N(0, $σ_{n}^{2}$ ),噪声为0表示高斯过程回归对原样本完全插值,因此 $σ_{n}^{2}$ 能够防止回归出现过拟合.

多元高斯过程可定义为任意输入变量x, x'∈R^k均满足高斯过程贝叶斯先验分布为

χ(x)~G(m(x), k(x, x'))

(5)

式中:m(x)为均值函数,实际使用中一般设置m(x)=0以简化后验概率分布求解;k(x, x')为核函数.

高斯过程回归常用核函数包括线性核函数、P阶多项式核函数、径向基核函数等.符合各向异性输入特征条件的6种常用核函数如表2所示.表中:x_i、x_j为输入数据点;θ为核函数的参数向量;σ_l为长度尺度参数,控制核函数的光滑度和相关性范围;σ²为核函数的方差参数; r为x_i和x_j之间的距离,可以使用欧氏距离或其他距离度量.在实际模型中,需要根据具体情况选择恰当的核函数以达到最优效果.

表2 GPR常用核函数

Tab.2 Common kernel functions for GPR

核函数	函数关系式
Matern 3/2	k(x_i, x_j\|θ)=σ²exp $(1 + \frac{\sqrt{3 r}}{σ_{l}})$ exp $(- \frac{\sqrt{3 r}}{σ_{l}})$ , r= $\sqrt{(x_{i} - x_{j})^{T} (x_{i} - x_{j})}$
Matern 5/2	k(x_i, x_j\|θ)=σ² $(1 + \frac{\sqrt{3 r}}{σ_{l}} + \frac{5 r^{2}}{3 σ^{2}})$ exp $(- \frac{\sqrt{5 r}}{σ_{l}})$
ARD Matern 3/2	k(x_i, x_j\|θ)=σ²(1+ $\sqrt{3 r}$ )exp(- $\sqrt{3 r}$ ), r= $\sqrt{\overset{d}{\sum_{m = 1}} \frac{(x_{i m} - x_{j m})^{2}}{σ_{m}^{2}}}$
ARD Matern 5/2	k(x_i, x_j\|θ)=σ² $(1 + \sqrt{5} r + \frac{5 r^{2}}{3})$ exp(- $\sqrt{5 r}$ )
Squared exponential	k(x_i, x_j\|θ)=σ²exp $[- \frac{1}{2} \frac{(x_{i} - x_{j})^{T} (x_{i} - x_{j})}{σ_{l}^{2}}]$
Absolute exponential	k(x_i, x_j\|θ)=σ²exp $(- \frac{r}{σ_{l}})$ , r= $\sqrt{(x_{i} - x_{j})^{T} (x_{i} - x_{j})}$

新窗口打开| 下载CSV

此外,由于多维参数输入可能导致特征量差异性较大,从而出现大变量主导等缺陷,所以在进行机器学习特征融合之前,标准化方法可以被用来消除不同维度之间的差异.在输入量和输出量均为正数的情况下,最大值标准化可以被应用,将不同维度的变量都缩放到0~1之间.具体而言,数学表达式如下所示:

x'=

$\frac{x}{x_{m a x}}$

(6)

式中:x为原变量值;x'为标准化后的变量值;x_max为对应变量的最大值.

2.3 GPR-TD3方法

结合GPR和DRL两者对数据探索和特征提取的优势,提出一种新的优化方法GPR-TD3,利用少量的学习样本快速得到扑翼推进的参数选择模型,训练后的模型可对最佳推进性能所对应的扑翼运动参数以及特定扑翼推进状态下的推荐扑翼运动参数进行快速生成.

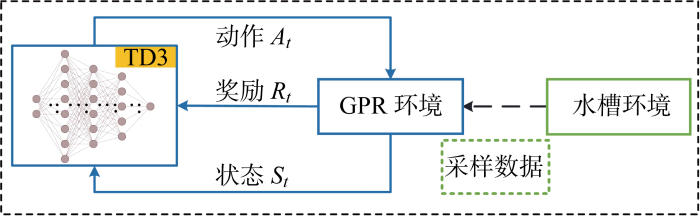
本文所提出的GPR-TD3方法整体框架如图3所示.通过实验装置进行采样,每组多维参数变量样本均由拉丁超采样方法分层随机抽取得出,以保证样本全面性并提升采样效率.实验利用适用于小样本学习的机器学习方法GPR模拟水槽环境,并在GPR环境上使用双延迟深度确定性策略梯度(TD3)算法进行环境交互以验证其可行性.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 GPR-TD3方法整体流程图

Fig.3 Overall flow chart of GPR-TD3 method

3 实验设置

3.1 实验装置

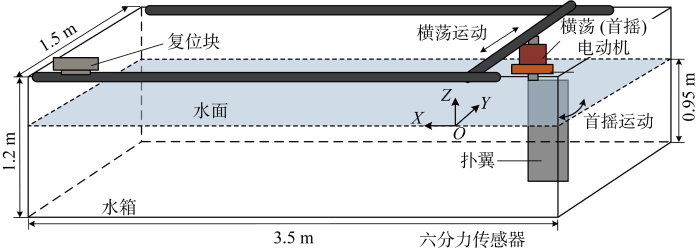
实验装置如图4所示,扑翼推进装置被架设于静水水槽上方,水槽的尺寸为长3.5 m、宽1.5 m、高1.2 m,水深为0.95 m.扑翼主体完全浸没在水面下,入水深度为440 mm,扑翼扑动初始运动位置统一为设定坐标系原点.实验装置整体由方钢构成长方体框架,沿X轴向设置一对平行滑动导轨,沿Y轴向设置可供扑翼滑动的导轨.在实验中,电控箱接收扑翼参数后通过横荡(首摇)电动机驱动扑翼的耦合运动,单扑翼耦合运动结合沿Y轴向的横荡线运动与绕Z轴向的首摇角运动,扑翼通过该耦合运动自驱动其本身沿X轴向运动.扑翼停止运动后,复位电动机驱动复位块推动扑翼回到初始点位.位于X轴导轨上的位移传感器用于记录推进过程中的扑翼位移,力、力矩则通过安装于扑翼上方的六分力传感器进行测量记录.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 扑翼推进装置布置示意图

Fig.4 Layout of flapping foil propulsion device

水下扑翼的三维模型如图5所示,该实体模型由连接件和扑翼两部分构成.扑翼的跨度为500 mm.实体模型安装中心与横荡(首摇)电动机中轴线一致,且连接件和电动机之间设置有六分力传感器.Garnier等^[11]的研究指出,在较低雷诺数条件下,薄扑翼推进效能高于厚扑翼.在综合考虑实际疲劳情况后,本研究设定扑翼后缘厚度为1.33 mm.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 扑翼三维示意图

Fig.5 Three-dimensional diagram of flapping foil

采集不同运动参数组合对应的六分力传感器数据、扑翼行进位移和推进时长,从而得出扑翼推进速度和扑翼推进效率.扑翼推进速度计算公式为

v_f=

$\frac{y_{d}}{t_{t}}$

(7)

式中:y_d为扑翼沿y向的推进位移;t_t为扑翼单次实验中自开始运动到位移达最大值时的时间.

扑翼推进效率按以下公式计算:

η_f=

$\frac{P_{o}}{P_{p} + P_{h}}$ =

$\frac{v_{f} \int_{0}^{T} F_{X} d t}{\int_{0}^{T} (M_{Z} {\overset{\cdot}{z}}_{0} + F_{Y} {\overset{\cdot}{y}}_{0}) d t}$

(8)

式中:P_o为扑翼输出推进功率;P_p、P_h分别为扑翼横荡(首摇)运动功率;F_X、F_Y分别为X、Y方向推力;M_Z为绕Z轴弯矩; ${\overset{\cdot}{z}}_{0}$ 为首摇运动Z向角速度; ${\overset{\cdot}{y}}_{0}$ 为横荡运动Y向线速度.

3.2 验证方法

GPR使用的总样本数为290组,为了评估GPR算法对水槽环境的建模效果以及所建立非参数模型的泛化性和抗噪性,本研究使用6种核函数在特定输入点进行预测,然后将预测值与实际值比较,以判断各模型优劣,从而选择最优模型.首先,机器学习对超参数初始值非常敏感,GPR涉及到的初始超参数包括长度尺度L_s,噪声方差N_l和边际最大似然估计法更新次数O_n.本文使用贝叶斯优化方法进行超参数优化选取,并以平均绝对误差(MAE)最小化为目标进行GPR超参数动态搜索.同时验证阶段选择3项指标作为衡量标准系数,分别是平均绝对误差M、均方误差R、皮尔逊系数P:

$\frac{1}{N} \overset{N}{\sum_{i = 1}} |y_{e, i} - y_{p, i}|$

(9)

$\frac{1}{N} \sqrt{\overset{N}{\sum_{i = 1}} (y_{e, i} - y_{p, i})^{2}} \frac{n!}{r! (n - r)!}$

(10)

$\frac{\overset{N}{\sum_{i = 1}} (y_{e, i} - {\bar{y}}_{e}) (y_{p, i} - {\bar{y}}_{p})}{\sqrt{\overset{N}{\sum_{i = 1}} (y_{e, i} - {\bar{y}}_{e}) (y_{p, i} - {\bar{y}}_{p})^{2}}}$

(11)

式中:N代表样本总数;y_e,_i表示实验真实值;y_p,_i为算法预测值; ${\bar{y}}_{e}$ 为实验平均值; ${\bar{y}}_{p}$ 为预测平均值.

就评价指标而言,M、R越小,代表模型适用性更高,且两者均为正数.P越接近1,代表模型预测准确性越高,且该值区间位于-1~1之间.

在深度强化学习任务中,观测值的优化目标被设定为扑翼推进速度、推进效率的大小.动作被选定为[f z₀y₀ϕ]向量组合形式.本研究参考Scott等^[8]设定不同工况下TD3算法的初始超参数,在实验中学习率均设为0.001.为了避免模型陷入局部最优解,同时也为了增加探索性,在训练过程中给予高斯噪声.为激励学习算法较快选择到速度值和效率值的最优解,奖励设为二次函数形式并根据量级大小进行缩放:

$\begin{array}{l} R_{v} = (O_{v} {/ 100)}^{2} \\ R_{e} = (1 000 O_{e})^{2} \end{array}\}$

(12)

式中:R_v、R_e分别为观测值为动作、效率的奖励值;O_v、O_e为环境观测值,即扑翼推进速度和扑翼推进效率.

此外,为了在实际应用中控制扑翼速度,GPR-TD3方法可以通过修改奖励函数来获得对应的推进动作值.例如,在要求速度达到80 mm/s时,可以设置如下的奖励函数:

R₈₀=-(O₈₀/80-1)²+1

(13)

式中:O₈₀为扑翼推进速度.

3.3 验证工况

为验证GPR-TD3方法在该扑翼推进问题上的可行性,本研究首先在全定义域范围内验证扑翼推进效率以及扑翼推进速度最优解.其次,验证在任意给定速度70、80、100 mm/s这3种工况下训练给出的推荐动作组合解.

4 结果分析

4.1 高斯过程回归模型

在使用GPR算法构建运动参数与扑翼推进速度之间的非参数模型时,本研究针对6种常用核函数进行优化选取,并列出了相应的指标值和最终超参数,详见表3.从ARD Matern 3/2和Matern 3/2以及ARD Matern 5/2和Matern 5/2这两对数据可以看出:在对初始输入特征进行归一化处理后,使用单向量核函数以及多维向量核函数(ARD类核函数)得到的结果在保留3位小数后相同.因此,在建立运动参数与扑翼推进效率之间非线性映射关系时,本研究将对比的核函数类型调整为4组,具体如表4所示.

表3 联合运动参数与扑翼推进速度的GPR算法参数

Tab.3 GPR model parameters of motion parameters and flapping foil propulsion speed

核函数	L_s	N_l	O_n	M	R	P
Matern 3/2	0.000 688	71 523	16	2.128	3.108	0.864
Matern 5/2	0.000 562	11 281	12	12.597	16.011	0.640
ARD Matern 3/2	[2.385 7.976 6.998 4.158]	39 948	1	2.128	3.108	0.864
ARD Matern 5/2	[5.088 1.123 8.345 5.086]	32 307	18	12.597	16.011	0.640
Squared exponential	0.008 38	19 108	7	1.274	1.516	0.956
Absolute exponential	0.007 72	32 667	100	1.006	1.832	0.957

新窗口打开| 下载CSV

表4 联合运动参数与扑翼推进效率的GPR算法参数

Tab.4 GPR model parameters of motion parameters and flapping foil propulsion efficiency

核函数	L_s	N_l	O_n	M	R	P
Matern 3/2	0.689	11 820	13	0.010 9	0.014 6	-0.645
Matern 5/2	0.946	79 233	3	0.010 9	0.014 7	-0.621
Squared exponential	0.001 12	39 666	2	0.010 9	0.014 6	0.250
Absolute exponential	0.043 3	46 725	5	0.010 9	0.014 7	-0.931

新窗口打开| 下载CSV

在对运动参数与扑翼推进速度以及运动参数与扑翼推进效率之间的GPR算法建模效果进行比较时,经过多组核函数优化与选取的结果显示,选用Absolute exponential核函数可获得最优的运动参数与扑翼推进速度之间的非参数模型.同时,选用Squared exponential核函数可在建立运动参数与扑翼推进效率的非线性映射关系时获得最佳的建模效果.

4.2 深度强化学习结果

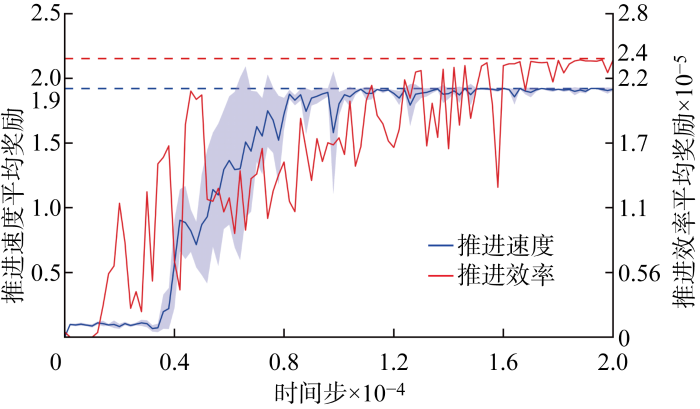
经过2万次训练后,TD3算法针对推进速度、推进效率的奖励最大化曲线如图6所示.其中,纵坐标为每100组训练的奖励平均值,就推进速度而言图中阴影部分表示对任意5组随机种子情况进行计算得出的标准偏差区域,就推进效率而言图中给出强化学习算法习得的最优效率曲线,虚线表示奖励最终收敛平稳后的平均值.研究结果表明,TD3算法寻找到的推进速度最优解平均奖励为1.901,即最优推进速度平均值为137.9 mm/s;推进效率最优解最优奖励为 239 032,即推进效率为48.9%.此外,结合图6奖励曲线尾段稳定趋势能够计算得出推进速度的局部最优解仅存在最大约 4 mm/s 的浮动范围,速度最优值几乎稳定后其最小值为 136.3 mm/s.而推进效率最终稳定在48.9%附近,效率最优值几乎稳定后其最小值为46.2%.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 推进速度平均奖励曲线和推进效率最优奖励曲线

Fig.6 Average reward curve for propulsion speed and optimal reward curves for propulsion efficiency

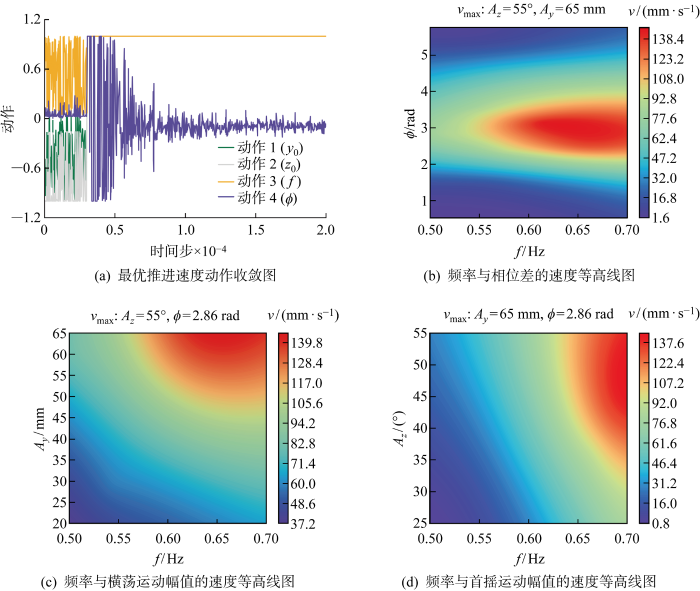
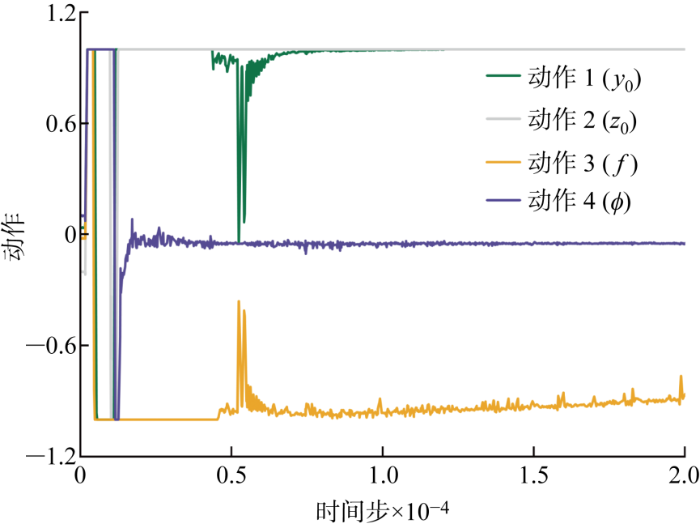
TD3算法在定义域全局中搜索到的推进速度及相应最优动作在GPR模型中的二维切片等高线图如图7所示,推进效率动作最优解如图8所示.图7中:v为GPR模型速度拟合值;v_max为TD3于全域中搜索到的局部最优解.图7(a)中,动作参数归一化范围为[-1,1].实验结果表明,针对推进速度而言,最优推进速度动作向量前3个变量均为定值1,即为定义域上界值,而相位差的最优值则在-0.1上下较小的范围内摆动.这说明TD3算法学习到了多个仅在较小区域内波动的局部最优解.以其中一个局部最优解[1 1 1 -0.017] 为例,即真实动作向量为[0.700 55 65 2.860]时,给出其在GPR中的分布规律.结果显示, TD3算法给出的最优解与GPR模型中的局部最大值区域吻合情况较好,说明该优化方法在使用GPR模拟环境时具有较好的收敛性和泛化能力.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 推进速度动作收敛位置及对应GPR二维等高线图

Fig.7 Convergence position of propulsion velocity action and corresponding GPR 2D contour map

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 推进效率动作收敛位置

Fig.8 Convergence position of propulsion efficiency action

针对推进效率而言,全局范围内的最优动作收敛位置为:首摇运动幅值与横荡运动幅值为上界最大值,频率趋近于下届最小值,相位差在-0.046 2 上下轻微摆动.以其中一个局部最优解[-0.862 1 1 -0.048 3]为例,即真实动作向量为[0.514 55 65 3.015]时,结果表明TD3算法给出的推进效率对应最优解依旧落在GPR模拟环境中局部最大值区域.需要说明的是,推进效率存在多个不连续的局部最优解,其在全局上的数据不平衡会导致可视化阅读的不便利,因此在此不予展示相关效率等高线图.

4.3 任意速度时GPR-TD3结果

图9展示了速度目标值与GPR-TD3速度实际值的绝对数值大小.其中,局部最优解的速度目标值为推进速度最优动作在实际水池环境中工作时产生的推进速度,此时两者相对误差为3.61%.速度需求值为70、80、100 mm/s时,GPR-TD3速度实际值与目标值的相对误差范围为0.23%~6.68%,相对误差最大的情况位于速度需求值为80 mm/s时.表5中给出了不同速度需求情况下GPR-TD3方法提供的推荐动作组合解.

图9

新窗口打开| 下载原图ZIP| 生成PPT

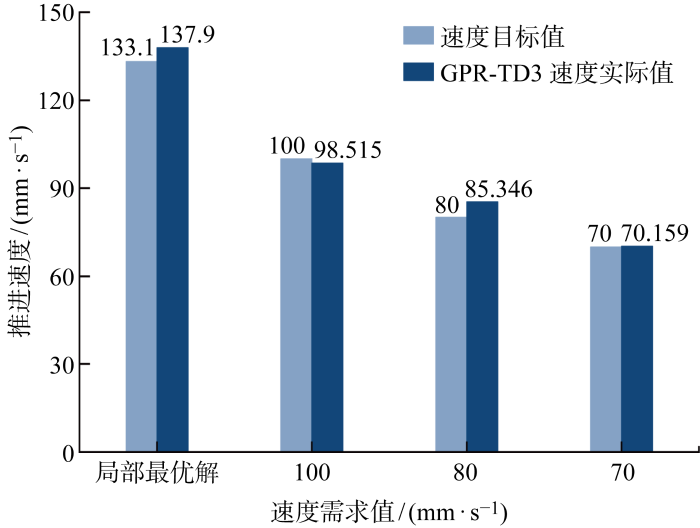
图9 速度目标值与GPR-TD3速度实际值对比结果

Fig.9 Comparison of speed target value and actual value of GPR-TD3 speed

表5 传统TD3算法与GPR-TD3方法所需样本数量及习得动作

Tab.5 Number of samples and learned actions required by traditional reinforcement learning and GPR-TD3 methods

类别	传统强化学习样本数量	GPR-TD3样本数量	动作向量
推进速度局部最优	9 200	290	[ $\begin{array}{l} 0.700 & 55 & 65 & 2.860 \end{array}$ ]
推进效率局部最优	6 200	290	[ $\begin{array}{l} 0.700 & 55 & 65 & 2.837 \end{array}$ ]
推进速度100 mm/s	5 300	290	[ $\begin{array}{l} 0.501 & 55 & 65 & 3.630 \end{array}$ ]
推进速度80 mm/s	5 900	290	[ $\begin{array}{l} 0.500 & 55 & 53.615 & 4.500 \end{array}$ ]
推进速度70 mm/s	4 300	290	[ $\begin{array}{l} 0.675 & 55 & 52.178 & 2.734 \end{array}$ ]

新窗口打开| 下载CSV

表5列出了传统TD3算法与GPR-TD3方法所需样本数量及习得动作.结果表明, GPR-TD3方法相对于直接运用深度强化学习方法在所需样本数量上具有较大优势,是传统深度强化学习的 0.031 5~0.067 4.由此可见,GPR-TD3方法能够极大地提高深度强化学习训练效率,降低训练成本.

5 结论

本研究基于GPR-TD3方法建立了一个在水槽环境下识别扑翼最优推进速度或最优推进效率的模型.该方法利用拉丁超采样采集扑翼的扑动参数和推进性能数据,通过TD3算法对接GPR模拟水槽环境从而实现自主深度强化学习,获得不同推进性能下的推荐动作参数组合解.结果表明:

(1) TD3算法经过2万次训练后,能够在全局定义域中搜索到多个推进速度和推进效率的最优解,并且在局部最优解处也能得到较好结果.TD3算法习得的最优推进速度平均值为 137.9 mm/s 且最小值为136.3 mm/s,在实际水池环境中验证模型习得最优动作下的推进速度为 133.1 mm/s;最优推进效率最高可达48.9%.

(2) 通过修改奖励函数,GPR-TD3方法能够给出任意速度需求下的推荐动作向量.目标值和GPR-TD3方法推荐值之间的相对误差范围为0.23%~6.68%,以局部最优解为例验证得出模拟水槽环境与真实水槽环境之间的相对误差为3.61%.

(3) 通过与直接使用深度强化学习方法所需样本量对比,GPR-TD3方法大大缩减了实验成本和实验时长.GPR-TD3方法在290组样本前提下能够得出可应用的动作解,所需样本数量是传统深度强化学习的0.031 5~0.067 4.

需要注意的是,GPR-TD3方法目前仅被用于单扑翼推进性能的动作参数控制,且水槽环境为静水状态.因此,其抗环境干扰能力以及在复杂水动力环境下的泛化能力、鲁棒性还有待验证.后续的研究可以选择更为复杂的水池环境并对运动模式和扑翼特性进行优化,以更好地应用于实际工程.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

MANNAM

, KRISHNANKUTTY

, VIJAYAKUMARAN

, et al.

Experimental and numerical study of penguin mode flapping foil propulsion system for ships

[J]. Journal of Bionic Engineering, 2017, 14(4): 770-780.

[本文引用: 1]

[2]

, ZHANG

, TIAN

, et al.

A review on fluid dynamics of flapping foils

[J]. Ocean Engineering, 2020, 195: 106712.

[本文引用: 1]

[3]

ASHRAF

M A

, YOUNG

, LAI

J C A

, et al.

Oscillation frequency and amplitude effects on plunging airfoil propulsion and flow periodicity

[J]. AIAA Journal, 2012, 50(11): 2308-2324.

[本文引用: 1]

[4]

KHALID

, AKHTAR

, IMTIAZ

, et al.

On the hydrodynamics and nonlinear interaction between fish in tandem configuration

[J]. Ocean Engineering, 2018, 157: 108-120.

[本文引用: 1]

[5]

DAS

, SHUKLA

R K

, GOVARDHAN

R N

Existence of a sharp transition in the peak propulsive efficiency of a low-Re pitching foil

[J]. Journal of Fluid Mechanics, 2016, 800: 307-326.

[本文引用: 1]

[6]

MACKOWSKI

A W

, WILLIAMSON

C H K

Direct measurement of thrust and efficiency of an airfoil undergoing pure pitching

[J]. Journal of Fluid Mechanics, 2015, 765: 524-543.

[本文引用: 1]

[7]

AMIRALAEI

M R

, ALIGHANBARI

, HASHEMI

S M

An investigation into the effects of unsteady parameters on the aerodynamics of a low Reynolds number pitching airfoil

[J]. Journal of Fluids and Structures, 2010, 26(6): 979-993.

[本文引用: 1]

[8]

SCOTT

, HERKE

, DAVID

Addressing function approximation error in actor-critic methods

[C]// Proceedings of the 35th International Conference on Machine Learning. Stockholm, Sweden: PMLR, 2018: 1587-1596.

[本文引用: 2]

[9]

THAKOR

, KUMAR

, DAS

, et al.

Investigation of asymmetrically pitching airfoil at high reduced frequency

[J]. Physics of Fluids, 2020, 32(5): 053607.

[本文引用: 1]

[10]

CHENG

, JIAO

, YAN

, et al.

Prediction of surface residual stress in end milling with Gaussian process regression

[J]. Measurement, 2021, 178(11): 109333.

[本文引用: 1]

[11]

GARNIER

, VIQUERAT

, RABAULT

, et al.

A review on deep reinforcement learning for fluid mechanics

[J]. Computers & Fluids, 2021, 225: 104973.

[本文引用: 1]

Experimental and numerical study of penguin mode flapping foil propulsion system for ships

2017

... 海洋航行物的动力推进一直是一项热门研究话题.考虑到操纵性、环保性、推进效率等因素,越来越多的水面航行物如各类船舶、自主水面航行器(ASV)和水下航行物如自主水下航行器(AUV)、水下滑翔机、无人潜航器等倾向于采用仿生扑翼推进手段^[1]. ...

A review on fluid dynamics of flapping foils

2020

... 20世纪初至今,针对扑翼运动参数对水动力性能的影响是一个备受关注的研究方向^[2],目前集中在针对单一变量和离散变量的研究.其中,扑翼运动的拍动频率和振幅等参数设定对于推力、功率系数和推进效率等研究目标的优化至关重要^[3].已有研究表明,推力系数与振幅大小呈先增后减或单调递增趋势,推进效率的变化趋势则取决于推力系数与功率系数之间的相对增幅^[4⇓-6].此外,Amiralaei等^[7]的研究显示选取适当的扑翼运动参数可以有效提升扑翼推进性能,但是在单扑翼水动力性能与拍动频率、耦合运动相位差之间还未发现必然规律.因此,在连续运动区间内快速寻找单扑翼最佳水动力性能对应的耦合运动参数具有相当的应用价值和研究前景. ...

Oscillation frequency and amplitude effects on plunging airfoil propulsion and flow periodicity

2012

On the hydrodynamics and nonlinear interaction between fish in tandem configuration

2018

Existence of a sharp transition in the peak propulsive efficiency of a low-Re pitching foil

2016

Direct measurement of thrust and efficiency of an airfoil undergoing pure pitching

2015

An investigation into the effects of unsteady parameters on the aerodynamics of a low Reynolds number pitching airfoil

2010

Addressing function approximation error in actor-critic methods

2018

... 为了建立准确的扑翼运动模型并考虑到水下环境力的强非线性影响,本研究采用高斯过程回归(GPR)算法对扑翼推进运动进行非参数建模.与此同时,深度强化学习(DRL)可以通过水下扑翼与环境之间的实时交互以获取经验进行自主优化学习,具备着对多维参数进行自主特征提取、重构和优化的优势^[8].本文结合高斯过程回归和深度强化学习提出一种新的优化方法,能够在小样本基础上快速获取扑翼推进的非参数化模型,且该方法可对最佳推进性能以及特定推进性能需求下的扑翼运动参数进行优化结果选取. ...

... 在深度强化学习任务中,观测值的优化目标被设定为扑翼推进速度、推进效率的大小.动作被选定为[f z₀ y₀ ϕ]向量组合形式.本研究参考Scott等^[8]设定不同工况下TD3算法的初始超参数,在实验中学习率均设为0.001.为了避免模型陷入局部最优解,同时也为了增加探索性,在训练过程中给予高斯噪声.为激励学习算法较快选择到速度值和效率值的最优解,奖励设为二次函数形式并根据量级大小进行缩放: ...

Investigation of asymmetrically pitching airfoil at high reduced frequency

2020

... 据Thakor等^[9]的研究显示,无论是针对水下扑翼还是空中扑翼,通常情况下扑翼运动研究所采用的扑翼正弦运动公式为 ...

Prediction of surface residual stress in end milling with Gaussian process regression

2021

... 高斯过程回归是一种机器学习非参数建模手段,能够有效处理小样本数据下的非线性多维参数回归问题^[10].高斯回归可以为深度学习中的海量样本需求问题提供解决方法.高斯过程回归的算法本质是基于多元高斯过程和贝叶斯推理对非线性系统进行建模.假设一个具有任意有限数量样本的空间D={(X,y_i)

$|i = 1, 2, \dots, n}$

={X, Y_D}.其中:X=[x₁ x₂ … x_n]^T为n维输入矩阵,x_i∈R^k为k维输入向量;y_i∈R为对应输出标量;Y_D为输出向量.回归过程将根据样本集学习输入X与输出Y_D的非线性映射关系,该回归模型表述为 ...

A review on deep reinforcement learning for fluid mechanics

2021

... 水下扑翼的三维模型如图5所示,该实体模型由连接件和扑翼两部分构成.扑翼的跨度为500 mm.实体模型安装中心与横荡(首摇)电动机中轴线一致,且连接件和电动机之间设置有六分力传感器.Garnier等^[11]的研究指出,在较低雷诺数条件下,薄扑翼推进效能高于厚扑翼.在综合考虑实际疲劳情况后,本研究设定扑翼后缘厚度为1.33 mm. ...

〈

〉