机动目标跟踪是目标跟踪领域的重要研究方向,随着空中飞行器的机动性能不断增强,对机动目标进行有效跟踪的重要性愈发凸显.当跟踪的目标发生机动时,其运动模式会发生剧烈变化,此时单模型算法往往难以适用,而基于多模型思想的机动目标跟踪算法则具有更好的表现.定结构的交互式多模型(Interacting Multi-Model, IMM)方法假设目标存在多种可能的运动模式,能够处理复杂的运动模式[1 ] ,对目标机动有一定的自适应性.相比于定结构的IMM方法,以模型集自适应(Model-Set Adaption, MSA)为核心的变结构交互式多模型(Variable Structure Interacting Multi-Model, VSIMM)方法具有更好的性能,其中可能模型集(Likely Model-Set, LMS)、模型群切换(Model Group Switch, MGS)、期望模式扩增(Expected-Model Augmentation, EMA)和自适应网格(Adaptive Grid,AG)等[2 ⇓ ⇓ -5 ] 都较为典型.王昱淇等[6 ] 则提出了一种复合的EMA-LMS算法,一定程度上综合了LMS的复杂度优点和EMA的估计精度优点.
然而考虑到场景中目标机动不确定性和量测噪声的影响,多模型方法在自适应方面仍然存在问题.首先,传统多模型算法依赖于先验参数的设置,针对这一问题,学者们提出了基于模型自身概率变化情况[7 ⇓ -9 ] 和基于机动判别[10 ] 的模型转移概率自适应调节方法,以改善相应算法在不同机动情况下的收敛性能.其次,多模型方法依赖的模型后验概率与模型的似然值有关,而似然值受到量测噪声的影响,不准确的似然值将为MSA过程带来不利影响.对于该问题,潘媚媚[10 ] 尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节.
更进一步,研究者们引入模糊控制系统,以减少多模型方法对先验参数设置的依赖,并且增强对模型后验概率不确定性的自适应能力.Enu等[11 ] 基于T-S推理模型动态调节模型概率转移矩阵,增强各模型概率的区分度;Li等[12 ] 则引入模糊逻辑,对模型进行基于各运动特征的模糊分类,并基于T-S模型隶属度函数重新定义转移概率,设计各模型的概率计算及交互过程,提高了IMM方法的跟踪精度.邵堃等[13 ] 在AGIMM算法中引入T-S模型,通过最大模型后验概率、模型网格大小计算机动置信度、选择自适应网格的更新方式,改良了AG方法的收敛性.
模糊推理能够以非精确的输入推理出非精确的结果,而T-S模糊推理具有语义信息引入简明和对不同形态系统泛用的优势[14 ] ,利用T-S模糊推理进行机动判别,能够有效增强对目标机动不确定性和量测噪声的适应性.当前模糊推理方法在多模型方法中的应用主要集中于与IMM算法和AG算法的结合,但已有研究关注的模型类型较为单一,考虑的输入变量较为简单.T-S模糊推理与LMS、EMA等模型集自适应方法的结合尚没有相关研究.
本文针对机动目标跟踪中VSIMM方法对于目标机动不确定性和量测噪声的自适应能力不足的问题,提出了基于模糊推理的机动自适应目标跟踪算法.首先引入模糊推理,设计能够自适应调节MSA过程的双级机动判别模型,该模型能够通过模糊逻辑进行主模型可信度推理和机动判别推理;又将双级机动判别模型引入EMA-LMS框架,提出基于模糊推理的机动自适应目标跟踪算法,算法对目标机动的不确定性和量测噪声具有良好的自适应能力.仿真实验表明,本文算法能够有效提高机动目标跟踪精度.
1 问题描述
1.1 系统模型
在目标跟踪问题中,目标状态的状态转移方程和量测方程可以写为
(1) ${{x}_{k}}={{F}_{k}}_{-1}{{x}_{k}}_{-1}+{{G}_{k}}_{-1}{{u}_{k}}_{-1}+{{\Gamma }_{k}}_{-1}{{w}_{k}}_{-1}$
(2) ${{z}_{k}}={{H}_{k}}{{x}_{k}}+{{v}_{k}}$
式中:k 为采样时刻;xk 为状态向量;Fk -1 为状态转移矩阵;Gk -1 为加速度输入矩阵;Γk -1 为过程噪声输入矩阵;wk -1 ~N (0, Qk ),为服从高斯分布的过程噪声,其均值为0,方差为Qk ;zk 为量测向量;Hk 为量测矩阵;vk ~N (0, Rk ),为服从高斯分布的量测噪声,其均值为0,方差为Rk ;uk -1 为目标运动模式,其模式空间为A ,模式空间是所有目标运动模式的集合,目标运动模式的转换可以用一阶马尔可夫过程描述.
1.2 VSIMM方法
VSIMM方法通过设计一个可变的模型集去匹配目标的运动模式,模型之间的转换过程用一阶马尔可夫过程描述, 假设k -1时刻模型集Mk -1 已知,且当前时刻已经通过MSA方法获得了模型集Mk ,以i 、j 表示模型序号,从k -1到k 时刻,模型m k - 1 j Mk -1 向模型m k i Mk 转移的概率为
(3) π j i = P m k i | m k - 1 j
对于模型mi ∈Mk ,其相应的状态转移方程和量测方程记为
(4) x k i = F k - 1 i x k - 1 i + G k - 1 i u k - 1 i + Γ k - 1 i w k - 1 i
(5) z k i = H k i x k i + v k i
假设基于模型集Mk -1 的目标状态估计{ x ^ k - 1 k - 1 i } m i ∈ M k - 1 { P k - 1 | k - 1 i } m i ∈ M k - 1 { μ k - 1 k - 1 i } m i ∈ M k - 1
(1) 模型交互.对于所有mi ∈Mk ,计算模型预测概率:
(6) μ k | k - 1 i = ∑ m j ∈ M k - 1 π j i μ k - 1 k - 1 j
(7) $\mu _{k-1}^{j|i}={{\pi }_{ji}}\frac{\mu _{k-1\left| k \right.-1}^{j}}{\mu _{k|k-1}^{i}},{{m}^{j}}\in {{M}_{k}}_{-1}$
(8) x - k - 1 | k - 1 i = ∑ m j ∈ M k - 1 μ k - 1 j | i x ^ k - 1 k - 1 j
(9) $\bar{P}_{k-1\left| k \right.-1}^{\text{i}}=\underset{{{m}^{j}}\in {{M}_{k-1}}}{\mathop \sum }\,\mu _{k-1}^{j|i}\left[ P_{\text{k}-1|\text{k}-1}^{j}+(\bar{x}_{\text{k}-1|\text{k}-1}^{i}-\hat{x}_{k-1\left| k \right.-1}^{\text{j}}){{(\bar{x}_{\text{k}-1|\text{k}-1}^{i}-\hat{x}_{k-1\left| k \right.-1}^{\text{j}})}^{T}} \right]$
(2) 模型条件滤波.对于所有mi ∈Mk ,将x - k - 1 | k - 1 i P ^ k - 1 k - 1 i mi 对应滤波器的输入,可以得到状态估计x ^ k | k i P k | k i z ~ k i S k i .
(3) 模型概率更新.对于所有mi ∈Mk ,计算模型似然:
(10) Λ k i = 1 ( 2 π ) N m | S k i | × e x p - 1 2 z ~ k i T S k i - 1 z ~ k i
(11) μ k | k i = Λ k i μ k | k - 1 i ∑ m j ∈ M k Λ k j μ k | k - 1 j
上述过程即为VSIMM方法的通式.根据模型集自适应方法不同,VSIMM方法又包含了EMA、LMS,以及二者结合的EMA-LMS等算法.然而这些算法仍存在一些问题,首先,LMS算法依赖于先验阈值的设定,参数缺乏自适应性,导致算法对目标机动不确定性自适应能力不足;此外,EMA和LMS都依赖于模型后验概率,后验概率的准确性受到模型似然的影响,由式(10)可知,模型似然计算与测量残差有关,因此会受到噪声影响,这将为EMA和LMS算法带来不利影响.本文为了解决上述问题,在EMA-LMS算法框架下引入基于模糊推理的双级机动判别方法,以增强对目标机动和量测噪声的自适应性.
2 基于模糊推理的双级机动判别方法
基于模糊推理的双级机动判别方法包含主模型可信度推理和机动判别推理两个层级,将后验概率最高的模型称为主模型,主模型可信度推理描述了主模型信息的可信程度,机动判别推理则进一步利用主模型残差加权范数推理了目标机动的可能性.这两个层级的推理结果能够为MSA方法的参数自适应调整提供依据.
2.1 主模型可信度推理
主模型可信度推理能够反映主模型的“代表性”,也即算法认为主模型信息作为机动判别依据的可信程度.选取以下指标作为主模型可信度推理的输入.
(12) ${{P}_{\max,k}}=\max {{\{\mu _{k|k}^{i}\}}_{{{m}^{i}}\in {{M}_{k}}}}$
该指标能够直接反映主模型的代表性,P max, k
(13) ${{P}_{\text{diff},k}}={{P}_{\max }}_{,k}-\max \left( {{\{\mu _{k|k}^{i}\}}_{{{m}^{i}}\in {{M}_{k}}}}-\left\{ {{P}_{\text{max},k}} \right\} \right)$
该指标间接反映了主模型的代表性,当仅靠P max, k P diff, k
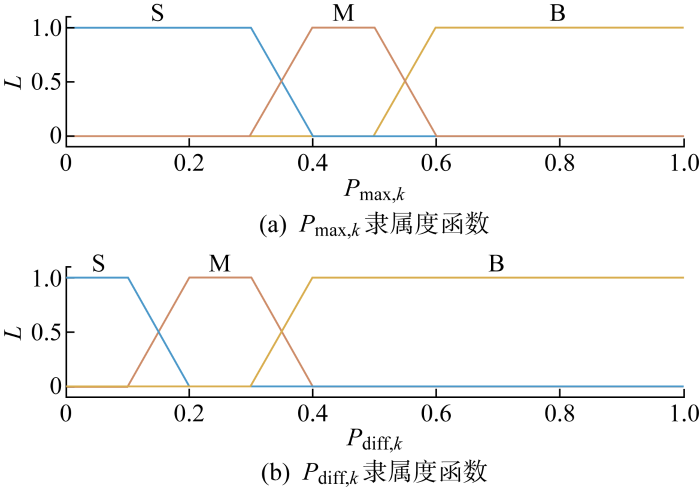
将以上两个指标输入T-S模糊推理模型,输出主模型可信度P Main, k .
其中:P max 、P diff 分别为P max, k P diff, k L ,P max, k P diff, k 图1 所示.
图1
图1
主模型可信度推理输入变量隶属度函数
Fig.1
Inputs variable membership function of main model reliability inference
主模型可信度推理有N Main 条模糊规则,第n 条规则可以表述为
(14) $\begin{matrix} & \text{if }{{P}_{\max }}_{,k}\text{ is }{{A}^{n}}_{\text{Main}}\text{ and }{{P}_{\text{diff},k}}\text{ is }{{B}^{n}}_{\text{Main}} \\ & \text{then }{{P}^{n}}_{\text{Main},k}=c_{\text{Main}}^{n,0}+c_{\text{Main}}^{n,1}{{P}_{\max,k}}+c_{\text{Main}}^{n,2}{{P}_{\text{diff},k}} \\ \end{matrix}$
式中:A n M a i n B n M a i n max ,k 、Pdiff ,k 对应的模糊子集;P n M a i n , k c M a i n n , 0 c M a i n n , 1 c M a i n n , 2 .
运用Sugeno 方法[15 ] 进行推理,推理规则如表1 所示. 通过各条模糊规则计算输出后,再利用加权平均法进行解模糊化,获得最终输出PMain , k :
(15) ${{P}_{Main}}_{,k}=\frac{\overset{{{\text{N}}_{Main}}}{\mathop{\mathop{\sum }_{\text{n}=1}}}\,{{\text{w}}^{\text{n}}}\text{P}_{Main,\text{k}}^{\text{n}}}{\overset{{{\text{N}}_{Main}}}{\mathop{\mathop{\sum }_{\text{n}=1}}}\,{{\text{w}}^{\text{n}}}}$
式中:wn 为对应的第n条推理规则的输出权重,其实质为第n条推理规则的适用度,通过各输入变量隶属度的乘积求取.
2.2 机动判别推理
该级推理模型的作用是推理目标发生机动的可能性.选取以下指标作为模糊推理模型的输入.
(1) 主模型残差加权范数Dk , 滤波残差加权范数能够较好反映目标当前时刻的状态变化[16 ] .记当前时刻后验概率最大的模型序号为r ,此时mr 为主模型,则主模型的残差加权范数定义为
(16) D k = d k r T S k r - 1 d k r
(17) d k r = z k r - H k r x ^ k | k - 1 r
(18) S k r = H k r P k | k - 1 r ( H k r ) T + R k r
式中:x ^ k | k - 1 r P k | k - 1 r .Dk 反映了量测值和主模型预测值的偏离程度,若该指标较大,则认为机动可能性较大.
(19) ${{D}_{i}}_{,k}=0.5{{D}_{k}}+0.3{{D}_{k}}_{-1}+0.2{{D}_{k}}_{-2}$
由于噪声的影响,目标机动后模型集调整并不总是能一步完成.若Di ,k 较大,则认为当前属于“后机动”时刻,仍需要机动性调整的可能性较大.
(20) ${{D}_{d}}_{,k}={{D}_{k}}-{{D}_{k}}_{-1}$
若该指标为正值且绝对值较大,则认为机动可能性较大;若为负值且绝对值较大,则认为机动可能性较小.
将以上3个指标输入T-S模糊推理模型,输出机动判别指标P MD, k
其中:D 为Dk 对应的论域,包含模糊子集S、M和B;D i 为Di ,k 对应的论域,包含模糊子集S、M和B;D d 为D d, k
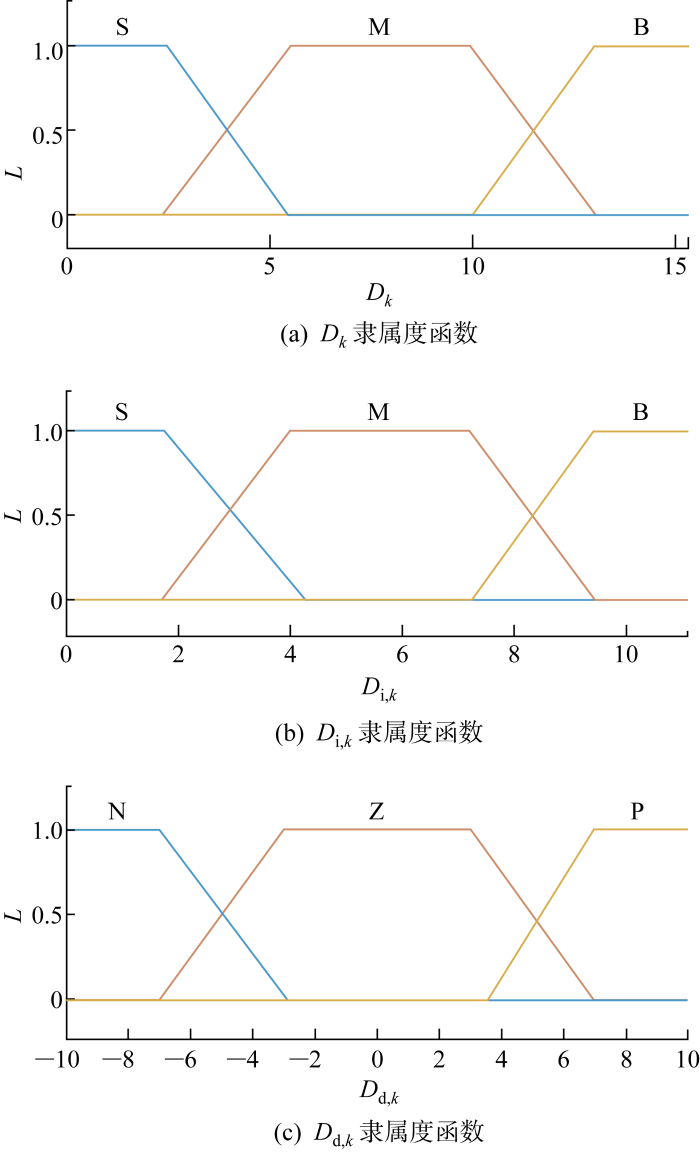
在机动判别推理模型中,采用模糊神经网络进行训练,设定D 、D i 、D d 的模糊分割数分别为3、3、3,最终得到的输入隶属度函数如图2 所示.
图2
图2
机动判别推理输入变量隶属度函数
Fig.2
Inputs variable membership function of maneuvering discrimination inference
机动判别推理有N MD 条模糊规则,第n 条规则可以表述为
(21) $\begin{matrix} & \text{if }{{D}_{k}}\text{ is }A_{MD}^{n}\text{ and }{{D}_{i}}_{,k}\text{ is }B_{MD}^{n}\text{ and }{{D}_{d}}_{,k}\text{ is }C_{MD}^{n}, \\ & \text{then }p_{MD,k}^{n}=c_{MD}^{n,0}+c_{MD}^{n,1}{{D}_{k}}+c_{MD}^{n,2}{{D}_{i}}_{,k}+c_{MD}^{n,3}{{D}_{d}}_{,k} \\ \end{matrix}$
式中:A n M D B n M D C n M D n 条规则下Dk 、Di ,k 、Dd ,k 对应的模糊子集;p M D , k n n 条规则对应的输出;c M D n , 0 c M D n , 1 c M D n , 2 c M D n , 3 n 条规则对应的后件参数.
运用Sugeno方法进行推理,推理规则及相应的线性输出函数由模糊神经网络训练生成[15 ] . 完成推理后同样需要进行解模糊化得到最终输出,解模糊方法同主模型可信度推理.
至此,给出了主模型可信度推理和机动判别推理过程,二者共同构成了双级机动判别算法,算法以模型后验概率{ μ k | k i } m i ∈ M k Dk 、Dk -1 、Dk -2 作为输入,输出主模型可信度P Main, k P MD, k
(1) 根据式(12)计算主模型概率值P max, k
(2) 根据式(13)计算主次模型概率偏差值P diff, k
(3) 根据表1 计算每条推理规则对应的主模型可信度P M a i n , k n n =1, 2, …, N Main .
(4) 根据式(15),使用加权平均法进行解模糊化,计算主模型可信度P Main, k .
(5) 根据式(19)计算主模型残差加权范数积分D i, k .
(6) 根据式(20)计算主模型残差加权范数微分D d, k .
(7) 根据模糊神经网络训练生成的规则与输出函数,计算每条规则对应的机动判别指标P M D , k n n =1, 2, …, N MD .
(8) 通过加权平均法解模糊化计算机动判别指标P MD, k .
3 基于模糊推理的机动自适应目标跟踪算法
在EMA-LMS框架下引入基于模糊推理的双级机动判别,从两个方面增强机动目标跟踪算法对目标不确定和量测不确定的自适应性:一方面辅助EMA部分生成更加稳定、贴近目标真实模式的期望模型,提高状态估计精度;另一方面辅助LMS部分根据目标运动状况自适应调整模型概率阈值参数,更好地对模型进行取舍.
3.1 基于双级机动判别的EMA期望模型计算
EMA将模型集分为基础模型集和期望模型集,基础模型集是算法开始前设计好的模型集,而期望模型集需要在线计算和调整.在计算期望模型集Ek 时引入了双级机动判别,以实现模型权重的自适应调节.
假设已通过双级机动判别算法得到主模型可信度P M a i n , k E P M D , k E
(22) α = e x p [ c α ( P M D , k E - T M D ) ] , P M a i n , k E ≥ T M a i n e x p [ c α c M a i n E ( P M D , k E - T M D ) ] , P M a i n , k E < T M a i n
式中:T MD 为机动判别阈值;T Main 为主模型可信度阈值;cα 为常数调节系数;c M a i n E P M a i n , k E
(23) c M a i n E = e x p ( P M a i n , k E - T M a i n )
在主模型可信度推理级,若输出的P M a i n , k E P M a i n , k E P M D , k E α >1,调节因子起增幅作用,指标值越大增幅作用越强;反之则有α <1,调节因子起削弱作用,指标值越小削弱作用越强.
加入调节因子后,计算期望模型集Ek ,一般取期望模型集内的模型数为1,该期望模型m E, k
(24) m E , k = α ( 1 - μ E , k - 1 k - 1 ) m ' E , k + μ E , k - 1 k - 1 m E , k - 1 | k - 1 / α α ( 1 - μ E , k - 1 k - 1 ) + μ E , k - 1 k - 1 / α
(25) m ' E , k = ∑ m i ∈ M f k - 1 μ k - 1 k - 1 i m i ∑ m i ∈ M f k - 1 μ k - 1 k - 1 i
式中:M f k - 1 Mk -1 中基础模型的集合;μ E, k -1| k -1 表示上一时刻的期望模型概率;m' E, k
3.2 基于双级机动判别的LMS模型概率阈值调节
LMS算法是一种模型激活和终止的方法,它以模型概率为依据对模型进行取舍,但LMS算法效果受到预先设置的模型概率阈值影响.通过引入双级机动判别自适应调整模型概率阈值.
假设当前已通过双级机动判别算法得到主模型可信度P M a i n , k L P M D , k L
(26) β 1 = e x p [ c β 1 ( P M D , k L - T M D ) ] , P M a i n , k L ≥ T M a i n e x p [ c β 1 c M a i n L ( P M D , k L - T M D ) ] , P M a i n , k L < T M a i n
(27) β 2 = e x p [ c β 2 ( P M D , k L - T M D ) ] , P M a i n , k L ≥ T M a i n e x p [ c β 2 c M a i n L ( P M D , k L - T M D ) ] , P M a i n , k L < T M a i n
式中:c β 1 c β 2 c M a i n L P M a i n , k L
(28) c M a i n L = e x p ( P M a i n , k L - T M a i n )
β 1 和β 2 分别用来调节LMS中的“不太可能”模型概率门限t 1 和“主要”模型概率门限t 2 .
(29) t 1 = m a x t 1 , m i n , m i n t ' 1 / β 1 , t 1 , m a x
(30) t 2 = m a x t 2 , m i n , m i n t ' 2 / β 2 , t 2 , m a x
式中:t' 1 和t' 2 分别为t 1 和t 2 的初始值;t 1,min 和t 2,min 为最小值;t 1,max 和t 2,max 为最大值. 主模型可信度推理级作用与3. 1节相同;在机动判别推理级,当判定目标发生机动的可能性较大时,有β 1 >1和β 2 >1,在调节因子作用下两个模型概率门限降低,使得LMS算法能够纳入更多的模型,以实现对目标真实模式的迅速逼近;反之当判定发生机动的可能性较小,则有β 1 <1和β 2 <1,调节因子使得模型概率门限提高,以尽量从滤波过程中排除不必要的模型,使模型集的匹配更加准确.
3.3 模糊推理EMA-LMS算法
结合3.1和3.2节对于EMA和LMS算法的改进,将基于模糊推理的双级机动判别引入EMA-LMS框架,得到模糊推理EMA-LMS算法,算法在一个时间周期内的流程如下.
(1) 设当前时刻为k ,根据k -1时刻的模型后验概率和主模型残差加权范数,利用双级机动判别算法计算主模型可信度P M a i n , k E P M D , k E . 1节所述方法计算期望模型集Ek .
(2) 根据上一时刻的模型集Mk -1 和当前时刻的期望模型集Ek 、基础模型集M f k Mk -1 -Ek -1 ,利用VSIMM方法分别计算{ x ^ k | k i } m i ∈ E k { P k | k i } m i ∈ E k { μ k | k i } m i ∈ E k { x ^ k | k i } m i ∈ M f k { P k | k i } m i ∈ M f k { μ k | k i } m i ∈ M f k .
(3) 对模型概率集合{ μ k | k i } m i ∈ E k { μ k | k i } m i ∈ M f k E k ∪ M f k { μ k | k i } m i ∈ ( E k ⋃ M f k ) . 将上述计算结果作为双级机动判别算法的输入,计算新的主模型可信度P M a i n , k L P M D , k L . 2节所述方法计算模型概率阈值t 1 和t 2 .
根据{ μ k | k i } m i ∈ M f k M f k M p (μ k | k i t 2 )、“重要模型集”M s (t 1 ≤μ k | k i t 2 )和“不太可能模型集”M u (μ k | k i t 1 ). 设模型集M a 为所有与M p 内模型连通的模型构成的集合,定义新增模型集合M n =M a ∩M - k M - k Mk 的补集.
(4) 若M n =⌀,融合M f k Ek 两模型集的估计结果,融合规则参考文献[4 ],得到基于模型集Mk =M f k Ek 的状态估计{ x ^ k | k i } m i ∈ M k { P k | k i } m i ∈ M k { μ k | k i } m i ∈ M k . 若M n ≠⌀,利用VSIMM方法计算{ x ^ k | k i } m i ∈ M n { P k | k i } m i ∈ M n { μ k | k i } m i ∈ M n M f k Ek 两模型集的估计结果进行融合,获得基于Mk =M f k Ek ∪M n 的状态估计{ x ^ k | k i } m i ∈ M k { P k | k i } m i ∈ M k { μ k | k i } m i ∈ M k .
(5) 根据Mk 模型集的估计结果,通过加权得到当前时刻的状态估计和协方差矩阵:
(31) x ^ k | k = ∑ m i ∈ M k μ k | k i x ^ k | k i
(32) P k | k = ∑ m i ∈ M k μ k | k i [ P k | k i + ( x ^ k | k - x ^ k | k i ) ( x ^ k | k - x ^ k | k i ) T ]
(6) 若M u ≠⌀,定义可丢弃模型集M d =M u ∩M - a M u 中与M p 不连通的部分. 若M d ≠⌀,则从Mk 中删除M d 中概率较小的模型,直到M d 中所有模型都被删除,或Mk 中剩下K 个模型,K 为Mk 的最小模型数.
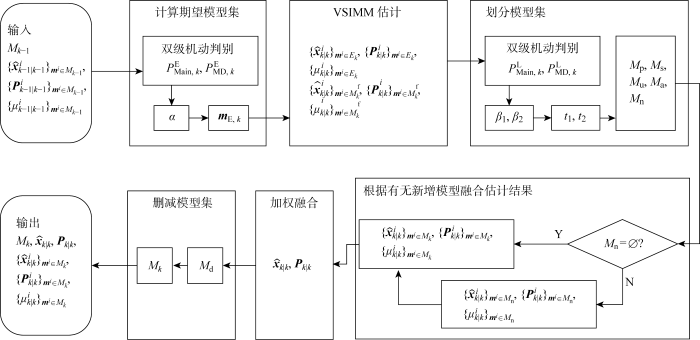
基于上述算法流程,图3 给出了模糊推理EMA-LMS算法的流程图.从图中可以看出,相比于EMA-LMS算法,本文算法在计算期望模型集和划分模型集阶段都引入了双级机动判别算法,以辅助进行MSA参数的自适应调节.
图3
图3
模糊推理EMA-LMS算法流程图
Fig.3
Flow chart of fuzzy inference-based EMA-LMS algorithm
4 仿真分析
仿真实验根据目标运动的机动性不同,设计两种场景,并在不同量测噪声条件下进行验证,通过对比多种算法的目标跟踪误差,证明本文提出的模糊推理EMA-LMS算法能够有效提高机动目标跟踪精度.
4.1 仿真场景与参数设置
假设一目标在二维平面内进行机动运动,其状态向量为X =[x x · y y · T ,其中x 、y 分别为x 、y 轴方向上的位置,x · y · . 目标状态转移方程为式(1),状态转移矩阵Fk 、加速度输入矩阵Gk 和过程噪声输入矩阵Γk 分别为
(33) F k = 1 t 0 0 0 1 0 0 0 0 1 t 0 0 0 1
(34) G k = Γ k = t 2 / 2 0 t 0 0 t 2 / 2 0 t
(35) ${{Q}_{k}}=\text{diag}({{(0.1\text{ }m)}^{2}},{{(0.1\text{ }m)}^{2}})$
目标运动模型为二维加速度模型,目标加速度输入为uk =[ax ay ]T ,其模式空间A ={(ax , ay )|a x 2 + a y 2 2 }. 量测方程为式(2),量测矩阵:
(36) H k = 1 0 0 0 0 0 1 0
量测噪声vk ~N (0, Rk ),量测噪声在两个方向的标准差均为σ R =50 m,有:
(37) ${{R}_{k}}=\text{diag}({{(50\text{ }m)}^{2}},{{(50\text{ }m)}^{2}})$
目标初始状态X 0 =[8000 m 25 m/s 8000 m 200 m/s]T ,且在仿真时间内进行多次机动,机动模式参考同类仿真中采用较多的加速度阶跃变化模式.为充分对比算法对目标机动的自适应性,设计两种目标机动场景,两场景的主要区别在于目标状态发生改变时加速度阶跃变化的幅度,场景1中目标的加速度变化幅度大于场景2,机动性也更强.两种场景的目标加速度设置如表2 所示.
参与仿真对比的算法包括模糊推理EMA-LMS算法、IMM算法、EMA算法[4 ] 、LMS算法[2 ] 、EMA-LMS算法[6 ] 和当前统计自适应网格(Current Statistical Adaptive Grid, CS-AG)算法[17 ] .
前5种算法使用相同的基础模型集.各模型加速度如下,单位均为m/s2 :a 1 =[0 0]T ,a 2 =[60 0]T ,a 3 =[0 60]T ,a 4 =[-60 0]T ,a 5 =[0 -60]T ,a 6 =[60 60]T ,a 7 =[-60 60]T ,a 8 =[-60 -60]T ,a 9 =[60 -60]T ,a 10 =[120 0]T ,a 11 =[0 120]T ,a 12 =[-120 0]T ,a 13 =[0 -120]T .
IMM和LMS算法模型初始概率μ 0 i / 13,mi ∈M 0 ,转移概率矩阵:
(38)
EMA 、EMA-LMS 、模糊推理EMA-LMS 算法模型初始概率μ 0 i mi ∈M 0 ,转移概率矩阵:
(39)
式(39)中期望模型编号为14. 模糊推理EMA-LMS 算法设置如下参数:TMain . 5,TMD . 6,t '1 =0. 1,t1, min . 01,t1, max . 3,t' 2 =0. 7,t2, min . 5,t2, max . 95,cα =2. 4,c β 1 = 0 . 96 c β 2 = 0 . 48 . LMS 算法、EMA-LMS 算法模型概率门限t1 =0. 1,t2 =0. 9. LMS 算法、EMA-LMS 算法和模糊推理EMA-LMS 算法的最小滤波模型数都为K=4. CS-AG 算法的参数配置参照文献[17 ].
4.2 仿真结果与分析
在设计的两种仿真场景下,分别进行500次蒙特卡洛仿真实验,仿真结果如下.
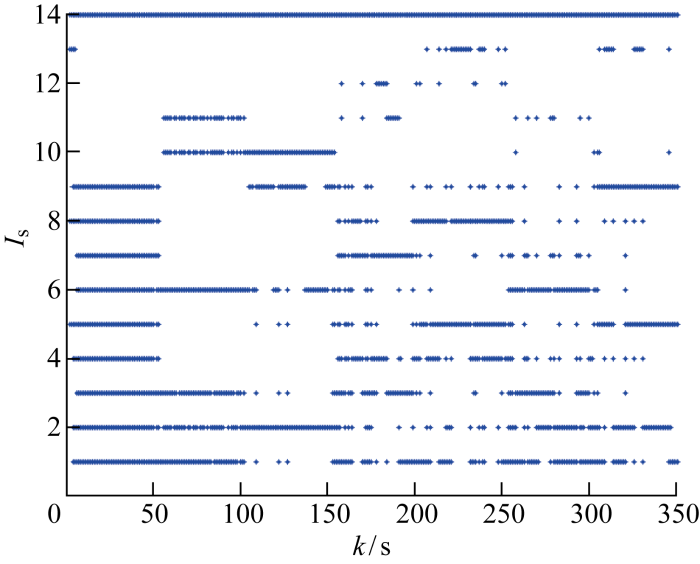
(1) 场景1:量测噪声标准差σR m ,记选择的模型编号为Is 图4 所示.
图4
图4
模糊推理EMA-LMS算法模型选择结果(场景1)
Fig.4
Model selection result of fuzzy inference-based EMA-LMS algorithm (Scenario 1)
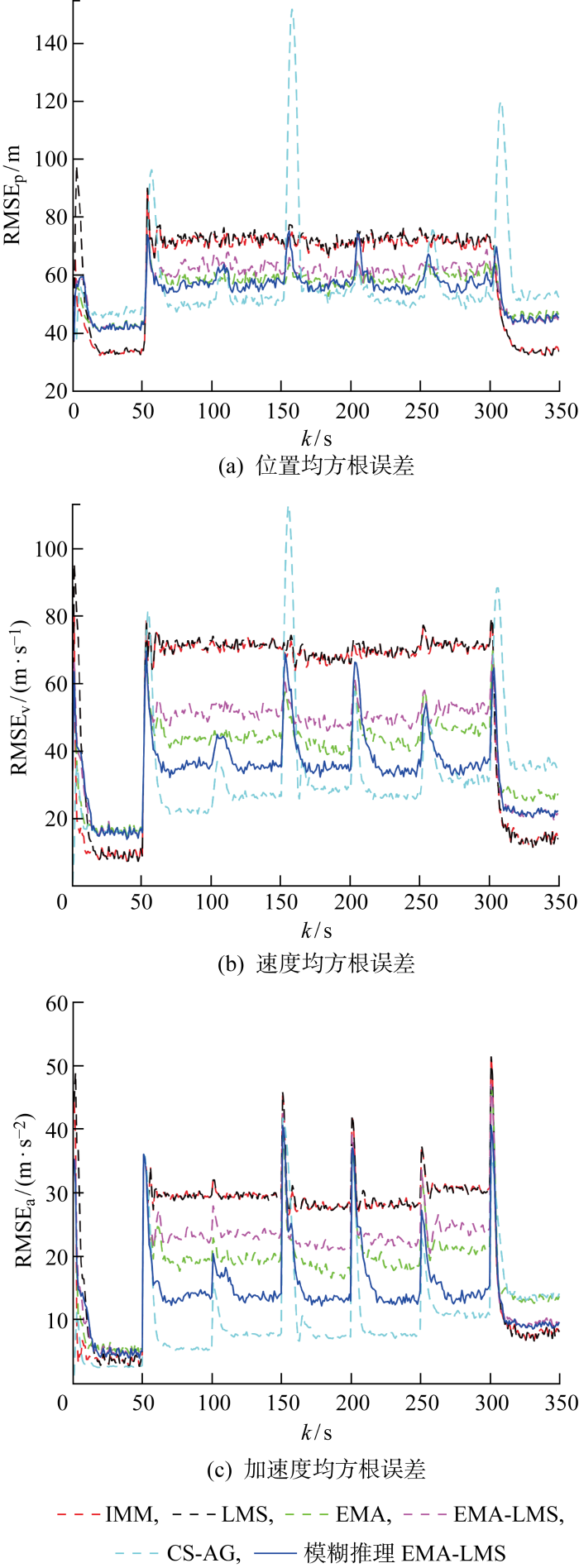
仿真实验采用均方根误差(Root Mean Square Error ,RMSE )作为评价指标,将位置、速度、加速度RMSE 分别记为RMSEp 、RMSEv 和RMSEa ,所有时刻的目标跟踪误差如图5 所示.
图5
图5
各算法跟踪指标对比(场景1)
Fig.5
Comparison on tracking indexes of algorithms (Scenario 1)
将一段时间内的位置、速度、加速度平均 RMSE 分别记为ARMSEp 、ARMSEv 和ARMSEa ,各算法跟踪指标平均值如表3 所示. 根据仿真设计,k =1~ 100 s ,目标的真实运动模式恰巧与各算法基础模型集中的模型匹配(CS-AG 无基础模型集);k =101~ 350 s ,真实模式与基础模型集不匹配,处于其“间隙”之中. 从实际角度出发,机动目标模式与基础模型不匹配更可能是常态,故第2阶段的结果更具有参考意义.
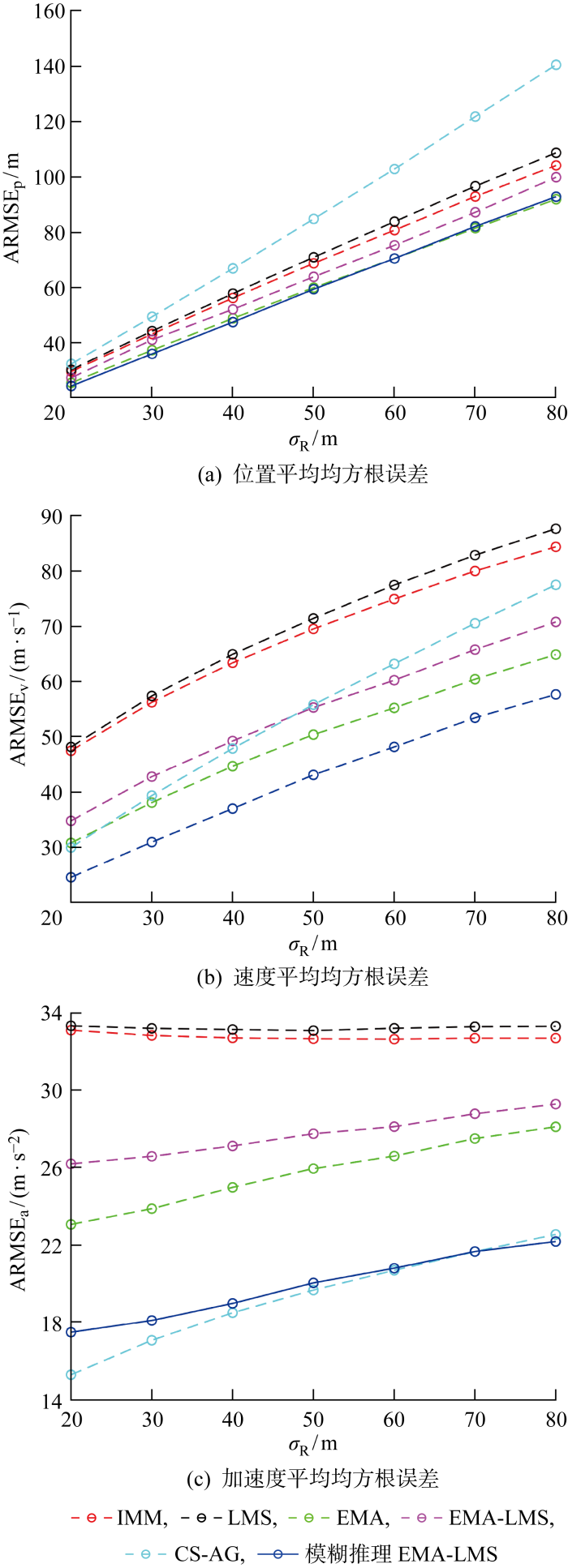
为充分对比算法对噪声的自适应性,进一步对比不同量测噪声水平下各算法在模式不匹配阶段的跟踪性能指标,结果如图6 所示.
图6
图6
不同量测噪声下各算法跟踪指标对比(场景1)
Fig.6
Comparison of tracking indexes of algorithms at different measurement noises (Scenario 1)
(2) 场景2:量测噪声标准差σR m ,所有时刻的模型选择结果与目标跟踪误差对比如图7 和图8 所示.
图7
图7
模糊推理EMA-LMS模型选择结果(场景2)
Fig.7
Model selection result of fuzzy inference-based EMA-LMS algorithm (Scenario 2)
图8
图8
各算法跟踪指标对比(场景2)
Fig.8
Comparison of tracking indexes of algorithms (Scenario 2)
各算法在全仿真过程内的平均估计误差如表4 所示. 根据仿真条件的设计,k=1~ 50 s 和k=301~ 350 s 为模式匹配阶段,k=51~ 300 s 为模式不匹配阶段.
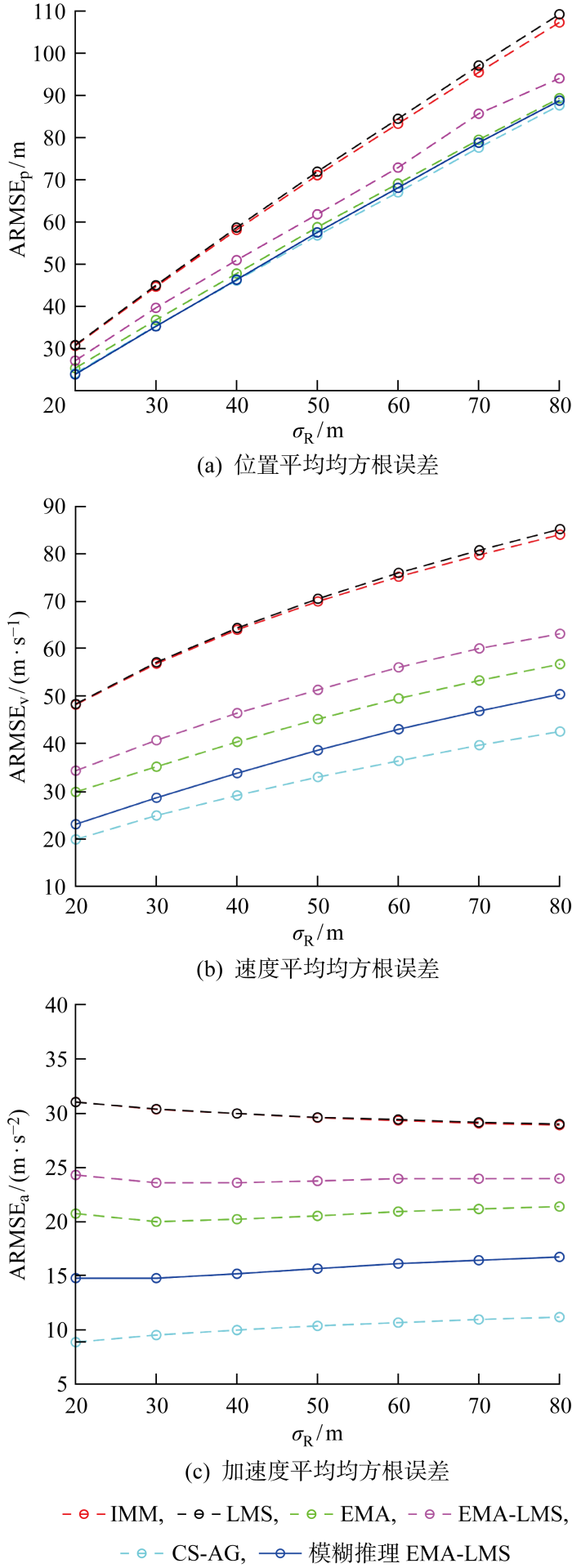
进一步对比不同量测噪声水平下各算法在模式不匹配阶段的跟踪性能指标,结果如图9 所示.
图9
图9
不同量测噪声下各算法跟踪指标对比(场景2)
Fig.9
Comparison of tracking indexes of algorithms at different measurement noises (Scenario 2)
对于上述仿真结果,由图4 和图7 可知,两种场景下模糊推理EMA-LMS 算法都能够有效地自适应选择模型. 从状态估计的误差方面,首先对前4种同类算法进行分析,重点比较EMA 、EMA-LMS 和本文算法在跟踪精度方面的表现. 仿真表明:在两场景的真实模式匹配基础模型阶段,基础的IMM 算法、LMS 算法都取得了较好的效果;此阶段运用了EMA 思想的3类算法由于存在扩增模式的干扰反而误差略大,表现差距也较小;但在真实模式不匹配的阶段,EMA 、EMA-LMS 和模糊推理EMA-LMS 的效果显著较优,同时可看出本文所提出的模糊推理EMA-LMS 的估计误差总体优于EMA 和EMA-LMS ,且优势在不同噪声水平下均有体现. 以具体场景为例,量测噪声标准差为50 m ,在场景1(不匹配阶段)中,本文算法的位置、速度、加速度估计误差分别比 EMA 降低了 0. 96% 、14. 44% 、22. 80% ,比EMA-LMS 降低了7. 04% 、22. 01% 、27. 83% ;在场景2(不匹配阶段)中,分别比 EMA 降低了 2. 11% 、14. 53% 、23. 65% ,比EMA-LMS 降低了6. 91% 、24. 83% 、34. 02%.
除上述同类算法外,又与CS-AG 算法进行对比,CS-AG 算法为多模型跟踪领域较近的研究成果. 仿真结果表明,在目标运动模式变化较小时,CS-AG 平均估计误差较优,在场景2(不匹配阶段)中,量测噪声标准差为50 m ,本文算法的位置和速度估计误差比CS-AG 算法分别高1. 26% 和17. 22% ,原因在于目标运动模式稳定时,CS-AG 算法模型集自适应效果更好,估计精度也更高;但在运动模式变化时刻及其后续时刻,CS-AG 算法出现了较为显著的误差“峰值”,特别是在目标的运动模式有较大变化时,其适应能力显然存在不足,在场景1(不匹配阶段)中,量测噪声标准差为50 m ,本文算法的位置、速度估计误差分别比CS-AG 算法低29. 97% 、22. 73%. 此外,由图5 和图8 的位置和速度误差曲线可以看出,本文算法在目标运动模式发生较大变化时刻,误差“峰值”显著低于CS-AG 算法,说明本文算法的状态估计更加稳定. 综合考虑估计误差、场景通用性和估计稳定性,本文算法仍然具有优势.
5 结语
针对现有多模型算法在目标运动状态和量测不确定条件下自适应性不足的问题,从优化MSA算法策略和参数的角度入手,提出了基于模糊推理的双级机动判别方法,并基于EMA-LMS框架设计了一种基于模糊推理的机动自适应目标跟踪算法,通过目标机动状态判别,对MSA策略进行自适应的优化.仿真验证了在多种机动目标场景下,本文算法能有效适应目标机动和量测噪声的不确定性,提高机动目标跟踪精度.
参考文献
View Option
[1]
陈晓 , 李亚安 , 李余兴 , 等 . 基于距离加权的概率数据关联机动目标跟踪算法
[J]. 上海交通大学学报 2018 , 52 (4 ): 474 -479 .
DOI:10.16183/j.cnki.jsjtu.2018.04.013
[本文引用: 1]
为了提高杂波环境下机动目标跟踪的实时性和精确性,在概率数据关联算法的基础上,引入距离加权的概念,以区分来自于目标的量测概率和来自于杂波的虚假概率,在一定程度上提高了概率数据关联算法在密集杂波环境下的非机动目标的跟踪性能.针对机动目标的跟踪,提出了一种适用于密集杂波环境下的联合交互式多模型概率数据关联跟踪算法,该算法利用距离加权的概率数据关联算法进行滤波.模拟实验结果表明:该算法可以在一定程度上提高密集杂波环境下机动目标跟踪的性能,能够更加有效、可靠地实现机动目标跟踪的目的.
CHEN Xiao LI Ya’an LI Yuxing , et al Maneuvering target tracking algorithm based on weighted distance of probability data association
[J]. Journal of Shanghai Jiao Tong University 2018 , 52 (4 ): 474 -479 .
[本文引用: 1]
[2]
LI X R ZHANG Y . Multiple-model estimation with variable structure. V. Likely-model set algorithm
[J]. IEEE Transactions on Aerospace and Electronic Systems 2000 , 36 (2 ): 448 -466 .
DOI:10.1109/7.845222
URL
[本文引用: 2]
[3]
LI X R ZHI X ZHANG Y . Multiple-model estimation with variable structure. III. Model-group switching algorithm
[J]. IEEE Transactions on Aerospace and Electronic Systems 1999 , 35 (1 ): 225 -241 .
DOI:10.1109/7.745694
URL
[本文引用: 1]
[4]
LI X R JILKOV V P RU J . Multiple-model estimation with variable structure—Part VI: Expected-mode augmentation
[J]. IEEE Transactions on Aerospace and Electronic Systems 2005 , 41 (3 ): 853 -867 .
DOI:10.1109/TAES.2005.1541435
URL
[本文引用: 3]
[5]
JILKOV V P ANGELOVA D S SEMERDJIEV T Z A . Design and comparison of mode-set adaptive IMM algorithms for maneuvering target tracking
[J]. IEEE Transactions on Aerospace and Electronic Systems 1999 , 35 (1 ): 343 -350 .
DOI:10.1109/7.745704
URL
[本文引用: 1]
[6]
王昱淇 , 卢宙 , 蔡云泽 . 基于一致性的分布式变结构多模型方法
[J]. 自动化学报 2021 , 47 (7 ): 1548 -1557 .
[本文引用: 2]
WANG Yuqi LU Zhou CAI Yunze . Consensus-based distributed variable structure multiple model
[J]. Acta Automatica Sinica 2021 , 47 (7 ): 1548 -1557 .
[本文引用: 2]
[7]
郭志 , 董春云 , 蔡远利 , 等 . 时变转移概率IMM-SRCKF机动目标跟踪算法
[J]. 系统工程与电子技术 2015 , 37 (1 ): 24 -30 .
[本文引用: 1]
GUO Zhi DONG Chunyun CAI Yuanli , et al Time-varying transition probability based IMM-SRCKF algorithm for maneuvering target tracking
[J]. Systems Engineering and Electronics 2015 , 37 (1 ): 24 -30 .
DOI:10.3969/j.issn.1001-506X.2015.01.05
[本文引用: 1]
An on-line updating method of Markov transition probability for the interacting multiple model(IMM)algorithm is proposed, and the square-root cubature Kalman filter(SRCKF)is introduced into IMM, so a novel time-varying Markov transition IMM-SRCKF algorithm is obtained.Using real-time recursive estimation method based on the system mode information implicit in the current measurements, the proposed algorithm effectively avoids the problem of prior determination of the Markov transition probability matrix in traditional IMM. Furthermore, SRCKF propagates the square root of the covariance in filter interaction so that it guarantees the symmetry and positive semi-definiteness of the covariance matrix and greatly improves the numerical stability and numerical accuracy. Simulation results show that the proposed algorithm has better tracking performance and higher efficiency compared with the conventional IMM and IMMCKF.
[8]
游航航 , 韩其松 , 余敏建 , 等 . 基于AIGWO-IMMUKF 的目标跟踪算法
[J]. 北京航空航天大学学报 2020 , 46 (10 ): 1826 -1833 .
[本文引用: 1]
YOU Hanghang HAN Qisong YU Minjian , et al Target tracking algorithm based on AIGWO-IMMUKF
[J]. Journal of Beijing University of Aeronautics and Astronautics 2020 , 46 (10 ): 1826 -1833 .
[本文引用: 1]
[9]
XIE G SUN L WEN T , et al Adaptive transition probability matrix-based parallel IMM algorithm
[J]. IEEE Transactions on Systems , Man , and Cybernetics: Systems 2019 , 51 (5 ): 2980 -2989 .
DOI:10.1109/TSMC.2019.2922305
URL
[本文引用: 1]
[10]
潘媚媚 . 高速高机动目标自适应跟踪算法研究 [D]. 西安 : 西安电子科技大学 , 2019 .
[本文引用: 2]
PAN Meimei . Research on adaptive algorithms for highly maneuvering target tracking [D]. Xi’an : Xi-dian University , 2019 .
[本文引用: 2]
[11]
EUN Y JEON D . Fuzzy inference-based dynamic determination of IMM mode transition probability for multi-radar tracking
[C]// Proceedings of the 16th International Conference on Information Fusion Istanbul, Turkey : IEEE , 2013 : 1520 -1525 .
[本文引用: 1]
[12]
LI L Q ZHAO D LUO C D . A novel interacting TS fuzzy multiple model by using UKF for maneuvering target tracking
[C]// 2019 22th International Conference on Information Fusion Ottawa, Canada : IEEE , 2019 : 1 -7 .
[本文引用: 1]
[13]
邵堃 , 雷迎科 . 基于模糊逻辑和机动检测的AGIMM跟踪算法
[J]. 空军工程大学学报(自然科学版) 2020 , 21 (4 ): 80 -87 .
[本文引用: 1]
SHAO Kun LEI Yingke. AGIMM tracking algorithm based on fuzzy logic and maneuvering detection
[J]. Journal of Air Force Engineering University (Natural Science Edition) 2020 , 21 (4 ): 80 -87 .
[本文引用: 1]
[15]
雷英杰 , 路艳丽 , 王毅 , 等 . 模糊逻辑与智能系统 [M]. 西安 : 西安电子科技大学出版社 , 2016 .
[本文引用: 2]
LEI Yingjie LU Yanli WANG Yi , et al Fuzzy logic with intelligent systems [M]. Xi’an : Xidian University Press , 2016 .
[本文引用: 2]
[16]
罗晓勇 . 无线传感网络中基于交互式多模型目标跟踪算法研究 [D]. 重庆 : 重庆邮电大学 , 2020 .
[本文引用: 1]
LUO Xiaoyong . Research on target tracking algorithm based on interaction multiple model in wireless sensor networks [D]. Chongqing : Chongqing University of Posts and Telecommunications , 2020 .
[本文引用: 1]
[17]
傅虹景 , 于守江 , 吉峰 , 等 . 基于“当前”统计模型的变结构交互多模型算法
[J]. 无线电工程 2020 , 50 (4 ): 318 -322 .
[本文引用: 2]
FU Hongjing YU Shoujiang JI Feng , et al Variable structure interactive multiple model algorithm based on current statistical model
[J]. Radio Engineering 2020 , 50 (4 ): 318 -322 .
[本文引用: 2]
基于距离加权的概率数据关联机动目标跟踪算法
1
2018
... 机动目标跟踪是目标跟踪领域的重要研究方向,随着空中飞行器的机动性能不断增强,对机动目标进行有效跟踪的重要性愈发凸显.当跟踪的目标发生机动时,其运动模式会发生剧烈变化,此时单模型算法往往难以适用,而基于多模型思想的机动目标跟踪算法则具有更好的表现.定结构的交互式多模型(Interacting Multi-Model, IMM)方法假设目标存在多种可能的运动模式,能够处理复杂的运动模式[1 ] ,对目标机动有一定的自适应性.相比于定结构的IMM方法,以模型集自适应(Model-Set Adaption, MSA)为核心的变结构交互式多模型(Variable Structure Interacting Multi-Model, VSIMM)方法具有更好的性能,其中可能模型集(Likely Model-Set, LMS)、模型群切换(Model Group Switch, MGS)、期望模式扩增(Expected-Model Augmentation, EMA)和自适应网格(Adaptive Grid,AG)等[2 ⇓ ⇓ -5 ] 都较为典型.王昱淇等[6 ] 则提出了一种复合的EMA-LMS算法,一定程度上综合了LMS的复杂度优点和EMA的估计精度优点. ...
Maneuvering target tracking algorithm based on weighted distance of probability data association
1
2018
... 机动目标跟踪是目标跟踪领域的重要研究方向,随着空中飞行器的机动性能不断增强,对机动目标进行有效跟踪的重要性愈发凸显.当跟踪的目标发生机动时,其运动模式会发生剧烈变化,此时单模型算法往往难以适用,而基于多模型思想的机动目标跟踪算法则具有更好的表现.定结构的交互式多模型(Interacting Multi-Model, IMM)方法假设目标存在多种可能的运动模式,能够处理复杂的运动模式[1 ] ,对目标机动有一定的自适应性.相比于定结构的IMM方法,以模型集自适应(Model-Set Adaption, MSA)为核心的变结构交互式多模型(Variable Structure Interacting Multi-Model, VSIMM)方法具有更好的性能,其中可能模型集(Likely Model-Set, LMS)、模型群切换(Model Group Switch, MGS)、期望模式扩增(Expected-Model Augmentation, EMA)和自适应网格(Adaptive Grid,AG)等[2 ⇓ ⇓ -5 ] 都较为典型.王昱淇等[6 ] 则提出了一种复合的EMA-LMS算法,一定程度上综合了LMS的复杂度优点和EMA的估计精度优点. ...
Multiple-model estimation with variable structure. V. Likely-model set algorithm
2
2000
... 机动目标跟踪是目标跟踪领域的重要研究方向,随着空中飞行器的机动性能不断增强,对机动目标进行有效跟踪的重要性愈发凸显.当跟踪的目标发生机动时,其运动模式会发生剧烈变化,此时单模型算法往往难以适用,而基于多模型思想的机动目标跟踪算法则具有更好的表现.定结构的交互式多模型(Interacting Multi-Model, IMM)方法假设目标存在多种可能的运动模式,能够处理复杂的运动模式[1 ] ,对目标机动有一定的自适应性.相比于定结构的IMM方法,以模型集自适应(Model-Set Adaption, MSA)为核心的变结构交互式多模型(Variable Structure Interacting Multi-Model, VSIMM)方法具有更好的性能,其中可能模型集(Likely Model-Set, LMS)、模型群切换(Model Group Switch, MGS)、期望模式扩增(Expected-Model Augmentation, EMA)和自适应网格(Adaptive Grid,AG)等[2 ⇓ ⇓ -5 ] 都较为典型.王昱淇等[6 ] 则提出了一种复合的EMA-LMS算法,一定程度上综合了LMS的复杂度优点和EMA的估计精度优点. ...
... 参与仿真对比的算法包括模糊推理EMA-LMS算法、IMM算法、EMA算法[4 ] 、LMS算法[2 ] 、EMA-LMS算法[6 ] 和当前统计自适应网格(Current Statistical Adaptive Grid, CS-AG)算法[17 ] . ...
Multiple-model estimation with variable structure. III. Model-group switching algorithm
1
1999
... 机动目标跟踪是目标跟踪领域的重要研究方向,随着空中飞行器的机动性能不断增强,对机动目标进行有效跟踪的重要性愈发凸显.当跟踪的目标发生机动时,其运动模式会发生剧烈变化,此时单模型算法往往难以适用,而基于多模型思想的机动目标跟踪算法则具有更好的表现.定结构的交互式多模型(Interacting Multi-Model, IMM)方法假设目标存在多种可能的运动模式,能够处理复杂的运动模式[1 ] ,对目标机动有一定的自适应性.相比于定结构的IMM方法,以模型集自适应(Model-Set Adaption, MSA)为核心的变结构交互式多模型(Variable Structure Interacting Multi-Model, VSIMM)方法具有更好的性能,其中可能模型集(Likely Model-Set, LMS)、模型群切换(Model Group Switch, MGS)、期望模式扩增(Expected-Model Augmentation, EMA)和自适应网格(Adaptive Grid,AG)等[2 ⇓ ⇓ -5 ] 都较为典型.王昱淇等[6 ] 则提出了一种复合的EMA-LMS算法,一定程度上综合了LMS的复杂度优点和EMA的估计精度优点. ...
Multiple-model estimation with variable structure—Part VI: Expected-mode augmentation
3
2005
... 机动目标跟踪是目标跟踪领域的重要研究方向,随着空中飞行器的机动性能不断增强,对机动目标进行有效跟踪的重要性愈发凸显.当跟踪的目标发生机动时,其运动模式会发生剧烈变化,此时单模型算法往往难以适用,而基于多模型思想的机动目标跟踪算法则具有更好的表现.定结构的交互式多模型(Interacting Multi-Model, IMM)方法假设目标存在多种可能的运动模式,能够处理复杂的运动模式[1 ] ,对目标机动有一定的自适应性.相比于定结构的IMM方法,以模型集自适应(Model-Set Adaption, MSA)为核心的变结构交互式多模型(Variable Structure Interacting Multi-Model, VSIMM)方法具有更好的性能,其中可能模型集(Likely Model-Set, LMS)、模型群切换(Model Group Switch, MGS)、期望模式扩增(Expected-Model Augmentation, EMA)和自适应网格(Adaptive Grid,AG)等[2 ⇓ ⇓ -5 ] 都较为典型.王昱淇等[6 ] 则提出了一种复合的EMA-LMS算法,一定程度上综合了LMS的复杂度优点和EMA的估计精度优点. ...
... (4) 若M n =⌀,融合 M f k Ek 两模型集的估计结果,融合规则参考文献[4 ],得到基于模型集Mk = M f k Ek 的状态估计 { x ^ k | k i } m i ∈ M k { P k | k i } m i ∈ M k { μ k | k i } m i ∈ M k . 若M n ≠⌀,利用VSIMM方法计算 { x ^ k | k i } m i ∈ M n { P k | k i } m i ∈ M n { μ k | k i } m i ∈ M n M f k Ek 两模型集的估计结果进行融合,获得基于Mk = M f k Ek ∪M n 的状态估计 { x ^ k | k i } m i ∈ M k { P k | k i } m i ∈ M k { μ k | k i } m i ∈ M k . ...
... 参与仿真对比的算法包括模糊推理EMA-LMS算法、IMM算法、EMA算法[4 ] 、LMS算法[2 ] 、EMA-LMS算法[6 ] 和当前统计自适应网格(Current Statistical Adaptive Grid, CS-AG)算法[17 ] . ...
Design and comparison of mode-set adaptive IMM algorithms for maneuvering target tracking
1
1999
... 机动目标跟踪是目标跟踪领域的重要研究方向,随着空中飞行器的机动性能不断增强,对机动目标进行有效跟踪的重要性愈发凸显.当跟踪的目标发生机动时,其运动模式会发生剧烈变化,此时单模型算法往往难以适用,而基于多模型思想的机动目标跟踪算法则具有更好的表现.定结构的交互式多模型(Interacting Multi-Model, IMM)方法假设目标存在多种可能的运动模式,能够处理复杂的运动模式[1 ] ,对目标机动有一定的自适应性.相比于定结构的IMM方法,以模型集自适应(Model-Set Adaption, MSA)为核心的变结构交互式多模型(Variable Structure Interacting Multi-Model, VSIMM)方法具有更好的性能,其中可能模型集(Likely Model-Set, LMS)、模型群切换(Model Group Switch, MGS)、期望模式扩增(Expected-Model Augmentation, EMA)和自适应网格(Adaptive Grid,AG)等[2 ⇓ ⇓ -5 ] 都较为典型.王昱淇等[6 ] 则提出了一种复合的EMA-LMS算法,一定程度上综合了LMS的复杂度优点和EMA的估计精度优点. ...
基于一致性的分布式变结构多模型方法
2
2021
... 机动目标跟踪是目标跟踪领域的重要研究方向,随着空中飞行器的机动性能不断增强,对机动目标进行有效跟踪的重要性愈发凸显.当跟踪的目标发生机动时,其运动模式会发生剧烈变化,此时单模型算法往往难以适用,而基于多模型思想的机动目标跟踪算法则具有更好的表现.定结构的交互式多模型(Interacting Multi-Model, IMM)方法假设目标存在多种可能的运动模式,能够处理复杂的运动模式[1 ] ,对目标机动有一定的自适应性.相比于定结构的IMM方法,以模型集自适应(Model-Set Adaption, MSA)为核心的变结构交互式多模型(Variable Structure Interacting Multi-Model, VSIMM)方法具有更好的性能,其中可能模型集(Likely Model-Set, LMS)、模型群切换(Model Group Switch, MGS)、期望模式扩增(Expected-Model Augmentation, EMA)和自适应网格(Adaptive Grid,AG)等[2 ⇓ ⇓ -5 ] 都较为典型.王昱淇等[6 ] 则提出了一种复合的EMA-LMS算法,一定程度上综合了LMS的复杂度优点和EMA的估计精度优点. ...
... 参与仿真对比的算法包括模糊推理EMA-LMS算法、IMM算法、EMA算法[4 ] 、LMS算法[2 ] 、EMA-LMS算法[6 ] 和当前统计自适应网格(Current Statistical Adaptive Grid, CS-AG)算法[17 ] . ...
Consensus-based distributed variable structure multiple model
2
2021
... 机动目标跟踪是目标跟踪领域的重要研究方向,随着空中飞行器的机动性能不断增强,对机动目标进行有效跟踪的重要性愈发凸显.当跟踪的目标发生机动时,其运动模式会发生剧烈变化,此时单模型算法往往难以适用,而基于多模型思想的机动目标跟踪算法则具有更好的表现.定结构的交互式多模型(Interacting Multi-Model, IMM)方法假设目标存在多种可能的运动模式,能够处理复杂的运动模式[1 ] ,对目标机动有一定的自适应性.相比于定结构的IMM方法,以模型集自适应(Model-Set Adaption, MSA)为核心的变结构交互式多模型(Variable Structure Interacting Multi-Model, VSIMM)方法具有更好的性能,其中可能模型集(Likely Model-Set, LMS)、模型群切换(Model Group Switch, MGS)、期望模式扩增(Expected-Model Augmentation, EMA)和自适应网格(Adaptive Grid,AG)等[2 ⇓ ⇓ -5 ] 都较为典型.王昱淇等[6 ] 则提出了一种复合的EMA-LMS算法,一定程度上综合了LMS的复杂度优点和EMA的估计精度优点. ...
... 参与仿真对比的算法包括模糊推理EMA-LMS算法、IMM算法、EMA算法[4 ] 、LMS算法[2 ] 、EMA-LMS算法[6 ] 和当前统计自适应网格(Current Statistical Adaptive Grid, CS-AG)算法[17 ] . ...
时变转移概率IMM-SRCKF机动目标跟踪算法
1
2015
... 然而考虑到场景中目标机动不确定性和量测噪声的影响,多模型方法在自适应方面仍然存在问题.首先,传统多模型算法依赖于先验参数的设置,针对这一问题,学者们提出了基于模型自身概率变化情况[7 ⇓ -9 ] 和基于机动判别[10 ] 的模型转移概率自适应调节方法,以改善相应算法在不同机动情况下的收敛性能.其次,多模型方法依赖的模型后验概率与模型的似然值有关,而似然值受到量测噪声的影响,不准确的似然值将为MSA过程带来不利影响.对于该问题,潘媚媚[10 ] 尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节. ...
Time-varying transition probability based IMM-SRCKF algorithm for maneuvering target tracking
1
2015
... 然而考虑到场景中目标机动不确定性和量测噪声的影响,多模型方法在自适应方面仍然存在问题.首先,传统多模型算法依赖于先验参数的设置,针对这一问题,学者们提出了基于模型自身概率变化情况[7 ⇓ -9 ] 和基于机动判别[10 ] 的模型转移概率自适应调节方法,以改善相应算法在不同机动情况下的收敛性能.其次,多模型方法依赖的模型后验概率与模型的似然值有关,而似然值受到量测噪声的影响,不准确的似然值将为MSA过程带来不利影响.对于该问题,潘媚媚[10 ] 尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节. ...
基于AIGWO-IMMUKF 的目标跟踪算法
1
2020
... 然而考虑到场景中目标机动不确定性和量测噪声的影响,多模型方法在自适应方面仍然存在问题.首先,传统多模型算法依赖于先验参数的设置,针对这一问题,学者们提出了基于模型自身概率变化情况[7 ⇓ -9 ] 和基于机动判别[10 ] 的模型转移概率自适应调节方法,以改善相应算法在不同机动情况下的收敛性能.其次,多模型方法依赖的模型后验概率与模型的似然值有关,而似然值受到量测噪声的影响,不准确的似然值将为MSA过程带来不利影响.对于该问题,潘媚媚[10 ] 尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节. ...
Target tracking algorithm based on AIGWO-IMMUKF
1
2020
... 然而考虑到场景中目标机动不确定性和量测噪声的影响,多模型方法在自适应方面仍然存在问题.首先,传统多模型算法依赖于先验参数的设置,针对这一问题,学者们提出了基于模型自身概率变化情况[7 ⇓ -9 ] 和基于机动判别[10 ] 的模型转移概率自适应调节方法,以改善相应算法在不同机动情况下的收敛性能.其次,多模型方法依赖的模型后验概率与模型的似然值有关,而似然值受到量测噪声的影响,不准确的似然值将为MSA过程带来不利影响.对于该问题,潘媚媚[10 ] 尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节. ...
Adaptive transition probability matrix-based parallel IMM algorithm
1
2019
... 然而考虑到场景中目标机动不确定性和量测噪声的影响,多模型方法在自适应方面仍然存在问题.首先,传统多模型算法依赖于先验参数的设置,针对这一问题,学者们提出了基于模型自身概率变化情况[7 ⇓ -9 ] 和基于机动判别[10 ] 的模型转移概率自适应调节方法,以改善相应算法在不同机动情况下的收敛性能.其次,多模型方法依赖的模型后验概率与模型的似然值有关,而似然值受到量测噪声的影响,不准确的似然值将为MSA过程带来不利影响.对于该问题,潘媚媚[10 ] 尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节. ...
2
2019
... 然而考虑到场景中目标机动不确定性和量测噪声的影响,多模型方法在自适应方面仍然存在问题.首先,传统多模型算法依赖于先验参数的设置,针对这一问题,学者们提出了基于模型自身概率变化情况[7 ⇓ -9 ] 和基于机动判别[10 ] 的模型转移概率自适应调节方法,以改善相应算法在不同机动情况下的收敛性能.其次,多模型方法依赖的模型后验概率与模型的似然值有关,而似然值受到量测噪声的影响,不准确的似然值将为MSA过程带来不利影响.对于该问题,潘媚媚[10 ] 尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节. ...
... [10 ]尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节. ...
2
2019
... 然而考虑到场景中目标机动不确定性和量测噪声的影响,多模型方法在自适应方面仍然存在问题.首先,传统多模型算法依赖于先验参数的设置,针对这一问题,学者们提出了基于模型自身概率变化情况[7 ⇓ -9 ] 和基于机动判别[10 ] 的模型转移概率自适应调节方法,以改善相应算法在不同机动情况下的收敛性能.其次,多模型方法依赖的模型后验概率与模型的似然值有关,而似然值受到量测噪声的影响,不准确的似然值将为MSA过程带来不利影响.对于该问题,潘媚媚[10 ] 尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节. ...
... [10 ]尝试通过机动判别方法对基于滤波残差模型似然值的模型集自适应方法进行补充调节. ...
Fuzzy inference-based dynamic determination of IMM mode transition probability for multi-radar tracking
1
2013
... 更进一步,研究者们引入模糊控制系统,以减少多模型方法对先验参数设置的依赖,并且增强对模型后验概率不确定性的自适应能力.Enu等[11 ] 基于T-S推理模型动态调节模型概率转移矩阵,增强各模型概率的区分度;Li等[12 ] 则引入模糊逻辑,对模型进行基于各运动特征的模糊分类,并基于T-S模型隶属度函数重新定义转移概率,设计各模型的概率计算及交互过程,提高了IMM方法的跟踪精度.邵堃等[13 ] 在AGIMM算法中引入T-S模型,通过最大模型后验概率、模型网格大小计算机动置信度、选择自适应网格的更新方式,改良了AG方法的收敛性. ...
A novel interacting TS fuzzy multiple model by using UKF for maneuvering target tracking
1
2019
... 更进一步,研究者们引入模糊控制系统,以减少多模型方法对先验参数设置的依赖,并且增强对模型后验概率不确定性的自适应能力.Enu等[11 ] 基于T-S推理模型动态调节模型概率转移矩阵,增强各模型概率的区分度;Li等[12 ] 则引入模糊逻辑,对模型进行基于各运动特征的模糊分类,并基于T-S模型隶属度函数重新定义转移概率,设计各模型的概率计算及交互过程,提高了IMM方法的跟踪精度.邵堃等[13 ] 在AGIMM算法中引入T-S模型,通过最大模型后验概率、模型网格大小计算机动置信度、选择自适应网格的更新方式,改良了AG方法的收敛性. ...
基于模糊逻辑和机动检测的AGIMM跟踪算法
1
2020
... 更进一步,研究者们引入模糊控制系统,以减少多模型方法对先验参数设置的依赖,并且增强对模型后验概率不确定性的自适应能力.Enu等[11 ] 基于T-S推理模型动态调节模型概率转移矩阵,增强各模型概率的区分度;Li等[12 ] 则引入模糊逻辑,对模型进行基于各运动特征的模糊分类,并基于T-S模型隶属度函数重新定义转移概率,设计各模型的概率计算及交互过程,提高了IMM方法的跟踪精度.邵堃等[13 ] 在AGIMM算法中引入T-S模型,通过最大模型后验概率、模型网格大小计算机动置信度、选择自适应网格的更新方式,改良了AG方法的收敛性. ...
LEI Yingke. AGIMM tracking algorithm based on fuzzy logic and maneuvering detection
1
2020
... 更进一步,研究者们引入模糊控制系统,以减少多模型方法对先验参数设置的依赖,并且增强对模型后验概率不确定性的自适应能力.Enu等[11 ] 基于T-S推理模型动态调节模型概率转移矩阵,增强各模型概率的区分度;Li等[12 ] 则引入模糊逻辑,对模型进行基于各运动特征的模糊分类,并基于T-S模型隶属度函数重新定义转移概率,设计各模型的概率计算及交互过程,提高了IMM方法的跟踪精度.邵堃等[13 ] 在AGIMM算法中引入T-S模型,通过最大模型后验概率、模型网格大小计算机动置信度、选择自适应网格的更新方式,改良了AG方法的收敛性. ...
A novel approach to implement Takagi-Sugeno fuzzy models
1
2017
... 模糊推理能够以非精确的输入推理出非精确的结果,而T-S模糊推理具有语义信息引入简明和对不同形态系统泛用的优势[14 ] ,利用T-S模糊推理进行机动判别,能够有效增强对目标机动不确定性和量测噪声的适应性.当前模糊推理方法在多模型方法中的应用主要集中于与IMM算法和AG算法的结合,但已有研究关注的模型类型较为单一,考虑的输入变量较为简单.T-S模糊推理与LMS、EMA等模型集自适应方法的结合尚没有相关研究. ...
2
2016
... 运用Sugeno 方法[15 ] 进行推理,推理规则如表1 所示. 通过各条模糊规则计算输出后,再利用加权平均法进行解模糊化,获得最终输出PMain , k : ...
... 运用Sugeno方法进行推理,推理规则及相应的线性输出函数由模糊神经网络训练生成[15 ] . 完成推理后同样需要进行解模糊化得到最终输出,解模糊方法同主模型可信度推理. ...
2
2016
... 运用Sugeno 方法[15 ] 进行推理,推理规则如表1 所示. 通过各条模糊规则计算输出后,再利用加权平均法进行解模糊化,获得最终输出PMain , k : ...
... 运用Sugeno方法进行推理,推理规则及相应的线性输出函数由模糊神经网络训练生成[15 ] . 完成推理后同样需要进行解模糊化得到最终输出,解模糊方法同主模型可信度推理. ...
1
2020
... (1) 主模型残差加权范数Dk , 滤波残差加权范数能够较好反映目标当前时刻的状态变化[16 ] .记当前时刻后验概率最大的模型序号为r ,此时mr 为主模型,则主模型的残差加权范数定义为 ...
1
2020
... (1) 主模型残差加权范数Dk , 滤波残差加权范数能够较好反映目标当前时刻的状态变化[16 ] .记当前时刻后验概率最大的模型序号为r ,此时mr 为主模型,则主模型的残差加权范数定义为 ...
基于“当前”统计模型的变结构交互多模型算法
2
2020
... 参与仿真对比的算法包括模糊推理EMA-LMS算法、IMM算法、EMA算法[4 ] 、LMS算法[2 ] 、EMA-LMS算法[6 ] 和当前统计自适应网格(Current Statistical Adaptive Grid, CS-AG)算法[17 ] . ...
... 式(39)中期望模型编号为14. 模糊推理EMA-LMS 算法设置如下参数:TMain . 5,TMD . 6,t '1 =0. 1,t1, min . 01,t1, max . 3,t' 2 =0. 7,t2, min . 5,t2, max . 95,cα =2. 4, c β 1 = 0 . 96 c β 2 = 0 . 48 . LMS 算法、EMA-LMS 算法模型概率门限t1 =0. 1,t2 =0. 9. LMS 算法、EMA-LMS 算法和模糊推理EMA-LMS 算法的最小滤波模型数都为K=4. CS-AG 算法的参数配置参照文献[17 ]. ...
Variable structure interactive multiple model algorithm based on current statistical model
2
2020
... 参与仿真对比的算法包括模糊推理EMA-LMS算法、IMM算法、EMA算法[4 ] 、LMS算法[2 ] 、EMA-LMS算法[6 ] 和当前统计自适应网格(Current Statistical Adaptive Grid, CS-AG)算法[17 ] . ...
... 式(39)中期望模型编号为14. 模糊推理EMA-LMS 算法设置如下参数:TMain . 5,TMD . 6,t '1 =0. 1,t1, min . 01,t1, max . 3,t' 2 =0. 7,t2, min . 5,t2, max . 95,cα =2. 4, c β 1 = 0 . 96 c β 2 = 0 . 48 . LMS 算法、EMA-LMS 算法模型概率门限t1 =0. 1,t2 =0. 9. LMS 算法、EMA-LMS 算法和模糊推理EMA-LMS 算法的最小滤波模型数都为K=4. CS-AG 算法的参数配置参照文献[17 ]. ...