变负载条件下多体折展机翼改进自抗扰控制方法

doi:10.16183/j.cnki.jsjtu.2024.208

变负载条件下多体折展机翼改进自抗扰控制方法

韩一凡¹^,², 陈柏屹^,¹^,², 刘燕斌¹^,², 陈金宝¹^,²

1.南京航空航天大学航天学院,南京 211106

2.南京航空航天大学宇航空间机构全国重点实验室,南京 211106

Improved Active Disturbance Rejection Control for Multibody Folding Wing Under Variable Loads

HAN Yifan¹^,², CHEN Boyi^,¹^,², LIU Yanbin¹^,², CHEN Jinbao¹^,²

1. College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China

2. National Key Laboratory of Aerospace Mechanism, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China

通讯作者: 陈柏屹,副研究员;E-mail:chenboyi1989@nuaa.edu.cn.

责任编辑: 王一凡

收稿日期: 2024-06-6 修回日期: 2024-07-3 接受日期: 2024-07-8

基金资助:

国家自然基金青年基金资助项目(62103187)

Received: 2024-06-6 Revised: 2024-07-3 Accepted: 2024-07-8

作者简介 About authors

韩一凡(2000—),硕士生,从事多体飞行器动力学建模与控制研究.

摘要

针对多体折展机翼在协调倾转过程中受到气动负载变化、重力换向及受外部干扰的问题,提出基于双曲正切函数与调相补偿结合的改进自抗扰控制策略.通过拉格朗日方程,将单元翼的气动负载作用于质心处,并给出重力项随机体姿态角的偏置,从而建立多体折展机翼的动力学模型.设计改进自抗扰控制器实现折展机翼的期望角度轨迹的跟踪,并选取合理的控制器参数对关节振动进行抑制.仿真结果表明,改进自抗扰控制方法在变负载条件下可以有效实现轨迹跟踪和关节振动的抑制,并在受到外界扰动时具有更小的跟踪误差和更好的动态性能及鲁棒性.

关键词： 多体折展机翼; 拉格朗日法建模; 变负载; 自抗扰控制

Abstract

To address the issue of multi-body folding wings being subjected to aerodynamic load changes, gravity reversal, and external disturbances during coordinated tilting, an improved active disturbance rejection control (ADRC) strategy based on the combination of hyperbolic tangent function and phase compensation is proposed. Using the Lagrange equation, the aerodynamic load on the unit wing is applied to the center of mass, and the offset of the gravity term with the attitude angle of the body is provided, thereby establishing the dynamic model of the multi-body folding wing. An improved ADRC controller is designed to track the desired angular trajectory of the folding wing, and appropriate controller parameters are selected to suppress joint vibration. The simulation results show that the improved ADRC method can effectively achieve trajectory tracking and joint vibration suppression under variable load conditions, and it demonstrates smaller tracking errors and better dynamic performance and robustness when subjected to external disturbances.

Keywords： multi-body folding wing; Lagrange modeling; variable load; active disturbance rejection control (ADRC)

PDF (1921KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

韩一凡, 陈柏屹, 刘燕斌, 陈金宝. 变负载条件下多体折展机翼改进自抗扰控制方法[J]. 上海交通大学学报, 2024, 58(11): 1762-1771 doi:10.16183/j.cnki.jsjtu.2024.208

HAN Yifan, CHEN Boyi, LIU Yanbin, CHEN Jinbao. Improved Active Disturbance Rejection Control for Multibody Folding Wing Under Variable Loads[J]. Journal of Shanghai Jiaotong University, 2024, 58(11): 1762-1771 doi:10.16183/j.cnki.jsjtu.2024.208

变构型飞行器起源于仿生学,它可以根据飞行任务和工作环境自主改变几何构型,兼顾各个任务段的性能,从而使综合性能达到最佳.20世纪初在美国的一个专利申请里提出了变形翼飞机的概念,随后英美、苏联相继都有变后掠翼飞机问世^[1].随着材料、驱动技术和计算机技术的发展,许多学者提出了更先进的变形方式,例如气动弹性机翼、柔性舵面、折叠翼、滑动蒙皮等^[2],以前的很多复杂的结构现在可以比较轻松地实现或者通过其他变构型方式进行替代,变形机翼飞行器逐渐受到了国内外研究人员的重视.变形机翼不仅是指机翼外形的变化,而且还涵盖了机翼特性和性能变化的特点,可以说是一个科学研究的整体,对军事和民用航空部门的进步都有启发作用^[3].

目前,洛克希德·马丁公司(Lockheed Martin)和新一代航空技术公司(Hypercomp/NexGen)正同时开展“变形机翼”项目的研究,该项目是美国国防部先进研究项目局(DARPA)^[4]开展的“变体飞行器结构”(MAS)^[5]研发项目的其中一部分.MAS计划旨在通过改变飞机的气动外形,使飞机在执行不同任务时都能保持最佳性能.2019年,北京航空航天大学团队在大型鸟类飞行运动启发下,提出了一种变形翼飞行器设计方案,飞行器以平面连杆机构为主要变形机构,可实现滑翔、下降和高机动3种飞行状态^[6].Ryu等^[7]以扑翼和折叠运动为研究对象,设计了两种基于四杆机构的扑翼机构,推导了两种机构的运动学方程,并进行了优化以最大化扑翼角.Wang^[8]针对三段折叠机翼的气动稳定性进行了研究.使用多体动力学分析方法,研究了飞行器在折叠飞行过程中基于飞行稳定性的轨迹跟踪算法.赵亚鲁^[9]简化折叠机翼的三维模型,利用ANSYS软件分析了折叠机翼在不同尺寸和不同折叠角度下单、双向流固耦合动力学特性及其参数影响规律.郭秋亭等^[10]使用数值模拟方法研究折叠翼飞行器机翼折叠和展开过程的动态气动特性,仿真结果表明气动力受机翼折叠的扰动流场影响较大,且机翼折叠速度越快影响越大.Hu等^[11]主要研究折叠翼在变形过程中的气动弹性特性.采用柔性多体动力学方法对折叠翼结构进行建模,提出了一种计算折叠翼变形过程气动力的有效方法.

以上研究主要针对于多体折展机翼变形方案以及气动耦合特性的分析,但在飞行过程中机翼折叠对飞行稳定性及操作性影响严重,因此对多体折展机翼的控制提出了挑战.

比例微分(PD)、比例积分微分(PID)、自适应算法、积分阻抗技术等被广泛地应用于控制器设计^{[12⇓⇓-15]}.刘志豪等^[16]基于垂直起降无人机,提出了经典PID、最快模式转换及最快模式转换定高3种控制策略并对模拟结果进行对比.陶晓荣等^[17]基于变体飞行器模型设计了鲁棒最优控制方法,实现了机翼扭转变形跟踪控制.宋慧心等^[18]提出了一种基于自抗扰理论的飞行器变形过程中的稳定控制方法,实现了速度通道和高度通道的解耦控制.周林阳等^[19]提出了基于反正切非线性函数的自抗扰控制,针对输出带有测量噪声的控制对象均取得较好的控制效果.

针对折展机翼在协调倾转过程受到作用于3个单元翼上的时变气动负载、重力换向以及受到零件摩擦等内部因素对于系统扰动较多的问题.经过综合考虑,本文选择自抗扰控制(ADRC)方法来实现多体折展机翼在协调倾转过程中的指令跟踪.主要工作如下:

(1) 在考虑气动负载作用于单元翼质心以及重力项随机体姿态角的偏置的条件下,结合多体折展机翼气动耦合特性利用拉格朗日方程建立了系统模型.

(2) 设计了自抗扰控制器对折展机翼的运动轨迹进行跟踪,并实现振动的快速抑制.

(3) 仿真结果表明本文设计的控制方法在应对动态负载和姿态变化时,相比传统的控制方法具有显著的优势.

1 系统建模

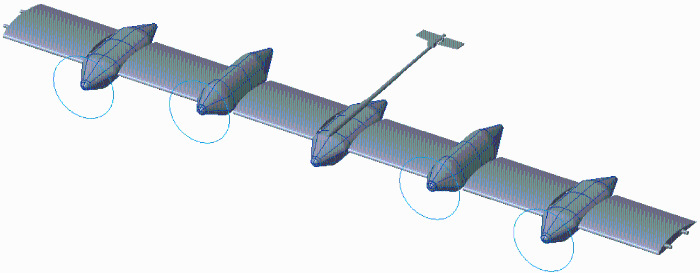
由于变构型飞行器存在大型的变形结构,所以不能将其视为单个刚体进行建模.针对整体式的变形,可以忽略变构型飞行器的形变,将其视为通过铰链连接的多刚体系统,使用描述多刚体运动的方法进行研究可以得到较为精确的动力学模型.变构型飞行器结构如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 变构型飞行器结构

Fig.1 Structure of variable-configuration aircraft

考虑到实际的折展机翼的结构相对较复杂,很难进行精确的描述,因此,需要利用简化的数学模型进行讨论.简化条件如下:

(1) 假设折展机翼是刚性结构,不考虑形变.

(2) 忽略各构件之间的摩擦力.

(3) 假设折展机翼的各单元翼是密度均匀的刚体.

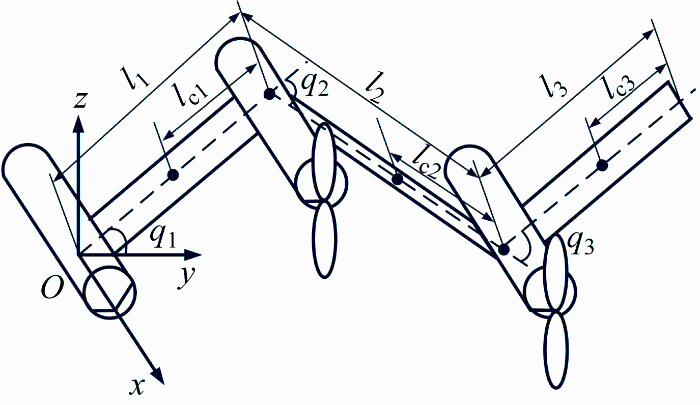
平面多体折展机翼模型结构如图2所示.图中:q_i为第i单元翼的旋转角度,i=1, 2, 3;m_i为第i单元翼的质量;l_i为第i单元翼的长度;l_c_i为第i单元翼的质心到前一关节的长度;J_i为第i单元翼的转动惯量.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 多体折展机翼示意图

Fig.2 Diagram of multi-body folding wing

对于平面多体折展机翼而言,q₁、q₂、q₃唯一地确定了其位置,q₁、q₂、q₃的一阶导数和二阶导数确定了其运动状态,它们是动力学描述所需的基础变量.

1.1 动力学模型

折展机翼在垂直平面运动及未加入气动负载的情况下其动力学方程为^[20]

(1)$\boldsymbol{M}(q) \ddot{\boldsymbol{q}}+\boldsymbol{C}(q, \dot{q}) \dot{\boldsymbol{q}}+\boldsymbol{G}(q)=\boldsymbol{\tau}(t)$

式中:$\boldsymbol{\tau}=\left[\begin{array}{lll}\tau_{1} & \tau_{2} & \tau_{3}\end{array}\right]^{\mathrm{T}}$为控制力矩向量;$\ddot{\boldsymbol{q}}= \left[\begin{array}{lll}\ddot{q}_{1} & \ddot{q}_{2} &\ddot{q}_{3}\end{array}\right]^{\mathrm{T}}$为系统的角加速度向量;$\boldsymbol{M}(q)= \boldsymbol{M}_{0}(q)+\boldsymbol{M}_{\Delta}(q) \in \mathbf{R}^{3 \times 3}$为惯性矩阵;$\boldsymbol{C}(q, \dot{q})= \boldsymbol{C}_{0}(q, \dot{q})+\boldsymbol{C}_{\Delta}(q, \dot{q}) \in \mathbf{R}^{3 \times 1}$为科氏力和离心力的结合矩阵;$ \boldsymbol{G}(q)=\boldsymbol{G}_{0}(q)+\boldsymbol{G}_{\Delta}(q) \in \mathbf{R}^{3 \times 1}$为重力矩阵.$\boldsymbol{M}_{0}(q) 、 \boldsymbol{C}_{0}(q, \dot{q}) 、 \boldsymbol{G}_{0}(q)$已知,是对动力学模型参数的估计量;$\boldsymbol{M}_{\Delta}(q) 、 \boldsymbol{C}_{\Delta}(q, \dot{q}) 、 \boldsymbol{G}_{\Delta}(q)$未知但有界.具体形式如下:

(2)$\begin{array}{l}\boldsymbol{M}(q)=\left[\begin{array}{lll}M_{11} & M_{12} & M_{13} \\M_{21} & M_{22} & M_{23} \\M_{31} & M_{32} & M_{33}\end{array}\right] \end{array}$

(3)$\begin{array}{l}\boldsymbol{C}(q, \dot{q})=\left[\begin{array}{l}C_{1} \\C_{2} \\C_{3}\end{array}\right] \end{array}$

(4)$\begin{array}{l}\boldsymbol{G}(q)=\left[\begin{array}{l}G_{1} \\G_{2} \\G_{3}\end{array}\right]\end{array}$

(5)

\begin{array}{l} M_{11} (q) = m_{1} l_{c 1}^{2} + J_{1} + (m_{2} + m_{3}) l_{1}^{2} + J_{2} + \\ m_{2} l_{c 2}^{2} + m_{3} l_{2}^{2} + J_{3} + m_{3} l_{2}^{2} + \\ 2 (m_{2} l_{c 2} + m_{3} l_{2}) l_{1} c o s q_{2} + \\ 2 m_{3} l_{c 3} l_{1} c o s (q_{2} + q_{3}) + \\ 2 m_{3} l_{c 3} l_{2} c o s q_{3} \\ M_{12} (q) = J_{2} + m_{2} l_{c 2}^{2} + m_{3} l_{2}^{2} + J_{3} + m_{3} l_{2}^{2} + \\ (m_{2} l_{c 2} + m_{3} l_{2}) l_{1} c o s q_{2} + \\ c o s (q_{2} + q_{5}) + 2 m_{3} l_{c 3} l_{2} c o s q_{3} \\ M_{13} (q) = J_{3} + m_{3} l_{2}^{2} + m_{3} l_{c 3} l_{1} c o s (q_{2} + q_{3}) + \\ m_{3} l_{c 3} l_{2} c o s q_{3} \\ M_{21} (q) = M_{12} (q) \\ M_{22} (q) = J_{2} + m_{2} l_{c 2}^{2} + m_{3} l_{2}^{2} + J_{3} + \\ m_{3} l_{2}^{2} + 2 m_{3} l_{c 3} l_{2} c o s q_{3} \\ M_{23} (q) = J_{3} + m_{3} l_{2}^{2} + m_{3} l_{c 3} l_{2} c o s q_{3} \\ M_{31} (q) = M_{13} (q) \\ M_{32} (q) = M_{23} (q) \\ M_{33} (q) = J_{3} + m_{3} l_{2}^{2} \end{array}\}

C(q, $\overset{\cdot}{q}$ )中的系数如下:

(6)

\begin{array}{l} C_{1} = - m_{3} l_{c 3} l_{1} (2 {\overset{\cdot}{q}}_{1} + {\overset{\cdot}{q}}_{2} + {\overset{\cdot}{q}}_{3}) \\ ({\overset{\cdot}{q}}_{2} + {\overset{\cdot}{q}}_{3}) s i n (q_{2} + q_{3}) - \\ m_{3} l_{c 3} l_{2} (2 {\overset{\cdot}{q}}_{1} + {\overset{\cdot}{q}}_{2} + {\overset{\cdot}{q}}_{3}) {\overset{\cdot}{q}}_{3} s i n q_{3} - \\ (m_{2} l_{c 2} + m_{3} l_{2}) l_{1} (2 {\overset{\cdot}{q}}_{1} + {\overset{\cdot}{q}}_{2}) {\overset{\cdot}{q}}_{2} s i n q_{2} \\ C_{2} = (m_{2} l_{c 2} + m_{3} l_{2}) l_{1} {\overset{\cdot}{q}}_{1}^{2} s i n q_{2} + \\ m_{3} l_{c 3} l_{1} {\overset{\cdot}{q}}_{1}^{2} s i n (q_{2} + q_{3}) - \\ m_{3} l_{c 3} l_{2} (2 {\overset{\cdot}{q}}_{1} + {\overset{\cdot}{q}}_{2} + {\overset{\cdot}{q}}_{3}) {\overset{\cdot}{q}}_{3} s i n q_{3} \\ C_{3} = m_{3} l_{c 3} l_{1} {\overset{\cdot}{q}}_{1}^{2} s i n (q_{2} + q_{3}) + \\ m_{3} l_{c 3} l_{2} ({\overset{\cdot}{q}}_{1} + {\overset{\cdot}{q}}_{2})^{2} s i n q_{3} \end{array}\}

重力项G的每一行正是每个关节需要克服的在它之后所有单元翼的重力作用在它身上的分量.其中,在地面坐标系下重力项G'中的系数如下:

(7)

\begin{array}{l} G'_{1} = m_{3} g [l_{1} c o s q_{1} + l_{2} c o s (q_{1} + q_{2}) + \\ l_{c 3} c o s (q_{1} + q_{2} + q_{3})] + \\ m_{2} g [l_{1} c o s q_{1} + l_{c 2} c o s (q_{1} + q_{2})] + \\ m_{1} g l_{c 1} c o s q_{1} \\ G'_{2} = m_{3} g [l_{2} c o s (q_{1} + q_{2}) + \\ l_{c 3} c o s (q_{1} + q_{2} + q_{3})] + \\ m_{2} g [l_{c 2} c o s (q_{1} + q_{2})] \\ G'_{3} = m_{3} g [l_{c 3} c o s (q_{1} + q_{2} + q_{3})] \end{array}\}

需要将重力项转换到机体坐标系,转换矩阵计为

(8)$\boldsymbol{S}_{\theta \text { 外 }}=\left[\begin{array}{ccc}\cos \theta \cos \psi & \cos \theta \sin \psi & -\sin \theta \\\sin \theta \cos \psi \sin \phi-\sin \psi \cos \phi & \sin \theta \sin \psi \sin \phi+\cos \psi \cos \phi & \cos \theta \sin \phi \\\sin \theta \cos \psi \cos \phi+\sin \psi \sin \phi & \sin \theta \sin \psi \cos \phi-\cos \psi \sin \phi & \cos \theta \cos \phi\end{array}\right]$

式中:θ为俯仰角;ψ为偏航角;ϕ为滚转角.则重力项偏置后的表达式为

(9)$\boldsymbol{G}=\boldsymbol{S}_{\theta \varphi \phi} \boldsymbol{G}^{\prime}$

1.2 气动耦合特性

研究多体折展机翼的气动耦合特性时,主要考虑多体折展机翼作为整个浮动基转动时的力和力矩.故选择单元翼质心作为气动负载的作用点.

升力与阻力计算公式为

(10)

\begin{array}{l} D_{i} = 0.5 ρ v_{i}^{2} S_{r e f} C_{d i} \\ L_{i} = 0.5 ρ v_{i}^{2} S_{r e f} C_{l i} \end{array}\}

式中:ρ为大气密度;v_i为各单元翼在其局部机体坐标系下的速度;S_ref为单元翼参考面积;C_l为升力系数;C_d为阻力系数.基于计算流体力学方法(computational fluid dynamics, CFD)计算所得的折展机翼气动数据进行多项式代理建模,得到C_l、C_d的表达式为

(12)$\begin{array}{l}\boldsymbol{X}_{\text {body }}=\boldsymbol{S}_{\alpha \beta}^{\mathrm{T}} \boldsymbol{X}_{\text {wind }}\end{array}$

(13)$\begin{array}{l}\boldsymbol{S}_{\alpha \beta}^{\mathrm{T}}=\left|\begin{array}{ccc}\cos \alpha \cos \beta & -\cos \alpha \sin \beta & -\sin \alpha \\\sin \beta & \cos \beta & 0 \\\sin \alpha \cos \beta & -\sin \alpha \sin \beta & \cos \alpha\end{array}\right|\end{array}$

式中:X_body是机体坐标系下表达的气动力和力矩向量;X_wind是气流的坐标系下表达的气动力和力矩向量;α是迎角;β是侧滑角.

将升力和阻力转换到机体坐标系相加后得到:

(14)$\boldsymbol{F}_{i}=\left[\begin{array}{l}L_{i x} \\L_{i y} \\L_{i z}\end{array}\right]+\left[\begin{array}{l}D_{i x} \\D_{i y} \\D_{i z}\end{array}\right]$

式中:F_i为第i单元翼质心所受外力.

由于多体折展机翼只在机体坐标系y-z平面内进行折展运动,所以本文假设可以忽略气动力在机体系x轴方向上的分量.得到F_i的形式为2×1的矩阵.

在静态情况下,关节力矩与作用在单元翼上的外力达到平衡.根据笛卡尔空间中力的功应等于关节空间中力矩的功的原理,具体表达式如下:

(15)$\boldsymbol{F}^{\mathrm{T}} \delta x=\boldsymbol{\tau}^{\mathrm{T}} \delta q$

式中:x为系统的广义坐标变化.

单元翼在笛卡尔空间中的位姿,可以通过单元翼在关节空间中的位姿左乘一个和位姿相关的矩阵T(q):

(16)$x=\boldsymbol{T}(q) q$

对上式求偏导可得

(17)$\delta x=\boldsymbol{J}(q) \delta q$

J(q)即单元翼对应驱动关节的雅克比矩阵,因此可以得到:

(18)$\boldsymbol{F}^{\mathrm{T}} \boldsymbol{J} \delta q=\boldsymbol{\tau}^{\mathrm{T}} \delta q $

(19)$\boldsymbol{\tau}=\boldsymbol{J}^{\mathrm{T}} \boldsymbol{F}$

由此可以得出雅可比矩阵的转置将作用在单元翼上的气动力映射成了等效关节力矩.根据多体折展机翼的几何关系可以求得各单元翼质心处的雅各比矩阵:

(20)

\begin{array}{l} J_{1} = [\begin{array}{l} - l_{c 1} s i n q_{1} \\ l_{c 1} c o s q_{1} \end{array}] \\ J_{2} = [\begin{array}{l} - l_{1} s i n q_{1} - l_{c 2} s i n (q_{1} + q_{2}) & - l_{c 2} s i n (q_{1} + q_{2}) \\ l_{1} c o s q_{1} + l_{c 2} c o s (q_{1} + q_{2}) & l_{c 2} c o s (q_{1} + q_{2}) \end{array}] \\ J_{3} = [\begin{array}{l} - l_{1} s i n q_{1} - l_{2} s i n (q_{1} + q_{2}) - l_{c 3} s i n (q_{1} + q_{2} + q_{3}) \\ l_{1} c o s q_{1} + l_{2} c o s (q_{1} + q_{2}) + l_{c 3} c o s (q_{1} + q_{2} + q_{3}) \end{array} \dots \\ \begin{array}{l} - l_{2} s i n (q_{1} + q_{2}) - l_{c 3} s i n (q_{1} + q_{2} + q_{3}) & - l_{c 3} s i n (q_{1} + q_{2} + q_{3}) \\ l_{2} c o s (q_{1} + q_{2}) + l_{c 3} c o s (q_{1} + q_{2} + q_{3}) & l_{c 3} c o s (q_{1} + q_{2} + q_{3}) \end{array}] \end{array}\}

气动力作用于折展机翼产生了接触力的情况,通常把它转为等效的关节力矩,加入等式左侧作为模型的一部分.将式(1)更新为加入气动负载影响的表达形式:

(21)$\begin{array}{c}\boldsymbol{M}(q) \ddot{\boldsymbol{q}}+\boldsymbol{C}(q, \dot{q}) \dot{\boldsymbol{q}}+\boldsymbol{G}(q)+ \\\boldsymbol{J}^{\mathrm{T}}(q) \boldsymbol{F}(t)=\boldsymbol{\tau}(t)\end{array}$

式中:F(t)为气动负载.

在考虑单元翼受到的气动负载和重力项随机体姿态角的偏置的条件下,通过拉格朗日方程推导建立了多体折展机翼的动力学模型.动力学方程的形式体现系统是一个具有强耦合和非线性的复杂系统,系统在运动过程中,各个关节相互影响^[21].基于拉格朗日方程得到的折展机翼动力学模型,建立起了单元翼关节驱动力矩与单元翼运动参数和机械参数之间的关系.

2 控制器设计

在实际应用中,可以利用编码器获取各单元翼的角度信息.同时,通过使用跟踪微分器(TD)可以获得各单元翼折展角度的一阶和二阶导数,即单元翼的角速度和角加速度^[22].扩张状态观测器(ESO)通常被应用于非线性系统或那些具有未建模动态的线性系统中.它通过对系统状态的估计,克服了传统控制器无法处理的挑战,如模型不确定性、外部扰动以及传感器噪声等.ESO基于系统的数学模型和输出信息,利用状态观测器来估计系统的扰动状态,并将这些估计值整合到控制器中,以实现对扰动的补偿.

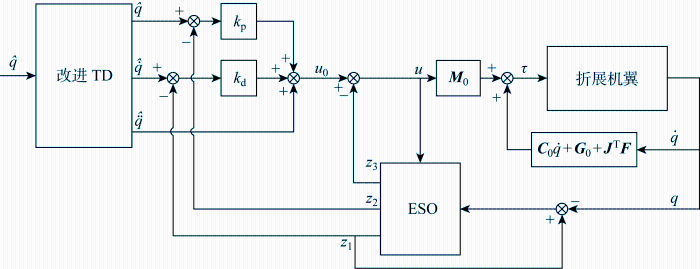
多体折展机翼的控制框图如图3所示.图中: $\hat{q}$ 为期望轨迹;k_p、k_d分别为比例系数和微分系数;u₀为初步生成的控制信号;u为经过扰动补偿后的控制信号;z₁~z₃为ESO的状态变量.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 控制器结构示意图

Fig.3 Controller structure diagram

将跟踪微分器获取的信息与ESO的观测值作差,得到线性状态误差,并将其送入反馈控制器,得到虚拟控制输入u.然后,将虚拟控制输入u与M₀相乘,并与式(6)、式(9)和式(19)计算得到的前馈项C₀ $\overset{\cdot}{q}$ +G₀+J^TF,计算出实际的折展力矩.

2.1 扩张状态观测器

针对式(21)所表示的二阶系统可以设计出连续形式的三阶ESO算法:

(22)

\begin{array}{l} {\overset{\cdot}{z}}_{1} = z_{2} - β_{i 1} e_{1} \\ {\overset{\cdot}{z}}_{2} = z_{3} - β_{i 2} f a l (e_{1}, a, δ) + u \\ {\overset{\cdot}{z}}_{3} = - β_{i 3} f a l (e_{1}, a, δ) \end{array}\}

式中:β_i1、β_i2、β_i3、a均为可调参数;δ为线性段的区间长度;e₁为跟踪误差.fal( )函数为

(23)$\operatorname{fal}(e, a, \delta)=\left\{\begin{array}{ll}\left|e_{1}\right|^{a} \operatorname{sgn} e_{1}, & \left|e_{1}\right|>\delta \\e_{1} / \delta^{1-a}, & \left|e_{1}\right| \leqslant \delta\end{array}\right.$

为了方便观测器的设计及参数整定,选择将β_i1、β_i2、β_i3配置为3ω₀、3 $ω_{0}^{2}$ 、 $ω_{0}^{3}$ 的形式,其中ω₀为扩张观测器的带宽^[23].

2.2 改进跟踪微分器

根据葛倩等^[24]设计的新型跟踪微分器,可以得到如下表达式:

(24)$\left.\begin{array}{l}\dot{x}_{1}=x_{2} \\\dot{x}_{2}=R^{2}\left[-b_{1} \tanh \left(x_{1}-u\right)-b_{2} \tanh \left(\frac{x_{2}}{R}\right)\right]\end{array}\right\}$

式中:x₁代表对输入指令的跟踪;x₂代表对输入指令的微分;b₁、b₂、R为待设计参数.

双曲正切函数可以保证微分跟踪器收敛的快速性并能有效消除输出颤振.该跟踪微分器简化了设计参数并能够提供输入信号的任意阶导数,但是忽略了提取的平滑信号滞后于输入指令的情况.周浩等^[25]所提出的调相补偿方法基于fal函数的滤波特性与相位补偿机理,从而对跟踪微分器的输出进行改造,以实现对指令信号的稳定跟踪.本文基于该方法进行了简化,对提取到的平滑信号的微分信号进行相位补偿之前使用二级跟踪微分器对微分信号进行处理,估计出微分信号的平滑信号及其微分信号.针对微分信号的调相补偿设计如下:

(25)

\begin{array}{l} x_{f 2} = c_{1} f a l (x_{2} - x_{f 2}, c_{2}, σ) \\ x_{2} = (x_{1} + λ x_{f 2}) / γ \end{array}\}

式中:x_f2表示经过fal函数处理的输出;c₁、c₂、σ为原微分信号的滤波系数;λ为预测补偿步数;γ为尺度调节参数.

2.3 状态误差反馈率(LSEF)

自抗扰控制器的控制律为

(26)u=u₀-z₃

式中:u₀的形式为虚拟控制量,即

(27)$u_{0}=\hat{\ddot{q}}+k_{\mathrm{p}}\left(\hat{q}-z_{1}\right)+k_{\mathrm{d}}\left(\hat{\dot{q}}-z_{2}\right)$

因此,折展机翼的力矩输入设计为

(28)$\begin{aligned}\tau= & \boldsymbol{M}_{0}\left[\hat{\tilde{q}}+k_{\mathrm{p}}\left(\hat{q}-z_{1}\right)+k_{\mathrm{d}}\left(\hat{\dot{q}}-z_{2}\right)-z_{3}\right]+ \\& \boldsymbol{C}_{0} \dot{q}+\boldsymbol{G}_{0}+\boldsymbol{J}^{\mathrm{T}} \boldsymbol{F}_{0}\end{aligned}$

3 稳定性分析

将式(28)代入式(21)所示的动力学方程化简为标准形式,系统表示为

(29)

\ddot{q}

=u+f

式中:f定义为动力学模型估计量误差与系统外扰之和的总扰动.在控制设计中,为了使用ESO进行扰动观测和补偿,需要将系统表示为标准的二阶形式.将上面的方程写为状态空间形式:

(30)

\begin{array}{l} {\overset{\cdot}{x}}_{1} = x_{2} \\ {\overset{\cdot}{x}}_{2} = u + f \end{array}\}

式中:定义状态变量x₁=q, x₂= $\overset{\cdot}{q}$ .

在扰动条件下,如果观测器是渐近稳定的,并且假设扰动和建模误差有界(即总扰动f有界),那么基于ADRC的结构,可以推导出整个闭环系统是渐近稳定的.因此,接下来将证明在扰动条件下观测器的渐近稳定性.

定理1 对于系统式(30),使用ESO对系统进行观测,参数满足

$\begin{array}{l}\eta>0, \quad \chi>0, \quad \zeta>0, \quad 4 \eta \zeta>\chi^{2}\left|e_{1}\right|^{\frac{1}{2}} \\3 \frac{\eta}{\chi}>2 \frac{\beta_{\mathrm{i} 1}}{\beta_{\mathrm{i} 2}}, \quad \chi \beta_{\mathrm{i} 2}\left(2 \zeta \beta_{\mathrm{i} 1}-\chi\right)>0, \quad 3 \eta>4 \zeta \beta_{\mathrm{i} 2}\end{array}$

时可以保证观测器的稳定性.

证明由式(22)可以得到此时观测器的形式为

(31)

\begin{array}{l} {\overset{\cdot}{z}}_{1} = z_{2} - β_{i 1} e_{1} \\ {\overset{\cdot}{z}}_{2} = z_{3} - β_{i 2} f a l (e_{1}, a, δ) + u \end{array}\}

将式(31)、式(30) 相减可以得到误差系统为

(32)

\begin{array}{l} {\overset{\cdot}{e}}_{1} = {\overset{\cdot}{z}}_{1} - {\overset{\cdot}{x}}_{1} = z_{2} - β_{i 1} e_{1} - x_{2} \\ {\overset{\cdot}{e}}_{2} = {\overset{\cdot}{z}}_{2} - {\overset{\cdot}{x}}_{2} = z_{3} - β_{i 2} f a l (e_{1}, a, δ) - f \end{array}\}

当系统达到稳定状态时,满足 ${\overset{\cdot}{e}}_{1}$ = ${\overset{\cdot}{e}}_{2}$ =0:

(33)$e_{3}-\beta_{i 2} \operatorname{fal}\left(e_{1}, a, \delta\right)=e_{2}-\beta_{i 1} e_{1}=0$

当|e₁|>δ, a=1/2,即误差较大时,

(34)$\operatorname{fal}\left(e_{1}, a, \delta\right)=\left|e_{1}\right|^{\frac{1}{2}} \operatorname{sgn} e_{1}$

取如下形式的李雅普诺夫函数:

(35)$\begin{aligned}V & =\eta|e_{1}|^{\frac{3}{2}}-\chi e_{1}e_{2}+\zeta e_{2}^{2}= \\ & (|e_{1}|^{\frac{3}{4}}\quad e_{2})\begin{pmatrix}\eta & -\frac{1}{2}\chi|e_{1}|^{\frac{1}{4}} \\ \\-\frac{1}{2}\chi|e_{1}|^{\frac{1}{4}} & \zeta\end{pmatrix}\times \\ & \begin{pmatrix}|e_{1}|^{\frac{3}{4}} \\ \\e_{2}\end{pmatrix}\end{aligned}$

式中:η>0; ζ>0; 4ηζ>χ² ${|e_{1}|}^{\frac{1}{2}}$ .则所选的李雅普诺夫函数是正定的,且有

(36)\begin{aligned}\dot{V}= & \frac{V}{e_{1}} \dot{e}_{1}+\frac{V}{e_{2}} \dot{e}_{2}= \\& \left(\frac{3}{2} \eta\left|e_{1}\right|^{\frac{1}{2}} \operatorname{sgn} e_{1}-\chi e_{2}\right)\left(e_{2}-\beta_{\mathrm{i} 1} e_{1}\right)+ \\& \left(-\chi e_{1}+2 \zeta e_{2}\right)\left(e_{3}-\beta_{\mathrm{i} 2}\left|e_{1}\right|^{\frac{1}{2}} \operatorname{sgn} e_{1}\right)= \\& \left(\frac{3}{2} \eta\left|e_{1}\right|^{\frac{1}{2}} \operatorname{sgn} e_{1} e_{2}-\chi e_{2}^{2}-\right. \\& \left.\frac{3}{2} \eta \beta_{\mathrm{i} 1}\left|e_{1}\right|^{\frac{3}{2}}+\chi \beta_{\mathrm{i} 1} e_{1} e_{2}\right)+ \\& \left(-\chi e_{3} e_{1}+2 e_{3} \zeta e_{2}+\chi \beta_{\mathrm{i} 2}\left|e_{1}\right|^{\frac{3}{2}}\right)- \\& 2 \zeta \beta_{\mathrm{i} 2}\left|e_{1}\right|^{\frac{1}{2}} \operatorname{sgn} e_{1} e_{2}= \\& \left(\frac{3}{2} \eta-2 \zeta \beta_{\mathrm{i} 2}+\chi \beta_{\mathrm{i} 1}\left|e_{1}\right|^{\frac{1}{2}}\right) \times \\& \left|e_{1}\right|^{-\frac{1}{4}}\left|e_{1}\right|^{\frac{3}{4}} \operatorname{sgn} e_{1} e_{2}-\chi e_{2}^{2}- \\& \left(\frac{3}{2} \eta \beta_{\mathrm{i} 1}-\chi \beta_{\mathrm{i} 2}\right)\left|e_{1}\right|^{\frac{3}{2}}+ \\& \left(-\chi e_{3} e_{1}+2 e_{3} \zeta e_{2}\right)\end{aligned}

定义:

$\begin{array}{l}C=\chi, \quad B=\left(\frac{3}{2} \eta-2 \zeta \beta_{\mathrm{i} 2}+\chi \beta_{\mathrm{i} 1}\left|e_{1}\right|^{\frac{1}{2}}\right)\left|e_{1}\right|^{-1 / 4} \\A=\frac{3}{2} \eta \beta_{\mathrm{i} 1}-\chi \beta_{\mathrm{i} 2}, \quad x_{1}=\left|e_{1}\right|^{\frac{3}{4}} \operatorname{sgn} e_{1}, \quad x_{2}=e_{2}\end{array}$

则式(36)可以表示为如下形式:

(37)$\begin{aligned}\dot{V}= & B\left|e_{1}\right|^{\frac{3}{4}} \operatorname{sgn} e_{1} e_{2}-C e_{2}^{2}-A\left|e_{1}\right|^{2\left(\frac{3}{4}\right)}+ \\& \left(\chi e_{3} e_{1}-2 \zeta e_{3} e_{2}\right)=B x_{1} x_{2}-C x_{2}^{2}- \\& A x_{1}^{2}+\left(-\chi e_{3} e_{1}+2 \zeta e_{3} e_{2}\right)\end{aligned}$

取

(38)$\left.\begin{array}{l}V_{1}=B x_{1} x_{2}-C x_{2}^{2}-A x_{1}^{2} \\V_{2}=-\chi e_{3} e_{1}+2 \zeta e_{3} e_{2}\end{array}\right\}$

当A>0, C>0, B²-4AC<0时,有V₁<0.进一步求解可得:

$\chi>0, \quad 3 \frac{\eta}{\chi}>2 \frac{\beta_{i 2}}{\beta_{i 1}}$

$\chi \beta_{\mathrm{i} 2}\left(2 \zeta \beta_{\mathrm{i} 1}-\chi\right)>0, \quad 3 \eta>4 \zeta \beta_{\mathrm{i} 2}$

时, $\overset{\cdot}{V}$ 在很大范围内都是负定函数,由此可以证明状态观测器在很大范围内都是渐近稳定的.

4 数值仿真验证与分析

为了验证本文提出的针对折展机翼变负载情况下的自抗扰控制器性能,本节进行了仿真实验,利用Simulink完成了以下实验.首先,设计了轨迹跟踪实验,旨在验证本文控制方法在轨迹跟踪方面的效果,并分析流固耦合特性对多体折展机翼控制的影响.其次,设计了标准的ADRC、PD与改进自抗扰控制器的抗扰对比实验并进行对比分析.

折展机翼操作空间为{q₁, q₂, q₃| q₁∈[-π/2, π/2], q₂∈[-π/2, π/2], q₃∈[-π/2, π/2]},设置反馈参数k_p1=600和k_d1=30,k_p2=600和k_d2=30,k_p3=800和k_d3=30.ESO的带宽设置为:ω₀₁=170,ω₀₂=170,ω₀₃=170.改进跟踪微分器的参数设置为:R₁₁=600,b₁₁=0.8,b₁₂=0.02,R₁₂=40,b₂₁=0.8,b₂₂=0.8,c₁=0.42,c₂=2,δ=1,λ=0.1,γ=1.03.

4.1 轨迹跟踪实验

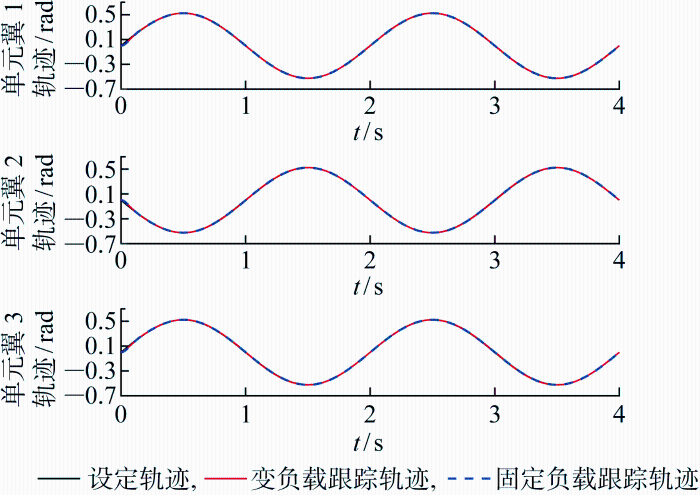
为了验证多体折展机翼在不同条件下对给定轨迹的跟踪情况,实验对比了考虑流固耦合特性与不考虑流固耦合特性两种情况下的轨迹跟踪效果.旨在深入探究负载变化对多体折展机翼控制带来的影响,并验证自抗扰控制器在解决变负载控制问题方面的优越性.在设计实验时,将折展机翼的跟踪轨迹设定为: ${\hat{q}}_{1}$ = ${\hat{q}}_{2}$ =π/6sin(πt), ${\hat{q}}_{3}$ =-π/6sin(πt),仿真时间为4 s.折展机翼分别在考虑流固耦合特性(变负载)与不考虑流固耦合特性(固定负载)条件下的轨迹跟踪曲线如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 固定负载和变负载条件下的轨迹跟踪曲线

Fig.4 Trajectory tracking curves under fixed load and variable load conditions

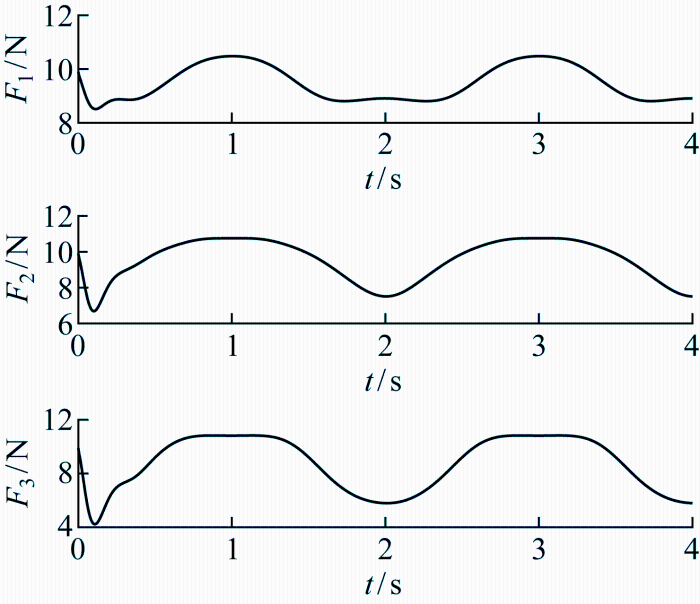
改进自抗扰控制器的引入使得无论考虑流固耦合特性(变负载)还是不考虑流固耦合特性(固定负载),折展机翼都能够实现精确的目标轨迹跟踪.图5显示了折展机翼各单元翼质心处所受气动负载的曲线,图6显示了在变负载和固定负载条件下的位置跟踪误差曲线.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 折展机翼气动负载曲线

Fig.5 Aerodynamic load curves of folding wing

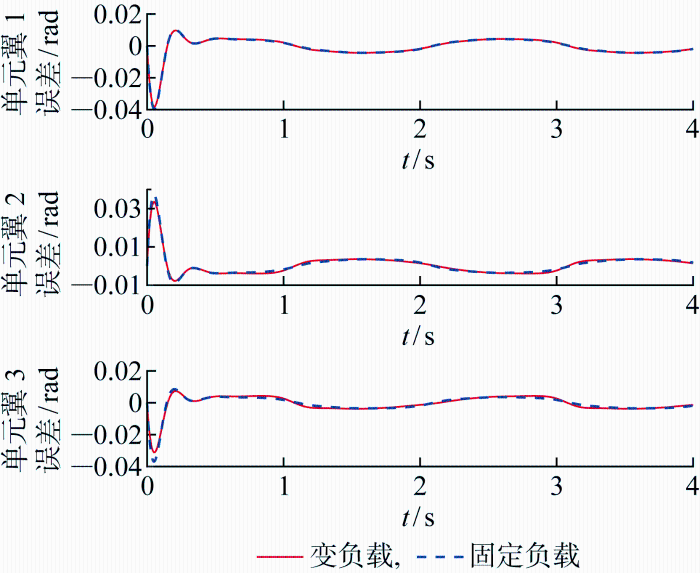
图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 变负载和固定负载情况下的位置跟踪误差曲线

Fig.6 Error curves of position tracking under variable load and fixed load conditions

在考虑流固耦合特性(变负载)和不考虑流固耦合特性(固定负载)两种条件下,跟踪误差曲线在初始阶段(0~0.5 s)存在明显波动,随后趋于平稳并几乎重合,都能保持在±0.01 rad之间.表明多体折展机翼在变负载条件下的指令跟踪性能较好,尤其在初始调整阶段过后,系统能够稳定地跟踪目标信号.图7显示了在变负载和固定负载条件下的力矩曲线.

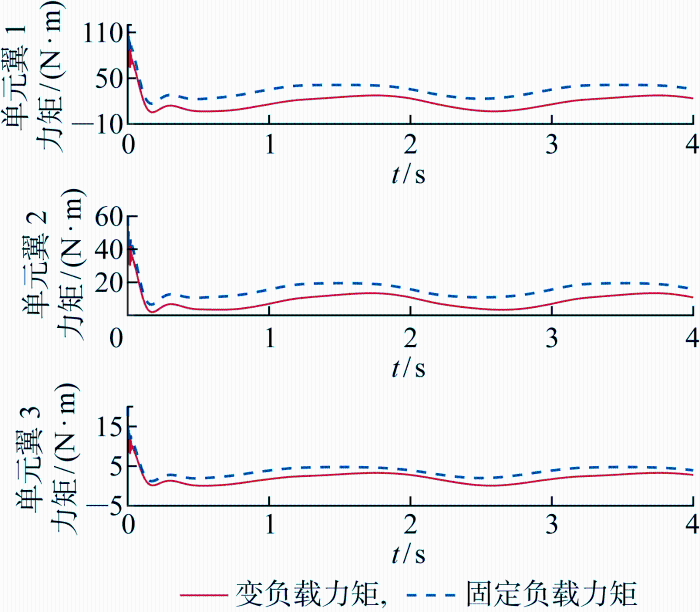
图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 变负载和固定负载情况下的力矩曲线

Fig.7 Torque curves under variable load and fixed load conditions

在变负载条件下,折展力矩在初始波动之后显著低于固定负载条件下的折展力矩.这表明气动负载(主要是升力)有效地平衡了单元翼的重力,从而减小了折展力矩.仿真结果表明,自抗扰控制能够有效应对多体折展机翼在协调倾转过程中受到的时变气动负载所带来的挑战,从而确保轨迹跟踪控制的准确性.这些结果验证了气动负载对折展力矩的影响,进一步说明在设计和控制单元翼时考虑气动负载的重要性.

4.2 抗扰对比实验

在3.1节的实验中,改进自抗扰控制取得了较好的轨迹跟踪效果.为了对比本文所设计控制方法的效果,采用与3.1节相同的控制输入,分别用改进自抗扰控制器、ADRC控制器和PD控制器在设定的同一扰动条件下对多体折展机翼进行控制.

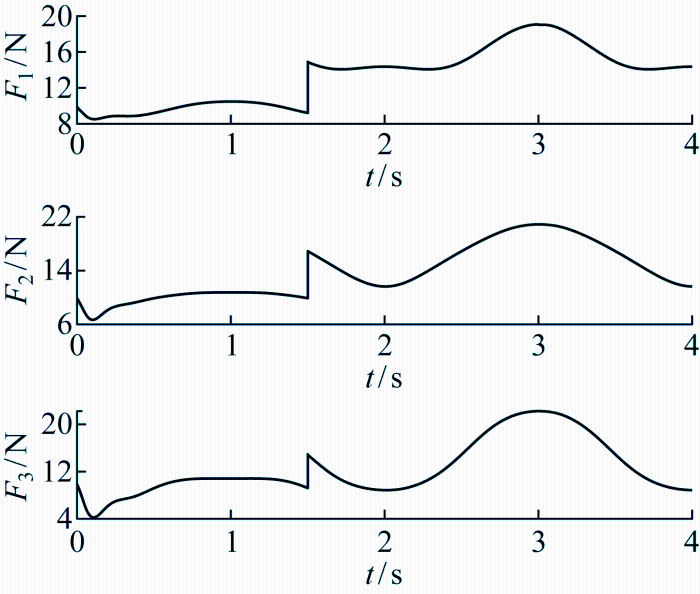
给定扰动为在1.5 s处机体全局坐标系下x轴速度v_x由10 m/s阶跃为15 m/s,另一扰动为在3 s处滚转角偏转3° 带来重力项偏置.图8展示了在加入扰动条件下各单元翼所受气动负载的变化情况.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 加入扰动条件下的气动负载

Fig.8 Aerodynamic load with disturbance

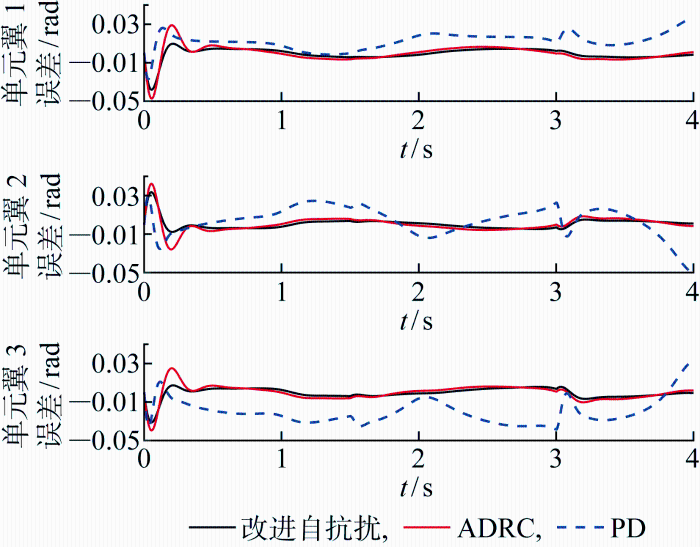
观察图中发现,在时间点1.5 s处,由于v_x阶跃,导致气动负载也产生突变.扰动条件下的位置跟踪误差曲线如图9所示.可以看到,3种控制器都可以实现对设定轨迹的跟踪,且误差较小.在受到扰动后,PD控制则会在受到外界扰动后导致跟踪误差不能有效控制在较小的区间范围之内,而自抗扰控制可以很好地将误差始终保持在±0.01 rad之间.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 加入扰动条件下的位置跟踪误差曲线

Fig.9 Error curves of position tracking under disturbed condition

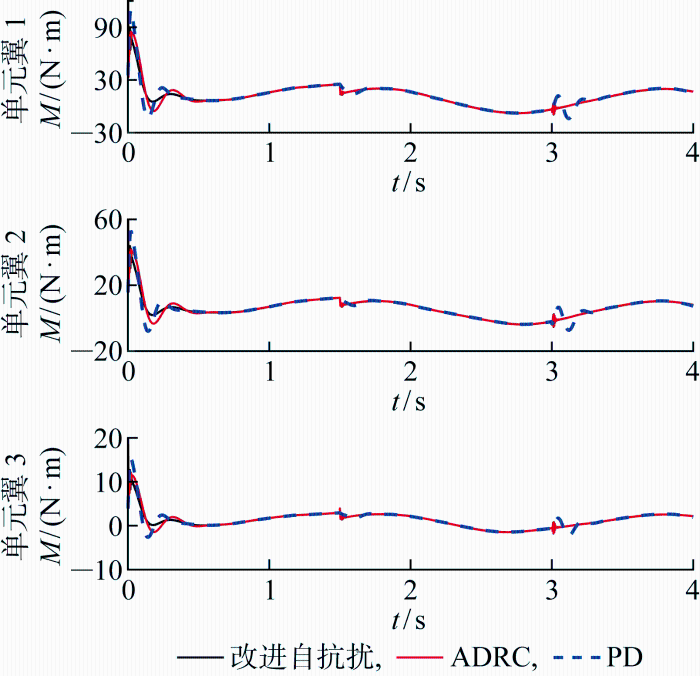
加入扰动条件下各单元翼的力矩曲线如图10所示.PD控制在某些时刻出现较大的偏差,表现出较低的鲁棒性.说明PD控制在处理变负载时的性能不如改进自抗扰控制和ADRC.改进自抗扰控制在初始阶段(0~0.5 s)的响应速度明显快于 ADRC 和PD控制,迅速达到稳定值.改进自抗扰控制的超调显著小于ADRC和PD控制,这表明其在处理负载变化时具有更优的稳定性.仿真结果表明,改进自抗扰控制方法在应对多体折展机翼的时变负载时,能够快速、稳定地减小折展力矩的波动,从而提高轨迹跟踪控制的准确性.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 加入扰动条件下的力矩曲线

Fig.10 Torque curves under disturbed condition

5 结论

本文通过对多体折展机翼在变负载条件下的轨迹跟踪控制问题进行了仿真实验,最终得出以下结论:

(1) 在协调倾转过程中,多体折展机翼必须考虑气动作用的影响,包括气动负载的变化、重力换向以及内部干扰.因此,本文所提出的变负载控制方法具有明显的优势,能够有效解决变负载对折展机翼控制所带来的影响并实现较为精确的轨迹跟踪.

(2) 本文设计的控制方法能够更好地抑制外界扰动并减少抖振,具有在初始阶段响应快、超调小的优势.当受到外界扰动时,改进自抗扰控制能够提高系统的鲁棒性,从而更好地将轨迹跟踪误差控制在较小范围内.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

冷劲松, 孙健, 刘彦菊.

智能材料和结构在变体飞行器上的应用现状与前景展望

[J]. 航空学报, 2014, 35(1): 29-45.

DOI:10.7527/S1000-6893.2013.0265 [本文引用: 1]

变体飞行器可以根据不同的飞行条件改变自身形状以获得最优的气动性能，大大提高飞行器的综合性能，是未来飞行器发展的重要方向之一。新型智能材料和结构具有驱动、变形、承载、传感等特点，为变体飞行器的设计提供了新的技术途径。本文根据不同可变形机翼结构分类，详细阐述了智能材料和结构在自适应结构、智能驱动器和变形蒙皮等方面的研究现状。变体飞行器的实现亟需解决变形/承载一体化蒙皮技术、轻质大输出力驱动器技术和自适应结构技术等关键技术，本文还对智能材料和结构未来在变体飞行器上的应用前景进行了展望。

LENG

Jinsong

, SUN

Jian

, LIU

Yanju

Application status and future prospect of smart materials and structures in morphing aircraft

[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 29-45.

DOI:10.7527/S1000-6893.2013.0265 [本文引用: 1]

Morphing aircraft can alter their shapes to achieve optimal aerodynamic performance under different flight conditions, which will greatly improve the comprehensive performance of the aircraft. Their emergence and development is one of the most important trends of future aircraft. Smart materials and structures have the properties of actuating, morphing, loading, sensing etc., which provide a new technological approach to morphing aircraft design. In this paper, research status is elaborated of smart materials and structures in adaptive structures, smart actuators, and morphing skins. Some key technologies are addressed in detail, such as deformation/loading integrative skins, lightweight high-output actuators, and adaptive structures. The future prospect of the application of smart materials and structures in morphing aircraft is also discussed.

[2]

BOWMAN

, SANDERS

, CANNON

et al.

Development of next generation morphing aircraft structures

[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Waikiki, Hawaii, USA: 2007: 1730.