仿人柔性关节耦合建模及变负载振动抑制

doi:10.16183/j.cnki.jsjtu.2021.342

仿人柔性关节耦合建模及变负载振动抑制

宋传明, 杜钦君^,, 李存贺, 罗永刚

山东理工大学电气与电子工程学院,山东淄博 255049

Coupling Modeling of Humanoid Flexible Joint and Vibration Suppression at Variable Load

SONG Chuanming, DU Qinjun^,, LI Cunhe, LUO Yonggang

School of Electrical and Electronic Engineering, Shandong University of Technology, Zibo 255049, Shandong, China

通讯作者: 杜钦君,教授,博士生导师;E-mail:duqinjun@sdut.edu.cn.

责任编辑: 孙启艳

收稿日期: 2021-09-10 修回日期: 2022-10-28 接受日期: 2021-12-8

基金资助:

国家自然科学基金项目(62076152)
山东省自然科学基金(ZR2020MF096)

Received: 2021-09-10 Revised: 2022-10-28 Accepted: 2021-12-8

作者简介 About authors

宋传明(1995-),博士生,从事仿人机器人驱动控制技术、特种电机控制技术研究.

摘要

针对仿人柔性关节负载突变引起的关节振动问题,提出一种基于状态观测器的转矩补偿控制方法.通过控制电动机输出与扰动力矩等值的转矩增量,使关节力矩快速平衡变化后的负载力矩,缩短弹性元件被动适应负载变化的振荡过程.设计了估计负载扰动转矩和电动机转速的状态观测器,并利用Lyapunov函数证明其收敛性;建立基于比例积分-积分比例(PI-IP)转速调节器的驱动系统控制结构,并将观测器的输出前馈输入到转速调节器中,提高系统抗干扰能力.仿真结果表明,与比例积分微分(PID)控制和关节力反馈比例微分(PD)控制相比,所提方法能够在负载变化后的0.6 s内使电动机转速恢复稳定,并在1 s内实现关节振动抑制,关节转速调节时间分别缩短了约1.8 s和0.9 s,有效提升系统动态调节能力.最后,通过在一体化柔性关节测试平台上的实验,验证了所提方法的有效性.

关键词： 仿人柔性关节; 变负载振动抑制; 力矩补偿控制; 状态观测器

Abstract

Aimed at the joint vibration problem caused by the load change of humanoid flexible joint, a torque compensation control method based on state observer is proposed. By controlling the motor to output a torque increment equivalent to the disturbance torque, the joint torque can quickly balance the load torque and shorten the oscillation process of the elastic element passively adapting to the load change. A state observer for estimating load disturbance torque and motor speed is designed, whose convergence is proved by the Lyapunov function. The control structure of the drive system based on the proportional integral-intergral proportional (PI-IP) speed regulator is established, and the observer output feedforward link is added to the speed regulator to improve the anti-interference ability of the system. The simulation results show that compared with proportional integral differential (PID) control and joint force feedback proportional differential (PD) control, the proposed method can restore the motor speed to stability within 0.6 s after load change and realize joint vibration suppression within 1 s. Besides, the joint speed adjustment time is shortened by about 1.8 s and 0.9 s respectively, which effectively improves the dynamic adjustment ability of the system. Finally, the effectiveness of the proposed method was verified by experiments on an integrated flexible joint testing platform.

Keywords： humanoid flexible joint; vibration suppression; torque compensation control; state observer

PDF (5177KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

宋传明, 杜钦君, 李存贺, 罗永刚. 仿人柔性关节耦合建模及变负载振动抑制[J]. 上海交通大学学报, 2023, 57(5): 601-612 doi:10.16183/j.cnki.jsjtu.2021.342

SONG Chuanming, DU Qinjun, LI Cunhe, LUO Yonggang. Coupling Modeling of Humanoid Flexible Joint and Vibration Suppression at Variable Load[J]. Journal of Shanghai Jiaotong University, 2023, 57(5): 601-612 doi:10.16183/j.cnki.jsjtu.2021.342

仿人柔性关节因其独特的关节柔性而被广泛应用于工业生产、航空航天和交互服务等领域^[1-2],这对柔性关节的控制精度提出了更高要求.然而减速器和弹簧缸等弹性元件的引入降低了关节稳定性,系统极易在外部负载突变的干扰下引发振动问题,严重影响关节控制效果^[3-4].因此,在负载变化的情况下有效解决关节振动问题,是提高仿人柔性关节控制效果的关键.

由于柔性关节是在电动机(以下简称电机)的驱动下实现指定动作,所以电机的驱动特性对关节的控制性能有重要影响.传统的建模方法通常只关注关节的机械特性,如Spong^[5]建立的柔性关节简化模型和Bridges等^[6]提出的具有摩擦项以及非线性项的模型均只考虑关节的力学因素,而将电机控制力矩视为系统外部力矩引入模型,无法体现柔性关节系统的机电耦合过程.为解决这一问题,Li等^[7]提出一种涵盖电机电气动力学的柔性关节动力学模型,建立电机输入电流、电压与电机输出转矩之间的简化模型,但该模型无法描述电机电磁耦合场的数学关系.Maiti等^[8]主要研究了刚性机器人关节系统的电气量与机械量的能量守恒问题,并构建了用于机器人开发的仿真模型,该模型不考虑关节柔性,且将系统电气部分和机械部分分开建模,难以设计有效的控制器结构.Ji等^[9]提出了控制器耦合问题,研究机电耦合对机器人控制精度的影响,但其分析方法仅针对双履带机器人,不具有普适性.文献[7 ⇓-9]提出了机器人机电耦合的概念并分析了耦合影响,但未形成具体的建模方法.在此基础上,娄军强^[10]完善了耦合作用下关节驱动电机输入电流到输出转速的传递模型.鞠锦勇^[11]则进一步提出一种针对具有臂杆柔性的直角操作臂的机电耦合建模方法,虽然其模型不适用于仿人柔性关节系统,但是基于Lagrange-Maxwell方程的建模方法具有一定的普适意义.

早期对柔性关节振动抑制方法的研究多采用变刚度结构(VSA)的被动控制或附加传感器的主动控制^[12-13],这使关节结构复杂度增加、体积增大.目前则重点研究基于状态反馈的末端位置控制、阻抗控制、力矩反馈控制等方法.Liu等^[14]提出一种VSA力矩控制方法,通过调整输出力矩实现不同负载状况下的关节刚度变化;Yoo等^[15]提出一种采用观测器反馈连杆侧运动信息的关节力矩控制方法,通过补偿弹簧形变实现振动抑制.但这两类方法仅针对Kelly等^[16]提出基于重力矩补偿的比例-微分(PD)控制方法,解决了负载变化导致的手臂平衡位置偏差问题;Gupta等^[17]设计了轮式机器人的3级轨迹跟踪控制器,并采用模型逆运算实现对电机转矩的估算;Chen等^[18]设计了一种用于踝关节的力矩补偿比例-积分(PI)控制器,实现了不同倾角时的力矩稳定输出.虽然上述方法存在未考虑关节柔性、应用对象具有局限性以及仅考虑稳态误差而忽略动态性能等问题,但采用力矩补偿实现振动抑制的方法具有推广意义.实现力矩补偿控制的前提,是对外部扰动力矩进行精确估计,并准确跟踪系统状态变化.Song等^[19]提出一种采用负载力矩观测器估计电机输出转矩的方法,判断机械臂是否发生碰撞振动.Cui等^[20]则提出采用扩展状态观测器的方法,估计水下机器人的不可测量线速度和扰动力矩.Yabuki等^[21]提出一种基于瞬时状态观测器的关节加速度控制方法,采用状态反馈的积分-比例微分(I-PD)控制器实现对关节力矩的稳定控制.王漪梦等^[22]提出一种基于干扰观测器的扰动补偿方法,并设计双位置闭环控制器来提高机械臂跟踪精度.Cheng等^[23]提出一种利用非线性干扰观测器估计外部扰动的方法,并采用积分反步法设计关节跟踪控制器,提高了系统鲁棒性.这些研究成果为关节振动抑制提供了有效的状态跟踪和扰动估计方法.

针对关节复杂的机电耦合特性,建立了基于Lagrange-Maxwell方程的仿人柔性关节系统机电耦合模型,分析了关节柔性机理及负载变化时关节的振动机理;提出一种基于观测器的负载转矩补偿控制方法,并给出了负载变化后的电机期望转角增量控制方程.设计了估计电机输出转速和负载转矩的状态观测器,实现对期望转角计算过程中负载扰动转矩的准确测量;同时建立基于前馈补偿和比例积分-积分比例(PI-IP)转速调节器的关节驱动系统闭环控制结构,提高系统控制精度和抗干扰能力.

1 仿人柔性关节的物理结构与耦合模型

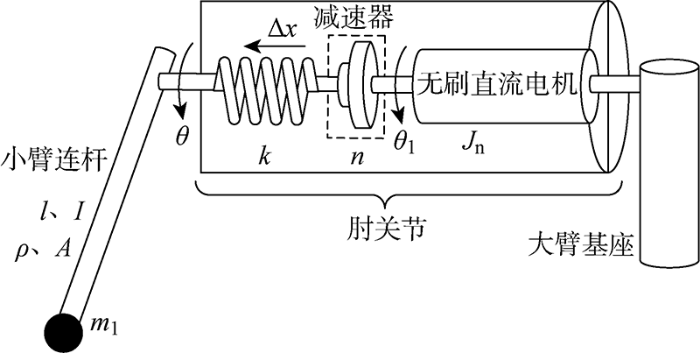
仿人机械臂的执行机构由肩关节、大臂、肘关节、小臂和腕关节等构成.以大臂为基座、小臂为执行机构,对肘部关节开展单关节变负载振动抑制的研究.图1所示为仿人柔性关节机械臂的肘关节物理模型,主要包括无刷直流电机(BLDCM)、谐波减速器、弹性元件以及与肘关节相连接的小臂连杆.假定小臂绕连杆一端的轴旋转,且运动平面与电机输出轴方向垂直.图中,θ₁为柔性关节的电机输出转角;θ为手臂连杆的输出转角;n为减速器的减速比;k为关节刚度系数;Δx为弹簧旋进量;J_n为电机转子转动惯量;m_l为手臂端负载质量;I为手臂转动惯量;l、ρ和A分别为手臂连杆的长度、材料密度和横截面积.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 仿人柔性关节机械臂的肘关节物理模型

Fig.1 Physical model of elbow joint of humanoid flexible joint robotic arm

采用Lagrange-Maxwell方程对关节进行建模.通过构造关节驱动电机的磁场广义坐标,将驱动电机磁场能引入关节动力学方程中,进而建立控制量输入到机械量输出的完整机电耦合模型.定义系统的广义坐标如表1所示.电磁部分包括BLDCM的三相定子电量和转子磁链,机械传动部分包括电机转角和手臂转角.表1中,q_a、q_b和q_c为电机三相定子电量;i_a、i_b和i_c为三相定子绕组电流;ψ_r为转子磁链;A_j (j=1, 2, 3, 4, 5)为广义坐标; $Q_{j}^{A}$ 为对应于广义坐标A_j的非保守广义力;F_j为与广义坐标相对应的坐标广义力; ${\overset{\cdot}{A}}_{j}$ 、 ${\overset{\cdot}{θ}}_{1}$ 和 $\overset{\cdot}{θ}$ 分别为A_j、θ₁和θ对时间t的导数,后文中均以“ $\overset{\cdot}{}$ ”表示各函数、变量对时间t的导数.

表1 广义坐标定义

Tab.1 Definition of generalized coordinates

广义坐标与广义力标识	电磁部分				机械传动部分
	定子			转子	电机转角 j=4	手臂转角 j=5
	j=1	j=2	j=3	转子	电机转角 j=4	手臂转角 j=5
A_j	q_a	q_b	q_c	ψ_r	θ₁	θ
${\overset{\cdot}{A}}_{j}$	i_a	i_b	i_c	—	${\overset{\cdot}{θ}}_{1}$	$\overset{\cdot}{θ}$
$Q_{j}^{A}$	F₁	F₂	F₃	—	F₄	F₅

注:表中“—”表示无法对转子磁链进行求导,并找到其对应的广义力.

新窗口打开| 下载CSV

Lagrange-Maxwell方程的广义坐标形式^[11,24]如下:

(1)

\frac{d}{d t} (\frac{\partial L}{\partial {\overset{\cdot}{A}}_{j}})

\frac{\partial L}{\partial A_{j}}

\frac{\partial H}{\partial {\overset{\cdot}{A}}_{j}}

Q_{j}^{A}

j=1, 2, 3, 4, 5

式中:L为Lagrange-Maxwell算子;H为系统耗散函数.算子L的一般形式可以表示为

(2)L=T+W_m-E_p

式中:T为系统动能;W_m为驱动电机磁场能;E_p为系统势能.

驱动与传动部分的动能T_dt主要包括电机转子动能、减速器和输出轴动能;手臂端的动能T_arm主要包括连杆动能和负载动能.系统的势能E_p主要包括弹簧的弹性势能和关节及负载的重力势能,由于重力势能只改变关节的最终平衡位置,对关节的振动状态没有主动影响,所以重力势能可忽略.系统的电磁能W_m主要包括BLDCM的定子电流产生的磁能W_m₁以及转子磁链与定子电流相互作用产生的磁能W_m₂.式(2)中的各项可以表示为

T=T_dt+T_arm= $\frac{1}{2}$ J_n ${\overset{\cdot}{θ}}_{1}^{2}$ + $\frac{1}{2}$ J_r ${(\frac{1}{n} {\overset{\cdot}{θ}}_{1})}^{2}$ + $(\frac{1}{6} ρ A l^{2} + \frac{1}{2} m_{l}) {\overset{\cdot}{θ}}^{2}$

E_p= $\frac{1}{2}$ k ${(\frac{1}{n} θ_{1} - θ)}^{2}$

(3)W_m=W_m1+W_m2=

\frac{1}{2}

L_a

i_{a}^{2}

\frac{1}{2}

L_b

i_{b}^{2}

\frac{1}{2}

L_c

i_{c}^{2}

+Mi_ai_b+Mi_ai_c+Mi_bi_c+i_aψ_r(θ₁)+i_bψ_r

(θ_{1} - \frac{2}{3} π)

+i_cψ_r

(θ_{1} + \frac{2}{3} π)

其中:J_r为减速器及输出轴惯量;L_a、L_b和L_c为电机三相绕组自感;M为三相绕组互感;ψ_r随永磁体磁场在气隙中的分布而变化.BLDCM的转子气隙磁场在定子表面呈梯形分布,当转子逆时针转动时,以a相为基准,假设转子与a相夹角为β,则a相磁链可以表示为

ψ_r(β)=NS $\int_{- \frac{π}{2} + β}^{\frac{π}{2} + β}$ B(θ₁)dθ₁

其中:B(θ₁)为转子磁体在气隙径向的磁密分布;N为绕组匝数;S为定子内表面绕组面积.a相磁链ψ_r(β)对时间t求导即可得到a相绕组反电动势e_a,同理可得b、c相绕组反电动势e_b、e_c.

系统耗散能函数H主要包括电机绕组发热产生的耗散能H_e、转子旋转摩擦耗散能 $H_{θ_{1}}$ 和手臂连杆末端旋转摩擦产生的耗散能H_θ:

(4)H=H_e+

H_{θ_{1}}

+H_θ=

\frac{1}{2}

R_a

i_{a}^{2}

\frac{1}{2}

R_b

i_{b}^{2}

\frac{1}{2}

R_c

i_{c}^{2}

\frac{1}{2}

B_v

{\overset{\cdot}{θ}}_{1}^{2}

\frac{1}{2}

D_f

{\overset{\cdot}{θ}}^{2}

式中:R_a、R_b和R_c为电枢绕组的等效电阻;B_v为电机电磁阻尼系数;D_f为关节机械阻尼系数.

根据式(3),算子L可表示为

(5)L=

\frac{1}{2}

J_n

{\overset{\cdot}{θ}}_{1}^{2}

\frac{1}{2}

J_r

{(\frac{1}{n} {\overset{\cdot}{θ}}_{1})}^{2}

(\frac{1}{6} ρ A l^{2} + \frac{1}{2} m_{l}) {\overset{\cdot}{θ}}^{2}

\frac{1}{2}

L_a

i_{a}^{2}

\frac{1}{2}

L_b

i_{b}^{2}

\frac{1}{2}

L_c

i_{c}^{2}

+Mi_ai_b+Mi_ai_c+ Mi_bi_c+i_aψ_r(θ₁)+i_bψ_r

(θ_{1} - \frac{2}{3} π)

+i_cψ_r

(θ_{1} + \frac{2}{3} π)

\frac{1}{2}

{(\frac{1}{n} θ_{1} - θ)}^{2}

由式(5)求解式(1)各项,取广义坐标为a相定子电量,即A₁=q_a,则有:

(6)

\begin{array}{l} \frac{\partial L}{\partial A_{1}} = \frac{\partial L}{\partial q_{a}} = 0 \\ \frac{\partial L}{\partial {\overset{\cdot}{A}}_{1}} = \frac{\partial L}{\partial i_{a}} = L_{a} i_{a} + M i_{b} + M i_{c} + ψ_{r} (θ_{1}) \\ \frac{d}{d t} (\frac{\partial L}{\partial {\overset{\cdot}{A}}_{1}}) = L_{a} \frac{d i_{a}}{d t} + M \frac{d i_{b}}{d t} + M \frac{d i_{c}}{d t} + e_{a} \\ \frac{\partial H}{\partial {\overset{\cdot}{A}}_{1}} = \frac{\partial H}{\partial i_{a}} = R_{a} i_{a} \end{array}\}

对电机而言,非保守广义力分别对应电机三相电压u_a、u_b和u_c,即F₁对应u_a,F₂对应u_b,F₃对应u_c.所以将式(6)写作式(1)的形式,即可表示驱动电机a相绕组电压方程,取广义坐标为b和c相的定子电量时,同理可得b和c相的电压方程:

(7)

\begin{array}{l} u_{a} = L_{a} \frac{d i_{a}}{d t} + M \frac{d i_{b}}{d t} + M \frac{d i_{c}}{d t} + R_{a} i_{a} + e_{a} \\ u_{b} = L_{b} \frac{d i_{b}}{d t} + M \frac{d i_{a}}{d t} + M \frac{d i_{c}}{d t} + e_{b} + R_{b} i_{b} \\ u_{c} = L_{c} \frac{d i_{c}}{d t} + M \frac{d i_{a}}{d t} + M \frac{d i_{b}}{d t} + e_{c} + R_{c} i_{c} \end{array}\}

与式(6)的推导过程相同,当广义坐标取电机输出转角θ₁时,可以得到柔性关节系统驱动与传动部分的转矩方程:

(8)

(J_{n} + \frac{1}{n^{2}} J_{r}) {\ddot{θ}}_{1}

-i_aψ_r(

{\overset{\cdot}{θ}}_{1}

)-i_bψ_r

({\overset{\cdot}{θ}}_{1} - \frac{2}{3} π)

-i_cψ_r

({\overset{\cdot}{θ}}_{1} + \frac{2}{3} π)

\frac{k}{n} (\frac{1}{n} θ_{1} - θ)

+B_v

{\overset{\cdot}{θ}}_{1}

式中: ${\ddot{θ}}_{1}$ 为电机转子加速度; $(J_{n} + \frac{1}{n^{2}} J_{r}) {\ddot{θ}}_{1}$ 为驱动环节机械部分的加速力矩.在忽略耗散能的前提下,当系统保持匀速转动时,加速力矩为0,电机经减速器输出的电磁力矩与关节弹性力矩保持平衡.

当广义坐标取手臂转角θ时,同理可得手臂部分的运动方程:

(9)

(\frac{1}{3} ρ A l^{2} + m_{l}) \ddot{θ}

+D_f

\overset{\cdot}{θ}

-k

(\frac{1}{n} θ_{1} - θ)

τ_{m_{l}}

式中: $\ddot{θ}$ 为关节加速度; $(\frac{1}{3} ρ A l^{2} + m_{l}) \ddot{θ}$ 为连杆及负载的加速力矩; $τ_{m_{l}}$ 为连杆外部作用力矩,即末端负载重力矩.在忽略耗散能的前提下,当外部负载保持不变时,关节弹性力矩与负载重力矩和为0,连杆保持静止或匀速运动.式(7)~(9)共同构成了仿人柔性手臂系统机电耦合模型:

(10)

\begin{array}{l} u_{a} = L_{a} \frac{d i_{a}}{d t} + M \frac{d i_{b}}{d t} + M \frac{d i_{c}}{d t} + R_{a} i_{a} + e_{a} \\ u_{b} = L_{b} \frac{d i_{b}}{d t} + M \frac{d i_{a}}{d t} + M \frac{d i_{c}}{d t} + e_{b} + R_{b} i_{b} \\ u_{c} = L_{c} \frac{d i_{c}}{d t} + M \frac{d i_{a}}{d t} + M \frac{d i_{b}}{d t} + e_{c} + R_{c} i_{c} \\ (J_{n} + \frac{1}{n^{2}} J_{r}) {\ddot{θ}}_{1} - i_{a} ψ_{r} ({\overset{\cdot}{θ}}_{1}) - i_{b} ψ_{r} ({\overset{\cdot}{θ}}_{1} - \frac{2}{3} π) - \\ i_{c} ψ_{r} ({\overset{\cdot}{θ}}_{1} + \frac{2}{3} π) + \frac{k}{n} (\frac{1}{n} θ_{1} - θ) + B_{v} {\overset{\cdot}{θ}}_{1} = 0 \\ (\frac{1}{3} ρ A l^{2} + m_{l}) \ddot{θ} + D_{f} \overset{\cdot}{θ} - k (\frac{1}{n} θ_{1} - θ) = τ_{m_{l}} \end{array}\}

该模型包括输入电流建立的磁场电气方程以及关节驱动力矩带动手臂运动的机械方程,完整描述了关节系统机电耦合过程.模型式(10)中第4和第5个方程描述了柔性关节的动力学特性.用τ_e等效替换模型中的驱动电机电磁力项,可以得到简化的关节动力学方程:

(11)

\begin{array}{l} (J_{n} + \frac{1}{n^{2}} J_{r}) {\ddot{θ}}_{1} + \frac{k}{n} (\frac{1}{n} θ_{1} - θ) + B_{v} {\overset{\cdot}{θ}}_{1} = τ_{e} \\ (\frac{1}{3} ρ A l^{2} + m_{l}) \ddot{θ} + D_{f} \overset{\cdot}{θ} - k (\frac{1}{n} θ_{1} - θ) = τ_{m_{l}} \end{array}\}

根据模型式(11)可以得出:

(1) 弹性元件的引入使手臂转角滞后于减速器输出转角,电机的输出动能转化为弹簧的弹性势能,且这部分能量在为手臂连杆提供驱动力矩的同时,减缓了手臂对电机输出的响应速度,实现了近似柔性.

(2) 手臂的运动状态同时受到负载重力矩和关节弹性力矩的影响,负载力矩的变化将使关节运动产生加速力矩,同时受运动惯性影响,关节的加速运动又将进一步改变关节弹性力矩,进而引起系统振动.如果此时电机输出转矩不能主动调整关节运动状态,手臂将呈现出与弹性元件相似的二阶振荡状态.

综上所述,在负载力矩变化打破系统力矩平衡状态后,所引起的关节加速运动与关节弹性的相互作用是导致关节产生振动现象的主要原因.

2 基于状态观测器的负载转矩补偿控制

关节弹性力矩对负载力矩变化的被动适应过程是造成关节振动的核心原因.提出一种负载力矩补偿控制方法,通过电动机输出与负载力矩变化量等值的转矩增量,实现对关节弹性力矩的主动调节,使关节力矩能够快速平衡变化后的负载力矩,缩短振动过程.

2.1 控制方程设计

根据式(9)已知,当手臂处于匀速运动时,手臂转角加速度 $\ddot{θ}$ 为0,此时手臂的运动方程可以表示如下:

(12)D_f

\overset{\cdot}{θ}

-k

(\frac{1}{n} θ_{1} - θ)

τ_{m_{l}}

当产生负载力矩增量Δ $τ_{m_{l}}$ 时,期望的控制目标为手臂转角加速度为0,手臂转角无变化,即 $\ddot{θ}$ =0、Δθ=0.因此,期望的手臂运动方程表示为

(13)D_f

\overset{\cdot}{θ}

[k (\frac{1}{n} θ_{1} - θ) + Δ τ_{k}]

τ_{m_{l}}

+Δ

τ_{m_{l}}

式中:Δτ_k为应对负载变化而产生的转矩弹簧弹性力矩增量.式(13)表明,负载变化后在系统新的力矩平衡过程中,弹簧的弹性力矩变化量可直接抵消负载力矩的变化,从而避免由负载力矩变化导致的连杆加速力矩的动态平衡过程,实现避免手臂抖动的目的.

由式(11)已知,弹簧弹性力矩同时受手臂末端负载和电机输出端的影响,若令Δθ=0,则Δτ_k完全由电机输出转角增量提供,表示为

(14)Δτ_k=k

\frac{Δ θ_{1}}{n}

=-Δ

τ_{m_{l}}

式中:Δθ₁为驱动电机输出转角的增量;Δθ₁/n为电机经减速器后的输出转角增量.

将式(14)带入式(13),可得:

(15)D_f

\overset{\cdot}{θ}

-k

[(\frac{1}{n} θ_{1} + \frac{1}{n} Δ θ_{1}) - θ]

τ_{m_{l}}

+Δ

τ_{m_{l}}

根据式(15),已知负载转矩增量Δ $τ_{m_{l}}$ ,即可得到能够补偿负载力矩增量的电机期望转角增量Δθ₁,并将其作为给定信号控制驱动电机.当关节负载发生突变时,电机输出的转角增量Δθ₁能够使关节产生弹性力矩增量Δτ_k,而根据式(14)已知,Δτ_k与Δ $τ_{m_{l}}$ 大小相等、方向相反,能够快速弥补负载突变后关节弹性力矩与负载力矩之间的差值.这表明,在不改变关节转角θ的情况下,驱动电机通过主动输出Δθ₁,实现对关节力矩的调整,使关节力矩能够快速平衡变化后的负载力矩.

该方法理论上可以在维持手臂连杆转动角度和角加速度不变的情况下,使变负载系统达到新的平衡,并且在负载突变引起的手臂稳态情况下,避免角加速度的突变和转矩弹簧不可控的阻尼振荡,进而抑制负载突变时柔性关节机械臂的振动问题.

2.2 观测器设计

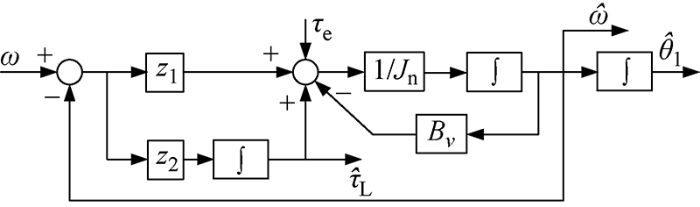
根据方程式(15)可知,为了计算期望的电机转角增量Δθ₁,需要在负载突变后获取准确的电机负载转矩值和实际输出转速值.设计合理的转速、转矩观测器能够有效避免因关节内部空间小而导致的检测困难、检测精度低的问题.

已知BLDCM运动方程为

(16)τ_e=J_n

\frac{d ω}{d t}

+B_vω+τ_L

式中:τ_L为电机负载转矩;ω为电机输出转速.

取ω和τ_L为状态变量,将式(16)写作矩阵形式:

(17)

\begin{array}{l} \overset{\cdot}{x} = A x + B u \\ y = C x \end{array}\}

式中:x= ${[\begin{array}{l} ω & τ_{L} \end{array}]}^{T}$ ,y=ω,u=τ_e,

A= $[\begin{array}{l} - \frac{B_{v}}{J_{n}} & - \frac{1}{J_{n}} \\ 0 & 0 \end{array}]$ ,B= ${[\begin{array}{l} \frac{1}{J_{n}} & 0 \end{array}]}^{T}$ ,C= $[\begin{array}{l} 1 & 0 \end{array}]$ .

构造状态观测器为

(18)

\overset{\cdot}{\hat{x}}

\hat{A x}

+Bu+Z(y-

\hat{y}

)

(19)

\hat{y}

\hat{C x}

式中:“^”为对应量的估计值;Z= ${[\begin{array}{l} z_{1} & z_{2} \end{array}]}^{T}$ 为观测器比例增益矩阵.

根据式(17)和(19),观测器方程式(18)可以改写为

(20)

[\begin{array}{l} \overset{\cdot}{\hat{ω}} \\ {\overset{\cdot}{\hat{τ}}}_{L} \end{array}]

[\begin{array}{l} - B_{v} J_{n} \hat{ω} - \frac{1}{J_{n}} {\hat{τ}}_{L} + \frac{1}{J_{n}} τ_{e} + z_{1} (ω - \hat{ω}) \\ z_{2} (ω - \hat{ω}) \end{array}]

根据式(20),观测器的物理结构如图2所示.图2中,∫表示对输入信号进行积分.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 状态观测器结构

Fig.2 Structure of state observer

定义状态误差 $\tilde{x}$ =x- $\hat{x}$ ,转速估计误差 $\tilde{ω}$ = ω- $\hat{ω}$ ,转矩估计误差 ${\tilde{τ}}_{L}$ =τ_L- ${\hat{τ}}_{L}$ .由式(17)~(19)可得 $\overset{\cdot}{\tilde{x}}$ = $\tilde{A x}$ - $\tilde{Z C x}$ =(A-ZC) $\tilde{x}$ ,即:

(21)

[\begin{array}{l} \overset{\cdot}{\tilde{ω}} \\ {\overset{\cdot}{\tilde{τ}}}_{L} \end{array}]

[\begin{array}{l} - \frac{B_{v}}{J_{n}} - z_{1} & - \frac{1}{J_{n}} \\ - z_{2} & 0 \end{array}] [\begin{array}{l} \tilde{ω} \\ {\tilde{τ}}_{L} \end{array}]

定义Lyapunov函数为

(22)V(

\tilde{x}

{\tilde{x}}^{T} \tilde{P x}

式中:P为对称正定矩阵,则有

(23)

\overset{\cdot}{V}

(

\tilde{x}

{\overset{\cdot}{\tilde{x}}}^{T} \tilde{P x}

{\tilde{x}}^{T}

\overset{\cdot}{\tilde{x}}

{[(A - Z C) \tilde{x}]}^{T} \tilde{P x}

{\tilde{x}}^{T}

[(A - Z C) \tilde{x}]

{\tilde{x}}^{T} [{(A - Z C)}^{T} P + P (A - Z C)] \tilde{x}

由于矩阵P正定,则V( $\tilde{x}$ )正定.若要求观测器的状态观测误差收敛至0,则需要 $\overset{\cdot}{V}$ ( $\tilde{x}$ )负定,即选取合适的矩阵Z,使矩阵(A-ZC)^TP+P(A-ZC)负定.令:

(24)(A-ZC)^TP+P(A-ZC)=-Q

式中:Q为正定对称矩阵,取Q= $[\begin{array}{l} 1 & 0 \\ 0 & 1 \end{array}]$ ;取P= $[\begin{array}{l} p_{11} & p_{12} \\ p_{21} & p_{22} \end{array}]$ ,且p₁₂=p₂₁.则有

(25)(A-ZC)^TP+P(A-ZC)=

[\begin{array}{l} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}]

[\begin{array}{l} - 1 & 0 \\ 0 & - 1 \end{array}]

其中:

a₁₁=-2p₁₁ $(\frac{B_{v}}{J_{n}} + z_{1})$ -z₂(p₁₂+p₂₁)

a₁₂=-p₁₁ $\frac{1}{J_{n}}$ - $(\frac{B_{v}}{J_{n}} + z_{1})$ p₁₂-z₂p₂₂

a₂₁=-p₁₁ $\frac{1}{J_{n}}$ - $(\frac{B_{v}}{J_{n}} + z_{1})$ p₂₁-z₂p₂₂

a₂₂=-p₁₂ $\frac{1}{J_{n}}$ -p₂₁ $\frac{1}{J_{n}}$

所以有

(26)P=

[\begin{array}{l} \frac{1 - J_{n} z_{2}}{2 (\frac{B_{v}}{J_{n}} + z_{1})} & \frac{J_{n}}{2} \\ \frac{J_{n}}{2} & - \frac{(J_{n} z_{1} + B_{v})^{2} + (1 - J_{n} z_{2})}{2 z_{2} (B_{v} + J_{n} z_{1})} \end{array}]

如式(26)所示,通过选取合适的增益矩阵Z,可以找到对称正定矩阵P,使V( $\tilde{x}$ )正定,且 $\overset{\cdot}{V}$ ( $\tilde{x}$ )负定.此时,状态观测器是渐进稳定的,即观测器的输出 $\tilde{x}$ 收敛于系统实际输出x.根据式(21)可知系统的极点为

s_1,2=- $\frac{1}{2} (\frac{B_{v}}{J_{n}} + z_{1})$ ± $\frac{1}{2} \sqrt{{(\frac{B_{v}}{J_{n}} + z_{1})}^{2} + \frac{4 z_{2}}{J_{n}}}$

当极点位于复频域的左半平面时系统稳定,令s₁=s₂=v,v是任意给定的正实数,则有z₁=2v- $\frac{B_{v}}{J_{n}}$ ,z₂=-J_nv². v的大小决定了估计值的收敛速度.

2.3 转速调节器设计

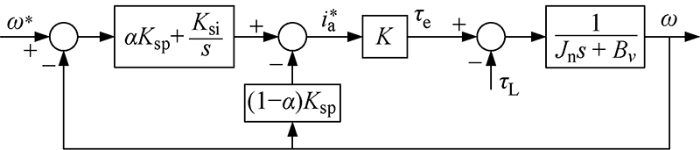
在得到负载转矩增量并计算出期望的电机转角增量后,转速调节器将给定的增量信号输出为电机的控制信号.IP控制器是PI控制器的一种改型.根据文献[25-26],在采用相同的控制器参数时,IP控制器相较于PI控制器具有更大的带宽和更小的超调量,但在跟踪连续变化的输入信号时,PI控制器具有更小的跟踪误差.因此,综合利用PI和IP控制器的优势,采用PI-IP控制器作为转速调节器的主要结构.PI-IP控制器的结构如图3所示.图3中,ω^*为给定转速; $i_{a}^{*}$ 为电机电枢电流的期望值;s为经过拉普拉斯变换后的复频域变量;K_sp和K_si分别为调节器的比例系数和积分系数;K为转矩系数,当忽略电枢感应和其他因素时,可以认为直流电机的输出转矩与电枢电流成正比.混合因数α∈[0,1]为PI控制器和IP控制器的混合因子,当α= 1时,转速调节器为PI调节器;当α= 0时,转速调节器为IP调节器.所以,当α减小时,会增强IP控制器的控制作用,能够有效降低响应超调;当α增大时,PI控制器的控制作用会有所增强,可以减小跟踪误差.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 PI-IP控制器结构

Fig.3 Structure of PI-IP controller

根据图3,输出转速的传递函数为

(27)

\frac{ω (s)}{ω^{*} (s)}

\frac{K (α K_{s p} s + K_{s i})}{J_{n} s^{2} + (B_{v} + K K_{s p}) s + K K_{s i}}

将图3做等效替换可以得到图4.根据图4,给定转速信号在经过低通滤波环节的优化后输入到闭环调节器,而负载转矩的响应通过闭环调节器得到调节.因此,PI-IP控制器可以同时提高信号的跟踪能力和抗干扰能力.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 PI-IP控制器的等效结构

Fig.4 Equivalent structure of PI-IP controller

综上所述,混合因数α的引入使控制系统更灵活应对仿人柔性关节系统复杂的控制要求,通过选择合适的α值可以调节PI和IP控制器的占比,进而获得期望的动态性能.而且,PI-IP控制器抗干扰能力强、跟踪精度高、结构简单稳定性好,不会给控制系统带来额外的不利因素,适用于仿人柔性关节系统.

2.4 控制器结构设计

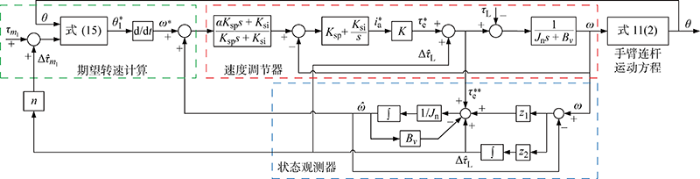
根据前述分析,给出柔性关节驱动系统控制器结构框图,如图5所示.图5中,状态观测器环节用于观测负载扰动转矩,因此,将扰动观测器的前馈输入量由参考转矩 $τ_{e}^{*}$ 调整为 $τ_{e}^{* *}$ ,其表示 $τ_{e}^{*}$ 与补偿扰动转矩Δ ${\hat{τ}}_{L}$ 之和,观测器增益矩阵的整定方法不变.此外,期望转速计算环节中,方程式(15)需要手臂端负载的变化量,因此在观测器输出的扰动转矩估计值后面增加增益系数,即减速比n.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 关节驱动系统控制框图

Fig.5 Control block diagram of joint drive system

图5所示的控制器结构由PI-IP转速调节器实现电机调速;由状态观测器对电机输出转速及电机负载扰动转矩进行估计,并将转矩估计值代入到方程式(15)中,计算负载变化后的期望转角增量;计算得到的期望转速先与观测器得到的转速估计值进行比较,再将比较值经过低通滤波器处理后与转速实际值进行比较,有助于提高转速调节精度.同时,将观测得到的扰动转矩估计值反馈到转速调节器中,有助于提高系统的抗干扰能力.此外,图5中的式11(2)指式(11)中的第二个方程,其为手臂连杆的运动方程.

3 仿真与实验验证

为了验证所提方法的有效性,根据图5所示控制系统结构搭建仿真模型,分别对观测器的跟踪效果、控制器的调节能力进行仿真验证.关节硬件参数如表2所示.

表2 柔性关节驱动系统参数

Tab.2 System parameters of flexible joint drive system

参数	设定值
驱动电机额定电压/V	12
驱动电机额定转速/(r·min^-1)	1200
电枢绕组等效电感/mH	1.4
电枢绕组等效电阻/Ω	24
转子转动惯量/(kg·m²)	0.062
手臂转动惯量/(kg·m²)	0.45
电机电磁阻尼系数/(N·m·s·rad^-1)	0.2
关节机械阻尼系数/(N·m·s·rad^-1)	0.5
关节刚度系数/(N·m·rad^-1)	10
减速器减速比	100∶1

新窗口打开| 下载CSV

3.1 扰动观测器仿真

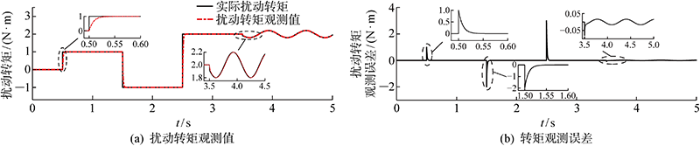
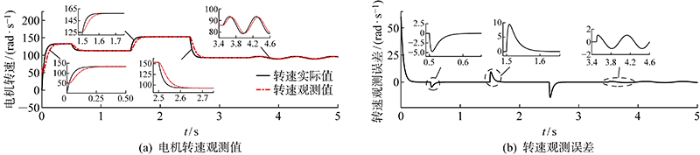
扰动观测器对扰动转矩和电机转速的跟踪效果决定了期望转角增量计算的准确性.在图5控制器结构的模型基础上去掉闭环反馈,以凸显负载变化时观测器对电机转速变化的跟踪效果.将电机端负载转矩变化量看作扰动转矩,定义与关节运动方向相反的负载力矩为正,与关节运动方向相同的负载力矩为负,输出观测器估计转矩值和估计转速值.取观测器增益矩阵为Z=[56.8 -55.8]^T,并设定仿真场景:驱动电机从启动加速到额定转速,在0.5 s时,负载转矩由0上升至1 N·m,1.5 s时负载转矩下降至-1 N·m,2.5 s时负载转矩上升至2 N·m,3.5 s时负载转矩取幅值为0.2 N·m,周期为0.2π的正弦扰动信号.

图6为扰动转矩观测值与转矩观测误差值曲线.当负载转矩发生阶跃变化时,观测器估计转矩值可在0.035 s内完成对转矩变化的跟踪,观测误差在短暂的增大后迅速收敛到0;当负载转矩发生周期性正弦波动时,观测输出与实际变化之间存在最大约0.01 s的延时,最大观测误差出现在扰动转矩突变的瞬间,约为-0.075 N·m,随后观测误差迅速衰减并保持在 ±0.02 N·m左右.图7为负载转矩变化时相应的电机转速观测曲线与转速观测误差曲线,纵坐标换算为电机角速度.在开环控制下,当负载转矩变化时,电机输出转速随之发生变化.当负载呈现阶跃变化时,观测器对电机转速的观测误差可在0.08 s内收敛到0,实现对转速实际值的跟踪;当负载呈现正弦趋势变化时,实际转速值周期性波动,观测器输出转速估计值与实际输出转速之间存在最大约0.04 s的延迟时间,且观测误差保持在 ±1 rad·s^-1 左右. 仿真结果表明, 观测器具有快速跟踪扰动转矩值和电机转速值的能力.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 扰动转矩观测值及观测误差

Fig.6 Observed value and observation error of disturbance torque

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 电机转速观测值及观测误差

Fig.7 Observed value and observation error of motor speed

3.2 转矩增量补偿控制方法仿真

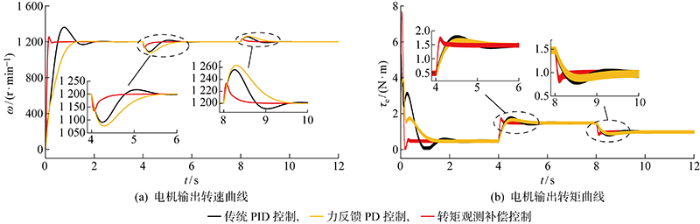
利用MATLAB/Simulink搭建了柔性关节控制系统模型,分别对转速反馈定值比例积分微分(PID)控制、关节力反馈PD控制以及基于转矩观测补偿的PI-IP控制方法进行仿真对比,系统参数如表2所示.关节力反馈PD控制是根据关节弹性力矩反馈值设计的控制律,电机输出的控制力矩为τ_m=K_pe+K_v $\overset{\cdot}{e}$ ,其中,K_p和K_v为增益系数,e为电机转角误差,结合模型式(11),此时关节弹性力矩的控制方程为τ_k=n(J_m ${\ddot{θ}}_{1}$ + $τ_{B_{v}}$ -τ_m),其中,τ_k=k $(θ - θ_{1} / n)$ 为关节弹性力矩; $τ_{B_{v}}$ =B_v ${\overset{\cdot}{θ}}_{1}$ 为摩擦力矩;J_m=J_n+J_r/n²为关节总惯量,表示为电机惯量与减速器惯量之和.力反馈PD控制相比于传统的转速反馈PID控制,具有更好的应对关节力矩突变的能力,且控制器不含积分项,具有更小的超调量和稳态误差,因此将该方法作为对比方法之一.

PID控制器参数取比例系数为10,积分系数为0.1,微分系数为0.5;PD控制器参数取比例系数和开环增益均为10;PI-IP调节器参数取比例系数为10,积分系数为0.1,α=0.5;观测器增益矩阵取Z=[56.8-55.8]^T.设定仿真场景:电机初始负载力矩为0.5 N·m,在4 s时增大至1.5 N·m,在8 s时减小至1 N·m.容许误差为2%,观察电机输出转速、转矩以及关节轨迹的变化趋势.

电机输出转速和转矩曲线如图8所示.由图8(a)可知,当负载力矩发生变化时,传统PID控制下的电机转速产生了最大约100 r/min的波动,并在约2.3 s内恢复对给定转速的跟踪;力反馈PD控制下的电机输出转速,在负载力矩发生变化时产生了最大约130 r/min的波动,并在约1.45 s内恢复对给定转速的跟踪;转矩观测补偿控制下的电机转速,在负载力矩变化时产生了最大约65 r/min的转速波动,并在约0.6 s内恢复对给定转速的跟踪.相比之下,转矩补偿控制下的电机输出具有更短的转速调节时间和更小的转速波动.由图8(b)可知,3种控制方法均能实现对负载力矩变化的跟踪,PID控制和力反馈PD控制下的系统力矩调节时间分别约为1.7 s 和1.5 s,而转矩补偿控制下的力矩调节时间约为0.5 s,因此转矩补偿控制具有更快跟踪负载力矩的能力.同时,在电机启动过程中,若忽略观测器的延迟时间,观测器观测到的初始扰动转矩等于负载力矩本身,启动时会产生较大的期望转角值,进而产生较大的启动转矩超调量.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 驱动电机输出曲线

Fig.8 Output curve of drive motor

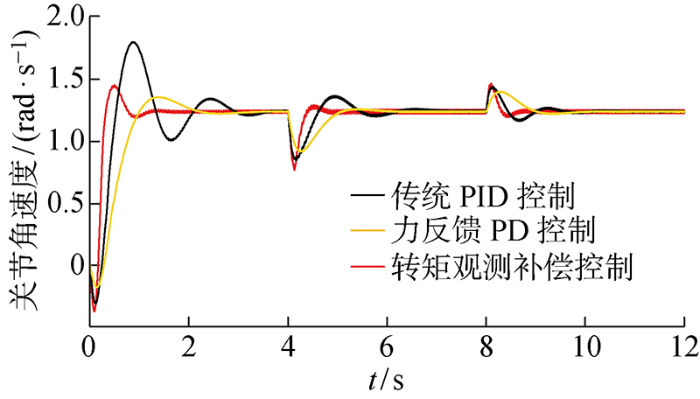
关节角速度曲线如图9所示.对比图8(a),由于弹性元件将部分电机转子动能转化为弹性势能,所以关节的响应速度略滞后于电机的响应速度,验证了前文模型对关节柔性的描述.当负载力矩发生变化时,PID控制下的关节转速调节时间约为2.8 s,力反馈PD控制下的关节转速调节时间约为1.9 s,转矩补偿控制下的关节转速调节时间约为1 s.相比之下,本文提出的控制方法可以有效抑制因负载变化引起的关节振动,并且具有更短的调节时间.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 关节角速度曲线

Fig.9 Curve of joint angular velocity

3.3 转矩增量补偿方法实验分析

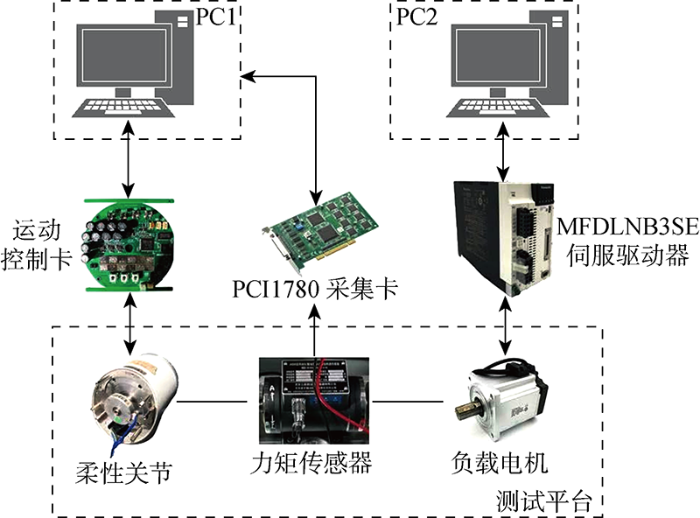
为了验证所提负载转矩增量补偿控制方法在实际柔性关节运动控制中的有效性,在含有一体化柔性关节的测试平台上进行实验.一体化柔性关节的硬件结构如图10(a)所示,实验测试平台如图10(b)所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 实验设备现场

Fig.10 Site of experimental equipment

在图10(a)中,关节驱动电机采用额定电压为48 V、额定输出转矩为0.3 N·m、额定转速为 1000 r/min、额定功率为100 W的永磁无刷直流电机;减速器采用减速比为100∶1的谐波减速器;磁编码器采集关节及电机转子的位置信号;运动控制板根据反馈信号计算电机期望转角和估计负载扰动力矩值,并输出电机驱动信号.

在图10(b)中,实验测试平台左侧为安装了固定外壳和固定支架的一体化柔性关节,右侧采用松下 1000 W 低惯量伺服电机MSMF作为负载电机,并采用配套的A6SE系列的MFDLNB3SE伺服驱动器进行驱动控制.实验中,通过调节负载侧伺服电机模拟柔性关节系统的负载力矩突变.柔性关节与负载电机之间安装有0~100 N·m的应变片式力矩传感器,其输出的关节力矩信号通过PCI1780数据采集卡传输至计算机端,观测关节输出转矩跟随负载力矩变化的调节过程.图11所示为实验平台的结构示意图.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 实验平台结构示意图

Fig.11 Schematic diagram of experimental platform

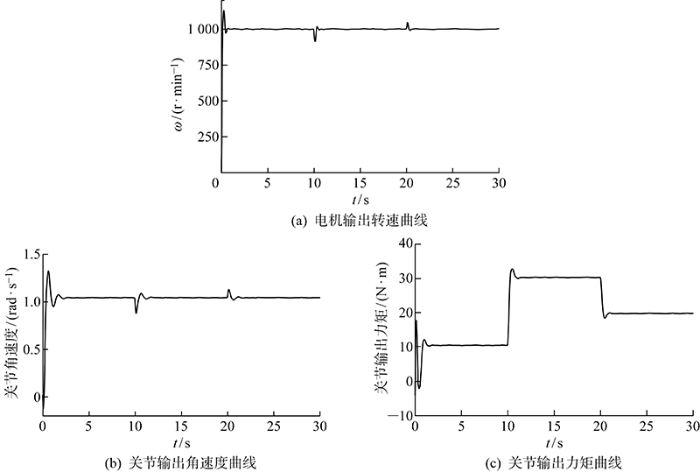
测试时关节电机经启动达到额定转速,负载电机初始输出力矩为10 N·m,在10 s时将负载电机输出力矩调整为30 N·m,在20 s时将负载电机输出力矩调整为20 N·m.

图12为关节驱动电机转速、关节输出端角速度和关节输出力矩曲线.图12(a)和12(b)表明,在额定情况下,驱动电机和关节输出角速度可以有效跟踪给定信号;随着在10 s和20 s处的负载力矩发生变化,关节角速度和电机转速产生波动,但可以看出负载变化并没有引起系统的长时间振动,电机转速在0.8 s内恢复稳定,而关节角速度的波动在1.4 s内得到有效抑制.图12(c)表明,在转矩补偿控制的作用下,关节输出转矩可以在1 s内实现对负载力矩的有效跟踪,且调节过程中振动幅度小、跟踪精度高.实验结果证明所提出的转矩观测补偿控制方法能够有效应对负载突变引起的关节振动问题,且实验结果与仿真结果具有一致性.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 负载力矩变化时的转矩补偿控制方法实验结果

Fig.12 Experimental results of torque compensation control method at variation in load torque

4 结论

研究仿人柔性关节变负载情况下的振动问题,主要结论如下:

(1) 基于Lagrange-Maxwell方程构建了仿人柔性关节系统的机电耦合模型.该模型通过定义驱动电机电磁项为系统广义坐标,解决了传统动力学建模只能将电机电磁力矩作为外力矩引入模型的问题.基于模型分析了关节柔性机理与负载变化后的关节振动机理.分析认为,负载力矩的突变会导致关节产生加速力矩并进一步改变关节弹性力矩,而弹性力矩对负载力矩的被动适应过程是引发关节振动的核心原因.

(2) 针对负载变化导致关节振动的问题,提出一种基于观测器的转矩补偿控制方法.该方法以负载变化后手臂零加速度、零转角增量为期望控制目标,构建驱动电机转角增量控制方程,并通过控制驱动电机输出转角增量来主动调节关节弹性力矩,从而实现对关节振荡过程的主动抑制.为了准确计算负载转矩增量所对应的驱动电机转角增量,设计了用于估计负载转矩增量和电机输出转速的状态观测器,并利用Lyapunov稳定性原理给出了观测器增益矩阵的整定方法;设计了基于PI-IP调节器的关节驱动系统闭环控制结构,并将扰动力矩的观测结果前馈输入到驱动电机的参考转矩中,以提高系统控制精度和抗干扰能力.

(3) 仿真结果表明,本文设计的状态观测器能够快速有效跟踪负载力矩变化引起的系统状态变化,与定值PID控制和关节力反馈PD控制相比,转矩观测补偿控制下的电机转速调节时间分别降低了1.7、0.85 s,关节转速的调节时间分别降低了约1.8、0.9 s,关节振动在1 s内得到有效抑制,提高了系统动态调节能力.最后通过实验验证了该方法在实际柔性关节中的控制效果,结果表明转矩观测补偿控制方法能够有效应对负载变化时引起的关节振动问题.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ASFOUR

, KAUL

, WÄCHTER

, et al.

ARMAR-6: A collaborative humanoid robot for industrial environments[C]//2018 IEEE-RAS 18th International Conference on Humanoid Robots

Beijing, China: IEEE, 2018: 447-454.

[本文引用: 2]

[2]

JIANG

Z H

, XU

J F

, LI

, et al.

Stable parking control of a robot astronaut in a space station based on human dynamics

[J]. IEEE Transactions on Robotics, 2020, 36(2): 399-413.

DOI:10.1109/TRO.8860 URL [本文引用: 1]

[3]

ITO

, IWASAKI

State feedback-based vibration suppression for multi-axis industrial robot with posture change[C]//IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society

Florence, Italy: IEEE, 2016: 5119-5124.