高温热管工作温度较高,且碱金属工质的化学性质活泼,因此目前针对高温碱金属热管的实验研究集中于吸液芯选型的影响以及宏观传热性能的测量.Manoj等[4]对环形吸液芯结构和复合吸液芯结构的高温钠热管的性能进行了实验研究,结果表明,复合吸液芯结构的热管热阻更低,性能更好,在充液率为40%、倾角为30°时表现出较好的传热特性.Cisterna等[5]研究了充注过程对钠热管性能的影响,结果表明在受控气氛中充注液态钠、热管封闭后进行不凝性气体吹扫过程的热管热传输能力更强.田智星等[6]通过实验对高温热管的管壁温度、蒸汽温度、压力进行检测,研究了倾角、加热/冷却功率对热管传热极限的影响.针对高温碱金属热管的理论和数值模拟[7
不难发现,当前针对高温热管传热性能的研究鲜有考虑碱金属工质在三相接触线附近的微观传热机理的影响.而针对水[12]、制冷剂(NH3[13]、辛烷[14]、R134a [15]、HFE-7100 [15]、FC-72 [16])等工质的理论、实验和数值研究表明,汽-液-固三相接触线附近蒸发弯月面区域的微观传热机理对核态沸腾、薄液膜蒸发等汽液相变传热过程的总体传热性能存在显著影响[14-15,17
1 计算模型
1.1 接触线传热模型
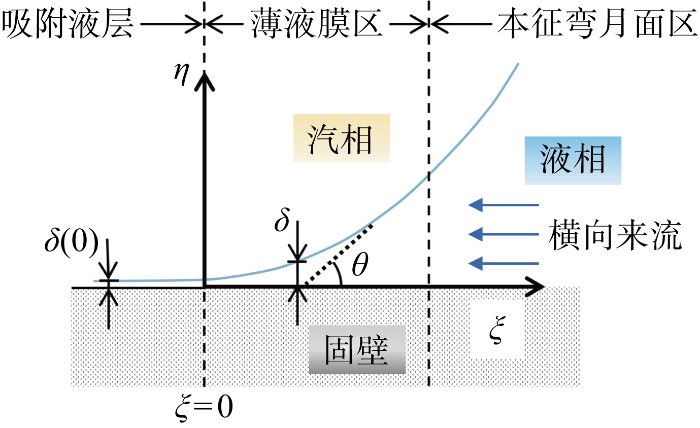
在三相接触线附近区域,液体和固体表面间的相互作用起到了关键的作用,需要考虑分离压力的影响[22].根据接触线传热理论,汽液界面靠近壁面时形成的蒸发弯月面可以分为如图1所示的3个区域.图中: ξ表示液膜的延展方向;η表示液膜厚度方向;δ为局部液膜厚度;δ(0)为初始液膜厚度;θ 为接触角.3个区域分别为:① 吸附液层,该区域的流-固分子间吸附力即分离压力很强,使得液膜紧紧吸附在固体壁面上无法蒸发;② 薄液膜区,液膜厚度上升,因而分离压力开始迅速下降,本文规定当分离压力下降到吸附液层区分离压力值的1/5 000 时为薄液膜区的边界[14]; ③ 本征弯月面区,分离压力的影响逐渐消失,该区域由毛细压力占主导,汽液界面的曲率几乎维持不变.
图1
图1
蒸发弯月面以及接触线传热模型示意图
Fig.1
Schematic of evaporating meniscus and contact line heat transfer model
1.2 模型假设
(1) 计算区域内的液体流动为稳态层流流动.
(2) 由于 ξ方向的长度远大于η方向的长度,液体的流动可以用润滑近似理论来描述,忽略η 方向的压力变化及流动.
(3) 壁面为等温壁面,传热为一维导热且垂直于壁面.
(4) 壁面处无滑移,汽液界面无剪切力.
(5) 由于液膜的斜率较小,可认为通过壁面的导热面积和界面蒸发面积近似相等[14].
(7) 假设表面张力为常数,忽略Marangoni流的影响[15].
1.3 模型方程
在上述的模型假设下,可得到三相接触线附近微观区域的动量守恒、质量守恒、压力平衡以及能量守恒方程式.
1.3.1 动量守恒 由润滑近似可得到ξ方向的纳维-斯托克斯方程:
式中: pl为液相压力;μl为液体动力黏度; u表示液相平行于ξ 方向的速度.
壁面、汽液界面处的边界条件分别为
η=0: u=0
η=δ:
对式(1)进行求解,得到沿液膜厚度η方向的速度分布u如下:
1.3.2 质量守恒 将速度分布 u沿η方向进行积分,得到ξ 位置处的质量流量:
式中:ρl为液相密度.
质量流量沿ξ方向的变化率等于ξ位置处由于液体蒸发所损失的质量即蒸发速率:
式中:q″为局部热流密度;hlv为蒸发潜热.
1.3.3 压力平衡
基于修正的Young-Laplace方程[26],汽液两相的压差Δp由3部分组成:液体分子和固体表面相互作用而产生的分离压力pd、界面曲率引起的毛细压力pc以及蒸发过程中由于汽液两相密度不同引起的动量变化从而产生的蒸汽反冲力pr.也即
式中:pv为汽相的饱和压力.分离压力pd、毛细压力pc以及蒸汽反冲力pr由下式给出:
1.3.4 能量守恒
通过液膜的一维导热量为
式中:Tw和Ti分别为壁面温度(与液膜接触的一侧的壁面温度)和汽液界面温度;λl为液体热导率.
通过汽液界面的相变传热量可由Schrage方程[28]得到:
式中:piv为液相对应的平衡蒸汽压力;
因为Tsat/Ti≈1 [15],所以式(10)化简为
汽液相压差Δp使得平衡蒸汽压piv偏离汽液界面温度Ti对应的饱和压力psat(Ti),由Thomson方程[29]可得piv与Δp的关系:
又由ρv≪ρl可得,
由Clausius-Clapeyron方程[30]可得饱和压力-温度的关系:
由于汽液界面和汽相的压力、温度变化较小,所以可由式(14)得:
将式(13)、(15)代入式(11),可得到q″表达式:
式中:Ri为汽液界面蒸发热阻,
汽液界面的局部平衡温度Tiv定义为
结合式(4)、(9)和(16)得:
结合上述动量守恒、质量守恒、压力平衡以及能量守恒的关系式,整理得到如下的四阶常微分方程:
式中: Q=
1.4 边界条件
由吸附液层的热流密度为0可得计算区域的起点处 Q(0) = 0、Q'(0)=0.将Q'(0)=0代入式(23)得到Δp(0).此外,起点与斜率以及曲率为0的吸附液膜相连,因此可得δ'(0)=0、δ″(0)=0.将δ″(0)=0代入式(21)可以得到吸附液膜的厚度δ(0). 总的边界条件如下:
2 计算设置
为了避免数值求解过程中各物理量数值量级差异过大,对式(20)~(23)进行无量纲化,同时在求解过程中对 Q(0)进行微小扰动直到接触角θ (θ=arctan δ' )在求解范围内接近恒定值[23].数值模拟结果发现当色散常数A值增大时,需要增加对Q(0) 扰动的精度,以期得到碱金属在三相接触线处微观传热特性的数值解.对pv = 1 atm(1 atm=101 325 Pa),过热度Tw-Tsat=0.5~5 K工况下的水以及钾、钠、锂的三相接触线传热特性进行数值模拟,参照文献[15,31-32]选取pv=1 atm条件下的饱和物性参数,列于表1.当pv=1 atm, 过热度在Tw-Tsat=0.5~5 K 内变化时,碱金属工质钠、钾、锂的表面张力变化分别约为0.5%、0.3%和0.6%.因此,在计算时可以合理地忽略温度对表面张力的影响.
表1 水、钾、钠及锂的物性参数 (pv = 1 atm)
Tab.1
| 水参数 | 取值 | 水参数 | 取值 |
|---|---|---|---|
| Tsat /K | 373.15 | ρl/(kg·m-3) | 958.35 |
| A/J | 6.45×10-21 | μl /(Pa·s) | 2.82×10-4 |
| 1 | ρv/(kg·m-3) | 0.598 1 | |
| σ/(N·m-1) | 0.058 9 | λl/(W·m-1·K-1) | 0.679 1 |
| hlv/(J·kg-1) | 2.256 5×106 | Rg/(J·kg-1·K-1) | 461.89 |
| 碱金属参数 | 取值 | ||
| 钾 | 钠 | 锂 | |
| Tsat/K | 1 032.40 | 1 159.30 | 1 616.80 |
| A/J | 1.0×10-20 | 1.0×10-20 | 1.0×10-20 |
| 1 | 1 | 1 | |
| σ/(N·m-1) | 0.072 0 | 0.116 1 | 0.236 5 |
| hlv/(J·kg-1) | 1.870 0×106 | 3.867 1×106 | 1.927 8×107 |
| ρl/(kg·m-3) | 663.49 | 739.82 | 399.60 |
| μl/(Pa·s) | 1.30×10-4 | 1.56×10-4 | 1.61×10-4 |
| ρv/(kg·m-3) | 0.506 4 | 0.283 9 | 0.060 8 |
| λl/(W·m-1·K-1) | 30.259 4 | 48.933 8 | 69.002 9 |
| Rg/(J·kg-1·K-1) | 212.63 | 361.48 | 1 204.93 |
3 模型验证
图2
考虑到接触线传热模型的核心是考虑了分离压力效应的影响,本文采用的计算分离压力的方法 (pd=A/δ3) 是基于分子间微观作用势得到的,对不同流-固分子组合是一种普适的方法,该模型同样适用于碱金属工质的蒸发弯月面区域微观传热特性研究[32].
4 结果与讨论
在蒸发弯月面区域,和热质传递密切相关的特性包括液膜厚度、局部接触角变化、热阻分布、压力分布、热流密度变化等.本文从这几个方面入手,对不同工质及不同过热度下的蒸发弯月面区域微观传热特性进行分析和研究.
4.1 不同工质的蒸发弯月面区域微观传热特性
热管是一种利用汽液相变进行传热的装置,因此常基于饱和蒸汽压力确定工质的工作温度范围.过高的饱和蒸汽压力对热管壁材料的结构强度要求较高,而过低的饱和蒸汽压力则会导致不凝性气体进入热管从而影响其传热性能[31].因此,本文分别以水和碱金属钾、钠、锂为工质,研究了当工质饱和蒸汽压pv=1 atm,Tw-Tsat=2 K 时,不同工质在蒸发弯月面区域的微观传热特性.
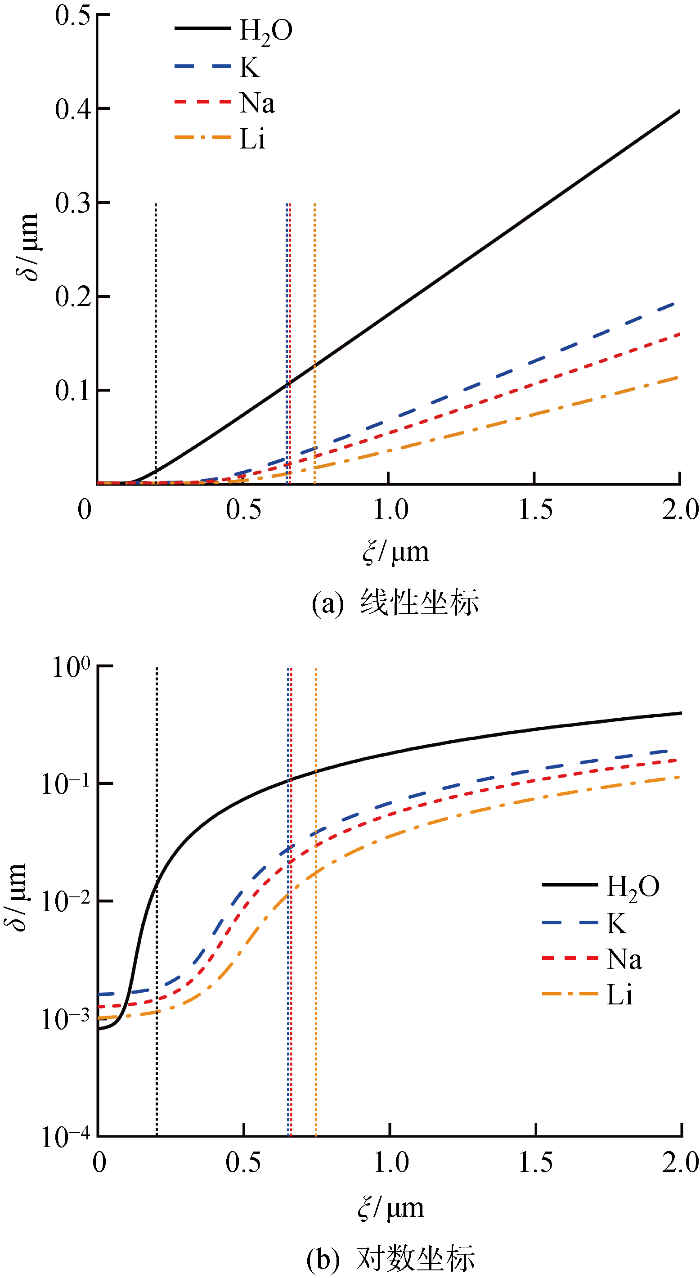
图3为水、钾、钠、锂的液膜厚度分布示意图,与ξ方向垂直的虚线表示不同工质在计算区域内薄液膜区和本征弯月面区的分界线(左侧为薄膜区域,右侧为本征弯月面区).在薄液膜区,液膜厚度从吸附液膜的厚度δ(0)开始增加,并最终在本征弯月面区达到一个固定的曲率.由图3(b)可知,水的吸附液膜厚度最小,δ(0)由色散常数A、蒸发潜热hlv、液相密度ρl以及汽相饱和温度Tsat决定(见式(24)).随着弯月面的延展,水的液膜厚度逐渐超过了锂、钠、钾,其更小的色散常数A使之在相同的液膜厚度下分离压力减小,液膜厚度变化更快,薄液膜区的长度随之减小(为0.202 μm).工质钾、钠、锂的液膜厚度依次降低,薄液膜区的长度增加,分别为0.651、0.662、0.747 μm.这主要是由于三者的蒸发潜热hlv依次升高(锂的蒸发潜热比钠、钾高出一个量级),由式(24)可知,锂的初始液膜厚度δ(0)最小.因此,锂的分离压力效应更强,固液分子间的强吸引力使液膜厚度增加的速度减缓,薄液膜区的长度变长.
图3
图3
蒸发弯月面区域液膜厚度分布(pv=1 atm,Tw-Tsat=2 K)
Fig.3
Film thickness profile in evaporating meniscus region (pv=1 atm,Tw-Tsat=2 K)
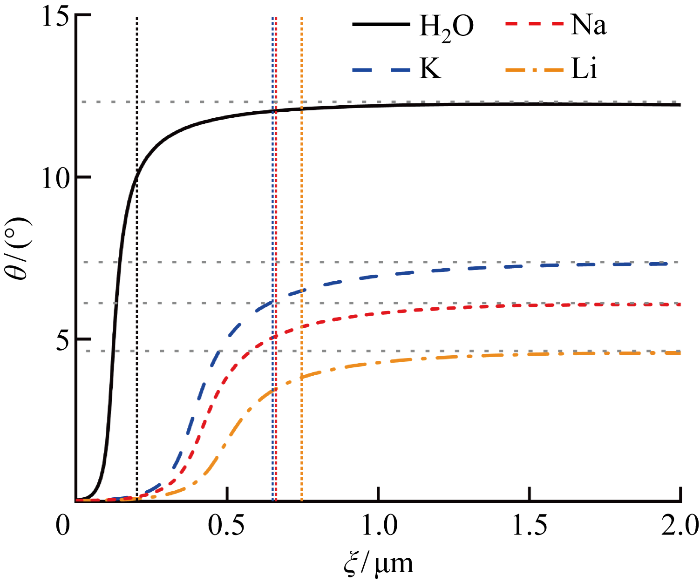
不同工质的接触角特性与液膜厚度的变化密切相关,如图4所示:在薄液膜区,接触角θ从0° 开始不断增加;在本征弯月面区,θ趋近一恒定值,这一恒定值即为表观接触角.由前文讨论可知,在本征弯月面区,水的液膜厚度变化最快,钾、钠次之,锂最慢,它们的表观接触角依次减小,分别为12.2°、7.3°、6.1°和4.6°.
图4
图4
蒸发弯月面区域接触角分布(pv=1 atm,Tw-Tsat=2 K)
Fig.4
Contact angle profile in evaporating meniscus region (pv=1 atm,Tw-Tsat=2 K)
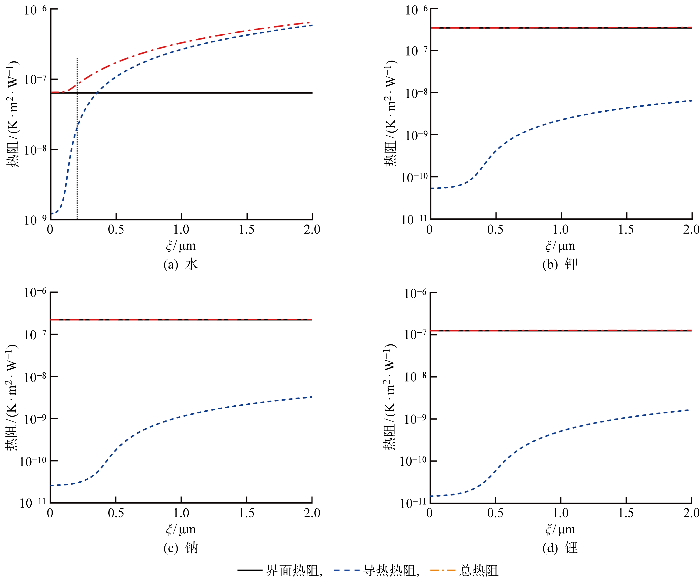
液膜厚度及导热系数会对导热热阻δ/λl产生影响.由于碱金属的导热系数远高于水,钾、钠、锂在蒸发弯月面区域的热阻分布与水相比有显著的不同,如图5所示.在三相接触线附近微观区域内,总热阻由界面热阻Ri和导热热阻δ/λl两部分组成.如图5(a)所示,在薄液膜区,水的液膜厚度介于1~15 nm,相对于导热热阻δ/λl,界面蒸发热阻Ri占据主导地位;而在本征弯月面区,随着液膜厚度的增加,由于水的液体热导率λl仅为 0.679 1 W/(m·K),导热热阻δ/λl以较快的速度增加,总热阻由界面蒸发热阻主导转变为导热热阻主导.相比之下,如图5(b)、5(c)和5(d)所示,碱金属钾、钠、锂的液体热导率λl超过30 W/(m·K),在计算的微观区域内,导热热阻与界面蒸发热阻相比小了2~4个数量级,总热阻可认为是一个定值,近似等于界面蒸发热阻.
图5
图5
蒸发弯月面区域界面蒸发热阻、导热热阻及总热阻分布(pv=1 atm,Tw-Tsat=2 K)
Fig.5
Interfacial, conductive, and total thermal resistance profile in evaporating meniscus region (pv=1 atm,Tw-Tsat=2 K)
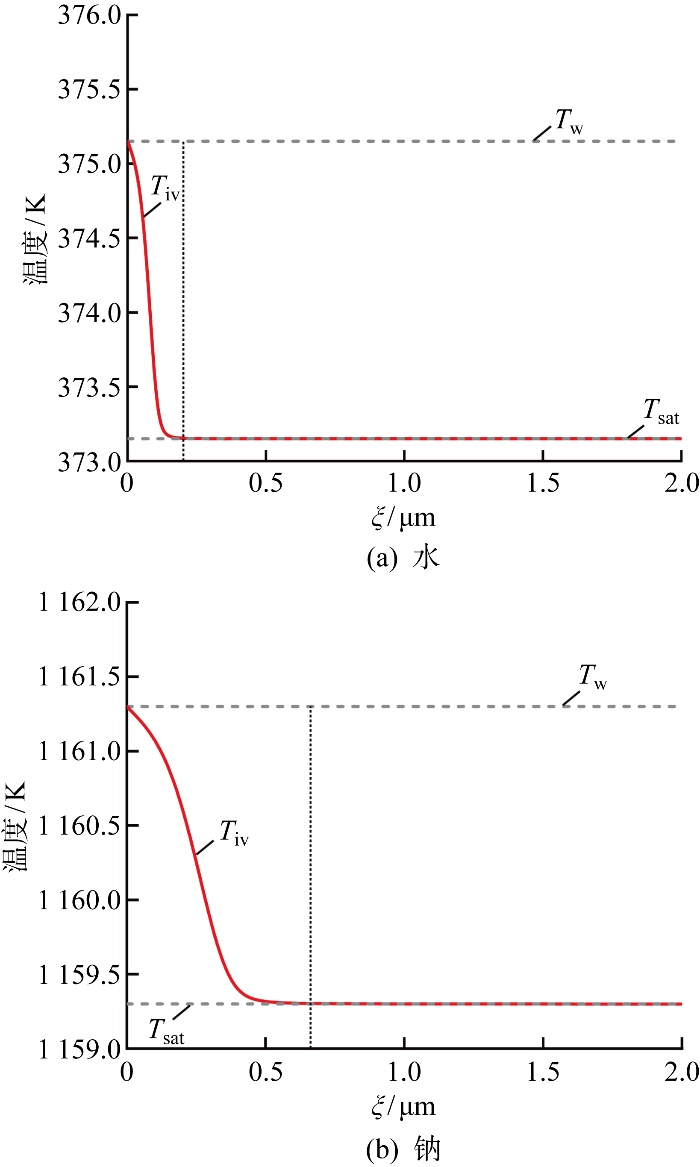
由式(19)可得,热流密度q″的驱动温差为壁面温度Tw与汽液界面局部平衡温度Tiv之差.图6展示了水和钠汽液界面局部平衡温度Tiv的分布.在薄液膜区,Tiv由Tw(此时式(19)中的q″= 0,分离压力效应导致与超薄吸附液膜平衡的蒸汽压力降低,从而抑制蒸发[34])下降至接近汽相饱和温度Tsat(薄液膜区的液膜厚度增加,分离压力显著降低,式(5)的汽相和液相的总压差Δp呈现出快速下降的趋势导致式(18)中的局部平衡温度Tiv迅速下降),在本征弯月面区则基本保持不变.Stephan等[13]指出,在蒸发弯月面附近的微观区域内,受界面曲率和分离压力效应的影响,Tiv会偏离Tsat.若假设汽液界面局部平衡温度Tiv等于汽相饱和温度Tsat,会大幅高估热管蒸发端的径向传热系数.
图6
图6
蒸发弯月面区域汽液界面局部平衡温度分布(pv=1 atm,Tw-Tsat=2 K)
Fig.6
Local equilibrium temperature profile at vapor-liquid interface in evaporating meniscus region (pv=1 atm,Tw-Tsat=2 K)
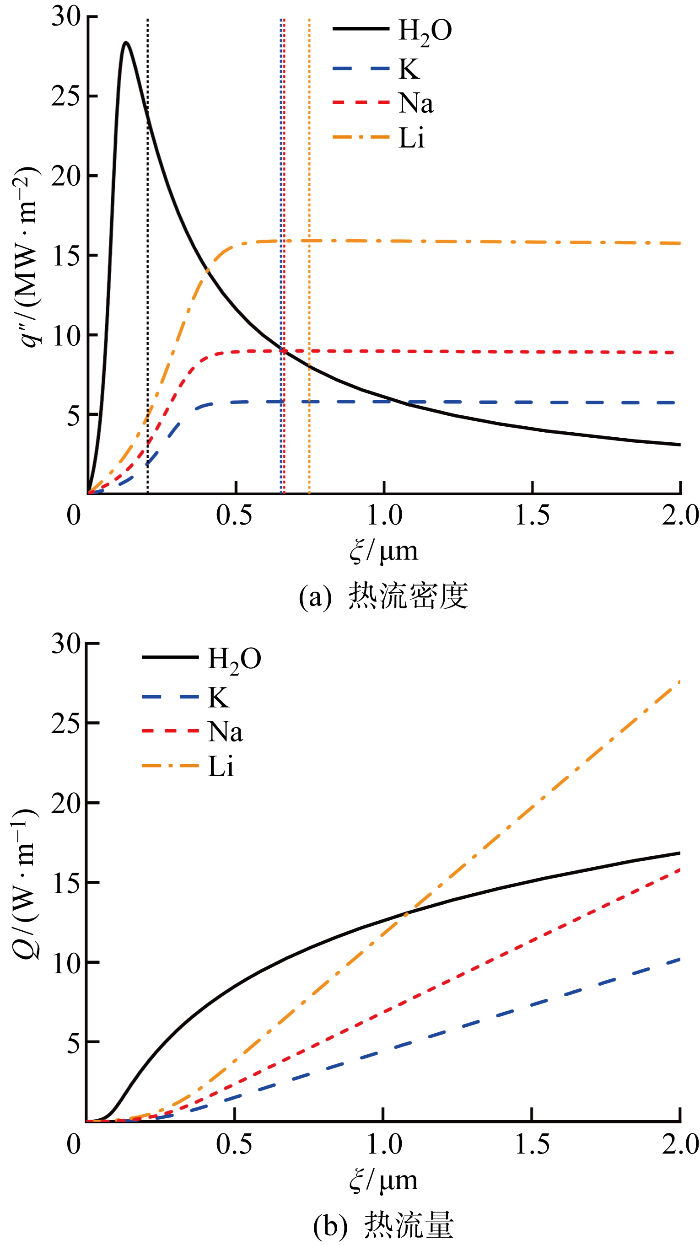
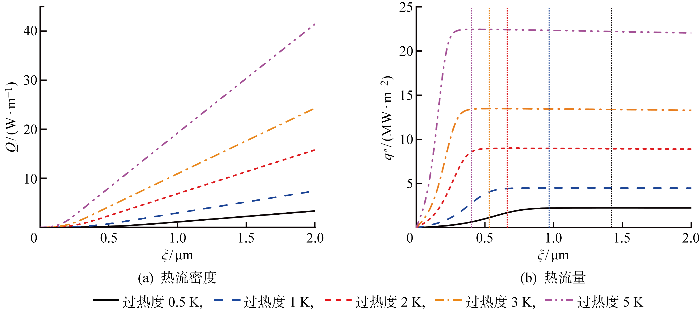
局部热流密度 q″ = (Tw-Tiv)/(Ri+δ/λl), 热阻和汽液界面局部平衡温度的分布决定了热流密度的分布.图7为水和碱金属钾、钠、锂在蒸发弯月面区域的热流密度及热流量分布.在薄液膜区,总热阻由界面蒸发热阻主导且量级较小(10-8~10-7 K·m2/W),随着液膜厚度的增加,分离压力抑制蒸发的效应减弱,Tw-Tiv从0迅速增大到2 K,热流密度从0升高到5~30 MW/m2(见图7(a)).由图5可见,水的总热阻最低,因此其热流密度最高.在本征弯月面区,液膜厚度的增加导致水的导热热阻显著增加,热流密度下降到3.0 MW/m2(见图7(a)).然而,对于碱金属钾、钠、锂,总热阻几乎不变,热流密度在达到峰值后几乎保持恒值,随着液膜厚度的增加稍有下降,锂在微观区域的热流量可达27.6 W/m(见图7(b)).在三相接触线附近的微观区域,锂的热流量最大.
图7
图7
蒸发弯月面区域热流密度及热流量分布(pv=1 atm,Tw-Tsat=2 K)
Fig.7
Heat flux and cumulative heat flux profile in evaporating meniscus region (pv=1 atm,Tw-Tsat=2 K)
本文对碱金属在微观区域的传热特性进一步分析:钾、钠、锂的界面蒸发热阻分别为3.426×10-7、2.216×10-7、1.252×10-7 K·m2/W.对于钾、钠、锂等在微观区域由界面蒸发热阻主导的工质,和文献[35-36]中类似,本文提出一个与式(17)汽液界面蒸发热阻表达式有关的品质因数 M,M=
4.2 不同过热度下的接触线微观传热特性
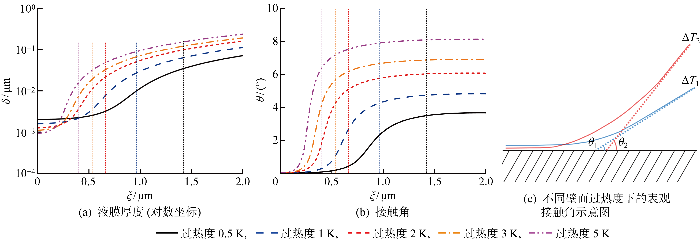
吸附液膜的厚度和表观接触角均随着壁面过热度的增加而自适应调节.当壁面过热度增加时,微观区域的蒸发传热增强,更多的液体进入微观区域进行补液;液膜的厚度、表观接触角等发生变化以促进液体流动.图8为不同壁面过热度下钠在蒸发弯月面区域的液膜厚度及接触角分布.如图8(a)所示,与ξ方向垂直的虚线表示不同过热度下在计算区域内薄液膜区和本征弯月面区的分界线.当壁面过热度从0.5 K升高到5 K时,吸附液膜的厚度降低,初始的分离压力效应增强以抑制蒸发;薄液膜区内液膜厚度的变化速度加快,薄液膜区的长度从1.421 μm减小到0.402 μm.壁面过热度升高时,本征弯月面区液膜厚度和界面斜率增大,表观接触角(见图8(b))从3.7° 变化到 8.1°,此时微观区域的汽液界面面积增大,更多液体流入微观区域进行补充.图8(c) 为不同壁面过热度-表观接触角示意图,可以看出,当过热度从ΔT1增大到ΔT2时,由于液膜厚度的变化速率加快,表观接触角从θ1变为θ2,θ2> θ1.
图8
图8
不同壁面过热度下蒸发弯月面区域液膜厚度及接触角分布(钠)
Fig.8
Film thickness (logarithmic scale),contact angle profile, and schematic of apparent contact angle at different wall superheats for sodium in evaporating meniscus region
图9
图9
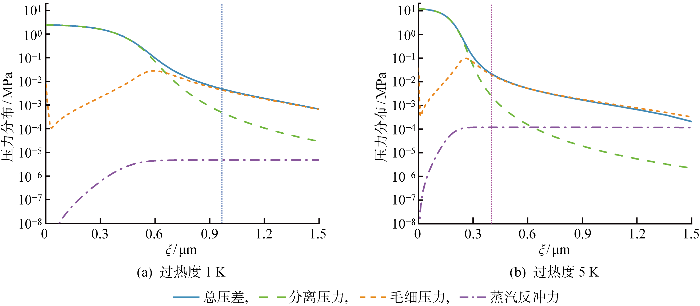
不同壁面过热度下蒸发弯月面区域压力分布(钠)
Fig.9
Pressure profile at different wall superheats for sodium in evaporating meniscus region
当壁面过热度升高时,蒸发弯月面区域内液膜的压力梯度增加,补液能力增强.壁面过热度为5 K时的压力分布如图9(b)所示.当壁面过热度升高时,初始分离压力值更高、下降速度更快;更剧烈的液膜厚度变化使得液膜曲率增大,毛细压力的峰值上升,同时峰值位置随着薄液膜区的变化前移;汽液相总压差Δp在蒸发弯月面区域内的变化增大,即液膜的压力梯度增加,亦促使更多液体流入蒸发弯月面区域.
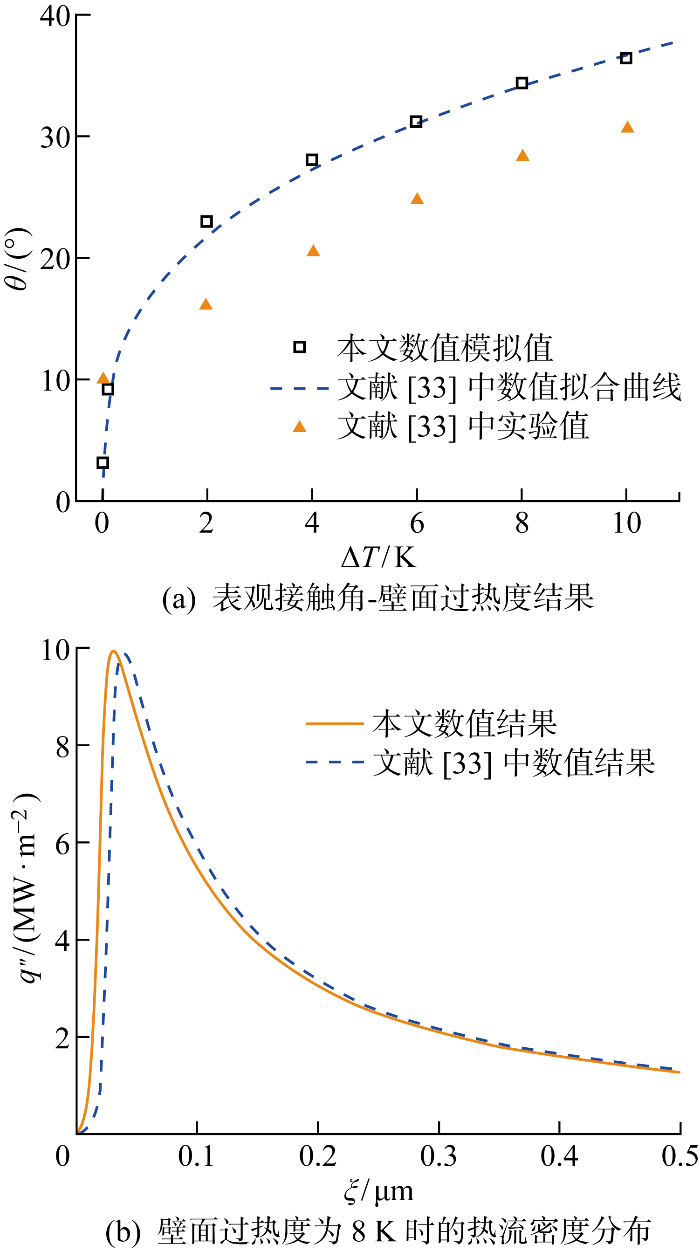
此外,在薄液膜区,蒸汽反冲力可忽略不计;而在本征弯月面区,随着分离压力和毛细压力的进一步降低,蒸汽反冲力则超过分离压力,和毛细压力一起构成了总压差.此时的蒸汽反冲力不会对表观接触角产生影响,与文献[33]中的结论一致.
图10
图10
不同壁面过热度下蒸发弯月面区域热流密度及热流量分布(钠)
Fig.10
Heat flux and cumulative heat flux profile at different wall superheats for sodium in evaporating meniscus region
5 结论
采用描述蒸发弯月面附近传质传热特性的接触线传热模型对高温热管吸液芯内碱金属工质发生汽液相变时的微观传热特性进行了模拟,获得了液膜厚度、接触角、压力分布、热流密度等物理量分布,得到了以下结论.
(1) 在本文计算的三相接触线附近微观区域内(0~2 μm),碱金属工质钾、钠、锂的传热性能与水显著不同:水的总热阻由界面蒸发热阻主导转变为导热热阻主导,而钾、钠、锂的总热阻则近似等于界面蒸发热阻.
(2) 本文提出了一个与汽液界面蒸发热阻有关的品质因数 M;碱金属钾、钠、锂的M 值依次升高,表明蒸发弯月面区域的微观传热性能依次提升;而在宏观尺度下,导热热阻为主导热阻,其中锂的导热系数最高,因此其宏观传热性能亦最佳.
(3) 随着壁面过热度的增加,吸附液膜厚度、表观接触角和压力梯度均自适应调节,其中吸附液膜厚度降低、表观接触角增加、液膜压力梯度增加,从而促使更多液体进入到微观区域进行补液,汽液界面的蒸发传热增强.
参考文献
高温钠热管传热性能试验研究
[J].
DOI:10.7538/yzk.2021.youxian.0115
[本文引用: 1]

为获得高温钠热管传热性能,开展真空条件下钠热管启动性能和等温性能试验,获得了钠热管真空条件下启动速度与等温性能数据;开展强制冷却工况条件下传热性能试验,获得了钠热管声速限特性与试验工况下的最大传热功率。经试验验证,所研制高温钠热管在真空条件下,580 ℃时完全启动,启动用时20 min,轴向壁面温差低于11 ℃,等温性能良好;钠热管传热功率在工作温度为500~650 ℃时受声速极限限制,在650 ℃以上受携带极限限制;在750 ℃和850 ℃时,测得热管最大散热功率分别为4.78 kW与8.02 kW,对应的最大轴向热流密度分别为1.51 kW/cm<sup>2</sup>与2.53 kW/cm<sup>2</sup>。试验结果表明,所研制钠热管具有较强传热能力,可满足热管式核反应堆等工程应用需求。
Experimental study on heat transfer performance of high temperature sodium heat pipe
[J].
DOI:10.7538/yzk.2021.youxian.0115
[本文引用: 1]

In order to obtain the heat transfer performance of high temperature sodium heat pipe, the start-up performance and isothermal performance tests of sodium heat pipe under vacuum conditions were carried out, and the start-up speed and isothermal performance data of sodium heat pipe under vacuum conditions were obtained. Heat transfer performance tests under the forced cooling conditions were carried out, and the sonic limit characteristics of sodium heat pipe and the maximum heat transfer power under test conditions were obtained. The experimental results show that the developed high temperature sodium heat pipe is fully started at 580 ℃ under vacuum condition, and the start-up time is 20 minutes, the axial wall temperature difference is lower than 11 ℃, and the isothermal performance is good. The heat transfer power of sodium heat pipe is limited by the sonic limit in the temperature range of 500-650 ℃, and is limited by carrying limit in the operating temperature above 650 ℃. When the working temperature is 750 ℃ and 850 ℃, the measured maximum heat transfer power of the heat pipe is 4.78 kW and 8.02 kW, respectively, and the maximum axial heat flux density was 1.51 kW/cm<sup>2</sup> and 2.53 kW/cm<sup>2</sup>, respectively. The test results show that the developed sodium heat pipe has strong heat transfer capability which can meet the needs of heat pipe nuclear reactors and other engineering applications.
基于CFD方法的高温热管特性研究
[J].
CFD analysis on characteristics of high temperature heat pipe
[J].
高温热管传热特性实验研究
[J].
Experimental study on heat transfer performance of high temperature potassium heat pipe
[J].
Performance evaluation of sodium heat pipe through parametric studies
[J].
Charging procedures: Effects on high temperature sodium thermosyphon performance
[J].
热管冷却反应堆中高温钠热管传热极限实验研究
[C]//
Experimental investigation on heat transfer limit of high-temperature sodium heat pipe
[C]//
Numerical simulation of high temperature sodium heat pipe for passive heat removal in nuclear reactors
[J].
海洋静默式热管反应堆热工水力特性研究
[J].
DOI:10.7538/yzk.2022.youxian.0339
[本文引用: 1]

安全可靠的能源供给是无人水下潜航器(UUV)发展的关键基础,本研究面向我国重型海洋UUV研发的能源需求,提出了海洋静默式热管反应堆(NUSTER-100)小型核电源概念设计。建立了包括堆芯功率模型、堆芯通道传热模型、热管传热模型、热电转换模型及冷端换热模型等热管反应堆系统数学物理模型,基于高效稳健的数值算法和模块化编程思想,开发了具有自主知识产权的热管反应堆稳态和瞬态热工水力特性分析程序HEART,采用热管实验、温差发电实验等数据对HEART程序关键模块进行了验证与确认。采用HEART程序对NUSTER-100的稳态、冷启动瞬态及反应性引入瞬态工况进行了计算分析,获得了NUSTER-100满功率稳态工况下的热工水力特性,基于冷启动瞬态热工水力分析,提出了具有较高安全性的三段式热管反应堆启动方案,评估了反应性引入瞬态工况下热管反应堆的自稳特性和安全性。本研究可为我国UUV及热管反应堆技术的发展提供理论和技术支持。
Study on thermal-hydraulic characteristics of ocean silent heat pipe cooled reactor
[J].
DOI:10.7538/yzk.2022.youxian.0339
[本文引用: 1]

Safe and reliable energy supply is the key foundation for the development of unmanned underwater vehicle (UUV). Unlike land and space missions, underwater missions are more demanding on energy, which requires higher power level, longer operating time, faster response time, and better concealment. Heat pipe cooled reactor has the advantages of large power capacity, simple structure, easy control of reactivity, and rapid thermal response. The solid-state reactor core does not require coolant and relies entirely on heat pipes to dissipate heat, thereby providing good inherent safety, controllability and concealment. Therefore, heat pipe cooled reactor is considered as one of the most promising options for UUV energy supply. In this study, a conceptual design of Nuclear Silent Thermal-Electrical Reactor (NUSTER-100) was proposed to meet the energy requirement of China’s heavy ocean UUV research and development. 109 sodium heat pipes were arranged in the reactor core for passive cooling, and the thermoelectric generators (TEGs) were employed in the reactor to convert fission heat to electric power. A set of heat pipe cooled reactor system-wild mathematical and physical models were established, including core neutron physics model, core channel heat transfer model, heat pipe model, thermoelectric conversion model and cold junction heat transfer mode. Based on the efficient and robust numerical algorithm and modular modeling ideas, heat pipe advanced reactor transient analysis code HEART was developed with independent intellectual property rights, and the key modules of HEART were validated and verified by heat pipe experiment and thermoelectric power experiment. The steady-state, cold-start transient and reactivity insertion transient conditions of NUSTER-100 were calculated and analyzed by HEART, and the full power operation characteristics of NUSTER-100 were obtained. Steady-state performance of the NUSTER-100 indicates that the solid-state core has good temperature flattening ability. The surface temperature of the heat pipe is less than 1 300 K, and the average temperature drop of the TEG module in central channel is 724 K, which can produce an electrical power of 1 207.8 W. Based on the cold-start transient thermal-hydraulic analysis, a three-stage heat pipe cooled reactor start-up scheme with high safety was proposed, and the stability and safety of heat pipe reactor under reactivity insertion transient were evaluated. The results show that the three-stage heat pipe cooled reactor start-up scheme can improve the reactor start-up efficiency. This study can provide support for the development of UUV and heat pipe cooled reactor technology in China.
A two-phase three-field modeling framework for heat pipe application in nuclear reactors
[J].
Bubble dynamics and heat transfer during nucleate boiling in a microchannel
[J].
Analysis of the heat transfer coefficient of grooved heat pipe evaporator walls
[J].
Characteristics of an evaporating thin film in a microchannel
[J].
Shape of a vapor stem during nucleate boiling of saturated liquids
[J].
Nanoengineered materials for liquid-vapour phase-change heat transfer
[J].
Ultrafast diameter-dependent water evaporation from nanopores
[J].
DOI:10.1021/acsnano.8b09258
PMID:30836750

Evaporation from nanopores plays an important role in various natural and industrial processes that require efficient heat and mass transfer. The ultimate performance of nanopore-evaporation-based processes is dictated by evaporation kinetics at the liquid-vapor interface, which has yet to be experimentally studied down to the single nanopore level. Here we report unambiguous measurements of kinetically limited intense evaporation from individual hydrophilic nanopores with both hydrophilic and hydrophobic top outer surfaces at 22 °C using nanochannel-connected nanopore devices. Our results show that the evaporation fluxes of nanopores with hydrophilic outer surfaces show a strong diameter dependence with an exponent of nearly -1.5, reaching up to 11-fold of the maximum theoretical predication provided by the classical Hertz-Knudsen relation at a pore diameter of 27 nm. Differently, the evaporation fluxes of nanopores with hydrophobic outer surfaces show a different diameter dependence with an exponent of -0.66, achieving 66% of the maximum theoretical predication at a pore diameter of 28 nm. We discover that the ultrafast diameter-dependent evaporation from nanopores with hydrophilic outer surfaces mainly stems from evaporating water thin films outside of the nanopores. In contrast, the diameter-dependent evaporation from nanopores with hydrophobic outer surfaces is governed by evaporation kinetics inside the nanopores, which indicates that the evaporation coefficient varies in different nanoscale confinements, possibly due to surface-charge-induced concentration changes of hydronium ions. This study enhances our understanding of evaporation at the nanoscale and demonstrates great potential of evaporation from nanopores.
Evaporation in nano/molecular materials
[J].
Edge-enhanced ultrafast water evaporation from graphene nanopores
[J].
Micro-scale heat transfer modelling of the contact line region of a boiling-sodium bubble
[J].
Interfacial transport of evaporating water confined in nanopores
[J].
DOI:10.1021/la201807a
PMID:21749136
[本文引用: 1]

A semianalytical, continuum analysis of evaporation of water confined in a cylindrical nanopore is presented, wherein the combined effect of electrostatic interaction and van der Waals forces is taken into account. The equations governing fluid flow and heat transfer between liquid and vapor phases are partially integrated analytically, to yield a set of ordinary differential equations, which are solved numerically to determine the flow characteristics and effect on the resulting shape and rate of evaporation from the liquid-vapor interface. The analysis identifies three important parameters that significantly affect the overall performance of the system, namely, the capillary radius, pore-wall temperature, and the degree of saturation of vapor phase. The extension of meniscus is found to be prominent for smaller nanoscale capillaries, in turn yielding a greater net rate of evaporation per unit pore area. The effects of temperature and ambient vapor pressure on net rate of evaporation are shown to be analogous. An increase in pore-wall temperature, which enhances saturation pressure, or a decrease in the ambient vapor pressure result in enhancing the net potential for evaporation and increasing the curvature of the interface.© 2011 American Chemical Society
Surface charge enhanced kinetically-limited evaporation in nanopores
[J].
The interline heat-transfer coefficient of an evaporating wetting film
[J].
On the equilibrium of vapour at a curved surface of liquid
[J].
Contact line behavior for a highly wetting fluid under superheated conditions
[J].
Mesoscopic model for disjoining pressure effects in nanoscale thin liquid films and evaporating extended meniscuses
[J].
DOI:10.1021/acs.langmuir.3c02068
PMID:37677082
[本文引用: 1]

Disjoining pressure effect is the key to describe contact line dynamics, micro/nanoscale liquid-vapor phase change heat transfer, and liquid transport in nanopores. In this paper, by combining a mesoscopic approach for nanoscale liquid-vapor interfacial transport and a mean-field approximation of the long-range solid-fluid molecular interaction, a mesoscopic model for the disjoining pressure effect in nanoscale thin liquid films is proposed. The capability of this model to delineate the disjoining pressure effect is validated. We demonstrate that the Hamaker constant determined from our model agrees very well with molecular dynamics (MD) simulation and that the transient evaporation/condensation mass flux predicted by this mesoscopic model is also consistent with the kinetic theory. Using this model, we investigate the characteristics of the evaporating extended meniscus in a nanochannel. The nonevaporating film region, the evaporating thin-film region, and the intrinsic meniscus region are successfully captured by our model. Our results suggest that the apparent contact angle and thickness of the nonevaporating liquid film are self-tuned according to the evaporation rate, and a higher evaporation rate results a in larger apparent contact angle and thinner nonevaporating liquid film. We also show that disjoining pressure plays a dominant role in the nonevaporating film region and suppresses the evaporation in this region, while capillary pressure dominates the intrinsic meniscus region. Strong evaporation takes place in the thin-film region, and both the disjoining pressure and capillary pressure contribute to the total pressure difference that delivers the liquid from the intrinsic meniscus region to the evaporating thin-film region, compensating for the liquid mass loss due to strong evaporation. Our work provides a new avenue for investigating thin liquid film spreading, liquid transport in nanopores, and microscopic liquid-vapor phase change heat/mass transfer mechanisms near the three-phase contact line region.
High heat flux evaporation of low surface tension liquids from nanoporous membranes
[J].
Capillary-fed, thin film evaporation devices
[J].