Processing math: 6%
上海交通大学学报

上海交通大学学报, 2024, 58(4): 525-533 doi: 10.16183/j.cnki.jsjtu.2022.423

电子信息与电气工程

基于增量式等距映射同双重局部密度方法的工业过程故障检测

冯立伟1,2, 孙立文2,3, 顾欢2,3, 李元,1

1.沈阳化工大学 理学院,沈阳 110142

2.沈阳化工大学 计算机科学与技术学院,沈阳 110142

3.辽宁省化工过程工业智能化技术重点实验室, 沈阳 110142

Industrial Process Fault Detection Based on Incremental Isometric Mapping and Double Local Density Method

FENG Liwei1,2, SUN Liwen2,3, GU Huan2,3, LI Yuan,1

1. College of Science, Shenyang University of Chemical Technology, Shenyang 110142, China

2. College of Computer Science and Technology, Shenyang University of Chemical Technology, Shenyang 110142, China

3. Key Laboratory of Intelligent Technology for Chemical Process Industry of Liaoning Province, Shenyang 110142, China

通讯作者: 李 元,教授,博士生导师; E-mail:li-yuan@mail.tsinghua.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-10-28   修回日期: 2022-12-9   接受日期: 2022-12-30  

基金资助: 国家自然科学基金(61673279)
国家自然科学基金(62273242)

Received: 2022-10-28   Revised: 2022-12-9   Accepted: 2022-12-30  

作者简介 About authors

冯立伟(1980-),讲师,从事基于数据驱动复杂过程故障监控与诊断研究.

摘要

针对工业过程的非线性和动态性问题,提出一种基于流形学习下的增量式等距映射(IISOMAP)与双重局部密度(DLD)相结合的故障检测方法(IISOMAP-DLD).利用 IISOMAP 将原始数据映射到低维流形特征子空间和剩余子空间;然后,在两个子空间中分别引入双重局部密度方法构建统计量对过程进行监控;最后,将IISOMAP-DLD方法应用到田纳西-伊斯曼(TE)过程.实验结果表明,IISOMAP-DLD对比其他方法有更高的故障检测率.IISOMAP在保留数据内在特征的同时,解决了过程的非线性问题,而双重局部密度方法可消除过程的动态性.

关键词： 流形学习; 等距映射; 局部密度; 故障检测; 动态性

Abstract

To address the nonlinearity and dynamics of industrial processes, an incremental isometric mapping (IISOMAP) in combination with double local density (DLD) is proposed as a fault detection method (IISOMAP-DLD) based on stream shape learning. First, IISOMAP is used to map the raw data into a low-dimensional manifold feature subspace and a residual subspace. Then, the double local density method is introduced in the two subspaces respectively to construct statistics to monitor the process. Finally, the IISOMAP-DLD method is applied to the Tennessee-Eastman (TE) process, and the experimental results show that IISOMAP-DLD has a higher fault detection rate than the other methods. IISOMAP preserves the intrinsic characteristics of the data and solves the nonlinear problems of the process, while the double local density method can eliminate the dynamic of the process.

Keywords： manifold learning; isometric mapping (ISOMAP); local density; fault detection; dynamic

PDF (2253KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

冯立伟, 孙立文, 顾欢, 李元. 基于增量式等距映射同双重局部密度方法的工业过程故障检测[J]. 上海交通大学学报, 2024, 58(4): 525-533 doi:10.16183/j.cnki.jsjtu.2022.423

FENG Liwei, SUN Liwen, GU Huan, LI Yuan. Industrial Process Fault Detection Based on Incremental Isometric Mapping and Double Local Density Method[J]. Journal of Shanghai Jiaotong University, 2024, 58(4): 525-533 doi:10.16183/j.cnki.jsjtu.2022.423

随着工业产品质量和操作安全要求的不断提高,过程监控在工业生产过程中得到了更多的关注和重视[1-2].过程监控方法主要分为基于模型的方法、基于知识的方法和基于数据的方法[3].其中,过程数据易于收集与分析,具有更高的通用性,因此基于数据的方法得到了迅速发展.

为了获得稳定的产品质量和持续的利润,基于过程数据的多元统计分析方法已经被广泛应用[4-5],由于实际工业过程中数据往往具有动态性和非线性等特征,所以传统的线性方法在实际工业过程监控中会出现故障漏报和误报的现象[6-7].针对非线性特征,Lee等[8]提出核主成分分析(Kernel Principal Component Analysis, KPCA),通过核映射把数据映射到高维空间使之线性可分.邓佳伟等[9]提出加权统计局部核主成分分析,研究全新的局部加权策略,提高了核主成分分析对微小故障检测的能力.考虑到工业过程具有动态性的特点,Ku等[10]提出动态主成分分析(Dynamic Principal Component Analysis, DPCA),该方法对主成分分析(PCA)引入时滞矩阵,捕获了过程的动态信息.为了解决过程的动态非线性问题,张佳鑫等[11]提出时间逻辑算法和动态核主成分分析(DKPCA),此方法分析变量之间的时间特性和相关性,对动态数据矩阵分段捕获故障信息,有效提高了故障检测效果.冯立伟等[12]提出PCA与加权k近邻相结合的故障检测方法,将局部近邻的平均距离作为权重,构建加权距离,有效解决工况中心漂移和方差差异显著等问题.Zhang等[13]考虑到微弱故障发生在密集过程处,提出加权k近邻策略消除多模态的影响,降低统计量的自相关性.Wang等[14]提出多维敏感性特征的加权k近邻(WKNN)方法,计算滚动轴承数据的每个特征权重获得高维敏感特征集,使用WKNN模型进行分类诊断,有效提高检测精度.

考虑到过程的动态变化,慢特征分析(Slow Feature Analysis, SFA)被应用到过程监控领域[15].SFA方法从过程数据中提取过程变化的最缓慢信息,适用于动态过程检测.Bohmer等[16]首次将核技巧应用到SFA中提出核慢特征分析(Kernel SFA,KSFA),实现音频数据的分类.卢依容[17]将KSFA运用到过程监控中,实验结果证明了KSFA在故障检测方面的有效性和可行性.Zhang等[18]提出了核慢特征判别分析(Kernel Slow Feature Discriminant Analysis,KSFDA),将局部判别分析与核SFA方法相结合来识别故障数据.黄健等[19]提出在线故障相关特征选择SFA策略,将在线数据超过阈值的特征作为故障特征,对过程进行监控.上述方法仅是从局部结构出发来寻找样本间的结构关系,忽略了全局结构信息对过程监控的影响.

从数据的全局结构出发,Tenenbaum等[20]首次提出等距映射(Isometric Mapping, ISOMAP)方法,解决了非线性问题,并应于计算机视觉领域.Zhang等[21]将ISOMAP方法应用于滚动轴承机械故障分类中,提出局部线性回归方法.此方法处理新样本数据低维映射的问题,解决了传统故障模式识别的缺陷,提高了故障分类性能.张妮等[22]提出相对测地距离ISOMAP,并使用核岭回归计算新样本的低维输出,从而提高了故障检测率.但是以上ISOMAP方法均未考虑过程具有动态性的问题,当数据具有动态性时,以上方法的监控性能较弱.

针对过程具有非线性和动态性特征的故障检测问题,本文提出了一种基于增量式等距映射同双重局部密度(Incremental Isometric Mapping-Double Local Density, IISOMAP-DLD)的故障检测策略.首先,采用IISOMAP在保持样本间测地距离近似不变的情况下,提取数据的低维流形结构;其次,对特征数据采用双重局部密度(DLD)方法消除动态性并构建统计量τ;最后,采用统计量τ对过程进行监控.

1 等距映射方法

等距映射方法采用“测地线距离”替代欧氏距离,从全局结构来表示特征空间内数据点之间存在的几何关系,对多维尺度变换(Multidimensional Scaling,MDS)方法[23-24]实现进一步优化,即高维空间数据Xn×m=[x1x2…xn]T,xi∈Rm, i=1, 2, …, n,经ISOMAP方法提取的低维特征数据为Tn×d=[t1t2…tn]T,ti∈Rd.

ISOMAP的基本步骤可分为以下3步.

(1) 使用数据点间的欧氏距离D=[dE(xi, xj)](dE(xi, xj)表示第i个样本到第j个样本间的欧氏距离),选择k近邻或ε邻域法确定近邻关系,构造邻域图G.

(2) 采用Floyd算法或Dijkstra算法,使用邻域图G上两点之间的最短路径逼近流形上的测地距离:

dM(xi,xj)=min
(1)

p=1, 2, …, n

(3) 将测地距离矩阵DM代入MDS方法,计算内积:

{{b}_{ij}}=-\frac{1}{2}\times \left( d_{ij}^{2}-\frac{1}{n}\overset{n}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,d_{ij}^{2}-\frac{1}{n}\overset{n}{\mathop{\underset{j=1}{\mathop \sum }\,}}\,d_{ij}^{2}+\frac{1}{{{n}^{2}}}\overset{n}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,\overset{n}{\mathop{\underset{j=1}{\mathop \sum }\,}}\,{{d}_{ij}} \right)
(2)

式中:dij为样本xi与xj在高维空间测地距离.对内积矩阵B进行特征值分解,

B=V\Lambda {{V}^{T}}
(3)

获得特征向量矩阵V和特征值矩阵Λ.

最后,选择前K个最大特征值及对应的特征向量分别组成矩阵VK和ΛK.原始数据X在低维空间的流形结构为

T={{V}_{K}}\Lambda _{K}^{1/2}
(4)

不同于线性投影方法,ISOMAP方法无映射矩阵,不能直接对新样本进行高效投影.

2 基于增量式等距映射同双重局部密度检测策略

2.1 增量式等距映射

为了实现非线性过程中新样本的在线投影,引入增量式方法[25]将ISOMAP改进为IISOMAP方法.增量式等距映射解决了等距映射方法缺少映射矩阵对新样本在线投影的问题,IISOMAP的基本步骤可分为以下3步.

(1) 更新邻域图Gnew.计算新样本到原始样本的欧氏距离Dnew=[dE(xnew, xi)],寻找新样本点xnew在原始样本中的k个近邻xnew, 1, xnew, 2, …, xnew, k,更新邻域关系Gnew.

(2) 计算测地距离.计算新样本到原始样本的测地线距离:

\begin{matrix} & {{d}_{Mnew}}({{x}_{new}},{{x}_{i}})=~\min \{{{d}_{E}}({{x}_{new}},{{x}_{new,1}})+{{d}_{M}}({{x}_{new,1}},{{x}_{i}}),\ldots, \\ & {{d}_{E}}({{x}_{new}},{{x}_{new,k}})+{{d}_{M}}({{x}_{new,k}},{{x}_{i}})\} \\ & ~i=1,2\ldots,n \\ \end{matrix}
(5)

(3) 寻找新样本的低维输出.用训练样本间测地距离和新样本到训练样本的测地距离dnew,i来表示tnew和ti的内积:

{{f}_{i}}={{t}_{i}}t_{new}^{\text{T}}=-\frac{1}{2}\left( d_{\text{new}, ~ i}^{2}-\frac{1}{n}\underset{i=1}{\mathop \sum }\,d_{\text{new}, ~ i}^{2}+\frac{1}{{{n}^{2}}}\underset{ij}{\mathop \sum }\,{{d}_{ij}}-\frac{1}{n}\underset{j}{\mathop \sum }\,{{d}_{ij}} \right)
(6)

由式(6)得线性方程组:

TtnewT=f
(7)

式中: T=λ1ν1…λKνK为原始训练样本集X经ISOMAP降维后的样本集.求解式(7)得到降维后新的投影点:

tnew=1λ1fTν1…1λKfTνK
(8)

IISOMAP通过更新邻域图和测地线距离,保持高维空间数据的全局非线性结构,解决了新样本的非线性映射问题.

2.2 双重局部密度

动态性是指在非稳态工况下过程变量与时间相关的特性,即采样的数据呈现出随着时间变化的特征.过程当前时刻的状态被前面时刻所影响,最终造成数据不服从多元高斯分布.因此,使用经典的多元统计方法进行过程监控,会出现误报和漏报的问题.为了消除数据的动态性,提出双重局部密度策略.

计算经IISOMAP降维后ti与tj间的欧氏距离:

{{L}_{2}}({{t}_{i}},{{t}_{j}})={{\left( {{t}_{i}}-{{t}_{j}} \right)}^{2}}
(9)

根据欧氏距离确定邻域半径ε:

\varepsilon =\kappa (\min ({{L}_{2}}({{t}_{i}},{{t}_{j}})))
(10)

式中:κ为参数.

计算第1层密度:

{{\rho }_{i}}=\text{num}(\Theta {{t}_{i}},{{\varepsilon }_{1}})
(11)

式中:ρi表示以ti为圆心,以ε1为邻域半径的圆所包含样本Θti={ti1, …, tif, …, tiε}的个数.

然后再对Θti中每个样本tif以ε2为邻域半径,计算第2层密度:

{{\zeta }_{i}}=\frac{1}{{{\rho }_{i}}}\overset{{{\rho }_{i}}}{\mathop{\underset{i=1}{\mathop \sum }\,}}\,\text{num}((\Theta t_{i}^{f},{{\varepsilon }_{1}}))
(12)

最后对ti进行双重局部密度处理,构造统计量:

{{\tau }_{i}}=\frac{1}{{{\rho }_{i}}}{{\zeta }_{i}}
(13)

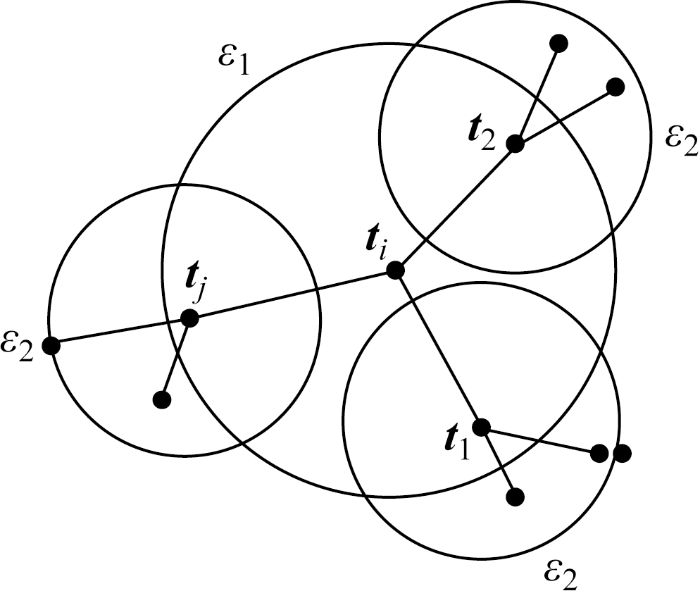
图1为ti双重局部密度示意图.ti的第1层密度以ε1为邻域半径,用来确定邻域内包含的样本个数.在第1层密度包含的所有样本的基础上分别确定以ε2为半径的第2层密度值,将此值作为权重施加在第1层上.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   双重局部密度示意图

Fig.1   Diagram of double local density


DLD方法之所以能够解决动态性问题,是因为该方法在统计量的构建过程中,第1层邻域密度体现了数据所处位置的稀疏情况,第2层密度调整了同一个阶段数据的疏密程度,使整个数据的疏密程度近似相同,样本当前时刻的结果被前面时刻所影响的问题得到解决.此外,τ为一组独立同分布的随机变量,具有共同的累积分布函数H(τ).定义样本的最大值Mn=max{τ1, τ2, …, τn},存在常数列{an>0}和{bn},使得下式成立:

limn→∞Pr Mn-bnan≤τ=H(τ), 　τ∈R
(14)

根据Fisher-Tippett极值I类型定理[26], 可以判定统计量服从Gumbel极值分布.

2.3 基于IISOMAP-DLD的故障检测策略

IISOMAP方法单独计算新样本的低维映射,避免了训练样本重复计算的问题,但是提取的特征数据动态性仍然存在.因此,为了消除过程存在的动态性,提出IISOMAP与DLD方法相结合的策略.

在2.1节中IISOMAP方法是通过测地距离矩阵,经内积变换获得低维空间的流形展开.该方法在故障检测中存在以下两个问题:一是重构问题,IISOMAP 方法是获取高维数据的低维流形展开,无法还原回去,得不到残差空间;二是IISOMAP方法对高维数据进行低维流形展开时,出现部分故障落入正常数据中的问题.采用一个非线性动态数值模拟过程进行问题2的论述,数值模型如下:

x1=tcostx2=1.5hx3=tsint
(15)

该过程包含5个变量,h, t为潜隐变量, 其中采样时间t∈[0,10] min;h~U(0, 1).

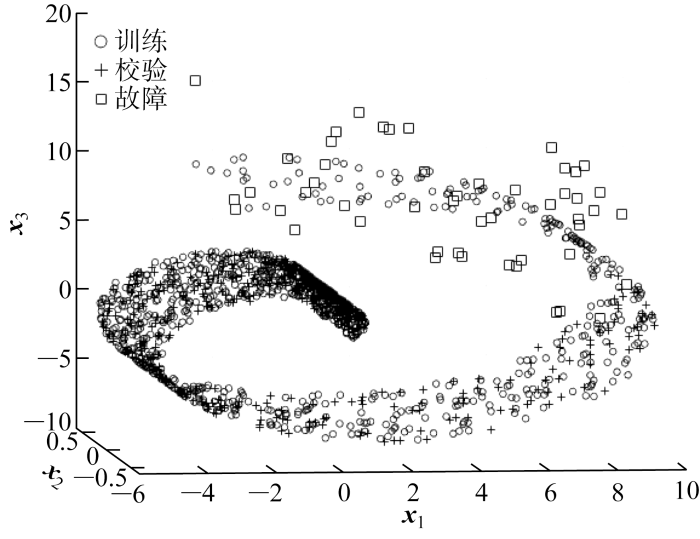
正常运行过程中,采样间隔为0.01 min,产生 1 001 个正常样本数据建立监控模型.过程再次正常运行时,以0.02 min的采样间隔,第9 min时刻后在变量x3增加 -6.5 ~6.5之间的随机扰动.变量x1和x3随时间t发生变化,以曲线形式波动,使过程呈现出非线性和动态性特点,图2为原始数据中心化后的散点图.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   中心化后数据散点图

Fig.2   Data scatter plot after centralization


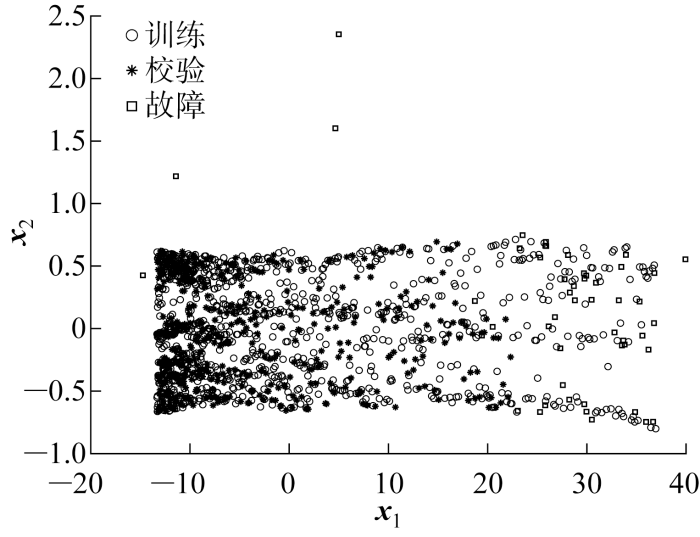
IISOMAP方法通过流形展开,将数据投影到低维流形特征空间中.由于故障发生在变量x3上,所以可以发现大部分故障数据展开后都落入训练数据中,如图3所示.虽然特征子空间构造的统计量τ反映了模型内部的数据变化状态,但也会出现占据主导地位的主元数目选择不合适或故障发生位置并不在主导变量上的问题.因此,按以下公式利用剩余非主元构建剩余子空间,并用式(13)计算其统计量τe补偿这种损失.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   IISOMAP特征空间中样本

Fig.3   Samples in IISOMAP feature space


训练数据集X在剩余子空间的投影为

E={{V}_{e}}\Lambda _{\text{e}}^{\frac{1}{2}}
(16)

新样本xnew在剩余子空间的投影为

{{e}_{new}}={{f}^{T}}{{V}_{e}}/\sqrt{{{\Lambda }_{\text{e}}}}
(17)

式中:Ve和Λe分别为剩余的特征值及对应的特征向量组成的矩阵.

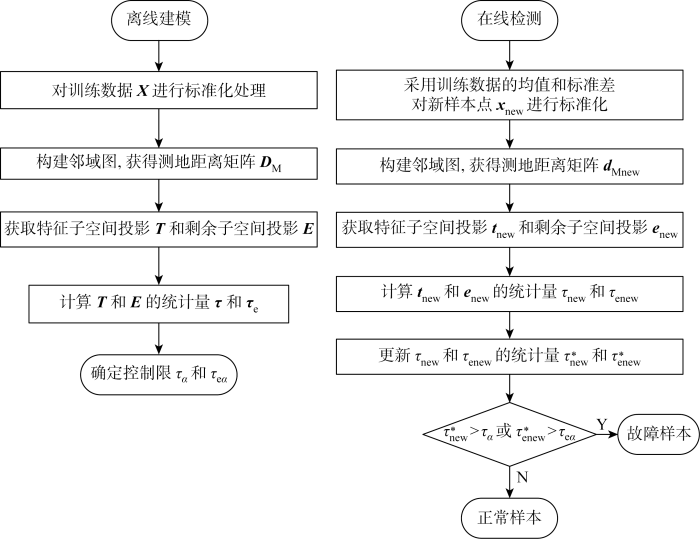
图4为IISOMAP-DLD方法的故障检测流程图,故障检测过程分为两个阶段:离线建模和在线检测.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   IISOMAP-DLD方法的故障检测流程图

Fig.4   Flow chart of fault detection of IISOMAP-DLD method


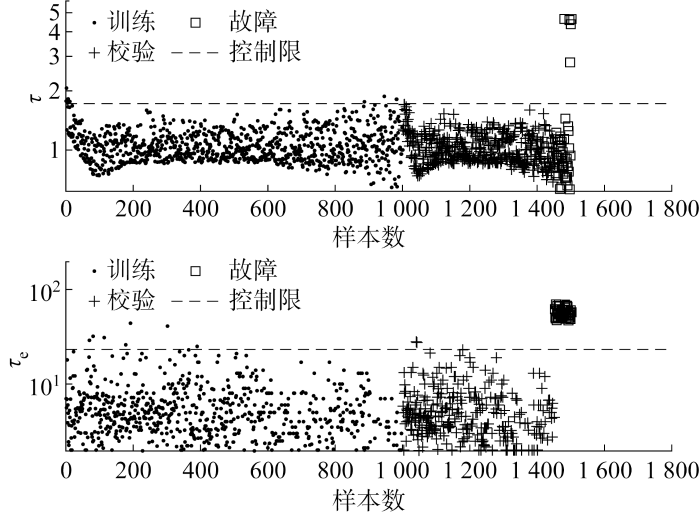
图5为IISOMAP-DLD方法检测出的全部故障点.图3为高维空间提取的低维流形结构,因为故障样本的主要信息处于剩余子空间中,所以在特征空间中方框故障点大部分落在正常数据中,流形特征空间检测结果不理想,而剩余子空间的检测率为100%.图5统计量的分布显示动态性大幅度降低,因此,IISOMAP-DLD方法能很好地处理非线性动态过程.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   IISOMAP-DLD检测图

Fig.5   Diagram of IISOMAP-DLD detection


通过下式计算Gumbel极限分布概率密度函数(PDF):

f(τ;μ, β)=e-z-e-z,　z=τ-μβ
(18)

式中:μ为位置参数(在Gumbel中为众数);β为尺度系数.

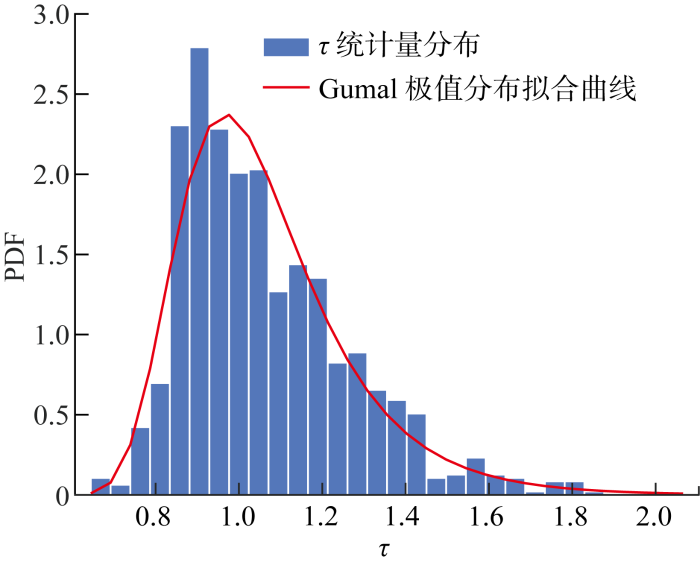
对DLD处理后统计量作拟合,拟合结果如图6所示.可以看出计算的PDF使统计量得到了很好的拟合,因此,统计量近似服从Gumbel极限分布得到证明.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   DLD拟合结果

Fig.6   Result of DLD fitting


3 Tennessee Eastman 过程监控

采用一个具有非线性和动态特性的通用测试平台田纳西-伊斯曼(Tennessee Eastman, TE)过程[17,22,27⇓⇓ -30],将本文所提方法与KPCA、DKPCA、WKNN、KSFA方法的检测结果进行对比分析,验证IISOMAP-DLD的有效性.TE过程是Downs和Vogel根据伊斯曼化学公司的实际化工反应过程开发的标准测试实验平台,其数据具有非线性、强耦合和时变等特性,是典型的复杂工业过程.TE过程由5个主要操作单元组成: 反应器、冷凝器、压缩机、汽提器和分离器.TE过程包含22个连续测量变量、19个组分测量变量和12个操纵变量[27],过程的详细解释参考文献[6-7,9⇓-11,28].

反应时间设为10 h,采样时间设为0.01 h,其余参数使用系统默认值,获得一批正常数据用于训练模型.过程多次运行在3 h后引入21类故障,生成21组测试数据,编号为f1~f21.由于过程的3个控制变量恒定不变,所以本文选择50个重要变量作为监控变量.表1为各种方法对TE过程进行故障检测的结果.表中:T2为霍特林统计量;Te2为由残余慢特征计算的霍特林统计量;SPE为平方预测误差统计量;D为加权距离统计量.

表1   TE过程中各方法的故障检测率

Tab.1  Fault detection rate of each method in TE process

组别KPCADKPCAWKNN
D/%		KSFAIISOMAP-DLD
T2/%SPE/%T2/%SPE/%T2/%Te2/%τ/%τe/%
f198.8699.1498.5499.4398.8699.0098.5799.1499.54
f294.0194.8692.4494.1596.5797.0094.8699.0099.54
f30.4315.550.571.4120.8625.0052.2969.0019.86
f499.7199.7110010099.8699.8699.8610099.86
f5030.1000.7037.7142.0057.7173.7114.71
f699.7199.7110010099.8699.8699.8610099.86
f799.7199.7110010099.8699.8699.8610099.86
f886.8889.8785.8489.8488.4388.7188.7190.0086.00
f93.4217.261.573.3422.0017.7147.0062.1415.57
f1085.1689.3083.1284.5588.1490.8687.2990.4383.00
f1196.8698.4394.1398.0097.8698.1492.0098.7195.29
f1236.0980.8824.7546.3570.8660.5773.2979.7142.57
f1394.0195.0194.2894.999494.4393.7195.5793.71
f1498.5798.7298.7198.8698.7198.7191.4399.0098.00
f1503.570013.297.2958.8667.147.57
f161.281.281.291.000.860.710.7129.8616.43
f1783.1784.8882.9884.5584.7184.5782.4386.8683.00
f1849.0763.6249.5058.0856.8655.5759.8668.8662.00
f1991.8795.7289.5694.4294.5796.0094.4396.7195.14
f2084.8885.1684.9885.4184.2984.4381.8685.1483.71
f211.431.281.431.000.710.711.4129.2915.86

新窗口打开| 下载CSV


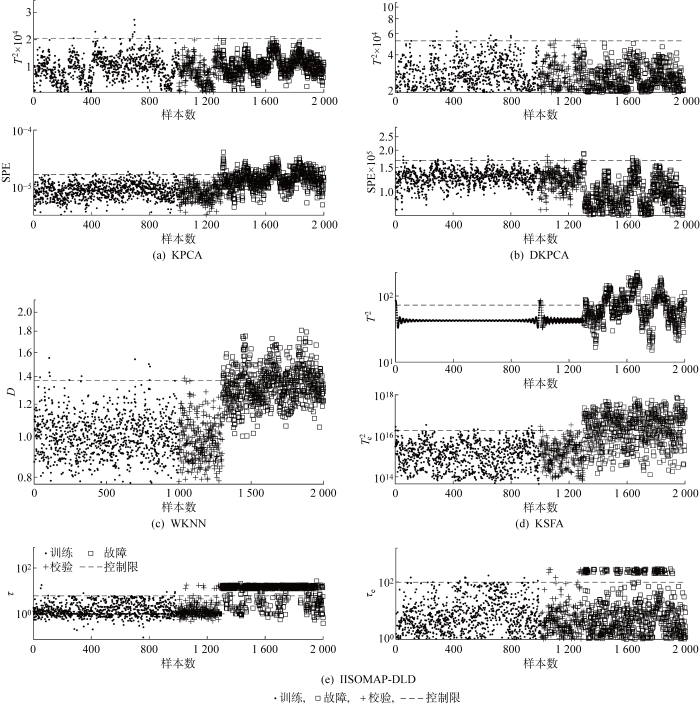
对于大多数故障,IISOMAP-DLD比KPCA、DKPCA、WKNN和KSFA具有更好的监控性能,其中故障f5、f9、f15、f16等为偏离幅度小的故障.表1表明,KPCA和DKPCA检测效果最差,WKNN和KSFA检测率一般,而IISOMAP-DLD具有最高的检测率.以施加在冷凝器冷却水的入口温度变化产生的故障f5为例,此时冷凝器到分离器的输出流速增加,导致分离器内的温度和分离器冷却水的输出口温度增加,从而引起阶跃故障.5种方法的检测结果如图7所示,其中前 1 000 个为训练样本,后 1 000 个为测试样本.因为TE过程数据并不服从高斯分布,所以KPCA和DKPCA并不能很好地把故障点分离开,导致检测率不高.WKNN和KSFA算法能处理部分动态信息,检测结果有所提高,但由于施加的阶跃故障不明显,所以WKNN中故障样本的加权k近邻计算的统计值低于控制限.此外,微小故障导致KSFA提取的慢特征和正常样本接近,因此这两种方法并不能很好地将故障信息和正常信息区分开.IISOMAP-DLD方法采用IISOMAP提取了样本的非线性特征,且从图7(e)的统计量分布能看出双重密度操作消除了过程的动态特征,因此故障检测率较高.实验结果显示,本文所提方法能有效提取非线性特征和消除过程的动态性.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   5种方法的检测图

Fig.7   Diagrams of detection of five methods


4 结语

针对传统多元统计方法对非线性动态过程进行故障检测时存在的漏报和误报的问题,提出一种基于IISOMAP-DLD的过程监控方法,解决了等距映射对新样本无法映射的问题,通过调整样本间的疏密程度消除了动态性问题.理论分析和实验结果均表明,本文方法相对于KPCA、DKPCA、WKNN、KSFA方法具有更高的检测效率,这对工业发展以及生产安全管理具有一定指导性的理论意义.

参考文献

RAMAKRISHNA K, MRINMAYEE B, MUDDU M.

Kantorovich distance based fault detection scheme for non-linear processes

[J]. IEEE Access, 2022, 10: 1051-1067

DOI:10.1109/ACCESS.2021.3138696      URL     [本文引用: 1]

陈法法, 杨晓青, 陈保家, 等.

基于正交邻域保持嵌入与多核相关向量机的滚动轴承早期故障诊断

[J]. 计算机集成制造系统, 2018, 24(8): 1946-1954.

[本文引用: 1]

CHEN Fafa, YANG Xiaoqing, CHEN Baojia, et al.

Early fault diagnosis of rolling bearing based on orthogonal neighbourhood preserving embedding and multi-kernel relevance vector machine

[J]. Computer Integrated Manufacturing Systems, 2018, 24(8): 1946-1954.

[本文引用: 1]

GUO J Y, ZHONG L L, LI Y.

Fault detection of multi-mode batch process based on statistics difference LPP

[J]. Application Research of Computers, 2019, 36(1): 123-126.

[本文引用: 1]

CAO L J, CHUA K S, CHONG W K, et al.

A comparison of PCA, KPCA and ICA for dimensionality reduction in support vector machine

[J]. Neurocomputing, 2003, 55(1/2): 321-336.

DOI:10.1016/S0925-2312(03)00433-8      URL     [本文引用: 1]

赵小强, 姚红娟.

改进邻域保持嵌入—独立元分析的间歇过程故障检测算法

[J]. 计算机集成制造系统, 2021, 27(4): 1062-1071.

DOI:10.13196/j.cims.2021.04.010      [本文引用: 1]

针对间歇过程数据的非线性和高斯与非高斯混合分布特性导致故障检测效果不佳的问题,提出了基于多向差分邻域保持嵌入—加权差分独立元分析(MDNPE-WDICA)的间歇过程故障检测算法。首先采用Jarque-Bera检验方法(J-B test)将原始数据空间划分为高斯和非高斯子空间;然后,在高斯子空间,将差分策略与NPE算法结合提出MDNPE算法,对高斯空间数据进行维数约简,在保持其局部结构不变的同时处理非线性,并克服传统非线性处理方法由于引入核函数带来的计算复杂的问题;在非高斯子空间,将加权差分策略与ICA算法结合提出WDICA算法,在充分提取数据非高斯信息的同时解决其非线性,并有效利用数据的局部信息;最后,通过贝叶斯推断构建一个新的监测统计量,实现整个间歇过程数据的故障检测。通过青霉素生产过程仿真结果验证了所提算法的可行性和有效性。

ZHAO Xiaoqiang, YAO Hongjuan.

Fault detection algorithm of batch process based on improved neighborhood preserving embedding-independent component analysis

[J]. Computer Integrated Manufacturing Systems, 2021, 27(4): 1062-1071.

[本文引用: 1]

KONG X Y, LI Q, AN Q S, et al.

Quality-related fault detection based on partial least squares score reconstruction

[J]. Control Theory and Applications, 2020, 37(11): 2321-2332.

[本文引用: 2]

董顺, 李益国, 孙栓柱, 等.

基于状态空间主成分分析网络的故障检测方法

[J]. 化工学报, 2018, 69(8): 237-245.

[本文引用: 2]

DONG Shun, LI Yiguo, SUN Shuanzhu, et al.

Fault detection method based on state space principal component analysis network

[J]. CIESC Journal, 2018, 69(8): 237-245.

[本文引用: 2]

LEE J, YOO C, LEE I.

Fault detection of batch processes using multiway kernel principal component analysis

[J]. Computers and Chemical Engineering, 2004, 28(9): 1837-1847.

DOI:10.1016/j.compchemeng.2004.02.036      URL     [本文引用: 1]

邓佳伟, 邓晓刚, 曹玉苹, 等.

基于加权统计局部核主元分析的非线性化工过程微小故障诊断方法

[J]. 化工学报, 2019, 70(7): 2594-2605.

DOI:10.11949/j.issn.0438-1157.20181307      [本文引用: 2]

传统统计局部核主元分析（statistical local kernel principal component analysis, SLKPCA）在构造改进残差时未考虑样本的差异性，使得故障样本信息易于被其他样本所掩盖，针对该问题，提出一种基于加权统计局部核主元分析（weighted statistical local kernel principal component analysis, WSLKPCA）的非线性化工过程微小故障诊断方法。该方法首先利用KPCA获取过程的得分向量和特征值并构建初始残差。然后设计了一种基于测试样本与训练样本之间距离的加权策略构建加权改进残差，对含有较强微小故障信息的样本赋予较大权值，以增强故障样本的影响。最后，采用基于测量变量与监控统计量之间的加权互信息构建贡献图以识别故障源变量。在连续搅拌反应釜和田纳西伊斯曼（Tennessee Eastman, TE）化工过程上的仿真结果表明,所提方法具有良好的微小故障检测与识别性能。

DENG Jiawei, DENG Xiaogang, CAO Yuping, et al.

Incipient fault diagnosis method of nonlinear chemical process based on weighted statistical local KPCA

[J]. CIESC Journal, 2019, 70(7): 2594-2605.

[本文引用: 2]

KU W, ROBERT H, CHRISTOS G.

Disturbance detection and isolation by dynamic principal component analysis

[J]. Chemometrics and Intelligent Laboratory Systems, 1995, 30: 175-196.

[本文引用: 2]

张佳鑫, 罗文嘉, 戴一阳.

基于CTA-DKPCA的化工过程故障诊断

[J]. 控制工程, 2021, 28(5): 844-850.

[本文引用: 2]

ZHANG Jiaxin, LUO Wenjia, DAI Yiyang.

Chemical process fault diagnosis based on CTA-DKPCA

[J]. Control Engineering, 2021, 28(5): 844-850.

[本文引用: 2]

冯立伟, 张成, 李元.

基于PC-WKNN的多工况间歇过程故障检测方法研究

[J]. 计算机应用研究, 2018, 35(4): 1130-1134.

[本文引用: 1]

FENG Liwei, ZHANG Cheng, LI Yuan.

Research on fault detection method of multi-mode intermittent process based on PC-WKNN

[J]. Application Research of Computers, 2018, 35(4): 1130-1134.

[本文引用: 1]

ZHANG C, GAO X W, LI Y, et al.

Fault detection strategy based on weighted distance of k nearest neighbors for semiconductor manufacturing processes

[J]. IEEE Transactions on Semiconductor Manufacturing, 2018, 32(1): 75-81.

DOI:10.1109/TSM.2018.2857818      URL     [本文引用: 1]

WANG Q F, WANG S, WEI B K, et al.

Weighted k-NN classification method of bearings fault diagnosis with multi-dimensional sensitive features

[J]. IEEE Access, 2021, 9: 45428-45440.

DOI:10.1109/ACCESS.2021.3066489      URL     [本文引用: 1]

SHANG C, HUANG B, YANG F, et al.

Probabilistic slow feature analysis-based representation learning from massive process data for soft sensor modeling

[J]. AIChE Journal, 2015, 61(12): 4126-4139.

DOI:10.1002/aic.v61.12      URL     [本文引用: 1]

BOHMER W, GRUNEWALDER S, NICKISCH H, et al.

Regularized sparse kernel slow feature analysis

[C]// European Conference on Machine Learning and Knowledge Discovery in Databases-Volume Part I. Heidelberg, Germany: Springer, 2011: 235-248.

[本文引用: 1]

卢依容. 基于核慢特征分析算法的故障检测与诊断[D]. 上海: 上海交通大学, 2015.

[本文引用: 2]

LU Yirong. Fault detection and diagnosis based on kernel slow feature analysis algorithm[D]. Shanghai: Shanghai Jiao Tong University, 2015.

[本文引用: 2]

ZHANG H, TIAN X, CAI L.

Nonlinear process fault diagnosis using kernel slow feature discriminant analysis

[J]. IFAC Papersonline, 2015, 48(21): 607-612.

DOI:10.1016/j.ifacol.2015.09.593      URL     [本文引用: 1]

黄健, 杨旭, 陈先中.

基于故障相关慢特征分析的过程监测方法

[J]. 高校化学工程学报, 2020, 34(5): 1290-1296.

[本文引用: 1]

HUANG Jian, YANG Xu, CHEN Xianzhong.

Process monitoring method based on fault related slow characteristic analysis

[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(5): 1290-1296.

[本文引用: 1]

TENENBAUM J, SILVA V, LANGFORD J.

A global geometric framework for nonlinear dimensionality reduction

[J]. Science, 2000, 290(5500): 2319-2323.

DOI:10.1126/science.290.5500.2319      PMID:11125149      [本文引用: 1]

Scientists working with large volumes of high-dimensional data, such as global climate patterns, stellar spectra, or human gene distributions, regularly confront the problem of dimensionality reduction: finding meaningful low-dimensional structures hidden in their high-dimensional observations. The human brain confronts the same problem in everyday perception, extracting from its high-dimensional sensory inputs-30,000 auditory nerve fibers or 10(6) optic nerve fibers-a manageably small number of perceptually relevant features. Here we describe an approach to solving dimensionality reduction problems that uses easily measured local metric information to learn the underlying global geometry of a data set. Unlike classical techniques such as principal component analysis (PCA) and multidimensional scaling (MDS), our approach is capable of discovering the nonlinear degrees of freedom that underlie complex natural observations, such as human handwriting or images of a face under different viewing conditions. In contrast to previous algorithms for nonlinear dimensionality reduction, ours efficiently computes a globally optimal solution, and, for an important class of data manifolds, is guaranteed to converge asymptotically to the true structure.

ZHANG Y, LI B W, WANG Z B, et al.

Fault diagnosis of rotating machine by isometric feature mapping

[J]. Journal of Mechanical Science & Technology, 2013, 27(11): 3215-3221.

[本文引用: 1]

张妮, 田学民, 蔡连芳.

基于RISOMAP的非线性过程故障检测方法

[J]. 化工学报, 2013, 64(6): 2125-2130.

DOI:10.3969/j.issn.0438-1157.2013.06.031      [本文引用: 2]

化工过程监控数据存在非线性特点,且过程常常运行于多个模态,针对该类问题,提出基于相对等距离映射(relative isometric mapping, RISOMAP)的过程故障检测方法,该方法采用相对测地距离构造高维空间的距离关系阵,运用多维尺度变换(MDS)计算其低维嵌入输出,从高维数据中提取子流形信息和残差信息分别构造监控统计量进行故障检测,同时运用核ridge回归在线计算测试数据的低维输出,核矩阵通过综合相似度进行更新。数值算例和TE过程的仿真结果表明,RISOMAP方法可以更为有效地实施故障检测,故障检测的灵敏度较高,同时也为基于流形学习的多模态过程故障检测的实施提供了一条思路。

ZHANG Ni, TIAN Xuemin, CAI Lianfang.

Nonlinear process fault detection method based on RISOMAP

[J]. CIESC Journal, 2013, 64(6): 2125-2130.

[本文引用: 2]

COX T, COX M.

Multidimensional scaling

[J]. Journal of the Royal Statistical Society, 2001, 46(2): 1050-1057.

[本文引用: 1]

NASIR S, HAEWOON N, MIAN I U H, et al.

A survey on multidimensional scaling

[J]. ACM Computing Surveys (CSUR), 2018, 51(3): 471-496.

[本文引用: 1]

LAW M, JAIN A.

Incremental nonlinear dimensionality reduction by manifold learning

[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 28(3): 377-391.

[本文引用: 1]

SHANBHAG D N, RAO C R. Handbook of statistics stochastic processes: Theory and methods[M]. Amsterdam,Netherlands: Elsevier, 2001.

[本文引用: 1]

DENG X, TIAN X, CHEN S, et al.

Nonlinear process fault diagnosis based on serial principal component analysis

[J]. IEEE Transactions on Neural Networks & Learning Systems, 2018, 29(3): 560-572.

[本文引用: 2]

郭金玉, 李文涛, 李元.

在线压缩核主元分析的自适应过程监控

[J]. 上海交通大学学报, 2022, 56(10): 1397-1408.

DOI:10.16183/j.cnki.jsjtu.2021.084      [本文引用: 2]

对于动态系统,传统的核主元分析(KPCA)方法处理的效果不理想.滑动窗口核主元分析方法能适应动态系统的正常参数漂移,但是该方法处理大量的样本时需要较长的运算时间.因此,提出一种在线压缩核主元分析的自适应过程监控方法.该方法在大量的样本中选定较小的训练集作为初始压缩集进行建模,对在线实时采集的数据进行分析,判断新的样本是否正常.若为正常样本,判断该样本是否加入压缩集中,在加入压缩集的同时自动更新在线KPCA模型.将该方法应用到数值例子和田纳西-伊斯曼(TE)过程,仿真结果验证了该方法的有效性.

GUO Jinyu, LI Wentao, LI Yuan.

Adaptive process monitoring based on on-line compressed kernel principal component analysis

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(10): 1397-1408.

[本文引用: 2]

ZHONG X, HAN M, QIU T, et al.

Fault diagnosis of complex process using sparse kernel local fisher discriminant analysis

[J]. IEEE Transactions on Neural Networks & Learning Systems, 2020, 31(5): 1581-1591.

[本文引用: 1]

BATHELT A, RICKER N, JELALI M.

Revision of the Tennessee Eastman process model

[J]. IFAC PapersOnLine, 2015, 48(8): 309-314.

[本文引用: 1]

/

〈 〉