多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义.
为实现异构多智能体系统输出一致性,国内外专家将鲁棒控制[11 ] 、滑模控制[12 ] 、自适应控制[13 ] 等方法与协同控制理论相结合,提出了许多有效的输出一致性控制方案.其中,自适应控制不依赖精确的系统模型,能够有效地处理多智能体系统在复杂任务场景下遇到的系统参数不确定问题[14 -15 ] .文献[16 ]中针对具有外部干扰的异构多智能体系统,分别设计了有限时间自适应控制器和固定时间自适应控制器,实现有限时间和固定时间下的多智能体系统二部平均输出一致性.文献[17 ]中通过设计观测器估计领导者输出信号,并设计分布式自适应极点配置控制器实现非最小相位异构多智能体系统的领导者-跟随者输出一致性.文献[18 ]中构造了一种将观测器估计得到的领导者输出信号作为参考输入的参考模型系统,并设计基于事件触发机制的模型参考自适应控制方法,实现了异构多智能体系统的输出一致性.
上述研究虽然有效地解决了异构多智能体系统的输出一致性问题,但是要求所有跟随者都能够获取领导者信息.实际上,智能体之间存在着通信距离的限制,因而领导者及所有跟随者信息都无法全局可达;并且,多智能体系统在固定通信拓扑下执行复杂任务时存在最大通信距离无法满足实际所需通信距离的问题,此时智能体原有通信链接将会断开并与通信范围内的智能体建立新的通信链接,造成通信拓扑结构突变的情况[19 ] .因此,文献[20 ]中提出了一种分布式输出反馈模型参考自适应控制策略,仅利用相邻智能体信息进行控制器设计,实现异构多智能体领导者-跟随者输出一致性.在此基础上,文献[21 ]中提出了基于切换控制策略的分布式自适应控制器,实现了突变通信拓扑结构的异构多智能体领导者-跟随者输出一致性.但是,文献[21 -22 ]中所设计的控制策略需要满足较为复杂的模型匹配条件.
为解决具有不确定系统参数和突变通信拓扑的异构多智能体系统领导者-跟随者输出一致性问题,本文提出一种基于切换拓扑策略的分布式状态反馈模型参考自适应控制方案.本文的主要贡献为:① 针对领导者-跟随者输出一致性问题,引入局部输出跟踪误差,将全局输出一致性问题转化为相邻智能体局部输出一致性问题;② 针对系统参数已知的情况,为每个跟随者设计对应的参考模型系统,基于切换拓扑策略设计仅依赖邻居信息的分布式参考输入信号和跟随者标称控制器,实现切换拓扑下参考模型-领导者匹配和跟随者-参考模型匹配,进而达成异构多智能体系统在突变通信拓扑结构下的输出一致性;③ 针对系统参数未知的情况,设计分布式自适应控制器和自适应律,实现跟随者对参考模型的渐近输出跟踪,进而实现具有突变通信拓扑的异构多智能体的输出一致性.
1 问题描述
1.1 领导者-跟随者系统
本文考虑一个由N 个异构跟随者与1个虚拟领导者构成的多智能体系统.第i 个跟随者的状态空间方程如下:
(1) $\left.\begin{array}{l}\dot{\boldsymbol{x}}_{i}(t)=\boldsymbol{A}_{i} \boldsymbol{x}_{i}(t)+\boldsymbol{B}_{i} u_{i}(t) \\y_{i}(t)=\boldsymbol{C}_{i} \boldsymbol{x}_{i}(t), \quad i=1,2, \cdots, N\end{array}\right\}$
式中:$\boldsymbol{A}_{i} \in \mathbf{R}^{p_{i} \times p_{i}}, \boldsymbol{B}_{i} \in \mathbf{R}^{p_{i}}, \boldsymbol{C}_{i} \in \mathbf{R}^{1 \times p_{i}} $是未知参数矩阵,pi 为矩阵的维数;$\boldsymbol{x}_{i}(t) \in \mathbf{R}^{p_{i}}$是第i 个跟随者的状态向量;$u_{i}(t) \in \mathbf{R}^{1}$是第i 个跟随者的控制输入信号;$y_{i}(t) \in \mathbf{R}^{1}$是第i 个跟随者的输出信号.每个跟随者系统也可由以下输入-输出形式描述:
(2) $\left.\begin{array}{l}y_{i}(t)=G_{i}(s)\left[u_{i}\right](t), \quad i=1,2, \cdots, N \\G_{i}(s)=k_{\mathrm{p} i} \frac{Z_{i}(s)}{P_{i}(s)}=\boldsymbol{C}_{i}\left(s \boldsymbol{I}_{i}-\boldsymbol{A}_{i}\right)^{-1} \boldsymbol{B}_{i}\end{array}\right\}$
式中:s 表示拉普拉斯变换变量;$ P_{i}(s)=\operatorname{det}\left(s \boldsymbol{I}_{i}-\right. \boldsymbol{A}_{i} )$是pi 阶首一多项式;$Z_{i}(s)$是mi 阶首一多项式$\left(m_{i} \geqslant 0\right) ; k_{\mathrm{p} i}=\boldsymbol{C}_{i} \boldsymbol{A}_{i_{i}-1}^{\rho_{i}-1} \boldsymbol{B}_{i}$为第i 个跟随者系统的高频增益,ρi =pi -mi 为相应跟随者系统的相对阶;“[ ]”是一种连接时域和复域的混合域运算符.yi (t )=Gi (s )[ui ](t )表示为:系统传递函数为Gi (s ),系统输入为ui (t )时的系统输出,这是在自适应控制中常见的符号[23 -24 ] .
(3) y 0 (t)=Wm0 (s)[r0 ](t), Wm0 (s)= 1 ξ m 0 ( s )
式中:r 0 (t )是有界的参考输入信号;ξ m0 (s )是理想的p 0 阶稳定首一多项式. 因此虚拟领导者系统的相对阶ρ 0 =p 0 . 考虑虚拟领导者和跟随者相对阶相同,则有ρ 0 =ρi =ρ ,i =1, 2, …, N.
注1 本文所考虑的多智能体系统属于网络互联系统,智能体之间不存在机械耦合,仅通过通信网络相互连接以进行信息交互,并通过协同控制器设计实现群体目标,例如机器人编队、飞行器编队等[25 ⇓ -27 ] ,各智能体状态方程表示为
其中:ui (t )为产生第i 个智能体与其他智能体之间的耦合效应的协同控制器.而当各个子系统之间存在机械耦合,此时每个子系统的状态将会受到其他子系统状态的直接影响,定义$\mathcal{P}_{i}$为与第i 个子系统存在机械耦合的子系统的集合,则每个子系统的状态方程表示为
其中:$\sum_{j \in \mathcal{P}_{i}} \boldsymbol{A}_{i j} \boldsymbol{x}_{j}(t)$表示第i 个子系统与其他子系统之间的耦合效应,针对这类机械互联系统控制方案的研究可参考文献[25 ,28 ⇓ -30 ].
1.2 通信网络拓扑描述
由于智能体之间通信距离有限,所以领导者信息及各跟随者信息无法全局共享;进一步地,多智能体系统在执行任务时,可能发生原本处于信息交互中的智能体的实际通信所需距离超出其最大通信距离的情况,此时断开原有通信链接的智能体需要与其通信距离内的智能体建立新的链接,造成原有通信网络拓扑结构突变.本文将通信拓扑结构突变视为切换拓扑的情况,对多智能体系统的通信网络进行描述.
为描述通信拓扑结构突变,本文考虑的N +1个智能体之间的信息交互通过时变有向图$\mathcal{G}(t)= \mathcal{G}_{\sigma(t)} $表示,其中$\mathcal{G}_{\sigma(t)}=\left(\mathcal{V}, \mathcal{E}_{\sigma(t)}\right), \mathcal{V}=\left\{v_{0}, v_{1}, \cdots\right. , \left.v_{N}\right\}$为顶点集,$\mathcal{E}_{\sigma(t)} \subseteq \mathcal{V} \times \mathcal{V}$为有向边集.σ (t )是时变有向图$\mathcal{G}(t)$在若干个固定有向图$\mathcal{G}_{p}=\left(\mathcal{V}, \mathcal{E}_{p}\right), p= 1,2, \cdots$, M 中切换的开关信号,其在$t \in[0, \infty)$上具有映射关系$\sigma:[0, \infty) \rightarrow p $.顶点v 0 表示虚拟领导者智能体,vi 代表第i 个跟随者智能体. 有向边$\left(v_{j}, v_{i}\right) \in \mathcal{E}_{\sigma(t)}$代表智能体vi 可以单向地从智能体vj 处获取信息,因此称vj 是vi 的邻居(领导者也可作为vi 的邻居,即$\left.\left(v_{0}, v_{i}\right) \in \mathcal{E}_{\sigma(t)}\right)$.
为了描述通信拓扑结构突变下智能体vi 与其他智能体间的通信关系,定义$\mathcal{N}_{i}(t) $为包含了智能体vi 在t 时刻下所有现有邻居的集合,并定义Σi vi 在t ∈[0, ∞)中所有可能邻居的集合. 因此有集合$\overline{\mathcal{N}}_{i}(t)=\left\{v_{j} \mid v_{j} \in \Sigma_{i}, v_{j} \notin\right. \left.\mathcal{N}_{j}(t)\right\} $表示t 时刻智能体vi 除现有邻居外,所有可能邻居的集合. 当通信网络拓扑结构突变时,若$v_{j} \in \mathcal{N}_{i}(t)$,智能体vi 可获取vj 的正确信息;若$v_{j} \in \overline{\mathcal{N}}_{i}(t)$,原本接收到的vj 的信息将变为0或卡停在某一错误的值上,无法再用于控制器的设计.
1.3 通信拓扑结构突变下输出一致性控制问题
根据上述对领导者-跟随者系统及其通信网络拓扑的描述,领导者信息及所有跟随者信息无法全局共享,且智能体间的邻居关系也可能发生改变.为实现突变通信拓扑结构下异构多智能体系统领导者-跟随者全局输出一致性,给出本文的控制目标.
控制目标 针对具有N 个跟随者和1个虚拟领导者的异构多智能体系统,考虑系统参数不确定以及通信拓扑突变的情况,为每一个跟随者设计一个控制器ui (t ),该控制器仅根据自身以及邻居信息即可使所有跟随者的输出yi (t )渐近跟踪领导者的输出y 0 (t ),达成领导者-跟随者全局输出一致性,即
(4) $\begin{array}{c}\lim _{t \rightarrow \infty} e_{i 0}(t)=\lim _{t \rightarrow \infty}\left(y_{i}(t)-y_{0}(t)\right)=0, \\i=1,2, \cdots, N\end{array}$
为实现上述控制目标,对时变有向图$\mathcal{G}(t)$以及跟随者智能体系统Gi (s )做出以下假设.
假设1 对于每个智能体vi ,至少存在一条始于领导者v 0 ,终于智能体vi 的有向路径.
假设2 本文考虑的有向图$\mathcal{G}(t)$是没有自回路和平行边的简单图.
假设3 (Ai , Bi , Ci )是可稳定的和可观测的.
假设4 系统Gi (s )的零点多项式Zi (s )是稳定的多项式,其阶数mi 是已知的.
注2 假设1和假设2是实现领导者-跟随者一致性的基本假设;假设3 保证了跟随者的输出跟踪及其内部信号的有界性;假设4中,Zi (s )稳定是为了实现模型参考控制,mi 已知是为了选取跟随者参考模型实现自适应控制;假设5是为了设计稳定的自适应律.
2 标称控制器设计
2.1 局部输出跟踪误差
在假设1和2的前提下,Song等[31 ] 中构造了一种局部状态跟踪误差,并获得了若智能体vi 的局部状态跟踪误差收敛,则达成全局状态一致性的结论. 类似地,首先给出当前智能体vi 与其邻居智能体vj 的输出误差eij (t )=yi (t )-yj (t ),并定义如下局部输出跟踪误差:
(5) $\begin{aligned}e_{i}(t)= & \frac{1}{n_{i}(t)} \sum_{v_{j} \in \mathcal{N}_{i}(t)} e_{i j}(t)= \\& y_{i}(t)-\frac{1}{n_{i}(t)} \sum_{v_{j} \in \mathcal{N}_{i}(t)} y_{j}(t)\end{aligned}$
式中:i =1, 2, …, N ;ni (t )是智能体vi 在时刻t 下的邻居数. 当时间趋于无穷时,若局部输出误差ei (t )收敛,则称之为达到了局部输出一致性,而以下给出的引理1则将局部输出一致性推广至全局的领导者-跟随者输出一致性.
引理1 在假设1和假设2的前提下,若跟随者局部输出跟踪误差ei (t )有界,则跟随者输出yi (t )也是有界的,其中i =1, 2, …, N. 更进一步地,若满足局部输出一致性l i m t → ∞ ei (t )=0,则实现领导者- 跟随者全局输出一致性l i m t → ∞ ei 0 (t )=0,其中ei 0 (t )=yi (t )-y 0 (t )为跟随者vi 与领导者v 0 的输出误差,i =1, 2, …, N.
引理1证明过程见附录A.对于具有1个领导者和N 个跟随者的多智能体系统,由引理1可知,只需要每个跟随者vi (i =1, 2, …, N )满足与其邻居智能体的局部输出一致性:
l i m t → ∞ ei (t )=l i m t → ∞ y i ( t ) - 1 n i ( t ) ∑ v j ∈ N i ( t ) y j ( t )
l i m t → ∞ ei 0 (t )=l i m t → ∞ ( yi (t )-y 0 (t ))=0
因此,为实现本文领导者-跟随者全局输出一致性控制目标,将该控制问题进一步分解:① 为每个跟随者设计对应的参考模型,实现参考模型系统的局部输出一致性,进而达成参考模型-领导者匹配,实现各参考模型系统对领导者的全局输出一致性;② 达成跟随者-参考模型匹配,实现各跟随者对其相应参考模型的渐近输出跟踪,进而实现多智能体系统领导者-跟随者全局输出一致性.下面给出标称控制器设计过程.
2.2 参考模型-领导者匹配
(6) $y_{\mathrm{m} i}(t)=W_{\mathrm{m} i}(s)\left[r_{i}\right](t), \quad i=1,2, \cdots, N$
式中:W m i s )=ξ m i - 1 ( s )是一个稳定的传递函数,ξ m i s )=s ρ i a i ρ i - 1 s ρ i - 1 ai 1 s +ai 0 ,通过给定参考输入信号ri (t ),可获得理想的参考输出y m i t ). 进而,由虚拟领导者系统式(3)和跟随者参考模型系统式(6)组成的虚拟多智能体系统可通过以下可控状态空间实现进行表示:
(7) $\left.\begin{array}{l}\dot{\boldsymbol{x}}_{\mathrm{m} i}(t)=\boldsymbol{A}_{\mathrm{m}} \boldsymbol{x}_{\mathrm{m} i}(t)+\boldsymbol{B}_{\mathrm{m} i} r_{i}(t) \\y_{\mathrm{m} i}(t)=\boldsymbol{C}_{\mathrm{m}} \boldsymbol{x}_{\mathrm{m} i}(t), \quad i=0,1,2, \cdots, N\end{array}\right\}$
式中:当i =0时,x m0 (t )∈R p 0 r 0 (t )∈R1 、y m0 (t )=y 0 (t )∈R1 分别为虚拟领导者系统的状态信号、控制输入信号和输出信号,A m0 ∈R p 0 × p 0 B m0 ∈R p 0 C m0 ∈R 1 × p 0 i =1, 2, …, N 时,x m i t )∈R p i ri (t )∈R1 、y m i t )∈R1 分别为跟随者参考模型系统的状态信号、参考输入信号和输出信号,A m i R p i × p i B m i R p i C m i R 1 × p i . 考虑通信距离的限制,跟随者vi 只能获取其邻居的信息(领导者也可以是邻居),因此设计跟随者参考模型式(6)的分布式参考输入信号ri (t )如下所示:
(8) $\begin{aligned}r_{i}(t)= & \boldsymbol{K}_{\mathrm{r} 1 i}^{* \mathrm{~T}} \boldsymbol{x}_{\mathrm{m} i}(t)+\frac{1}{n_{i}(t)} \sum_{v_{j} \in \Sigma_{i}}\left(\boldsymbol{K}_{\mathrm{r} 2 i j}^{* \mathrm{~T}} \delta_{i j}(t) \boldsymbol{x}_{m j}(t)+\right. \\& \left.K_{\mathrm{r} 3 i j}^{*} \delta_{i j}(t) r_{j}(t)\right), \quad i=1,2, \cdots, N\end{aligned}$
式中:K r 1 i * T R 1 × p i vi 的参考模型系统的闭环稳定,K r 2 i j * T R 1 × p j K r 3 i j * 1 保证了参考模型-领导者匹配的实现;δij (t )是用于区分与vi 是否有邻居关系的指示函数,
(9) $\delta_{i j}(t)=\left\{\begin{array}{ll}1, & v_{j} \in \mathcal{N}_{i}(t) \\0, & v_{j} \in \overline{\mathcal{N}}_{i}(t)\end{array}\right.$
指示函数δij (t )用于决定跟随者vi 的参考模型系统是否可以获取vj (vj ∈Σi vi 现有邻居集内的智能体才能共享其参考模型信息用于设计分布式参考输入信号ri (t ). 下面考虑多智能体领导者-跟随者系统通信拓扑结构突变的情况,给出定理1.
定理1 针对跟随者vi (i =1, 2, …, N )的参考模型系统式(6),在满足假设1和假设2的条件下,存在分布式参考输入信号ri (t )使参考模型系统闭环稳定,达成相邻参考模型系统间的局部输出一致性,即
(10) $\begin{array}{l} \lim _{t \rightarrow \infty} e_{\mathrm{r} i}(t)=\lim _{t \rightarrow \infty}\left(y_{\mathrm{m} i}(t)-\right. \\\left.\frac{1}{n_{i}(t)} \sum_{v_{j} \in \Sigma_{i}(t)} \delta_{i j}(t) y_{\mathrm{m} j}(t)\right)=0\end{array}$
进而根据引理1,实现参考模型-领导者匹配,达成各参考模型系统对领导者的全局输出一致性,即
(11) $\begin{array}{c}\lim _{t \rightarrow \infty} e_{\mathrm{m} i 0}(t)=\lim _{t \rightarrow \infty}\left(y_{\mathrm{m} i}(t)-y_{0}(t)\right)=0, \\i=1,2, \cdots, N\end{array}$
证明 首先考虑固定拓扑的情况,此时跟随者vi 的邻居vj (vj ∈i t ))不会改变,因此vi 的邻居数为常值ni (t )=n i * . 记y m i t )的第k 阶导数为
(12) $\begin{array}{c}y_{\mathrm{m} i}^{(k)}(t)=\boldsymbol{C}_{\mathrm{m} i} \boldsymbol{A}_{\mathrm{m} i}^{k} \boldsymbol{x}_{\mathrm{m} i}(t)+\boldsymbol{C}_{\mathrm{m} i} \boldsymbol{A}_{\mathrm{m} i}^{k-1} \boldsymbol{B}_{\mathrm{m} i} r_{i}(t), \\i=1,2, \cdots, N, \quad k=0,1, \cdots, \rho_{i}\end{array}$
当k =0, 1, …, ρi -1时,C m i A m i k - 1 B m i k =ρi 时,C m i A m i k - 1 B m i . 因此设计
(13) $\begin{array}{c}r_{i}(t)=-\boldsymbol{C}_{\mathrm{m} i} \boldsymbol{A}_{\mathrm{m} i}^{\rho_{i}} \boldsymbol{x}_{\mathrm{m} i}(t)-\xi_{\mathrm{m} i}(s)\left[y_{\mathrm{m} i}\right](t)+ \\y_{\mathrm{m} i}^{\left(\rho_{i}\right)}(t)+\frac{1}{n_{i}^{*}} \sum_{v_{j} \in \mathcal{N}_{i}(t)} \xi_{\mathrm{m} i}(s)\left[y_{\mathrm{m} j}\right](t), \\i=1,2, \cdots, N\end{array}$
每个智能体具有相同的相对阶,即ρ 0 =ρi =ρj =ρ ,因此式(13)可以写为
(14) $\begin{aligned}r_{i}(t)= & \boldsymbol{K}_{\mathrm{r} 1 i}^{* \mathrm{~T}} \boldsymbol{x}_{\mathrm{m} i}(t)+\frac{1}{n_{i}^{*}} \sum_{v_{j} \in \mathcal{N}_{i}(t)}\left(\boldsymbol{K}_{\mathrm{r} 2 i j}^{* \mathrm{~T}} \boldsymbol{x}_{\mathrm{m} j}(t)+\right. \\& \left.K_{\mathrm{r} 3 i j}^{*} r_{j}(t)\right), \quad i=1,2, \cdots, N \end{aligned}$
(15) $\begin{aligned}\boldsymbol{K}_{\mathrm{r} 1 i}^{* \mathrm{~T}}= & -\boldsymbol{C}_{\mathrm{m} i} \boldsymbol{A}_{\mathrm{m} i}^{\rho}-a_{i p_{i}-1} \boldsymbol{C}_{\mathrm{m} i} \boldsymbol{A}_{\mathrm{m} i}^{\rho-1}-\cdots-a_{i 0} \boldsymbol{C}_{\mathrm{m} i} \\\boldsymbol{K}_{\mathrm{r} 2 i j}^{* \mathrm{~T}}= & \boldsymbol{C}_{\mathrm{m} j} \boldsymbol{A}_{\mathrm{m} j}^{\rho}+a_{i \rho_{i}-1} \boldsymbol{C}_{\mathrm{m} j} \boldsymbol{A}_{\mathrm{m} j}^{\rho-1}+\cdots+a_{i 0} \boldsymbol{C}_{\mathrm{m} j} \\K_{\mathrm{r} 3 i j}^{*}= & \boldsymbol{C}_{\mathrm{m} j} \boldsymbol{A}_{\mathrm{m} j}^{\sigma_{j}^{-1} \boldsymbol{B}_{\mathrm{m} j}}\end{aligned}$
将ri (t )代入y m i ( ρ i ) ( t )并化简,得到:
(16) ym i (t)= 1 n i * ∑ v j ∈ N i ( t ) m j (t), i=1, 2, …, N
因此有l i m t → ∞ ( y m i t )-1 n i * ∑ v j ∈ N i ( t ) y m j t ))=0,达成了固定拓扑下的参考模型系统局部输出一致性.根据引理1,则达成了固定拓扑下的参考模型系统对领导者的全局输出一致性,即
(17) l i m t → ∞ m i (t)-y0 (t))=0, i=1, 2, …, N
下面考虑通信拓扑突变的情况,此时vi 的邻居集$\mathcal{N}_{i}(t)$是时变的,vi 的邻居数ni (t )也不再为常值. 因此引入指示函数式(9),将vi 的邻居集范围从当前时刻的邻居集$ \mathcal{N}_{i}(t)$扩大至包含所有可能邻居的集合Σi i
(18) $\begin{array}{c}r_{i}(t)=\boldsymbol{K}_{\mathrm{r} 1 i}^{* \mathrm{~T}} \boldsymbol{x}_{\mathrm{m} i}(t)+\frac{1}{n_{i}(t)} \sum_{v_{j} \in \mathcal{N}_{i}^{\prime}(t)}\left(\boldsymbol{K}_{\mathrm{r} 2 i j}^{* \mathrm{~T}} \delta_{i j}(t) \boldsymbol{x}_{\mathrm{m} j}(t)+\right. \\\left.K_{\mathrm{r} 3 i j}^{*} \delta_{i j}(t) r_{j}(t)\right)+\frac{1}{n_{i}(t)} \sum_{v_{j} \in \overline{\mathcal{N}}_{i}^{(t)}}\left(\boldsymbol{K}_{\mathrm{r} 2 i j}^{* \mathrm{~T}} \delta_{i j}(t) \boldsymbol{x}_{\mathrm{m} j}(t)+\right. \\\left.K_{\mathrm{r} 3 i j}^{*} \delta_{i j}(t) r_{j}(t)\right)=\boldsymbol{K}_{\mathrm{r} 1 i}^{* \mathrm{~T}} \boldsymbol{x}_{\mathrm{m} i}(t)+ \\\frac{1}{n_{i}(t)} \sum_{v_{j} \in \Sigma_{i}}\left(\boldsymbol{K}_{\mathrm{r} 2 i j}^{* \mathrm{~T}} \delta_{i j}(t) \boldsymbol{x}_{\mathrm{m} j}(t)+K_{\mathrm{r} 3 i j}^{*} \delta_{i j}(t) r_{j}(t)\right), \\i=1,2, \cdots, N\end{array}$
由于指示函数δij (t )的引入,邻居共享信号x m j t )和rj (t )被替换成了δij (t )x m j t )和δij (t )rj (t ). 当邻居vj 与vi 保持通信,此时δij (t )=1,可以获取邻居的精确信息,而当vj 与vi 的通信断开,此时δij (t )=0,所以其信息不再参与ri (t )的计算. 此时将式(18)代入y m i ( ρ i ) ( t ),则有
(19) ym i (t)= 1 n i ( t ) ∑ v j ∈ Σ i ij (t)ym j (t),
且跟随者vi 与其邻居vj (vj ∈Σi
(20) $\begin{array}{l}\sum_{v_{j} \in \Sigma_{i}} \boldsymbol{C}_{\mathrm{m} i}\left(s \boldsymbol{I}_{\mathrm{m} i}-\boldsymbol{A}_{\mathrm{m} i}-\boldsymbol{B}_{\mathrm{m} i} \boldsymbol{K}_{\mathrm{rl} 1 i}^{* \mathrm{~T}}\right)^{-1} \boldsymbol{B}_{\mathrm{m} i} \xi_{\mathrm{m} i}(s) \xi_{\mathrm{m} j}^{-1}(s)= \\\sum_{v_{j} \in \Sigma_{i}} W_{\mathrm{m} j}(s), \quad i=1,2, \cdots, N\end{array}$
(21) $ \begin{aligned}\lim_{t}e_{{\mathrm{r}i}}(t)&=\\\lim_{t}&_{\infty}\Bigl(y_{{\mathrm{m}i}}(t)-\frac{1}{n_{i}(t)}_{{v_{j}\in\Sigma_{i}}}\delta_{ij}(t)y_{{\mathrm{m}j}}(t)\Bigr)=0,\\&i=1,2,\ldots,N&\end{aligned}$
因此在突变通信拓扑结构下,ri (t )实现了每个跟随者对应的参考模型系统的局部输出一致性.基于引理1,对于具有1个领导者和N 个跟随者的多智能体系统,只需要每个跟随者满足其与邻居智能体的局部输出一致性,则可达到领导者-跟随者全局输出一致性.故根据各参考模型系统间的局部输出一致性式(21),则实现了参考模型-领导者匹配:
(22) l i m t → ∞ m i 0 (t)= l i m t → ∞ m i (t)-y0 (t))=0,
达成了跟随者参考模型系统对领导者的全局输出一致性.
在标称情况下,定理1通过设计参考模型输入信号ri (t )实现了参考模型-领导者匹配,下面给出标称情况下跟随者控制输入信号ui (t )的设计以实现跟随者-参考模型匹配,进而实现领导者-跟随者全局输出一致性.
2.3 跟随者-参考模型匹配
考虑跟随者智能体系统式(1)的状态xi (t )均可测量,状态反馈控制器结构为
(23) $\begin{array}{c}u_{i}(t)=\boldsymbol{K}_{1 i}^{* \mathrm{~T}} \boldsymbol{x}_{i}(t)+K_{2 i}^{*} r_{i}(t) \\i=1,2, \cdots, N\end{array}$
式中:标称参数K 1 i * T R 1 × p i K 2 i * 1 实现对参考模型输出的渐近跟踪;分布式参考输入信号ri (t )由式(8)计算得到.
定理2 在满足假设3和假设4的条件下,针对第i 个跟随者智能体系统式(1),存在标称控制器式(23)使得闭环系统稳定且实现跟随者-参考模型匹配,达成跟随者对参考模型的输出跟踪,即
(24) $y_{i}(t)=W_{\mathrm{m} i}(s)\left[r_{i}\right](t), \quad i=1,2, \cdots, N$
进而达成多智能体系统领导者-跟随者全局输出一致性,即
(25) $\begin{array}{c}\lim _{t \rightarrow \infty} e_{i 0}(t)=\lim _{t \rightarrow \infty}\left(y_{i}(t)-y_{0}(t)\right)=0, \\i=1,2, \cdots, N\end{array}$
(26) $\begin{array}{l}y_{i}^{(k)}(t)=\boldsymbol{C}_{i} \boldsymbol{A}_{i}^{k} \boldsymbol{x}_{i}(t)+\boldsymbol{C}_{i} \boldsymbol{A}_{i}^{k-1} \boldsymbol{B}_{i} u_{i}(t), \\i=1,2, \cdots, N, \quad k=0,1, \cdots, \rho_{i}\end{array}$
当k =0, 1, …, ρi -1时,Ci A i k - 1 Bi =0. 根据k p i Ci A i ρ i - 1 Bi ,设计ui (t )为
(27) $\begin{aligned}u_{i}(t)= & k_{\mathrm{p} i}^{-1}\left(-\boldsymbol{C}_{i} \boldsymbol{A}_{i}^{\rho_{i}} \boldsymbol{x}_{i}(t)-\xi_{\mathrm{m} i}(s)\left[y_{i}\right](t)+\right. \\& \left.y_{i}^{\left(\rho_{i}\right)}(t)+r_{i}(t)\right), \quad i=1,2, \cdots, N\end{aligned}$
(28) $\begin{array}{l}\xi_{\mathrm{m} i}(s)\left[y_{i}\right](t)=y_{i}^{\left(\rho_{i}\right)}(t)+ \\a_{i \rho_{i}-1} y_{i}^{\left(\rho_{i}-1\right)}(t)+\cdots+a_{i 0} y_{i}(t)\end{array}$
(29) $y_{i}^{\left(\rho_{i}\right)}(t)+a_{i \rho_{i}-1} y_{i}^{\left(\rho_{i}-1\right)}+\cdots+a_{i 0} y_{i}(t)=r_{i}(t)$
(30) $\begin{array}{c}u_{i}(t)=\boldsymbol{K}_{1 i}^{* \mathrm{~T}} \boldsymbol{x}_{i}(t)+K_{2 i}^{*} r_{i}(t), \\i=1,2, \cdots, N\end{array}$
(31) $\begin{array}{c}u_{i}(t)=\boldsymbol{K}_{1 i}^{* \mathrm{~T}} \boldsymbol{x}_{i}(t)+K_{2 i}^{*} r_{i}(t), \\i=1,2, \cdots, N\end{array}$
式中:K 1 i * T k p i - 1 (- Ci A i ρ i - a i ρ i - 1 Ci A i ρ i - 1 - …-ai 1 Ci Ai -ai 0 Ci );K 2 i * k p i - 1 . 将式(31)代入跟随者智能体系统式(1),得到闭环系统:
(32) $y_{i}(t)=W_{\mathrm{m} i}(s)\left[r_{i}\right](t), \quad i=1,2, \cdots, N$
(33) $\begin{array}{c}\boldsymbol{C}_{i}\left(s \boldsymbol{I}_{i}-\boldsymbol{A}_{i}-\boldsymbol{B}_{i} \boldsymbol{K}_{1 i}^{* \mathrm{~T}}\right)^{-1} \boldsymbol{B}_{i} K_{2 i}^{*}=W_{\mathrm{m} i}(s), \\i=1,2, \cdots, N\end{array}$
由式(31)和假设4可知,所设计的控制器ui (t )实现了跟随者智能体闭环系统稳定,xi (t )和yi (t )有界,且实现跟随者-参考模型匹配,达成各跟随者对相应参考模型系统的输出跟踪yi (t )=W m i s )[ri ](t )=y m i t ), i =1, 2, …, N. 更进一步,结合定理1,根据跟随者参考模型系统对领导者的全局输出一致性 l i m t → ∞ ( y m i t )-y 0 (t ))=0, i =1, 2, …, N ,可得到
(34) $\begin{array}{c}\lim _{t \rightarrow \infty} e_{i 0}(t)=\lim _{t \rightarrow \infty}\left(y_{i}(t)-y_{0}(t)\right)=0, \\i=1,2, \cdots, N\end{array}$
即达成突变通信拓扑下被控多智能体系统的领导者-跟随者全局输出一致性.
3 自适应控制器设计
3.1 自适应控制器
由于跟随者系统参数Ai 、Bi 、Ci 不确定,标称控制器式(23)的控制器参数K 1 i * T K 2 i *
控制器结构 基于标称控制器式(23),设计自适应控制器如下:
(35) $\begin{array}{c}u_{i}(t)=\boldsymbol{K}_{1 i}^{\mathrm{T}}(t) \boldsymbol{x}_{i}(t)+K_{2 i}(t) r_{i}(t), \\i=1,2, \cdots, N\end{array}$
式中:K T 1 i ( t )和K 2 i t )分别为K 1 i * T K 2 i *
(36) $\begin{aligned}r_{i}(t)= & \boldsymbol{K}_{\mathrm{r} 1 i}^{* \mathrm{~T}} \boldsymbol{x}_{\mathrm{m} i}(t)+ \\& \frac{1}{n_{i}(t)} \sum_{v_{j} \in \Sigma_{i}}\left(\boldsymbol{K}_{\mathrm{r} 2 i j}^{* \mathrm{~T}} \delta_{i j}(t) \boldsymbol{x}_{\mathrm{m} j}(t)+\right. \\& \left.K_{\mathrm{r} 3 i j}^{*} \delta_{i j}(t) r_{j}(t)\right), \\& i=1,2, \cdots, N\end{aligned}$
参数K r 1 i * T K r 2 i j * T K r 3 i j *
误差方程 将式(35)应用于系统式(1)得到闭环系统,并根据式(6)得到跟随者系统与其参考模型的输出跟踪误差e m i t )=yi (t )-y m i t ),忽略渐近收敛项f p i t )=Ci e ( A i + B i K 1 i * T ) t xi (0),则有
(37) $e_{\mathrm{m} i}(t)=\Psi_{i}^{*} W_{\mathrm{m} i}(s)\left[\widetilde{\boldsymbol{\Theta}}_{i}^{\mathrm{T}} \boldsymbol{\omega}_{i}\right](t)$
(38) $\left.\begin{array}{l}\boldsymbol{\Theta}_{i}^{\mathrm{T}}(t)=\left[\begin{array}{ll}\boldsymbol{K}_{1 i}^{\mathrm{T}}(t) & \boldsymbol{K}_{2 i}(t)\end{array}\right] \\\boldsymbol{\Theta}_{i}^{* \mathrm{~T}}=\left[\begin{array}{ll}\boldsymbol{K}_{1 i}^{* \mathrm{~T}} & \boldsymbol{K}_{2 i}^{*}\end{array}\right] \\\widetilde{\boldsymbol{\Theta}}_{i}^{\mathrm{T}}=\boldsymbol{\Theta}_{i}^{\mathrm{T}}(t)-\boldsymbol{\Theta}_{i}^{* \mathrm{~T}} \\\boldsymbol{\omega}_{i}(t)=\left[\begin{array}{ll}\boldsymbol{x}_{i}^{\mathrm{T}}(t) & r_{i}(t)\end{array}\right]^{\mathrm{T}}\end{array}\right\}$
(39) $\varepsilon_{i}(t)=e_{\mathrm{m} i}(t)+\Psi_{i}(t) \xi_{i}(t)$
(40) $\left.\begin{array}{l}\xi_{i}(t)=\boldsymbol{\Theta}_{i}^{\mathrm{T}}(t) \boldsymbol{\zeta}_{i}(t)-W_{\mathrm{m} i}(s)\left[\boldsymbol{\Theta}_{i}^{\mathrm{T}} \boldsymbol{\omega}_{i}\right](t) \\\boldsymbol{\zeta}_{i}(t)=W_{\mathrm{m} i}(s)\left[\boldsymbol{\omega}_{i}\right](t)\end{array}\right\}$
自适应律 根据跟随者系统与其参考模型系统的输出跟踪误差方程式(37),估计误差信号式(39)可整理为
(41) $\varepsilon_{i}(t)=\widetilde{\Psi}_{i}(t) \xi_{i}(t)+\Psi_{i}^{*} \widetilde{\boldsymbol{\Theta}}_{i}^{\mathrm{T}}(t) \boldsymbol{\zeta}_{i}(t)$
式中:Ψ ~ i ( t )=Ψi (t )-Ψ i * . 根据式(41),设计自适应律:
(42) $\left.\begin{array}{l}\dot{\boldsymbol{\Theta}}_{i}(t)=-\frac{\operatorname{sign}\left[\Psi_{i}^{*}\right] \boldsymbol{\Gamma}_{i} \boldsymbol{\zeta}_{i}(t) \varepsilon_{i}(t)}{m_{i}^{2}(t)} \\\dot{\Psi}_{i}(t)=-\frac{\gamma_{i} \xi_{i}(t) \varepsilon_{i}(t)}{m_{i}^{2}(t)} \\m_{i}^{2}(t)=1+\boldsymbol{\zeta}_{i}^{\mathrm{T}}(t) \boldsymbol{\zeta}_{i}(t)+\xi_{i}^{2}(t)\end{array}\right\}$
式中:Γi =Γ T i γi >0. 且自适应律式(42)具有如下性质.
(1) Θi (t )∈L ∞ ,Ψi (t )∈L ∞ ,ε i ( t ) m i ( t ) L 2 ∩L ∞ .
(2) Θ · i ( t )∈L 2 ∩L ∞ ,Ψ · i ( t )∈L 2 ∩L ∞ .
3.2 稳定性分析
定理3 在满足假设1到假设5的条件下,针对系统参数不确定的跟随者智能体式(1),选取参考模型式(6),采用自适应控制器式(35)和自适应律式(42),则可实现闭环系统所有信号有界,且实现跟随者对其参考模型的渐近输出跟踪,即l i m t → ∞ e m i t )=l i m t → ∞ ( yi (t )-y m i t ))=0,进而实现突变通信拓扑下领导者- 跟随者全局输出一致性,即l i m t → ∞ ei 0 (t )=l i m t → ∞ ( yi (t )-y 0 (t ))=0,i =1, 2, …, N.
证明 定理3的证明过程分为以下两步:首先证明单个跟随者智能体对其参考模型系统的渐近输出跟踪,进而证明领导者-跟随者全局输出一致性.其中,针对单个跟随者系统的闭环稳定性及跟踪性能分析可参考文献[24 ],由于篇幅限制,本文仅进行简要的说明.引入以下全阶状态观测器:
(43) $\dot{\hat{\boldsymbol{x}}}_{i}(t)=\left(\boldsymbol{A}_{i}-\boldsymbol{L}_{i} \boldsymbol{C}_{i}\right) \hat{\boldsymbol{x}}_{i}(t)+\boldsymbol{B}_{i} u_{i}(t)+\boldsymbol{L}_{i} y_{i}(t)$
由于假设3中设定了(Ai , Ci )是可观测的,所以存在增益矩阵Li ∈R p i × 1 Ai -Li Ci 稳定.进一步地,得到观测器状态为
(44) $\begin{aligned}\hat{\boldsymbol{x}}_{i}(t)= & \frac{\boldsymbol{G}_{\mathrm{u} i}(s)}{\Lambda_{i}(s)}\left[u_{i}\right](t)+\frac{\boldsymbol{G}_{y i}(s)}{\Lambda_{i}(s)}\left[y_{i}\right](t)+ \\& \mathrm{e}^{\left(\boldsymbol{A}_{i}-L_{i} C_{i}\right) t} \hat{\boldsymbol{x}}_{i}(0)\end{aligned}$
式中:l i m t → ∞ e ( A i - L i C i ) t x ^ i (0) =0;G u i s )∈R p i × 1 G y i s )∈R p i × 1 Λi (s )=det(sIi -Ai -Li Ci ). 并且可以进一步得到l i m t → ∞ ( x ^ i ( t )-xi (t ))=0. 因此可将自适应控制器式(35)中的K T i 1 ( t )xi (t )用K T i 1 ( t )x ^ i ( t )代替,进而将其参数化为
(45) $u_{i}(t)=\boldsymbol{\Theta}_{i}^{\mathrm{T}}(t) \boldsymbol{\omega}_{i}(t)$
(46) $\left.\begin{array}{l}\boldsymbol{\Theta}_{i}^{\mathrm{T}}(t)=\left[\begin{array}{lll}\boldsymbol{\Theta}_{i 1}^{\mathrm{T}}(t) & \boldsymbol{\Theta}_{i 2}^{\mathrm{T}}(t) & K_{2 i}(t)\end{array}\right] \\\boldsymbol{\omega}_{i}(t)=\left[\begin{array}{lll}\boldsymbol{\omega}_{i 1}^{\mathrm{T}}(t) & \boldsymbol{\omega}_{i 2}^{\mathrm{T}}(t) & r_{i}(t)\end{array}\right]^{\mathrm{T}}\end{array}\right\}$
式中:ωi 1 (t )=a i ( s ) Λ i ( s ) ui ](t );ωi 2 =G y i ( s ) Λ i ( s ) yi ](t );Λi (s )是特征值与Ai -Li Ci 相同的pi 阶稳定多项式;ai (s )=[1 s … s p i - 1 T ;Θ T i 1 ( t )、Θ T i 2 ( t )由自适应律式(42)估计得到. 接着需要为系统yi (t )=Gi (s )[ui ](t )引入3个如下形式的滤波器:
(47) $\left.\begin{array}{l}s H_{f i \mu}(s)=1-K_{\mathrm{fi} \mathrm{\mu}}(s) \\K_{f i \mu}(s)=\frac{\hat{\alpha}_{i_{\mu}}^{\rho_{i}}}{\left(s+\hat{\alpha}_{i \mu}\right)^{\rho_{i}}}\end{array}\right\}$
式中:μ =1, 2, 3表示滤波器的序号;α ^ i μ .H f iμ s )的脉冲响应为
(48) $h_{\mathrm{f} i \mu}(t)=\mathrm{e}^{-\hat{\alpha}_{i \mu}} \sum_{d=1}^{\rho_{i}} \frac{\hat{\alpha}_{i \mu}^{\rho_{i}-d}}{\left(\rho_{i}-d\right)!} t^{\rho_{i}-d}$
(49) $\left\|h_{\mathrm{f} j \mu}(\cdot)\right\|_{1}=\int_{0}^{\infty}\left|h_{\mathrm{f} j \mu}(t)\right| \mathrm{d} t=\frac{\rho_{i}}{\hat{\alpha}_{i \mu}}$
在虚拟滤波器的作用下,经过一系列转换,ui (t )可被整理为以下形式:
(50) $u_{i}(t)=G_{i 7}(s, \cdot)\left[y_{f i}\right](t)+G_{i 8}(s, \cdot)\left[r_{i}\right](t)$
式中:y f i t )=hi (s )[yi ](t ). 对于单输入单输出系统式(1)来说,hi (s )可由式(39)中的W m i s )表示.Gi 7 (s , ·)和Gi 8 (s , ·)是具有有限增益的适当稳定算子.ri (s )是有界的,因此y f i t )具有如下性质:
(51) $\begin{aligned}y_{f i}(t) \leqslant & x_{i 0}+\beta_{i 1} \int_{0}^{t} \mathrm{e}^{-\hat{\alpha}_{i 1}(t-\phi)} x_{i 1}(\phi) \times \\& \left(\int_{0}^{\phi} \mathrm{e}^{-\hat{\alpha}_{i 2}(\phi-w)}\left\|y_{f i}(w)\right\| \mathrm{d} w\right) \mathrm{d} \phi\end{aligned}$
式中:βi 1 ,α ^ i 1 α ^ i 2 xi 0 ∈L ∞ ;xi 1 (t )=Θ · i ( t ) ε i ( t ) mi (t )∈L 2 ∩L ∞ . 因此根据小增益引理[24 ] 可得y f i t )∈L ∞ ,进而有ui (t )∈L ∞ ,yi (t )∈L ∞ . 因此ωi (t )∈L ∞ ,ξi (t )∈L ∞ ,ζi (t )∈L ∞ ,mi (t )∈L ∞ 得到保障. 根据引理2,有ε i ( t ) m i ( t ) L 2 ,Θ · i ( t )∈L 2 ,Ψ · i ( t )∈L 2 ,并且可得ξi (t )∈L 2 ,l i m t → ∞ ξi (t )=0. 更进一步地,有
(52) $\left\|e_{\mathrm{m} i}(t)\right\| \leqslant c_{i 3}\left\|h_{f i 3}\right\|+z_{i 1}(t) \leqslant \frac{c_{i 4}}{\hat{\alpha}_{i 3}}+z_{i 1}(t)$
式中:ci 3 ,ci 4 >0;l i m t → ∞ zi (t )=0. α ^ i 3 l i m t → ∞ e m i t )=l i m t → ∞ ( yi (t )-y m i t ))=0,实现了跟随者系统对其参考模型系统的输出渐近跟踪,达成了跟随者-参考模型匹配.
上述内容在文献[24 ]中的框架下证明了跟随者系统参数未知时,跟随者输出对其参考模型输出的渐近跟踪性能,若每个参考模型系统都可实现对领导者系统的输出跟踪,即可达成领导者-跟随者全局输出一致性.因此结合定理1,根据参考模型系统对领导者的全局输出一致性l i m t → ∞ e m i 0 (t )=l i m t → ∞ ( y m i t )-y 0 (t ))=0,可得
即达成突变通信拓扑下领导者-跟随者全局输出一致性.证明完毕.
综上所述,在具有不确定系统参数和突变通信拓扑的情况下,本文设计的基于领导者-模型-跟随者匹配的分布式自适应协同控制方法能够有效实现异构多智能体系统领导者-跟随者全局输出一致性,保证定理3所述的跟随者智能体闭环系统所有信号有界以及系统输出对领导者输出的渐近跟踪性能.
4 仿真分析
为体现本文所设计的控制方法的有效性,本节采用由1个虚拟领导者、2个无人机跟随者、2个无人车跟随者组成的异构多智能体系统进行仿真.
对于2个无人机跟随者智能体,四轴无人机偏航运动动力学方程[21 ] 如下所示:
(53) $\ddot{\psi}_{i}=I_{y i}^{-1} \tau_{\psi_{i}}$
式中:ψi 、Iyi 、τ ψ i i 架无人机的偏航角、y 轴上的转动惯量、偏航角上的转动力矩.对于2个无人车跟随者智能体,无人车横向动力学方程[31 ] 如下所示:
(54) $\left.\begin{array}{rl}\dot{\beta}_{i}= & -\frac{k_{f i}+k_{\mathrm{ri}}}{m_{i} v_{y i}} \beta_{i}+\left(\frac{k_{f i} l_{f i}-k_{\mathrm{ri}} l_{\mathrm{r} i}}{m_{i} v_{y i}^{2}}+1\right) \dot{\phi}_{i}- \\& \frac{k_{f i}}{m_{i} v_{y i}} \delta_{f i} \\\ddot{\phi_{i}}= & \frac{k_{f i} l_{f i}-k_{\mathrm{r} i} l_{\mathrm{r} i}}{I_{y i}} \beta_{i}-\frac{k_{f i} l_{\mathrm{fi}}^{2}+k_{\mathrm{r} i} l_{\mathrm{ri}}^{2}}{I_{y i} v_{y i}} \dot{\phi}_{i}+\frac{k_{f i} l_{\mathrm{fi}}}{I_{y i}} \delta_{\mathrm{fi}}\end{array}\right\}$
式中:βi 和ϕi 为第i 辆无人车的侧滑角和偏航角;δ f i i 辆无人车的前轮转角;mi 和vyi 为第i 辆无人车的车辆质量和车辆纵向速度(此处假设速度为常数);Iyi 为第i 辆无人车相对于纵轴的转动惯量;k f i k r i i 辆无人车前轮和后轮的侧偏刚度;l f i l r i i 辆无人车重心到车辆前桥和后桥的距离.根据式(53)和式(54),可以得到4个跟随者系统的状态空间方程为
其中:当i =1, 2时,xi (t )=[ψi ψ · i T 、ui (t )=τ ψ i yi (t )=ψi 分别为第1、第2个跟随者(无人机)的状态信号、控制输入信号和输出信号;当i =3, 4时,xi (t )=[βi ϕi ϕ · i T 、ui (t )=δ f i yi (t )=ϕi 分别为第3、第4个跟随者(无人车)的状态信号、控制输入信号和输出信号;Ai 、Bi 、Ci 为相应的系统参数矩阵.根据文献[21 ,31 ],跟随者智能体的系统参数矩阵选取为
(55) $y_{0}(t)=\frac{1}{(s+2)^{2}}\left[r_{0}\right](t)$
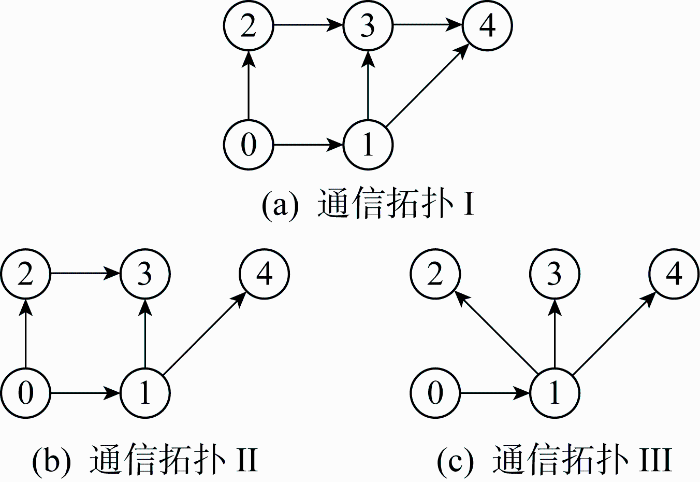
多智能体系统的通信拓扑结构如图1 所示,以30 s的时间间隔按照图1 所示顺序进行突变.
图1
图1
通信链接改变导致的拓扑结构突变
Fig.1
Topology structural abrupt changes caused by communication connection changes
领导者系统与跟随者系统的相对阶为ρ 0 =ρi =2;因此选择多项式:ξ m1 (s )=(s +2. 5)2 ,ξ m2 (s )=(s +0. 5)2 ,ξ m3 (s )=(s +1)2 ,ξ m4 (s )=(s +1. 5)2 . 设定领导者输入r 0 (t )=sin(0. 14t ),系统参数初值为真实值的70%,仿真结果如图2 ~4 所示.
图2
图2
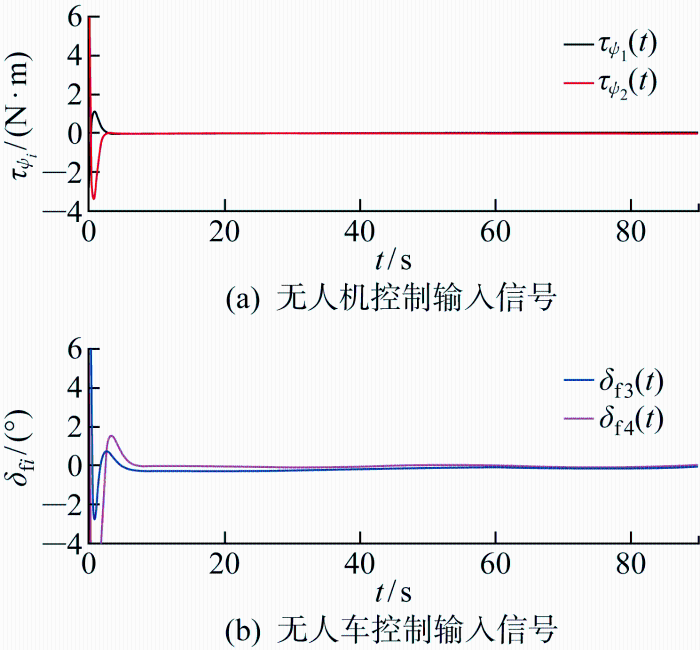
跟随者控制输入信号
Fig.2
Control input signal of follower
图3
图3
领导者-跟随者系统输出信号
Fig.3
Output signals of leader-follower system
图4
图4
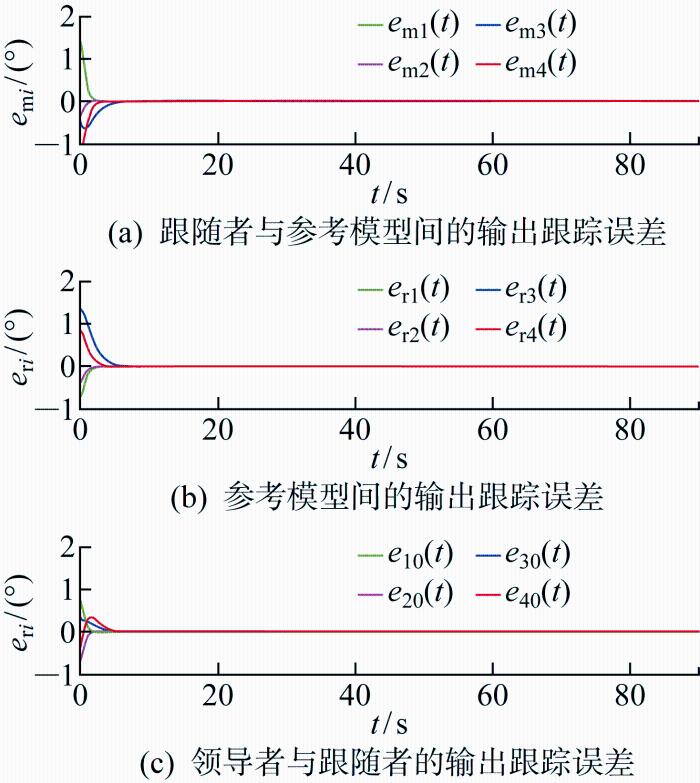
领导者-跟随者系统输出跟踪误差
Fig.4
Output tracking error of leader-follower system
图2 和图3 分别为由无人机和无人车以及虚拟领导者组成的异构多智能体系统的控制输入信号ui (t )和输出信号yi (t)的仿真图.当i =1, 2时, ui (t )=τ ψ i ( t )为无人机偏航角转动力矩,yi (t )=ψi (t )为无人机偏航角;当i =3, 4时,ui (t )=δ f i t )为无人车前轮转角,yi (t )=ϕi (t )为无人车偏航角. 图4 为跟随者与其对应的参考模型之间的输出跟踪误差e m i t ),各参考模型系统间的局部输出跟踪误差e r i t )以及领导者与跟随者之间的输出跟踪误差ei 0 (t )的仿真图.
由图2 和图3 可见,在具有不确定系统参数和突变通信拓扑结构的情况下,各个跟随者智能体输出信号在其控制输入信号的作用下实现了对领导者输出信号的渐近跟踪.由图4(b) 可见,参考模型间局部输出跟踪误差的收敛达成了参考模型间的局部输出一致性,进而实现参考模型输出与领导者输出的全局一致性;而图4(a) 中跟随者与其相应参考模型的输出跟踪误差的收敛进一步地实现了领导者-跟随者全局输出一致性,如图4(c) 所示.因此,在参考模型系统的引导下,跟随者系统在不依赖全局信息的情况下实现了对领导者的输出一致性.可以看出本文的控制策略可以实现各智能体系统闭环稳定以及突变通信拓扑下的异构多智能体领导者-跟随者输出一致性.
5 结语
针对具有不确定系统参数和突变通信拓扑的异构多智能体系统,设计了一种基于领导者-模型-跟随者匹配的分布式模型参考自适应控制方法.与现有的基于模型参考自适应控制的异构多智能体控制方法相比,本文所提出的方案具有更简单的匹配条件,且适用于各异构智能体状态维数不同的情况.通过引入表征邻居智能体通信情况的指示函数,本文设计的自适应控制器可以在不依赖全局信息的情况下,使异构多智能体系统实现突变通信拓扑结构下的领导者-跟随者输出一致性.最后,仿真结果表明了本文所设计的方案的有效性.目前,针对复杂不确定环境下多智能体系统因故障或不确定外部扰动而无法完成任务的问题仍有待进一步研究,这将是未来的主要研究工作之一.
附录见本刊网络版(xuebao.sjtu.edu.cn/article/2024/1006-2467/1006-2467-58-11-1805.shtml)
参考文献
View Option
[1]
GONG J JIANG B MA Y Adaptive fault tolerant supervisory consensus control for nonlinear strict-feedback multiagent systems
[C]//International Conference on Guidance , Navigation and Control . Singapore , Singapore : Springer , 2022 : 1603 -1703 .
[本文引用: 1]
[2]
CHU H CAI Y ZHANG W Consensus tracking for multi-agent systems with directed graph via distributed adaptive protocol
[J]. Neurocomputing 2015 , 166 : 8 -13 .
[本文引用: 1]
[3]
BAO G MA L YI X Recent advances on cooperative control of heterogeneous multi-agent systems subject to constraints: A survey
[J]. Systems Science & Control Engineering 2022 , 10 (1 ): 539 -551 .
[本文引用: 1]
[4]
CANESE L CARDARILLI G C DI N L et al Multi-agent reinforcement learning: A review of challenges and applications
[J]. Applied Sciences 2021 , 11 (11 ): 1 -25 .
[本文引用: 1]
[5]
AMIRKHANI A BARSHOOI A H Consensus in multi-agent systems: A review
[J]. Artificial Intelligence Review 2022 , 55 (5 ): 3897 -3935 .
[本文引用: 1]
[6]
SKEIK O LANZON A Robust output consensus of homogeneous multi-agent systems with negative imaginary dynamics
[J]. Automatica 2020 , 113 : 108799 .
[本文引用: 1]
[7]
BHATTACHARYYA S PATRA S Positive consensus of multi-agent systems with hierarchical control protocol
[J]. Automatica 2022 , 139 : 110191 .
[本文引用: 1]
[8]
YU P LIU K LIU X et al Robust consensus tracking control of uncertain multi-agent systems with local disturbance rejection
[J]. IEEE/CAA Journal of Automatica Sinica 2023 , 10 (2 ): 427 -438 .
[本文引用: 1]
[9]
沈林成 , 牛轶峰 , 朱华勇 . 多无人机自主协同控制理论与方法 [M]. 北京 : 国防工业出版社 , 2013 .
[本文引用: 1]
SHEN Lincheng NIU Yifeng ZHU Huayong Theories and methods of autonomous cooperative control for multiple UAVs [M]. Bejing : National Defense Industry Press , 2013 .
[本文引用: 1]
[10]
HU D VINCENT J L G WANG T et al Multi-agent robotic system (MARS) for UAV-UGV path planning and automatic sensory data collection in cluttered environments
[J]. Building and Environment 2022 , 221 : 109349 .
[本文引用: 1]
[11]
YAN B SHI P LIM C C Robust formation control for nonlinear heterogeneous multiagent systems based on adaptive event-triggered strategy
[J]. IEEE Transactions on Automation Science and Engineering 2022 , 19 (4 ): 2788 -2800 .
[本文引用: 1]
[12]
YAO D LI H LU R et al Distributed sliding-mode tracking control of second-order nonlinear multiagent systems: An event-triggered approach
[J]. IEEE Transactions on Cybernetics 2020 , 50 (9 ): 3892 -3902 .
DOI:10.1109/TCYB.2019.2963087
PMID:31995513
[本文引用: 1]
The event-triggered tracking control problem of second-order multiagent systems in consideration of system nonlinearities is investigated by utilizing the distributed sliding-mode control (SMC) approach. An event-triggered strategy is proposed to decrease the controller sampling frequency and save the network communication resources; the triggering condition is then established for leader-following multiagent systems. In this article, by utilizing the distributed event-based sliding-mode controller, the system state of second-order multiagent systems with system nonlinearities is capable of approaching the integral sliding-mode surface in finite time. A novel integral sliding-mode surface is constructed in this article to guarantee the consensus tracking performance in the existence of system nonlinearities as the state trajectories of second-order integrator systems move on the constructed sliding manifold. By employing the Lyapunov approach, sufficient conditions are deduced to ensure that the consensus tracking performance is obtained for the closed-loop system. Furthermore, it is presented that the triggering scheme can effectively reduce state updates and eliminate the Zeno behavior. A simulation example is provided to testify the validity of our proposed methodology.
[13]
ZHANG J ZHANG H LU Y et al Cooperative output regulation of heterogeneous linear multi-agent systems with edge-event triggered adaptive control under time-varying topologies
[J]. Neural Computing and Applications 2020 , 32 (19 ): 15573 -15584 .
[本文引用: 1]
[14]
WEN L TAO G YANG H et al Adaptive actuator failure compensation for possibly nonminimum-phase systems using control separation based LQ design
[J]. IEEE Transactions on Automatic Control 2018 , 64 (1 ): 143 -158 .
[本文引用: 1]
[15]
WEN L TAO G JIANG B et al Adaptive LQ control using reduced hamiltonian for continuous-time systems with unmatched input disturbances
[J]. SIAM Journal on Control and Optimization 2021 , 59 (5 ): 3625 -3660 .
[本文引用: 1]
[16]
HAN T GUAN Z XIAO B et al Bipartite average tracking for multi-agent systems with disturbances: Finite-time and fixed-time convergence
[J]. IEEE Transactions on Circuits and Systems I: Regular Papers 2021 , 68 (10 ): 4393 -4402 .
[本文引用: 1]
[17]
CAO W LIU L FENG G Distributed adaptive output consensus of unknown heterogeneous non-minimum phase multi-agent systems
[J]. IEEE/CAA Journal of Automatica Sinica 2023 , 10 (4 ): 997 -1008 .
[本文引用: 1]
[18]
YANG R LIU L FENG G Cooperative output tracking of unknown heterogeneous linear systems by distributed event-triggered adaptive control
[J]. IEEE Transactions on Cybernetics 2020 , 52 (1 ): 3 -15 .
[本文引用: 1]
[19]
马思迁 , 董朝阳 , 马鸣宇 , 等 . 基于自适应通信拓扑四旋翼无人机编队重构控制
[J]. 北京航空航天大学学报 2018 , 44 (4 ): 841 -850 .
[本文引用: 1]
MA Siqian DONG Chaoyang MA Mingyu et al Formation reconfiguration control of quadrotor UAVs based on adaptive communication topology
[J]. Journal of Beijing University of Aeronautics and Astronasutics 2018 , 44 (4 ): 841 -850 .
[本文引用: 1]
[20]
BALDI S YUAN S PAOLO F Output synchronization of unknown heterogeneous agents via distributed model reference adaptation
[J]. IEEE Transactions on Control of Network Systems 2018 , 6 (2 ): 515 -525 .
[本文引用: 1]
[21]
ROSA M R Adaptive synchronization for heterogeneous multi-agent systems with switching topologies
[J]. Machines 2018 , 6 (1 ): 1 -18 .
[本文引用: 4]
[22]
SONG G TAO G TAN C A distributed adaptive state feedback control scheme for output consensus of multi-agent systems
[C]//Asian Control Conference . Piscataway , USA : IEEE , 2019 : 1149 -1154 .
[本文引用: 1]
[23]
WEN L TAO G YANG H et al Aircraft turbulence compensation using adaptive multivariable disturbance rejection techniques
[J]. Journal of Guidance , Control , and Dynamics 2015 , 38 (5 ): 954 -963 .
[本文引用: 2]
[24]
TAO G Adaptive control design and analysis [M]. New York, USA : John Wiley & Sons , 2003 .
[本文引用: 5]
[25]
杨浩 , 姜斌 , 周东华 . 互联系统容错控制的研究回顾与展望
[J]. 自动化学报 2017 , 43 (1 ): 9 -19 .
[本文引用: 2]
YANG Hao JIANG Bin ZHOU Donghua Review and perspectives on fault tolerant control for interconnected systems
[J]. Acta Automatica Sinica 2017 , 43 (1 ): 9 -19 .
[本文引用: 2]
[26]
ESTEBAN R ANTONIO L LOANNIS S et al Robust consensus of high-order systems under output constraints: Application to rendezvous of underactuated UAVs
[J]. IEEE Transactions on Automatic Control 2023 , 68 (1 ): 329 -342 .
[本文引用: 1]
[27]
CHANG J SHI H ZHU S et al Time cost for consensus of stochastic multiagent systems with pinning control
[J]. IEEE Transactions on Systems , Man
and Cybernetics: Systems , 2023 , 53 (1 ): 94 -104 .
[本文引用: 1]
[28]
XU H YU T REN C et al Finite-time decentralized sliding mode control for interconnected systems and its application to electrical power systems: A GA-assisted design method
[J]. IEEE Transactions on Circuits and Systems I: Regular Papers 2024 , 71 (6 ): 2835 -2847 .
[本文引用: 1]
[29]
DI G S Output stabilization of flexible spacecraft with active vibration suppression
[J]. IEEE Transactions on Aerospace and Electronic Systems 2003 , 39 (3 ): 747 -759 .
[本文引用: 1]
[30]
VOURNAS C D PAPADIAS B C Power system stabilization via parameter optimization-application to the hellenic interconnected system
[J]. IEEE Transactions on Power Systems 1987 , 2 (3 ): 615 -622 .
[本文引用: 1]
[31]
SONG G TAO G Adaptive leader-following state consensus of multiagent systems with switching topology
[J]. International Journal of Adaptive Control and Signal Processing 2018 , 32 (10 ): 1508 -1528 .
[本文引用: 3]
Adaptive fault tolerant supervisory consensus control for nonlinear strict-feedback multiagent systems
1
2022
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
Consensus tracking for multi-agent systems with directed graph via distributed adaptive protocol
1
2015
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
Recent advances on cooperative control of heterogeneous multi-agent systems subject to constraints: A survey
1
2022
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
Multi-agent reinforcement learning: A review of challenges and applications
1
2021
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
Consensus in multi-agent systems: A review
1
2022
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
Robust output consensus of homogeneous multi-agent systems with negative imaginary dynamics
1
2020
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
Positive consensus of multi-agent systems with hierarchical control protocol
1
2022
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
Robust consensus tracking control of uncertain multi-agent systems with local disturbance rejection
1
2023
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
1
2013
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
1
2013
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
Multi-agent robotic system (MARS) for UAV-UGV path planning and automatic sensory data collection in cluttered environments
1
2022
... 多智能体系统因其在无人机、航天器、机器人编队等领域的广泛应用而得到了迅速发展[1 ⇓ ⇓ ⇓ -5 ] .目前,针对同构多智能体系统的状态一致性问题已有许多研究成果[6 ⇓ -8 ] .但是,日益复杂的任务需求往往需要多种智能体相互配合[9 -10 ] .不同类型的智能体组成的异构多智能体系统除了各智能体的系统参数存在差异外,其动态模型甚至状态维度都可能是不同的,此时状态一致性大多无法实现,因此针对异构多智能体系统的输出一致性研究具有重要意义. ...
Robust formation control for nonlinear heterogeneous multiagent systems based on adaptive event-triggered strategy
1
2022
... 为实现异构多智能体系统输出一致性,国内外专家将鲁棒控制[11 ] 、滑模控制[12 ] 、自适应控制[13 ] 等方法与协同控制理论相结合,提出了许多有效的输出一致性控制方案.其中,自适应控制不依赖精确的系统模型,能够有效地处理多智能体系统在复杂任务场景下遇到的系统参数不确定问题[14 -15 ] .文献[16 ]中针对具有外部干扰的异构多智能体系统,分别设计了有限时间自适应控制器和固定时间自适应控制器,实现有限时间和固定时间下的多智能体系统二部平均输出一致性.文献[17 ]中通过设计观测器估计领导者输出信号,并设计分布式自适应极点配置控制器实现非最小相位异构多智能体系统的领导者-跟随者输出一致性.文献[18 ]中构造了一种将观测器估计得到的领导者输出信号作为参考输入的参考模型系统,并设计基于事件触发机制的模型参考自适应控制方法,实现了异构多智能体系统的输出一致性. ...
Distributed sliding-mode tracking control of second-order nonlinear multiagent systems: An event-triggered approach
1
2020
... 为实现异构多智能体系统输出一致性,国内外专家将鲁棒控制[11 ] 、滑模控制[12 ] 、自适应控制[13 ] 等方法与协同控制理论相结合,提出了许多有效的输出一致性控制方案.其中,自适应控制不依赖精确的系统模型,能够有效地处理多智能体系统在复杂任务场景下遇到的系统参数不确定问题[14 -15 ] .文献[16 ]中针对具有外部干扰的异构多智能体系统,分别设计了有限时间自适应控制器和固定时间自适应控制器,实现有限时间和固定时间下的多智能体系统二部平均输出一致性.文献[17 ]中通过设计观测器估计领导者输出信号,并设计分布式自适应极点配置控制器实现非最小相位异构多智能体系统的领导者-跟随者输出一致性.文献[18 ]中构造了一种将观测器估计得到的领导者输出信号作为参考输入的参考模型系统,并设计基于事件触发机制的模型参考自适应控制方法,实现了异构多智能体系统的输出一致性. ...
Cooperative output regulation of heterogeneous linear multi-agent systems with edge-event triggered adaptive control under time-varying topologies
1
2020
... 为实现异构多智能体系统输出一致性,国内外专家将鲁棒控制[11 ] 、滑模控制[12 ] 、自适应控制[13 ] 等方法与协同控制理论相结合,提出了许多有效的输出一致性控制方案.其中,自适应控制不依赖精确的系统模型,能够有效地处理多智能体系统在复杂任务场景下遇到的系统参数不确定问题[14 -15 ] .文献[16 ]中针对具有外部干扰的异构多智能体系统,分别设计了有限时间自适应控制器和固定时间自适应控制器,实现有限时间和固定时间下的多智能体系统二部平均输出一致性.文献[17 ]中通过设计观测器估计领导者输出信号,并设计分布式自适应极点配置控制器实现非最小相位异构多智能体系统的领导者-跟随者输出一致性.文献[18 ]中构造了一种将观测器估计得到的领导者输出信号作为参考输入的参考模型系统,并设计基于事件触发机制的模型参考自适应控制方法,实现了异构多智能体系统的输出一致性. ...
Adaptive actuator failure compensation for possibly nonminimum-phase systems using control separation based LQ design
1
2018
... 为实现异构多智能体系统输出一致性,国内外专家将鲁棒控制[11 ] 、滑模控制[12 ] 、自适应控制[13 ] 等方法与协同控制理论相结合,提出了许多有效的输出一致性控制方案.其中,自适应控制不依赖精确的系统模型,能够有效地处理多智能体系统在复杂任务场景下遇到的系统参数不确定问题[14 -15 ] .文献[16 ]中针对具有外部干扰的异构多智能体系统,分别设计了有限时间自适应控制器和固定时间自适应控制器,实现有限时间和固定时间下的多智能体系统二部平均输出一致性.文献[17 ]中通过设计观测器估计领导者输出信号,并设计分布式自适应极点配置控制器实现非最小相位异构多智能体系统的领导者-跟随者输出一致性.文献[18 ]中构造了一种将观测器估计得到的领导者输出信号作为参考输入的参考模型系统,并设计基于事件触发机制的模型参考自适应控制方法,实现了异构多智能体系统的输出一致性. ...
Adaptive LQ control using reduced hamiltonian for continuous-time systems with unmatched input disturbances
1
2021
... 为实现异构多智能体系统输出一致性,国内外专家将鲁棒控制[11 ] 、滑模控制[12 ] 、自适应控制[13 ] 等方法与协同控制理论相结合,提出了许多有效的输出一致性控制方案.其中,自适应控制不依赖精确的系统模型,能够有效地处理多智能体系统在复杂任务场景下遇到的系统参数不确定问题[14 -15 ] .文献[16 ]中针对具有外部干扰的异构多智能体系统,分别设计了有限时间自适应控制器和固定时间自适应控制器,实现有限时间和固定时间下的多智能体系统二部平均输出一致性.文献[17 ]中通过设计观测器估计领导者输出信号,并设计分布式自适应极点配置控制器实现非最小相位异构多智能体系统的领导者-跟随者输出一致性.文献[18 ]中构造了一种将观测器估计得到的领导者输出信号作为参考输入的参考模型系统,并设计基于事件触发机制的模型参考自适应控制方法,实现了异构多智能体系统的输出一致性. ...
Bipartite average tracking for multi-agent systems with disturbances: Finite-time and fixed-time convergence
1
2021
... 为实现异构多智能体系统输出一致性,国内外专家将鲁棒控制[11 ] 、滑模控制[12 ] 、自适应控制[13 ] 等方法与协同控制理论相结合,提出了许多有效的输出一致性控制方案.其中,自适应控制不依赖精确的系统模型,能够有效地处理多智能体系统在复杂任务场景下遇到的系统参数不确定问题[14 -15 ] .文献[16 ]中针对具有外部干扰的异构多智能体系统,分别设计了有限时间自适应控制器和固定时间自适应控制器,实现有限时间和固定时间下的多智能体系统二部平均输出一致性.文献[17 ]中通过设计观测器估计领导者输出信号,并设计分布式自适应极点配置控制器实现非最小相位异构多智能体系统的领导者-跟随者输出一致性.文献[18 ]中构造了一种将观测器估计得到的领导者输出信号作为参考输入的参考模型系统,并设计基于事件触发机制的模型参考自适应控制方法,实现了异构多智能体系统的输出一致性. ...
Distributed adaptive output consensus of unknown heterogeneous non-minimum phase multi-agent systems
1
2023
... 为实现异构多智能体系统输出一致性,国内外专家将鲁棒控制[11 ] 、滑模控制[12 ] 、自适应控制[13 ] 等方法与协同控制理论相结合,提出了许多有效的输出一致性控制方案.其中,自适应控制不依赖精确的系统模型,能够有效地处理多智能体系统在复杂任务场景下遇到的系统参数不确定问题[14 -15 ] .文献[16 ]中针对具有外部干扰的异构多智能体系统,分别设计了有限时间自适应控制器和固定时间自适应控制器,实现有限时间和固定时间下的多智能体系统二部平均输出一致性.文献[17 ]中通过设计观测器估计领导者输出信号,并设计分布式自适应极点配置控制器实现非最小相位异构多智能体系统的领导者-跟随者输出一致性.文献[18 ]中构造了一种将观测器估计得到的领导者输出信号作为参考输入的参考模型系统,并设计基于事件触发机制的模型参考自适应控制方法,实现了异构多智能体系统的输出一致性. ...
Cooperative output tracking of unknown heterogeneous linear systems by distributed event-triggered adaptive control
1
2020
... 为实现异构多智能体系统输出一致性,国内外专家将鲁棒控制[11 ] 、滑模控制[12 ] 、自适应控制[13 ] 等方法与协同控制理论相结合,提出了许多有效的输出一致性控制方案.其中,自适应控制不依赖精确的系统模型,能够有效地处理多智能体系统在复杂任务场景下遇到的系统参数不确定问题[14 -15 ] .文献[16 ]中针对具有外部干扰的异构多智能体系统,分别设计了有限时间自适应控制器和固定时间自适应控制器,实现有限时间和固定时间下的多智能体系统二部平均输出一致性.文献[17 ]中通过设计观测器估计领导者输出信号,并设计分布式自适应极点配置控制器实现非最小相位异构多智能体系统的领导者-跟随者输出一致性.文献[18 ]中构造了一种将观测器估计得到的领导者输出信号作为参考输入的参考模型系统,并设计基于事件触发机制的模型参考自适应控制方法,实现了异构多智能体系统的输出一致性. ...
基于自适应通信拓扑四旋翼无人机编队重构控制
1
2018
... 上述研究虽然有效地解决了异构多智能体系统的输出一致性问题,但是要求所有跟随者都能够获取领导者信息.实际上,智能体之间存在着通信距离的限制,因而领导者及所有跟随者信息都无法全局可达;并且,多智能体系统在固定通信拓扑下执行复杂任务时存在最大通信距离无法满足实际所需通信距离的问题,此时智能体原有通信链接将会断开并与通信范围内的智能体建立新的通信链接,造成通信拓扑结构突变的情况[19 ] .因此,文献[20 ]中提出了一种分布式输出反馈模型参考自适应控制策略,仅利用相邻智能体信息进行控制器设计,实现异构多智能体领导者-跟随者输出一致性.在此基础上,文献[21 ]中提出了基于切换控制策略的分布式自适应控制器,实现了突变通信拓扑结构的异构多智能体领导者-跟随者输出一致性.但是,文献[21 -22 ]中所设计的控制策略需要满足较为复杂的模型匹配条件. ...
Formation reconfiguration control of quadrotor UAVs based on adaptive communication topology
1
2018
... 上述研究虽然有效地解决了异构多智能体系统的输出一致性问题,但是要求所有跟随者都能够获取领导者信息.实际上,智能体之间存在着通信距离的限制,因而领导者及所有跟随者信息都无法全局可达;并且,多智能体系统在固定通信拓扑下执行复杂任务时存在最大通信距离无法满足实际所需通信距离的问题,此时智能体原有通信链接将会断开并与通信范围内的智能体建立新的通信链接,造成通信拓扑结构突变的情况[19 ] .因此,文献[20 ]中提出了一种分布式输出反馈模型参考自适应控制策略,仅利用相邻智能体信息进行控制器设计,实现异构多智能体领导者-跟随者输出一致性.在此基础上,文献[21 ]中提出了基于切换控制策略的分布式自适应控制器,实现了突变通信拓扑结构的异构多智能体领导者-跟随者输出一致性.但是,文献[21 -22 ]中所设计的控制策略需要满足较为复杂的模型匹配条件. ...
Output synchronization of unknown heterogeneous agents via distributed model reference adaptation
1
2018
... 上述研究虽然有效地解决了异构多智能体系统的输出一致性问题,但是要求所有跟随者都能够获取领导者信息.实际上,智能体之间存在着通信距离的限制,因而领导者及所有跟随者信息都无法全局可达;并且,多智能体系统在固定通信拓扑下执行复杂任务时存在最大通信距离无法满足实际所需通信距离的问题,此时智能体原有通信链接将会断开并与通信范围内的智能体建立新的通信链接,造成通信拓扑结构突变的情况[19 ] .因此,文献[20 ]中提出了一种分布式输出反馈模型参考自适应控制策略,仅利用相邻智能体信息进行控制器设计,实现异构多智能体领导者-跟随者输出一致性.在此基础上,文献[21 ]中提出了基于切换控制策略的分布式自适应控制器,实现了突变通信拓扑结构的异构多智能体领导者-跟随者输出一致性.但是,文献[21 -22 ]中所设计的控制策略需要满足较为复杂的模型匹配条件. ...
Adaptive synchronization for heterogeneous multi-agent systems with switching topologies
4
2018
... 上述研究虽然有效地解决了异构多智能体系统的输出一致性问题,但是要求所有跟随者都能够获取领导者信息.实际上,智能体之间存在着通信距离的限制,因而领导者及所有跟随者信息都无法全局可达;并且,多智能体系统在固定通信拓扑下执行复杂任务时存在最大通信距离无法满足实际所需通信距离的问题,此时智能体原有通信链接将会断开并与通信范围内的智能体建立新的通信链接,造成通信拓扑结构突变的情况[19 ] .因此,文献[20 ]中提出了一种分布式输出反馈模型参考自适应控制策略,仅利用相邻智能体信息进行控制器设计,实现异构多智能体领导者-跟随者输出一致性.在此基础上,文献[21 ]中提出了基于切换控制策略的分布式自适应控制器,实现了突变通信拓扑结构的异构多智能体领导者-跟随者输出一致性.但是,文献[21 -22 ]中所设计的控制策略需要满足较为复杂的模型匹配条件. ...
... ]中提出了基于切换控制策略的分布式自适应控制器,实现了突变通信拓扑结构的异构多智能体领导者-跟随者输出一致性.但是,文献[21 -22 ]中所设计的控制策略需要满足较为复杂的模型匹配条件. ...
... 对于2个无人机跟随者智能体,四轴无人机偏航运动动力学方程[21 ] 如下所示: ...
... 其中:当i =1, 2时,xi (t )=[ψi ψ · i T 、ui (t )= τ ψ i yi (t )=ψi 分别为第1、第2个跟随者(无人机)的状态信号、控制输入信号和输出信号;当i =3, 4时,xi (t )=[βi ϕi ϕ · i T 、ui (t )=δ f i yi (t )=ϕi 分别为第3、第4个跟随者(无人车)的状态信号、控制输入信号和输出信号;Ai 、Bi 、Ci 为相应的系统参数矩阵.根据文献[21 ,31 ],跟随者智能体的系统参数矩阵选取为 ...
A distributed adaptive state feedback control scheme for output consensus of multi-agent systems
1
2019
... 上述研究虽然有效地解决了异构多智能体系统的输出一致性问题,但是要求所有跟随者都能够获取领导者信息.实际上,智能体之间存在着通信距离的限制,因而领导者及所有跟随者信息都无法全局可达;并且,多智能体系统在固定通信拓扑下执行复杂任务时存在最大通信距离无法满足实际所需通信距离的问题,此时智能体原有通信链接将会断开并与通信范围内的智能体建立新的通信链接,造成通信拓扑结构突变的情况[19 ] .因此,文献[20 ]中提出了一种分布式输出反馈模型参考自适应控制策略,仅利用相邻智能体信息进行控制器设计,实现异构多智能体领导者-跟随者输出一致性.在此基础上,文献[21 ]中提出了基于切换控制策略的分布式自适应控制器,实现了突变通信拓扑结构的异构多智能体领导者-跟随者输出一致性.但是,文献[21 -22 ]中所设计的控制策略需要满足较为复杂的模型匹配条件. ...
Aircraft turbulence compensation using adaptive multivariable disturbance rejection techniques
2
2015
... 式中:s 表示拉普拉斯变换变量;$ P_{i}(s)=\operatorname{det}\left(s \boldsymbol{I}_{i}-\right. \boldsymbol{A}_{i} )$是pi 阶首一多项式;$Z_{i}(s)$是mi 阶首一多项式$\left(m_{i} \geqslant 0\right) ; k_{\mathrm{p} i}=\boldsymbol{C}_{i} \boldsymbol{A}_{i_{i}-1}^{\rho_{i}-1} \boldsymbol{B}_{i}$为第i 个跟随者系统的高频增益,ρi =pi -mi 为相应跟随者系统的相对阶;“[ ]”是一种连接时域和复域的混合域运算符.yi (t )=Gi (s )[ui ](t )表示为:系统传递函数为Gi (s ),系统输入为ui (t )时的系统输出,这是在自适应控制中常见的符号[23 -24 ] . ...
... 引理2 自适应律式(42)保证了[23 -24 ] : ...
5
2003
... 式中:s 表示拉普拉斯变换变量;$ P_{i}(s)=\operatorname{det}\left(s \boldsymbol{I}_{i}-\right. \boldsymbol{A}_{i} )$是pi 阶首一多项式;$Z_{i}(s)$是mi 阶首一多项式$\left(m_{i} \geqslant 0\right) ; k_{\mathrm{p} i}=\boldsymbol{C}_{i} \boldsymbol{A}_{i_{i}-1}^{\rho_{i}-1} \boldsymbol{B}_{i}$为第i 个跟随者系统的高频增益,ρi =pi -mi 为相应跟随者系统的相对阶;“[ ]”是一种连接时域和复域的混合域运算符.yi (t )=Gi (s )[ui ](t )表示为:系统传递函数为Gi (s ),系统输入为ui (t )时的系统输出,这是在自适应控制中常见的符号[23 -24 ] . ...
... 引理2 自适应律式(42)保证了[23 -24 ] : ...
... 证明 定理3的证明过程分为以下两步:首先证明单个跟随者智能体对其参考模型系统的渐近输出跟踪,进而证明领导者-跟随者全局输出一致性.其中,针对单个跟随者系统的闭环稳定性及跟踪性能分析可参考文献[24 ],由于篇幅限制,本文仅进行简要的说明.引入以下全阶状态观测器: ...
... 式中:βi 1 , α ^ i 1 α ^ i 2 xi 0 ∈L ∞ ;xi 1 (t )= Θ · i ( t ) ε i ( t ) mi (t )∈L 2 ∩L ∞ . 因此根据小增益引理[24 ] 可得y f i t )∈L ∞ ,进而有ui (t )∈L ∞ ,yi (t )∈L ∞ . 因此ωi (t )∈L ∞ ,ξi (t )∈L ∞ ,ζi (t )∈L ∞ ,mi (t )∈L ∞ 得到保障. 根据引理2,有 ε i ( t ) m i ( t ) L 2 , Θ · i ( t )∈L 2 , Ψ · i ( t )∈L 2 ,并且可得ξi (t )∈L 2 , l i m t → ∞ ξi (t )=0. 更进一步地,有 ...
... 上述内容在文献[24 ]中的框架下证明了跟随者系统参数未知时,跟随者输出对其参考模型输出的渐近跟踪性能,若每个参考模型系统都可实现对领导者系统的输出跟踪,即可达成领导者-跟随者全局输出一致性.因此结合定理1,根据参考模型系统对领导者的全局输出一致性 l i m t → ∞ e m i 0 (t )= l i m t → ∞ ( y m i t )-y 0 (t ))=0,可得 ...
互联系统容错控制的研究回顾与展望
2
2017
... 注1 本文所考虑的多智能体系统属于网络互联系统,智能体之间不存在机械耦合,仅通过通信网络相互连接以进行信息交互,并通过协同控制器设计实现群体目标,例如机器人编队、飞行器编队等[25 ⇓ -27 ] ,各智能体状态方程表示为 ...
... 其中:$\sum_{j \in \mathcal{P}_{i}} \boldsymbol{A}_{i j} \boldsymbol{x}_{j}(t)$表示第i 个子系统与其他子系统之间的耦合效应,针对这类机械互联系统控制方案的研究可参考文献[25 ,28 ⇓ -30 ]. ...
Review and perspectives on fault tolerant control for interconnected systems
2
2017
... 注1 本文所考虑的多智能体系统属于网络互联系统,智能体之间不存在机械耦合,仅通过通信网络相互连接以进行信息交互,并通过协同控制器设计实现群体目标,例如机器人编队、飞行器编队等[25 ⇓ -27 ] ,各智能体状态方程表示为 ...
... 其中:$\sum_{j \in \mathcal{P}_{i}} \boldsymbol{A}_{i j} \boldsymbol{x}_{j}(t)$表示第i 个子系统与其他子系统之间的耦合效应,针对这类机械互联系统控制方案的研究可参考文献[25 ,28 ⇓ -30 ]. ...
Robust consensus of high-order systems under output constraints: Application to rendezvous of underactuated UAVs
1
2023
... 注1 本文所考虑的多智能体系统属于网络互联系统,智能体之间不存在机械耦合,仅通过通信网络相互连接以进行信息交互,并通过协同控制器设计实现群体目标,例如机器人编队、飞行器编队等[25 ⇓ -27 ] ,各智能体状态方程表示为 ...
IEEE Transactions on Systems , Man
1
2023
... 注1 本文所考虑的多智能体系统属于网络互联系统,智能体之间不存在机械耦合,仅通过通信网络相互连接以进行信息交互,并通过协同控制器设计实现群体目标,例如机器人编队、飞行器编队等[25 ⇓ -27 ] ,各智能体状态方程表示为 ...
Finite-time decentralized sliding mode control for interconnected systems and its application to electrical power systems: A GA-assisted design method
1
2024
... 其中:$\sum_{j \in \mathcal{P}_{i}} \boldsymbol{A}_{i j} \boldsymbol{x}_{j}(t)$表示第i 个子系统与其他子系统之间的耦合效应,针对这类机械互联系统控制方案的研究可参考文献[25 ,28 ⇓ -30 ]. ...
Output stabilization of flexible spacecraft with active vibration suppression
1
2003
... 其中:$\sum_{j \in \mathcal{P}_{i}} \boldsymbol{A}_{i j} \boldsymbol{x}_{j}(t)$表示第i 个子系统与其他子系统之间的耦合效应,针对这类机械互联系统控制方案的研究可参考文献[25 ,28 ⇓ -30 ]. ...
Power system stabilization via parameter optimization-application to the hellenic interconnected system
1
1987
... 其中:$\sum_{j \in \mathcal{P}_{i}} \boldsymbol{A}_{i j} \boldsymbol{x}_{j}(t)$表示第i 个子系统与其他子系统之间的耦合效应,针对这类机械互联系统控制方案的研究可参考文献[25 ,28 ⇓ -30 ]. ...
Adaptive leader-following state consensus of multiagent systems with switching topology
3
2018
... 在假设1和2的前提下,Song等[31 ] 中构造了一种局部状态跟踪误差,并获得了若智能体vi 的局部状态跟踪误差收敛,则达成全局状态一致性的结论. 类似地,首先给出当前智能体vi 与其邻居智能体vj 的输出误差eij (t )=yi (t )-yj (t ),并定义如下局部输出跟踪误差: ...
... 式中:ψi 、Iyi 、 τ ψ i i 架无人机的偏航角、y 轴上的转动惯量、偏航角上的转动力矩.对于2个无人车跟随者智能体,无人车横向动力学方程[31 ] 如下所示: ...
... 其中:当i =1, 2时,xi (t )=[ψi ψ · i T 、ui (t )= τ ψ i yi (t )=ψi 分别为第1、第2个跟随者(无人机)的状态信号、控制输入信号和输出信号;当i =3, 4时,xi (t )=[βi ϕi ϕ · i T 、ui (t )=δ f i yi (t )=ϕi 分别为第3、第4个跟随者(无人车)的状态信号、控制输入信号和输出信号;Ai 、Bi 、Ci 为相应的系统参数矩阵.根据文献[21 ,31 ],跟随者智能体的系统参数矩阵选取为 ...