基于矢量场制导法和模型预测控制的船舶路径跟踪与避碰

doi:10.16183/j.cnki.jsjtu.2023.121

基于矢量场制导法和模型预测控制的船舶路径跟踪与避碰

何宇¹, 欧阳子路¹, 邹璐^,¹^,², 陈伟民³, 邹早建¹^,²

1.上海交通大学船舶海洋与建筑工程学院,上海 200240

2.上海交通大学海洋工程国家重点实验室,上海 200240

3.上海船舶运输科学研究所有限公司,上海 200135

Ship Path Following and Collision Avoidance Based on Vector Field Guidance Law and Model Predictive Control

HE Yu¹, OUYANG Zilu¹, ZOU Lu^,¹^,², CHEN Weimin³, ZOU Zaojian¹^,²

1. School of Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

3. Shanghai Ship and Shipping Research Institute Co., Ltd., Shanghai 200135, China

通讯作者: 邹璐,副教授,博士生导师,电话(Tel.):021-34208149;E-mail:luzou@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-04-3 修回日期: 2023-05-29 接受日期: 2023-07-3

基金资助:

水动力学国家重点实验室开放基金(6142203210205)
中央高校基本科研业务费专项资金(AF0100142/005/002)
航运技术与安全国家重点实验室、交通行业重点实验室开放课题基金(W22CG000114)

Received: 2023-04-3 Revised: 2023-05-29 Accepted: 2023-07-3

作者简介 About authors

何宇(2000—),硕士生,现主要从事船舶运动控制研究.

摘要

为提高船舶路径跟踪和避碰效果,提出了一种基于矢量场制导法的模型预测控制方法.首先,采用矢量场制导算法将船舶的路径跟踪和船舶避碰问题转换为航向控制问题;然后,采用一阶 Nomoto 响应模型作为模型预测控制的动力学模型,考虑船舶的舵角输入受限问题,引入干扰观测器对模型误差项和环境扰动进行补偿,并应用Lyapunov理论证明了所设计的路径跟踪控制系统的稳定性;最后,设计了基于矢量场制导法的避碰策略,使船舶在路径跟踪的过程中同时完成自主避碰.仿真计算结果表明,开发的方法可以使船舶在波浪干扰作用下准确地跟踪目标路径并有效实现避碰.

关键词： 船舶路径跟踪; 避碰; 模型预测控制; 矢量场制导法; 干扰观测器

Abstract

A model predictive control (MPC) method based on the vector field guidance law is proposed to improve the effectiveness of path following and collision avoidance for ships. First, the path following and collision-avoidance problems are transformed into heading-control problems by the vector field guidance law. Then, the first-order Nomoto response model is adopted as the ship dynamic model for the model predictive control. Considering the input limitation of the rudder angle, the disturbance observer is introduced to compensate the model error and the environmental disturbances. The stability of the designed path following control system is verified by the Lyapunov theory. Finally, a collision avoidance strategy based on the vector field guidance law is designed to enable the ship to avoid collision autonomously in the process of path following. The simulation results indicate that the proposed methods can make the ship track the target path accurately and realize collision avoidance under the impacts of wave disturbances.

Keywords： ship path following; collision avoidance; model predictive control (MPC); vector field (VF) guidance law; disturbance observer

PDF (3125KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

何宇, 欧阳子路, 邹璐, 陈伟民, 邹早建. 基于矢量场制导法和模型预测控制的船舶路径跟踪与避碰[J]. 上海交通大学学报, 2024, 58(11): 1644-1653 doi:10.16183/j.cnki.jsjtu.2023.121

HE Yu, OUYANG Zilu, ZOU Lu, CHEN Weimin, ZOU Zaojian. Ship Path Following and Collision Avoidance Based on Vector Field Guidance Law and Model Predictive Control[J]. Journal of Shanghai Jiaotong University, 2024, 58(11): 1644-1653 doi:10.16183/j.cnki.jsjtu.2023.121

船舶的路径跟踪是指在空间维度上,船舶于有限时间内跟踪并收敛到一条预先设好的目标路径上,因此路径跟踪只有空间上的限制而没有时间上的限制.一般来说,船舶的路径跟踪可以大致分为两个模块,分别是制导算法和控制算法.制导算法可将船舶三自由度的运动控制问题简化为一个自由度的航向控制问题,由此解决船舶的欠驱动问题.在众多制导算法中,视线 (line-of-sight, LOS) 制导法及其改进形式因易于理解与实施,被广泛使用^[1⇓⇓-4].相比于LOS法,矢量场(vector field, VF)制导法是一种结构更灵活的数学方法.其主要思想是建立一个矢量空间,空间中所有的矢量都平稳地指向路径,如果船舶跟随矢量场中设定的期望航向角,最终会收敛到目标路径上.矢量场制导法被广泛用于无人机的制导^[5-6],但将该方法应用于水面船舶运动控制领域的研究较少:Xu等^[7]设计了用于船舶直线路径和曲线路径跟踪控制的时变矢量场制导律,并通过Lyapunov理论给出了制导律的一致半全局指数稳定性证明;Xu等^[8]通过设置自适应参数对矢量场制导法进行改进,使船舶能准确地跟踪预设的直线路径.

对于水面船舶来说,在航行过程中遇到障碍物是不可避免的.传统的避碰通常强调在船舶完全控制的前提下使碰撞风险最小化,因此一般被视为一个独立于控制器的规划问题^[9-10].此外,也有学者将船舶避碰集成到跟踪控制上,使船舶能同时完成这两项任务^{[8,11 -12]}.对于处理船舶系统的输入约束,已经积累了许多研究成果.陆潇杨等^[13]针对水面船舶航向运动中出现的输入约束和非零漂角问题,结合反步控制算法提出了一种鲁棒自适应航向控制器.Qiu等^[14]提出了一种实用的欠驱动无人船的自适应滑模控制方案,并采用辅助动态系统技术处理输入约束问题.模型预测控制 (model predictive control, MPC) 作为一种先进的控制算法,可以在求解优化问题的过程中处理船舶系统的输入约束,在解决船舶运动控制问题上具有独特的优势.柳晨光等^[15]设计线性模型预测控制器以解决船舶控制输入及其增量的约束问题.Wang等^[16]提出了一种数据驱动预测控制方法,该方法采用弹性网络回归算法对船舶操纵运动过程中收集的数据进行拟合,并根据拟合得到的数据驱动模型与模型预测控制实现准确地船舶路径跟踪.除了船舶的输入约束问题,模型的建模误差和干扰问题也是不能忽视的.船舶的动力学模型会随着航行环境干扰的变化而改变,这对控制器的鲁棒性提出了更高的要求.Zhang等^[17]、Yang等^[18]、贺宏伟等^[19]通过引入干扰观测器估计环境扰动或者采用神经网络逼近非线性项等手段以增强不确定条件下控制系统的自适应能力与鲁棒性.

本文首先设计了一种基于矢量场制导法的路径跟踪制导律,并给出了一种障碍物矢量场的生成方法.通过改进的矢量场制导法,可以将船舶路径跟踪与自主避碰问题转化为航向控制问题.考虑到船舶控制器设计模型误差和环境扰动等问题,设计了干扰观测器进行观测,以提高船舶操纵运动控制的有效性与鲁棒性.然后,采用考虑了干扰项的模型预测控制准确跟踪矢量场制导法生成的期望航向角,以同时实现船舶的路径跟踪与自主避碰.最后,建立带有波浪干扰的仿真模型进行计算机仿真,对本文所提出方法进行验证.

1 矢量场制导法

1.1 坐标系以及运动模型建立

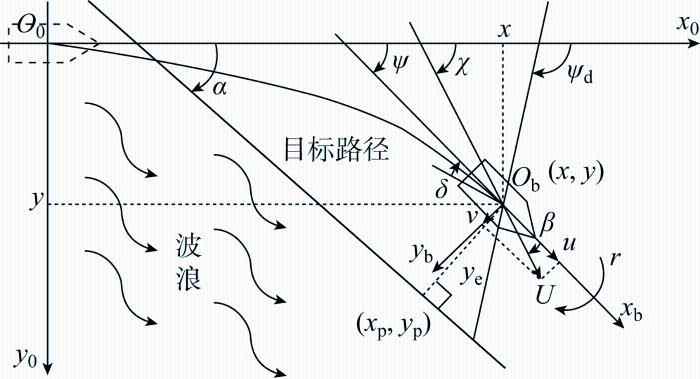
为便于分析三自由度船舶操纵运动,构建如图1所示的两个右手坐标系:惯性坐标系O₀-x₀y₀z₀和船体坐标系O_b-x_by_bz_b.惯性坐标系固定在地球表面,x₀轴指向船舶初始直航方向,y₀轴指向初始状态时的船体右舷,z₀轴垂直向下为正;船体坐标系固定在船中,其中O_b-x_by_b平面与静水面重合,x_b轴指向船艏,y_b轴指向船体右舷,z_b轴垂直向下为正.在图1中:(x, y)为船舶在惯性坐标系中的位置;ψ为船舶艏向角;u、v和r分别表示在船体坐标系下的纵向速度、横向速度和转艏角速度;β=arctan(v/u)为漂角;χ=ψ+β为航速角;U= $\sqrt{u^{2} + v^{2}}$ 表示船舶合速度;δ为舵角;(x_p, y_p)为船舶中心O_b在目标路径上的投影;α是目标路径与惯性坐标系x₀轴正向之间的夹角;y_e为船舶与目标路径之间的横向误差;ψ_d为制导的期望航向角,通过矢量场制导法求出.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 船舶平面位置与运动参数

Fig.1 Ship planar position and motion parameters

通过矢量场制导法可以将船舶的路径跟踪问题转化为对期望航向角的跟踪问题.构建水面三自由度船舶的运动模型:

(1)

\begin{array}{l} \overset{\cdot}{x} = u c o s ψ - v s i n ψ \\ \overset{\cdot}{y} = u s i n ψ + v c o s ψ \\ \overset{\cdot}{ψ} = r \end{array}\}

船舶与目标路径之间的横向误差可以表示为

(2)y_e=-(x-x_p)sin α+(y-y_p)cos α

对式(2)求导并将式(1)代入可以得到:

(3)$\begin{aligned}\dot{y}_{\mathrm{e}}= & -\dot{x} \sin \alpha+\dot{y} \cos \alpha= \\& -(u \cos \psi-v \sin \psi) \sin \alpha+ \\& (u \sin \psi+v \cos \psi) \cos \alpha= \\& -U(\cos \beta \cos \psi-\sin \beta \sin \psi) \sin \alpha+ \\& U(\cos \beta \sin \psi+\sin \beta \cos \psi) \cos \alpha= \\& -U \cos (\psi+\beta) \sin \alpha+U \sin (\psi+\beta) \cos \alpha= \\& U \sin (\psi-\alpha+\beta)\end{aligned}$

1.2 路径跟踪矢量场生成

基于矢量场制导法对船舶进行路径跟踪,船舶在某位置处期望的行进方向(航速角)即为该处矢量的方向.将平行于目标路径与垂直于目标路径的两个矢量场进行叠加,构成平滑指向目标路径的矢量场,两个矢量场以及叠加后的矢量场如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 目标路径(红线)周围的矢量场

Fig.2 Vector field around target path (red line)

图2(a)矢量场的矢量方向平行于目标路径且指向目标路径点,矢量大小不随位置而改变,引导船舶前进;图2(b)矢量场的矢量方向垂直并指向目标路径,矢量大小随着船舶与目标路径之间横向误差的减小而减小,引导船舶收敛于目标路径.矢量的欧氏范数设置如下:

(4)$\left.\begin{array}{l}\left\|\boldsymbol{v}_{1}\right\|_{2}=1 \\\left\|\boldsymbol{v}_{2}\right\|_{2}=a_{1} \tanh \left(a_{2}\left|y_{\mathrm{e}}\right|\right)\end{array}\right\}$

式中:a₁和a₂均为大于0的常数.

叠加后的矢量为

(5)$\boldsymbol{v}_{\mathrm{s}}=\boldsymbol{v}_{1}+\boldsymbol{v}_{2}$

叠加后矢量场中在各个位置矢量的方向即表示船舶的期望航速角χ_d,考虑到漂角的存在,期望航向角ψ_d表示为

(6)

\begin{array}{l} χ_{d} = α - s i g n (y_{e}) a r c t a n [a_{1} t a n h (a_{2} | y_{e} |)] \\ ψ_{d} = χ_{d} - β \end{array}\}

假设船舶能跟踪上期望航向角,即ψ=ψ_d,将式(6)代入式(3)可以得到:

(7)$\begin{aligned}\dot{y}_{\mathrm{e}}= & U \sin (\psi-\alpha+\beta)= \\& U \sin \left(\psi_{\mathrm{d}}-\alpha+\beta\right)=U \sin \left(\chi_{\mathrm{d}}-\alpha\right)= \\& U \sin \left\{\alpha-\left(y_{\mathrm{e}}\right) \arctan \left[a_{1} \tanh \left(a_{2}\left|y_{e}\right|\right)\right]-\alpha\right\}= \\& -U \frac{a_{1} \operatorname{sign}\left(y_{\mathrm{e}}\right) \tanh \left(a_{2}\left|y_{\mathrm{e}}\right|\right)}{\sqrt{1+\left[a_{1} \tanh \left(a_{2} y_{\mathrm{e}}\right)\right]^{2}}}\end{aligned}$

选择如下Lyapunov函数以证明本文中路径跟踪引导律的稳定性:

(8)V₁=

\frac{1}{2} y_{e}^{2}

对式(8)求导并代入式(7)可得:

(9)$\begin{aligned}\dot{V}_{1}= & y_{e} \dot{y}_{e}=-U \frac{a_{1} \operatorname{sign}\left(y_{e}\right) y_{\mathrm{e}} \tanh \left(a_{2}\left|y_{e}\right|\right)}{\sqrt{1+\left[a_{1} \tanh \left(a_{2} y_{e}\right)\right]^{2}}}= \\& -U \frac{a_{1}\left|y_{e}\right| \tanh \left(a_{2}\left|y_{e}\right|\right)}{\sqrt{1+\left[a_{1} \tanh \left(a_{2} y_{e}\right)\right]^{2}}} \leqslant 0\end{aligned}$

根据Lyapunov定理,制导系统是稳定的,且 y_e=0是系统的平衡点.

1.3 避碰矢量场生成

若在目标路径上有一静态障碍物,为避开障碍物,需要改变矢量场的方向,以实现跟踪目标路径并安全避障的任务.假设障碍物的影响范围为圆形,设计以障碍物为中心、R_o为半径的圆形危险区域,同时考虑障碍物半径、船舶尺度和安全距离,将船舶视为一个质点:

(10)R_o=R_ob+

\frac{L_{p p}}{2}

+D_safe

式中:R_ob为障碍物的圆形包络半径;L_pp是船长;D_safe是船舶和障碍物间的最小安全距离.当船舶质点在圆形危险区域外时,认为船舶是安全的.

设置以障碍物中心为圆心、R_co为半径的圆形碰撞范围.当船舶在碰撞范围以外时,路径跟踪的矢量场不会受到障碍物所产生的矢量场影响;而当船舶进入碰撞范围内时,障碍物会产生矢量场,从而影响船舶的期望航向角.R_co可表示为

(11)R_co=R_o+L_co

式中:扩张距离L_co>0.L_co的大小与船舶回转性能有关,回转性能较好的船舶L_co较小,回转性能较差的船舶L_co较大.

设置障碍物所产生矢量总是垂直于目标路径,且朝向远离障碍物的方向.当障碍物与船舶的连线与目标路径平行时,矢量方向指向船舶右舷,障碍物产生的矢量场如图3所示.障碍物产生矢量的大小随船舶和障碍物之间的距离的减小而增大,其欧氏范数设置如下:

(12)$\left\|\boldsymbol{v}_{3}\right\|_{2}=\frac{a_{3}}{\left(L-R_{\circ}\right)^{a_{4}}}$

式中:υ₃表示障碍物产生的矢量;L表示船舶中心与障碍物中心之间的距离;a₃和a₄均为大于0的常数.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 障碍物产生的矢量场

Fig.3 Vector field generated by the obstacle

同时,考虑到:① 随着障碍物的增大,即使船舶与障碍物保持相同的距离,碰撞危险度也会增加;因此,障碍物产生的矢量场强度应随着障碍物的增大而增大;② 即使与同一障碍物保持相同的距离,碰撞危险度会随着船舶行进方向逐渐偏离障碍物而下降;因此设θ为船舶行进方向的向量与由船舶中心指向障碍物中心的向量之间的夹角,将障碍物所产生矢量的强度设计成与θ有关的函数;在其他条件相同的情况下,矢量强度随着θ的增大而减小,对应船舶由驶向障碍物到驶离障碍物过程中碰撞危险度的衰减;③ 船舶的航速对碰撞危险度也会有影响,航速越快碰撞危险度越大.

按照上述方法对式(12)进行改写:

(13)$\left.\begin{array}{l}\left\|\boldsymbol{v}_{3}\right\|_{2}=\frac{a_{3} \eta R_{0}\left(a_{5} U+1\right)}{\left(L-R_{0}\right)^{a_{4}}} \\\eta=\sqrt{\frac{\cos \theta+1}{2}}\end{array}\right\}$

式中:η为障碍物产生矢量的衰减系数;a₅为大于0的常数,a₅越大表示航速对碰撞危险度的影响越大.

有障碍物时叠加后的矢量场将表示为

(14)$\boldsymbol{v}_{\mathrm{s}}=\boldsymbol{v}_{1}+\boldsymbol{v}_{2}+\boldsymbol{v}_{3}$

根据上式得到路径周围存在障碍物时的矢量场后,期望的航速角即为船舶所在位置处矢量的方向.

2 航向控制器设计

本文中解决船舶的路径跟踪以及避碰问题的方法是:采用矢量场制导法生成期望航向角,然后基于MPC方法进行航向控制.航向控制的准确与否最终将影响路径跟踪和避碰的效果,控制器结构如图4所示.图中: $\hat{d}$ 为干扰项的观测值.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 控制器结构

Fig.4 Structure of controller

2.1 响应模型

通常采用响应模型描述船舶转艏运动的动力学过程.本文采用一阶Nomoto响应模型进行船舶航向控制器的设计:

(15)$T \dot{r}+r=K \delta$

式中:K和T为操纵性指数.考虑到一阶Nomoto模型可能的建模误差以及受环境干扰的问题,将式(15)改写为

(16)$\dot{r}=-\frac{1}{T}r+\frac{K}{T}\delta+d$

式中:d为建模误差项和环境扰动项的合并项,称之为干扰项.

一般建模误差项较小,而海洋环境的变化在通常情况下是缓慢的,且波浪的能量是有限的,因此可以假设干扰项d是时变的,但其变化率是有界的^[20],故存在一个正的常数ε使下式成立:

(17)$\mid\dot{d}\mid\leqslant\varepsilon$

2.2 干扰观测器

假设u、v、r等船舶系统状态可测,设计以下干扰观测器对式(16)中的干扰项进行估计,以提高航向控制的准确性:

(18)$\hat{d}=l r+p$

(19)$\dot{p}=-l p-l\left(-\frac{1}{T} r+\frac{K}{T} \delta+l r\right) $

(20)$\tilde{d}=d-\hat{d}$

式中: $\tilde{d}$ 为观测误差;p为中间变量;l为大于0的常数.

对式(18)进行求导,并将式(19)代入:

(21)$\begin{array}{c}\dot{\hat{d}}=l \dot{r}+\dot{p}=l\left(-\frac{1}{T} r+\frac{K}{T} \delta+d\right)- \\l p-l\left(-\frac{1}{T} r+\frac{K}{T} \delta+l r\right)= \\l(d-p-l r)=l(d-\hat{d})=l \tilde{d}\end{array}$

选择如下Lyapunov函数:

(22)V₂=

\frac{1}{2} {\tilde{d}}^{2}

对式(22)求导可得:

(23)$\begin{aligned}\dot{V}_{2}= & \tilde{d} \dot{\tilde{d}}=\tilde{d}(\dot{d}-\dot{\vec{d}})=\tilde{d}(\dot{d}-l \tilde{d})= \\& -l \widetilde{d}^{2}+\widetilde{d} \dot{d} \leqslant-l \widetilde{d}^{2}+\frac{1}{2} \xi \widetilde{d}^{2}+\frac{1}{2 \xi} \dot{d}^{2}= \\& -\left(l-\frac{1}{2} \xi\right) \widetilde{d}^{2}+\frac{1}{2 \xi} \dot{d}^{2} \leqslant \\& -(2 l-\xi) V_{2}+\frac{1}{2 \xi} \varepsilon^{2}\end{aligned}$

式中:ξ为大于0的常数;选择l>ξ/2,即l-ξ/2>0.

对式(23)进行求解:

(24)$\begin{aligned}V_{2} \leqslant & \frac{\varepsilon^{2}}{2 \xi(2 l-\xi)}+ \\& {\left[V_{2}(0)-\frac{\varepsilon^{2}}{2 \xi(2 l-\xi)}\right] \mathrm{e}^{-(2 l-\xi) t} }\end{aligned}$

根据式(22)和式(24)可以得到:

(25)

|\tilde{d}|

≤

\sqrt{\frac{ε^{2}}{ξ (2 l - ξ)} + [2 V_{2} (0) - \frac{ε^{2}}{ξ (2 l - ξ)}] e^{- (2 l - ξ) t}}

由式(25)可知,当ε=0时,即干扰恒定时,观测误差 $\tilde{d}$ 是全局渐近稳定的;当ε≠0时,观测误差 $\tilde{d}$ 是全局一致最终有界的.

2.3 模型预测控制器

将式(16)改写成状态空间方程的形式,并用干扰项的观测值 $\hat{d}$ 代替干扰项的真实值d:

(26)$\dot{\boldsymbol{X}}(t)=\boldsymbol{A}_{t} \boldsymbol{X}(t)+\boldsymbol{B}_{t} \delta(t)+\boldsymbol{C}_{t}$

(27)$\left.\begin{array}{l}\boldsymbol{X}(t)=\left[\begin{array}{l}\psi(t) \\ r(t)\end{array}\right], \quad \boldsymbol{A}_t=\left[\begin{array}{cc}0 & 1 \\ 0 & -\frac{1}{T}\end{array}\right] \\ \boldsymbol{B}_t=\left[\begin{array}{l}0 \\ \frac{K}{T}\end{array}\right], \quad \boldsymbol{C}_t=\left[\begin{array}{l}0 \\ \hat{d}\end{array}\right]\end{array}\right\}$

采用欧拉法对式(26)进行离散:

(28)$\boldsymbol{X}(k+1)=\boldsymbol{A}_{k} \boldsymbol{X}(k)+\boldsymbol{B}_{k} \delta(k)+\boldsymbol{C}_{k}$

(29)$\left.\begin{array}{l}\boldsymbol{X}(k)=\left[\begin{array}{c}\psi(k) \\ r(k)\end{array}\right], \quad \boldsymbol{A}_k=\left[\begin{array}{cc}1 & T_{\mathrm{s}} \\ 0 & 1-\frac{1}{T} T_{\mathrm{s}}\end{array}\right] \\ \boldsymbol{B}_k=\left[\begin{array}{c}0 \\ \frac{K}{T} T_{\mathrm{s}}\end{array}\right], \quad \boldsymbol{C}_k=\left[\begin{array}{c}0 \\ \hat{d} T_{\mathrm{s}}\end{array}\right]\end{array}\right\}$

式中:T_s表示采样时间.

将模型预测控制中的控制时域和预测时域分别设置为N_c和N_p,且N_c≤N_p.在已知当前时刻系统状态的前提下,根据式(28)对预测时域内的状态进行预测,并且假设系统输入δ在控制时域N_c内是变化的,之后则保持不变.在预测时域内的系统状态可表示为

(30)$\left.\begin{array}{l}\boldsymbol{X}(k+1)=\boldsymbol{A}_k \boldsymbol{X}(k)+\boldsymbol{B}_k \delta(k)+\boldsymbol{C}_k \\ \boldsymbol{X}(k+2)=\boldsymbol{A}_k \boldsymbol{X}(k+1)+\boldsymbol{B}_k \delta(k+1)+\boldsymbol{C}_k \\ \ldots \\ \boldsymbol{X}\left(k+N_{\mathrm{c}}\right)=\boldsymbol{A}_k \boldsymbol{X}\left(k+N_{\mathrm{c}}-1\right)+ \\ \quad \boldsymbol{B}_k \delta\left(k+N_c-1\right)+\boldsymbol{C}_k \\ \ldots \\ \boldsymbol{X}\left(k+N_{\mathrm{p}}\right)=\boldsymbol{A}_k \boldsymbol{X}\left(k+N_{\mathrm{p}}-1\right)+ \\ \quad \boldsymbol{B}_k \delta\left(k+N_{\mathrm{c}}-1\right)+\boldsymbol{C}_k\end{array}\right\}$

根据预测时域内的状态向量以及目标向量计算跟踪偏差:

(31)$\left.\begin{array}{l}\boldsymbol{e}(k+1)=\boldsymbol{X}(k+1)-\boldsymbol{X}_{\mathrm{d}}(k+1) \\\cdots \\\boldsymbol{e}\left(k+N_{\mathrm{p}}\right)=\boldsymbol{X}\left(k+N_{\mathrm{p}}\right)-\boldsymbol{X}_{\mathrm{d}}\left(k+N_{\mathrm{p}}\right)\end{array}\right\}$

式中:X_d表示需要跟踪的目标向量.同时,在用预测控制解决船舶航向控制问题时,通常假定期望航向角在预测时间范围内是一个常数,因此X_d(k+i)=[ψ_d(k) 0]^T, i=1, 2, …, N_p.

在船舶航行的过程中应尽量避免高频操舵,因此在模型预测控制进行滚动优化的过程中需对舵角变化量进行考虑,计算舵角变化量:

(32)

\begin{array}{l} Δ δ (k) = δ (k) - δ (k - 1) \\ \dots \\ Δ δ (k + N_{c} - 1) = \\ δ (k + N_{c} - 1) - δ (k + N_{c} - 2) \end{array}\}

根据跟踪偏差以及舵角变化量设计代价函数:

(33)$\begin{aligned}f(\boldsymbol{X}, \boldsymbol{\delta})= & \sum_{i=1}^{N_{\mathrm{p}}-1} \boldsymbol{e}(k+i)^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{e}(k+i)+ \\& \boldsymbol{e}\left(k+N_{\mathrm{p}}\right)^{\mathrm{T}} \boldsymbol{F} \boldsymbol{e}\left(k+N_{\mathrm{p}}\right)+ \\& \sum_{j=0}^{N_{\mathrm{c}}-1} R[\Delta \delta(k+j)]^{2}\end{aligned}$

式中:Q和R分别为跟踪误差和舵角变化量的权值矩阵与权重系数;F为跟踪误差在预测时域终端的权值矩阵;控制序列δ=[δ(k) δ(k+1) … δ(k+N_c-1)].

模型预测控制能够考虑系统约束,对代价函数进行在线求解,得出状态反馈δ(k)=g(X(k), δ(k-1))在预测时域上的最优控制^[21],并仅将控制序列中的第1项作为控制指令:

(34)$\min _{\substack{\delta_{\min } \leqslant \delta \leqslant \delta_{\max } \\ \Delta \delta_{\min } \leqslant \Delta \delta \leqslant \Delta \delta_{\max }}} f(\boldsymbol{X}, \boldsymbol{\delta})$

3 结果及讨论

3.1 船舶动力学仿真模型

本文采用三自由度MMG船舶操纵数学模型作为船舶动力学模型^[22-23].MMG模型将作用在船舶上的水动力(纵向力X,横向力Y)和力矩(转艏力矩N)分为船体、螺旋桨和舵上的三部分,还可计入波浪等环境力的影响,表示为

(35)

\begin{array}{l} (m + m_{x}) \overset{\cdot}{u} - (m + m_{y}) v r - m x_{G} r^{2} = \\ X_{S} + X_{P} + X_{R} + X_{W} \\ (m + m_{y}) \overset{\cdot}{v} + (m + m_{x}) u r + m x_{G} \overset{\cdot}{r} = \\ Y_{S} + Y_{P} + Y_{R} + Y_{W} \\ (I_{z} + J_{z z}) \overset{\cdot}{r} + m x_{G} (\overset{\cdot}{v} + u r) = \\ N_{S} + N_{P} + N_{R} + N_{W} \end{array}\}

式中:下标S、P、R分别表示船体、螺旋桨、舵,W表示波浪;m为船舶质量;m_x、m_y分别为船体沿x_b、y_b轴运动的附加质量;x_G为船体坐标系下船舶重心纵向坐标;I_z为船体绕z_b轴的惯性矩;J_zz为绕z_b轴的附加惯性矩.

波浪干扰力可以分为两类:一阶高频波浪力和二阶慢漂波浪力.参考文献[24]中采用二阶传递函数的形式对波浪力以及波浪力矩进行建模,三自由度水面船舶的波浪力以及波浪力矩的传递函数表达式为

(36)$\left.\begin{array}{l}X_{\mathrm{W}}=\frac{K_{\mathrm{W}}^{\{1\}} s}{s^{2}+2 \lambda^{\{1\}} \omega_{\mathrm{e}}^{\{1\}} s+\left(\omega_{\mathrm{e}}^{\{1\}}\right)^{2}} \bar{\omega}_{1}+d_{1} \\Y_{\mathrm{W}}=\frac{K_{\mathrm{W}}^{\{2\}} s}{s^{2}+2 \lambda^{\{2\}} \omega_{\mathrm{e}}^{\{2\}} s+\left(\omega_{\mathrm{e}}^{\{2\}}\right)^{2}} \bar{\omega}_{2}+d_{2} \\N_{\mathrm{W}}=\frac{K_{\mathrm{W}}^{\{6\}} s}{s^{2}+2 \lambda^{\{6\}} \omega_{\mathrm{e}}^{\{6\}} s+\left(\omega_{\mathrm{e}}^{\{6\}}\right)^{2}} \bar{\omega}_{3}+d_{3}\end{array}\right\}$

式中:K_W为增益,波浪力以及波浪力矩的大小可由K_W进行调整,$ K_{\mathrm{w}}=2 \lambda \omega_{0} \sigma$,λ为阻尼系数,σ为波浪强度,与不同海况下的波高和波浪主频率有关,且不同的波浪谱表达式不同;上标{1}、{2}、{6}表示沿x_b、y_b的平动和绕z_b轴的转动;遭遇频率$\omega_{\mathrm{e}}=\omega_{0}- \omega_{0}^{2} U \cos \beta_{\mathrm{c}} / g, \omega_{0}$为波浪主频率,g为重力加速度,β_c为遭遇角,即船舶艏向与波浪方向之间的夹角,表示为$\beta_{\mathrm{c}}=\psi-\beta_{\mathrm{w}}, \beta_{\mathrm{w}} $为波浪方向; $ \omega_{i}(i=1,2,3) $为随机零均值的高斯白噪声;$ d_{i}(i=1,2,3)$表示二阶波浪慢漂力.

二阶波浪慢漂力d_i(i=1, 2, 3)被建模为缓慢变化的偏差项:

(37)$\left.\begin{array}{l}\dot{d}_{1}=\bar{\omega}_{4} \\\dot{d}_{2}=\bar{\omega}_{5} \\\dot{d}_{3}=\bar{\omega}_{6}\end{array}\right\}$

式中:$ \tilde{\omega}_{i}(i=4,5,6)$同样为随机零均值的高斯白噪声.

3.2 仿真结果与分析

本文以双桨双舵船ONRT船模为研究对象,船模的主尺度等信息见文献[25].取文献[26]中的水动力导数,并以 Modified P-M 波浪谱^[24]来模拟高频波浪响应,波浪参数设置:β_w=45°,ω₀=1.1,λ=0.258 8,σ=0.988 2;同时,加入缓慢时变干扰力模拟慢漂波浪力.惯性坐标系下,仿真得到三自由度上波浪力(矩)的时历曲线如图5所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 作用在船舶上的波浪力(矩)

Fig.5 Wave force (moment) on the ship

为验证本文提出的基于矢量场制导法的MPC控制器的有效性,开展波浪干扰下船舶路径跟踪和避碰问题的仿真计算,并与经典MPC以及比例-积分-微分(proportion integration differentiation, PID) 控制的仿真结果进行对比.PID控制是一种基于误差进行反馈的控制方法,具有结构简单、易于工程实现等诸多优点,因此被广泛采用.设置船舶的初始速度以及初始转艏角速度:u₀=1.1 m/s,v₀=0 m/s,r₀=0 rad/s, 螺旋桨转速设置为n=538 r/min,舵角值限制为|δ|≤35°,转舵速率值限制在| $\overset{\cdot}{δ}$ |≤10 (°)/s.设置采样时间T_s为0.2 s,δ_min=-35°,δ_max=35°,Δδ_min=-2°, Δδ_max=2°;一阶Nomoto模型参数K=0.3,T=0.5.控制器参数设计如下:矢量场制导法参数a₁=20,a₂=0.003,a₃=0.12,a₄=0.5,a₅=0.1,L_co=40 m;干扰观测器参数l=1,p初值为0;MPC相关参数为N_c=3,N_p=20,Q=diag[0,1],R=20,F=40Q;PID控制参数为K_p=1.6,K_i=0,K_d=5.

3.2.1 航向控制效果

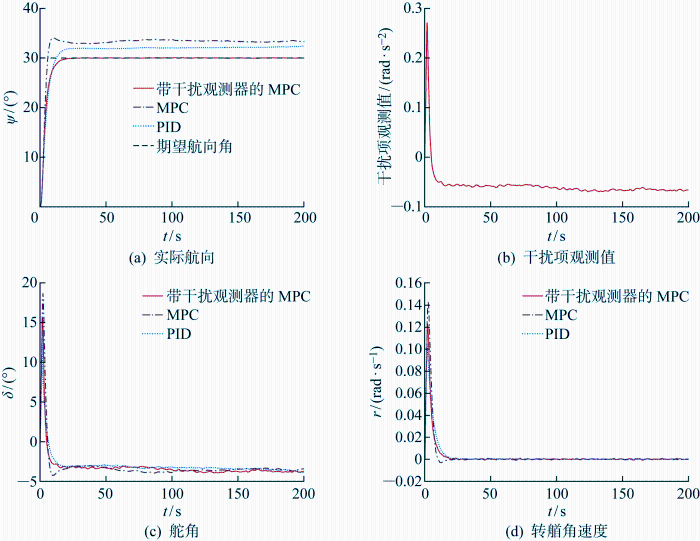
首先验证带干扰观测器的MPC在船舶航向控制中的抗干扰能力,对仿真模型施加波浪力以及波浪力矩.设置船舶初始航向角 ψ₀=0°,期望航向角ψ_d=30°.3种控制方法的仿真结果如图6所示.由图6(a)可知,在波浪力的干扰下经典的MPC以及PID控制均明显存在稳态误差,而带有干扰观测器的MPC能够使船舶航向角收敛至期望值,说明带有干扰观测器的MPC面对建模误差项与环境干扰作用具有较强的鲁棒性.图6(b)展示了本文设计的干扰观测器对干扰项的观测值,由图可知 $\hat{d}$ 最终存在一个较为稳定的非零值,包含建模的不准确项以及环境扰动项.经典的MPC未对干扰项进行考虑,使响应模型与真实模型间有较大误差,从而导致了较大稳态误差的产生.图6(c)和6(d)给出了采用3种方法进行航向控制时的舵角与转艏角速度时历曲线.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 船舶航向控制仿真结果

Fig.6 Simulation results of ship course control

采用均方根误差 (root mean square error, RMSE) 和稳态误差对不同控制方法的效果进行衡量,表1列出了3种控制方法的量化对比结果.由表1可以看到,采用带干扰观测器的MPC进行航向控制时,航向角的RMSE值最小,为0.61°,并且其稳态误差接近于0°.因此,相较于经典的MPC与PID控制,带干扰观测器的MPC具有最好的控制效果.两种MPC以及PID航向控制效果的对比说明:① MPC控制是基于模型的控制方法,模型精度对MPC控制效果有较为明显的影响;② PID是一种无模型的控制方法,干扰对其控制效果的影响较小.因此,在有干扰时PID控制效果优于经典的MPC,而带有干扰观测器的MPC通过提高模型精度达到了提升控制效果的目的,增强了控制系统的鲁棒性.

表1 航向控制仿真结果对比

Tab.1 Comparison of course-control simulation results

控制方法	航向角的 RMSE/(°)	航向角稳态误差/(°)
带干扰观测器的MPC	0.61	0
MPC	2.84	3.44
PID	1.28	2.10

新窗口打开| 下载CSV

3.2.2 路径跟踪效果

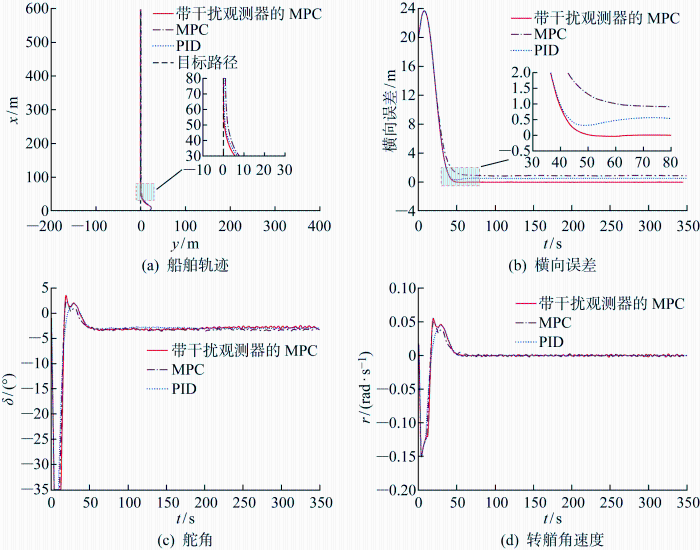
为验证矢量场制导法的有效性,对波浪中的船舶路径跟踪进行仿真计算.设置船舶的初始位置和艏向角:x₀=0 m,y₀=20 m,ψ₀=30°.选择路径y=0 m进行跟踪,图7给出了仿真结果.由图7(a)和7(b)可知,本文提出的矢量场制导法可以引导船舶对目标路径进行较为准确地跟踪.相比于PID控制与经典MPC,带干扰观测器的MPC以最快的速度收敛到目标路径,且在路径跟踪的过程中基本没有外漂现象出现,稳定后横向误差较小:稳定后,PID的横向误差约为0.6 m,经典MPC的横向误差约为1.0 m,带有干扰观测器的MPC的横向误差约为0 m.图7(c)和7(d)展示了采用3种方法进行路径跟踪控制时的舵角与转艏角速度时历曲线.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 船舶路径跟踪控制仿真结果

Fig.7 Simulation results of ship path following

3.2.3 避碰效果

对欠驱动船舶的避碰问题进行仿真研究来检验矢量场制导法避碰的有效性,仿真结果如图8所示,分别给出了R_o=10,20,30,40 m时基于矢量场避碰方法的船舶避碰情况,并将带有衰减系数a₃与不带衰减系数时的仿真进行对比.由图8可知,面对不同大小的障碍物,矢量制导法均能使船舶在保证路径跟踪效果的前提下安全地避开障碍物,证明了本文所提基于矢量场制导法的避碰策略具有较强的鲁棒性.由图8还可看出,当船舶位于障碍物的碰撞范围外时,障碍物对船舶的期望航向没有影响,即船舶与障碍物发生碰撞的风险为0;在这个阶段,只有目标路径产生的矢量场起作用;当船舶进入障碍物的碰撞区域后,船舶与障碍物碰撞的风险不再为0,这时障碍物将产生矢量场引导船舶避障.同时通过对比有无衰减系数时船舶的实际路径可知,通过设置衰减系数可以令船舶的避碰路径更加光顺,并且可以使船舶在航行安全的前提下与障碍物之间距离最小,即拥有更好的避碰效果.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 船舶避碰仿真结果

Fig.8 Simulation results of ship collision avoidance

4 结语

本文提出了一种欠驱动水面船舶的路径跟踪方法及避碰控制算法,基于矢量场制导法将路径跟踪和避碰问题转换为航向控制问题,并通过设计带有干扰观测器的MPC控制器实现对期望航向角的准确跟踪.仿真结果表明,通过采用干扰观测器的方法对模型不准确项以及波浪的时变干扰进行估计可以较好地提升MPC控制器的跟踪效果.设计的矢量场制导法能够使船舶对目标路径进行准确跟踪,并使船舶在进行路径跟踪的同时,也能安全地避开障碍物.在后续研究中,将考虑动态障碍物以及多障碍物等更加复杂的情况,并尝试把海事规则融入到控制器的设计中.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

MOREIRA

, FOSSEN

T I

, GUEDES SOARES

Path following control system for a tanker ship model

[J]. Ocean Engineering, 2007, 34(14): 2074-2085.