双线平行顶管上跨地铁盾构隧道施工环境影响实测分析

doi:10.16183/j.cnki.jsjtu.2022.290

双线平行顶管上跨地铁盾构隧道施工环境影响实测分析

应宏伟¹^,², 姚言¹, 王奎华^,¹, 张昌桔³

1.浙江大学滨海和城市岩土工程研究中心, 杭州 310058

2.河海大学岩土力学与堤坝工程教育部重点实验室, 南京 210024

3.杭州市市政工程集团有限公司, 杭州 310014

Observed Environment Response Caused by Construction of Double-Line Parallel Pipe Jacking Crossing over Metro Shield Tunnels

YING Hongwei¹^,², YAO Yan¹, WANG Kuihua^,¹, ZHANG Changju³

1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China

2. Key Laboratory for Geomechanics and Embankment Engineering of the Ministry of Educational, Hohai University, Nanjing 210024, China

3. Hangzhou Municipal Engineering Group Co., Ltd., Hangzhou 310014, China

通讯作者: 王奎华,教授,博士生导师;E-mail:zdwkh0618@zju.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-07-25 修回日期: 2022-09-12 接受日期: 2022-09-22

基金资助:

国家自然科学基金项目(51678523)
中央高校基本科研业务费资助项目(B200201012)
浙江省建设科研项目(2018K025)
杭州市建设科研项目(2018027)

Received: 2022-07-25 Revised: 2022-09-12 Accepted: 2022-09-22

作者简介 About authors

应宏伟(1971-),教授,博士生导师,主要从事岩土工程的教学和科研工作.

摘要

基于现场实测数据,详尽分析了某粉砂性地层中近距离双线顶管从上方穿越既有运营地铁隧道过程中的环境影响,包括横向地表沉降分布、沉降随时间发展、地铁隧道上浮等规律.研究发现:单线顶管横向地表沉降曲线呈现为“V”形,双线顶管横向地表沉降曲线为不对称“W”形,且后行顶管轴线上方的地面沉降大于先行顶管;后行顶管施工期间,先行顶管轴线上方地面也产生明显沉降.Peck公式在顶管施工引起的地表沉降曲线预测中适用性较好:案例中对于单线顶管,沉降槽宽度参数为0.79,土体损失率为1.6%;对于双线顶管,先行、后行顶管的沉降槽宽度参数分别为0.74和0.58,前者是后者的1.28倍;先行、后行顶管土体损失率分别为2.41%和3.11%,后者是前者的1.29倍.顶管顶进使下卧地铁隧道的纵向产生“W”形竖向位移分布曲线,顶管穿越完成后隧道的上浮存在滞后性;平行顶管上跨施工对下方地铁盾构隧道的纵向影响范围约为4~6倍顶管管径.后行顶管穿越监测断面时产生的瞬时沉降大于先行顶管;采用全方位高压喷射(MJS)工法预加固隧道上方粉砂土时降低了原状土的渗透性,顶管穿越后地面沉降仍将持续一段时间,可采用指数函数描述瞬时沉降发生后沉降随时间的发展规律.

关键词： 双线平行顶管; 地表沉降; 隧道上浮; 沉降槽; Peck公式

Abstract

Based on the field measured data of a double-line parallel power pipe jacking upper span subway shield tunnel, the environmental impact of a short-distance double-line pipe jacking in sandy silt stratum in the process of crossing over the existing subway tunnel was analyzed in detail, including the transverse surface settlement distribution, the development of settlement with time, and the floating of subway tunnels. The results show that the horizontal surface settlement curve of single pipe jacking presents a “V” shape, while the horizontal surface settlement curve of double line pipe jacking is an asymmetric “W” shape. The settlement of ground surface above the axis of the later pipe jacking is larger than that of the first pipe jacking. During the construction of the later pipe jacking, the settlement above the axis of the first pipe jacking is also obvious. The Peck formula has a good applicability in predicting surface settlement curve caused by pipe-jacking construction. For single-line pipe-jacking, the width parameter of settlement trough is 0.79, and the ground loss ratio is 1.6%. For double-line pipe jacking, the width parameter of settlement trough of the first and later pipe jacking are 0.74 and 0.58 respectively, and the former is 1.28 times of the latter. The soil loss ratio of the first and the second pipe jacking are 2.41% and 3.11% respectively, and the latter is 1.29 times of the former. Pipe jacking causes the vertical displacement distribution curve of the “W” shape in the longitudinal direction of the underlying subway tunnel. There is a lag in the up-floating of the tunnel after the completion of pipe jacking crossing. The longitudinal influence range of the parallel pipe jacking construction on the subway shield tunnel is about 4~6 times the pipe jacking diameter. The instantaneous settlement generated by the later pipe jacking across the monitoring section is greater than that generated by the first pipe jacking. The permeability of the undisturbed soil is reduced when the silty soil above the tunnel is pre-reinforced by the metro jet system (MJS). The ground settlement will continue for a period of time after the pipe jacking crossing. The exponential function can be used to describe the development of the settlement with time after the instantaneous settlement occurs.

Keywords： double-line parallel pipe jacking; ground surface settlement; floating of subway tunnel; settlement trough; the Peck formula

PDF (2687KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

应宏伟, 姚言, 王奎华, 张昌桔. 双线平行顶管上跨地铁盾构隧道施工环境影响实测分析[J]. 上海交通大学学报, 2023, 57(12): 1639-1647 doi:10.16183/j.cnki.jsjtu.2022.290

YING Hongwei, YAO Yan, WANG Kuihua, ZHANG Changju. Observed Environment Response Caused by Construction of Double-Line Parallel Pipe Jacking Crossing over Metro Shield Tunnels[J]. Journal of Shanghai Jiaotong University, 2023, 57(12): 1639-1647 doi:10.16183/j.cnki.jsjtu.2022.290

随着经济的发展与人口的增长,城市化进程对空间与资源的有效利用提出了更高的要求,地下空间的开发逐渐成为城市规划的重要方向.顶管施工技术是继盾构施工技术之后发展起来的一种非开挖隧道施工技术,常用于各种地下管线、通道的建设.目前顶管法隧道的施工环境越来越复杂,顶管施工不可避免地会对周围建(构)筑物产生影响,因此研究顶管施工对诸如地表沉降、隧道变形等周围环境影响具有重要意义.

在隧道施工引起的地表沉降研究中,有理论解析法、数值模拟法、经验公式法、模型试验法等方法.而对于经验公式的研究,又以Peck^[1]于1969年提出的基于实测数据的地表横向沉降预测公式最具影响力.Peck公式是基于有限地区实测资料提出的经验公式,在我国各地应用时需考虑其适用性及其沉降槽宽度系数i、土体损失率η等参数的选取.国内外学者^[2⇓-4]提出了很多理论方法计算i与η,由于这些计算方法最终还是取决于其他相关参数经验值的选取,所以直接基于实测数据通过Peck公式反分析得到沉降槽宽度参数和土体损失率应用更为广泛,使用更加简便.

国内有不少学者收集了我国各地隧道施工引起地表沉降实测数据,通过反分析得到相关参数,为Peck公式在我国各地的适用性提供了丰富的参考依据.韩煊等^[5]通过对30多组不同工法及开挖方式隧道实测数据的分析,肯定了Peck在我国的适用性;吴昌胜等^[6]收集并分析了各地区盾构隧道施工引起的土体损失率和沉降槽宽度参数,完善了我国各地Peck公式经验参数的取值;马克栓^[7]、丁智等^[8]基于多线平行隧道的实测数据,得到了相关参数的经验值,进一步肯定了Peck公式在多线隧道中的适用性.

在新建隧道上穿对下方既有隧道影响实测与模型试验研究方面.朱蕾等^[9]基于上海地铁13号线上穿地铁4号线施工期隧道变形监测数据,指出既有隧道的隆起具有滞后性且纵向变形曲线近似成正态分布.黄德中等^[10]采用离心模型试验与现场实测结合的方法,指出新建盾构施工对既有隧道的影响主要在两隧道交点左右两倍盾构直径范围内.

在隧道施工引起的环境影响实测研究中,学者们多将目光聚焦于盾构隧道,而顶管隧道施工虽与盾构施工有诸多相似之处,但在顶进、注浆方式等方面还是有较大差异,因此对于盾构隧道的研究结论可参考而不能照搬.在顶管施工环境影响的理论与数值研究中,以黄宏伟等^[11]、魏纲等^[12]为代表的学者们常将顶管施工中的作用概括为土体损失等位移作用以及正面附加推力、管壁摩擦力、注浆压力等荷载作用分别加以研究.在顶管施工环境影响的地表实测研究中,周顺华等^[13]对单线顶管实测地表沉降进行了分析,魏纲等^[14]对双线平行顶管实测沉降进行了分析.

可见顶管施工引起的环境影响,特别是顶管穿越引起下方隧道隆沉的研究较少.本文以杭州砂质粉土地层中某大直径双线平行电力顶管隧道为研究对象,整理了顶管从上方穿越地铁隧道过程中地表沉降、地铁道面隆沉的实测数据,详尽分析了地表横向沉降分布、地表沉降随时间的发展、下方地铁隧道隆沉发展变化的规律.

1 工程概况

1.1 场地环境及工程地质条件

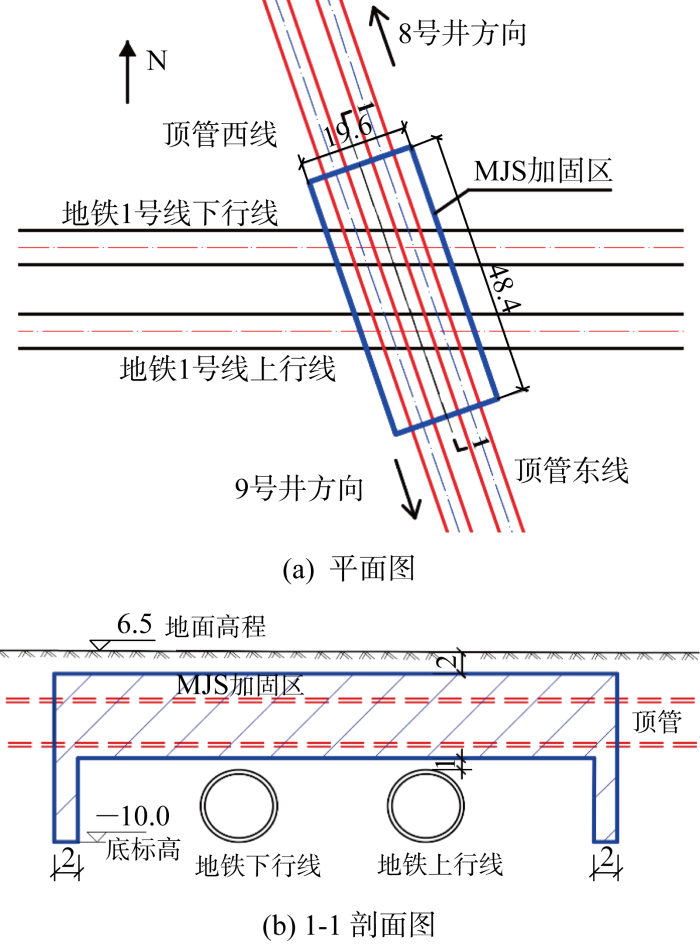
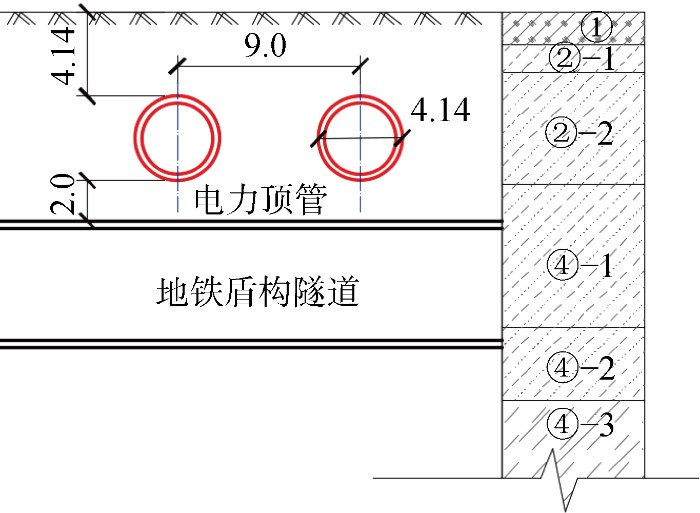
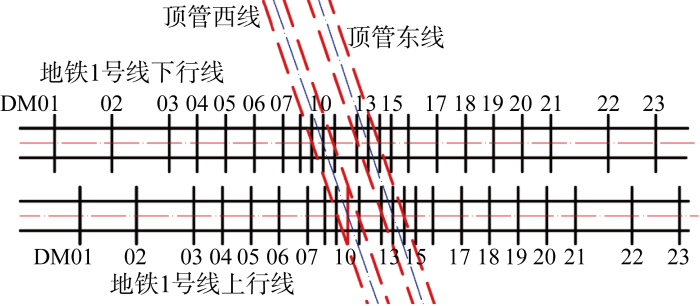
案例为城市高压线路上改下工程,里程总长度2 044.4 m,双线顶管长约285 m,埋深约4.14 m,管节内径3 500 mm,外径4 140 mm,壁厚320 mm,单节长度2.5 m,采用泥水平衡顶管机施工.顶管从北至南由8号井推至9号井,西线顶管先行施工.

顶管上穿杭州地铁1号线盾构隧道,穿越角度为71°,顶管与地铁盾构隧道的平面位置关系如图1(a)所示.盾构隧道埋深约10.28 m,管片内径5 500 mm,外径6 200 mm,壁厚350 mm.为了减少顶管穿越对地铁的影响,控制地铁设施的受力与变形,地铁隧道上方采用全方位高压喷射(MJS)工法进行水泥土加固,加固深度为地表以下2.0 m到盾构隧道拱顶上方 1.0 m, 加固区平面图和剖面图如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 顶管上跨地铁盾构隧道与MJS工法桩加固区的平面图和剖面图(m)

Fig.1 Plan view and sectional view of pipe jacking crossing over subway shield tunnel and reinforcement area of MJS method (m)

施工场地第四纪覆盖层厚度约为70 m,其上部为河口相地层,系钱塘江口近、现代冲海积沉积的粉砂性土地层.施工场地地面高程6.5 m左右,各土层物理力学参数如表1所示.表中:h为隧道轴线埋深;w为含水量;a_1-2为压缩系数;E_S1-2为压缩模量;c为黏聚力;φ为内摩擦角;k_h为水平渗透系数;k_v为垂直渗透系数.本工程地铁区间隧道位于④-1、④-2砂质粉土层,电力顶管隧道主要穿越②-2砂质粉土层,剖面图如图2所示.

表1 土层物理力学参数

Tab.1 Physical and mechanical parameters of soils

地层编号	地层名称	h/m	w/%	a_1-2/ MPa^-1	E_S1-2/MPa	直剪固快		k_h×10⁴/ (cm·s^-1)	k_v×10⁴/ (cm·s^-1)
地层编号	地层名称	h/m	w/%	a_1-2/ MPa^-1	E_S1-2/MPa	c/kPa	φ/(°)	k_h×10⁴/ (cm·s^-1)	k_v×10⁴/ (cm·s^-1)
②-1	黏质粉土	1.6	28.1	0.21	8.75	9.1	27.8	3.1	2.7
②-2	砂质粉土	3.0	26.5	0.17	10.38	7.5	28.8	5.2	4.9
④-1	砂质粉土	8.2	26.1	0.16	10.88	8.0	29.4	4.4	3.6
④-2	砂质粉土	14.0	26.0	0.17	10.64	8.7	27.7	6.5	5.8
④-3	粉土夹黏性土	18.6	28.6	0.21	9.53	10.9	26.5	2.8	1.8
④-5	粉质黏土夹粉土	24.5	34.5	0.43	4.60	24.6	14.3	—	—
⑤-1	淤泥质黏土	33.8	44.2	0.74	3.24	11.7	9.5	—	—

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 电力顶管隧道剖面图(m)

Fig.2 Profile of the power pipe jacking (m)

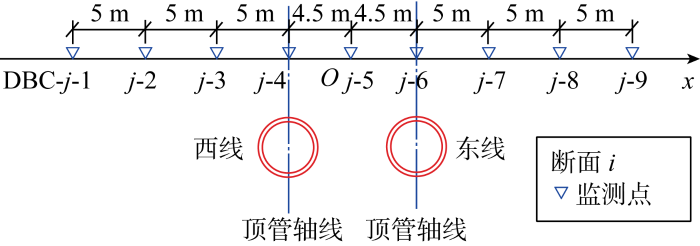
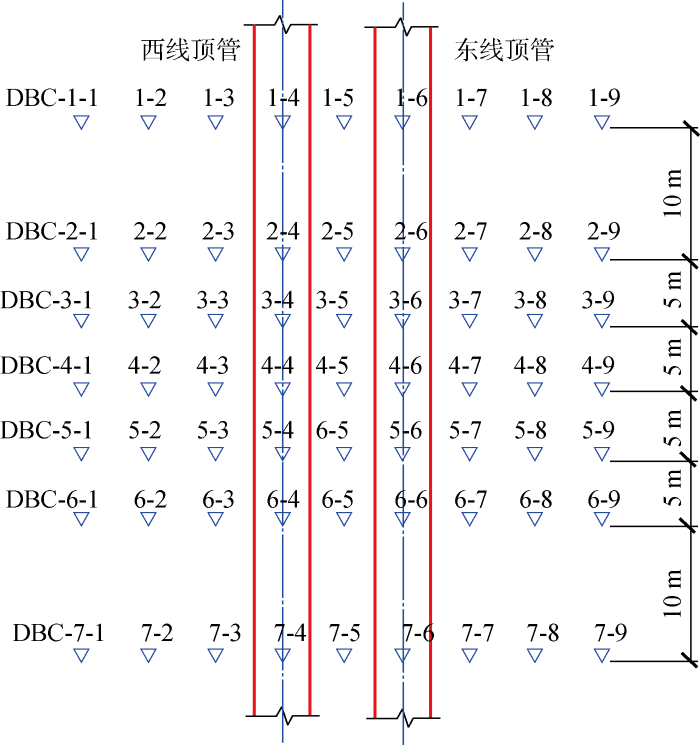
1.2 监测点位布设

为了监测双线顶管施工过程产生的地表沉降,沿顶管轴线方向进行地表沉降监测点的布设.顶管断面j的地表沉降监测点布置情况如图3所示.图中:DBC表示地表沉降监测断面.沿顶管轴线在穿越地铁区域共布置7个监测断面,监测平面图如图4所示.同时为了监测顶管穿越期间地铁道面隆沉,沿地铁方向布置2×23个监测断面如图5所示.图中:DM表示地铁盾构隧道监测断面.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 地表沉降监测断面

Fig.3 Monitoring section of surface settlement

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 地表沉降监测平面图

Fig.4 Plan of surface settlement monitoring

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 地铁隧道监测断面布置平面图

Fig.5 Layout plan of subway tunnel monitoring section

2 顶管施工实测结果分析

2.1 地表横向沉降规律

顶管穿越地铁盾构隧道区间典型沉降监测断面DBC-1不同施工阶段的地表横向沉降监测曲线如图6所示.图中:坐标原点位置与x轴方向如图3所示,坐标原点位于双线顶管中轴线与地面的交点;S为地表竖向位移,负值表示沉降、正值表示隆起,下同.本文地表横向沉降曲线图坐标系均与图3保持一致,不再赘述.

图6

新窗口打开| 下载原图ZIP| 生成PPT

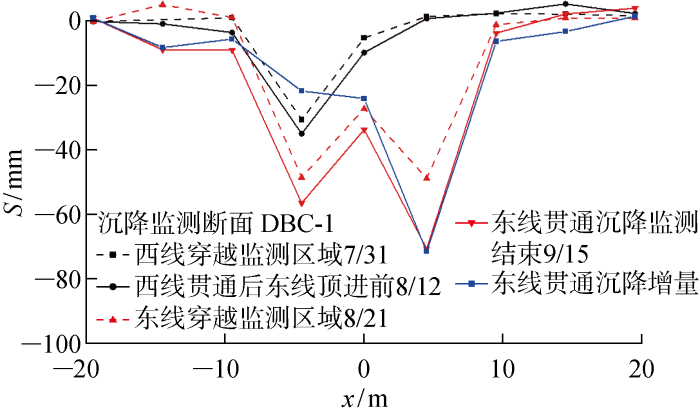
图6 监测断面DBC-1各施工阶段地表沉降

Fig.6 Surface settlement of monitoring section DBC-1 in each construction stage

以图6所示断面DBC-1为例进行分析,西线顶管穿过地表监测区域后,地表沉降槽发展为明显的“V”形,最大沉降量发生在西线顶管轴线上方地表处,占该处最终沉降量的52.7%.西线贯通后,沉降槽保持“V”形,变形基本稳定,轴线上方地面沉降值相对穿越DBC-1断面时仅有少量增长,增量占最终沉降量的9%.当东线顶管贯通后,地表沉降槽由“V”形变为不对称的“W”形,后行顶管轴线上方沉降大于先行顶管.

顶管施工时需要克服开挖面的土压力、刀盘的切削阻力、顶管机外壳和衬砌与土体之间的摩擦力等阻力,这些力的反作用于周围土体使其经历了挤压、剪切等复杂的应力路径并产生附加荷载.顶管通过后,顶管机与衬砌间的管径差形成建筑间隙,土体向建筑间隙内移动,引起土体松动卸荷.在上述附加荷载与卸荷作用反复扰动下,顶管周围加固土体力学性质降低,文献[15]中采用室内模型试验验证了先行隧道对周围土体扰动的现象.因此在经过先行顶管穿越期间对周围土体的扰动后,后行顶管施工将引起更大的土体损失,造成更大的沉降量.

从图6中还可发现,东线顶管顶进时,除了在自身轴线上方产生较大的沉降增量外,在西线顶管上方也产生了较大的沉降增量.原因有:① 如前文所述,东线顶管施工也对周围土体产生了扰动,造成先行顶管四周土体强度降低;② 后行顶管施工过程中产生的力学效应传递到先行顶管衬砌上,使其产生位移和变形,造成先行顶管周围土体发生应力重分布.因此在东线后行顶管的二次扰动下,西线先行顶管地层损失增大,最终使地表沉降量增加^[16].由二次扰动引起的西线顶管上方的沉降增量占最终沉降量的38.3%.由此可见,近距离双线平行顶管的开挖顶进是一个相互影响的过程,既要考虑先行顶管对周围土体的扰动,也要考虑后行顶管对先行顶管的二次扰动.

2.2 地铁盾构隧道竖向位移规律

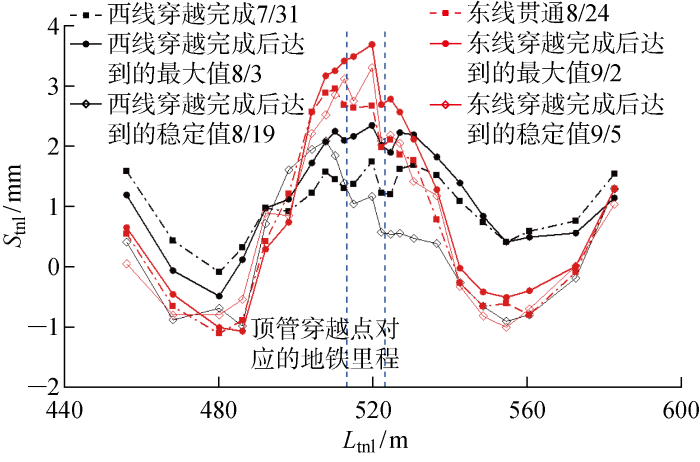
以顶管顶进到影响区域为时间零点,对下方地铁区间的道面累计竖向位移进行统计分析.如图7所示.图中:S_tnl为地铁隧道竖向位移,正值表示上浮,负值表示下沉;L_tnl为地铁隧道里程.西线顶管在里程513 m左右处穿越,东线顶管在里程522 m左右处穿越.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 顶管不同施工阶段地铁隧道纵向竖向位移

Fig.7 Settlement of subway tunnel at different construction stages of pipe jacking

当西线顶管穿越完成后(7月31日),如图7中黑色虚线所示,地铁隧道竖向位移曲线表现为“W”形,以两穿越点中线为对称轴呈现较为明显的对称性,竖向位移在数值不大,上浮最大值约为1.70 mm,占最大上浮量的72%;西线穿越完成至西线贯通(8月3日)期间,地铁隧道持续上浮达到最大值2.36 mm,曲线形状基本保持不变,相对于刚穿越完成时,上浮增量为0.66 mm,占最大上浮量的28%.盾构隧道在西线顶管穿越完成后持续上浮直至贯通结束,说明顶管施工过程中管节周围持续的注浆压力等因素对下方盾构隧道上浮有一定影响,造成了上浮的滞后.

东线顶进期间地铁隧道上行线的竖向位移规律与西线顶进期间类似.在东线顶管贯通后(8月24日),曲线峰值对应里程附近隧道继续发生持续上浮,在9月2日达到上浮的最大值,约为3.5 mm.

从图7所示的地铁隧道竖向位移曲线来看,顶管顶进引起的沉降与上浮数值不大,但是影响范围约为穿越点两侧4~6倍顶管管径,远大于文献 [9-10] 中提到的影响范围.

3 Peck沉降预测公式的适用性

3.1 单线顶管

目前工程界对单线顶管施工由土体损失引起的横向地面沉降计算方法主要采用Peck提出的地面沉降横向分布估算公式^[1]:

(1)S(x)=-S_maxexp

(- \frac{x^{2}}{2 i^{2}})

(2)S_max=

\frac{π R^{2} η}{i \sqrt{2 π}}

式中:S_max为隧道轴线上方最大地面沉降;R为隧道半径;i=Kh^[2],K为地面沉降槽宽度参数.

在东线顶管穿越前,可以将西线顶管当做单线顶管加以研究.通过式(1)对西线先行顶管贯通后断面DBC-1的地表沉降曲线进行拟合,得到曲线如图8所示,其余断面的拟合参数如表2所示.拟合曲线表明Peck公式可以较好预测单线顶管施工引起的地表沉降,西线顶管贯通沉降达到基本稳定后,各断面K范围在0.63~0.90之间,平均值为0.79,η范围在1.22~1.93%,平均值为1.60%.

图8

新窗口打开| 下载原图ZIP| 生成PPT

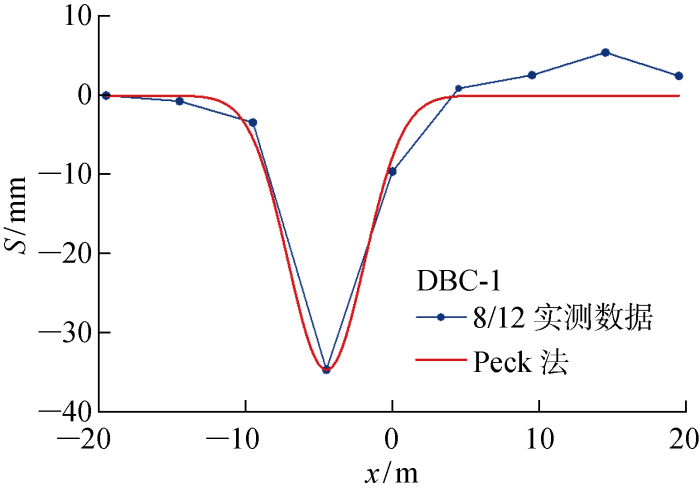
图8 单线顶管断面DBC-1横向地面沉降

Fig.8 Transverse surface settlement of single-line pipe jacking in section DBC-1

表2 单线顶管Peck法横向地面沉降拟合参数

Tab.2 Transverse surface settlement fitting parameters of Peck formula of single-line pipe jacking

断面	S_max/mm	i/m	K	η/%
DBC-1	34.78	2.60	0.63	1.65
DBC-2	26.89	3.17	0.77	1.56
DBC-3	29.64	3.40	0.82	1.84
DBC-4	31.53	3.35	0.81	1.93
DBC-5	18.14	3.71	0.90	1.23
DBC-6	—	—	—	—
DBC-7	19.2	3.47	0.84	1.22
平均	26.7	3.28	0.79	1.60

新窗口打开| 下载CSV

3.2 双线顶管

对于双线平行隧道的地面横向沉降预测,常采用将两条单线隧道地面沉降横向分布公式叠加的方法^[7],并将重点放在先行、后行隧道的沉降槽宽度和土体损失率的选取上.

(3)$\begin{array}{c} S(x)=-\left\{S_{\max, 1} \exp \left[-\frac{\left(x-\frac{L}{2}\right)^{2}}{2 i_{1}^{2}}\right]+\right. \\ \left.S_{\max, 2} \exp \left[-\frac{\left(x-\frac{L}{2}\right)^{2}}{2 i_{2}^{2}}\right]\right\} \end{array}$

式中:S_max_,1= $\frac{π R^{2} η_{1}}{i_{1} \sqrt{2 π}}$ 、S_max_,2= $\frac{π R^{2} η_{2}}{i_{2} \sqrt{2 π}}$ 分别为先行、后行隧道轴线上方最大沉降值;i₁、i₂分别为先行、后行隧道的地表沉降槽宽度系数;η₁、η₂分别为先行、后行隧道的土体损失率;L为隧道轴间距.O’Reilly等^[2]认为i与h成正比,其比值取决于地层性质,但实际工况中考虑到平行顶管施工相互影响,因此先行、后行顶管上方的沉降槽宽度必然有所不同.

通过双线隧道沉降预测式(3)对双线顶管断面DBC-1的地表横向沉降实测数据进行拟合,结果如图9所示,其余各断面的沉降槽宽度及土体损失率参数如表3所示.表中:K₁、K₂分别为先后行顶管的地面沉降槽宽度参数;η_avg为先后行顶管的平均土体损失率.

图9

新窗口打开| 下载原图ZIP| 生成PPT

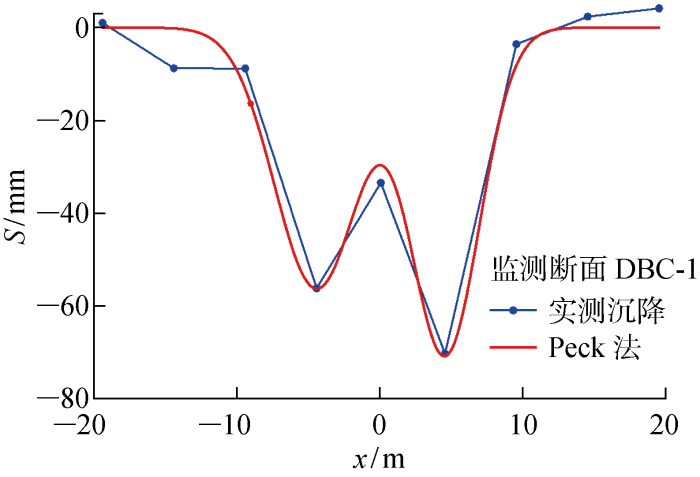
图9 双线顶管断面DBC-1横向地表沉降

Fig.9 Transverse surface settlement of double-line pipe jacking in section DBC-1

表3 双线顶管地表沉降曲线拟合参数

Tab.3 Fitting parameters of the transverse surface settlement curve of Peck formula of double-line pipe jacking

断面	S_max,1/mm	S_max,2/mm	i₁/m	i₂/m	K₁	K₂	η₁/%	η₂/%	η_avg/%
DBC-1	56.31	70.41	2.94	2.41	0.71	0.58	3.02	3.10	3.06
DBC-2	44.6	65.34	3.17	2.28	0.77	0.55	2.58	2.72	2.65
DBC-3	49.96	51.21	2.96	2.57	0.71	0.62	2.70	2.40	2.55
DBC-4	55.07	93.83	3.04	2.19	0.73	0.53	3.06	3.75	3.41
DBC-5	37.31	96.44	2.94	2.39	0.71	0.58	2.00	4.21	3.11
DBC-6	28.9	68.01	2.87	2.37	0.69	0.57	1.52	2.94	2.23
DBC-7	29.29	47.56	3.56	2.71	0.86	0.65	1.90	2.35	2.13
平均	43.06	70.4	3.07	2.42	0.74	0.58	2.41	3.11	2.76

新窗口打开| 下载CSV

从图9可以发现,式(3)可以较好地预测双线顶管施工引起的地表沉降曲线.案例中的双线平行顶管,先行顶管的沉降槽宽度参数K平均值为0.74,大于后行顶管的0.58,是后行顶管的1.28倍;后行顶管土体损失率平均值为3.11%,是先行顶管的1.29倍.

4 地表沉降的时间效应

4.1 地表沉降时间曲线特征

图10、图11所示为7个监测断面顶管轴线上方地表沉降随时间t的变化曲线.

图10

新窗口打开| 下载原图ZIP| 生成PPT

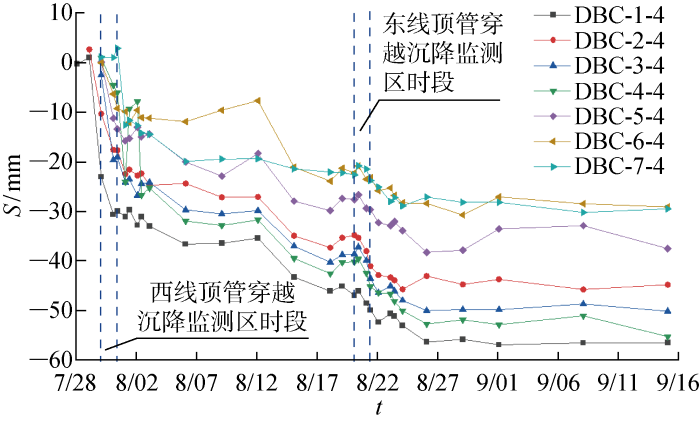
图10 西线顶管上方地表沉降随时间变化

Fig.10 Time-dependent surface settlements above the pipe jacking of the western line

图11

新窗口打开| 下载原图ZIP| 生成PPT

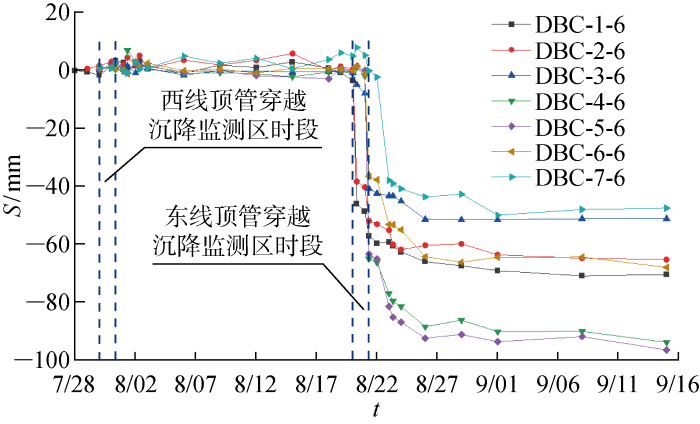
图11 东线顶管轴线上方沉降测点沉降随时间变化

Fig.11 Time-dependent surface settlements above the pipe jacking of the eastern line

由图可见,无论是西线顶管还是东线顶管,在顶管接近沉降监测断面及其后的穿越期间,绝大部分测点观测到较为剧烈的沉降;而在东线顶管接近沉降监测断面及其穿越期间,可以在西线顶管轴线上方各沉降点观测到轻微隆起,且这7个点的隆起特征较为一致,观测到的隆起发生时间主要在穿越开始前一天,此时顶管已顶进66环,推测顶管顶进至接近监测断面时可能发生隆起.

在图10中,可明显发现后行顶管对于先行顶管二次扰动的影响.在先行顶管穿越完成后,先行顶管轴线上方沉降发展若干天后保持稳定甚至有轻微的回弹,但自东线顶管开始顶进以后,先行顶管轴线上方沉降速率明显增大,在穿越完成后的若干天后沉降发展稳定且基本保持不变直至监测结束.

4.2 考虑时间效应的地表沉降预测

由地表沉降的时间曲线(图10、图11)可知,顶管轴线上方沉降观测点的沉降规律具有明显的时间效应.根据地表沉降的时间曲线特征,可以看到其发展趋势与软黏土地基地面堆载引起的地面沉降发展趋势有相似之处^[17],这里借鉴采用指数曲线拟合法对顶管引起的地表沉降时间曲线进行拟合:

(4)S_max(t)=S_max₀+α[1-

e^{- β (t - t_{0})}

]

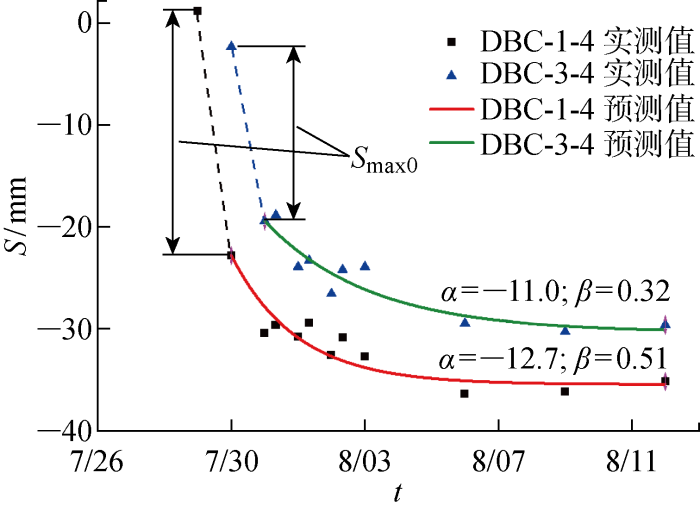
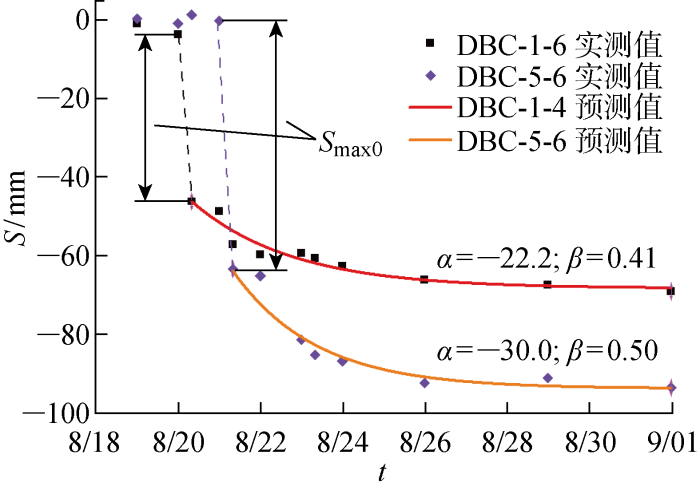
式中:S_max(t)为顶管穿越当前断面后轴线上方任意时刻t的地表竖向位移;S_max₀为顶管穿越当前监测断面后t₀时刻的瞬时竖向位移;α为反映最终竖向位移的参数;β为反映竖向位移发展快慢的无量纲参数.

对西线、东线顶管顶进期间上方实测沉降曲线进行拟合,同时将参数α、β标注在各曲线附近,分别如图12、图13所示.结合图10、图11,西线顶管穿越完成后至东线顶管顶进前,其轴线上方测点先产生较小的瞬时沉降,随后的沉降发展规律符合指数曲线的发展规律;东线顶管穿越完成后,其轴线上方测点将产生较大的瞬时沉降,之后的沉降发展曲线也比较符合指数曲线发展规律.对于参数α,东线顶管大于西线顶管,说明对于具有时间效应的曲线段,后行顶管轴线上方产生更大的最终沉降;对于参数β,东、西线顶管较为接近,说明两顶管轴线上方地表在发生瞬时沉降后的沉降发展速率和形式较为接近.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 西线顶管上方地面沉降发展预测值与实测值对比

Fig.12 Comparison of predicted and measured values of surface settlement development over pipe-jacking of western line

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 东线顶管上方地面沉降发展预测值与实测值的对比

Fig.13 Comparison of predicted and measured values of surface settlement development over pipe-jacking of eastern line

由于案例所在场地⑤-1淤泥质黏土层埋深33.8 m,距离盾构隧道与顶管较远,所以不考虑该土层对地表沉降的影响.MJS工法以水泥为固化剂对原状土进行加固,通过水泥的水化、凝固作用填充原状土孔隙,改善原状土结构,以提高其强度与抗渗性能.已有研究表明^[18],经水泥土加固后,砂质土的渗透系数可以降低两个数量级以上.案例中MJS加固区域如图1所示,可见顶管穿越全程在加固土中进行.由此推测粉砂土地层中顶管施工引起地面沉降呈现时间效应的原因为,顶管顶进前现场采用MJS工法对地铁隧道上方的土体进行了加固,使之形成了具有较高强度和较低渗透性的水泥土,顶管施工产生的超静孔隙水压力消散较慢,在顶管顶进后一段时间内,顶管轴线上方将持续产生沉降后再趋于稳定.

5 结论

通过对杭州砂质粉土地层中大直径双线平行电力顶管上穿已有地铁盾构隧道过程中地表沉降、隧道内道面隆沉的实测数据分析,得到以下主要结论:

(1) 单线顶管横向地表沉降曲线为“V”形,双线顶管横向地表沉降曲线为不对称“W”形,且后行顶管轴线上方沉降大于先行顶管,平行双线顶管施工存在交叉影响.

(2) Peck公式在顶管施工引起的地表沉降曲线预测中适用性较好.本案例对于单线顶管,沉降槽宽度参数K取0.79,土体损失率η取1.6%;对于双线顶管,先行、后行顶管的沉降槽宽度参数K分别取0.74和0.58,前者是后者的1.28倍;先行、后行顶管土体损失率η分别为2.41%和3.11%,后者是前者的1.29倍.

(3) 顶管上跨使地铁隧道产生“W”形沉降曲线,顶管穿越完成后隧道持续上浮至最大值,存在一定的滞后性,顶管贯通暂停施工后隧道产生一定回落.平行顶管上跨施工对下方地铁盾构隧道的影响范围约为4~6倍顶管管径.

(4) 顶管穿越监测断面后产生瞬时地面沉降,且后行顶管的影响大于先行顶管.考虑MJS工法桩加固将降低原状粉砂土的渗透系数,可采用指数函数描述顶管穿越引起地面瞬时沉降后的沉降随时间继续发展规律.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

PECK

R B

Deep excavations and tunneling in soft ground

[C]// Proceedings of the 7th International Conference of Soil Mechanics and Foundation Engineering. Mexico City, Mexico:[s.n.], 1969: 225-290.

[本文引用: 2]

[2]

O’REILLY

M P

, NEW

B M

Settlements above tunnels in the United Kingdom-Their magnitude and prediction

[C]// Proceedings Tunnelling 82. London, UK: Institution of Mining and Metallurgy, 1982: 173-181.

[本文引用: 3]

[3]

M N

, BROERE

, BOSCH

J W

Volume loss in shallow tunneling

[J]. Tunnelling and Underground Space Technology, 2016, 59(10): 77-90.

DOI:10.1016/j.tust.2016.06.011 URL [本文引用: 1]

[4]

孙玉永, 周顺华, 宫全美.

软土地区盾构掘进引起的深层位移场分布规律

[J]. 岩石力学与工程学报, 2009, 28(3): 500-506.