共轴双旋翼动力学建模与验证

doi:10.16183/j.cnki.jsjtu.2021.044

共轴双旋翼动力学建模与验证

胡金硕¹, 黄健哲^,²

1.中国民航科学技术研究院无人机适航审定中心,北京 100020

2.上海交通大学航空航天学院,上海 200240

Dynamics Modeling and Validation of Coaxial Lifting Rotors

HU Jinshuo¹, HUANG Jianzhe^,²

1. UAS Airworthiness Certification Center, China Academy of Civil Aviation Science and Technology, Beijing 100020, China

2. School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 黄健哲,男,副教授,博士生导师,电话(Tel.):021-34204112;E-mail:huangdeng9@sjtu.edu.cn.

责任编辑: 石易文

收稿日期: 2021-02-5

基金资助:

国家自然科学基金(11901385)
上海市扬帆计划资助项目(19YF1421600)

Received: 2021-02-5

作者简介 About authors

胡金硕(1988-),男,山东省滨州市人,助理研究员,主要从事无人机动力学与控制.

摘要

建立共轴双旋翼动力学模型可用于共轴多旋翼飞行器的控制器设计、飞行模拟等研究,需要同时兼顾模型的计算实时性和精度.首先,基于伴随理论推导包含旋翼尾迹的全流场诱导速度计算模型.然后,在单旋翼有限状态入流模型基础上进行扩展,建立考虑尾迹倾斜的共轴双旋翼有限状态动力学模型.最后,推导共轴双旋翼悬停状态上下旋翼推力计算公式,并进行试验验证.研究结果表明:所建立的动力学模型计算复杂度在可接受的范围内,推力计算值与测试值在一定转速范围内基本吻合,并可很好地反映出共轴双旋翼推力损失趋势.

关键词： 共轴双旋翼; 动力学建模; 有限入流; 流场干涉

Abstract

The dynamics model for coaxial lifting rotors can be used to study the controller design and flight simulation for coaxial-rotor aerial vehicles. However, both the computational efficiency and the accuracy should be considered. First, the computational model of the induced velocity of lifting rotor everywhere including the wake region is derived based on adjoint theorem. Then, the finite state dynamics model for coaxial lifting rotors with wake skew considered is developed by extending the finite state inflow model for single rotor. Finally, the equations for calculating the thrust of coaxial lifting rotors in the hover condition are given, and the test is conducted. The results show that the computational complexity of the proposed dynamics model for coaxial lifting rotors is acceptable, and the computational thrusts are almost close to the test results when the rotational speed is within a certain range, which can also reflect the trend of the thrust lost for coaxial lifting rotors.

Keywords： coaxial lifting rotors; dynamics modeling; finite-state inflow; flow field interaction

PDF (0KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

胡金硕, 黄健哲. 共轴双旋翼动力学建模与验证[J]. 上海交通大学学报（自然版）, 2022, 56(3): 395-402 doi:10.16183/j.cnki.jsjtu.2021.044

HU Jinshuo, HUANG Jianzhe. Dynamics Modeling and Validation of Coaxial Lifting Rotors[J]. Journal of shanghai Jiaotong University, 2022, 56(3): 395-402 doi:10.16183/j.cnki.jsjtu.2021.044

由于共轴双旋翼直升机上下主旋翼产生的扭矩可相互抵消,所以比传统单旋翼带尾浆的直升机结构更简单,气动对称性也更好^[1].另外,对于多旋翼无人机,共轴旋翼的引入将大大提高无人机的抗风能力和稳定性^[2].因此,人们对共轴双旋翼的研究和研制一直都没有停止.从俄罗斯卡莫夫设计局研发的卡-8和美国西科斯基的XH-59A验证机开始,经过半个多世纪的发展,共轴双旋翼构型的直升机越来越受到业内的关注和重视.针对共轴双旋翼飞行器的控制和飞行模拟仿真器的研发也已成为研究的热点之一.

不同于旋翼计算流体力学(CFD)的研究,针对旋翼飞行器控制设计和飞行仿真的动力学模型需要有更好的实时性,同时对计算精度也有一定的要求.1989年文献[3]开发的Peters-He模型是目前最广泛应用的旋翼有限状态模型,可以用于计算旋翼盘上任意位置的诱导速度,进而实时计算单旋翼的推力.该理论隐含了著名的动态入流理论、Pradtl/Galdstein静态入流分布和Theodorsen理论,并且计算结果和试验数据有很好的吻合度.此后,一种被称为Morillo模型^[4]的动态入流模型由Peters教授团队提出,它对旋翼上方流场的求解有其优越性.由于共轴双旋翼之间流场的干扰,上下旋翼的拉力性能将下降^[5],所以用于计算单旋翼诱导速度和推力的Peters-He模型和针对旋翼上方流场计算的Morillo模型,它们均无法直接用于对共轴双旋翼的动力学建模.基于当前的有限入流建模理论,文献[6]利用关联上下旋翼入流系数和压强场系数的入流影响系数矩阵来计算每个旋翼产生的诱导速度.该入流影响系数矩阵包含了旋翼自诱导速度信息和上下旋翼之间互诱导速度信息,由于当时缺少互诱导速度的封闭计算公式,所以互诱导速度需要通过数值计算得到.其开发出的模型在XV-15倾转旋翼机上得到了试验验证.由于该模型需要进行数值计算,所以其计算的实时性能还有一定的提升空间.2015年,文献[7,8]提出了混合势流模型,建立了Peters-He模型和Morillo模型非线性混合函数,对旋翼盘上和旋翼上方流场的计算精度做了进一步提升,更重要的是,该模型对旋翼尾迹进行了建模,给出了旋翼尾迹流场计算的封闭形式解.文献[9]在旋翼悬停地效建模上应用了该混合势流模型,并与试验数据和RotCFD计算结果进行了对比,验证了模型有效性.文献[10]基于运动嵌套网格方法,建立了一套适合于悬停状态下共轴刚性双旋翼非定常干扰流场分析的计算流体力学方法.该研究运用了计算流体力学方法,可以给出共轴双旋翼更加细致的动态流场信息,提高了计算精度,但是存在很大的计算复杂度.文献[11]对倾转过渡状态共轴倾转旋翼进行了研究,考虑了尾流倾斜和收缩的上下旋翼的相互干扰,通过能量方程推导了诱导速度的计算公式,最后利用迭代方法求解了上下旋翼的载荷.由于整个计算过程需要迭代,所以通过此方法进行共轴多旋翼动力学建模也具有一定的计算复杂度.文献[12]结合叶素理论和Pitt-Peters 动态入流模型对共轴双旋翼的气动干涉和挥舞运动进行了近似建模,其他未准确建模的部分用控制算法进行补偿,并在Simulink搭建了控制器进行联合仿真.该方法利用动态入流模型计算诱导速度,仿真实时性好.但是Pitt-Peters 模型结构简单,是Peters教授团队最初提出的三状态动态入流模型^[13],对于一些复杂的飞行状态难以保证较好的计算效果.此外,若仅采用诱导速度干扰系数表示上、下旋翼之间的气动干涉,需要较为充分的理论支撑.现有研究中主要考虑了上下旋翼的流场干扰,并对其进行了相应的数学建模,但还未见到有基于时滞伴随理论的势流模型来建立共轴双旋翼动力学模型的研究.

针对共轴双旋翼上旋翼入流受到下旋翼上游流场影响,以及下旋翼入流受到上旋翼尾流影响的问题,本文提出一种基于势流模型的共轴双旋翼动力学建模方法,并设计了共轴双旋翼的推力测试装置,验证了悬停状态下共轴双旋翼的推力计算准确性.本文研究可为共轴双旋翼飞行器的旋翼初步设计、控制和飞行仿真提供理论基础.

1 共轴双旋翼有限状态模型

根据文献[4],上下旋翼在其各自平面和上方位置 (ν≥0)产生的诱导速度v⁽^u⁾(ν, η, ψ, t)和v⁽^l⁾(ν, η, ψ, t) 分别表示为

v⁽^u⁾(ν, η, ψ, t)=

$\overset{\infty}{\sum_{m = 0}} \overset{\infty}{\sum_{n = m}} a_{n}^{m (u)}$

(t)

$P_{n}^{m}$

(ν)

$Q_{n}^{m}$

(iη)cos(mψ)

(1)

v⁽^l⁾(ν, η, ψ, t)=

$\overset{\infty}{\sum_{m = 0}} \overset{\infty}{\sum_{n = m}} a_{n}^{m (l)}$

(t)

$P_{n}^{m}$

(ν)

$Q_{n}^{m}$

(iη)cos(mψ)

(2)

式中: $P_{n}^{m}$ (ν)和 $Q_{n}^{m}$ (iη)分别为正则化的第一类和第二类勒让德函数; m和n分别为谐波次数和旋翼径向多项式数;ν,η,ψ为椭圆坐标系坐标; $a_{n}^{m (u)}$ (t)和 $a_{n}^{m (l)}$ (t)分别为上下旋翼在t 时刻的诱导速度因子.上标u和l分别为上旋翼和下旋翼.椭圆坐标系和机体坐标系的转换关系为

$\begin{array}{l} ν = \frac{- sgn (z)}{\sqrt[]{2}} \sqrt[]{1 - A + \sqrt[]{{(A - 1)}^{2} + 4 z^{2}}} \\ η = \frac{1}{\sqrt[]{2}} \sqrt[]{A - 1 + \sqrt[]{{(A - 1)}^{2} + 4 z^{2}}} \\ ψ = ta n^{- 1} (- y / x) \\ A = x^{2} + y^{2} + z^{2} \end{array}\}$

(3)

式中:x,y,z为计算点在体坐标系中的正则化坐标位置,则在旋翼边缘有A=1.

由于上旋翼的尾迹会对下旋翼产生影响,所以需要给出上旋翼的尾迹速度的计算公式.根据文献[8],上旋翼在 (ν, η, ψ)位置的尾迹速度v⁽^u⁾(ν, η, ψ, t)(v<0) 表示为

$v^{(\mathrm{u})}(\nu, \eta, \psi, t)=v^{(\mathrm{u})}\left(0, \eta_{0}, \psi_{0}, t-\tau\right)-\omega^{(\mathrm{u})}\left(0, \eta_{0}, \psi_{0}+\pi, t-\tau\right)$

(4)

式中: v⁽^u⁾(0, η₀, ψ₀, t-τ)为上旋翼在(0, η₀, ψ₀)位置的诱导速度; $\bar{\omega}$ ⁽^u⁾(0, η₀, ψ₀+π, t-τ)为上旋翼在(0, η₀, ψ₀+π)位置的伴随速度;τ为时滞量.由于椭圆坐标系与体坐标系的转换比较复杂,η₀、ψ₀与η、ψ 之间的关系可用如下关系式进行表述:

如果(x, y, 0)→(0, η, ψ),那么(x+ $\bar{d}$ tanχ, y, 0)→(0, η₀, ψ₀)

其中: 为正则化的旋翼轴向距离(距离与旋翼半径的比值);χ为上旋翼的尾迹倾斜角. $\bar{\omega}$ ⁽^u⁾(ν, η, ψ, t) 为上旋翼的伴随速度,可通过下式计算得到:

$\bar{\omega}$ ⁽^u⁾(ν, η, ψ, t)=

$\overset{\infty}{\sum_{m = 0}} \overset{\infty}{\sum_{n = m}} Δ_{n}^{m (u)}$

(t)

$P_{n}^{m}$

(ν)

$Q_{n}^{m}$

(iη)cos(mψ)

(5)

式中: $Δ_{n}^{m (u)}$ 为上旋翼的伴随速度因子.

如果诱导速度和伴随速度计算式包含 N次谐波,即m=0, 1, …, N, 定义诱导速度因子和伴随速度因子的状态向量为 a^(u)、a^(l)、Δ^(u). 根据文献[7],压强势用于计算旋翼周围的压强,而压强势可用压强因子 $τ_{n}^{m}$ 分谐次叠加来表示,分别定义上、下旋翼的压强因子向量为τ^(u)、τ^(l). 具体表示如下式所示.

$\begin{array}{l} a^{(u)} ≜ [a_{n}^{m (u)}] \equiv {[\begin{array}{l} a_{1}^{0 (u)} & a_{3}^{0 (u)} & \dots & a_{N + 1}^{0 (u)} & \dots & a_{i + 1}^{i (u)} & \dots & a_{N + 1}^{N (u)} & a_{0}^{0 (u)} & a_{2}^{0 (u)} & \dots & a_{N}^{0 (u)} & \dots & a_{N}^{N (u)} \end{array}]}^{T} \\ a^{(l)} ≜ [a_{n}^{m (l)}] \equiv {[\begin{array}{l} a_{1}^{0 (l)} & a_{3}^{0 (l)} & \dots & a_{N + 1}^{0 (l)} & \dots & a_{i + 1}^{i (l)} & \dots & a_{N + 1}^{N (l)} & a_{0}^{0 (l)} & a_{2}^{0 (l)} & \dots & a_{N}^{0 (l)} & \dots & a_{N}^{N (l)} \end{array}]}^{T} \\ Δ^{(u)} ≜ [Δ_{n}^{m (u)}] \equiv \\ {[\begin{array}{l} Δ_{1}^{0 (u)} & Δ_{3}^{0 (u)} & \dots & Δ_{N + 1}^{0 (u)} & \dots & Δ_{i + 1}^{i (u)} & \dots & Δ_{N + 1}^{N (u)} & Δ_{0}^{0 (u)} & Δ_{2}^{0 (u)} & \dots & Δ_{N}^{0 (u)} & \dots & Δ_{N}^{N (u)} \end{array}]}^{T} \end{array}\}$

(6)

$\begin{array}{l} τ^{(u)} ≜ [τ_{n}^{m (u)}] \equiv {[\begin{array}{l} τ_{1}^{0 (u)} & τ_{3}^{0 (u)} & \dots & τ_{N + 1}^{0 (u)} & \dots & τ_{i + 1}^{i (u)} & \dots & τ_{N + 1}^{N (u)} & τ_{0}^{0 (u)} & τ_{2}^{0 (u)} & \dots & τ_{N}^{0 (u)} & \dots & τ_{N}^{N (u)} \end{array}]}^{T} \\ τ^{(l)} ≜ [τ_{n}^{m (l)}] \equiv {[\begin{array}{l} τ_{1}^{0 (l)} & τ_{3}^{0 (l)} & \dots & τ_{N + 1}^{0 (l)} & \dots & τ_{i + 1}^{i (l)} & \dots & τ_{N + 1}^{N (l)} & τ_{0}^{0 (l)} & τ_{2}^{0 (l)} & \dots & τ_{N}^{0 (l)} & \dots & τ_{N}^{N (l)} \end{array}]}^{T} \end{array}\}$

(7)

其中,当 m+n为偶数时, $τ_{n}^{m (u)}$ = $τ_{n}^{m (l)}$ =0;当m+n 为奇数时,

$\begin{array}{l} τ_{n}^{0 (i)} = \frac{1}{2 π} \overset{Q}{\sum_{q = 1}} \int_{0}^{1} \frac{L_{q}^{(i)} (r)}{2 ρR} J_{0} (0) ϕ_{n}^{0} (r) d r \\ τ_{n}^{m (i)} = \frac{1}{π} \overset{Q}{\sum_{q = 1}} \int_{0}^{1} \frac{L_{q}^{(i)} (r)}{2 ρR} \times \\ J_{0} (\bar{mb} / r) ϕ_{n}^{m} (r) d r \cos (m ψ_{q}^{(i)}), m \neq 0 \end{array}\}$

(8)

式中: Q和R分别为旋翼的叶片数和半径;ρ为空气密度; $L_{q}^{(u)}$ (r)和 $L_{q}^{(l)}$ (r)分别为上、下旋翼第q个叶片微元的升力;r为叶片微元沿桨叶径向方向距离桨叶中心的距离;J₀(x)为第一类贝塞尔函数; $ϕ_{n}^{m}$ (r)= $P_{n}^{m}$ (ν)/ν; $\bar{b}$ 为旋翼叶片在r处的归一化半弦长; $ψ_{q}^{(i)}$ 为第q 个叶片的方位角, i∈{u, l}.

通过低速流体的质量守恒和动量守恒定律公式,代入用勒让德函数表示的速度和压强表达式^[7],并通过伽辽金变换可得到一组以诱导速度因子和伴随速度因子为状态量的常微分方程:

$[\begin{array}{l} {\overset{\cdot}{a}}^{(u)} \\ {\overset{\cdot}{a}}^{(l)} \end{array}]$

$[\begin{array}{l} K^{(u)} & 0 \\ 0 & K^{(l)} \end{array}] [\begin{array}{l} a^{(u)} \\ a^{(l)} \end{array}]$

$[\begin{array}{l} τ^{(u)} \\ τ^{(l)} \end{array}]$

(9)

-RM

${\overset{\cdot}{Δ}}^{(u)}$

+K^(u)Δ^(u)=D

${\tilde{τ}}^{(u)}$

(10)

其中

${K}^{(\mathrm{u})}={D} {V}_{(\mathrm{u})} {L}_{(\mathrm{u})}^{-1} {M}$

${K}^{(\mathrm{1})}={D} {V}_{(\mathrm{l})} {L}_{(\mathrm{l})}^{-1} {M}$

$\widetilde{\tau}^{(\mathrm{u})}=(-1)^{n+1} \tau_{n}^{m(\mathrm{u})}$

式中:M和D分别为表观质量矩阵和阻尼矩阵; $L_{(u)}^{- 1}$ 和 $L_{(l)}^{- 1}$ 分别为上、下旋翼的入流影响矩阵,和上、下旋翼的尾迹倾斜角有关;V_(u)和V_(l)分别为上、下旋翼的入流矩阵.上述矩阵的计算表达式可参见文献[7].V_(u)和V_(l)的表达式分别为

V₍_i₎=

$[\begin{array}{l} V_{T}^{(i)} \\ V_{1}^{(i)} \\ ⋱ \\ V_{1}^{(i)} \end{array}]$

, i∈{u, l}

(11)

其中

$V_{T}^{(u)}$ = $\sqrt[]{U_{a}^{2} + (V_{a} + {\bar{v}}^{(u)} + {\bar{v}}^{(ul)})^{2}}$

$V_{T}^{(l)}$ = $\sqrt[]{U_{a}^{2} + (V_{a} + {\bar{v}}^{(l)} + {\bar{v}}^{(lu)})^{2}}$

$V_{1}^{(u)}$ = $\frac{U_{a}^{2} + (V_{a} + {\bar{v}}^{(u)} + {\bar{v}}^{(ul)}) (V_{a} + 2 {\bar{v}}^{(u)} + {\bar{v}}^{(ul)})}{V_{T}^{(u)}}$

$V_{1}^{(l)}$ = $\frac{U_{a}^{2} + (V_{a} + {\bar{v}}^{(l)} + {\bar{v}}^{(lu)}) (V_{a} + 2 {\bar{v}}^{(l)} + {\bar{v}}^{(lu)})}{V_{T}^{(l)}}$

式中: U_a和V_a分别为体坐标系下相对气流速度的x和y分量; ${\bar{v}}^{(u)}$ 和 ${\bar{v}}^{(l)}$ 分别为上、下旋翼盘内平均诱导速度,可分别通过式(1)和(2)计算各自旋翼盘内每一点诱导速度的总和再除以旋翼面积得到; ${\bar{v}}^{(ul)}$ 为上旋翼盘内的下旋翼诱导速度的平均值,为第一类互诱导速度,可通过式(2)计算上旋翼盘内每一点诱导速度的总和再除以旋翼面积得到; ${\bar{v}}^{(lu)}$ 为下旋翼盘内的上旋翼诱导速度的平均值,为第二类互诱导速度,由于下旋翼处于上旋翼的下方,所以需通过式(4)计算下旋翼盘内每一点诱导速度的总和再除以旋翼面积得到.

由于式(9)中的入流矩阵需要 τ时刻前的伴随速度因子信息,所以需要同时对式(9)进行时间正向数值积分,并对式(10)采取计算时刻t₁为初始的时间反向数值积分,同时求得速度因子和伴随速度因子的时间序列信息.对于式(10)的时间反向数值积分,需要在每一个计算时刻进行时长为τ的反向数值迭代,计算量比较大.通过以下计算步骤可以通过更少的计算量,求得在t₁时刻伴随速度因子τ时刻前的数值Δ⁽^u⁾(t₁-τ).

步骤1 求解 R^-1M^-1K^(u)的特征值和特征向量分别为λ_i(i=1, 2, …, G),φ, 使得:

φ^-1(R^-1M^-1K^(u))φ= $[\begin{array}{l} λ_{1} \\ λ_{2} \\ ⋱ \\ λ_{G} \end{array}]$

其中:G为矩阵M的维数.

步骤2 给出 t₁时刻前 ${\tilde{τ}}^{(u)}$ 的全部时间序列信息;

步骤3 通过下式计算Δ^(u)(t₁-τ):

Δ^(u)(t₁-τ)=

$\int_{t_{1}}^{-}$

$[\begin{array}{l} e^{- λ_{1} (t - t_{1} + τ)} \\ e^{- λ_{2} (t - t_{1} + τ)} \\ ⋱ \\ e^{- λ_{G} (t - t_{1} + τ)} \end{array}]$

×φ^-1

${[K^{(u)}]}^{- 1}$

${\tilde{τ}}^{(u)}$

(12)

式(8)中,求解 $L_{q}^{(u)}$ (r)和 $L_{q}^{(l)}$ (r) 可分别通过叶片单元法进行计算,如下式所示:

$L_{q}^{(u)}$

(r)=

$\frac{1}{2}$

ρw_sc(r)[(ω_uRr-U_asin

$ψ_{q}^{(u)}$

)²θ-(ω_uRr-U_asin

$ψ_{q}^{(u)}$

)(V_a+

${\bar{v}}^{(u)}$

${\bar{v}}^{(ul)}$

${\overset{\cdot}{β}}_{q}^{(u)}$

Rr-U_acos

$ψ_{q}^{(u)} β_{q}^{(u)}$

)]

(13)

$L_{q}^{(l)}$

(r)=

$\frac{1}{2}$

ρw_sc(r)[(ω_lRr+U_asin

$ψ_{q}^{(l)}$

)²θ-(ω_lRr+U_asin

$ψ_{q}^{(l)}$

)(V_a+

${\bar{v}}^{(l)}$

${\bar{v}}^{(lu)}$

${\overset{\cdot}{β}}_{q}^{(l)}$

Rr-U_acos

$ψ_{q}^{(l)} β_{q}^{(l)}$

)]

(14)

式中: $β_{q}^{(u)}$ 和 $β_{q}^{(l)}$ 分别为上、下旋翼第q个叶片的挥舞角; ω_u和ω_l分别为上、下旋翼的转速;w_s为叶片翼型升力系数斜率;c(r)为距离桨叶中心r位置处的旋翼叶片微元的平均弦长;θ为叶片扭角.由式(8)、(11)、(13)、(14)可知,微分方程式(9)左边诱导速度因子系数矩阵需要右边压强因子来完成计算,并且平均诱导速度需要通过诱导速度因子进行叠加计算,同时,方程右边的压强因子又需要方程左边的诱导速度因子来完成计算.因此,共轴双旋翼诱导速度因子动力学模型式(9)是一组强耦合的非线性动力学方程.通过对式(9)进行数值积分,得到诱导速度因子每个时刻的数值以后,可通过式(13)和(14)计算上、下旋翼的推力F^(u)和F^(l) 分别为

$\begin{array}{l} F^{(u)} = \int_{0}^{1} L_{q}^{(u)} (r) d r \\ F^{(l)} = \int_{0}^{1} L_{q}^{(l)} (r) d r \end{array}\}$

(15)

2 计算结果验证

为了验证共轴双旋翼诱导速度动力学模型的正确性,选取悬停状态上、下旋翼的推力作为研究对象,搭建试验验证平台,平台实物图如图1所示.右侧旋翼为固定安装,旋翼轴高度和轴向位置不可调.左侧旋翼可沿轨道向前向后移动,用于调整双旋翼的轴向距离;左侧旋翼的离地高度也可进行调整,当高度调整至右侧旋翼高度相同时,为共轴状态.选取型号为1024的PVC螺旋桨作为测试桨叶,该桨叶直径约为254 mm,距桨叶中心点5 mm半径范围内为平直安装面(矩形翼型、无扭转角).桨叶桨距为119.38 mm,弦长沿桨叶径向位置连续可变,为了简化计算,将桨叶从平直安装面结束段开始,沿径向方向分为5部份,分别测量每一部分边缘位置的弦长,数据如表1所示.沿桨叶径向方向距离桨叶中心为r的截面,其扭角可根据下式计算:

θ(r)=ϑr

(16)

式中:ϑ为桨叶桨距.两侧旋翼分别由两套完全独立的动力系统提供旋转动力,两套动力系统的电机也由完全独立的控制系统来分别调节脉冲宽度调制(PWM)值,进而实现电机转速的独立控制.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 共轴双旋翼推力测试台架

Fig.1 Thrust test rig for coaxial lifting rotors

表1 测试旋翼叶片径向弦长分布

Tab.1 Chord length distribution in the radial direction for testing blade

r/mm	c/mm
5.0	13.0
25.4	20.8
50.8	29.7
71.2	32.5
91.6	31.0
117.0	24.8

新窗口打开| 下载CSV

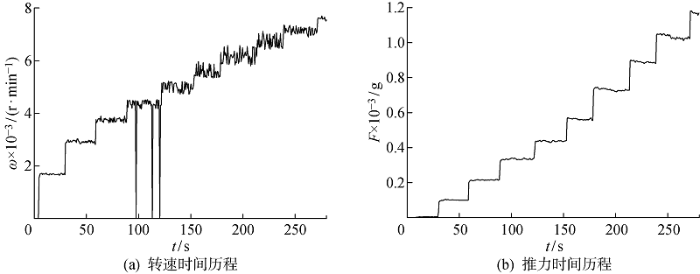
调整左、右电机旋转方向和旋翼桨叶安装方式,使得左、右旋翼旋转方向相反,且尾迹均朝左.此时,左旋翼处于右旋翼的尾迹(下方流场)中,可视为共轴双旋翼的下旋翼.首先,只为一侧旋翼电机通电,使其旋转并测量和记录不同转速下产生的推力,用于校验计算模型对单旋翼计算的准确性, 也为双旋翼计算提供准备.由于一侧旋翼旋转时,产生的诱导速度会成为另一侧旋翼的入流,带动另一侧旋翼随之旋转.所以,可连通右侧旋翼, 即使左侧旋翼被动旋转,右侧旋翼处于左侧旋翼的上游流场,产生的影响较小.图2(a)和2(b)分别给出了单轴旋翼旋转时转速和对应推力测试结果的时间历程图,其中:F为推力测试值;ω为旋翼转速.测试采取逐渐增加转速的方式,并在每个转速停留一段时间使流场充分发展.截取每一转速段中间时刻0.8 s长度数据,分别计算平均转速和平均推力,并用上一节提出的方法对不同转速下的单轴旋翼进行计算.这里估计旋翼升力线斜率为6.11 rad^-1,且因为大于 5000 r/min后转速波动过于激烈,而 1800 r/min时旋翼推力极小,使得力传感器几乎感受不到旋翼产生的推力,因此只对 3000 r/min和 5000 r/min之前的数据进行计算和对比.计算值与测试值的对比如图3所示.在不同转速下,推力的计算值和测试值的偏差如表2所示.其中: $\tilde{F}$ 为推力计算值;e_F为偏差.当偏差大于0时,表示推力计算值高于测试值.图1所示的试验台架拉力测试精度为0.1%±20 g,因此在低转速推力测试值仅为65.7 g时,测试值和计算值之间的偏差率非常大.在旋翼转速为 3500 r/min和 4000 r/min时,测试值和计算值偏差分别为24.23 g和 -1.19 g,偏差率均不大于20%.当旋翼转速为 5000 r/min时,推力计算值小于实际测试值,可能是旋翼在高速旋转时流场产生了复杂流动,而计算模型基于势流理论造成的,此时的计算偏差率为21%.同时,小型直流无刷电机在高速旋转时,由于桨叶的不平衡引发耦合振动,也可能产生额外侧推力.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 单轴旋翼测试结果

Fig.2 Test results for single rotor

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 单轴旋翼推力计算结果

Fig.3 Computational thrust results of single rotor

采用MATLAB中的Curve Fitting Tool工具包,对数据进行拟合,可得到转速与推力的特性关系式,如下式所示:

$\begin{array}{l} F = 1.221 \times 10^{- 5} ω^{2} \\ \tilde{F} = 1.111 \times 10^{- 5} ω^{2} \end{array}\}$

(17)

表2 单旋翼不同转速下的推力

Tab.2 Thrusts at different rotor speeds for single rotor

ω/(r·min^-1)	F/g	$\tilde{F}$ /g	e_F/g
3000	65.7	111.80	46.10
3500	128.0	152.23	24.23
4000	200.0	198.81	-1.19
5000	393.0	310.59	-82.41

新窗口打开| 下载CSV

对于测试数据,拟合的误差平方和(SSE)为 0.7526,而对于计算数据,拟合的误差平方和为1.908×10^-7.由式(16)可知,推力系数的计算值和测试值仅有9%的偏差.

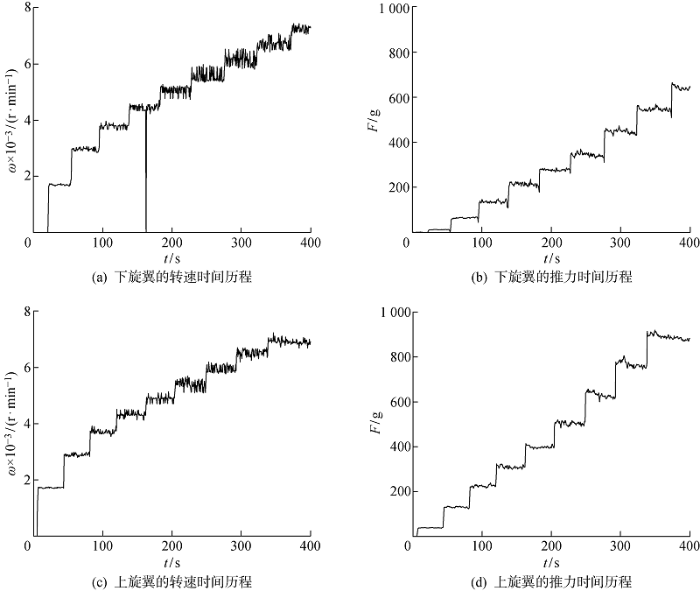
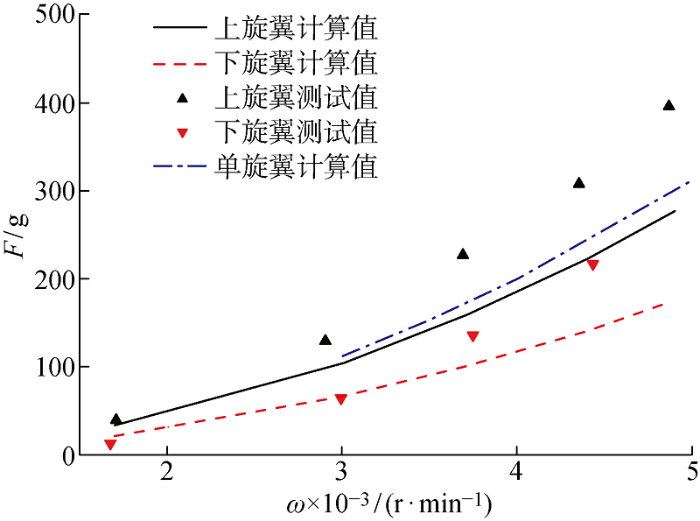
对于共轴双旋翼的测试,设置旋翼轴向距离为一个旋翼半径长度,即127 mm.同时调节左、右旋翼电机PWM值,使得左、右旋翼转速基本稳定在某一设定值附近,并分别记录下对应的PWM值.采用试验出的PWM值,同时对左、右旋翼进行升转速测试,并测试对应的左、右旋翼推力值,如图4所示.由于实际条件限制,左、右电机不可能同时开机,并且升转速的起始点也无法做到完全同步,从时序图上看,出现不完全同步的现象.因此,可选取左、右电机转速同步时间段的转速和推力数据进行平均,获得不同转速下左、右旋翼平均推力的测试值.利用上一节推导的模型,对相应的测试工况进行计算,测试值与计算值的对比如图5所示.不同转速下左、右旋翼的计算值、测试值和偏差如表3所示.其中: $e_{F}^{(l)}$ 为左旋翼偏并; $e_{F}^{(u)}$ 为右旋翼偏差.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 双轴旋翼测试结果

Fig.4 Test results for coaxial rotors

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 共轴双旋翼推力计算结果(轴距127 mm)

Fig.5 Computational thrusts results of coaxial lifting rotor (axial distance=127 mm)

表3 双旋翼不同转速下的推力

Tab.3 Thrusts at different rotor speeds for coaxial lifting rotor

ω/(r·min^-1)	F^(l)/g	${\tilde{F}}^{(1)}$ /g	$e_{F}^{(l)}$ /g	F^(u)/g	${\tilde{F}}^{(u)}$ /g	$e_{F}^{(u)}$ /g
1700	39.30	33.11	-6.19	12.75	20.99	8.24
3000	129.21	103.11	-26.10	64.34	65.36	1.02
3700	227.02	156.87	-70.15	135.82	99.44	-36.38
4400	307.86	221.80	-86.06	216.77	140.60	-76.17
4900	395.95	275.13	-120.82	276.72	174.41	-102.31

新窗口打开| 下载CSV

由图5可知,在 3000~5000 r/min转速范围内,相较于单轴旋翼,对于共轴双旋翼左、右旋翼在相同转速下均出现推力损失,并且由于左旋翼位于右旋翼尾迹之中,造成的推力损失更大.所提出的模型可以较好的反应出这种规律,并且趋势与测试值大致相同.和单轴旋翼类似,随着转速的提高,推力测试值越高于计算值.同样地,通过数据拟合,可以分别得到左、右旋翼的转速与推力特性关系式,如下式所示:

$\begin{array}{l} F^{(u)} = 1.47 \times 10^{- 5} ω^{2} \\ {\tilde{F}}^{(u)} = 1.025 \times 10^{- 5} ω^{2} \end{array}\}$

(18)

$\begin{array}{l} F^{(l)} = 9.426 \times 10^{- 6} ω^{2} \\ {\tilde{F}}^{(l)} = 6.498 \times 10^{- 6} ω^{2} \end{array}\}$

(19)

对于测试数据,右旋翼拟合的SSE为 0.02175, 左旋翼拟合的SSE为 0.1522.对于计算数据,右旋翼拟合的SSE为1.354×10^-7,左旋翼拟合的SSE为6.538×10^-8.

3 结语

本文研究了基于有限状态模型的共轴双旋翼动力学建模方法,利用伴随理论推导了上旋翼尾迹诱导速度表达式,拓展了传统的单轴旋翼有限状态模型.上旋翼动力学模型中的入流矩阵包含了上旋翼的平均自诱导速度信息和下旋翼的平均互诱导速度信息,下旋翼动力学模型中的入流矩阵包含了下旋翼的平均自诱导速度信息和上旋翼的平均互诱导速度信息,其中上旋翼的平均互诱导速度需要利用上旋翼尾迹诱导速度计算式来求取.动力学模型的载荷输入表达式也包含了诱导速度信息,由此可见,该动力学模型是入流和载荷、上旋翼和下旋翼耦合的强非线性动力学模型.跟一般的经验模型不同,此模型需要输入共轴双旋翼桨叶几何信息、气动参数、轴向间距、转速等实际物理信息,因此更具有普适性,能够适应更多的应用环境.通过试验数据验证,此模型具有一定的计算准确度,可用于共轴双旋翼的设计初步计算、控制器设计与实时仿真,有一定的工程应用价值.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

陈铭

共轴双旋翼直升机的技术特点及发展

[J]. 航空制造技术, 2009, 52(17):26-31.

[本文引用: 1]

CHEN

Ming

Technology characteristic and development of coaxial rotor helicopter

[J]. Aeronautical Manufacturing Technology, 2009, 52(17):26-31.

[本文引用: 1]

[2]

MARQUÉS

, DA RONCH

Advanced UAV aerodynamics, flight stability and control

[M]. Chichester, UK: John Wiley & Sons, Ltd, 2017.

[本文引用: 1]

[3]

PETERS D

, BOYD D

, HE C

Finite-state induced-flow model for rotors in hover and forward flight

[J]. Journal of the American Helicopter Society, 1989, 34(4):5-17.

DOI:10.4050/JAHS.34.5 URL [本文引用: 1]

[4]

MORILLO J

, PETERS D

Velocity field above a rotor disk by a new dynamic inflow model

[J]. Journal of Aircraft, 2002, 39(5):731-738.

DOI:10.2514/2.3019 URL [本文引用: 2]

[5]

许和勇, 叶正寅.

悬停共轴双旋翼干扰流动数值模拟

[J]. 航空动力学报, 2011, 26(2):453-457.

[本文引用: 1]

Heyong

, YE

Zhengyin

Numerical simulation of interaction unsteady flows around co-axial rotors in hover

[J]. Journal of Aerospace Power, 2011, 26(2):453-457.

[本文引用: 1]

[6]

PRASAD J V

, NOWAK

, XIN

. Finite state inflow models for a coaxial rotor in hover[EB/OL]. (2012-01-02)[2021-01-20]. https://www.researchgate.net/publication/283484243_Finite_state_inflow_models_for_a_coaxial_rotor_in_hover

URL [本文引用: 1]

[7]

HUANG J

Potential-flow inflow model including wake distortion and contraction

[D]. St. Louis,USA: Washington University, 2015.

[本文引用: 4]

[8]

HUANG J

, PETERS D

, PRASAD

J V R

Converged velocity field for rotors by a blended potential flow method

[J]. GSTF Journal on Aviation Technology, 2015, 1(2):1-10.

[本文引用: 2]

[9]

NAIR S

, JOSEPH

, MOHAN

. An evaluation of ground effect modeling for rotors in hover[EB/OL]. (2017-11-01)[2021-01-20]. https://www.researchgate.net/publication/321184068_An_Evaluation_of_Ground_Effect_Modelling_for_Rotors_in_Hover

URL [本文引用: 1]

[10]

朱正, 招启军, 李鹏.

悬停状态共轴刚性双旋翼非定常流动干扰机理

[J]. 航空学报, 2016, 37(2):568-578.

[本文引用: 1]

ZHU

Zheng

, ZHAO

Qijun

, LI

Peng

Unsteady flow interaction mechanism of coaxial rigid rotors in hover

[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2):568-578.

[本文引用: 1]

[11]

陆陶冶, 陈仁良, 曾丽芳, 等.

共轴倾转旋翼性能计算方法

[J]. 南京航空航天大学学报, 2017, 49(3):396-402.

[本文引用: 1]

Taoye

, CHEN

Renliang

, ZENG

Lifang

, et al.

Mathematical model for performance of coaxial tilt-rotor

[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2017, 49(3):396-402.

[本文引用: 1]

[12]

陈汉, 李科伟, 邓宏彬, 等.

一种共轴双旋翼飞行器悬停控制联合仿真

[J]. 兵工学报, 2019, 40(2):303-313.

[本文引用: 1]

CHEN

Han

, LI

Kewei

, DENG

Hongbin

, et al.

Hover control co-simulation of a coaxial dual-rotor aircraft

[J]. Acta Armamentarii, 2019, 40(2):303-313.

[本文引用: 1]

[13]

PITT

, PETERS D

Theoretical prediction of dynamic-inflow derivatives

[J]. Vertica, 1981, 5(1):21-34.

[本文引用: 1]

共轴双旋翼直升机的技术特点及发展

2009

... 由于共轴双旋翼直升机上下主旋翼产生的扭矩可相互抵消,所以比传统单旋翼带尾浆的直升机结构更简单,气动对称性也更好^[1].另外,对于多旋翼无人机,共轴旋翼的引入将大大提高无人机的抗风能力和稳定性^[2].因此,人们对共轴双旋翼的研究和研制一直都没有停止.从俄罗斯卡莫夫设计局研发的卡-8和美国西科斯基的XH-59A验证机开始,经过半个多世纪的发展,共轴双旋翼构型的直升机越来越受到业内的关注和重视.针对共轴双旋翼飞行器的控制和飞行模拟仿真器的研发也已成为研究的热点之一. ...

共轴双旋翼直升机的技术特点及发展

2009

Advanced UAV aerodynamics, flight stability and control

2017

Finite-state induced-flow model for rotors in hover and forward flight

1989

... 不同于旋翼计算流体力学(CFD)的研究,针对旋翼飞行器控制设计和飞行仿真的动力学模型需要有更好的实时性,同时对计算精度也有一定的要求.1989年文献[3]开发的Peters-He模型是目前最广泛应用的旋翼有限状态模型,可以用于计算旋翼盘上任意位置的诱导速度,进而实时计算单旋翼的推力.该理论隐含了著名的动态入流理论、Pradtl/Galdstein静态入流分布和Theodorsen理论,并且计算结果和试验数据有很好的吻合度.此后,一种被称为Morillo模型^[4]的动态入流模型由Peters教授团队提出,它对旋翼上方流场的求解有其优越性.由于共轴双旋翼之间流场的干扰,上下旋翼的拉力性能将下降^[5],所以用于计算单旋翼诱导速度和推力的Peters-He模型和针对旋翼上方流场计算的Morillo模型,它们均无法直接用于对共轴双旋翼的动力学建模.基于当前的有限入流建模理论,文献[6]利用关联上下旋翼入流系数和压强场系数的入流影响系数矩阵来计算每个旋翼产生的诱导速度.该入流影响系数矩阵包含了旋翼自诱导速度信息和上下旋翼之间互诱导速度信息,由于当时缺少互诱导速度的封闭计算公式,所以互诱导速度需要通过数值计算得到.其开发出的模型在XV-15倾转旋翼机上得到了试验验证.由于该模型需要进行数值计算,所以其计算的实时性能还有一定的提升空间.2015年,文献[7,8]提出了混合势流模型,建立了Peters-He模型和Morillo模型非线性混合函数,对旋翼盘上和旋翼上方流场的计算精度做了进一步提升,更重要的是,该模型对旋翼尾迹进行了建模,给出了旋翼尾迹流场计算的封闭形式解.文献[9]在旋翼悬停地效建模上应用了该混合势流模型,并与试验数据和RotCFD计算结果进行了对比,验证了模型有效性.文献[10]基于运动嵌套网格方法,建立了一套适合于悬停状态下共轴刚性双旋翼非定常干扰流场分析的计算流体力学方法.该研究运用了计算流体力学方法,可以给出共轴双旋翼更加细致的动态流场信息,提高了计算精度,但是存在很大的计算复杂度.文献[11]对倾转过渡状态共轴倾转旋翼进行了研究,考虑了尾流倾斜和收缩的上下旋翼的相互干扰,通过能量方程推导了诱导速度的计算公式,最后利用迭代方法求解了上下旋翼的载荷.由于整个计算过程需要迭代,所以通过此方法进行共轴多旋翼动力学建模也具有一定的计算复杂度.文献[12]结合叶素理论和Pitt-Peters 动态入流模型对共轴双旋翼的气动干涉和挥舞运动进行了近似建模,其他未准确建模的部分用控制算法进行补偿,并在Simulink搭建了控制器进行联合仿真.该方法利用动态入流模型计算诱导速度,仿真实时性好.但是Pitt-Peters 模型结构简单,是Peters教授团队最初提出的三状态动态入流模型^[13],对于一些复杂的飞行状态难以保证较好的计算效果.此外,若仅采用诱导速度干扰系数表示上、下旋翼之间的气动干涉,需要较为充分的理论支撑.现有研究中主要考虑了上下旋翼的流场干扰,并对其进行了相应的数学建模,但还未见到有基于时滞伴随理论的势流模型来建立共轴双旋翼动力学模型的研究. ...

Velocity field above a rotor disk by a new dynamic inflow model

2002

... 根据文献[4],上下旋翼在其各自平面和上方位置 (ν≥0)产生的诱导速度v⁽^u⁾(ν, η, ψ, t)和v⁽^l⁾(ν, η, ψ, t) 分别表示为 ...

悬停共轴双旋翼干扰流动数值模拟

2011

悬停共轴双旋翼干扰流动数值模拟

2011

2021

Potential-flow inflow model including wake distortion and contraction

2015

... 如果诱导速度和伴随速度计算式包含 N次谐波,即m=0, 1, …, N, 定义诱导速度因子和伴随速度因子的状态向量为 a^(u)、a^(l)、Δ^(u). 根据文献[7],压强势用于计算旋翼周围的压强,而压强势可用压强因子

$τ_{n}^{m}$

分谐次叠加来表示,分别定义上、下旋翼的压强因子向量为τ^(u)、τ^(l). 具体表示如下式所示. ...

... 通过低速流体的质量守恒和动量守恒定律公式,代入用勒让德函数表示的速度和压强表达式^[7],并通过伽辽金变换可得到一组以诱导速度因子和伴随速度因子为状态量的常微分方程: ...

... 式中:M和D分别为表观质量矩阵和阻尼矩阵;

$L_{(u)}^{- 1}$

和

$L_{(l)}^{- 1}$

分别为上、下旋翼的入流影响矩阵,和上、下旋翼的尾迹倾斜角有关;V_(u)和V_(l)分别为上、下旋翼的入流矩阵.上述矩阵的计算表达式可参见文献[7].V_(u)和V_(l)的表达式分别为 ...

Converged velocity field for rotors by a blended potential flow method

2015

... 由于上旋翼的尾迹会对下旋翼产生影响,所以需要给出上旋翼的尾迹速度的计算公式.根据文献[8],上旋翼在 (ν, η, ψ)位置的尾迹速度v⁽^u⁾(ν, η, ψ, t)(v<0) 表示为 ...

2021

悬停状态共轴刚性双旋翼非定常流动干扰机理

2016

悬停状态共轴刚性双旋翼非定常流动干扰机理

2016

共轴倾转旋翼性能计算方法

2017

共轴倾转旋翼性能计算方法

2017

一种共轴双旋翼飞行器悬停控制联合仿真

2019

一种共轴双旋翼飞行器悬停控制联合仿真

2019

Theoretical prediction of dynamic-inflow derivatives

1981

〈

〉