基于优先权与双可变时间窗的大型热轧生产线机会维护建模

doi:10.16183/j.cnki.jsjtu.2023.173

基于优先权与双可变时间窗的大型热轧生产线机会维护建模

毛雯欣, 周晓军^,

上海交通大学机械与动力工程学院,上海 200240

Opportunistic Maintenance Modeling of Large-Scale Hot Rolling Production Line Based on Maintenance Priority and Dual Variable Time Window

MAO Wenxin, ZHOU Xiaojun^,

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 周晓军,副教授,博士生导师; E-mail:zzhou745@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-05-4 修回日期: 2023-09-11 接受日期: 2023-09-20

基金资助:

国家重点研发计划(2020YFB1711103)
国家自然科学基金(52075336)

Received: 2023-05-4 Revised: 2023-09-11 Accepted: 2023-09-20

作者简介 About authors

毛雯欣(1998-),硕士生,从事设备维护决策研究.

摘要

为解决大型热轧生产线日常动态维护和支撑辊定期更换带来的维护需求差异问题,综合考虑长距离条件下的维护资源及停机时间限制,引入维护优先权规则识别部件的组合维护判断次序,构建双可变时间窗规则辨别部件是否维护并区分维护需求,进而建立系统整体动态机会维护模型.实例分析表明,该模型可有效解决维护资源和停机时间限制下大型热轧生产线的差异化维护调度问题,且比传统基于时间窗的模型更具成本优势.

关键词： 大型热轧生产线; 机会维护; 预防维护; 维护优先权; 可变时间窗

Abstract

To solve the problem of differential maintenance demand caused by daily dynamic maintenance and periodic replacement of support rolls in large-scale hot rolling lines, a maintenance priority rule is introduced to identify maintenance judgment order of components under long distance condition and downtime constraint. A dual variable time window rule is constructed to identify whether components should be maintained and distinguish maintenance demand, and then a dynamic opportunity maintenance model is established for the system. The case study shows that the model can effectively solve the problem of differential maintenance scheduling for large-scale hot rolling lines under the constraints of maintenance resources and downtime, and has more cost advantages than the traditional time-window-based model.

Keywords： large-scale hot rolling line; opportunistic maintenance; preventive maintenance; maintenance priority; variable time window

PDF (1391KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

毛雯欣, 周晓军. 基于优先权与双可变时间窗的大型热轧生产线机会维护建模[J]. 上海交通大学学报, 2024, 58(8): 1221-1230 doi:10.16183/j.cnki.jsjtu.2023.173

MAO Wenxin, ZHOU Xiaojun. Opportunistic Maintenance Modeling of Large-Scale Hot Rolling Production Line Based on Maintenance Priority and Dual Variable Time Window[J]. Journal of Shanghai Jiaotong University, 2024, 58(8): 1221-1230 doi:10.16183/j.cnki.jsjtu.2023.173

大型热轧生产线是钢铁制造流程的重要组成部分.由于热轧生产的高温、高负荷、高磨损特性,设备工作环境极其恶劣且易发故障,预防性维护是保障其生产效率的重要手段.对于大型热轧生产线,不仅有部件日常动态预防维护机会,还存在支撑辊更换带来的定期预防维护机会,且热轧产线的连续生产特性导致可用的维护停机时间有限,如何综合考虑各部件的维护需求并区分两种维护机会,是亟待解决的问题.

早期的研究常采用定周期预防维护策略^[1⇓-3],该策略下预防维护时间点的确定较为便捷,然而对于热轧生产线,由于部件特性差异大,定周期的预防维护策略实施效果不理想.为解决这一问题,一些学者采用机会维护策略来规划系统预防维护方案,在此策略下,系统中任一设备的预防性维护均可为其他设备带来维护机会,以减少系统停机成本.

现有的机会维护建模方法可主要分为两种,分别为基于动态特性的机会维护建模及基于静态规则的机会维护建模.动态方法^{[4⇓⇓⇓⇓-9]}常根据每个系统维护周期内的目标函数值来动态决策当前的机会维护方案,其一般为短时决策.Lu 等^[4]考虑设备间的经济依赖性,提出一种基于可靠性阈值的滚动方法动态更新维护计划.Xia等^[5]使用基于多属性模型与维护时间窗结合的多目标动态机会维护决策方式降低串并联生产系统的生产成本.Zhou等^[6]通过引入质量-衰退链来考虑设备与产品质量之间相互影响带来的随机依赖性,构建基于扩展成本节约方法的预防维护模型.动态机会维护方法可以很好地反映设备短期内的动态维护需求,但由于其需要列举所有维护方案,且方案数量与设备数量呈指数级相关,其易给方案求解带来维数灾难.为此,一些学者提出了基于静态规则的机会维护建模方法^{[10⇓⇓⇓⇓-15]}.Lu等^[10]针对串并行多级制造系统,引入基于设备故障率的预防维护紧急系数型可靠窗,并据此构建系统的机会维护模型.俞梦琦等^[11]针对多设备串行系统构建基于双维护时间窗的机会维护模型.Zhou等^[12]引入设备维护时间窗之间的引力概念构建与目标成本直接相关的引力窗,实现随机性条件下的机会维护决策.以上基于静态规则的建模方法可大幅降低机会维护决策复杂度,然而现有的规则没有考虑到在维护资源限制以及停机时间限制下,不同部件参与组合维护的机会大小差异,也难以利用生产中存在的额外维护机会,不适用于大型热轧生产线.

部分学者针对维护资源限制进行了研究,如Cavalca^[16]针对串联系统,综合考虑部件的冗余度和维护团队工作量限制的影响,优化了系统的可用性.韩李杰^[17]针对串联系统,综合考虑了维护人力资源成本和备件资源成本,构建基于设备可靠度的系统机会维护决策模型.Qin等^[18]考虑了包括人力资源约束在内的多种复杂约束,开发了一种两阶段的优化方法调整维护计划.然而,这些研究仅仅从数量的角度考虑维护资源,没有涉及大型产线中设备间距离对维护资源使用的影响,缺乏对停机时间约束的考虑,也难以识别两种维护机会带来的维护需求,同样不适用于大型热轧生产线.

本文以串行连续大型热轧生产线为研究对象,通过引入基于维护优先权的判断规则,考虑设备间距离对于维护资源准备时长的影响,决策部件参与机会维护的判断顺序,进而构建基于双可变时间窗的系统机会维护模型,获取日常动态维护机会及支撑辊更换带来的定期维护机会不同场景下的部件预防维护组合.

1 问题描述和维护策略

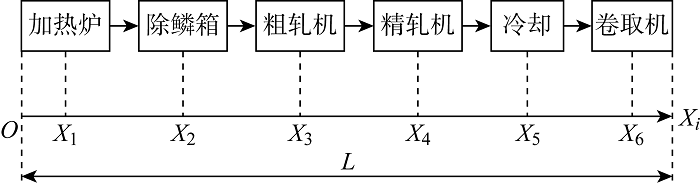
考虑一条由大型设备组成的热轧串行生产线,如图1所示,钢坯通过加热炉加热后经除鳞箱去除表面氧化皮,再先后使用粗轧机和精轧机轧制成钢板,经过层流冷却后使用卷取机将钢板打成卷.假定设备i含有M_i个关键部件,整条生产线的长度为L,设备i的坐标为X_i,设备i的第j个部件可表示为部件E_i_,_j.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 产线示意图

Fig.1 Schematic diagram of production line

该产线最主要的生产特性是需要在高温高负荷下连续运行,导致部件不断磨损,进而增加故障停机的风险.在运行过程中,部件一旦发生故障,需立即使用小修修复,使其恢复工作状态,但无法通过小修改变部件的故障率,且小修时间一般较短,可以忽略不计.故障停机将导致高昂的生产损失,为保证生产稳定性,须按需对产线实施预防性维护.

热轧生产线上的设备均为大型设备,对其进行维护时需要用到维护辅助装置,且产线上有众多的支撑辊需要定期停机更换.当串行生产线中任一部件达到其最佳预防维护时间点时,所有设备均需停机,给产线上其他部件带来预防维护机会.对于大型热轧生产线,高昂的停机成本限制了每次预防维护的停机时长,此外对大型设备维护时需要用到脚手架、行车、电动葫芦等辅助装置,这些维护资源的数量有限,且维护资源在使用之前需对其进行设置.由于大型连续生产线设备间的距离较大,所以维护资源在设备之间移动需要时间,维护资源的设置时间和移动时间可看作维护资源的准备时间,在停机时间有限的条件下,维护资源准备时间不可忽略.此外,大型热轧生产线需定期更换支撑辊,由于支撑辊数量众多,所以停机时间大于一般日常预防维护可用的停机时间,给产线上的其他部件带来预防维护的机会.维护建模的目的是在考虑大型热轧生产线特征下充分利用维护资源,同时有效识别日常动态维护机会和支撑辊更换带来的定期维护机会之间的差别性维护需求.

本文的其他假设如下:① 同一设备上部件间的距离忽略不计;② 维护资源在靠近的设备之间移动可以节约准备时间;③ 触发系统预防维护的部件的准备时间仅包括设置时间;④ 同一时间内仅能够使用维护资源维护一台设备上的一个部件.

2 基于优先权规则及双可变维护时间窗的系统机会维护建模与决策

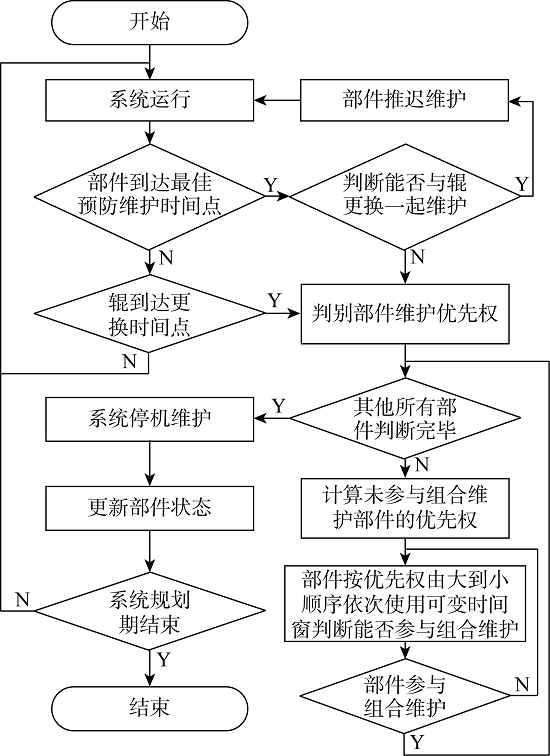
大型热轧生产线的主要特点包括产线距离长、维护资源需预先准备、停机时间有限且存在额外的定期维护机会.传统的时间窗模型能够解决部件是否参与机会维护的问题,但无法考虑部件进入维护组合的次序,在距离及维护资源的约束下,部件进入维护组合的先后会极大程度影响其他部件能否进入维护组合,因此本模型在决策部件是否加入维护组合前引入维护优先权规则以决策部件进入维护组合的次序.此外,为区分日常动态维护机会和定期维护机会之间的不同维护需求,需建立双时间窗,并采用可变时间窗的方式体现不同部件参与组合维护的机会大小差异,可变时间窗通过基准时间窗的压缩及扩张获得.如图2所示,当系统开始运行后,一旦有部件到达最佳预防维护时间点或支撑辊到达更换时间点,便存在系统维护机会,此时使用维护优先权规则及双可变时间窗判别进入维护组合的部件,判别完毕后部件更新状态,系统继续运行直到下一个维护机会出现,整个过程的决策步骤如下.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 机会维护决策流程

Fig.2 Decision process of opportunistic maintenance

步骤1 系统开始运行,各部件处于全新的状态.

步骤2 维护机会出现在部件到达最佳预防维护时间点或支撑辊更换时间点时,针对部件到达最佳预防维护时间点,首先判断能否延后至与支撑辊更换一起维护,若可以延迟,则重复步骤2,否则,计算剩余部件的维护优先权并以此进行排序.

步骤3 使用可变时间窗判断维护优先权最大的部件能否参与机会维护.如确认参与,则更新剩余部件维护优先权并排序,进而重复该步骤对下一部件进行机会维护判别;如确认不参与,则直接进入下一部件的机会维护判别.重复步骤3直至所有部件被判别.

步骤4 系统停机预防维护或更换支撑辊并对部件进行预防维护,更新各部件的状态.

步骤5 若规划期未结束,转至步骤2.

步骤6 以最小化系统总成本为目标,决策优化双基准时间窗的值.

基于以上决策步骤,维护建模中首先需通过单部件维护建模获取各部件的预防维护周期,其次是制定有效的机会维护判断规则获取机会维护组合.判断规则分为两部分,一是解决部件维护优先权问题以识别组合维护判断顺序,二是对日常动态维护机会和支撑辊更换带来的定期维护机会分别定义可变时间窗,以解决两种情况下的维护需求差异问题.在此基础上构建决策目标函数,优化获取系统预防维护策略及维护计划.

2.1 部件预防维护周期决策建模

参与机会维护将使部件改变预防维护时间点,其下一维护时间点随之发生变化.机会维护的动态特性极易导致基于长周期的预防维护时间点决策方法失效,为此,首先以部件单一维护周期的总成本率最低为目标,优化获取当前周期的最佳预防维护时间点.E_i_,_j第k个预防维护周期的总成本率为

(1)

R_{i, j, k}^{P M}

\frac{C_{i, j, k}}{T_{i, j, k}}

\frac{C_{i, j, k}}{t_{i, j, k}^{P M} - t_{i, j, k - 1}^{P M}}

式中:T_i_,_j_,_k为E_i_,_j第k个预防维护周期长度; $t_{i, j, k}^{P M}$ 表示E_i_,_j第k个预防维护周期的维护时间点;C_i_,_j_,_k为E_i_,_j第k个预防维护周期的总成本,

(2)C_i_,_j_,_k=

c_{i, j}^{P M}

C_{i, j, k}^{D}

C_{i, j, k}^{M R}

$c_{i, j}^{P M}$ 为E_i_,_j单次预防维护成本; $C_{i, j, k}^{D}$ 为E_i_,_j第k个预防维护周期的维护停机成本; $C_{i, j, k}^{M R}$ 为E_i_,_j第k个预防维护周期的小修成本.对于停机成本 $C_{i, j}^{D}$ ,定义为

(3)

C_{i, j}^{D}

=c^D

τ_{i, j}^{P M}

式中:c^D为系统单位时间停机成本; $τ_{i, j}^{P M}$ 为E_i_,_j的预防性维护时长.对于小修成本 $C_{i, j, k}^{M R}$ ,定义为

(4)

C_{i, j, k}^{M R}

c_{i, j}^{M R} N_{i, j, k}^{f} (t_{i, j, k}^{P M})

c_{i, j}^{M R} \int_{A_{i, j, k}}^{A_{i, j, k} + t_{i, j, k}^{P M} - t_{i, j, k - 1}^{P M}}

h_i_,_j(t)dt

式中: $c_{i, j}^{M R}$ 为E_i_,_j单次小修成本; $N_{i, j, k}^{f}$ ( $t_{i, j, k}^{P M}$ )表示从E_i_,_j上一次维护至 $t_{i, j, k}^{P M}$ 间的期望故障次数;h_i_,_j(t)为E_i_,_j的故障率函数;A_i_,_j_,_k为E_i_,_j第k个预防维护周期起始点的虚拟役龄.预防性维护通常难以将部件恢复到全新状态,已有研究中,虚拟役龄是常用的表征修复非新的方式^[19],引入预防维护修复率θ_i_,_j(0<θ_i_,_j<1)来表示部件的修复特性,A_i_,_j_,_k可定义为

(5)A_i_,_j_,_k=A_i_,_j_,_k_-1+θ_i_,_jT_i_,_j_,_k_-1

通过最小化单周期维护总成本率 $R_{i, j, k}^{P M}$ ,可获得E_i_,_j第k个维护周期内的最佳预防维护时间点 $t_{i, j, k}^{P M *}$ ,则E_i_,_j第k个维护周期长度为 $t_{i, j, k}^{P M *}$ - $t_{i, j, k - 1}^{P M *}$ .

2.2 基于维护优先权规则的双可变时间窗建模

2.2.1 维护优先权判断规则

由于每次系统停机预防维护的总时间有限,且维护资源准备时间不可忽略,两台距离较远设备上的部件共同维护将产生更多的维护资源准备时间,减小其他部件共同维护的机会.为避免维护资源准备时间在可用停机时间中占比过大,引入维护优先权规则,综合考虑设备间距离、部件最佳预防维护时间点等因素,决策出优先权最大的部件最先判断能否参与机会维护.一旦有部件被纳入机会维护,更新剩余部件的维护优先权,直至所有部件判断完毕.E_i_,_j参与系统第r次预防维护的维护优先权p_i_,_j_,_r可定义为

(6)p_i_,_j_,_r=

\frac{c^{D} (T_{i, j, 0}^{p r e} - T_{i, j, r}^{p r e}) c_{i, j}^{M R} [N_{i, j, k}^{f} (t_{i, j, k}^{P M}) - N_{i, j, k}^{f} (t_{r}^{P M})]}{|t_{i, j, k}^{P M} - t_{r}^{P M}|}

\frac{c^{D} (T_{i, j, 0}^{p r e} - T_{i, j, r}^{p r e}) c_{i, j}^{M R} \int_{A_{i, j, k} + t_{r}^{P M} - t_{i, j, k - 1}^{P M}}^{A_{i, j, k} + t_{i, j, k}^{P M} - t_{i, j, k - 1}^{P M}} h_{i, j} (t) d t}{|t_{i, j, k}^{P M} - t_{r}^{P M}|}

式中: $|t_{i, j, k}^{P M} - t_{r}^{P M}|$ 表示E_i_,_j第k次预防维护时间点与系统第r次预防维护时间点 $t_{r}^{P M}$ 之间的距离; $c_{i, j}^{M R}$ [ $N_{i, j, k}^{f} (t_{i, j, k}^{P M})$ - $N_{i, j, k}^{f} (t_{r}^{P M})$ ]表示E_i_,_j提前至系统第r次预防维护可节约的小修成本;c^D( $T_{i, j, 0}^{p r e}$ - $T_{i, j, r}^{p r e}$ )可表示E_i_,_j参与系统第r次预防维护相比其单独维护可以节约的停机成本; $T_{i, j, 0}^{p r e}$ 为E_i_,_j的基础准备时间,包括基础移动时间和基础设置时间,可表示为

(7)

T_{i, j, 0}^{p r e}

T_{i, j, 0}^{m o v}

T_{i, j, 0}^{s e t}

$T_{i, j, 0}^{s e t}$ 为部件E_i_,_j的基础设置时间,即维护资源设置时间T^res; $t_{i, j, 0}^{m o v}$ 为E_i_,_j的基础移动时间,

(8)

T_{i, j, 0}^{m o v}

\frac{X_{i}}{v^{r e s}}

v^res为维护资源的移动速度.E_i_,_j参与系统第r次预防维护的维护资源准备时间 $T_{i, j, r}^{p r e}$ 可定义为

(9)

T_{i, j, r}^{p r e}

T_{i, j, r}^{m o v}

T_{i, j, r}^{s e t}

式中: $T_{i, j, k}^{m o v}$ 为E_i_,_j参与系统第r次预防维护的维护资源移动时间,

(10)

T_{i, j, r}^{m o v}

(1 - y_{i, j, r}) \frac{\underset{E_{i_{1} j_{1}} \in Ω_{r}}{m i n} D_{i, i_{1}}}{v^{r e s}}

Ω_r表示参与系统第r次预防维护的部件集合; $D_{i, i_{1}}$ 为设备i和设备i₁之间的距离;y_i_,_j_,_r为布尔变量.如E_i_,_j为第1个被纳入系统第r次预防维护的部件,y_i_,_j_,_r=1;否则y_i_,_j_,_r=0. $T_{i, j, r}^{s e t}$ 为E_i_,_j参与系统第r次预防维护的维护资源设置时间,

(11)

T_{i, j, r}^{s e t}

=y_i_,_j_,_rT^res+

(1 - y_{i, j, r})

T^resr^sav(

\underset{E_{i_{1}, j_{1}} \in Ω_{r}}{m i n} D_{i, i_{1}}

)

r^sav( $\underset{E_{i_{1}, j_{1}} \in Ω_{r}}{m i n} D_{i, i_{1}}$ )为E_i_,_j参与系统第r次预防维护的维护资源设置时间节约率,与设备i和其在Ω_r中最短设备间距离有关,可定义为

(12)r^sav(

\underset{E_{i_{1}, j_{1}} \in Ω_{r}}{m i n} D_{i, i_{1}}

\frac{(\underset{E_{i_{1}, j_{1}} \in Ω_{r}}{m i n} D_{i, i_{1}})^{b}}{(\underset{i, i' \in I}{m a x} D_{i, i'})^{b}}

b为节约系数;I为设备集合;i'为i以外的另一设备.维护资源设置时间节约率与设备间的距离非线形相关,对于同一台设备上的不同部件组合维护,维护资源不需要重新设置;对于两台距离较近的设备,维护资源在两者之间时可以不完全拆卸,从而节约设置时间.

2.2.2 双可变时间窗

为体现维护资源限制、系统最长停机时间限制以及设备间距离对于部件维护机会的影响,设置可变时间窗,由维护基准时间窗扩张及压缩获得,以体现各因素影响的大小.由于日常动态维护机会和支撑辊更换带来的定期维护机会可用停机时长不同,所以需分别设置基准时间窗.针对日常动态维护机会,E_i_,_j参与系统第r次维护的可变维护时间窗可定义为

(13)

T_{i, j, r}^{D}

{T^{W}}_{1} r_{i, j, r}^{s} r_{i, j, r}^{p}

式中: ${T^{W}}_{1}$ 为日常动态维护机会的基准时间窗; $r_{i, j, r}^{s}$ 为E_i_,_j参与系统第r次维护的维护时间窗扩张率; $r_{i, j, r}^{p}$ 为E_i_,_j参与系统第r次维护的维护时间窗压缩率.类似,针对支撑辊更换带来的定期维护机会,E_i_,_j可变维护时间窗可定义为

(14)

T_{i, j, r}^{R}

{T^{W}}_{2} r_{i, j, r}^{s} r_{i, j, r}^{p}

式中: $T_{2}^{W}$ 为定期维护机会的基准时间窗.

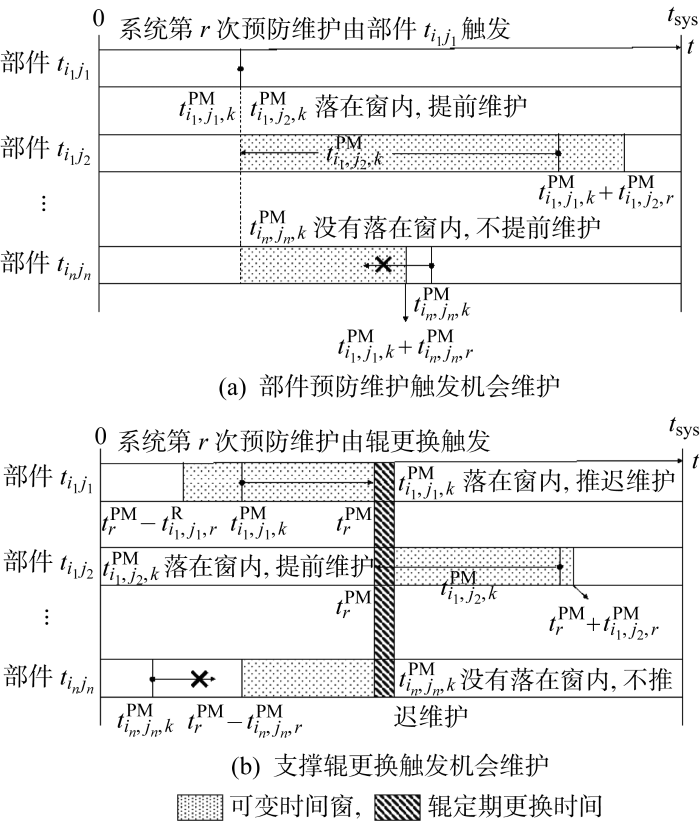
图3给出了基于以上规则的机会维护判定过程,t_sys为系统规划期结束的时刻.系统的预防维护机会由部件 $E_{i_{1}, j_{1}}$ 到达最佳预防维护时间点触发,此时,首先如图3(b)左半部分所示判断能否与支撑辊更换一起维护,若 $t_{i_{1}, j_{1}, k}^{P M}$ 落在可变时间窗内,则推迟至与支撑辊更换一起维护;否则,计算剩余部件的维护优先权,按维护优先权大小依次判断部件的最佳预防维护时间点是否落在可变时间窗内,如图3(a) 所示,若落在窗内,该部件提前维护,并重新计算剩余设备的维护优先权.当系统的预防维护机会由支撑辊更换触发,则计算剩余部件的维护优先权,按维护优先权大小依次判断设备的最佳预防维护时间点是否落在可变时间窗内,如图3(b)右半部分所示,该部件提前维护,并重新计算剩余设备的维护优先权.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 双可变时间窗策略

Fig.3 Dual variable time window strategy

由于每次系统停机进行预防维护的时长有限,为限制部件不断纳入维护导致超出最长可停机时间,引入压缩率对时间窗的长度进行压缩,压缩程度通过剩余维护可用时长体现.对于E_i_,_j,第r次系统预防维护的压缩率 $r_{i, j, r}^{p}$ 可定义为

(15)

r_{i, j, r}^{p}

=1-

\frac{\sum_{E_{i, j} \in Ω_{r}}^{} τ_{i, j}^{P M} + τ_{i, j}^{P M}}{{τ^{d}}_{r}}

式中: ${τ^{d}}_{r}$ 为系统第r次可用停机时长.

在第r次系统预防维护中,若Ω_r中有与E_i_,_j距离较近的部件,则E_i_,_j参与机会维护可节约维护资源准备时间,因此需扩大时间窗,以给予其更大的维护机会.基准时间窗扩大的程度由扩张率决定,对于E_i_,_j,第r次系统预防维护的扩张率 $r_{i, j, r}^{s}$ 可定义为

(16)

r_{i, j, r}^{s}

\frac{T_{i, j, 0}^{p r e} + τ_{i, j}^{P M}}{T^{r e s} r^{s a v} (\underset{E_{i_{1}, j_{1}} \in Ω_{r}}{m i n} D_{i, i_{1}}) + τ_{i, j}^{P M}}

2.3 系统机会维护决策建模

基于上述规则,可不断决策系统每次机会维护部件集合,直到规划期结束.通过调整决策变量 $T_{1}^{W}$ 、 $T_{2}^{W}$ 的大小,最小化规划期内系统总成本C,获取系统预防维护策略.系统总成本C由预防维护成本、小修成本、停机成本3个部分组成,规划期内总预防维护成本 $C_{s y s}^{P M}$ 可定义为

(17)

C_{s y s}^{P M}

\sum_{i = 1}^{N} \sum_{j = 1}^{M_{i}}

m_i_,_j

c_{i, j}^{P M}

式中:N为设备总数;m_i_,_j为E_i_,_j规划期内预防维护次数.规划期内总小修成本 $C_{s y s}^{M R}$ 可定义为

(18)

C_{s y s}^{M R}

\sum_{i = 1}^{N} \sum_{j = 1}^{M_{i}} \sum_{k = 1}^{m_{i, j}} c_{i, j}^{M R}

n_i_,_j_,_k=

\sum_{i = 1}^{N} \sum_{j = 1}^{M_{i}} \sum_{k = 1}^{m_{i, j}} c_{i, j}^{M R} \int_{A_{i, j, k - 1}}^{A_{i, j, k - 1} + T_{i, j, k}}

h_i_,_j(t)dt

规划期内总停机成本 $C_{s y s}^{D}$ 可定义为

(19)

C_{s y s}^{D}

=c^D(n^PMτ^PM+n^SWτ^SW)

式中:n^PM为日常动态预防维护次数;τ^PM日常动态预防维护可用停机时长;n^SW为支撑辊更换次数;τ^SW为支撑辊更换可用停机时长.因此,规划期内总成本为

(20)C=

\sum_{i = 1}^{N} \sum_{j = 1}^{M_{i}}

m_i_,_j

c_{i, j}^{P M}

+c^D(n^PMτ^PM+n^SWτ^SW)+

\sum_{i = 1}^{N} \sum_{j = 1}^{M_{i}} \sum_{k = 1}^{m_{i, j}} c_{i, j}^{M R}

n_i_,_j_,_k

3 实例分析

3.1 实例概览与结果分析

针对问题描述章节中图1所示的大型热轧生产线,加热炉主要由炉体、余热回收及通风装置和燃烧装置4个部件组成;除鳞箱主要由夹送辊装置、传动装置和高压除鳞集管3个部件组成;粗轧机主要由传动系统、辊道、扎制液压装置和轧辊平衡装置4个部件组成;精轧机主要由传动系统、辊道、扎制液压装置、轧辊平衡装置和弯辊装置5个部件组成;层流冷却装置主要由上喷装置、侧喷装置和下喷装置3个部件组成;卷取机主要由卷轴、辅助卷取设备和液压装置3个部件组成.Weibull分布常被用于描述机械设备或部件故障率趋势,由于该生产线上关键部件均为机械部件,所以假设所有部件的故障率均服从Weibull分布,则E_i_,_j的故障率函数可定义为

(21)h_i_,_j(t)=

\frac{α_{i, j}}{β_{i, j}} {(\frac{t}{β_{i, j}})}^{α_{i, j} - 1}

,
i=1, 2, …, 6; j=1, 2, …, M _i

式中:α_i_,_j和β_i_,_j分别表示E_i_,_j的尺度参数和形状参数.若产线上存在具有其他衰退特性的部件,如电子部件等,可将式(21)中的故障率函数替换为其他分布的故障率函数.

设备的坐标及部件参数如表1及表2所示,表2中E_i_,_j维护持续时间 $τ_{i, j}^{P M}$ 以及成本参数可基于统计获得的车间维护历史数据均值获得,成本参数包括 $c_{i, j}^{M R}$ 、 $c_{i, j}^{P M}$ 及c^D,计算成本参数时主要考虑了产线停机造成的生产损失、故障停机造成的废料损失、用于维护及维修的零部件成本、维护操作工的人力资源成本等因素;基于部件历史故障及维修信息,α_i_,_j、β_i_,_j以及θ_i_,_j可通过最大似然估计获得^[20].

表1 设备坐标

Tab.1 Equipment parameters

i	X_i/m
1	36
2	48
3	147.3
4	251
5	338.7
6	517

新窗口打开| 下载CSV

表2 部件维护参数及故障参数

Tab.2 Component maintenance parameters and fault parameters

i	j	α_i,j	β_i,j	θ_i,j	$c_{i, j}^{M R}$ /元	$c_{i, j}^{P M}$ /元	c^D/元	$τ_{i, j}^{P M}$ /h
1	1	1.91	190.30	0.99	19 955.75	10 022.30	63 926.94	0.26
1	2	2.11	572.81	0.99	14 660.86	7 338.08	63 926.94	0.29
1	3	3.19	262.87	0.99	19 628.20	9 834.12	63 926.94	0.34
2	1	2.15	190.81	0.97	21 364.43	10 778.73	63 926.94	0.23
2	2	2.89	336.95	0.97	24 905.46	12 551.00	63 926.94	0.30
2	3	2.38	298.07	0.97	11 100.67	5 552.24	63 926.94	0.30
3	1	2.05	323.81	0.98	19 687.53	9 845.41	63 926.94	0.34
3	2	1.40	218.42	0.98	21 586.06	10 854.72	63 926.94	0.33
3	3	2.42	226.00	0.97	16 004.07	8 068.35	63 926.94	0.23
3	4	2.34	189.25	0.98	18 473.28	8 274.24	63 926.94	0.29
4	1	2.44	289.29	0.98	11 235.69	8 163.95	63 926.94	0.26
4	2	2.91	450.77	0.96	7 524.52	3 765.91	63 926.94	0.24
4	3	1.96	360.03	0.97	23 924.34	11 962.74	63 926.94	0.21
4	4	1.65	240.31	0.98	24 208.23	12 198.36	63 926.94	0.29
4	5	2.04	352.06	0.98	11 982.24	6 026.53	63 926.94	0.23
5	2	2.42	253.50	0.96	10 127.18	5 139.05	63 926.94	0.34
5	3	2.18	277.35	0.99	15 932.36	8 253.69	63 926.94	0.32
5	4	2.08	244.23	0.96	20 118.95	10 129.69	63 926.94	0.25
6	1	2.78	190.87	0.99	15 752.26	7 950.42	63 926.94	0.30
6	2	1.90	356.04	0.99	10 034.88	5 073.03	63 926.94	0.36
6	3	3.91	239.46	0.97	8 474.86	4 303.24	63 926.94	0.27

新窗口打开| 下载CSV

系统总规划期长度为T^sys=2 880 h,基于车间实验数据均值可得维护资源设置时间T^res=0.2 h,维护资源移动速度v^res=0.5 m/s,节约系数b=1.2.支撑辊需每月更换,即每720 h带来一次定期维护机会,支撑辊定期更换时可用预防维护时长为τ^SW=3 h,系统日常动态预防维护可用停机时长为τ^PM=1 h.根据式(20),通过最小化规划期内系统总成本,对基准时间窗进行双参数优化,使用软件MATLAB编程遍历求解,根据经验值,基准时间窗 $T_{1}^{W}$ 、 $T_{2}^{W}$ 的搜索范围均为[0,100] h,搜索步长为 1 h.计算求解可得系统的最优维护策略( $T_{1}^{W}$ , $T_{2}^{W}$ )的取值为(60, 50) h,该策略下的部分系统预防维护计划如表3所示. 表中:“⚪”表示E_i_,_j参与此次系统机会维护.由表3可得,在本文的策略下部件进行了动态维护组合,且同一设备上的部件或相邻设备上的部件有更多的机会进行组合维护.在时间t=720 h时,支撑辊更换带来系统预防维护机会,可用停机时长更长,因此有更多的部件参与组合维护.

表3 规划期内部分系统预防维护决策

Tab.3 Partial system preventive maintenance decisions during the planning period

i	j	参与系统维护的时间/h
i	j	558	602	604	615	720	750	800	837	845	904	915
1	1				⚪				⚪
1	2					⚪
1	3					⚪
2	1	⚪				⚪						⚪
2	2	⚪								⚪
2	3					⚪
3	1						⚪
3	2
3	3				⚪				⚪
3	4						⚪					⚪
4	1					⚪
4	2
4	3					⚪
4	4					⚪
4	5										⚪
5	2			⚪
5	3			⚪
5	4							⚪
6	1					⚪					⚪
6	2		⚪
6	3		⚪					⚪

新窗口打开| 下载CSV

3.2 策略对比

为验证基于维护优先权与双可变时间窗策略(策略1)的有效性,设置基于双时间窗的预防维护策略(策略2)以及基于单时间窗的预防维护策略(策略3)进行对比.上述两种策略的具体内容如下.

策略2 系统内任一部件到达其最佳预防维护时间点或支撑辊更换时,假设为系统第r次预防维护时间点 $t_{r}^{P M}$ ,分别针对日常动态维护以及支撑辊更换带来的定期维护机会设置时间窗 ${T^{W}}_{1}$ 和 ${T^{W}}_{2}$ ,按照最佳预防维护时间点的先后依次将剩余部件中最佳预防维护时间落在[ $t_{r}^{P M}$ , $t_{r}^{P M}$ + ${T^{W}}_{1}$ ](日常动态维护机会)或[ $t_{r}^{P M}$ , $t_{r}^{P M}$ + ${T^{W}}_{2}$ ](支撑辊更换定期维护机会)内部件纳入机会维护部件集合,直至到达停机时长限制.

策略3 判断逻辑同策略2,两者的区别在于策略3下日常动态维护机会及支撑辊定期更换带来的机会采用同一个时间窗.

各策略下的结果如表4所示,比较不同策略下的成本,策略1的系统总成本最低,且大幅降低了系统小修成本以及停机成本,这是由于策略1基于维护优先权规则决策部件参与机会维护的判断次序,在此过程中同时考虑了设备间距离的影响及部件小修成本,进而获得机会维护组合,而其他两种策略仅仅按照最佳预防维护时间点的先后来决策机会维护组合.此外,不可变的时间窗也无法体现不同部件的维护机会大小差异.

表4 不同策略下的结果对比

Tab.4 Comparison of results of different strategies

策略	$T_{1}^{W}$ /h	$T_{2}^{W}$ /h	C/元	$C_{s y s}^{P M}$ /元	$C_{s y s}^{M R}$ /元	$C_{s y s}^{D}$ /元
1	60	50	11 906 720.0	1 804 806.52	5 237 031.37	4 864 882.08
2	30	70	12 245 530.1	1 752 787.59	5 383 183.74	5 109 558.77
3	120	120	12 331 983.3	1 805 587.98	5 502 394.46	5 024 000.91

新窗口打开| 下载CSV

停机时长限制是本文研究的核心问题之一,大型热轧生产线产能高,停机的高生产损失导致高昂的停机成本,故产线停机时长有限.停机成本主要取决于钢板的价格,而钢板的价格会因市场因素而波动.为验证策略1在市场波动时的有效性,引入停机成本变化因子r^D, 令单位时间停机成本 $c_{n e w}^{D}$ =r^Dc^D,保持其他参数不变,调节停机成本变化因子的大小,各策略下的系统总成本C如表5所示.结果表明当停机成本波动时,策略1依然有效,能够获得比其他两种策略更低的系统总成本.

表5 停机成本变化时不同策略下的总成本对比

Tab.5 Comparison of total cost of different strategies at different downtime costs

r^D	C/元
r^D	策略1	策略2	策略3
0.5	9620459.5	9 705 047.2	9 809 341.9
0.8	11137170.5	11 253 346.3	13 177 470.9
0.9	11645926.6	11 758 861.0	11 857 452.1
1.1	12450669.2	12 649 852.0	12 649 851.9
1.2	12836969.8	13 147 182.0	13 177 470.9
1.3	13182547.6	13 467 639.1	13 467 639.1
1.4	13692836.8	13 982 316.3	14 003 082.2
1.5	13974578.3	14 177 837.0	14 221 703.6
1.6	14529246.8	14 712 756.4	14 740 627.2
1.7	14872695.2	15 225 633.6	15 260 733.4
1.8	15225633.5	15 472 867.0	15 482 514.8
1.9	15668527.0	15 928 027.0	16 020 137.9
2.0	16004840.5	16 334 781.7	16 337 258.5
3.0	18962605.2	19 118 940.2	19 430 157.4
4.0	21386509.9	21 932 994.6	22 347 742.4

新窗口打开| 下载CSV

此外,大型热轧生产线在进行预防性维护或小修时,需要多名操作工对设备进行检修及更换零件,因此维护人员和零件的成本波动也会影响部件单次预防维护成本及小修成本.引入单次预防维护成本变化因子r^PM及单次小修成本变化因子r^MR,令单次小修成本 $c_{n e w, i, j}^{M R}$ =r^MR $c_{i, j}^{M R}$ 、单次预防维护成本 $c_{n e w, i, j}^{P M}$ =r^PM $c_{i, j}^{P M}$ ,保持其他参数不变,分别改变单次预防维护成本变化因子及单次小修成本变化因子的大小,各策略下的系统总成本C如表6所示.结果表明当单次预防维护成本及单次小修成本波动时,策略1始终具有成本优势.

表6 单次预防维护成本及单次小修成本变化时不同策略下的总成本对比

Tab.6 Comparison of total cost of different strategies at different preventive maintenance costs and minimal repair costs

r^PM	C/元			r^MR	C/元
r^PM	策略1	策略2	策略3	r^MR	策略1	策略2	策略3
0.4	10842663	11 058 172	11 076 813	0.4	7617885	7 675 420	7 773 159
0.6	11092007	11 218 433	11 289 565	0.6	9362511	9 483 791	9 532 783
0.8	11431720	11 585 273	11 585 273	0.8	10756493	10 879 263	10 896 904
1.0	11737294	11 900 250	11 951 963	1.0	11906720	12 245 530	12 331 983
1.2	11906720	12 245 530	12 331 983	1.2	13240993	13 287 997	13 501 420
1.4	12377192	12 434 377	12 434 377	1.4	14353124	14 578 590	14 631 391
1.6	12711406	12 832 599	12 892 816	1.6	15347480	15 612 128	15 612 128
1.8	12881166	13 030 062	13 030 062	1.8	16355153	16 522 962	16 634 735
2.0	13139298	13 348 537	13 348 537	2.0	17233474	17 371 955	17 602 482

新窗口打开| 下载CSV

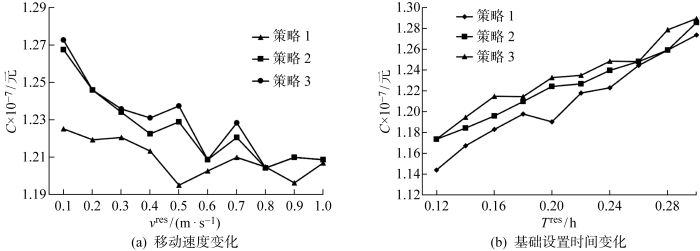
大型热轧生产线中维护资源是本文研究的重点,维护资源准备时间是影响部件机会维护的主要因素,其又取决于设置时间及移动时间两部分,为进一步验证策略1的有效性,保持其他参数不变的条件下,分别改变维护资源设置时间T^res及移动速度v^res,对比3种策略下的成本,结果如图4所示.由图4(a)可得,各策略下系统总成本随移动速度的降低而增加,但策略1始终具有成本优势,策略2的系统总成本不高于策略3.当移动速度降低时,维护资源准备时间在停机可用时间中的占比增大,停机时长限制及设备间距的影响被放大,而策略1中优先权规则及可变时间窗将设备间距离纳入考量,能决策出进入组合维护的更优部件集合,因此在此情况下,策略1与策略2和3之间的差距拉大,策略1的成本优势更为突出.由图4(b)可得,各策略下系统总成本与维护资源设置时间呈正相关,且策略1的系统总成本始终低于策略2、3,进一步表明了策略1在大型热轧生产线上应用的优越性.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 维护资源参数变化时不同策略下的结果对比

Fig.4 Comparison of results total cost of different strategies at different parameters of maintenance resource

4 结语

本文针对大型热轧生产线,综合考虑维护资源限制、停机时间约束以及设备间距离对于部件机会维护的影响,提出维护优先权规则,决策部件组合维护判别次序,并构建基于双可变时间窗的机会维护模型,识别日常动态维护机会及支撑辊更换带来的定期维护机会之前的维护需求差别,通过压缩及扩张基准时间窗的方式体现不同部件参与组合维护机会的差异.实例分析表明,该模型能够有效降低系统总成本,在维护资源设置时间变化时,仍能够取得比传统时间窗模型更低的系统总成本,当维护资源移动速度降低时,采用基于维护优先权规则与双可变时间窗模型更利于节约成本.此外,在停机成本波动时,该模型始终能获得比传统时间窗模型更低的系统总成本,证明该方法具有广泛的适应性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LIM

J H

, PARK

D H

Optimal periodic preventive maintenance schedules with improvement factors depending on number of preventive maintenances

[J]. Asia-Pacific Journal of Operational Research, 2007, 24(1): 111-124.

i	j	参与系统维护的时间/h
i	j	558	602	604	615	720	750	800	837	845	904	915
1	1				⚪				⚪
1	2					⚪
1	3					⚪
2	1	⚪				⚪						⚪
2	2	⚪								⚪
2	3					⚪
3	1						⚪
3	2
3	3				⚪				⚪
3	4						⚪					⚪
4	1					⚪
4	2
4	3					⚪
4	4					⚪
4	5										⚪
5	2			⚪
5	3			⚪
5	4							⚪
6	1					⚪					⚪
6	2		⚪
6	3		⚪					⚪

i	j	参与系统维护的时间/h
i	j	558	602	604	615	720	750	800	837	845	904	915
1	1				⚪				⚪
1	2					⚪
1	3					⚪
2	1	⚪				⚪						⚪
2	2	⚪								⚪
2	3					⚪
3	1						⚪
3	2
3	3				⚪				⚪
3	4						⚪					⚪
4	1					⚪
4	2
4	3					⚪
4	4					⚪
4	5										⚪
5	2			⚪
5	3			⚪
5	4							⚪
6	1					⚪					⚪
6	2		⚪
6	3		⚪					⚪