基于双惯容调谐质量系统的半潜式海上风力机振动控制

doi:10.16183/j.cnki.jsjtu.2023.019

基于双惯容调谐质量系统的半潜式海上风力机振动控制

曾伟杰¹, 张颖^,², 邓燕飞³, 郭川睿¹, 任伟新¹

1.深圳大学土木与交通工程学院,广东深圳 518061

2.广东工业大学机电学院,广州 510006

3.哈尔滨工业大学深圳智能海洋工程研究院,广东深圳 518055

Vibration Control of Semi-Submersible Offshore Wind Turbines Using Inerter-Based Absorbers

ZENG Weijie¹, ZHANG Ying^,², DENG Yanfei³, GUO Chuanrui¹, REN Weixin¹

1. College of Civil and Transportation Engineering, Shenzhen University, Shenzhen 518061, Guangdong, China

2. School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou 510006, China

3. Intelligent Ocean Engineering Research Institute, Harbin Institute of Technology, Shenzhen 518055, Guangdong, China

通讯作者: 张颖,副教授;E-mail:sara.zhangying@gdut.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-01-16 修回日期: 2023-03-7 接受日期: 2023-03-14

基金资助:

国家自然科学基金(52008259)
深圳市海上基础设施安全与监测重点实验室(筹建启动)(ZDSYS20201020162400001)

Received: 2023-01-16 Revised: 2023-03-7 Accepted: 2023-03-14

作者简介 About authors

曾伟杰(1997-),硕士生,从事海上风力机减振减载研究.

摘要

与固定式海上风力机相比,漂浮式海上风力机的振动问题更为突出,进一步控制漂浮式海上风力机的振动成为了工程难题.针对此问题,探索了惯容调谐质量阻尼器(惯容-TMD,即IBA)系统对半潜式海上风力机的振动抑制效果,并提出一种基于结构阻抗的惯容-TMD综合优化设计方法,从整个设计空间出发保证惯容-TMD的最优性.为寻求最优的减振效果,基于达朗贝尔原理建立风力机-惯容-TMD动力学模型,采用双IBA的控制策略同时对半潜式海上风力机浮台和塔筒的振动响应进行抑制,并从增益效果角度,比较了双IBA与双TMD的减振性能.最后对OpenFAST软件进行二次开发,数值验证了风浪联合作用下双IBA相对于双TMD减振性能的提升.结果表明:双减振装置的减振性能相较于单个减振装置有明显提升,且双IBA振动控制效果要优于双TMD;此外,基于惯容器质量增益效果,在达到最优TMD相同减振效果的情况下,机舱惯容-TMD (NIBA)和浮台惯容-TMD (PIBA)分别可将结构减振器中质量元件的质量减少23.9%和32.2%,大幅降低装置成本.

关键词： 漂浮式海上风力机; 惯容; 调谐质量阻尼器; 振动控制

Abstract

Compared with fixed offshore wind turbines, the vibration problem of floating offshore wind turbines is particularly prominent, and further reduction of the vibration of floating offshore wind turbines has become an engineering challenge. In order to solve this problem, a novel vibration suppression device, inerter-based absorber (IBA) is introduced, and the vibration control of semi-submersible offshore wind turbines is studied. A comprehensive optimization method, namely the structure-immittance approach, is utilized to design the IBA in a systematic way. In order to search for the optimum vibration suppression performance, a simplified dynamic model of the semi-submersible offshore wind turbine, and the IBA dynamic equations are established using D’Alembert’s principle. Simultaneous suppression of the vibration response of the floating platform and tower of a semi-submersible offshore wind turbine is realized using the dual IBA control strategy. Furthermore, by implementing the optimum IBA in the OpenFAST software, the vibration suppression benefits of the dual IBA compared with the dual tuned mass damper (TMD) are verified under the coupling effects of wind and waves. The results show that the vibration control performance of the dual IBA control strategy is significantly better than that of the single one, and that of the dual IBA is better than that of the dual TMD. In addition, under the condition of achieving the same suppression performance as the TMD, IBA installed at the nacelle and the platform can respectively decrease the required absorber mass by 23.9% and 32.2%, which can greatly reduce the manufacture cost of the device.

Keywords： floating wind turbines; inerter; tuned mass dampers (TMD); vibration control

PDF (3460KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

曾伟杰, 张颖, 邓燕飞, 郭川睿, 任伟新. 基于双惯容调谐质量系统的半潜式海上风力机振动控制[J]. 上海交通大学学报, 2024, 58(7): 983-994 doi:10.16183/j.cnki.jsjtu.2023.019

ZENG Weijie, ZHANG Ying, DENG Yanfei, GUO Chuanrui, REN Weixin. Vibration Control of Semi-Submersible Offshore Wind Turbines Using Inerter-Based Absorbers[J]. Journal of Shanghai Jiaotong University, 2024, 58(7): 983-994 doi:10.16183/j.cnki.jsjtu.2023.019

随着能源需求的增长和温室效应加剧,世界各地对清洁能源的需求日益迫切.海上风力发电作为清洁能源,得到了快速发展,近海风场资源的开发已近饱和.由于中远海的平均风速高、湍流小,近年来漂浮式海上风力机受到了广泛的关注.根据全球风能理事会(GWEC)发布的《Global Wind Report 2022》,2021年全球范围内新装57 MW漂浮式海上风力机,其中中国新装5.5 MW,实现了零的突破,而全球范围内累计安装的漂浮式海上风电已达到121.4 MW^[1].漂浮式海上风力机正在从科研逐步走向工程应用,预计在2030年实现全面的商业化^[2].

漂浮式海上风力机所受的环境载荷复杂多变,振动问题突出,在极端海况下甚至会发生倾覆,如何进一步减小漂浮式海上风力机振动,提高其稳定性成为了近年来的研究热点.为了降低漂浮式海上风力机的振动幅值,提高风力机整体稳定性,2011年Lackner等^[3]将被动结构减振装置调谐质量阻尼器(TMD)用于大型漂浮式海上风力机中进行减振减载研究,表明了TMD提高漂浮式海上风力机稳定性的潜力;Stewart等^[4]研究了放置在机舱的TMD对立柱式、张力腿式和驳船式海上风力机的影响;Si等^[5]则建立6自由度的立柱式海上风力机简化模型来进行减振研究;贺尔铭等^[6⇓⇓-9]将TMD放置于驳船式漂浮风力机的浮台中;Guimaraes等^[10]提出了一种新型倒立摆TMD放置于风力机机舱; Li等^[11]则研究在半潜式海上风力机的机舱和塔架中使用前后TMD进行被动控制的效果.为了寻求更优的控制效果,Zhang等^[12]则研究调谐液柱阻尼器(TLCD)在立柱型浮式海上风力机振动控制中的应用;Wei等^[13]通过结合双向调谐液柱阻尼器(BTLCD)和TMD的优点来减轻驳船式海上风力机的俯仰和横摇运动.

惯容器(Inerter)是一种具有两个独立自由端点的机械装置,其两端等大反向的力与两端的相对加速度成正比,目前已被应用于一级方程式赛车^[14]和土木工程结构的振动控制中,其性能优势已得到充分证明^[15⇓-17].而针对海上风力机结构,Zhang等^[18]提出一种转动惯性双调谐质量阻尼器(RIDTMD)放置于风力机机舱;Li等^[19]将惯容器与TMD结合放置于机舱,并对其减振性能进行评估.

目前大量关于漂浮式海上风力机减振减载的研究大都针对立柱式和驳船式漂浮风力机,对半潜式风力机研究较少,且大都集中于在塔顶机舱中安装各种减振装置,对浮台纵摇减振效果不佳.此外,目前研究大都局限在几种给定结构的TMD或惯容系统,未能从整个设计空间考虑,无法保证给定TMD或惯容系统结构的最优性.

本文提出一种将多个弹簧、阻尼和惯容器串联或并联组合形成的惯容-TMD (Inerter-Based Absorbers,IBA),以半潜式海上风力机为对象,利用达朗贝尔原理建立相应的半潜式海上风力机-惯容-TMD动力学模型,采用双惯容-TMD的控制策略同时对半潜式海上风力机浮台和塔筒的振动响应进行抑制,并提出一种新型无源网络综合理论——结构阻抗法进行惯容系统拓扑结构与参数优化研究,在满足系统经济性要求的前提下,使得所提出的惯容-TMD减振系统减振性能最优,最后对OpenFAST进行二次开发,进行风浪联合工况数值模拟,对惯容-TMD 的减振性能进行验证.

1 半潜式海上风力机-惯容-TMD 简化动力学模型

本研究选择IEA-OC4项目中的基准模型OC4-DeepCwind半潜式基础海上风力机作为研究对象.IEA-OC4是由国际能源署(IEA)牵头开发的项目,旨在验证各种漂浮式海上风力机分析工具的准确性.在OC4-DeepCwind模型中,由美国国家可再生能源实验室(NREL)设计的5 MW风力机被安装在半潜式浮式平台上,OC4-DeepCwind的各项参数^[20-21]如表1所示.

表1 半潜式海上风力机模型参数^[20-21]

Tab.1 Model parameters of semi-submersible offshore wind turbine^[20-21]

参数	取值
功率/MW	5
风轮,轮毂直径/m	126, 3
切入、额定、切出风速/(m·s^-1)	3, 11.4, 25
机舱尺寸/(m×m×m)	18× 6 × 6
风轮质量/kg	110 000
机舱质量/kg	240 000
风塔质量/kg	347 460
风塔惯性矩/(kg·m²)	2.721 8×10⁹
塔基(浮台顶部)标高/m	10
风力机塔顶标高/m	87.6
浮台吃水深度/m	20
平台质量(包括压载物)/kg	1.347 3×10⁷
浮台质心位置(基于海平面)/m	-13.46

新窗口打开| 下载CSV

1.1 简化模型的建立

在漂浮的海工结构中通常有纵荡(Surge)、横荡(Sway)、垂荡(Heave)、纵摇(Pitch)、横摇(Roll)和艏摇(Yaw)6个自由度的运动响应,其中与风浪方向平行的纵摇响应最大,也是漂浮式风力机振动的主要原因之一.而对于上部风力机结构,风力机塔筒变形位移(Tower Deflection)是风力机塔架振动的主要表现形式,也是引起塔基弯矩增大,导致风力机塔筒疲劳损伤的主要原因.

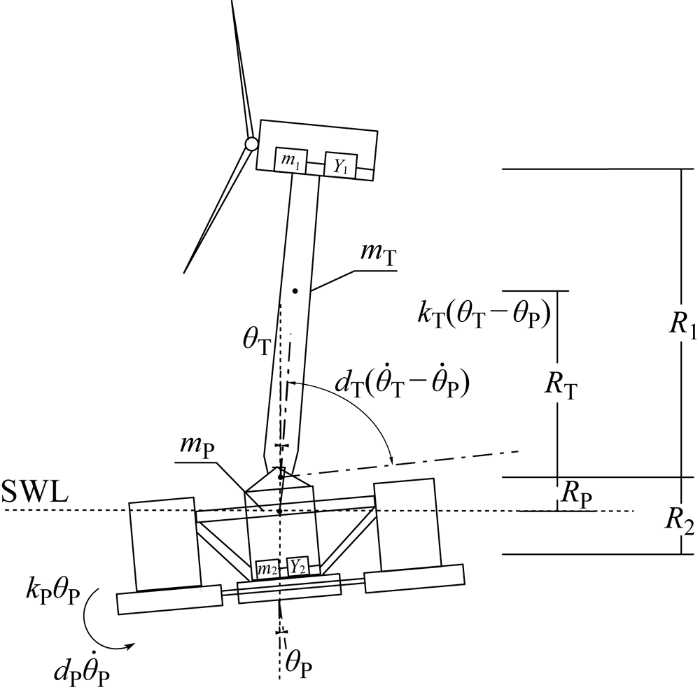
因此本文以半潜式海上风力机作为研究对象,建立包含风力机塔筒角度( ${\tilde{θ}}_{T}$ )、浮台的纵摇( ${\tilde{θ}}_{P}$ )、机舱结构减振器质量块运动位移(x₁)以及浮台结构减振器质量块运动位移(x₂)4个自由度的半潜式海上风力机动力学模型,如图1所示.图中:m_T、m_P、m₁和m₂分别为风塔、浮台、机舱减振装置和浮台减振装置的质量;R_T和R_P分别为风塔和浮台质心到风塔和浮台链接点的距离;R₁和R₂分别为机舱减振装置和浮台减振装置质量块质心到风塔和浮台链接点的距离;k_P和d_P分别为半潜式浮台纵摇的刚度和阻尼系数;k_T和d_T分别为塔筒前后变形的刚度和阻尼系数;θ_T和θ_P分别为风塔的角度和浮台的纵摇; ${\overset{\cdot}{θ}}_{T}$ 和 ${\overset{\cdot}{θ}}_{P}$ 分别为风塔角度和浮台纵摇的运动速度;Y₁和Y₂分别为m₁和m₂的传递函数;SWL为海平面.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 半潜式海上风力机简化动力学模型

Fig.1 Simplified model of semi-submersible offshore wind turbine

为了便于对不同类型结构减振装置的参数进行优化研究,本文以传递函数Y的形式表示不同结构形式的减振装置.其中拉普拉斯域中的传递函Y(s)如下所示:

(1)Y(s)=

\frac{F (s)}{Δ V (s)}

式中:F(s)为结构减振器的输出力;ΔV(s)是质量m与机舱或浮台之间的相对速度的变化量;s为拉普拉斯变换的复频率.例如,普通TMD的传递函数为Y(s)=k/s+c,表示一个刚度为k的弹簧和一个阻尼为c的阻尼器并联连接,而简单相互并联的惯容-TMD传递函数为Y(s)=k/s+c+bs,其中b为惯容器惯质系数.

根据达朗贝尔原理和小角度近似原则,4自由度的半潜式海上风力机-惯容-TMD动力学模型在拉普拉斯域的动力学方程如下:

(2)

\begin{array}{l} I_{T} {\tilde{θ}}_{T} (s) s^{2} = - (d_{T} s + k_{T}) ({\tilde{θ}}_{T} (s) - {\tilde{θ}}_{P} (s)) - \\ R_{1} Y_{1} (s) {\tilde{x}}_{1} (s) s + m_{1} {\tilde{g x}}_{1} (s) + \\ m_{T} g R_{T} {\tilde{θ}}_{T} (s) + M_{w i n d} \\ I_{P} {\tilde{θ}}_{P} (s) s^{2} = (d_{T} s + k_{T}) ({\tilde{θ}}_{T} (s) - {\tilde{θ}}_{P} (s)) + \\ R_{2} Y_{2} (s) {\tilde{x}}_{2} (s) s - m_{2} {\tilde{g x}}_{2} (s) - \\ (d_{P} s + k_{P}) {\tilde{θ}}_{P} (s) + M_{w a v e} - \\ m_{P} g R_{P} {\tilde{θ}}_{P} (s) \\ m_{1} {\tilde{x}}_{1} (s) s^{2} = m_{1} g {\tilde{θ}}_{T} (s) - Y_{1} (s) {\tilde{x}}_{1} (s) s - \\ m_{1} R_{1} {\tilde{θ}}_{T} (s) s^{2} \\ m_{2} {\tilde{x}}_{2} (s) s^{2} = m_{2} g {\tilde{θ}}_{P} (s) - Y_{2} (s) {\tilde{x}}_{2} (s) s - \\ m_{2} R_{2} {\tilde{θ}}_{P} (s) s^{2} \end{array}\}

式中:I_T和I_P分别为风塔和平台的惯性矩,下标T和P分别表示风塔和浮台;M_wind和M_wave分别是输入到半潜式海上风力机简化模型的风载荷和波浪力矩; ${\tilde{x}}_{1}$ 和 ${\tilde{x}}_{2}$ 分别为机舱和浮台减振装置的质量块位移;g为重力加速度.

为了得到准确的半潜式海上风力机动力学模型,首先需要确定模型参数.根据DeepCwind半潜式平台说明文件^[19]、NREL 5 MW标准风力机介绍书^[20]和OpenFAST的输入文件等参考资料, m_T、m_P、R_T、R_P等参数可由表1计算得出,而参数d_P、d_T、k_P、k_T和I_P则需利用MATLAB进行识别.

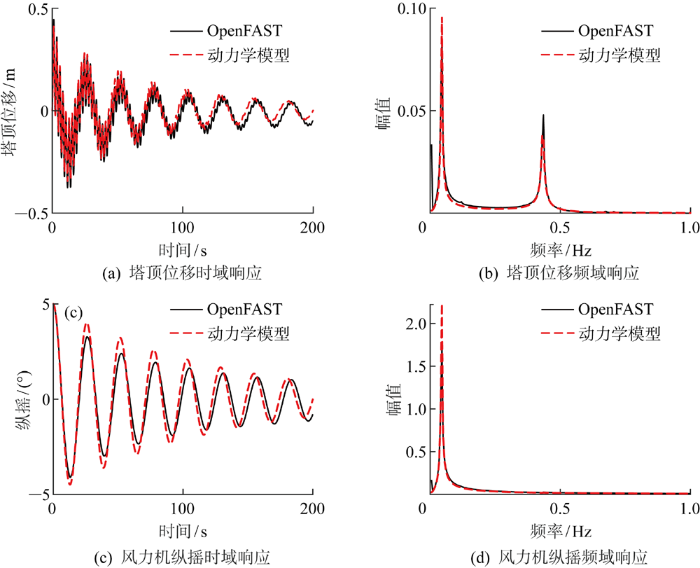
将OpenFAST中的OC4海上风力机模型浮台纵摇设置为5°,得到其自由衰减响应曲线,通过最小化OpenFAST输出的风塔前后变形响应与简化模型的风塔前后变形响应之间的均方根误差S,使用MATLAB中的Pattern Search算法对上述5个参数进行识别,得到相应的简化模型参数结果和拟合图分别如表2和图2所示,表3为半潜式风力机

表2 参数估算结果

Tab.2 Estimation results of parameter

类别	d_P/[N·(m· s^-1)^-1]	d_T/[N·(m· s^-1)^-1]	k_P/(N· m^-1)	k_T/(N·m^-1)	I_P/(kg·m²)
初始值	6.5×10⁸	2.0×10⁸	0.0	1.4×10¹⁰	3.0×10⁹
估计值	9.5×10⁸	1.2×10⁸	1.0	1.9×10¹⁰	4.2×10⁹

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 简化动力学模型时域和频域拟合结果

Fig.2 Fitting results of time and frequency domain of simplified dynamic model

表3 模型频率

Tab.3 Frequency of model

类别	简化模型频率/Hz	OpenFAST模型频率/Hz
纵摇	0.039	0.040
塔筒前后变形	0.422	0.420

新窗口打开| 下载CSV

海上风力机浮台纵摇和塔筒前后变形的频率.

均方根误差表示为

(3)S=

\sqrt{\overset{n}{\sum_{i = 1}} (X_{O, i} - X_{S, i})^{2} / n}

式中:n为数据总量;X_O_,i为OpenFAST输出的第i个结果;X_S_,i为简化动力学模型输出的第i个结果.

应该指出的是,最优惯容-TMD安装位置和参数也可通过由NREL开发的软件OpenFAST进行优化,但为了找到最优安装位置和最优参数,需要调用OpenFAST中数千个函数进行计算,这需要耗费大量的计算资源和时间成本.

1.2 风力机性能指标

风塔的变形位移是漂浮式海上风力机风塔振动的主要表现形式,而风塔的变形位移是导致风力机塔筒底部疲劳损伤的主要因素,因此,为了减小风力机塔筒疲劳损伤,将风塔变形位移大小的离散程度作为性能指标,目标函数定义如下:

(4)J₁=

{‖T_{M_{w i n d} \to (θ_{T} - θ_{P})}‖}_{2}

{‖T_{M_{w a v e} \to (θ_{T} - θ_{P})}‖}_{2}

式中:J₁为风、浪荷载输入对风塔变形位移的H₂范数之和; $T_{M_{w i n d} \to (θ_{T} - θ_{P})}$ 为风载荷引起风力机塔筒变形的传递函数; $T_{M_{w a v e} \to (θ_{T} - θ_{P})}$ 为波浪载荷引起风力机塔筒变形的传递函数.

同时,漂浮式海上风力机浮台的纵摇响应不仅关系着整个风力机的整体稳定,也是造成风塔变形,引起风塔振动的主要原因,为了进一步提升漂浮式风力机的稳定性和减小浮式风力机塔筒底部的最大弯矩,以减小浮台纵摇最值作为性能指标,目标函数定义如下:

(5)J₂=

{‖T_{M_{w i n d} \to θ_{P}}‖}_{\infty}

{‖T_{M_{w a v e} \to θ_{P}}‖}_{\infty}

式中:J₂为风、浪荷载输入对浮台纵摇的H_∞无穷范数之和; $T_{M_{w i n d} \to θ_{P}}$ 为风载荷引起风力机浮台纵摇的传递函数; $T_{M_{w a v e} \to θ_{P}}$ 为波浪载荷引起风力机浮台纵摇的传递函数.

2 TMD参数优化及其减振性能分析

为突出惯容-TMD的性能优势和达到最优的振动控制效果,本文利用半潜式海上风力机简化动力学模型研究TMD安装在风力机不同位置的减振性能,并应用粒子群算法(Particle Swarm Algorithm,PSO)对TMD的参数进行优化.相比于遗传算法,粒子群算法由于没有交叉和变异的运算过程,靠其粒子速度进行寻优,并在迭代过程中只传递最优值,优化速度更快,所以选择利用粒子群算法对TMD和惯容-TMD参数进行优化.TMD和惯容-TMD中各个参数的上下限设置为1 000~500 000,粒子群大小为20.

本文旨在研究TMD和惯容-TMD的减振性能对比,考虑到工程实际应用和简便,根据文献[3-4],将机舱TMD质量块质量选定为 20 t,与半潜式海上风力机风塔结构的质量比为3.04%,浮台TMD质量块质量选定为 200 t,与半潜式海上风力机浮台的质量比为1.48%,其中机舱TMD置于在机舱坐标系原点位置处,而浮台TMD置于浮台中轴线-30 m的底部.

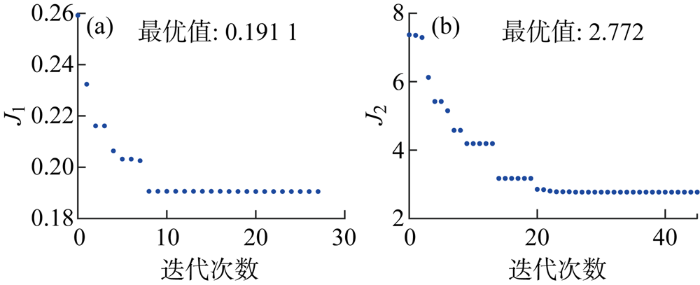
将风力机机舱TMD和浮台TMD传递函数代入半潜式海上风力机简化模型,分别以J₁和J₂为优化目标,利用粒子群优化算法对其中参数进行优化,以达到其对半潜式海上风力机最优的减振性能,粒子群优化算法的迭代过程如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 粒子群算法优化TMD参数迭代过程

Fig.3 PSO for optimizing iterative process of TMD parameters

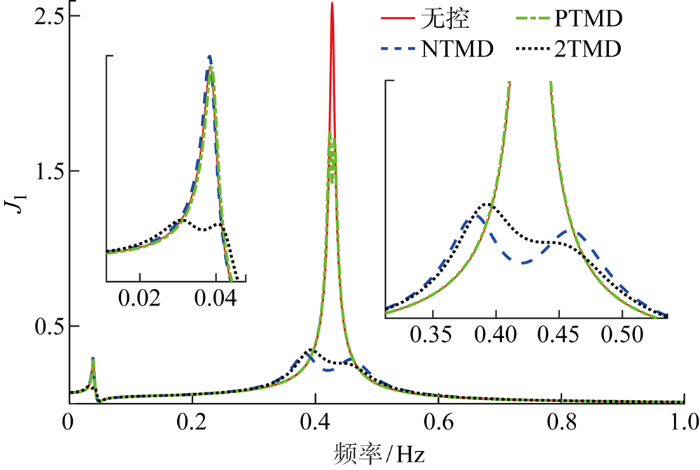
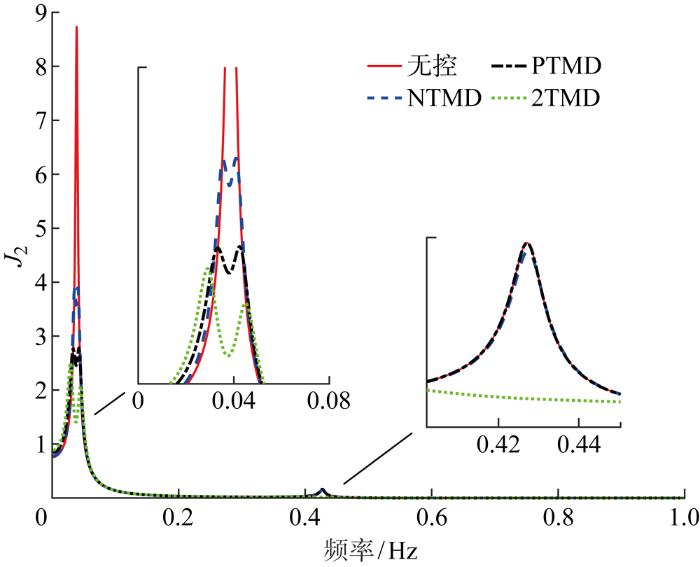
机舱TMD(NTMD)、浮台TMD(PTMD)以及双TMD(2TMD)的减振效果对比如图4和图5所示.可以看出,针对风力机塔筒的变形位移,相较于安装在浮台的TMD,TMD安装在机舱中减振效果更好;若要抑制漂浮式海上风力机风塔变形,在风力机机舱中安装结构减振装置是更理想的方法.然而基于TMD的减振机理,单个TMD只能对主结构某一特定频率进行有效的调谐.因此,利用双TMD的减振策略,在风力机浮台和机舱同时加入TMD,NTMD、PTMD和2TMD参数优化结果如表4所示.从优化结果来看,相较于单个浮台TMD和机舱TMD,无论是风力机塔筒的变形位移,还是风力机浮台的纵摇,2TMD的效果都要优于单个TMD,且2TMD还能同时抑制风力机的塔筒变形位移和浮台纵摇.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 NTMD、PTMD及2TMD对风塔变形位移抑制效果对比

Fig.4 Comparison of suppression performance of NTMD, PTMD, and 2TMD on the tower deflection

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 NTMD、PTMD及2TMD对浮台纵摇抑制效果对比

Fig.5 Comparison of suppression performance of NTMD, PTMD, and 2TMD on the pitch angle

表4 TMD参数优化结果

Tab.4 Optimization results of TMD parameters

类别	m/t	k/ (kN·m^-1)	c/[(kN· (m·s^-1)^-1]	J₁		J₁提升比例/%	J₂		J₂提升比例/%
类别	m/t	k/ (kN·m^-1)	c/[(kN· (m·s^-1)^-1]	无TMD	有TMD	J₁提升比例/%	无TMD	有TMD	J₂提升比例/%
NTMD	20	135 116	10 578	0.470	0.191	59.6	8.730	8.775	-0.5
	20	1 150	1 074	0.470	0.455	3.20	8.730	3.919	55.1
PTMD	200	1 434 100	8 899	0.470	0.411	12.8	8.730	8.656	0.8
	200	12 100	17 900	0.470	0.465	1.10	8.730	2.772	68.0
2TMD	20	139 200	13 700	0.470	0.187	60.2	8.730	2.702	69.1
	200	11 200	18 300

新窗口打开| 下载CSV

综合上述单TMD和2TMD参数优化的结果可知,相较于单个浮台TMD和单个机舱TMD分别只能对风力机浮台纵摇和风力机风塔变形位移表现出良好抑制效果,在风力机的机舱和浮台中均安装TMD的多TMD联合布置方式不仅可以同时对风力机风塔变形位移和浮台纵摇都进行良好抑制,且抑制效果还均优于单个TMD.

3 惯容-TMD拓扑结构优化

为了寻求更好更经济可行的减振策略,引入惯容器对TMD的减振性能和结构形式作进一步的改善,经过拓扑结构优化,提出一种最优的惯容-TMD组合形式,并给出其最优参数组合.

惯容器两端等大反向的力F与两端的相对加速度的比值b称为惯质系数,其理论控制方程为

(6)F=b(

{\ddot{x}}_{1}

{\ddot{x}}_{2}

)

式中: ${\ddot{x}}_{1}$ 和 ${\ddot{x}}_{2}$ 为惯容器两端加速度.

惯容器的出现突破了传统减振形式,为无源结构控制发展带来了新的契机.然而基于Hu等^[22]的研究,惯容器、弹簧和阻尼器之间的简单串并联组合对漂浮式海上风力机这类大型柔性结构的减振性能相比于TMD并没有明显的性能优势.因此,为了探究惯容器和TMD应该如何组合才能充分发挥惯容器的性能优势,本文从输出阻抗角度下系统分析整个减振系统设计空间结构的同时保证结构的可行性,并针对风力机不同的振动响应,得到惯容-TMD减振系统最优拓扑结构及其最优参数,确保在满足减振系统可行性的前提下保证所提出的惯容-TMD减振系统减振性能最优.

基于本课题组Zhang等^[23-24]提出的用于被动阻尼器拓扑结构优化的方法-结构阻抗法,可得到一组包含4个元件惯容-TMD所有拓扑结构可能性的结构阻抗函数.

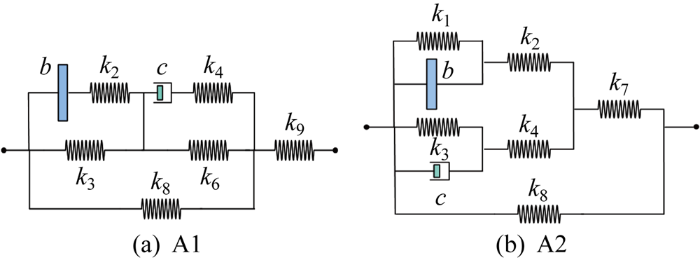
具体地,对于2个弹簧、1个阻尼器和1个惯容器的4元件惯容系统来说,理论上共有18种可能的惯容减振系统拓扑结构.通过结构推导,可以得到2个包含上述18种拓扑结构的通用网络,称为A1和A2,如图6所示.图中:k₁~k₉为弹性元件的刚度系数;A1网络和A2网络中需要满足最多只有2个弹性元件存在的条件,如当k₁和k₃均不为0和无穷大时,k₂和k₄~k₉必须为0或无穷大.

通用网络A1和A2对应的结构阻抗函数如下:

(7)Y_j(s)=

\frac{n_{j} (s)}{m_{j} (s)}

(j=1, 2)

(8)

\begin{array}{l} n_{1} (s) = b c (k_{3} / k_{2} + k_{8} / k_{2} + k_{6} / k_{4} + \\ k_{8} / k_{4} + 1) s^{3} + b (k_{6} + k_{8}) s^{2} + \\ c (k_{3} + k_{8}) s + k_{3} k_{8} + k_{6} k_{8} \\ m_{1} (s) = b c s (1 / k_{2} + 1 / k_{4} + 1 / k_{9}) s^{3} + \\ b s (k_{3} / k_{2} + k_{6} / k_{2} + k_{6} / k_{9} + \\ k_{8} / k_{9} + 1) s^{2} + c s (k_{3} / k_{4} + \\ k_{3} / k_{9} + k_{6} / k_{4} + k_{8} / k_{9} + 1) s + \\ k_{3} s + k_{6} s \\ n_{2} (s) = b c (1 / k_{2} + 1 / k_{4}) s^{3} + b (k_{3} / k_{2} + \\ k_{3} / k_{4} + k_{8} / k_{2} + k_{8} / k_{7} + 1) s^{2} + \\ k_{1} + k_{3} + k_{8} + c (k_{1} / k_{2} + k_{8} / k_{4} + \\ k_{1} / k_{4} + k_{8} / k_{7} + 1) s \\ m_{2} (s) = b c s [1 / (k_{2} k_{4}) + 1 / (k_{2} k_{7}) + \\ 1 / (k_{4} k_{7})] s^{3} + b s (1 / k_{2} + 1 / k_{7}) s^{2} \\ + c s (1 / k_{4} + 1 / k_{7}) + (k_{1} / k_{2} + \\ k_{1} / k_{7} + k_{3} / k_{4} + k_{3} / k_{8}) s \end{array}\}

式中:Y₁(s)和Y₂(s)包括2个弹簧、1个阻尼器和1个惯容器的所有可能组合.在Y₁(s)中, 1/k₂、 k₃、 1/k₄、 k₆、 k₈和1/k₉中只能存在2个是正的,其他则均为0或无穷大,同理,而在Y₂(s)中, k₁、 1/k₂、 k₃、 1/k₄、 1/k₇和k₈中也只能存在2个是正的,其他则都等于0或无穷大.通常把这个规定称为特定的约束条件.对于给定的系统和目标函数,这些传递函数可用于识别优化包含2个弹簧、1个阻尼器和1个惯容器的最佳拓扑结构及其最优参数.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 包含2个弹簧、1个阻尼器和1个惯容器的通用网络

Fig.6 Universal network of two springs, a damper, and an inerter

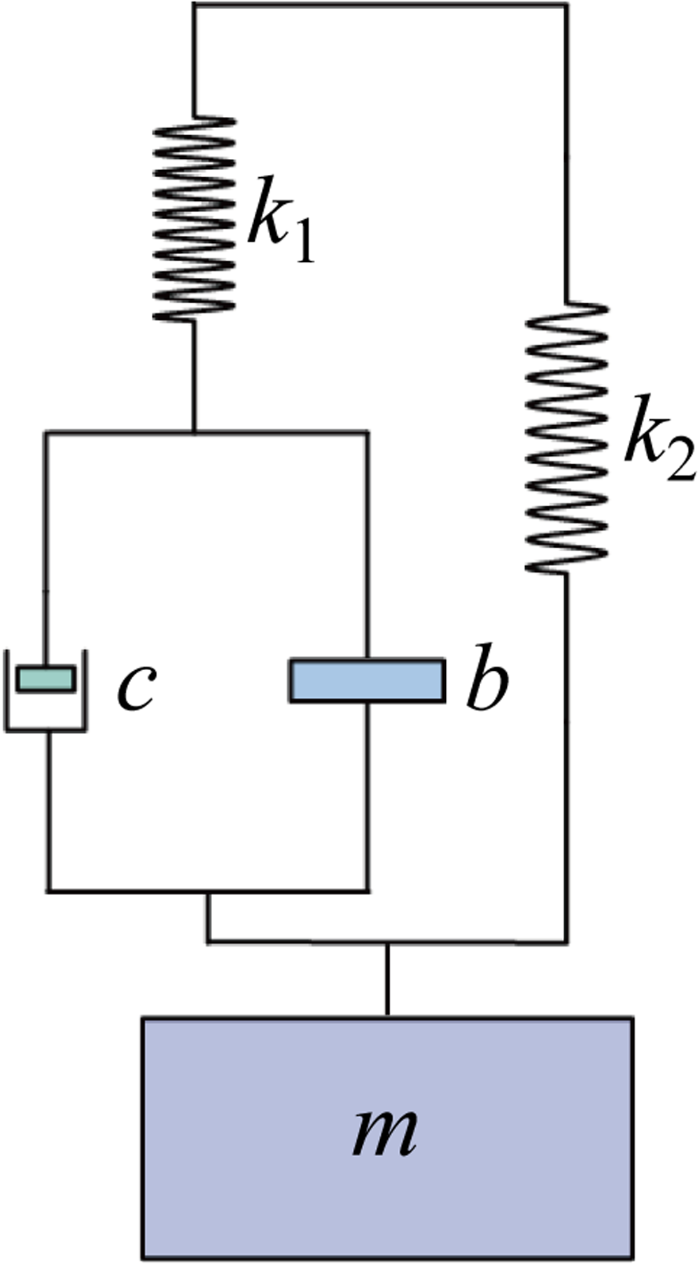
利用式(4)和(5)中定义的目标函数,采用结构阻抗方法在半潜式海上风力机简化模型中对包含4个元件(2弹簧、1阻尼器、1惯容器)的惯容系统进行了优化研究.经结构阻抗法对包含4个元件的IBA系统进行优化得到其最优的拓扑结构布局如图7所示,优化后的最优惯容-TMD传递函数如下:

(9)Y(s)=

\frac{(b k_{1} + b k_{2}) s^{2} + (c k_{1} + c k_{2}) s + k_{1} k_{2}}{b s^{3} + c s^{2} + k_{1} s}

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 4元件IBA拓扑结构优化结果

Fig.7 Optimization results of 4-element IBA topology

4 惯容-TMD的减振性能分析

为了研究本文所优化的惯容-TMD相比于TMD的性能提升,本节以在机舱和浮台同时安装TMD为对比对象,对IBA的参数进行优化,并对比分析2IBA相较于2TMD对半潜式海上风力机减振性能的提升.此外,基于惯容器的增益效益,对IBA的质量增益效果进行分析.

4.1 惯容-TMD参数优化及其性能提升

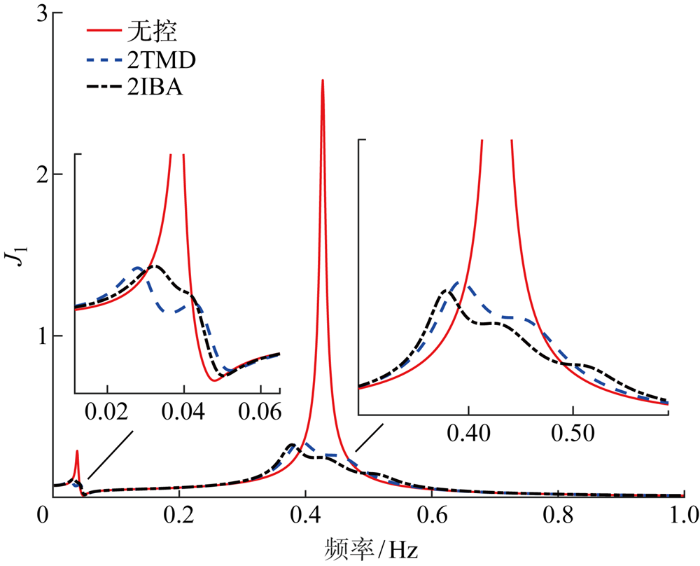
同理,利用粒子群算法对惯容-TMD参数进行优化,优化结果如表5所示.表中:NIBA为机舱惯容-TMD;PIBA为浮台惯容-TMD.2IBA相较于2TMD分别将风塔变形位移J₁和浮台纵摇J₂进一步提升了4.3%和5.3%.图8和图9为风力机机舱和浮台同时放置TMD或惯容-TMD时的风塔变形位移和浮台纵摇频响对比图,从图中可以看出,风塔变形位移和浮台纵摇响应的模态频率均被TMD分解为两个小波峰,而惯容-TMD则可将风塔变形位移响应的模态频率进一步分成3个小波峰,拥有更宽的减振频带,且相比于普通TMD,惯容-TMD结构减振器拥有进一步调节结构的某一特定频率的能力,其效果均优于普通TMD.

表5 2TMD和2IBA优化结果

Tab.5 Optimization results of 2TMD and 2IBA

类别		m/t	k/ (kN·m^-1)	k₁/ (kN·m^-1)	k₂/ (kN·m^-1)	c/[(kN· (m·s^-1)^-1]	b/kg	J₁	J₂
2TMD	NTMD	20	139.2	—	—	13.7	—	0.187	2.702
	PTMD	200	11.2	—	—	18.3	—
2IBA	NIBA	20	—	13.7	142.3	1.68	1 602.5	0.179	2.560
	PIBA	200	—	7.9	8.5	30.4	3 471.4

新窗口打开| 下载CSV

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 2TMD和2IBA对风塔变形位移抑制效果对比

Fig.8 Comparison of suppression performance of 2TMD and 2IBA on the tower deflection

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 2TMD和2IBA对浮台纵摇抑制效果对比

Fig.9 Comparison of suppression performance of 2TMD and 2IBA on the pitch angle

4.2 惯容-TMD质量增益效果分析

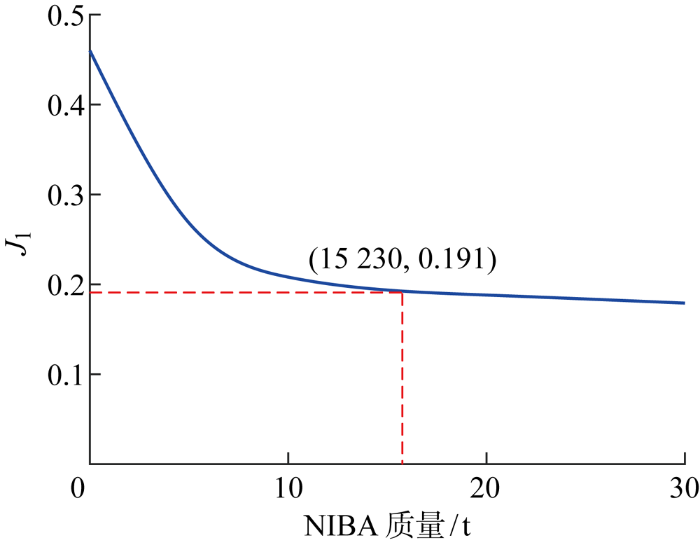
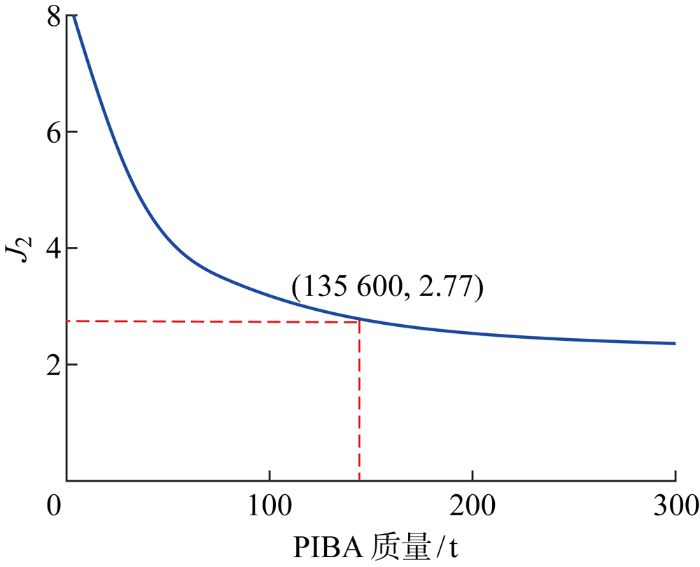
值得注意的是,惯容器的显著优点是其质量增益作用,为了更直观地表明惯容-TMD相较于TMD的经济优势,本节研究了惯容-TMD质量元件的质量值与其减振性能的关系.一般来说,减振性能的改进会随着惯容-TMD质量元件质量的增加而增加,但在这种趋势中可以看到其收益是递减的.图10与图11显示了性能指标J₁和J₂与惯容-TMD质量值之间的关系.结果表明,达到最优机舱TMD相同减振性能的机舱IBA(NIBA)的质量值为15.23 t,相较于最优机舱TMD减少了23.9%,此时NIBA的k₁=7.673 kN/m,k₂=102.011 kN/m,c=0.940 kN/(m·s^-1),b=991 kg.而若要达到与最优浮台TMD(PTMD) 相同的性能,浮台IBA(PIBA)的质量值为135.6 t,比最优浮台TMD减少了32.2%,此时PIBA的最佳参数值为k₁=2.060 kN/m,k₂=6.524 kN/m,c=7.391 kN/(m· s^-1),b=30.034 t.在达到最优TMD相同减振性能的情况下,NIBA和PIBA分别可将结构减振器中质量元件的质量减少23.9%和32.2%,大幅降低装置成本.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 NIBA质量值与其减振性能关系

Fig.10 Relationship between NIBA mass value and suppression performance

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 PIBA质量值与其减振性能关系

Fig.11 Relationship between PIBA mass value and suppression performance

5 数值分析与验证

为了评估TMD和惯容-TMD在半潜式海上风力机上的减振性能,有必要进行风浪联合数值模拟,进一步验证上述优化所获结论.

对于评估TMD在真实海况上对海上风力机的减振性能,Lackner等^[3]在最新版的OpenFAST3.0中将之前版本FAST_V8中的TMD模块整合成了Structural Control模块,并在其中新增了调谐液柱阻尼器(TLCD)模型,研究人员可在OpenFAST中使用不同种类的结构减振器和针对海上风力机不同位置安装结构减振器的耦合模拟.为了验证IBA对漂浮式海上风力机在风浪联合作用下的减振性能,本文对OpenFAST3.0中的Structural Control模块进行了二次开发,使其能够进行半潜式海上风力机-IBA的耦合模拟.

根据IBA的性质,定义Y'(s)为力f(s)到加速度Δa(s)的传递函数:

(10)Y'(s)=

\frac{Y (s)}{s}

\frac{f (s)}{Δ a (s)}

对于被动结构减振器,Y'(s)总是正实数,因此它可以写成如下的非唯一正则状态空间方程形式:

(11)Y'(s)=C(sI-A)^-1B+d

式中:A、B、C和d分别为分别是系统状态系数矩阵Rⁿ^×ⁿ、系统状态控制矩阵Rⁿ^×1、系统状态输出矩阵R^1×ⁿ和前馈值,而内部状态变量 $\overset{\cdot}{ω}$ ∈Rⁿ^×1和输出力f如下:

(12)

\overset{\cdot}{ω}

=Aω+

{\ddot{B x}}_{I B A}

(13)f=Cω+

{\ddot{d x}}_{I B A}

(14)

\overset{\cdot}{f}

\overset{\cdot}{ω}

{\overset{\dots}{d x}}_{I B A}

=C(Aω+

{\ddot{B x}}_{I B A}

{\overset{\dots}{d x}}_{I B A}

式中:x_IBA是IBA质量块元件的位移; ${\ddot{x}}_{I B A}$ 则是其相应的加速度.

在OpenFAST-Structural Control模块中的StrucCtrl.f90文件里,TMD振动控制模块被编译为状态空间方程,并利用四阶龙格-库塔方法进行求解.根据Li等^[19]和Stewart等^[25-26]的研究,OpenFAST中TMD模块的运动方程如下:

(15)m_TMD

{\ddot{x}}_{T M D}

-m_TMD(

{\overset{\cdot}{ω}}_{P 1}^{2}

{\overset{\cdot}{ω}}_{P 2}^{2}

)x_TMD+ k_TMDx_TMD+c_TMD

{\overset{\cdot}{x}}_{T M D}

= m_TMDg+m_TMD

{\ddot{x}}_{P}

+f_stop+f_ext

式中:m_TMD、k_TMD、c_TMD分别为TMD的质量、刚度和阻尼;x_TMD为TMD质量块相对于初始位置的位移; ${\ddot{x}}_{P}$ 为质量块随风力机全局坐标系运动的加速度;f_stop为停止力;f_ext 为用户自定的外力; ${\overset{\cdot}{ω}}_{P 1}$ 和 ${\overset{\cdot}{ω}}_{P 2}$ 为转动速度.

现引入包含惯容器的传递函数,将式(15)改写为

(16)m_IBA

{\ddot{x}}_{I B A}

-m_IBA(

{\overset{\cdot}{ω}}_{P 1}^{2}

{\overset{\cdot}{ω}}_{P 2}^{2}

)x_IBA+Y'(s)

{\ddot{x}}_{I B A}

= m_IBAg-m_IBA

{\ddot{x}}_{P}

+f_stop+f_ext

根据式(10)可知,Y'(s) ${\ddot{x}}_{I B A}$ 为IBA系统输出力f,式(16)可改写为

(17)m_IBA

{\ddot{x}}_{I B A}

-m_IBA(

{\overset{\cdot}{ω}}_{P 1}^{2}

{\overset{\cdot}{ω}}_{P 2}^{2}

)x_IBA+C(A∫ω +

{\overset{\cdot}{B x}}_{I B A}

{\ddot{d x}}_{I B A}

=m_IBAg-m_IBA

{\ddot{x}}_{P}

+f_stop+f_ext

设M_IBA=m_IBA+d;K_IBA=-m_IBA( ${\overset{\cdot}{ω}}_{P 1}^{2}$ + ${\overset{\cdot}{ω}}_{P 2}^{2}$ ); C_IBA=CB;U∈R^1×ⁿ为输入向量.式(17)可整理得:

(18)M_IBA

{\ddot{x}}_{I B A}

+C_IBA

{\ddot{x}}_{I B A}

+K_IBAx_IBA+CA∫ω = m_IBAg-m_IBA

{\ddot{x}}_{P}

+f_stop+f_ext

令B₁U=m_IBAg-m_IBA ${\ddot{x}}_{P}$ +f_stop+f_ext,故整个IBA运动方程可在时域中以状态空间方程形式表述:

(19)

\overset{\cdot}{X}

=A_IBAX+B_IBAUX=

(\begin{array}{l} {\ddot{x}}_{I B A} \\ x_{I B A} \\ \int ω \end{array})

A_IBA=

(\begin{array}{l} - M_{I B A}^{- 1} C_{I B A} & - M_{I B A}^{- 1} K_{I B A} & - M_{I B A}^{- 1} C A \\ 1 & 0 & 0 \\ B & 0 & A \end{array})

B_IBA=

(\begin{array}{l} - M_{I B A}^{- 1} B_{1} \\ 0 \\ 0 \end{array})

基于上述公式,整个IBA系统的传递函数在时域内被重写为状态空间方程形式,而在基于Fortran语言的OpenFAST-Structural Control模块中TMD也是基于状态空间方程形式所编译的,因此,不同传递函数的IBA系统都可以被编译到基于Fortran语言所开发的OpenFAST-Structural Control模块中,实现IBA-OpenFAST的耦合数值模拟.

最后将传递函数Y(s)设置为普通TMD形式,即Y(s)=k/s+c,通过在编译的OpenFAST-IBA-V3.0和原版OpenFAST-V3.0运行相同的工况得到的TMD质量块行程一致,从而验证了其正确性,运行结果如图12所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同OpenFAST版本输出的TMD行程

Fig.12 TMD stroke for output of different OpenFAST versions

根据规范IEC 61400-1^[27],选取5种风浪荷载工况对TMD和IBA的减振效果进行综合评估.其中波浪谱是由OpenFAST中HydroDyn模块所生成的JONSWAP随机波浪谱,而风谱则是由TurbSim软件生成的KAIMAL湍流风风谱.5种工况如表6所示,其中工况1~4为风力机正常运行工况,工况5为风力机风暴停机的极端工况.值得注意的是,在进行极端工况模拟时需在OpenFAST中关闭风力发电机的转动自由度,并将叶片浆距角设置为90°,每次模拟持续630 s,省略前30 s数据以保证发电机转矩和叶片运动处于正常运行状态.

表6 风浪荷载工况

Tab.6 Load cases

工况编号	风速/ (m·s^-1)	湍流强度/%	有效波高/m	波谱周期/s
1	8	16.0	1.31	5.67
2	12	14.6	1.70	5.88
3	16	13.9	2.19	6.37
4	20	13.4	2.76	6.99
5	41.5	11.7	4.90	9.43

新窗口打开| 下载CSV

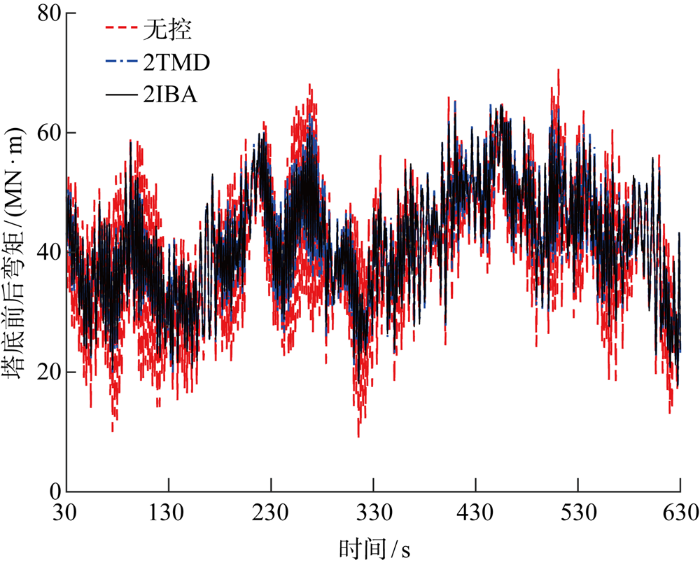
表7为风力机各个工况下塔底前后弯矩和塔底侧向弯矩的标准差和最大值,图13为工况1下塔底前后弯矩的时域图.可以看出,在低风浪的工况1情况下,2TMD可使塔底前后弯矩和塔底侧向弯矩的标准差降低16.82%和54.80%,最大值分别降低7.65%和41.82%,而2IBA对塔底前后弯矩和塔底侧向弯矩的标准差抑制效果进一步提升至18.86%和59.39%,最大值抑制效果进一步提升至8.53%和43.10%,TMD和惯容-TMD在低风浪工况下均表现出良好的减振性能.但随着波浪工况越来越高,波浪荷载所引起的半潜式海上风力机的低频运动难以抑制,结构减振装置对风力机的低频运动(如纵摇)的抑制性能也随之转弱.

表7 风力机塔基弯矩标准差和最大值

Tab.7 Standard deviation and maximum value of tower base bending moment

工况	塔底前后弯矩最大值/(kN·m)			塔底侧向弯矩最大值/(kN·m)			塔底前后弯矩标准差/(kN·m)			塔底侧向弯矩标准差/(kN·m)
工况	无控	2TMD	2IBA	无控	2TMD	2IBA	无控	2TMD	2IBA	无控	2TMD	2IBA
1	70 679	65 273	64 648	13 787	8 021	7 844	10 993	9 144	8 920	3 088	1 395	1 254
2	99 725	101 712	101 037	13 228	12 572	12 789	12 155	12 273	12 289	2 068	1 741	1 745
3	88 950	94 178	94 132	16 771	14 967	14 945	12 986	13 124	13 130	2 403	2 101	2 100
4	87 679	93 941	93 018	21 057	18 120	18 043	13 831	14 052	14 046	3 483	2 834	2 808
5	114 155	115 743	113 147	53 659	43 393	41 439	20 293	20 196	20 123	12 926	9 613	9 427

新窗口打开| 下载CSV

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 工况1塔底前后弯矩的时域图

Fig.13 Time domain diagram of fore-aft tower base load of Case 1

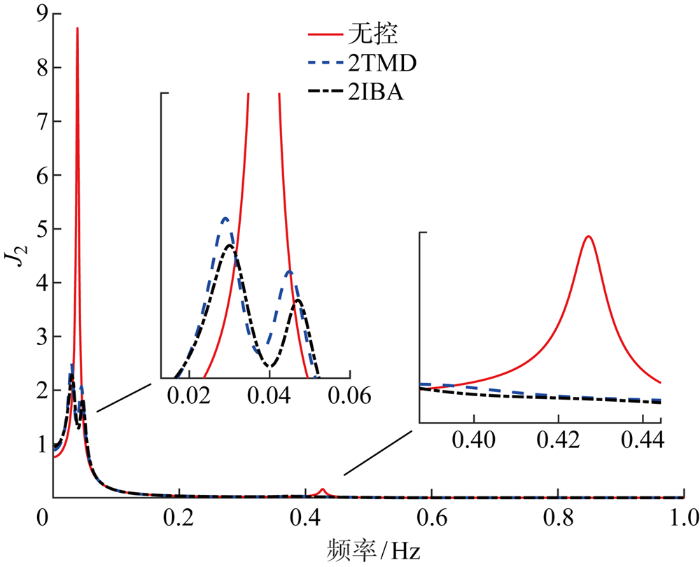
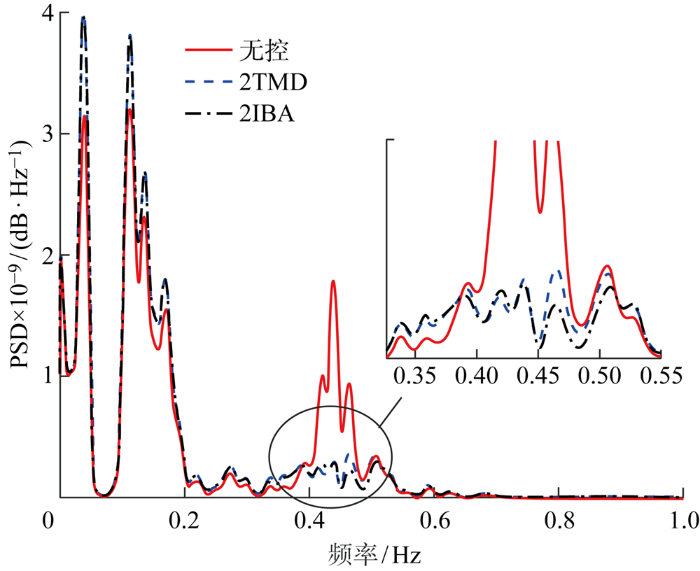
图14为极端工况下塔底前后弯矩的功率谱密度图(Power Spectral Density,PSD),极端工况下2TMD和2IBA减振性能分析如表8所示.可以看出在极端工况下,2IBA对塔顶前后变形位移的最大值相较于2TMD提升了2.65%,抑制率为 0.47%,2TMD抑制率为 -2.24%,此外,2IBA对频域响应的塔顶前后和侧向变形位移的功率谱密度相较于2TMD分别提升了16.86%和18.14%,抑制率分别为83.01%和80.32%.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 工况5塔底前后弯矩频域图

Fig.14 Frequency domain diagram of fore-aft tower base load of Case 5

表8 极端工况(工况5)分析

Tab.8 Analysis of extreme conditions (Case 5)

分析类型	参数	无TMD/IBA	2TMD (抑制率)		2IBA (抑制率)
时域分析	塔顶前后变形位移最大值/m	0.596 9	0.610 3	(-2.24%)	0.594 1	(0.47%)
	塔顶侧向变形位移最大值/m	0.294 8	0.245 8	(16.62%)	0.235 3	(20.18%)
	塔底前后弯矩最大值/(kN·m)	114 155	115 743	(-1.39%)	113 147	(0.88%)
	塔底侧向弯矩最大值/(kN·m)	53 660	43 394	(19.13%)	41 439	(22.77%)
频域分析 (0.4~0.6 Hz)	塔顶前后变形位移功率谱密度/(dB·Hz^-1)	0.053 62	0.010 96	(79.56%)	0.009 112	(83.01%)
	塔顶侧向变形位移功率谱密度/(dB·Hz^-1)	0.059 61	0.014 33	(75.96%)	0.011 73	(80.32%)
	塔底前后弯矩功率谱密度/(dB·Hz^-1)	1.798×10⁹	3.766×10⁸	(79.05%)	3.081×10⁸	(82.86%)
	塔底侧向弯矩功率谱密度/(dB·Hz^-1)	2.043×10⁹	4.897×10⁸	(76.03%)	4.028×10⁸	(80.28%)

新窗口打开| 下载CSV

值得注意的是,对于极端工况,由于风浪频率占据了风力机振动的主要成分,而TMD及惯容-TMD的减振效果与系统响应谱的成分构成和能量分布特征密切相关,风力机浮台纵摇响应中存在显著的波浪激励频率成分(非固有频率成分),导致减振效果变弱,但对于固有频率振动占比较大的情况(风塔振动),其减振效果依然显著.

6 结论

以半潜式海上风力机为研究对象,本文提出一种多元件惯容-TMD减振策略及其综合优化设计方法,且为了寻求最优的振动控制效果,对TMD安装位置进行了研究,最后采用二次开发后的OpenFAST软件,验证风浪联合作用下最优惯容-TMD相对于TMD减振性能的提升,结论如下:

(1) 相比于单个惯容-TMD的减振策略,双惯容-TMD的减振策略能同时对半潜式海上风力机浮台和风塔振动响应进行有效抑制,且其减振效果有进一步的提升.

(2) 基于传递函数分析结果表明:相较于最优参数的2TMD,最优参数的2IBA分别将半潜式海上风力机风塔变形位移标准差和风力机纵摇最大值的抑制率分别提升了4.3%和5.3%,即同等附加质量的情况下,惯容-TMD的减振性能要优于TMD.

(3) 基于惯容器的质量增益效应,达到最优TMD相同减振性能所需的附加质量值明显减小,最优机舱IBA的附加质量值可减少23.9%,最优浮台IBA的附加质量值可减少32.2%,附加质量值大幅减少,使得其在漂浮式海上风力机上的工程应用成为可能.

(4) 在基于OpenFAST软件风浪联合作用数值模拟的验证下,通过简化模型优化所得结论与数值模拟所得结果一致,经结构阻抗法优化所得最优拓扑结构形式的惯容-TMD对比普通TMD的减振性能有明显的提升.

(5) 根据数值模拟结果显示,TMD和惯容-TMD在低风浪工况下均表现出良好的减振性能,对于极端工况,风浪频率占据了风力机振动的主要成分,而TMD及惯容-TMD的减振效果与系统响应谱的成分构成和能量分布特征密切相关,风力机浮台纵摇响应中存在显著的波浪激励频率成分(非固有频率成分),导致减振效果变弱,但对于固有频率振动占比较大的情况(风塔振动),其减振效果显著.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[5]

, KARIMI

H R

, GAO

Modelling and optimization of a passive structural control design for a spar-type floating wind turbine

[J]. Engineering Structures, 2014, 69: 168-182.