在国家战略“双碳”目标下,构建以新能源为主体的新型电力系统成为能源电力行业共同奋进的方向[1 ] .风光等新能源存在随机波动性,为解决其出力波动对电力系统运行的影响,据北极星储能网报道,国家及地方于2021年陆续出台相关政策,规定新增风电光伏场站需要配套建设10%~20%左右的储能.因此,储能将成为许多新能源场站的有机整体.
目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式.
然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论.
综上可见,目前针对跟网或构网同构型电源的暂态稳定机理与稳定性定量分析问题都有较为明晰的研究方法和结论.然而,针对跟-构网暂态交互作用下的暂态交互与瞬时频率稳定问题,虽有一些初步研究成果,但在分析中均进行了大量简化,比如未考虑电流幅值以及故障穿越下电流控制策略切换的影响,导致所得频率失稳机理难以有效指导工程实际;另外,研究中较多依赖定性分析和特定参数下的数值求解,缺少对于失稳物理过程的揭示.因此,贴合实际的异构电源系统暂态交互机理仍待深入研究,这对于指导并形成含储能的异构型风电场暂态控制方法具有理论和实际意义.
以集成构网型储能的跟网型风电场为研究对象,探索异构电源系统电网短路故障下瞬时频率交互机理及其影响因素.首先,建立含跟网型风电机组和构网型储能的异构型风电场的暂态分析模型;然后,根据上述模型揭示该异构电源系统在电网短路故障下的瞬时频率交互机理,发现了故障期间具有较慢功角动态的构网型电源对具有较快功角动态的跟网型电源的“频率牵引效应”,以及在满足频率牵引条件下后者对于前者的“功角联合驱动效应”;其次,分别分析参数变化与故障穿越控制方式对所揭示暂态频率交互机理的影响;最后,通过MATLAB/Simulink仿真详细验证了所提机理及相应结论.
1 含构网型储能的异构型风电场的暂态分析建模
1.1 含构网型储能的异构型风电场的系统拓扑
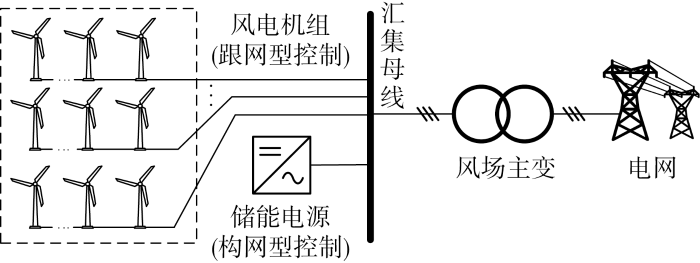
含构网型储能电源的异构型风电场拓扑如图1 所示,该新能源场站部分在现有风电场的基础上增加了储能电源,与风场馈线一同连接至汇集母线上,再经过风场主变压器升压至高压,连接至大电网.储能电源可以兼做无功补偿,因此站内可以不再设置无功补偿装置.
图1
图1
含构网型储能的异构型风电场拓扑结构
Fig.1
Topological structure of heterogeneous windfarms with grid-forming energy storage
风电机组均采用全功率型(Type-4)风力发电机,网侧变换器采用经典跟网型控制,外环控制目标为直流侧电压.储能电源的拓扑一般为多台低压分布式储能或集中式高压直挂储能[19 ] ,前者一般采用两电平或三电平拓扑,后者则采用模块化拓扑结构,可节省交流变压器.
1.2 含构网型储能的异构型风电场的暂态分析模型
1.2.1 跟网型控制的全功率风电机组的暂态稳定分析建模
采用跟网型控制的全功率风电机组建模方法较为成熟,目前普遍采用受控电流源代替变换器的特性,且在暂态稳定性分析中一般只保留锁相环的动态[20 ] .如图2 所示.图中:ω pll 为锁相环角频率;ω n 为额定角频率.锁相环的动态方程为
(1) δ · p l l = k p U c q + x i n t x · i n t = k i U c q
式中:δ pll =θ pll -θ g 为锁相环相对于电网电压的角度,其中θ pll 为锁相环输出的角度,θ g 为电网电压的角度;x int 为锁相环积分器的输出;U c q U c e - j θ p l l ) 为并网点电压相量U c 在锁相环参考系下的电压q 轴分量; k p 、k i 为锁相环的PI控制器参数.受控电流源输出的电流相量为
(2) Ic =(Ic d +jIc q ) e j θ p l l
式中:I c d I c q d 轴和q 轴电流.由于电流环控制的时间尺度一般在数毫秒内,锁相环的时间尺度往往在几十毫秒以上,所以在暂态稳定性分析中通常假设变换器的输出电流等于其参考值[12 ] ,而变换器的参考值由外环控制器提供.
图2
图2
跟网型控制的全功率风电机组的暂态稳定分析模型
Fig.2
Modeling of full-capacity wind turbine with grid-following control for transient stability analysis
1.2.2 构网型控制的储能电源的暂态稳定分析建模
对于采用构网型控制的储能电源而言,由于构网型控制实现方式众多,目前尚无模型对构网型控制进行统一表征[21 ] ,所以采用典型的虚拟同步控制,控制框图如图3 所示.其中,功率同步环对于暂态过程中的功角摇摆起重要作用,其动态方程为
(3) δ · v = ω v 2 H ω · v = ( P r e f - P v ) - D ω v
图3
图3
采用虚拟同步控制的构网型储能电源的暂态稳定分析模型
Fig.3
Modeling of grid-forming battery energy storage system using virtual synchronous control for transient stability analysis
式中:δ v =θ v -θ pll 为储能的内电势功角,其中θ v 为构网型储能的电压相角;H 为惯量时间常数;ω v 为构网型储能的角频率;P ref 为有功功率参考值;P v 为构网型储能的有功功率;D 为有功频率下垂系数.在功角运动的时间尺度内,认为电流内环的控制到达稳态.当电流指令I v, cmd 未到达限幅值时,满足如下关系[22 ] :
(4) Iv =Iv, cmd = Z v - 1 v )
式中:I v 为购网型储能的输出电流;Z v =R v +jX v 为虚拟阻抗的大小,其中R v 、X v 分别为购网型储能控制环节中的虚拟电阻、虚拟电抗;E 为内电势;U v 为储能的并网点电压. 当电流指令到达限幅值后,由于采用dq 轴平均限幅的电流限幅器只改变电流矢量幅值而不改变相位,所以电流限幅器相当于一个增益环节[22 ] . 假该缩放比例为k ,则有
(5) I v =k -1 I v , cmd =(kZ v )-1 (E -U v )
这表明在电流指令超过最大限幅值时,电流限幅器的作用相当于将虚拟阻抗Z v 增大至kZ v ,这样就能得到基于虚拟同步控制的储能电源的等效电路模型[22 ] ,如图3 所示.图中:s 为拉普拉斯算子;E 为内电势幅值;p.u.表示标幺值.该模型不仅体现了对功角运动起主导作用的功率同步环动态,而且将虚拟阻抗及电流限幅的影响考虑在内.正常情况下,电流指令值一般不会到达饱和值,此时有k =1;而当电网电压较低或者功角与电网偏差过大时,电流指令将会到达饱和,此时有k >1.
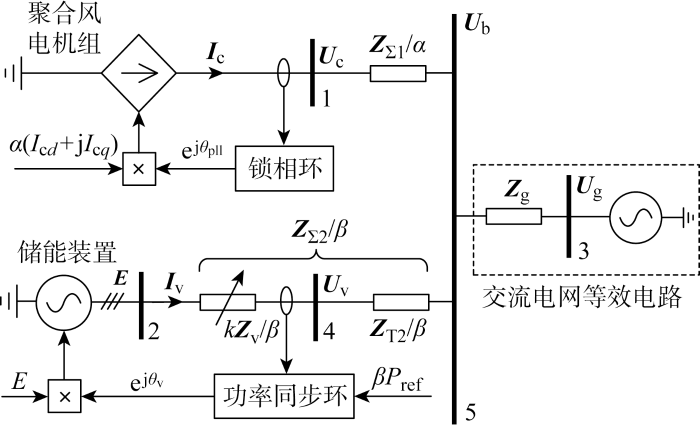
1.2.3 异构系统的暂态分析等效模型
异构控制风储联合新能源场站的暂态稳定性分析等效模型如图4 所示,跟网型风电场和构网型储能电源的等效电路分别用上述受控电流源和受控电压源表示.图中:1~5为母线编号;U b 为母线电压;Z g 为电网阻抗;U g 为电网电压.为了简化分析,将整个风电场聚合为单台风电机组进行建模.Z Σ1 表示风电机组升压变与风场内网的聚合阻抗之和,由于升压变的漏抗远大于线路阻抗,故Z Σ1 略大于风电机组升压变的漏抗大小.Z Σ2 =kZ v +Z T2 表示储能电源的虚拟内电势到风场汇集母线的阻抗大小,其中Z T2 表示分布式储能的升压变漏抗,如果采用高压直挂储能,则Z T2 =0.此外,考虑风电机组并网发电率即风电开机率为α ,储能的装机容量与风电总装机容量的比值为β ,则有
(6) α= S W T , o n S W F S B E S S S W F
图4
图4
异构控制风储联合新能源场站的暂态稳定性分析等效模型
Fig.4
Equivalent model of heterogeneous windfarm for transient stability analysis
式中:S WT, on 为并网的风电机组容量;S WF 为风电场的总装机容量;S BESS 为储能的装机容量.为了在同一功率基准下进行定量分析,图4 中的阻抗、电流及有功参考值从每台电源自身的标幺值重新缩放至以风电总装机容量为基准功率的标幺值下.此外,为了便于计算,假设所有阻抗均为感性,即Z =jX ,X 为感抗.先得到该系统的节点导纳矩阵,再利用Kron消元法消去母线4和5,可以得到降维节点导纳矩阵的表达式:
(7) $\begin{aligned} \boldsymbol{Y}= & \frac{1}{\mathrm{j}}\left[\begin{array}{lll} Y_{\mathrm{cc}} & Y_{\mathrm{cv}} & Y_{\mathrm{cg}} \\ Y_{\mathrm{vc}} & Y_{\mathrm{vv}} & Y_{\mathrm{vg}} \\ Y_{\mathrm{gc}} & Y_{\mathrm{gv}} & Y_{\mathrm{gg}} \end{array}\right]= \\ & \frac{\mathrm{j}\left(X_{1} X_{2}+X_{1} X_{\mathrm{g}}+X_{2} X_{\mathrm{g}}\right)}{} \times \\ & {\left[\begin{array}{ccc} X_{2}+X_{\mathrm{g}} & -X_{\mathrm{g}} & -X_{2} \\ -X_{\mathrm{g}} & X_{1}+X_{\mathrm{g}} & -X_{1} \\ -X_{2} & -X_{1} & X_{1}+X_{2} \end{array}\right] } \end{aligned}$
式中:Yxy , x , y ∈[c, v, g]表示节点x 和y 之间的自导纳(x =y )和互导纳(x ≠y ),c、v、g分别表示跟网型风电机组节点、构网型储能节点、电网节点.X 1 =X Σ1 /α ,X 2 =X Σ2 /β ,X Σ1 、X Σ2 分别表示Z Σ1 、Z Σ2 的感性部分. 对应的节点导纳关系满足I =YU ,其中电流向量I =[I c I v I g ]T ,I g 为电网节点电流;电压向量U =[U c E U g ]T .由此可以推导出风电机组和储能节点的电流表达式:
(8) I c = Y c c U c + Y c v E + Y c g U g I v = Y v c U c + Y v v E + Y v g U g
根据式(8),跟网型电源节点处的电压表达式可以进一步推导为
(9) $\begin{array}{r} \boldsymbol{U}_{\mathrm{c}}=\boldsymbol{Y}_{\mathrm{cc}}^{-1} \boldsymbol{I}_{\mathrm{c}}-\boldsymbol{Y}_{\mathrm{c}-1}^{-1} \boldsymbol{Y}_{\mathrm{cv}} \boldsymbol{E}-\boldsymbol{Y}_{\mathrm{cc}}^{-1} \boldsymbol{Y}_{\mathrm{cg}} \boldsymbol{U}_{\mathrm{g}}= \\ \mathrm{j} Y_{\mathrm{cc}}^{-1} \boldsymbol{I}_{\mathrm{c}}-Y_{\mathrm{cc}}^{-1} Y_{\mathrm{cv}} \boldsymbol{E}-Y_{\mathrm{cc}}^{-1} Y_{\mathrm{cg}} \boldsymbol{U}_{\mathrm{g}}= \\ \mathrm{j} Y_{\mathrm{cc}}^{-1} \boldsymbol{I}_{\mathrm{c}}+\frac{X_{\mathrm{g}}}{X_{2}+X_{\mathrm{g}}} \boldsymbol{E}+\frac{X_{2}}{X_{2}+X_{\mathrm{g}}} \boldsymbol{U}_{\mathrm{g}} \end{array}$
式中:Y c c - 1 X 1 X 2 + X 1 X g + X 2 X g X 2 + X g X g 为电网阻抗的虚部.
(10) $\begin{array}{l} \boldsymbol{E}=E \mathrm{e}^{\mathrm{j} \theta_{\mathrm{v}}}, \quad \boldsymbol{U}_{\mathrm{g}}=U_{\mathrm{g}} \mathrm{e}^{\mathrm{j} \theta_{\mathrm{g}}} \\ \boldsymbol{I}_{\mathrm{c}}=\alpha\left(I_{\mathrm{cd}}+\mathrm{j} I_{\mathrm{cq}}\right) \mathrm{e}^{\mathrm{j}\left(\theta_{\mathrm{pll}}+\varphi_{\mathrm{c}}\right)} \end{array}$
式中:U g 为电网电压幅值;θ g 为电网角度;φ c 为电流相角.将式(9)进行旋转坐标变化,并代入上述电压和电流表达式,可得
(11) $\begin{array}{l} \boldsymbol{U}_{\mathrm{c}} \mathrm{e}^{-\mathrm{j} \theta_{\mathrm{pll}}}=\mathrm{j} Y_{\mathrm{cc}}^{-1} \alpha\left(I_{\mathrm{cd}}+\mathrm{j} I_{\mathrm{cq}}\right) \mathrm{e}^{\mathrm{j} \varphi_{\mathrm{c}}}+ \\ \quad \frac{X_{\mathrm{g}}}{X_{2}+X_{\mathrm{g}}} E \mathrm{e}^{\mathrm{j}\left(\delta_{\mathrm{v}}-\delta_{\mathrm{plll}}\right)}+\frac{X_{2}}{X_{2}+X_{\mathrm{g}}} U_{\mathrm{g}} \mathrm{e}^{-\mathrm{j} \hat{\mathrm{o}}_{\mathrm{pll}}} \end{array}$
(12) $\begin{aligned} U_{\mathrm{cq}}= & \operatorname{lm}\left(\boldsymbol{U}_{\mathrm{c}} \mathrm{e}^{-\mathrm{j} \theta_{\mathrm{pll}}}\right)=\alpha Y_{\mathrm{cc}}^{-1} I_{\mathrm{cd}}- \\ & \lambda E \sin \left(\delta_{\mathrm{pll}}-\delta_{\mathrm{v}}\right)-(1-\lambda) U_{\mathrm{g}} \sin \delta_{\mathrm{pll}} \end{aligned}$
另一方面,根据式(8)~(10),可以得到储能电源输出的有功功率:
(13) $\begin{aligned} P_{\mathrm{v}}= & \operatorname{Re}\left(\boldsymbol{U}_{\mathrm{v}} \boldsymbol{I}_{\mathrm{v}}^{*}\right)= \\ & \operatorname{Re}\left\{U _ { \mathrm { v } } \mathrm { e } ^ { \mathrm { j } \delta _ { \mathrm { v } } } \left[Y_{\mathrm{vc}} Y_{\mathrm{cc}}^{-1} \alpha\left(I_{\mathrm{cd}}+\mathrm{j} I_{\mathrm{cq}}\right) \mathrm{e}^{-\mathrm{j}\left(\delta_{\mathrm{pll}}+\varphi_{\mathrm{c}}\right)}-\right.\right. \\ & \mathrm{j}\left(Y_{\mathrm{vc}} Y_{\mathrm{cc}}^{-1} Y_{\mathrm{cv}}-Y_{\mathrm{vv}}\right) E \mathrm{e}^{-\mathrm{j} \delta_{\mathrm{v}}}- \\ & \left.\left.\mathrm{j}\left(Y_{\mathrm{vc}} Y_{\mathrm{cc}}^{-1} Y_{\mathrm{cg}}-Y_{\mathrm{vg}}\right) U_{\mathrm{g}} \mathrm{e}^{-\mathrm{j} \delta_{\mathrm{g}}}\right]\right\}= \\ & \alpha E Y_{\mathrm{vc}} Y_{\mathrm{cc}}^{-1}\left(I_{\mathrm{cd}}+\mathrm{j} I_{\mathrm{cq}}\right) \cos \left(\delta_{\mathrm{v}}-\delta_{\mathrm{pll}}-\varphi_{\mathrm{c}}\right)+ \\ & E\left(Y_{\mathrm{vc}} Y_{\mathrm{cc}}^{-1} Y_{\mathrm{cg}}-Y_{\mathrm{vg}}\right) U_{\mathrm{g}} \sin \delta_{\mathrm{v}}= \\ & E U_{\mathrm{g}} Y_{\mathrm{vg}}^{\prime} \sin \delta_{\mathrm{v}}-\alpha \lambda E I_{\mathrm{cd}} \cos \left(\delta_{\mathrm{v}}-\delta_{\mathrm{pll}}\right)- \\ & \alpha \lambda E I_{\mathrm{cq}} \sin \left(\delta_{\mathrm{v}}-\delta_{\mathrm{pll}}\right) \end{aligned}$
式中:δ g 为电网电压矢量的角度;Y' vg =Y vc Y c c - 1 Y cg -Y vg =(X 2 +X g )-1 .
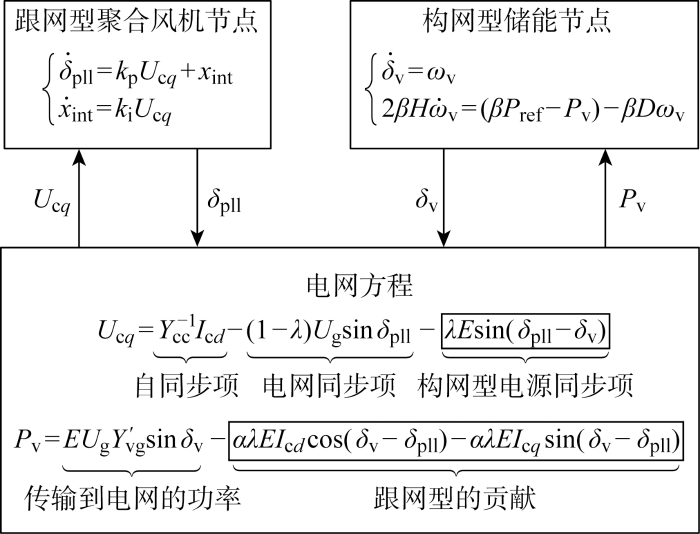
将方程式(1)、式(3)、式(12)、式(13)联立,即可得到异构系统在暂态分析中的总方程,如图5 所示.由图可见,跟网型电源锁相环的驱动力包含3个部分,其中自同步项和电网同步项是单台跟网型电源所固有驱动力,λE sin(δ pll -δ v )则代表构网型电源对跟网型电源锁相环频率驱动的影响;构网型电源同步环的驱动力包括固有的参考值P ref 、阻尼项Dω v 以及与电网交互的功率P v ,其中P v 不仅包含传输到电网的功率,还包含与跟网型电源之间的功率交互.当电网发生严重故障后,两个电源与电网电压之间的交互基本跌落至零,彼此通过上述耦合项产生频率交互行为.
图5
图5
面向暂态稳定性分析的异构控制风储联合新能源场站系统动力学方程
Fig.5
Dynamic equation of heterogeneous windfarm for transient stability analysis
2 电网故障期间异构电源系统的频率交互机制
根据以往的认知,一旦电网发生严重故障,系统将不存在静态工作点,风电机组的锁相环和储能电源的功率同步环将不可避免地出现转子加速现象.由于锁相环的时间尺度远远快于功率同步环,所以锁相环的频率加速度远远大于后者,从而导致异构系统的电源频率出现分离[11 ] .然而,本节内容将揭示,即使当系统不存在平衡点,但满足一定条件时,跟网型风电机组的锁相环频率能够被构网型储能牵引,从而使异构系统的电源频率在故障期间保持一致,即实现整场站在频率牵引作用下的同步运行.
2.1 频率牵引机制分析
2.1.1 牵引机制分析
对于平衡点不存在的情况,假设发生三相短路故障,故障时电网的戴维南等效电压U g =0,此时式(12)可以写为
(14) Uc q =α Y c c - 1 c d -λEsin(δpll -δv )
当λ 越大,故障期间跟网型电源越有可能同步到构网型电源上.根据式(14),跟网型满足静态稳定的条件为
(15) α Y c c - 1 I c d λ E α I c d Y c v E
(16) $\begin{aligned} Y_{\mathrm{cv}}= & \frac{X_{\mathrm{g}}}{X_{1} X_{2}+X_{1} X_{\mathrm{g}}+X_{2} X_{\mathrm{g}}}= \\ & \frac{\alpha \beta X_{\mathrm{g}}}{X_{\Sigma 1} X_{\Sigma 2}+\beta X_{\Sigma 1} X_{\mathrm{g}}+\alpha X_{\Sigma 2} X_{\mathrm{g}}} \end{aligned}$
(17) $\begin{array}{l} \left|I_{\mathrm{cd}}\right| \leqslant I_{\mathrm{cd}, \mathrm{cr}}= \\ \quad\left|\frac{\beta X_{\mathrm{g}} E}{X_{\Sigma 1} X_{\Sigma 2}+\left(\beta X_{\Sigma 1}+\alpha X_{\Sigma 2}\right) X_{\mathrm{g}}}\right| \end{array}$
式(17)的物理意义为:如果跟网型风机所注入的d 轴电流不大于临界值I c d ,cr ,即使电网电压跌落为0,锁相环依然可以通过锁住构网型电源的电压相位来使自身存在静态工作点.这表明构网型储能在电网低电压期间对跟网型风电机组的锁相环频率起到牵引作用,该牵引作用取决于式(17)是否成立,同时还取决于故障期间的状态是否在稳定域内.
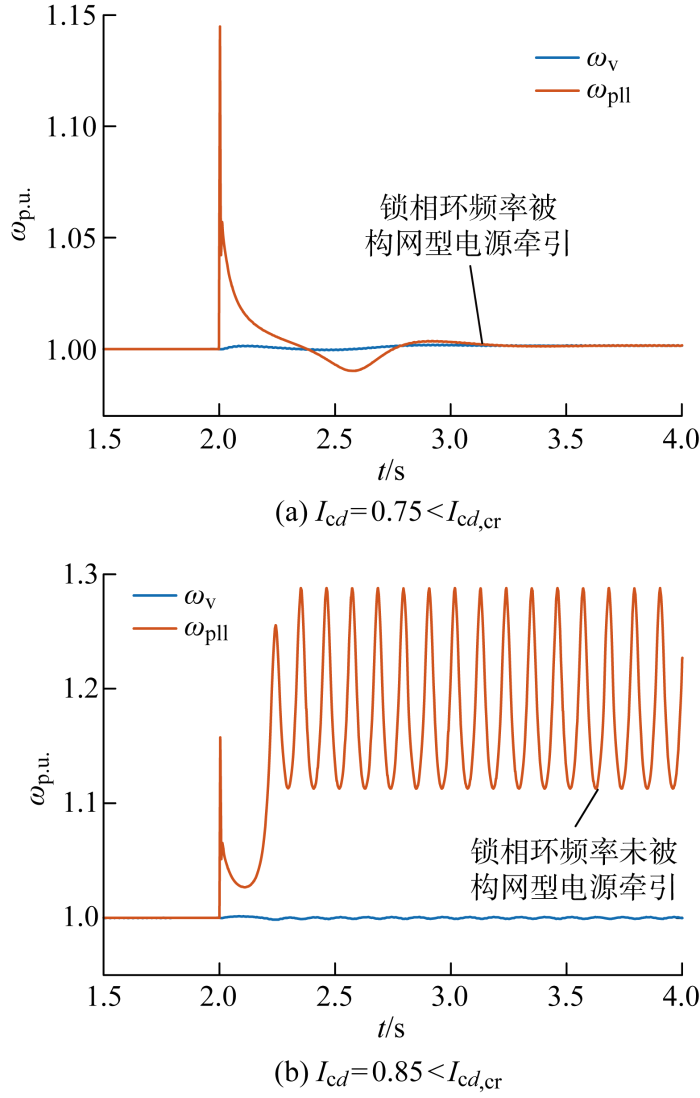
(18) X Σ 1 p . u . = 0.1 , X Σ 2 p . u . = 0.3 , X g p . u . = 0.4 α = 50 % , β = 20 % , E p . u . = 1.0
根据式(17)可以计算得到I c d , c r p . u . I c d I c d , cr 和I c d I c d , cr ,设置t =2 s时电网电压为0,仿真结果如图6 所示.可以看出当跟网型电源的d 轴电流小于临界值时,锁相环的频率能够被构网型电源牵引,尽管此时电网电压为0,但跟网型电源的频率依然不会发散;而当d 轴电流大于临界值时,构网型电源不足以牵引跟网型电源的频率,从而体现为跟网型电源的频率发散.为了便于观察,在仿真中对锁相环的PI控制器设置积分限幅,从而限制频率发散的幅度.
图6
图6
频率牵引效应的时域仿真分析
Fig.6
Simulation waveforms of frequency pinning effect
2.1.2 参数影响分析
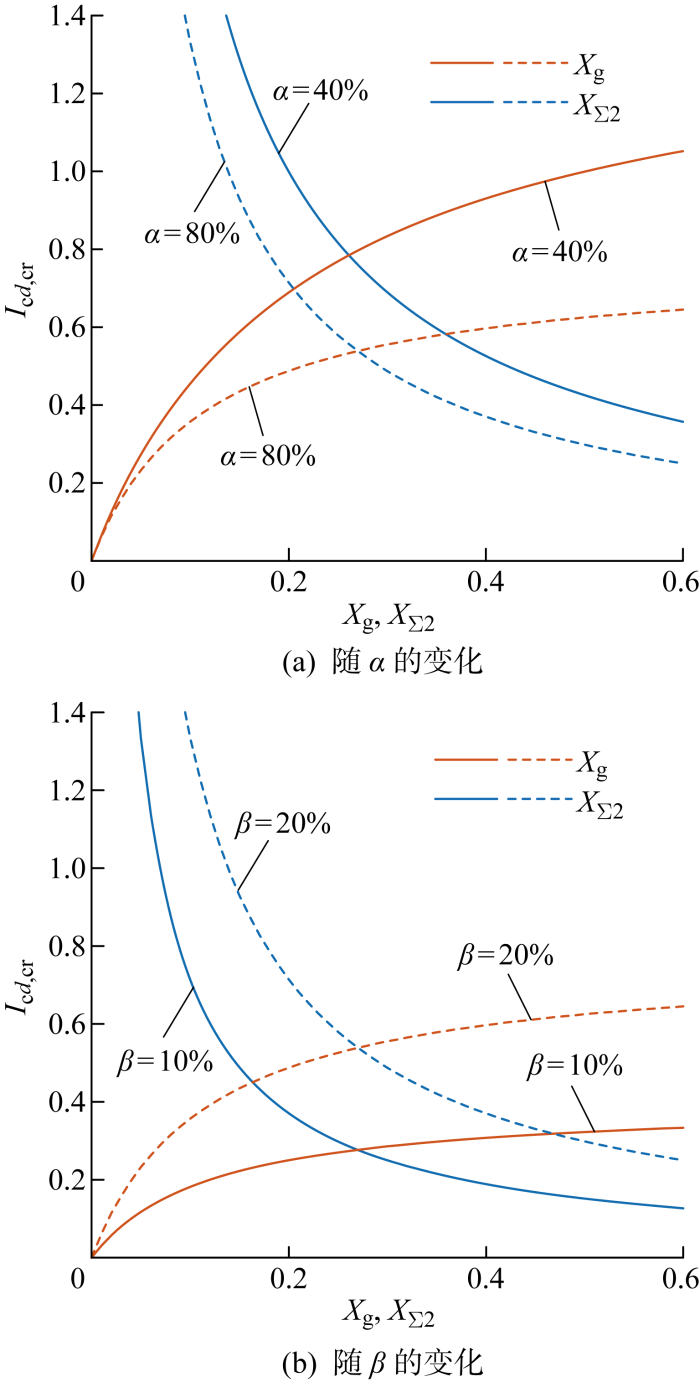
进一步分析关键参数对于频率牵引效应的影响.分别改变X Σ2 和X g 的大小,选取不同风电并网比例α 和储能装机容量β 代入式(17)中得到I c d , cr 的大小,结果如图7 所示.可以看出I c d , cr 随电网阻抗X g 的增大而增大,这是因为公共连接点(point of common coupling, PCC)电压在较大的等效电网阻抗下比较高,有利于构网型电源对跟网型电源起到频率牵引作用;I c d , cr 随构网型电源到PCC的阻抗X Σ2 的增大而减小,这是因为X Σ2 增加会导致跟网型和构网型两个电源之间的电气距离增大,从而减弱了频率牵引效应.此外,I c d , cr 随着风电机组并网率α 增大而降低,这是因为α 增大会提升风场整体d 轴电流;I c d , cr 随着构网型储能的容量占比β 增大而增大,这是因为构网型储能的容量增大后,等效阻抗X Σ2 /β 将减小,从而使得跟网型电源更容易同步到构网型电源的电压上.
图7
图7
临界d轴电流随参数变化的影响
Fig.7
Parametric investigation of critical d -axis current
2.2 跟网对构网频率的驱动机制
分析跟网型电源对构网型电源频率的联合驱动作用.令故障期间电网电压U g =0,且假设式(17)成立,则有λE sin(δ pll -δ v )=α Y c c - 1 I c d
(19) Pv =- α λ 2 E 2 - ( α Y c c - 1 I c d ) 2 - α 2 I c q Y c c - 1 c d
(20) δ · v = ω v 2 H ω · v = P r e f + P v / β - D ω v
根据式(20),令ω · v
(21) $\begin{array}{l} \omega_{\mathrm{v} 0}=\frac{1}{D}\left(P_{\mathrm{ref}}-\frac{P_{\mathrm{v}}}{\beta}\right)=\frac{1}{D}\left[P_{\mathrm{ref}}+\right. \\ \\ \left.\quad \frac{1}{\beta}\left(\alpha \sqrt{\lambda^{2} E^{2}-\left(\alpha Y_{\mathrm{cc}}^{-1} I_{\mathrm{c} d}\right)^{2}}-\alpha^{2} I_{\mathrm{cq}} Y_{\mathrm{cc}}^{-1}\right) I_{\mathrm{cd}}\right] \end{array}$
为了验证以上推导的正确性,在式(18)参数的基础上,进一步设置:
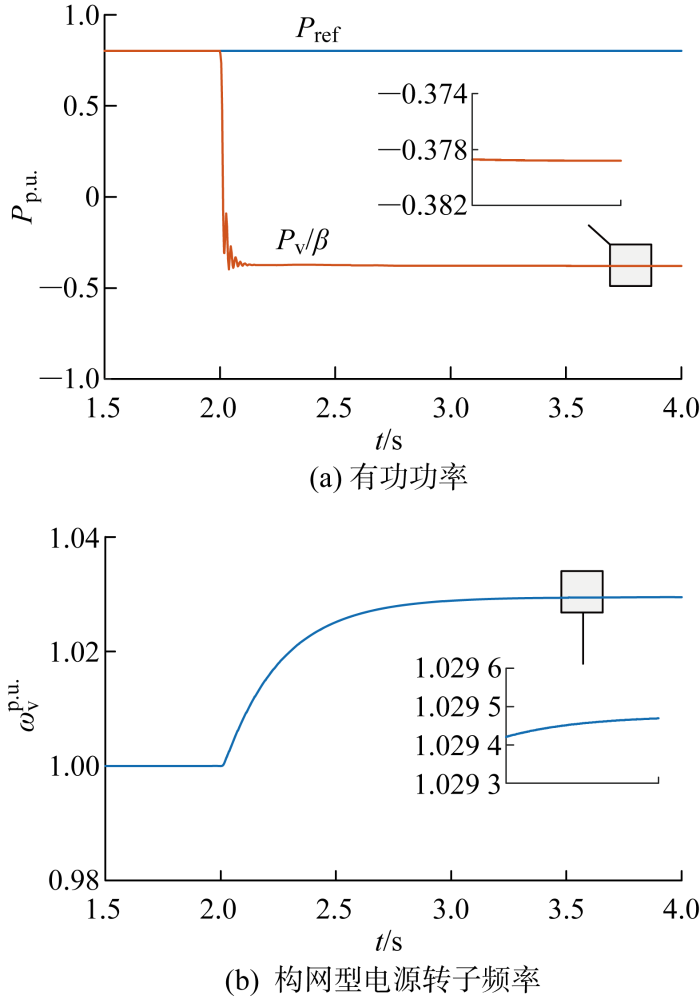
(22) D = 40 , P r e f = 0.8 I c q = - 0.5 , I c d = 0.5
计算得到P v /β =-0. 369,ω v0 =1. 029 2. 设置与2. 1节同样的故障,仿真波形如图8 所示. 由图可见,P v /β =-0. 379,ω v0 =1. 029 5,与理论值均比较接近,由此证明理论分析正确性.
图8
图8
功角联合驱动机制仿真
Fig.8
Simulation waveform of rotor angle co-driving effect
(23) F=βPref + α λ 2 E 2 - ( α Y c c - 1 I c d ) 2 - α 2 I c q Y c c - 1 c d
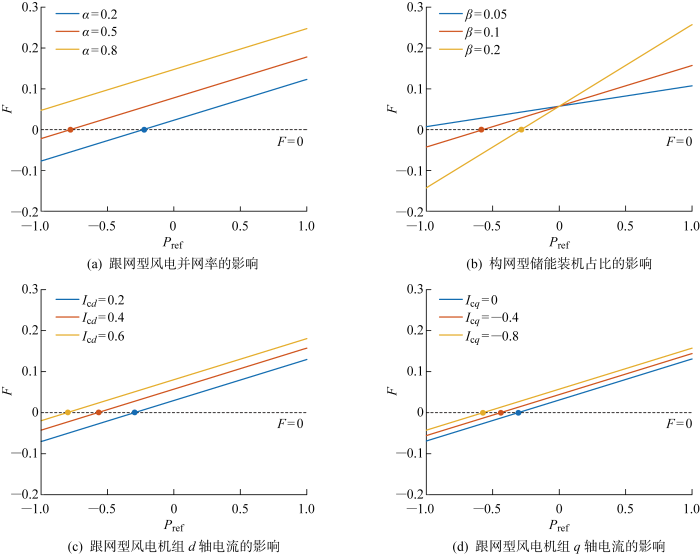
从式(20)中可以看出,在电网低电压期间,跟网型电源会向构网型电源倒灌有功功率,有可能进一步造成构网型电源频率加速,从而引发其功角失稳.如果F >0,那么构网型电源频率将在故障期间增加,且d 轴电流越大、感性无功电流即负的I c q F <0,那么构网型电源频率将在故障期间减小;如果F =0,则构网型电源的功角在故障期间恰好保持不变.一般而言,希望构网型电源频率尽可能保持静止,且考虑到通常有I c d P ref <0来抵消频率加速.
以α =0. 4, β =0. 1, I c d . 4, I c q . 8为初始参数,以P ref 为横坐标变量,同时改变相应参数的大小,可以得到如图9 所示的功角驱动力F 的曲线.可以看出,F =0所对应的P ref 值均小于0,这说明只有设置构网型储能的有功参考值小于0即吸功率状态,才能抵消跟网型电源注入有功对功角运动的影响.当风电并网比例α 到达80%时,在 P ref ∈[-1, 1]区间内不存在F =0,这说明如果风电并网率过高的话,储能电源可能无法完全吸收跟网型风电机组所发出的有功功率;而当储能的装机占比β 低至5%时,在P ref ∈[-1, 1]区间内也不存在满足F =0,这说明如果储能的占比过低,储能电源也无法完全吸收跟网型风电机组所发出的有功功率;此外,增大d 轴电流或注入更多感性q 轴电流,均需要构网型储能吸收更多有功功率,相应地也需要设置更大的负有功参考值.
图9
图9
功角驱动力F随参数变化的影响
Fig.9
Parametric investigation of equivalent driving force F
2.3 故障穿越控制的影响分析
2.3.1 跟网型风机的动态无功电流注入影响
在故障期间,风电机组的网侧变换器需要依照国家标准向电网提供动态无功电流,剩余容量用来传输有功电流,在《风电场接入电力系统设计技术规定——第1部分:陆上风电》(GB/T 19963.1—2021)中其相应的表达式为
(24) $\begin{array}{l} I_{\mathrm{cq}, \mathrm{ref}}=-K\left(0.9-U_{\mathrm{c}}\right) \\ I_{\mathrm{cd}, \mathrm{ref}}=\min \left\{I_{\mathrm{cd}, \mathrm{cmd}}, \sqrt{I_{\mathrm{lim}}^{2}-I_{\mathrm{cq}, \mathrm{ref}}^{2}}\right\} \end{array}$
式中:I c q , ref 、I c d , ref 分别为从外环传递过来的q 、d 轴电流参考值;K 为动态无功电流注入系数;U c 为并网点电压幅值; I c d , cmd 为从外环传递过来的d 轴电流指令值;I lim 为跟网型风电机组的电流限幅值.通常而言,当电网发生严重故障时,由于功率送出受限,功率全部积累在风电机组变换器的直流侧,导致直流侧电压上升,所以需要通过卸荷电路将直流电压标幺值控制在1.1左右.在这种情况下,直流电压控制器始终处于最大饱和限幅状态,即I c d , c m d p . u . q 轴无功电流,那么所有电流容量均用来输出d 轴有功电流,根据前文分析,此时风电机组的频率很可能在严重电网故障期间持续增大,从而导致暂态同步失稳;如果风电机组在故障期间向电网提供q 轴无功电流,那么d 轴有功电流的参考值会相应减少,从而有利于达到频率牵引条件,即式(17). 此外,动态无功电流注入的K 系数越大,那么所注入的q 轴电流越多,从而导致故障期间d 轴电流的参考值越低,系统越容易达到频率牵引条件.
2.3.2 构网型储能的电流限幅的影响
基于电力电子变换器的构网型储能电源在故障期间存在过流风险,因此必须在控制中采用电流限幅策略以防止发生长期过电流.根据1.2.2节的分析,一旦构网型电源输出的电流到达限幅值,其电流限幅环节作用相当于增大了虚拟阻抗Z v 的大小,此时有k >1.由方程式X Σ2 =kZ v +Z T2 可得,虚拟阻抗增大会进一步导致X Σ2 增大,即构网型变换器与PCC点之间的等价电气距离增加,跟网型风电机组电源与构网型储能电源之间的耦合将会减弱,故频率牵引机制和功角联合驱动机制均会减弱.电流限幅值设置得越小,则k 值越大,从而导致X Σ2 越大;而根据图7 ,X Σ2 越大则I c d , cr 越小,频率牵引条件越不容易达到,从而增大风电机组锁相环在故障期间失稳的风险.以上分析说明,构网型储能的电流限幅会减弱构网型储能对风电机组的频率牵引效应,且电流限幅值越小,频率牵引效应越弱.
3 仿真验证
3.1 仿真场景与工况设置
为验证以上分析的正确性,在 MATLAB/Simulink 中搭建风电装机容量为100 MW的异构风电场模型,场站的基本架构见图1 ,其中风电机组采用等值聚合模型.仿真依然采用式(18)中的参数 β =20%;风电机组在正常运行时的出力标幺值为0.5,储能在正常时的有功设定值为P r e f p . u . 表1 所示.表中: I max 为储能电源的电流限幅值;t flt,dur 为故障持续时间;P ref,flt 为故障期间储能电源的有功功率参考值;空白表示不适用.
所有算例在仿真时间t =2.0 s时电网电压跌落至0,算例1~4的故障持续时间较长,以充分观察故障异构系统在故障期间的频率交互机理;算例 5~6的故障持续时间为0.5 s,以分析故障期间的频率交互机制对故障后系统的影响.
3.2 算例分析
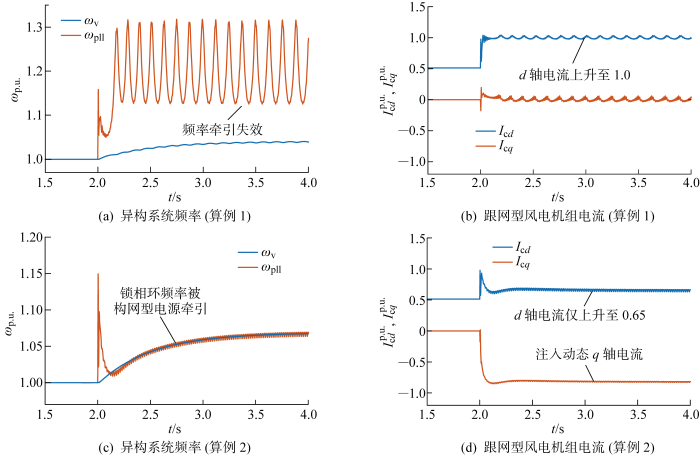
首先,在不考虑构网型储能电源电流限幅的情况下,利用算例1和算例2验证风电机组动态无功电流注入的影响.如图10 所示,在算例1不注入动态无功电流的情况下,风电机组的频率ω pll 不能被储能电源成功牵引住,如图10(a) 所示;而在算例2中,当风电机组注入了动态无功电流时,锁相环的频率能够被成功牵引住,如图10(c) 所示.这是因为在故障期间,直流电压控制回路出现饱和,d 轴电流的参考值到达最大值1.0 p.u.,如图10(b) 所示,超过了临界d 轴电流,从而使得频率牵引失效;而一旦注入动态无功电流即q 轴电流,根据式(24),d 轴电流会相应减小,如图10(d) 所示,从而使得锁相环频率被成功牵引.图中:ω 为角频率.
图10
图10
动态无功电流注入的影响
Fig.10
Impact of dynamic reactive current injection
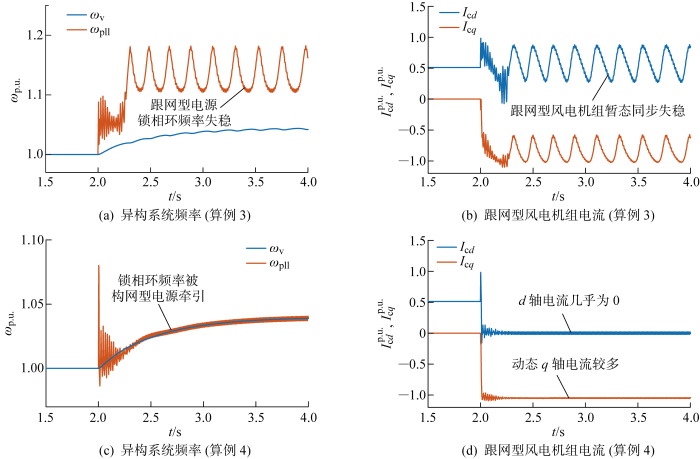
接着,当考虑了构网型电源的电流限幅后,分别设置风电机组按照K =1.5(算例3)和K =3.0(算例4)注入动态无功功率,发现前者发生锁相环频率失稳而后者的锁相环频率被成功牵引住,如图11 所示.根据2.3.2节的分析,这是因为构网型电源的电流限幅器一旦起作用,就等价于增大X Σ2 ,再根据图7 中临界d 轴电流随X Σ2 的变化情况,考虑电流限幅后的临界d 轴电流会进一步降低. 因此,只有采用更大的K 系数以注入更多的q 轴无功电流,才能将d 轴电流降低至临界d 轴电流以下,从而使锁相环频率被成功牵引.
图11
图11
构网型储能电源电流限幅的影响
Fig.11
Impact of current limitation on grid-forming battery storage energy system
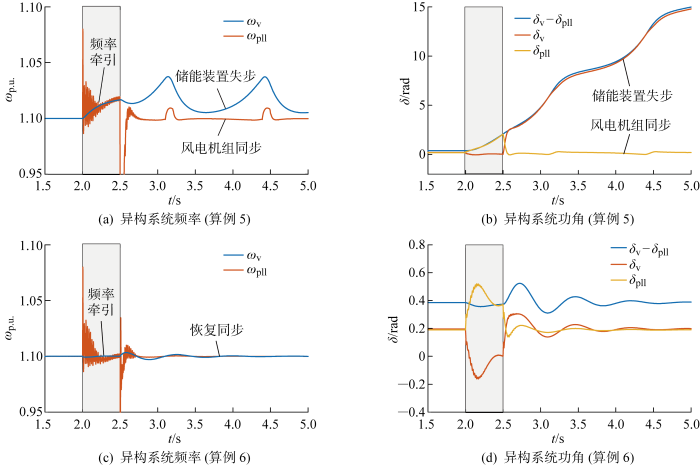
最后,利用仿真进一步探讨异构系统的暂态频率交互对于故障清除后系统的暂态稳定性的影响.如图12 所示,δ 为功角,每个分图中的灰色区域代表故障期间,此时电网电压为0.可以看出故障期间跟网型风电机组的频率均被成功牵引,防止了故障后风电机组锁相环无法锁相的问题[11 ] .由图可见,风电机组频率在故障清除后均恢复电网同步,没有出现失稳的情况.另一方面,如果在故障期间有功参考值较大,即P ref,flt =0.8(算例5),那么故障期间构网型储能电源的转子角将加速较多,使得故障期间积累较多能量,从而导致储能电源在故障后发生同步失稳,如图12(a) 和12(b) 所示;而根据1.2.3节的分析,通过设置故障期间有供参考值P ref,flt <0以减小联合功角驱动力F 的大小,能够减缓故障期间储能电源的虚拟转子加速,从而有利于提高其在故障后的电网同步能力.为此,设置P ref,flt =-0.1(算例6),发现故障后系统能够恢复同步, 由此证明在故障期间减缓构网型电源功角运动的必要性.
图12
图12
暂态频率交互对于故障后异构系统暂态稳定性的影响
Fig.12
Impact of transient frequency interaction on post-fault transient stability of heterogenerous system
4 结论
分析了含构网型储能的异构型风电场在电网严重短路故障下,构网型电源对跟网型电源的频率牵引机制和满足牵引性下的跟网对构网频率的驱动机制及影响.基于该交互机制,分析故障穿越控制影响.具体结论如下:
(1) 当电网发生严重短路故障时,如果风电机组的d 轴电流大小低于临界值,那么具有较快时间尺度的跟网型风电机组的频率能够被具有较慢时间尺度的构网型储能电源的频率所牵引,避免锁相环频率在暂态期间发散.
(2) 临界d 轴电流大小随风电机组并网率增加而减小,随储能装机占比增加而增大,故较大的风电机组并网率容易导致频率牵引失效,而增大储能容量能够提升频率牵引的可能性;此外减小d 轴电流大小也有利于实施频率牵引.
(3) 当考虑构网型储能的电流限幅因素后,满足频率牵引效应的临界d 轴电流会下降,从而可能导致风电机组锁相环失步的情况;而根据并网导则注入动态无功电流能够降低风电机组在故障期间的d 轴电流,从而增大频率牵引的可能性;此外,较大的动态无功电流注入系数有利于构网型储能电源实施频率牵引.
(4) 当频率牵引条件成立时,风电机组在故障期间所发出的部分有功功率将会输出到构网型储能电源中,从而参与驱动后者的功角运动,通过合理设置储能电源在故障期间的有功参考值为负,能够改善整个发风储联合场站的暂态稳定性.
综上,本文为理解异构型新能源发电系统受瞬时频率特性影响下的暂态稳定机理提供了探索性思路.根据所得相关机理,后续将提出基于频率牵引的异构电源系统频率致稳控制方法.此外,未来还将针对该系统在考虑电流限幅下的暂态频率及功角特性进行更深入的定量分析.
参考文献
View Option
[1]
黄强 , 郭怿 , 江建华 , 等 . “双碳” 目标下中国清洁电力发展路径
[J]. 上海交通大学学报 , 2021 , 55 (12 ): 1499 -1509 .
DOI:10.16183/j.cnki.jsjtu.2021.272
[本文引用: 1]
目前,第三次能源革命已经开始,为了减少碳排放,发达国家先后制定了清洁能源发展战略,并公布了放弃火电、核电的时间表.与此同时,中国也向世界作出承诺:2030年前碳排放达峰,2060年实现碳中和.因此,在“双碳”目标下,研究清洁电力发展路径具有重要意义.分析了中国水、风、光等清洁能源储量及其特征,预测了中长期电力需求,依据电力电量平衡原理,估算了2030和2050规划水平年电力系统结构组成,并分析了未来CO<sub>2</sub>排放趋势,提出了未来中国清洁电力的发展对策与建议.结果表明:预计2027年中国电力系统将实现“碳达峰”;2030年中国清洁电力发电量将超过总发电量的50%;2050年火电、核电将被水、风、光等清洁电力全部取代,电力行业将实现CO<sub>2</sub>的“零排放”,基本全面实现电力系统的绿色转型,以响应国家的“双碳”目标.
HUANG Qiang GUO Yi JIANG Jianhua et al Development pathway of China’s clean electricity under carbon peaking and carbon neutrality goals
[J]. Journal of Shanghai Jiao Tong University , 2021 , 55 (12 ): 1499 -1509 .
[本文引用: 1]
[2]
黄远明 , 张玉欣 , 夏赞阳 , 等 . 考虑需求响应资源和储能容量价值的新型电力系统电源规划方法
[J]. 上海交通大学学报 , 2023 , 57 (4 ): 432 -441 .
DOI:10.16183/j.cnki.jsjtu.2021.477
[本文引用: 1]
高比例可再生能源的接入对电力系统容量充裕性带来了新的挑战,系统必须具备充足的置信容量应对可再生能源的出力波动性和随机性.由于储能置信容量与电源规划结果的非线性关系,传统电源规划方法难以准确计算储能置信容量并建立系统置信容量充裕度约束.通过综合考虑火电、可再生能源、储能以及需求侧响应建立了电源规划模型,内嵌全年8 760时段生产运行模拟以确保系统具有充足灵活性,同时改进容量充裕性约束以考虑需求响应资源和储能的容量价值.针对储能置信容量的非线性问题,设计了迭代算法进行求解,并用某区域电力系统验证了模型的有效性.结果表明,高比例可再生能源系统中,影响系统成本的主要因素是灵活性约束,引入少量需求侧响应资源可大幅降低系统成本,为未来高比例可再生资源电力系统规划问题提供了新的思路.
HUANG Yuanming ZHANG Yuxin XIA Zanyang et al Power system planning considering demand response resources and capacity value of energy storage
[J]. Journal of Shanghai Jiao Tong University , 2023 , 57 (4 ): 432 -441 .
[本文引用: 1]
[3]
KATIRAEI F IRAVANI R HATZIARGYRIOU N et al Microgrids management
[J]. IEEE Power and Energy Magazine , 2008 , 6 (3 ): 54 -65 .
[本文引用: 1]
[4]
马宁宁 , 谢小荣 , 贺静波 , 等 . 高比例新能源和电力电子设备电力系统的宽频振荡研究综述
[J]. 中国电机工程学报 , 2020 , 40 (15 ): 4720 -4732 .
[本文引用: 1]
MA Ningning XIE Xiaorong HE Jingbo et al Review of wide-band oscillation in renewable and power electronics highly integrated power systems
[J]. Proceedings of the CSEE , 2020 , 40 (15 ): 4720 -4732 .
[本文引用: 1]
[5]
张志强 , 李秋彤 , 余浩 , 等 . 海上直驱风电经柔直并网系统的次/超同步振荡特性分析
[J]. 上海交通大学学报 , 2022 , 56 (12 ): 1572 -1583 .
DOI:10.16183/j.cnki.jsjtu.2021.434
[本文引用: 1]
海上直驱风电经柔性直流输电并网系统由多变流器构成,具有不同时间尺度的控制回路和复杂的动态特性.基于双风电场经柔性直流并网系统算例,采用状态空间分析法研究系统次/超同步振荡模态与电流控制回路的关联关系.研究表明,系统存在3种与变流器电流环相关的主导振荡模态,分别对应于风场-柔直模态、风场间模态以及柔直-交流系统模态,风场侧的模态与柔直-交流系统模态是解耦的,相关变流器控制参数、系统的运行工况对3种模态稳定性具有重要影响;单个主导模态失稳引起的振荡会波及到柔直的另一端,需要甄别引起振荡的根本原因,以利于针对性设计抑制策略.研究结果对于认识海上风电经柔直并网系统动态特性、参数设计以及振荡抑制具有指导作用.
ZHANG Zhiqiang LI Qiutong YU Hao et al Analysis of sub/super-synchronous oscillation of direct-drive offshore wind power grid-connected system via VSC-HVDC
[J]. Journal of Shanghai Jiao Tong University , 2022 , 56 (12 ): 1572 -1583 .
[本文引用: 1]
[6]
RATHNAYAKE D B AKRAMI M PHURAILATPAM C et al Grid forming inverter modeling, control, and applications
[J]. IEEE Access , 2021 , 9 : 114781 -114807 .
[本文引用: 1]
[7]
DENIS G PREVOST T DEBRY M et al The Migrate project: The challenges of operating a transmission grid with only inverter-based generation. A grid-forming control improvement with transient current-limiting control
[J]. IET Renewable Power Generation , 2018 , 12 (5 ): 523 -529 .
[本文引用: 1]
[8]
ROCABERT J LUNA A BLAABJERG F et al Control of power converters in AC microgrids
[J]. IEEE Transactions on Power Electronics , 2012 , 27 (11 ): 4734 -4749 .
[本文引用: 1]
[9]
沈阳武 , 宋兴荣 , 罗紫韧 , 等 . 基于模型预测控制的分布式储能型风力发电场惯性控制策略
[J]. 上海交通大学学报 , 2022 , 56 (10 ): 1285 -1293 .
DOI:10.16183/j.cnki.jsjtu.2022.134
[本文引用: 1]
分布式储能型(DES)风力发电机组是解决规模化风力发电接入引起系统频率稳定问题的有效手段.提出一种基于模型预测控制(MPC)的分布式储能型风力发电场惯性控制方法,首先建立分布式储能型风力发电场的线性化预测模型,在此基础上结合MPC控制框架,设计考虑储能损耗成本和风机转子转速均衡变化的MPC惯性控制优化模型和策略,以实现惯量控制期间风力发电机组转子转速的均衡变化.仿真结果表明:所提控制策略可以有效协调分布式储能型风力发电机组中风力发电单元和储能系统单元的有功功率输出,降低储能系统的充放电损耗成本,并保证风力发电场内所有风机转速在惯性控制期间趋于平均,避免由于风机转速下降过度而导致风力发电机组退出调频的问题.分布式储能型风力发电场惯性控制策略有利于提高电网频率稳定性,对保障电网的安全运行具有重要意义.
SHEN Yangwu SONG Xingrong LUO Ziren et al Inertial control strategy for wind farm with distributed energy storage system based on model predictive control
[J]. Journal of Shanghai Jiao Tong University , 2022 , 56 (10 ): 1285 -1293 .
[本文引用: 1]
[10]
张宇 , 蔡旭 , 张琛 , 等 . 并网变换器的暂态同步稳定性研究综述
[J]. 中国电机工程学报 , 2021 , 41 (5 ): 1687 -1702 .
[本文引用: 1]
ZHANG Yu CAI Xu ZHANG Chen et al Transient synchronization stability analysis of voltage source converters: A review
[J]. Proceedings of the CSEE , 2021 , 41 (5 ): 1687 -1702 .
[本文引用: 1]
[11]
张琛 , 蔡旭 , 李征 . 全功率变换风电机组的暂态稳定性分析
[J]. 中国电机工程学报 , 2017 , 37 (14 ): 4018 -4026 .
[本文引用: 3]
ZHANG Chen CAI Xu LI Zheng Transient stability analysis of wind turbines with full-scale voltage source converter
[J]. Proceedings of the CSEE , 2017 , 37 (14 ): 4018 -4026 .
[本文引用: 3]
[12]
QORIA T GRUSON F COLAS F et al Critical clearing time determination and enhancement of grid-forming converters embedding virtual impedance as current limitation algorithm
[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics , 2020 , 8 (2 ): 1050 -1061 .
[本文引用: 2]
[13]
ZHANG Y ZHANG C YANG R X et al Current-constrained power-angle characterization method for transient stability analysis of grid-forming voltage source converters
[J]. IEEE Transactions on Energy Conversion , 2023 , 38 (2 ): 1338 -1349 .
[本文引用: 1]
[14]
SHEN C SHUAI Z K SHEN Y et al Transient stability and current injection design of paralleled current-controlled VSCs and virtual synchronous generators
[J]. IEEE Transactions on Smart Grid , 2021 , 12 (2 ): 1118 -1134 .
[本文引用: 1]
[15]
沈超 , 帅智康 , 程慧婕 . 虚拟同步机并联电流控制型变换器系统暂态同步稳定性分析
[J]. 电力系统自动化 , 2021 , 45 (10 ): 115 -123 .
[本文引用: 1]
SHEN Chao SHUAI Zhikang CHENG Huijie Transient synchronization stability analysis of system with paralleled virtual synchronous generators and current-controlled converters
[J]. Automation of Electric Power Systems , 2021 , 45 (10 ): 115 -123 .
[本文引用: 1]
[16]
HE X Q GENG H Transient stability of power systems integrated with inverter-based generation
[J]. IEEE Transactions on Power Systems , 2021 , 36 (1 ): 553 -556 .
[本文引用: 1]
[17]
黎晓 , 李剑泽 , 苏晨博 , 等 . 锁相环失步对同步发电机暂态功角稳定性的影响机理分析
[J]. 电力系统自动化 , 2022 , 46 (22 ): 101 -110 .
[本文引用: 1]
LI Xiao LI Jianze SU Chenbo et al Influence mechanism analysis of phase locked loop out-of-synchronization on transient power angle stability of synchronous generators
[J]. Automation of Electric Power Systems , 2022 , 46 (22 ): 101 -110 .
[本文引用: 1]
[18]
LI M F QUAN X J WU Z J et al Modeling and transient stability analysis of mixed-GFM-GFL-based power system
[C]// 2021 IEEE Sustainable Power and Energy Conference. Nanjing , China : IEEE , 2021 : 2755 -2759 .
[本文引用: 1]
[19]
蔡旭 , 李睿 , 刘畅 , 等 . 高压直挂储能功率变换技术与世界首例应用
[J]. 中国电机工程学报 , 2020 , 40 (1 ): 200 -211 .
[本文引用: 1]
CAI Xu LI Rui LIU Chang et al Transformerless high-voltage power conversion system for battery energy storage system and the first demonstration application in world
[J]. Proceedings of the CSEE , 2020 , 40 (1 ): 200 -211 .
[本文引用: 1]
[20]
ZHANG Y ZHANG C CAI X Large-signal grid-synchronization stability analysis of PLL-based VSCs using Lyapunov’s direct method
[J]. IEEE Transactions on Power Systems , 2022 , 37 (1 ): 788 -791 .
[本文引用: 1]
[21]
秦世耀 , 齐琛 , 李少林 , 等 . 电压源型构网风电机组研究现状及展望
[J]. 中国电机工程学报 , 2023 , 43 (4 ): 1314 -1334 .
[本文引用: 1]
QIN Shiyao QI Chen LI Shaolin et al Review of the voltage-source grid forming wind turbine
[J]. Proceedings of the CSEE , 2023 , 43 (4 ): 1314 -1334 .
[本文引用: 1]
[22]
张宇 , 张琛 , 蔡旭 , 等 . 虚拟同步机电流受限暂态电压支撑机理与改进故障穿越控制研究
[J]. 中国电机工程学报 , 2024 , 44 (15 ): 5996 -6009 .
[本文引用: 3]
ZHANG Yu ZHANG Chen CAI Xu et al Current Constrained Transient Voltage Response Analysis and An Improved Fault Ride Through Control of the Virtual Synchronous Generator
[J]. Proceedings of the CSEE , 2024 , 44 (15 ): 5996 -6009 .
[本文引用: 3]
“双碳” 目标下中国清洁电力发展路径
1
2021
... 在国家战略“双碳”目标下,构建以新能源为主体的新型电力系统成为能源电力行业共同奋进的方向[1 ] .风光等新能源存在随机波动性,为解决其出力波动对电力系统运行的影响,据北极星储能网报道,国家及地方于2021年陆续出台相关政策,规定新增风电光伏场站需要配套建设10%~20%左右的储能.因此,储能将成为许多新能源场站的有机整体. ...
Development pathway of China’s clean electricity under carbon peaking and carbon neutrality goals
1
2021
... 在国家战略“双碳”目标下,构建以新能源为主体的新型电力系统成为能源电力行业共同奋进的方向[1 ] .风光等新能源存在随机波动性,为解决其出力波动对电力系统运行的影响,据北极星储能网报道,国家及地方于2021年陆续出台相关政策,规定新增风电光伏场站需要配套建设10%~20%左右的储能.因此,储能将成为许多新能源场站的有机整体. ...
考虑需求响应资源和储能容量价值的新型电力系统电源规划方法
1
2023
... 目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式. ...
Power system planning considering demand response resources and capacity value of energy storage
1
2023
... 目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式. ...
Microgrids management
1
2008
... 目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式. ...
高比例新能源和电力电子设备电力系统的宽频振荡研究综述
1
2020
... 目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式. ...
Review of wide-band oscillation in renewable and power electronics highly integrated power systems
1
2020
... 目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式. ...
海上直驱风电经柔直并网系统的次/超同步振荡特性分析
1
2022
... 目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式. ...
Analysis of sub/super-synchronous oscillation of direct-drive offshore wind power grid-connected system via VSC-HVDC
1
2022
... 目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式. ...
Grid forming inverter modeling, control, and applications
1
2021
... 目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式. ...
The Migrate project: The challenges of operating a transmission grid with only inverter-based generation. A grid-forming control improvement with transient current-limiting control
1
2018
... 目前,电化学储能得益于部署便捷、维护简单等特点成为新能源场站内部储能的主流选择[2 ] .风电机组及电化学储能都要通过并网变换器实现电能转换与并网,因此,变换器控制方式将对储能、风电并网动态特性起到主导作用.基于锁相环同步的跟网型控制和通过控制功角运动实现同步的构网型控制是两类主要的变换器电网同步与并网功率控制方法[3 ] .跟网型控制下新能源的功率跟踪能力较强,但主动阻尼电网频率和电压波动的能力较弱,同时也面临较严峻的弱电网稳定运行问题[4 -5 ] .相比于跟网型控制,构网型控制能够自主支撑电网电压和频率;并具有较强的弱电网稳定运行能力,这对于以新能源为主体的电源运行具有重要意义[6 ] .针对维持新能源高渗透电力系统基本运行稳定所需的构网型电源占比问题已有一定研究,如欧洲MIGRATE项目研究[7 ] 显示,只要构网型控制的应用比例不低于30%,就能够支撑100%新能源渗透率的电网运行.《能源产业聚集》内部资料显示,对于电网中大部分新能源场站短路比不足的场合,配置15%具有短时1.5倍10 s过载能力的构网储能系统,基本可以缓解新能源场站由于短路比不足引发的稳定运行问题.基于上述研究结论,如果让风电场内的储能以构网型控制运行,那么风电机组无需进行构网型改造而维持其常规跟网控制,这有效避免了机组做构网控制运行可能带来的整机安全性降低的问题,如频繁进行惯量和频率响应对整机载荷及寿命带来的不利影响.因此,跟网机组与构网储能结合的异构电源系统有望成为未来风电场站的典型形式. ...
Control of power converters in AC microgrids
1
2012
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
基于模型预测控制的分布式储能型风力发电场惯性控制策略
1
2022
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
Inertial control strategy for wind farm with distributed energy storage system based on model predictive control
1
2022
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
并网变换器的暂态同步稳定性研究综述
1
2021
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
Transient synchronization stability analysis of voltage source converters: A review
1
2021
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
全功率变换风电机组的暂态稳定性分析
3
2017
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
... 根据以往的认知,一旦电网发生严重故障,系统将不存在静态工作点,风电机组的锁相环和储能电源的功率同步环将不可避免地出现转子加速现象.由于锁相环的时间尺度远远快于功率同步环,所以锁相环的频率加速度远远大于后者,从而导致异构系统的电源频率出现分离[11 ] .然而,本节内容将揭示,即使当系统不存在平衡点,但满足一定条件时,跟网型风电机组的锁相环频率能够被构网型储能牵引,从而使异构系统的电源频率在故障期间保持一致,即实现整场站在频率牵引作用下的同步运行. ...
... 最后,利用仿真进一步探讨异构系统的暂态频率交互对于故障清除后系统的暂态稳定性的影响.如图12 所示,δ 为功角,每个分图中的灰色区域代表故障期间,此时电网电压为0.可以看出故障期间跟网型风电机组的频率均被成功牵引,防止了故障后风电机组锁相环无法锁相的问题[11 ] .由图可见,风电机组频率在故障清除后均恢复电网同步,没有出现失稳的情况.另一方面,如果在故障期间有功参考值较大,即P ref,flt =0.8(算例5),那么故障期间构网型储能电源的转子角将加速较多,使得故障期间积累较多能量,从而导致储能电源在故障后发生同步失稳,如图12(a) 和12(b) 所示;而根据1.2.3节的分析,通过设置故障期间有供参考值P ref,flt <0以减小联合功角驱动力F 的大小,能够减缓故障期间储能电源的虚拟转子加速,从而有利于提高其在故障后的电网同步能力.为此,设置P ref,flt =-0.1(算例6),发现故障后系统能够恢复同步, 由此证明在故障期间减缓构网型电源功角运动的必要性. ...
Transient stability analysis of wind turbines with full-scale voltage source converter
3
2017
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
... 根据以往的认知,一旦电网发生严重故障,系统将不存在静态工作点,风电机组的锁相环和储能电源的功率同步环将不可避免地出现转子加速现象.由于锁相环的时间尺度远远快于功率同步环,所以锁相环的频率加速度远远大于后者,从而导致异构系统的电源频率出现分离[11 ] .然而,本节内容将揭示,即使当系统不存在平衡点,但满足一定条件时,跟网型风电机组的锁相环频率能够被构网型储能牵引,从而使异构系统的电源频率在故障期间保持一致,即实现整场站在频率牵引作用下的同步运行. ...
... 最后,利用仿真进一步探讨异构系统的暂态频率交互对于故障清除后系统的暂态稳定性的影响.如图12 所示,δ 为功角,每个分图中的灰色区域代表故障期间,此时电网电压为0.可以看出故障期间跟网型风电机组的频率均被成功牵引,防止了故障后风电机组锁相环无法锁相的问题[11 ] .由图可见,风电机组频率在故障清除后均恢复电网同步,没有出现失稳的情况.另一方面,如果在故障期间有功参考值较大,即P ref,flt =0.8(算例5),那么故障期间构网型储能电源的转子角将加速较多,使得故障期间积累较多能量,从而导致储能电源在故障后发生同步失稳,如图12(a) 和12(b) 所示;而根据1.2.3节的分析,通过设置故障期间有供参考值P ref,flt <0以减小联合功角驱动力F 的大小,能够减缓故障期间储能电源的虚拟转子加速,从而有利于提高其在故障后的电网同步能力.为此,设置P ref,flt =-0.1(算例6),发现故障后系统能够恢复同步, 由此证明在故障期间减缓构网型电源功角运动的必要性. ...
Critical clearing time determination and enhancement of grid-forming converters embedding virtual impedance as current limitation algorithm
2
2020
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
... 式中:I c d I c q d 轴和q 轴电流.由于电流环控制的时间尺度一般在数毫秒内,锁相环的时间尺度往往在几十毫秒以上,所以在暂态稳定性分析中通常假设变换器的输出电流等于其参考值[12 ] ,而变换器的参考值由外环控制器提供. ...
Current-constrained power-angle characterization method for transient stability analysis of grid-forming voltage source converters
1
2023
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
Transient stability and current injection design of paralleled current-controlled VSCs and virtual synchronous generators
1
2021
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
虚拟同步机并联电流控制型变换器系统暂态同步稳定性分析
1
2021
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
Transient synchronization stability analysis of system with paralleled virtual synchronous generators and current-controlled converters
1
2021
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
Transient stability of power systems integrated with inverter-based generation
1
2021
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
锁相环失步对同步发电机暂态功角稳定性的影响机理分析
1
2022
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
Influence mechanism analysis of phase locked loop out-of-synchronization on transient power angle stability of synchronous generators
1
2022
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
Modeling and transient stability analysis of mixed-GFM-GFL-based power system
1
2021
... 然而,异构电源系统涉及异构控制特性、暂态控制策略切换以及电力电子变流器电流限幅等复杂的非线性过程,其暂态特性与交互稳定机理十分复杂,这给其运行控制带来极大挑战,是当今的研究热点[8 -9 ] .为厘清这些机理,可以从单机同构电源的暂稳问题出发.目前,针对电网短路故障下跟网和构网并网变换器的暂态稳定性已有大量研究,包括定性的机理分析和定量的稳定性评估,如极限切除时间[10 ] .文献[11 ]中建立了锁相型并网变换器的暂态同步稳定性分析模型,揭示了以锁相环“瞬时频率”快速失稳为典型特征的跟网型电源暂态同步失稳问题;文献[12 -13 ]中研究了构网型控制的暂态稳定机理.在涉及两者暂态交互的异构电源系统研究方面,文献[14 -15 ]中分析了跟网型变换器瞬时频率波动引发的功角动态对于构网型变换器暂态稳定性的影响,并估计了故障清除时间;文献[16 ]中揭示了跟网型变流器可能由于同步机功角摇摆中位置变化而失去静态工作点从而引发暂态失稳的机理;文献[17 ]中基于一种非线性方法进一步刻画静态工作点丢失后的跟网型变流器的锁相环轨迹;文献[18 ]中建立异构电源系统的暂态稳定交互数学模型,主要分析跟、构网型变换器对于彼此静态工作点的影响,并得出增大跟网型变换器端电流可以增强构网型变换器暂态稳定性的结论. ...
高压直挂储能功率变换技术与世界首例应用
1
2020
... 风电机组均采用全功率型(Type-4)风力发电机,网侧变换器采用经典跟网型控制,外环控制目标为直流侧电压.储能电源的拓扑一般为多台低压分布式储能或集中式高压直挂储能[19 ] ,前者一般采用两电平或三电平拓扑,后者则采用模块化拓扑结构,可节省交流变压器. ...
Transformerless high-voltage power conversion system for battery energy storage system and the first demonstration application in world
1
2020
... 风电机组均采用全功率型(Type-4)风力发电机,网侧变换器采用经典跟网型控制,外环控制目标为直流侧电压.储能电源的拓扑一般为多台低压分布式储能或集中式高压直挂储能[19 ] ,前者一般采用两电平或三电平拓扑,后者则采用模块化拓扑结构,可节省交流变压器. ...
Large-signal grid-synchronization stability analysis of PLL-based VSCs using Lyapunov’s direct method
1
2022
... 采用跟网型控制的全功率风电机组建模方法较为成熟,目前普遍采用受控电流源代替变换器的特性,且在暂态稳定性分析中一般只保留锁相环的动态[20 ] .如图2 所示.图中:ω pll 为锁相环角频率;ω n 为额定角频率.锁相环的动态方程为 ...
电压源型构网风电机组研究现状及展望
1
2023
... 对于采用构网型控制的储能电源而言,由于构网型控制实现方式众多,目前尚无模型对构网型控制进行统一表征[21 ] ,所以采用典型的虚拟同步控制,控制框图如图3 所示.其中,功率同步环对于暂态过程中的功角摇摆起重要作用,其动态方程为 ...
Review of the voltage-source grid forming wind turbine
1
2023
... 对于采用构网型控制的储能电源而言,由于构网型控制实现方式众多,目前尚无模型对构网型控制进行统一表征[21 ] ,所以采用典型的虚拟同步控制,控制框图如图3 所示.其中,功率同步环对于暂态过程中的功角摇摆起重要作用,其动态方程为 ...
虚拟同步机电流受限暂态电压支撑机理与改进故障穿越控制研究
3
2024
... 式中:δ v =θ v -θ pll 为储能的内电势功角,其中θ v 为构网型储能的电压相角;H 为惯量时间常数;ω v 为构网型储能的角频率;P ref 为有功功率参考值;P v 为构网型储能的有功功率;D 为有功频率下垂系数.在功角运动的时间尺度内,认为电流内环的控制到达稳态.当电流指令I v, cmd 未到达限幅值时,满足如下关系[22 ] : ...
... 式中:I v 为购网型储能的输出电流;Z v =R v +jX v 为虚拟阻抗的大小,其中R v 、X v 分别为购网型储能控制环节中的虚拟电阻、虚拟电抗;E 为内电势;U v 为储能的并网点电压. 当电流指令到达限幅值后,由于采用dq 轴平均限幅的电流限幅器只改变电流矢量幅值而不改变相位,所以电流限幅器相当于一个增益环节[22 ] . 假该缩放比例为k ,则有 ...
... 这表明在电流指令超过最大限幅值时,电流限幅器的作用相当于将虚拟阻抗Z v 增大至kZ v ,这样就能得到基于虚拟同步控制的储能电源的等效电路模型[22 ] ,如图3 所示.图中:s 为拉普拉斯算子;E 为内电势幅值;p.u.表示标幺值.该模型不仅体现了对功角运动起主导作用的功率同步环动态,而且将虚拟阻抗及电流限幅的影响考虑在内.正常情况下,电流指令值一般不会到达饱和值,此时有k =1;而当电网电压较低或者功角与电网偏差过大时,电流指令将会到达饱和,此时有k >1. ...
Current Constrained Transient Voltage Response Analysis and An Improved Fault Ride Through Control of the Virtual Synchronous Generator
3
2024
... 式中:δ v =θ v -θ pll 为储能的内电势功角,其中θ v 为构网型储能的电压相角;H 为惯量时间常数;ω v 为构网型储能的角频率;P ref 为有功功率参考值;P v 为构网型储能的有功功率;D 为有功频率下垂系数.在功角运动的时间尺度内,认为电流内环的控制到达稳态.当电流指令I v, cmd 未到达限幅值时,满足如下关系[22 ] : ...
... 式中:I v 为购网型储能的输出电流;Z v =R v +jX v 为虚拟阻抗的大小,其中R v 、X v 分别为购网型储能控制环节中的虚拟电阻、虚拟电抗;E 为内电势;U v 为储能的并网点电压. 当电流指令到达限幅值后,由于采用dq 轴平均限幅的电流限幅器只改变电流矢量幅值而不改变相位,所以电流限幅器相当于一个增益环节[22 ] . 假该缩放比例为k ,则有 ...
... 这表明在电流指令超过最大限幅值时,电流限幅器的作用相当于将虚拟阻抗Z v 增大至kZ v ,这样就能得到基于虚拟同步控制的储能电源的等效电路模型[22 ] ,如图3 所示.图中:s 为拉普拉斯算子;E 为内电势幅值;p.u.表示标幺值.该模型不仅体现了对功角运动起主导作用的功率同步环动态,而且将虚拟阻抗及电流限幅的影响考虑在内.正常情况下,电流指令值一般不会到达饱和值,此时有k =1;而当电网电压较低或者功角与电网偏差过大时,电流指令将会到达饱和,此时有k >1. ...