如果一个编码符号可以通过访问最多r个其他编码符号来恢复,那么该编码符号具有修复局部性,该参数用r表示,这r个编码符号的集合称为修复集[4-5].Gopalan等[5]提出了修复局部性r,这一参数是衡量修复效率的重要指标,对于信息符号具有局部性r的LRCs,给出了码的最小距离上界.文献[6⇓⇓-9]中给出了最小距离达到此上界的LRCs的相关构造.除了局部性r外,LRCs的另一个重要特性是可用性.如果一个编码符号具有t个修复集,那么称该编码符号具有可用性,该参数用t表示.这个特性与热数据密切相关,具有可用性的LRCs可以确保对热数据进行并行读取和多路径修复[10].为了在多个节点故障的情况下实现局部恢复,Rawat等[11]提出了(r,t)局部性的概念,并且证明了信息符号具有(r,t)局部性的单校验LRCs最小距离的上界.Tamo等[12]提出并证明了所有符号具有(r,t)局部性的LRCs的最小距离和码率上界.
目前大量文献对具有(r,t)局部性的LRCs构造进行研究.文献[12]中基于t个二进制(r+1,r)奇偶校验码的直积,构造具有(r,t)局部性的二元局部修复码(binary locally repairable codes, BLRCs),该BLRCs虽然能够实现任意的局部性r和可用性t,但是其码率较小.文献[13]中利用有限域上的迹函数构造了一类循环(r,t) 局部修复码,构造出的BLRCs达到了最优最小距离,但是此构造方法只能构造特定参数的BLRCs且码率较小.Hao等[14]采用有限几何低密度奇偶校验码(LDPC)和阵列LDPC 构造了具有 (r,t) 局部性的BLRCs,该BLRCs虽然达到了最优最小距离,不足之处是参数条件限制较多且码率较小.文献[15]中基于分区和特定结构的函数构造了两种具有严格可用性t的BLRCs,然而提出的两种LRCs只在某些参数条件下存在.文献[16]中基于超图构造的BLRCs达到了最优最小距离界,但是超图的存在需要满足一些参数条件的限制,参数选择不够灵活,并且码率较小.
为了解决上述LRCs构造中存在的参数限制较多且码率较小的问题,基于三角形结合方案,提出具有(r,t)局部性的最优BLRCs的构造方法.首先利用三角形结合方案的结合关系,基于校验矩阵构造可用性t=2的BLRCs,进一步基于生成矩阵构造局部性r=2的BLRCs;为了使BLRCs的参数选择更加灵活,对基于三角形结合方案构造的BLRCs进行扩展,构造能够实现任意局部性r>2和任意可用性t>2的BLRCs.通过性能分析,基于三角形结合方案构造的具有(r,2)局部性的BLRCs达到了最优码率界,构造的具有任意局部性r>2和可用性t>2的BLRCs达到了最优最小距离界.与基于近正则图构造的BLRCs和基于直积码构造的BLRCs等方法相比,本文BLRCs在码率上表现更优且参数选择更灵活.
1 预备知识
1.1 局部修复码
设C是有限域Fq上的(n,k)线性码,其中n为码长,k为维度.给定[n]={1,2,…,n},c=(c1,c2,…,cn)是一个码字,下面给出具有(r,t)局部性的码C定义.
定义1[11] 如果编码符号ci具有(r,t)局部性,那么需要满足下列条件:
(1) 存在t个子集,满足φ1(i),…,φi(i)⊂[n]\{i},需ci能够从φj(i) (j∈[t])中恢复出来,φj(i) (j∈[t])称为ci的修复集.
(2) |φj(i)|≤r,j∈[t].
(3) φj(i)∩φl(i)=⌀,j≠l∈[t].
如仅有信息符号具有(r,t)局部性,则此码称作(n, k, r, t)i LRCs.如所有符号具有(r,t)局部性,则此码称作(n, k, r, t)a LRCs.
定义2[15] 对于v=[v1v2 … vn]∈
定理1[17] 对于信息位具有(r,t)局部性的(n,k,d) LRCs,最小距离应满足:
定理2[11] 若LRCs的所有信息位码元的每个修复集中只包含一个校验位,那么该单校验(n, k, r, t)i LRCs的最小距离满足:
称达到边界式(3)的LRCs是最小距离最优的单校验(n, k, r, t)i LRCs.
定理3[13] 若(n,k,r,t) LRCs的每个码元具有t个大小为r的不相交修复集,那么该码码率满足:
称达到边界式(4)的LRCs是码率最优的(n,k,r,t) LRCs.
定理4 特别地,Prakash等[18]进一步提出了(n,k,r,t=2) LRCs的码率上界:
称达到边界式(5)的LRCs是码率最优的(n, k, r, 2) LRCs.
定理5 对于具有严格可用性的LRCs,Balaji等[19]提出其码长需要满足:
1.2 三角形结合方案
结合方案是关于集合Ω中元素对之间的关系,Ω×Ω是Ω中有序元素对的集合,即Ω×Ω={(α,β): α∈Ω, β∈Ω}.令B是Ω×Ω的任意子集,其对偶子集是B',其中B'={(β, α): (α, β)∈B},如果B=B',则称B是对称的.一个特殊的对称子集是对角子集,对角子集Diag(Ω)可以表示为Diag(Ω)={(ω,ω): ω∈Ω}.
定义3[20] 称为结合方案.有限集Ω上具有s个结合类的结合方案是将Ω×Ω划分成集合D0, D1, …, Ds,称为结合类,满足以下条件:
(1) D0=Diag(Ω).
(2) Di是对称的,其中i=1,2,…,s.
(3) 对于{0,1,…,s}中所有的i,j,k,有正整数
定义4[20] 称为三角形结合方案.设Ω是由m元集Γ中所有二元子集构成的集合族,对于Ω中的元素α,令
D1(α)={β∈Ω: |α∩β|=1}
D2(α)={β∈Ω: α∩β=⌀}
若β∈D1(α),即满足|α∩β|=1,则称α与β具有第一类结合关系;若β∈D2(α),则称α与β具有第二类结合关系,即三角形结合方案.
2 基于三角形结合方案构造BLRCs
基于三角形结合方案中的结合关系可构造可用性t=2的BLRCs,进一步基于生成矩阵可构造出局部性r=2的BLRCs;为了使BLRCs的参数更加灵活,对基于三角形结合方案构造的BLRCs进行扩展,进一步构造能够实现任意局部性r>2和任意可用性t>2的BLRCs.
2.1 构造可用性t=2的BLRCs
首先基于三角形结合方案构造关联矩阵,基于关联矩阵构造可用性t=2的BLRCs.通过构造生成矩阵进一步得到局部性r=2的BLRCs.构造关联矩阵的具体步骤如下:
步骤1 用Ω表示三角形结合方案中m+1元集Γ={1,2,…,m+1}全部二元子集构成的集合族,则此集合族中共有m(m+1)/2个元素,其中m≥2.
步骤2 对任意二元子集L∈Ω,令Bi={L|i∈L},B={B1,B2,…,Bm+1},其中i∈Γ.
步骤3 构造关联矩阵
其中
由|Bi|=m可知,关联矩阵M的行重为m;对任意二元子集L∈Ω,必定存在
基于以上关联矩阵构造校验矩阵,考虑由校验矩阵定义二元码,有如下构造.
构造1 由校验矩阵H1=[M|I(m+1)]构造的码C1是所有符号具有局部性r和可用性t的单校验(n, k, r, t)aBLRCs,其中满足参数条件
证明 由文献[15]可知,如果C中的每个码元符号ci(i∈[n]),在对偶码中都存在t个码字
对于码元符号ci
例1 以m=4为例构造可用性t=2的BLRCs,则$\Gamma=\{1,2,3,4,5\}, \Omega=\{(i, j\} \mid i<j \in \Gamma\}, B=\{\{\{1,2\},\{1,3\},\{1,4\},\{1,5\}\},\{\{1,2\}, \\ \{2,3\},\{2,4\},\{2,5\}\},\{\{1,3\},\{2,3\},\{3,4\}, \{3,5\}\},\{\{1,4\},\{2,4\},\{3,4\},\{4,5\}\},\{\{1,5\}, \{2,5\}, \{3,5\},\{4,5\}\}\}$,将B中元素与矩阵的行关联,将Ω中元素与矩阵的列关联,那么可知关联矩阵M是一个5×10阶的正则矩阵,关联矩阵M可具体表示如下:
M=
由校验矩阵H1=[M|I5]构造的码是所有符号具有局部性r和可用性t的(n=15, k=10, r=4, t=2)aBLRCs,码的最小距离d=3.若信息位c1发生故障,则由BLRCs的校验矩阵H1可知,信息位c1可用c1=c11-c2-c3-c4=c12-c5-c6-c7来恢复,那么信息位c1的修复集可表示为
φ1(1)={2,3,4,11}, φ2(1)={5,6,7,12}
每个信息符号的修复集均含有一个校验位符号.若校验位c11发生故障,则由BLRCs的校验矩阵H1可知,校验位c11可用c11=c1+c2+c3+c4=c12+c13+c14+c15来恢复,那么校验位c11的修复集可表示为
φ1(11)={1,2,3,4}, φ2(11)={12,13,14,15}
可以看出校验符号同样具有两种修复方式.
推论1 由生成矩阵
G=[Im+1|M]
定义的码C2是所有符号具有局部性r和可用性t的单校验(n, k, r, t)aBLRCs,其中参数满足条件
n=(m+1)(m+2)/2
k=m+1, r=2, t=m
证明 该推论的证明与构造1相似.
推论2 由关联矩阵M作为校验矩阵定义的码C3是所有符号具有严格可用性的(n, k, r, t)aBLRCs,其中参数满足条件
n=m(m+1)/2, k=(m-1)m/2
r=m-1, t=2
且构造的BLRCs 的码长达到了Balaji等[19]提出的具有严格可用性的BLRCs的码长界.
证明 若a×b阶校验矩阵的行重为r+1,列重为t,满足bt=a(r+1),且校验矩阵中第i列具有非零项的行的支持集由
由此类校验矩阵构造的码称为具有严格可用性t的码[15].因此,由关联矩阵M作为校验矩阵定义的码是具有严格可用性的码.
由关联矩阵M的形式可以确定码C3的码长、所有符号局部性和可用性.然后对码C3的维度进行证明.由于构造的关联矩阵M的秩为行数减1,所以码C3的维度
k=n-rank(M)=m(m+1)/2-(m+1-1)=(m-1)m/2
由码C3的参数条件可知
(r+1)2-r(r+1)/t=m2-(m-1)m/2= m(m+1)/2=n
即构造出的码长达到了Balaji等[19]提出的具有严格可用性的码具有的码长界.
2.2 构造具有任意局部性和可用性的BLRCs
现有码结构主要是针对给定参数的系统,因此缺乏适应系统参数变化的能力.使用构造1仅能构造可用性t=2的BLRCs.本文对构造1进行推广,进一步构造具有任意局部性r>2和可用性t>2的BLRCs.
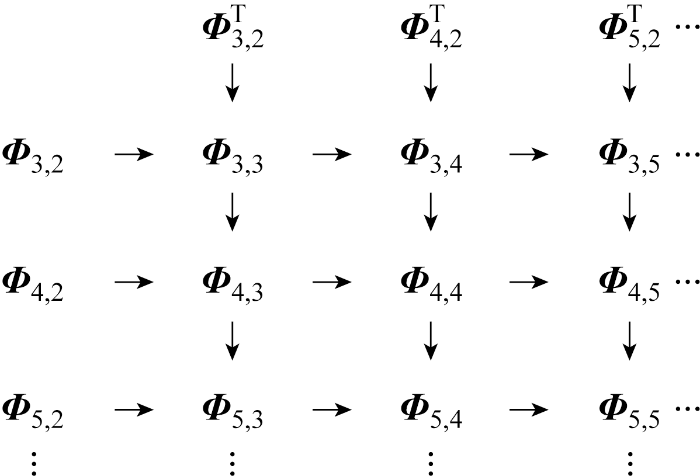
矩阵构造示意图如图1所示.用Φm,p表示行重为m、列重为p的正则矩阵.由于基于三角形结合方案构造的关联矩阵M的行重为m,列重为2,因此,用Φm,2表示行重为m的关联矩阵M.当m, p>2时,给定m, p,使用矩阵
Φm,p=
图1
可进一步构造行重为m、列重为p的正则矩阵.矩阵Φm,p中的块最终均能用Φl,2(2<l≤m)、
Φ3, 3=
其中:Φ3,2即为由三角形结合方案构造得到的行重为3、列重为2的关联矩阵.
构造2 由校验矩阵
H2=
定义的码C4是信息符号,可以实现任意局部性r>2和任意可用性t>2的(n=(m+1)(m+2)… (m+p)/p!, k=m(m+1)…(m+p-1)/p!, r=m, t=p)iBLRCs.
证明 首先计算矩阵Φm,p的大小.由构造1可知Φm,2的行数为m+1,列数为m(m+1)/2.由于矩阵
根据矩阵形式,Φm,3的行数可表示为
m+1+
Φm,3的列数可表示为
Φm,4的行数可表示为
Φm,4的列数可表示为
当p>2时,假设Φm,p的行数为(m+1)(m+2)…(m+p-1)/(p-1)!,Φm,p的列数为m(m+1)…(m+p-1)/p!.由于矩阵
矩阵Φm,p+1的行数为
矩阵Φm,p+1的列数为
假设成立.
因此,当p>2时,Φm,p的行数为(m+1)(m+2)…(m+p-1)/(p-1)!,Φm,p的列数为m(m+1)…(m+p-1)/p!.则由校验矩阵H2=[Φm,p|I]定义的码长
n=(m+1)(m+2)…(m+p)/p!
维度
k=m(m+1)…(m+p-1)/p!
当需要构造给定局部性r及可用性t的BLRCs时,可以基于三角形结合方案构造所需的列重为2的关联矩阵,由这些关联矩阵构造得到校验矩阵H2=[Φr, t|I]进而构造BLRCs.
例2 以r=3, t=5为例构造BLRCs,由上述构造方法可知:
Φ3,5=
其中,基于三角形结合方案构造关联矩阵的方法,矩阵Φ3,2可以表示为
Φ3,2=
矩阵Φ4,2、Φ5,2也同样可以表示出来.可以看出,矩阵Φ3,5中的块最终能用Φ3,2、
3 性能分析
3.1 最小距离
定理6 由构造1中校验矩阵H1构造得到的(n, k, r, 2)aBLRCs的最小距离为d=3.
证明 通过观察构造1中校验矩阵H1可知,由于关联矩阵M的列重为2,且关联矩阵M的右边是一个单位矩阵,所以校验矩阵H1中存在线性相关的3列.因此,构造得到的LRCs的最小距离d≤3.另一方面,从校验矩阵中任取两列,若两列都来自关联矩阵M或两列都来自单位矩阵I(m+1),显然它们线性无关;若一列来自关联矩阵M,另一列来自单位矩阵I(m+1),由于列重不同,它们必然线性无关.因此,构造得到的BLRCs的最小距离d≥3.综上可知,构造1构造的BLRCs的最小距离为d=3.
定理7 由构造2中校验矩阵H2构造得到的信息符号可以实现任意局部性r>2和任意可用性t>2的(n, k, r, t)iBLRCs是最小距离最优的BLRCs,且码的最小距离d=t+1.
证明 由构造2中的校验矩阵H2可知,矩阵Φm,p的列重为p,且矩阵Φm,p的右边是一个单位矩阵,可知从矩阵Φm,p中任选一列是单位阵中p列的线性组合,即校验矩阵H2中存在线性相关的p+1列.因此,由校验矩阵H2构造得到的BLRCs的最小距离d≤p+1.另一方面,根据矩阵Φm,p的形式可知,矩阵Φm,p的行重为m,列重为p,每列“1”元素所在p行中任意两行的支撑集只在该元素处相交,因此每个信息符号的修复局部性为m且具有p个不相交的修复集.根据定理1,最小距离应满足d≥p+1.综上所述,可知由校验矩阵H2构造所得的BLRCs的最小距离d=p+1.
又因为由校验矩阵H2构造的BLRCs的参数满足
n=(m+1)(m+2)…(m+p)/p!
k=m(m+1)…(m+p-1)/p!
r=m, t=p
将这些参数代入式(3),可得:
因为p=t,所以构造出的BLRCs的最小距离d=t+1,且达到了式(3)中的最小距离边界,即该码是最小距离最优的BLRCs,证毕.
3.2 构造参数分析
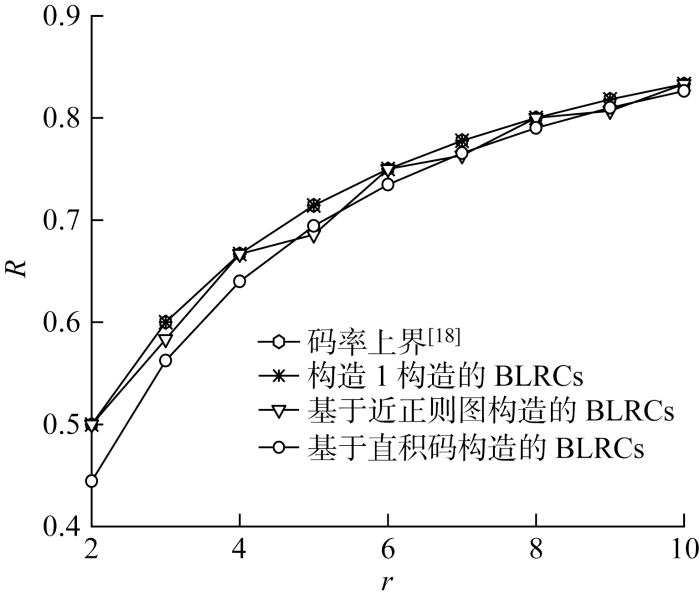
由表1可知,当可用性t=2时,有
表1 构造1参数比较分析
Tab.1
即由构造1构造的BLRCs的码率高于基于直积码构造的BLRCs的码率.虽然基于直积码构造的BLRCs 的最小距离大于构造1构造的BLRCs最小距离,但当局部性r>1时,由于
即构造1构造的BLRCs的相对距离大于基于直积码构造的BLRCs的相对距离.当r|2k且2k=r(r+2)时,基于近正则图构造的BLRCs的相对距离
即基于近正则图构造的BLRCs的相对距离小于构造1构造的BLRCs.构造1构造的BLRCs与基于单位矩阵变换构造的BLRCs能够达到相同的最小距离和码率,但是当局部性r取相同值并且r>1时,可知其相对距离
即构造1构造的BLRCs的相对距离大于基于单位矩阵变换构造的BLRCs.
图2
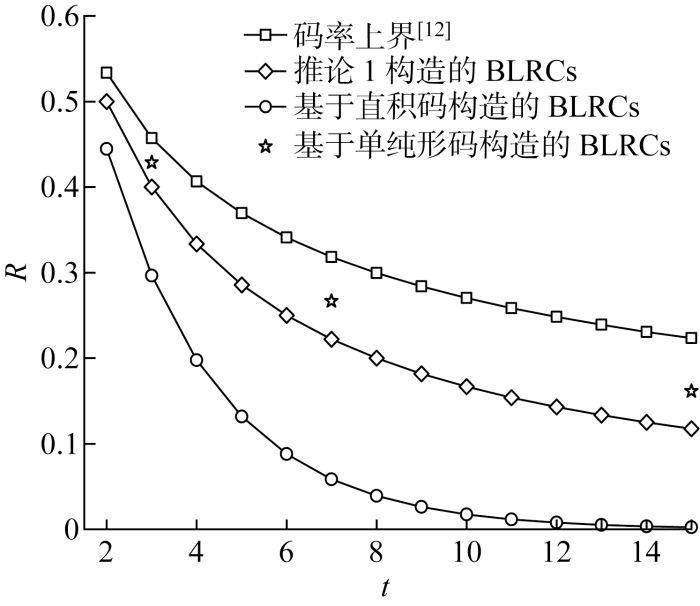
由于推论1仅能构造局部性r=2的BLRCs,将其与基于单纯形码构造的BLRCs以及基于直积码构造的BLRCs进行比较.由表2可知,当基于直积码构造的BLRCs的局部性取为(2,t)且t>1时,有
表2 推论1参数比较分析
Tab.2
即由推论1得到的BLRCs的码率高于基于直积码构造的BLRCs.此外,由推论1得到的BLRCs的相对距离也大于基于直积码构造的BLRCs.基于单纯形码仅能构造可用性t=2m-1-1的BLRCs,限制了可用性的参数选择,而基于推论1可以构造具有任意可用性的BLRCs.
图3
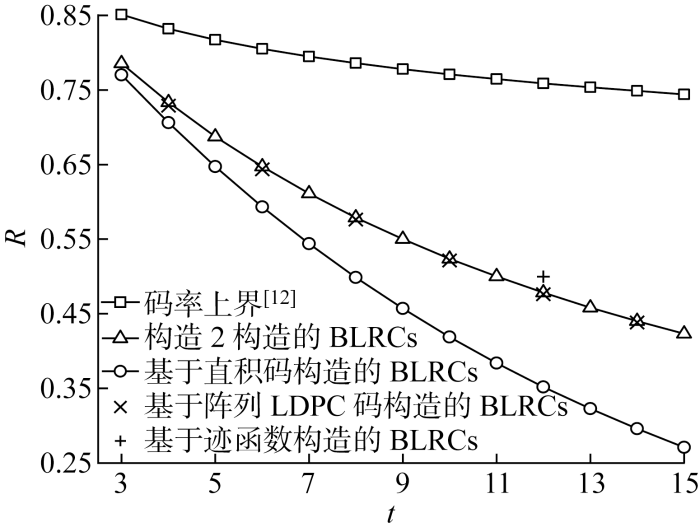
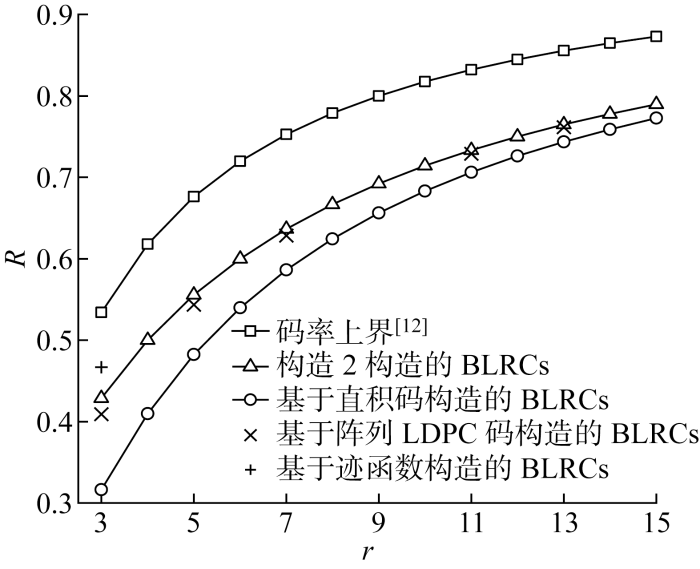
由构造2可以构造任意局部性r>2和可用性t>2的BLRCs,将其与基于迹函数构造的BLRCs、基于超图构造的BLRCs、基于阵列LDPC码构造的BLRCs以及基于直积码构造的BLRCs进行比较.由表3可知,将码的局部性都取为(r,t),当t>2时,可知
表3 构造2构造参数比较分析
Tab.3
因此基于直积码构造的BLRCs的码率
经分析可知,构造2构造的BLRCs的码率总高于基于直积码构造的BLRCs.由于
即构造2构造的BLRCs的码率总高于基于阵列LDPC码构造的BLRCs.基于迹函数构造出的BLRCs 需要满足可用性t=r+1,只能构造特定参数的BLRCs,具有较大的参数限制,并且仅能构造码率
图4
图5
4 结语
局部修复码能够有效实现分布式存储系统对海量数据的高可靠、高效率存储.提出基于三角形结合方案及其扩展的BLRCs构造方法,可以得到具有任意(r,t)局部性BLRCs.运用三角形结合方案的结合关系,基于校验矩阵构造可用性t=2的BLRCs,进一步基于生成矩阵构造局部性r=2的BLRCs;为了使BLRCs的参数选择更加灵活,对基于三角形结合方案构造的BLRCs进行扩展,进一步构造能够实现任意局部性r>2和任意可用性t>2的BLRCs.构造的具有(r,2)局部性的BLRCs达到了最优码率界;构造的具有任意局部性r>2和可用性 t>2的BLRCs达到了最优最小距离界.分析表明,与基于近正则图构造的BLRCs以及基于直积码构造的BLRCs等相比,本文构造的BLRCs在码率上表现更优且参数选择更灵活.
参考文献
Singleton-optimal LRCs and perfect LRCs via cyclic codes
[C]//
Locally repairable codes: Joint sequential-parallel repair for multiple node failures
[J].
Locally repairable codes
[J].
Bounds for binary linear locally repairable codes via a sphere-packing approach
[J].
On the locality of codeword symbols
[J].
Optimal locally repairable codes of distance 3 and 4 via cyclic codes
[J].
Explicit construction of optimal locally recoverable codes of distance 5 and 6 via binary constant weight codes
[J].
Bounds and constructions of locally repairable codes: Parity-check matrix approach
[J].
On the locality of some optimal ternary codes with dimension 6
[C]//
Optimal locally repairable systematic codes based on packings
[J].
Locality and availability in distributed storage
[J].
Bounds on locally recoverable codes with multiple recovering sets
[C]//
Two classes of (r, t)-locally repairable codes
[C]//
On the single-parity locally repairable codes with availability
[C]//
Bounds on the rate and minimum distance of codes with availability
[C]//
Hypergraph-based binary locally repairable codes with availability
[J].
Two classes of optimal LRCs with information (r, t)-locality
[J].
Codes with locality for two erasures
[J].
Binary codes with locality for multiple erasures having short block length
[C]//
Construction of binary locally repairable codes with optimal distance and code rate
[J].
Achieving arbitrary locality and availability in binary codes
[C]//