基于灰狼算法的风-光-抽水蓄能联合系统多目标优化策略

doi:10.16183/j.cnki.jsjtu.2023.049

基于灰狼算法的风-光-抽水蓄能联合系统多目标优化策略

张良¹, 郑丽冬^,¹, 冷祥彪², 吕玲¹, 蔡国伟¹

1.东北电力大学电气工程学院,吉林吉林 132012

2.南方电网能源发展研究院有限责任公司,广州 510670

Multi-Objective Optimization Strategy for Wind-Photovoltaic-Pumped Storage Combined System Based on Gray Wolf Algorithm

ZHANG Liang¹, ZHENG Lidong^,¹, LENG Xiangbiao², LÜ Ling¹, CAI Guowei¹

1. School of Electrical Engineering, Northeast Electric Power University, Jilin 132012, Jilin, China

2. Southern Power Grid Energy Development Research Institute Co., Ltd., Guangzhou 510670, China

通讯作者: 郑丽冬,硕士生;E-mail:1579745352@qq.com.

责任编辑: 王历历

收稿日期: 2023-02-13 修回日期: 2023-04-28 接受日期: 2023-05-19

基金资助:

吉林省科技厅重点研发项目资助(20220203052SF)
吉林省科技厅国际科技合作项目(20210402080GH)

Received: 2023-02-13 Revised: 2023-04-28 Accepted: 2023-05-19

作者简介 About authors

张良(1985—),博士,副教授,从事智能微电网、V2G信息交互等方向的研究.

摘要

风电、光伏的出力具有随机性、波动性以及间歇性,直接并网将会造成电站发电收益降低和电能并网波动性较大以及风、光弃电量较多等问题,降低碳减排量.抽水蓄能电站的加入可在一定程度上缓解上述问题.因此,针对风-光-抽水蓄能联合发电应用场景进行研究,建立综合考虑联合系统经济收益最大化、系统功率波动最小化以及碳减排量最大化3个目标的多目标优化模型,并通过归一化处理,将多目标问题转换成单一目标问题进行求解.采用能够实现局部搜索与全局搜索自适应调整的灰狼算法,对风电、光伏以及抽水蓄能的并网电量进行优化仿真.仿真结果表明:所建立的模型能够有效提高系统的经济收益,大大降低电能并网波动性.同时,新能源的高效利用也使得联合系统的碳减排能力显著提高,模型具备较高的可行性.

关键词： 碳减排; 多目标优化; 归一化处理; 灰狼算法

Abstract

The output of wind power and photovoltaic has the characteristics of randomness, volatility, and intermittency. Direct grid connection will lead to a lower power generation income of the power station, a greater volatility of grid connection of electric energy, and more wind and photovoltaic power discards, resulting in lower carbon emission reductions. The addition of pumped storage power plants effectively reduces the above impacts. Therefore, this paper studies the application scenario of wind photovoltaic and pumped storage combined power generation, establishes a multi-objective optimization model that comprehensively considers the three objectives of maximizing the economic benefits of the combined system, minimizing the system power fluctuation, and maximizing carbon emission reduction, and converts the multi-objective problem into a single objective problem for solution by normalization. In this paper, the gray wolf algorithm, which can realize the adaptive adjustment of local search and global search, is used to simulate and optimize the grid connected power of wind power, photovoltaic, and pumped storage. The optimization results show that the established model can effectively improve the economic benefits of the system and greatly reduce the fluctuation of power grid connection. In addition, the efficient use of new energy also greatly improves the carbon emission reduction capacity of the joint system, which proves that the model has high feasibility.

Keywords： carbon emission reduction; multi-objective optimization; normalization; gray wolf algorithm

PDF (4752KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张良, 郑丽冬, 冷祥彪, 吕玲, 蔡国伟. 基于灰狼算法的风-光-抽水蓄能联合系统多目标优化策略[J]. 上海交通大学学报, 2024, 58(10): 1554-1566 doi:10.16183/j.cnki.jsjtu.2023.049

ZHANG Liang, ZHENG Lidong, LENG Xiangbiao, LÜ Ling, CAI Guowei. Multi-Objective Optimization Strategy for Wind-Photovoltaic-Pumped Storage Combined System Based on Gray Wolf Algorithm[J]. Journal of Shanghai Jiaotong University, 2024, 58(10): 1554-1566 doi:10.16183/j.cnki.jsjtu.2023.049

工业革命以来,化石能源的大量开采以及二氧化碳的过度排放导致全球气候变暖,给人类的生产生活造成多方面的影响.为了阻止人类与自然环境相互危害的恶性循环,中国主动采取措施,提出“双碳”目标,力争二氧化碳排放在2030年前达到峰值,并在2060年前实现碳中和.“双碳”目标愿景推动了可再生能源发展,构建以新能源为主体的新型电力系统上升为国家战略层面的重大决策部署.

我国是一个风、光资源丰富的国家,对新能源的利用已遍布众多领域.但由于天气具有不确定性,风力发电和光伏发电出力的周期性、间歇性和随机性都很强,导致风、光发电量波动性较大,并网将对电网稳定运行造成严重影响^[1⇓-3].为风、光发电配备一定的储能装置可以在很大程度上提升电网对风、光电站波动性出力的消纳能力,从而增强电网的稳定性^[4].抽水蓄能方式具有技术较为成熟、启停迅速、灵活可靠、容量大等优点,在有利环境下是储能设备的首选,在社会上也引起广泛关注^[5].

文献[6]中以最小化风电-抽水蓄能联合系统发电成本为目标,在目标求解过程中确定最佳自弹性系数和互弹性系数,运用基于实时电价的需求价格来弹性引导电力用户以实现负荷转移.仿真结果表明,需求侧资源主动参与优化调度可降低负荷峰谷差,利于系统稳定运行,并且可以减少发电成本,提高联合系统经济性.

文献[7]中将风电场和抽水蓄能电站联合调度,建立风-蓄联合运行效益最大和风-蓄联合出力波动方差最小的多目标优化调度模型,模型求解采用归一化的多目标处理策略,实验结果验证了抽水蓄能电站在提高风电场运行效益以及风电接入能力方面的优势,也证明了该多目标模型的可行性和有效性.

文献[8]中针对风电和抽水蓄能以及火电出力的不同特性,建立内外两层模型嵌套求解.内层模型为风蓄联合运行收益最大和风电入网波动最小的双目标模型,决定了抽水蓄能机组的抽水功率或发电功率,再在外层建立计及不同置信水平风电预测误差的风蓄火联合收益最大的目标模型.采用粒子群优化-遗传算法混合优化算法求解模型,并利用IEEE 30节点系统验证了该模型在增加系统经济效益的同时可以降低风电出力波动性.

文献[9]中建立抽水蓄能与风电、光伏多能互补系统综合出力与需求偏差最小为目标函数的优化模型,利用整型非线性规划优化模型分析规模配比和初始蓄能量对多能互补系统出力效果的影响.结果表明,经抽水蓄能调节,综合出力与需求偏差的均方差可大幅度减小.

文献[10]中构建不同装机容量场景下风电-光伏-抽水蓄能混合发电系统的包括技术经济效益、财务效益、社会效益和环境效益的经济评价模型,并且在社会和环境效益指数中考虑碳排放的影响.采用组合加权法对各指标进行加权,再采用非线性加权法计算总分.最后,应用该模型对22种场景下的混合动力系统进行求解和分析.结果表明,综合经济效益与装机容量之间存在非线性相关关系,并在一定范围内存在经济效益的局部最大值.

文献[11]中以风-光-抽水蓄能联合系统的经济收益最大化为目标建立优化配置模型;文献[12 ⇓-14]中同时兼顾联合系统经济收益最大以及系统功率波动最小两个目标,建立联合系统优化模型.以上文献通过算法求解均验证了模型的有效性以及联合系统的优越性.

然而,上述文献中不论是风-蓄联合运行还是风-光-蓄联合运行,都仅考虑系统的经济效益、功率波动中的一个或者两个目标,并没有考虑到当前全球碳排放形势,将碳排放指标加入在内.在上述文献基础上,采用灰狼优化(grey wolf optimization, GWO)算法对风电、光伏与抽水蓄能电站联合调度策略进行研究,通过建立考虑联合系统经济收益最大化、并网有功功率平均波动率最小化以及碳减排量最大化的多目标优化模型,对风电、光伏和抽水蓄能机组的出力进行优化.求解过程中,分时电价机制可能导致在某些电价低谷时段联合系统为追求整体经济效益最优而减小并网电量.并网电量减小会使碳减排量降低,这与碳减排量最大的目标矛盾.为此,另外考虑到联合系统并网电量尽可能大以及弃电量尽可能小两个因素,将3个目标函数归一化处理,并结合我国某地实际案例,验证所提风-光-抽水蓄能联合运行优化方法的可行性与有效性.

1 风-光-抽水蓄能联合系统结构

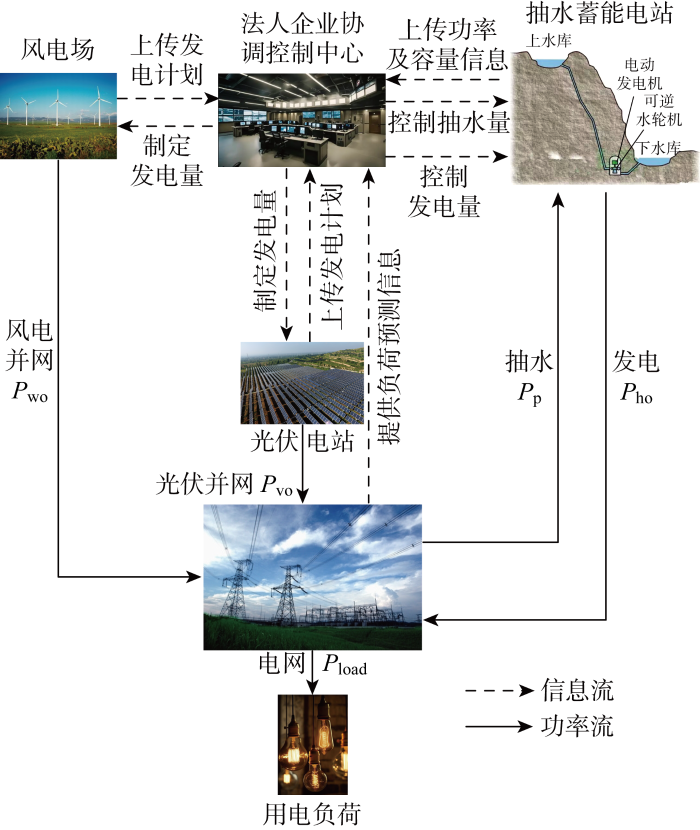
风、光是两种不稳定的能源.通常,我国大部分地区夜间风速较大而白天尤其是中午光照强度较强,这段时间内将出现较为严重的弃电情况.相反,在其他时段,风、光出力大大降低,无法维持电力用户正常的用电需求.抽水蓄能作为一种特殊的储能装置,其时空转移特性能够将风、光发电高峰时段的发电量存储起来并转移到低谷时段发出,从而实现将不稳定的电源转变成可调控的稳定电源发电供电,达到能源高效利用的目的^[15].然而,风电场、光伏电站、抽水蓄能电站不归属于同一发电公司管理,三方均作为独立主体参与电力市场交易.为了对其进行统一的能量调度,采取“联合”经营模式,将风、光发电机组以及抽水蓄能机组组成运行联合体,并使其由同一法人企业管理^[16].法人企业建立协调控制中心收集风、光发电计划以及抽水蓄能的功率和库容信息,并获取到电网的负荷预测信息,从而制定各个发电单元的发电或用电计划.为此,建立风-光-抽水蓄能联合系统,其结构如图1所示.图中:P_wo、P_vo、P_ho分别为风电、光伏、抽水蓄能的上网功率;P_p为抽水蓄能的抽水功率;P_load为电力系统用户负荷功率.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 风-光-抽水蓄能联合系统结构

Fig.1 Structure of wind-photovoltaic-pumped storage combined system

在风、光子系统发电量较高,甚至超过系统负荷时,超出的能量就可以用来启动水泵,将抽水蓄能电站下水库的水抽到上水库,实现电能到水的重力势能的转移和储存.当风、光子系统发电量不足时,抽水蓄能电站将水从上水库放回到下水库,并带动水轮机组运行,将水的重力势能转变回电能,以满足电网用电需求^[17].

2 风-光-抽水蓄能联合系统多目标优化模型

综合考虑风-光-抽水蓄能联合系统经济收益最大化、并网有功功率平均波动率最小化以及碳减排量最大化3个目标,建立风-光-抽水蓄能联合系统优化模型^{[18⇓⇓-21]}.

2.1 目标函数

2.1.1 经济效益最大化目标

考虑联合系统并网运行的经济效益最大化,同时也考虑到弃风弃光的惩罚费用,但不考虑抽水蓄能机组启停成本,所得目标函数如下:

(1)$ \begin{aligned} F_{1}= & \sum_{i=1}^{T} C_{i}\left(P_{i}^{\mathrm{wo}}+P_{i}^{\mathrm{vo}}+P_{i}^{\mathrm{ho}}\right)- \\ & C_{i}^{\mathrm{p}} P_{i}^{\mathrm{p}}-C^{\mathrm{r}}\left(P_{i}^{\mathrm{wr}}+P_{i}^{\mathrm{vr}}\right) \end{aligned}$

(2)$ \left.\begin{array}{l} P_{i}^{\mathrm{ho}}=P_{i}^{\mathrm{ph}}, \quad P_{i}^{\mathrm{ph}}>0 \\ P_{i}^{\mathrm{p}}=-P_{i}^{\mathrm{ph}}, \quad P_{i}^{\mathrm{ph}}<0 \end{array}\right\}$

式中: $P_{i}^{w o}$ 、 $P_{i}^{v o}$ 、 $P_{i}^{h o}$ 分别为第i时刻风电、光伏、抽水蓄能的上网功率; ${P^{p}}_{i}$ 为第i时刻抽水蓄能的抽水功率; $P_{i}^{p h}$ 为第i时刻抽水蓄能机组的功率; $P_{i}^{w r}$ 、 $P_{i}^{v r}$ 分别为弃风、弃光量;C_i为上网电价; ${C^{p}}_{i}$ 为抽水电价;C^r为弃风弃光惩罚电价.

2.1.2 碳减排量最大化目标

考虑将火力发电机组替换为风-光-抽水蓄能联合发电系统,反映碳减排量的目标函数^[22⇓-24]如下:

(3)$ \max F_{2}=G_{\mathrm{CO}_{2}} S_{\text {coal }} \sum_{i=1}^{T} t\left(P_{i}^{\mathrm{wo}}+P_{i}^{\mathrm{vo}}+P_{i}^{\mathrm{ho}}\right)$

式中: $G_{C O_{2}}$ 为煤燃烧产生二氧化碳的量;S_coal为清洁能源发电换算成火力发电的煤耗量; $\overset{T}{\sum_{i = 1}}$ t( $P_{i}^{w o}$ + $P_{i}^{v o}$ + $P_{i}^{h o}$ )为联合系统发电并网的总电量;t为时间长度.

2.1.3 并网有功功率平均波动率最小化目标

考虑联合系统发电并网对电网稳定性以及电能质量影响,需要使联合系统发电功率波动最小.采用功率平均波动指数来衡量联合系统输出功率的平稳度,目标函数如下:

(4)λ=

\frac{1}{P_{r e f}} \sqrt{\frac{1}{T} \overset{T}{\sum_{t = 1}} (P_{e} (t) - P_{r e f})^{2}}

式中:P_e(t)为t时刻联合系统输出功率;P_ref为联合系统输出功率的平均值;T为优化周期.

2.2 约束条件

2.2.1 输出功率平衡约束

表示为

(5)

{P^{w}}_{i}

{P^{v}}_{i}

P_{i}^{w o}

P_{i}^{v o}

{P^{p}}_{i}

P_{i}^{w r}

P_{i}^{v r}

(6)

\begin{array}{l} 0 \leq P_{i}^{w o} \leq {P^{w}}_{i} \\ 0 \leq P_{i}^{v o} \leq {P^{v}}_{i} \end{array}\}

式中: ${P^{w}}_{i}$ 、 ${P^{v}}_{i}$ 分别为第i时刻风电和光伏的预测出力.

2.2.2 电网接收功率约束

表示为

(7)(1-ω)

P_{i}^{l o a d}

P_{i}^{w o}

P_{i}^{v o}

P_{i}^{h o}

≤(1+ω)

P_{i}^{l o a d}

式中: $P_{i}^{l o a d}$ 为第i时刻的预测负荷值;ω为上网功率与负荷的最大允许偏差,根据文献[25],最大允许偏差取10%相比于无最大允许偏差,收益下降0.2%,但惩罚费用下降49.1%;而最大允许偏差取5%相比于10%,收益下降0.4%,但惩罚费用下降38.5%,因此最大允许偏差取ω=5%.

2.2.3 正负旋转备用约束

表示为

(8)

\begin{array}{l} ({P^{w}}_{i} - P_{i}^{w o}) + ({P^{v}}_{i} - P_{i}^{v o}) + \\ (P_{i}^{p h, m a x} - P_{i}^{p h}) \geq {R^{u}}_{i} \\ P_{i}^{p h} - P_{i}^{p h, m i n} \geq {R^{d}}_{i} \end{array}\}

式中: $P_{i}^{p h, m a x}$ 、 $P_{i}^{p h, m i n}$ 分别为第i时刻抽水蓄能的最大和最小输出功率; ${R^{u}}_{i}$ 、 ${R^{d}}_{i}$ 分别为系统第i时刻的正、负旋转备用需求.

《电力系统事故备用容量配置技术规范》指出,负荷备用容量的大小一般为最大负荷的2%~5%,大型电力系统采用较小值,小型电力系统采用较大值.本文按照小型电力系统标准取5%.

2.2.4 抽水蓄能输出功率约束

表示为

(9)

P_{i}^{p h, m i n}

≤

P_{i}^{p h}

≤

P_{i}^{p h, m a x}

(10)

\begin{array}{l} P_{i}^{p h, m i n} = m a x {- ({P^{w}}_{i} + {P^{v}}_{i}), \\ - P^{p, m a x}, - \frac{{E^{d}}_{i}}{t η_{p}}} \\ P_{i}^{p h, m a x} = m i n \{P^{h o, m a x}, \frac{{E^{u}}_{i}}{t η_{h}}\} \end{array}\}

式中:P^p^,^max为抽水功率最大值;P^ho^,^max为发电功率最大值;η_p、η_h分别为水泵的抽水效率和水轮机组的发电效率; ${E^{u}}_{i}$ 、 ${E^{d}}_{i}$ 分别为第i时刻上下水库的容量.

2.2.5 抽水蓄能水库库容约束

表示为

(11)

\begin{array}{l} E_{m i n}^{u} \leq {E^{u}}_{i} \leq E_{m a x}^{u} \\ E_{m i n}^{d} \leq {E^{d}}_{i} \leq E_{m a x}^{d} \end{array}\}

(12)

\begin{array}{l} {E^{u}}_{i + 1} = {E^{u}}_{i} + (t {P^{p}}_{i} η_{p} - \frac{t P_{i}^{h o}}{η_{h}}) \\ {E^{d}}_{i + 1} = {E^{d}}_{i} + (\frac{t P_{i}^{h o}}{η_{h}} - t {P^{p}}_{i} η_{p}) \end{array}\}

式中: $E_{m i n}^{u}$ 、 $E_{m a x}^{u}$ 分别为上水库容量的最小值和最大值; $E_{m i n}^{d}$ 、 $E_{m a x}^{d}$ 分别为下水库容量的最小值和最大值.

2.3 多目标问题处理方法

所建立的模型包含3个优化目标,采用归一化的处理方式,将多目标问题转换成单目标问题进行求解,从而降低求解难度.

由于3个目标函数的数量级以及量纲之间不同,所以不能简单地通过对目标加权求和来求解.为了如实反映引入抽水蓄能前后风光发电厂的经济性、风光并网波动性以及碳减排量的变化,可以将风光联合系统并网运行时,系统的经济效益、输出功率平均波动率以及碳减排量作为衡量基准,将3个目标函数做归一化处理,则原来的多目标函数^[14]可以表示为

(13)$ \begin{aligned} \min F= & \omega_{1}\left(F_{1 \mathrm{wp}}^{\prime} / F_{1}\right)+\omega_{2}\left(F_{2 \mathrm{wp}}^{\prime} / F_{2}\right)+ \\ & \omega_{3}\left(\lambda / \lambda_{\mathrm{wp}}^{\prime}\right) \end{aligned}$

式中:F为多目标函数归一化值;F'₁_wp为风光发电系统联合运行时的总收益;F'₂_wp 为风光系统联合运行时的碳减排量;λ'_wp为风光系统联合运行时输出功率的平均波动率;ω₁、ω₂、ω₃为3个子目标所赋予的权重值.

ω₁、ω₂、ω₃的值通过层次分析法(analytical hierarchy process, AHP)来确定,主要步骤如下:

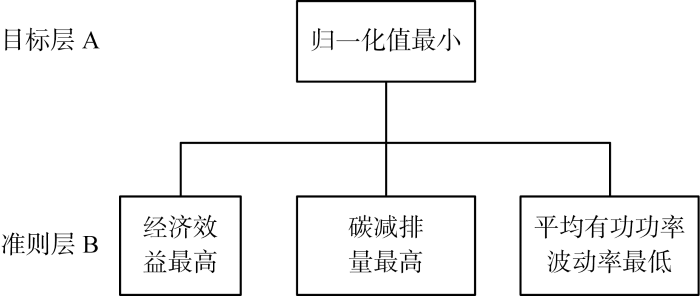
(1) 建立层次结构模型.首先,将模型分为目标类及其准则类;然后,根据构建各因素之间相互关联的层次结构对各因素赋权;最后,计算相对权数,得到优劣次序.AHP的层次结构模型如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 层次结构模型

Fig.2 Hierarchy model of AHP

(2) 构建判断矩阵.对各因素进行两两比较,使用1~9标度法将其重要程度赋予相应的数值,其中1~9标度定义如表1所示.专家根据表1打分,量化后得到的判断矩阵如下:

(14)A=

[\begin{array}{l} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{array}]

表1 1~9标度定义表

Tab.1 Definition of Scale 1~9

标度	定义
1	表示两个元素相比,具有同等重要性
3	表示两个元素相比,一个元素比另一个元素稍微重要
5	表示两个元素相比,一个元素比另一个元素明显重要
7	表示两个元素相比,一个元素比另一个元素强烈重要
9	表示两个元素相比,一个元素比另一个元素极端重要
2,4,6,8	上述相邻判断的中值

新窗口打开| 下载CSV

(3) 层次单排序及一致性检验.计算判断矩阵每行所有元素积的方根如下:

(15)$ \bar{\omega}_{l}=\sqrt[n]{\prod_{j=1}^{n} b_{l j}}, \quad l=1,2,3$

(16)$ \bar{\omega}=\left\{\bar{\omega}_{1}, \bar{\omega}_{2}, \bar{\omega}_{3}\right\}$

将 $\bar{ω}$ 进行归一化,即

(17)ω_l=

\frac{{\bar{ω}}_{l}}{\overset{3}{\sum_{j = 1}} {\bar{ω}}_{j}}

, l=1, 2, 3

由此可以得到ω₁、ω₂、ω₃的值.

3 灰狼优化算法

GWO通过模拟灰狼种群捕食猎物的行为,并基于种群内部相互协作的机制达到优化的目的.GWO算法具有结构简单、需要调节的参数少、容易实现等特点,存在能够自适应调整的收敛因子以及信息反馈机制,能够在局部寻优与全局搜索之间实现平衡,因此在对问题的求解精度和收敛速度方面都有良好性能^[26-27].

3.1 灰狼算法优化原理

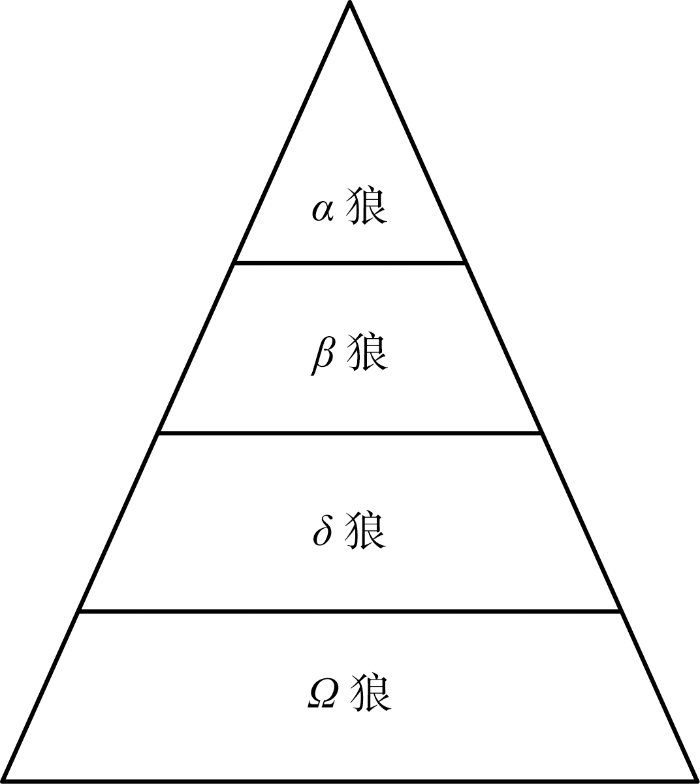
(1) 狼群等级划分.狼群中每匹狼都有自己的角色定位,它们的社会等级制度如图3所示.其中,α狼为狼群的决策者,代表模型的最优解;β狼负责协助α狼进行决策,代表模型的次优解;δ狼听从α狼以及β狼的命令,代表模型的一般解;Ω狼是最底层的狼,主要作用是维持狼群内部关系平衡,代表模型的候选解.在寻优过程中,Ω狼会根据α、β以及δ狼的位置来更新自己的位置,如果上层狼的适应度不好,则会逐级被下一层的狼所取代.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 灰狼的社会等级制度

Fig.3 Social hierarchy of gray wolves

(2) 包围猎物.在狼群捕食猎物过程中,将它们的行为作如下定义:

(18)D=

|C X_{P} (k) - X (k)|

(19)X(k+1)=X(k)-AD

式(18)表示灰狼个体与猎物之间的距离,式(19)表示灰狼位置的更新.另外,D为灰狼个体与猎物间距离;k为当前种群迭代次数,X_P、X分别为猎物的位置和灰狼的位置.A和C为系数向量,计算公式如下:

(20)A=2ar₁-a

(21)C=2r₂

式中:a为收敛因子,数值从2线性减小到0;r₁和r₂的大小取[0,1]之间的随机数.当 $|A|$ >1时,候选解远离最优解,进行全局搜索;当 $|A|$ <1时,候选解逼近最优解,进行局部搜索.C的作用是在整个迭代过程中,提供种群在决策空间中的全局搜索,避免寻优过程陷入局部最优. $|C|$ >1表示狼所在位置对猎物的影响权重大,反之则表示影响权重小.

(3) 捕食猎物.狼群在α、β以及δ狼的带领下不断靠近猎物,在这个过程中,它们的位置永远在动态变化,直到捕猎成功为止.这个过程可以用如下公式表示:

(22)

\begin{array}{l} D_{α} = |C_{1} X_{α} - X| \\ D_{β} = |C_{2} X_{β} - X| \\ D_{δ} = |C_{3} X_{δ} - X| \end{array}\}

(23)

\begin{array}{l} X_{1} = X_{α} - A_{1} D_{α} \\ X_{2} = X_{β} - A_{2} D_{β} \\ X_{3} = X_{δ} - A_{3} D_{δ} \end{array}\}

(24)$ \boldsymbol{X}(t+1)=\frac{\boldsymbol{X}_{1}+\boldsymbol{X}_{2}+\boldsymbol{X}_{3}}{3}$

式中:D_α、D_β、D_δ分别为狼群中其他个体与α、β以及δ之间的距离;X_α、X_β、X_δ分别为α、β以及δ狼当前的位置;X₁、X₂、X₃分别为受α、β以及δ狼的影响,种群其他个体所需要调整的位置, 式(24)则确定了它们的最终位置;A₁、A₂、A₃为系数向量,数值是[-2, 2]间的随机数.

3.2 灰狼算法参数调整策略

3.2.1 收敛因子非线性调整

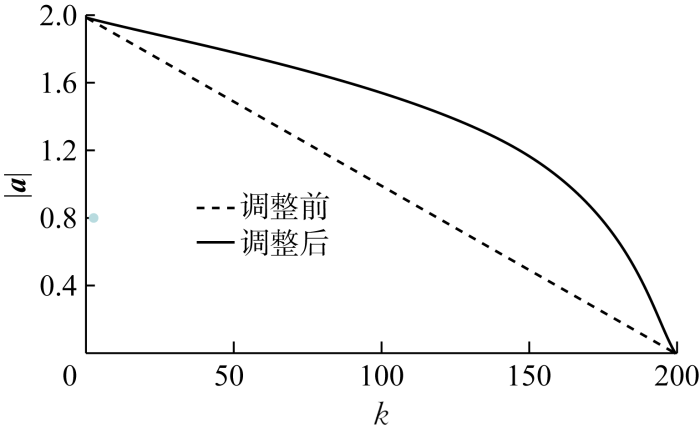
在基本灰狼算法中,收敛因子a的数值由2线性递减到0,控制灰狼对猎物进行搜索或攻击,这种方法的弊端是算法在迭代前期和后期搜索重点不明确,不利于搜寻全局最优解.对a进行非线性的调整如下:

(25)|a|=2

[1 - c o s (\frac{π}{2} \frac{k}{k_{m a x}})]

式中:k_max为灰狼种群最大迭代次数.

调整前和调整后的a收敛曲线如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 收敛因子调整前后对比

Fig.4 Convergence factors before and after adjustment

对于算法而言,较大的a值可以增大灰狼搜索步长,提高全局搜索能力;较小a值可以减小灰狼搜索步长,提高局部搜索能力.调整后的收敛因子a能够使算法在迭代前期更加注重全局搜索,在迭代中后期更加注重局部搜索,提高算法的收敛速度.

3.2.2 α、β以及δ狼的位置动态置信调整策略

基本灰狼算法的位置更新是将α、β以及δ狼在搜索猎物过程中置于同等地位,通过平均分配权重的方式来更新其他灰狼的位置,这并未体现出不同等级灰狼个体所具有的不同重要性.针对这种问题,给出一种基于高等级灰狼位置的动态置信调整策略,具体表达式如下:

(26)$ \begin{array}{l} \boldsymbol{X}(t+1)=\omega_{1}^{\prime} \boldsymbol{X}_{1}+\omega_{2}^{\prime} \boldsymbol{X}_{2}+\omega_{3}^{\prime} \boldsymbol{X}_{3} \\ \omega_{1}^{\prime}=4 / 9-3 k /\left(9 k_{\max }\right) \\ \omega_{2}^{\prime}=3 / 9 \\ \omega_{3}^{\prime}=2 / 9+3 k /\left(9 k_{\max }\right) \end{array}$

式中:ω'₁、ω'₂、ω'₃分别为α、β以及δ狼的置信度.

3.3 调整后的灰狼优化算法与灰狼优化算法、粒子

群优化算法的优劣性对比

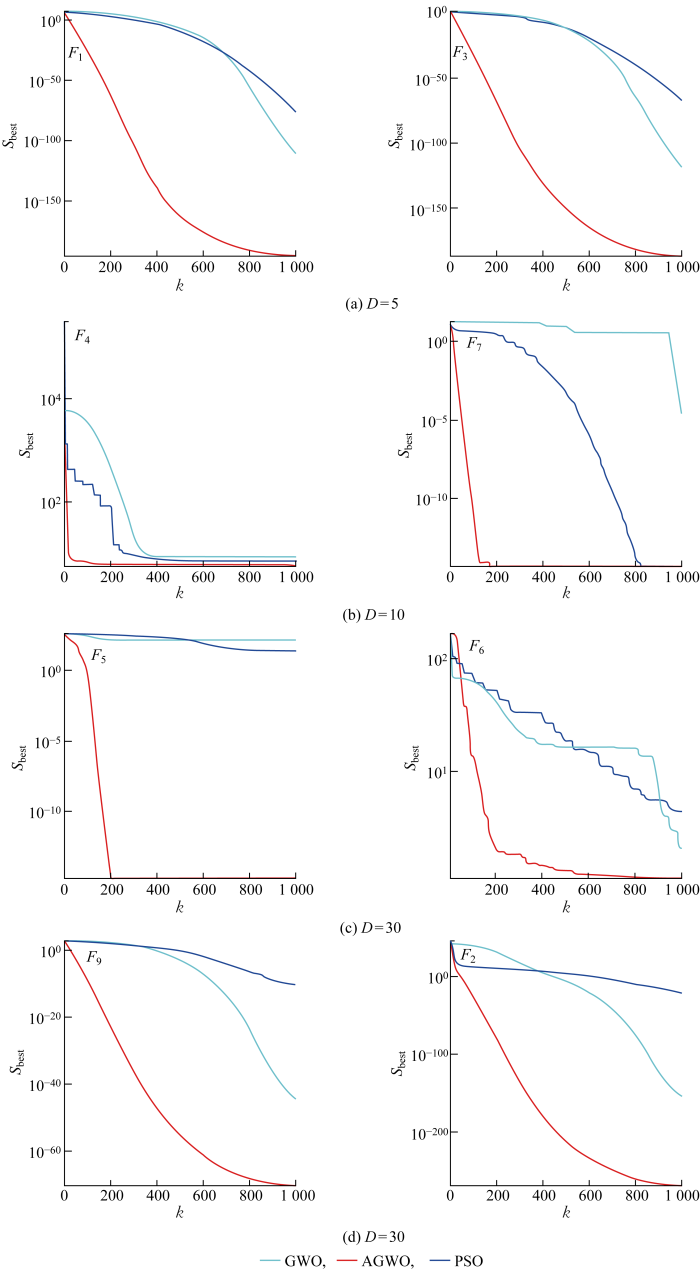
为了验证采用的调整后的灰狼优化(adjusted grey wolf optimization, AGWO)算法的寻优效果,将其与GWO、粒子群优化(particle swarm optimization, PSO)算法针对CEC测试函数的寻优结果进行对比分析.CEC标准测试函数集包括37个测试函数,维度从2~30不等,选取其中8个分别为5、10、30维度的测试函数进行测试.各个算法的参数具体设定如下:PSO的学习因子c₁、c₂设定为2,粒子的最大移动速度设定为6,惯性权重的最大值和最小值分别取为0.9、0.2;GWO的收敛因子a初值设定为2,并线性减小到0,系数A 赋予 [-2, 2]区间内的随机初值,C 赋予[0,2]区间内的随机初值;AGWO的收敛因子a初值设定为2,并非线性减小到0,系数A和C的赋值方式同GWO相同.3种算法的种群规模与迭代次数分别设为100、1 000,得到的寻优结果迭代曲线如图5所示.图中:F₁~F₇、F₉为测试函数;S_best为当前最优解.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 AGWO与GWO以及PSO的寻优结果对比

Fig.5 Comparison of optimization results of AGWO, GWO and PSO

由图5可知,AGWO在求解过程中,在收敛速度以及求解精度方面都具有明显优势.使用算法对8个测试函数进行30次运行,取30次运行的平均值、标准差、最优值以及最小运行时间进行记录,如表2所示.

表2 CEC标准测试函数测试结果

Tab.2 Test results of CEC standard test function

测试函数	维度	指标	GWO	PSO	AGWO	函数最优解
F₁	5	平均值	1.0586×10^-111	1.56837×10^-75	2.8089×10^-189	0
		标准差	2.0204×10^-111	4.78018×10^-75	0
		最优值	4.7246×10^-117	5.66403×10^-82	2.0224×10^-200
		最小运行时间/s	0.0625	0.0938	0.0625
F₃	5	平均值	5.1416×10^-110	3.03639×10^-66	5.6786×10^-185	0
		标准差	1.562×10^-109	9.38151×10^-66	0
		最优值	4.9023×10^-120	2.03774×10^-70	2.0189×10^-189
		最小运行时间/s	0.1250	0.1250	0.0313
F₄	10	平均值	8.206186494	6.925003246	6.038853119	0
		标准差	0.976010289	0.14160085	0.740366322
		最优值	6.25242962	6.662404072	4.946185531
		最小运行时间/s	0.1406	0.1406	0.0938
F₇	10	平均值	0.001194785	3.9968×10^-15	3.9968×10^-15	0
		标准差	0.003769227	0	0
		最优值	3.9968×10^-15	3.9968×10^-15	3.9968×10^-15
		最小运行时间/s	0.0938	0.125	0.0781
F₅	30	平均值	114.3494578	38.2086689	0	0
		标准差	19.73841416	9.941091481	0
		最优值	94.33174368	22.88404825	0
		最小运行时间/s	0.2031	0.2188	0.1406
F₆	30	平均值	23.30240464	4.262098719	0.916806479	0
		标准差	18.33678485	2.204487459	0.253678272
		最优值	2.041006692	2.295927461	0.382751422
		最小运行时间/s	0.3133	0.3159	0.1560
F₉	30	平均值	1.2887×10^-43	7.0961×10^-12	1.58352×10^-72	0
		标准差	1.49665×10^-43	1.17089×10^-11	1.9561×10^-72
		最优值	5.75044×10^-45	1.34152×10^-13	1.41472×10^-73
		最小运行时间/s	0.1563	0.2031	0.0781
F₂	30	平均值	1.8676×10^-154	1.85983×10^-17	6.2139×10^-269	0
		标准差	5.8446×10^-154	5.86839×10^-17	0
		最优值	7.8137×10^-168	5.39049×10^-24	7.041×10^-285
		最小运行时间/s	0.4063	0.4219	0.3594

新窗口打开| 下载CSV

3.4 调整后灰狼算法优化流程

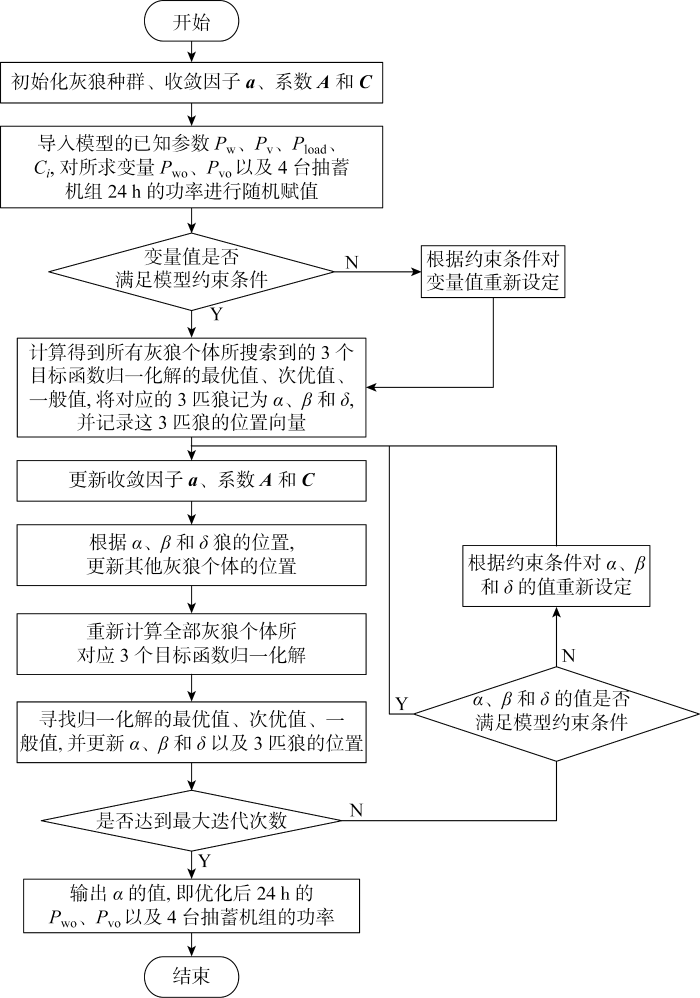
调整后GWO的流程图如图6所示,图中:P_w、P_v分别为风电和光伏输出功率.模型具体寻优步骤如下.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 调整后GWO优化流程图

Fig.6 Flow chart of adjusted GWO algorithm

(1) 对灰狼种群、收敛因子 a、系数A和C进行初始赋值,同时导入系统模型相关已知参数,对模型所求变量赋予随机初值,并确定算法的最大迭代次数.

(2) 判断对模型所求变量所赋的初始值是否满足模型的约束条件.若不满足,则需要对所赋初始值进行相应的调整;若满足,跳转到下一步.

(3) 计算出所有灰狼个体所搜索到得3个目标函数归一化解3个最优值,将对应的3匹狼记为α、β、δ.同时保存他们的位置向量,记为X_α、X_β、X_δ.

(4) 对收敛因子a、系数A和C按照式(20)、(21)、(25)进行更新.

(5) 根据公式(22)、(23)、(26)更新当前其他灰狼的位置.

(6) 重复步骤(3)并更新α、β、δ狼的适应度和位置.

(7) 判断是否达到最大迭代次数.若未达到最大迭代次数,判断α、β、δ的值是否满足模型约束条件.若不满足,则根据约束条件重新设定数值并跳转到步骤(4);若满足则直接跳转到步骤(4);若达到最大迭代次数,输出联合系统优化后的24 h的P_wo、P_vo以及4台抽蓄机组的功率值,算法结束.

4 算例分析

以中国某一包含一个风电场、一个光伏电站和一个抽水蓄能电站的电网为研究对象,以小时为时间节点,对该系统一天24 h的调度情况进行优化研究,并针对优化结果进行对比分析.

4.1 模型参数设置

4.1.1 风、光发电站输出功率及电力负荷预测值

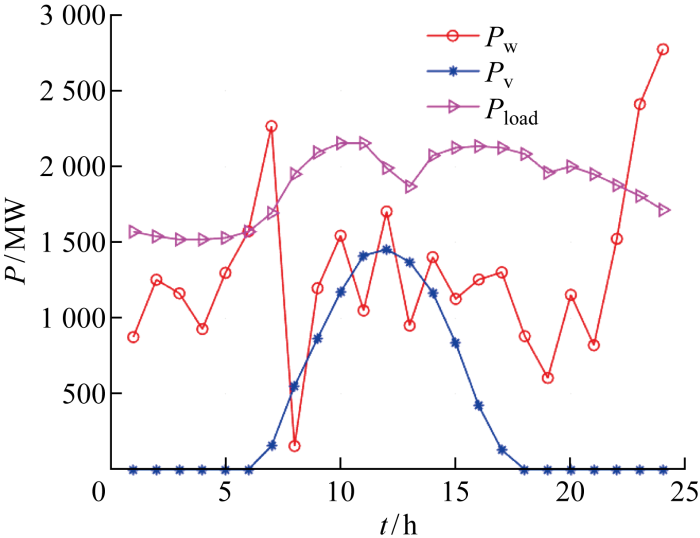
联合发电系统中风力发电和光伏发电的输出功率以及电力系统的负荷预测值如图7所示.图中:P为功率.由图可见,风光发电本身具有一定的互补特性,但当其无法满足电力系统负荷需求时,根据本文研究方向,采用抽水蓄能设备能够对其进行有效调节.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 风、光发电输出功率及电力负荷预测值

Fig.7 Output power of wind and photovoltaic power plants and power load forecast values

4.1.2 抽水蓄能电站基本参数

联合发电系统的功率范围及抽水蓄能系统的容量以及工作效率参数分别为:风力发电最大功率 $P_{m a x}^{w}$ 和光伏发电最大功率 $P_{m a x}^{v}$ 分别为 3000 和 1600 MW,最小功率 $P_{m i n}^{w}$ 、 $P_{m i n}^{v}$ 均为0 MW;抽水蓄能最大抽水功率 $P_{m a x}^{p}$ 及最大发电功率 $P_{m a x}^{h o}$ 均为300 MW,抽水效率η_p为0.87,发电效率η_h为0.9;抽水蓄能上下水库最大库容 $E_{m a x}^{u}$ 、 $E_{m a x}^{d}$ 及最小库容 $E_{m i n}^{u}$ 、 $E_{m i n}^{d}$ 分别为 2000 和 500 MW·h.

采用4台抽水蓄能机组同时工作,设定4台机组工作状态一致,即同时抽水或同时发电.另外,抽水蓄能上水库初始容量设定为 1500 MW·h,下水库初始容量设定为 1000 MW·h.

4.1.3 碳减排相关参数

根据中国煤炭燃烧实测平均数据,煤炭燃烧产生的CO₂量 $G_{C O_{2}}$ 的值为 1730.97 kg/t;根据2020年12月18日发布的《全国电力工业统计》,清洁能源发电转换成火力发电的煤耗量S_coal为304.7 g/(kW·h).

4.1.4 分时段电价

充分考虑电力市场峰平谷时段电价差异,结合本文研究区域电价情况,制定一天24 h电价如表3所示.

表3 研究区域24 h分时段电价

Tab.3 Twenty-four hours electricity price in study area

时间	C_i/[元·(MW·h)^-1]	时段
10:00—15:00	1289.3	峰值
18:00—21:00	1289.3	峰值
7:00—10:00	873.1	平值
15:00—18:00	873.1	平值
21:00—23:00	873.1	平值
23:00—7:00	457.0	谷值

新窗口打开| 下载CSV

采用分时段电价,可以更好地跟踪负荷变化,有利于算法的寻优进程,同时也能够提高社会效益与经济效益.此外,抽水蓄能的抽水电价 ${C^{p}}_{i}$ =0.25C_i,弃风弃光惩罚电价C^r=600元/(MW·h).

4.2 仿真结果分析

4.2.1 加入抽水蓄能前后模型目标函数值对比分析

抽水蓄能系统加入后,分别运用AGWO、GWO以及PSO对联合系统的经济效益、碳减排量及输出功率平均波动率进行优化,结果如表4所示.由表可见,加入抽水蓄能后,应用3种优化方法所得到的系统输出功率平均波动率较为接近,但针对系统经济效益以及碳减排量,AGWO具有较为明显的优势.AGWO优化后,平均每天的系统经济效益相比于GWO与PSO优化后分别提高290、270万元,系统碳减排量相比于GWO与PSO优化后分别高200、600 t.

表4 抽水蓄能加入前后模型目标函数值对比

Tab.4 Comparison of model objective function values before and after participation of pumped storage

算法	系统经济效益/ (元·d^-1)	系统碳减排量/ (kg·d^-1)	系统输出功率平均波动率
加入前	2.85×10⁷	1.86×10⁷	0.3287
加入后AGWO优化	3.99×10⁷	2.36×10⁷	0.1314
加入后GWO优化	3.70×10⁷	2.34×10⁷	0.1174
加入后PSO优化	3.72×10⁷	2.30×10⁷	0.1210

新窗口打开| 下载CSV

与未加入抽水蓄能之前作比较,在AGWO的优化作用下,系统的经济效益每天增加 1140 万元,每年收入将增加41.61亿元.系统碳减排量每天增加 5000 t,每年则碳减排182.5×10⁴ t,参照研究区域内碳排放平均价格30元/t,系统的收入每年又将增加 5475 万元.另外,系统输出功率的平均波动率由 0.3287 降到 0.1314,系统有功功率并网的稳定性得到较大提升.因此,为风电和光伏合理的配置抽水蓄能设备能够大大增加系统的经济效益与环境效益,同时也能够降低新能源的波动性对电网的危害,在促进新能源发展的同时为我国“双碳”目标也提供了巨大助力.

4.2.2 联合系统功率优化结果分析

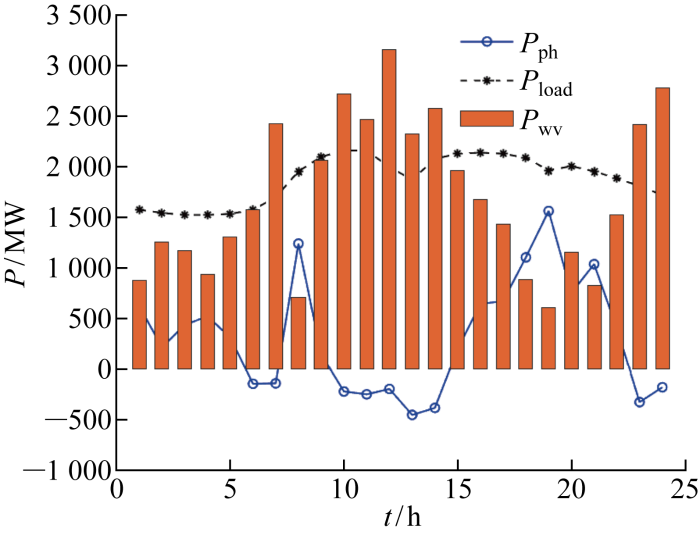
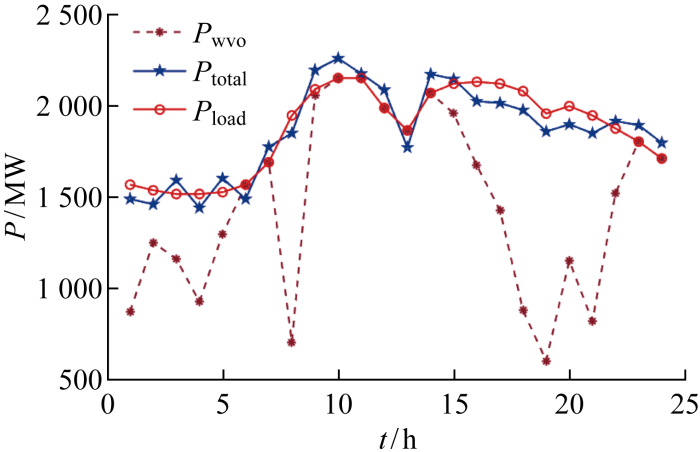
为风、光发电引入抽水蓄能并经过灰狼算法的优化作用后,抽水蓄能系统在各个时段的工作状态以及功率情况如图8所示.图中,P_wv为风光输出功率之和.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 抽水蓄能系统各个时段的工作状态及其功率情况

Fig.8 Working state and power of pumped storage system in each period

图8中,当风电和光伏总输出功率小于电力系统负荷时,抽水蓄能处于发电状态.当风电和光伏总输出功率大于电力系统负荷时,抽水蓄能转换工作状态,进行抽水储存电能以备后续需要.若仅考虑抽水蓄能机组的发电状态,结合风电、光伏并网电量的优化结果,得到风电、光伏以及抽水蓄能的并网电量情况如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 风电、光伏及其抽水蓄能并网电量

Fig.9 Grid connected power of wind power, photovoltaic, and pumped storage

图9中,各个时段风、光、抽水蓄能并网电量求和即为联合系统的总并网电量.将其与未加入抽水蓄能时风、光的总并网电量进行对比,其功率波动情况以及与电力系统负荷需求对比情况如图10所示.图中:P_wvo为未加入抽水蓄能时风、光的总并网电量,P_total为加入抽水蓄能后联合系统总并网电量.由图可见,加入抽水蓄能前,风、光总并网电量波动较大,且在多个时段与电力系统负荷需求差距较大,无法满足电力用户的负荷需要.加入抽水蓄能后,联合系统并网电量波动大大降低,且能够较好地贴近电力系统负荷需求,有利于电网稳定可靠运行.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 抽水蓄能加入前后系统并网电量对比

Fig.10 Comparison of grid connected power before and after participation of pumped storage

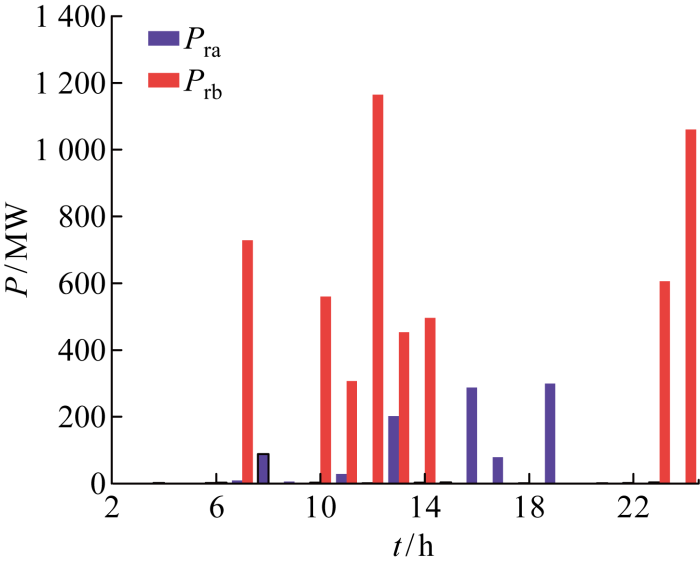
此外,加入抽水蓄能前后,风、光发电站在各个具体时间段的弃电量如图11所示.图中:P_ra为加入抽水蓄能后弃电量,P_rb为加入抽水蓄能前弃电量.由图可见,在抽水蓄能系统加入后,风、光弃电量大幅度降低.每天弃电量由之前的 5379.09 MW降低到 1019.49 MW,占风、光总发电量 40714.09 MW的比例由13.21%降低到2.50%.对比可知,加入抽水蓄能系统后,系统的弃电量降低 4359.60 MW,弃电惩罚金额减少261.58万元.因此,为风光系统配置抽水蓄能设备在提高新能源利用率的同时,也有助于提高系统的经济效益,在风、光发电系统建设中值得大力提倡.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 抽蓄加入前后各个时段弃电量

Fig.11 Abandoned electricity in each period before and after participation of pumped storage

5 结论

综合考虑风-光-抽水蓄能联合系统经济收益最大化、系统平均有功功率波动率最小化以及碳减排量最大化3个目标,建立风-光-抽水蓄能联合系统多目标优化模型.通过归一化处理将多目标优化问题转换为单目标优化问题,并采用灰狼算法进行求解.得到如下结论:

(1) 所提经过改进的灰狼算法与基本灰狼算法以及当前较为常用的粒子群算法相比,具有较为明显的优势.该算法在调整后非线性变化的收敛因子a的作用下,在迭代前期更加注重全局搜索,在中后期更加注重局部搜索,收敛速度大大提高.同时,算法对于不同等级的灰狼个体,通过引入置信度系数,赋予不同权重话语权,使得收敛精度大大提升.另外,算法在陷入局部最优情况时,非线性变化的系数C可以使算法跳出局部搜索,进行全局搜索.

(2) 所提风-光-抽水蓄能联合系统优化调度模型综合考虑联合系统经济收益、碳减排量以及系统并网有功功率波动3个目标,与风、光发电系统对比表明,联合系统每年可增加的收益为 41.61 亿元,每年可以额外减少的碳排放量为182.5×10⁴ t,并且可以大大降低电网有功功率的波动性.这种清洁、低碳、可靠、高效的系统运行方式,为新型电力系统的建立与发展提供了有益参考.

(3) 所建立的模型还存在一定局限性,将一日划分为24个时段,可能导致风光输出功率与电力负荷预测出现较大误差,影响优化结果.并且对于抽水蓄能系统,未考虑机组启停成本,仅仅考虑单一机组容量,未选取不同容量机组对优化结果进行对比分析.对于上述问题,后续将展开进一步研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

樊肖杰, 迟永宁, 马士聪, 等.

大规模海上风电接入电网关键技术与技术标准的研究及应用

[J]. 电网技术, 2022, 46(8): 2859-2870.