基于底质力时历计算的沉船打捞离底过程动力特性分析及系泊系统优化

图1 打捞系统布置情况

Fig.1 Configuration of salvage system

表1 驳船和沉船的主要尺寸

Tab.1 Major dimensions of barge and wreck

参数	驳船	沉船
长度/m	120	46
宽度/m	34	17
高度/m	9	6.67
初始吃水/m	3.75	-
水线面面积/m²	3 230.57	-
质量/t	6 000	9 500
水下质量/t	-	4 151.67

表2 系泊和提升缆的性能

Tab.2 Properties of mooring and lifting cables

参数	系泊缆	提升缆
长度/m	800	-
数量	8	20
质量/(kg·m^-1)	273.95	26
刚度/GN	1.454	0.246
直径/m	0.12	0.078
最小断裂载荷/MN	6.786	3.5

2 打捞系统动力特性模拟方法

2.1 沉船-土体相互作用模型

底质阻力又称“海底突破力”,是指沉船出土时受到周围土壤的阻力.其主要包括两部分: 一是由相对运动趋势造成的摩擦力;二是土壤内部的负超孔隙流体压力^{[7⇓⇓⇓-11]}.负的超孔压产生的原因可以简单地用土壤的有效应力原理来解释,其表达式为

σ = σ' + p

其中: $σ$ 是在土壤某一截面上的总应力; $σ^{'}$ 是作用在土粒骨架上的有效应力; $p$ 是孔隙压力.可见,土壤骨架和孔隙水共同分担来自外部的荷载.当荷载减小时,有效应力瞬间下降,接着土体骨架产生松弛趋势,土体孔隙趋于扩张.然而,在排水不良条件下,孔隙水的流动受到严重限制,因此相对封闭的孔隙空间的膨胀最终导致孔隙压力发生了负向变化,最终表现为对沉没目标物的吸力.为方便叙述,下文中讨论的“孔隙压力”实际上就是这种超孔压(后文图中将以大写P标识,以示含义区分).

本文所述海床分为4个不同土层.土的物理性质如表3所示.表中:S_a为饱和度;φ为内摩擦角;C_y为黏聚力屈服应力;C_f为摩擦因数;C_p为渗透系数.

表3 现场地质勘察结果总结

Tab.3 Summary of geotechnical investigation results

序号	厚度/m	密度/(t·m^-3)	泊松比	孔隙比	S_a/%	φ/(°)	C_y/kPa	C_f	C_p/(cm·s^-1)
①	1.04	1.949	0.25	0.743	93	30	7	0.577	5.56×10^-7
④	17.85	1.724	0.42	1.364	98	11.5	12	0.203	1.58×10^-5
⑤1	8.4	1.765	0.42	1.225	96	13	17	0.231	8.79×10^-6
⑤3	22.71	1.898	0.35	0.894	96	18	20	0.325	1.56×10^-6

在每一控制体内,海床土体的平衡方程可以基于虚功原理来表示,写作:

\begin{array}{l} \int_{V} σ : δ ε d V = \int_{S} t \cdot δ v d S + \int_{V} f \cdot δ v d V + \\ \int_{V} n_{f} ρ_{w} g \cdot δ v d V \end{array}

其中: $σ$ 为柯西应力; $δ ε$ 是虚变形率;V为控制体体积;t是单位面积的表面牵引力; $δ v$ 是一个虚速度场;S是控制体表面积;f是除了孔隙液体(这里是海水)重力的所有体积力;n_f为多孔液体(自由液体加上固着液体)的总体积;ρ_w为液体密度(此处取值为 1 025 kg/m³);g是重力加速度.

海底土弹性阶段采用各向同性线弹性模型,塑性行为采用Mohr-Coulomb模型来描述^[12].该模型具有参数简单易得、对静水压力敏感、能区分拉压工况差异等优点,故在工程实践中得到广泛应用.Mohr-Coulomb模型的屈服函数可以写成如下形式:

(σ_{1} - σ_{3}) - (σ_{1} + σ_{3}) s i n φ - 2 c c o s φ = 0

其中:σ₁是最大主应力;σ₃是最小主应力;c是土体材料的黏聚力.

由于沉船数值模型在xz和yz平面上都是对称的,所以仅取其1/4进行水-土-沉船相互作用模拟.此外,建模范围扩大到沉船尺寸的6倍左右(140 m× 50 m× 50 m),以尽量减少边界效应的影响.

利用有限元程序包,采用牛顿法隐式求解了水-土-沉船相互作用的控制方程.本文中假定孔隙流体海水是不可压缩的.求取了 4 000 s 的海底阻力数值解时历,将之用于下一步的数据分析当中(将在后文中论述).海底土壤超孔隙水压力分布如图2所示,其中蓝色区域即为负超孔隙压力区域.总提升力曲线(海底阻力和沉船沉重之和)如图3所示,图中横坐标表示沉船的归一化垂直位移,定义为沉船实时垂直位移与其初始埋深(此处为 6.67 m)之比.图中还显示了接触面中心处的孔压变化.孔压在初始阶段急剧下降,迅速达到负向峰值,然后再缓慢上升.也就是说,在打捞阶段开始时,沉船与土壤有分离倾向,此时海底阻力中的吸附力成分将急剧增大.同时,一旦土壤与沉船的接触不再那么紧密,这种巨大的吸力又会重新下降.

图2

图2 海床土体超孔隙水压力云图(XZ截面)

Fig.2 Distribution of excess pore water pressure in seabed (XZ plane)

图3

图3 沉船离底阶段所需总提升力(方向相对于母船)及土体超孔压变化情况

Fig.3 Seabed resistance and negative pore pressure

2.2 考虑吃水变化的驳船-系泊缆耦合模拟方法

基于Cummins理论开发了考虑吃水变化和底质力时历的模拟程序,用于计算驳船-系泊缆系统在沉船离底阶段的动力学响应,所述控制方程^[13-14]可写为

\begin{array}{l} (M^{O} + M^{A}) \ddot{X} + \int_{0}^{t} H (t - τ) \overset{\cdot}{X} (τ) d τ + K X = \\ F_{e} + F_{m} + F_{l} \end{array}

其中:M^O为驳船的原始质量矩阵;M^A为附加质量矩阵;X为驳船上参考点的全局坐标向量; $\ddot{X}$ 和 $\overset{\cdot}{X}$ 分别为驳船的加速度和速度向量;H为时延函数矩阵;K为静水回复力矩阵;F_e、F_m、F_l为作用在驳船上的外力,分别代表海洋环境力、系泊力和提升力.F_l的垂直分量将克服海底阻力,使沉船能够被向上提升.

2.2.1 水动力系数及变吃水模块

采用基于势流理论的面元法计算了一组水动力系数,包括附加质量系数、阻尼系数、静水回复力、一阶波浪力传递函数和慢漂力二阶传递函数.本文采用Newman近似,避免了双重求和带来的计算量过大的问题^[15-16].

如前文所述,打捞前沉船嵌入海底,由海底土颗粒骨架支撑.在提升过程中,沉船开始脱离海底,沉船载荷(即沉船的湿重)逐渐由土壤转移到驳船上.因此,在作业过程中驳船吃水会显著增加.同时,这种情况也导致了水动力系数的大范围变化,从而导致基于固定平均吃水的水动力数据不能准确地描述驳船的行为.图4展示了5组不同吃水情况下的驳船一阶波浪力传递函数的变化情况,从中可见吃水增加时这些系数的显著变化.为此,需要考虑驳船在每个时间步长内的实时吃水.为了涵盖所有可能的情况,考虑了从2 m到9 m,间隔0.5 m的吃水变化序列,并计算了每个吃水对应的水动力数据.最终生成包含15个吃水、20个浪向(0°~190°, 间隔10°)、2个水深(20 m、50 m)、40个波浪频率(0~2 rad/s, 间隔0.05 rad/s)的多维数据库.模拟开始后,每一个时间步内都会实时抓取驳船的吃水,并通过插值的方式从数据库中提取水动力系数.这些功能最终都集成到一个变吃水程序模块中进行调用.

图4

图4 吃水2~6 m情况下驳船各一阶波浪力传递函数的变化

Fig.4 Variation of first-order wave load transfer function of six motion modes at draughts of 2 to 6 m

2.2.2 集中质量法

系泊缆的动力学模拟通过集中质量法来实现.集中质量法作为一种实用且应用广泛的数值建模方法,已经得到了很好的阐述和验证.在较平静海况下,集中质量法的精度足以用于研究所述系泊系统的性能.本文不再赘述相关的求解过程,因为文献[17 ⇓-19]中已有很充分的论述.图5展示了本文模拟中涉及的几种不同的节点类型.节点在其平衡位置的控制方程均可表示为 $\begin{array}{l} (m^{O} + m^{A}) \ddot{Y} = W + T + F^{D} + F^{I} + F^{s} \end{array}$ 其中:m^O为节点原始质量矩阵;m^A为附加质量矩阵;Y为全局坐标向量.根据节点类型,外力由不同的分量组成:湿重W、弹性系泊张力T、水动力载荷F^D和F^I、海底支撑力F^s.系泊缆的弯曲和扭转的影响较小故忽略不计.

图5

图5 集中质量法中系泊缆的离散示意图及各类型节点

Fig.5 Schematic diagram of lumped-mass model and different node types

最终形成的整套模拟流程如图6所示.

图6

图6 考虑精确底质力时历的沉船打捞离底过程模拟流程图

Fig.6 Workflow of entire simulation including seabed resistance time history

3 沉船离底阶段中驳船动力响应特性

本节模拟了一种典型海况下的沉船离底过程.入射波由JONSWAP谱产生,水深H=20 m,有义波高H_s=1 m,浪向角D_w=135°,谱峰周期T_p=7 s.提升阶段(即 1 000~3 383.1 s)的几个关键参数值汇总在表4中.沉船的垂直位置是相对于大地坐标而言的.驳船六自由度运动的 5 000 s 时历曲线如图7所示,每根系泊缆的最大张力曲线如图8所示.图中:T_1.max~T_8.max为整根缆上张力的空间极值,对应图1中的系泊缆标号.出于安全考虑,本文中的“张力值”指的是都是这个极值.图中用红色虚线标出了提升作业的起始时刻和结束时刻,本文将两条线划分的3个区域分别称为提升前阶段、提升阶段和提升后阶段.具体而言,提升前阶段是指系泊系统和打捞缆具均已就位,但打捞机构尚未执行提升动作的阶段,此时提升缆完全松弛;提升阶段是指提升机构开始发力运行,牵动沉船向上脱离海底的阶段,此时提升缆张力将随时间发生变化,这一阶段将一直持续到沉船最低点完全与土体脱离为止;提升后阶段是指沉船“悬挂”于母船下方,此时提升缆总张力等于沉船水下重量,不再发生显著变化.

表4 提升阶段提升缆关键参数的起始值、极值和终末值

Tab.4 Starting, extreme, and ending key parameter values of lifting cables in lifting phase

参数	起始值	极值	终末值
驳船平均吃水/m	3.76	5.13	5.01
提升缆长度/m	25.24	17.19	17.31
沉船垂直位置/m	-23.24	-16.66	-16.66
总提升张力/kN	0	44 345.18	40 686.30

图7

图7 离底过程中驳船的各自由度运动时历

Fig.7 Time history of 6DOF motions of barge in off-bottom stage

图8

图8 离底过程中各系泊缆张力变化时历

Fig.8 Time history of mooring tensions in off-bottom stage

时历曲线为描述系泊系统的动力行为提供了一个整体的视角.不同运动自由度或不同系泊缆在同一提升过程中表现出不同的响应特性.具体观察如下:

(1) 对于纵荡. 提升阶段的纵荡运动明显呈现出不规则振荡特征;提升阶段的首尾时刻纵荡值均出现突变;且该阶段纵荡极值明显超过其他两个阶段,波动范围也明显变大.

(2) 对于横荡. 与提升前阶段相比,横荡最大值和最小值均减小,运动幅度变化不大;提升后阶段的运动幅度最小.

(3) 对于垂荡. 在提升阶段初期,驳船会快速下沉一段时间,达到最低点后略有反弹,这与海底阻力的变化趋势是一致的.

(4) 对于横摇. 除了在提升阶段较早的时刻出现两个极值(一个为正,一个为负)外,3个阶段的横摇幅度差异不太显著.

(5) 对于纵摇. 3个阶段的纵摇运动趋势基本不变.

(6) 对于首摇. 首摇幅值逐阶段增大,但无异常突变值.

(7) 对于缆#1和缆#7. 最小张力值出现在提升阶段.

(8) 对于缆#2、#3、#5、#6. 提升阶段的最大和最小张力值都不是全局极值.

(9) 对于缆#4. 在提升阶段结束时出现全局最大张力值,波动范围扩大.

(10) 对于缆#8. 整个模拟的张力峰值出现在缆#8处;最高、最低两个张力极值均出现在提升阶段,且波动幅度明显大于其他两个阶段.

上述分析揭示了考虑提升操作的扰动时,系泊系统行为的复杂性.虽然所有系泊缆在提升阶段的平均张力水平似乎都小于提升前,但母船的运动结果仍然截然不同.很难找到一个统一的规律来概括驳船在提升阶段的运动.沉船在提升阶段的作用类似于一个特殊的锚,对驳船施加了额外的垂向载荷.同时,提升缆可能会随着驳船的移动而偏离竖直位置,因此驳船也会受到X或Y方向上的水平分力.这些力(或力矩)加强了对驳船的约束.然而,这样的附加约束不一定能降低驳船运动振幅.其中一种可能的情况是: 提升开始,驳船受到提升缆的反作用力→驳船下降,系泊缆略微松弛→系泊张力下降→驳船运动幅度增加→一些系泊缆再次张紧.系泊张力与驳船运动之间的相互作用可能在提升阶段变得难以捉摸,因此在初步设计阶段就应重点关注这种不确定性,以便更好地控制母船运动.下一节将介绍几种不同系泊系统布置下的模拟,以测试其对上述不确定性的影响.

4 不同系泊缆布置方案的影响

为了进一步研究提升阶段系泊系统的动力特性,设计了6种系泊系统布置方案.XOY平面第1象限的系泊缆排列如图9所示,其余3个象限为对称布置.布置方案A为原设计方案,B~F为系泊缆在A基础上的修改版本.根据系泊缆的方位,可分为3种类型: 类型I,缆#2与Y轴平行;类型 II,缆#1与缆#2的夹角平分线指向45° 方向[如图 1(b)所示]; 类型 III,缆#1与X轴平行.定义缆 #1 和缆#2之间的角度为θ,每种类型包括两个不同的θ.在与前一节相同的海况下对每个构型分别开展模拟.

图9

图9 6种不同的系泊系统布置方案(以XOY平面第一象限为例)

Fig.9 Six different mooring line arrangements in first quadrant of XOY plane

与其他阶段相比,提升阶段的运动和张力曲线相对更为复杂.因此,这里单独分析了该阶段,以了解不同方案的性能区别.图10所示为6种运动模态在提升作业中的运动极值,峰值缆张力绘制在图11中.图中:T_1.peak~T_8.peak是T_1.max~T_8.max曲线的全时历最大值,即某根缆上各点在一段时间内出现的最危险张力峰值.

图10

图10 不同系泊缆布置情况下提升阶段驳船的六自由度运动极值统计

Fig.10 Maximum and minimum 6DOF motion values of six mooring configurations in lifting phase

图11

图11 不同系泊缆布置情况下提升阶段系泊缆的全时历张力峰值

Fig.11 Peak cable tensions of six mooring configurations in lifting phase

对于不同的运动自由度,系泊缆布置方式带来的影响可能是相反的.例如,当缆布置方案从A变化到C时,最大绝对纵荡幅值减小,而横荡最大值增大,纵摇峰值先减小后增大.此外,垂荡受系泊布置的影响较小,而其他5种自由度较为敏感.由于不同自由度之间的不一致性,在打捞工程设计中可能需要进行一些权衡,以首先确保最关注运动模态的控制效果.

最大运动幅值和峰值张力相对原始系泊布置的增量百分比分别绘制在图12和图13中.图中:峰值张力简记为T₁~T₈.图12、13中, 雷达图曲线围合面积越大,驳船运动/张力的控制效果越好.为清晰起见,原布置方案的参考值特别用点划线标出.两幅图的最后一个子块是6个自由度运动/8根缆张力指标的平均值.由图12可见,只有方案C和F在提升阶段发挥了有效的运动控制作用,且C的优化效果最好.布置方案F可作为备选,因为其能够最大程度地降低系泊张力.D是唯一一个实现更好横荡控制的方案,然而其各自由度的平均效果不尽如人意.结果表明,通过调整系泊缆布置可以抑制提升阶段某些运动模态和缆张力的异常增大(或剧烈波动).

图12

图12 提升阶段不同系泊缆布置下驳船六自由度运动的优化情况

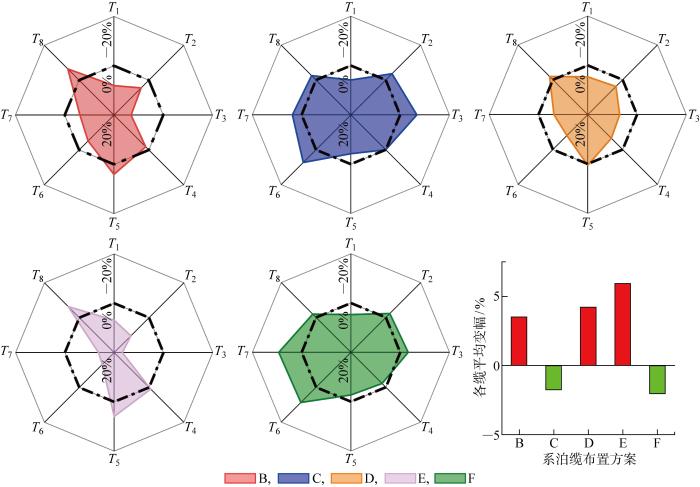
Fig.12 Increments of motion responses of barge with different mooring configurations in lifting phase

图13

图13 提升阶段不同系泊缆布置下各系泊缆峰值张力的优化情况

Fig.13 Increments of peak tensions of different mooring configurations in lifting phase

布置B、D、E中的缆张力水平增加,但相应的驳船运动幅度并没有减少,这再次说明在提升阶段需要注意驳船运动-缆张力的复杂耦合作用.在当前较为温和的海况下,暂未发现超出最小破断水平的缆张力值.尽管如此,目前的一些极端张力值也可能成为危险因素,如E中的T_7.peak.这是因为本文的模拟也在一定程度上反映了打捞系统的固有特性.

若考虑所有3个阶段,驳船运动和系泊缆张力在整个离底过程中的优化效果如图14和图15所示.在前面的分析中,对于提升阶段而言,方案C是耦合系统的最佳运动控制方案,但其在整个打捞过程中的总体结果表明,驳船各自由度平均运动情况较原设计增加了6.46%,其中一个重要原因是整个离底过程中方案C的最大横荡值比原方案A增加了74.9%.

图14

图14 整个离底过程中不同系泊缆布置下驳船六自由度运动的优化情况

Fig.14 Increments of motion responses of barge with different mooring configurations in simulation

图15

DOI:10.1016/j.scitotenv.2010.07.031 URL [本文引用: 2]

图15 整个离底过程中不同系泊缆布置下各系泊缆峰值张力的优化情况

Fig.15 Increments of peak tensions of different mooring configurations in simulation

最终,F可被视作一种合理的系泊布置优化方案,它在控制驳船运动和缆张力方面均有较好表现.虽然对不同打捞系统的优化方法可能并不统一,但本文已经证明,在打捞作业之前,应进行基于数值模拟的综合案例研究,因为设计其他系泊系统的一般经验可能尚不足以充分预判打捞工程的系统风险.

5 结论

提升阶段动力响应的复杂性使得打捞系统的设计与其他常见的系泊系统有所不同.本文提出了一种新的基于底质力时历曲线的沉船打捞离底过程数值模拟方法.不同的运动模态或系泊缆在打捞过程中受到的影响是不同的,从本文的结果中可以得出以下关键点:

(1) 提升阶段驳船运动和系泊缆张力与未进行作业时的系统原始状态相比,会出现运动幅值的整体异常激励或个别时刻的极端值,其中纵荡运动的异常增大最为显著.

(2) 合理的系泊系统布置不仅可以实现更好的运动控制,还可以降低系泊缆的峰值张力.对于当前打捞系统,系泊缆方位角设置组合(0°,45°)为合理方案.

受目前条件所限,本文所述方法尚未开展完全匹配的相关全耦合模型试验.未来将进一步开展波浪中执行打捞任务的试验验证工作,并进一步优化本文所述的模拟算法.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ROGOWSKA

, WOLSKA

, NAMIEŚNIK

Impacts of pollution derived from ship wrecks on the marine environment on the basis of s/s “Stuttgart” (Polish Coast, Europe)

[J]. Science of The Total Environment, 2010, 408(23): 5775-5783.

[2]

VELAYUDHAN

A K D

Design of a supervisory fuzzy logic controller for monitoring the inflow and purging of gas through lift bags for a safe and viable salvaging operation

[J]. Ocean Engineering, 2019, 171: 193-201.

DOI:10.1016/j.oceaneng.2018.10.049 URL [本文引用: 1]

[3]

HAHLADAKIS

J N

, STYLIANOS

, GIDARAKOS

Assessment of released heavy metals from electrical and electronic equipment (EEE) existing in shipwrecks through laboratory-scale simulation reactor

[J]. Journal of Hazardous Materials, 2013(250-251): 256-264.

[4]

LEE

H J

Breakout of partially embedded objects from cohesive seafloor soils

[C]\\Offshore Technology Conference. Houston, Texas, USA: Offshore Technology Conference, 1973: II-789-795.

[5]

BARTHOLOMEW

C A

, MARSH

, HOOPER

US navy salvage engineer’s handbook

[M]. Washington D.C., USA: Naval Sea Systems Command, 1992.

DOI:10.1016/j.oceaneng.2016.02.038 URL [本文引用: 1]

[6]

LEE

, JANG

B S

, KIM

Development of procedure for structural safety assessment of energy saving device subjected to nonlinear hydrodynamic load

[J]. Ocean Engineering, 2016, 116: 165-183.

[7]

VESIC

A S

Breakout resistance of objects embedded in ocean bottom

[J]. Journal of the Soil Mechanics and Foundations Division, 1971, 97(9): 1183-1205.

DOI:10.1061/JSFEAQ.0001659 URL [本文引用: 1]

[8]

NINOMIYA

, TAGAYA

, MURASE

A study on suction breaker and scouring of a submersible offshore structure

[C]\\Offshore Technology Conference. Houston, Texas,USA: OnePetro, 1971.

[9]

NINOMIYA

, TAGAYA

, MURASE

A study on suction and scouring of sit-on-bottom type offshore structure

[C]\\Offshore Technology Conference. Houston, Texas,USA: OnePetro, 1972.

DOI:10.2118/3416-PA URL [本文引用: 1]

[10]

NINOMIYA

, TAGAYA

, MURASE

A study of suction and scouring of bottom-sitting offshore structures

[J]. Journal of Petroleum Technology, 1973, 25(3): 279-287.

[11]

SMALL

, THORNE

, TA

Effect of pore pressure dissipation on the behaviour of anchors in clay

[C]\\The Eighth International Offshore and Polar Engineering Conference. Montreal, Canada: OnePetro, 1998.

[12]

CHEN

W F

, HAN

D J

Plasticity for structural engineers[M]. New York, USA: Springer-Verlag, 1988.

[13]

CUMMINS

W E

The impulse response function and ship motions

[J]. Schiffstechnik, 1962, 9: 101-109.

[14]

OGILVIE

T F

Recent progress toward the understanding and prediction of ship motions

[C]\\5th ONR Symposium on Naval Hydrodynamics. Bergen, Norway: David Taylor Model Basin, 1964.

[15]

NEWMAN

J N

Second-order slowly varying forces on vessels in irregular waves

[C]\\Proceedings of the International Symposium on Dynamics of Marine Vehicles and Structures in Waves. London, UK: IMechE, 1974.