基于预定时间一致性的直流微电网分布式协同控制

doi:10.16183/j.cnki.jsjtu.2022.050

基于预定时间一致性的直流微电网分布式协同控制

周儒畅, 王子强, 王杰^,

上海交通大学电子信息与电气工程学院, 上海 200240

Distributed Prescribed-Time Consensus Based Cooperative Control for DC Microgrids

ZHOU Ruchang, WANG Ziqiang, WANG Jie^,

School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 王杰,教授;E-mail:jiewangxh@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2022-03-5 修回日期: 2022-05-9 接受日期: 2022-06-17

Received: 2022-03-5 Revised: 2022-05-9 Accepted: 2022-06-17

作者简介 About authors

周儒畅(1997-),硕士生,从事直流微电网控制研究.

摘要

为解决直流微电网中分布式电源的协同控制问题,提出了一种基于预定时间一致性的微电网控制方法.首先提出一种基于预定时间控制的电流控制方法,能够实现在预先设定的时间内各分布式电源按比例输出功率,同时可以调节各分布式电源出口电压,将其恢复至额定值附近.然后通过MATLAB/Simulink建立微电网仿真系统,在不同工况下验证了所提出控制策略的有效性.最后在仿真系统中建立有限时间控制策略,并与预定时间控制策略下系统电流的电能质量与系统收敛预估时间的保守性进行比较,说明与验证了所提出的控制策略的优点.

关键词： 直流微电网; 下垂控制; 分布式控制; 二次控制; 预定时间一致性

Abstract

A microgrid control method based on prescribed time control is proposed to solve the cooperative control problem of distributed energy resources (DER) in DC microgrid. First, a current control method based on prescribed time control is proposed, which can allocate the power output of each DER proportionally within a pre-defined time. Meanwhile, the outlet voltage of each distributed power supply can be adjusted to be near the rated value and the observation value can be kept at the rated value. Then, the microgrid system is simulated through MATLAB/Simulink and the effectiveness of the proposed control strategy is verified in different working conditions. Afterward, the finite-time control strategy is established in the simulated system. A comparison of the conservative power quality of the system current with the estimated time of system convergence in the scheduled-time control strategy verifies the advantages of the proposed strategy.

Keywords： direct current (DC) microgrids; droop control; distributed control; secondary control; prescribed-time consensus

PDF (1964KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

周儒畅, 王子强, 王杰. 基于预定时间一致性的直流微电网分布式协同控制[J]. 上海交通大学学报, 2023, 57(7): 824-834 doi:10.16183/j.cnki.jsjtu.2022.050

ZHOU Ruchang, WANG Ziqiang, WANG Jie. Distributed Prescribed-Time Consensus Based Cooperative Control for DC Microgrids[J]. Journal of Shanghai Jiaotong University, 2023, 57(7): 824-834 doi:10.16183/j.cnki.jsjtu.2022.050

作为集成分布式发电(Distributed Generator, DG)、负载和储能的一种技术方案,微电网(Microgrid, MG)以其能够接入大量分布式电源并消纳新能源的特点得到了充分关注^{[1⇓⇓⇓-5]}.随着微电网中直流分布式电源与直流负荷的逐渐增加,由于直流微电网具有变流环节少与不需要考虑无功问题等优点,这一技术得到了迅速发展^[6⇓-8].一般而言,微电网可以作为主网的一部分工作在并网状态,也可以与独立工作于孤岛状态.由于孤岛MG与大电网隔离,所以通常需要利用储能系统等分布式电源维持电压的稳定并优化能量管理,改善电能质量^[9-10].为了实现这些目标,孤岛直流MG的分层控制结构得到了广泛研究.

目前对于控制结构而言,主流微电网分层控制框架主要由3个级别的控制组成,每个层级的控制对应着不同的响应时间尺度需求^[11].一次控制的目标是实现对MG的功率与电压的动态调节,一般采用下垂控制;二次控制用于补偿初级控制带来的功率分配偏差与电压偏差^[12].对于控制模式,较早被研究的集中式二次控制依赖于中央控制器的参考指令,对单点故障敏感^[13].因此,分布式二次控制被广泛研究以达到对初级控制偏差的修正^[14].

在稀疏通信拓扑的基础上,基于一致性的分布式二次控制具有良好的灵活性和可靠性.由于加快收敛速度可以提高电能质量,为了实现这一目标,并且在有限时间内实现分布式电源的电流均衡输出,根据参数确定收敛时间上限的有限时间一致性理论被提出^[15-16].之后固定时间一致性理论因为其收敛时间不受系统初始状态的影响而得到进一步研究.

但是目前的主流控制策略仍然存在一些不足^[17].首先,对于有限时间一致性而言,文献[18]中应用符号函数sgn(x)来提高MG中的有限时间收敛速度.文献[19]中同时应用信号函数sgn(x)与分数阶状态反馈来构造有限时间控制方法.但是在有限时间一致性控制方法中使用的分数阶非平滑控制会降低系统的电能质量^[20].此外符号函数的应用虽然提高了MG应对外界干扰的鲁棒性,但是会给控制过程带来不可避免的抖振,若考虑到MG中具有随机性的可再生能源接入,系统电能质量的问题将会更为严重.文献[21]中应用饱和函数减少抖振现象,代价是降低了应对外界扰动的鲁棒性.同样地,有限时间一致性控制方法的收敛时间估计上限具有很大的保守性,并且取决于系统中DG状态的初值^[20].易知功率分配与电压恢复的加速能够有效改善电能质量并降低运行损耗,故降低收敛时间估计上界的保守性并提高其对初值的独立性十分必要.

而在采用固定时间一致性方法的工作中,文献[22]中采用了分数阶状态反馈,文献[23-24]中采用了分数阶反馈与信号函数.文献[25]中采用了tanh函数,并且通过一个基于分段函数的近似方法得到了一个保守不足的收敛时间上界.虽然固定时间算法取得了显著的进步,但是除了电能质量问题之外,Lyapunov稳定性分析确定的收敛时间的估计上界仍然具有一定的保守性,大约为仿真确定的实际收敛时间的数倍,并且为控制参数的函数,不能够预先给定.

提出一种基于预定时间一致性的直流微电网分布式分层控制策略,以实现微电网运行时的功率按比例分配与电压恢复.此策略利用分布式智能体间的通信交互收集电压与电流信息,能够在预先确定收敛时间的基础上实现系统的快速收敛,提高电能质量.此外,相比于有限时间一致性方法与固定时间一致性方法,本文中采用的控制方法收敛时间不仅与系统初值无关,而且能够预先根据生产场景的应用需要确定收敛时间,同时具有收敛时间估计上限保守性低和函数不含有抖振的优点.之后,在此基础上通过对多种场景的仿真对文中提出的控制方法的控制效果进行了验证.

1 多智能体系统的预定时间一致性控制

直流微电网的无向通信拓扑G(V, ε, A)由微电网中的可控制单元集合V={1,2,…,N}与通信链路集合ε∈V×V构成.有加权邻接矩阵A={a_ij}_N_×_N, ε_ji∈ε⇔a_ij>0,其中ε_ji为节点i与节点j之间的信息交换渠道,a_ij为伴随矩阵的权重系数.N_i={j∈V|(i,j)∈ε}被称为节点i的邻居节点集合.若ε_ji∉ε,则a_ij=0,此外若j=i,则a_ij=0.微电网拓扑的度矩阵D=diag{d₁,d₂,…,d_N}满足d_i= $\overset{N}{\sum_{j = 1}}$ a_ij,而拓扑的Laplace矩阵L=[l_ij]∈Rⁿ^×ⁿ满足:

(1)l_ij=

\{\begin{array}{l} \overset{n}{\sum_{j = 1}} a_{i j}, & i = j \\ - a_{i j}, & i \neq j \end{array}

主要研究一阶多智能体系统的预定时间控制问题.一阶系统输入可以描述如下:

(2)

{\overset{\cdot}{x}}_{i}

=u_i, i=1,2,…,n

式中:x_i∈Rⁿ,u_i∈Rⁿ分别为系统的状态变量和输入变量;n为智能体的个数.每个智能体只能与通信拓扑中的相邻智能体通信并进行状态信息交互.

为实现直流微电网不同工况下的有效控制,将收敛时间设定为扰动开始时间,引入分段时间标度函数^[20]为

(3)ζ_m(t)=

\{\begin{array}{l} \frac{T_{p}^{α}}{(T_{p} + t_{d + m - 1} {- t)}^{α}}, \\ t \in [t_{d + m - 1}, t_{d + m - 1} + T_{p}) \\ 1, t \in [t_{d + m - 1} + T_{p}, t_{d + m}) \end{array}

式中:t_d为控制方法投入的时间,d=1, 2, …, n;T_p为事先预定的系统收敛时间;α为可以选择的实数,α>2;m为自然数.式(3)表明分段时间标度函数ζ_m(t)是在时间区间[t_d₊_m_-1,t_d₊_m)上的分段函数,也即第m个时间区间上的函数.

由式(3)可得:

(4)

{\overset{\cdot}{ζ}}_{m}

(t)=

\{\begin{array}{l} \frac{α}{T_{p}} ζ_{m}^{1 + \frac{1}{α}}, & t \in [t_{d + m - 1}, t_{d + m - 1} + T_{p}) \\ 0, & t \in [t_{d + m - 1} + T_{p}, t_{d + m}) \end{array}

构造误差:

(5)e_i=

\sum_{j \in N_{i}}

a_ij(x_i-x_j), i=1,2,…,n

则区间t∈[t_d₊_m_-1, t_d₊_m)上的预定时间控制方案为

(6)u_i=-

(b + k \frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}})

e_i

式中:k与b为大于0 的实数.

取t_d₊_m_-1=0.考虑系统y(t)≥0,满足 $\overset{\cdot}{y}$ (t)=-by(t)-k( ${\overset{\cdot}{ζ}}_{m}$ /ζ_m)y(t)^[26].同时,取文献[22]、文献[24]与文献[25]中的有限时间控制算法与预定时间一致性控制方案进行比较,对比其总谐波失真(Total Harmonic Distortion, THD),并以参数H_THD代表THD含量,如表1所示.

表1 不同控制方法H_THD对比

Tab.1 Comparison of H_THD of different control methods

控制方法	控制输入	H_THD/%
固定时间方法1^[22]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$	23.32
固定时间方法2^[24]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$ -k₃sgn(y)	17.17
固定时间方法3^[25]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$ -k₃tanh(y)	22.13
预定时间方法参数1	T_p=0.05, b=60, k=2, α=3	9.12
预定时间方法参数2	T_p=0.3, b=30, k=2, α=3	16.93

新窗口打开| 下载CSV

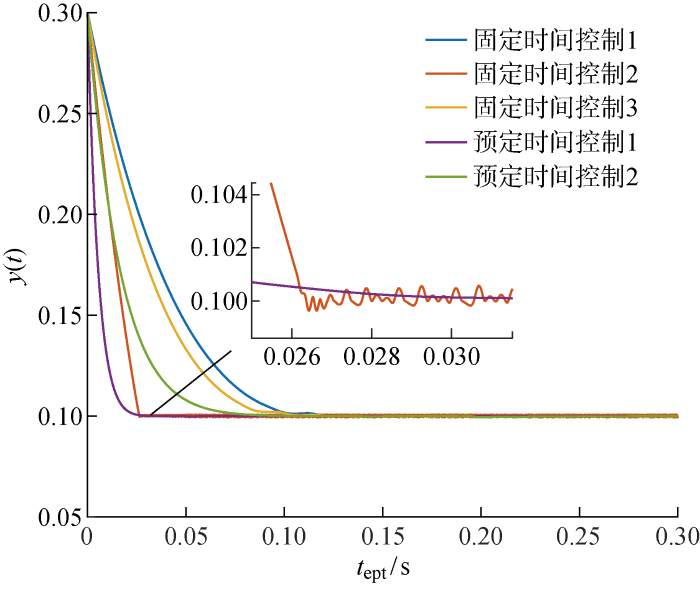
此时引入实验来说明不同控制方法的收敛特性,表1中sig(x $)^{\frac{p}{q}}$ =sgn(x)|x $|^{\frac{p}{q}}$ , p=3,q=5,且k₁=k₂=10,并设置预定时间收敛的起始时间t_d₊_m_-1为0 s,系统状态变量y的稳态值为0.1.经过ode45方法在时间区间[0, 0.4] s上对表1中5种方法进行数值求解,以t_ept表示实验时间,结果如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 不同控制方法收敛过程比较

Fig.1 Comparison of convergence process of different control methods

根据文献[24],表1中固定时间控制方法1、2与3控制下系统收敛时间的上限可以计算为T_f≤ ${\bar{T}}_{f}$ =πq/[2(q-p) $\sqrt{k_{1} k_{2}}$ ]=0.392 s.图1中固定时间控制1、2、3的实际收敛时间分别为0.14、0.027、0.12 s,与预估的收敛时间上限相比,保守性分别为180%、1 352%、227%.与之相比,预定时间控制的预定收敛时间T_p分别为0.05 s与0.3 s,而保守性为66.7%与50%.图1不仅说明了预定时间控制拥有比固定时间控制更快的收敛特性,还验证了表1中3个固定时间控制方法的估计上界要比预定时间控制的预定时间拥有更大的保守性.

此外,通过对信号进行Fourier分解能够得到在时间区间[0, 0.2] s内5种不同控制下的总谐波失真H_THD,如表1最右列所示.如图1所示,固定时间控制方法2中的sgn函数和固定时间控制3中的tanh函数可以加速系统的收敛速度,与固定时间控制1曲线相比,说明收敛速度的提高可以改善电能质量,表现为H_THD的减小.同时,3个固定时间控制下的H_THD均大于预定时间控制方法1,说明分数功率状态反馈的非平滑控制动作会带来额外的电能质量问题.

此外,通过改变预定收敛时间等参数引入了预定时间控制方法2.由图1可得,虽然预定时间控制方法2的收敛速度较固定时间控制方法2慢,但是前者的H_THD略优于后者,再次验证了固定时间控制中的分数阶反馈会影响电能质量的观点.

2 直流微电网分层控制策略

基于改进的预定时间分布式控制方案直流微电网的分层控制与交流微电网类似,包括一次控制和二次控制.不同的是交流微电网中要考虑频率-有功功率与电压-无功功率关系,而直流微电网中只需要维持电压-电流关系即可维持系统稳定.

2.1 一次控制

孤岛直流微电网的一次控制旨在快速维持系统中电压与电流的稳定并保证功率平衡,采用对等控制中的下垂控制,通过对下垂系数比例的调节实现诸分布式电源之间功率的按比例分配.当分布式电源容量相同时,功率的按比例分配输出即成为平均输出.此种控制方法仅需要接入控制单元的本地端口电压与输出功率、电流等信息而无需依赖通信拓扑中的信息交流机制.直流微电网中与电压功率有关一次控制可以被描述为

(7)v_i=U_i_,ref-k_iI_i

式中:v_i为分布式电源变流器出口的测量电压值;U_i_,ref为设定的下垂控制参考电压;I_i为分布式电源变流器出口的输出电流测量值;k_i为本地下垂控制的下垂系数.

2.2 二次控制

传统的下垂控制手段由于下垂曲线的特性,无法同时满足端口电压恢复与按分布式电源容量分配输出功率的控制目标,无法进行无差调节^[27].因此,需要采取二次控制对一次控制的控制量进行补偿,产生合适的电压参考值并提供给分布式控制器用于分布式电源端口电压与输出功率的控制.

二次控制需要对式(7)中的参考电压进行修正,参考电压U_i_,ref的修正项分为两个部分,分别对应二次控制的两个目标,即分别为负责功率均分的电流修正项与负责电压恢复的电压修正项,可以写成:

(8)

\begin{array}{l} U_{i, r e f} = v_{i} - k_{i} I_{i} + Δ U_{i} \\ Δ U_{i} = Δ U_{i}^{V} + Δ U_{i}^{I} \end{array}\}

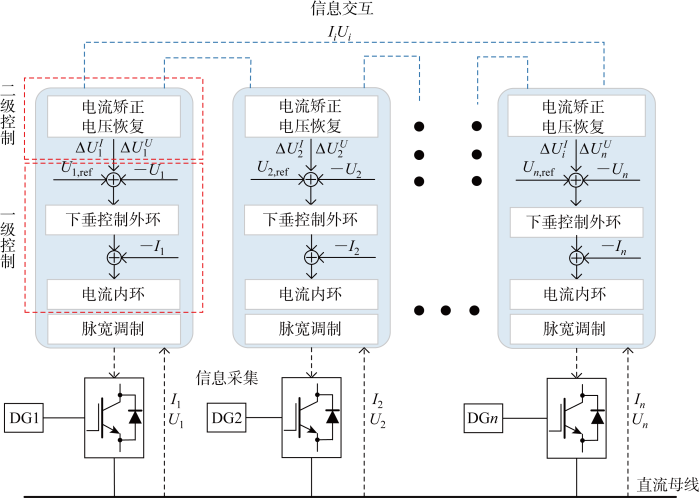
式中:ΔU_i为下垂控制的二次修正项;Δ $U_{i}^{V}$ 表示用于解决下垂控制造成的电压偏差问题的电压修正项;Δ $U_{i}^{I}$ 表示用于解决按比分配负荷问题的电流修正项.

如图2所示,微电网中的各智能体单元监测其对应的分布式电源输出的电压与电流信息,并将其应用于一次控制.同时,各邻居智能体单元通过通信拓扑进行信息交换得到网络中其余分布式电源的电压与电流信息,并协同生成电流校正与电压恢复修正项,最后通过比例积分(PI)控制器将其输出添加到下垂控制器中.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 直流微电网分层控制结构

Fig.2 Hierarchical control structure of DC microgrid

3 基于预定时间一致性的分布式控制策略

本文中构造的直流微电网控制架构可以抽象为一个多智能体系统,每个参与控制的分布式电源可以看成一个智能体,利用多智能体系统的自治性,每个分布式电源可以进行本地决策从而进行独立本地控制,而无需中央控制器的参与.利用多智能体系统的稀疏通信拓扑可以使得分布式电源间完成信息交互及协同,从而达成系统的全局控制目标.各智能体间通过通信耦合进行信息交互,实现输出电流信息的全局共享,并获得二次控制的电流及电压修正指令.利用智能体的主动性及适应性可以适应通信拓扑变化.当直流微电网通信拓扑发生突然改变时——包括通信线路断开或分布式电源投入、退出等时刻,多智能体系统能够进行自发调整从而维持正常运行.

3.1 电流控制策略

3.1.1 电流校正控制

基于第1节中讨论的控制方法,在电流校正控制中,分布式电源智能体i采集自身输出电流,并同时通过通信拓扑交换各智能体的电流信息,进行预定时间控制.由式(5)与式(6),时间区间[t_d₊_m_-1,t_d₊_m)预定时间控制的电流修正控制可以写成:

(9)Δ

{\overset{\cdot}{U}}_{i}^{I}

(- b + k \frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}})

e_i= h

(- b + k \frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}) \sum_{j \in N_{i}}

a_ij(I_i-I_j)

式中:I_i与I_j为本地变流器输出的电流;h为电压与电流间的耦合系数.

首先根据文献[28]中的引理1给出,当系统拓扑G为无向连接图时,若存在一个实数常数g>0使得在区间[t_d₊_m_-1,t_d₊_m)上有:

(10)

\begin{array}{l} V_{m} (0, t) = 0 \\ V_{m} (x (t), t) > 0, x \neq 0 \\ {\overset{\cdot}{V}}_{m} = - g V_{m} - 2 \frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}} V_{m} \end{array}\}

式中:函数V_m为定义在时间区间[t_d₊_m_-1,t_d₊_m)上的连续可导函数.则系统原点在式(3)中给出的预定时间T_p下是稳定的.对于时间区间[t_d₊_m_-1,t_d₊_m_-1+T_p),有:

(11)V_m(t)≤

ζ_{m}^{- 2}

exp[-g(t-t_d₊_m_-1)]V(t_d₊_m_-1)

成立.而对于时间区间[t_d₊_m_-1+T_p, t_d₊_m)有:

(12)V_m(t)≡0

由于直流微电网中不存在频率-有功功率与电压-无功功率的对应关系,所以仅采用预定时间一致性理论使电流达到平均一致性完成均流目标,平均一致性目标可以写成:

(13)e_c=x_i-

\frac{1}{n} (\overset{n}{\sum_{i = 1}} x_{i})

令智能体的状态平均值x^*= $\frac{1}{n} (\overset{n}{\sum_{i = 1}} x_{i} (t))$ ,智能体状态与平均值的差δ_i(t)=x(t)-x(t)^*.若 X=[x₁x₂ … x_n]^T且δ=[δ₁δ₂ … δ_n]^T,则有:

(14)δ=X-

\frac{1}{n}

(1_N

{1^{T}}_{N}

式中:1_N为N阶单位矩阵.

3.1.2 电流校正控制相关证明

选择Lyapunov函数的形式为

(15)V=

\frac{1}{2}

δ^Tδ

函数式(15)定义在时间区间[t_d₊_m_-1,t_d₊_m)上.考虑到式(4),且由Laplace矩阵L性质可得L1_N=0_N, ${1^{T}}_{N}$ = ${0^{T}}_{N}$ ,那么有:

(16)

{1^{T}}_{N} \overset{\cdot}{X}

{1^{T}}_{N} [- (b + k \frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}) L X]

= -

(b + k \frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}})

(

{1^{T}}_{N}

L)X=0

这意味着:

(17)

\overset{\cdot}{δ}

\overset{\cdot}{X}

\frac{1}{N}

(1_N

{1^{T}}_{N}

)

\overset{\cdot}{X}

\overset{\cdot}{X}

同时有:

(18)Lδ=LX-

\frac{1}{N}

L1_N

{1^{T}}_{N}

X=LX

则对Lyapunov函数式(15)求导,则有:

(19)

\overset{\cdot}{V}

=δ^T

\overset{\cdot}{δ}

=δ^T

\overset{\cdot}{X}

=δ^T

[- (b + k \frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}) (L X)]

= -bδ^TLδ-k

\frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}

δ^TLδ

引入基本假设,在连通无向图G中,若1_NX=0,则有X^TLX≥λ₂(L)X^TX.式中λ₂(L)>0为系统Laplace矩阵L中的次小特征值.

注意到:

(20)

{1^{T}}_{N}

δ=

{1^{T}}_{N}

(X-

\frac{1}{N}

1_N

{1^{T}}_{N}

X)=0

因此对Lyapunov函数式(15)求导有:

(21)

\overset{\cdot}{V}

=-bδ^TLδ-k

\frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}

δ^TLδ≤ -bλ₂(L)δ^Tδ-k

\frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}

λ₂(L)δ^Tδ

由于条件k≥ $λ_{2}^{- 1}$ (L),上式可以变化为

(22)

\overset{\cdot}{V}

≤-bλ₂(L)δ^Tδ-

\frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}

δ^Tδ= -2bλ₂(L)V-2

\frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}

考虑 $\frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}$ = $\frac{α}{T_{p}} ζ^{\frac{1}{α}}$ , 那么根据文献[28],在时间段[t_d₊_m_-1, t_d₊_m_-1+T_p]上有:

(23)V(t)≤

ζ_{m}^{- 2}

exp[-2bλ₂(L)(t-t_d₊_m_-1)]V(t_d₊_m_-1)

即在[t_d₊_m_-1, t_d₊_m_-1+T_p)上有:

(24)

{(δ (t))}^{2}

≤ζ_m(t)²×exp[-2bλ₂(L)(t-t_d₊_m_-1)]

{(δ (t_{d + m - 1}))}^{2}

在上式中,若t→(t_d₊_m_-1+T_p)^-,则ζ_m(t)^-2→0,那么可以得出 $(δ (t))$ →0.也即系统在预定时间T_d内能够达到如式(13)所述的平均一致性.

在系统到达预定时间T_d后,ζ(t)=1, $\overset{\cdot}{ζ}$ (t)=0,那么可以证明当t∈[t_d₊_m_-1+T_p,t_d₊_m)时控制输入与系统保持稳定.由于V= $\frac{1}{2}$ δ^Tδ,所以有:

(25)

\overset{\cdot}{V}

(t)≤-2bλ₂(L)≤0

且V(t_d₊_m_-1+T_p)= $\underset{t \to (t_{d + m - 1} + T_{p})}{l i m}$ V(t)=0,则:

(26)0≤V(t)≤V(t_d₊_m_-1)=0

式中:t∈[t_d₊_m_-1+T_p,t_d₊_m).说明电流的预定时间一致性控制在预定时间内能够达到平均一致性,并在到达预定时间后保持稳定的平均一致性控制.

从时间区间[t_d₊_m_-1, t_d₊_m)的证明中,可以看到平均一致性共识是在预先指定的有限时间T_p内实现的,并保持在[t_d₊_m_-1+T_p, t_d₊_m)上.此外,文献[20]中指出控制输入在上至少为C¹平滑且均匀有界.则相对于有限时间控制方法里的非平滑控制函数,预定时间一致性控制方法的输入一直是平滑的(见图1实验结果).

3.2 电压控制策略

分布式电源电压控制的目标是使得在微电网正常运行并且分布式电源输出均衡功率时输出电压能够保持在电压参考值U_i_,ref,故采用在下垂控制参考电压中加入电压偏移补偿项的方式进行来恢复直流电压.电压偏移补偿项可以写成^[29]:

(27)Δ

U_{i}^{V} (k_{P}^{v} + \frac{k_{I}^{v}}{s})

(U_i_,ref-

v_{i}^{*}

)

(28)

v_{i}^{*}

=U_i+

\int_{0}^{t} \sum_{j \in N_{i}}

a_ij(

v_{j}^{*}

(τ)-

v_{i}^{*}

(τ))dτ

式中:s为拉普拉斯算子;U_i为采集到的本地变流器出口电压; $v_{i}^{*}$ 与 $v_{j}^{*}$ 分别为本地变流器与相邻变流器的估计电压; $k_{P}^{v}$ 与 $k_{I}^{v}$ 分别为PI控制器的比例系数与积分系数.参考电压与本地估计电压的差值通过PI控制器生成电压恢复修正项注入下垂控制器.节点的电压若出现任何变化,本估计电压 $v_{i}^{*}$ 都会立即响应并且通过通信网络传播,影响到其他估计值.

令v^*=[ $v_{1}^{*}$ $v_{2}^{*}$ … $v_{n}^{*}$ ]^T,U=[U₁U₂ … U_n]^T, 对 $v_{i}^{*}$ 求导可得:

(29)

{\overset{\cdot}{v}}_{i}^{*}

{\overset{\cdot}{v}}_{i}^{*}

\sum_{j \in N_{i}}

a_ij(

v_{j}^{*}

v_{i}^{*}

{\overset{\cdot}{v}}_{i}

\sum_{j \in N_{i}}

a_ij

v_{j}^{*}

-d_i

v_{i}^{*}

写成矩阵形式有:

(30)

{\overset{\cdot}{v}}^{*}

\overset{\cdot}{v}

-(D-A)v=

\overset{\cdot}{v}

-Lv

同样地,在频域中,

(31)sV^*-V^*(0)=

\bar{s V}

\bar{V}

(0)-

\bar{L V}

式中:V^*与 $\bar{V}$ 分别为v^*与U经过Laplace变换之后的形态.由式(28)可得V^*(0)= $\bar{V}$ (0),因此:

(32)V^*=s(sI_N+L)^-1

\bar{V}

式中:I_N为单位矩阵.式(32)表示电压观测器的全局动态.文献[29]表明,若Laplace矩阵L是平衡的,则估计电压向量V^*中的所有元素能够收敛到共识值,也即平均电压的真实值.此共识值也即向量 $\bar{V}$ 中所有元素的平均值,通过PI控制器可以使这个值不断接近给出的直流母线电压参考值,并得到电压恢复修正项,完成直流母线电压恢复.

4 仿真分析

综合第1节与第2节,将不同控制方法的特点对比如表2所示.

表2 不同控制方法特点对比

Tab.2 Comparison of feature of different control methods

方法	收敛时间与系统初值是否有关	函数抖振	收敛时间估计上限保守性	能否预先确定收敛时间
有限时间一致性	√	√	高	×
固定时间一致性	×	√	高	×
预定时间一致性	×	×	低	√

新窗口打开| 下载CSV

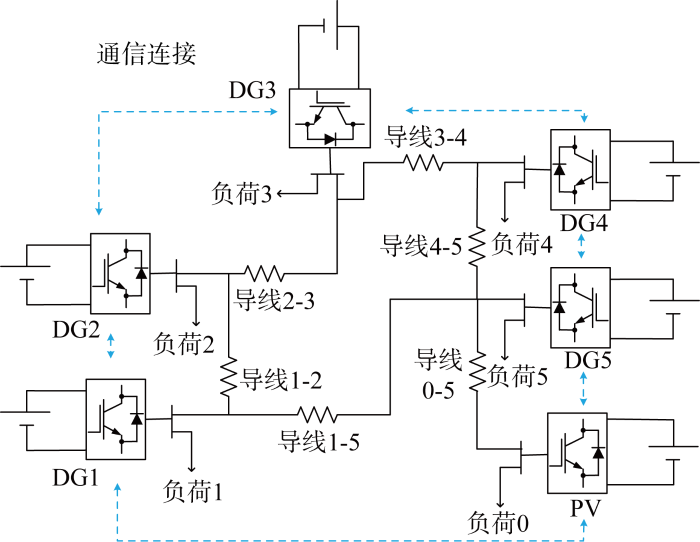
为了验证提出的控制策略在系统不同工况中的可行性与有效性,在仿真软件MATLAB/ Simulink中建立了包含5个分布式储能和一个光伏电源的直流微电网模型.微电网模型的物理构成如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 微电网模型的物理构成与通信拓扑

Fig.3 Physical composition and communication topology of microgrid model

分布式储能及其对应的分布式智能体采用一致性算法进行控制,光伏电源通过最大功率点跟踪(Maximum Power Point Tracking,MPPT)算法进行控制,各储能电池均通过DC-DC变流器接入直流母线.系统的拓扑如图3所示,每个分布式电源所带负荷均为6.25 kW,线路电阻均为0.2 Ω,光伏电源光照强度为 1 000 W/m²,并伴有幅值为50 W/m²的随机波动.其余控制参数中,K_P1,K_I1表示下垂控制中电流内环的PI参数;K_P2,K_I2表示下垂控制中电压外环的控制参数;K_P3,K_I3表示电流补偿项的PI参数;K_P4,K_I4表示电压补偿项的控制参数.参数设置如表3所示.

表3 控制器与系统参数

Tab.3 Controller and system parameters

参数	取值	参数
DG控制器下垂系数k_i	0.2	直流母线额定电压/V	500
DC/DC滤波电容/mF	0.5	DC/DC滤波电感/mH	0.1
电流内环PI	K_P1=0.1	电压外环PI	K_P2=0.1
	K_I1=1		K_I2=1
电流补偿项PI	K_P3=0	电压补偿项PI	K_P4=1
	K₁₃=1		K₁₄=5

新窗口打开| 下载CSV

4.1 负荷突增工况

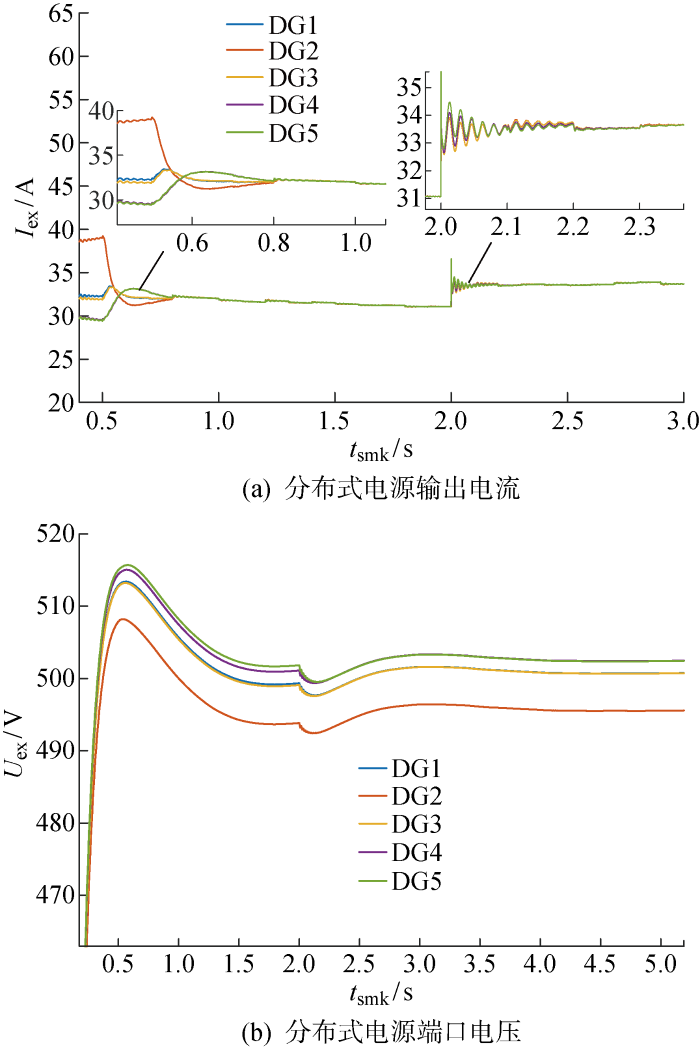
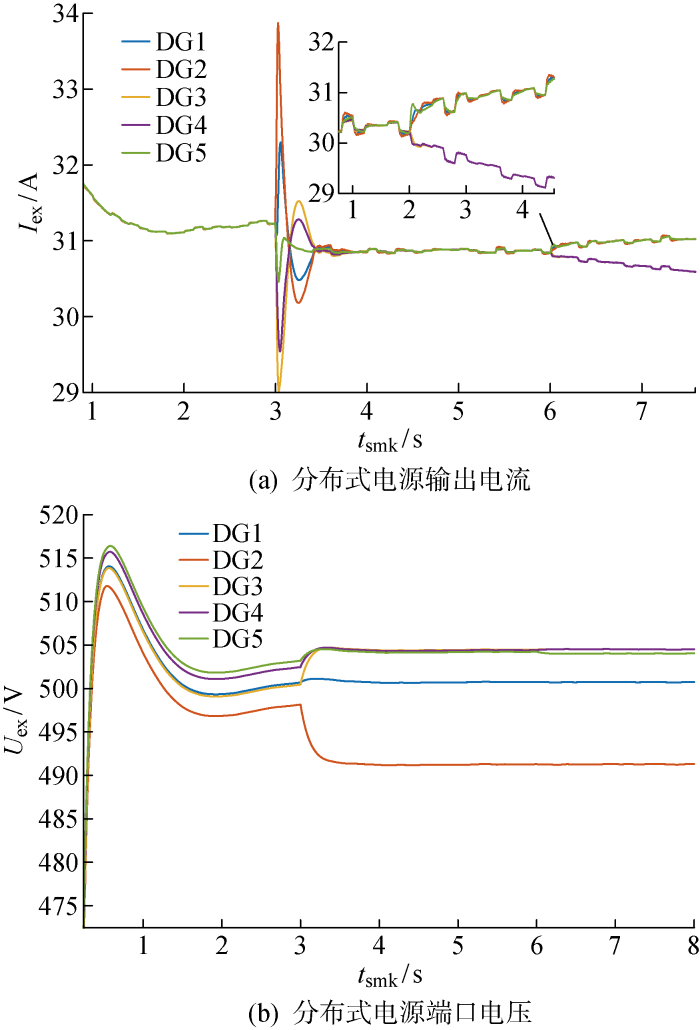
仿真系统中原负荷为31.25 kW,令仿真时间为参数t_smk,在仿真时间t_smk=0.5 s时启动控制策略,t_smk=2 s开始负荷突增6.25 kW.使用I_ex代表各DG的输出电流,U_ex代表各DG的出口电压,则系统负荷突增工况动态曲线如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 系统负荷突增工况动态曲线

Fig.4 Dynamic curves of system load under sudden surge condition

图4(a)中所示为系统分布式电源的输出电流曲线.在t_smk=0.5 s之前电流控制策略没有启动,各分布式电源输出电流不一致;在t_smk=0.5 s之后启动电流控制策略,收敛时限T_p=1 s,各分布式电源电流输出值能够在预先设定的收敛时限内快速收敛,并在时间达到收敛时限后保持不变,与前文理论部分相符,验证了分布式电源一致性控制方法的有效性.在t_smk=2 s时,DG5出口附近的系统负荷突增,分布式电源的输出电流值,在极短时间内再次达到平均一致性收敛.

如图4(b)为分布式电源输出的电压曲线.在仿真开始时分布式电源输出电压高于直流母线额定电压500 V,在t_smk=2 s前完成电压恢复.在负荷突增时分布式电源迅速恢复电压至额定电压并保持稳定.

4.2 通信拓扑断开

本工况下的仿真验证了通信拓扑断开的情况下所述控制方法的有效性.

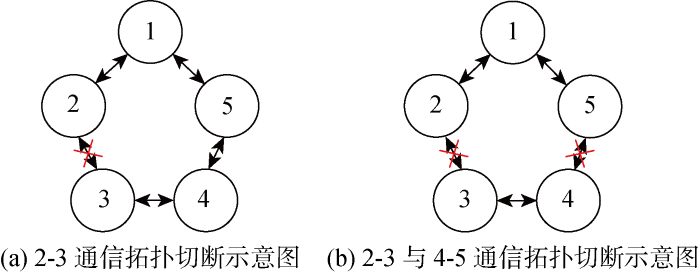
图5是系统通信拓扑的切断情况示意图.在t_smk=3 s时通信拓扑故障出现,2-3之间的通信拓扑切断.之后在t_smk=6 s时4-5的通信拓扑中断.使用本文中的控制策略对其进行负荷均衡分配,并恢复、调整电压到额定值500 V.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 系统通信拓扑示意图

Fig.5 Topology diagram of system communication

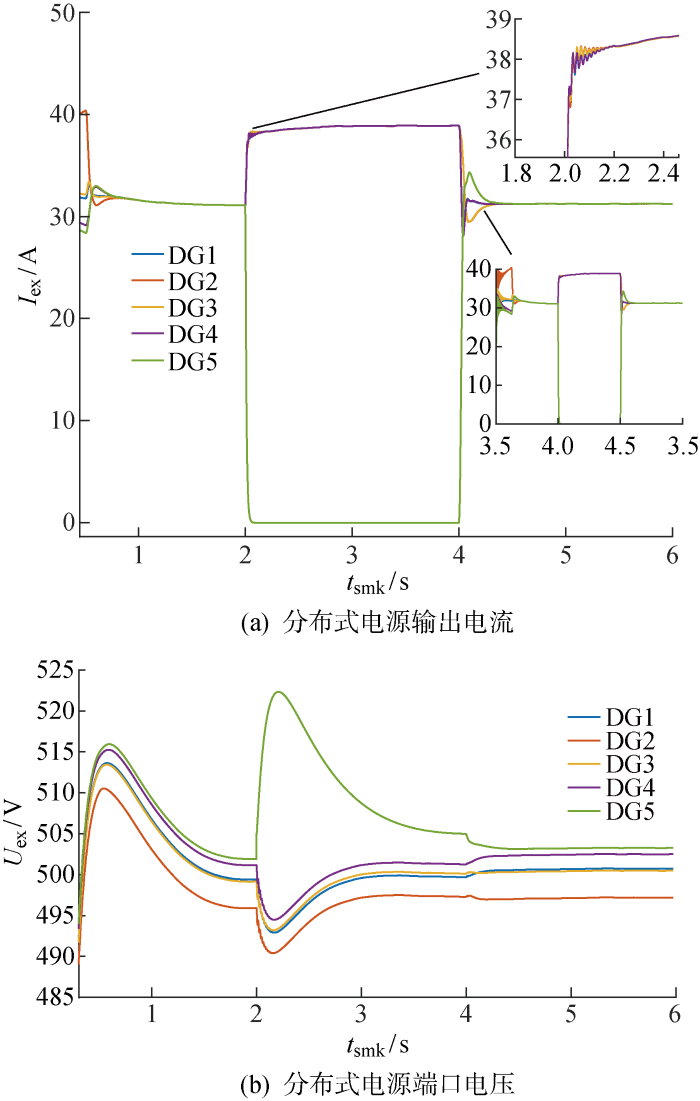
系统通信拓扑断开工况动态曲线如图6所示.图6(a)为此工况下切断先后切断2-3与4-5之间通信拓扑的分布式电源输出电流图像,在t_smk=0.5 s时,电流校正控制被投入.t_smk∈[0,3) s时,系统在图5(a)所示环形拓扑下保持稳定运行.在t_smk=3 s时节点2-3的通信拓扑被切断,由于系统本身的通信拓扑仍然是连通图,故系统的电流输出在经过了小幅振荡后仍然能够保持一致性,即环型拓扑下一条通信线路故障不会影响系统的运行与收敛.在t_smk=6 s时节点4-5的通信拓扑被切断,此时2-3通信拓扑并未恢复,系统无法构成连通图,故根据图6(a)的电流曲线,节点1、2、5与节点3、4变成两个非联通网络,此时分布式电源1、2、5与分布式电源3、4的输出电流分别达到一致性,如图5(b)所示的情况.这说明虽然系统整体通信拓扑被切断,有多条通信线路发生故障,但是各部分内部均能够达到均流输出.由于电压恢复的目标是将分布式电源出口电压恢复至500 V,故通信拓扑的切断并不影响分布式电源的电压恢复.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 系统通信拓扑断开工况动态曲线

Fig.6 Topology disconnection dynamic curve of system communication

4.3 退出与投入分布式电源

在t_smk=3 s时将分布式电源DG5从系统中切除,此后在t_smk=6 s时将分布式电源DG5重新并网并且投入运行,得到如图7所示的图像.图7(a)是系统在切除与重新加入DG5时的分布式电源输出电流曲线.当t_smk=0.5 s时,电流校正控制被投入.当t_smk=3 s时分布式电源DG5被切除,此时原来由5个分布式电源分担的负荷输出改由4个分布式电源承担,故每个分布式电源的输出功率均上升,在图7(a)中表现为输出电流上升.同时分布式电源的出口电压也发生突变.当t_smk=6 s时,退出的分布式电源DG5重新接入系统,此时系统拓扑与退出前系统保持一致,系统中每一个分布式电源的输出功率又回到DG5退出前的水平.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 系统投退分布式电源动态曲线

Fig.7 Dynamic curve of switching on and off of distributed power system

4.4 控制方法参数对比

表4是预定时间控制方法下系统切除分布式电源的工况下,对两种控制方法取不同的系统控制参数,考察电流曲线的H_THD,比较不同情况下的电能质量,结果如表4所示.表4中实际收敛时间项通过观察不同参数下电流曲线的收敛速度得到.然后就预定时间控制与有限时间控制的保守性进行对比,结果如表5所示.表5中的准确度Z_Q为实际收敛时间T_r与预计收敛时间上限 ${\bar{T}}_{p}$ 之比.

表4 不同控制参数下系统电流曲线H_THD

Tab.4 H_THD of system current curve of different control parameters

控制参数	H_THD
控制参数	t_smk= [0.5,3) s	t_smk= [3,6) s	t_smk= [6,8) s
T_p=0.5, α =3, b=50	1.02	0.49	1.42
T_p=0.2, α =3, b=50	0.89	0.48	1.42
k₁=500, k₂=500, p=7, q=9	1.53	0.50	2.05
k₁=1 000, k₂=1 000, p=7, q=9	1.61	0.50	2.31
k₁=1 500, k₂=1 500, p=7, q=9	1.64	0.50	2.52
k₁=2 000, k₂=2 000, p=7, q=9	1.68	0.52	2.64
k₁=2 500, k₂=2 500, p=7, q=9	1.93	0.64	2.68
k₁=3 000, k₂=3 000, p=7, q=9	1.95	0.66	2.78

新窗口打开| 下载CSV

表5 不同控制参数下系统收敛时间及准确度

Tab.5 Convergence time and accuracy of different control parameters

参数	T_r/s	${\bar{T}}_{p}$ /s	Z_Q/%
T_p=0.5, α =3, b=50	0.19	0.2	95
k₁=500, k₂=500, p=7, q=9	0.72	4.50	16
k₁=1 000, k₂=1 000, p=7, q=9	0.55	2.62	20.9
k₁=1 500, k₂=1 500, p=7, q=9	0.49	1.91	25.7
k₁=2 000, k₂=2 000, p=7, q=9	0.41	1.53	26.8
k₁=2 500, k₂=2 500, p=7, q=9	0.39	1.29	30.2
k₁=3 000, k₂=3 000, p=7, q=9	0.27	0.82	32.9

新窗口打开| 下载CSV

对分布式电源切除工况t_smk∈[0.5,3) s阶段下不同控制参数下的收敛时间、预计收敛时间上限进行比较.而收敛时间上限项中,预定时间控制下系统的收敛时间上限 ${\bar{T}}_{p}$ =T_p,固定时间控制的收敛时间上限由文献[25]得出.通过表5可知,随着固定时间有关控制参数的增加,实际收敛时间降低,收敛时间估计准确度上升——这意味着保守性的下降,但是仍然远不如预定时间控制下系统收敛时间估计的准确程度.

而根据表2对比结果可以得知,电能质量应该随着实际收敛时间T_r的降低而提高.从表4与表5的对比中可以得到,对于固定时间控制方法,参数k₁与k₂的上升会缩小系统的实际收敛时间,但是降低输出电流的电能质量.这就意味着在同一个工况下,通过增加控制参数来降低预计收敛时间将加剧非平滑控制动作对电能质量的恶化.因此,很难通过设置分布式固定时间二次控制的控制参数和降低预计收敛时间来同时加速收敛过程和提高电能质量.但是,提出的预定时间二次控制具有更少的预估收敛时间上限保守性,并且可以轻松预先设置收敛时间以根据实际需要实现快速收敛,并提高系统电能质量.

5 结语

提出一种基于预定时间控制方法的直流微电网控制策略.此种策略在下垂控制的基础上,应用了一种能够同时满足功率均分输出与电压校正的二次控制策略,并且通过仿真验证了所提出策略的有效性和相较于目前主流控制策略的优越性.文中提出的分布式电流控制策略能够在预先预定的时间内完成分布式电源的均流控制,并且将偏移额定电压的母线电压值恢复至额定电压.同时,仿真结果表明,文中提出的预定时间方法比主流的有限时间方法能使系统的收敛时间拥有更低的保守度,并且在相似的收敛时间下系统拥有更高的电能质量.这说明采用的预定时间控制方法具有更好的收敛性能与控制性能,提高了系统的适应性与可操作性.下一步的研究将考虑预定时间控制方法在更复杂工况下的应用方法,以及对预定时间控制下系统的鲁棒性进行优化.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

董旭柱, 华祝虎, 尚磊, 等.

新型配电系统形态特征与技术展望

[J]. 高电压技术, 2021, 47(9): 3021-3035.

[本文引用: 1]

DONG

Xuzhu

, HUA

Zhuhu

, SHANG

Lei

, et al.

Morphological characteristics and technology prospect of new distribution system

[J]. High Voltage Engineering, 2021, 47(9): 3021-3035.

[本文引用: 1]

[2]

MATHEW

, MADICHETTY

, MISHRA

A multilevel distributed hybrid control scheme for islanded dc microgrids

[J]. IEEE Systems Journal, 2019, 13(4): 4200-4207.

DOI:10.1109/JSYST.4267003 URL [本文引用: 1]

[3]

文云峰, 杨伟峰, 汪荣华, 等.

构建100%可再生能源电力系统述评与展望

[J]. 中国电机工程学报, 2020, 40(6): 1843-1855.

[本文引用: 1]

WEN

Yunfeng

, YANG

Weifeng

, WANG

Ronghua

, et al.

Review and prospect of toward 100% renewable energy power systems

[J]. Proceedings of the CSEE, 2020, 40(6): 1843-1855.

[本文引用: 1]

[4]

韩肖清, 李廷钧, 张东霞, 等.

双碳目标下的新型电力系统规划新问题及关键技术

[J]. 高电压技术, 2021, 47(9): 3036-3046.

[本文引用: 1]

HAN

Xiaoqing

, LI

Tingjun

, ZHANG

Dongxia

, et al.

New issues and key technologies of new power system planning under double carbon goals

[J]. High Voltage Engineering, 2021, 47(9): 3036-3046.

[本文引用: 1]

[5]

肖先勇, 郑子萱.

“双碳”目标下新能源为主体的新型电力系统: 贡献、关键技术与挑战

[J]. 工程科学与技术, 2022, 54(1): 47-59.

[本文引用: 1]

XIAO

Xianyong

, ZHENG

Zixuan

New power systems dominated by renewable energy towards the goal of emission peak &carbon neutrality: Contribution, key techniques, and challenges

[J]. Advanced Engineering Sciences, 2022, 54(1): 47-59.

[本文引用: 1]

[6]

姜淞瀚, 彭克, 徐丙垠, 等.

直流配电系统示范工程现状与展望

[J]. 电力自动化设备, 2021, 41(5): 219-231.

[本文引用: 1]

JIANG

Songhan

, PENG

, XU

Bingyin

, et al.

Current situation and prospect of demonstration projects of DC distribution system

[J]. Electric Power Automation Equipment, 2021, 41(5): 219-231.

[本文引用: 1]

[7]

卓振宇, 张宁, 谢小荣, 等.

高比例可再生能源电力系统关键技术及发展挑战

[J]. 电力系统自动化, 2021, 45(9): 171-191.

[本文引用: 1]

ZHUO

Zhenyu

, ZHANG

Ning

, XIE

Xiaorong

, et al.

Key technologies and developing challenges of power system with high proportion of renewable energy

[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.

[本文引用: 1]

[8]

李玲芳, 陈占鹏, 胡炎, 等.

基于灵活性和经济性的可再生能源电力系统扩展规划

[J]. 上海交通大学学报, 2021, 55(7): 791-801.

[本文引用: 1]

Lingfang

, CHEN

Zhanpeng

, HU

Yan

, et al.

Expansion planning of renewable energy power system considering flexibility and economy

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(7): 791-801.

[本文引用: 1]

[9]

杨丘帆, 黄煜彬, 石梦璇, 等.

基于一致性算法的直流微电网多组光储单元分布式控制方法

[J]. 中国电机工程学报, 2020, 40(12): 3919-3927.

[本文引用: 1]

YANG

Qiufan

, HUANG

Yubin

, SHI

Mengxuan

, et al.

Consensus based distributed control for multiple pv-battery storage units in DC microgrid

[J]. Proceedings of the CSEE, 2020, 40(12): 3919-3927.

[本文引用: 1]

[10]

李霞林, 郭力, 黄迪, 等.

直流配电网运行控制关键技术研究综述

[J]. 高电压技术, 2019, 45(10): 3039-3049.

[本文引用: 1]

Xialin

, GUO

, HUANG

, et al.

Research review on operation and control of DC distribution networks

[J]. High Voltage Engineering, 2019, 45(10): 3039-3049.

[本文引用: 1]

[11]

顾伟, 楼冠男, 柳伟. 微电网分布式控制理论与方法[M]. 北京: 科学出版社, 2019.

[本文引用: 1]

Wei

, LOU

Guannan

, LIU

Wei

. Distributed control theory and method of microgrid[M]. Beijing: Science Press, 2019.

[本文引用: 1]

[12]

李一琳

. 基于有限时间一致性的直流微电网分布式协调控制[D]. 广州: 华南理工大学. 2019.

[本文引用: 1]

Yilin

. Distributed coordinated control for DC microgrid based on finite-time consensus algorithm[D]. Guangzhou: South China University of Technology, 2019.

[本文引用: 1]

[13]

CHEN

, GUO

Distributed secondary and optimal active power sharing control for islanded microgrids with communication delays

[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 2002-2014.

DOI:10.1109/TSG.5165411 URL [本文引用: 1]

[14]

马宇辰

. 直流微电网分布式单元协同控制与负荷分配研究[D]. 上海: 上海电力大学, 2021.

[本文引用: 1]

Yuchen

. Research on cooperative control and load distribution of distributed units on DC microgrids[D]. Shanghai: Shanghai University of Electric Power, 2021.

[本文引用: 1]

[15]

WANG

Z Q

, WANG

, MA

M L

, et al.

A distributed event-triggered fixed-time fault-tolerant secondary control framework of islanded AC microgrid against faults and communication constraints

[J]. IEEE Transactions on Power Systems, 2022, 37(5): 3817-3833.

DOI:10.1109/TPWRS.2022.3143138 URL [本文引用: 1]

[16]

WANG

Z Q

, WANG

, MA

M L

, et al.

Distributed event-triggered fixed-time fault-tolerant secondary control of islanded AC microgrid

[J]. IEEE Transactions on Power Systems, 2022, 37(5): 4078-4093.

DOI:10.1109/TPWRS.2022.3142153 URL [本文引用: 1]

[17]

NETO

P J

, BARROS

T A

, SILVEIRA

P C

, et al.

Power management strategy based on virtual inertia for DC microgrids

[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12472-124857.

DOI:10.1109/TPEL.63 URL [本文引用: 1]

[18]

, SUN

, GU

, et al.

Optimal distributed control for secondary frequency and voltage regulation in an islanded microgrid

[J]. IEEE Transactions on Industrial Informatics, 2019, 15(1): 225-235.

DOI:10.1109/TII.2018.2795584 URL [本文引用: 1]

[19]

DEHKORDI

N M

, SADATI

, HAMZEH

Distributed robust finite-time secondary voltage and frequency control of islanded microgrids

[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3648-3659.

DOI:10.1109/TPWRS.2016.2634085 URL [本文引用: 1]

[20]

WANG

, SONG

, HILL

D J

, et al.

Prescribed-time consensus and containment control of networked multiagent systems

[J]. IEEE Transactions on Cybernetics, 2019, 49(4): 1138-1147.

DOI:10.1109/TCYB.2017.2788874 PMID:29994574 [本文引用: 4]

In this paper, we present a new prescribed-time distributed control method for consensus and containment of networked multiple systems. Different from both regular finite-time control (where the finite settling time is not uniform in initial conditions) and the fixed-time control (where the settling time cannot be preassigned arbitrarily), the proposed one is built upon a novel scaling function, resulting in prespecifiable convergence time (the settling time can be preassigned as needed within any physically allowable range). Furthermore, the developed control scheme not only ensures that all the agents reach the average consensus in prescribed finite time under undirected connected topology, but also ensures that all the agents reach a prescribed-time consensus with the root's state being the group decision value under the directed topology containing a spanning tree with the root as the leader. In addition, we extend the result to prescribed-time containment control involving multiple leaders under directed communication topology. Numerical examples are provided to verify the effectiveness and the superiority of the proposed control.

[21]

SAHOO

, MISHRA

A distributed finite-time secondary average voltage regulation and current sharing controller for DC microgrids

[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 282-292.

DOI:10.1109/TSG.2017.2737938 URL [本文引用: 1]

[22]

WANG

, HUANG

, ZAERY

, et al.

A fully distributed fixed-time secondary controller for DC microgrids

[J]. IEEE Transactions on Industry Applications, 2020, 56(6): 6586-6597.

DOI:10.1109/TIA.28 URL [本文引用: 3]

[23]

, SUN

Distributed finite-time convergence control of an islanded low-voltage AC microgrid

[J]. IEEE Transactions on Power Systems, 2018, 33(3): 2339-2348.

DOI:10.1109/TPWRS.59 URL [本文引用: 1]

[24]

ZHAO

, ZHANG

, LI

, et al,

Distributed robust frequency restoration and active power sharing for autonomous microgrids with event-triggered strategy

[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 3819-3834.

DOI:10.1109/TSG.2021.3087960 URL [本文引用: 4]

[25]

SARRAFAN

, ROSTAMI

M A

, ZAREI

, et al.

Improved distributed prescribed finite-time secondary control of inverter-based microgrids: Design and real-time implementation

[J]. IEEE Transactions on Industrial Electronics, 2021, 68(11): 11135-11145.

DOI:10.1109/TIE.2020.3031522 URL [本文引用: 4]

[26]

SONG

, WANG

, HOLLOWAY

, et al.

Time-varying feedback for finite-time robust regulation of normal-form nonlinear systems

[C]// 2016 IEEE 55th Conference on Decision and Control. Las Vegas, NV, USA: IEEE, 2016: 3837-3842.

[本文引用: 1]

[27]

, XU

, WU

X Y

, et al.

A two-layer distributed cooperative control method for islanded networked microgrid systems

[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 942-957.

DOI:10.1109/TSG.5165411 URL [本文引用: 1]

[28]

WANG

, SONG

, HILL

D J

, et al.

Prescribed finite time consensus of networked multi-agent systems

[C]// 2017 IEEE 56th Annual Conference on Decision and Control. Melbourne, VIC, Australia: IEEE, 2017: 4088-4093.

[本文引用: 2]

[29]

ZAERY

, WANG

, et al.

Distributed global economical load sharing for a cluster of DC microgrids

[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3410-3420.

DOI:10.1109/TPWRS.59 URL [本文引用: 2]

新型配电系统形态特征与技术展望

2021

... 作为集成分布式发电(Distributed Generator, DG)、负载和储能的一种技术方案,微电网(Microgrid, MG)以其能够接入大量分布式电源并消纳新能源的特点得到了充分关注^{[1⇓⇓⇓-5]}.随着微电网中直流分布式电源与直流负荷的逐渐增加,由于直流微电网具有变流环节少与不需要考虑无功问题等优点,这一技术得到了迅速发展^[6⇓-8].一般而言,微电网可以作为主网的一部分工作在并网状态,也可以与独立工作于孤岛状态.由于孤岛MG与大电网隔离,所以通常需要利用储能系统等分布式电源维持电压的稳定并优化能量管理,改善电能质量^[9-10].为了实现这些目标,孤岛直流MG的分层控制结构得到了广泛研究. ...

新型配电系统形态特征与技术展望

2021

A multilevel distributed hybrid control scheme for islanded dc microgrids

2019

构建100%可再生能源电力系统述评与展望

2020

构建100%可再生能源电力系统述评与展望

2020

双碳目标下的新型电力系统规划新问题及关键技术

2021

双碳目标下的新型电力系统规划新问题及关键技术

2021

“双碳”目标下新能源为主体的新型电力系统: 贡献、关键技术与挑战

2022

“双碳”目标下新能源为主体的新型电力系统: 贡献、关键技术与挑战

2022

直流配电系统示范工程现状与展望

2021

直流配电系统示范工程现状与展望

2021

高比例可再生能源电力系统关键技术及发展挑战

2021

高比例可再生能源电力系统关键技术及发展挑战

2021

基于灵活性和经济性的可再生能源电力系统扩展规划

2021

基于灵活性和经济性的可再生能源电力系统扩展规划

2021

基于一致性算法的直流微电网多组光储单元分布式控制方法

2020

基于一致性算法的直流微电网多组光储单元分布式控制方法

2020

直流配电网运行控制关键技术研究综述

2019

直流配电网运行控制关键技术研究综述

2019

... 目前对于控制结构而言,主流微电网分层控制框架主要由3个级别的控制组成,每个层级的控制对应着不同的响应时间尺度需求^[11].一次控制的目标是实现对MG的功率与电压的动态调节,一般采用下垂控制;二次控制用于补偿初级控制带来的功率分配偏差与电压偏差^[12].对于控制模式,较早被研究的集中式二次控制依赖于中央控制器的参考指令,对单点故障敏感^[13].因此,分布式二次控制被广泛研究以达到对初级控制偏差的修正^[14]. ...

2019

Distributed secondary and optimal active power sharing control for islanded microgrids with communication delays

2019

2021

A distributed event-triggered fixed-time fault-tolerant secondary control framework of islanded AC microgrid against faults and communication constraints

2022

... 在稀疏通信拓扑的基础上,基于一致性的分布式二次控制具有良好的灵活性和可靠性.由于加快收敛速度可以提高电能质量,为了实现这一目标,并且在有限时间内实现分布式电源的电流均衡输出,根据参数确定收敛时间上限的有限时间一致性理论被提出^[15-16].之后固定时间一致性理论因为其收敛时间不受系统初始状态的影响而得到进一步研究. ...

Distributed event-triggered fixed-time fault-tolerant secondary control of islanded AC microgrid

2022

Power management strategy based on virtual inertia for DC microgrids

2020

... 但是目前的主流控制策略仍然存在一些不足^[17].首先,对于有限时间一致性而言,文献[18]中应用符号函数sgn(x)来提高MG中的有限时间收敛速度.文献[19]中同时应用信号函数sgn(x)与分数阶状态反馈来构造有限时间控制方法.但是在有限时间一致性控制方法中使用的分数阶非平滑控制会降低系统的电能质量^[20].此外符号函数的应用虽然提高了MG应对外界干扰的鲁棒性,但是会给控制过程带来不可避免的抖振,若考虑到MG中具有随机性的可再生能源接入,系统电能质量的问题将会更为严重.文献[21]中应用饱和函数减少抖振现象,代价是降低了应对外界扰动的鲁棒性.同样地,有限时间一致性控制方法的收敛时间估计上限具有很大的保守性,并且取决于系统中DG状态的初值^[20].易知功率分配与电压恢复的加速能够有效改善电能质量并降低运行损耗,故降低收敛时间估计上界的保守性并提高其对初值的独立性十分必要. ...

Optimal distributed control for secondary frequency and voltage regulation in an islanded microgrid

2019

Distributed robust finite-time secondary voltage and frequency control of islanded microgrids

2017

Prescribed-time consensus and containment control of networked multiagent systems

2019

... [20].易知功率分配与电压恢复的加速能够有效改善电能质量并降低运行损耗,故降低收敛时间估计上界的保守性并提高其对初值的独立性十分必要. ...

... 为实现直流微电网不同工况下的有效控制,将收敛时间设定为扰动开始时间,引入分段时间标度函数^[20]为 ...

... 从时间区间[t_d₊_m_-1, t_d₊_m)的证明中,可以看到平均一致性共识是在预先指定的有限时间T_p内实现的,并保持在[t_d₊_m_-1+T_p, t_d₊_m)上.此外,文献[20]中指出控制输入在上至少为C¹平滑且均匀有界.则相对于有限时间控制方法里的非平滑控制函数,预定时间一致性控制方法的输入一直是平滑的(见图1实验结果). ...

A distributed finite-time secondary average voltage regulation and current sharing controller for DC microgrids

2019

A fully distributed fixed-time secondary controller for DC microgrids

2020

... 而在采用固定时间一致性方法的工作中,文献[22]中采用了分数阶状态反馈,文献[23-24]中采用了分数阶反馈与信号函数.文献[25]中采用了tanh函数,并且通过一个基于分段函数的近似方法得到了一个保守不足的收敛时间上界.虽然固定时间算法取得了显著的进步,但是除了电能质量问题之外,Lyapunov稳定性分析确定的收敛时间的估计上界仍然具有一定的保守性,大约为仿真确定的实际收敛时间的数倍,并且为控制参数的函数,不能够预先给定. ...

... 取t_d₊_m_-1=0.考虑系统y(t)≥0,满足

\overset{\cdot}{y}

(t)=-by(t)-k(

{\overset{\cdot}{ζ}}_{m}

/ζ_m)y(t)^[26].同时,取文献[22]、文献[24]与文献[25]中的有限时间控制算法与预定时间一致性控制方案进行比较,对比其总谐波失真(Total Harmonic Distortion, THD),并以参数H_THD代表THD含量,如表1所示. ...

... Comparison of H_THD of different control methods

Tab.1

控制方法	控制输入	H_THD/%
固定时间方法1^[22]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$	23.32
固定时间方法2^[24]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$ -k₃sgn(y)	17.17
固定时间方法3^[25]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$ -k₃tanh(y)	22.13
预定时间方法参数1	T_p=0.05, b=60, k=2, α=3	9.12
预定时间方法参数2	T_p=0.3, b=30, k=2, α=3	16.93

Distributed finite-time convergence control of an islanded low-voltage AC microgrid

2018

Distributed robust frequency restoration and active power sharing for autonomous microgrids with event-triggered strategy

2021

... 取t_d₊_m_-1=0.考虑系统y(t)≥0,满足

\overset{\cdot}{y}

(t)=-by(t)-k(

{\overset{\cdot}{ζ}}_{m}

... Comparison of H_THD of different control methods

Tab.1

控制方法	控制输入	H_THD/%
固定时间方法1^[22]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$	23.32
固定时间方法2^[24]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$ -k₃sgn(y)	17.17
固定时间方法3^[25]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$ -k₃tanh(y)	22.13
预定时间方法参数1	T_p=0.05, b=60, k=2, α=3	9.12
预定时间方法参数2	T_p=0.3, b=30, k=2, α=3	16.93

... 根据文献[24],表1中固定时间控制方法1、2与3控制下系统收敛时间的上限可以计算为T_f≤

{\bar{T}}_{f}

=πq/[2(q-p)

\sqrt{k_{1} k_{2}}

]=0.392 s.图1中固定时间控制1、2、3的实际收敛时间分别为0.14、0.027、0.12 s,与预估的收敛时间上限相比,保守性分别为180%、1 352%、227%.与之相比,预定时间控制的预定收敛时间T_p分别为0.05 s与0.3 s,而保守性为66.7%与50%.图1不仅说明了预定时间控制拥有比固定时间控制更快的收敛特性,还验证了表1中3个固定时间控制方法的估计上界要比预定时间控制的预定时间拥有更大的保守性. ...

Improved distributed prescribed finite-time secondary control of inverter-based microgrids: Design and real-time implementation

2021

... 取t_d₊_m_-1=0.考虑系统y(t)≥0,满足

\overset{\cdot}{y}

(t)=-by(t)-k(

{\overset{\cdot}{ζ}}_{m}

... Comparison of H_THD of different control methods

Tab.1

控制方法	控制输入	H_THD/%
固定时间方法1^[22]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$	23.32
固定时间方法2^[24]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$ -k₃sgn(y)	17.17
固定时间方法3^[25]	$\overset{\cdot}{y}$ =-k₁sig(y $)^{\frac{p}{q}}$ -k₂sig(y $)^{2 - \frac{p}{q}}$ -k₃tanh(y)	22.13
预定时间方法参数1	T_p=0.05, b=60, k=2, α=3	9.12
预定时间方法参数2	T_p=0.3, b=30, k=2, α=3	16.93

... 对分布式电源切除工况t_smk∈[0.5,3) s阶段下不同控制参数下的收敛时间、预计收敛时间上限进行比较.而收敛时间上限项中,预定时间控制下系统的收敛时间上限

{\bar{T}}_{p}

=T_p,固定时间控制的收敛时间上限由文献[25]得出.通过表5可知,随着固定时间有关控制参数的增加,实际收敛时间降低,收敛时间估计准确度上升——这意味着保守性的下降,但是仍然远不如预定时间控制下系统收敛时间估计的准确程度. ...

Time-varying feedback for finite-time robust regulation of normal-form nonlinear systems

2016

... 取t_d₊_m_-1=0.考虑系统y(t)≥0,满足

\overset{\cdot}{y}

(t)=-by(t)-k(

{\overset{\cdot}{ζ}}_{m}

A two-layer distributed cooperative control method for islanded networked microgrid systems

2020

... 传统的下垂控制手段由于下垂曲线的特性,无法同时满足端口电压恢复与按分布式电源容量分配输出功率的控制目标,无法进行无差调节^[27].因此,需要采取二次控制对一次控制的控制量进行补偿,产生合适的电压参考值并提供给分布式控制器用于分布式电源端口电压与输出功率的控制. ...

Prescribed finite time consensus of networked multi-agent systems

2017

... 首先根据文献[28]中的引理1给出,当系统拓扑G为无向连接图时,若存在一个实数常数g>0使得在区间[t_d₊_m_-1,t_d₊_m)上有: ...

... 考虑

\frac{{\overset{\cdot}{ζ}}_{m}}{ζ_{m}}

\frac{α}{T_{p}} ζ^{\frac{1}{α}}

, 那么根据文献[28],在时间段[t_d₊_m_-1, t_d₊_m_-1+T_p]上有: ...

Distributed global economical load sharing for a cluster of DC microgrids

2020

... 分布式电源电压控制的目标是使得在微电网正常运行并且分布式电源输出均衡功率时输出电压能够保持在电压参考值U_i_,ref,故采用在下垂控制参考电压中加入电压偏移补偿项的方式进行来恢复直流电压.电压偏移补偿项可以写成^[29]: ...

... 式中:I_N为单位矩阵.式(32)表示电压观测器的全局动态.文献[29]表明,若Laplace矩阵L是平衡的,则估计电压向量V^*中的所有元素能够收敛到共识值,也即平均电压的真实值.此共识值也即向量

\bar{V}

中所有元素的平均值,通过PI控制器可以使这个值不断接近给出的直流母线电压参考值,并得到电压恢复修正项,完成直流母线电压恢复. ...

〈

〉