极限学习机及其在质子交换膜燃料电池参数辨识中的应用

doi:10.16183/j.cnki.jsjtu.2021.453

极限学习机及其在质子交换膜燃料电池参数辨识中的应用

杨博, 曾春源, 陈义军, 束洪春, 曹璞璘^,

昆明理工大学电力工程学院, 昆明 650500

Extreme Learning Machine and Its Application in Parameter Identification of Proton Exchange Membrane Fuel Cell

YANG Bo, ZENG Chunyuan, CHEN Yijun, SHU Hongchun, CAO Pulin^,

Faculty of Electric Power Engineering, Kunming University of Science and Technology, Kunming 650500, China

通讯作者: 曹璞璘,副教授;E-mail:pulincao_kust@sina.com.

责任编辑: 王历历

收稿日期: 2021-11-11 修回日期: 2022-02-23 接受日期: 2022-02-24

基金资助:

国家自然科学基金(61963020)
云南省重大科技专项计划(202002AF080001)
云南省自然科学基金(202001AT070096)

Received: 2021-11-11 Revised: 2022-02-23 Accepted: 2022-02-24

作者简介 About authors

杨博(1988-),教授,从事新能源发电/储能系统优化与控制,以及人工智能在智能电网中应用方面的研究.

摘要

为对质子交换膜燃料电池(PEMFC)进行精确建模,需要准确辨识PEMFC中的未知参数.然而,PEMFC的参数辨识是一个多变量、多峰值和强耦合的非线性优化问题,传统的参数辨识方法往往得不到满意的结果.此外,不同运行条件下产生的噪声会阻碍启发式算法(MhAs)获取精确的参数.针对该问题,提出一种基于极限学习机(ELM)的MhAs策略——ELM-MhAs,以实现PEMFC的参数辨识.利用ELM对数据进行训练以降低或消除噪声,为MhAs提供更为准确可靠的适应度函数,从而保证MhAs对PEMFC参数的精确辨识.为验证该策略的可行性和有效性,在低温、低相对湿度和高温、高相对湿度两种条件下,分别对25组电压-电流数据进行不降噪、贝叶斯正则神经网络(BRNN)降噪以及ELM降噪处理,随后对比不同数据中6种MhAs和列文伯格-马夸尔特反向传播法的参数辨识结果.实验结果表明,与不降噪和BRNN降噪处理相比,应用ELM能够显著减少数据噪声对实验数据的影响,从而有效提高MhAs的参数辨识精度.

关键词： 质子交换膜燃料电池; 参数辨识; 极限学习机; 启发式算法; 降噪处理

Abstract

In order to develop an accurate model of proton exchange membrane fuel cell (PEMFC), it is essential to exactly identify unknown parameters in PEMFC. However, parameter identification of PEMFC is a multi-variable, multi-peak, and strongly coupled nonlinear optimization problem, of which traditional parameter identification methods often fail to achieve satisfactory results. In addition, noises generated under different operation conditions will hinder meta-heuristic algorithms (MhAs) to obtain accurate parameters. To handle these thorny obstacles, extreme learning machine based MhAs (ELM-MhAs) are proposed for PEMFC parameter identification, which can achieve denoising through ELM. ELM is used to train data to reduce or eliminate noises and provide more accurate and reliable fitness functions for MhAs, thus ensuring the accurate identification of PEMFC parameters by MhAs. To verify the feasibility and effectiveness of this strategy, 25 groups of voltage-current data are processed without denoising, with Bayesian regularization neural network (BRNN) denoising or with ELM denoising under two conditions—low temperature and low relative humidity; high temperature and high relative humidity, respectively. Subsequently, parameter identification results of six MhAs and a Levenberg-Marquardt backpropagation of different data are thoroughly compared. The simulation results indicate that ELM can significantly reduce the impact of noise on the data, while effectively improving the parameter identification accuracy of MhAs, compared with no denoising and BRNN denoising.

Keywords： proton exchange membrane fuel cell (PEMFC); parameter identification; extreme learning machine (ELM); meta-heuristic algorithms (MhAs); denoising

PDF (4860KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨博, 曾春源, 陈义军, 束洪春, 曹璞璘. 极限学习机及其在质子交换膜燃料电池参数辨识中的应用[J]. 上海交通大学学报, 2023, 57(4): 482-494 doi:10.16183/j.cnki.jsjtu.2021.453

YANG Bo, ZENG Chunyuan, CHEN Yijun, SHU Hongchun, CAO Pulin. Extreme Learning Machine and Its Application in Parameter Identification of Proton Exchange Membrane Fuel Cell[J]. Journal of Shanghai Jiaotong University, 2023, 57(4): 482-494 doi:10.16183/j.cnki.jsjtu.2021.453

日益增长的能源需求、传统燃料资源的枯竭和环境污染给社会的可持续发展带来巨大的挑战^[1].为缓解上述问题,优化能源结构,发展绿色能源技术势在必行^[2].其中,燃料电池(Fuel Cell, FC)系统以其高效、低污染、可持续发展等优点得到广泛的应用.燃料电池一般可分为4种类型,即质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell, PEMFC)^[3-4]、磷酸燃料电池、固体氧化燃料电池(Solid Oxide Fuel Cell, SOFC)和熔融碳酸盐燃料电池.

PEMFC具有响应速度快、启动速度快、工作温度低、无污染等优点,已广泛应用于航空、电动汽车和分布式发电等领域.此外,为获得准确可靠的电压-电流(V-I)特性,研究人员开发了多种PEMFC模型,如三维稳态模型^[5]、物理电解槽模型^[6]、电化学稳态模型^[7]等.尤其是由半经验方程推导出的电化学稳态模型能够很好地预测PEMFC的稳态和瞬时状态,该模型中包含的一些未知参数对PEMFC的准确性和可靠性有很大影响.

然而,PEMFC的高度非线性、强耦合和多峰值特性严重阻碍人们利用传统方法获得满意的参数辨识结果.近年来,启发式算法(Meta-Heuristic Algorithms, MhAs)^[4]以其极大的灵活性被广泛应用于PEMFC模型的参数辨识.例如,文献[8]采用粒子群优化算法对Nexa 1.2 kW PEMFC进行离线参数辨识.文献[9]模拟遗传学和自然选择的自然进化行为,利用改进遗传算法(Genetic Algorithm, GA)辨识PEMFC参数.同时,其他先进的MhAs也用于PEMFC参数辨识,例如,灰狼优化(Grey Wolf Optimizer, GWO)算法^[10]、鲸鱼优化算法(Whale Optimization Algorithm, WOA)^[11]、飞蛾扑火算法^[12]、差分进化算法^[13]、蚁狮优化(Antlion Optimization, ALO)算法^[14]、蜻蜓算法(Dragonfly Algorithm, DA)^[14]、平衡优化器(Equilibrium Optimizer, EO)^[15]等.到目前为止,MhAs在提高搜索能力和效率方面已取得显著进展.但是,上述文献忽略了数据噪声对PEMFC参数辨识的干扰,而由于测量误差或环境影响,这种情况在实际应用中不可避免且普遍存在.噪声的存在会导致MhAs的收敛速度减慢,PEMFC的参数辨识误差增大,使得后续的建模准确性降低.因此,需要采用一种切实有效的手段对数据噪声进行处理.

在数据降噪处理领域中,传统的方法有回归分析、聚类分析和分箱方法等.这些方法只能通过处理临近数据来确定最终解,没有自主学习能力,具有一定的缺陷.而人工神经网络(Artificial Neural Network, ANN)有强大的学习和适应能力,能够模拟人脑神经元的协同以实现信息的传递和处理,在数据降噪方面得到广泛研究.

因此,提出一种基于极限学习机(Extreme Learning Machine, ELM)的MhAs——ELM-MhAs来提高PEMFC的参数辨识性能.同时,对比ELM和另一种ANN策略——贝叶斯正则神经网络(Bayesian Regularization Neural Network, BRNN)^[16]的噪声性能.主要贡献和创新点可以总结如下:

(1) 考虑数据噪声对PEMFC参数辨识的影响,利用ELM策略减少或滤除数据噪声,以获得PEMFC更准确的V-I数据.

(2) 结合ELM降噪策略和多种先进MhAs,在低温、低相对湿度和高温、高相对湿度两个算例下全面比较6种主流MhAs性能,全面评价与分析ELM-MhAs的性能.

(3) 综合对比ELM-MhAs策略和BRNN-MhAs策略的降噪性能,仿真结果表明ELM-MhAs能够更有效地辨识PEMFC参数,且辨识精度高、速度快、稳定性好.

(4) 基于ELM和BRNN两种降噪策略,全面对比神经网络训练端到端参数辨识模型,即列文伯格-马夸尔特反向传播法(Levenberg-Marquardt Backpropagation, LMBP)^[17]与6种MhAs算法的PEMFC参数辨识结果,验证ELM降噪策略具有较强的泛化能力,能够与其他参数辨识算法结合.

1 质子交换膜燃料电池建模

1.1 电化学反应

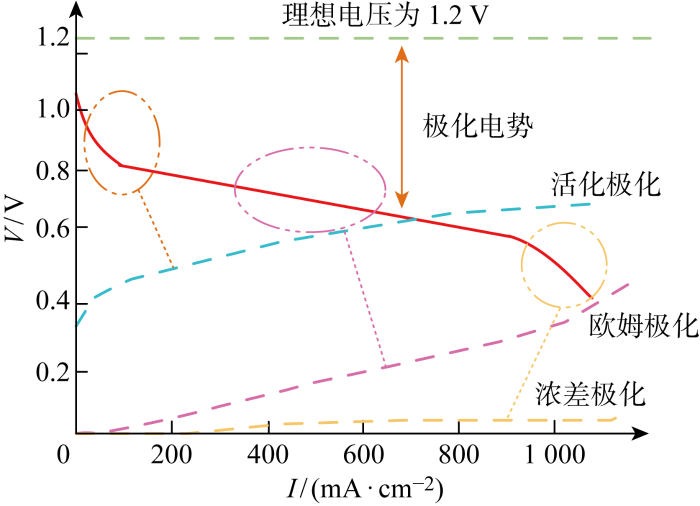
在实际运用中,PEMFC的电势会逐渐降低,这是因为电池内部存在不可逆的损失,这些不可逆的损失又被称为过电压或极化电势.PEMFC的极化曲线主要受3部分影响,即活化极化、欧姆极化、浓差极化,如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 PEMFC极化曲线

Fig.1 Polarization curve of PEMFC

PEMFC内部的电化学反应^[18]可表示为

阳极:

(1)H₂→2H⁺+2e^-

阴极:

(2)2H⁺+2e^-+

\frac{1}{2}

O₂→H₂O

总反应:

(3)2H₂+O₂→2H₂O

该反应放能.

1.2 数学建模

在考虑电化学反应的极化情况下,单个PEMFC输出电压^[17]为

(4)V_c=E_nerns-V_act-V_ohmic-V_con

式中:E_nerns为能斯特电动势;V_act为活化过电压;V_ohmic为欧姆过电压;V_con为浓差过电压.

能斯特电动势为热力学电动势,指理想情况下的输出电压,表示为

(5)

\begin{array}{l} E_{n e r n s} = \frac{Δ G}{2 F} + \frac{Δ S}{2 F} (T_{k} - T_{r e f}) + \\ \frac{R T_{k}}{2 F} (l n p_{H_{2}} + \frac{1}{2} p_{O_{2}}) \end{array}

式中:ΔG为吉布斯自由能的变化;F为法拉第常数,取96.487 C/mol;ΔS为熵变;R为气体常数,取8.314 J/(K·mol);T_k和T_ref分别为实际工作温度和参考温度; $p_{H_{2}}$ 和 $p_{O_{2}}$ 分别为氢分压和氧分压,可描述为

(6)

p_{H_{2}} = \frac{1}{2} H_{r, a} p_{H_{2} O}^{s a t} \times [{(\frac{H_{r, a} p_{H_{2} O}^{s a t}}{p_{a}} e x p (\frac{1.635 \frac{i_{c e l l}}{A}}{T_{k}^{1.334}}))}^{- 1} - 1]

(7)

p_{O_{2}} = H_{r, c} p_{H_{2} O}^{s a t} \times [{(\frac{H_{r, a} p_{H_{2} O}^{s a t}}{p_{c}} e x p (\frac{4.192 \frac{i_{c e l l}}{A}}{T_{k}^{1.334}}))}^{- 1} - 1]

式中:H_r,a和H_r,c分别为阴极和阳极气体相对湿度;p_a和p_c分别为阳极和阴极的进口压强;i_cell为实际电流; $p_{H_{2} O}^{s a t}$ 为水蒸气的饱和压强;A为膜的有效面积.定义一个便于 $p_{H_{2} O}^{s a t}$ 计算的温度值T_c,受电池温度的影响,则

(8)

T_{c} = T_{k} - 273.15

(9)

l g p_{H_{2} O}^{s a t} = 2.95 \times 10^{- 2} T_{c} - 9.19 \times 10^{- 5} T_{c}^{2} + 1.44 \times 10^{- 7} T_{c}^{3} - 2.18

活化过电压^[19]可表示为

(10)

\begin{matrix} V_{a c t} = ε_{1} + ε_{2} T_{k} + ε_{3} T_{k} l n c_{O_{2}} + ε_{3} T_{k} l n i_{c e l l} \end{matrix}

式中:ε_i' (i'=1, 2, 3, 4)为半经验系数; $c_{O_{2}}$ 为氧催化界面氧气浓度,可描述为

(11)

\begin{matrix} c_{O_{2}} = \frac{p_{O_{2}}}{5.08 \times 10^{6} e x p (- \frac{498}{T_{k}})} \end{matrix}

欧姆过电压计算如下:

(12)

\begin{matrix} V_{o h m i c} = i_{c e l l} (R_{m} + R_{c}) \end{matrix}

式中:R_c为电子传导的等效接触电阻;R_m为质子传导的等效膜电阻,表示为

(13)

\begin{matrix} R_{m} = ρ_{m} \frac{l}{A} \end{matrix}

式中:l为膜厚度;ρ_m为膜电阻率,描述为

(14)

\begin{array}{l} ρ_{m} = \\ \frac{181.6 [1 + 0.03 \frac{i_{c e l l}}{A} + 0.062 {(\frac{T_{k}}{303})}^{2} {(\frac{i_{c e l l}}{A})}^{2.5}]}{(λ - 0.634 - 3 \frac{i_{c e l l}}{A}) e x p (4.18 \frac{T_{k} - 303}{T_{k}})} \end{array}

式中:λ为经验系数,表示膜的含水量.

浓差过电压受氢、氧浓度的影响^[20],可表示为

(15)

\begin{matrix} V_{c o n} = - b l n (l n \frac{J}{A J_{m a x}}) \end{matrix}

式中:b为经验系数;J和J_max分别为实际电流密度和最大电流密度.

从式(4)~(15)可以看出PEMFC模型需要确定7个未知参数,即ε₁,ε₂,ε₃,ε₄,b,λ和R_c.

1.3 目标函数

为准确辨识PEMFC的7个参数,需设计合理的目标函数,使实际值与估计值之间的误差最小.选用均方根误差(RMSE)作为目标函数,如下:

(16)

R M S E (x') = \sqrt{\frac{1}{N} \overset{N}{\sum_{n = 1}} (V_{a v, n} - V_{e s t, n} (x', I_{n} {))}^{2}}

式中: $x'$ 为待优化变量,即 $x' = (ε_{1}, ε_{2}, ε_{3}, ε_{4}, b, λ, R_{c})$ ;N为实际数据量; $I_{n}$ 为实际数据集中第n个电流值; $V_{a v, n}$ 和 $V_{e s t, n}$ 为实际数据集中第n个输出电压值以及 $I_{n}$ 对应的估计电压值.

同时,为高效实现参数辨识,对待辨识的PEMFC参数上下边界进行约束,有

(17)

s . t . \{\begin{array}{l} ε_{i', m i n} \leq ε_{i'} \leq ε_{i', m a x} \\ λ_{m i n} \leq λ \leq λ_{m a x} \\ R_{c, m i n} \leq R_{c} \leq R_{c, m a x} \\ b_{m i n} \leq b \leq b_{m a x} \end{array} \forall i' \in {1,2, 3,4}

2 PEMFC参数辨识的 ELM-MhAs设计

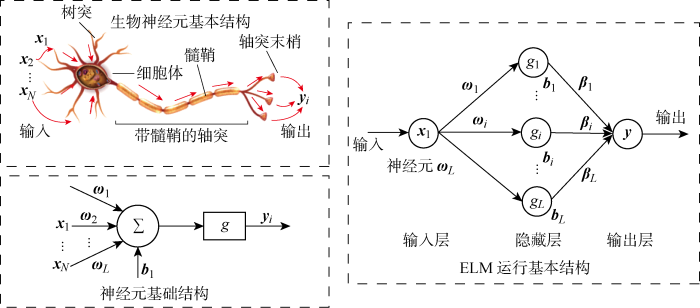
2.1 ELM基本原理

与其他常规的前馈神经网络相比,ELM^[21]能显著提高鲁棒性、泛化能力、学习速度和训练精度.ELM的拓扑结构如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 ELM的拓扑结构图

Fig.2 Topological structure of ELM

训练开始时,ELM能随机初始化输入权重和偏置,且在后续训练中无需进行调整,仅需设定隐藏层的神经元个数,即可在输出层获得全局最优解.

详细论证ELM主要数学机理^[22-23]:假设ELM的输入层有N个神经元,对应N个输入变量;隐藏层有L个神经元;输出层有M个神经元,对应M个输出变量. 当有N个训练数据 $(x_{i}, t_{i}), x_{i} = (x_{i 1}, x_{i 2}, \dots, x_{i n})^{T} \in R^{n}, t_{i} = (t_{i 1}, t_{i 2}, \dots, t_{i m})^{T} \in R^{m}$ 时,对应于该ELM的输出计算如下:

(18)

y_{i} = \overset{L}{\sum_{j = 1}} β_{j} \cdot g (ω_{j} \cdot x_{i} + b_{j}), i = 1,2, \dots, N

式中:x_i为ELM的第i个输入; $ω_{j} = (ω_{j 1}, ω_{j 2}, \dots, ω_{j n})^{T}$ 为输入层神经元和第j个隐藏层神经元之间的权重; $b_{j}$ 为第j个隐藏层神经元的偏置; $g (\cdot)$ 为激活函数; $β_{j} = (β_{j 1}, β_{j 2}, \dots, β_{j m})^{T}$ 为第j个隐藏层神经元与输出层神经元之间的权重.

此外,性能良好的ELM能够近似获得零误差的训练数据,即 $\overset{N}{\sum_{i = 1}} |y_{i} - t_{i}| = 0$ ,即存在 $ω_{j} 、 x_{i}$ 和 $b_{j}$ 使得ELM第i个训练数据的输出 $t_{i}$ 可以满足^[24]:

(19)

t_{i} = \overset{L}{\sum_{j = 1}} β_{j} \cdot g (ω_{j} \cdot x_{i} + b_{j}), i = 1,2, \dots, N

将式(18)和式(19)以矩阵的方式表达为

(20)

H β = T

(21)

H = [\begin{array}{l} h (x_{1}) \\ h (x_{2}) \\ ︙ \\ h (x_{N}) \end{array}] = {[\begin{array}{l} g (ω_{1} \cdot x_{1} + b_{1}) & \dots & g (ω_{L} \cdot x_{1} + b_{L}) \\ ︙ & ︙ \\ g (ω_{1} \cdot x_{N} + b_{1}) & \dots & g (ω_{L} \cdot x_{N} + b_{L}) \end{array}]}_{N \times L}

(22)

β = {[\begin{array}{l} β_{1} \\ β_{2} \\ ︙ \\ β_{L} \end{array}]}^{T}_{L \times m}, T = {[\begin{array}{l} t_{1} \\ t_{2} \\ ︙ \\ t_{N} \end{array}]}^{T}_{N \times m}

式中:H为隐藏层的输出矩阵;T为期望输出向量;β表示隐藏层神经元与输出层神经元之间的权向量^[25-26],可表示为

(23)

\begin{matrix} (H \tilde{β} - T) = \underset{β}{m i n} (H β - T) \end{matrix}

式中: $\tilde{β}$ 为对应于β的理想权向量^[27],表示为

(24)

\begin{matrix} \tilde{β} = H^{†} T \end{matrix}

式中:H^†为隐藏层输出矩阵H的Moore-Penrose广义逆矩阵.

在各种实际运行条件下,V-I测量数据中不可避免地存在噪声,这通常会导致MhAs参数辨识不理想甚至出现严重错误.因此,需要通过改变输入层和隐藏层神经元之间的权重,即对随机初始化的权重进行一定范围的限制以强化泛化能力并降低过拟合的情况.随后,对比多种范围限制的结果,选择对原始数据拟合效果最好的一组,进而实现ELM减少或滤除噪声.

2.2 PEMFC参数辨识

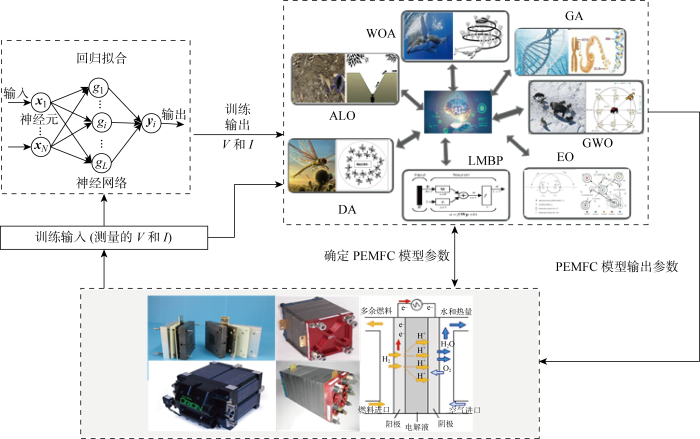
基于ELM-MhAs的PEMFC参数辨识过程主要包括数据采集、数据预处理和参数辨识3个部分,如图3所示.首先,收集PEMFC的V-I测量数据,并传输到ELM.然后,利用ELM训练测量V-I数据,进行数据预处理.最后,运用MhAs进行一系列的全局搜索和局部探索,根据处理后的数据精确辨识出PEMFC模型参数.ELM-MhAs详细执行步骤如下.其中:N_p为初始种群大小.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 PEMFC基于ELM算法的参数辨识总体框架

Fig.3 Overall framework of ELM-algorithms based PEMFC parameter identification

算法1:ELM-MhAs的实现步骤

步骤1: 构建PEMFC模型;

步骤2: 采集PEMFC的V-I数据;

步骤3: 使用ELM对V-I数据进行训练;

步骤4: 初始化MhAs参数;

步骤5: 设置t=0;

步骤6: WHILE t≤t_max

步骤7: FOR1 p=1

步骤8: 通过式(16)计算第p个个体的适应度值;

步骤9: END FOR1

步骤10: 根据每个个体的适应度值来调整其角色;

步骤11: FOR2 p=1: N_p

步骤12: 基于第p个个体搜索规则更新解;

步骤13: END FOR2

步骤14: 设置t=t+1;

步骤15: END WHILE

步骤16: 输出PEMFC全局最优参数.

需要说明的是,目前燃料电池参数辨识研究忽视了客观存在的数据噪声带来的干扰,绝大部分PEMFC参数辨识的研究没有运用相应策略进行滤波降噪处理,且仅采用单一启发式算法进行参数辨识^[4].ELM作为一种成熟的人工神经网络策略,能够很好地减少或滤除数据噪声,具有较强的泛化能力,因此其应用不局限于对燃料电池数据的处理.

3 算例分析

温度、阴极和阳极气体相对湿度对PEMFC的V-I曲线和参数都有影响.因此,在低温T_k=333.15 K、低相对湿度H_r,a=50%和H_r,c=50%以及高温T_k=353.15 K、高相对湿度H_r,a=100%和H_r,c=100%条件下,运用6种MhAs(ALO^[14]、DA^[14]、EO^[15]、GA^[9]、GWO^[10]、WOA^[11])和LMBP^[17,28]进行PEMFC的7个参数(ε₁、ε₂、ε₃、ε₄、b、λ和R_c)辨识.同时,为提高效率和准确性,对参数边界条件进行限制^[10],如表1所示.值得注意的是,目前绝大部分燃料电池数据采集主要依赖于测量精度为mV的数据采集系统^[29].由于电池内部环境复杂,采集的信号不可避免地会受到一些噪声等高频信号的干扰,故用信号调理电路对这些信号进行处理^[30],但技术的限制使得当前精度的信号调理电路无法完全滤除这些干扰信号^[31].为增强研究的实用性和准确性,目前多用白噪声数据模拟这些噪声信号.从Ballard-Mark-V PEMFC中取25组V-I数据^[32]作为无噪声的原始数据,并设置随机独立分布3 mV级别的白噪声以获取噪声数据,电池膜厚 178 μm,有效面积为50.6 cm².

表1 PEMFC参数辨识的范围^[10]

Tab.1 PEMFC parameter range for identification^[10]

参数	ε₁	ε₂	ε₃	ε₄	λ	R_c/Ω	b/V
最小值	-1.1997	0.0010	3.6000×10^-5	-2.6000×10^-4	10	1.0000×10^-4	0.0136
最大值	-0.8531	0.0050	9.8000×10^-5	-9.5400×10^-5	23	8.0000×10^-4	0.5000

新窗口打开| 下载CSV

特别地,BRNN和ELM都属于ANN技术,BRNN具有良好的学习能力和降噪效果,其性能已在文献[16]中充分验证.在后续PEMFC研究中发现ELM降噪处理精度更高,能够处理更小的噪声数据,故采用BRNN和ELM进行滤波降噪效果的对比研究.此外,亦在SOFC研究中运用神经网络训练端到端参数辨识模型LMBP^[28],并充分验证其稳定性、准确性和效率.因此,为区别于MhAs对PEMFC的参数辨识,采用LMBP与MhAs进行对比研究.

基于BRNN和ELM两种降噪策略实现数据噪声的处理,并结合上述7种算法进行已降噪和未降噪数据的参数辨识;最后,综合比较基于BRNN和ELM降噪下各算法参数辨识的结果和最小RMSE,以充分验证ELM-MhAs辨识参数的良好性能.

为确保所有算法在相同条件下运行,设置最大迭代次数k_max=120、初始种群N_p=40,均独立运行15次.仿真在2.9 GHz Intel^R CoreTMi7 CPU和16 GB RAM配置的个人计算机上运行,模型利用MATLAB/Simulink2019a搭建.

3.1 低温、低相对湿度

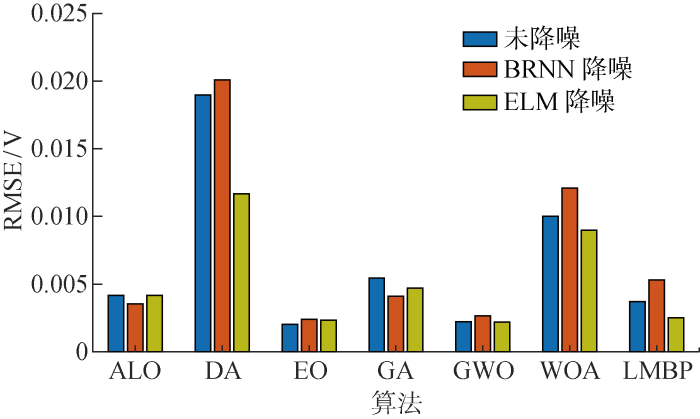
表2为无降噪处理、BRNN以及ELM降噪处理下7种算法的最优参数辨识结果和最小RMSE,其中符号‘N’表示无降噪处理,‘B’表示由BRNN降噪处理,‘E’表示由ELM降噪处理(最优值加粗表示,后同).从表中可以看出,降噪处理后各算法得到的RMSE要明显小于无降噪处理的RMSE;相比于BRNN降噪,ELM降噪后参数辨识精度更高,性能更优良.例如,相较于无降噪和BRNN降噪处理后算法的准确性,ELM降噪处理后ALO准确性分别提高22.03%和2.72%,GWO准确性分别提高24.80%和21.68%,EO准确性分别提高52.63%和58.80%,DA准确性分别提高0.82%和6.63%,LMBP准确性分别提高4.81%和14.07%.

表2 低温低相对湿度下的参数辨识结果

Tab.2 Parameter identification results obtained at a low temperature and low relative humidity

算法	符号	ε₁	ε₂	ε₃	ε₄	λ	R_c/Ω	b/V	RMSE/V
ALO	N	-1.1997	0.0038	4.7755×10^-5	-1.9539×10^-4	22.7213	8.0000×10^-4	0.0136	1.4918×10^-3
	B	-0.8531	0.0027	4.6077×10^-5	-1.9240×10^-4	17.2486	3.0088×10^-4	0.0148	1.1955×10^-3
	E	-1.0622	0.0039	8.3563×10^-5	-1.9076×10^-4	19.5346	2.1396×10^-4	0.0162	1.1631×10^-3
DA	N	-1.1997	0.0038	4.4140×10^-5	-1.9063×10^-4	14.1016	4.8523×10^-4	0.0157	1.3099×10^-3
	B	-0.9920	0.0031	4.4408×10^-5	-1.9707×10^-4	15.4621	3.3040×10^-4	0.0136	1.3915×10^-3
	E	-0.8531	0.0030	7.0217×10^-5	-1.9588×10^-4	14.1585	5.2635×10^-4	0.0136	1.2992×10^-3
EO	N	-0.8828	0.0033	8.8483×10^-5	-1.8694×10^-4	20.2055	5.1412×10^-4	0.0180	1.7501×10^-3
	B	-1.1997	0.0041	6.8525×10^-5	-1.8486×10^-4	22.2448	8.0000×10^-4	0.0181	2.0123×10^-3
	E	-0.9576	0.0032	5.9925×10^-5	-1.9073×10^-4	17.4769	1.1767×10^-4	0.0152	8.2907×10^-4
GA	N	-0.8952	0.0033	8.1726×10^-5	-1.9717×10^-4	17.9935	1.0162×10^-4	0.0150	1.4024×10^-3
	B	-1.0374	0.0032	3.9417×10^-5	-1.9576×10^-4	22.9887	1.0260×10^-4	0.0143	1.7726×10^-3
	E	-0.8727	0.0034	9.4426×10^-5	-1.9046×10^-4	20.1161	2.1615×10^-4	0.0174	1.1935×10^-3
GWO	N	-0.8558	0.0026	4.1166×10^-5	-1.8835×10^-4	22.5918	6.0519×10^-4	0.0180	1.6007×10^-3
	B	-1.0634	0.0040	9.4119×10^-5	-1.8632×10^-4	20.0275	6.5140×10^-4	0.0173	1.5371×10^-3
	E	-1.1301	0.0041	8.3065×10^-5	-1.8739×10^-4	14.2505	1.9414×10^-4	0.0157	1.2038×10^-3
WOA	N	-0.8535	0.0026	4.3311×10^-5	-1.9027×10^-4	13.3911	1.0890×10^-4	0.0180	3.2404×10^-3
	B	-1.0351	0.0037	7.8048×10^-5	-1.8972×10^-4	14.7768	1.0000×10^-4	0.0136	1.5500×10^-3
	E	-1.1995	0.0041	6.3044×10^-5	-1.9065×10^-4	16.7606	4.0499×10^-4	0.0143	1.1961×10^-3
LMBP	N	-1.0282	0.0031	3.7294×10^-5	-1.8648×10^-4	20.7773	1.0000×10^-4	0.0193	2.5661×10^-3
	B	-1.1028	0.0039	7.5117×10^-5	-1.8040×10^-4	10.2563	8.0000×10^-4	0.0136	2.8427×10^-3
	E	-1.0619	0.0036	6.3838×10^-5	-1.8326×10^-4	19.4747	8.0000×10^-4	0.0188	2.4426×10^-3

新窗口打开| 下载CSV

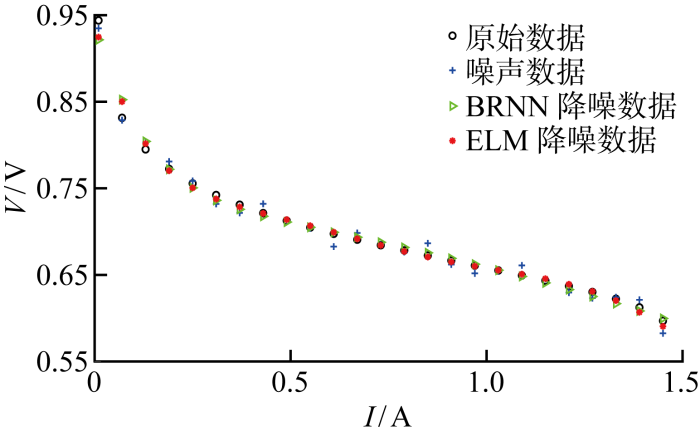
图4给出不同数据在低温、低相对湿度下的极化拟合曲线.由图可知,数据噪声对原始数据干扰性较强,导致偏差较大,数据重合点较少;而ELM和BRNN降噪数据与原始数据重合点多,表明降噪技术能实现更好的数据拟合.其中,ELM降噪数据的拟合情况优于BRNN降噪数据,证明ELM能够更有效减少或滤除噪声,使数据更准确可靠.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 低温、低相对湿度下的数据拟合

Fig.4 Data fitting obtained at a low temperature and low relative humidity

图5为各算法分别基于无降噪、BRNN降噪和ELM降噪进行15次独立参数辨识后的RMSE.大部分基于BRNN降噪的RMSE均大于基于ELM的RMSE,表明ELM-MhAs能找到更好的全局最优解,从而更准确、稳定地实现PEMFC的参数辨识.由图可知,ELM降噪处理后,DA的RMSE约为无降噪处理的40%,BRNN降噪处理的35%,算法的准确性和稳定性显著提高.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 低温、低相对湿度下7种算法的RMSE

Fig.5 RMSE of seven algorithms obtained at a low temperature and low relative humidity

图6为7种算法的箱形图.由图可见,经过BRNN和ELM降噪处理后,大部分算法的误差及分布范围明显减小.特别地,ELM降噪后所有算法的RMSE波动范围更小,异常值也更少,进一步验证ELM降噪处理能够增强算法在参数辨识中的全局搜索能力和寻优稳定性.例如,ELM-DA较DA和BRNN-DA误差分布范围显著减小,ELM-LMBP较LMBP和BRNN-LMBP整体误差减小且剔除异常值.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 低温、低相对湿度下7种算法的箱形图

Fig.6 Boxplot of seven algorithms obtained at a low temperature and low relative humidity

图7给出所有算法在无降噪处理和两种降噪策略处理后的收敛曲线.图中:k为迭代次数.由图可知,经过BRNN或ELM降噪处理后,算法在迭代后期能较为稳定地进行参数寻优,而未降噪处理的算法受数据噪声干扰大,误差波动大,难以趋于平稳.对比BRNN和ELM降噪处理后的收敛曲线,ELM降噪策略保证更多算法只需更少的迭代次数就能辨识到高准确性的参数,进一步验证ELM-MhAs辨识参数的稳定性、精确性和快速性.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 低温低相对湿度下7种算法收敛曲线

Fig.7 Convergence curves of seven algorithms obtained at a low temperature and low relative humidity

3.2 高温、高相对湿度

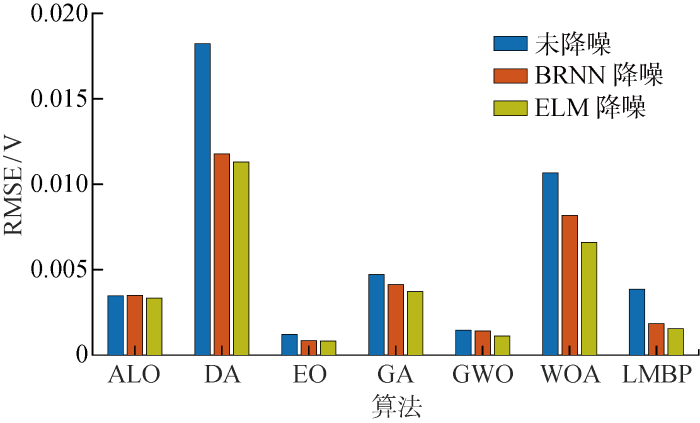
6种MhAs和LMBP最优参数辨识结果和最小RMSE如表3所示.从表中可以看出,相较于基于BRNN和ELM降噪策略的算法,无降噪处理算法的最优参数辨识误差更大,精确性不足.对比两种降噪策略,ELM降噪后ALO、EO、GA、GWO、WOA和LMBP共6种算法得到的RMSE比BRNN降噪的RMSE更小,表明ELM能够显著提高数据噪声干扰下各算法的全局搜索能力并降低陷入局部最优解的概率,从而实现更高精度的参数辨识.例如,ELM-GA的准确性较GA和BRNN-GA分别显著提高43.84%和42.74%;ELM-ALO的准确性较ALO和BRNN-ALO分别显著提高22.75%和15.50%;ELM-LMBP的准确性较LMBP和BRNN-LMBP分别显著提高44.95%和2.27%.

表3 高温、高相对湿度下的参数辨识结果

Tab.3 Parameter identification results obtained at a high temperature and high relative humidity

算法		ε₁	ε₂	ε₃	ε₄	λ	R_c/Ω	b/V	RMSE/V
ALO	N	-0.8531	0.0028	5.4224×10^-5	-1.9381×10^-4	17.1927	1.6728×10^-4	0.0136	1.4200×10^-3
	B	-0.9590	0.0030	4.6983×10^-5	-1.9038×10^-4	15.0582	1.0000×10^-4	0.0136	1.2983×10^-3
	E	-0.8531	0.0027	4.5276×10^-5	-1.9218×10^-4	18.1940	4.4457×10^-4	0.0136	1.0970×10^-3
DA	N	-0.9377	0.0029	4.2164×10^-5	-1.9321×10^-4	18.9210	4.1854×10^-4	0.0136	1.1348×10^-3
	B	-1.1997	0.0040	6.2009×10^-5	-1.9179×10^-4	18.2714	3.5924×10^-4	0.0136	8.6808×10^-4
	E	-0.8531	0.0028	5.2448×10^-5	-1.9155×10^-4	20.7451	8.0000×10^-4	0.0136	7.9570×10^-4
EO	N	-0.9304	0.0032	6.7696×10^-5	-1.9272×10^-4	19.8194	1.6251×10^-4	0.0136	7.9879×10^-4
	B	-0.8564	0.0032	8.3113×10^-5	-1.9239×10^-4	22.0052	1.0000×10^-4	0.0136	6.8046×10^-4
	E	-1.1996	0.0040	6.3959×10^-5	-1.9278×10^-4	22.9997	2.3671×10^-4	0.0136	6.8623×10^-4
GA	N	-1.0365	0.0035	6.5236×10^-5	-1.9455×10^-4	22.8470	1.2145×10^-4	0.0137	1.1852×10^-3
	B	-1.0737	0.0033	4.0511×10^-5	-1.9059×10^-4	22.8380	1.1889×10^-4	0.0141	1.1625×10^-3
	E	-1.1406	0.0043	9.2910×10^-5	-1.9165×10^-4	22.7392	7.9682×10^-4	0.0136	6.6562×10^-4
GWO	N	-1.1997	0.0043	8.1015×10^-5	-1.9245×10^-4	22.3827	2.3883×10^-4	0.0136	6.6925×10^-4
	B	-0.8894	0.0027	4.1693×10^-5	-1.9289×10^-4	21.8924	4.9842×10^-4	0.0136	6.9529×10^-4
	E	-1.1327	0.0035	4.4503×10^-5	-1.9136×10^-4	19.5772	1.9583×10^-4	0.0137	6.3941×10^-4
WOA	N	-1.1493	0.0038	5.9464×10^-5	-1.8838×10^-4	17.7311	1.0096×10^-4	0.0151	1.7329×10^-3
	B	-0.8531	0.0026	3.8977×10^-5	-1.9118×10^-4	13.0255	1.0991×10^-4	0.0136	1.9095×10^-3
	E	-1.1540	0.0041	7.6040×10^-5	-1.9381×10^-4	18.6908	1.0000×10^-4	0.0136	1.2166×10^-3
LMBP	N	-0.97694	0.0033	5.9833×10^-5	-1.9507×10^-4	21.1973	1.0000×10^-4	0.0136	1.5649×10^-3
	B	-1.1155	0.0036	5.6620×10^-5	-1.9381×10^-4	22.3659	1.0000×10^-4	0.0136	8.8141×10^-4
	E	-1.1823	0.0036	3.8790×10^-5	-1.9396×10^-4	23.0000	1.0000×10^-4	0.0136	8.6141×10^-4

新窗口打开| 下载CSV

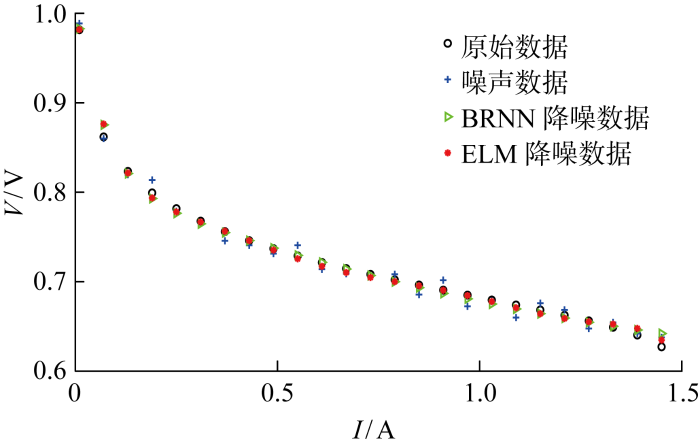
高温、高相对湿度下,4种数据的拟合对比如图8所示.由图可以明显看出,相较于无降噪处理和BRNN降噪处理的数据,ELM降噪处理的数据与原始数据重合点多,数据偏差小,拟合效果优良.进一步验证ELM降噪策略能显著减少数据中的噪声,使拟合数据更为理想.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 高温高相对湿度下的数据拟合

Fig.8 Data fitting obtained at a high temperature and high relative humidity

图9给出7种算法在无降噪以及两种降噪策略处理下独立运行15次的RMSE对比.由图可见,经过BRNN或ELM降噪后,所有算法的RMSE都较未降噪处理算法的RMSE更小.其中,基于ELM策略得到的参数辨识误差较BRNN更小,ELM-MhAs能获得更好的全局最优解.ELM降噪算法较BRNN降噪算法性能优化程度最好的为WOA,其次为DA、GA、GWO、LMBP、ALO以及EO.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 高温、高相对湿度下7种算法的RMSE

Fig.9 RMSE of seven algorithms obtained at a high temperature and high relative humidity

7种优化算法独立运行15次的误差箱形图如图10所示.可以看出,利用噪声数据进行辨识的误差和误差波动范围皆大于降噪数据的误差和误差波动范围,说明引入降噪技术能够切实减小数据噪声的干扰,从而提高辨识参数的精度.此外,基于ELM降噪处理的各算法误差区间远小于基于BRNN降噪处理的误差区间,且异常值亦更少.例如,ELM-LMBP的误差上下限小于BRNN-LMBP的误差上下限,并且ELM-LMBP辨识PEMFC参数的稳定性和精确性也进一步提升.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 高温、高相对湿度下7种算法的箱形图

Fig.10 Boxplot of seven algorithms obtained at a high temperature and high relative humidity

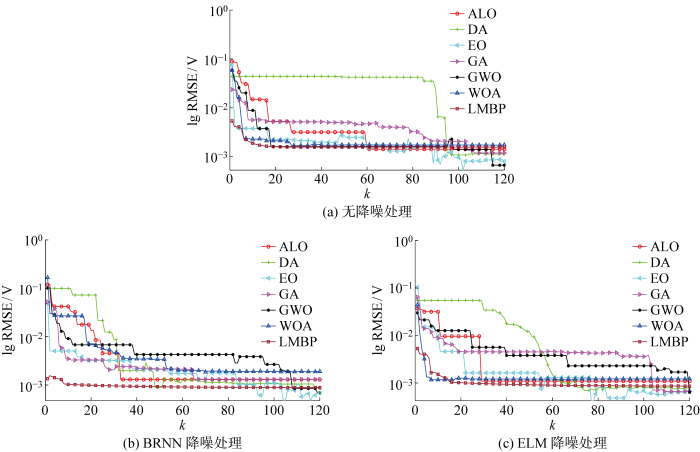
图11(a)、11(b)和11(c)分别为基于无降噪、BRNN和ELM降噪处理下7种算法迭代120次的收敛曲线.对比3组迭代收敛曲线,可以看出基于噪声数据算法比基于降噪数据算法的迭代收敛RMSE更大,寻优收敛速度更慢.从图11(b)和11(c)可知,ELM降噪处理后,各算法的收敛速度更快,收敛误差更小,能够更好地平衡局部探索和全局搜索,不容易陷入局部最优解.其中,WOA算法的性能得到显著优化,BRNN-WOA约迭代55次收敛,ELM-WOA只需迭代7次即可收敛且其RMSE小于BRNN-WOA的RMSE.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 高温高相对湿度下7种算法收敛曲线

Fig.11 Convergence curves of five algorithms obtained at a high temperature and high relative humidity

4 结论

针对PEMFC提出一种基于ELM降噪处理的MhAs参数辨识策略,其贡献可概括为以下4个方面:

(1) 充分考虑数据噪声对PEMFC参数辨识精度的影响,引入降噪技术以获得更准确的V-I数据,从而提高电化学稳态建模的精确性.

(2) 相较于单一MhAs策略,ELM-MhAs策略能够显著减少数据噪声对辨识参数的干扰,保证更有效、可靠的全局搜索和局部探索,具有高准确性、快速性和鲁棒性.

(3) 全面综合地比较基于ELM-MhAs策略和BRNN-MhAs策略的参数辨识结果.算例研究表明,ELM降噪后获得的辨识精度、收敛稳定性和快速性皆优于BRNN降噪.例如,低温、低相对湿度情况下,ELM-EO参数精确性最多提高58.80%;高温、高相对湿度情况下,ELM-GA准确性最多提高42.74%.

(4) 对比神经网络训练端到端参数辨识模型LMBP与6种MhAs算法的PEMFC参数辨识结果.算例研究表明,在低温、低相对湿度情况下,ELM-LMBP参数精确性较LMBP和BRNN-LMBP精确性分别提高4.81%和14.07%,优化精度高于ELM-DA增加的0.82%和6.63%;在高温、高相对湿度情况下,ELM-LMBP参数精确性较LMBP和BRNN-LMBP精确性分别提高44.95%和2.27%,优化精度高于ELM-ALO增加的22.75%和15.50%.

ELM-MhAs具有普遍适用性,不受模型限制.未来可将其应用于光伏电池、固体氧化燃料电池等其他参数辨识问题.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

孙立明, 杨博.

蓄电池/超导混合储能系统非线性鲁棒分数阶控制

[J]. 电力系统保护与控制, 2020, 48(22): 76-83.

[本文引用: 1]

SUN

Liming

, YANG

Nonlinear robust fractional-order control of battery/SMES hybrid energy storage systems

[J]. Power System Protection and Control, 2020, 48(22): 76-83.

[本文引用: 1]

[2]

陈国平, 董昱, 梁志峰.

能源转型中的中国特色新能源高质量发展分析与思考

[J]. 中国电机工程学报, 2020, 40(17): 5493-5506.

[本文引用: 1]

CHEN

Guoping

, DONG

, LIANG

Zhifeng

Analysis and reflection on high-quality development of new energy with Chinese characteristics in energy transition

[J]. Proceedings of the CSEE, 2020, 40(17): 5493-5506.

[本文引用: 1]

[3]

李奇, 王晓锋, 孟翔, 等.

基于在线辨识和极小值原理的PEMFC混合动力系统综合能量管理方法

[J]. 中国电机工程学报, 2020, 40(21): 6991-7002.

[本文引用: 1]

, WANG

Xiaofeng

, MENG

Xiang

, et al.

Comprehensive energy management method of PEMFC hybrid power system based on online identification and minimal principle

[J]. Proceedings of the CSEE, 2020, 40(21): 6991-7002.

[本文引用: 1]

[4]

YANG

, WANG

J B

, YU

, et al.

A critical survey on proton exchange membrane fuel cell parameter estimation using meta-heuristic algorithms

[J]. Journal of Cleaner Production, 2020, 265: 121660.

DOI:10.1016/j.jclepro.2020.121660 URL [本文引用: 3]

[5]

MACEDO-VALENCIA

, SIERRA

J M

, FIGUEROA-RAMÍREZ

S J

, et al.

3D CFD modeling of a PEM fuel cell stack

[J]. International Journal of Hydrogen Energy, 2016, 41(48): 23425-23433.

DOI:10.1016/j.ijhydene.2016.10.065 URL [本文引用: 1]

[6]

OLIVIER

, BOURASSEAU

, BOUAMAMA

Dynamic and multiphysic PEM electrolysis system modelling: A bond graph approach

[J]. International Journal of Hydrogen Energy, 2017, 42(22): 14872-14904.

DOI:10.1016/j.ijhydene.2017.03.002 URL [本文引用: 1]

[7]

潘文霞, 陈健强, 张阳, 等.

混合发电系统中的质子交换膜燃料电池建模及其应用

[J]. 电力系统保护与控制, 2012, 40(12): 13-18.

[本文引用: 1]

PAN

Wenxia

, CHEN

Jianqiang

, ZHANG

Yang

, et al.

Modeling of PEMFC and application in hybrid power system

[J]. Power System Protection and Control, 2012, 40(12): 13-18.

[本文引用: 1]

[8]

SALIM

, NABAG

, NOURA

, et al.

The parameter identification of the Nexa 1.2 kW PEMFC’s model using particle swarm optimization

[J]. Renewable Energy, 2015, 82: 26-34.

DOI:10.1016/j.renene.2014.10.012 URL [本文引用: 1]

[9]

TIAN

E L

, EBADI

A G

, MAVALURU

, et al.

Parameter derivation of a proton exchange membrane fuel cell based on coevolutionary ribonucleic acid genetic algorithm

[J]. Computational Intelligence, 2019, 35(4): 1021-1041.

DOI:10.1111/coin.v35.4 URL [本文引用: 2]

[10]

ALI

, EL-HAMEED

M A

, FARAHAT

M A

Effective parameters’ identification for polymer electrolyte membrane fuel cell models using grey wolf optimizer

[J]. Renewable Energy, 2017, 111: 455-462.

DOI:10.1016/j.renene.2017.04.036 URL [本文引用: 5]

[11]

EL-FERGANY

A A

, HASANIEN

H M

, AGWA

A M

Semi-empirical PEM fuel cells model using whale optimization algorithm

[J]. Energy Conversion and Management, 2019, 201: 112197.

DOI:10.1016/j.enconman.2019.112197 URL [本文引用: 2]

[12]

BEN

MESSAOUD R

, MIDOUNI

, HAJJI

PEM fuel cell model parameters extraction based on moth-flame optimization

[J]. Chemical Engineering Science, 2021, 229: 116100.

DOI:10.1016/j.ces.2020.116100 URL [本文引用: 1]

[13]

SUN

, WANG

, BI

Y R

, et al.

Parameter identification of PEMFC model based on hybrid adaptive differential evolution algorithm

[J]. Energy, 2015, 90: 1334-1341.

DOI:10.1016/j.energy.2015.06.081 URL [本文引用: 1]

[14]

ISA

Z M

, NAYAN

N M

, ARSHAD

M H

, et al.

Optimizing PEMFC model parameters using ant lion optimizer and dragonfly algorithm: A comparative study

[J]. International Journal of Electrical and Computer Engineering, 2019, 9(6): 5295.

[本文引用: 4]

[15]

SELEEM

S I

, HASANIEN

H M

, EL-FERGANY

A A

Equilibrium optimizer for parameter extraction of a fuel cell dynamic model

[J]. Renewable Energy, 2021, 169: 117-128.

DOI:10.1016/j.renene.2020.12.131 URL [本文引用: 2]

[16]

YANG

, LI

D Y

, ZENG

C Y

, et al.

Parameter extraction of PEMFC via Bayesian regularization neural network based meta-heuristic algorithms

[J]. Energy, 2021, 228: 120592.

DOI:10.1016/j.energy.2021.120592 URL [本文引用: 2]

[17]

YANG

, ZENG

C Y

, WANG

, et al.

Parameter identification of proton exchange membrane fuel cell via Levenberg-Marquardt backpropagation algorithm

[J]. International Journal of Hydrogen Energy, 2021, 46(44): 22998-23012.

DOI:10.1016/j.ijhydene.2021.04.130 URL [本文引用: 3]

[18]

王筱彤, 李奇, 王天宏, 等.

基于离散区间二进制序列激励信号的燃料电池EIS测量及故障诊断方法

[J]. 中国电机工程学报, 2020, 40(14): 4526-4537.

[本文引用: 1]

WANG

Xiaotong

, LI

, WANG

Tianhong

, et al.

EIS measurement based on DIBS excitation signal and fault diagnosis method of fuel cell

[J]. Proceedings of the CSEE, 2020, 40(14): 4526-4537.

[本文引用: 1]

[19]

孙术发, 杨洁, 唐华林, 等.

PEMFC输出特性建模与多因素仿真分析

[J]. 哈尔滨工业大学学报, 2019, 51(10): 144-151.

[本文引用: 1]

SUN

Shufa

, YANG

Jie

, TANG

Hualin

, et al.

PEMFC output characteristics modeling and multi-factor simulation analysis

[J]. Journal of Harbin Institute of Technology, 2019, 51(10): 144-151.

[本文引用: 1]

[20]

BLANCO-COCOM

, BOTELLO-RIONDA

, ORDOÑEZ

L C

, et al.

Robust parameter estimation of a PEMFC via optimization based on probabilistic model building

[J]. Mathematics and Computers in Simulation, 2021, 185: 218-237.

DOI:10.1016/j.matcom.2020.12.021 URL [本文引用: 1]

[21]

殷豪, 曾云, 孟安波, 等.

基于奇异谱分析-模糊信息粒化和极限学习机的风速多步区间预测

[J]. 电网技术, 2018, 42(5): 1467-1474.

[本文引用: 1]

YIN

Hao

, ZENG

Yun

, MENG

Anbo

, et al.

Wind speed multi-step interval prediction based on singular spectrum analysis-fuzzy information granulation and extreme learning machine

[J]. Power System Technology, 2018, 42(5): 1467-1474.

[本文引用: 1]

[22]

吴忠强, 戚松岐, 尚梦瑶, 等.

基于优化极限学习机的直流微电网并网等效建模

[J]. 电力自动化设备, 2020, 40(6): 43-49.

[本文引用: 1]

Zhongqiang

, QI

Songqi

, SHANG

Mengyao

, et al.

Grid-connected equivalent modeling of DC microgrid based on optimized extreme learning machine

[J]. Electric Power Automation Equipment, 2020, 40(6): 43-49.

[本文引用: 1]

[23]

邵宇鹰, 彭鹏, 张秋桥, 等.

基于极限学习机与负荷密度指标法的空间负荷预测

[J]. 电力工程技术, 2021, 40(1): 86-91.

[本文引用: 1]

SHAO

Yuying

, PENG

Peng

, ZHANG

Qiuqiao

, et al.

Spatial load forecasting based on ELM and clustering algorithm

[J]. Electric Power Engineering Technology, 2021, 40(1): 86-91.

[本文引用: 1]

[24]

周锋, 孙廷玺, 权少静, 等.

基于集合经验模态分解和极限学习机的变压器油中溶解气体体积分数预测方法

[J]. 高电压技术, 2020, 46(10): 3658-3665.

[本文引用: 1]

ZHOU

Feng

, SUN

Tingxi

, QUAN

Shaojing

, et al.

Predication of dissolved gases concentration in transformer oil based on ensemble empirical mode decomposition and extreme learning machine

[J]. High Voltage Engineering, 2020, 46(10): 3658-3665.

[本文引用: 1]

[25]

孙莉, 李静, 李继云, 等.

基于稀疏贝叶斯极限学习机的光伏电站设备故障诊断研究

[J]. 太阳能学报, 2020, 41(8): 221-226.

[本文引用: 1]

SUN

, LI

Jing

, LI

Jiyun

, et al.

Research on fault diagnosis of photovoltaic power station equipment based on sparse Bayesian extreme learning machine

[J]. Acta Energiae Solaris Sinica, 2020, 41(8): 221-226.

[本文引用: 1]

[26]

陈谦, 王朝辉, 陈渊召, 等.

基于极限学习机的钢桥面板腐蚀评估及预测

[J]. 材料导报, 2020, 34(14): 14099-14104.

[本文引用: 1]

CHEN

Qian

, WANG

Chaohui

, CHEN

Yuanzhao

, et al.

Corrosion assessment and prediction of steel bridge deck based on extreme learning machine

[J]. Materials Reports, 2020, 34(14): 14099-14104.

[本文引用: 1]

[27]

汪颖, 王欢, 张姝.

基于优化极限学习机的电压暂降源识别方法

[J]. 电力系统自动化, 2020, 44(9): 135-143.

[本文引用: 1]

WANG

Ying

, WANG

Huan

, ZHANG

Shu

Recognition method of voltage sag source based on optimized extreme learning machine

[J]. Automation of Electric Power Systems, 2020, 44(9): 135-143.

[本文引用: 1]

[28]

YANG

, CHEN

Y J

, GUO

Z X

, et al.

Levenberg-Marquardt backpropagation algorithm for parameter identification of solid oxide fuel cells

[J]. International Journal of Energy Research, 2021, 45(12): 17903-17923.

DOI:10.1002/er.v45.12 URL [本文引用: 2]

[29]

游志宇, 汪立伟.

高速PEMFC单片电压监测系统设计

[J]. 西南民族大学学报(自然科学版), 2019, 45(5): 499-506.

[本文引用: 1]

YOU

Zhiyu

, WANG

Liwei

Design of high speed PEMFC single cell voltage monitoring system

[J]. Journal of Southwest Minzu University (Natural Science Edition), 2019, 45(5): 499-506.

[本文引用: 1]

[30]

刘佼龙, 杨莉, 刘教瑜, 等.

PEMFC电压监控系统设计

[J]. 微型机与应用, 2017, 36(3): 85-87.

[本文引用: 1]

LIU

Jiaolong

, YANG

, LIU

Jiaoyu

, et al.

Design of PEMFC voltage monitoring system

[J]. Microcomputer & Its Applications, 2017, 36(3): 85-87.

[本文引用: 1]

[31]

钟崇霖, 马天才.

基于LTC6803的低成本燃料电池单体电压监测器设计

[J]. 机电一体化, 2017, 23(1): 48-52.

[本文引用: 1]

ZHONG

Chonglin

, MA

Tiancai

Low-cost fuel cell monomer voltage monitor design based on LTC6803

[J]. Mechatronics, 2017, 23(1): 48-52.

[本文引用: 1]

[32]

KLER

, RANA

K P S

, KUMAR

Parameter extraction of fuel cells using hybrid interior search algorithm

[J]. International Journal of Energy Research, 2019, 43(7): 2854-2880.

DOI:10.1002/er.v43.7 URL [本文引用: 1]

蓄电池/超导混合储能系统非线性鲁棒分数阶控制

2020

... 日益增长的能源需求、传统燃料资源的枯竭和环境污染给社会的可持续发展带来巨大的挑战^[1].为缓解上述问题,优化能源结构,发展绿色能源技术势在必行^[2].其中,燃料电池(Fuel Cell, FC)系统以其高效、低污染、可持续发展等优点得到广泛的应用.燃料电池一般可分为4种类型,即质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell, PEMFC)^[3-4]、磷酸燃料电池、固体氧化燃料电池(Solid Oxide Fuel Cell, SOFC)和熔融碳酸盐燃料电池. ...

蓄电池/超导混合储能系统非线性鲁棒分数阶控制

2020

能源转型中的中国特色新能源高质量发展分析与思考

2020

能源转型中的中国特色新能源高质量发展分析与思考

2020

基于在线辨识和极小值原理的PEMFC混合动力系统综合能量管理方法

2020

基于在线辨识和极小值原理的PEMFC混合动力系统综合能量管理方法

2020

A critical survey on proton exchange membrane fuel cell parameter estimation using meta-heuristic algorithms

2020

... 然而,PEMFC的高度非线性、强耦合和多峰值特性严重阻碍人们利用传统方法获得满意的参数辨识结果.近年来,启发式算法(Meta-Heuristic Algorithms, MhAs)^[4]以其极大的灵活性被广泛应用于PEMFC模型的参数辨识.例如,文献[8]采用粒子群优化算法对Nexa 1.2 kW PEMFC进行离线参数辨识.文献[9]模拟遗传学和自然选择的自然进化行为,利用改进遗传算法(Genetic Algorithm, GA)辨识PEMFC参数.同时,其他先进的MhAs也用于PEMFC参数辨识,例如,灰狼优化(Grey Wolf Optimizer, GWO)算法^[10]、鲸鱼优化算法(Whale Optimization Algorithm, WOA)^[11]、飞蛾扑火算法^[12]、差分进化算法^[13]、蚁狮优化(Antlion Optimization, ALO)算法^[14]、蜻蜓算法(Dragonfly Algorithm, DA)^[14]、平衡优化器(Equilibrium Optimizer, EO)^[15]等.到目前为止,MhAs在提高搜索能力和效率方面已取得显著进展.但是,上述文献忽略了数据噪声对PEMFC参数辨识的干扰,而由于测量误差或环境影响,这种情况在实际应用中不可避免且普遍存在.噪声的存在会导致MhAs的收敛速度减慢,PEMFC的参数辨识误差增大,使得后续的建模准确性降低.因此,需要采用一种切实有效的手段对数据噪声进行处理. ...

... 需要说明的是,目前燃料电池参数辨识研究忽视了客观存在的数据噪声带来的干扰,绝大部分PEMFC参数辨识的研究没有运用相应策略进行滤波降噪处理,且仅采用单一启发式算法进行参数辨识^[4].ELM作为一种成熟的人工神经网络策略,能够很好地减少或滤除数据噪声,具有较强的泛化能力,因此其应用不局限于对燃料电池数据的处理. ...

3D CFD modeling of a PEM fuel cell stack

2016

... PEMFC具有响应速度快、启动速度快、工作温度低、无污染等优点,已广泛应用于航空、电动汽车和分布式发电等领域.此外,为获得准确可靠的电压-电流(V-I)特性,研究人员开发了多种PEMFC模型,如三维稳态模型^[5]、物理电解槽模型^[6]、电化学稳态模型^[7]等.尤其是由半经验方程推导出的电化学稳态模型能够很好地预测PEMFC的稳态和瞬时状态,该模型中包含的一些未知参数对PEMFC的准确性和可靠性有很大影响. ...

Dynamic and multiphysic PEM electrolysis system modelling: A bond graph approach

2017

混合发电系统中的质子交换膜燃料电池建模及其应用

2012

混合发电系统中的质子交换膜燃料电池建模及其应用

2012

The parameter identification of the Nexa 1.2 kW PEMFC’s model using particle swarm optimization

2015

Parameter derivation of a proton exchange membrane fuel cell based on coevolutionary ribonucleic acid genetic algorithm

2019

... 温度、阴极和阳极气体相对湿度对PEMFC的V-I曲线和参数都有影响.因此,在低温T_k=333.15 K、低相对湿度H_r,a=50%和H_r,c=50%以及高温T_k=353.15 K、高相对湿度H_r,a=100%和H_r,c=100%条件下,运用6种MhAs(ALO^[14]、DA^[14]、EO^[15]、GA^[9]、GWO^[10]、WOA^[11])和LMBP^[17,28]进行PEMFC的7个参数(ε₁、ε₂、ε₃、ε₄、b、λ和R_c)辨识.同时,为提高效率和准确性,对参数边界条件进行限制^[10],如表1所示.值得注意的是,目前绝大部分燃料电池数据采集主要依赖于测量精度为mV的数据采集系统^[29].由于电池内部环境复杂,采集的信号不可避免地会受到一些噪声等高频信号的干扰,故用信号调理电路对这些信号进行处理^[30],但技术的限制使得当前精度的信号调理电路无法完全滤除这些干扰信号^[31].为增强研究的实用性和准确性,目前多用白噪声数据模拟这些噪声信号.从Ballard-Mark-V PEMFC中取25组V-I数据^[32]作为无噪声的原始数据,并设置随机独立分布3 mV级别的白噪声以获取噪声数据,电池膜厚 178 μm,有效面积为50.6 cm². ...

Effective parameters’ identification for polymer electrolyte membrane fuel cell models using grey wolf optimizer

2017

... [10],如表1所示.值得注意的是,目前绝大部分燃料电池数据采集主要依赖于测量精度为mV的数据采集系统^[29].由于电池内部环境复杂,采集的信号不可避免地会受到一些噪声等高频信号的干扰,故用信号调理电路对这些信号进行处理^[30],但技术的限制使得当前精度的信号调理电路无法完全滤除这些干扰信号^[31].为增强研究的实用性和准确性,目前多用白噪声数据模拟这些噪声信号.从Ballard-Mark-V PEMFC中取25组V-I数据^[32]作为无噪声的原始数据,并设置随机独立分布3 mV级别的白噪声以获取噪声数据,电池膜厚 178 μm,有效面积为50.6 cm². ...

... PEMFC参数辨识的范围^[10] ...

... PEMFC parameter range for identification^[10] ...

Semi-empirical PEM fuel cells model using whale optimization algorithm

2019

PEM fuel cell model parameters extraction based on moth-flame optimization

2021

Parameter identification of PEMFC model based on hybrid adaptive differential evolution algorithm

2015

Optimizing PEMFC model parameters using ant lion optimizer and dragonfly algorithm: A comparative study

2019

... [14]、平衡优化器(Equilibrium Optimizer, EO)^[15]等.到目前为止,MhAs在提高搜索能力和效率方面已取得显著进展.但是,上述文献忽略了数据噪声对PEMFC参数辨识的干扰,而由于测量误差或环境影响,这种情况在实际应用中不可避免且普遍存在.噪声的存在会导致MhAs的收敛速度减慢,PEMFC的参数辨识误差增大,使得后续的建模准确性降低.因此,需要采用一种切实有效的手段对数据噪声进行处理. ...

... [14]、EO^[15]、GA^[9]、GWO^[10]、WOA^[11])和LMBP^[17,28]进行PEMFC的7个参数(ε₁、ε₂、ε₃、ε₄、b、λ和R_c)辨识.同时,为提高效率和准确性,对参数边界条件进行限制^[10],如表1所示.值得注意的是,目前绝大部分燃料电池数据采集主要依赖于测量精度为mV的数据采集系统^[29].由于电池内部环境复杂,采集的信号不可避免地会受到一些噪声等高频信号的干扰,故用信号调理电路对这些信号进行处理^[30],但技术的限制使得当前精度的信号调理电路无法完全滤除这些干扰信号^[31].为增强研究的实用性和准确性,目前多用白噪声数据模拟这些噪声信号.从Ballard-Mark-V PEMFC中取25组V-I数据^[32]作为无噪声的原始数据,并设置随机独立分布3 mV级别的白噪声以获取噪声数据,电池膜厚 178 μm,有效面积为50.6 cm². ...

Equilibrium optimizer for parameter extraction of a fuel cell dynamic model

2021

Parameter extraction of PEMFC via Bayesian regularization neural network based meta-heuristic algorithms

2021

... 因此,提出一种基于极限学习机(Extreme Learning Machine, ELM)的MhAs——ELM-MhAs来提高PEMFC的参数辨识性能.同时,对比ELM和另一种ANN策略——贝叶斯正则神经网络(Bayesian Regularization Neural Network, BRNN)^[16]的噪声性能.主要贡献和创新点可以总结如下: ...

... 特别地,BRNN和ELM都属于ANN技术,BRNN具有良好的学习能力和降噪效果,其性能已在文献[16]中充分验证.在后续PEMFC研究中发现ELM降噪处理精度更高,能够处理更小的噪声数据,故采用BRNN和ELM进行滤波降噪效果的对比研究.此外,亦在SOFC研究中运用神经网络训练端到端参数辨识模型LMBP^[28],并充分验证其稳定性、准确性和效率.因此,为区别于MhAs对PEMFC的参数辨识,采用LMBP与MhAs进行对比研究. ...

Parameter identification of proton exchange membrane fuel cell via Levenberg-Marquardt backpropagation algorithm

2021

... (4) 基于ELM和BRNN两种降噪策略,全面对比神经网络训练端到端参数辨识模型,即列文伯格-马夸尔特反向传播法(Levenberg-Marquardt Backpropagation, LMBP)^[17]与6种MhAs算法的PEMFC参数辨识结果,验证ELM降噪策略具有较强的泛化能力,能够与其他参数辨识算法结合. ...

... 在考虑电化学反应的极化情况下,单个PEMFC输出电压^[17]为 ...

基于离散区间二进制序列激励信号的燃料电池EIS测量及故障诊断方法

2020

... PEMFC内部的电化学反应^[18]可表示为 ...

基于离散区间二进制序列激励信号的燃料电池EIS测量及故障诊断方法

2020

... PEMFC内部的电化学反应^[18]可表示为 ...

PEMFC输出特性建模与多因素仿真分析

2019

... 活化过电压^[19]可表示为 ...

PEMFC输出特性建模与多因素仿真分析

2019

... 活化过电压^[19]可表示为 ...

Robust parameter estimation of a PEMFC via optimization based on probabilistic model building

2021

... 浓差过电压受氢、氧浓度的影响^[20],可表示为 ...

基于奇异谱分析-模糊信息粒化和极限学习机的风速多步区间预测

2018

... 与其他常规的前馈神经网络相比,ELM^[21]能显著提高鲁棒性、泛化能力、学习速度和训练精度.ELM的拓扑结构如图2所示. ...

基于奇异谱分析-模糊信息粒化和极限学习机的风速多步区间预测

2018

... 与其他常规的前馈神经网络相比,ELM^[21]能显著提高鲁棒性、泛化能力、学习速度和训练精度.ELM的拓扑结构如图2所示. ...

基于优化极限学习机的直流微电网并网等效建模

2020

... 详细论证ELM主要数学机理^[22-23]:假设ELM的输入层有N个神经元,对应N个输入变量;隐藏层有L个神经元;输出层有M个神经元,对应M个输出变量. 当有N个训练数据

(x_{i}, t_{i}), x_{i} = (x_{i 1}, x_{i 2}, \dots, x_{i n})^{T} \in R^{n}, t_{i} = (t_{i 1}, t_{i 2}, \dots, t_{i m})^{T} \in R^{m}

时,对应于该ELM的输出计算如下: ...

基于优化极限学习机的直流微电网并网等效建模

2020

(x_{i}, t_{i}), x_{i} = (x_{i 1}, x_{i 2}, \dots, x_{i n})^{T} \in R^{n}, t_{i} = (t_{i 1}, t_{i 2}, \dots, t_{i m})^{T} \in R^{m}

时,对应于该ELM的输出计算如下: ...

基于极限学习机与负荷密度指标法的空间负荷预测

2021

(x_{i}, t_{i}), x_{i} = (x_{i 1}, x_{i 2}, \dots, x_{i n})^{T} \in R^{n}, t_{i} = (t_{i 1}, t_{i 2}, \dots, t_{i m})^{T} \in R^{m}

时,对应于该ELM的输出计算如下: ...

基于极限学习机与负荷密度指标法的空间负荷预测

2021

(x_{i}, t_{i}), x_{i} = (x_{i 1}, x_{i 2}, \dots, x_{i n})^{T} \in R^{n}, t_{i} = (t_{i 1}, t_{i 2}, \dots, t_{i m})^{T} \in R^{m}

时,对应于该ELM的输出计算如下: ...

基于集合经验模态分解和极限学习机的变压器油中溶解气体体积分数预测方法

2020

... 此外,性能良好的ELM能够近似获得零误差的训练数据,即

\overset{N}{\sum_{i = 1}} |y_{i} - t_{i}| = 0

,即存在

ω_{j} 、 x_{i}

和

b_{j}

使得ELM第i个训练数据的输出

t_{i}

可以满足^[24]: ...

基于集合经验模态分解和极限学习机的变压器油中溶解气体体积分数预测方法

2020

... 此外,性能良好的ELM能够近似获得零误差的训练数据,即

\overset{N}{\sum_{i = 1}} |y_{i} - t_{i}| = 0

,即存在

ω_{j} 、 x_{i}

和

b_{j}

使得ELM第i个训练数据的输出

t_{i}

可以满足^[24]: ...

基于稀疏贝叶斯极限学习机的光伏电站设备故障诊断研究

2020

... 式中:H为隐藏层的输出矩阵;T为期望输出向量;β表示隐藏层神经元与输出层神经元之间的权向量^[25-26],可表示为 ...

基于稀疏贝叶斯极限学习机的光伏电站设备故障诊断研究

2020

... 式中:H为隐藏层的输出矩阵;T为期望输出向量;β表示隐藏层神经元与输出层神经元之间的权向量^[25-26],可表示为 ...

基于极限学习机的钢桥面板腐蚀评估及预测

2020

... 式中:H为隐藏层的输出矩阵;T为期望输出向量;β表示隐藏层神经元与输出层神经元之间的权向量^[25-26],可表示为 ...

基于极限学习机的钢桥面板腐蚀评估及预测

2020

... 式中:H为隐藏层的输出矩阵;T为期望输出向量;β表示隐藏层神经元与输出层神经元之间的权向量^[25-26],可表示为 ...

基于优化极限学习机的电压暂降源识别方法

2020

... 式中:

\tilde{β}

为对应于β的理想权向量^[27],表示为 ...

基于优化极限学习机的电压暂降源识别方法

2020

... 式中:

\tilde{β}

为对应于β的理想权向量^[27],表示为 ...

Levenberg-Marquardt backpropagation algorithm for parameter identification of solid oxide fuel cells

2021

高速PEMFC单片电压监测系统设计

2019

高速PEMFC单片电压监测系统设计

2019

PEMFC电压监控系统设计

2017

PEMFC电压监控系统设计

2017

基于LTC6803的低成本燃料电池单体电压监测器设计

2017

基于LTC6803的低成本燃料电池单体电压监测器设计

2017

Parameter extraction of fuel cells using hybrid interior search algorithm

2019

〈

〉