考虑频率稳定约束的电-氢互补多楼宇协调优化调度

doi:10.16183/j.cnki.jsjtu.2022.380

考虑频率稳定约束的电-氢互补多楼宇协调优化调度

范宏^,¹, 王兰坤¹, 邢梦晴¹, 田书欣¹, 于伟南²

1.上海电力大学电气工程学院,上海 200090

2.国网内蒙古东部电力有限公司电力科学研究院,呼和浩特 010020

Coordinated Scheduling of Multiple Buildings with Electric-Hydrogen Complementary Considering Frequency Stability Constraints

FAN Hong^,¹, WANG Lankun¹, XING Mengqing¹, TIAN Shuxin¹, YU Weinan²

1. College of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China

2. The Electric Power Research Institute of State Grid Inner Mongolia Eastern Power Co., Ltd., Hohhot 010020, China

责任编辑: 王一凡

收稿日期: 2022-09-29 修回日期: 2022-11-15 接受日期: 2023-02-15

基金资助:

国家自然科学基金(52007112)

Received: 2022-09-29 Revised: 2022-11-15 Accepted: 2023-02-15

作者简介 About authors

范宏(1978-),副教授,从事综合能源系统优化及实时仿真的研究;E-mail:fan_honghong@126.com.

摘要

为实现“碳达峰、碳中和”的双碳目标,电-氢互补综合能源系统的推进意义重大,但随着可再生能源的渗透率逐渐提高,系统的惯量水平下降,频率安全受到威胁.针对传统的优化调度方法无法保证系统的频率稳定性这一问题,提出了一种考虑频率稳定约束的电-氢互补多楼宇协调优化调度方法.首先,建立了以楼宇为底层单元的电-氢综合能源系统架构,系统内的可再生能源发电机组采用虚拟同步发电机技术进行控制,以提高系统的惯量水平;其次,以调度周期内系统总运行成本最小为目标,并考虑了并网和孤岛不同运行模式下系统的惯量需求,建立了考虑系统频率稳定约束的优化调度模型;最后,通过算例仿真验证了所提方法对系统频率稳定的有效性、经济性和环保性.

关键词： 双碳目标; 氢储能系统; 虚拟惯量; 频率稳定约束; 优化调度

Abstract

In order to achieve the dual carbon goal of “carbon peak and carbon neutrality”, it is of great significance to promote the electric and hydrogen complementary integrated energy system. However, with the gradual increase of the penetration rate of renewable energy, the inertia level of the system decreases, and the frequency security is threatened. Aimed at the problem that the traditional optimization scheduling method cannot guarantee the frequency stability of the system, a coordinated optimization scheduling method of electric-hydrogen complementary multiple buildings considering the frequency stability constraint is proposed. First, the architecture of the electric-hydrogen integrated energy system with the building as the ground floor unit is established, and the renewable energy generator sets in the system are controlled by the virtual synchronous generator technology to improve the inertia level of the system. Then, aimed at minimizing the total operating cost of the system in the scheduling period, and considering the inertia requirements of the system in different operation modes of grid-connected and islanding, an optimal scheduling model considering the system frequency stability constraint is established. Finally, an example is given to verify the effectiveness, economy, and environmental protection of the proposed method for frequency stability of the system.

Keywords： dual carbon targets; hydrogen storage system; virtual moment of inertia; frequency stability constraint; optimal dispatch

PDF (2948KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

范宏, 王兰坤, 邢梦晴, 田书欣, 于伟南. 考虑频率稳定约束的电-氢互补多楼宇协调优化调度[J]. 上海交通大学学报, 2023, 57(12): 1559-1570 doi:10.16183/j.cnki.jsjtu.2022.380

FAN Hong, WANG Lankun, XING Mengqing, TIAN Shuxin, YU Weinan. Coordinated Scheduling of Multiple Buildings with Electric-Hydrogen Complementary Considering Frequency Stability Constraints[J]. Journal of Shanghai Jiaotong University, 2023, 57(12): 1559-1570 doi:10.16183/j.cnki.jsjtu.2022.380

为实现“3060”双碳目标,需要加快建设多元化、低碳化的清洁能源供给体系,大力推广可再生能源发电^[1].综合能源系统(Integrated Energy System,IES)集成多种可再生能源、负荷、氢储能以及其他智能元件于一体,可协调可再生能源发电、转换、存储与消费^[2],氢作为一种清洁无污染的优质二次能源,能够和电互补,可以进一步提高可再生能源占比,降低碳排放量^[3].然而,随着可再生能源的渗透率逐渐增加,系统惯量水平逐渐降低,系统发生有功扰动时的频率调节能力逐渐减弱^[4-5].而氢储能系统在1~2 s内对系统频率的快速响应能力,能大大改善系统的频率响应特征,因此含氢储能系统的电-氢互补综合能源系统在系统频率响应上具有很大的挖掘潜力^[6-7].

含氢储能系统的智慧楼宇^[8-9]是典型的电-氢互补综合能源系统,它具有灵活调节和协调调度能力,通过智慧楼宇集群的集中管理和调度可提高系统灵活运行能力,增强系统的频率稳定性^[10-11].文献[12]中在电解水制氢中加入储氢罐构建氢储能系统,以提高系统的能源利用率与运行的经济性.文献[13]中构建了完整的电氢能源系统,并从经济性等不同角度详细阐述了对电氢能源系统的展望.文献[14]中基于液态储氢技术构建了楼宇中的氢储能系统,并采用深度强化学习方法实现智慧园区内的多楼宇的协调调度.上述文献都基于氢储能系统对IES实现优化调度,但是都仅考虑了系统的成本优化问题,并未将系统的安全运行考虑其中.

为保障电-氢互补综合能源系统安全稳定运行,需要提高系统的惯量支撑,充分挖掘系统中可再生能源的调频潜力^[15-16].文献[17]中阐述了如何利用虚拟惯性控制使得可再生能源和负荷像常规机组一样共同参与电网的频率调节.文献[18]中分析了系统的惯量需求,并提出了考虑频率变化率(Rate of Change of Frequency,RoCoF)及频率最低点约束的系统最小惯量评估新方法.文献[19]中提出了一种由氢电解槽提供频率控制服务的模型,采用虚拟同步机控制令氢电解槽提供虚拟惯性响应.文献[20]中研究了氢燃料电池堆的动态响应特性,并对燃料电池发电系统的频率响应特性进行了仿真分析.以上工作仅针对系统惯量评估以及氢储能系统的频率响应特性,并未将其考虑到系统的优化调度中.文献[21-22]中基于交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)构建了多主体的综合能源系统分布式优化调度模型.文献[23]中提出了一种基于频率感知约束的微电网优化调度方法,通过预留足够的备用容量确保系统能够过渡到孤岛状态.文献[24]中在孤岛微电网调度模型中增加了极值频率约束,使扰动后最大频率偏差被限制在规定范围内.文献[25]中提出了一种包含多类型虚拟同步机的微电网频率稳定约束优化调度模型,确保系统在不同有功扰动下的频率稳定性.以上调度模型和方法都并未考虑包含氢储能系统的IES在调度时系统的惯量支撑与频率控制备用需求.

基于以上分析,提出了一种考虑频率稳定约束电-氢互补多楼宇协调优化调度方法.首先,根据包含氢储能系统的IES运行机理,构建了模块化的智慧楼宇单体模型,针对海岛供能体系特点搭建了IES的整体架构.其次,针对有功扰动下系统的频率稳定问题,构建了风力机和光伏-氢储能系统的虚拟惯量模型、系统的惯性需求模型和频率控制备用模型.在此基础上,以系统运行总成本最小为目标,建立了考虑频率稳定约束的电-氢互补智慧楼宇协调调度模型,通过麦考密克松弛法将模型线性化处理,对各机组的出力和备用以及负荷的削减进行优化.最后通过仿真验证,验证了在该优化调度方法下系统能够同时保证系统频率安全及经济运行.

1 电-氢互补的智慧楼宇结构设计及频率响应

1.1 系统架构

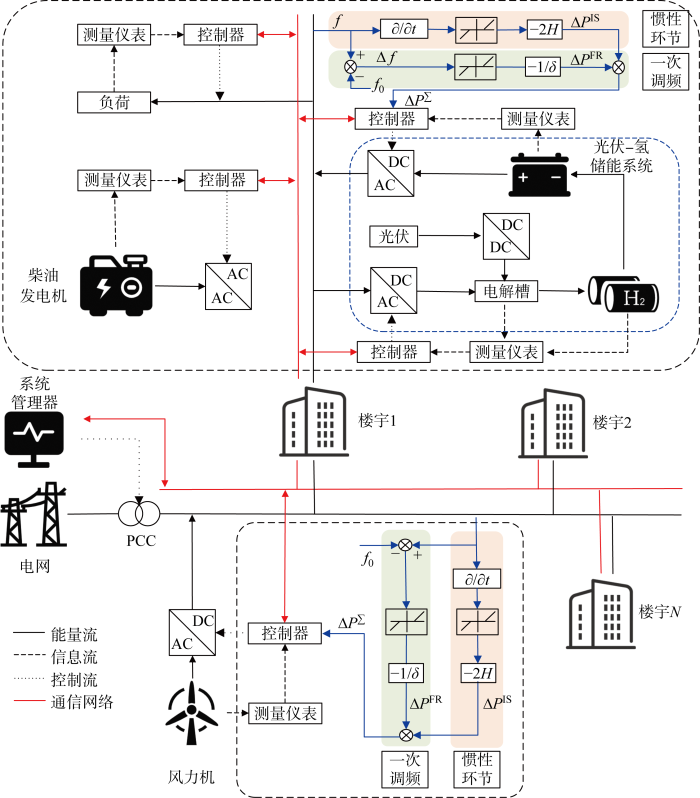
为了保证系统在不同模式切换过程中平滑过渡、提高综合能源系统在不同模式下的灵活运行能力以及保持系统频率稳定的能力,建立了以智慧楼宇为模块化单元的海岛电-氢综合能源系统,系统结构如图1所示.图中:f为系统频率;f₀为系统初始时刻的频率;Δf为系统的频率偏差;t为时间;H为机组的虚拟惯性时间常数;δ为机组的等效调差系数;ΔP^IS为机组的惯性响应功率;ΔP^FR为机组的一次调频功率;ΔP^∑为系统总的功率支撑;AC为交流输出;DC为直流输出;PCC为系统与配电网的公共连接点.系统内包含风力机,且每栋楼宇配备光伏面板和柴油机组以及氢储能系统,风力机和氢储能系统采用虚拟同步发电机技术控制,在系统有功扰动下,配合柴油发电机组,向系统提供惯量支撑,并且可以对楼宇内一部分柔性负荷进行削减,增强系统在负荷波动、联络线中断等情况下系统的频率稳定性.在IES中,楼宇之间通过一条母线连接,进行电力交互.此外,每栋楼宇都配有单独的测量装置和控制器,通过通信网络与系统管理器进行交互,以实现对发电机组、氢储能系统、负荷以及联络线功率进行监测和控制.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 电-氢互补的智慧楼宇结构及IES示意图

Fig.1 Schematic diagram of electrical-hydrogen complementary smart building structure and IES

1.2 智慧楼宇的频率动态响应

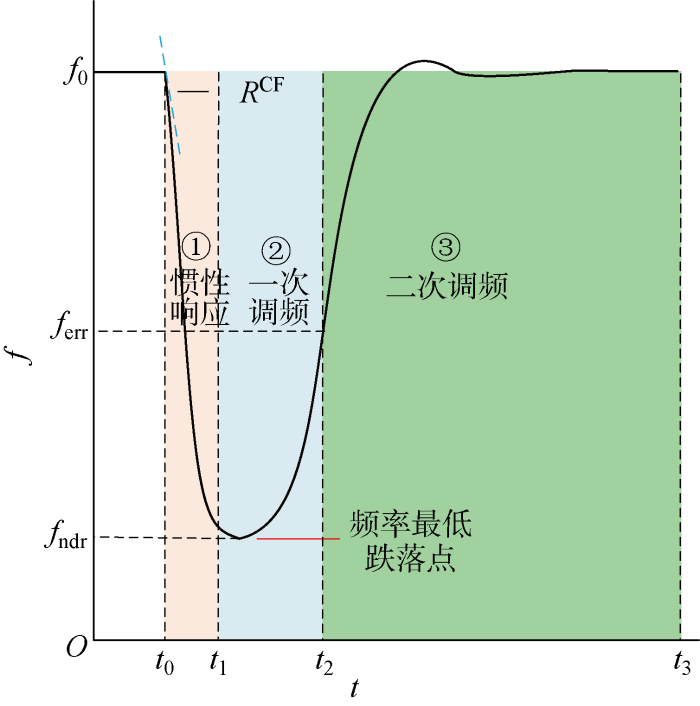
正常状态时,IES与电网相连,当联络线中断时,不平衡功率会使得系统频率下降,发电机组根据系统频率的变化调整输出,使得系统的频率逐渐恢复到额定水平.系统的频率响应过程分为3个阶段,分别为惯性响应、一次调频和二次调频,如图2所示.图中: f_err为一次调频后系统的频率稳定值;f_ndr为系统的频率最低值;R^CF为系统的频率变化率.t₀—t₁时段为惯性响应过程,有功功率扰动后,系统的R^CF依赖于系统的惯量水平,由于孤岛使得系统惯量水平较低,此时系统的频率将会大幅下降,频率变化率最大.t₁—t₂时段为一次调频过程,此时调速器动作,调整发电机组出力,系统的频率恢复到稳态水平f_err.t₂—t₃时段为二次调频过程,系统通过自动发电控制改变机组出力,将系统频率慢速恢复到额定水平.本文考虑风力机和氢储能系统对综合能源系统的频率支撑作用,采用虚拟同步发电机技术控制,当系统内检测到频率变化时,根据频率变化率调整出力,为系统提供短暂的惯量支撑;同时根据频率偏差,为系统提供一次调频功率,减小不平衡功率维持频率稳定.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 系统频率响应过程

Fig.2 System frequency response process

在满足系统功率平衡与备用需求的同时充分考虑频率稳定约束,对风力机、智慧楼宇内的光伏、氢储能系统以及柴油机组的出力和系统内负荷的功率需求进行协调优化.仅对惯性响应和一次调频过程进行分析,不考虑二次调频过程,系统模型如下.

2 电-氢互补的智慧楼宇模型

2.1 风力机模型

传统的风力机不能对电网频率起到支撑作用,可以采用虚拟同步发电机技术,使其具有与同步发电机相似的频率调节能力来为系统提供惯性支撑.风力机的惯性支撑包括惯性响应功率和一次调频功率,惯性响应功率表示为

(1)Δ

P_{w}^{I S}

=-2

{H^{W}}_{w} \frac{\partial f}{\partial t} \frac{P_{w}^{W, m a x}}{f_{0}}

式中:Δ $P_{w}^{I S}$ 为风力机的惯性响应功率; ${H^{W}}_{w}$ 为风力机的虚拟惯性时间常数;W为风力机类型;w为风力机机组编号; $P_{w}^{W, m a x}$ 为风力机的额定功率.

当频率变化超过调频死区后,开始一次调频,此时风力机的一次调频功率,表示为

(2)Δ

P_{w}^{F R}

\frac{1}{{δ^{W}}_{w}} \frac{P_{w}^{m a x}}{f_{0}}

Δf

式中:Δ $P_{w}^{F R}$ 为风力机的一次调频功率; ${δ^{W}}_{w}$ 为风力机的等效调差系数.

2.2 光伏-氢储能系统的模型

光伏面板不同于风力机,没有机械旋转部件,无法参与系统频率调节且出力具有随机性,而氢储能系统包括制氢系统、储氢罐和燃料电池,具有的功率双向调节功能,能够削弱可再生能源出力的随机性,平抑可再生能源功率的波动性.楼宇中光伏面板搭配氢储能系统,可以在系统发生功率扰动时,快速提供功率支撑,提高系统的频率稳定性和抵御风险的能力.

楼宇i氢储能系统的荷载状态表示为

(3)

S_{i, t}^{O C}

=(1-μ_lossΔt)

S_{i, t, 0}^{O C}

\frac{η^{c h} P_{i, t}^{E L} - η^{d i s} P_{i, t}^{F C}}{Q}

Δt

式中: $S_{i, t}^{O C}$ 为楼宇i氢储能系统的荷载状态;μ_loss为储氢罐的损失系数且μ_loss≈0; $S_{i, t, 0}^{O C}$ 为楼宇i氢储能系统初始时刻的荷载状态;η^ch、η^dis分别为氢储能系统消耗电能和释放电能的效率; $P_{i, t}^{E L}$ 、 $P_{i, t}^{F C}$ 分别为制氢系统消耗的功率和燃料电池释放的功率;Q为储氢罐的容量.

氢储能系统提供的支撑功率表示为

(4)Δ

P_{i, t}^{H S}

=-2

H_{i, t}^{H S} \frac{\partial f}{\partial t} \frac{P_{i}^{F C, m a x}}{f_{0}}

\frac{1}{δ_{i}^{H S}} \frac{P_{i}^{F C, m a x}}{f_{0}}

Δf

式中:Δ $P_{i, t}^{H S}$ 为楼宇i氢储能系统的暂态支撑功率; $P_{i}^{F C, m a x}$ 为氢储能系统输出的额定功率; $δ_{i}^{H S}$ 为楼宇i氢储能系统的调差系数; $H_{i, t}^{H S}$ 为楼宇i氢储能系统的等效虚拟惯性时间常数,表示为

(5)

H_{i, t}^{H S}

\frac{S_{i, t}^{O C} η_{d i s}}{S_{0}} γ_{i}^{m a x}

式中:S₀为单位基准功率; $γ_{i}^{m a x}$ 为氢储能系统的最大充/放电倍率^[26].

2.3 系统惯性需求模型

系统中的风力机和氢储能系统进行虚拟同步发电机技术控制,可以配合柴油发电机组对系统提供惯性支撑,保证系统在功率扰动时能够保持频率稳定.系统的整体惯性需求表征为

(6)$\begin{aligned}H_{\text {Eneed }}= & {\left[\Delta P_{t, 0}^{\text {loss }}-\sum_{i=1}^{N_{i}}\left(\Delta P_{i, t, n}^{\mathrm{G}}+\Delta P_{i, t, n}^{\mathrm{HS}}-\right.\right.} \\& \left.\left.\frac{P_{i, t}^{\mathrm{d}} \Delta f_{t, n}}{f_{0} D^{-1}}\right)-\sum_{w=1}^{N_{w}} \Delta P_{w, i, n}^{\mathrm{W}}\right] /\left(2 R_{t, n}^{\mathrm{CF}}\right) \end{aligned}$

式中:系统的初始有功功率扰动量Δ $P_{t, 0}^{l o s s}$ 为外部电网的注入功率; ${P^{G}}_{i, t, n}$ 为楼宇i柴油发电机组的输出功率; ${P^{d}}_{i, t}$ 为楼宇i的负荷需求;Δf_t_,_n为故障后第n个步长时系统的频率偏差(固定步长Δn为0.1 s);D为负荷的阻尼系数; $R_{t, n}^{C F}$ 为t时段系统的频率变化率.

系统的整体惯量水平H_ine包括风力机、氢储能系统的虚拟惯量和柴油发电机组的惯量,具体表征为

(7)H_ine=

\overset{N_{t}}{\sum_{t = 1}} [\overset{N_{i}}{\sum_{i = 1}} ({H^{G}}_{i} {P^{G}}_{i, t} + H_{i, t}^{H S} P_{i, t}^{H S}) + \overset{N_{w}}{\sum_{w = 1}} {H^{W}}_{w, t} {P^{W}}_{w, t}]

式中:N_t为总调度时段数; ${H^{G}}_{i}$ 为楼宇i柴油发电机组的惯性时间常数.

2.4 系统旋转备用模型

当系统发生有功扰动时,足够的系统旋转备用能够有效抑制频率变化.传统的备用模型只考虑同步机组的备用容量,而在本文的综合能源系统中,备用容量由风力机、氢储能系统和柴油发电机组共同提供.系统的总备用容量表示如下:

(8)∑R_t=

\overset{N_{i}}{\sum_{i = 1}}

(

{R^{G}}_{i, t}

R_{i, t}^{H S}

\overset{N_{w}}{\sum_{w = 1}} {R^{W}}_{w, t}

式中:∑R_t为t时段系统的总备用容量; $\overset{N_{i}}{\sum_{i = 1}}$ ( ${R^{G}}_{i, t}$ + $R_{i, t}^{H S}$ )、 $\overset{N_{w}}{\sum_{w = 1}} {R^{W}}_{w, t}$ 分别为t时段楼宇i内柴油发电机组和氢储能系统所提供的备用容量以及风力机提供的备用容量.

(9)

{R^{W}}_{w, t}

=β

P_{w, t}^{p r e}

(10)

R_{i, t}^{H S}

γ_{i}^{m a x} P_{i}^{F C, m a x}

P_{i, t}^{F C}

式中:β为各时段各时段风力机的减载系数(本文中取β=0.1); $P_{w, t}^{p r e}$ 为t时段风力机的最大功率预测值.

3 多智慧楼宇协调优化调度的数学模型

本文综合考虑系统内风力机和光伏-氢储能系统的虚拟惯量支撑,构建考虑频率稳定约束的电-氢互补多楼宇协调优化调度模型.在并网模式下,模型主要确保系统在最优运行时具有足够的旋转备用容量,确保系统避免频率崩溃,能够在有功扰动时平滑的切换到孤岛模式;在孤岛模式下,模型需要对发电机组、氢储能系统的出力以及负荷的切除进行调度,保证系统的频率稳定性.

3.1 目标函数

模型以调度周期内系统总运行成本最小为优化目标,主要考虑系统的运行成本 ${C^{G}}_{t}$ 、碳排放成本 $C_{t}^{C B}$ 、备用成本 ${C^{R}}_{t}$ 、设备维护成本 $C_{t}^{M T}$ 、购电成本 $C_{t}^{g r i d}$ 、切负荷惩罚成本 $C_{t}^{c u t}$ 以及楼宇间售电收益 $C_{t}^{c e l l}$ ,忽略系统内氢储能系统的损耗成本.具体的目标函数如下:

(11)min F=

\overset{N_{t}}{\sum_{t = 0}}

(

{C^{G}}_{t}

C_{t}^{C B} C_{t}^{R}

C_{t}^{M T}

C_{t}^{g r i d}

C_{t}^{c u t}

C_{t}^{c e l l}

)

柴油发电机的运行成本主要为燃料成本,表示为

(12)

{C^{G}}_{t}

=σ^G

\overset{N_{i}}{\sum_{i = 1}} {P^{G}}_{i, t}

式中;σ^G为柴油发电机的成本系数.

碳排放成本主要是由柴油发电机发电和配电购电产生的,表示如下:

(13)

C_{t}^{C B}

=σ^G^,^CB

\overset{N_{i}}{\sum_{i = 1}} {P^{G}}_{i, t}

+σ^grid^,^CB

P_{t}^{g r i d}

式中:σ^G,CB、σ^grid,CB分别为柴油发电机和电网购电的碳排放成本系数; $P_{t}^{g r i d}$ 为系统从电网购入的电量.

备用成本主要包括柴油发电机的旋转备用成本和风力机的备用成本,表示为

(14)

{C^{R}}_{t}

=σ^G^,^R

\overset{N_{i}}{\sum_{i = 1}} {R^{G}}_{i, t}

+σ^W^,^R

\overset{N_{w}}{\sum_{w = 1}} {R^{W}}_{w, t}

式中:σ^G,R为柴油发电机备用成本系数;σ^W,R为风力机的弃风惩罚成本系数.

设备的运行维护成本主要包括风力机、光伏和柴油发电机组的维护成本,表示为

(15)

C_{t}^{M T}

=α^W

\overset{N_{w}}{\sum_{w = 1}} {P^{W}}_{w, t}

+α^PV

\overset{N_{i}}{\sum_{i = 1}} P_{i, t}^{P V}

+α^G

\overset{N_{i}}{\sum_{i = 1}} {P^{G}}_{i, t}

式中:α^W、α^PV、α^G分别为风力机、光伏、柴油发电机组的维护费用.

楼宇的购电成本包括向其他楼宇购电成本以及向电网购电成本,表示为

(16)

C_{t}^{g r i d}

=σ^s^,^b

\overset{N_{i}}{\sum_{i = 1}} \overset{N_{i}}{\sum_{l \in N_{i}, l \neq i}} P_{l, t}^{l 2 i}

+σ^grid(1-τ^PCC)

\overset{N_{i}}{\sum_{i = 1}} P_{i, t}^{g r i d}

式中:σ^s,b为楼宇间的购电成本系数;σ^grid为电网购电成本系数; $P_{l, t}^{l 2 i}$ 为楼宇i向楼宇l的购电量;τ^PCC为综合能源系统运行模式的表征量,当系统处于并网模式时τ^PCC=0,当系统处于孤岛模式时τ^PCC=1.

切负荷惩罚成本表示为

(17)

C_{t}^{c u t}

=σ^cutτ^PCC

\overset{N_{i}}{\sum_{i = 1}} P_{i, t}^{c u t}

式中:σ^cut为切负荷成本系数; $P_{t}^{c u t}$ 为系统的切负荷量.

楼宇间售电收益表示为

(18)

C_{t}^{c e l l}

=σ^s^,^b

\overset{N_{i}}{\sum_{i = 1}} \overset{N_{i}}{\sum_{l \in N_{i}, l \neq i}} P_{l, t}^{i 2 l}

式中, $P_{l, t}^{i 2 l}$ 为楼宇l向楼宇i的售电量.

3.2 约束条件

3.2.1 设备运行约束

综合能源系统内关键设备的运行约束如下.

(1) 风力机运行约束.

(19)

\begin{array}{l} {P^{W}}_{w, t} = P_{w, t}^{I S} + P_{w, t}^{F R} = (1 - β) P_{w, t}^{p r e} \\ P_{w, t}^{p r e} \geq 0.2 P_{w}^{W, m a x} \end{array}\}

当风力机的有功输出大于0.2 $P_{w}^{W, m a x}$ 时,可以预留一部分备用功率参与系统一次调频.

(2) 氢储能系统运行约束.

(20)

\begin{array}{l} P_{i}^{F C, m i n} \leq P_{i, t}^{F C} \leq P_{i}^{F C, m a x} \\ P_{i}^{E L, m i n} \leq P_{i, t}^{E L} \leq P_{i}^{E L, m a x} \\ S_{i}^{O C - m i n} \leq S_{i, t} \leq S_{i}^{O C - m a x} \end{array}\}

式中: $S_{i}^{O C - m i n}$ 和 $S_{i}^{O C - m a x}$ 为氢储能系统的载荷状态.

(3) 柴油发电机组运行约束.

(21)

\begin{array}{l} P_{i}^{G, m i n} \leq {P^{G}}_{i, t} + {R^{G}}_{i, t} \leq P_{i}^{G, m a x} \\ - v_{R D, i} \leq {P^{G}}_{i, t} - {P^{G}}_{i, t - 1} \leq v_{R U, i} \end{array}\}

式中: $P_{i}^{G, m i n}$ 、 $P_{i}^{G, m a x}$ 和v_RD_,i、v_RU_,i分别为楼宇i柴油发电机组的最小/最大稳定出力和最大向下/向上爬坡速率限值.

3.2.2 机组功率调整量约束

为实现调频资源间的协同配合,维持系统的频率稳定,需要对各调频机组出力采用离散化处理,每隔固定步长Δn对系统内调频机组的支撑功率进行更新,调度时段t内各调频机组在故障后第n个步长时的功率调整量表示为

(22)

\begin{array}{l} Δ {P^{G}}_{i, t, n} = Δ {P^{G}}_{i, t, n - 1} - \frac{(Δ f_{t, n} + Δ f_{f d}) P_{i}^{G, m a x}}{{δ^{G}}_{i} f_{0}} \\ n \geq \frac{{ε^{G}}_{i}}{Δ n} \\ Δ P_{i, t, n}^{H S} = Δ P_{i, t, n - 1}^{H S} - \frac{(Δ f_{t, n} + Δ f_{f d}) P_{i}^{F C, m a x}}{δ_{i}^{H S} f_{0}} \\ n \geq \frac{ε_{i}^{H S}}{Δ n} \\ Δ {P^{W}}_{w, t, n} = Δ {P^{W}}_{w, t, n - 1} - \frac{(Δ f_{t, n} + Δ f_{f d}) P_{w}^{W, m a x}}{{δ^{W}}_{i} f_{0}} \\ n \geq \frac{{ε^{W}}_{w}}{Δ n} \end{array}\}

(23)

\begin{array}{l} {P^{G}}_{i, t} + Δ {P^{G}}_{i, t, n} \leq P_{i}^{G, m a x} \\ Δ P_{i, t, n}^{H S} \leq R_{i, t}^{H S} \\ Δ {P^{W}}_{w, t, n} \leq {R^{W}}_{w, t} \end{array}\}

式中: ${δ^{G}}_{i}$ 为楼宇i柴油机组的调差系数;Δf_fd为系统的频率死区; ${ε^{G}}_{i}$ 、 $ε_{i}^{H S}$ 和 ${ε^{W}}_{w}$ 分别为柴油机组、光伏-氢储能系统以及风力机的调频响应时间,当机组的调频时间小于该值时对应机组功率调整量为0.

3.2.3 频率稳定约束

R^CF与Δf是衡量系统频率稳定的关键指标.系统的频率变化率约束,表示为

(24)-

R_{m a x}^{C F}

≤

R_{t, n}^{C F}

≤

R_{m a x}^{C F}

式中: $R_{m a x}^{C F}$ 为频率变化率的阈值.

综合能源系统的频率偏差表征为

(25)Δf_t_,_n=Δf_t_,_n_-1+

R_{t, n}^{C F}

Δn

频率偏差Δf_t_,_n约束表示为^[23]

(26)-Δf_max≤Δf_t_,_n≤Δf_max

3.2.4 系统运行备用约束

为了保障综合能源系统一次调频具有足够的备用容量,需要构建系统运行备用约束,考虑系统中可再生能源发电和负荷的预测误差以及故障时的功率扰动量,系统的备用约束表征为

(27)∑R_t≥max{ζ_NDP_ND,Δ

P_{m a x}^{l o s s}

}

式中:ζ_ND、P_ND分别为可靠性系数和等效净负荷的误差标准差;Δ $P_{m a x}^{l o s s}$ 为系统最大的有功功率扰动量.

3.2.5 并网模式下的约束条件

并网模式下,综合能源系统通过联络线与电网相连,可从电网直接购买电量.因此,需要系统功率平衡和联络线功率传输进行约束,系统的功率平衡约束表征为

(28)

\overset{N_{i}}{\sum_{i = 1}}

(

{P^{G}}_{i, t}

P_{i, t}^{P V}

P_{i, t}^{F C}

\overset{N_{w}}{\sum_{w = 1}} {P^{W}}_{w, t}

P_{t}^{g r i d}

\overset{N_{i}}{\sum_{i = 1}}

(

{P^{d}}_{i, t}

P_{i, t}^{E L}

)

功率传输约束包括楼宇与配电网联络线传输约束、楼宇与楼宇的功率交互约束,表征为

(29)

\begin{array}{l} 0 \leq P_{i, t}^{g r i d} \leq P_{m a x}^{g r i d} \\ 0 \leq P_{i, t}^{l 2 i} \leq P_{m a x}^{l 2 i} \\ 0 \leq P_{i, t}^{i 2 l} \leq P_{m a x}^{i 2 l} \end{array}\}

本文模型仅从配电网购电,不向配电网售电.

3.2.6 孤岛模式下的约束条件

孤岛模式下,综合能源系统失去了外部电网的支撑,极易遭受功率扰动的影响,系统需要发电机组的惯性支撑外,还需要留有一定的切负荷裕度.因此,孤岛模式下的功率平衡约束与并网模式下的功率平衡约束存在差异,表征为

(30)

\overset{N_{i}}{\sum_{i = 1}}

(

{P^{G}}_{i, t}

P_{i, t}^{P V}

P_{i, t}^{F C}

\overset{N_{w}}{\sum_{w = 1}} {P^{W}}_{w, t}

\overset{N_{i}}{\sum_{i = 1}}

(

{P^{d}}_{i, t}

P_{i, t}^{E L}

P_{i, t}^{c u t}

)

孤岛模式下联络线功率传输约束仅包括楼宇与楼宇间的功率交互约束.

系统负荷切除约束表征为

(31)0≤

P_{i, t}^{c u t}

≤

ζ_{i}^{m a x} {P^{d}}_{i, t}

式中: $ζ_{i}^{m a x}$ 为楼宇i在孤岛模式下所允许的最大负荷切除率.

3.3 约束条件线性化

本文模型中存在非线性部分的约束为式(24)系统频率变化率约束.根据式(6)和式(7),系统的频率变化率可以表征为

(32)

R_{t, n}^{C F} [\overset{N_{i}}{\sum_{i = 1}} ({H^{G}}_{i} {P^{G}}_{i, t} + H_{i, t}^{H S} P_{i, t}^{H S}) + \overset{N_{w}}{\sum_{w = 1}} {H^{W}}_{w, t} {P^{W}}_{w, t}]

\frac{Δ P_{t, n}^{l o s s}}{2}

式中:Δ $P_{t, n}^{l o s s}$ 为故障后第n个步长时系统的有功功率扰动量.由于 $H_{i, t}^{H S}$ 变量跟氢储能系统的荷电状态相关,与 $R_{t, n}^{C F}$ 的乘积使得非线性式(32)无法直接求解,需要对系统的频率变化率进行线性化处理^[25],采用文献[27]中的麦考密克松弛法将其线性化为二次约束规划,利用更收敛的边界约束可更快进行求解.

4 算法求解

ADMM算法是一种被广泛应用于解决大型优化问题的算法,将问题分解为子问题进行分布式交替求,解能够通过交互少量信息实现系统整体最优目标.随着人工智能及数据挖掘行业的不断发展,目前ADMM方法已在电力系统的优化运行中获得了诸多应用.上文建立的优化调度模型根据ADMM算法的基础理论^[28],构造建立目标函数的增广拉格朗日函数:

(33)$\begin{aligned} L= & \sum_{i=1}^{N_{i}}\left\{F\left(\boldsymbol{x}_{i}\right)+g\left(\boldsymbol{z}_{i}\right)+\sum_{t=1}^{N_{t}}\left[\boldsymbol{\pi}_{i}^{\mathrm{T}}\left(\boldsymbol{x}_{i}^{\mathrm{bs}}-\boldsymbol{z}_{i}\right)+\right.\right. \\ & \left.\left.\frac{\rho}{2}\left\|\boldsymbol{x}_{i}^{\mathrm{bs}}-\boldsymbol{z}_{i}\right\|_{2}^{2}\right]\right\} \end{aligned}$

式中:x_i=[ $P_{t}^{g r i d}$ ${P^{W}}_{w, t}$ ${P^{G}}_{i, t}$ $P_{i, t}^{P V}$ $P_{i, t}^{c u t}$ $P_{i, t}^{F C}$ $P_{i, t}^{E L}$ $P_{l, t}^{i 2 l}$ $P_{l, t}^{l 2 i}$ ]为决策变量; $x_{i}^{b s}$ =[ $P_{l, t}^{i 2 l}$ $P_{l, t}^{l 2 i}$ ]为楼宇i和楼宇l之间交换的电能;z_i为辅助变量且 $x_{i}^{b s}$ -z_i=0;g(z_i)为指示函数,当z_i满足约束条件时g(z_i)=0,当z_i不满足约束条件时g(z_i)=∞;π_i为 $x_{i}^{b s}$ -z_i=0的对偶变量;ρ为惩罚参数.

因此,可以将原问题分解为

(34)

\begin{array}{l} x_{i}^{k + 1} = \underset{x}{a r g m i n} {F (x_{i}) + \\ \overset{N_{i}}{\sum_{t = 0}} [(π_{i}^{k})^{T} (x_{i}^{b s} - z_{i}^{k}) + \frac{ρ}{2} {‖x_{i}^{b s} - z_{i}^{k}‖}_{2}^{2}]} \\ z_{i}^{k + 1} = \underset{z}{a r g m i n} {g (z_{i}) + \\ \overset{N_{t}}{\sum_{t = 0}} [(π_{i}^{k})^{T} (x_{i}^{b s, k + 1} - z_{i}) + \\ \frac{ρ}{2} {‖x_{i}^{b s, k + i} - z_{i}‖}_{2}^{2}]} \\ π_{i}^{k + 1} = π_{i}^{k} + ρ (x_{i}^{b s, k + 1} - z_{i}^{k + 1}) \end{array}\}

式中: $x_{i}^{k + 1}$ 、 $z_{i}^{k + 1}$ 表示第k+1次迭代的变量.

x_i和z_i交替迭代,以原始残差r^k和对偶残差s^k作为收敛判据,当满足收敛精度时,可输出系统内各机组最优出力.

(35)

{‖r^{k}‖}_{2}^{2}

\overset{N_{t}}{\sum_{t = 0}} \overset{N_{i}}{\sum_{i = 1}} {‖x_{i}^{b s, k + 1} - z_{i}^{k + 1}‖}_{2}^{2}

≤ε^pri

(36)

{‖s^{k}‖}_{2}^{2}

\overset{N_{t}}{\sum_{t = 0}} \overset{N_{i}}{\sum_{i = 1}} {‖z_{i}^{k} - z_{i}^{k - 1}‖}_{2}^{2}

≤ε^dual

式中:ε^pri和ε^dual分别为原始残差和对偶残差的收敛精度.

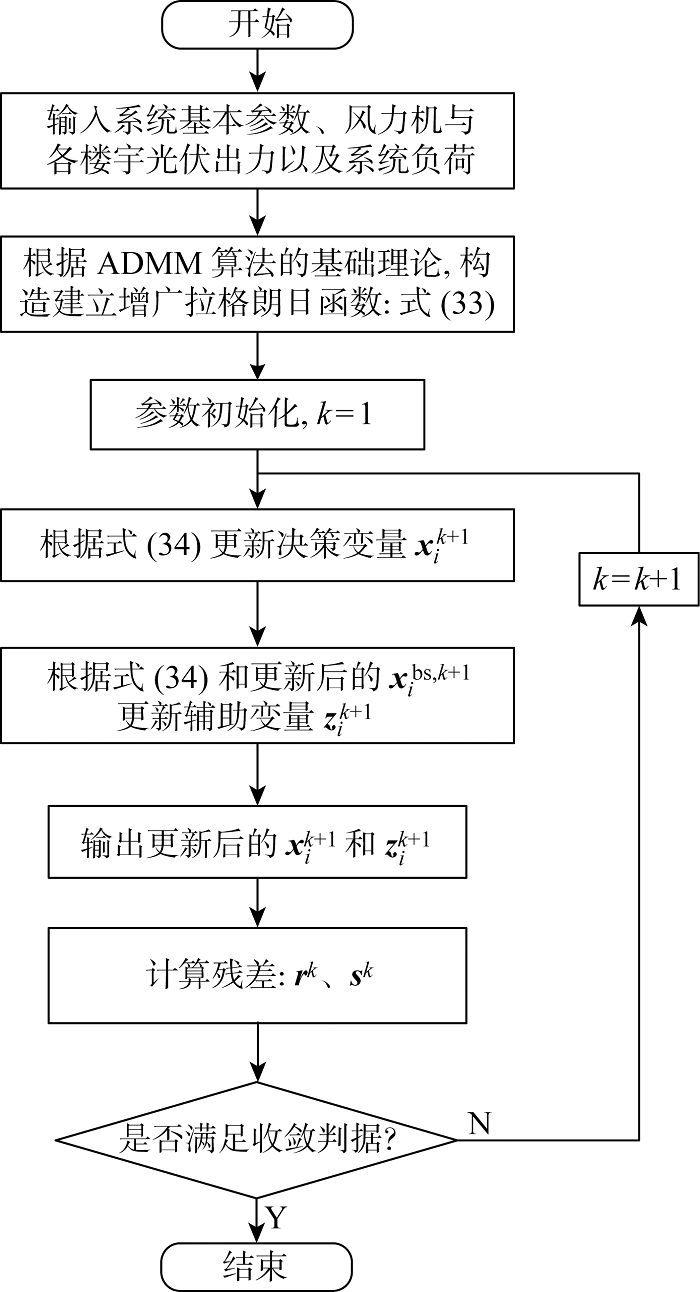
求解流程图如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 基于ADMM算法的优化调度求解流程

Fig.3 Optimal scheduling solution flow based on ADMM algorithm

5 算例分析

为验证所提优化调度方法在包含氢储能系统的IES中的经济性和适用性,对上海某装设了氢储能系统的IES示范工程进行仿真,IES中包含两台风力机W1~W2以及3栋智慧楼宇,3栋楼宇内分别装设光伏面板PV1~PV3、氢储能系统HS1~HS3以及柴油发电机G1~G3.系统的发电机组参数和关键参数分别如表1、表2所示,系统的运行成本系数以及碳排放成本系数如表3所示.系统以24 h 为调度周期,共划分24个时段,每个时段为1 h,图4所示为调度周期内各楼宇的光伏出力和系统总负荷.仿真基于MATLAB R2019a环境下编程并调用CPLEX求解器完成.

表1 发电机组参数

Tab.1 Parameters of generator set

参数	取值	参数	取值
$P_{1}^{W, m a x}$ /kW	100	$P_{3}^{G, m a x}$ /kW	100
$H_{1}^{W}$ /s	8	$H_{3}^{G}$ /s	5
$δ_{1}^{W}$ /%	4	$δ_{3}^{G}$ /%	5
$P_{2}^{W, m a x}$ /kW	120	$P_{1}^{F C, m a x}$ /kW	70
$H_{2}^{W}$ /s	8	$H_{1}^{H S}$ /s	1~3
$δ_{2}^{W}$ /%	5	$δ_{1}^{H S}$ /%	3
$P_{1}^{G, m a x}$ /kW	80	$P_{2}^{F C, m a x}$ /kW	90
$H_{1}^{G}$ /s	4.8	$H_{2}^{H S}$ /s	1~3
$δ_{1}^{G}$ /%	4.5	$δ_{2}^{H S}$ /%	3.5
$P_{2}^{G, m a x}$ /kW	80	$P_{3}^{F C, m a x}$ /kW	100
$H_{2}^{G}$ /s	4.8	$H_{3}^{H S}$ /s	1~3
$δ_{2}^{G}$ /%	4.5	$δ_{3}^{H S}$ /%	3.5

新窗口打开| 下载CSV

表2 系统关键参数

Tab.2 Key parameters of system

参数	取值	参数	取值
$P_{m a x}^{g r i d}$ /kW	80	\|Δf_max\|/Hz	0.8
η^ch/%	70	\| $R_{m a x}^{C F}$ \|/(Hz·s^-1)	1
η^dis/%	80	$S_{i}^{O C - m i n}$ /%	10
γ^max	3	$S_{i, t_{0}}^{O C}$ /%	50
D	1.0	$S_{i}^{O C - m a x}$ /%	100

新窗口打开| 下载CSV

表3 系统运行成本

Tab.3 System operating cost

参数/ [元·(kW·h)^-1]	取值	参数/ [元·(kW·h)^-1]	取值
σ^G,CB	0.01	σ^grid	0.49
σ^grid,CB	0.014 02	α^W	0.016 4
σ^G,R	0.065 7	α^PV	0.013 5
σ^G	0.674	α^G	0.085 9
σ^s,b	0.3

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

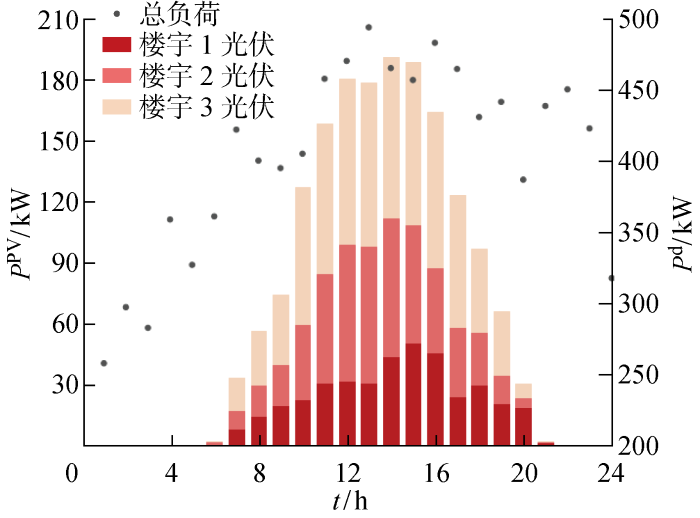
图4 系统总负荷需求和各楼宇光伏出力

Fig.4 Total system load demand and photovoltaic output of each building

5.1 频率稳定约束的有效性分析

在电-氢IES优化调度时同时考虑系统的频率稳定,增加频率稳定约束,用R^CF和Δf表征系统的频率稳定性.为了简化求解,在处理频率稳定约束时采用了线性化的方法,在时域仿真软件中搭建等效模型模拟系统频率响应过程,验证求得的频率稳定约束的有效性.在整个调度周期内,分别在并网模式和孤岛模式下选取3个节点,对比基于相同参数下由仿真系统和本文计算模型所得的R^CF和Δf,对比结果如表4所示.

表4 R^CF和Δf结果对比

Tab.4 Results contrast of R^CF and Δf

运行方式	Δf/Hz		R^CF/(Hz·s^-1)
运行方式	本文模型	仿真模型	本文模型	仿真模型
并网时刻1	-0.21	-0.23	-0.28	-0.27
并网时刻2	-0.35	-0.38	-0.47	-0.49
并网时刻3	-0.12	-0.11	-0.25	-0.26
孤岛时刻1	-0.35	-0.33	-0.47	-0.47
孤岛时刻2	-0.41	-0.47	-0.55	-0.56
孤岛时刻3	-0.32	-0.36	-0.50	-0.49

新窗口打开| 下载CSV

从表4的对比中可以看出,采用本文模型和采用时域仿真模型得到的R^CF和Δf基本相近,Δf的最大偏差为0.06 Hz,R^CF的最大偏差为0.02 Hz/s,均在可接受范围内.

5.2 调度结果分析

为了验证本文所提调度方法的有效性,模拟了3种不同场景下IES在并网模式和孤岛模式下的调度情况并进行对比分析.

场景1,系统采用相同的优化调度方法且考虑频率稳定约束,但不考虑光伏-氢储能系统对频率的支撑作用.

场景2,系统采用相同的优化调度方法且考虑频率稳定约束,但不考虑氢储能系统对频率的支撑作用,仅由风力机和柴油机组承担调频任务.

场景3,可再生能源发电系统不允许调度,不考虑频率稳定约束,仅由柴油机组承担调频任务.

5.2.1 并网模式下

场景1在并网模式下的调度结果和楼宇间功率交互情况分别如图5、图6所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

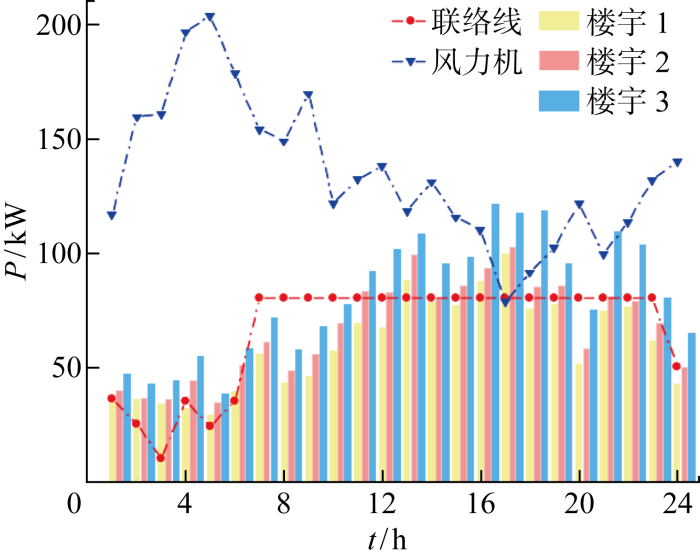
图5 并网模式下场景1优化调度结果

Fig.5 Optimization scheduling results of scenario 1 in grid-connected mode

图6

新窗口打开| 下载原图ZIP| 生成PPT

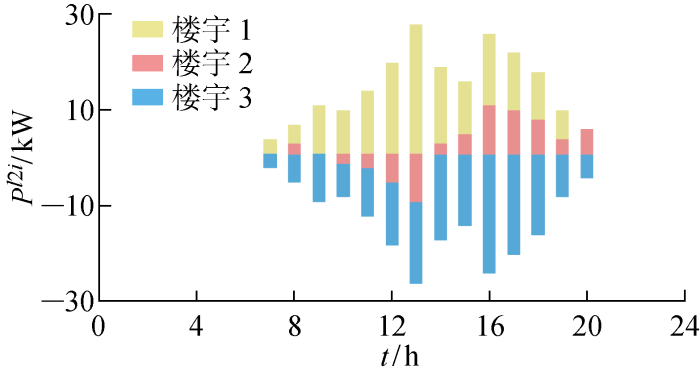
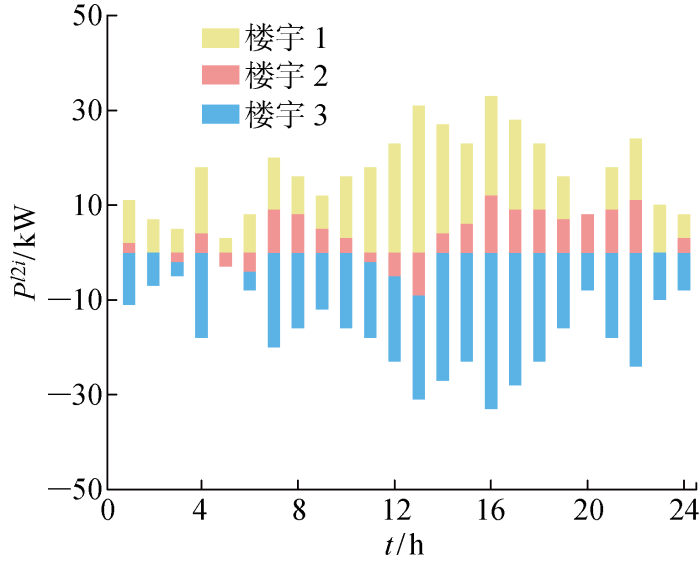
图6 并网模式下场景1楼宇交互功率

Fig.6 Interactive power of buildings of Scenario 1 in grid-connected mode

由图5和图6可以看出,在23:00—次日6:00时段,由于负荷需求较低,风力机出力较高,此时系统的负荷需求主要由风力机进行满足,楼宇间无功率交互;在7:00—20:00时段,负荷需求增加,风力机功率逐渐减小,楼宇内的光伏面板输出功率逐渐增加,楼宇间通过功率交互弥补功率缺额,剩余电量缺额从配电网购入补足,此时联络线处于满额运行状态;在21:00—23:00时段,负荷需求升高,由于风力机和光伏面板的输出功率减少,此时需从配电网购入电量,联络线仍处于满额运行状态.并网模式下,由于风力机和氢储能系统对系统频率的支撑,场景1的系统总运行成本 2 232.62 元低于场景2的系统总运行成本 2 345.325 元,虽然高于场景3的系统总运行成本 2 153.316 元,但是由于考虑了频率稳定约束,提高了系统频率的稳定性.

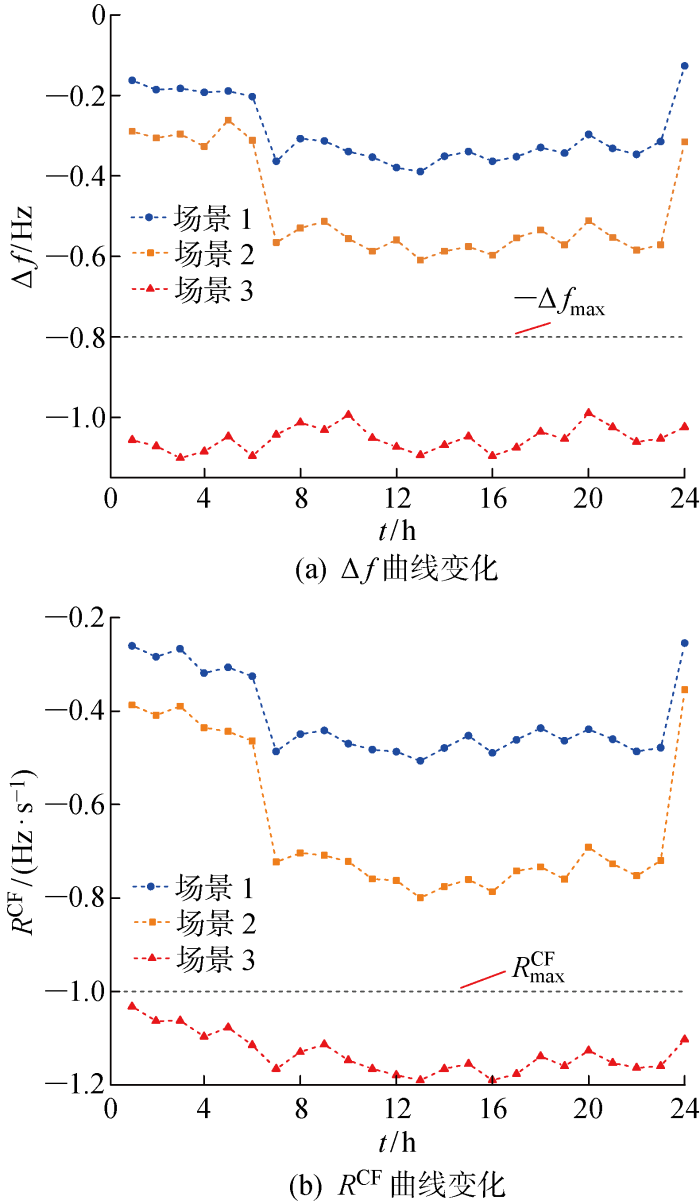
当系统在预想故障时,系统的频率指标R^CF和Δf在调度时段内的变化情况如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 并网模式下系统频率指标的变化

Fig.7 Change of system frequency index in grid-connected mode

由图7可以看出,在发生联络线中断故障时,由于场景1和2均有发电机组配合柴油机组对频率进行支撑,因此R^CF和Δf均在安全限值之内,有效抑制了频率快速跌落情况.场景1与场景2相比,由于氢储能系统参与到系统的惯性响应和一次调频阶段,为系统提供额外的惯量支撑,所以,R^CF和Δf均比场景2的变化幅度小,可以在更严重的有功扰动下维持系统的频率稳定.由于场景3中的调频机组功率有限,所以R^CF和Δf均越限,若不对场景3及时进行控制,会引发频率崩溃等恶性事件.

5.2.2 孤岛模式下

场景1在孤岛模式下的优化调度结果和楼宇间功率交互情况分别如图8、图9所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

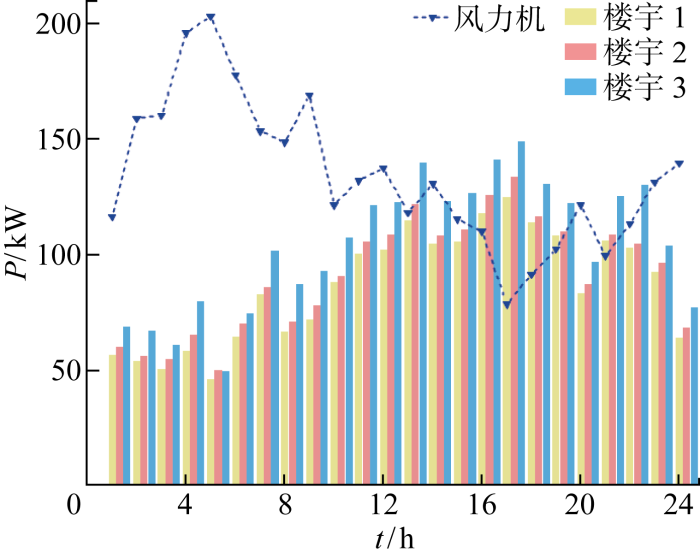
图8 孤岛模式下场景1优化调度结果

Fig.8 Optimization scheduling results of Scenario 1 in island mode

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 孤岛模式下场景1楼宇交互功率

Fig.9 Interactive power of buildings of Scenario 1 in island mode

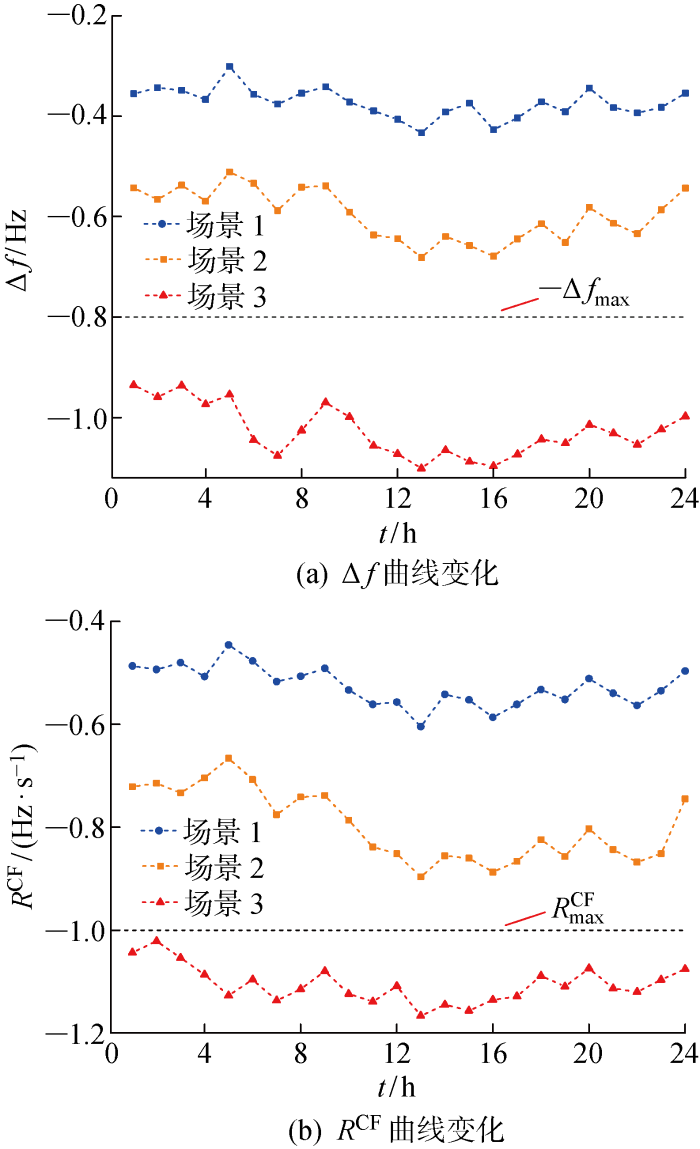
结合图8和图9可以看出,孤岛模式下场景1系统在孤岛模式下由于失去了外部电网的支撑,楼宇的电量缺额主要由楼宇间交互功率和楼宇内柴油发电机组进行补足,此时系统的总运行成本 2 658.478 元低于场景2的总运行成本 2 686.184 元,与场景3的总运行成本 2 594.384 元接近.虽然孤岛模式下系统的总运行成本相差不大,但是场景1中考虑了氢储能系统的虚拟惯量支撑,分担了系统的调频压力,增强了系统抵抗有功扰动的能力.

在系统频率稳定性方面,预设楼宇2中的柴油发电机G2因故退出运行,系统的频率指标R^CF和Δf在调度时段内的变化情况如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 孤岛模式下系统频率指标的变化

Fig.10 Change of system frequency index in island mode

由图10可以看出,在预设故障下,场景1由于风力机和氢储能系统的虚拟惯量加入,缓解了柴油发电机的调频压力,为系统提供了充足的备用容量,所以R^CF和Δf均在安全限值内,并且留有足够多的波动空间.场景2的R^CF和Δf相较于场景1的变化幅度更大,更加临近于安全限值.场景3的频率指标与并网模式下的相同,由于只有柴油发电机组进行调频,所以R^CF和Δf均在安全限值之外,系统的频率稳定性受到严重威胁.

不同模式下各场景的碳排放成本如表5所示.在并网模式下,由于场景3始终选择满额从外部电网购电,所以碳排放成本最高,场景1对比于场景2,由于氢储能系统对柴油发电机组的调频任务进行了分担,所以,碳排放成本较低.在孤岛模式下,由于停止从外部购电后,场景3中柴油发单机的调频压力最大,所以碳排放成本最高,由于场景1充分利用系统中的氢储能系统的虚拟惯量和旋转备用,所以场景1的碳排放成本低于场景2的碳排放成本,拥有较高的环保性.

表5 不同模式下各场景的碳排放成本

Tab.5 Carbon emission cost of different scenarios in different modes

运行方式	碳排放成本/元
运行方式	场景1	场景2	场景3
并网模式	66.838	69.958	73.676
孤岛模式	41.295	42.726	43.674

新窗口打开| 下载CSV

综合以上分析可知,本文所提的优化调度方法拥有较好的经济性.在此基础上,考虑频率稳定性约束,可以充分挖掘系统内的调频潜力,降低系统频率越限的风险,提高系统抵抗有功扰动的能力,同时考虑氢储能系统对系统的惯量支撑,可以进一步提高系统的频率稳定性,并且能够降低系统的碳排放成本,提高系统的运行经济性和环保性.

6 结论

为充分利用IES中的可再生能源发电以及其调频潜力,提出了一种考虑频率稳定约束的电-氢互补多楼宇协调优化调度方法,主要总结如下:

(1) 由于综合能源系统缺少惯性支撑,本文根据风力机和氢储能系统的虚拟惯性响应和一次调频过程,构建系统惯性需求和旋转备用模型,并将频率指标R^CF和Δf作为频率稳定约束,算例表明所提方法能够在有功扰动时有效地保持系统频率稳定.

(2) 综合考虑系统的频率稳定性与经济调度,建立包含频率稳定约束在内的多楼宇协调优化调度模型,给出不同运行模式下系统风力机和各楼宇出力的优化调度方案,保证系统频率稳定的同时能够经济运行.

(3) 充分挖掘系统内风力机和氢储能系统的调频潜力,减少外部购电和柴油发电机组的调频压力,在提高系统频率稳定性的同时,减少碳排放量,提高系统的环保性.

本文的研究成果为IES维持频率稳定和优化运行提供了思路和方法,后续将考虑在IES中更多楼宇的配合参与以及在多IES互联结构下考虑频率稳定性的优化调度.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

国家电网.

国家电网公司“碳达峰、碳中和”行动方案

[J]. 国家电网, 2021(3): 50+52.