考虑地区发展阶段不确定性的电网投资决策鲁棒优化

doi:10.16183/j.cnki.jsjtu.2022.053

考虑地区发展阶段不确定性的电网投资决策鲁棒优化

黄琬迪¹, 张沈习^,¹, 程浩忠¹, 陈丹², 翟晓萌², 吴霜²

1.上海交通大学电力传输与功率变换控制教育部重点实验室, 上海 200240

2.国网江苏省电力有限公司经济技术研究院,南京 210008

Robust Optimization of Power Grid Investment Decision-Making Considering Regional Development Stage Uncertainties

HUANG Wandi¹, ZHANG Shenxi^,¹, CHENG Haozhong¹, CHEN Dan², ZHAI Xiaomeng², WU Shuang²

1. Key Laboratory of Control of Power Transmission and Conversion of the Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China

2. Economic and Technological;Research Institute, State Grid Jiangsu Electric Power Co., Ltd., Nanjing 210008, China

通讯作者: 张沈习,副研究员,博士生导师;E-mail:willzsx@sjtu.edu.cn.

责任编辑: 王历历

收稿日期: 2022-03-5 修回日期: 2022-06-14 接受日期: 2022-07-13

基金资助:

国家自然科学基金青年基金(51907123)
国网江苏省电力有限公司科技项目(J2021153)

Received: 2022-03-5 Revised: 2022-06-14 Accepted: 2022-07-13

作者简介 About authors

黄琬迪(1997-),硕士生,从事电网投资优化、电力系统规划相关研究.

摘要

针对地区发展阶段具有不确定性和不同发展阶段下地区投资需求难以量化的问题,提出一种考虑地区发展阶段不确定性的电网投资决策鲁棒优化方法,以保证电网投资决策与实际发展需求的匹配程度,提高决策结果对投资组合风险与发展阶段不确定性的应对能力.首先,基于现代投资组合理论构建投资风险约束;其次,采用箱型不确定集对地区发展阶段不确定性进行表征,建立考虑发展阶段不确定性的电网投资决策鲁棒优化模型,模型中外层最小化问题求解最恶劣场景下的地区发展阶段不确定性变量,内层最大化问题求解最恶劣场景下能够使投资收益最大的决策方案;再次,根据强对偶理论将双层优化模型转化为可直接求解的单层模型,采用大M法对模型进行求解;最后,利用我国某东部沿海省份中13个地市的实际算例验证了该电网投资决策模型的适用性与有效性.

关键词： 发展阶段不确定性; 电网投资决策; 投资组合风险; 鲁棒优化; 强对偶理论

Abstract

Aimed at the problem of uncertainties in the regional development stage and the difficulties in quantifying regional investment demand in different development stages, a robust optimization method for power grid investment decision-making considering regional development stage uncertainties is proposed to promise the matching degree between power grid investment decisions and development needs, and to improve the ability of decision-making results to deal with portfolio risks and uncertainties in regional development stage. First, investment risk constraints are constructed based on the modern portfolio theory. Then, a box uncertainty set is used to characterize uncertainties in regional development stage, and a robust optimization model for power grid investment decision-making considering uncertainties in development stage is established. In the optimization model, the outer minimization problem is used to solve the uncertain variables in regional development stage in the worst scenario, while inner maximization problem is used to obtain the decision-making plan that can maximize investment return in the worst scenario. Furthermore, according to the strong duality theory, the double-layer optimization model is transformed into a single-layer model that can be solved directly, and the big-M method is used to solve the model proposed. Finally, an actual example of 13 cities in an eastern coastal province verifies the applicability and effectiveness of the power grid investment decision-making model.

Keywords： uncertainty in development stage; power grid investment decision-making; portfolio risk; robust optimization; strong dual theory

PDF (2782KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄琬迪, 张沈习, 程浩忠, 陈丹, 翟晓萌, 吴霜. 考虑地区发展阶段不确定性的电网投资决策鲁棒优化[J]. 上海交通大学学报, 2023, 57(11): 1455-1464 doi:10.16183/j.cnki.jsjtu.2022.053

HUANG Wandi, ZHANG Shenxi, CHENG Haozhong, CHEN Dan, ZHAI Xiaomeng, WU Shuang. Robust Optimization of Power Grid Investment Decision-Making Considering Regional Development Stage Uncertainties[J]. Journal of Shanghai Jiaotong University, 2023, 57(11): 1455-1464 doi:10.16183/j.cnki.jsjtu.2022.053

在国民经济不断发展的背景下,我国电网投资规模始终保持较高水平,优化电网投资决策对电力行业的健康发展与投资效率的提升都具有重要影响^[1-2].由于电网发展规模和完善程度均与地区发展阶段有较强相关性,所以不同发展阶段地区的电网投资需求与投资能力有所差别.电网投资对投资风险的承受能力有限,在投资策略制定过程中,综合考虑投资风险、发展阶段差异,能够优化电网投资模式,提高投资效率^[3].在影响地区电网发展阶段的多项因素中,地区用电负荷种类增多、分布式电源渗透率逐渐增加,受政策制定、经济技术发展等影响,地区电网发展具有较大随机性与波动性,提高了地区电网发展阶段的不确定程度^[4].因此,准确表征地区发展阶段不确定性,合理分配电网投资,研究精准投资决策方法是实现高效投资的关键.

目前,电网投资决策优化主要分为构建投资决策模型的数学建模分析以及构建指标体系、投资评价模型的投资方案评估两种方法.在数学建模分析方法中,文献[5]中综合考虑自然灾害及电网老化等极端因素,建立给定预算约束下的投资决策模型,对输电线路、变电站等进行投资优化;文献[6]中在分布式电源渗透率逐渐增大的背景下,建立优化模型以提高输电网投资效率;文献[7]中考虑电网的灾害恢复能力,以光伏和储能接入作为投资对象进行优化模型构建,以提升投资决策效益.在投资方案评估方法中,文献[8]中基于反向传播神经网络对电网投资决策风险进行评估,减少电力企业的投资风险与经济损失;文献[9]中采用迁移学习技术挖掘小样本情况下的电网投入-产出关系,对投资效果进行评估,辅助配电网投资规划方案优选.然而,上述研究在进行电网投资决策优化的过程中,通常仅将经济效益作为优化与评价目标,较少考虑不同地区的发展差异与投资风险,使优化模型无法保证稳定的投资效益,投资分配结果与地区实际需求有所差异.此外,在经济、电网发展影响因素日益复杂的背景下,上述研究基于确定性优化制定电网投资决策,无法保证优化结果满足所有投资环境下的约束条件.

在考虑不确定性的电网规划与投资优化研究中,文献[10]中以多场景表征分布式电源出力不确定性,优化电网投资决策,提高电网投资收益.此外,鲁棒优化^[11-12]、随机规划^[13-14]、分布鲁棒优化^[15-16]等方法也在不确定性量化中有所应用.以上研究大多仅将分布式电源出力、用电负荷等作为不确定性因素,优化对象也多为分布式电源与储能投资容量等,并未应用在地区发展差异分析、电网投资分配等方面.

电网建设成本回收期长、初期投入较大、对风险的承受能力有限,不同发展阶段地区的电网投资需求与投资能力也有所差别.针对地区发展情况及其不确定性制定投资策略,可有效提升资源配置效率与能源利用率,优化投资效果.基于上述考虑,提出一种考虑地区发展阶段不确定性的电网投资决策鲁棒优化方法.首先,利用箱型不确定集表征地区发展阶段不确定性;其次,基于现代投资组合理论,建立电网投资组合风险约束,考虑地区发展阶段不确定性建立电网投资决策鲁棒优化模型,基于强对偶理论等方法对模型进行转化和求解;最后,选取某省13个地市作为实际算例,验证对电网投资决策的有效性.

1 投资组合风险建模

1.1 现代投资组合理论

多元投资组合可对电网投资收益进行优化,采用分散原理建立电网投资组合,可以有效降低投资过程中的非系统风险^[17].在解决省级投资分配问题时,不同地区间投资额具有一定组合风险,为表征这一非系统风险,确保投资结果符合决策者的风险承受能力,应对投资风险进行构建.根据现代投资组合理论相关定义,以资产组合的投资回报期望E(R)表示资产组合的最终收益,其表达式为

(1)E(R)=

\overset{n}{\sum_{i = 1}}

ω_iE(r_i)

式中:ω_i为第i项要素资产最终投资额在投资总额中权重值;n为要素资产总数;E(r_i)为投资组合中第i项要素资产的期望投资回报,计算表达式为

(2)E(r_i)=

\overset{m}{\sum_{j = 1}}

r_ijp_j

式中:r_ij为第j种经济情况下资产i产生的投资回报;p_j为第j种经济状况的出现概率;m为总经济情况数目.由式(1)和式(2)总结可得,资产组合的投资回报期望E(R)可表示为投资组合中各要素资产的期望报酬E(r_i)的加权平均值.

资产组合中的非系统风险可表示为该组合获得的投资回报少于投资回报期望的可能性.考虑到投资回报期望由无风险收益、预期通货膨胀溢价与风险溢价等因素共同决定,投资组合风险可由组合中各资产投资回报的方差和各资产间投资回报的协方差进行计算,形成投资风险均值-方差模型,衡量投资组合期望收益与波动风险.因此,在均值-方差模型中,投资组合风险主要由投资回报方差与投资组合回报协方差之和表征,具体表达式为

(3)Var(R)=

\overset{n}{\sum_{i = 1}} ω_{i}^{2} σ_{i}^{2}

\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1, j \neq i}}

ω_iω_jCov(r_i,r_j)

式中:σ_i为资产i的投资回报; $ω_{i}^{2} σ_{i}^{2}$ 为投资主体回报方差项;Cov(r_i,r_j)为资产i与资产j间投资回报的协方差;ω_iω_jCov(r_i,r_j)为投资组合回报协方差项.根据协方差物理意义,此时的协方差项表征2项投资资产收益的联合变化程度.根据定义,采用相关系数等变量进行计算,Cov(r_i,r_j)计算表达式为

(4)Cov(r_i,r_j)=

\overset{m}{\sum_{k = 1}}

p_k(r_ik-r_i)(r_jk-r_j)=ρ_ijσ_iσ_j

式中:p_k为第k种经济状况的出现概率;ρ_ij为资产i与资产j间投资收益相关系数,ρ_ij∈[-1, 1];σ_j为资产j的投资回报.

1.2 投资组合风险约束建模

采用现代投资组合理论中均值-方差模型,以投资回报方差表示各投资主体的投资风险,以投资回报协方差表示不同投资主体的组合风险.根据定义,电网投资分配主体在第t年的回报方差 $σ_{t}^{2}$ 可采用离散方差的计算形式,其计算方法为

(5)

σ_{t, i}^{2}

=(v_NPV,_t_,_i-E(v_NPV,_t))²

(6)E(v_NPV,_t)=

\overset{N_{c i t y}}{\sum_{i = 1}}

v_NPV,_t_,_ip_i

式中: $σ_{t, i}^{2}$ 为第t年第i项电网投资主体的离散方差;v_NPV,_t_,_i为时间t时投资分配主体i的电网投资回报净现值;E(v_NPV,_t)为第t年的平均电网投资回报净现值;p_i为第i项电网投资主体的出现概率;N_city为投资主体总数.

结合式(5)和式(6),类比证券收益协方差物理意义,由式(3)和式(4)可总结出电网投资分配主体i与投资分配主体j在第t年的投资回报协方差Cov(v_NPV,_t_,_i, v_NPV,_t_,_i)计算方法如下:

(7)Cov(v_NPV,_t_,_i, v_NPV,_t_,_j)=ρ_ijσ_t_,_iσ_t_,_j

式中:v_NPV,_t_,_j为时间t时投资分配主体j的电网投资回报净现值.

由此可得,投资期每一投资阶段内投资组合风险约束可表示为

(8)

\begin{array}{l} \overset{T}{\sum_{t = 1}} (C_{S q} + C_{C o v}) \leq σ^{2} \\ C_{S q} = \frac{1}{F_{t}^{2}} \overset{N_{c i t y}}{\sum_{i = 1}} f_{t, i}^{2} σ_{t, i}^{2} \\ C_{C o v} = \frac{1}{F_{t}^{2}} \overset{N_{c i t y}}{\sum_{i = 1}} \overset{N_{c i t y}}{\sum_{j = 1, j \neq i}} f_{t, i} f_{t, j} \times \\ C o v (v_{N P V, t, i}, v_{N P V, t, j}) \end{array}\}

式中:T为投资年限;C_Sq、C_Cov分别为投资组合风险方差项和协方差项;F_t为第t年的投资总额;f_t_,_i为投资分配主体i在第t年的投资分配额;σ²为决策者可接受的投资组合风险上限.

2 电网投资决策优化模型

在影响地区发展阶段的各项因素中,地区用电负荷、人均GDP等因素均存在较大不确定性,因此需要对地区电网发展不确定性进行建模.采用鲁棒优化方法制定出具有鲁棒性的最优方案,使得最终投资决策在不确定性因素“最恶劣”环境下仍可满足优化模型约束条件,得到目标函数最优情况下的投资决策结果.

2.1 地区发展不确定性建模

利用箱型不确定集对地区发展阶段不确定性进行表征,其数据波动范围可表示为

(9)P_dev,_i∈(

{\hat{P}}_{d e v, i}

-Δ

P_{d e v, i}^{m a x} {\hat{P}}_{d e v, i}

+Δ

P_{d e v, i}^{m i n}

),∀i∈N_city

式中:P_dev,_i为考虑不确定性后引入的第i项投资主体中地区电网发展阶段不确定变量; ${\hat{P}}_{d e v, i}$ 为第i项投资主体地区电网发展数据值;Δ $P_{d e v, i}^{m a x}$ 、Δ $P_{d e v, i}^{m i n}$ 为第i项投资主体地区电网发展阶段不确定性允许的最大、最小波动偏差,Δ $P_{d e v, i}^{m a x}$ 为正数.采用不确定性辅助向量对地区电网发展阶段不确定性进行等效,则有

(10)$\begin{array}{c}P_{\mathrm{dev}, i}=\hat{P}_{\mathrm{dev}, i}+u_{\mathrm{dev}, i}^{\min } P_{\mathrm{dev}, i}^{\min }-u_{\mathrm{dev}, i}^{\max } P_{\mathrm{dev}, i}^{\max }, \\\forall i \in N_{\mathrm{city}}\end{array}$

式中: $P_{d e v, i}^{m a x}$ 、 $P_{d e v, i}^{m i n}$ 分别第i项投资主体地区电网发展阶段不确定性允许的最大、最小波动值; $u_{d e v, i}^{m i n}$ 、 $u_{d e v, i}^{m a x}$ 为表征第i项投资主体地区电网发展阶段不确定性的辅助变量,其可行域为D=[0,1].

2.2 目标函数

考虑各年投资资金流入现值、以输配电成本为主的资金流出现值与上缴税额,采用净现值描述电网投资效益.净现值是指投资方案在投资期内,综合考虑现金流入流出值,在给定利率的条件下折现到“0”时点的代数和.投资净现值具体表达式为

(11)v_NPV=

\overset{T}{\sum_{t = 1}}

(V_in-V_out)_t(1+I)^-^t

式中:V_in与V_out分别为现金流入和流出值;I为折现率,国民经济评价常用社会折现率,财务评价则用基准折现率,一般为8%.其中,采用输配电价改革后电网投资成本分析方法,不考虑电网缺电与停运成本时,现金流出值的计算表达式为

(12)V_out=

\overset{N_{c i t y}}{\sum_{i = 1}}

[p_trans

P_{e l e}^{i}

(1-R_s)]

式中:p_trans为输配电单位成本; ${P^{i}}_{e l e}$ 为地区i用电负荷;R_s为电网公司所得税率.

电网投资中,各年投资资金流入现值主要受售电收益影响,售电收益与用户用电量和电价有关.采用输配电价改革后的成本收益核算方式,电网投资收益主要由售电收益决定,输配电价则主要由电度电价与容量电价构成.因此,电网投资的现金流入值计算等式可表示为

(13)

\begin{array}{l} V_{i n} = \overset{N_{c i t y}}{\sum_{i = 1}} {[p_{e l e} (1 - r_{l o s s}^{i}) P_{e l e}^{i} + p_{c a p} P_{c a p}^{i}] R_{t a x}} \\ R_{t a x} = (1 - R_{s}) (1 - R_{z}) \end{array}\}

式中:p_ele、p_cap分别为单位电度电价与单位容量电价; ${r^{i}}_{l o s s}$ 为投资主体i的综合线损率; ${P^{i}}_{c a p}$ 为地区i的容量需求;R_tax为去税金额比例;R_z为电网公司增值税率.

确定性优化下,考虑地区发展阶段差异性的电网精准投资决策模型的目标函数可表示为

(14)max v_NPV=max[

\overset{T}{\sum_{t = 1}}

(V_in-V_out)_t(1+I)^-^t]

根据电网企业成本收益计算方法,地区电网发展阶段不确定性可能会对企业现金流入产生限制作用,进而限制电网投资经济性效益.为使最终投资分配结果在地区电网发展阶段不确定性最恶劣条件下也具有可行性,采用鲁棒优化模型以寻找在地区电网发展阶段不确定性朝最恶劣场景变化下的经济性最优投资决策方案.由式(14)进行对偶转换可得,在鲁棒优化模型中,目标函数为

(15)

\underset{u \in D}{m i n}

\underset{y, z \in Ω_{\tilde{u}}}{m a x}

(

{f^{T}}_{1}

{f^{T}}_{2}

式中:u为地区电网发展阶段不确定性辅助向量,包括 $u_{d e v, i}^{m i n}$ 和 $u_{d e v, i}^{m a x}$ 2个元素;y、z为列向量,其中y表示第i项投资主体在第t年的投资分配结果f_t_,_i,在省级电网投资分配中,表征地区i的投资额;z则表示电网特征变量P_cap等;f₁、f₂分别为y、z的系数矩阵; $Ω_{\tilde{u}}$ 为地区发展阶段一定情况下的投资分配结果可行域,其中最优解 $\tilde{u}$ 在外层最小化问题中确定.

目标函数中,外层最小化问题优化变量为地区电网发展指数P_dev,_i,目的在于寻找当前地区发展阶段不确定变量在不确定集内使得电网投资效益最低的最恶劣场景;内层最大化问题优化变量为投资分配结果与电网特征变量等,目的在于寻找最恶劣场景下使得投资收益最大的投资决策方案.

2.3 约束条件

(1) 投资组合风险约束.

基于现代投资组合理论的投资组合风险约束可表示为式(8).

(2) 投资总额约束.

总投资期内,投资总额不能超过一定范围,即

(16)F_t≤

F_{t}^{m a x}

式中: $F_{t}^{m a x}$ 为第t年的投资总额上限.

(3) 系统协调性约束.

容载比反映电网容量备用情况,可有效体现各区域电力系统协调性.电网容载比过高代表大量供电设备闲置,降低电网投资效率;容载比过低则会抑制电能消费,限制经济发展.因此,电网投资应在电网容量备用与投资成本控制间寻求动态平衡,使所增加的变电容量与供电区负荷所成比例保持在一定范围内.使用容载比的经济化表示对电网协调性进行描述,地区电网容载比可根据下式进行计算.

(17)C_cap,_i=

\frac{P_{c a p, i}}{P_{l o a d, i}^{m a x}}

式中:C_cap,_i为地区i容载比计算结果;P_cap,_i为地区i主变容量; $P_{l o a d, i}^{m a x}$ 为地区i的年最大负荷.

根据Q/GDW 156—2006《城市电力网规划设计导则》规定,各电压等级容载比上下限如表1所示.因此,使用容载比经济化进行表征的系统协调性约束可表示为

(18)

C_{c a p}^{m i n}

≤C_cap≤

C_{c a p}^{m a x}

式中: $C_{c a p}^{m a x}$ 、 $C_{c a p}^{m i n}$ 分别为容载比经济化数值上下限.

表1 各电压等级容载比上下限

Tab.1 Upper and lower limits of capacitance-to-load ratio of each voltage level%

城网负荷增长情况	较慢增长率	中等增长率	较快增长率
年负荷平均增长率(建议值)	(0,7)	[7,12]	(12, +∞)
500 kV及以上	1.5~1.8	1.6~1.9	1.7~2.0
220~330 kV	1.6~1.9	1.7~2.0	1.8~2.1
35~110 kV	1.8~2.0	1.9~2.1	2.1~2.2

新窗口打开| 下载CSV

(4) 各地区投资需求约束.

为明确各地区在投资期内的发展阶段与投资需求,收集相关发展数据,采用改进Logistic模型对地区发展阶段进行划分.根据定义,改进Logistic生长曲线模型可表示为

(19)y_t=

\frac{c}{(1 + e^{a - b s (t + l)})^{\frac{1}{s}}}

式中:a,b,c>0,a为函数初始值相关参数,b为增长速度参数,c为函数饱和值相关参数;0<s<+∞,s为密度约束参数;l、o为坐标校正参数.

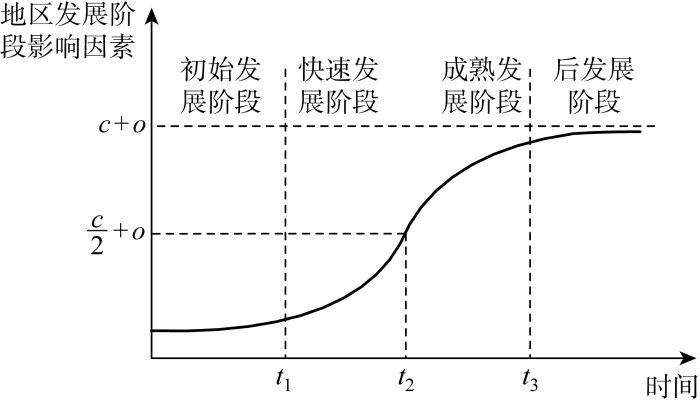
因此,改进Logistic生长曲线模型特征如图1所示,根据发展特征将地区电网发展阶段划分为初始发展阶段、快速发展阶段、成熟发展阶段与后发展阶段.各地区所处发展阶段不同,其投资需求也有所差异.令各阶段划分时间节点分别为t₁、t₂与t₃,不同阶段发展特征可总结为表2.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 改进Logistic模型特征

Fig.1 Features of improved Logistic model

表2 地区发展阶段特征

Tab.2 Characteristics of regional development stage

发展阶段	对应时段	发展潜力	发展增速	发展加速度
初始发展阶段	[0, t₁)	大	小	正
快速发展阶段	[t₁, t₂)	大	大	正
成熟发展阶段	[t₂, t₃)	小	大	负
后发展阶段	[t₃, ∞)	小	小	负

新窗口打开| 下载CSV

根据表2中不同发展阶段的发展特征可划分各地区的投资需求,即各地区投资分配金额,具体约束可表示为

(20)

f_{t, i}^{m i n}

≤f_t_,_i≤

f_{t, i}^{m a x}

式中: $f_{t, i}^{m a x}$ 与 $f_{t, i}^{m i n}$ 分别为对不同地区电网发展阶段

进行计算后,投资分配主体i在第t年的投资需求上限与下限.实际决策过程中,应根据地区发展特征、生长曲线走势等特性确定 $f_{t, i}^{m a x}$ 与 $f_{t, i}^{m i n}$ 变量取值.

(5) 净现值约束.

当净现值v_NPV≥0时,该投资决策方案在经济上可行.因此,净现值约束可表示为

(21)v_NPV,_t≥0, t∈[0,T]

3 电网投资决策优化模型求解

投资风险约束中,引入辅助变量α_2,_t_,_i= $f_{t, i}^{2}$ 对模型中待优化变量进行代换,投资风险约束式(8)中方差风险值变量可替换为

(22)

\overset{T}{\sum_{t = 1}} \frac{1}{F_{t}^{2}} \overset{N_{c i t y}}{\sum_{i = 1}}

α_2,_t_,_i

σ_{t, i}^{2}

≤σ²

由于各投资主体间相互独立,投资组合风险由方差风险值构成.考虑到F_t与σ_t_,_i的变量对应关系,同理可引入辅助变量α_d_,_t_,_i对投资组合方差风险值进行变量代换,得到可进行对偶转化的线性约束条件.根据变量代换原则,各辅助变量约束可总结为

(23)(

f_{t, i}^{m i n}

)^d≤α_d_,_t_,_i≤(

f_{t, i}^{m i n}

)^d, d∈{2,3,4}

鲁棒优化模型目标函数为min-max双层优化模型,优化变量为各地区投资分配金额,求解过程中可基于对偶理论^[18],将内层优化求解最大化问题转化为最小化问题,从而与外层优化问题合并,将双层模型转化为单层优化模型.对于转化前后的最大化问题与最小化问题,如果其中一个问题存在最优解,则对应最优值也同时为另一问题的最优解.

使用一般化形式对电网投资决策模型进行描述,采用向量y,u,z分别表征投资分配结果、地区电网发展阶段不确定性辅助变量与投资决策经济性变量,其中,投资分配结果即最终投资决策中各地区投资额分配情况,投资经济决策经济性变量包括输配电价、电网容载比等影响电网投资效益的相关变量.因此,各变量的具体映射关系为

(24){f_j_,_i}→y

(25){

u_{c o n s, n}^{m i n}

u_{c o n s, n}^{m a x}

}→u

(26){P_cap,P_ele,C_cap,α,γ}→z

式中:f_j_,_i为投资分配额,即投资分配结果; $u_{c o n s, n}^{m i n}$ 、 $u_{c o n s, n}^{m a x}$ 分别为地区发展阶段不确定性最低值、最高值辅助变量; α为方差风险值辅助变量;γ为发展阶段不确定性最大偏差值与原确定值之比,即不确定性最大偏差值比例.

则模型一般化形式可初步表示为

(27)

\underset{u \in D}{m i n}

\underset{y, z \in Ω_{\tilde{u}}}{m a x}

(

{f^{T}}_{1}

{f^{T}}_{2}

(28)

\begin{array}{l} s . t . & H_{1, j} y + H_{2, j} u + H_{3, j} z = h \\ G_{1, j} y + G_{2, j} u + G_{3, j} z \leq g_{1} \\ G_{4} z \leq g_{2} \\ y, z \geq 0 \end{array}\}

式中:H和h为等式约束参数矩阵;G_1,_j~G_3,_j与g₁分别为第j阶段不等式约束的系数矩阵与常数列向量;G₄与g₂分别为与投资阶段无关的不等式约束z的系数矩阵与常数列向量.

根据强对偶理论,引入对偶变量,将内层最大化问题转化为对偶形式,即可以与外层进行合并的最小化问题.对于对偶问题的不确定性变量来说,其最优解位于取值范围的边界处,因此在对偶问题中,可将变量u中元素的取值范围改为D'={0,1}.假设式(28)中,前3组约束对应的对偶变量分别为λ₁_i、λ₂_i与λ₃,将原问题与对偶问题的价值系数与右端项分别对应,得到原始模型中的最大化型原问题转化结果为

(29)

\underset{u, λ}{m i n}

(

{λ^{T}}_{1 j}

{λ^{T}}_{2 j}

g₁+

{λ^{T}}_{3}

g₂-

{λ^{T}}_{1 j}

H_2,_ju-

{λ^{T}}_{2 j}

G_2,_ju)

(30)

\begin{array}{l} s . t . & H_{1, j}^{T} λ_{1 j} + G_{1, j}^{T} λ_{2 j} \geq f_{1} \\ H_{3, j}^{T} λ_{1 j} + G_{3, j}^{T} λ_{2 j} + G_{4}^{T} λ_{3} \geq f_{2} \\ u \in D', λ_{2 j}, λ_{3} \in Λ \end{array}\}

式中:Λ为非负矩阵; $λ_{1 j}^{T}$ H_2,_ju项与 $λ_{2 j}^{T}$ G_2,_ju项是地区发展阶段不确定性辅助变量与对偶变量的乘积,为双线性项,采用大M法^[19]对其进行消除,将双线性项转化为含0~1整数变量和大M数的不等式约束,具体过程如下.

(1) 引入辅助变量矩阵ω_t,设列向量λ₁_j中第p个元素为λ₁_j_,_p,列向量u中第q个元素为u_q,则矩阵ω_t中第p行、第q列的元素可表示为ω_t_,_p_,_q.

(2) 引入极大数M,使得ω_t_,_p_,_q满足:

(31)$\begin{array}{l}-M u_{q} \leqslant \omega_{t, p, q} \leqslant M u_{q} \\\lambda_{1 j, p}-M\left(1-u_{q}\right) \leqslant \omega_{l, p, q} \leqslant\end{array}$

(32)λ₁_j_,_p+M(1-u_q)

因此,可利用ω_t_,_p_,_q替代 ${λ^{T}}_{1 j}$ H_2,_ju与 ${λ^{T}}_{2 j}$ G_2,_ju项中的双线性项λ₁_j_,_pu_q.

此外,在表征发展阶段不确定性过程中,假设变量的正、负最大偏差量相等,即可采用式(33)替换式(10),表征发展阶段不确定性.

(33)u_i_,_t=

{\hat{u}}_{i, t}

+(1+

{\bar{u}}_{i, t}

γ-

{\underline{u}}_{i, t}

γ), ∀i∈N

式中:u_i_,_t为表征第i项投资主体在t时段的地区电网发展阶段不确定性的辅助变量; ${\bar{u}}_{i, t}$ 、 ${\underline{u}}_{i, t}$ 分别为其最大、最小偏差值; ${\hat{u}}_{i, t}$ 为发展阶段不确定性初始值.

4 电网投资决策优化流程

综上所述,电网投资决策优化流程可概括为图2.

图2

新窗口打开| 下载原图ZIP| 生成PPT

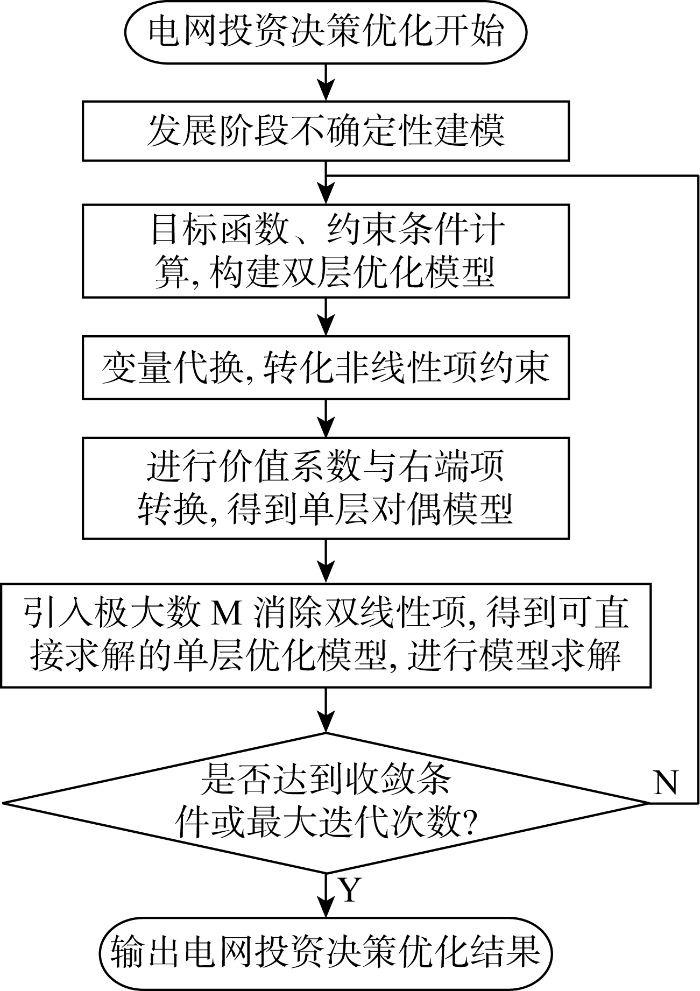
图2 电网投资决策优化流程

Fig.2 Flow chart of optimization of grid investment decision-making

5 算例分析

5.1 算例设置

为验证所提考虑地区发展不确定性的电网精准投资决策模型与求解方法的有效性,选取我国某东部沿海省份中13个地市作为实际算例进行电网投资决策分析.算例建模与求解基于MATLAB R2020b程序开发与仿真平台,采用YALMIP工具箱调用Gurobi 9.0.2商用求解器对优化模型进行求解.

根据历史数据获取情况,投资周期设置为2020—2027年,共8年.在电网企业成本收益核算中,采用各地市实际线损率、输配电价、税率、折现率与输配电单位成本进行核算.根据该省电网销售电价表,以大工业用电销售电价对电网企业成本收益进行核算,选取电度电价0.532元/(kW·h),容量电价每月40元/kW.对于电网企业增值税与所得税税率,依据《中华人民共和国增值税暂行条例》及《国家发展改革委关于电网企业增值税税率调整相应降低一般工商业电价的通知》(发改价格〔2019〕559号),电网企业增值税税率选取13%;根据《中华人民共和国税收征收管理法》及其实施细则、《中华人民共和国企业所得税暂行条例》及其实施细则和有关规定,电网企业所得税税率选取25%.在成本收益核算中,根据该省历史数据,折现率选取基准折现率,即8%;成本核算中,输配电单位成本选取0.187元/(kW·h).

根据电网投资历史数据,投资期内首年投资上限选取350亿元,而后每年以3%的速度增长.投资组合风险约束中,由于投资总额受投资上限约束,并不是确定值,所以任意两市投资收益间并不存在线性相关关系,认为两市间投资收益不相关,因此此时投资组合风险主要由均值-方差模型中的方差项决定.以历史数据与实地调研结果为基础,并计算投资期内可接受的最大风险值,设定投资期内投资组合风险约束值为10(亿元)².

综合考虑各地区供电量、期末发电装机台数、地区生产总值等历史数据,对地区电网发展阶段进行划分,计算各市地区电网发展阶段划分节点.对于系统协调性约束,选取220 kV电压等级,以各地市负荷增速对容载比上下限进行划分.根据计算结果,容载比上下限约束、各地市发展阶段划分结果及时间节点如表3所示.

表3 地区发展阶段及容载比上下限划分结果

Tab.3 Division results of regional development stage and upper and lower limits of capacitive-to-load ratio

地区	t₁	t₂	t₃	容载比上下限
A	1994	2015	2031	1.7~2.0
B	1998	2016	2035	1.7~2.0
C	1990	2011	2030	1.6~1.9
D	1987	2006	2025	1.6~1.9
E	1990	2010	2026	1.6~1.9
F	1982	2008	2030	1.6~1.9
G	1992	2012	2030	1.6~1.9
H	1987	2010	2037	1.7~2.0
I	1997	2016	2032	1.6~1.9
J	1983	2010	2034	1.7~2.0
K	1977	2012	2046	1.8~2.1
L	1990	2014	2040	1.7~2.0
M	2000	2015	2030	1.6~1.9

新窗口打开| 下载CSV

根据表2中各阶段发展指数增长潜力、增长速度与增长加速度等特征,划分各地市投资需求上下限.其中,在投资期内位于快速、成熟发展阶段内的投资需求发展加速度较大,而位于后发展阶段内的投资需求增速较为稳定.以上述特征为基础,计算改进Logistic模型中发展数值增速及增长加速度,设定各发展阶段地区投资需求增速范围如表4所示.

表4 发展阶段与投资需求增速范围对应

Tab.4 Correspondence between development stage and investment demand growth rate

发展阶段	投资需求增速范围
初始发展阶段	0.80~1.05
快速发展阶段	0.90~1.15
成熟发展阶段	0.90~1.20
后发展阶段	0.80~1.05

新窗口打开| 下载CSV

5.2 投资决策优化结果

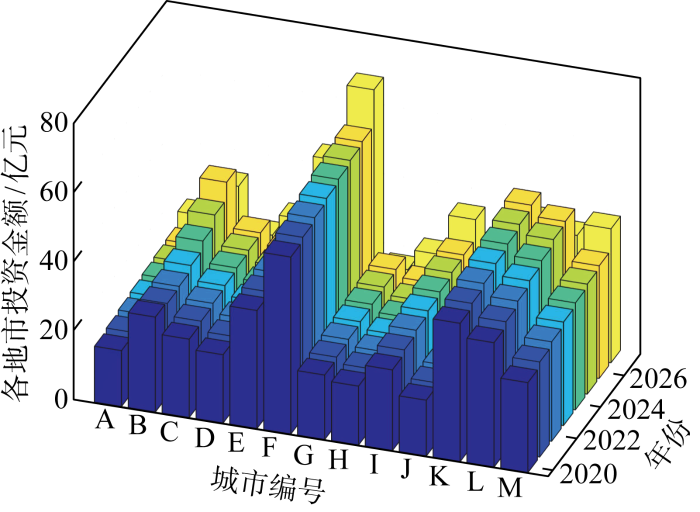
首先设置最大偏差值比例γ为0.1,对上述鲁棒优化模型进行求解,得到最终投资期内各地市的投资分配结果如图3所示.由图可见,此时由于投资额上限逐渐增长,各地市投资额分配整体为上升趋势,但上升幅度各有差别.其中,E、F等市的投资额在投资期内始终位于较高水平.对比其实际发展情况,E、F市工业、经济较为发达,维持较为完善的电网运行需要加大投资力度,始终保持较高的投资水平并逐渐增加投资额,符合城市经济、社会及电网发展需求.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 γ=0.1时投资决策结果

Fig.3 Results of investment decision at γ=0.1

对于I、M等市,发达程度相对较低,在分配结果中,其投资额起始值较低,与发展情况匹配.但其在投资期内处于高速发展时期,因此较为快速的投资额增速也与其投资需求相符.考虑到这类地区具有较大的发展潜力与投资需求,当前结果满足预期电网发展需要,也同时能够保证较低的投资风险.

5.3 地区发展不确定性影响

5.3.1 最大偏差值比例γ=0.2时投资优化结果

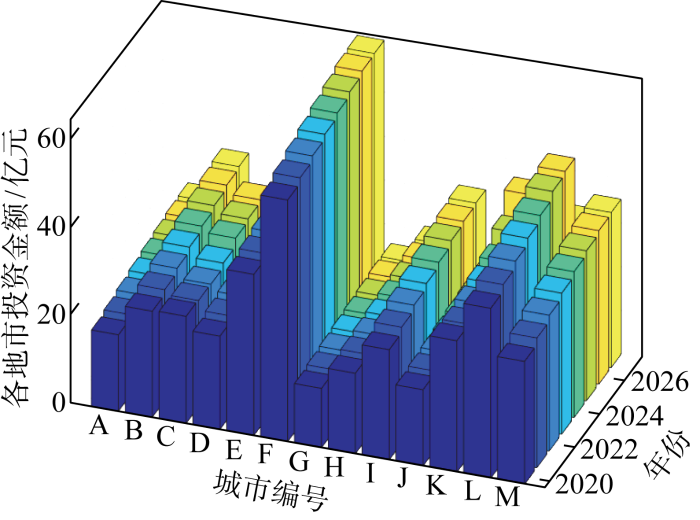
当模拟地区电网发展阶段不确定性较大的场景,研究鲁棒区间宽度对投资决策结果影响时,可适当调高最大偏差值参数.设置最大偏差值比例γ为0.2,增大鲁棒区间宽度,对上述模型进行求解,得到投资期内各地市的投资分配结果,如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 γ=0.2时投资决策结果

Fig.4 Results of investment decision at γ=0.2

对比可得,增大偏差值参数,各地市投资分配结果随时间变化趋于平缓,投资结果更为保守.此时,不仅不同城市间的投资金额变化趋势类似,各城市的投资金额变化幅度也更加平缓.以F市为例,根据发展阶段划分结果可得,由于其在投资期内存在较大的投资需求,偏差值比例γ增大,F市投资额分配结果仍旧处于较高水平,但2020—2027年投资额变化率由37.81%变为12.29%.由此可得,增大鲁棒区间宽度可使投资分配结果变化幅度减小,经济性降低,但对不确定性的抵御能力增强,投资结果趋于保守.

因此,增大鲁棒区间宽度不仅能保证更低的投资风险,也能保证各年投资能力位于地区电网发展阶段的约束范围内,使投资决策结果能够满足发展阶段不确定性较大时的各项约束条件.

5.3.2 投资决策风险与投资效益对比

参考式(8),采用现代投资组合理论中的均值-方差模型对不同优化方式下的投资风险值进行对比,分别求取确定性优化模型与γ=0.1时的鲁棒优化模型的投资风险值,如表5所示.

表5 投资风险对比

Tab.5 Comparison of investment risk

年份	投资风险/(亿元)²
年份	γ=0	γ=0.1
2020	0.315	0.319
2021	0.389	0.353
2022	0.478	0.414
2023	0.584	0.514
2024	0.706	0.678
2025	0.861	0.946
2026	1.015	1.433
2027	1.205	1.524
总计	5.554	5.181

新窗口打开| 下载CSV

由表5分析可得,鲁棒优化的保守性有效降低了各时段的投资风险,相比于考虑地区发展阶段的确定性规划,γ=0.1时的鲁棒优化模型风险值下降幅度为6.72%,提高了电网投资决策的稳定性.

当模拟地区电网发展阶段不确定性较大的场景、研究鲁棒区间宽度对投资决策结果影响时,可适当调高最大偏差值参数.鲁棒优化模型首先寻找地区发展阶段不确定性最恶劣场景,进而进行投资分配优化,使投资分配结果满足鲁棒区间内最恶劣场景下所有约束条件.为更加直观地对比不同鲁棒区间时鲁棒优化与确定性优化结果,验证鲁棒优化的保守性,调节鲁棒区间宽度并计算不同区间宽度分别对应的投资分配决策净利润,结果如表6所示.

表6 不同鲁棒区间宽度下的投资决策净利润

Tab.6 Net profit of investment decision-making at different robust interval widths

年份	投资决策净利润/亿元
年份	γ=0	γ=0.05	γ=0.1	γ=0.15	γ=0.2
2020	57.514	57.719	57.536	57.241	56.324
2021	58.502	58.598	58.403	58.094	57.080
2022	59.483	59.535	59.334	59.003	57.941
2023	60.454	60.538	60.332	60.006	58.922
2024	61.417	61.605	61.395	61.066	60.018
2025	62.414	62.732	62.533	62.203	61.194
2026	63.282	63.855	63.700	63.373	62.471
2027	64.162	61.361	60.725	59.612	57.757
总计	651.879	649.001	644.620	641.418	629.283

新窗口打开| 下载CSV

表6中,γ=0对应不确定性变量最大偏差值为0,即为确定性优化.对比表6中各情况下投资决策净利润可知,与确定性优化结果对比,考虑发展阶段不确定性的情况下,鲁棒优化的投资分配决策净利润更低.随着最大偏差值γ不断增大,投资决策净利润逐渐减小,优化模型保守度提高.当γ=0.2,优化模型投资总利润下降3.46%,以保证更低的投资风险.随着鲁棒区间宽度增大,鲁棒优化模型中的发展阶段不确定性进一步增强,模型通过舍弃部分经济效益得到更为稳定、保守的投资决策结果.实际投资决策过程中,应调节模型鲁棒性使投资决策结果在经济性与稳定性中寻求平衡,使投资结果满足决策者需求.综上,该结果进一步证实调整偏差值参数可控制模型不确定性集合的鲁棒性.实际投资决策时,可根据对于发展阶段不确定性的接受程度、投资风险的承受能力与各约束越限风险的适应程度调整偏差值参数.

6 结论

提出考虑地区发展阶段不确定性的电网投资决策鲁棒优化模型,并采用变量代换、对偶变换、大M法等方法将模型转化为单层鲁棒优化模型进行求解.通过实际算例分析,可得到如下结论:

(1) 考虑地区发展阶段不确定性的电网精准投资决策模型可对投资分配决策进行优化,得到的决策方案符合地区电网发展需求与投资能力.

(2) 与确定性优化相比,鲁棒优化模型计算结果具有更强的保守性,投资决策净利润降低.计算可得,γ=0.1时的鲁棒优化模型风险值下降幅度为6.72%,投资组合风险更小.鲁棒区间宽度增加可增强投资决策方案保守性.与确定性优化相比,鲁棒区间γ上升至0.2,投资总利润有3.46%的降幅.实际投资决策时,投资者可根据风险承受能力调节偏差值参数,获得不同场景下的决策方案.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘巍, 李锰, 李秋燕,

等.

基于改进遗传算法的电网投资组合预测方法

[J]. 电力系统保护与控制, 2020, 48(8): 78-85.

[本文引用: 1]

LIU

Wei

, LI

Meng

, LI

Qiuyan

et al.

Power grid portfolio forecasting method based on an improved genetic algorithm

[J]. Power System Protection & Control, 2020, 48(8): 78-85.

[本文引用: 1]

[2]

张华一, 文福拴, 张璨,

等.

基于前景理论的电网建设项目组合多属性决策方法

[J]. 电力系统自动化, 2016, 40(14): 8-14.

[本文引用: 1]

ZHANG

Huayi

, WEN

Fushuan

, ZHANG

Can

et al.

Prospect theory based multiple-attribute decision-making method for determining portfolio of construction projects in power systems

[J]. Automation of Electric Power Systems, 2016, 40(14): 8-14.

[本文引用: 1]

[3]

杨娜, 刘敦楠, 刘明光,

等.

考虑地市发展阶段的省级电网差异化投资策略

[J]. 电力系统自动化, 2020, 44(7): 115-122.

[本文引用: 1]

YANG

, LIU

Dunnan

, LIU

Mingguang

et al.

Differentiated investment strategy of provincial power grid considering development stage of city region

[J]. Automation of Electric Power Systems, 2020, 44(7): 115-122.

[本文引用: 1]

[17]

YUN

Qiuchen

, TIAN

Liting

, QI

Ning

et al.

Optimization method of resource combination for virtual power plant based on modern portfolio theory

[J]. Automation of Electric Power Systems, 2022, 46(1): 146-154.

[本文引用: 1]

[18]

H R

, WANG

C S

, LI

et al.

Robust operation of soft open points in active distribution networks with high penetration of photovoltaic integration

[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 280-289.

DOI:10.1109/TSTE.2018.2833545 URL [本文引用: 1]

[4]

李林晏, 韩爽, 乔延辉,

等.

面向高比例新能源并网场景的风光-电动车协同调度方法

[J]. 上海交通大学学报, 2022, 56(5): 554-563.

[本文引用: 1]

Linyan

, HAN

Shuang

, QIAO

Yanhui

et al.

A wind-solar-electric vehicles coordination scheduling method for high proportion new energy grid-connected scenarios

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(5): 554-563.

[本文引用: 1]

[5]

GARIFI

, JOHNSON

E S

, ARGUELLO

et al.

Transmission grid resiliency investment optimization model with SOCP recovery planning

[J]. IEEE Transactions on Power Systems, 2022, 37(1): 26-37.

DOI:10.1109/TPWRS.2021.3091538 URL [本文引用: 1]

[6]

CEBECI

M E

, TOR

O B

, OPREA

S V

et al.

Consecutive market and network simulations to optimize investment and operational decisions under different RES penetration scenarios

[J]. IEEE Transactions on Sustainable Energy, 2019, 10(4): 2152-2162.

DOI:10.1109/TSTE.5165391 URL [本文引用: 1]

[7]

KUSHAL

T R B

, ILLINDALA

M S

Decision support framework for resilience-oriented cost-effective distributed generation expansion in power systems

[J]. IEEE Transactions on Industry Applications, 2021, 57(2): 1246-1254.

DOI:10.1109/TIA.28 URL [本文引用: 1]

[8]

CHEN

S J

, JIANG

, HE

Y Q

et al.

A BP neural network-based hierarchical investment risk evaluation method considering the uncertainty and coupling for the power grid

[J]. IEEE Access, 2020, 8: 110279-110289.

DOI:10.1109/Access.6287639 URL [本文引用: 1]

[9]

杨建平, 向月, 刘俊勇.

面向配电网投资决策的小样本关联规则自适应迁移学习方法

[J]. 中国电机工程学报, 2022, 42 (16): 5823-5834.

[本文引用: 1]

YANG

Jianping

, XIANG

Yue

, LIU

Junyong

Adaptive transfer learning of small sample correlation rules for distribution network investment decision

[J]. Proceedings of the CSEE, 2022, 42 (16): 5823-5834.

[本文引用: 1]

[10]

MUÑOZ-DELGADO

, CONTRERAS

, ARROYO

J M

et al.

Integrated transmission and distribution system expansion planning under uncertainty

[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 4113-4125.

DOI:10.1109/TSG.2021.3071385 URL [本文引用: 1]

[11]

方一晨, 张沈习, 程浩忠,

等.

含智能软开关的主动配电网分布式光伏准入容量鲁棒优化

[J]. 电力系统自动化, 2021, 45(7): 8-17.

[本文引用: 1]

FANG

Yichen

, ZHANG

Shenxi

, CHENG

Hao-zhong

et al.

Robust optimization of distributed photovoltaic hosting capacity of active distribution network with soft open point

[J]. Automation of Electric Power Systems, 2021, 45(7): 8-17.

[本文引用: 1]

[12]

周士超, 刘晓林, 熊展,

等.

考虑韧性提升的交直流配电网线路加固和储能配置策略

[J]. 上海交通大学学报, 2021, 55(12): 1619-1630.

[本文引用: 1]

ZHOU

Shichao

, LIU

Xiaolin

, XIONG

Zhan

et al.

Line hardening and energy storage system configuration strategies for resilience enhancement of a hybrid AC-DC distribution system

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(12): 1619-1630.

[本文引用: 1]

[13]

刘明涛, 谢俊, 张秋艳,

等.

碳交易环境下含风电电力系统短期生产模拟

[J]. 上海交通大学学报, 2021, 55(12): 1598-1607.

[本文引用: 1]

LIU

Mingtao

, XIE

Jun

, ZHANG

Qiuyan

et al.

Short-term production simulation of power system containing wind power under carbon trading environment

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(12): 1598-1607.

[本文引用: 1]

[14]

BHATTACHARYA

, KHAROUFEH

J P

, ZENG

Managing energy storage in microgrids: A multistage stochastic programming approach

[J]. IEEE Transactions on Smart Grid, 2018, 9(1): 483-496.

DOI:10.1109/TSG.2016.2618621 URL [本文引用: 1]

[15]

, WU

Q W

, YANG

et al.

Distributed distributionally robust dispatch for integrated transmission-distribution systems

[J]. IEEE Transactions on Power Systems, 2021, 36(2): 1193-1205.

DOI:10.1109/TPWRS.59 URL [本文引用: 1]

[16]

陈泽雄, 张新民, 王雪锋,

等.

分布式光伏电站接入配电网的分布鲁棒优化配置方法

[J]. 电力系统保护与控制, 2021, 49(13): 30-42.

[本文引用: 1]

CHEN

Zexiong

, ZHANG

Xinmin

, WANG

Xuefeng

et al.

A distributionally robust optimal allocation method for distributed photovoltaic generation stations integrated into a distribution network

[J]. Power System Protection & Control, 2021, 49(13): 30-42.

[本文引用: 1]

[17]

云秋晨, 田立亭, 齐宁,

等.

基于投资组合理论的虚拟电厂资源优化组合方法

[J]. 电力系统自动化, 2022, 46(1): 146-154.

[本文引用: 1]

[19]

DING

, LI

, YANG

Y H

et al.

A two-stage robust optimization for centralized-optimal dispatch of photovoltaic inverters in active distribution networks

[J]. IEEE Transactions on Sustainable Energy, 2017, 8(2): 744-754.

DOI:10.1109/TSTE.2016.2605926 URL [本文引用: 1]

基于改进遗传算法的电网投资组合预测方法

2020

... 在国民经济不断发展的背景下,我国电网投资规模始终保持较高水平,优化电网投资决策对电力行业的健康发展与投资效率的提升都具有重要影响^[1-2].由于电网发展规模和完善程度均与地区发展阶段有较强相关性,所以不同发展阶段地区的电网投资需求与投资能力有所差别.电网投资对投资风险的承受能力有限,在投资策略制定过程中,综合考虑投资风险、发展阶段差异,能够优化电网投资模式,提高投资效率^[3].在影响地区电网发展阶段的多项因素中,地区用电负荷种类增多、分布式电源渗透率逐渐增加,受政策制定、经济技术发展等影响,地区电网发展具有较大随机性与波动性,提高了地区电网发展阶段的不确定程度^[4].因此,准确表征地区发展阶段不确定性,合理分配电网投资,研究精准投资决策方法是实现高效投资的关键. ...

基于改进遗传算法的电网投资组合预测方法

2020

基于前景理论的电网建设项目组合多属性决策方法

2016

基于前景理论的电网建设项目组合多属性决策方法

2016

考虑地市发展阶段的省级电网差异化投资策略

2020

考虑地市发展阶段的省级电网差异化投资策略

2020

基于投资组合理论的虚拟电厂资源优化组合方法

2022

... 多元投资组合可对电网投资收益进行优化,采用分散原理建立电网投资组合,可以有效降低投资过程中的非系统风险^[17].在解决省级投资分配问题时,不同地区间投资额具有一定组合风险,为表征这一非系统风险,确保投资结果符合决策者的风险承受能力,应对投资风险进行构建.根据现代投资组合理论相关定义,以资产组合的投资回报期望E(R)表示资产组合的最终收益,其表达式为 ...

Robust operation of soft open points in active distribution networks with high penetration of photovoltaic integration

2019

... 鲁棒优化模型目标函数为min-max双层优化模型,优化变量为各地区投资分配金额,求解过程中可基于对偶理论^[18],将内层优化求解最大化问题转化为最小化问题,从而与外层优化问题合并,将双层模型转化为单层优化模型.对于转化前后的最大化问题与最小化问题,如果其中一个问题存在最优解,则对应最优值也同时为另一问题的最优解. ...

面向高比例新能源并网场景的风光-电动车协同调度方法

2022

面向高比例新能源并网场景的风光-电动车协同调度方法

2022

Transmission grid resiliency investment optimization model with SOCP recovery planning

2022

... 目前,电网投资决策优化主要分为构建投资决策模型的数学建模分析以及构建指标体系、投资评价模型的投资方案评估两种方法.在数学建模分析方法中,文献[5]中综合考虑自然灾害及电网老化等极端因素,建立给定预算约束下的投资决策模型,对输电线路、变电站等进行投资优化;文献[6]中在分布式电源渗透率逐渐增大的背景下,建立优化模型以提高输电网投资效率;文献[7]中考虑电网的灾害恢复能力,以光伏和储能接入作为投资对象进行优化模型构建,以提升投资决策效益.在投资方案评估方法中,文献[8]中基于反向传播神经网络对电网投资决策风险进行评估,减少电力企业的投资风险与经济损失;文献[9]中采用迁移学习技术挖掘小样本情况下的电网投入-产出关系,对投资效果进行评估,辅助配电网投资规划方案优选.然而,上述研究在进行电网投资决策优化的过程中,通常仅将经济效益作为优化与评价目标,较少考虑不同地区的发展差异与投资风险,使优化模型无法保证稳定的投资效益,投资分配结果与地区实际需求有所差异.此外,在经济、电网发展影响因素日益复杂的背景下,上述研究基于确定性优化制定电网投资决策,无法保证优化结果满足所有投资环境下的约束条件. ...

Consecutive market and network simulations to optimize investment and operational decisions under different RES penetration scenarios

2019

Decision support framework for resilience-oriented cost-effective distributed generation expansion in power systems

2021

A BP neural network-based hierarchical investment risk evaluation method considering the uncertainty and coupling for the power grid

2020

面向配电网投资决策的小样本关联规则自适应迁移学习方法

2022

面向配电网投资决策的小样本关联规则自适应迁移学习方法

2022

Integrated transmission and distribution system expansion planning under uncertainty

2021

... 在考虑不确定性的电网规划与投资优化研究中,文献[10]中以多场景表征分布式电源出力不确定性,优化电网投资决策,提高电网投资收益.此外,鲁棒优化^[11-12]、随机规划^[13-14]、分布鲁棒优化^[15-16]等方法也在不确定性量化中有所应用.以上研究大多仅将分布式电源出力、用电负荷等作为不确定性因素,优化对象也多为分布式电源与储能投资容量等,并未应用在地区发展差异分析、电网投资分配等方面. ...

含智能软开关的主动配电网分布式光伏准入容量鲁棒优化

2021

含智能软开关的主动配电网分布式光伏准入容量鲁棒优化

2021

考虑韧性提升的交直流配电网线路加固和储能配置策略

2021

考虑韧性提升的交直流配电网线路加固和储能配置策略

2021

碳交易环境下含风电电力系统短期生产模拟

2021

碳交易环境下含风电电力系统短期生产模拟

2021

Managing energy storage in microgrids: A multistage stochastic programming approach

2018

Distributed distributionally robust dispatch for integrated transmission-distribution systems

2021

分布式光伏电站接入配电网的分布鲁棒优化配置方法

2021

分布式光伏电站接入配电网的分布鲁棒优化配置方法

2021

基于投资组合理论的虚拟电厂资源优化组合方法

2022

A two-stage robust optimization for centralized-optimal dispatch of photovoltaic inverters in active distribution networks

2017

... 式中:Λ为非负矩阵;

λ_{1 j}^{T}

H_2,_ju项与

λ_{2 j}^{T}

G_2,_ju项是地区发展阶段不确定性辅助变量与对偶变量的乘积,为双线性项,采用大M法^[19]对其进行消除,将双线性项转化为含0~1整数变量和大M数的不等式约束,具体过程如下. ...

〈

〉