近年来,由于自主水下机器人(AUV)在水文测量、水下探测巡检作业等方面的优势,其在商业和科研方面的应用愈发广泛[1].为成功完成指定任务,路径跟踪运动控制是不可或缺的一个环节,因此相关研究倍受国内外学者关注.针对外界时变扰动影响下的控制问题,Do等[2]基于反步法和投影算法设计了一个鲁棒控制器实现全局渐近稳定,并利用模型船开展了实验验证.Wang等[3]设计了模糊未知观测器对扰动进行在线观测补偿.考虑未精确建模及参数摄动问题,余亚磊等[4]通过坐标变换对模型进行转化,随后利用反步自适应算法对不确定项进行补偿.此外,文献[5]中所采用的模糊逼近方法也可有效处理这一问题.考虑到实际物理条件限制,执行器所产生的控制输入是受限的,因而输入饱和问题也是一个需要解决的问题.常见的一种方法是设计辅助动力系统[6]进行处理, 此外还可采用平滑饱和函数[7]、边界李雅普诺夫函数[8]和饱和滤波器[9]等策略.
面向海底起伏地形跟踪作业需求,航行安全约束需在全过程得到保障,如控制器响应过慢或超调过大均有可能对AUV安全性带来问题,因而需要寻求一种有效的解决方案以实现对控制系统瞬态性能的安全约束.传统的控制器设计仅能保障系统的稳态性能,有限时间[15]和固定时间控制[16]可对收敛时间起到约束,但是超调量仍难以约束.针对这一问题,Bechlioulis等[17]于2008年提出预设性能控制技术,随后在水下机器人中得到了成功的应用[18].此外,Dai等[19]和Zheng[20]在预设性能路径跟踪方面也开展了相关工作,但多是针对水平面的,且未考虑系统执行机构时滞特性.为此,本文针对带有时滞特性的AUV深度面路径跟踪控制问题,提出了一种基于预设性能技术的控制器设计方法.与现有文献相比,本文主要贡献如下:
(1) 面向AUV海底起伏地形跟踪任务的需求,本文中结合预设性能与时变视线角制导技术,设计了一种预设性能制导律,在确保系统误差收敛的同时还兼顾了瞬态跟踪性能,有利于提升AUV在海底起伏地形跟踪控制的航行安全.
(2) 针对执行器由于物理性能约束所固有的时滞特性,本文基于径向基函数(RBF)神经网络和时滞动力学模型方程设计了一种鲁棒时滞控制器,避免了未考虑时滞特性导致实艇算法移植稳定性下降的问题,使其更符合航行控制需求.
1 控制对象模型建立
欠驱动AUV在深度面的简化运动学模型如下所示:
式中:x,z分别为定义在惯性坐标系
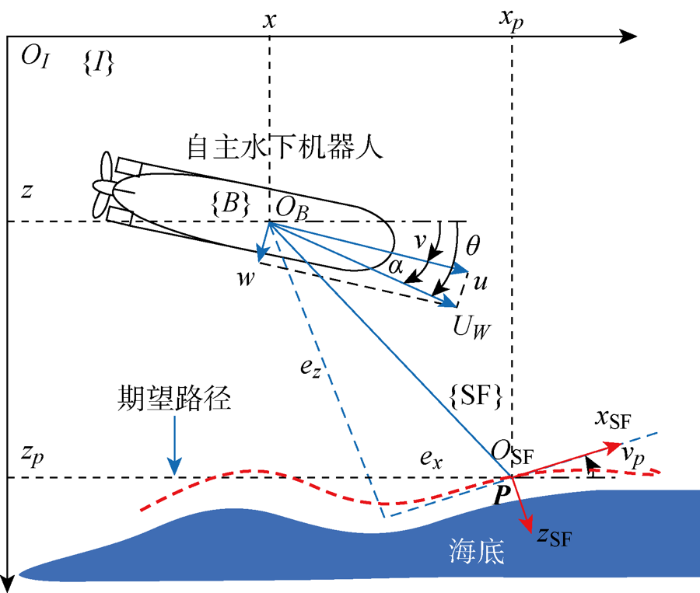
图1
式中:vp为虚拟点的潜伏角.进一步,其运动误差动态可作如下表达:
式中:UW=
具有时滞特性的动力学模型可以作如下表述[21]:
式中:gq为舵角增益;λδ为舵机时滞系数;δs为考虑时滞的真实舵角;δsc为舵角指令; fq为水动力函数,具体定义如下:
式中:xg,zg为重心在垂直面的坐标;W为AUV重力;Iyy为转动惯量;Muq,Muw,
假设1 航行过程中AUV的速度以经济航速稳定航行.
注1 因本文中所研究的问题为路径跟踪问题,对AUV到达路径时间无明确要求,因而对前向速度控制无特殊要求.此外,为确保AUV的续航性,执行任务时往往以经济航速前行,同时前向速度通常具有单独控制系统,稳定航行波动较小,因而本文中作出上述假设.
2 控制器设计
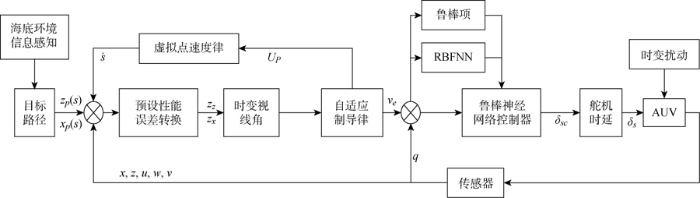
为实现水下机器人深度面路径跟踪目标,本文分别从运动学和动力学入手进行控制器设计.首先,基于预设性能函数进行误差转换,随后在转换系统基础上设计相应的虚拟点速度及预设性能制导律用以引导水下机器人趋近目标路径.同时,考虑系统所存在时滞特性,为确保水下机器人可与参考输入姿态同步,基于RBF神经网络(RBFNN)和自适应技术设计了鲁棒动力学控制器,具体控制框图如图2所示.
图2
图2
基于预设性能制导律的鲁棒时滞控制器框图
Fig.2
Block diagram of the prescribed performance guidance law based robust time-delay controller
2.1 运动学设计
预设性能控制技术由Bechlioulis等[17]于2008年提出,其本质是通过预设性能误差转换将具有受限误差的原始系统转换为一新系统.通过设计控制器镇定这一系统,可确保误差全过程处于给定界限内.本文中所给定预设性能误差范围如下:
式中:i=x, z;ei,l,ei,u分别为预设性能上下界限.ei,l(t)=(ρli0-ρli∞)
注2 显然性能函数会从初值ρ*i0以指数速度趋近于ρ*i∞,这一收敛速度也是系统误差收敛速度的下界,ρ*i∞是系统误差在稳态阶段的上界,适当选取这一参数使得其小于目标路径与海底的深度差,可对航行安全起到保障作用.此外,为确保预设性能界限不被违背,ρ**0的选取必须确保ρ**0>
为后续预设性能控制技术实施,引入如下预设性能函数[22]:
式中:i=x, z; ei为原始系统误差变量; p(ei)为随误差切换的变量,其定义为p(ei)=
基于预设性能函数可将原始路径跟踪系统的误差方程重构为如下新系统:
式中:i=x, z.为便于后续表达,记λi=
注3 为简化控制器设计,使其结构更为简捷,便于实艇移植验证,本文中令ex,u=ex,l= ez,u=ez,l=elim=(ρ0-ρ∞)e-ξt+ρ∞.由于这是由控制工程师预设的性能界限,通过调整参数ρ*i0、ρ*i∞、ξ*i即可实现这一要求.
在这一转换系统的基础之上,可设计虚拟速度律和制导律,为AUV路径跟踪控制提供参考输入,引导AUV趋近于目标路径.定义时变视线制导角为vTLOS=arctan
求导可得:
同时,注意到:
将式(11)代入式(12)~(15),可化为
根据上式,可设计运动学控制律如下:
式中:k1和k2为待整定控制参数.
考虑到:
进一步可得所跟踪虚拟点的俯仰角速度为
注4 若所设计的制导律是连续且非奇异的,则控制过程中AUV不会因参考俯仰角速度跳变而造成控制性能振荡.证明如下:
式(18)中仅考虑ve-vTLOS这一分母项,确实会在ve→vTLOS出现奇异现象,但是由于在控制器设计中引入了sinve-sinvTLOS这一分子项可以避免这一问题,此时,
由等价无穷小可知
进而避免了奇异现象,确保了制导律的连续性和非奇异性.
2.2 动力学设计
运动学层面给出了参考的俯仰角,若水下机器人姿态角可与参考角实时匹配,则会逐渐向目标路径收敛,且收敛过程中的误差时刻处于预设的上下界内.为实现这一目标,下一步将在动力学层面设计相应的控制律.定义俯仰角跟踪误差为qe=q-qd,选择第2个李雅普诺夫函数:
对其求导可得:
结合其时滞动力学模型的特性,利用线性化反馈技术可设计如下动力学控制器:
式中:k3为一待设定正常数.值得一提的是,在实际控制过程中,尤其是小型水下机器人所搭载的传感器往往是有限的,且感知精度难以得到保障.因此
式中:ω*为理想权值;ϑ为有界高斯基;
式中:τNN=-ϑ, 其自适应律 =qeϑ(k4为控制参数).由于神经网络逼近误差
2.3 稳定性分析
定理 在假设1条件下,水下自主机器人系统式(4)在所设计虚拟点速度律式(17)、预设性能制导律式(18)和考虑时滞的鲁棒神经网络控制器式(26)作用下,通过适当选取参数可实现深度面路径跟踪需求,路径跟踪位姿误差渐近稳定收敛,并且深度和前向误差时刻处于预设性能界限内.
证明 选取最终的李雅普诺夫预选函数为
对其求导可得:
代入所设计的制导律及控制律可得:
代入所设计自适应律可得:
注5 若要确保系统稳定,参数选取需要满足k1>ξ,k2>0,k3>0.此外还需制导系数0<ke<
显然,若控制参数选取满足注5所述要求,可得
注6 从工程实践角度,考虑到机器人执行任务时由水面开始下潜,初始纵倾角θ(0)接近0°,且此时下潜态势尚未形成,攻角α(0)可近似为0°.同时,恰当选取参数ke可使vTLOS(0)很小,通过选取合适的目标路径虚拟点初始位置,可使得ve(0)-vTLOS(0)=0.因此,若系统初始误差处于Ω=
3 仿真研究
为验证本文中所提出控制算法的有效性,利用REMUS自主水下机器人作为研究对象开展仿真试验,其模型参数如表1所示.仿真中施加时变海流干扰,其对应的数学表达式为τdq=0.005d,d=1+0.1sin 0.25t.
表1 仿真对象水动力模型参数表
Tab.1
| 参数 | 取值 |
|---|---|
| m/kg | 30.48 |
| W/N | 299 |
| B/N | 306 |
| Iyy/(N·kg·m2) | 3.45 |
| xg/m | 0 |
| zg/m | 0.019 6 |
| -4.88 | |
| -1.93 | |
| Mw|w|/kg | 3.18 |
| Mq|q|/(kg·m2·rad-2) | -188 |
| Muq/(kg·m·rad-1) | -2 |
| Muw/kg | 24 |
| Muuδ/(kg·rad-1) | -6.15 |
| -35.5 | |
| zw|w|/(kg·m-1) | -131 |
| zq|q|/(kg·m2·rad-2) | -0.632 |
| zuw/(kg·m-1) | -28.6 |
| zuq/(kg·rad-1) | -5.22 |
| λδ/s | 1.2 |
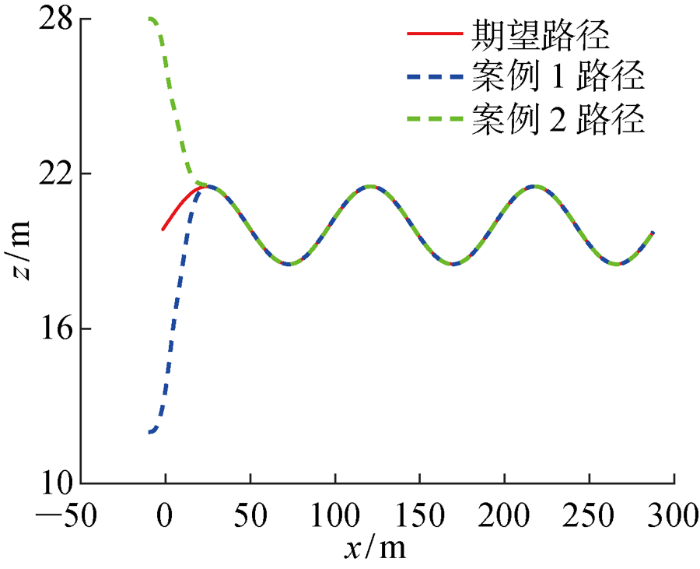
仿真过程中令机器人跟踪一深度面变深路径,用以模拟水下机器人起伏地形航行.同时为更好地测试所提控制器性能,令机器人从两个不同初始位姿出发,形成两个仿真案例,对应初始状态分别为:案例1 [x(0) z(0) θ(0)]T=[-10m 12m 0°]T,案例2 [x(0) z(0) θ(0)]T=[-10m 28m 0°]T.机器人速度的初始状态为 [u(0) w(0) q(0)]T=[1.5m/s 0m/s 0m/s]T,稳定航行前向速度为1.5 m/s.同时,考虑到为保证舵的响应和对执行机构的保护,工程实践中一般将水下机器人舵角限幅在30° 以内,因此本仿真将实际执行器机构饱和限幅为30°.控制器设计参数选取为k1=1, k2=1, k3=0.5, k4=0.005, k5=2, ke=1.5.预设性能参数为ρ0=12.5, ρ∞=1.25, ξ=0.1.
仿真结果如图3~8所示.同时,为更好地评价所设计控制器的表现,本文中采用下式计算控制性能指标:
式中:t0和t∞分别为开始和结束时间;MAEx为前向通道的平均绝对误差;MAEz为垂向通道的平均绝对误差,用以衡量控制器的响应能力;MIA为平均积分绝对值,可用于测量控制输入所带来的消耗;MTV为平均变化绝对值,可用于评价控制舵角的平滑性.
图3
图4
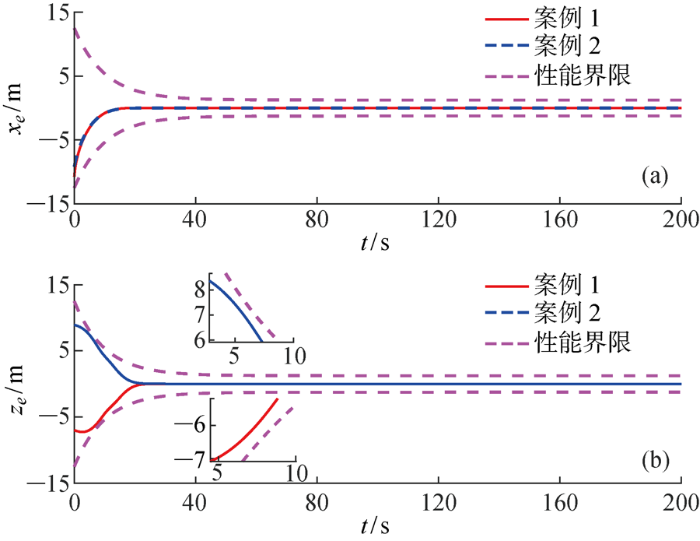
图4
系统状态误差及预设性能界限图
Fig.4
Path following errors and prescribed performance limits of different cases
图5
图6
图7
图8
由图3可以看出,所设计的控制器会趋使水下机器人迅速向目标路径收敛,且即使在不同初始状态一样可起到作用.各自由度的具体误差曲线在图4中给出,可见误差时刻处于所限定的性能区域内,进一步证实了预设性能策略的有效性.此外,由图4和表2可以看出,得益于预设性能控制技术对收敛速度下界的约束,可以实现误差的快速收敛.图5刻画了系统的潜伏角误差跟踪曲线,显然水下机器人经过短暂调整后潜伏角跟踪误差会趋近于0°.由图6和图7可以看出,由于执行机构的时滞迟特性,真实舵角需要延迟几个周期才可达到所给控制指令,但即使是在这种情况下,所设计的时滞控制器仍可保证路径跟踪控制的效果.此外,结合表2中的MIA及MTV指标可以看出,除了初期的误差较大时控制舵角会有较大波动外,其总体的能量较小、信号较为平滑.图8给出了速度时历曲线,在前期收敛过程由于水下机器人姿态有较大变化,相应垂向速度和俯仰速度略有波动, 但在抵达路径后速度仅跟随周期性路径而平稳变化.
表2 控制性能指标
Tab.2
| 初始状态 | txs/s | tzs/s | MAEx/m | MAEz/m | MIA/(°) | MTV/(°) |
|---|---|---|---|---|---|---|
| (-10 m, 12 m, 0°)T | 15.1 | 22.1 | 0.1912 | 0.1912 | 0.0790 | 0.0031 |
| (-10 m, 12 m, 0°)T | 16.1 | 22.0 | 0.1943 | 0.1945 | 0.0762 | 0.0030 |
由式(30)计算得到的性能参数如表2所示.表中tis(i=x, z)为到达时间, 即系统误差收敛至小于0.1 m的时间,用于表征误差收敛的快速性.
4 结语
考虑执行器固有时滞特性,为实现水下机器人近海底起伏地形航行作业过程中的路径跟踪,本研究引入预设性能控制技术以确保前向跟踪及垂向跟踪精度可时刻处于设定范围内. 在运动学阶段设计了虚拟点速度律以及预设制导律用以引导机器人在兼顾瞬态性能的前提下趋向目标路径.随后,为确保水下机器人可达到参考输入姿态角,在动力学阶段基于RBF神经网络及自适应技术设计了鲁棒时滞动力学控制器,达到期望的路径跟踪性能.最后,通过李雅普诺夫稳定性理论证明了闭环系统中信号的有界性.仿真结果进一步证实了所设计控制器可确保水下机器人完成起伏地形下的路径跟踪任务,同时跟踪误差时刻处于预设性能范围之内,有利于提高航行安全性能.
参考文献
Finite-time consensus of nonlinear multi-agent system with prescribed performance
[J].DOI:10.1007/s11071-017-4020-1 URL [本文引用: 1]
基于反步法的欠驱动水下机器人鲁棒定深控制
[J].
Robust depth control of under-actuated underwater vehicles based on backstepping
[J],
Robust path-following of underactuated ships: Theory and experiments on a model ship
[J].DOI:10.1016/j.oceaneng.2005.07.011 URL [本文引用: 1]
Fuzzy unknown observer-based robust adaptive path following control of underactuated surface vehicles subject to multiple unknowns
[J].DOI:10.1016/j.oceaneng.2019.02.017 URL [本文引用: 1]
基于速变LOS的无人船反步自适应路径跟踪控制
[J].
Tracking control of backstepping adaptive path of unmanned surface vessels based on surge-varying LOS
[J].
Guidance-error-based robust fuzzy adaptive control for bottom following of a flight-style AUV with saturated actuator dynamics
[J].DOI:10.1109/TCYB.2018.2890582 URL [本文引用: 1]
Path following of a surface vessel with prescribed performance in the presence of input saturation and external disturbances
[J].DOI:10.1109/TMECH.2017.2756110 URL [本文引用: 1]
Robust adaptive control of uncertain nonlinear systems
[J].DOI:10.1109/TAC.2011.2122730 URL [本文引用: 1]
Fault tolerant finite-time leader-follower formation control for autonomous surface vessels with LOS range and angle constraints
[J].DOI:10.1016/j.automatica.2016.01.064 URL [本文引用: 1]
Neural adaptive robust control of underactuated marine surface vehicles with input saturation
[J].DOI:10.1016/j.apor.2015.09.010 URL [本文引用: 1]
Safety performance monitoring of autonomous marine systems
[J].DOI:10.1016/j.ress.2016.11.024 URL [本文引用: 1]
Design and evaluation of a driving mode decision algorithm for automated driving vehicle on a motorway
[J].
Development of safety envelopes and subsea traffic rules for autonomous remotely operated vehicles
[J].DOI:10.1016/j.jlp.2019.03.006 URL [本文引用: 1]
智能水下机器人自救模糊专家系统研究
[J].
Fuzzy expert system of AUV self rescue
[J].
AUV主动应急自救机制与策略
[J].
AUV emergency self-rescue mechanism and strategy
[J].
Distributed finite-time fault-tolerant containment control for multiple ocean bottom flying node systems with error constraints
[J].DOI:10.1016/j.oceaneng.2019.106341 URL [本文引用: 1]
Distributed adaptive fixed-time consensus tracking for second-order multi-agent systems using modified terminal sliding mode
[J].DOI:10.1016/j.amc.2017.05.049 URL [本文引用: 1]
Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance
[J].DOI:10.1109/TAC.2008.929402 URL [本文引用: 2]
Adaptive neural network control of underactuated surface vessels with guaranteed transient performance: Theory and experimental results
[J].DOI:10.1109/TIE.2019.2914631 URL [本文引用: 1]
Adaptive neural control of underactuated surface vessels with prescribed performance guarantees
[J].DOI:10.1109/TNNLS.2018.2876685 URL [本文引用: 1]
Moving path following control for a surface vessel with error constraint
[J].DOI:10.1016/j.automatica.2020.109040 URL [本文引用: 1]