基于FAHP法和区间数改进TOPSIS法的盾构隧道下穿建筑物风险评估

doi:10.16183/j.cnki.jsjtu.2021.018

基于FAHP法和区间数改进TOPSIS法的盾构隧道下穿建筑物风险评估

陈仁朋¹^,²^,³, 王志腾¹^,²^,³, 吴怀娜^,¹^,²^,³, 刘源¹^,²^,³, 孟凡衍¹^,²^,³

1.湖南大学地下空间开发先进技术研究中心

2.建筑安全与节能教育部重点实验室

3.土木工程学院, 长沙 410082

Risk Assessment for Shield Tunneling Beneath Buildings Based on Interval Improved TOPSIS Method and FAHP Method

CHEN Renpeng¹^,²^,³, WANG Zhiteng¹^,²^,³, WU Huaina^,¹^,²^,³, LIU Yuan¹^,²^,³, MENG Fanyan¹^,²^,³

1. Research Center of Underground Space Advance Technology

2. Key Laboratory of Building Safety and Energy Efficiency of the Ministry of Education

3. College of Civil Engineering, Hunan University, Changsha 410082, China

通讯作者: 吴怀娜,女,教授,电话(Tel. ):0731-88821441;E-mail:wuhn@hnu.edu.cn.

责任编辑: 孙启艳

收稿日期: 2021-01-18

基金资助:

国家自然科学基金重点项目(51938005)
湖南省创新平台与人才计划-湖湘高层次人才聚集工程-创新团队项目(2019RS1030)

Received: 2021-01-18

作者简介 About authors

陈仁朋(1972-),男,浙江省衢州市人,教授,博士生导师,现主要从事地下空间灾变控制研究.

摘要

为评估盾构隧道施工对邻近建筑物的影响,提出一种基于模糊层次分析法(FAHP)和区间数改进优劣解距离(TOPSIS)法相结合的风险评估方法.通过调研建立基于土体性质、建筑物因素、隧道因素、盾构掘进参数等影响因素为主的风险评估体系,基于专家打分利用FAHP判断因素权重.利用传统TOPSIS法,根据因素分级标准选取6个典型样本,确定非等分风险等级判断标准.首次将区间数改进TOPSIS法运用到盾构隧道下穿建筑物的风险评估中,采用区间数描述工程情况.该评估过程均采用量化方式,比传统风险评估方法的准确性更高,受主观因素影响较少,客观性更强.利用该方法对某砌体建筑物进行风险评估,结果与实际情况相符,证明了该方法的有效性,可为类似工程风险评估提供参考.

关键词： 盾构隧道; 模糊层次分析法; TOPSIS法; 风险评估

Abstract

In order to evaluate the impact of shield tunnel construction on adjacent buildings, a method based on the fuzzy analytic hierarchy process (FAHP) and the interval number improvement technique for order preference by similarity to ideal solution (TOPSIS) is proposed. A risk assessment system based on soil properties, building factors, tunnel factors, shield tunneling parameters, and other factors is established after investigation. The FAHP is used to determine the weight of factors based on expert scoring. Based on the traditional TOPSIS method, 6 typical samples are selected according to the factor grading standard to determine the non-uniform risk rating criteria. For the first time, the interval improved TOPSIS method is applied to the risk assessment of shield tunneling beneath buildings. The engineering situation can be better represented by the interval number. Compared with traditional risk assessment methods, this method is more accurate, less affected by subjective factors, and more objective. The proposed method has been used to evaluate the risk of a certain masonry building, and the result is consistent with the actual situation, which proves its effectiveness of. Thus, the proposed method can provide reference for risk assessment of similar projects.

Keywords： shield tunnel; fuzzy analytic hierarchy process (FAHP); technique for order preference by similarity to ideal solution (TOPSIS); risk assessment

PDF (1682KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈仁朋, 王志腾, 吴怀娜, 刘源, 孟凡衍. 基于FAHP法和区间数改进TOPSIS法的盾构隧道下穿建筑物风险评估[J]. 上海交通大学学报, 2022, 56(12): 1710-1719 doi:10.16183/j.cnki.jsjtu.2021.018

CHEN Renpeng, WANG Zhiteng, WU Huaina, LIU Yuan, MENG Fanyan. Risk Assessment for Shield Tunneling Beneath Buildings Based on Interval Improved TOPSIS Method and FAHP Method[J]. Journal of Shanghai Jiaotong University, 2022, 56(12): 1710-1719 doi:10.16183/j.cnki.jsjtu.2021.018

随着城市地铁建设的发展,越来越多的地铁隧道采用盾构法施工.盾构掘进过程由于盾尾土体损失、开挖面支护力过大或不足、盾壳与地层摩擦,会不可避免地造成地层变形,进而引发上部建筑物不均匀沉降或隆起,严重时可造成建筑物开裂损坏.因此,地铁盾构施工对周围建筑物的风险评估是非常重要的研究课题.

近年来,盾构隧道下穿建筑物的风险评估已成为国内外学者的研究热点之一^[1⇓-3].于丹丹等^[2]分析了地铁隧道施工对邻近建筑物的影响因素,利用可变模糊集理论构建风险模型,确定风险等级;魏纲等^[3]将层次分析法引入对盾构隧道邻近建筑物的安全风险评估中,结合模糊综合评价法获得评价等级;王烨晟等^[4]利用模糊综合评价法对影响建筑物安全的各因素进行半定量分析.上述风险评估方法虽然取得一定效果,但权重确定过程较粗糙,主观性强且准确性不高.相较于传统层次分析法,模糊层次分析法(FAHP)在计算步骤等方面进行了改进,用模糊数替代具体数值进行计算.隧道工程问题不确定因素较多且受主观因素影响,用模糊数计算更能准确反映专家想法,从而科学合理地分配各因素权重.

传统风险评估方法过于主观,风险分级的确定需要人为设定隶属函数或者依照均匀等分风险分级标准划分,而优劣解距离(TOPSIS)法受主观因素影响较少,无需人为设定隶属函数,可以根据计算得出具体非等分风险分级标准,相较于均匀等分风险分级标准,计算结果也更为客观准确.目前运用TOPSIS法确定风险等级已被广泛应用到风险评估中^[5-6],针对具体工程风险评估时,因地下工程的不确定性,区间数可以更准确地反映风险因素的取值范围.

本文基于FAHP和区间数改进TOPSIS法相结合的盾构隧道下穿建筑物风险评估方法,建立新的风险指标体系,以某砌体建筑物为例进行分析,研究成果对类似工程案例具有参考意义.

1 盾构隧道下穿建筑物风险评估原理

结合FAHP和区间数改进TOPSIS法评估盾构隧道下穿建筑物风险,其基本原理如下:首先,确定盾构隧道下穿建筑物的主要风险因素,运用FAHP法把风险因素层层分级,通过专家打分赋予因素权重;其次,通过参考相关文献及规范结合专家意见,明确各因素风险分级标准,根据具体工程背景确定相关因素风险取值范围;再次,根据确定的各因素风险分级标准,运用传统TOPSIS法计算出以相对接进度(E⁺)作为评判工程整体风险等级标准;最后,利用区间数改进TOPSIS法对具体工程进行计算,得出相对接近度,结合风险评级标准得出风险等级.

1.1 FAHP原理

1.1.1 判断矩阵构造

组织专家在熟悉实际工程的情况下,识别各层次风险因素,构建多层次模型.再由专家评审团根据表1所示的因素重要性评判标准,对因素进行评判,确定所对应的模糊数a=(l, m, u),其中l、m、n代表模糊数的3个无量纲参数.

根据打分结果构造 $n$ 阶判断矩阵:

\begin{array}{l} A = (a_{i j})_{n \times n} = (\begin{array}{l} a_{11} & a_{12} & \dots & a_{1 n} \\ a_{21} & a_{22} & \dots & a_{2 n} \\ \dots & \dots & \dots & \dots \\ a_{n 1} & a_{n 2} & \dots & a_{n n} \end{array}) \\ i = 1, 2, \dots, n; j = 1, 2, \dots, m \end{array}

其中: $a_{i j}$ 表示因素 $C_{i}$ 相比于因素 $C_{j}$ 的重要程度. $a_{i j}$ 的值越大,表示因素 $C_{i}$ 相比于因素 $C_{j}$ 的重要性越大. $a_{i j}$ 取值根据表1得到.

表1 因素重要性评判标准

Tab.1 The criteria factor importance

语言描述	a	l	m	u
同等重要	$\tilde{1}$	1	1	1
稍微重要	$\tilde{3}$	1	3	5
明显重要	$\tilde{5}$	3	5	7
强烈重要	$\tilde{7}$	5	7	9
极端重要	$\tilde{9}$	7	9	9
稍微不重要	${\tilde{3}}^{- 1}$	$\frac{1}{5}$	$\frac{1}{3}$	1
明显不重要	${\tilde{5}}^{- 1}$	$\frac{1}{7}$	$\frac{1}{5}$	$\frac{1}{3}$
强烈不重要	${\tilde{7}}^{- 1}$	$\frac{1}{9}$	$\frac{1}{7}$	$\frac{1}{5}$
极端不重要	${\tilde{9}}^{- 1}$	$\frac{1}{9}$	$\frac{1}{9}$	$\frac{1}{7}$

新窗口打开| 下载CSV

1.1.2 因素的模糊权重确定

计算因素权重主要分为3步.

步骤一计算综合模糊值.

定义因素C_i的综合模糊值D_i为

(1)

D_{i} = \overset{n}{\sum_{j = 1}} a_{i j} \otimes {(\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} a_{i j})}^{- 1}

(2)

\overset{n}{\sum_{j = 1}} a_{i j} = (\overset{n}{\sum_{j = 1}} l_{i j}, \overset{n}{\sum_{j = 1}} m_{i j}, \overset{n}{\sum_{j = 1}} u_{i j})

(3)

\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} a_{i j} = (\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} l_{i j}, \overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} m_{i j}, \overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} u_{i j})

(4)

{(\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} a_{i j})}^{- 1} = (\frac{1}{\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} u_{i j}}, \frac{1}{\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} m_{i j}}, \frac{1}{\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} l_{i j}})

步骤二去模糊化.

$a_{1} = (l_{1}, m_{1}, u_{1}), a_{2} = (l_{2}, m_{2}, u_{2})$ 为两个三角模糊数,则 $a_{1} \geq a_{2}$ 的可能性定义为

(5)

\begin{array}{l} P (a_{1} \geq a_{2}) = \\ \{\begin{array}{l} 1, & m_{1} \geq m_{2} \\ \frac{l_{2} - u_{1}}{(m_{1} - u_{1}) - (m_{2} - l_{2})}, & u_{1} \geq l_{2}, m_{1} < m_{2} \\ 0, & 其 他 \end{array} \end{array}

步骤三获得权重.

一个模糊数大于其他k个模糊数的可能度(d)定义为:

(6)

\begin{array}{l} d (C) = P (D \geq D_{1}, D_{2}, \dots, D_{k}) = \\ m i n P (D \geq D_{i}) \end{array}

式中:C为因素;D为综合模糊值.

通过上述计算得到各因素权重为

(7)$W=(d(C_{1})d(C_{2})...d(C_(n)))^{t}$

标准化后,最终权重为

(8)

\begin{matrix} W = (w_{1} w_{2} \dots w_{n})^{T} \end{matrix}

式中:w₁为第1个因素所代表的最终权重;w_n为第n个因素所代表的最终权重.

1.2 区间数改进TOPSIS法原理

1.2.1 传统TOPSIS法

通过传统TOPSIS法计算出以相对接近度E⁺作为风险分级标准,具体计算步骤如下.

步骤一构造风险因素评价矩阵.

针对n个评价方案,分别对应m个评价指标,构造评价矩阵:

(9)

\begin{matrix} R = (r_{i j})_{n \times m} = [\begin{array}{l} r_{11} & r_{12} & \dots & r_{1 m} \\ r_{21} & r_{22} & \dots & r_{2 m} \\ \dots & \dots & \dots & \dots \\ r_{n 1} & r_{n 2} & \dots & r_{n m} \end{array}] \end{matrix}

式中: $r_{i j} 为第 i 个评价方案的第 j$ 个评价指标.

步骤二构造加权风险因素评价矩阵.

对因素之间进行比较,对初始风险因素评价矩阵R进行归一化,并与相应因素权重相乘,得到加权风险因素评价矩阵:

(10)

\begin{array}{l} V = (v_{i j})_{n \times m} = [\begin{array}{l} v_{11} & v_{12} & \dots & v_{1 m} \\ v_{21} & v_{22} & \dots & v_{2 m} \\ \dots & \dots & \dots & \dots \\ v_{n 1} & v_{n 2} & \dots & v_{n m} \end{array}] \\ v_{i j} = w_{j} s_{i j} \end{array}

(11)

s_{i j} = \frac{r_{i j}}{\sqrt{\overset{n}{\sum_{i = 1}} r_{i j}^{2}}}

式中: $w_{j}$ 为由式(8)计算得到的最终权重; $v_{i j} 和 s_{i j}$ 为归一化后的第i个评价方案的第j个评价指标.因素权重可由模糊层次分析法得到.

步骤三确定风险最小方案和风险最大方案.

根据加权规范矩阵,确定风险最小方案A⁺和风险最大方案A^-,分别为

(12)

A^{+} = {(\underset{i}{m a x} v_{i j} |j \in J_{1}), (\underset{i}{m i n} v_{i j} |j \in J_{2} |i \in n)} = [v_{1}^{+} v_{2}^{+} \dots v_{m}^{+}]

(13)

A^{-} = {(\underset{i}{m i n} v_{i j} |j \in J_{1}), (\underset{i}{m a x} v_{i j} |j \in J_{2} |i \in n)} = [v_{1}^{-} v_{2}^{-} \dots v_{m}^{-}]

式中: $J_{1}$ 为正向指标,即指标越大越好; $J_{2}$ 为负向指标,即指标越低越好; $v_{1}^{+}$ 为在归一化后的矩阵V中第一行中数值最大的值; $v_{m}^{+}$ 为第m行中数值最大的值; $v_{1}^{-}$ 为在归一化后的矩阵V中第一行中数值最小的值; $v_{m}^{-}$ 为第m行中数值最小的值.

步骤四计算评价方案与风险最小(大)方案距离.

(14)

\begin{array}{l} \begin{matrix} z_{i}^{+} = \sqrt{\overset{m}{\sum_{j = 1}} (v_{i j} - v_{j}^{+})^{2}} \end{matrix} \end{array}

(15)

z_{i}^{-} = \sqrt{\overset{m}{\sum_{j = 1}} (v_{i j} - v_{j}^{-})^{2}}

式中: $z_{i}^{+} 为 i 方案与风险最小方案的距离; z_{i}^{-} 为 i$ 方案与风险最大方案的距离.

步骤五计算相对接近度.

(16)

\begin{matrix} E_{i}^{+} = \frac{z_{i}^{-}}{z_{i}^{-} + z_{i}^{+}} \end{matrix}

式中: $E_{i}^{+}$ 为相对接近度,取值范围为[0, 1],越接近1表示该方案越理想,风险越小,越接近0表示该方案越差,风险越大.

通过不同风险方案计算,得到不同的相对接近度,由此形成以相对接近度为标准的风险评价等级.结合具体工程,采用区间数改进TOPSIS法计算该工程的相对接近度,判断该工程的具体风险等级.

1.2.2 区间数改进TOPSIS法

传统TOPSIS法只能采用具体数值进行评估分析,某些情况下,由于数据的不完整和不确定性,难以获得精确数值,引入区间数改进TOPSIS法可以增加评估准确性和实用性.采用区间数改进TOPSIS法评估工程风险,根据相对接近度判断风险等级.定义区间数为

(17)

\hat{x} = (\underline{x}, \bar{x}) = {x |\underline{x} \leq x \leq \bar{x}, |\underline{x}, \bar{x} \in R}

具体计算步骤如下.

步骤一构造评价矩阵.针对n个评价方案,且分别对应m个评价指标,构造评价矩阵:

(18)

\begin{matrix} N = ({\hat{x}}_{i j})_{n \times m} = [\begin{array}{l} {\hat{x}}_{11} & {\hat{x}}_{12} & \dots & {\hat{x}}_{1 m} \\ {\hat{x}}_{21} & {\hat{x}}_{22} & \dots & {\hat{x}}_{2 m} \\ \dots & \dots & \dots & \dots \\ {\hat{x}}_{n 1} & {\hat{x}}_{n 2} & \dots & {\hat{x}}_{n m} \end{array}] \end{matrix}

步骤二矩阵归一化.

根据因素属性的不同,归一化方法分为两种.

针对优势型因素,归一化方法为

(19)

\begin{matrix} {\hat{r}}_{i j} = (\frac{{\underline{x}}_{i j}}{m a x ({\bar{x}}_{i j})}, \frac{{\bar{x}}_{i j}}{m a x ({\bar{x}}_{i j})}) \end{matrix}

针对劣势型因素,归一化方法为

(20)

\begin{matrix} {\hat{r}}_{i j} = (1 - \frac{{\bar{x}}_{i j}}{m a x ({\bar{x}}_{i j})}, 1 - \frac{{\underline{x}}_{i j}}{m a x ({\bar{x}}_{i j})}) \end{matrix}

式中: ${\overset{^{}}{r}}_{i j}$ 为归一化后的第i个评价方案的第j个评价指标.

步骤三确定风险最小方案和风险最大方案.

(21)

A^{+} = {(\underset{i}{m a x} {\bar{r}}_{i j} |j \in J_{1}), (\underset{i}{m i n} {\underline{r}}_{i j} |j \in J_{2} |i \in n)} = [r_{1}^{+} r_{2}^{+} \dots r_{m}^{+}]

(22)

A^{-} = {(\underset{i}{m i n} {\underline{r}}_{i j} |j \in J_{1}), (\underset{i}{m a x} {\bar{r}}_{i j} |j \in J_{2} |i \in n)} = [r_{1}^{-} r_{2}^{-} \dots r_{m}^{-}]

式中: $r$ 可由式(19)和式(20)计算得到.

步骤四计算与风险最小(大)方案距离.

(23)

\begin{array}{l} d_{i}^{+} = \sqrt{\frac{1}{2} \overset{m}{\sum_{j = 1}} w_{j} ({|r_{j}^{+} - {\underline{r}}_{i j}|}^{2} + {|r_{j}^{+} - {\bar{r}}_{i j}|}^{2})} \end{array}

(24)

d_{i}^{-} = \sqrt{\frac{1}{2} \overset{m}{\sum_{j = 1}} w_{j} ({|r_{j}^{-} - {\underline{r}}_{i j}|}^{2} + {|r_{j}^{-} - {\bar{r}}_{i j}|}^{2})}

式中: $d_{i}^{-} 为评价方案与风险最大方案的距离; d_{i}^{+}$ 为评价方案与风险最小方案的距离.

步骤五计算相对接近度.

(25)

\begin{matrix} E_{i}^{+} = \frac{d_{i}^{-}}{d_{i}^{-} + d_{i}^{+}}, 0 \leq E_{i}^{+} \leq 1 \end{matrix}

2 盾构隧道下穿建筑物风险评估流程及指标体系

2.1 风险评估流程

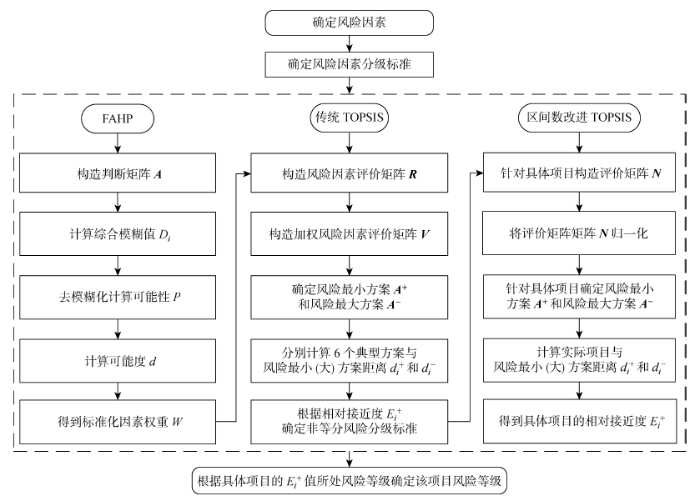
风险评估流程主要分为3个阶段,每一个阶段分别应用一种方法.首先,结合专家意见和相关资料,运用FAHP确定风险因素权重;其次,根据因素分级标准,从因素最好值到最差值依次选取6组数据,构建6个典型样本,运用TOPSIS法计算得出6个典型样本的 $E^{+} 值, 确定基于相对接近度 E^{+}$ 的非等分风险分级标准;最后,针对具体工程项目,运用区间数改进TOPSIS法,确定项目的相对接近度E⁺,再根据风险分级标准,确定项目的风险等级.具体风险评估流程如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 风险评估流程图

Fig.1 Flow chart of risk assessment

2.2 风险评估指标体系

根据文献[7-8]及《GB 50652—2011城市轨道交通地下工程建设风险管理规范》^[9]等相关规范,确定盾构隧道下穿建筑物风险评级因素:土体性质、建筑物因素、隧道因素和盾构掘进参数.从4个方面分析盾构掘进对上部建筑物的安全影响.

汇总10位专家对因素之间相对重要性的评判结果后,通过式(1)~(8)对各层次因素进行权重计算,得到因素权重如表2所示.土地性质中,内摩擦角为基础底面接触土层的内摩擦角;黏聚力为基础底面接触土层的黏聚力;压缩模量为基础底面接触土层的压缩模量;地下水深度指从地表到地下水位的距离;复合地层指在同一位置处存在两种及以上地层;软硬交界指软弱地层与硬岩存在交界;特殊地质指是否存在岩溶、断裂构造等.建筑物因素中,基础形式为建筑物基础类型,包括桩基础、条形基础、筏板基础等;上部结构形式为建筑物上部结构材料的不同形式;重要性程度根据建筑物的使用及用途划分,建筑物重要性程度越大,造成的损失就越大,风险等级越高;完损现状为建筑物的完整度,即是否受到损伤.隧道因素中,隧道直径为隧道的设计直径;隧道埋深为隧道中心距离地表的距离;隧道与建筑物的水平距离为隧道中心与建筑物形心的距离.盾构掘进参数均为盾构机下穿建筑物时的掘进参数值.

表2 风险因素权重分布

Tab.2 Weight distribution of risk factors

第一层次因素	权重	第二层次因素	权重	最终权重
土体性质	0.43	内摩擦角	0.14	0.060
		黏聚力	0.06	0.026
		压缩模量	0.14	0.060
		地下水深度	0.16	0.069
		复合地层	0.13	0.056
		软硬交界	0.19	0.082
		特殊地质	0.18	0.077
建筑物因素	0.23	基础形式	0.30	0.069
		上部结构形式	0.22	0.051
		重要性程度	0.27	0.062
		完损现状	0.21	0.048
隧道因素	0.23	隧道直径	0.20	0.046
		隧道埋深	0.47	0.108
		隧道与建筑物水平距离	0.33	0.076
盾构掘进参数	0.11	掘进速度	0.25	0.028
		推力	0.01	0.001
		转矩	0.02	0.002
		注浆量	0.39	0.043
		土仓压力	0.33	0.036

新窗口打开| 下载CSV

由表2可知,影响盾构隧道下穿建筑物风险的最重要的一级指标是土体性质,权重为0.43.其次分别是建筑物因素和隧道因素,权重均为0.23,所占权重最小的一级指标是盾构掘进参数,权重为0.11.经过与专家求证,权重计算结果符合专家的判断,证明了FAHP的有效性.

结合文献[5 ⇓⇓-8]及咨询相关专家意见,将盾构隧道下穿建筑物风险因素分为5级.1级表示安全,2级表示较安全,3级表示一般,4级表示较危险,5级表示危险.19个风险因素中有一部分因素可以直接量化,通过具体监测数据表示,如土体内摩擦角、黏聚力和压缩模量等.有些因素很难通过具体监测数据表示,只能通过专家评分,如复合地层、软硬交界和特殊地质等.相关风险因素分级如表3所示.

表3 风险指标因素分级

Tab.3 Classification of risk indicator factors

评价指标		指标取值
评价指标		1级	2级	3级	4级	5级
土体性质	内摩擦角/(°)	[25, 45]	[15, 25)	[10, 15)	[5, 10)	[0, 5)
	黏聚力/kPa	[20, 25]	[15, 20)	[10, 15)	[5, 10)	[0, 5)
	压缩模量/MPa	[40, 60]	[20, 40)	[10, 20)	[5, 10)	[0, 5)
	地下水深度/m	[30, 50]	[20, 30)	[10, 20)	[5, 10)	[0, 5)
	复合地层专家评分	[80, 100] 不存在复合地层	[60, 80) 间断存在复合地层	[40, 60) 水平方向存在复合地层	[20, 40) 垂直方向存在复合地层	[0, 20) 垂直水平方向均存在复合地层
	软硬交界专家评分	[80, 100] 不存在软硬交界	[60, 80) 间断存在其他形式软硬交界地层	[40, 60) 间断存在上软下硬地层	[20, 40) 存在其他形式软硬交界地层	[0, 20) 存在上软下硬地层
	特殊地质专家评分	[80, 100] 不存在特殊地质	[60, 80) 间断存在特殊地质	[40, 60) 存在其他种类特殊地质	[20, 40) 存在断裂构造地质	[0, 20) 存在岩溶地质
建筑物因素	基础形式专家评分	[80, 100] 桩基础	[60, 80) 箱型或筏板基础	[40, 60) 条形基础	[20, 40) 混合基础或毛石基础	[0, 20) 无基础或形式不详
	上部结构形式专家评分	[80, 100] 框剪结构	[60, 80) 现浇式框架结构	[40, 60) 装配式框架结构	[20, 40) 砖混结构	[0, 20) 木结构
	重要性程度专家评分	[0, 20) 简易、临时建筑物	[20, 40) 普通建筑物	[40, 60) 比较重要的公共建筑和居住建筑	[60, 80) 重要的公共建筑物	[80, 100] 具有历史性、代表性的重要建筑物
	完损现状专家评分	[80, 100] 完好	[60, 80) 基本完好	[40, 60) 一般损坏	[20, 40) 严重损坏	[0, 20) 危险
隧道因素	隧道直径/m	[0, 5)	[5, 8)	[8, 12)	[12, 16)	[16, 20]
	隧道埋深/m	[30, 40]	[20, 30)	[15, 20)	[10, 15)	[0, 10)
	隧道与建筑物水平距离/m	[30, 40]	[20, 30)	[10, 20)	[5, 10)	[0, 5)
盾构掘进参数	掘进速度/ (mm·min^-1)	[0, 15)	[15, 30)	[30, 45)	[45, 60)	[60, 75]
	推力/MN	[0, 10)	[10, 15)	[15, 20)	[20, 25)	[25, 35]
	转矩/(MN·m)	[0, 1)	[1, 2)	[2, 3)	[3, 4)	[4, 5]
	注浆量/m³	[0, 7)	[7, 10)	[10, 12)	[12, 15)	[15, 25]
	土仓压力×10^-5/Pa	[0, 0.9)	[0.9, 1.8)	[1.8, 2.7)	[2.7, 3.6)	[3.6, 4.5]

新窗口打开| 下载CSV

3 工程实例分析

3.1 工程概况

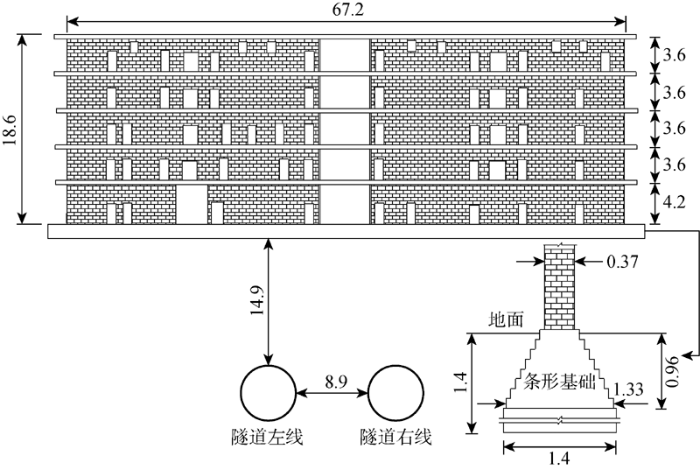
某地铁盾构隧道为双线平行隧道,隧道轴线相距14.9 m.施工过程下穿某砌体建筑物,该建筑物为6层砖混结构,长为67.2 m,高为18.6 m,由砖墙和砖柱承重.建筑物基础为墙下条形基础,基础埋深为1.4 m.建筑物主体部分位于隧道正上方,隧道顶部距建筑物基础14.9 m,隧道与建筑物相对位置关系如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 隧道与建筑物相对位置关系图(m)

Fig.2 Diagram of relative position of tunnel and building (m)

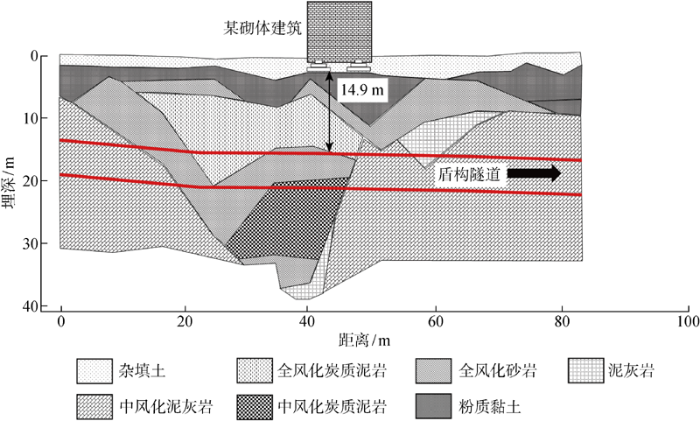
隧道左线沿线地质剖面如图3所示.场地地质条件复杂,最上层为杂填土,条形基础位于粉质黏土层,地层中分布着一定厚度的中风化、全风化炭质泥岩、泥灰岩及全风化砂岩.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 左线地质剖面图

Fig.3 Left geological profile

在建筑物正下方,全风化炭质泥岩、中风化炭质泥岩、全风化砂岩和中风化炭质泥岩均发生突变(见图3).根据勘察时水位观测情况,稳定水位埋深为0.00~9.60 m,略具承压性.

盾构隧道主要穿过中风化泥灰岩和全风化砂岩等土层.盾构机在掘进过程中主要掘进参数:掘进速度为45~60 mm/min,推力为 8~10 MN,刀盘转矩为 1000~2000 kN·m,土仓压力为 (1.6~2.6)×10⁵ Pa,注浆量为6~7 m³.

3.2 基于TOPSIS法计算风险分级

根据表3风险因素分级,取因素分级标准中最好值与最差值及相邻分级的交界值,建立6个典型样本,建立初始评价矩阵:

$\begin{array}{l} R = [\begin{array}{l} 45 & 25 & 15 & 10 & 5 & 0 \\ 25 & 20 & 15 & 10 & 5 & 0 \\ 60 & 40 & 20 & 10 & 5 & 0 \\ 50 & 30 & 20 & 10 & 5 & 0 \\ 100 & 80 & 60 & 40 & 20 & 0 \\ 100 & 80 & 60 & 40 & 20 & 0 \\ 100 & 80 & 60 & 40 & 20 & 0 \\ 100 & 80 & 60 & 40 & 20 & 0 \\ 100 & 80 & 60 & 40 & 20 & 0 \\ 100 & 80 & 60 & 40 & 20 & 0 \\ 100 & 80 & 60 & 40 & 20 & 0 \\ 0 & 5 & 8 & 12 & 16 & 20 \\ 40 & 30 & 20 & 15 & 10 & 0 \\ 40 & 30 & 20 & 10 & 5 & 0 \\ 0 & 15 & 30 & 45 & 60 & 75 \\ 0 & 10 & 15 & 20 & 25 & 35 \\ 0 & 1 & 2 & 3 & 4 & 5 \\ 0 & 7 & 10 & 12 & 15 & 25 \\ 0 & 0.9 & 1.8 & 2.7 & 3.6 & 4.5 \end{array}] \end{array}$

由式(10)~(11),计算得到加权规范矩阵: $\begin{array}{l} V = \\ {[\begin{array}{l} 0.0493 & 0.0274 & 0.0164 & 0.0110 & 0.0055 & 0.0000 \\ 0.0175 & 0.0140 & 0.0105 & 0.0070 & 0.0035 & 0.0000 \\ 0.0476 & 0.0317 & 0.0159 & 0.0079 & 0.0040 & 0.0000 \\ 0.0551 & 0.0330 & 0.0220 & 0.0110 & 0.0055 & 0.0000 \\ 0.0378 & 0.0302 & 0.0227 & 0.0151 & 0.0076 & 0.0000 \\ 0.0553 & 0.0442 & 0.0332 & 0.0221 & 0.0111 & 0.0000 \\ 0.0519 & 0.0415 & 0.0311 & 0.0208 & 0.0104 & 0.0000 \\ 0.0465 & 0.0372 & 0.0279 & 0.0186 & 0.0093 & 0.0000 \\ 0.0344 & 0.0275 & 0.0206 & 0.0138 & 0.0069 & 0.0000 \\ 0.0418 & 0.0334 & 0.0251 & 0.0167 & 0.0084 & 0.0000 \\ 0.0324 & 0.0259 & 0.0194 & 0.0129 & 0.0065 & 0.0000 \\ 0.0000 & 0.0077 & 0.0123 & 0.0185 & 0.0247 & 0.0309 \\ 0.0761 & 0.0571 & 0.0380 & 0.0285 & 0.0190 & 0.0000 \\ 0.0553 & 0.0415 & 0.0276 & 0.0138 & 0.0069 & 0.0000 \\ 0.0000 & 0.0038 & 0.0076 & 0.0113 & 0.0151 & 0.0189 \\ 0.0000 & 0.0002 & 0.0003 & 0.0004 & 0.0005 & 0.0007 \\ 0.0000 & 0.0003 & 0.0005 & 0.0008 & 0.0011 & 0.0013 \\ 0.0000 & 0.0089 & 0.0127 & 0.0153 & 0.0191 & 0.0318 \\ 0.0000 & 0.0049 & 0.0097 & 0.0146 & 0.0194 & 0.0243 \end{array}]}^{T} \end{array}$

由式(12)~(13),确定风险最小方案A⁺和风险最大方案A^-:

\begin{array}{l} A^{+} = [0.0493 0.0175 0.0476 0.0551 0.0378 0.0553 0.0519 0.0465 0.0344 0.0418 0.0324 0.0000 0.0761 0.0553 0.0000 0.0000 0.0000 0.0000 0.0000] \\ A^{-} = [0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0309 0.0000 0.0000 0.0189 0.0007 0.0013 0.0318 0.0243] \end{array}

根据式(14)~(15),计算典型样本分别与风险最小(大)方案的距离:

\begin{array}{l} z^{+} = {[0.0000 0.0499 0.0896 0.1216 0.1489 0.1819]}^{T} \\ z^{-} = {[0.1819 0.1349 0.0958 0.0638 0.0356 0.0000]}^{T} \end{array}

由式(16)计算相对接近度,得到各风险等级所对应的相对接近度,如表4所示.

表4 风险等级分级标准

Tab.4 Criteria of risk rating

风险等级	E⁺
1级	(0.7300, 1]
2级	(0.5165, 0.7300]
3级	(0.3440, 0.5165]
4级	(0.1930, 0.3440]
5级	[0, 0.1930]

新窗口打开| 下载CSV

根据相对接近度大小判断风险等级.其中1级表示安全,不需要采取措施进行防护;2级表示较安全,可以针对建筑物采取实时监测手段,必要时采取防护措施;3级表示一般,需采取必要的防护措施,并且加强实时监测;4级表示较危险,必须采取防护措施,进行实时监测,邀请相关专家实地考察并分析可能出现的损伤;5级表示危险,必须采取防护措施,进行实时监测,采集现场土样进行实验分析,根据现场情况和专家意见优化施工计划.

3.3 采用改进TOPSIS法风险评价

根据实际情况结合专家打分,确定某教学楼风险因素取值,如表5所示.

表5 某教学楼风险因素取值

Tab.5 Value of risk factors of a teaching building

风险因素	参数	取值
土体性质	内摩擦角/(°)	[16.5, 17.5]
	黏聚力/kPa	[5, 10]
	压缩模量/MPa	[5, 11]
	地下水深度/m	[1.5, 2]
	复合地层专家评分	[40, 50]
	软硬交界专家评分	[25, 45]
	特殊地质专家评分	[55, 65]
建筑物因素	基础形式专家评分	[45, 55]
	上部结构形式专家评分	[20, 40]
	重要性程度专家评分	[85, 95]
	完损现状专家评分	[55, 65]
隧道因素	隧道直径/m	[6, 6]
	隧道埋深/m	[16, 16.5]
	隧道与建筑物水平距离/m	[0, 0]
盾构掘进参数	掘进速度/(mm·min^-1)	[45, 60]
	推力/(MN)	[8, 14]
	转矩/(MN·m)	[1, 2]
	注浆量/m³	[6, 7]
	土仓压力×10^-5/Pa	[1.6, 2.6]

新窗口打开| 下载CSV

由式(19)~(20)构造归一化评价矩阵:

R = [(0.3667, 0.3889) (0.2000, 0.4000) (0.0833, 0.1833) (0.0300, 0.0400) (0.4000, 0.5000) (0.2500, 0.4500) (0.5500, 0.6500) (0.4500, 0.5500) (0.2000, 0.4000) (0.8500, 0.9500) (0.5500, 0.6500) (0.7000, 0.7000) (0.4000, 0.4125) (0.0000, 0.0000) (0.2000, 0.4000) (0.6000, 0.7714) (0.6000, 0.8000) (0.7200, 0.7600) (0.4222, 0.6444)]

根据式(21)~(22)确定风险最小(大)方案:

A⁺=[1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 0 0 0 0]

A^-=[0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1]

通过式(23)~(24)计算评价单元与风险最小(大)方案的距离:

\begin{array}{l} d^{+} = 0.6614 \\ d^{-} = 0.4478 \end{array}

由式(25)计算得出相对接近度:

E⁺=0.4037

通过改进TOPSIS法计算得到相对接近度为0.4037,根据表4确定风险等级为3级,即建筑物风险处于一般状态.结合实际施工情况,根据基于损伤现象的损伤评估,建筑物处于“轻微损伤”至“中等损伤”^[10],与风险评估结果相符,验证了评估方法的有效性.

4 结论

(1) 通过参考相关文献规范及咨询专家意见,确定盾构隧道下穿建筑物的主要影响因素,构建了包含土体性质、建筑物因素、隧道因素和盾构掘进参数的风险评估体系.根据风险因素不同,制定相应的分级标准,将因素分为5个等级.

(2) 利用传统TOPSIS法基于风险因素分级标准,确定基于相对接近度E⁺的非等分风险分级标准,相较传统等分风险分级标准更具科学性.

(3) 首次将区间数改进TOPSIS法应用于盾构隧道下穿建筑物风险评估中,采用区间数描述实际工程信息,更好地反映实际工程情况.

(4) 结合模糊层次分析法、TOPSIS法和区间数改进TOPSIS法形成了新的风险评估方法,评估过程均采用量化方式,相较于传统风险评估方法准确性更高,受主观因素影响较少,客观性更强.将该方法运用于某地铁下穿砖混结构的工程实例中,评估结果与实际相符,证明了该评估方法的有效性,可为类似工程风险评估提供参考.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

CLARKE

J A

, LAEFER

D F

Evaluation of risk assessment procedures for buildings adjacent to tunnelling works

[J]. Tunnelling and Underground Space Technology, 2014, 40: 333-342.

DOI:10.1016/j.tust.2013.10.014 URL [本文引用: 1]

[2]

于丹丹, 双晴.

地铁隧道施工邻近建筑物安全风险评价

[J]. 城市轨道交通研究, 2013, 16(4): 32-37.

[本文引用: 2]

Dandan

, SHUANG

Qing

Safety risk evaluation of adjacent buildings during metro tunneling construction

[J]. Urban Mass Transit, 2013, 16(4): 32-37.

[本文引用: 2]

[3]

魏纲, 周琰.

邻近盾构隧道的建筑物安全风险模糊层次分析

[J]. 地下空间与工程学报, 2014, 10(4): 956-961.

[本文引用: 2]

WEI

Gang

, ZHOU

Yan

Fuzzy assessment method combining AHP for safety risk of buildings caused by adjacent shield tunnel construction

[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(4): 956-961.

[本文引用: 2]

[4]

王烨晟, 陈文华.

受地铁工程影响建筑物安全风险等级评定研究

[J]. 路基工程, 2015(3): 42-46.

[本文引用: 1]

WANG

Yesheng

, CHEN

Wenhua

Study on security risk grade evaluation standard of buildings influnced by metro tunneling construction

[J]. Subgrade Engineering, 2015(3): 42-46.

[本文引用: 1]

[5]

彭道刚, 卫涛, 赵慧荣, 等.

基于D-AHP和TOPSIS的火电厂控制系统信息安全风险评估

[J]. 控制与决策, 2019, 34(11): 2445-2451.

[本文引用: 2]

PENG

Daogang

, WEI

Tao

, ZHAO

Huirong

, et al.

Cyber security risk assessment of power plant control system based on D-AHP and TOPSIS

[J]. Control and Decision, 2019, 34(11): 2445-2451.

[本文引用: 2]

[6]

TAYLAN

, BAFAIL

A O

, ABDULAAL

R M S

, et al.

Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies

[J]. Applied Soft Computing, 2014, 17: 105-116.

DOI:10.1016/j.asoc.2014.01.003 URL [本文引用: 2]

[7]

ZHANG

L M

, WU

X G

, DING

L Y

, et al.

Decision support analysis for safety control in complex project environments based on Bayesian networks

[J]. Expert Systems With Applications, 2013, 40(11): 4273-4282.

DOI:10.1016/j.eswa.2012.11.022 URL [本文引用: 2]

[8]

ZHANG

L M

, DING

L Y

, WU

X G

, et al.

An improved Dempster-Shafer approach to construction safety risk perception

[J]. Knowledge-Based Systems, 2017, 132: 30-46.

DOI:10.1016/j.knosys.2017.06.014 URL [本文引用: 2]

[9]

中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 城市轨道交通地下工程建设风险管理规范: GB 50652—2011[S]. 北京: 中国建筑工业出版社, 2012.

[本文引用: 1]

Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Qua-rantine of the People’s Republic of China. Code for risk management of underground works in urban rail transit: GB 50652—2011[S]. Beijing: China Architecture & Building Press, 2012.

[本文引用: 1]

[10]

陈仁朋, 曾巍, 吴怀娜, 等.

盾构隧道下穿引起砌体结构建筑沉降损伤实例研究

[J]. 岩土工程学报, 2020, 42(12): 2301-2307.

[本文引用: 1]

CHEN

Renpeng

, ZENG

Wei

, WU

Huaina

, et al.

Case study of tunneling-induced settlement and da-mage of masonry buildings

[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2301-2307.

[本文引用: 1]

Evaluation of risk assessment procedures for buildings adjacent to tunnelling works

2014

... 近年来,盾构隧道下穿建筑物的风险评估已成为国内外学者的研究热点之一^[1⇓-3].于丹丹等^[2]分析了地铁隧道施工对邻近建筑物的影响因素,利用可变模糊集理论构建风险模型,确定风险等级;魏纲等^[3]将层次分析法引入对盾构隧道邻近建筑物的安全风险评估中,结合模糊综合评价法获得评价等级;王烨晟等^[4]利用模糊综合评价法对影响建筑物安全的各因素进行半定量分析.上述风险评估方法虽然取得一定效果,但权重确定过程较粗糙,主观性强且准确性不高.相较于传统层次分析法,模糊层次分析法(FAHP)在计算步骤等方面进行了改进,用模糊数替代具体数值进行计算.隧道工程问题不确定因素较多且受主观因素影响,用模糊数计算更能准确反映专家想法,从而科学合理地分配各因素权重. ...

地铁隧道施工邻近建筑物安全风险评价

2013

... [2]分析了地铁隧道施工对邻近建筑物的影响因素,利用可变模糊集理论构建风险模型,确定风险等级;魏纲等^[3]将层次分析法引入对盾构隧道邻近建筑物的安全风险评估中,结合模糊综合评价法获得评价等级;王烨晟等^[4]利用模糊综合评价法对影响建筑物安全的各因素进行半定量分析.上述风险评估方法虽然取得一定效果,但权重确定过程较粗糙,主观性强且准确性不高.相较于传统层次分析法,模糊层次分析法(FAHP)在计算步骤等方面进行了改进,用模糊数替代具体数值进行计算.隧道工程问题不确定因素较多且受主观因素影响,用模糊数计算更能准确反映专家想法,从而科学合理地分配各因素权重. ...

地铁隧道施工邻近建筑物安全风险评价

2013

邻近盾构隧道的建筑物安全风险模糊层次分析

2014

... [3]将层次分析法引入对盾构隧道邻近建筑物的安全风险评估中,结合模糊综合评价法获得评价等级;王烨晟等^[4]利用模糊综合评价法对影响建筑物安全的各因素进行半定量分析.上述风险评估方法虽然取得一定效果,但权重确定过程较粗糙,主观性强且准确性不高.相较于传统层次分析法,模糊层次分析法(FAHP)在计算步骤等方面进行了改进,用模糊数替代具体数值进行计算.隧道工程问题不确定因素较多且受主观因素影响,用模糊数计算更能准确反映专家想法,从而科学合理地分配各因素权重. ...

邻近盾构隧道的建筑物安全风险模糊层次分析

2014

受地铁工程影响建筑物安全风险等级评定研究

2015

受地铁工程影响建筑物安全风险等级评定研究

2015

基于D-AHP和TOPSIS的火电厂控制系统信息安全风险评估

2019

... 传统风险评估方法过于主观,风险分级的确定需要人为设定隶属函数或者依照均匀等分风险分级标准划分,而优劣解距离(TOPSIS)法受主观因素影响较少,无需人为设定隶属函数,可以根据计算得出具体非等分风险分级标准,相较于均匀等分风险分级标准,计算结果也更为客观准确.目前运用TOPSIS法确定风险等级已被广泛应用到风险评估中^[5-6],针对具体工程风险评估时,因地下工程的不确定性,区间数可以更准确地反映风险因素的取值范围. ...

... 结合文献[5⇓⇓-8]及咨询相关专家意见,将盾构隧道下穿建筑物风险因素分为5级.1级表示安全,2级表示较安全,3级表示一般,4级表示较危险,5级表示危险.19个风险因素中有一部分因素可以直接量化,通过具体监测数据表示,如土体内摩擦角、黏聚力和压缩模量等.有些因素很难通过具体监测数据表示,只能通过专家评分,如复合地层、软硬交界和特殊地质等.相关风险因素分级如表3所示. ...

基于D-AHP和TOPSIS的火电厂控制系统信息安全风险评估

2019

Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies

2014

Decision support analysis for safety control in complex project environments based on Bayesian networks

2013

... 根据文献[7-8]及《GB 50652—2011城市轨道交通地下工程建设风险管理规范》^[9]等相关规范,确定盾构隧道下穿建筑物风险评级因素:土体性质、建筑物因素、隧道因素和盾构掘进参数.从4个方面分析盾构掘进对上部建筑物的安全影响. ...

An improved Dempster-Shafer approach to construction safety risk perception

2017

2012

盾构隧道下穿引起砌体结构建筑沉降损伤实例研究

2020

... 通过改进TOPSIS法计算得到相对接近度为0.4037,根据表4确定风险等级为3级,即建筑物风险处于一般状态.结合实际施工情况,根据基于损伤现象的损伤评估,建筑物处于“轻微损伤”至“中等损伤”^[10],与风险评估结果相符,验证了评估方法的有效性. ...

盾构隧道下穿引起砌体结构建筑沉降损伤实例研究

2020

〈

〉