深空探测器接近段自主导航的滑动窗口自适应滤波方法

图1 恒星和导航天体之间的角度

Fig.1 Angle between the star and Mars

在火星探测器导航系统中,星光角距量测模型可以表示为

$\begin{array}{l} θ_{m i} = a r c c o s (- l_{p m} \cdot s_{m i}) + v_{m} \\ θ_{p i} = a r c c o s (- l_{p p} \cdot s_{p i}) + v_{p} \\ θ_{d i} = a r c c o s (- l_{p d} \cdot s_{d i}) + v_{d} \end{array}\}$

(3)

式中:i=1, 2, 3;θ_m_i为第i颗恒星与火星之间的角度;l_pm为火星到探测器的视线矢量;s_m_i, s_d_i分别为第i颗恒星在火星、火卫二传感器视场的矢量;v_m, v_p, v_d分别为第i颗恒星与火星、火卫一、火卫二之间的量测噪声.

设量测矢量Z=[θ_m_i θ_p_i θ_d_i]^T,h(·)为量测模型函数,V为量测噪声,式(3)可写为

Z(t)=h(X(t), t)+V(t)

(4)

1.3 不确定性误差及其传递特性

1.3.1 积分误差分析

无论何种数值积分方法,都是轨道动力学微分方程的近似解,因此会产生计算误差.由于计算过程可以等效于前后两步之间斜率的加权平均值与积分步长的乘积,所以斜率的加权平均值会产生较大的近似误差(即非线性微分方程误差的截断).积分步长越小,近似误差越小.因此,积分误差主要受数值积分步长的影响.另外,由数值积分方法引起的摄动加速度误差可以表示为

δ_a(t)=

$\overset{\infty }{\mathop{\underset{i=p}{\mathop \sum }\,}}\,\frac{{{H}^{p+1}}}{\left( p+1 \right)!}\frac{{{\text{d}}^{p+1}}}{\text{d}{{t}^{p+1}}}$ f(t, a(t))

(5)

式中:f(t, a(t))为航天器轨道动力学模型;p为数值积分的阶数;H为积分步长.尽管误差模型可以描述轨道积分误差,但这种误差不仅难以使用统计方法来描述,而且航天器轨道动力学模型随着 $\frac{d^{p}}{d t^{p}}$ f(t, a(t))的高阶变化也难以准确表示.因此,轨道动力学模型的积分误差可视为复杂的不确定误差,该误差在轨道动力学模型中积分两次,直接影响航天器的导航精度.

1.3.2 积分误差传递分析

轨道动力学模型积分误差传播模型可以表示为

$\begin{array}{l} δ_{\overset{\cdot}{r}} = δ_{v} \\ δ_{v} = \int_{t_{1}}^{t_{2}} δ_{a} (t) d t \end{array}\}$

(6)

式中:t₁和t₂分别为起、止时间.

在接近阶段结束时,四阶数值积分的误差为

δ_a(t)=

$\frac{{{H}^{5}}}{5!}\frac{{{\text{d}}^{5}}}{\text{d}{{t}^{5}}}$ f(t, a(t))

(7)

以中心天体重力加速度为例可得:

$\frac{d^{5}}{d t^{5}}$ f(t, a(t))=

$\frac{720 μ r^{(5)}}{r^{7}}$ +

$\frac{1 200 μ {\overset{\cdot}{r}}^{3} \ddot{r}}{r^{6}}$ -

$\frac{360 μ \overset{\cdot}{r} \ddot{r}}{r^{5}}$ -

$\frac{1 200 μ {\overset{\cdot}{r}}^{3} \ddot{r}}{r^{6}}$ +

$\frac{60 μ {\ddot{r}}^{2} r^{(3)}}{r^{4}}$ +

$\frac{30 μ \overset{\cdot}{r} r^{(4)}}{r^{4}}$ -

$\frac{2 μ r^{(5)}}{r^{3}}$

(8)

式中:μ为中心天体的引力常数; $\overset{\cdot}{r}$ =v= $\sqrt{μ (\frac{2}{r} - \frac{1}{a_{x}})}$ ,v为航天器速度,a_x为轨道半长轴; $\ddot{r}$ =a= $\frac{μ}{r^{2}}$ ,r⁽³⁾=-2μ $\frac{v}{r^{3}}$ ,r⁽⁴⁾=6μ $\frac{v^{2}}{r^{4}}$ -2μ $\frac{a}{r^{3}}$ ,r⁽⁵⁾=-24μ $\frac{v^{3}}{r^{5}}$ +18μ $\frac{v^{3} a}{r^{4}}$ -2μ $\frac{r^{(3)}}{r^{3}}$ ,a为航天器加速度.

如式(6)所示,轨道动力学模型的积分误差随积分步长而变化.当轨道高度为距火星200 km、积分步长为250 s时,轨道动力学模型引起的加速度误差约为 0.002 1 m/s².刹车后,继续飞行约10 min,速度误差约为1.26 m/s,位置误差为750 m.因此,积分误差会影响导航精度,尤其是在接近阶段.

当航天器遇到目标天体时,目标天体会导致航天器加速度急剧增加.如果积分时间步长较大,则无法快速跟踪加速度的变化,会引入较大的积分误差.因此,状态模型的误差在接近段急剧增加,过程噪声在航天器接近目标时无法保持不变.为准确估计航天器的位置和速度,需要采用自适应非线性滤波估计过程噪声协方差.一方面,为保证导航精度,需要减小状态模型误差;另一方面,为获得更好的导航性能,应该跟踪或估计状态模型的变化.

2 自适应无迹卡尔曼滤波

2.1 传统无迹卡尔曼滤波

非线性离散随机系统在特定时刻k的状态模型考虑如下:

$\begin{array}{l} X_{k + 1} = f (X_{k}, k) + w_{k} \\ Z_{k} = h (X_{k}, k) + v_{k} \end{array}\}$

(9)

式中:X_k和Z_k分别为k时刻的状态矢量和观测矢量;w_k和v_k分别为k时刻的过程噪声和量测噪声.假设量测噪声和过程噪声是具有可加性的零均值高斯白噪声且互不相关,则

E(w_k

${w^{T}}_{j}$

)=δ_kjQ_k

E(v_k

${v^{T}}_{j}$

)=δ_kjR_k

E(v_k

${w^{T}}_{j}$

)=0, ∀k, j

(10)

式中: Q_k和R_k分别为k时刻的过程噪声协方差和量测噪声协方差;当k=j时,克罗内克函数δ_kj取值为1,当k≠j时,δ_kj取值为0.

对于具有可加性噪声的非线性系统式(9),传统的UKF计算过程如下.

步骤1 设定滤波初值.当k=0,有

${\overset{\cdot}{X}}_{0}$

=E(X₀)

P₀=E[(X₀-

${\hat{X}}_{0}$ )(X₀-

${\hat{X}}_{0}$ )^T]

(11)

式中:P₀为协方差矩阵P的初始值.

步骤2 计算k-1时刻的Sigma点:

$\begin{array}{l} χ_{k - 1}^{0} = {\hat{X}}_{k - 1} \\ χ_{k - 1}^{i} = {\hat{X}}_{k - 1} + \sqrt{(n + λ) P_{k - 1}} \\ i = 1, 2, \dots, n \\ χ_{k - 1}^{i} = {\hat{X}}_{k - 1} - \sqrt{(n + λ) P_{k - 1}} \\ i = n + 1, n + 2, \dots, 2 n \end{array}\}$

(12)

步骤3 计算k时刻的一步预测值.首先根据非线性函数f(·),计算Sigma点的变换结果:

$χ_{k / k - 1}^{i}$ =f(

$χ_{k - 1}^{i}$ ), i=0, 1, …, 2n

(13)

然后计算出一步预测结果和对应的协方差矩阵:

${\hat{X}}_{k / k - 1}$

$\overset{2 n}{\sum_{i = 0}} ω_{i}^{m} χ_{k / k - 1}^{i}$

(14)

P_k/k_-1=

$\overset{2 n}{\sum_{i = 0}} ω_{i}^{c}$ [

$χ_{k / k - 1}^{i}$ -

${\hat{X}}_{k / k - 1}$ ][

$χ_{k / k - 1}^{i}$ -

${\hat{X}}_{k / k - 1}$ ]^T+Q_k_-1

(15)

步骤4 计算k时刻的一步预测Sigma样本点:

$\begin{array}{l} χ_{k / k - 1}^{0} = {\hat{X}}_{k / k - 1} \\ χ_{k / k - 1}^{i} = {\hat{X}}_{k / k - 1} + \sqrt{(n + λ) P_{k / k - 1}} \\ i = 1, 2, \dots, n \\ χ_{k / k - 1}^{i} = {\hat{X}}_{k / k - 1} - \sqrt{(n + λ) P_{k / k - 1}} \\ i = n + 1, n + 2, \dots, 2 n \end{array}\}$

(16)

步骤5 计算一步预测量测值及其自协方差矩阵、互协方差矩阵.根据非线性函数h(·),量测Sigma样本点的变换为

$γ_{k / k - 1}^{i}$ =h(

$χ_{k / k - 1}^{i}$ )

(17)

那么一步预测量测值为

${\hat{Z}}_{k / k - 1}$ =

$\overset{2 n}{\sum_{i = 0}} ω_{i}^{m} γ_{k / k - 1}^{i}$ =

$\overset{2 n}{\sum_{i = 0}} ω_{i}^{m}$ h(

$χ_{k / k - 1}^{i}$ )

(18)

自协方差矩阵为

$P_{{\hat{z}}_{k / k - 1}}$ =

$\overset{2 n}{\sum_{i = 0}} ω_{i}^{c}$ (

$γ_{k / k - 1}^{i}$ -

${\hat{Z}}_{k / k - 1}$ )(

$γ_{k / k - 1}^{i}$ -

${\hat{Z}}_{k / k - 1}$ )^T+R

(19)

与一步预测状态量之间的协方差矩阵为

$P_{{\hat{x}}_{k / k - 1} {\hat{z}}_{k / k - 1}}$ =

$\overset{2 n}{\sum_{i = 0}} ω_{i}^{c}$ (

$χ_{k / k - 1}^{i}$ -

${\hat{X}}_{k / k - 1}$ )(

$γ_{k / k - 1}^{i}$ -

${\hat{Z}}_{k / k - 1}$ )^T

(20)

步骤6 计算卡尔曼增益、状态估计结果及其协方差矩阵:

K_k=

${\hat{P}}_{{\hat{x}}_{k / k - 1} {\hat{z}}_{k / k - 1}} {\hat{P}}_{{\hat{z}}_{k / k - 1}}^{- 1}$

(21)

${\hat{X}}_{k}$ =

${\hat{X}}_{k / k - 1}$ +K_k(Z_k-

${\hat{Z}}_{k / k - 1}$ )

(22)

P_k=P_k/k_-1-K_k

$P_{{\hat{z}}_{k / k - 1}} {K^{T}}_{k}$

(23)

步骤7 对k+1重复执行步骤2~6.

对步骤2~6的参数设置如下:

$\begin{array}{l} ω_{0}^{m} = \frac{λ}{n + λ} \\ ω_{i}^{m} = \frac{λ}{2 (n + λ)}, i = 1, 2, \dots, 2 n \\ ω_{0}^{c} = \frac{λ}{n + λ} + 1 - α^{2} + β \\ ω_{i}^{c} = \frac{λ}{2 (n + λ)}, i = 1, 2, \dots 2 n \end{array}\}$

(24)

λ=α²(n+τ)-n

(25)

式中:α为很小的正数;β为X的分布信息;参数τ常取τ=3-n,故式(25)又可以写为

λ=3α²-n

(26)

2.2 自适应协方差调整的UKF

在确定的滤波器参数情况下,状态估计可能会有很大的估计误差.在实际应用中,量测噪声R_k可以根据传感器误差获取.与量测噪声相比,系统模型误差很难准确获取,因此实际应用中需要自适应地估计过程噪声协方差Q_k.假设过程噪声和量测噪声是零均值可加性的高斯白噪声,且量测噪声R_k是已知的恒定噪声.利用Maybeck的自适应线性卡尔曼滤波方法^[18]建立AQUKF方法,对Q_k的估计进行平稳化处理,使其在一个滑动窗口内是平稳的,并且k时刻的状态噪声估计 ${\hat{Q}}_{k}$ 利用[k-N+1,k]区间的差值,避免因某一时刻Q_k的突变而产生较大误差,并将改进方法与UKF方法相结合应用在火星探测器中.

根据Maybeck的理论,Q_k的观测值 $Q_{k}^{*}$ 通过量测更新前后状态估计之间的变化得出:

$Q_{k}^{*}$ =ΔX_kΔ

${X^{T}}_{k}$ -[P_k-(P_k/k_-1-

${\hat{Q}}_{k - 1}$ )]

(27)

式中:ΔX_k= ${\hat{X}}_{k}$ - ${\hat{X}}_{k / k - 1}$ 为量测更新前后的状态变化;P_k为状态估计协方差,P_k/k_-1为一步预测的状态协方差; ${\hat{Q}}_{k - 1}$ 为k-1时刻的状态噪声估计.式(27)表明, $Q_{k}^{*}$ 是残差减去两个相邻时刻之间后验协方差的变化.

将过程噪声协方差的观测值 $Q_{k}^{*}$ 与 ${\hat{Q}}_{k - 1}$ 线性组合可得:

${\hat{Q}}_{k}$ =

${\hat{Q}}_{k - 1}$ +ω_Q(

$Q_{k}^{*}$ -

${\hat{Q}}_{k - 1}$ )

(28)

式中:ω_Q为每次更新时的权重,如果ω_Q较小表示每次更新更倾向于与 ${\hat{Q}}_{k - 1}$ ,如果ω_Q较大表示相邻时刻之间Q_k发生较大变化.因此该自适应方法的性能对权重ω_Q的选择非常敏感,Busse等^[19]采用试错法来选择合适的ω_Q,但是所消耗的时间长,且没有一个直接的指标来衡量不同ω_Q的优良性;Lee等^[18]采用下降单纯性法来优化关于ω_Q的目标函数,但是计算量较大.另外,文献[18-19]只是针对ω_Q的选择采用不同的方法,没有改变模型对ω_Q的依赖性,方法性能仍然对ω_Q很敏感.

因此,使用宽度为N的滑动窗口对式(28)进行平稳化处理:

${\hat{Q}}_{k}$ =

${\hat{Q}}_{k - 1}$ +

$\frac{1}{N} \overset{k}{\sum_{j = k - N + 1}}$ (

$Q_{j}^{*}$ -

${\hat{Q}}_{j - 1}$ )

(29)

因为式(27)得到的噪声估计同时包含位置误差和速度误差,而位置误差比速度误差大几个量级,所以由此得到的噪声估计值并不准确,无法解决小干扰问题.为提高性能,将 ${\hat{Q}}_{k}$ 整合为连续形式.

如果

${\hat{Q}}_{k}$

$[\begin{array}{l} Q_{r r} & Q_{r v} \\ Q_{v r} & Q_{v v} \end{array}]$

(30)

令

q_vv=

$\frac{1}{T}$ diag(Q_vv)

(31)

式中:T为滤波周期.

那么,可以重新得到状态噪声估计:

${\hat{Q}}_{k}$

$[\begin{array}{l} 0 & 0 \\ 0 & q_{v v} \end{array}]$

(32)

然后,将 ${\hat{Q}}_{k}$ 作为k+1时刻的状态噪声.该方法将速度噪声引起的误差与位置噪声引起误差隔离开,解决小干扰问题.

3 仿真和分析

3.1 仿真参数设置

以火星探测器为例进行仿真分析,仿真数据由系统工具包产生.坐标系采用J2000.0火心惯性坐标系,轨迹参数如表1所示.表中:a'为长半轴;e为偏心率;i'为轨道倾角.

表1 火星探测器轨道参数

Tab.1 Orbit parameters of Mars probe

参数	数值
a'/km	1.932×10⁸
e	0.2364
i'/(°)	23.455
升交点赤经/(°)	0.258
近地点角距/(°)	71.347
真近角点/(°)	85.152
接近火星时间	1997-01-04T17:03:13.000

参考轨道由RKF89数字积分器生成,该积分器使用1 s的固定步长,时间为1997年7月1日0时0分0秒至1997年7月8日0时0分0秒.在接近段,火星和探测器之间的最小距离为 5 211 km.仿真中使用的行星星历和恒星数据库分别是JPL DE421星表和第谷恒星星表.量测中的导航天体为火星、火卫一和火卫二.火星、火卫一、火卫二和恒星传感器的精度设置为0.1像素,火星、火卫一和火卫二的光学传感器参数如表2所示.表中:f' 为焦距;FOV为视场角;R为分辨率.

表2 光学传感器的参数

Tab.2 Parameters of optical sensor

参数	数值
f'/mm	2 013.4
FOV/mrad	10×10
R/(rad·像素^-1)	10
CCD平面大小/像素	1024×1024
像素大小/m	21

滤波器的初始参数设置如下.

初始状态为

X₀=[r v]=[1.590 5×10⁹ 6.504 4×10⁸ 2.829 5×10⁷-4.925×10³ -2.030 5×10³ 76.742 2]

初始状态协方差为

P₀=diag(10⁶, 10⁶, 10⁶, 10², 10², 10²)

初始状态噪声协方差为

Q₀=diag(10^-3, 10^-3, 10^-3, 10^-8, 10^-8, 10^-8)

初始量测协方差为

R= $(\begin{array}{l} 9.6946 \times 10^{- 13} & 9.5472 \times 10^{- 13} & 3.3440 \times 10^{- 23} \\ 1.0432 \times 10^{- 23} & 9.4032 \times 10^{- 23} & 3.9301 \times 10^{- 23} \\ 2.5045 \times 10^{- 13} & 6.2661 \times 10^{- 13} & 1.0078 \times 10^{- 27} \end{array})$

窗口宽度N设置为10.

3.2 结果分析

分别使用UKF和扩展卡尔曼滤波方法对非线性模型式(9)进行滤波,然后与AQUKF进行比较分析,最后对AQUKF方法进行影响因素分析.

3.2.1 UKF与AQUKF滤波方法的结果比较

图2和图3分别给出了使用UKF和AQUKF方法的滤波结果.仿真结果的统计时间段从第1天开始至结束.图2中:D_r=‖D_r‖=‖[D_x D_y D_z]‖为航天器位置的误差; D_v=‖D_v‖=‖[D_vx D_vy D_vz]‖为航天器速度的误差.

图2

图2 UKF方法滤波结果

Fig.2 Results of UKF algorithm

图3

图3 AQUKF方法滤波结果

Fig.3 Results of AQUKF algorithm

表3给出了UKF和AQUKF方法滤波收敛后的平均误差和最大误差.由表3可知,本文提出的AQUKF方法位置精度比UKF提高90.97%;速度精度比UKF提高66.17%.从图2(a)可以看出,探测器在第3天末x方向和y方向的位置误差出现较大发散,并且直到第7天也没有收敛回来;从图2(b)可以看出,探测器在第3天末x方向和y方向的速度误差同样出现较大发散.与位置误差发散不同的是,速度误差在发散后出现短暂收敛,并在一个恒定误差上下波动.从图3可以看出,本文提出的AQUKF有效抑制了UKF带来的发散问题,提高了导航系统的稳定性和精度.

表3 UKF和AQUKF滤波方法的结果

Tab.3 Results of UKF and AQUKF filtering methods

滤波方法	估计误差平均值		估计误差最大值
滤波方法	位置/km	速度/ (m·s^-1)	位置/km	速度/ (m·s^-1)
UKF	92.221 2	0.879 7	355.462 5	11.166 9
AQUKF	8.323 4	0.297 6	146.019 5	11.173 0

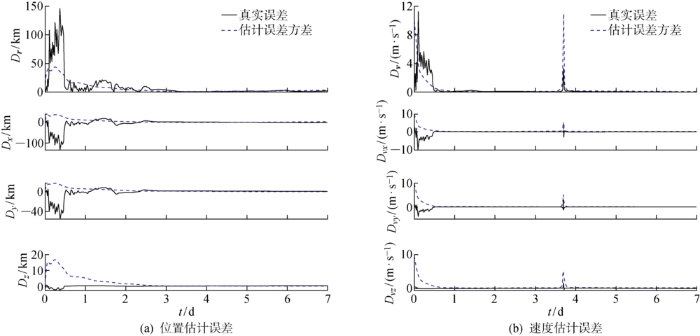
图4为UKF与AQUKF位置误差和速度误差对比.从图中可以清楚地看出,在约3.7 d时,UKF滤波位置误差和速度误差开始发散.从图4(b)中可以看出,3.7 d时AQUKF出现的尖峰比UKF稍大一些,约增加1.37 m/s,但是AQUKF可以在1.5 h内恢复收敛,而UKF并未恢复收敛.这说明探测器在某一时刻受到干扰时,利用AQUKF滤波可以很快恢复收敛,提高了导航系统的稳定性.另外从图4(b)可以看出,AQUKF在恢复收敛之后速度误差仍然很小.

图4

图4 UKF与AQUKF估计误差对比

Fig.4 Comparison of estimation error between UKF algorithm and AQUKF algorithm

3.2.2 影响因素分析

对基于AQUKF的火星探测器导航方法在不同影响因素下的滤波性能进行仿真分析,包括滤波周期、窗口大小.其余仿真条件与3.1节保持一致.

(1) 滤波周期对导航方法精度的影响.

表4和图5给出了窗口大小为10、不同滤波周期时的滤波结果.根据图表可知滤波周期越短导航系统性能越好,随着滤波周期减小,精度提升速度变慢,因此调整滤波周期的大小对导航滤波精度的提高是有限的.当滤波周期较长时,导航滤波结果所受影响较大,原因是系统轨道动力学模型的线性化误差随时间积分进一步增大,致使系统的性能下降.当采样周期大于600 s时,估计误差曲线波动幅度变大,特别是在接近火星时位置和速度均出现较大误差,导航性能较差.

表4 滤波周期对导航方法精度的影响

Tab.4 Influence of filtering period on accuracy of navigation algorithm

T/s	估计误差平均值		估计误差最大值
T/s	位置/km	速度/(m·s^-1)	位置/km	速度/(m·s^-1)
120	3.106 5	0.158 1	51.003	11.904 3
300	4.103 0	0.167 8	78.635	12.492 3
600	8.323 4	0.297 6	146.019	11.173 0
900	7.797 1	0.280 2	102.540	9.872 7
1 200	11.574 0	0.538 7	109.420	56.290 3

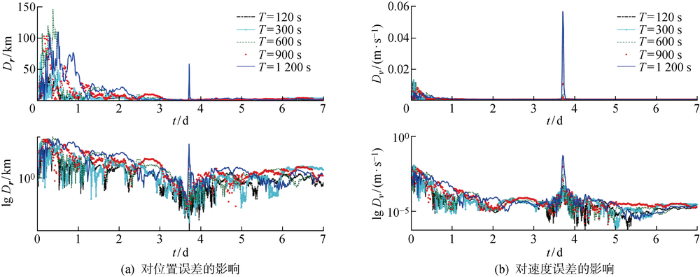
图5

图5 滤波周期对位置误差和速度误差的影响

Fig.5 Influence of filtering period on position error and velocity error

(2) 窗口大小对导航方法精度的影响.

图6和表5给出了滤波周期为600 s、不同窗口大小时的滤波结果.根据图表可知,窗口较大或者较小时导航系统性能均有所下降.当N<10,在探测器靠近火星时会利用更多当前时刻的信息去自适应过程噪声协方差,这样就会导致导航系统性能在该时刻附近突然降低,进而影响整个时间段的系统性能.而随着时间的增加,误差也会累积增加,因此当N>10时,在利用较多历史信息的同时,也导致误差的累积.当N=10时,平衡了当前时刻和历史时刻信息带来的误差,导航性能相对最佳.

图6

图6 窗口大小对位置误差和速度误差的影响

Fig.6 Influence of window size on position error and velocity error

表5 窗口大小对导航方法精度的影响

Tab.5 Influence of window size on accuracy of navigation algorithm

N	估计误差平均值		估计误差最大值
N	位置/km	速度/(m·s^-1)	位置/km	速度/(m·s^-1)
1	8.572 8	0.316 1	150.67	11.197 3
5	8.412 2	0.300 1	148.27	11.178 1
10	8.323 4	0.297 6	146.02	11.173 0
50	8.545 2	0.312 8	141.62	11.168 2
100	8.850 2	0.312 7	140.63	11.167 5
300	9.579 0	0.307 9	139.87	11.167 2

4 结语

本文提出一种深空探测器自主天文导航的滑动窗口自适应UKF方法,即AQUKF,相比于使用传统UKF的算法,AQUKF算法通过自适应调节系统噪声协方差,不仅解决系统发散问题,提高系统的稳定性,还可以大幅提高导航精度.由于AQUKF对窗口大小的敏感程度较小,所以不需要为选择合适的窗口消耗更多时间,也不需要通过优化目标方程选择窗口大小,损失系统的实时性.该方法可为我国未来深空探测器任务自主导航系统的研制提供参考.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

吴伟仁, 王大轶, 宁晓琳.

深空探测器自主导航原理与技术[M]. 北京: 中国宇航出版社, 2011.

Weiren

, WANG

Dayi

, NING

Xiaolin

Principle and technology of autonomous navigation for deep-space probe[M]. Beijing: China Astronautic Publishing House, 2011.

[2]

房建成, 宁晓琳.

深空探测器自主天文导航方法[M]. 西安: 西北工业大学出版社, 2010.

FANG

Jiancheng

, NING

Xiaolin

Autonomous celestial navigation method for a deep-space probe[M]. Xi’an: Northwestern Polytechnic University Press, 2010.

DOI:10.1016/j.paerosci.2017.08.002 URL [本文引用: 1]

[3]

Z S

, CUI

P Y

, CRASSIDIS

J L

Design and optimization of navigation and guidance techniques for Mars pinpoint landing: Review and prospect

[J]. Progress in Aerospace Sciences, 2017, 94: 82-94.

[4]

, NING

X L

, FANG

J C

Analysis of orbital dynamic equation in navigation for a Mars gravity-assist mission

[J]. The Journal of Navigation, 2012, 65(3): 531-548.

DOI:10.1017/S0373463312000100 URL [本文引用: 1]

[5]

BHASKARAN

Autonomous navigation for deep space missions

[C]∥SpaceOps 2012 Conference. Stockholm, Sweden: AIAA, 2012: 1267135.

DOI:10.1109/TIM.2010.2084710 URL [本文引用: 2]

[6]

FANG

J C

YANG Y, Study on innovation adaptive EKF for in-flight alignment of airborne POS

[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(4): 1378-1388.

[7]

NING

X L

, LI

, YANG

Y Q

, et al.

Analysis of ephemeris errors in autonomous celestial navigation during Mars approach phase

[J]. The Journal of Navigation, 2017, 70(3): 505-526.

DOI:10.1017/S0373463316000734 URL [本文引用: 3]

[8]

, ZHAO

, LIN

Y H

Adaptively tuning sampling weights of the unscented Kalman filter in starlight refraction navigation

[J]. Optik, 2017, 148: 300-311.

DOI:10.1016/j.ijleo.2017.08.097 URL [本文引用: 1]

[9]

XIONG

, WEI

C L

, LIU

L D

Multiple-model adaptive estimation for space surveillance with measurement uncertainty

[J]. Optimal Control Applications and Methods, 2016, 37(2): 404-423.

DOI:10.1002/oca.2176 URL [本文引用: 1]

[10]

LIU

W W

, LIU

Y C

, BUCKNALL

A robust localization method for unmanned surface vehicle (USV) navigation using fuzzy adaptive Kalman filtering

[J]. IEEE Access, 2019, 7: 46071-46083.

DOI:10.1109/ACCESS.2019.2909151 URL [本文引用: 1]

[11]

GAO

X L

, LUO

H Y

, BAO

B K

, et al.

RL-AKF: An adaptive Kalman filter navigation algorithm based on reinforcement learning for ground vehicles

[J]. Remote Sensing, 2020, 12(11): 1704.

DOI:10.3390/rs12111704 URL [本文引用: 1]

[12]

FRASER

C T

, ULRICH

Adaptive extended Kalman filtering strategies for spacecraft formation relative navigation

[J]. Acta Astronautica, 2021, 178: 700-721.

DOI:10.1016/j.actaastro.2020.10.016 URL [本文引用: 1]

[13]

卞鸿巍, 金志华, 王俊璞, 等.

组合导航系统新息自适应卡尔曼滤波算法

[J]. 上海交通大学学报, 2006, 40(6): 1000-1003.

BIAN

Hongwei

, JIN

Zhihua

, WANG

Junpu

, et al.

The innovation-based estimation adaptive Kalman filter algorithm for INS/GPS integrated navigation system

[J]. Journal of Shanghai Jiao Tong University, 2006, 40(6): 1000-1003.

[14]

HUANG

B H

, WANG

J J

, ZHANG

J F

, et al.

Variational bayesian adaptive Kalman filter for integrated navigation with unknown process noise covariance

[C]∥2022 2nd International Conference on Consumer Electronics and Computer Engineering. Guangzhou, China: IEEE, 2022: 436-443.