上海交通大学学报

上海交通大学学报, 2025, 59(8): 1156-1168 doi: 10.16183/j.cnki.jsjtu.2023.511

机械与动力工程

机匣组线加工装夹找正系统误差建模与精度优化方法

杜雪明, 向洋, 刘顺,, 金隼

上海交通大学 机械与动力工程学院, 上海 200240

Modeling of Systematic Errors and Precision Optimization Methods for Workpiece Clamping and Alignment System in Aeroengine Gearbox Automated Line Machining

DU Xueming, XIANG Yang, LIU Shun,, JIN Sun

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 刘 顺,助理研究员;E-mail:shunliu@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-10-10   修回日期: 2023-11-30   接受日期: 2023-12-4  

基金资助: 国防基础科研计划(JCKY 2021110B048)
国家自然科学基金(51975369)
上海交通大学“新进青年教师启动计划”(SFYS at SJTU 22X010503456)

Received: 2023-10-10   Revised: 2023-11-30   Accepted: 2023-12-4  

作者简介 About authors

杜雪明(2000—),博士生,从事航发环形薄壁件多工序误差传递累积机理研究.

摘要

在航空发动机机匣类零件自动化组线升级改造中,零点定位系统和辅助找正台等新设备的引入显著提升了生产效率,但同时也加剧了多工序加工中的系统误差累积.为降低新系统误差对加工精度的不利影响,研究了不确定性输入条件下找正系统的误差建模与精度优化方法.研究方法主要包括:首先,建立考虑零点定位系统子母盘装配差异的偏差分析模型,并采用K-S检验方法验证模型准确性;基于该模型,系统分析了多子盘-母盘互换过程中的精度损失规律.其次,创新性地提出基于输出分布差异与超差率差异的精度损失量化函数,通过对找正系统的基座结构进行优化,将系统精度损失由原先的11.53%降低至2.33%.同时,有效改善了由加工基准和定位基准不一致导致的工件径跳分布问题,其分布差异由 0.117 15 降至 0.039 54.本研究实现了零点装夹找正系统性能的显著提升,为产线的装夹定位精度分析和优化提供了理论支撑和实践指导.

关键词： 航发机匣; 零点定位系统; 误差建模; 精度优化

Abstract

In the upgrading and automation of aeroengine gearbox assembly line, the introduction of new equipment such as zero-point positioning systems and auxiliary alignment systems has significantly improved production efficiency. However, it has also brought about an increase in systematic errors during multi-process machining. To mitigate the adverse impact of these new systematic errors on machining accuracy, this paper investigates error modeling and precision optimization methods for the alignment system under uncertainty. First, it develops an assembly deviation analysis model, considering the differences between the master and sub-discs in the zero-point positioning system. It then designs a Kolmogorov-Smirnov (K-S) test to verify the accuracy of the model, based on which, the accuracy loss patterns during multi-sub-master disc to master disc interchange processes is analyzed. Afterwards, it defines a precision loss quantification function, incorporating both output distribution deviations and tolerance violation rates. By optimizing the bases structure of the alignment system, the precision loss is reduced from 11.53% to 2.33%. Additionally, the difference in radial runout distribution caused by misalignment between machining and positioning references is reduced from 0.117 to 0.039. These improvements significantly improve the performance of the zero-point clamping and alignment system, providing essential theoretical support for the analysis and optimization of clamping and positioning precision in automated production lines.

Keywords： aircraft gearbox; zero-point positioning system; error modeling; accuracy optimization

PDF (16254KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

杜雪明, 向洋, 刘顺, 金隼. 机匣组线加工装夹找正系统误差建模与精度优化方法[J]. 上海交通大学学报, 2025, 59(8): 1156-1168 doi:10.16183/j.cnki.jsjtu.2023.511

DU Xueming, XIANG Yang, LIU Shun, JIN Sun. Modeling of Systematic Errors and Precision Optimization Methods for Workpiece Clamping and Alignment System in Aeroengine Gearbox Automated Line Machining[J]. Journal of Shanghai Jiaotong University, 2025, 59(8): 1156-1168 doi:10.16183/j.cnki.jsjtu.2023.511

航空发动机机匣类环形薄壁零件制造过程中受到铸造毛坯误差、机加工变形、残余应力和温度等多物理场时变耦合影响[1].传统的3-2-1、N-2-1(N>3)等确定性定位难以保证定位精度.目前,主流的生产方式大多依赖单机生产,工人采用通用夹具、划线尺和千分表等工具进行工件的确定性定位,通过人工搬运进行工序流转.人工的介入导致生产过程呈现不连续性,且存在受主观因素影响大、测量精度不高、机床利用率低等问题[2].以某航空结构件加工为例[3],机床的平均空闲率约为60%,其中因找正、装夹造成的停工时间占一半以上,平均换装零件的时间为1 h,严重限制了数控设备的能力发挥.为充分发挥设备产能,实现航发机匣类零件的组线生产,零点定位系统[4]、地轨机器人、无人搬运车[5]、辅助找正台等设备被引入自动化产线中.将各个工序的人工干预过程集中在找正台上进行,并通过零点定位系统实现多工位的扭转,大幅度提高了机床的利用率.柔性产线涉及车削、铣削、三坐标测量等多个工序,各个工序又对应多台机床设备,会出现一个母盘与多个子盘配对或一个子盘与多个母盘配对的情况,导致装夹定位的基准与加工的基准存在差异.往往会出现在辅助找正台上定位精度测量满足要求,但在机床上进行定位精度测量时难以保证相同精度.鉴于上述问题,本文以装配定位偏差分析为切入点,详细分析一个母盘对应多个子盘以及一个子盘对应多个母盘的情况,构建误差传递链条,基于Vis~VSA三维偏差分析软件建模实现,之后对于误差传递模型进行优化分析.对于提高自动化组线加工模式下辅助找正台、零点定位系统在产线中的精度保持性,提升整线的精度和效率都具有重要的实际意义.

将仿真软件应用于装配偏差分析起始于Bjorke[6]提出的计算机辅助公差设计(CAT)的概念,各国学者和机构开发了以3DCS、VisVSA、CETOL 6σ等为主流的三维偏差分析软件[7],在焊接和装配模拟过程都发挥着重要的作用.王聪伟等[8]应用 VisVSA 建立了空气舵系统的装配尺寸链分析模型.林嘉等[9]利用VisVSA对某飞机后机身冲压排气管进行装配建模以及装配精度分析.王仲奇等[10]通过3DCS模拟计算飞机舱门某结构件的装配分析偏差过程.姚利民等[11]通过3DCS仿真探究焊接变形对动车组装配尺寸精度产生的影响.Tang等[12]利用UG二次开发工具和VisVSA软件分析了船舶螺旋桨的装配偏差分析过程.Ramnath等[13]指出基于VisVSA的装配偏差仿真结果,倾向于用户和专业知识.Litwa等[14]提出基于3DCS的公差耦合优化方法,对于产品和工艺过程信息进行优化.

装配精度和装配成本往往呈指数级正相关[15],目前的容差设计大多依靠经验,过于保守.相关学者在容差设计优化方面做出了大量工作,主要分为公差再设计和结构优化设计.在公差优化设计方面:刘鹏等[16]以某坐标镗床为研究对象,分析了尺寸链条中各大件的角度误差与装配精度的映射关系,利用自适应遗传算法,将涉及公差平均放宽了12%.王国亮等[17]对某车窗升降系统的三维装配进行建模,以公差收严的收益比为评价因素,实现了考虑车门内板变形的公差组合方案优化设计.刘奕颖等[18]利用自适应遗传算法对机床运动轴29个误差项的公差带进行了合理分配,放宽了9项机床装配精度指标,降低了装配成本.Wu等[19]针对于三轴机床的公差稳健性设计,基于正交试验溯源了13项关键误差,并将零部件的尺寸精度进行了不同公差等级的再分配.在结构设计方面:Wu等[20-21]对航发叶片进行分析建模,采用了有限元分析(FEA)和遗传算法对加工夹具的定位夹紧点进行了优化.一些学者考虑零点定位系统的几何结构、角度,选择最佳的数量和分布等,有效增加了重复定位精度,以满足各型工件多工序制造的需要[22-24].

综上所述,CAT凭借着建模过程简单、建模求解一体化的特点,在航空航天结构件的装配偏差分析建模中有了一定的基础,基于装配偏差模型的容差优化和结构优化在机床装备和零点定位系统得到了广泛应用.针对于机匣组线生产,装夹定位精度往往有着更高的要求[25],需考虑更全面的影响因素,产线中找正装备-快换系统-夹具系统对于工件定位精度的影响仍需进一步的研究.

结合找正台和零点定位系统刚性的特点,本文基于VisVSA实现找正台-零点定位系统-夹具-工件装配系统的装配偏差传递建模分析,通过K-S检验验证建模方法的准确性.通过分析单一子盘对应多母盘和单一母盘对应多子盘的两类装配过程,构建装配偏差传递模型,揭示了零点定位系统多子母盘差异输入情况下的精度损失规律,提出了基于输出分布差异的精度损失量化指标,以单一子盘对应多种母盘的情况为例进行了优化设计.提高零点定位系统、找正台设备在柔性产线中的普适性,为找正台改造设计提供理论支持,提高产线的精度和可靠性.

1 多子盘-母盘零点装夹找正与加工系统尺寸链模型

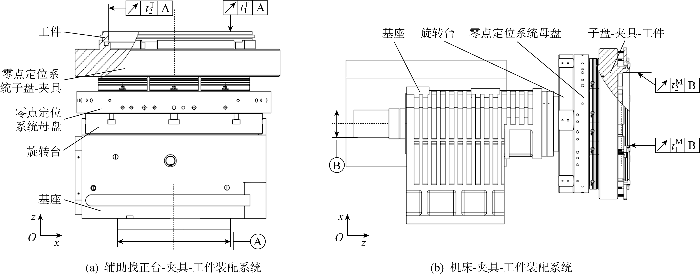
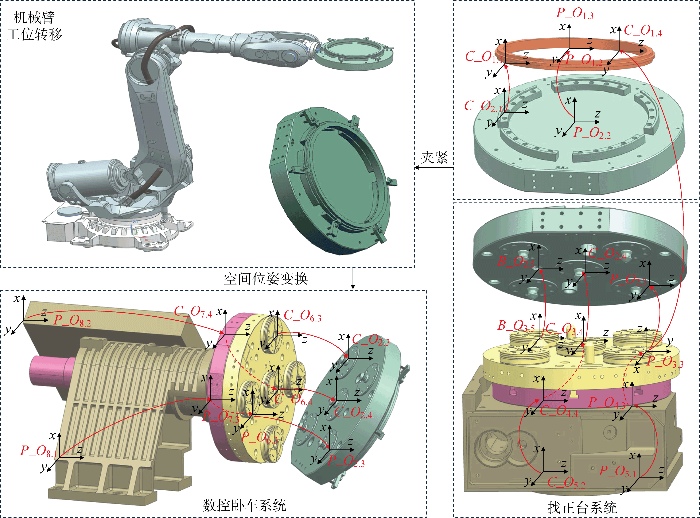
装配偏差模型的装配层级及装配特征是组成尺寸链模型的基本元素,是装配偏差分析的基础.通过分析辅助找正台和数控卧车复杂装配系统的基本装配信息,确定了装配层级、装配特征及测量目标特征(见图1),构建了基本的误差传递尺寸链.工件在辅助找正台系统中的测量分析目标为:工件相对于找正台基座基准A的轴向跳动${t}_{1}^{\mathrm{T}}$,工件相对于基准A的径向跳动${t}_{2}^{\mathrm{T}}$,如图1(a)所示;工件在数控卧车系统中的测量分析目标为:工件相对于主轴基座基准B的轴向跳动${t}_{1}^{\mathrm{M}}$,工件相对于基准B的径向跳动${t}_{2}^{\mathrm{M}}$,如图1(b)所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   尺寸链模型的装配偏差分析目标

Fig.1   Objective of assembly deviation analysis for dimensional chain model


1.1 多子盘差异输入装配信息模型

单一母盘多子盘差异输入的情况发生在多种类型的子盘-工件子装配体装在找正台上进行找正时.基于图1(a)所示的分析目标,为明确各关键部件尺寸和位置的相对关系,对于找正台的气动系统、夹具的夹紧系统等对装配偏差影响较小的部件进行简化.其简化后的三维模型如图2所示,主要包括基座、旋转台、零点定位系统的母盘、零点定位系统的子盘和夹具组成的子装配体、简化的航发机匣环形件.

图2

新窗口打开| 下载原图ZIP| 生成PPT

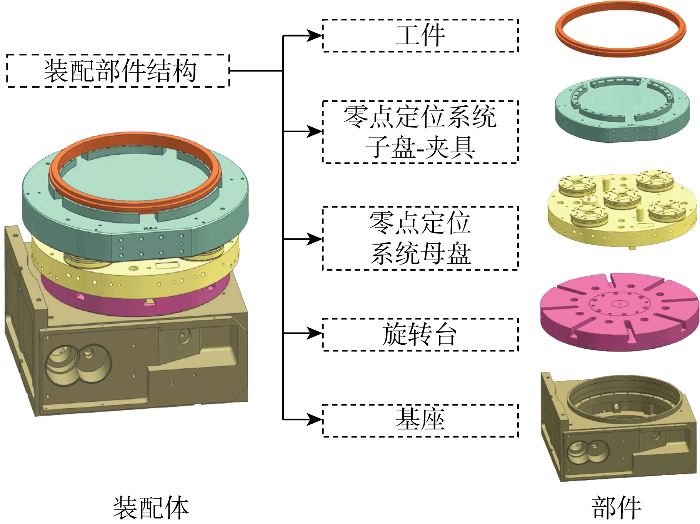
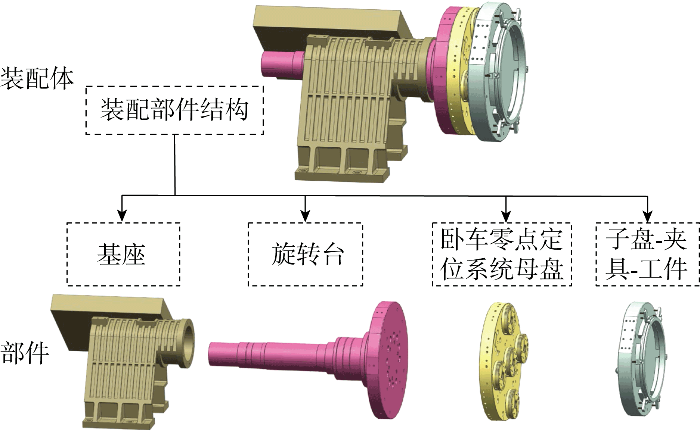
图2   找正台系统的简化装配模型和装配层级

Fig.2   Simplified assembly model and assembly level of the alignment table system


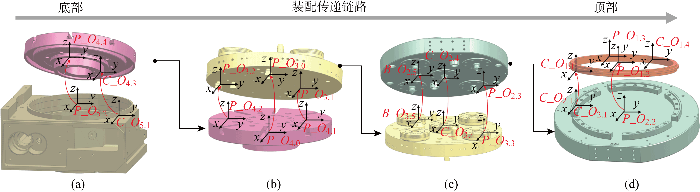
基于图2所示的简化数模,结合实际装配特征关系,分析找正台-零点定位系统-夹具-工件装配系统中的装配特征如图3所示.图中:P_Ox,y表示x零件上的平面特征y;C_Ox,y表示x零件上的孔销特征y;B_Ox,y表示x零件上的锥孔销特征y.在图3(a)中,基座与转台之间首先通过面面配合,限制z向平动($\stackrel{-}{z}$)、x向转动($\hat{x}$)、y向转动($\hat{y}$)自由度,余下x向平动($\stackrel{-}{x}$)、y向平动($\stackrel{-}{y}$)、z向转动($\hat{z}$)自由度,之后通过一浮动间隙较大的孔销配合进一步约束$\stackrel{-}{x}$、$\stackrel{-}{y}$,通过“一面一销”定位法保留了$\hat{z}$自由度;在图 3(b) 中,转台和零点定位系统母盘通过三面3-2-1定位完全限制6个自由度;在图3(c)中,零点定位系统母盘和子盘采用“一面两销”定位完全固定两构件;在图3(d)中,零点定位系统子盘-夹具和工件通过“一面一销”方式定位,仅剩$\hat{z}$自由度,基于夹紧力限制$\hat{z}$自由度,达到完全固定.分析可知,经由工件到转台的装配传递链路,工件相对于基座的$\hat{z}$自由度被保留.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   找正台-零点定位系统-夹具-工件装配系统中的装配特征

Fig.3   Assembly features in the alignment table-zero point positioning system-fixture-workpiece assembly system


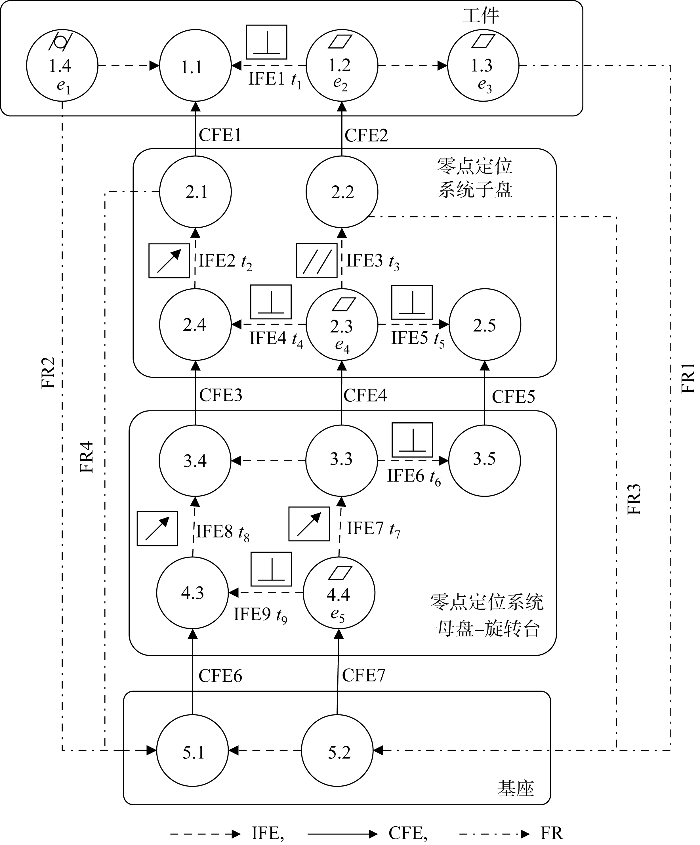
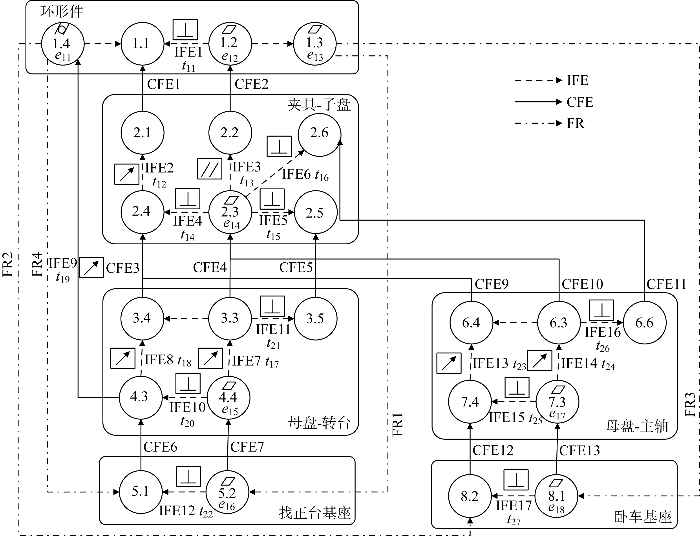
由装配特征、装配层级及测量目标确定的尺寸链模型如图4所示.图中:ti代表着第i个误差传递链路中平行度、垂直度、跳动、位置度等方向位置的公差值;ej代表着第j个特征平面度、圆柱度等形状公差的公差值,需要注意,形状公差无基准,ej是相对于名义位置的公差值;内部功能特征(IFE)代表着零件内的几何尺寸和公差(GD&T)关系;连接功能特征(CFE)代表着零件间的GD&T关系;功能需求(FR)为尺寸链的测量目标.由此,构建了找正台装配系统的基本的误差尺寸链路.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   找正台-零点定位系统-夹具-工件装配系统的基本尺寸链

Fig.4   Basic dimensional chain of alignment table-zero-point positioning system-fixture-workpiece assembly system


1.2 多母盘差异输入装配信息模型

单一子盘多母盘差异输入的情况发生在零点定位系统子盘-环形工件在找正台上定位夹紧后,由机械臂抓取子盘-工件装配体换装在机床母盘上时,如图5所示,整个快换过程包括:找正台系统进行工件找正夹紧、子盘-工件装配体与找正台母盘脱离、机械手夹持工件进行工位转移、子盘-工件装配体与数控卧车系统母盘连接.快换过程中,出现了单一子盘对应找正台母盘和卧车母盘的多母盘情况.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   单一子盘多母盘差异输入的情况

Fig.5   Differential inputs for multiple master in a single subpanel


现场加工工艺要求,工件在机床上的装夹定位精度通常由工件相对于机床基座的端面跳动和径向跳动表征.基于图1(b)所示的测量基准和测量特征,为明确各关键部件尺寸和位置的相对关系,对于机床的液压系统、气动系统、夹具的夹紧系统等对装配偏差影响较小的部件进行简化,其简化后的三维模型如图6所示.主要包括卧车基座、卧车主轴、卧车零点定位系统母盘、机械手换装转移的子盘-夹具-工件4部分.整体的装配过程为从左到右逐层装配.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   机床-夹具-工件装配系统的简化装配模型和装配层级

Fig.6   Simplified assembly model and assembly level of machine tool-fixture-workpiece assembly system


基于图6所示的简化数模,分析卧车-零点定位系统-夹具-工件装配系统中的装配特征如图6所示.首先,卧车基座与主轴之间通过“一面一销”定位法仅保留了$\hat{z}$自由度,即绕着转台轴向的旋转自由度;然后,主轴和数控卧车系统母盘通过三面3-2-1定位完全固定;最后,数控卧车系统母盘和子盘-夹具-工件组合体采用“一面两销”定位完全固定.因为从卧车主轴到最终工件,两两构件之间都为完全固定,经由装配传递链路可知,工件只有相对于卧车基座的绕轴线旋转的自由度被保留.

由装配特征、装配层级及测量目标确定的尺寸链模型如图7所示,传递链路分为了两条支路,涵盖了同一子盘分别在找正台上以及在卧车母盘上的尺寸链传递信息.由于两条支路的尺寸与公差信息差异,使得测量特征的功能需求FR存在差异, 难以保证相同精度.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   多母盘装配系统的装配偏差分析基本尺寸链

Fig.7   Basic dimensional chain for assembly deviation analysis of multi-master assembly system


2 装配偏差仿真分析模型的实现与验证

2.1 基于VisVSA的模型实现

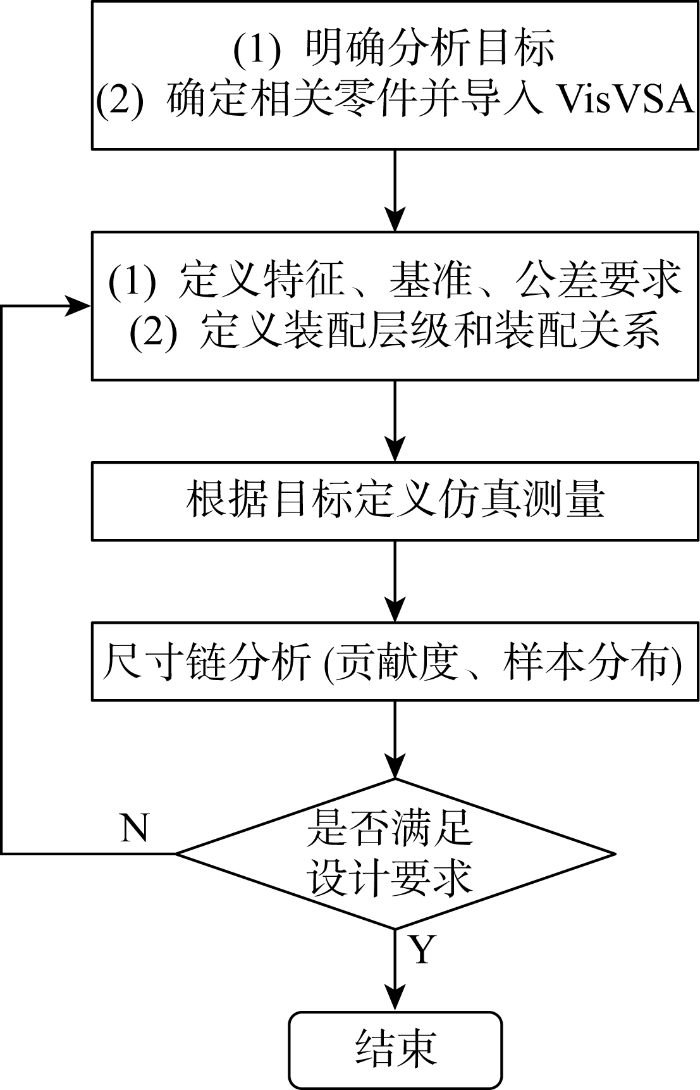
Teamcenter-VisVSA通过构建3D虚拟接触链模型的装配过程来预测产品的尺寸质量,被广泛应用于复杂系统的尺寸链分析,其分析流程如图8所示.首先,根据装配偏差分析的要求,定义装配特征,给出GD&T要求,明确装配顺序,建立了零件之间的装配关系,最后定义仿真测量目标.在研究中,仿真模型基于以下假设:

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   VisVSA装配偏差分析流程

Fig.8   Assembly deviation analysis process of VisVSA


(1) 在装配偏差分析建模过程中,所有公差及测量点的随机变动量在整体上趋向于以均值为中心的正态分布(+/-3σ分布);

(2) 仿真测量结果输出时,所有结果均基于 20 000 次Monte Carlo仿真去模拟真实的装配变动情况,同时运行偏差影响因子仿真,用来分析各装配特征对于目标特征的影响程度.

研究中,GD&T设计除已知结构件的设计公差外,其余在模型中未单独标注出的线性和角度公差参照ISO2768-1[26],截取部分标准如表1所示,研究中尺寸公差等级选取为中等(m)级别;未标注的形位公差参照ISO2768-2[27],截取部分标准如表2所示,研究中形位公差等级选取为H级.

表1   线性尺寸极限偏差数值

Tab.1  Limit deviation values for linear dimensionsmm

公差等级公差范围
标称尺寸
0.5~3 mm		标称尺寸
3~6 mm		标称尺寸
6~30 mm		标称尺寸
30~120 mm		标称尺寸
120~400 mm		标称尺寸
400~1 000 mm
f±0.05±0.05±0.10±0.15±0.20±0.30
m±0.10±0.10±0.20±0.30±0.50±0.80
c±0.15±0.20±0.50±0.80±1.20±2.00
v-±0.50±1.00±1.50±2.50±4.00

新窗口打开| 下载CSV


表2   平面度和直线度的一般公差

Tab.2  General tolerances for flatness and straightnessmm

公差等级公差范围
标称尺寸
0~10 mm		标称尺寸
10~30 mm		标称尺寸
30~100 mm		标称尺寸
100~300 mm		标称尺寸
300~1 000 mm		标称尺寸
1 000~3 000 mm
H0.020.050.10.20.30.4
K0.050.10.20.40.60.8
L0.10.20.40.81.21.6

新窗口打开| 下载CSV


2.2 准确性验证

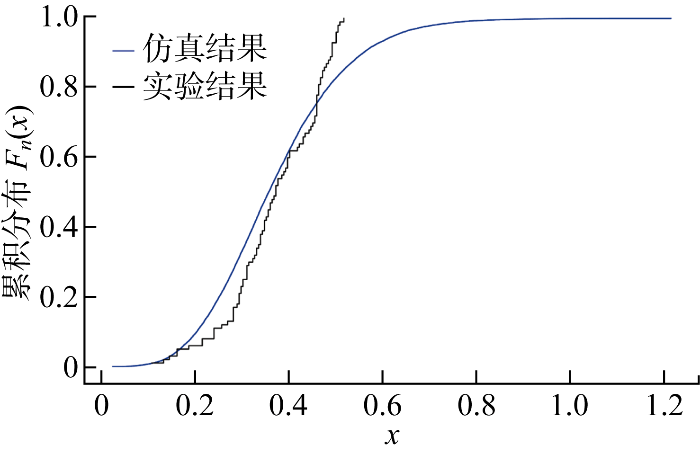
研究设计仿真实验以及批量的环形件径跳测量实验,采用K-S检验对实验结果进行评价,以此检验模型的准确性.本文设计的显著性水平α为0.01;原假设(H0)为:仿真模型的工件径向跳动输出和实验数据测量值来自同一分布;备择假设(H1):两个样本数据来自不同的分布.

为保证实验环境与仿真环境一致,对于2.1节的装配偏差模型进行调整,在原有的基础上增加人工找正约束,将特征1.4相对于基座的径跳控制在0.5 mm以内,与实验中人工找正误差控制限一致.在实验中,选取100个同一批次工件的径跳值.测量现场和径跳测量界面如图9所示;测量结果如表3所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   实验现场及测量界面

Fig.9   Experimental site and measurement interface


表3   实测数据

Tab.3  Measured datamm

序号测量值序号测量值序号测量值序号测量值序号测量值
10.52210.46410.40610.35810.30
20.46220.49420.47620.34820.49
30.22230.48430.51630.38830.46
40.34240.40440.46640.38840.46
50.37250.50450.40650.37850.47
60.37260.46460.51660.30860.37
70.50270.39470.50670.34870.15
80.49280.24480.22680.31880.14
90.49290.46490.47690.33890.36
100.49300.46500.33700.30900.36
110.46310.45510.33710.29910.36
120.16320.45520.32720.24920.36
130.46330.36530.31730.26930.32
140.50340.35540.31740.28940.19
150.39350.35550.31750.27950.51
160.39360.43560.28760.24960.34
170.30370.42570.30770.48970.34
180.45380.42580.30780.16980.47
190.44390.40590.28790.28990.50
200.43400.40600.30800.471000.11

新窗口打开| 下载CSV


本研究中,装配偏差分析结果基于Monte Carlo仿真所得结果的累积分布函数(CDF).取表3所示的测量结果为实验结果的CDF.两者的CDF如图10所示.计算得到p值为0.018,p值大于α则接受H0.由于样本量差异和测量系统误差,仿真分布与实际分布存在一定的差异,其量化指标为K-S统计量.计算方法为取两个样本数据中的最大观测值和最小观测值之间的差异.具体计算如下:

Dn,m=px|F1,n(x)-F2,m(x)|

式中:px|·|表示取所有x上的最大绝对差值;F1,n(x)为仿真样本的经验分布函数,n为样本量;F2,m(x)为实验样本的经验分布函数,m为样本量.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   K-S检验仿真结果和实验结果累积分布图

Fig.10   Cumulative distribution of simulation and experimental results of K-S test


经计算可知,仿真结果与测量结果分布的K-S统计量仅为0.152,结合上述的假设检验结果,验证了研究中提出的装配偏差传递模型的准确性.

3 多子盘-母盘互换过程中的精度损失规律研究

3.1 考虑多子盘差异输入的精度分析

3.1.1 仿真实验设计

对于多子盘差异输入模型,多个子盘装配到同一个母盘上.研究中采用Monte Carlo仿真不同的子盘输入情况,通过在子盘-工件子装配体的装配特征公差带中随机抽样m次,模拟得到多子盘输入下的m种可能装配状态.基于图8所示的模型实现流程,获得装配偏差分布的结果,研究中以装配偏差分布的6σ值对装配偏差分布进行量化,替代装配偏差分布情况,通过与零点定位系统子母盘出厂时的精度指标对比分析子盘差异输入时精度损失情况.

3.1.2 实验过程

模型的关键尺寸精度如表4所示(Normal表示正态分布),输入到如图4所示的误差分析链路中.基于2.1节中的假设,遵循实际工艺设计要求,设定偏差分析目标FR3子盘端跳${t}_{3}^{\mathrm{F}\mathrm{R}}$、FR4子盘径跳${t}_{4}^{\mathrm{F}\mathrm{R}}$上下限为:${t}_{3}^{\mathrm{F}\mathrm{R}}$的下控制限(LSL)为0,上控制限(USL)为0.012;${t}_{4}^{\mathrm{F}\mathrm{R}}$的LSL为0,USL为0.012.经过20 000次Monte Carlo仿真,其仿真结果如图11所示.

表4   多子盘装配偏差模型输入

Tab.4  Inputs to multi-subpanel assembly error transform modelmm

序号数值分布序号数值分布序号数值分布
e10.5Normalt1⌀0.4Normalt6⌀0.2Normal
e20.3Normalt20.012Normalt70.01Normal
e30.3Normalt30.012Normalt80.005Normal
e40.01Normalt4⌀0.2Normalt9⌀0.2Normal
e50.3Normalt5⌀0.2Normal

新窗口打开| 下载CSV


图11

新窗口打开| 下载原图ZIP| 生成PPT

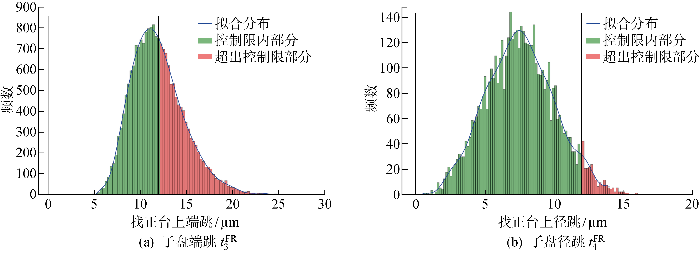
图11   子盘差异输入20 000次Monte Carlo仿真后的跳动分布情况

Fig.11   Distribution of radial runout for subpanel after 20 000 Monte Carlo simulations


3.1.3 实验结果分析

图11(a)为子盘差异输入情况下的零点定位系统子盘端跳分布情况,20 000 次Monte Carlo仿真结果分布在 0.004 7~0.031 8 区间内,与找正台-零点定位系统出厂精度小于0.012相比超差率(OOT)达到了46.32%,无法满足工艺要求;图11(b)为零点定位系统子盘径跳分布情况,20 000 次Monte Carlo仿真结果分布在0.007~0.016 1 区间内,OOT为4.98%近似满足工艺要求.通过对仿真数据统计分析计算均值(μ)、标准差(σ)、过程能力指数(CP)、过程能力K指数(CPK)、3σ下控制限(L3σ)、3σ上控制限(H3σ)等指标,如表5所示.其中针对端跳${t}_{3}^{\mathrm{F}\mathrm{R}}$的CPK为负值,径跳${t}_{4}^{\mathrm{F}\mathrm{R}}$的CPK为0.588,表明按照当前设计状态,多子盘差异输入情况下存在明显的装配超差,无法满足装配的工艺要求.

表5   子盘差异输入仿真结果

Tab.5  Simulation results of subpanel differential input

序号名义值μσOOT/%CPCPKLSLUSLL3σH3σ
FR1/${t}_{3}^{\mathrm{F}\mathrm{R}}$00.0120.002 946.320.670-0.00500.0120.004 70.031 8
FR2/${t}_{4}^{\mathrm{F}\mathrm{R}}$00.0010.007 64.980.8690.58800.0120.000 70.016 1

新窗口打开| 下载CSV


通过建立的多子盘差异输入装配偏差分析模型,得到了子盘差异输入情况下的精度损失规律,基于模型的输出分布能够对于找正台-零点定位系统的设计容差进行评估,并为后续的系统优化奠定基础.

3.2 考虑多母盘差异输入的精度分析

3.2.1 仿真实验设计

为研究子盘-夹具-工件装配体在找正台上装夹完成,由机械手转移到机床上后,工件装夹定位精度的损失情况,研究设计了多母盘差异输入误差传递模型,分析同一子盘在找正台上装配偏差分布与在机床上装配偏差分布的差异,揭示母盘差异输入时精度损失规律,模型的基本信息如1.2节所述.

3.2.2 实验过程

模型的关键尺寸精度如表6所示,将其输入到图7所示的误差分析链路中,基于2.1节中的假设,获得整个装配系统的装配偏差分析模型.设定偏差分析目标为工件相对机床基座端跳${t}_{3,\mathrm{M}}^{\mathrm{F}\mathrm{R}}$、工件相对找正台基座端跳${t}_{1,\mathrm{T}}^{\mathrm{F}\mathrm{R}}$、工件相对机床基座径跳${t}_{2,\mathrm{T}}^{\mathrm{F}\mathrm{R}}$、工件相对找正台基座径跳${t}_{4,\mathrm{T}}^{\mathrm{F}\mathrm{R}}$上下限为:${t}_{3,\mathrm{M}}^{\mathrm{F}\mathrm{R}}$和${t}_{1,\mathrm{T}}^{\mathrm{F}\mathrm{R}}$的LSL为0,USL为0.4;${t}_{2,\mathrm{M}}^{\mathrm{F}\mathrm{R}}$和${t}_{4,\mathrm{T}}^{\mathrm{F}\mathrm{R}}$的LSL为0,USL为0.5.仿真结果如图12所示.

表6   多母盘装配偏差模型输入

Tab.6  Inputs to multi-master assembly error transform model inputmm

序号数值分布序号数值分布序号数值分布
t11⌀0.4Normalt20⌀0.02Normale110.5Normal
t120.012Normalt21⌀0.2Normale120.3Normal
t130.012Normalt22⌀0.02Normale130.3Normal
t14⌀0.2Normalt230.005Normale140.01Normal
t15⌀0.2Normalt240.01Normale150.3Normal
t16⌀0.2Normalt25⌀0.02Normale160.1Normal
t170.01Normalt26⌀0.2Normale170.3Normal
t180.005Normalt270.02Normale180.1Normal
t19⌀0.2Normal

新窗口打开| 下载CSV


图12

新窗口打开| 下载原图ZIP| 生成PPT

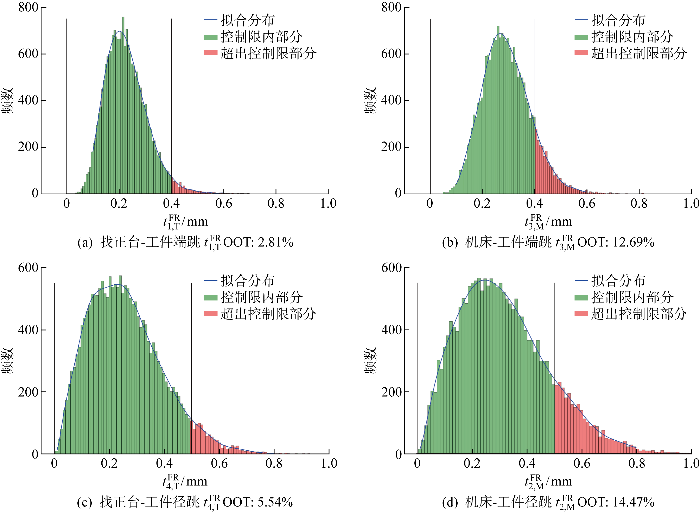
图12   母盘差异输入20 000次Monte Carlo仿真后的跳动分布情况

Fig.12   Runout distribution of master differential inputs after 20 000 Monte Carlo simulations


3.2.3 实验结果分析

图12(a)、12(b)为工件在找正台和机床上的端跳分布情况, OOT分别为2.81%和12.69%,图12(c)、12(d)为工件在找正台和机床上的径跳分布情况,OOT分别为5.54%和14.47%.当工件-子盘在找正台上找正完成,由机械手流转,将其装夹到机床母盘时,工件的端跳OOT增加了9.88%,工件的径跳OOT增加了8.93%,该数据与产线运行时工件在某道序加工完成后的超差率增加约10%的情况基本一致.

通过对仿真数据统计分析计算得到均值、标准差、超差率等指标,如表7所示.其中${t}_{3,\mathrm{M}}^{\mathrm{F}\mathrm{R}}$的CPK相较于找正台上降低了0.226,${t}_{2,\mathrm{M}}^{\mathrm{F}\mathrm{R}}$的CPK相较于找正台上降低了0.179,装夹定位的工艺能力下降,从而导致最终的工件加工超差.

表7   母盘差异输入仿真结果

Tab.7  Results of simulation of master differential input

序号名义值μσOOT/%CPCPKLSLUSLL3σH3σ
找正台/${t}_{1,\mathrm{T}}^{\mathrm{F}\mathrm{R}}$00.2290.079 12.810.8110.53600.40.0370.701
机床/${t}_{3,\mathrm{M}}^{\mathrm{F}\mathrm{R}}$00.2950.091 612.690.7080.31000.40.0520.821
找正台/${t}_{4,\mathrm{T}}^{\mathrm{F}\mathrm{R}}$00.2630.133 75.540.6740.48400.50.0110.752
机床/${t}_{2,\mathrm{M}}^{\mathrm{F}\mathrm{R}}$00.3210.164 014.470.5590.30500.50.0130.908

新窗口打开| 下载CSV


4 找正系统精度提升

找正系统精度可从装配工艺、公差设计两方面优化.研究以多母盘差异输入的装配偏差分析模型为基础,结合工件在找正台和机床上的径跳分布精度损失规律,提出基于输出分布差异与超差率差异的精度损失量化函数.通过优化找正台的基座结构,提升找正系统精度.

4.1 精度损失函数

为尽可能保证柔性产线运行时工件在机床上的装夹精度与找正台上的装夹精度一致,降低因多母盘差异输入导致的精度损失,分别设计了基于输出分布差异与超差率差异的精度损失量化函数.

量化函数g1(x):通过计算工件在不同母盘上的超差率差值量化精度损失.具体计算如下:

g1(x)=hm-ht

式中:hm为工件在机床上的超差率;ht为工件在找正台上的超差率.

量化指标g2(x):求解在不同母盘上的输出分布,通过计算分布之间的差异量化精度损失.具体计算如下:

g2(x)=px|FT,n(x)-FM,m(x)|

式中:FT,n(x)为工件在找正台母盘上的径跳/端跳累积分布函数;FM,m(x)为工件在机床母盘上的径跳/端跳累积分布函数.

4.2 优化案例

研究选取多母盘差异输入时工件的径跳损失为研究对象,以min g1(x)和min g2(x)为优化目标,装配系统的机械机构为优化变量.基于误差的“远端放大”效应,对找正台基座的向高度进行优化,综合考虑零点装夹找正系统精度与找正时间成本,选取找正策略为:基座数模向拉高100 mm.重新构建仿真模型,依照图8所示分析流程,得到优化后工件径跳在找正台和机床母盘上的分布情况,径跳分布优化前后结果对比如图13所示.

图13

新窗口打开| 下载原图ZIP| 生成PPT

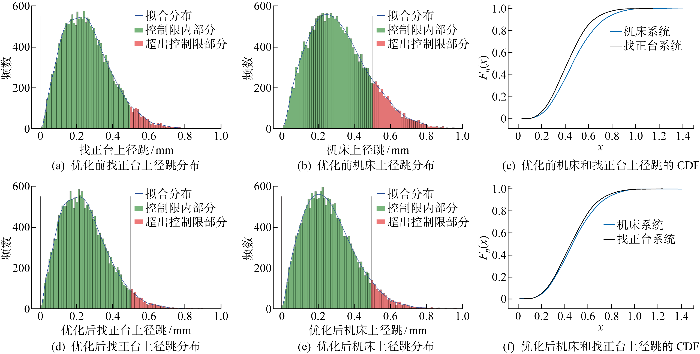
图13   工件径跳分布优化前后结果对比

Fig.13   Comparison of workpiece runout distribution before and after optimization


通过与优化前的径跳分布情况结果对比分析,基于式(2)计算g1(x),研究中提出的优化方案将多母盘差异输入时的超差率差异由11.53%降低到2.33%;通过对比分析优化前后机床和找正台上径跳的CDF,基于式(3)计算g2(x),输出分布的差异由 0.117 15 降低到 0.039 54,显著降低了多母盘差异输入带来的径跳误差分布差异,保证了组线模式下工件快换、流转加工的定位精度.

5 结论

本文针对不确定性输入下的找正系统,研究了误差传递累积规律与精度损失规律,建立了考虑零点定位系统子母盘差异的装配偏差分析模型,并通过实验验证了偏差传递模型的准确性.通过优化找正台基座结构,显著提升了多母盘差异输入时工件的径跳定位精度, 为航空发动机机匣自动化组线加工找正台-零点定位系统的优化设计及组线模式下工件装夹定位精度的提升提供了理论依据.本研究的研究内容和成果如下:

(1) 构建了考虑不确定性输入的找正台装配系统尺寸链分析模型,通过等效模拟各项尺寸公差,并采用显著性水平为0.01的K-S检验(p值大于α),验证了仿真结果与实验数据分布的一致,证明了模型的准确性.

(2) 建立了多子盘差异输入和多母盘差异输入两种工况下的装配偏差传递模型.通过仿真与实验对比分析,揭示了多子盘-母盘互换过程中的精度损失规律.研究发现:在子盘差异输入时,定位系统精度由小于0.012下降至 0.004 7~0.031 8;在母盘差异输入时,在机床上的超差率较找正台增加约10%.

(3) 提出了基于输出分布差异与超差率差异的精度损失量化函数.针对多母盘差异输入导致径跳精度损失问题,通过优化找正台基座的结构,超差率的差异值从11.53%降至2.33%;径跳输出分布差异从 0.117 15 降至0.039 54,显著提高了工件在机床上装夹精度与找正台上装夹精度的一致性.

参考文献

WANG X, ZHAO B, DING W, et al.

A short review on machining deformation control of aero-engine thin-walled casings

[J]. The International Journal of Advanced Manufacturing Technology, 2022, 121(5/6): 2971-2985.

[本文引用: 1]

周俊杰, 余建波.

基于机器视觉的加工刀具磨损量在线测量

[J]. 上海交通大学学报, 2021, 55(6): 741-749.

DOI:10.16183/j.cnki.jsjtu.2020.083      [本文引用: 1]

针对实际生产中测量刀具磨损需要人工操作、停机检测等问题,开发了一个基于机器视觉的加工刀具磨损测量系统.首先提出基于Laplacian算子边缘信息的Otsu分割算法将图像二值化,再通过基于形态学的Canny算子边缘检测粗定位及图像配准提取清晰的刀具磨损区域.最后,使用基于Zernike矩的亚像素边缘检测方法提高测量精度,并通过主曲线方法拟合亚像素边缘点得到光滑的边缘曲线,实现了刀具磨损量的在线测量.实际加工过程中的刀具磨损测试结果表明,该系统检测自动化程度高、运行速度快、测量精度可以达到微米级,可以有效地应用于工业上对加工刀具磨损的实时监控.

ZHOU Junjie, YU Jianbo.

Online measurement of machining tool wear based on machine vision

[J]. Journal of Shanghai Jiao Tong University, 2021, 55(6): 741-749.

[本文引用: 1]

唐林, 周良明, 刘卫武, 等.

基于零点定位技术的中小航空结构件快速换装技术研究

[J]. 制造业自动化, 2015, 37(21): 19-21.

[本文引用: 1]

TANG Lin, ZHOU Liangming, LIU Weiwu, et al.

Based on zero positioning technology of small and medium-sized aircraft structure metamorphosis technology research

[J]. Manufacturing Automation, 2015, 37(21): 19-21.

[本文引用: 1]

LI X, YANG Y, LI L, et al.

An approach for optimising the fixturing configuration in flexible machining fixtures

[J]. International Journal of Production Research, 2021, 59(20): 6223-6240.

[本文引用: 1]

董义军, 张功, 张洁.

单无人搬运车/单缓冲区约束的柔性生产系统调度研究

[J]. 上海交通大学学报, 2010, 44(4): 528-534.

[本文引用: 1]

DONG Yijun, ZHANG Gong, ZHANG Jie.

Scheduling with single AGV and single buffer area for flexible production on system

[J]. Journal of Shanghai Jiao Tong University, 2010, 44(4): 528-534.

[本文引用: 1]

BJORKE O. Computer-aided tolerancing[M]. 2nd ed. New York, USA: ASME Press, 1989.

[本文引用: 1]

余海东, 高畅, 赵勇, 等.

机械产品装配偏差分析方法研究进展与展望

[J]. 机械工程学报, 2023, 59(9): 212-229.

DOI:10.3901/JME.2023.09.212      [本文引用: 1]

机械产品装配是制造过程的最终阶段,装配质量对机械产品的服役性能和可靠性有直接影响。建立合理的数学模型描述机械产品装配过程中的偏差传递、累积和淹没规律,对产品的容差设计与故障诊断,并进一步提高产品性能和服役周期具有重要意义。归纳并总结了现有机械产品装配偏差分析的理论方法,从基于刚性假设的偏差分析与考虑柔性变形的偏差模型两个方面系统地论述了目前机械产品装配偏差传递分析的研究进展。刚性偏差分析围绕尺寸链模型与确定性定位模型展开,并对基于尺寸链理论的雅可比旋量方法做了详细介绍与具体的应用分析。对于主流的柔性装配偏差传递建模方法,详细论述了影响系数法与装配偏差场传递模型的理论建模过程与及其应用范围,并从大型结构装配的现场应用出发,对装配偏差场传递模型进行了具体的案例分析。针对目前航空航天等领域机械产品大尺寸、高承载的发展趋势,提出了对于局部刚性整体柔性的大型结构装配偏差预测的难点以及研究展望。

YU Haidong, GAO Chang, ZHAO Yong, et al.

Progress and prospect on assembly deviation propagation of mechanical products

[J]. Journal of Mechanical Engineering, 2023, 59(9): 212-229.

DOI:10.3901/JME.2023.09.212      [本文引用: 1]

Mechanical assembly is the final stage of the manufacturing process of the products. Assembly quality has a direct impact on the service performance and reliability of mechanical products. The establishment of the mathematical model, which may describe the transmission, accumulation and annihilation of deviation in the assembly process, is of great significance for tolerance design, fault diagnosis, and further improve the performance and service life of the products. The existing theoretical methods of assembly deviation analysis of mechanical products are summarized. Research progress of the assembly deviation analysis of the mechanical products is discussed through the deviation analysis based on rigid assumption and the analysis methods considering flexible deformation. The rigid deviation analysis is carried out around the dimension chain model and the deterministic locating method. The Jacobian-Torsor method based on dimension chain theory is introduced and analyzed in detail. The theoretical modeling process and application scope of the method of influence coefficient and assembly deviation field model are discussed in detail, which are the methods of flexible assembly deviation analysis. A specific case analysis of assembly deviation field model is carried out based on the engineering application of the assembly for large structure. Finally, the difficulties and research prospects of the analysis of the assembly deviation of the local rigid and integral flexible large-scale structure are discussed, which are aimed at the development trend of large size and high capacity of mechanical products in aerospace and other fields.

王聪伟, 于贺, 许俊伟, 等.

基于VisVSA的舵系统机械零位和活动间隙分析

[J]. 机械设计与研究, 2018, 34(2): 187-191.

[本文引用: 1]

WANG Congwei, YU He, XU Junwei, et al.

The mechanical zero and clearance analysis of rudder systems based on VisVSA

[J]. Machine Design and Research, 2018, 34(2): 187-191.

[本文引用: 1]

林嘉, 杨夫勇, 郑丞, 等.

定位方案三维稳健性分析及一般解推导

[J]. 上海交通大学学报, 2019, 53(4): 405-412.

DOI:10.16183/j.cnki.jsjtu.2019.04.003      [本文引用: 1]

空间三维定位涉及参数众多, 定位误差分析模型形式复杂, 现有研究多通过数值方法求解稳健方案, 只能得到特殊解而无法获得一般解, 难以揭示共性规律. 为此, 结合常用的工程条件和习惯引入2个附加假设, 在对三维确定性定位误差分析模型进行简化的基础上, 对定位方案的稳健性进行解析分析, 并给出最稳健方案的一般解. 以采用经典一面 (3定位块) 两销定位方式的某平板工件为例, 将该一般解与商用三维偏差分析软件VisVSA的分析结果进行了对比验证, 进而应用该一般解对某飞机后机身冲压排气管的安装定位方案进行了优化.

LIN Jia, YANG Fuyong, ZHENG Cheng, et al.

Robustness analysis of locating scheme for 3D workpieces and its general solution

[J]. Journal of Shanghai Jiao Tong University, 2019, 53(4): 405-412.

[本文引用: 1]

王仲奇, 杨盼, 陈世洁, 等.

飞机舱门数字孪生模型构建及偏差传递分析研究

[J]. 航空制造技术, 2022, 65(12): 36-47.

[本文引用: 1]

WANG Zhongqi, YANG Pan, CHEN Shijie, et al.

Research on construction of digital twin model and deviation transfer analysis of cabin door of airplane

[J]. Aeronautical Manufacturing Technology, 2022, 65(12): 36-47.

[本文引用: 1]

姚利民, 张道刘, 侯秀娟, 等.

考虑焊接变形的装配偏差分析在动力集中型动车组中的应用

[J]. 上海交通大学学报, 2019, 53(3): 260-268.

DOI:10.16183/j.cnki.jsjtu.2019.03.002      [本文引用: 1]

焊接是列车车体装配过程中应用最为广泛的连接方式，焊接变形会对动车组装配尺寸精度产生较大的影响.针对动车组侧墙窗口模块焊接装配尺寸控制问题，利用热弹塑性有限元法提取3种典型焊接接头的固有应变，并基于固有应变法得到窗口模块的焊后变形量；结合三维尺寸装配偏差分析，最终给出计及焊接收缩量变化的侧墙窗口模块的偏差结果.将模拟结果与实测数据进行对比分析，结果表明：考虑焊接变形因素的装配偏差模拟结果与实际测量值较为吻合，故该方法可对动车组侧墙窗口模块的焊接装配偏差进行有效且准确的预测.

YAO Limin, ZHANG Daoliu, HOU Xiujuan, et al.

Assembly deviation simulation considering welding deformation applied on electric multiple unit

[J]. Journal of Shanghai Jiao Tong University, 2019, 53(3): 260-268.

[本文引用: 1]

TANG S Y, GUAN D, WU X, et al.

Analysis on virtual assembly tolerance for pitch-adjustable lateral propulsion device

[J]. Procedia CIRP, 2015, 27: 131-136.

[本文引用: 1]

RAMNATH S, HAGHIGHI P, CHITALE A, et al.

Comparative study of tolerance analysis methods applied to a complex assembly

[J]. Procedia CIRP, 2018, 75, 208-213.

[本文引用: 1]

LITWA F, GOTTWALD M, SPUDEIKO S, et al.

Optimization coupling approach for/with non-static point 16 based CAT-models

[J]. Procedia CIRP, 2016,43:166-171.

[本文引用: 1]

倪军.

数控机床误差补偿研究的回顾及展望

[J]. 中国机械工程, 1997(1): 29-33.

[本文引用: 1]

NI Jun.

Review and prospect of error compensation for CNC machine tools

[J]. China Mechanical Engineering, 1997(1): 29-33.

[本文引用: 1]

刘鹏, 洪军, 刘志刚, 等.

采用自适应遗传算法的机床公差分配研究

[J]. 西安交通大学学报, 2016, 50(1): 115-123.

[本文引用: 1]

LIU Peng, HONG Jun, LIU Zhigang, et al.

Research on the tolerance allocation of machine tools based on adaptive genetic algorithm

[J]. Journal of Xi’an Jiaotong University, 2016, 50(1): 115-123.

[本文引用: 1]

钱鹏, 王国亮, 朱文峰.

柔性变形下车窗升降三维装配公差建模及优化

[J]. 上海交通大学学报, 2020, 54(11): 1134-1141.

[本文引用: 1]

QIAN Peng, WANG Guoliang, ZHU Wenfeng.

Modeling and optimization of 3D assembly tolerance for window lifting under flexible deformation

[J]. Journal of Shanghai Jiao Tong University, 2020, 54(11): 1134-1141.

[本文引用: 1]

刘奕颖, 郭俊康, 李宝童, 等.

精密机床加工误差灵敏度分析与公差设计

[J]. 机械工程学报, 2019, 55(17): 145-152.

DOI:10.3901/JME.2019.17.145      [本文引用: 1]

加工精度是衡量精密机床加工性能的重要指标，当前针对提高加工精度的研究主要围绕误差补偿展开，缺少根据加工件的精度要求而进行机床运动轴公差设计的研究。从公差设计的角度出发，通过机床空间运动误差建模、蒙特卡洛法模拟，实现最小二乘法评价零件加工精度；利用正交试验方法，得到某项精度要求与机床运动轴误差的公差带的多组对应数据，通过多元线性回归，进行灵敏度分析；同时基于自适应遗传算法，给出了运动轴误差的公差设计方法，保证所设计的公差带在装配工艺上的可行性。通过对某精密卧式坐标镗床29项误差公差带设计，验证了该方法的可行性。

LIU Yiying, GUO Junkang, LI Baotong, et al.

Sensitivity analysis and tolerance design for precision machine tool

[J]. Journal of Mechanical Engineering, 2019, 55(17): 145-152.

DOI:10.3901/JME.2019.17.145      [本文引用: 1]

The least squares method is used to evaluate the part machining precision from the perspective of tolerance design, by using the machine tool space motion error modeling, the Monte Carlo method and the Matlab software, and the precision requirements and the machine movement axis are obtained by the orthogonal test method. Multiple sets of corresponding data of the error tolerance band, through multiple linear regression, sensitivity analysis. At the same time based on adaptive genetic algorithm, a tolerance design method for motion axis error is given to ensure the feasibility of the designed tolerance zone in the assembly process. The feasibility of the method is verified through the design of 29 error tolerance bands for a precision horizontal coordinate boring machine.

WU H, ZHENG H, LI X, et al.

A geometric accuracy analysis and tolerance robust design approach for a vertical machining center based on the reliability theory

[J]. Measurement, 2020, 161: 107809.

[本文引用: 1]

WU D, ZHAO B, WANG H, et al.

Investigate on computer-aided fixture design and evaluation algorithm for near-net-shaped jet engine blade

[J]. Journal of Manufacturing Processes, 2020, 54: 393-412.

[本文引用: 1]

WU B, ZHENG Z, WANG J, et al.

Layout optimization of auxiliary support for deflection errors suppression in end milling of flexible blade

[J]. The International Journal of Advanced Manufacturing Technology, 2021, 115(5/6): 1889-1905.

[本文引用: 1]

MICHAEL THOMAS REX F, ANDREWS A, et al.

Optimization of flexible fixture layout to improve form quality using parametric finite element model and mixed discrete-integer genetic algorithm

[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2022, 236(1): 16-29.

[本文引用: 1]

DU J, LIU C, LIU J, et al.

Optimal design of fixture layout for compliant part with application in ship curved panel assembly

[J]. Journal of Manufacturing Science and Engineering, 2021, 143(6): 061007.

RAMESH M, SUNDARARAMAN K A, SABAREESWARAN M, et al.

Development of hybrid artificial neural network-particle swarm optimization model and comparison of genetic and particle swarm algorithms for optimization of machining fixture layout

[J]. International Journal of Precision Engineering and Manufacturing, 2022, 23(12): 1411-1430.

[本文引用: 1]

ZHOU X, MA J, ZHOU W, et al.

Forming-based geometric correction methods for thin-walled metallic components: A selective review

[J]. The International Journal of Advanced Manufacturing Technology, 2023: 1-23.

[本文引用: 1]

ISO/TC 3. General tolerances—Part 1: Tolerances for linear and angular dimensions without individual tolerance indications: ISO 2768-1[S]. Switzerland: International Organization for Standardization, 1989.

[本文引用: 1]

ISO/TC 3. General tolerances—Part2: Geometrical tolerances for features without individual tolerance indications: ISO 2768-2[S]. Switzerland: International Organization for Standardization, 1989.

[本文引用: 1]

/

〈 〉