裂纹形态对SG夹层玻璃开裂后硬化效应的影响机制

doi:10.16183/j.cnki.jsjtu.2023.549

裂纹形态对SG夹层玻璃开裂后硬化效应的影响机制

彭沈楠, 杨健^,, 王星尔, 陆敏铖, 朱禹翰

上海交通大学海洋工程国家重点实验室;上海市公共建筑和基础设施数字化运维重点实验室, 上海 200240

Influence and Mechanism of Crack Morphology on Post-Fracture Stiffening Effect of SG-laminated Glass

PENG Shennan, YANG Jian^,, WANG Xing’er, LU Mincheng, ZHU Yuhan

State Key Laboratory of Ocean Engineering; Shanghai Key Laboratory for Digital Maintenance of Buildings and Infrastructure, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 杨健,教授,博士生导师;E-mail:j.yang.1@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-10-31 修回日期: 2024-01-16 接受日期: 2024-02-19

基金资助:

国家自然科学基金(52078293)

Received: 2023-10-31 Revised: 2024-01-16 Accepted: 2024-02-19

作者简介 About authors

彭沈楠(1999—),硕士生,从事夹层玻璃开裂后力学性能研究.

摘要

SG离子型中间膜夹层热钢化玻璃(简称SG夹层玻璃)在拉伸硬化效应作用下,破坏后仍具有一定的残余强度,裂纹形态参数(如碎片密度和碎片分布)对其后破坏性能有显著影响.准确评估和预测夹层玻璃开裂后的性能,是提升其成本和性能综合效益的重要基础.目前,裂纹形态对夹层玻璃开裂后硬化效应及影响机制的研究尚显不足.首先通过SG夹层玻璃随机裂纹拉伸试验发现,碎片密度通过影响应力路径对夹层玻璃的开裂后性能产生影响,表现为抗拉强度和等效刚度随碎片密度增大分别呈线性和指数下降.随后,基于试验结果提出有效黏结区域假设,并建立精细化有限元模型,实现了对夹层玻璃开裂后抗拉性能的准确预测,同时探讨了碎片层交错程度对夹层玻璃开裂后硬化效应的影响规律.

关键词： 夹层热钢化玻璃; SG夹层玻璃; 开裂后硬化效应; 裂纹形态; 数值分析

Abstract

The effect of tension stiffening allows SG-laminated tempered glass to preserve specific post-fracture mechanical performance, which is significantly influenced by crack morphology, including fragment density and distribution. Accurately evaluating and predicting the post-fracture performance of laminated glass is essential for balancing cost and performance. However, limited work has addressed how crack morphology affects the stiffening behavior of laminated glass after fracture. In this paper, a series of random-cracked tensile tests on SG-laminated tempered glass is performed. The results reveal that the fragment density influences the post-fracture performance of SG-laminated glass by affecting the stress trajectory, and the tensile strength and equivalent stiffness decrease linearly and exponentially, respectively, with increasing fragment density. Afterwards, according to the experimental results, a hypothesis of the effective bonding is proposed and an improved finite element model is then developed. The proposed model accurately predicts the post-fracture tensile performance of laminated glass. Finally, the impact of fragment offset on the stiffening effect is discussed.

Keywords： laminated tempered glass; SG-laminated glass; post-fracture stiffening effect; crack morphology; numerical analysis

PDF (32854KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

彭沈楠, 杨健, 王星尔, 陆敏铖, 朱禹翰. 裂纹形态对SG夹层玻璃开裂后硬化效应的影响机制[J]. 上海交通大学学报, 2025, 59(8): 1123-1132 doi:10.16183/j.cnki.jsjtu.2023.549

PENG Shennan, YANG Jian, WANG Xing’er, LU Mincheng, ZHU Yuhan. Influence and Mechanism of Crack Morphology on Post-Fracture Stiffening Effect of SG-laminated Glass[J]. Journal of Shanghai Jiaotong University, 2025, 59(8): 1123-1132 doi:10.16183/j.cnki.jsjtu.2023.549

夹层玻璃因其通透、美观、高强的特点广泛用作建筑中的玻璃结构承重构件,被称为“结构玻璃”^[1-2].玻璃是典型的脆性材料^[3],易受到爆炸冲击^[4]或风致飞射物撞击^[5-6]而破坏,但由于中间层的作用,开裂后的夹层玻璃仍然具有一定的残余强度^[7-8].目前部分国家的规范^[9]已开始逐步在设计阶段考虑夹层玻璃的开裂后性能,然而相关理论与试验研究较少,规范未能给出具体的计算方法,普遍仍采用“牺牲层”^[10]概念来满足结构玻璃的设计安全要求,导致材料和成本耗费较高.为提升结构玻璃的性能和成本效益综合性,明确夹层玻璃开裂后力学性能的关键影响因素和潜在的调控方法尤为重要.

现有研究主要侧重于从黏结面性能、中间层材料、碎片尺寸等角度探讨夹层玻璃开裂后性能的影响因素.Samieian等^[11]通过随机裂纹拉伸试验(random-cracked tensile test, RCT)研究了界面黏结性能对夹层玻璃的开裂后力学性能影响,结果表明随着黏结性能的提升,开裂后夹层玻璃的初始弹性模量和极限应力逐步增大.Biolzi等^[12]对聚乙烯醇缩丁醛(PVB)中间层和PVB/聚碳酸酯(PC)复合中间层夹层热钢化玻璃梁的开裂后性能进行了试验研究,研究发现当两侧玻璃层完全开裂时,复合中间层相比PVB中间层能够为开裂后的夹层玻璃提供更高的抗弯能力和更长的持载时间.Biolzi等^[13]对SG离子型中间膜夹层热钢化玻璃(简称SG夹层玻璃)的开裂后力学性能进行了试验研究,指出由于玻璃碎片与SG中间层间的剪力传递,玻璃碎片能够对中间层产生拉伸硬化(tension stiffening)效应,显著提高开裂后夹层玻璃的整体抗拉刚度.Yang等^[14]对乙烯-醋酸乙烯酯共聚物(EVA)中间层和EVA/PC复合中间层的夹层玻璃试件进行贯穿裂纹拉伸试验(through-cracked tensile test, TCT),详细分析了不同温度、湿热、光照等老化条件对夹层玻璃试件开裂后性能的影响,并指出碎片间的局部桥接能力对于夹层玻璃的开裂后性能影响显著.Wang等^[15]通过离散元(DEM)方法建立了PVB夹层玻璃的多条贯穿裂纹拉伸试验(MTCT)数值模型,发现拉伸硬化效应通过应力路径来影响夹层玻璃的开裂后性能,并且碎片密度、裂纹交错、界面脱胶对应力路径均产生影响.朱禹翰等^[16-17]对物理热钢化玻璃裂纹形态的影响因素展开了试验研究,研究发现物理热钢化玻璃的碎片密度、圆度、周长等裂纹形态指标主要取决于玻璃厚度和表面应力,并指出裂纹形态与玻璃开裂时的应变能释放有关.陈素文等^[18]考虑了碎片边长大于15 mm、边长5~10 mm、边长小于5 mm 3种碎片尺寸范围来研究玻璃碎片尺寸对于浮法夹层玻璃开裂后性能的影响,研究发现,随着碎片尺寸减小,PVB浮法夹层玻璃承载能力降低、变形能力提高;对于SG浮法夹层玻璃,各尺寸碎片在加载过程中均会二次开裂成更致密的碎片,因此碎片尺寸对SG浮法夹层玻璃的承载力与变形能力影响较小.

尽管目前国内外对于夹层玻璃开裂后力学性能的影响因素已有部分研究,但针对玻璃层裂纹形态对SG夹层玻璃开裂后硬化效应及其影响机制的定量和系统分析仍不充分.本文以SG夹层玻璃的开裂后硬化效应为研究对象:首先,通过对不同钢化水平和厚度的SG夹层玻璃制成的随机裂纹试件进行准静态单轴拉伸试验,研究碎片密度对夹层热钢化玻璃开裂后硬化效应的影响机制;其次建立基于Voronoi几何重构和有效黏结假设的精细化有限元模型,用于预测开裂后夹层热钢化玻璃的抗拉性能,并分析碎片交错程度对开裂后硬化效应的影响规律.本研究拓展了夹层玻璃开裂后性能领域的研究深度,旨在为结构玻璃的性能分析和设计提供参考.

1 试验概况

1.1 试件设计与制备

全局碎片密度λ_G是描述热钢化玻璃裂纹形态的关键参数之一,其定义为单位面积内的碎片数量(单位为mm^-2),主要受玻璃的表面应力和厚度影响^[16,19].为研究碎片密度对夹层热钢化玻璃开裂后硬化效应的影响,玻璃层选用低、中、高3种钢化水平的6 mm厚钢化玻璃(依次编号为6a、6b、6c),以及8、12 mm厚低钢化水平的钢化玻璃(依次编号为8a、12a),长、宽分别为600、300 mm.中间层采用可乐丽集团的SentryGlas^®离子型中间膜,名义厚度为1.52 mm.夹层玻璃的构型信息如表1所示.

表1 夹层热钢化玻璃试件信息

Tab.1 Configurations of laminated tempered glass

试件编号	钢化水平	表面应力/MPa	夹层玻璃厚度/mm
6a	低	76.82	6/1.52/6
8a	低	69.53	8/1.52/8
12a	低	60.80	12/1.52/12
6b	中	91.50	6/1.52/6
6c	高	103.41	6/1.52/6

新窗口打开| 下载CSV

通过锥形金刚钻头垂直玻璃表面敲击的方式对夹层玻璃施加起裂荷载,起裂点位于玻璃长边中点.采用机械切割方式,从开裂后的大尺寸夹层热钢化玻璃中切割获得5块60 mm×300 mm的单轴拉伸 (UT)试件.试件两端夹持长度为60 mm,中间拉伸段长度为180 mm.为减少拉伸过程中试件与夹具间的滑移,在夹持两端黏结铝片增大试件与夹具间的摩擦.以8 mm厚低钢化水平的夹层热钢化玻璃试件为例,开裂后夹层热钢化玻璃单轴拉伸试件的制备方案和试件编号如图1所示,图中“×”形标记处为起裂点.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 开裂后夹层热钢化玻璃单轴拉伸试件制备(mm)

Fig.1 Preparation of UT specimens of fractured laminated tempered glass (mm)

采用高分辨率工业相机获取夹层热钢化玻璃单侧开裂后的裂纹图案,并通过识别裂纹图像中的闭合区域实现碎片密度统计.将每个试件视为独立工况,共计25个试验工况,如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 各试验工况的单轴拉伸试件碎片密度

Fig.2 Fragment density of each random-cracked UT specimens

1.2 试验加载方式与量测

试验中采用力试科仪公司的LE5504系列微机控制电子万能试验机进行加载,在试件两端利用液压夹具施加夹持荷载,防止拉伸过程中试件滑移,试验加载装置如图3所示.保持0.18 mm/s加载速率对试件进行准静态(应变率为0.001 s^-1)单轴拉伸,当试验机读数大幅下降或试件中间层断裂时停止加载.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 单轴拉伸试验装置

Fig.3 Setup of UT test

试验过程中通过万能试验机配套传感器获取加载过程中荷载-位移数据,采用高清相机对试件正面破坏和变形情况进行记录,以观察拉伸过程中碎片是否出现二次开裂现象.

2 试验分析

2.1 失效过程与失效模式

图4以试件6a-5和6b-4为例展示了不同碎片密度单轴拉伸试件的失效过程.试件6a-5的失效过程如图4(a)所示.可以观察到在加载过程中裂纹逐渐扩展增粗,碎片边缘逐步开裂形成致密的玻璃碎渣并掉落.当加载时间30 s时,试件下方的玻璃碎片有两处出现较为明显的二次开裂,并在前后两侧玻璃层形成对齐裂缝.随后,对齐裂缝处的SG中间层继续受拉伸长,当加载时间50 s时,可以明显观察到SG中间层断裂失效.此外,由于SG中间层优异的黏结性能,加载过程中碎片几乎不出现明显的脱胶现象.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 单轴拉伸试件失效过程

Fig.4 Failure process of UT specimens

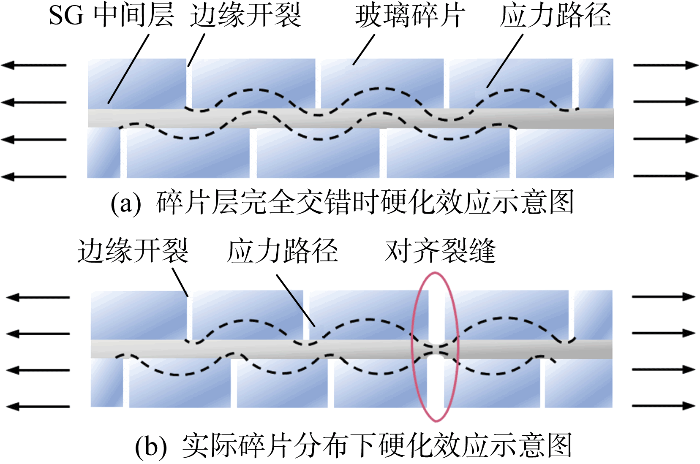
试件6b-4的失效过程如图4(b)所示.可以发现在加载开始前,相比于试件6a-5,碎片密度较大的试件6b-4存在较多边缘预开裂的玻璃碎片.这一方面是由于钢化水平越高,钢化玻璃开裂瞬间释放的应变能越大,更容易造成碎片边缘预开裂;另一方面是由于钢化玻璃在开裂后的一段时间内,残余应变能会持续释放,部分残余应变能较高的碎片会在此过程中发生二次开裂,并形成碎片团簇.试件6b-4在加载过程中,由于玻璃碎片尺寸较小,碎片仅在边缘产生局部二次开裂,且在预裂纹影响下未观察到明显的局部脱胶.当加载时间40 s时,试件上方在碎片边缘开裂处形成前后对齐裂缝,SG中间层在对齐裂缝处受拉变形并逐步撕裂.

受对齐裂缝的数量和位置影响,SG中间层的撕裂位置具有随机性,如图5所示.大部分试件撕裂起始位置位于中部拉伸段的1/4~1/3处,如图5中的试件6a-5,SG中间层在左侧下端1/4处起裂后,撕裂路径沿碎片轮廓先逐步向右上方延伸,后转为水平;靠近夹持端部区域亦有试件出现中间层断裂,如试件6b-3,并且其撕裂路径受碎片轮廓影响表现为锯齿状.此外,由于对齐裂缝未必会贯穿试件,SG中间层可能会发生多处撕裂,如试件6c-5中SG中间层先沿着对齐裂缝①撕裂,随后又沿着对齐裂缝②再次发生撕裂.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 SG中间层的断裂路径与断口形状

Fig.5 Tearing path and fracture shape of the SG interlayer

2.2 开裂后硬化效应

图6分区展示了不同钢化水平的6 mm厚单轴拉伸试件和不同厚度的低钢化水平单轴拉伸试件的荷载-位移曲线.由图6可见,在荷载达到峰值前,荷载-位移曲线近似呈抛物线型,并且相同厚度-钢化水平组合单轴拉伸试件的荷载-位移曲线具有较强一致性.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 开裂后夹层热钢化玻璃单轴拉伸的荷载-位移曲线

Fig.6 Force-displacement curves of UT tests of fractured laminated tempered glass specimens

定义抗拉强度σ_b为单轴拉伸试件的峰值荷载F_max与SG中间层名义截面面积S之比,等效抗拉刚度E_eff为抗拉强度σ_b与荷载-位移曲线上峰值荷载所在点的对应名义应变ε_b之比.抗拉强度与等效抗拉刚度的计算式如下:

(1)σ_b=

$\frac{{F}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{S}$

(2)E_eff=

$\frac{{\sigma }_{\mathrm{b}}}{{\epsilon }_{\mathrm{b}}}$

$\frac{{\sigma }_{\mathrm{b}}}{\delta /L}$

式中:δ为荷载峰值点对应的位移;L为试件有效变形长度,其值为180 mm.各组试件的平均抗拉强度和平均等效抗拉刚度如表2所示.表中:${\stackrel{-}{\sigma }}_{\mathrm{b}}$为平均抗拉强度;${\overline{E}}_{\mathrm{e}\mathrm{f}\mathrm{f}}$为平均等效抗拉刚度.

表2 单轴拉伸试件的平均抗拉强度与等效抗拉刚度

Tab.2 Mean tensile strength and effective stiffness of UT test specimens

试件编号	${\stackrel{-}{\sigma }}_{\mathrm{b}}$/MPa	${\stackrel{-}{\sigma }}_{\mathrm{b}}$增强率/%	${\overline{E}}_{\mathrm{e}\mathrm{f}\mathrm{f}}$/MPa	${\overline{E}}_{\mathrm{e}\mathrm{f}\mathrm{f}}$增强率/%
SG	28.38	—	570.89	—
6a	40.20	41.7	2 664.16	366.7
6b	36.72	29.4	1 166.13	104.3
6c	30.83	8.6	917.85	60.8
8a	37.66	32.7	4 770.89	735.7
12a	36.74	29.5	4 700.46	723.3

新窗口打开| 下载CSV

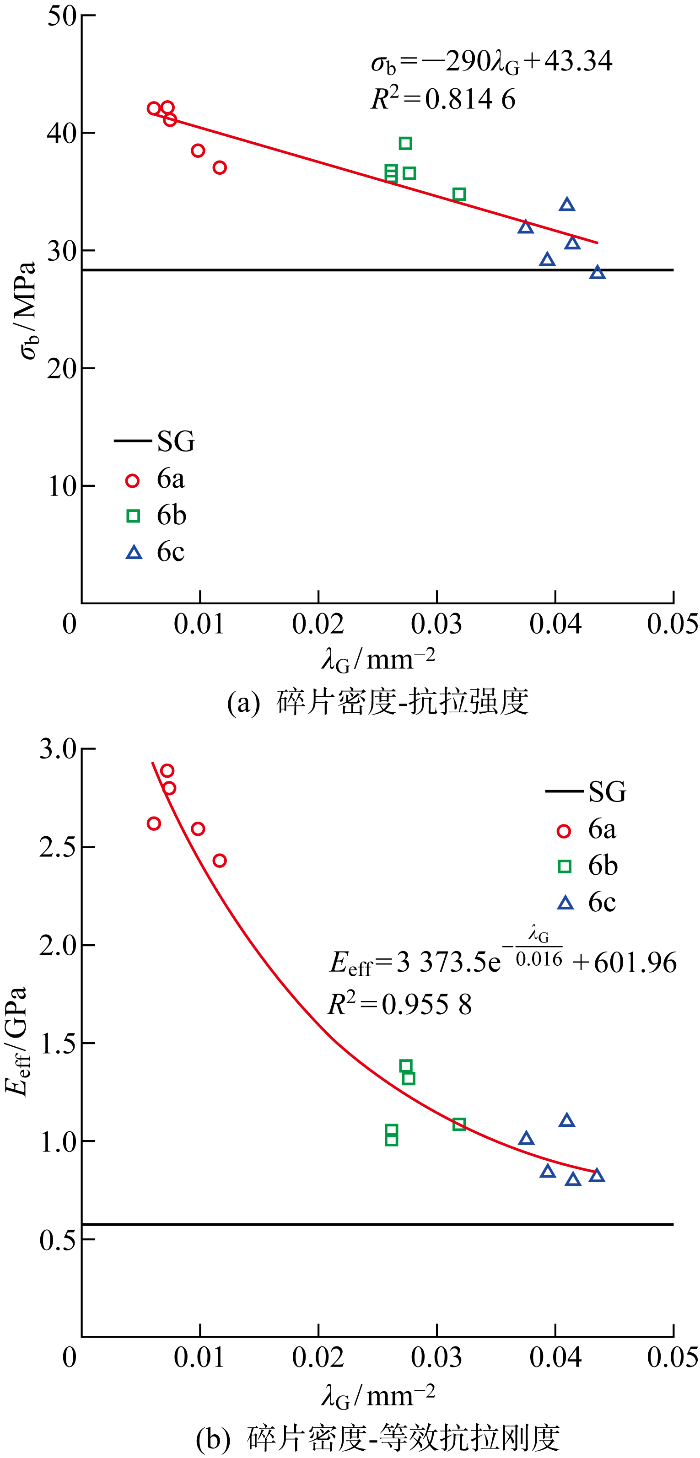
从表2可知,碎片层的存在使夹层玻璃展现出明显的开裂后硬化效应.单轴拉伸试件的抗拉强度与等效抗拉刚度相较于SG中间层均有较大程度提高:6 mm厚的低、中、高钢化水平试件的平均抗拉强度分别较SG中间层提升41.7%、29.4%、8.6%,平均等效抗拉刚度分别提升366.7%、104.3%、60.8%;低刚化水平的8、12 mm厚试件的平均抗拉强度分别较SG中间层提升32.7%、29.5%,平均等效抗拉刚度分别提升735.7%、723.3%.开裂后硬化效应的形成机制主要是通过玻璃碎片与中间层的相互作用,拉伸应力在玻璃碎片中形成新的应力路径,使得碎片层在加载过程中参与承受荷载,如图7所示.结合试验现象可以推断,SG夹层玻璃单轴拉伸试件的开裂后硬化效应主要受碎片密度、碎片交错程度等裂纹形态因素决定,裂纹形态通过影响应力路径对试件的开裂后硬化效应产生影响.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 拉伸硬化效应示意图

Fig.7 Diagram of tension stiffening effect

3 碎片密度对开裂后硬化效应影响分析

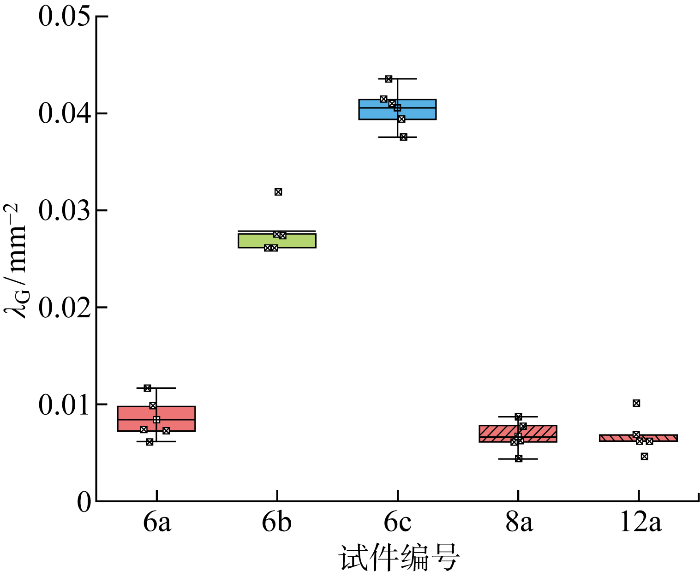
碎片密度是描述裂纹形态的重要指标之一,为进一步分析碎片密度对SG夹层玻璃开裂后硬化效应的影响,图8给出了6 mm厚各试件的抗拉强度和等效抗拉刚度随碎片密度的变化关系.图中:R²为决定系数.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 碎片密度对单轴拉伸试件抗拉性能的影响

Fig.8 Effect of fragment density on tensile performance of UT specimens

3.1 抗拉强度

碎片密度对单轴拉伸试件抗拉强度的影响如图8(a)所示.从图8(a)中可以看出,单轴拉伸试件的抗拉强度与碎片密度整体呈负相关,随着碎片密度从6.11×10^-3 mm^-2增大至4.35×10^-2 mm^-2,抗拉强度从42.09 MPa降低至28.11 MPa,与SG中间层的抗拉强度接近.对试验结果进行线性拟合,σ_b与λ_G的关系表达式为

(3)σ_b=-290λ_G+43.34

当玻璃层厚度为6 mm时,碎片密度λ_G与钢化玻璃表面应力σ_s满足如下线性关系^[17]:

(4)λ_G=(0.169σ_s-12.122)×10^-2

将式(4)代入式(3),可得到玻璃厚度为6 mm时,抗拉强度与表面应力满足如下关系:

σ_b=-0.49σ_s+78.49

3.2 等效抗拉刚度

碎片密度对单轴拉伸试件等效抗拉刚度的影响如图8(b)所示.由图8(b)可以发现,单轴拉伸试件的等效抗拉刚度随碎片密度增大整体呈指数下降,随着碎片密度从6.11×10^-3 mm^-2增大至4.35×10^-2 mm^-2,单轴拉伸试件的等效抗拉刚度从 2 429.06 MPa迅速降低至823.20 MPa,但仍比SG中间层的抗拉刚度高约44%,呈现显著的硬化效应.对试验结果进行指数拟合,等效抗拉刚度与碎片密度的关系表达式为

(5)$E_{\text {eff }}=3373.5 \mathrm{e}^{-\frac{\lambda_{G}}{0.016}}+601.96$

将式(4)代入式(5),可得到玻璃厚度为6 mm时,等效抗拉刚度与表面应力的关系表达式为

$E_{\text {eff }}=3373.5 \mathrm{e}^{-0.11 \sigma_{\mathrm{s}}+7.58}+601.96$

4 碎片交错对开裂后硬化效应影响的有限元分析

基于试件的真实碎片分布情况,采用Abaqus建立试件的精细化有限元模型,分析单轴拉伸荷载下裂纹形态对夹层热钢化玻璃开裂后硬化效应的影响机制,并在此基础上探究碎片交错程度对夹层热钢化玻璃开裂后硬化效应的影响规律.以模型6b-3为例对有限元分析方法进行介绍.

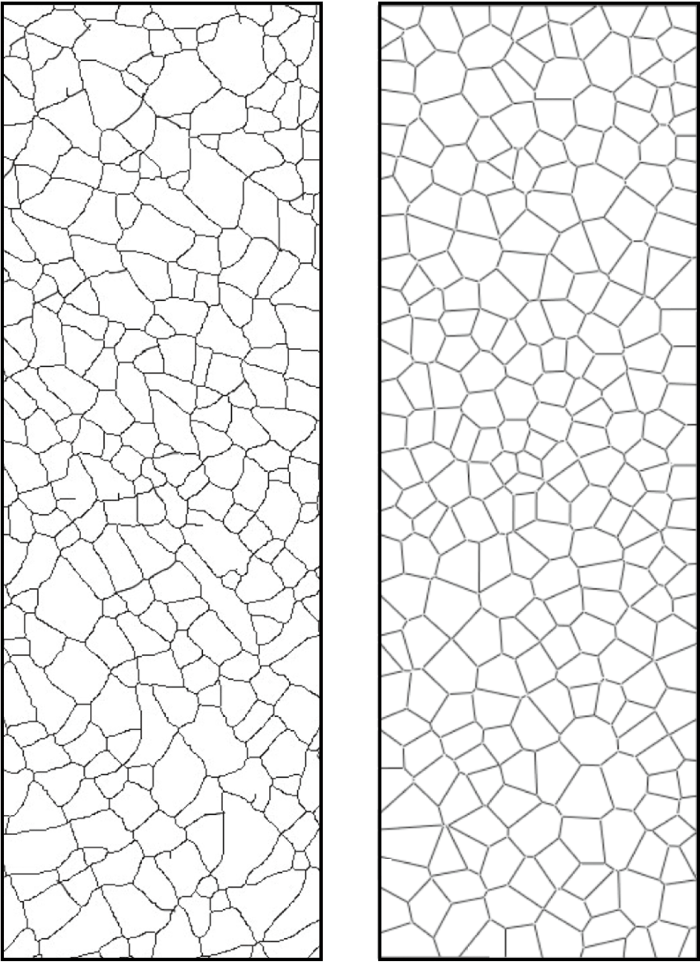
4.1 夹层热钢化玻璃开裂层重构

为最大程度还原开裂后玻璃层的裂纹形态,提升有限元模型的精细化程度,运用计算机视觉方法确定碎片形心位置,结合文献[16]中提出的Voronoi重构方法,分别对试件6a-3、6b-3、6c-3进行开裂碎片层重构.试件6b-3的碎片层重构效果如图9所示,能够较好地反映钢化玻璃开裂后的裂纹形态.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 试件6b-3碎片层重构效果

Fig.9 Reconstruction of fractured glass layer of UT specimen 6b-3

4.2 有限元模型建立与验证

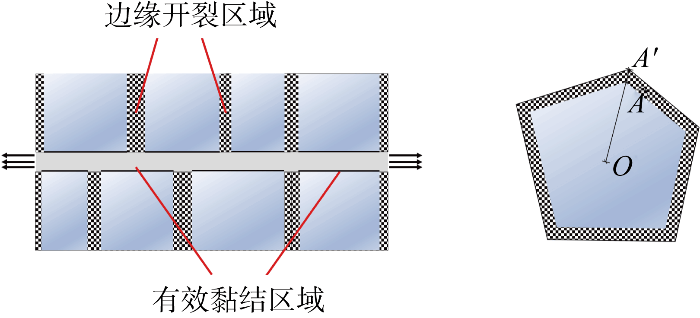
根据试件在拉伸过程中,玻璃碎片边缘局部开裂而核心区域通常不出现二次开裂,以及碎片密度较大的试件在拉伸荷载施加后期,可能同时存在边缘开裂和局部脱胶的现象,本文提出有效黏结假设:单轴拉伸试件在受拉过程中,应力路径只通过有效黏结区域,碎片边缘开裂区域对于试件的抗拉性能影响可以忽略,如图10所示.图中:O为碎片形心;A为有效黏结区域顶点;A'为碎片顶点.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 有效黏结区域示意图

Fig.10 Diagram of effective bonding area

为描述玻璃碎片的有效黏结区域范围,定义有效黏结系数ξ:

(6)ξ=1-l/l₀

式中:l为A到A'的距离;l₀为O到A'的距离.基于有效黏结区域假设,只需对有效黏结区域对应的碎片部分进行建模,同时可将玻璃碎片简化为线弹性材料,碎片与SG中间层间采用绑定约束进行连接.SG中间层在常温下呈现弹塑性特征,采用塑性本构模型和延性损伤模型模拟SG中间层的失效模态,材料参数取自于Yang等^[20]的试验结果,如表3所示.

表3 数值模型材料参数

Tab.3 Material parameters of numerical model

参数	取值
参数	玻璃	SG
弹性模量,E/GPa	70	1
泊松比,ν	0.22	0.4
密度,ρ/(kg·m^-3)	2 500	950
厚度,t/mm	6	1.52
断裂应变,${\epsilon }_{\mathrm{f}}^{\mathrm{p}\mathrm{l}}$		1.142
断裂能,E_f/(J·m^-2)		1.9

新窗口打开| 下载CSV

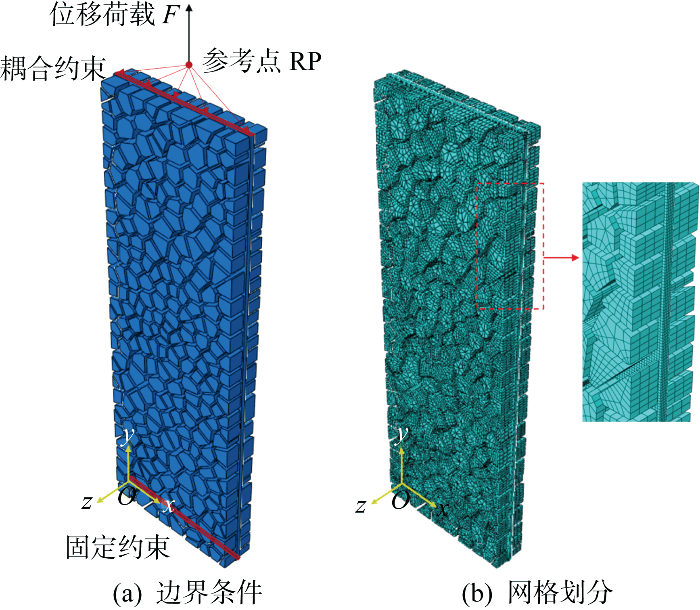
为提高计算效率,只对单轴拉伸试件中间拉伸段进行建模,并通过设置边界条件模拟试件的夹持和拉伸状态,有限元模型尺寸为180 mm×60 mm×13.52 mm.玻璃碎片和SG中间层均采用八节点六面体缩减积分实体单元(C3D8R)进行建模,SG中间层网格尺寸约0.5 mm×0.5 mm×0.4 mm,玻璃碎片设置相对粗糙的网格,尺寸约2.0 mm×1.0 mm×0.9 mm.试件6b-3数值模型的边界条件设置与网格划分如图11所示.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 单轴拉伸试件6b-3有限元模型

Fig.11 FEM model of UT specimen 6b-3

经过迭代计算,当模型6a-3、6b-3、6c-3的有效黏结系数分别为0.9、0.8、0.7时,有限元模拟结果与试验的荷载-位移曲线能够较好吻合,如图12所示.图13展示了模型6b-3的中间层失效过程,可以发现SG中间层在碎片边缘出现明显的应力集中现象,并在超出应变极限后逐步撕裂失效,能够较好体现SG中间层在玻璃碎片影响下的失效发展情况.

图12

新窗口打开| 下载原图ZIP| 生成PPT

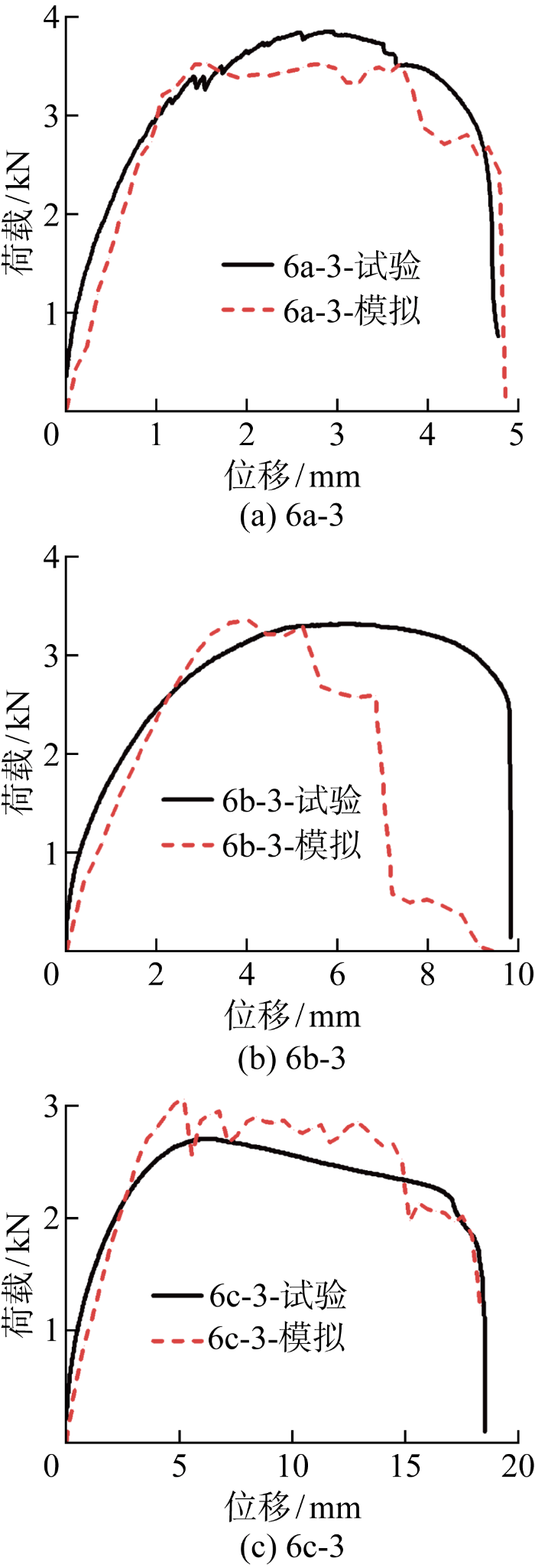
图12 荷载-位移曲线的模拟结果与试验结果的对比

Fig.12 Comparison of load-displacement between simulation and experiments

图13

新窗口打开| 下载原图ZIP| 生成PPT

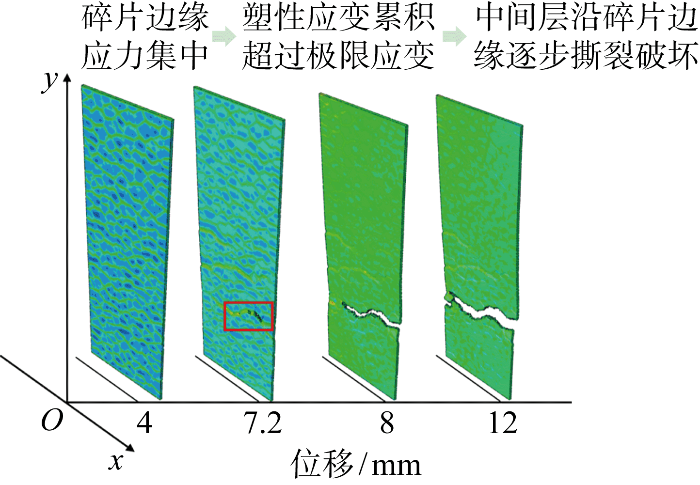
图13 单轴拉伸试件中间层失效过程模拟

Fig.13 Failure process of SG interlayer in fractured laminated tempered glass specimens

但模拟与试验结果仍存在一些差异:① 弹性阶段有限元模型的等效刚度略小于试验结果,这主要是由于在有效黏结假设下,所有碎片之间均相互分离,而试验中实际存在部分碎片通过互相嵌合形成团簇,具有放大碎片尺寸的效果;② 数值模型的峰值荷载与峰值位移和试验略有差别,这主要是由于模型两侧的碎片形态与试验不完全一致,碎片层的交错程度等其他因素对开裂后硬化效应也会造成一定影响;③ 图12(b)中,模型6b-3的荷载-位移曲线在中间层失效发展阶段与试验结果相差较大,主要原因仍是仿真模型与试验试件的碎片层分布差异.从图13可以发现,SG中间层在玻璃碎片影响下失效路径起伏式扩展,从而导致荷载-位移曲线阶梯式下降.

4.3 碎片交错程度对开裂后性能影响分析

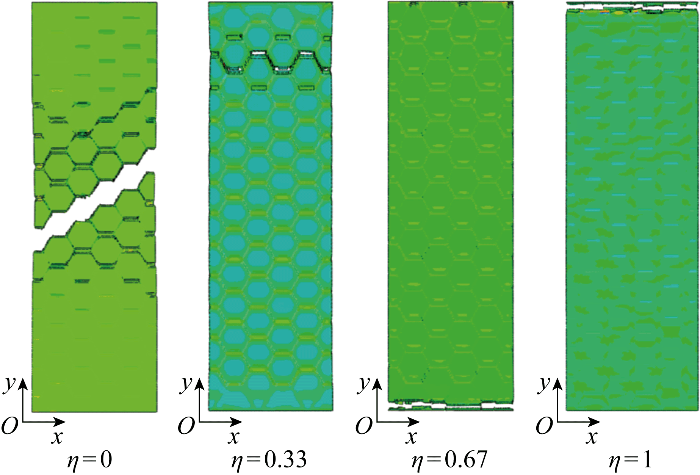
碎片交错程度是描述夹层玻璃裂纹形态的另一重要指标,夹层玻璃两侧碎片层有效黏结区域的重叠面积越大,碎片层交错程度越小.为进一步探究碎片交错程度对试件力学性能的影响规律,采用4.2节验证的有限元模型进行参数分析.根据试件6a-3、6b-3、6c-3的碎片密度分别建立有限元模型,并假设碎片形状为大小相同的正六边形^[17],定义交错比例η来量化碎片层的交错程度:

η=d/h

其中:d为中间层两侧最邻近玻璃碎片重心在xOy平面上的投影距离;h为正六边形碎片的边心距.碎片层交错程度设置如图14所示,η=0代表两侧碎片层完全重合,η=1代表两侧碎片层完全交错.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 模型6a-3各工况的碎片层偏置程度设置示意图

Fig.14 Offset degree of different test conditions of FEM model 6a-3

图15展示了碎片层交错程度对模型6a-3中间层失效模式的影响.由图15可见,SG中间层的撕裂位置随交错程度提升向两端过渡.当η=0.67,1时,SG中间层的失效位置靠近模型两端的夹持区域,这主要是由于随着碎片交错程度的增加,SG中间层的受力状态由抗拉转为抗剪,缓解碎片边缘处的应力集中;当两侧碎片层的有效黏结区域完全交错时,SG中间层的应力集中现象在靠近夹持端的位置最显著.但试验时试件的SG中间层的起裂位置通常在试件的中部拉伸段,而非靠近两夹持端,这主要是因为碎片层的随机分布特性使得中部拉伸段在加载过程中通常会出现对齐裂缝,SG中间层在对齐裂缝处受拉变形并最终失效开裂.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 模型6a-3不同交错程度时中间层的破坏模式

Fig.15 Failure modes of SG interlayer of FEM model 6a-3 with different η values

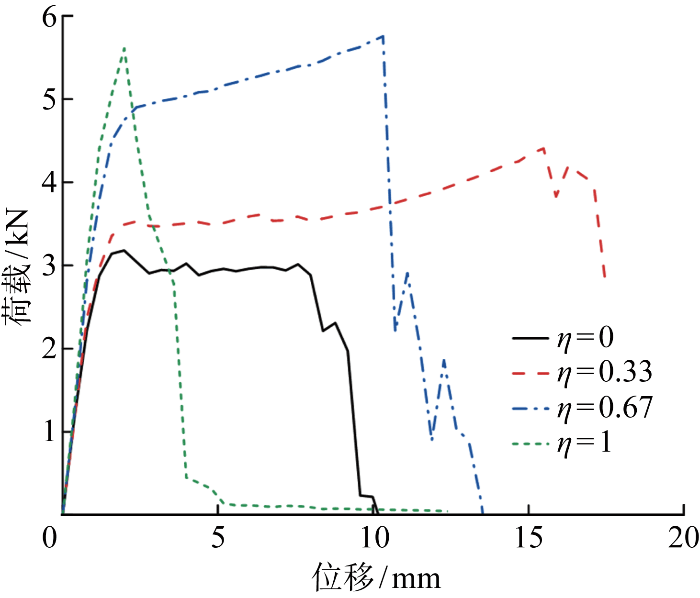
图16展示了模型6a-3不同碎片层交错程度时的荷载-位移曲线,表4展示了碎片层交错程度对不同碎片密度模型开裂后硬化效应的影响.从图16中可以发现,当η=0,0.33,0.67时,模型6a-3的荷载-位移曲线表现出延性特征;当η=1时,模型6a-3转为脆性破坏.随着碎片层交错比例η从0增加至1,模型6a-3的抗拉强度σ_b从34.9 MPa增大至61.5 MPa,等效抗拉刚度E_eff从 3 169.4 MPa增大至 5 586.4 MPa,这主要是因为随着两侧碎片层有效黏结区域从完全重合向完全交错过渡,模型所受的拉伸荷载从仅由碎片边缘开裂区域对应的SG中间层承受,转为由SG中间层与玻璃碎片在层间剪力作用下共同承受,且碎片与中间层间的应力路径分布更加均匀.而从表4可以看出,随着碎片密度的提升,碎片层交错程度对SG夹层玻璃开裂后硬化效应的影响会逐步减弱,这主要是由于碎片尺寸较小时难以形成连续的应力路径,影响玻璃碎片与SG中间层间的相互作用.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 模型6a-3不同交错程度有限元模型的荷载-位移曲线

Fig.16 Load-displacement of FEM model 6a-3 with different η values

表4 不同交错程度模型的开裂后力学性能

Tab.4 Post-breakage tensile strength and effective stiffness of FE models with different η values

η	抗拉强度/MPa			等效抗拉刚度/MPa
η	6a-3	6b-3	6c-3	6a-3	6b-3	6c-3
0	34.9	33.5	31.4	3 169.4	1 513.4	1 090.4
0.33	38.3	34.4	32.1	3 479.9	1 415.4	1 119.4
0.67	49.4	37.1	34.1	3 503.1	1 399.3	1 105.4
1	61.5	43.2	36.9	5 586.4	1 299.2	979.5

新窗口打开| 下载CSV

5 结论

本文通过试验和有限元模拟研究了SG夹层玻璃的开裂后硬化效应.采用准静态单轴拉伸试验,测定了随机裂纹试件的荷载-位移关系,并分析了碎片密度对SG夹层玻璃的抗拉强度与等效刚度的影响及作用机制.采用有限元模拟方法,建立了SG夹层玻璃试件单轴拉伸的精细化数值模型,并分析了碎片层交错程度对随机裂纹试件中间层失效模式和开裂后力学性能的影响规律.研究的具体结论如下:

(1) 绝大部分SG夹层玻璃单轴拉伸试件的玻璃碎片在加载过程中整体形态保持完好,并且未观察到明显的脱胶现象,但玻璃碎片边缘会出现局部二次开裂并形成致密的玻璃碎渣.SG中间层的起始失效位置和撕裂失效走向受碎片形状影响显著,起始失效位置主要出现在前后碎片层的对齐裂缝处.

(2) 夹层热钢化玻璃的开裂后抗拉强度与碎片密度近似呈线性负相关,等效抗拉刚度随碎片密度的增大呈指数型下降.当玻璃层厚度为6 mm时,随着钢化玻璃表面应力从75.34 MPa增大至97.47 MPa,抗拉强度从42.09 MPa降低至28.11 MPa,等效抗拉刚度迅速从 2 429.06 MPa降低至823.20 MPa,但仍比SG中间层的抗拉刚度高约44%.

(3) 基于Voronoi重构和有效黏结假设建立的夹层热钢化玻璃开裂后单轴拉伸的有限元模型能够有效反映SG中间层的损伤起始与扩展:SG中间层在碎片边缘出现明显的应力集中现象,并在超出应变极限后逐步撕裂失效.荷载-位移曲线的预测与试验结果吻合较好,可以预测和评估夹层热钢化玻璃的开裂后抗拉强度与等效抗拉刚度.

(4) 随着碎片层交错程度的增加,中间层失效位置逐步由中间向两端过渡,且SG夹层钢化玻璃的开裂后硬化效应显著增强:随着交错比例从0增大至1,模型6a-3的抗拉强度从34.9 MPa提升至61.5 MPa,等效抗拉刚度从 3 169.4 MPa提升至 5 586.4 MPa.但碎片层交错程度对SG夹层玻璃开裂后硬化效应的影响随碎片密度的提升逐步减弱,即当钢化玻璃表面应力较大时,碎片层交错程度对夹层热钢化玻璃开裂后力学性能的贡献较小.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

O’REGAN

Structural use of glass in buildings[M]. London, UK: Institution of Structural Engineers, 2014.