在土木工程领域,有限元仿真是一种常用的结构分析手段,但根据设计图纸或理想化假设建立的初始有限元模型往往存在建模误差、模型参数误差和测量误差等因素,导致了模型预测结果和实际结构响应的偏离[1 ] .为了保证结构有限元模型的准确性,应根据实际观测数据适当地调整有限元模型参数,以最小化测量值和有限元模型预测值的差异[2 ] .
传统的确定性模型更新方法不考虑测量信息和模型参数的不确定,更新后的有限元模型往往只能匹配某次测量的结构响应,难以准确预测结构在其他荷载条件下的响应.基于贝叶斯定理的模型更新是一种不确定性模型更新方法,综合考虑完整的测量信息和参数的先验信息,有效克服了确定性更新方法的不足,在模型更新领域得到广泛的应用[3 ] .1998年,Katafygiotis等[4 ] 和Beck等[5 ] 首次将贝叶斯理论应用于土木工程领域中的模型更新中,提出贝叶斯更新的基本框架.为了解决参数后验分布积分复杂的问题,Beck等[6 ] 将基于Metropolis-Hastings(MH)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法引入贝叶斯更新,利用剪切模型证明了该方法的可靠性.在Beck的理论基础上,诞生了许多优化的贝叶斯更新框架.刘纲等[7 ] 将延迟拒绝和自适应算法引入MH采样,结合相关向量机代理模型,更新了四层两跨钢框架结构弹性模量和质量密度.Lam等[8 ] 提出了一种可以同时计算多个马尔可夫链的并行MCMC算法,并将其应用于帆船形建筑的弹性模量更新.Luo等[9 ] 集成了粒子群优化中的粒子位置更新机制与MH算法,实现了三层框架结构的单元刚度更新.
但当前模型更新研究选用的待更新参数多为刚度、弹性模型和质量密度,将结构与基础的连接视为完全刚性约束,缺少对边界具体情况的考虑,容易导致更新结果精度不足,且传统的MH算法采样收敛速度较慢、更新效率低下,在参数增多时易陷入采样停滞.因此,本文将边界条件加入待更新参数,引入鲸鱼优化算法(whale optimization algorithm,WOA)以提升传统MH算法的采样效率,建立反映待更新参数和模态响应关系的径向基函数(radial basis functions,RBF)代理模型,以代理模型代替有限元模型完成模型更新.最后,将所提方法应用在简支梁数值算例和3层框架结构的更新上,通过振动台实验证明了方法的有效性.
1 基于改进MCMC的贝叶斯模型更新
1.1 基于改进MCMC的贝叶斯更新框架
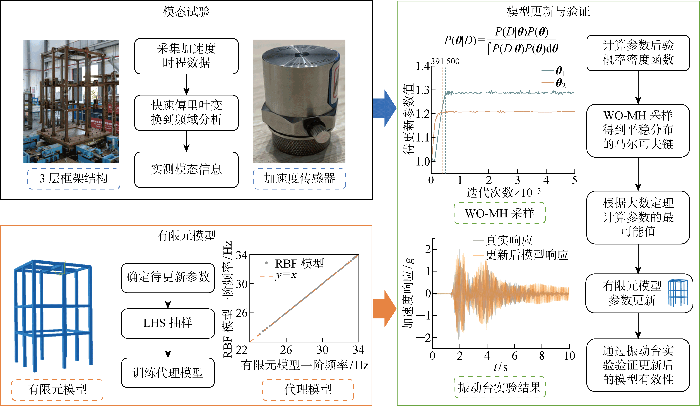
本文提出了有限元模型更新的框架,如图1 所示.具体步骤如下.
图1
图1
有限元模型更新的框架
Fig.1
Updating framework of finite element model
(1) 根据结构图纸建立初始有限元模型,基于Sobol灵敏度分析确定待更新参数.
(2) 使用拉丁超立方抽样(Latin hypercube sampling,LHS)抽取待更新参数样本,计算每个样本点对应的模态响应,建立RBF、随机森林(random forest,RF)和Kriging代理模型以拟合待更新参数和结构响应的映射关系.计算各代理模型的精度,选择精度最高的代理模型来代替有限元模型完成贝叶斯更新.
(3) 进行模态试验,利用加速度传感器采集加速度时程响应,识别结构的实测模态信息.
(4) 根据贝叶斯理论计算参数的后验概率密度函数,本文中采用无信息先验分布.构建基于鲸鱼优化的Metropolis-Hastings(WO-MH)采样序列,迭代采样得到一个平稳分布的马尔可夫链,根据大数定理计算不确定参数的最可能值,将其替换到有限元模型中完成模型更新.
1.2 贝叶斯更新原理
贝叶斯方法将参数视为随机变量,使用测量数据来更新参数的先验概率密度函数,得到后验概率密度函数[10 ] .其公式如下:
(1) $\begin{aligned}P(\boldsymbol{\theta} \mid D)= & \frac{P(D \mid \boldsymbol{\theta}) P(\boldsymbol{\theta})}{\int P(D \mid \boldsymbol{\theta}) P(\boldsymbol{\theta}) \mathrm{d} \boldsymbol{\theta}}= \\& { }_{c P}(D \mid \boldsymbol{\theta}) P(\boldsymbol{\theta})\end{aligned}$
式中:θ 是待更新参数组成的向量,θ =[θ 1 θ 2 … θN ]T ;D 是观测数据;P (θ )是θ 的先验分布,在没有历史经验的前提下常常将其视为广义无偏均匀分布;似然函数P (D |θ )是给定θ 时观测数据D 的条件概率;c =1/ ∫P (D |θ )P (θ )dθ ,是为了确保后验概率密度函数积分为1的归一化常数[11 ] .
本文选择模态数据(频率和振型)作为观测数据D ,假设D (θ )为有限元模型的计算模态. 根据最大熵原理,误差的后验分布可以假设为均值为0、协方差为Σ 的高斯分布[12 ] .则似然函数可以写作:
(2) $\begin{aligned}P(D \mid \boldsymbol{\theta})= & \frac{1}{\sqrt{2 \pi \Sigma}} \exp \left(-\frac{\varepsilon^{2}}{2 \Sigma}\right)= \\& \frac{1}{\sqrt{2 \pi \Sigma}} \exp \left[-\frac{(D-D(\boldsymbol{\theta}))^{2}}{2 \Sigma}\right]\end{aligned}$
假设所有模态的固有频率和振型是相互独立的,则P (D |θ )=P (f |θ )P (φ |θ ),又假设先验分布为均匀分布,则不确定参数的后验分布可以表示为
(3) $\begin{aligned}P(\boldsymbol{\theta} \mid D)= & c P(f \mid \boldsymbol{\theta}) P(\boldsymbol{\varphi} \mid \boldsymbol{\theta}) P(\boldsymbol{\theta})= \\& c \exp \left(-\frac{1}{2} J(\boldsymbol{\theta})\right)\end{aligned}$
(4) $ \begin{aligned}J(\boldsymbol{\theta})= & \sum_{r=1}^{s} \sum_{i=1}^{n}\left\{\frac{\left(\hat{f}_{r i}-f_{r}\right)^{2}}{\sum_{f r}}+\right. \\& {\left.\left[\frac{\left(\hat{\boldsymbol{\varphi}}_{r i}-\boldsymbol{\varphi}_{r}\right)^{\mathrm{T}}\left(\hat{\boldsymbol{\varphi}}_{r i}-\boldsymbol{\varphi}_{r}\right)}{\sum_{\varphi r}}\right]\right\} }\end{aligned}$
n 是模态试验的次数;s 是频率总阶数;${\hat{\mathrm{f}}}_{ri}$ ${\hat{\mathrm{\phi }}}_{ri}$ i 次实测第r 阶的频率和振型;fr 和φr 是有限元计算的第r 阶频率和振型;Σfr 和Σφr 分别是第r 阶的频率协方差和振型协方差[13 ] .
1.3 基于鲸鱼优化的MH采样
贝叶斯方法所得到的后验分布需要在参数空间上进行高维积分,难以直接计算其解析式,常引入MCMC算法来近似获得参数的后验分布[14 ] .MH算法是一种应用广泛的MCMC抽样方法,其从先验分布中采样,生成平稳分布的马尔可夫链,然后根据生成的样本获得待更新参数的统计特征[15 ] .
随着参数的增加和后验分布的复杂化,被拒绝的采样样本大大增加,传统的MH算法在采样过程中容易形成具有大量重复样本的马尔可夫链,进入非遍历状态[3 ] .因此引入WOA对MH采样中被拒绝的样本进行二次采样,利用WOA全局搜索能力强的特点选择下一个样本点,从而提高采样样本的多样性,避免陷入局部最优.WOA是模仿自然界中鲸鱼群体狩猎行为的新型启发式优化算法[16 ] .WOA包含3种种群更新机制,假定当前鲸鱼个体的位置为Xt ,当前最佳鲸鱼个体的位置为X* ,当前种群内随机鲸鱼个体位置为X rand ,则Xt 在X* 或X rand 影响下得到下一个位置Xt +1 ,3种更新机制下Xt +1 的计算公式分别为
(5) Xt +1 =$\left\{\begin{array}{l}{X}^{\mathrm{*}}-A|C{X}^{\mathrm{*}}-{X}_{t}|,\\ p<0.5\mathrm{且}\left|A\right|<1\\ |{X}^{\mathrm{*}}-{X}_{t}|{\mathrm{e}}^{bl}\mathrm{c}\mathrm{o}\mathrm{s}\left(2\mathrm{\pi }l\right)+{X}^{\mathrm{*}},\\ p\ge 0.5\\ {X}_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}-A|C{X}_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}-{X}_{t}|,\\ p<0.5\mathrm{且}\left|A\right|\ge 1\end{array}\right.$
(6) C =2r
(7) A =2ar -a
式中:r 和p 是0到1区间内的随机数; l 是-1到1间的随机数;a 随着迭代次数的增加由2线性递减到0;b 是对数螺旋形状常数.
(1) 指定样本初始值θ 0 并给定当前样本θj (j 表示样本标签);
(2) 构造建议分布q (θ' |θj ),从建议分布中生成候选样本θ' ;
(8) α (θj , θ' )=min$\left\{1,\frac{P\left(\theta \text{'}\right|D)}{P\left({\theta }_{j}\right|D)}\right\}$
(5) 若u ≤α ,则θj +1 =θ' ;若u >α ,则按照鲸鱼算法更新下一个采样点. 选取满足min J (θ )的θ 为最佳值θ* ,按照式(5)选取下一个采样点θ' ,再次计算接受率α ,如满足u ≤α ,则θj +1 =θ' ;否则θj +1 =θ.
(6) 对所有样本重复步骤(2)到步骤(5),得到一个收敛序列,即马尔可夫链.
1.4 代理模型
解决模型更新效率低下的另一种方法是建立高保真的代理模型来拟合结构响应和更新参数之间的关系,从而代替有限元模型进行计算[17 ] .常用的代理模型包括Kriging模型、RBF模型、RF模型、响应面模型、支持向量回归(support vector regression,SVR)等.本文选用RBF、RF和Kriging作为有限元模型的代理模型.
通过均方根误差(RMSE,记为e RMSE )和决定系数R 2 比较3种模型在低维和高维情况下的精度,其公式为
(9) e RMSE =$\sqrt{\frac{1}{k}\stackrel{k}{\sum _{m=1}}({\hat{\mathrm{y}}}_{\mathrm{m}}-{y}_{m}{)}^{2}}$
(10) R 2 =1-$\frac{\stackrel{k}{\sum _{m=1}}({\hat{\mathrm{y}}}_{\mathrm{m}}-{y}_{m}{)}^{2}}{\stackrel{k}{\sum _{m=1}}({\hat{\mathrm{y}}}_{\mathrm{m}}{-\stackrel{-}{y})}^{2}}$
式中:${\hat{\mathrm{y}}}_{\mathrm{m}}$ ym 分别表示理论响应和代理模型响应;$\stackrel{-}{y}$ k 为测试集样本数.
2 数值算例
为了验证WO-MH采样的有效性,建立一个钢结构简支梁有限元模型,如图2 所示.假定梁弹性模量的真实分布为均值E * =206 GPa的正态分布,质量密度的真实分布为均值m * =7 850 kg/m3 的正态分布,按照参数的真实分布随机生成20组参数样本,代入有限元模型计算得到20组前3阶频率和振型,作为仿真的实测模态信息.假定梁的初始弹性模量E 0 =160 GPa,初始质量密度m 0 =6 500 kg/m3 .初始值不代表实际工程情况,仅用来进行模型更新效果的数值验证.为避免参数数量级差别过大,以θ 1 =E/E 0 和θ 2 =m/m 0 为待更新参数.
图2
图2
简支梁模型
Fig.2
Simply supported beam model
通过拉丁超立方抽样均匀抽取 1 000 组样本,使用有限元计算相应的前3阶频率和振型,作为构建代理模型的数据集.取样本的80%为训练集,剩下20%为测试集.分别采用RBF、Kriging和RF模型构建基于样本的代理模型,利用遗传算法结合十折交叉验证计算各代理模型的最优超参数,从而得到优化后的代理模型.代理模型在测试集上预测的一阶频率和实际一阶频率的对比如图3 所示.由图3 可见,代理模型和有限元模型的频率点基本重合,表明3种代理模型精度都较高,较为准确地反映了有限元模型的自振特性.比较3种代理模型的计算精度,如表1 所示.其中RBF代理模型的RMSE最小,R 2 最接近1,拟合精度优于其他两种代理模型.因此,采用RBF模型代替有限元模型进行贝叶斯模型更新.
图3
图3
一阶频率预测值与实际值的比较
Fig.3
Comparison of predicted first-order frequency values and actual values
分别利用MH和WO-MH进行采样,经过 5 000 次迭代后得到参数的马尔可夫链,如图4 所示.引入WOA后,MH采样的收敛速度和平稳性大大提升.通过自相关函数(autocorrelation function,ACF)图[18 ] 来评估马尔可夫链的样本相关性,如图5 所示.与MH采样得到的ACF图相比,WO-MH采样得到的ACF图很快衰减到0,表明其样本之间相关度较低,在参数空间中收敛速率更快.
图4
图4
不确定参数的马尔可夫链
Fig.4
Markov chains of uncertain parameters
图5
图5
马尔可夫链的ACF图
Fig.5
ACF plots of Markov chains
利用time函数计算采样时间,得到MH采样总时间为46.62 s,WO-MH采样总时间为54.06 s.θ 1 的MH采样约在迭代807次后趋于平稳,此时已采样7.41 s;θ 1 的WO-MH采样约在迭代500次后趋于平稳,此时已采样6.38 s,更新效率提升13.9%.θ 2 的MH采样约在迭代562次后趋于平稳,此时已采样5.17 s;θ 2 的WO-MH采样约在迭代391次后趋于平稳,此时已采样5.04 s,更新效率提升2.5%.因此,虽然WO算法的引入增加了总采样时间,但加快了采样收敛的速度,总体上提高了模型更新的计算效率.
比较模型更新前后的参数值和真实参数值的误差,结果如表2 所示.两种方法更新的参数值均接近预设的真实参数值,误差均在1%以内,且WOMH-RBF的更新精度明显高于MH-RBF算法.
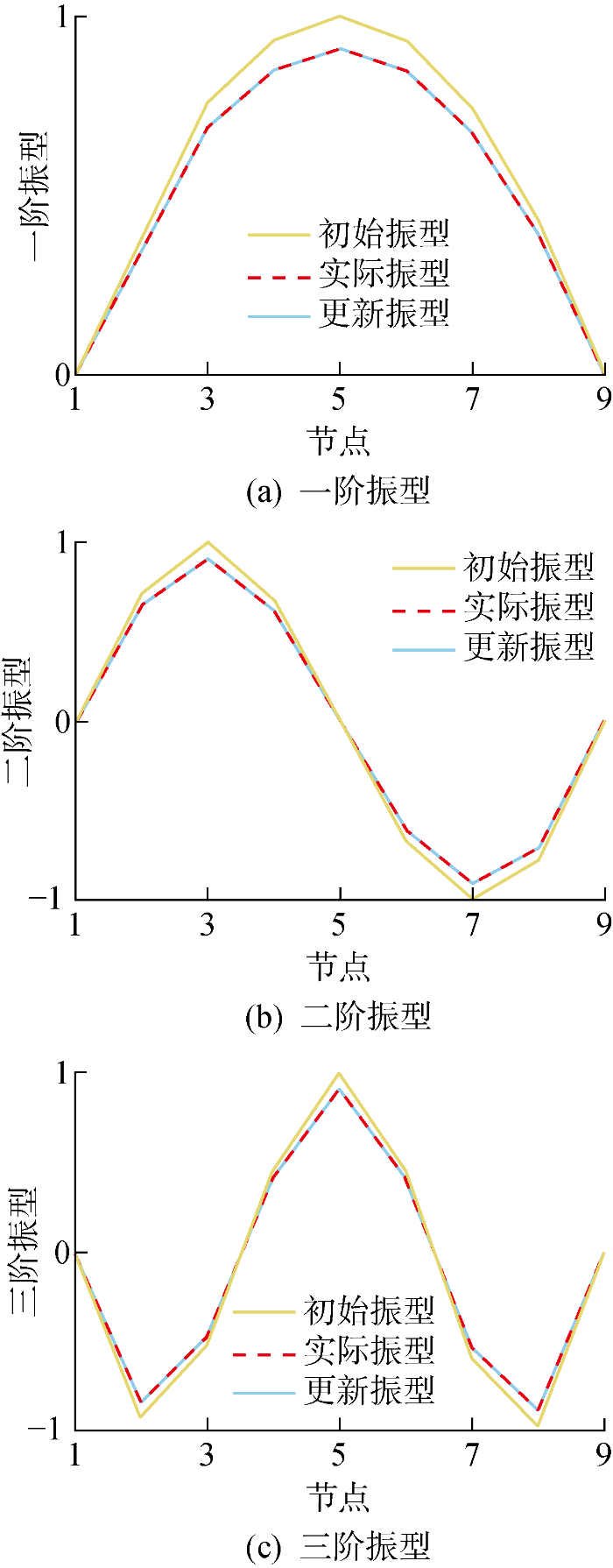
绘制模型更新前、模型更新后和真实的前3阶振型,如图6 所示.计算有限元模型在WO-MH更新前后的模态响应值及其和真实模态响应值的误差,结果如表3 所示.由表3 和图6 可知,更新后的有限元模型的响应精度大幅提升,最大误差为0.009%,最小误差为0%,且更新后的振型和真实振型吻合很好,参数更新的效果显著.
图6
图6
更新前后的振型对比
Fig.6
Comparison of mode shapes before and after updating
3 实验验证
为了证明所提算法应用于复杂结构的有效性,针对不确定参数更多的结构进行参数更新,可以进一步验证本文提出的基于WO-MH采样和RBF代理模型的有限元模型更新算法的通用性.
3.1 模态试验
研究对象为一个3层钢框架结构,如图7 所示.在模型的X 及Y 向安装单向加速度传感器,对模型施加X 向和Y 向的正弦波,通过快速傅里叶变换(fast Fourier transformation,FFT)将模态试验所得各组加速度数据转换成频域数据,提取结构的频率和振型.由于模态试验中高阶模态往往误差较大,采用X 方向和Y 方向的前两阶模态进行模型更新[19 ] .其中,试验测得频率的均值和方差如表4 所示.
图7
图7
3层钢框架试验模型
Fig.7
A three-story steel frame experimental model
3.2 模型更新
结构设计方案中所有钢材的弹性模量为206 GPa,质量密度为 7 850 kg/m3 ,框架与基础为完全刚接.参照结构设计方案设计有限元模型,钢构件使用线单元建模,梁中的支架简化为对应位置节点上的附加集中质量,此时模型X 向一阶频率18.707 Hz,与实测频率相差较大.考虑到施工完成的框架底板与基础之间以螺栓连接,并非完全固接,按照完全刚接考虑不够合理,因此将边界条件加入更新参数.将有限元模型中柱和基础之间的连接使用两根线性弹簧来表示,分别代表绕x 轴转动和绕y 轴转动的扭转刚度[20 ] .
设置所有钢材的初始弹性模量E 0 =206 GPa、初始质量密度ρ 0 =7 850 kg/m3 ,弹簧的初始刚度S 0 =0.1 MN·m/rad.将同一层梁的弹性模量E 看作一致,同一层梁的质量密度ρ 看作一致,最终得到12个待更新参数:一层梁的弹性模量E 1 和质量密度ρ 1 、二层梁的弹性模量E 2 和质量密度ρ 2 、三层梁的弹性模量E 3 和质量密度ρ 3 、大板梁的弹性模量E 4 和质量密度ρ 4 、柱的弹性模量E 5 和质量密度ρ 5 、弹簧绕x 轴转动刚度S 1 和绕y 轴转动刚度S 2 .
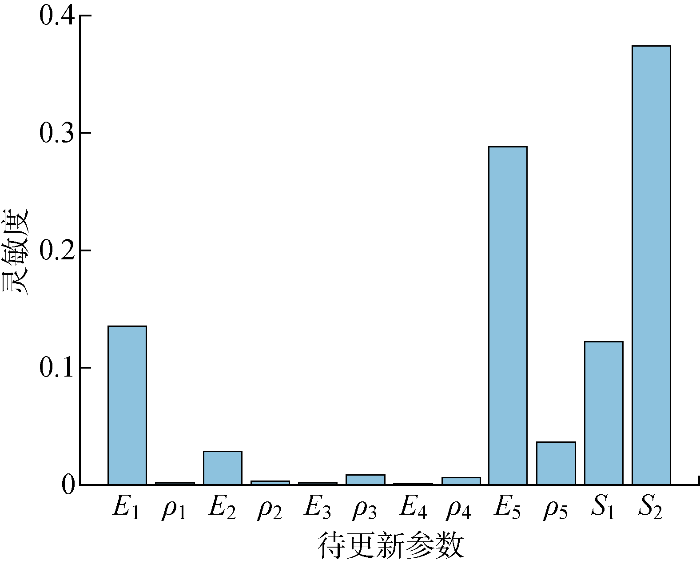
采用Sobol全局方差灵敏度分析对初始待更新参数进行筛选,图8 为3层框架模型中12个模型参数对一阶频率的灵敏度.根据灵敏度分析结果,选择灵敏度参数较大的前8个灵敏度参数为3层钢框架模型的待更新参数,分别为E 1 、E 2 、ρ 3 、ρ 4 、E 5 、ρ 5 、S 1 和S 2 .
图8
图8
参数对一阶频率的灵敏度
Fig.8
Sensitivities of parameters to the first-order frequency
采用Kriging、RBF和RF 3种方法建立代理模型,采用遗传算法对代理模型的超参数进行寻优,得到3种优化后模型的评价指标如表5 所示.输入参数由两维变为八维后,3种代理模型的精度都有所下降.由于RBF模型的精度最高,所以依然选择RBF模型进行模型更新.
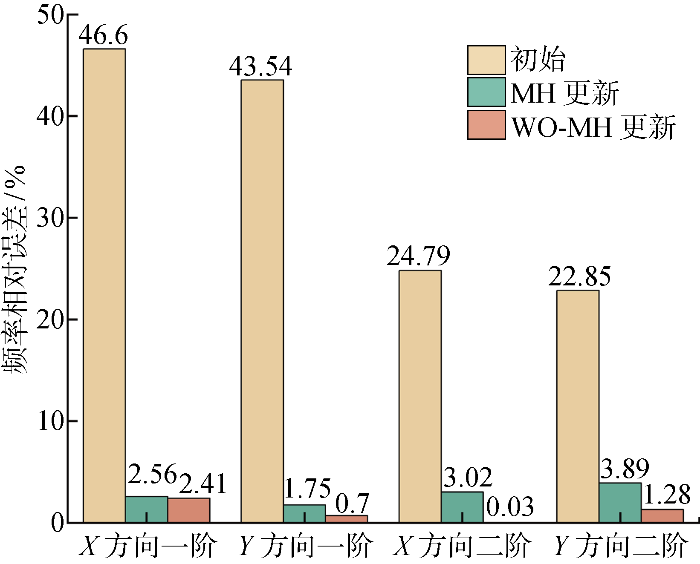
基于RBF代理模型完成MH采样和WO-MH采样,迭代 5 000 次后,将更新后的参数替换到初始有限元模型中,得到更新前后各阶频率值如表6 所示,更新前后各阶频率的相对误差分布如图9 所示.初始设计模型的频率和实测频率偏差较大,X 方向和Y 方向的前两阶频率相对误差分别为46.60%、43.54%、24.79%和22.85%,而MH更新后的频率相对误差分别为2.56%、1.75%、3.02%和3.89%,WO-MH更新后频率相对误差分别为2.41%、0.70%、0.03%和1.28%.更新后有限元模型的频率相对误差明显减小,且WO-MH算法相较于 MH算法在3层框架有限元模型更新中表现出更优的更新效果.
图9
图9
更新前后的频率相对误差
Fig.9
Frequency relative errors before and after updating
3.3 振动台实验验证
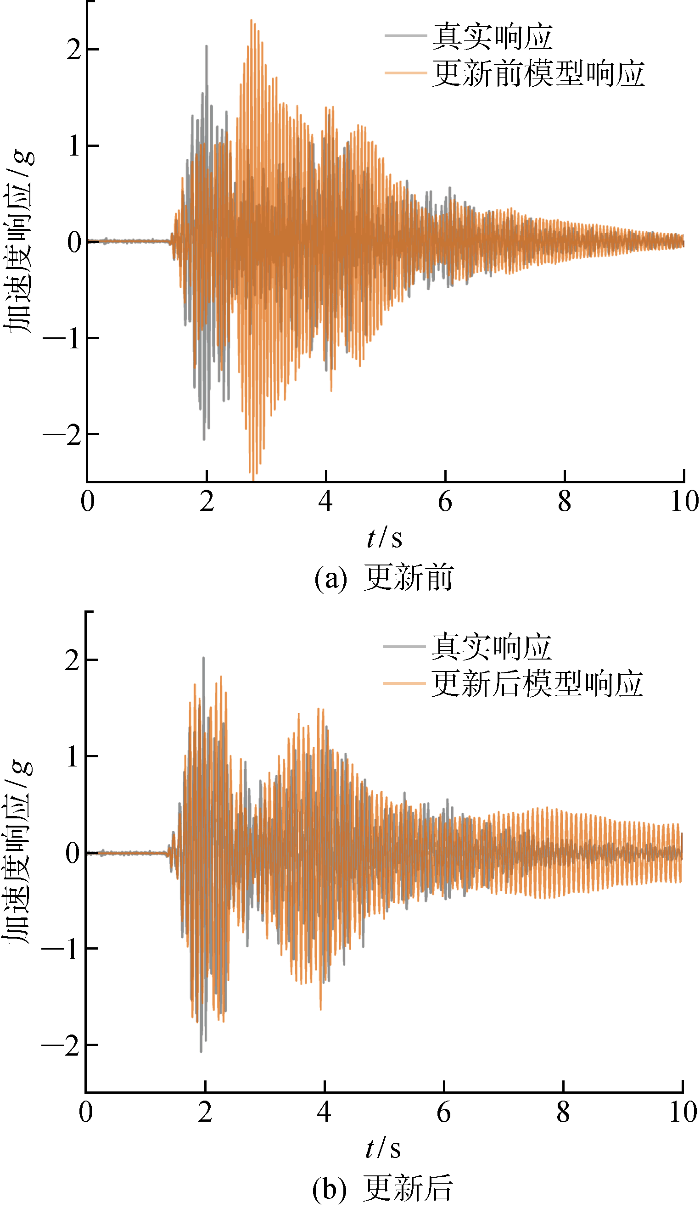
为了进一步验证模型更新效果,进行3层框架的振动台实验,对结构施加峰值加速度为0.4g 的El-Centro波,得到顶层x 方向的实际加速度时程曲线.利用更新后的有限元模型预测结构顶层x 方向的加速度时程曲线,并与实测的加速度时程曲线对比,如图10 所示.参数更新后,有限元模型预测的结构加速度响应与实测响应的峰值和形状更加接近,更能反映真实的结构特性.
图10
图10
有限元模型预测和实测的加速度响应比较
Fig.10
Acceleration response comparisons of finite model predictions and measurements
4 结论
针对传统MH采样收敛较慢、计算量大的问题,本文将鲸鱼优化算法引入MH采样,结合RBF代理模型提出一种新的贝叶斯模型更新框架,通过两参数的简支梁数值算例和八参数的实际框架结构验证了该方法的有效性,得到如下结论.
(1) 在低维和高维线性问题中,RBF代理模型的精度高于Kriging模型和RF模型,RMSE分别为 0.000 8 和 0.070 1,可以用来代替有限元模型完成模型更新,从而提高更新效率、减小计算成本.
(2) WO-MH算法克服了传统MH算法易陷入停滞的缺点,收敛速度和平稳性均优于传统MH 算法.本文数值算例表明,传统MH算法的弹性模量采样在迭代7.41 s后趋于平稳,本文优化算法在迭代6.38 s后趋于平稳,且WO-MH算法更新后的弹性模量相对误差仅为0.006%,小于MH算法的0.142%.经WO-MH更新后,简支梁数值模型的振型与实际振型吻合,频率最大相对误差仅为0.009%.
(3) 基于3层钢框架结构实验,验证了在多输入参数复杂模型的更新中,所提WO-MH算法仍具有较好的更新效果,与初始有限元模型相比,更新后的有限元模型在在El-Centro波下的顶层加速度时程曲线更接近实测加速度时程曲线.
参考文献
View Option
[1]
SONG M RENSON L NOEL J P et al Bayesian model updating of nonlinear systems using nonlinear normal modes
[J]. Structural Control & Health Monitoring 2018 , 25 (12 ): e2258 .
[本文引用: 1]
[2]
YIN T A practical Bayesian framework for structural model updating and prediction
[J]. Asce-Asme Journal of Risk and Uncertainty in Engineering Systems Part a: Civil Engineering 2022 , 8 (1 ): 04021073 .
[本文引用: 1]
[3]
BAISTHAKUR S CHAKRABORTY A Modified Hamiltonian Monte Carlo-based Bayesian finite element model updating of steel truss bridge
[J]. Structural Control & Health Monitoring 2020 , 27 (8 ): e2556 .
[本文引用: 2]
[4]
KATAFYGIOTIS L S BECK J L Updating models and their uncertainties. II: Model identifiability
[J]. Journal of Engineering Mechanics 1998 , 124 (4 ): 463 -467 .
[本文引用: 1]
[5]
BECK J L KATAFYGIOTIS L S Updating models and their uncertainties. I: Bayesian statistical framework
[J]. Journal of Engineering Mechanics 1998 , 124 (4 ): 455 -461 .
[本文引用: 1]
[6]
BECK J L AU S K Bayesian updating of structural models and reliability using Markov chain Monte Carlo simulation
[J]. Journal of Engineering Mechanics 2002 , 128 (4 ): 380 -391 .
[本文引用: 1]
[7]
刘纲 , 罗钧 , 秦阳 , 等 . 基于改进MCMC方法的有限元模型修正研究
[J]. 工程力学 2016 , 33 (6 ): 138 -145 .
[本文引用: 1]
LIU Gang LUO Jun QIN Yang et al A finite element model updating method based on improved MCMC method
[J]. Engineering Mechanics 2016 , 33 (6 ): 138 -145 .
[本文引用: 1]
[8]
LAM H F HU J ZHANG F L et al Markov chain Monte Carlo-based Bayesian model updating of a sailboat-shaped building using a parallel technique
[J]. Engineering Structures 2019 , 193 : 12 -27 .
[本文引用: 1]
[9]
LUO J HUANG M XIANG C et al Bayesian damage identification based on autoregressive model and MH-PSO hybrid MCMC sampling method
[J]. Journal of Civil Structural Health Monitoring 2022 , 12 (2 ): 361 -390 .
[本文引用: 1]
[10]
LIAO M RENAUD G BOMBARDIER Y Airframe digital twin technology adaptability assessment and technology demonstration
[J]. Engineering Fracture Mechanics 2020 , 225 : 106793 .
[本文引用: 1]
[11]
BEHMANESH I MOAVENI B Bayesian FE model updating in the presence of modeling errors
[C]// Model Validation and Uncertainty Quantification, Volume 3 Cham, Germany : Springer International Publishing , 2014 : 119 -133 .
[本文引用: 1]
[12]
CHING J Y MUTO M BECK J L Structural model updating and health monitoring with incomplete modal data using Gibbs sampler
[J]. Computer-Aided Civil and Infrastructure Engineering 2006 , 21 (4 ): 242 -257 .
[本文引用: 1]
[13]
黄民水 , 罗金 , 雷勇志 . 基于改进MH算法的结构损伤识别
[J]. 华中科技大学学报(自然科学版) 2022 , 50 (8 ): 136 -141 .
[本文引用: 1]
HUANG Minshui LUO Jin LEI Yongzhi Damage identification based on improved MH algorithm
[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition) 2022 , 50 (8 ): 136 -141 .
[本文引用: 1]
[14]
CHEUNG S H BECK J L Bayesian model updating using hybrid Monte Carlo simulation with application to structural dynamic models with many uncertain parameters
[J]. Journal of Engineering Mechanics 2009 , 135 (4 ): 243 -255 .
[本文引用: 1]
[15]
FENG K LU Z CHEN Z et al An innovative Bayesian updating method for laminated composite structures under evidence uncertainty
[J]. Composite Structures 2023 , 304 : 116429 .
[本文引用: 1]
[16]
MIRJALILI S LEWIS A The whale optimization algorithm
[J]. Advances In Engineering Software 2016 , 95 : 51 -67 .
[本文引用: 1]
[17]
XIAO J L NIE X LIU Y F et al Structural performance assessment of RC flexural members through crack-based fibre beam-column model updating
[J]. Computers & Structures 2023 , 281 : 107029 .
[本文引用: 1]
[18]
WAN H P REN W X Stochastic model updating utilizing Bayesian approach and Gaussian process model
[J]. Mechanical Systems and Signal Processing 2016 , 70-71 : 245 -268 .
[本文引用: 1]
[19]
陈辉 , 张衡 , 李烨君 , 等 . 测量模态不确定的梁式结构随机有限元模型修正
[J]. 振动工程学报 2019 , 32 (4 ): 653 -659 .
[本文引用: 1]
CHEN Hui ZHANG Heng LI Yejun et al Stochastic finite element model updating of beam structure based on uncertain measurement modes
[J]. Journal of Vibration Engineering 2019 , 32 (4 ): 653 -659 .
[本文引用: 1]
[20]
ZHOU X KIM C W ZHANG F L et al Vibration-based Bayesian model updating of an actual steel truss bridge subjected to incremental damage
[J]. Engineering Structures 2022 , 260 : 114226 .
[本文引用: 1]
Bayesian model updating of nonlinear systems using nonlinear normal modes
1
2018
... 在土木工程领域,有限元仿真是一种常用的结构分析手段,但根据设计图纸或理想化假设建立的初始有限元模型往往存在建模误差、模型参数误差和测量误差等因素,导致了模型预测结果和实际结构响应的偏离[1 ] .为了保证结构有限元模型的准确性,应根据实际观测数据适当地调整有限元模型参数,以最小化测量值和有限元模型预测值的差异[2 ] . ...
A practical Bayesian framework for structural model updating and prediction
1
2022
... 在土木工程领域,有限元仿真是一种常用的结构分析手段,但根据设计图纸或理想化假设建立的初始有限元模型往往存在建模误差、模型参数误差和测量误差等因素,导致了模型预测结果和实际结构响应的偏离[1 ] .为了保证结构有限元模型的准确性,应根据实际观测数据适当地调整有限元模型参数,以最小化测量值和有限元模型预测值的差异[2 ] . ...
Modified Hamiltonian Monte Carlo-based Bayesian finite element model updating of steel truss bridge
2
2020
... 传统的确定性模型更新方法不考虑测量信息和模型参数的不确定,更新后的有限元模型往往只能匹配某次测量的结构响应,难以准确预测结构在其他荷载条件下的响应.基于贝叶斯定理的模型更新是一种不确定性模型更新方法,综合考虑完整的测量信息和参数的先验信息,有效克服了确定性更新方法的不足,在模型更新领域得到广泛的应用[3 ] .1998年,Katafygiotis等[4 ] 和Beck等[5 ] 首次将贝叶斯理论应用于土木工程领域中的模型更新中,提出贝叶斯更新的基本框架.为了解决参数后验分布积分复杂的问题,Beck等[6 ] 将基于Metropolis-Hastings(MH)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法引入贝叶斯更新,利用剪切模型证明了该方法的可靠性.在Beck的理论基础上,诞生了许多优化的贝叶斯更新框架.刘纲等[7 ] 将延迟拒绝和自适应算法引入MH采样,结合相关向量机代理模型,更新了四层两跨钢框架结构弹性模量和质量密度.Lam等[8 ] 提出了一种可以同时计算多个马尔可夫链的并行MCMC算法,并将其应用于帆船形建筑的弹性模量更新.Luo等[9 ] 集成了粒子群优化中的粒子位置更新机制与MH算法,实现了三层框架结构的单元刚度更新. ...
... 随着参数的增加和后验分布的复杂化,被拒绝的采样样本大大增加,传统的MH算法在采样过程中容易形成具有大量重复样本的马尔可夫链,进入非遍历状态[3 ] .因此引入WOA对MH采样中被拒绝的样本进行二次采样,利用WOA全局搜索能力强的特点选择下一个样本点,从而提高采样样本的多样性,避免陷入局部最优.WOA是模仿自然界中鲸鱼群体狩猎行为的新型启发式优化算法[16 ] .WOA包含3种种群更新机制,假定当前鲸鱼个体的位置为Xt ,当前最佳鲸鱼个体的位置为X* ,当前种群内随机鲸鱼个体位置为X rand ,则Xt 在X* 或X rand 影响下得到下一个位置Xt +1 ,3种更新机制下Xt +1 的计算公式分别为 ...
Updating models and their uncertainties. II: Model identifiability
1
1998
... 传统的确定性模型更新方法不考虑测量信息和模型参数的不确定,更新后的有限元模型往往只能匹配某次测量的结构响应,难以准确预测结构在其他荷载条件下的响应.基于贝叶斯定理的模型更新是一种不确定性模型更新方法,综合考虑完整的测量信息和参数的先验信息,有效克服了确定性更新方法的不足,在模型更新领域得到广泛的应用[3 ] .1998年,Katafygiotis等[4 ] 和Beck等[5 ] 首次将贝叶斯理论应用于土木工程领域中的模型更新中,提出贝叶斯更新的基本框架.为了解决参数后验分布积分复杂的问题,Beck等[6 ] 将基于Metropolis-Hastings(MH)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法引入贝叶斯更新,利用剪切模型证明了该方法的可靠性.在Beck的理论基础上,诞生了许多优化的贝叶斯更新框架.刘纲等[7 ] 将延迟拒绝和自适应算法引入MH采样,结合相关向量机代理模型,更新了四层两跨钢框架结构弹性模量和质量密度.Lam等[8 ] 提出了一种可以同时计算多个马尔可夫链的并行MCMC算法,并将其应用于帆船形建筑的弹性模量更新.Luo等[9 ] 集成了粒子群优化中的粒子位置更新机制与MH算法,实现了三层框架结构的单元刚度更新. ...
Updating models and their uncertainties. I: Bayesian statistical framework
1
1998
... 传统的确定性模型更新方法不考虑测量信息和模型参数的不确定,更新后的有限元模型往往只能匹配某次测量的结构响应,难以准确预测结构在其他荷载条件下的响应.基于贝叶斯定理的模型更新是一种不确定性模型更新方法,综合考虑完整的测量信息和参数的先验信息,有效克服了确定性更新方法的不足,在模型更新领域得到广泛的应用[3 ] .1998年,Katafygiotis等[4 ] 和Beck等[5 ] 首次将贝叶斯理论应用于土木工程领域中的模型更新中,提出贝叶斯更新的基本框架.为了解决参数后验分布积分复杂的问题,Beck等[6 ] 将基于Metropolis-Hastings(MH)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法引入贝叶斯更新,利用剪切模型证明了该方法的可靠性.在Beck的理论基础上,诞生了许多优化的贝叶斯更新框架.刘纲等[7 ] 将延迟拒绝和自适应算法引入MH采样,结合相关向量机代理模型,更新了四层两跨钢框架结构弹性模量和质量密度.Lam等[8 ] 提出了一种可以同时计算多个马尔可夫链的并行MCMC算法,并将其应用于帆船形建筑的弹性模量更新.Luo等[9 ] 集成了粒子群优化中的粒子位置更新机制与MH算法,实现了三层框架结构的单元刚度更新. ...
Bayesian updating of structural models and reliability using Markov chain Monte Carlo simulation
1
2002
... 传统的确定性模型更新方法不考虑测量信息和模型参数的不确定,更新后的有限元模型往往只能匹配某次测量的结构响应,难以准确预测结构在其他荷载条件下的响应.基于贝叶斯定理的模型更新是一种不确定性模型更新方法,综合考虑完整的测量信息和参数的先验信息,有效克服了确定性更新方法的不足,在模型更新领域得到广泛的应用[3 ] .1998年,Katafygiotis等[4 ] 和Beck等[5 ] 首次将贝叶斯理论应用于土木工程领域中的模型更新中,提出贝叶斯更新的基本框架.为了解决参数后验分布积分复杂的问题,Beck等[6 ] 将基于Metropolis-Hastings(MH)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法引入贝叶斯更新,利用剪切模型证明了该方法的可靠性.在Beck的理论基础上,诞生了许多优化的贝叶斯更新框架.刘纲等[7 ] 将延迟拒绝和自适应算法引入MH采样,结合相关向量机代理模型,更新了四层两跨钢框架结构弹性模量和质量密度.Lam等[8 ] 提出了一种可以同时计算多个马尔可夫链的并行MCMC算法,并将其应用于帆船形建筑的弹性模量更新.Luo等[9 ] 集成了粒子群优化中的粒子位置更新机制与MH算法,实现了三层框架结构的单元刚度更新. ...
基于改进MCMC方法的有限元模型修正研究
1
2016
... 传统的确定性模型更新方法不考虑测量信息和模型参数的不确定,更新后的有限元模型往往只能匹配某次测量的结构响应,难以准确预测结构在其他荷载条件下的响应.基于贝叶斯定理的模型更新是一种不确定性模型更新方法,综合考虑完整的测量信息和参数的先验信息,有效克服了确定性更新方法的不足,在模型更新领域得到广泛的应用[3 ] .1998年,Katafygiotis等[4 ] 和Beck等[5 ] 首次将贝叶斯理论应用于土木工程领域中的模型更新中,提出贝叶斯更新的基本框架.为了解决参数后验分布积分复杂的问题,Beck等[6 ] 将基于Metropolis-Hastings(MH)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法引入贝叶斯更新,利用剪切模型证明了该方法的可靠性.在Beck的理论基础上,诞生了许多优化的贝叶斯更新框架.刘纲等[7 ] 将延迟拒绝和自适应算法引入MH采样,结合相关向量机代理模型,更新了四层两跨钢框架结构弹性模量和质量密度.Lam等[8 ] 提出了一种可以同时计算多个马尔可夫链的并行MCMC算法,并将其应用于帆船形建筑的弹性模量更新.Luo等[9 ] 集成了粒子群优化中的粒子位置更新机制与MH算法,实现了三层框架结构的单元刚度更新. ...
A finite element model updating method based on improved MCMC method
1
2016
... 传统的确定性模型更新方法不考虑测量信息和模型参数的不确定,更新后的有限元模型往往只能匹配某次测量的结构响应,难以准确预测结构在其他荷载条件下的响应.基于贝叶斯定理的模型更新是一种不确定性模型更新方法,综合考虑完整的测量信息和参数的先验信息,有效克服了确定性更新方法的不足,在模型更新领域得到广泛的应用[3 ] .1998年,Katafygiotis等[4 ] 和Beck等[5 ] 首次将贝叶斯理论应用于土木工程领域中的模型更新中,提出贝叶斯更新的基本框架.为了解决参数后验分布积分复杂的问题,Beck等[6 ] 将基于Metropolis-Hastings(MH)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法引入贝叶斯更新,利用剪切模型证明了该方法的可靠性.在Beck的理论基础上,诞生了许多优化的贝叶斯更新框架.刘纲等[7 ] 将延迟拒绝和自适应算法引入MH采样,结合相关向量机代理模型,更新了四层两跨钢框架结构弹性模量和质量密度.Lam等[8 ] 提出了一种可以同时计算多个马尔可夫链的并行MCMC算法,并将其应用于帆船形建筑的弹性模量更新.Luo等[9 ] 集成了粒子群优化中的粒子位置更新机制与MH算法,实现了三层框架结构的单元刚度更新. ...
Markov chain Monte Carlo-based Bayesian model updating of a sailboat-shaped building using a parallel technique
1
2019
... 传统的确定性模型更新方法不考虑测量信息和模型参数的不确定,更新后的有限元模型往往只能匹配某次测量的结构响应,难以准确预测结构在其他荷载条件下的响应.基于贝叶斯定理的模型更新是一种不确定性模型更新方法,综合考虑完整的测量信息和参数的先验信息,有效克服了确定性更新方法的不足,在模型更新领域得到广泛的应用[3 ] .1998年,Katafygiotis等[4 ] 和Beck等[5 ] 首次将贝叶斯理论应用于土木工程领域中的模型更新中,提出贝叶斯更新的基本框架.为了解决参数后验分布积分复杂的问题,Beck等[6 ] 将基于Metropolis-Hastings(MH)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法引入贝叶斯更新,利用剪切模型证明了该方法的可靠性.在Beck的理论基础上,诞生了许多优化的贝叶斯更新框架.刘纲等[7 ] 将延迟拒绝和自适应算法引入MH采样,结合相关向量机代理模型,更新了四层两跨钢框架结构弹性模量和质量密度.Lam等[8 ] 提出了一种可以同时计算多个马尔可夫链的并行MCMC算法,并将其应用于帆船形建筑的弹性模量更新.Luo等[9 ] 集成了粒子群优化中的粒子位置更新机制与MH算法,实现了三层框架结构的单元刚度更新. ...
Bayesian damage identification based on autoregressive model and MH-PSO hybrid MCMC sampling method
1
2022
... 传统的确定性模型更新方法不考虑测量信息和模型参数的不确定,更新后的有限元模型往往只能匹配某次测量的结构响应,难以准确预测结构在其他荷载条件下的响应.基于贝叶斯定理的模型更新是一种不确定性模型更新方法,综合考虑完整的测量信息和参数的先验信息,有效克服了确定性更新方法的不足,在模型更新领域得到广泛的应用[3 ] .1998年,Katafygiotis等[4 ] 和Beck等[5 ] 首次将贝叶斯理论应用于土木工程领域中的模型更新中,提出贝叶斯更新的基本框架.为了解决参数后验分布积分复杂的问题,Beck等[6 ] 将基于Metropolis-Hastings(MH)的马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)算法引入贝叶斯更新,利用剪切模型证明了该方法的可靠性.在Beck的理论基础上,诞生了许多优化的贝叶斯更新框架.刘纲等[7 ] 将延迟拒绝和自适应算法引入MH采样,结合相关向量机代理模型,更新了四层两跨钢框架结构弹性模量和质量密度.Lam等[8 ] 提出了一种可以同时计算多个马尔可夫链的并行MCMC算法,并将其应用于帆船形建筑的弹性模量更新.Luo等[9 ] 集成了粒子群优化中的粒子位置更新机制与MH算法,实现了三层框架结构的单元刚度更新. ...
Airframe digital twin technology adaptability assessment and technology demonstration
1
2020
... 贝叶斯方法将参数视为随机变量,使用测量数据来更新参数的先验概率密度函数,得到后验概率密度函数[10 ] .其公式如下: ...
Bayesian FE model updating in the presence of modeling errors
1
2014
... 式中:θ 是待更新参数组成的向量,θ =[θ 1 θ 2 … θN ]T ;D 是观测数据;P (θ )是θ 的先验分布,在没有历史经验的前提下常常将其视为广义无偏均匀分布;似然函数P (D |θ )是给定θ 时观测数据D 的条件概率;c =1/ ∫P (D |θ )P (θ )dθ ,是为了确保后验概率密度函数积分为1的归一化常数[11 ] . ...
Structural model updating and health monitoring with incomplete modal data using Gibbs sampler
1
2006
... 本文选择模态数据(频率和振型)作为观测数据D ,假设D (θ )为有限元模型的计算模态. 根据最大熵原理,误差的后验分布可以假设为均值为0、协方差为Σ 的高斯分布[12 ] .则似然函数可以写作: ...
基于改进MH算法的结构损伤识别
1
2022
... n 是模态试验的次数;s 是频率总阶数;${\hat{\mathrm{f}}}_{ri}$ ${\hat{\mathrm{\phi }}}_{ri}$ i 次实测第r 阶的频率和振型;fr 和φr 是有限元计算的第r 阶频率和振型;Σfr 和Σφr 分别是第r 阶的频率协方差和振型协方差[13 ] . ...
Damage identification based on improved MH algorithm
1
2022
... n 是模态试验的次数;s 是频率总阶数;${\hat{\mathrm{f}}}_{ri}$ ${\hat{\mathrm{\phi }}}_{ri}$ i 次实测第r 阶的频率和振型;fr 和φr 是有限元计算的第r 阶频率和振型;Σfr 和Σφr 分别是第r 阶的频率协方差和振型协方差[13 ] . ...
Bayesian model updating using hybrid Monte Carlo simulation with application to structural dynamic models with many uncertain parameters
1
2009
... 贝叶斯方法所得到的后验分布需要在参数空间上进行高维积分,难以直接计算其解析式,常引入MCMC算法来近似获得参数的后验分布[14 ] .MH算法是一种应用广泛的MCMC抽样方法,其从先验分布中采样,生成平稳分布的马尔可夫链,然后根据生成的样本获得待更新参数的统计特征[15 ] . ...
An innovative Bayesian updating method for laminated composite structures under evidence uncertainty
1
2023
... 贝叶斯方法所得到的后验分布需要在参数空间上进行高维积分,难以直接计算其解析式,常引入MCMC算法来近似获得参数的后验分布[14 ] .MH算法是一种应用广泛的MCMC抽样方法,其从先验分布中采样,生成平稳分布的马尔可夫链,然后根据生成的样本获得待更新参数的统计特征[15 ] . ...
The whale optimization algorithm
1
2016
... 随着参数的增加和后验分布的复杂化,被拒绝的采样样本大大增加,传统的MH算法在采样过程中容易形成具有大量重复样本的马尔可夫链,进入非遍历状态[3 ] .因此引入WOA对MH采样中被拒绝的样本进行二次采样,利用WOA全局搜索能力强的特点选择下一个样本点,从而提高采样样本的多样性,避免陷入局部最优.WOA是模仿自然界中鲸鱼群体狩猎行为的新型启发式优化算法[16 ] .WOA包含3种种群更新机制,假定当前鲸鱼个体的位置为Xt ,当前最佳鲸鱼个体的位置为X* ,当前种群内随机鲸鱼个体位置为X rand ,则Xt 在X* 或X rand 影响下得到下一个位置Xt +1 ,3种更新机制下Xt +1 的计算公式分别为 ...
Structural performance assessment of RC flexural members through crack-based fibre beam-column model updating
1
2023
... 解决模型更新效率低下的另一种方法是建立高保真的代理模型来拟合结构响应和更新参数之间的关系,从而代替有限元模型进行计算[17 ] .常用的代理模型包括Kriging模型、RBF模型、RF模型、响应面模型、支持向量回归(support vector regression,SVR)等.本文选用RBF、RF和Kriging作为有限元模型的代理模型. ...
Stochastic model updating utilizing Bayesian approach and Gaussian process model
1
2016
... 分别利用MH和WO-MH进行采样,经过 5 000 次迭代后得到参数的马尔可夫链,如图4 所示.引入WOA后,MH采样的收敛速度和平稳性大大提升.通过自相关函数(autocorrelation function,ACF)图[18 ] 来评估马尔可夫链的样本相关性,如图5 所示.与MH采样得到的ACF图相比,WO-MH采样得到的ACF图很快衰减到0,表明其样本之间相关度较低,在参数空间中收敛速率更快. ...
测量模态不确定的梁式结构随机有限元模型修正
1
2019
... 研究对象为一个3层钢框架结构,如图7 所示.在模型的X 及Y 向安装单向加速度传感器,对模型施加X 向和Y 向的正弦波,通过快速傅里叶变换(fast Fourier transformation,FFT)将模态试验所得各组加速度数据转换成频域数据,提取结构的频率和振型.由于模态试验中高阶模态往往误差较大,采用X 方向和Y 方向的前两阶模态进行模型更新[19 ] .其中,试验测得频率的均值和方差如表4 所示. ...
Stochastic finite element model updating of beam structure based on uncertain measurement modes
1
2019
... 研究对象为一个3层钢框架结构,如图7 所示.在模型的X 及Y 向安装单向加速度传感器,对模型施加X 向和Y 向的正弦波,通过快速傅里叶变换(fast Fourier transformation,FFT)将模态试验所得各组加速度数据转换成频域数据,提取结构的频率和振型.由于模态试验中高阶模态往往误差较大,采用X 方向和Y 方向的前两阶模态进行模型更新[19 ] .其中,试验测得频率的均值和方差如表4 所示. ...
Vibration-based Bayesian model updating of an actual steel truss bridge subjected to incremental damage
1
2022
... 结构设计方案中所有钢材的弹性模量为206 GPa,质量密度为 7 850 kg/m3 ,框架与基础为完全刚接.参照结构设计方案设计有限元模型,钢构件使用线单元建模,梁中的支架简化为对应位置节点上的附加集中质量,此时模型X 向一阶频率18.707 Hz,与实测频率相差较大.考虑到施工完成的框架底板与基础之间以螺栓连接,并非完全固接,按照完全刚接考虑不够合理,因此将边界条件加入更新参数.将有限元模型中柱和基础之间的连接使用两根线性弹簧来表示,分别代表绕x 轴转动和绕y 轴转动的扭转刚度[20 ] . ...