上海交通大学学报

上海交通大学学报, 2025, 59(8): 1081-1091 doi: 10.16183/j.cnki.jsjtu.2023.476

船舶海洋与建筑工程

海洋风电场尾流荷载作用下水平轴风力机结构动力响应

祝怡情1, 吴锋2, 周岱,1, 韩兆龙1, 卓杨2, 朱宏博1, 张凯1

1.上海交通大学 船舶海洋与建筑工程学院, 上海 200240

2.中交上海三航科学研究院有限公司, 上海 200032

Structural Dynamic Response of Offshore Horizontal Axis Wind Turbine Subjected to Wake-Induced Action

ZHU Yiqing1, WU Feng2, ZHOU Dai,1, HAN Zhaolong1, ZHUO Yang2, ZHU Hongbo1, ZHANG Kai1

1. School of Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. CCCC Shanghai Third Harbor Engineering Science and Technology Research Institute Co., Ltd., Shanghai 200032, China

通讯作者: 周 岱,教授,博士生导师;E-mail:zhoudai@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-09-18   修回日期: 2023-10-22   接受日期: 2023-10-26  

基金资助: 国家自然科学基金(42076210)
国家自然科学基金(52122110)
上海市教委重大科技创新计划(2019-01-07-00-02-E00066)

Received: 2023-09-18   Revised: 2023-10-22   Accepted: 2023-10-26  

作者简介 About authors

祝怡情(1998—),硕士生,从事水平轴风力机相关研究.

摘要

研究串列布置水平轴双风力机动力响应对保障风力机结构安全至关重要.基于计算流体动力学(CFD)方法,分析处于上游风力机近尾流区的下游风力机尾流场特性,获取双风力机气动荷载时程曲线.进而结合结构动力学与有限元数值方法,分析上、下游风力机结构的风致动力响应特性.研究发现:近尾流区尾流速度亏损显著,导致下游风力机的推力和扭矩分别减少54.94%和91.89%;同时,尾流湍流加剧了下游风力机的气动荷载的周期性波动.气动荷载波动性对下游风力机动力响应影响较小,其整体动力响应较弱,表现为塔顶推力方向的位移减小50.79%.研究成果可为海洋风电场风力机群结构气动响应分析提供技术参考.

关键词： 水平轴风力机; 海洋风电场; 气动性能; 尾流干扰效应; 动力响应

Abstract

The study of the dynamic response of a horizontal axis twin wind turbine in tandem arrangement is crucial for ensuring the structural safety of the wind turbine. Based on the computational fluid dynamics (CFD) method, the characteristics of the wake flow field of the downstream turbine, located in the near wake region of the upstream turbine, are analyzed. The time course curves of the aerodynamic loads on the twin turbines are obtained. Structural dynamics and finite element numerical methods are then used to analyze the wind-driven dynamic effects of the upstream and downstream turbine structures. It is found that the wake velocity deficit in the near wake region is significant, causing a reduction in thrust and torque of the downstream turbine by 54.94% and 91.89% respectively. Additionly, the wake turbulence increases cyclic fluctuation of aerodynamic load on the downstream turbine. While the aerodynamic load volatility has a small effect on the dynamic response of the downstream wind turbine, the overall dynamic response is weaker, and the displacement of the downstream wind turbine tower top in the thrust direction is reduced by 50.79%. The results provide technical references for the analysis of aerodynamic response of wind turbine cluster structures in offshore wind farms.

Keywords： horizontal axis wind turbine (HAWT); offshore wind farms; aerodynamic performance; wake interference effect; dynamic response

PDF (12106KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

祝怡情, 吴锋, 周岱, 韩兆龙, 卓杨, 朱宏博, 张凯. 海洋风电场尾流荷载作用下水平轴风力机结构动力响应[J]. 上海交通大学学报, 2025, 59(8): 1081-1091 doi:10.16183/j.cnki.jsjtu.2023.476

ZHU Yiqing, WU Feng, ZHOU Dai, HAN Zhaolong, ZHUO Yang, ZHU Hongbo, ZHANG Kai. Structural Dynamic Response of Offshore Horizontal Axis Wind Turbine Subjected to Wake-Induced Action[J]. Journal of Shanghai Jiaotong University, 2025, 59(8): 1081-1091 doi:10.16183/j.cnki.jsjtu.2023.476

风能是一种可再生能源,在全球可再生能源中的占比正逐步提升[1].随着风电技术发展,度电成本逐步下降.现阶段我国风电行业从陆地向海上拓展[2-3].海上风力机所处环境复杂,受到多种复杂组合载荷的影响显著[4],导致风力机动力响应更为复杂,安全性问题也随之凸显.

研究近尾流区风力机尾流特性以及下游风力机的气动荷载特性具有重要意义.随着海上风力机装机容量和轮毂高度不断增大,风力机塔筒顶部的大型转子和发电机质量和支撑塔筒的高度增大[5].目前,海上风电场中风力机常采用串列布局方式.然而,上游风力机尾流传播至下游风力机时,会对下游风力机的气动荷载特性造成干扰,进而影响其结构动力响应.许多研究者对水平轴风力机的振动特性进行了研究[6].柯世堂等[7]采用风力机塔架-叶片耦合模型,基于有限元方法分析了风力机塔架-叶片耦合系统在随机风荷载作用下的动力响应特性,并提出抗风设计应考虑塔架-叶片的耦合作用.丁勤卫等[8]考虑了风突变效应因素,分析了风力机叶片和塔架的位移和振动特性.周文平等[9]考虑了风剪切和动态来流因素对于风力机气动特性的影响,发现风剪切使得叶片载荷随时间呈周期性波动,增加了风力机的疲劳荷载.Kim等[10]分析了风电场对平均风速、风切变和湍流强度的尾流效应,发现风电场中尾流效应引起的高湍流强度会显著增加下游风力机的疲劳负荷.Clio等[11]研究了风电场中3台风力机的功率输出,发现由于上游风力机的影响,下游风力机的结构荷载和性能输出受到削弱.尽管目前已有关于单风力机在不同来流风下的结构振动分析,但关于双风力机的研究大多集中在风电场整体的功率输出及疲劳荷载方面,而针对风电场串列布置风力机结构风致振动响应的研究相对较少.

本文主要研究风电场串列布置水平轴双风力机结构动力响应.基于计算流体动力学(CFD)数值方法,运用Star CCM+商业计算软件,研究揭示两台NREL 5 MW[12]水平轴风力机(HAWT)旋转叶片的尾流气动荷载特性,对比分析两台风力机荷载大小、周期性、波动性等气动特性.在计算获取风力机气动荷载基础上,利用MATLAB软件中对该荷载进行拟合,以获得风力机叶片时序性荷载函数,将其施加于基于ANSYS软件建立的双风力机有限元计算模型,开展风力机结构动力学响应模拟,研究上、下游风力机位移、速度和加速度等动力学响应特性规律.

1 串列布置水平轴风力机

本文技术路线如图1所示.以NREL 5 MW水平轴风力机为对象,上、下游风力机间距设为5倍风轮直径,风力机间距布置如图2所示.该风力机模型为三叶片水平轴风力机,叶片结构为空心环型主梁加蒙皮结构,其几何模型和参数分别如图3和表1所示.风力机半径R=63 m,风轮直径D=126 m;塔筒高度H=90 m,塔筒底部直径D1=6 m,顶部直径D2=3.87 m.塔筒材料选用Q345钢材[12],密度ρ0=8 500 kg/m3(考虑了塔筒油漆、螺栓、焊接和法兰等零部件的质量),弹性模量E0=210 GPa,叶片蒙皮材料选择碳纤维环氧树脂,材料密度ρ1=1 620 kg/m3,弹性模量E1=120 GPa,泊松比γ=0.31.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   水平轴双风力机结构动力响应分析技术路线图

Fig.1   Technology flow chart for dynamic response analysis of HAWT


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   上、下游风力机间距布置图

Fig.2   Layout of upstream and downstream wind turbine distance


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   水平轴风力机几何模型

Fig.3   Geometric model of horizontal-axis wind turbine


表1   水平轴风力机模型的几何参数

Tab.1  Geometric properties of HAWT model

参数取值参数取值
额定输出功率/MW5额定风速/(m·s-1)11.4
叶片直径/m126轮毂高度/m90
叶片数3叶尖速比TSR8
切入风速/(m·s-1)3切出风速/(m·s-1)25
切入转速/(r·min-1)6.9额定转速/(r·min-1)12.1

新窗口打开| 下载CSV


2 数值方法

2.1 串列布置双风力机气动荷载

运用计算流体动力学CFD数值方法计算分析NREL 5 MW水平轴风力机气动荷载[13],即采用软件Star CCM+与重叠网格技术模拟上、下游风力机气动荷载,研究上、下游风力机气动响应.其中,空气假定为不可压缩流体.采用具有切应力输运(SST-ω)的非定常雷诺平均Navier-Stokes(URANS)湍流模型,对应的N-S方程如下:

$\frac{\partial \left(\rho {u}_{i}\right)}{\partial {x}_{i}}$=0
$\frac{\partial \left(\rho {u}_{i}\right)}{\partial t}$+$\frac{\partial \left(\rho {u}_{j}{u}_{i}\right)}{\partial {x}_{j}}$=-$\frac{\partial p}{\partial {x}_{i}}$+$\frac{\partial }{\partial {x}_{j}}\left[\mu \left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}-\frac{2}{3}{\mathrm{\delta }}_{ij}\frac{\partial {u}_{i}}{\partial {x}_{j}}\right)\right]$+$\frac{\partial }{\partial {x}_{i}}$(-$\overline{\rho u{\text{'}}_{i}u{\text{'}}_{j}}$)

式中:ui,uj分别为流体在i,j方向上的速度;xi,xj分别为流体在笛卡尔坐标系中i,j方向上的位置;μ为有效黏性系数;δij为克罗内克函数;t为时间;流体密度和流场中的压力用ρ和p表示;表达式 $\overline{\rho u{\text{'}}_{i}u{\text{'}}_{j}}$称为雷诺应力,表示湍流的影响.

建立如图4所示双风力机的计算域布局和边界条件.计算域入口采用速度入口条件,入口边界来流风速设置v∞=11.4 m/s,出口边界设置为压力出口,其余4个壁面均为滑移壁面条件,叶片表面为非滑移壁面.计算域尺寸20D×16D×8D,坐标原点设置在上游风力机轮毂中心处,原点距离速度入口边界的距离为4D,两风力机距离横向边界的距离均为8D,从原点到出口的长度为16D.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   水平轴风力机计算域及边界条件

Fig.4   Calculation domain and boundary conditions of horizontal axis wind turbine


计算域网格划分如图5所示,每个风力机叶片的旋转区域尺寸为Ω1(顺流向0.75D,横流向1.2D)的圆柱体,采用重叠网格技术生成.背景区域和旋转区域都使用Star CCM+ 18.02的网格生成器进行结构化网格划分.风场计算域划分时,为更好得获取上、下游风力机动力特性,旋转域到叶片边缘的网格呈逐渐加密,且由于叶片前缘的曲率较大,为保证计算结果的精确性,前缘网格尺寸更小,叶片表面采用棱柱层网格,总厚度为0.02 m.对模型雷诺数Re=11.4×106,在壁面处采用高y+值,以处理近壁区域湍流阻尼不佳的情况.这种处理可能对叶片阻力计算精度有一定影响,不过鉴于近叶片尖端区域流速很大,该阻力的计算精度误差很小.所以文中对无量纲化壁面距离,采用30<y+<300范围[14-15];同时,旋转域和计算域均采用切割体网格划分,总网格数3.35×107.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   水平轴风力机计算域网格

Fig.5   Computational domain grid of horizontal axis wind turbine


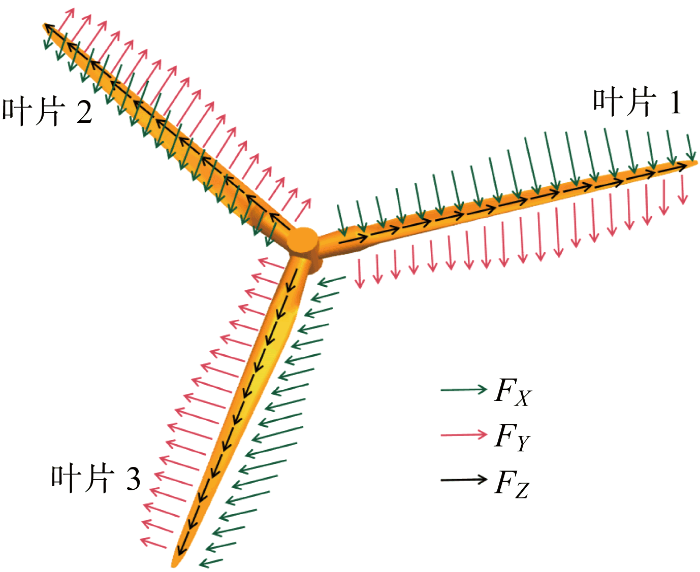
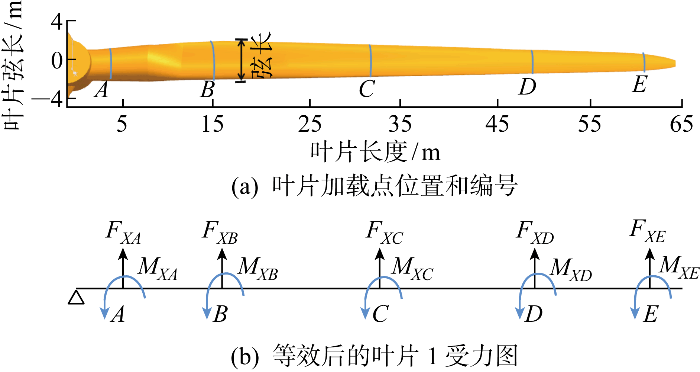
数值计算在稳态迭代约 2 000 次后,收敛误差小于1/104,且叶片气动载荷趋稳,以稳态解作为起点进行非稳态计算.叶片旋转一个完整周期耗时4.959 s,取计算时间步长为 27.5 ms,其对应叶片每时间步长旋转2° ;对每个时间步长迭代20次,总计算时长为500 s.为获得更准确的上、下游风力机叶片气动荷载,建模中将各叶片沿径向长度,按每段1 m,划分成63段,在Star CCM+软件中分别对每一段建立局部坐标系,得到上、下游风力机每段叶片的气动荷载,图6为施于叶片表面的气动荷载示意图.图中:FX为风力机叶片所受到的推力;FY为风力机叶片所受到的切向力;FZ为风力机叶片所受到的离心力.在风力机的每个叶片上取5个加载点,按照力等效原则,把通过函数拟合所得的叶片各段不均匀气动荷载分别等效加载于叶片的根部、中部和尖部的A、B、C、D、E等5个加载点,如图7所示.以下游风力机叶片1加载点C处的荷载为例,将推力及转矩时程曲线采用傅里叶级数进行拟合[16-17],得到风力机叶片加载点上任意时间序列的荷载函数方程为

$F_{X C}(t)=a_{0}+\sum_{j=1}^{8}\left[a_{j} \cos \left(\omega_{j} t\right)+b_{j} \sin \left(\omega_{j} t\right)\right]$
$M_{X C}(t)=c_{0}+\sum_{j=1}^{8}\left[c_{j} \cos \left(\omega_{j} t\right)+d_{j} \sin \left(\omega_{j} t\right)\right]$

式中:FXC(t)和MXC(t)分别叶片C点在t时刻下叶片的推力和推力形成的法向扭矩;a0、aj、bj、c0、cj、dj为傅里叶系数;ωj为基波圆频率;j∈N*.C点的推力、法向扭矩拟合曲线如图8所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   风力机叶片气动荷载示意图

Fig.6   Schematic diagram of aerodynamic loads on wind turbine blade


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   叶片等效荷载示意图

Fig.7   Diagram of blade equivalent loads


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   叶片中部加载点C处荷载拟合曲线

Fig.8   Load fitting curve at loading point C in the middle of the blade


2.2 风力机结构气动响应分析

运用ANSYS APDL软件计算上、下游风力机结构风致动力响应.建立风力机塔架-叶片耦合系统有限元模型时,采用梁单元BEAM 188,将节点部位约束条件设为刚接;依据效率和精度均衡的原则,模型划分2 981个单元,把拟合所得的叶片气动荷载函数分别施加于各叶片的5个加载点上.采用Newmark-β法中的平均常加速度法进行瞬态分析[18],该方法是二阶时间精度[19]的隐式时间积分方法,其中选用γ=0.5,β=0.25,采用瑞利阻尼,刚度阻尼系数取0.03[18].风力机结构系统风致动力方程为[19]

$\begin{array}{l}\boldsymbol{M} \ddot{\boldsymbol{u}}(t)+\boldsymbol{C} \ddot{\boldsymbol{i}}(t)+\boldsymbol{K} \boldsymbol{u}(t)= \\\quad \boldsymbol{F}_{\boldsymbol{I}}(t)+\boldsymbol{F}_{\boldsymbol{C}}(t)+\boldsymbol{F}_{\boldsymbol{K}}(t)=\boldsymbol{f}(t)\end{array}$

式中:$\ddot{u}$(t)、$\stackrel{·}{u}$(t)、u(t)分别为水平轴风力机节点的加速度响应、速度响应和位移响应;M、C、K分别为大型水平轴风力机结构的质量矩阵、阻尼矩阵和刚度矩阵;FI(t)、FC(t)、FK(t)分别为风力机的惯性力矩阵、阻尼力矩阵和恢复力矩阵;f(t)为激励荷载向量.

3 关键参数验证和选择

3.1 网格收敛性分析

当TSR为8时,选取NREL 5 MW上游水平轴风力机进行了千万级网格数的3种网格剖分方案(粗网格、中等网格、细网格)收敛性分析,相应的结果如表2所示.在不同的网格方案下,风力机扭矩和推力结果差异较小,中等网格和细网格计算结果相近.细网格计算成本较高,采用中等网格即可满足精度要求.

表2   网格独立性测试结果

Tab.2  Results of mesh independence test

网格网格数量推力/MN扭矩/(MN·m)
粗网格2.08×1070.753.59
中等网格3.35×1070.813.70
细网格4.57×1070.823.72

新窗口打开| 下载CSV


3.2 风力机功率与推力的验证

首先,分析验证上、下游风力机功率系数.图9为本文计算所得的上、下游风力机功率与相关文献结果的对比示意图.图9(a)中所示本文上游风力机功率结果为5.46 MW,文献[12,20-22]中的数值模拟结果均值为5.38 MW,误差1.5%,一致性较好.图9(b)为下游风力机功率的对比,本文结果为0.35 MW,文献[21,23-25]中的结果均值为0.86 MW.下游风力机功率计算结果与有关文献差别较大,主要原因之一是本文与参考文献双风力机间距不同,且未考虑风剪切作用.本文的下游风力机在5D近尾流位置处的入流风速显著降低,因此下游风力机输出功率较小;而参考文献下游风力机位于7D远尾流区域,叠加风剪切作用后,入流速度已得到恢复,由此导致下游风力机输出功率存在差异.此外,本文与文献中的风力机虽然保持相同转速,由于不同位置处下游风力机入流风速不同,所以风力机正常工作下的实际叶尖速比不同,导致两者输出功率有差异.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   上、下游风力机功率对比

Fig.9   Power comparison of upstream and downstream wind turbines


其次,分析验证风力机叶片不同位置处推力情况,图10为本文计算所得的单个风力机叶片不同位置处推力与相关文献结果的对比示意图.由图10可见,本文单风力机叶片不同位置处推力荷载结果和变化趋势与Nakhchi等[24,26 -27]的结果均较一致.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   单风力机叶片不同位置处推力对比

Fig.10   Comparison of thrust force at different positions of single wind turbine blade


3.3 时间步长选择

风力机结构动力效应求解,时间步长大小直接影响计算精度和效率.为兼顾计算效率和计算精度,需要审慎选择时间步长大小.利用ANSYS软件,分别选取计算时间步长为5、10、20、30 ms,以计算风力机塔筒底部扭矩M0.其中风力机关于y轴底部扭矩结果如表3所示.

表3   不同时间步长下风力机塔筒底部扭矩

Tab.3  Bottom bending moment at different time steps

时间步长/msM0/(MN·m)
5103.5
10103.0
20102.0
30101.0

新窗口打开| 下载CSV


风力机塔筒底部扭矩为

M0=$M_{0}=\int_{0}^{h_{k}} \int_{0}^{A_{k}} p(y) \mathrm{d} A \mathrm{~d} y$

式中:k为风力机内部质点;hi为结构物的高度;p(y)为y高度处结构表面压力;A,Ak为受力面积.

从表2可见,时间步长为10 ms时风力机底部所受扭矩大小M0=103 MN·m,与时间步长为5 ms时相比,误差仅为0.48%,计算结果较为相近.结构动力学算法受其模型中最小尺寸的网格影响,网格越小应力波传播速度越慢.保证计算稳定所需的时间步一般很小(仅为CFD时间步长的 1/1 000~1/100),从而导致计算量巨大.通过提高结构动力学计算的时间步长,可在较小影响结构特性分析前提下提高计算效率.本文中,采用10 ms的时间步长,既保证了计算精度,又提升了计算速度.

4 结果与分析

4.1 尾流场特性分析

图11给出计算时刻T=200,330,500 s的瞬时尾流场速度云图与时均流速云图.上游风力机不受尾流干扰影响,而下游风力机处于上游风力机的尾流场,其入流特性受到较强干扰,在下游风力机风轮前部出现尾流回旋,显著降低了下游风力机轮毂高度处的入流风速.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   不同时刻下流场速度云图

Fig.11   Velocity maps of lower flow field at different moments


在轮毂高度处,展向(X向)风速沿横向(Y向)的变化如图12所示.图中:vX为X方向上轮毂高度处的风速;vref为标准情况下的参考入流风速.在0<X/D<3处,展向平均风速剖线近似对称,平均风速在近中心线出现对称下凹.在4<X/D<6处,左右两边的下凹区发生一定偏移.7<X/D<8区域内,展向平均风速剖线变形较大,速度损失较明显.当X/D>8后,展向平均风速得到恢复.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   展向(X向)风速沿横向(Y向)的变化

Fig.12   Profile of spreading (X-direction) wind speed along the lateral (Y-direction) direction


4.2 串列布置双风力机气动荷载分析

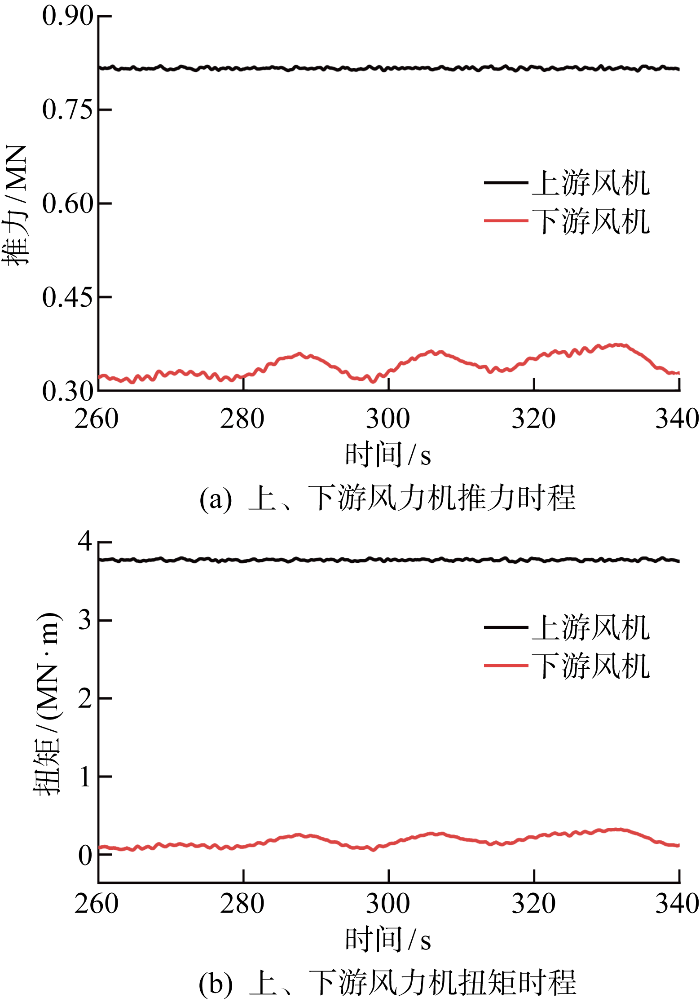
基于NREL 5 MW风力机,针对额定风速11.4 m/s、叶尖速比TSR为8、风力机额定转速为12.1 r/min的典型工况,运用STAR CCM+软件对上、下游风力机的扭矩和推力进行了计算,如图13所示.图13(a)、13(b)分别为上、下游风力机推力、扭矩时程曲线.可见上游风力机推力和扭矩均显著高于下游风力机.上游风力机推力范围在0.81 MN,扭矩则约为3.7 MN·m.相比之下,下游风力机因受上游风力机尾流的强烈干扰,其推力、扭矩均呈现周期性波动特征.下游推力波动区间为0.31~0.42 MN,其平均推力值比上游风力机减小了54.94%;而扭矩在0.1~0.5 MN·m范围内波动,平均扭矩值相较于上游风力机减少了91.89%.由此可见,下游风力机的推力和扭矩衰减十分显著.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   风力机叶片扭矩、推力时程

Fig.13   Torque and thrust time history of wind turbine


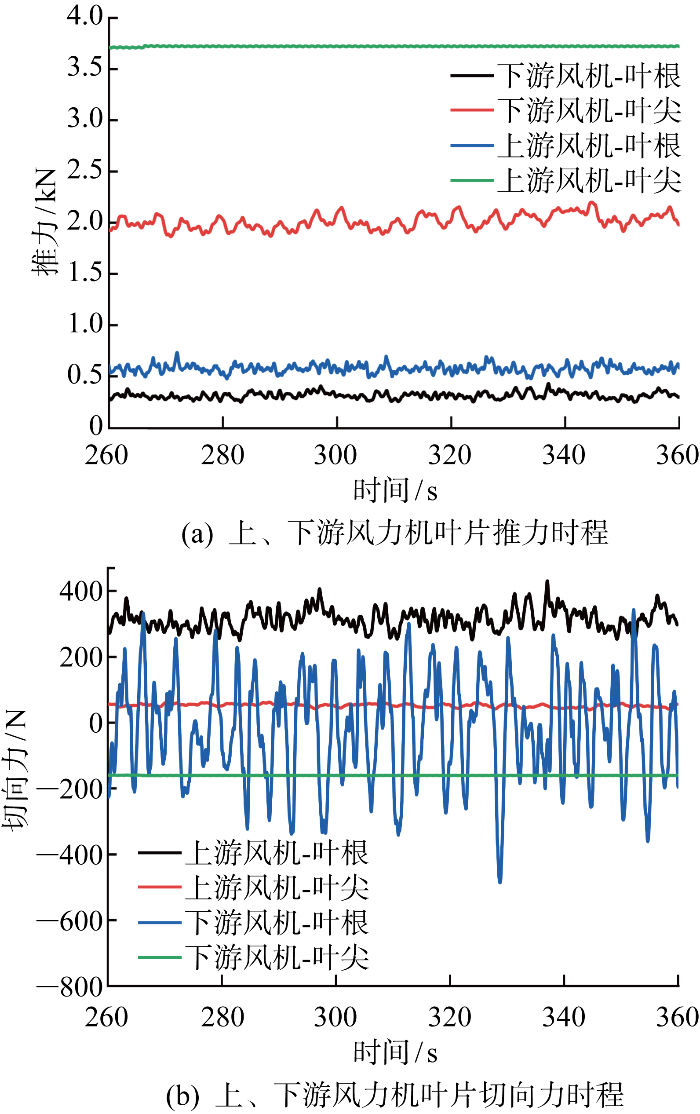
以上、下游风力机的叶片1为例,分析上、下游风力机进入稳态后的叶片荷载特性.图14所示为上、下游风力机叶片1在叶根和叶尖处的推力、切向力时程变化.结果显示,这些力均呈现一定波动性.在叶根处,下游风力机推力平均值较上游风力机减小了45.49%,但两者的推力波动性相近;而下游风力机切向力平均值仅为上游风力机的5.4%,但切向力时程变化的幅值达到了600 N,切向力的波动性达到上游风力机的4倍.在叶尖处,下游风力机推力平均值比上游风力机减小了45.94%,而上游风力机的推力波动特性迅速减弱,下游推力时程幅值达到了上游风力机的14.5倍,表现出显著荷载波动性.相比之下,两个风力机的切向力差异较小,且变化均较稳定,荷载波动性锐减.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   风力机叶片推力、切向力时程

Fig.14   Thrust and tangential force time history of wind turbine


4.3 双风力机结构风致动力响应分析

将上述所得的气动荷载施加于风力机结构系统,计算分析上、下游风力机动力响应.为简化计算,对叶片仅考虑箱型主梁刚度而忽略蒙皮效应.当风力机旋转20圈后,上游风力机气动特性趋稳,而下游风力机由于受到上游风力机尾流的影响,其气动特性初期明显不稳;下游风力机旋转30圈后,上、下游风力机气动特性均达到稳定状态.本文选取风力机转动的第260~360 s时段,对风力机的动力响应进行分析.

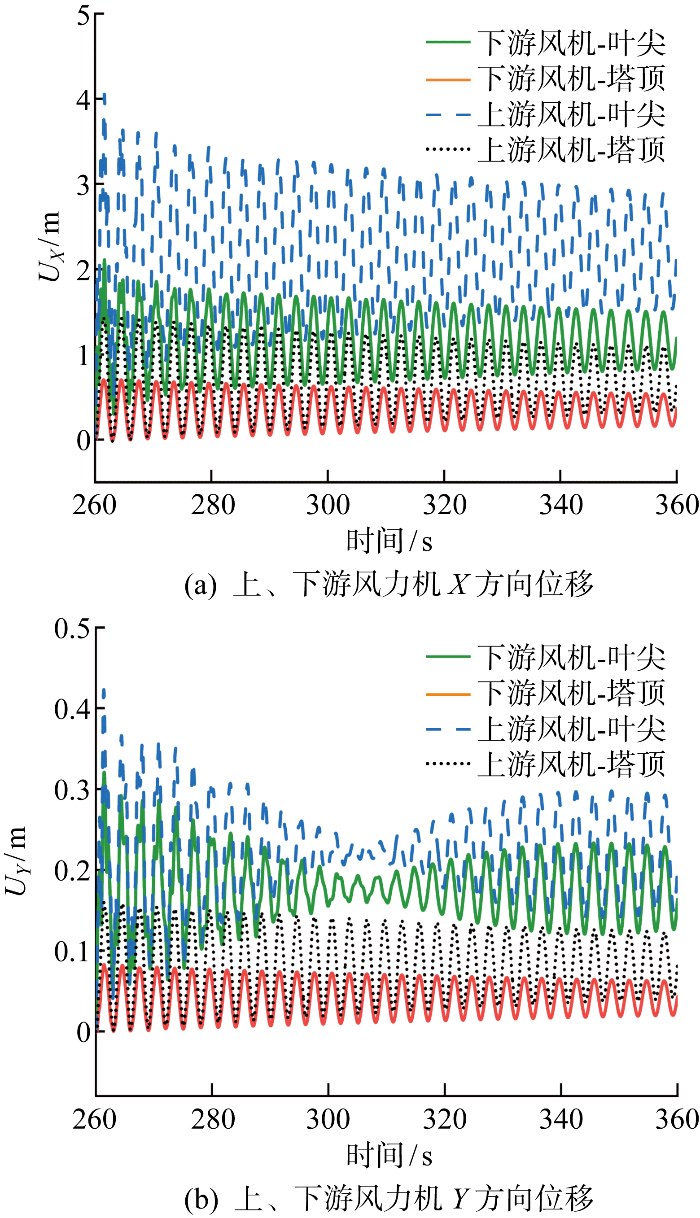
上、下游风力机塔顶、叶尖处的法向X、切向Y两个方向的位移响应极值如表4所示.表中:UX,max为X方向的最大位移;UX,min为X方向的最小位移;UY,max为Y方向的最大位移;UY,min为Y方向的最小位移;ΔX=UX,max-UX,min;ΔY=UY,max-UY,min.可见上游风力机结构风致动力响应较大,结构最大位移发生在叶尖处,应重点关注叶尖位移.

表4   风力机塔顶、叶尖处的位移响应极值

Tab.4  Extreme values of displacement response at top of the wind turbine tower and at tip of the blade

位置UX,max/mΔX/mUY,min/mUY,max/mmΔY/m
上游风力机塔顶-0.017 91.425 01.442 4-0.90.160 0
下游风力机塔顶-0.010 60.702 00.712 7-0.50.082 8
上游风力机叶尖0.004 04.053 04.048 90.20.423 0
下游风力机叶尖0.002 52.109 62.107 00.20.320 8

新窗口打开| 下载CSV


上、下游风力机的塔顶和叶尖在X、Y方向的位移时程曲线如图15所示.由图15(a)可见,上、下游风力机在X方向出现周期性位移波动,上游风力机动力响应大于下游风力机.在塔顶处,上游风力机位移时程波谷为 -18 mm,波峰为1.425 m,平衡位置为0.704 m;下游风力机位移时程波谷为-11 mm,波峰为0.702 m,平衡位置为0.347 m,上游风力机与下游风力机塔顶平衡位置幅值相差50.79%.叶尖处,上、下游风力机叶尖平衡位置幅值相差47.45%.风力机叶片顺风向即X方向振动响应比塔顶更剧烈,上、下游风力机振动响应在顺风向的差异显著.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   风力机位移时程曲线

Fig.15   Displacement time history of wind turbine


图15(b)给出风力机横风向即Y方向振动响应.由图可见,上、下游风力机叶尖响应相近,Y方向整体振动响应趋于缓和.塔顶处,上、下游风力机的位移平衡位置分别为81 mm和41 mm,两者相差19.63%.叶尖处,上、下游风力机位移平衡位置相差49.39%.可见,上、下游风力机横风向振动差异较小.

图16给出上、下游风力机在X、Y向的速度vX、vY时程,可见风力机在两个方向的速度幅值变化显著,在前20 s风力机动力响应强烈.进入平稳态后,速度趋稳,且上游风力机速度时程大于下游风力机.在X方向上,上、下游风力机在叶尖处的稳定速度时程变化幅度分别为5.08 m/s和2.67 m/s,两者相差50%,上、下游风力机塔顶速度变化幅值相近,但塔顶处整体速度响应比叶尖处弱.在Y方向上,叶尖与塔顶速度响应变化规律相同,上、下游风力机的稳定速度变化幅值较相近.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16   风力机速度时程曲线

Fig.16   Velocity time history of wind turbine


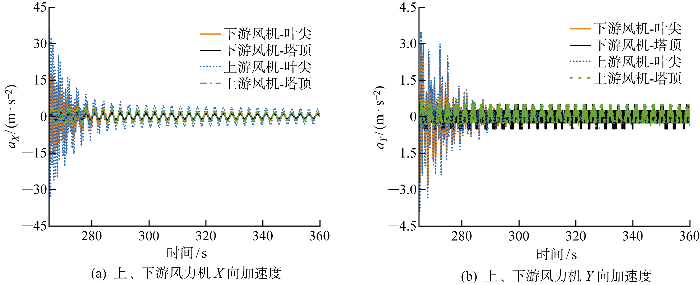
图17给出上、下游风力机在X、Y方向的加速度aX、aY时程,其变化趋势与速度时程相似.在X方向,上游风力机的叶尖加速度变化幅值为14.2 m/s2,下游风力机为7.40 m/s2,为上游风力机的52%,下游风力机的塔顶加速度变化幅值为上游风力机的55%.在Y方向,相同位置处上、下游风力机加速度响应变化相近,下游风力机的叶尖于塔顶处加速度变化幅值均为上游风力机的80%.

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17   风力机加速度时程曲线

Fig.17   Acceleration time history of wind turbine


5 结论

本文以NREL 5 MW水平轴风力机为研究对象,基于计算流体动力学CFD和结构动力学理论,运用STAR CCM+分析软件,数值模拟风力机运行旋转时的流场速度分布和叶片气动荷载,并将所得的风力机叶片时序荷载施加于风力机结构,利用ANSYS软件开展风力机结构动力响应时程计算,分析揭示上、下游风力机动力响应特性规律.主要结论如下:

(1) 尾流场特性方面.近尾流区域下游风力机尾流风速亏损严重,风速恢复较慢,导致下游风力机入流风速损失较大.下游风力机在近尾流区难以发挥较佳的输出功率,其输出功率仅为上游风力机的7%.

(2) 风力机气动荷载特性方面.上游风力机对下游风力机气动荷载的影响程度因方向和位置而异.上、下游风力机的推力和切向力荷载从叶根到叶尖均呈现先增大后减小趋势,但下游风力机整体气动荷载明显小于下游风力机,其中下游风力机整体推力比上游风力机减小约45%.下游风力机气动荷载呈现明显波动,越靠近叶尖,荷载波动性越强,其中叶片推力方向的气动荷载波动最显著,下游叶尖处推力时程幅值为上游风力机的14.5倍.

(3) 风力机气动振动响应方面.上游风力机所受气动荷载较大,其结构振动响应也较大.在推力方向上,上、下游风力机塔顶位移幅值相差50.79%,叶尖位移幅值相差47.45%.在切向力方向(Y方向),上、下游风力机位移振动响应相接近,叶尖处位移振动响应幅值差别较小.在X方向,上、下游风力机的速度和加速度响应均较大,且幅值差距均超过50%.同时,叶尖处的速度和加速度响应均大于塔顶处,而在Y方向上,上、下游风力机速度和、加速度响应差别不大.因此,在风力机设计和运行中,应重点关注风力机叶片尖部顺风向结构位移响应.

参考文献

JOSELIN HERBERT G M, INIYAN S, SREEVALSAN E, et al.

A review of wind energy technologies

[J]. Renewable & Sustainable Energy Reviews, 2007, 11 (6): 1117-145.

[本文引用: 1]

VARGAS S A, ESTEVES G R T, MAÇAIRA P M, et al.

Wind power generation: A review and a research agenda

[J]. Journal of Cleaner Production, 2019, 218: 850-70.

DOI:10.1016/j.jclepro.2019.02.015      [本文引用: 1]

The use of renewable energy resources, especially wind power, is receiving strong attention from governments and private institutions, since it is considered one of the best and most competitive alternative energy sources in the current energy transition that many countries around the world are adopting. Wind power also plays an important role by reducing greenhouse gas emissions and thus attenuating global warming. Another contribution of wind power generation is that it allows countries to diversify their energy mix, which is especially important in countries where hydropower is a large component. The expansion of wind power generation requires a robust understanding of its variability and thus how to reduce uncertainties associated with wind power output. Technical approaches such as simulation and forecasting provide better information to support the decision-making process. This paper provides an overview of how the analysis of wind speed/energy has evolved over the last 30 years for decision-making processes. For this, we employed an innovative and reproducible literature review approach called Systematic Literature Network Analysis (SLNA). The SLNA was performed considering 145 selected articles from peer-reviewed journals and through them it was possible to identify the most representative approaches and future trends. Through this analysis, we identified that in the past 10 years, studies have focused on the use of Measure-Correlate-Predict (MCP) models, first using linear models and then improving them by applying density or kernel functions, as well as studies with alternative techniques, like neural networks or other hybrid models. An important finding is that most of the methods aim to assess wind power generation potential of target sites, and, in recent years the most used approaches are MCP and artificial neural network methods. (C) 2019 Elsevier Ltd.

王思聪.

中国海陆风电成本研究

[J]. 宏观经济研究, 2019(8): 170-175.

[本文引用: 1]

WANG Sicong.

A study on onshore and offshore wind power cost in China

[J]. Macroeconomics, 2019(8): 170-175.

[本文引用: 1]

KAEWNIAM P, CAO M, ALKAYEM N F, et al.

Recent advances in damage detection of wind turbine blades: A state-of-the-art review

[J]. Renewable & Sustainable Energy Reviews, 2022, 167: 112723.

[本文引用: 1]

付杰, 施伟, 周惠蒙, 等.

固定式海上风力机实时混合试验加载方式研究

[J]. 湖南大学学报(自然科学版), 2023, 50 (7): 160-168.

[本文引用: 1]

FU Jie, SHI Wei, ZHOU Huimeng, et al.

Study on loading mode of real-time hybrid test for fixed offshore wind turbine

[J]. Journal of Hunan University (Natural Sciences), 2023, 50 (7): 160-168.

[本文引用: 1]

李飞. 极端风浪载荷激励下的海上漂浮式风力发电机组结构振动控制研究[D]. 重庆: 重庆大学, 2022.

[本文引用: 1]

LI Fei. Study on structural vibration control of offshore floating wind turbine under extreme wind and wave loads[D]. Chongqing: Chongqing University, 2022.

[本文引用: 1]

柯世堂, 曹九发, 王珑, 等.

风力机塔架-叶片耦合模型风致响应时域分析

[J]. 湖南大学学报(自然科学版), 2014, 41 (4): 87-93.

[本文引用: 1]

KE Shitang, CAO Jiufa, WANG Long, et al.

Time-domain analysis of the wind-induced responses of the coupled model of wind turbine tower-blade coupled system

[J]. Journal of Hunan University (Natural Sciences), 2014, 41 (4): 87-93.

[本文引用: 1]

丁勤卫, 李春, 叶舟, 等.

风突变效应对风力机振动特性影响研究

[J]. 振动与冲击, 2016, 35 (21): 47-52.

[本文引用: 1]

DING Qinwei, LI Chun, YE Zhou, et al.

Effects of wind gust on a wind turbine’s vibration characteristics

[J]. Journal of Vibration and Shock, 2016, 35 (21): 47-52.

[本文引用: 1]

周文平, 唐胜利, 吕红.

风剪切和动态来流对水平轴风力机尾迹和气动性能的影响

[J]. 中国电机工程学报, 2012, 32 (14): 122-127.

[本文引用: 1]

ZHOU Wenping, TANG Shengli, LÜ Hong.

Effect of transient wind shear and dynamic inflow on the wake structure and performance of horizontal axis wind turbine

[J]. Proceedings of the CSEE, 2012, 32 (14): 122-127.

[本文引用: 1]

KIM S H, SHIN H K, JOO Y C, et al.

A study of the wake effects on the wind characteristics and fatigue loads for the turbines in a wind farm

[J]. Renewable Energy, 2015, 74: 536-543.

[本文引用: 1]

CECCOTTI C, SPIGA A, BARTL J, et al.

Effect of upstream turbine tip speed variations on downstream turbine performance

[J]. Energy Procedia, 2016, 94: 478-486.

[本文引用: 1]

JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. USA: National Renewable Energy Lab, 2009.

[本文引用: 3]

张建, 杨庆山.

基于标准k-ε模型的平衡大气边界层模拟

[J]. 空气动力学学报, 2009(6): 729-735.

[本文引用: 1]

ZHANG Jian, YANG Qingshan.

Application of standard k-ε model to simulate the equilibrium ABL

[J]. Acta Aerodynamica Sinica, 2009 (6): 729-735.

[本文引用: 1]

MIAO W P, LI C, YANG J, et al.

Numerical investigation of the yawed wake and its effects on the downstream wind turbine

[J]. Renewable Sustainable Energy, 2016, 8 (3): 033303.

[本文引用: 1]

ZHANG Z H, KUANG L M, ZHAO Y S, et al.

Numerical investigation of the aerodynamic and wake characteristics of a floating twin-rotor wind turbine under surge motion

[J]. Energy Conversion and Management, 2023, 283: 116957

[本文引用: 1]

杨梦姚, 毛璐璐, 韩兆龙, 等.

三叶片H型垂直轴风力机风振与减振研究

[J]. 上海交通大学学报, 2021, 55 (4): 347-356.

DOI:10.16183/j.cnki.jsjtu.2020.054      [本文引用: 1]

针对三叶片H型垂直轴风机风振与减振问题,基于计算流体动力学(CFD)方法,采用数值方法模拟获得风机在转动周期内的叶片风压分布.将风压力时程荷载施加于风力机叶片表面,分析风机结构风振响应.在风力机不同位置处分别布置阻尼器,并数值模拟阻尼器耗能减振能力.结果表明:在垂直轴风力机主轴与支杆连接处布置阻尼器可降低结构位移响应,总位移最大降幅达44%.阻尼器位置与结构位移降低率密切相关,在近风机叶片顶端连杆处布置阻尼器,结构最大位移发生在风机叶片底端.在近风机叶片底端连杆处布置阻尼器,最大位移则发生在风机叶片顶端,下降达40.7%.研究成果可为垂直轴风力机减振研究提供技术参考.

YANG Mengyao, MAO Lulu, HAN Zhaolong, et al.

Wind vibration and vibration reduction of an H-rotor type three-bladed vertical axis wind turbine

[J]. Journal of Shanghai Jiao Tong University, 2021, 55 (4): 347-356.

[本文引用: 1]

何文君, 苏捷, 周岱, 等.

基于BESO算法的大型海洋垂直轴风力机支撑结构优化

[J]. 上海交通大学学报, 2023, 57 (2): 127-137.

DOI:10.16183/j.cnki.jsjtu.2021.448      [本文引用: 1]

大型海洋垂直轴风力机的研究对发展海洋风能具有重要意义,研究大型垂直轴风力机的合理支撑结构形式对风力发电结构安全至关重要.基于变删除率的双向渐进结构优化(BESO)算法,对大型海洋垂直轴风力机进行支撑结构优化,并通过风力机的动力响应特性分析,验证结构优化方法的可靠性.结果表明:反比例型变删除率的BESO算法能有效改善优化迭代速率,适用于垂直轴风力机的支撑结构优化设计;相比于初始结构,拓扑出的新结构模型在风荷载作用下的风致动力响应显著降低.研究成果可用于垂直轴风力机支撑结构设计优化.

HE Wenjun, SU Jie, ZHOU Dai, et al.

Supporting structure optimization of offshore large-scale vertical axis wind turbine based on BESO algorithm

[J]. Journal of Shanghai Jiao Tong University, 2023, 57 (2): 127-137.

[本文引用: 1]

KATONA M C, ZIENKIEWICZ O C.

A unified set of single step algorithms part 3: The beta-m method, a generalization of the Newmark scheme

[J]. International Journal for Numerical Methods in Engineering, 1985, 21 (7): 1345-1359.

[本文引用: 2]

NEWMARK NATHAN M.

A method of computation for structural dynamics

[J]. Journal of Engineering Mechanics Division, 1959, 85 (3): 67-94.

[本文引用: 2]

段鑫泽, 程萍, 万德成.

带偏航角串列式两风力机复杂尾流场数值模拟

[J]. 海洋工程, 2019, 37 (2): 50-58.

[本文引用: 1]

DUAN Xinze, CHENG Ping, WAN Decheng.

Numerical study of wake interaction between two wind turbines operating in different yaw angles

[J]. The Ocean Engineering, 2019, 37 (2): 50-58.

[本文引用: 1]

MIAO W P, LI C, GIORGIO P, et al.

Investigation of wake characteristics of a yawed HAWT and its impacts on the inline downstream wind turbine using unsteady CFD

[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 168: 60-71.

[本文引用: 1]

WEN B R, TIAN X L, DONG X J, et al.

Influences of surge motion on the power and thrust characteristics of an offshore floating wind turbine

[J]. Energy, 2017, 141: 2054-2068.

[本文引用: 1]

ZHANG W G, WANG Y Y, SHEN Y Z, et al.

CFD studies of wake characteristics and power capture of wind turbines with trailing edge flaps

[J]. IEEE Access, 2020, 8: 7349-7361.

[本文引用: 1]

NAKHCHI M E, WIN N.

A novel hybrid control strategy of wind turbine wakes in tandem configuration to improve power production

[J]. Energy Conversion and Management, 2022, 260: 115575.

[本文引用: 1]

TU Y, ZHANG K, HAN Z L, et al.

Aerodynamic characterization of two tandem wind turbines under yaw misalignment control using actuator line model

[J]. Ocean Engineering, 2023, 281: 114992.

[本文引用: 1]

ONEL H C, TUNCER I H.

Investigation of wind turbine wakes and wake recovery in a tandem configuration using actuator line model with LES

[J]. Computers & Fluids, 2021, 220: 104872.

[本文引用: 1]

DOSE B, RAHIMI H, HERRÁEZ I, et al.

Fluid-structure coupled computations of the NREL 5 MW wind turbine by means of CFD

[J]. Renewable Energy, 2018, 129: 591-605.

[本文引用: 1]

/

〈 〉