作为温差能发电平台以及深海养殖工船等生产设施的重要构件[1 -2 ] ,自由悬垂取水管受到的关注与日俱增.不同于两端约束的常规立管,悬垂取水管一端简支一端自由的边界条件使其在背景洋流作用下容易发生较大偏移,从而影响两侧的泄涡,导致相对复杂的涡激振动(VIV)响应与水动力特性[3 ] .悬垂连接双取水管结构与相同管径的单管结构相比,大幅提高了海水输送效率;当优先保障输送效率一致时,双管结构在实际生产中较之更大管径单管结构更加易于制造.在常规的多立管研究中,并联形式作为较为简单的双管配置情况成为了研究的焦点[4 ] .然而,关于并联悬垂连接双管结构的复杂涡激振动特性以及与单管结构的特性异同,目前工业界缺乏有效的分析手段与正确认识.因此,开展并联悬垂连接双取水管涡激振动载荷特性试验研究对悬垂输水管的设计与制造有着重要意义.
模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法.
因此,针对悬垂连接双输水管结构,本文提出了一种适用于大位移小变形的涡激振动水动力载荷识别方法.通过开展不同流速下悬垂双输水管的模型试验,基于载荷识别方法处理实验数据,分析了不同流速下悬垂连接双输水管的响应特征与涡激载荷系数特征,并与悬垂单管进行比较,为悬垂输水管结构的设计和选择提供了有价值的参考.
1 试验描述
1.1 试验装置
试验在上海交通大学多功能船模拖曳水池中开展,水池深7.5 m、长300 m.实验设施安装在拖曳小车的底部,拖曳小车驱动实验装置以一定的速度在水槽中移动,以模拟均匀流场.实验设施的照片如图1 所示,来流与悬垂双管模型成90°,悬垂双管间距为S ,与立管的水动力外径相同.以左管为例,悬垂管模型的顶部结构如图2 所示,悬垂双管模型在被夹具固定后,连接到万向节,顶端连接到三分力仪以测量悬垂管模型的动态张力变化.
图1
图1
试验装置在位图
Fig.1
Overview of the whole experiment
图2
图2
模型端部结构示意图
Fig.2
Structure of model end
1.2 试验模型
试验立管模型由3部分组成:中心缆、三型聚丙烯(PPR)管材、外层热缩管,实际加工制作的试验立管模型截面示意图如图3 所示.图中:CF1、CF2、IL1、IL2分别为横流向和顺流向的光纤应变片.
图3
图3
立管模型截面示意图
Fig.3
Cross section of pipe model
如图4 所示,无卡扣与底部单卡扣的布置方式均会发生双管的碰撞现象,因此采用中部与底部双卡扣布置方式来规避双管碰撞现象.
图4
图4
卡扣布置方式选择示意图
Fig.4
Selection of snap arrangement
根据实际工程参数,悬垂取水管的实尺度外径约为1.83 m,考虑到模型实际制作与拖曳水池尺度,本文采用的弗劳德相似(缩尺比λ =46.4),获得的试验模型参数如表1 所示,其中结构阻尼比为悬垂管模型在空气中的结构阻尼比.需要说明的是,受实验条件限制,本次实验中的取水管长度并未根据缩尺比选择,而是根据实际水池可以实现的最大长度来设计.
1.3 试验工况
试验过程中通过光纤光栅应变片采集悬垂管模型响应应变信号,光纤应变片被粘贴在模型表面上,不会影响悬垂管周围的流场分布与振动特性[17 ] .以左管为例,光纤光栅应变片的整体布置方式如图5 所示,在悬垂管表面分别沿CF和 IL两个方向上各布置了两组光纤光栅应变片CF1、CF2和IL1、IL2以采集悬垂管模型响应应变信号,IL方向布置12个应变片,间隔为0.46 m;CF方向布置10个应变片,间隔为0.55 m.试验中以250 Hz的采样频率同步采集顶部三分力仪信号、应变信号,不同测点处测得的应变信息之间没有相位延迟.除此以外,模型顶部安装倾角仪以获得顶部转角度时间历程.
图5
图5
光纤应变片布置示意图
Fig.5
Layout of fiber brag grating strain sensors
涡激振动主要的无量纲控制参数有约化速度和雷诺数,约化速度v r 表示为
(1) v r =u/ (f n1 D )
式中:f n1 为试验管1阶固有频率;u 为拖车运行速度.
(2) Re =ρuD/μ =uD/ν
设计背景流速范围为0.1~0.5 m/s,通过拖车带动试验管在x 方向运动以模拟背景洋流实现不同约化速度和雷诺数下的试验工况,最终确定共5个工况,其中u 由0.1 m/s增加至0.5 m/s,间隔0.1 m/s,雷诺数Re =2.54×103 ~1.27×104 ,约化速度v r =8.02~40.10.
1.4 试验数据预处理
在模型试验中,应变传感器记录到的应变ε 可以分为4个组成部分,分别是由涡激振动引起的弯曲应变ε b 、轴向拉伸应变ε T 、初始应变ε in 和高频噪声应变ε no :
(3) ε =ε in +ε T +ε no +ε b
经过数据处理,将初始应变和高频噪声应变移除之后,可以获得涡激振动应变在CF与IL两个方向上的表达式:
(4) $\left.\begin{array}{l}{\epsilon }_{\mathrm{C}\mathrm{F}\_\mathrm{V}\mathrm{I}\mathrm{V}}=\frac{{\epsilon }_{\mathrm{C}\mathrm{F}1}-{\epsilon }_{\mathrm{C}\mathrm{F}2}}{2}\\ {\epsilon }_{\mathrm{I}\mathrm{L}\_\mathrm{V}\mathrm{I}\mathrm{V}}=\frac{{\epsilon }_{\mathrm{I}\mathrm{L}1}-{\epsilon }_{\mathrm{I}\mathrm{L}2}}{2}-\frac{\overline{{\epsilon }_{\mathrm{I}\mathrm{L}1}-{\epsilon }_{\mathrm{I}\mathrm{L}2}}}{2}\end{array}\right\}$
式中:ε CF1 和ε CF2 分别为CF1和CF2方向的测点应变;ε IL1 和ε IL2 分别为IL1和IL2方向的测点应变.
其中在IL方向上的弯曲应变可以进一步细分为两个部分:一是由涡激振动引起的弯曲变形脉动值ε IL_VIV ,另一是由拖曳力导致的弯曲变形平均值ε mb ,如图6 所示.
图6
图6
IL方向变形示意图
Fig.6
Deformation in IL direction
2 水动力识别
2.1 位移重构
针对并联条件下的悬垂连接双输水管系统,左管与右管在理论上具有对称性.因此,本文以左管为例进行识别理论的推导与验证.由于悬垂输水管的顶端为自由边界条件,在流场作用在会发生刚体转动和弯曲变形[18 ] (如图7 所示,展示了均匀流下悬垂输水管的位移与变形).其中,弯曲变形由涡激振动引起,可视为围绕着中性轴的振动.设定全局坐标系OXYZ 与局部坐标系Oxyz 如图7 所示,在位移与变形发生前,规定立管中性轴位移位于Z 轴上,均匀流流向在XOZ 平面内;在位移与变形发生后,规定立管中性轴位于z 轴上,立管轴线与x 轴正交,IL方向平行于xOz 平面.θ R 为刚体转角,θε 为变形转角.
图7
图7
均匀流下悬垂管变形分解示意图
Fig.7
Diagram of free-hanging pipe deformation under uniform flow
在全局坐标系中,指定节点的位移X (z , t )与顶部转角θ 可以表示为
(5) $\left.\begin{array}{l}X(z,\mathrm{ }t)={X}_{\mathrm{R}}(z,\mathrm{ }t)+{X}_{\epsilon }(z,\mathrm{ }t)\\ {X}_{\mathrm{R}}(z,\mathrm{ }t)=z\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{ }{\theta }_{R}\\ {X}_{\epsilon }(z,\mathrm{ }t)={x}_{\epsilon }(z,\mathrm{ }t)\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{ }{\theta }_{\mathrm{R}}\\ \theta (0,\mathrm{ }t)={\theta }_{\mathrm{R}}(0,\mathrm{ }t)+{\theta }_{\epsilon }(0,\mathrm{ }t)\end{array}\right\}$
式中:t 为时间;X R (z , t )为刚体旋转位移;Xε (z , t )为变形位移的X 轴分量;xε (z , t )为局部坐标系下的变形位移;θ 为顶部转角(由顶部转角传感器求得).
考虑到变形位移是小变形,基于现有的模态叠加重构方法[10 ] ,将变形位移与应变间关系描述为
(6) $\left.\begin{array}{l}{x}_{\epsilon }(\mathrm{z},\mathrm{ }\mathrm{t})=\stackrel{k}{\sum _{i=1}}{p}_{i}\left(t\right){\phi }_{i}\left(z\right), z\in [0,\mathrm{ }L]\\ k(z,\mathrm{ }t)=\frac{{\partial }^{2}w(z,\mathrm{ }t)}{\partial {z}^{2}}=\\ \stackrel{n}{\sum _{i=1}}{p}_{i}\left(t\right)\phi {″}_{i}\left(z\right), z\in [0,\mathrm{ }L]\\ \epsilon (z,\mathrm{ }t)=-R\stackrel{k}{\sum _{i=1}}{p}_{i}\left(t\right)\phi ″, z\in [0,\mathrm{ }L]\end{array}\right\}$
式中:φi (z )是第i 阶位移振型;pi (t )是第i 阶位移模态权重;φ″i (z )是模型的第i 阶曲率振型函数;k (z , t )为模型涡激振动曲率时历;ε (z , t )是节点z 处结构表面的涡激振动弯曲应变;R 是模型半径.
由于悬垂双输水管振型不存在解析解,本文采用有限元软件Orcaflex求解双管结构的位移振型与固有频率.通过节点对应的方式求得左管与右管两个方向的位移振型φ (z ),分别如图8 、图9 所示.从图中可以看出,两种结构IL方向上的位移振型相差较小,而在CF方向上有较大差异;提取两种结构的固有频率如表2 所示,双管结构IL方向上的固有频率与单管结构接近,而在CF方向上有较大差异.
图8
图8
悬垂单管与悬垂双管IL方向位移振型
Fig.8
Mode shape of single pipe and double pipes in IL direction
图9
图9
悬垂单管与悬垂双管CF方向位移振型
Fig.9
Mode shape of single pipe and double pipes in CF direction
基于位移振型φ (z , t ),求导得到曲率振型φ″ (z , t ),通过式(6)求得位移模态权重pi (t )后,重构IL方向上的涡激振动响应,并通过中心差分法求得模型的变形转角,最终通过式(5)求得悬垂双输水管在全局坐标系下对应节点的位移.
悬垂双输水管模型在CF方向只有变形位移,没有刚体旋转位移.CF方向的涡激振动位移重构方式与IL方向相同.
2.2 水动力载荷识别
由于涡激振动变形位移属于小变形范畴,因此可以将单侧的悬垂输水管模型视为忽略扭转变形的欧拉-伯努利梁.基于欧拉-伯努利梁的控制方程,将t 时刻立管模型节点z 处的外部载荷表示为
(7) $\begin{aligned}f(z, t)= & m \frac{\partial^{2} x(z, t)}{\partial t^{2}}+c \frac{\partial x(z, t)}{\partial t}+ \\& E I \frac{\partial^{4} x(z, t)}{\partial z^{4}}-F_{\mathrm{T}}(z, t) \frac{\partial^{2} x(z, t)}{\partial z^{2}}- \\& \frac{\partial F_{\mathrm{T}}(z, t)}{\partial z} \frac{\partial x(z, t)}{\partial z}\end{aligned}$
式中:x (z , t )表示局部坐标系下模型节点处的位移;EI 表示弯曲刚度;F T (z , t )表示轴向张力,F T (z , t )=F T_top (t )-mg Δz cos θ R ,F T_top (t ) 表示顶部张力随时间的变化,m 为空气中双管模型单位长度的质量,g 为重力加速度,Δz 表示沿轴线的长度;c 表示双管模型的阻尼,c =4πζmf 1 ,ζ 表示空气中双管模型的阻尼比,f 1 表示双管模型的首阶固有频率.
在2.1节中获得立管上各节点的位移时历信息后,应用中心差分法计算位移相对于时间与相对于z 的各阶导数,基于控制方程式(7)可求出方程左端项,即立管模型所受的外部载荷.
本文选择立管模型上的微段进行受力分析以得到外部载荷的成分组成,如图10 所示.图中:fx 、fy 为IL和CF方向沿立管轴线方向的外部力;f drag 表示IL方向上立管单位长度的平均阻力;f IL 、f CF 表示IL和CF方向上的涡激力;f b 表示单位长度立管所受浮力.
图10
图10
均匀流下悬垂管微端受力示意图
Fig.10
Force of free-hanging pipe under uniform flow
(8) $\left.\begin{array}{l}{f}_{x}={f}_{\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}}cos\mathrm{ }{\theta }_{\mathrm{R}}+{f}_{\mathrm{I}\mathrm{L}}-(mg-{f}_{\mathrm{b}})sin\mathrm{ }{\theta }_{\mathrm{R}}\\ {f}_{y}={f}_{\mathrm{C}\mathrm{F}}\end{array}\right\}$
将由IL方向涡激振动速度导致的阻力变化考虑进f IL 中,而仅将莫里森载荷中来流速度所对应的项,即f drag =$\frac{1}{2}$ ρDC d (z )u 0 |u 0 | 视为作用于管道上的平均阻力,其中u 0 为来流速度.
(9) ${\stackrel{-}{f}}_{x}$ =${\stackrel{-}{f}}_{\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}}$ cos θ R +${\stackrel{-}{f}}_{\mathrm{I}\mathrm{L}}$ -(mg -f b )sin θ R
考虑到f drag 中仅计入针对来流速度的平均力项,因此有${\stackrel{-}{f}}_{\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}}$ f drag ; IL方向上的涡激力f IL 是一周期性载荷,其在时间上平均值为0,即${\stackrel{-}{f}}_{\mathrm{I}\mathrm{L}}$
(10) $f_{\mathrm{IL}}=f_{x}-\bar{f}_{x}$
(11) $\left.\begin{array}{l}{f}_{\mathrm{I}\mathrm{L}}={f}_{x}-{\stackrel{-}{f}}_{x}\\ {f}_{\mathrm{C}\mathrm{F}}={f}_{y}\end{array}\right\}$
2.3 水动力载荷系数识别
基于涡激载荷分解理论[7 ] ,以IL方向涡激振动为例,本文将涡激载荷分解为与速度同相位的激励力和与加速度同相位的附加质量力:
(12) $\begin{aligned}f_{\mathrm{IL}}(z, t)= & \frac{1}{2 \sqrt{2}} \rho D u^{2}(z, t) C_{\mathrm{e}}(z) \frac{\dot{x}(z, t)}{\dot{x}_{\mathrm{RMS}}(z)}- \\& \frac{\pi D^{2}}{4} \rho C_{\mathrm{a}}(z) \ddot{x}(z, t)\end{aligned}$
式中:ρ 为流体密度;u (z , t )=u 0 cos θ R ,是立管z 处的流速时历;$\stackrel{·}{x}$ ( z , t )和$\ddot{x}$ ( z , t )分别是z 处的速度和加速度;${\stackrel{·}{x}}_{\mathrm{R}\mathrm{M}\mathrm{S}}$ C e (z )和C a (z )分别为激励力系数和附加质量系数,在均匀流作用下,这两个系数不随时间变化.
在已知涡激载荷、速度和加速度的情况下,可以采用最小二乘法(LS)来识别涡激力系数[14 ] :
(13) $\left.\begin{array}{l}\Theta =({H}^{\mathrm{T}}{H)}^{-1}{H}^{\mathrm{T}}{F}_{\mathrm{I}\mathrm{L}}^{\mathrm{T}}\\ H=\left[\begin{array}{ll}{C}_{1}(z,\mathrm{ }t)& {C}_{2}(z,\mathrm{ }t)\end{array}\right]\\ \Theta =\left[\begin{array}{l}{C}_{\mathrm{e}}\left(z\right)\\ {C}_{\mathrm{a}}\left(z\right)\end{array}\right]\end{array}\right\}$
(14) $\left.\begin{array}{l}{C}_{1}(\mathrm{z},\mathrm{ }\mathrm{t})=\frac{\mathrm{\rho }\mathrm{D}{u}^{2}(\mathrm{z},\mathrm{ }\mathrm{t})}{2\sqrt{2}{\stackrel{·}{x}}_{\mathrm{R}\mathrm{M}\mathrm{S}}\left(z\right)}\stackrel{·}{x}(z,\mathrm{ }t)\\ {C}_{2}(z,\mathrm{ }t)=-\frac{1}{4}\rho \mathrm{\pi }{D}^{2}\ddot{x}(z,\mathrm{ }t)\end{array}\right\}$
在均匀流作用下,立管在CF方向上的激励力系数和附加质量系数可以采用与IL方向相同的方法进行求解.
2.4 重构方法验证
为了验证本节所提出的涡激振动响应及载荷重构方法的精度,根据表1 中的模型参数在有限元软件Abaqus中建立悬垂双管的有限元模型并施加分布载荷,以双管模型中的左管为例选取12个节点的应变模拟试验中的测量应变ε Aba (选取节点位置与试验中测点布放位置相同),应用重构方法得到提取得到结构节点处全局位移x 0 ,将其与Abaqus计算值x Aba 进行对比.
图11 为左管模型中点处重构位移与计算位移时历对比和相应的位移RMS值沿管长的分布情况.从图中可以看出,应用本文提出的位移重构方法获得的位移响应与软件计算结果吻合较好,误差仅7%,在可接受范围内,这说明了本文所提出的位移重构方法的准确性.
图11
图11
重构结果与Abaqus计算结果对比图
Fig.11
Comparison of reconstructed results and Abaqus computational results
在此基础上,应用本节所提出的载荷重构方法获得作用于立管模型上的外载荷,如图12 所示为重构的外载荷与施加的节点载荷RMS值沿管长的分布情况.可以看出,重构的外载荷RMS 值与导出值吻合良好,最大误差为12%,在数据分析可接受范围内.总体来看,本文所提出的位移及载荷重构方法能够较为准确地重构均匀流下自由悬垂双管的涡激载荷.
图12
图12
重构载荷与施加载荷的RMS值对比
Fig.12
Comparison of RMS values for reconstructed load and applied load
3 结果分析
本文主要研究对象为悬垂双管结构,包括左管和右管,同时选取物理参数与表1 一致的悬垂单管结构作为参照,将应用第2节中所提出的悬垂双管涡激载荷重构方法,以第1节中模型试验中所测量的应变信息为输入得到涡激振动位移与涡激载荷,开展悬垂双管结构涡激振动特性分析与悬垂单管结构特性的对比分析.针对u =0.1,0.3,0.5 m/s的试验工况进行分析.
3.1 涡激振动响应分析
图13 与图14 分别展示了CF方向和IL方向上不同流速下悬垂双管与悬垂单管在测点处应变信息的时空分布.
图13
图13
悬垂单管与悬垂双管CF方向应变信息时空分布图
Fig.13
Spatial and temporal distribution of strain in CF direction
图14
图14
悬垂单管与悬垂双管IL方向应变信息时空分布图
Fig.14
Spatial and temporal distribution of strain in IL direction
由图13 可以看出,相同流速同一涡激振动方向下,与悬垂单管相比,悬垂双管结构的应变幅值大小在同一量级,在CF方向上,当u =0.1,0.3 m/s时,两种结构的应变响应主要由驻波主导且比较稳定,激发模态数分别为1 阶与3阶;而当流速逐渐增加,u =0.5 m/s时,两种结构的应变响应显示出“驻波和行波”的分布特征,双管结构的激发模态为4阶,而单管结构的激发模态数由3阶转向了4阶,体现出应变响应的不稳定性.由图14 可以看出,在IL方向上,两种结构的应变响应始终呈现“驻波和行波”的分布特征,并在高流速下趋向于更不稳定的时空分布特征.两种悬垂管结构高流速下不稳定的振动特征,可能是由于悬垂管底部无约束的边界条件,高流速下管道整体倾斜角度更大,管道泄涡的轴向相关性更强,其与横流向耦合后使得管道出现不稳定泄涡[19 ] .同时与CF方向相比,IL方向上的行波现象相对显著,这可能是因为IL方向和CF方向的阻尼相等,并且在IL方向上激发的振动模态更高,更有利于行波的主导[20 ] ,这种显著的行波现象在双管结构上表现得更加突出.为进一步探究单管与双管结构间的振动频率差异,对各测点处的应变信息进行快速傅里叶(FFT)变换,如图15 所示,为不同流速下悬垂双管与悬垂单管在CF方向和IL方向应变的频率谱,并将各流速下主导频率整理到表3 中.
图15
图15
悬垂单管与悬垂双管CF和IL方向应变频率谱
Fig.15
Strain frequency spectrum of single pipe and double pipes in CF and IL directions
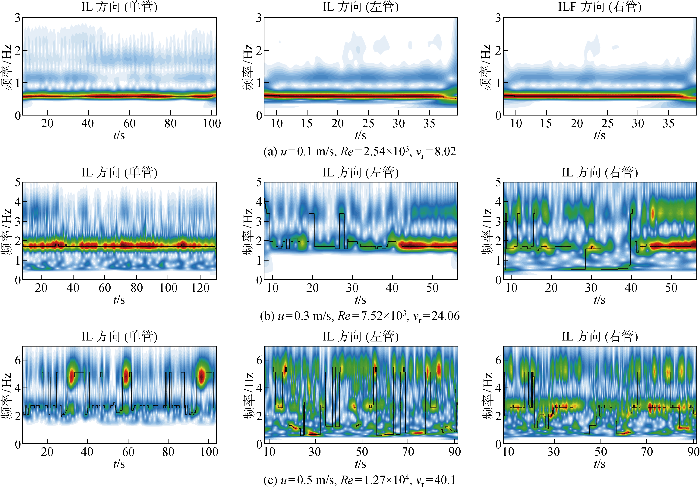
由图15 和表3 可以看出,当u =0.1 m/s时,同一方向上悬垂单管与悬垂双管的主导频率基本一致,其中IL方向上的主导频率约为CF方向上主导频率的2 倍,Fang等[19 ] 都发现了涡激振动中这种典型的频率加倍关系;当u =0.3 m/s时,CF方向上,悬垂单管与悬垂双管的主导频率基本一致, IL方向上,悬垂单管与悬垂双管(左管)的主导频率分别为1.73、3.45 Hz,而观察频谱图可以发现,此时悬垂单管同样激发出了3.45 Hz左右的应变幅值,且与主导频率幅值接近,说明此流速下尽管主导频率不同,但两种结构依然有着近似的激发频率;当 U =0.5 m/s时,同一方向上悬垂单管与悬垂双管的主导频率基本一致,同时CF与IL方向上的主导频率基本保持一致.Liu等[21 ] 进行的悬垂立管试验中也发现了两个方向主导频率一致的现象,这可能是悬垂管结构在大流速下发生偏转并倾斜,导致泄涡脱落模式发生变化,具体还需更为详细的计算流体力学(CFD)或者粒子观测实验(PIV)研究揭示.在频率分布上,当流速较低时,两种悬垂管结构的频率谱呈窄带状,主导频率明显;随着流速增加,频率谱逐渐呈宽带状,在IL方向上激发了更多高频成分,振动频率呈现出多频特征.
总体上看,在同一流速下,悬垂双管与悬垂单管有着相近的振动频率,这意味着对于悬垂双管结构,在保证管间距大于等于4倍管径的条件下,可以取与单管结构(管径相同)一致的斯特劳哈尔数开展涡激振动预报.
基于2.1节中的位移重构方法,获得不同流速下悬垂双管与悬垂单管在两个方向的位移响应.如图16 所示为不同流速下悬垂双管与悬垂单管在CF和 IL方向上位移RMS值的轴向分布.
图16
图16
悬垂单管与悬垂双管CF和IL方向位移RMS值的轴向分布
Fig.16
Axial distributions of displacement of single pipe and double pipes in CF and IL directions
从图16 可以看出,相同流速下,悬垂双管与悬垂单管在CF方向的涡激振动位移远大于IL方向的涡激振动位移.多个工况下的涡激振动最大位移均出现在结构底端,可能是由于底部无约束的边界条件所致.由于中部与底部夹具的存在,使得单双管CF方向上的位移振型有所不同,位移振型的差别也影响了两种结构的涡激振动位移沿管长的分布;IL方向上两种结构的涡激振动位移更加接近.总的来看,在低流速情况下,单、双管结构的位移幅值没有明显差异;随着流速的增大,涡激振动位移幅值差异也逐渐增大,u =0.5 m/s时,双管结构的涡激振动幅值略大于单管结构.
为进一步探究悬垂双管的涡激振动时频特性,对不同流速下悬垂双管与悬垂单管在CF和IL两个方向的中点处位移进行小波变换分析,如图17 与图18 所示.针对小波变换的结果分析,图中颜色深浅代表信号瞬时响应强度,颜色越红,表示对应频率的位移响应分量越大,黑色曲线是悬垂管模型此位置的涡激振动位移的主频时间历程.由图17 与图18 可得,当u =0.1 m/s时,悬垂双管与悬垂单管在CF与IL方向上的的红色区域主频曲线几乎没有波动,而随着流速逐渐增加到0.3 m/s甚至0.5 m/s时,悬垂双管与悬垂单管在CF与IL方向上的主频曲线波动剧烈,体现出明显的时变特征,这可能是由于行波及多模态竞争引起的.其中相比悬垂单管结构,悬垂双管结构主频曲线的波动出现在更低流速(u =0.3 m/s)下且更加剧烈,这说明双管间的干涉作用会使得结构的涡激振动不稳定性更加剧烈,值得更多关注.
图17
图17
悬垂单管与悬垂双管CF方向位移响应小波变换结果
Fig.17
Displacement response wavelet transform of single pipe and double pipes in CF direction
图18
图18
悬垂单管与悬垂双管IL方向位移响应小波变换结果
Fig.18
Displacement response wavelet transform of single pipe and double pipes in IL direction
3.2 涡激载荷系数分析
基于各测点的涡激振动位移响应,采用所提出的涡激载荷系数重构方法计算求得悬垂双管激励力系数和附加质量系数.图19 与图20 分别为不同流速下悬垂双管与悬垂单管在两个方向的涡激振动激励力系数C e 与附加质量系数C a 沿模型轴向的分布.
图19
图19
悬垂单管与悬垂双管CF和IL方向C e 轴向分布图
Fig.19
Axial distributions of excitation coefficients of single pipe and double pipes in CF and IL directions
图20
图20
悬垂单管与悬垂双管CF和IL方向C a 轴向分布图
Fig.20
Axial distributions of added-mass coefficients of single pipe and double pipes in CF and IL directions
激励力系数的正负代表着激励力做功的正负.图19 中,在中低流速下(u =0.1,0.3 m/s),单管结构与双管结构的激励力系数正负叠加后轴线围成的面积相似;考虑到整个结构的总能量大小与结构的振动幅值相匹配,与前文中低流速时,两种结构的涡激振动幅值相当这一现象对应;在高流速下(u =0.5 m/s),双管结构激励力系数正负叠加后轴线围成的面积大于单管结构,与前文高流速下,双管结构的涡激振动幅值略大于单管结构的现象对应.由图20 可以看出,单管与双管结构的附加质量系数相差较大.这主要是因为二者的固有频率(见表2 )相差较大,而泄涡频率基本一致;在这种情况下,二者的附加质量系数将起到不同的调制作用,使得二者在考虑附加质量之后的湿固有频率更接近泄涡频率,从而达到涡激振动共振.
4 结论
本文针对悬垂连接双管这一特殊构型立管在均匀流场下的涡激振动响应及载荷特性认识不清的问题,提出了一种适用于大位移耦合的涡激振动载荷识别方法,并开展了系列水池模型试验,对其涡激振动响应特性与涡激力载荷特性展开研究,并得到了以下结论.
(1) 试验中,在低流速下,悬垂双管与悬垂单管在CF方向和IL方向的涡激振动位移响应模态没有明显差异;随着流速的增加,二者被激发出的模态出现差异,特别是IL方向.
(2) 悬垂双管比悬垂单管在高流速下(u =0.5 m/s)更容易出现涡激振动不稳定的现象,如行波现象、瞬时多频响应等.针对高流速下悬垂双管的不稳定涡激振动,可尝试通过在双管结构部分区域添加螺旋列板来抑制涡激振动.
(3) 在相同流速下,悬垂双管与悬垂单管CF方向振动频率一致;据此,在悬垂双管的涡激振动预报中,可以采用与单管结构相同的斯特劳哈尔数来预报涡激振动频率.
(4) 悬垂双管与悬垂单管在CF方向上的附加质量系数差别较大,这主要是因为其参与调节立管结构的湿固有频率,使得模态信息不同的两个结构的涡激振动频率趋于一致.
需要注意的是,本次试验是依托于实际工程设计需求,确定了4倍管径的双管间距,本文以上结论均针对并联连接双管且双管间距为4倍管径.当双管之间为其他间距时,由于双管间不同的干涉作用,以上结论未必适用.后续研究中,可进一步针对其他间距下的涡激振动特性进行研究.
参考文献
View Option
[1]
董双林 . 黄海冷水团大型鲑科鱼类养殖研究进展与展望
[J]. 中国海洋大学学报(自然科学版) , 2019 , 49 (3 ): 1 -6 .
[本文引用: 1]
DONG Shuanglin Researching progresses and prospects in large salmonidae farming in cold water mass of Yellow Sea
[J]. Periodical of Ocean University of China 2019 , 49 (3 ): 1 -6 .
[本文引用: 1]
[2]
李大树 , 刘强 , 董芬 , 等 . 海洋温差能开发利用技术进展及预见研究
[J]. 工业加热 , 2021 , 50 (11 ): 1 -3 .
[本文引用: 1]
LI Dashu LIU Qiang DONG Fen et al Research on the progress and foresight of ocean thermal energy conversion
[J]. Industrial Heating 2021 , 50 (11 ): 1 -3 .
[本文引用: 1]
[3]
梁天纬 , 许玉旺 , 付世晓 , 等 . 悬垂立管波致疲劳与流致涡激振动疲劳特性研究
[J]. 振动与冲击 , 2023 , 42 (18 ): 313 -320 .
[本文引用: 1]
LIANG Tianwei XU Yuwang FU Shixiao et al Wave-induced fatigue and VIV-induced fatigue of a free-hanging riser
[J]. Journal of Vibration and Shock 2023 , 42 (18 ): 313 -320 .
[本文引用: 1]
[4]
JIANG Z LI P FENG L et al Experimental investigation on the VIV of two side-by-side risers fitted with triple helical strakes under coupled interference effect
[J]. Journal of Fluids and Structures 2021 , 101 : 103202 .
[本文引用: 1]
[5]
WANG J FU S WANG J et al Experimental investigation on vortex-induced vibration of a free-hanging riser under vessel motion and uniform current
[J]. Journal of Offshore Mechanics and Arctic Engineering 2017 , 139 (4 ): 041703 .
[本文引用: 1]
[6]
FU X FU S REN H et al Experimental investigation of vortex-induced vibration of a flexible pipe in bidirectionally sheared flow
[J]. Journal of Fluids and Structures 2022 , 114 : 103722 .
[本文引用: 1]
[7]
ZHANG M FU S LIU C et al Experimental investigation on vortex-induced force of a steel catenary riser under in-plane vessel motion
[J]. Marine Structures 2021 , 78 : 102882 .
[本文引用: 2]
[8]
DUAN J WANG X ZHOU J et al Effect of internal solitary wave on the dynamic response of a flexible riser
[J]. Physics of Fluids 2023 , 35 (1 ): 017107 .
[本文引用: 1]
[9]
DUAN J ZHOU J YOU Y et al Time-domain analysis of vortex-induced vibration of a flexible mining riser transporting flow with various velocities and densities
[J]. Ocean Engineering 2021 , 220 : 108427 .
[本文引用: 1]
[10]
MAO L ZENG S LIU Q et al Experimental investigation on vortex-induced vibrations of a hang-off evacuated drilling riser
[J]. Nonlinear Dynamics 2020 , 102 : 1499 -1516 .
[本文引用: 2]
[11]
QU Y FU S XU Y et al Application of a modified wake oscillator model to vortex-induced vibration of a free-hanging riser subjected to vessel motion
[J]. Ocean Engineering 2022 , 253 : 111165 .
[本文引用: 1]
[12]
HUSE E Experimental investigation of deep sea riser interaction
[C]// Offshore Technology Conference (OTC) 1996 : 97 -113 .
[本文引用: 1]
[13]
XU W CHENG A MA Y et al Multi-mode flow-induced vibrations of two side-by-side slender flexible cylinders in a uniform flow
[J]. Marine Structures 2018 , 57 : 219 -236 .
[本文引用: 1]
[14]
XU W ZHANG Q MA Y et al Hydrodynamic characteristics of two side-by-side flexible cylinders with different diameters experiencing flow-induced vibration
[J]. Ocean Engineering 2022 , 243 : 110199 .
[本文引用: 2]
[15]
REN T ZHANG M FU S et al Hydrodynamics of a flexible riser undergoing the vortex-induced vibration at high Reynolds number
[J]. China Ocean Engineering 2018 , 32 (5 ): 570 -581 .
[本文引用: 1]
[16]
LIU C FU S ZHANG M et al Time-varying hydrodynamics of a flexible riser under multi-frequency vortex-induced vibrations
[J]. Journal of Fluids and Structures 2018 , 80 : 217 -244 .
[本文引用: 1]
[17]
FU S REN T LI R et al Experimental investigation on VIV of the flexible model under full scale Re number
[C]// International Conference on Offshore Mechanics and Arctic Engineering 2011 : 43 -50 .
[本文引用: 1]
[18]
付雪鹏 , 黄维平 . 钢悬链式立管出平面运动刚体模态试验研究
[J]. 海洋工程 2018 , 36 (5 ): 114 -120 .
[本文引用: 1]
FU Xuepeng HUANG Weiping Experimental study of out-of-plane motion of steel catenary riser in rigid mode
[J]. The Ocean Engineering 2018 , 36 (5 ): 114 -120 .
[本文引用: 1]
[19]
FANG S M NIEDZWECKI J M FU S et al VIV response of a flexible cylinder with varied coverage by buoyancy elements and helical strakes
[J]. Marine Structures 2014 , 39 : 70 -89 .
[本文引用: 2]
[20]
CHEN Z S RHEE S H Effect of traveling wave on the vortex-induced vibration of a long flexible pipe
[J]. Applied Ocean Research 2019 , 84 : 122 -132 .
[本文引用: 1]
[21]
LIU Y JIANG Y ZHAO H et al Experimental investigation on vortex-induced vibration characteristics of a segmented free-hanging flexible riser
[J]. Ocean Engineering 2023 , 281 : 115032 .
[本文引用: 1]
黄海冷水团大型鲑科鱼类养殖研究进展与展望
1
2019
... 作为温差能发电平台以及深海养殖工船等生产设施的重要构件[1 -2 ] ,自由悬垂取水管受到的关注与日俱增.不同于两端约束的常规立管,悬垂取水管一端简支一端自由的边界条件使其在背景洋流作用下容易发生较大偏移,从而影响两侧的泄涡,导致相对复杂的涡激振动(VIV)响应与水动力特性[3 ] .悬垂连接双取水管结构与相同管径的单管结构相比,大幅提高了海水输送效率;当优先保障输送效率一致时,双管结构在实际生产中较之更大管径单管结构更加易于制造.在常规的多立管研究中,并联形式作为较为简单的双管配置情况成为了研究的焦点[4 ] .然而,关于并联悬垂连接双管结构的复杂涡激振动特性以及与单管结构的特性异同,目前工业界缺乏有效的分析手段与正确认识.因此,开展并联悬垂连接双取水管涡激振动载荷特性试验研究对悬垂输水管的设计与制造有着重要意义. ...
Researching progresses and prospects in large salmonidae farming in cold water mass of Yellow Sea
1
2019
... 作为温差能发电平台以及深海养殖工船等生产设施的重要构件[1 -2 ] ,自由悬垂取水管受到的关注与日俱增.不同于两端约束的常规立管,悬垂取水管一端简支一端自由的边界条件使其在背景洋流作用下容易发生较大偏移,从而影响两侧的泄涡,导致相对复杂的涡激振动(VIV)响应与水动力特性[3 ] .悬垂连接双取水管结构与相同管径的单管结构相比,大幅提高了海水输送效率;当优先保障输送效率一致时,双管结构在实际生产中较之更大管径单管结构更加易于制造.在常规的多立管研究中,并联形式作为较为简单的双管配置情况成为了研究的焦点[4 ] .然而,关于并联悬垂连接双管结构的复杂涡激振动特性以及与单管结构的特性异同,目前工业界缺乏有效的分析手段与正确认识.因此,开展并联悬垂连接双取水管涡激振动载荷特性试验研究对悬垂输水管的设计与制造有着重要意义. ...
海洋温差能开发利用技术进展及预见研究
1
2021
... 作为温差能发电平台以及深海养殖工船等生产设施的重要构件[1 -2 ] ,自由悬垂取水管受到的关注与日俱增.不同于两端约束的常规立管,悬垂取水管一端简支一端自由的边界条件使其在背景洋流作用下容易发生较大偏移,从而影响两侧的泄涡,导致相对复杂的涡激振动(VIV)响应与水动力特性[3 ] .悬垂连接双取水管结构与相同管径的单管结构相比,大幅提高了海水输送效率;当优先保障输送效率一致时,双管结构在实际生产中较之更大管径单管结构更加易于制造.在常规的多立管研究中,并联形式作为较为简单的双管配置情况成为了研究的焦点[4 ] .然而,关于并联悬垂连接双管结构的复杂涡激振动特性以及与单管结构的特性异同,目前工业界缺乏有效的分析手段与正确认识.因此,开展并联悬垂连接双取水管涡激振动载荷特性试验研究对悬垂输水管的设计与制造有着重要意义. ...
Research on the progress and foresight of ocean thermal energy conversion
1
2021
... 作为温差能发电平台以及深海养殖工船等生产设施的重要构件[1 -2 ] ,自由悬垂取水管受到的关注与日俱增.不同于两端约束的常规立管,悬垂取水管一端简支一端自由的边界条件使其在背景洋流作用下容易发生较大偏移,从而影响两侧的泄涡,导致相对复杂的涡激振动(VIV)响应与水动力特性[3 ] .悬垂连接双取水管结构与相同管径的单管结构相比,大幅提高了海水输送效率;当优先保障输送效率一致时,双管结构在实际生产中较之更大管径单管结构更加易于制造.在常规的多立管研究中,并联形式作为较为简单的双管配置情况成为了研究的焦点[4 ] .然而,关于并联悬垂连接双管结构的复杂涡激振动特性以及与单管结构的特性异同,目前工业界缺乏有效的分析手段与正确认识.因此,开展并联悬垂连接双取水管涡激振动载荷特性试验研究对悬垂输水管的设计与制造有着重要意义. ...
悬垂立管波致疲劳与流致涡激振动疲劳特性研究
1
2023
... 作为温差能发电平台以及深海养殖工船等生产设施的重要构件[1 -2 ] ,自由悬垂取水管受到的关注与日俱增.不同于两端约束的常规立管,悬垂取水管一端简支一端自由的边界条件使其在背景洋流作用下容易发生较大偏移,从而影响两侧的泄涡,导致相对复杂的涡激振动(VIV)响应与水动力特性[3 ] .悬垂连接双取水管结构与相同管径的单管结构相比,大幅提高了海水输送效率;当优先保障输送效率一致时,双管结构在实际生产中较之更大管径单管结构更加易于制造.在常规的多立管研究中,并联形式作为较为简单的双管配置情况成为了研究的焦点[4 ] .然而,关于并联悬垂连接双管结构的复杂涡激振动特性以及与单管结构的特性异同,目前工业界缺乏有效的分析手段与正确认识.因此,开展并联悬垂连接双取水管涡激振动载荷特性试验研究对悬垂输水管的设计与制造有着重要意义. ...
Wave-induced fatigue and VIV-induced fatigue of a free-hanging riser
1
2023
... 作为温差能发电平台以及深海养殖工船等生产设施的重要构件[1 -2 ] ,自由悬垂取水管受到的关注与日俱增.不同于两端约束的常规立管,悬垂取水管一端简支一端自由的边界条件使其在背景洋流作用下容易发生较大偏移,从而影响两侧的泄涡,导致相对复杂的涡激振动(VIV)响应与水动力特性[3 ] .悬垂连接双取水管结构与相同管径的单管结构相比,大幅提高了海水输送效率;当优先保障输送效率一致时,双管结构在实际生产中较之更大管径单管结构更加易于制造.在常规的多立管研究中,并联形式作为较为简单的双管配置情况成为了研究的焦点[4 ] .然而,关于并联悬垂连接双管结构的复杂涡激振动特性以及与单管结构的特性异同,目前工业界缺乏有效的分析手段与正确认识.因此,开展并联悬垂连接双取水管涡激振动载荷特性试验研究对悬垂输水管的设计与制造有着重要意义. ...
Experimental investigation on the VIV of two side-by-side risers fitted with triple helical strakes under coupled interference effect
1
2021
... 作为温差能发电平台以及深海养殖工船等生产设施的重要构件[1 -2 ] ,自由悬垂取水管受到的关注与日俱增.不同于两端约束的常规立管,悬垂取水管一端简支一端自由的边界条件使其在背景洋流作用下容易发生较大偏移,从而影响两侧的泄涡,导致相对复杂的涡激振动(VIV)响应与水动力特性[3 ] .悬垂连接双取水管结构与相同管径的单管结构相比,大幅提高了海水输送效率;当优先保障输送效率一致时,双管结构在实际生产中较之更大管径单管结构更加易于制造.在常规的多立管研究中,并联形式作为较为简单的双管配置情况成为了研究的焦点[4 ] .然而,关于并联悬垂连接双管结构的复杂涡激振动特性以及与单管结构的特性异同,目前工业界缺乏有效的分析手段与正确认识.因此,开展并联悬垂连接双取水管涡激振动载荷特性试验研究对悬垂输水管的设计与制造有着重要意义. ...
Experimental investigation on vortex-induced vibration of a free-hanging riser under vessel motion and uniform current
1
2017
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
Experimental investigation of vortex-induced vibration of a flexible pipe in bidirectionally sheared flow
1
2022
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
Experimental investigation on vortex-induced force of a steel catenary riser under in-plane vessel motion
2
2021
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
... 基于涡激载荷分解理论[7 ] ,以IL方向涡激振动为例,本文将涡激载荷分解为与速度同相位的激励力和与加速度同相位的附加质量力: ...
Effect of internal solitary wave on the dynamic response of a flexible riser
1
2023
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
Time-domain analysis of vortex-induced vibration of a flexible mining riser transporting flow with various velocities and densities
1
2021
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
Experimental investigation on vortex-induced vibrations of a hang-off evacuated drilling riser
2
2020
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
... 考虑到变形位移是小变形,基于现有的模态叠加重构方法[10 ] ,将变形位移与应变间关系描述为 ...
Application of a modified wake oscillator model to vortex-induced vibration of a free-hanging riser subjected to vessel motion
1
2022
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
Experimental investigation of deep sea riser interaction
1
1996
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
Multi-mode flow-induced vibrations of two side-by-side slender flexible cylinders in a uniform flow
1
2018
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
Hydrodynamic characteristics of two side-by-side flexible cylinders with different diameters experiencing flow-induced vibration
2
2022
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
... 在已知涡激载荷、速度和加速度的情况下,可以采用最小二乘法(LS)来识别涡激力系数[14 ] : ...
Hydrodynamics of a flexible riser undergoing the vortex-induced vibration at high Reynolds number
1
2018
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
Time-varying hydrodynamics of a flexible riser under multi-frequency vortex-induced vibrations
1
2018
... 模型试验是研究水下结构物涡激振动特性的重要手段,传统立管的试验条件主要有均匀流[5 ] 、剪切流[6 ] 、计及平台运动[7 ] 、考虑内波影响[8 -9 ] 等多个方面,研究较为广泛.而针对悬垂立管这种特殊边界条件下的涡激振动,Mao等[10 ] 通过水槽试验发现,柔性悬垂管在纵向(in-line,IL)和横向(cross-flow,CF)方向的响应主导频率相同.Qu等[11 ] 模拟了船体运动下的悬垂立管涡激振动,验证了一种新的尾流振子模型.针对双管结构的涡激振动,Huse[12 ] 通过试验发现相邻立管会在绕流流场作用下相互靠近乃至发生碰撞.Xu等[13 -14 ] 分别针对相同直径与不同直径的两端约束并联双管结构进行了系列实验,发现过小的间距比与不同的管径会使得IL与CF方向的涡激振动相互干扰.而在涡激振动载荷特性的研究方法上,Ren等[15 ] 利用模态分析方法和欧拉-伯努利梁方程得到了立管在IL和CF方向上的水动力分布,并使用最小二乘法计算了这两个方向上的水动力系数.Liu等[16 ] 进一步提出了遗忘因子最小二乘法,用于识别柔性立管在多频率和时分频率涡激振动下的时变涡激力系数.然而,上述研究存在一些限制:首先,现有大部分试验主要研究了悬垂边界条件下的单管模型或常规的两端约束并联双管模型,未有针对悬垂并联双输水管的涡激振动试验研究;其次,现有的涡激力识别方法主要适用于两端约束的小变形条件下的柔性立管,而自由悬垂取水管在背景洋流下的涡激振动属于刚体大位移和小变形的叠加,需要重新考虑识别方法. ...
Experimental investigation on VIV of the flexible model under full scale Re number
1
2011
... 试验过程中通过光纤光栅应变片采集悬垂管模型响应应变信号,光纤应变片被粘贴在模型表面上,不会影响悬垂管周围的流场分布与振动特性[17 ] .以左管为例,光纤光栅应变片的整体布置方式如图5 所示,在悬垂管表面分别沿CF和 IL两个方向上各布置了两组光纤光栅应变片CF1、CF2和IL1、IL2以采集悬垂管模型响应应变信号,IL方向布置12个应变片,间隔为0.46 m;CF方向布置10个应变片,间隔为0.55 m.试验中以250 Hz的采样频率同步采集顶部三分力仪信号、应变信号,不同测点处测得的应变信息之间没有相位延迟.除此以外,模型顶部安装倾角仪以获得顶部转角度时间历程. ...
钢悬链式立管出平面运动刚体模态试验研究
1
2018
... 针对并联条件下的悬垂连接双输水管系统,左管与右管在理论上具有对称性.因此,本文以左管为例进行识别理论的推导与验证.由于悬垂输水管的顶端为自由边界条件,在流场作用在会发生刚体转动和弯曲变形[18 ] (如图7 所示,展示了均匀流下悬垂输水管的位移与变形).其中,弯曲变形由涡激振动引起,可视为围绕着中性轴的振动.设定全局坐标系OXYZ 与局部坐标系Oxyz 如图7 所示,在位移与变形发生前,规定立管中性轴位移位于Z 轴上,均匀流流向在XOZ 平面内;在位移与变形发生后,规定立管中性轴位于z 轴上,立管轴线与x 轴正交,IL方向平行于xOz 平面.θ R 为刚体转角,θε 为变形转角. ...
Experimental study of out-of-plane motion of steel catenary riser in rigid mode
1
2018
... 针对并联条件下的悬垂连接双输水管系统,左管与右管在理论上具有对称性.因此,本文以左管为例进行识别理论的推导与验证.由于悬垂输水管的顶端为自由边界条件,在流场作用在会发生刚体转动和弯曲变形[18 ] (如图7 所示,展示了均匀流下悬垂输水管的位移与变形).其中,弯曲变形由涡激振动引起,可视为围绕着中性轴的振动.设定全局坐标系OXYZ 与局部坐标系Oxyz 如图7 所示,在位移与变形发生前,规定立管中性轴位移位于Z 轴上,均匀流流向在XOZ 平面内;在位移与变形发生后,规定立管中性轴位于z 轴上,立管轴线与x 轴正交,IL方向平行于xOz 平面.θ R 为刚体转角,θε 为变形转角. ...
VIV response of a flexible cylinder with varied coverage by buoyancy elements and helical strakes
2
2014
... 由图13 可以看出,相同流速同一涡激振动方向下,与悬垂单管相比,悬垂双管结构的应变幅值大小在同一量级,在CF方向上,当u =0.1,0.3 m/s时,两种结构的应变响应主要由驻波主导且比较稳定,激发模态数分别为1 阶与3阶;而当流速逐渐增加,u =0.5 m/s时,两种结构的应变响应显示出“驻波和行波”的分布特征,双管结构的激发模态为4阶,而单管结构的激发模态数由3阶转向了4阶,体现出应变响应的不稳定性.由图14 可以看出,在IL方向上,两种结构的应变响应始终呈现“驻波和行波”的分布特征,并在高流速下趋向于更不稳定的时空分布特征.两种悬垂管结构高流速下不稳定的振动特征,可能是由于悬垂管底部无约束的边界条件,高流速下管道整体倾斜角度更大,管道泄涡的轴向相关性更强,其与横流向耦合后使得管道出现不稳定泄涡[19 ] .同时与CF方向相比,IL方向上的行波现象相对显著,这可能是因为IL方向和CF方向的阻尼相等,并且在IL方向上激发的振动模态更高,更有利于行波的主导[20 ] ,这种显著的行波现象在双管结构上表现得更加突出.为进一步探究单管与双管结构间的振动频率差异,对各测点处的应变信息进行快速傅里叶(FFT)变换,如图15 所示,为不同流速下悬垂双管与悬垂单管在CF方向和IL方向应变的频率谱,并将各流速下主导频率整理到表3 中. ...
... 由图15 和表3 可以看出,当u =0.1 m/s时,同一方向上悬垂单管与悬垂双管的主导频率基本一致,其中IL方向上的主导频率约为CF方向上主导频率的2 倍,Fang等[19 ] 都发现了涡激振动中这种典型的频率加倍关系;当u =0.3 m/s时,CF方向上,悬垂单管与悬垂双管的主导频率基本一致, IL方向上,悬垂单管与悬垂双管(左管)的主导频率分别为1.73、3.45 Hz,而观察频谱图可以发现,此时悬垂单管同样激发出了3.45 Hz左右的应变幅值,且与主导频率幅值接近,说明此流速下尽管主导频率不同,但两种结构依然有着近似的激发频率;当 U =0.5 m/s时,同一方向上悬垂单管与悬垂双管的主导频率基本一致,同时CF与IL方向上的主导频率基本保持一致.Liu等[21 ] 进行的悬垂立管试验中也发现了两个方向主导频率一致的现象,这可能是悬垂管结构在大流速下发生偏转并倾斜,导致泄涡脱落模式发生变化,具体还需更为详细的计算流体力学(CFD)或者粒子观测实验(PIV)研究揭示.在频率分布上,当流速较低时,两种悬垂管结构的频率谱呈窄带状,主导频率明显;随着流速增加,频率谱逐渐呈宽带状,在IL方向上激发了更多高频成分,振动频率呈现出多频特征. ...
Effect of traveling wave on the vortex-induced vibration of a long flexible pipe
1
2019
... 由图13 可以看出,相同流速同一涡激振动方向下,与悬垂单管相比,悬垂双管结构的应变幅值大小在同一量级,在CF方向上,当u =0.1,0.3 m/s时,两种结构的应变响应主要由驻波主导且比较稳定,激发模态数分别为1 阶与3阶;而当流速逐渐增加,u =0.5 m/s时,两种结构的应变响应显示出“驻波和行波”的分布特征,双管结构的激发模态为4阶,而单管结构的激发模态数由3阶转向了4阶,体现出应变响应的不稳定性.由图14 可以看出,在IL方向上,两种结构的应变响应始终呈现“驻波和行波”的分布特征,并在高流速下趋向于更不稳定的时空分布特征.两种悬垂管结构高流速下不稳定的振动特征,可能是由于悬垂管底部无约束的边界条件,高流速下管道整体倾斜角度更大,管道泄涡的轴向相关性更强,其与横流向耦合后使得管道出现不稳定泄涡[19 ] .同时与CF方向相比,IL方向上的行波现象相对显著,这可能是因为IL方向和CF方向的阻尼相等,并且在IL方向上激发的振动模态更高,更有利于行波的主导[20 ] ,这种显著的行波现象在双管结构上表现得更加突出.为进一步探究单管与双管结构间的振动频率差异,对各测点处的应变信息进行快速傅里叶(FFT)变换,如图15 所示,为不同流速下悬垂双管与悬垂单管在CF方向和IL方向应变的频率谱,并将各流速下主导频率整理到表3 中. ...
Experimental investigation on vortex-induced vibration characteristics of a segmented free-hanging flexible riser
1
2023
... 由图15 和表3 可以看出,当u =0.1 m/s时,同一方向上悬垂单管与悬垂双管的主导频率基本一致,其中IL方向上的主导频率约为CF方向上主导频率的2 倍,Fang等[19 ] 都发现了涡激振动中这种典型的频率加倍关系;当u =0.3 m/s时,CF方向上,悬垂单管与悬垂双管的主导频率基本一致, IL方向上,悬垂单管与悬垂双管(左管)的主导频率分别为1.73、3.45 Hz,而观察频谱图可以发现,此时悬垂单管同样激发出了3.45 Hz左右的应变幅值,且与主导频率幅值接近,说明此流速下尽管主导频率不同,但两种结构依然有着近似的激发频率;当 U =0.5 m/s时,同一方向上悬垂单管与悬垂双管的主导频率基本一致,同时CF与IL方向上的主导频率基本保持一致.Liu等[21 ] 进行的悬垂立管试验中也发现了两个方向主导频率一致的现象,这可能是悬垂管结构在大流速下发生偏转并倾斜,导致泄涡脱落模式发生变化,具体还需更为详细的计算流体力学(CFD)或者粒子观测实验(PIV)研究揭示.在频率分布上,当流速较低时,两种悬垂管结构的频率谱呈窄带状,主导频率明显;随着流速增加,频率谱逐渐呈宽带状,在IL方向上激发了更多高频成分,振动频率呈现出多频特征. ...