附壁射流式多金属结核采集装置几何参数优化

doi:10.16183/j.cnki.jsjtu.2023.470

附壁射流式多金属结核采集装置几何参数优化

张栢源¹, 赵国成^,¹^,²^,³, 肖龙飞¹^,²^,³

1.上海交通大学海洋工程国家重点实验室, 上海 200240

2.上海交通大学海洋装备研究院, 上海 200240

3.上海交通大学三亚崖州湾深海科技研究院, 海南三亚 572024

Optimization of Geometrical Parameters of Coandă-Effect-Based Polymetallic Nodule Collection Device

ZHANG Baiyuan¹, ZHAO Guocheng^,¹^,²^,³, XIAO Longfei¹^,²^,³

1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

2. Institute of Marine Equipment, Shanghai Jiao Tong University, Shanghai 200240, China

3. SJTU Yazhou Bay Institute of Deepsea Sci-Tech, Sanya 572024, Hainan, China

通讯作者: 赵国成,助理研究员,电话(Tel.): 021-34207184;E-mail:guocheng.zhao@sjtu.edu.cn.

责任编辑: 王一凡

收稿日期: 2023-09-18 修回日期: 2023-10-22 接受日期: 2023-11-13

基金资助:

国家自然科学基金青年科学基金项目(52301332)
上海市“科技创新行动计划”扬帆专项(23YF1419800)
三亚市科技创新专项(2022KJCX67)

Received: 2023-09-18 Revised: 2023-10-22 Accepted: 2023-11-13

作者简介 About authors

张栢源(2000—),硕士生,从事深海水力集矿装置设计与优化研究.

摘要

采集海底矿石颗粒是开发深海矿产资源的核心技术.基于康达效应的附壁射流式集矿技术被认为是一种具有工程应用潜力的集矿方法.基于实验验证的计算流体力学-离散元(CFD-DEM)数值模拟方法,以提高矿粒采集率为优化目标,开展集矿装置几何参数优化研究.探究集矿装置凸曲壁曲率半径与矿粒直径之比(R/d)、射流切向弧度(θ)和射流厚度与矿粒直径之比(b/d)对临界无因次射流流量(q₀)的影响规律,并对各参数影响的显著性进行了比较.同时,结合集矿流场流速分布特征阐释矿粒受力运动特性.研究结果表明,b/d对集矿效率的影响最大,R/d次之,θ的影响最小.对比工况中,当R/d = 9、θ = 1.05 rad、b/d = 0.26时,矿粒采集效果最佳.本研究可为设计研发高效低扰动集矿装置提供理论支撑.

关键词： 多金属结核; 附壁射流采集; 计算流体力学-离散元法; 矿粒采集率; 参数优化

Abstract

The collection of seabed ore particles is a core technology of exploiting deep sea mineral resources, with wall-attached jet collection technology based on Coandă-effect being considered as a nodule collection method with engineering application potential. Based on the experimentally verified CFD-DEM numerical simulation, the optimization of geometric parameters of the collection device is conducted to improve pick-up efficiency. The influences of three geometric parameters, i.e., the ratio of the curvature radius of the convex curved wall to the diameter of the nodule particle R/d, the tangential radian of the jet θ, and the ratio of the thickness of the jet to the diameter of the nodule b/d on the critical unconditional jet flow rate q₀, are investigated and compared. The nodule collection characteristics are revealed through an analysis of the flow field characteristics. The results show that b/d has the greatest influence on the pick-up efficiency, followed by R/d, while θ has the least. The performance of nodule collection is optimal when R/d=9, θ=1.05 rad, and b/d=0.26 in contrast conditions. This research provides technical support for designing and developing the Coandă-effect-based collection devices.

Keywords： polymetallic nodule; Coandă-effect-based collection; computational fluid dynamics-discrete element method (CFD-DEM); nodule pick-up efficiency; parametric optimization

PDF (3985KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张栢源, 赵国成, 肖龙飞. 附壁射流式多金属结核采集装置几何参数优化[J]. 上海交通大学学报, 2025, 59(8): 1059-1066 doi:10.16183/j.cnki.jsjtu.2023.470

ZHANG Baiyuan, ZHAO Guocheng, XIAO Longfei. Optimization of Geometrical Parameters of Coandă-Effect-Based Polymetallic Nodule Collection Device[J]. Journal of Shanghai Jiaotong University, 2025, 59(8): 1059-1066 doi:10.16183/j.cnki.jsjtu.2023.470

全球能源结构转型使得风力发电、新能源汽车等产业迅猛发展,导致金属资源需求激增^[1].然而,随着陆地矿产资源的日益枯竭,深海矿产资源逐渐受到各国关注^[2].深海多金属结核以大尺寸颗粒形式广泛存在于海底表层沉积物中,因其金属元素种类多、储量大、品位和丰度高而极具开发利用价值^[3].目前,深海采矿系统主要包括海底作业、矿石输送和水面支持3个子系统构成,其中海底矿粒采集是海底作业子系统的核心技术^[4].集矿装置结构是影响矿粒采集效果的关键因素,合理的几何结构不仅能提高矿粒采集效率,还能减少集矿作业过程对海床表层沉积物的扰动,从而降低对底栖生物的影响.因此,开展集矿装置参数优化研究,对于研发高效、低扰动集矿装备具有重要意义.

国内外学者已经在集矿流场特征和集矿装置性能方面已开展大量研究.Zhao等^[5]利用粒子图像测速系统和融合视觉目标跟踪方法的高速摄像系统分别测量了集矿流场速度分布和矿粒的位置和速度.Rodman等^[6]通过射流实验,研究曲壁射流的曲率对流场的影响,提出求解曲壁射流流速和压力分布的半理论半经验方法.Hong等^[7]则研究射流冲采式集矿装置的集矿参数与其采集效率之间的关系,探究了底部的压力波动对采集效率的影响.赵国成等^[8]通过模型试验,研究不同集矿装置离底高度与矿粒直径比、集矿装置与矿粒之间的偏移角度和集矿装置拖曳速度对矿粒的垂向受力系数和径向受力系数的影响.Alhaddad等^[9]设计了一种基于康达效应的多金属结核采集装置,并进行实验测试其采集效率,发现矿粒处在集矿装置下方压力梯度场的时间是采集效率的重要因素.Yue等^[10]和李雨瑶等^[11]利用数值模拟,对现有3种主流集矿方法展开研究,从集矿性能和环境扰动两方面进行了比较.官雷等^[12]对比利时、韩国和中国设计的集矿装置的结构、参数和试验效果进行了比较,并初步得出了集矿参数的取值范围.总体来看,现有对集矿装置的研究大多关注于特定结构集矿装置的性能表现,缺乏从几何参数出发对集矿装置进行设计优化.

本研究基于传统附壁射流式集矿装置几何结构,设计一种双凸曲壁附壁射流式集矿装置,利用实验验证的计算流体力学-离散元法(CFD-DEM)进行数值模拟,探究3种无因次几何参数(凸曲壁曲率半径与矿粒直径之比R/d、射流切向弧度θ和射流厚度与矿粒直径之比b/d)对集矿流量需求的影响规律与b/d对水泵功率的特殊作用,并通过集矿流场射流半宽大小与最大流速的变化阐释矿粒受力运动特性,最终得出研究工况中各几何参数的最佳取值,从而提出集矿装置几何参数优化设计方法.

1 数值模拟方法

1.1 CFD-DEM与边界条件

本文使用软件STAR-CCM+12.02基于CFD-DEM对集矿过程数值模拟.采用一种适用于解决复杂壁面流动问题的可实现的k-ε两层湍流模型(RKE 2L)模拟集矿湍流演变,采用广泛应用于管道固液两相流的离散元方法(DEM)模拟矿粒受力运动^[13].采用Hertz-Mindlin无滑动接触理论模型^[14]对颗粒的碰撞进行模拟.

在RKE 2L模型中,湍动能k和湍流耗散率ε的输运方程为^[15]

(1)

$\begin{aligned}\frac{\partial}{\partial t}(\rho k) & +\boldsymbol{\nabla} \cdot(\rho k \overline{\boldsymbol{v}})= \\\boldsymbol{\nabla} \cdot & {\left[\left(\mu+\frac{\mu_{t}}{\sigma_{k}}\right) \boldsymbol{\nabla} k\right]+P_{k}-\rho\left(\varepsilon-\varepsilon_{0}\right)+S_{k} }\end{aligned}$

(2)

$\begin{array}{c}\frac{\partial}{\partial t}(\rho \varepsilon)+\nabla \cdot(\rho \varepsilon \overline{\boldsymbol{v}})=\nabla \cdot\left[\left(\mu+\frac{\mu_{\mathrm{t}}}{\sigma_{\varepsilon}}\right) \nabla \varepsilon\right]+ \\\frac{1}{T_{\varepsilon}} C_{\varepsilon 1} P_{\varepsilon}-C_{\varepsilon 2} f_{2} \rho\left(\frac{\varepsilon}{T_{\varepsilon}}-\frac{\varepsilon_{0}}{T_{0}}\right)+S_{\varepsilon}\end{array}$

式中:$\stackrel{-}{v}$为平均流速;μ为动力黏度;μ_t为湍流涡黏度;C_ε₁,C_ε₂= 1.9,σ_ε = 1.2,σ_k= 1均是模型系数;ε₀为抵消湍流衰减的环境湍流值;T₀为其单位时间尺度;P_k和P_ε是和k-ε模型相关的项;f₂为阻尼函数;T_ε= k/ε为大涡时间尺度;S_k和S_ε是自定义项.

计算域和边界条件的设置如图1所示.底面是速度U=0.2 m/s的滑移壁面,其余边界均为压力出口.在集矿装置前方贴靠底面处设置颗粒喷射器,使其沿X方向以0.2 m/s的初速度每秒释放10颗圆球形颗粒,模拟矿粒与集矿装置的相对运动.在凸曲壁最低点的正下方设置垂向流速监测线.采用trimmer模型对集矿计算域进行网格划分,并对射流口、凸曲面近壁面等区域进行逐层加密,网格划分结果如图2所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

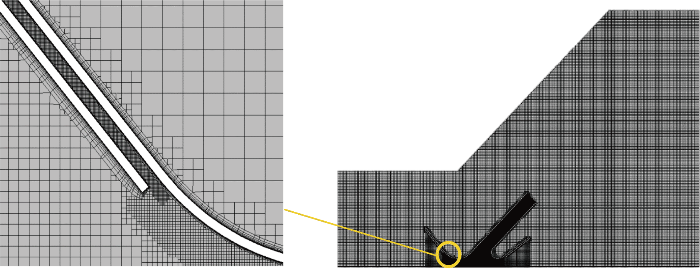
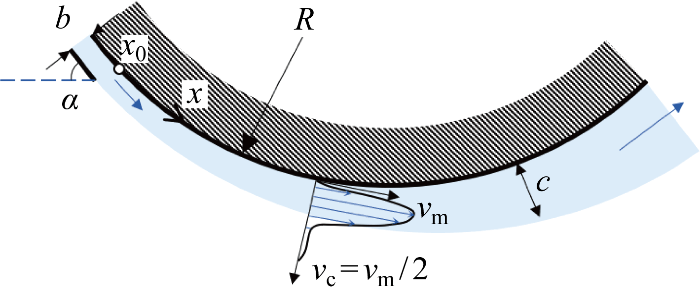
图1 计算域边界条件及流速监测线位置

Fig.1 Computational domain boundary conditions and location of flow monitoring line

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 网格划分与加密剖视图

Fig.2 Sectioned view of meshing and encryption

1.2 网格与时间步长无关性验证

对网格及时间步长做收敛性分析,验证物理量为矿粒采集率η.流场稳定后开启颗粒喷射器,获取前300 s内的矿粒采集情况,并根据以下公式计算矿粒的采集率:

(2)η=m_u/(m_u+m_d)

式中:m_u和m_d分别是成功采集和未成功采集的矿粒的质量.成功采集的颗粒被提升至输矿管内,其余未成功采集的颗粒则留在底面.

工况参数为曲率半径R=120 mm,射流切向角度α=35°,射流厚度b=3.125 mm,颗粒流率为10颗/s,射流流速v_j=6.8 m/s.表1为4种不同网格数量和4种不同时间步长下的采集率数值结果.

表1 网格与时间步长无关性验证

Tab.1 Verification of mesh and time step independence

编号	网格数量	时间步长/s	η/%	相对差值/%	编号	网格数量	时间步长/s	η/%	相对差值/%
M1	45 375	0.01	72.97	-	T1	73 506	0.020	72.52	-
M2	58 326	0.01	77.22	5.82	T2	73 506	0.015	77.20	6.45
M3	73 506	0.01	80.11	3.74	T3	73 506	0.010	80.11	3.77
M4	106 324	0.01	81.45	1.67	T4	73 506	0.005	81.26	1.44

新窗口打开| 下载CSV

由表1可见,工况M4相对于M3,η变化1.67%;工况T4相对于T3,η变化1.44%.由此可认为网格数量为 73 506、时间步长为 0.01 s 时数值结果收敛.

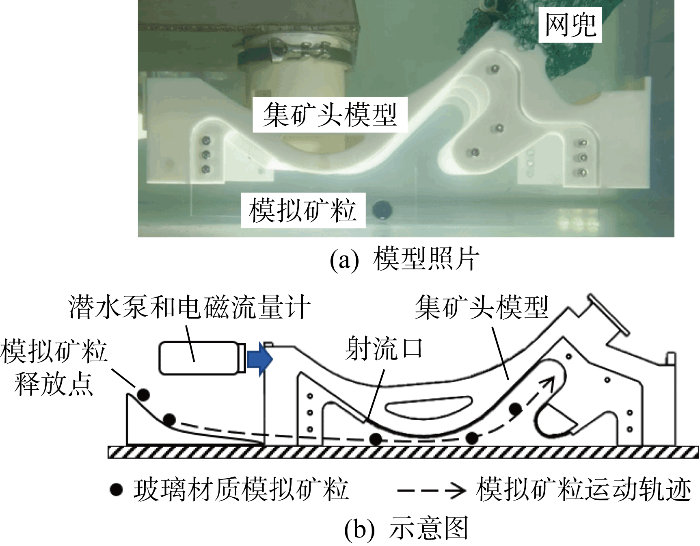
1.3 实验验证

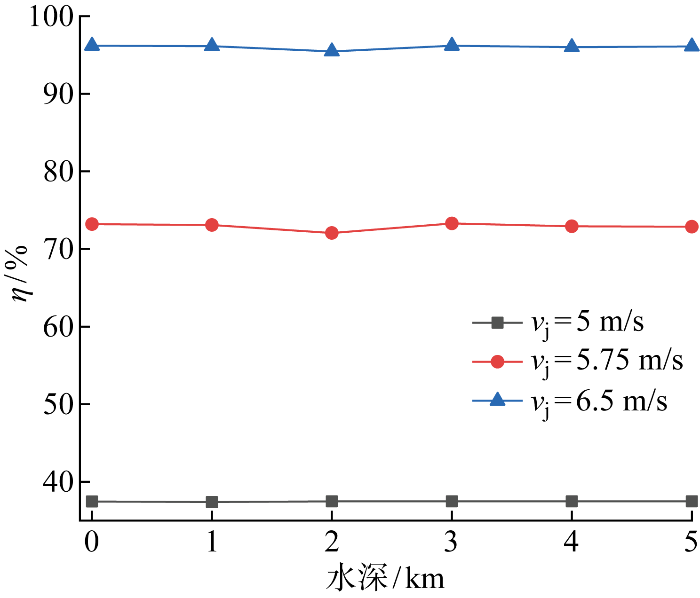
为了探究深水环境对集矿效率的影响,在数值模拟中计算3种射流流速(v_j=5,5.75,6.5 m/s)下矿粒采集率随水深的变化.通过改变压强基准值,在6个不同水深下(0.5~5 000 m)进行集矿过程模拟,结果如图3所示.由图可知,在同一射流流速下,矿粒采集率大小随水深增加基本保持不变.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同射流流速下水深对采集率的影响

Fig.3 Influence of water depth on pick-up efficiency at different jet velocities

深海大水压环境还可能会对沉积物力学特性产生影响.本文将底面简化为刚性平底,从而便于不同结构集矿装置的横向比较.此外,深海环境中平均洋流速度较小(0~0.15 m/s)^[16],占射流流速不到2%,而且实际采矿过程中,采矿装置行进方向与洋流的夹角不断变化,因此可忽略洋流速度的影响.综合以上结论,同时参考Hong等^[7]和Alhaddad等^[9]的实验研究,认为浅水的模型实验可用于模拟海底矿粒采集过程.

在高透明玻璃水槽(3 m×0.8 m×0.7 m)中开展采集率实验,以验证数值模拟结果的准确性.实验系统布置如图4所示,集矿装置模型采用3D打印技术制作,材质为光敏树脂(密度为1.15 g/cm³).实验时,将100颗玻璃材质的模拟矿粒分为10组,每次释放10颗.根据式(3)和网兜收集到的矿粒量即可计算矿粒采集率.实验工况参数如表2所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 矿粒采集实验系统

Fig.4 Particle collection experimental system

表2 实验工况参数

Tab.2 Experimental parameters

参数	取值
模拟矿粒密度,ρ_p/(kg·m^-3)	2 300
离底高度,h/mm	30
d/mm	20
R/mm	80
α/(°)	35
b/mm	3.125

新窗口打开| 下载CSV

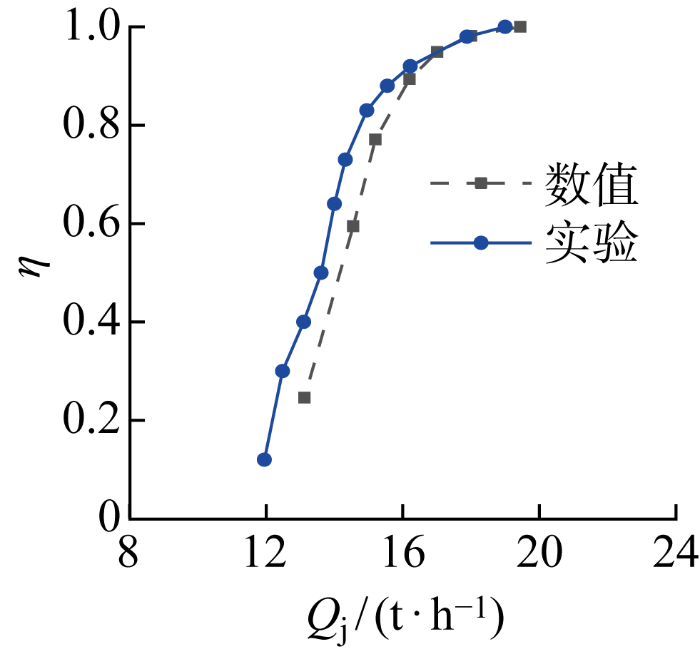
在数值模拟中进行与实验工况相同的模拟集矿过程,实验与数值模拟的采集率对比结果如图5所示,Q_j为射流流量.二者变化趋势相同,且随着采集率η升高而趋于一致,因此认为基于 RKE 2L 湍流模型和DEM模型的CFD-DEM数值模拟方法可用于准确预报矿粒采集过程.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 实验与模拟采集率结果对比

Fig.5 Comparison of experimental and simulated pick-up efficiency

1.4 工况设计

射流半宽c是附壁射流的关键特征参数,其定义为射流横断面处从壁面到最大流速v_m一半处的距离,直接反映了附壁射流的范围,如图6所示.图中:v_c为射流半宽处的流速.Rodman等^[6]通过实验得出了半理论半经验凸曲壁面射流半宽公式:

(4)$\frac{c}{b}=\frac{R}{b} \frac{\kappa}{n}\left[\exp \left(K \frac{n}{\kappa} \frac{x-x_{0}}{b} \frac{b}{R}\right)-1\right]$

式中:x- x₀为射流沿壁面的射程;K=0.073,为二维壁面射流发展速率(经验值);n与κ均为经验常数,n/κ约为7.式(4)适用于射流厚度b较小的情况,忽略了横向曲率的影响.由式(4)可知,c随x-x₀增大而增大,为便于比较不同结构的集矿流场,选取集矿装置凸曲壁面最低点(x-x₀=Rα)处的射流半宽c₁作为代表集矿附壁射流范围的关键特征参数.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 附壁射流参数示意图

Fig.6 Parameters of wall-attached jet

依据公式选取非耦合几何参数R、α和b,如图7所示,考虑R和b与d之比和射流切向弧度得到无因次几何参数:R/d、b/d、θ.设计参数取值如表3所示.根据矿粒直径计算雷诺数Re_p=1.07×10⁵.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 双曲壁附壁射流式集矿装置

Fig.7 Structure of the Coandă-effect-based collector

表3 数值模拟工况参数

Tab.3 Parameters of numerical simulation

几何参数	取值	其他参数	取值
R/mm	140~220	ρ_f/(kg·m^-3)	1 000
α/(°)	50~73	μ/(mPa·s)	1.31
b/mm	0.5~15	U/(m·s^-1)	0.2
h/mm	30	d/mm	20

新窗口打开| 下载CSV

同时定义无因次射流流量q:

(5)$q=\frac{Q_{\mathrm{j}}}{\rho_{\mathrm{f}} U d B}=\frac{v_{\mathrm{j}} b}{U d}$

式中:B为集矿装置宽度,取0.24 m.

利用临界无因次射流流量q₀,来衡量集矿装置的流量需求.一般情况下,随着q增加,集矿装置的矿粒采集率η会提升,而q₀为使得采集率达到99%以上所需要的最小q值,即

(6)$q_{0}=\{\min q \mid \eta(q ; R, \alpha, b) \geqslant 99 \%\}$

q₀越小,代表集矿装置在相同条件下达到较高的采集率对流量的需求越小,即集矿性能越优异.

2 几何参数对集矿性能的影响

2.1 凸曲壁曲率半径对集矿特性的影响

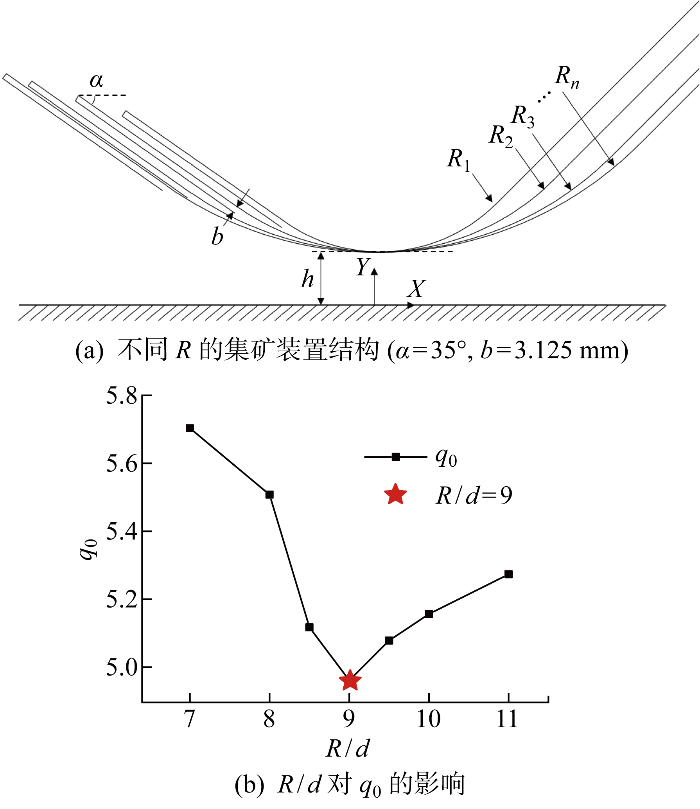
基于数值模拟,得到7组不同R/d下的q₀,结果如图8所示.由图可知,q₀-R/d曲线整体呈V形,q₀随R/d的增加先减小后增大,在R/d=9时达到最小值4.96.当R/d偏小时,由于流动分离或射流发展速率过大,导致矿粒周围的压力分布更为均匀,使其周围的垂向压差变小,举升力变小;而当R/d偏大时,随着R/d的增大,附壁射流沿凸曲壁流动至矿粒附近的距离增加,能量损耗增加且矿粒附近流场的非均匀性减小,矿粒举升力随之变小,从而导致需要的q₀增大.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 前凸曲壁曲率半径对流量需求的影响

Fig.8 Influence of curvature radius of convex wall on flow demand

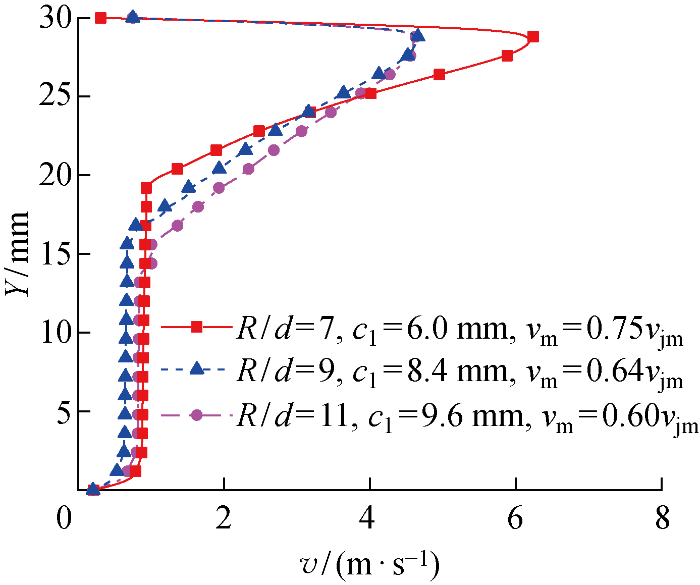
3种工况(R/d=7,9,11,q=q₀)下,垂向监测线上流体质点的流速v分布如图9所示.图中:v_jm是射流口处的最大流速.随着R/d的增大,v_m变小,射流半宽c₁增大,但变化速率减小;v_m的衰减量增大,其变化速率减小.R/d = 9时近底面处(Y<10 mm)流体质点的流速最小,说明集矿过程对底部区域的扰动也最小.因此,综合考虑矿粒采集效率和装置底部扰动情况,选取R/d=9为优化结果.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同R/d下的垂直监测线流速分布

Fig.9 Velocity distribution of monitoring line at different R/d values

2.2 射流切向角度对集矿特性的影响

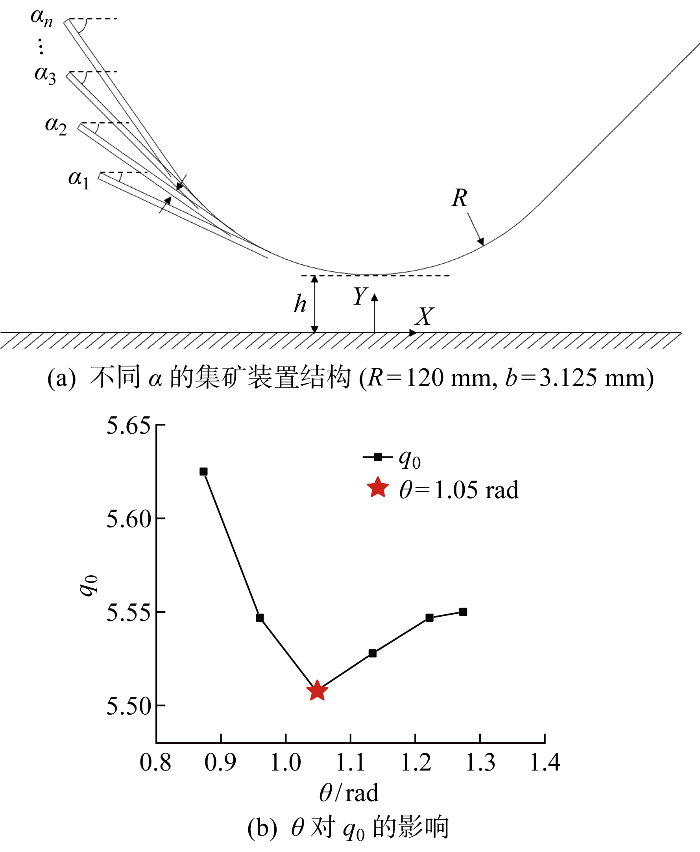
加大射流口处凸曲壁弧长以改变射流切向弧度θ,每个θ对应的q₀如图10所示.由图可知,θ对q₀的影响也呈V形发展,在θ=1.05 rad时,q₀达到最小值5.51.θ较小时,附壁射流发展不够充分,矿粒远离压力梯度场,相同流量下举升力较小;θ较大时,射流半宽显著增加,流场非均匀性降低,矿粒上下压力差异减小,受到的垂向举升力降低,因此流量需求升高.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 切向射流角度对流量需求的影响

Fig.10 Influence of curvature radius of jet angle on flow demand

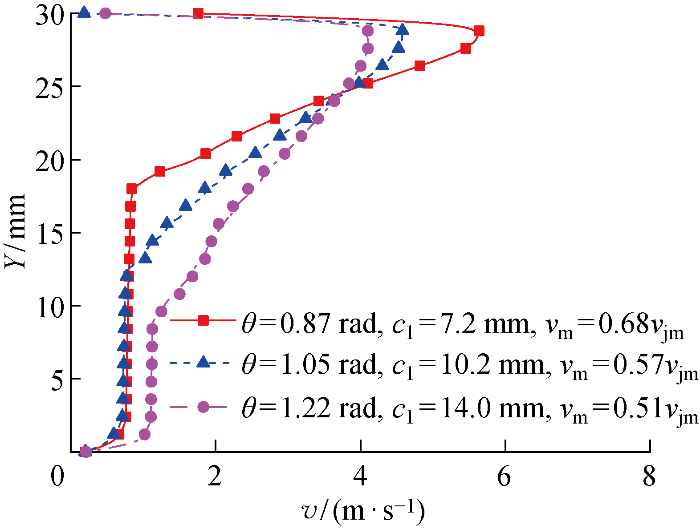
比较图8(b)与图10(b)可知,在R/d取值范围内,q₀最大相差0.78;而随着θ的变化,q₀最大相差0.13,仅为前者的16.7%.因此,R/d与θ虽然都直接改变了集矿流场的结构,但在影响程度上,θ要小于R/d.

对3种工况(θ=0.87,1.05,1.22 rad,q=q₀)监测线上的流速分布进行测量,如图11所示.随着θ增大,v_m变小,射流半宽c₁增大,且增大速率升高,θ从1.05提升到1.22 rad,c₁提升了39.22%;v_m衰减量增大,但变化速率减小.在近底面(Y<10 mm)处,工况θ=1.05 rad的流速最小,说明此时集矿流场对底部区域的扰动也最小.因此可选择θ=1.05 rad作为优化结果.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同θ下的垂直监测线流速分布

Fig.11 Velocity distribution of monitoring line at different θ values

2.3 射流厚度对集矿特性的影响

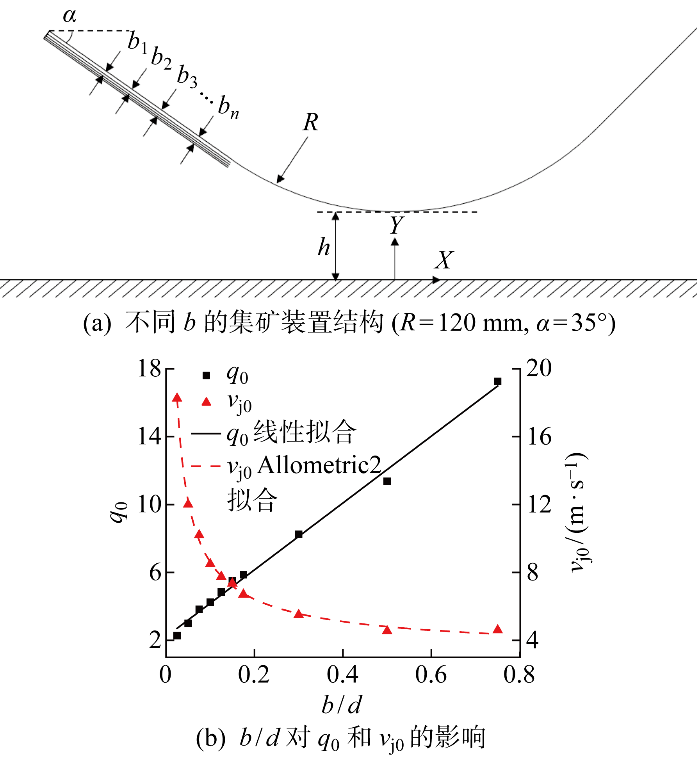
b/d对q₀的影响如图12所示,发现二者关系接近线性,对结果线性拟合,得到回归方程:

(7)q₀=a+s(b/d)

式中:a=2.21;s=19.69;拟合系数为0.994.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 射流厚度对流量需求的影响

Fig.12 Influence of jet thickness on flow demand

当b/d较小时,射流紧贴壁面,流场的非均匀性较强,矿粒所受举升力增加.随着b/d增加,矿粒上下压差逐渐降低,举升力减小,因此所需q₀增加.根据拟合公式,b/d每提升0.1,可使q₀提升约1.97,而R/d每变化0.1,q₀最大提升为0.08,仅为b/d变化值的4%;θ每变化0.1,q₀最大提升为0.09,仅为b/d变化值的4.6%.由此可知射流厚度对集矿性能的影响显著性远大于其他几何参数.

使用Allometric2模型对b/d和临界射流流速v_j0的关系进行拟合,得到如下方程:

(8)v_j0=m+n(b/d)^l

式中:m=3.11;n=1.02;l=-0.73;拟合系数为0.997,其影响规律符合幂函数特征.

由图12(b)可知,当b/d<0.2时,随着b/d的减小临界射流流速v_j0显著增大.在集矿过程中,不但使附壁射流更容易脱落,而且较大的射流流速会加剧集矿装置底部沉积物的受扰程度.因此考虑到集矿装置的稳定性与环境影响,b/d不宜小于0.2.

图13为水泵功率P_p随b/d的变化.在相同q下,随着b/d的减小P_p升高,且b/d越小,功率提升越显著(见图13(a)).这是因为较小的b/d使水射流在通过射流口时需克服更大的阻力,导致水泵需要消耗更大的功率.为确定不同b/d集矿装置在q=q₀工况下的水泵功率,进行了相应测量(见图13(b)).结果显示,当b/d=0.26时,P_p达到最小值1 kW.随着b/d继续增长,q₀的影响逐渐显现,水泵功率随之上升.因此,选取b/d=0.26为优化结果.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 b/d对水泵功率P_p的影响

Fig.13 Influence of jet b/d on pump power P_p

3 结论

本文针对双凸曲壁附壁射流式集矿装置几何参数优化问题,基于实验验证的CFD-DEM数值模拟方法,探究不同几何参数对集矿装置流量需求的影响规律,并结合集矿流场流速分布特性阐释矿粒受力运动特性,以高矿粒采集率、低流量需求和低能耗为优化目标,最终获得集矿参数的优化结果,主要结论如下.

(1) 通过比较实验结果和数值模拟结果,验证了RKE 2L湍流模型与DEM离散元模型相结合的CFD-DEM数值模拟矿粒采集过程的可行性和准确性.

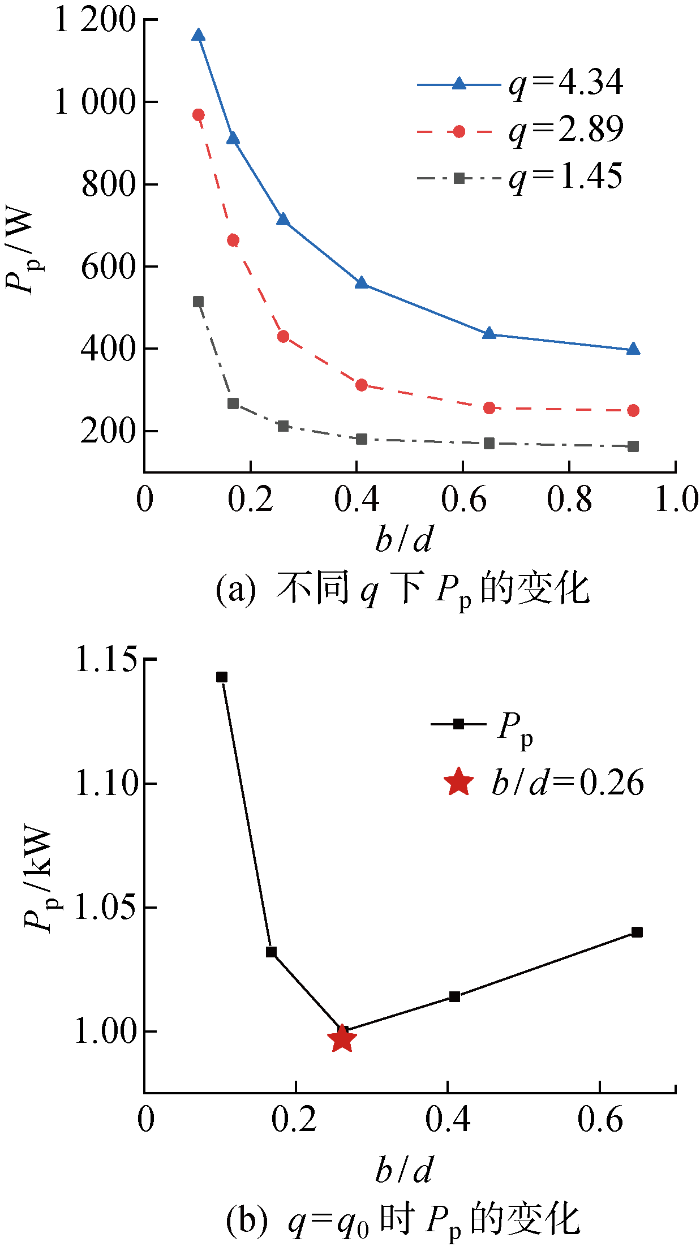
(2) b/d对集矿效率的影响最显著,R/d次之,θ影响最小.临界无因次射流流量q₀随R/d和θ的增加先减小后增大,分别在R/d=9,θ=1.05 rad时取得最小值;q₀随b/d的增加近似呈线性增大.水泵功率P_p随b/d的增加先减小后增大,在b/d = 0.26时取得最小值.最终优化几何参数为: R/d=9,θ=1.05 rad,b/d=0.26.

(3) 矿粒周围流场流速分布的非均匀性是影响其发生垂向起动的主要因素,而集矿装置几何参数的变化会显著影响集矿流场的分布特征.附壁射流下,R/d与c₁增长速率呈负相关,随着R/d和θ的增大,集矿头附近流体质点速度大小的差异性减小,从而导致流速分布非均匀性减弱.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

徐德义, 朱永光.

能源转型过程中关键矿产资源安全回顾与展望

[J]. 资源与产业, 2020, 22(4): 1-11.