基于神经网络分位数的分布式光伏发电功率异常识别方法

doi:10.16183/j.cnki.jsjtu.2023.412

基于神经网络分位数的分布式光伏发电功率异常识别方法

王晓倩, 周羽生, 毛源军, 李彬, 周文晴^,, 苏盛

长沙理工大学电气与信息工程学院,长沙 410114

Distributed Photovoltaic Power Outlier Detection Based on Quantile Regression Neural Network

WANG Xiaoqian, ZHOU Yusheng, MAO Yuanjun, LI Bin, ZHOU Wenqing^,, SU Sheng

School of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410114, China

通讯作者: 周文晴,博士生;E-mail:wenqingzhou2019@163.com.

责任编辑: 孙伟

收稿日期: 2023-08-24 接受日期: 2024-01-29

基金资助:

国家自然科学基金(51777015)

Received: 2023-08-24 Accepted: 2024-01-29

作者简介 About authors

王晓倩(1998—),硕士生,从事光伏发电状态异常检测研究.

摘要

分布式光伏发电系统点多面广,缺乏科学规范的运维管理体系,同时可用数据匮乏,难以准确识别由气象波动干扰导致的光伏设备异常.针对分布式光伏的运维现状和数据特征,提出一种基于神经网络分位数回归(QRNN)的光伏发电功率异常检测方法.首先分析晴天的太阳辐照度特性,利用晴朗日筛选方法排除阴雨天气的干扰影响;然后对不同电站的出力相关性进行分析,以获取出力相关性高的光伏电站作为横向参考;再将待测电站在不同晴朗日的出力曲线进行纵向对比,排除天气与环境条件等干扰因素.将排除干扰的计量出力有功功率数据输入QRNN模型,得到光伏正常有功功率出力区间,以正常出力区间的功率阈值识别光伏发电功率的异常.对某实际光伏系统数据进行仿真分析,结果表明:该方法能排除气象因素的干扰,准确识别出存在故障的光伏系统,推动分布式光伏的精细化运维.

关键词： 分布式光伏发电; 功率异常检测; 晴朗日筛选; 神经网络分位数; 出力相关性

Abstract

The distributed photovoltaic power generation system is widely dispersed and lacks a scientific and standardized operation and maintenance management system. Due to the limited availability of data, it is difficult to accurately detect abnormal conditions in photovoltaic devices caused by fluctuations in weather. In this paper, according to the operation and maintenance status and data characteristics of distributed photovoltaic, a quantile regression neural network (QRNN)-based method is proposed for detecting photovoltaic power outliers. First, the solar irradiance characteristics of sunny days are analyzed, and the influence of rainy weather is excluded by using a sunny day screening method. Then, the power output correlation of different power stations is analyzed to identify the photovoltaic stations with high power output correlation, which is used as a horizontal reference. Subsequently, the curves of the power output of the stations tested on different sunny days are compared vertically to eliminate the interfering factors such as weather and environmental conditions. The measured active power data is fed into the QRNN model to establish the normal active power range for the photovoltaic system, whose threshold is used to detect photovoltaic power outliers. The simulation results of actual photovoltaic system data show that the method proposed can eliminate the meteorological influence, accurately identify the faulty photovoltaic system, and promote the fine operation and maintenance of distributed photovoltaic.

Keywords： distributed photovoltaic power generation; power outlier detection; sunny day screening; quantile regression neural network (QRNN); power output correlation

PDF (3885KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王晓倩, 周羽生, 毛源军, 李彬, 周文晴, 苏盛. 基于神经网络分位数的分布式光伏发电功率异常识别方法[J]. 上海交通大学学报, 2025, 59(6): 836-844 doi:10.16183/j.cnki.jsjtu.2023.412

WANG Xiaoqian, ZHOU Yusheng, MAO Yuanjun, LI Bin, ZHOU Wenqing, SU Sheng. Distributed Photovoltaic Power Outlier Detection Based on Quantile Regression Neural Network[J]. Journal of Shanghai Jiaotong University, 2025, 59(6): 836-844 doi:10.16183/j.cnki.jsjtu.2023.412

分布式光伏发电近几年装机快速增长,但安装环境复杂多变^[1],家用屋顶分布式光伏在最优运维周期下的平均每日运维成本为116元/户^[2],发电收益无法覆盖运维成本,因此小容量分布式光伏出现了运维频率低、故障率高的现象.长期处于异常状态的光伏设备不仅影响用户利益,也给设备运行带来巨大安全隐患.如何准确感知设备状态,减少对运检人员诊断经验和高频率巡视的依赖,是目前光伏运维的关键技术课题.

近年来,针对光伏系统的故障诊断方法主要分为两种:红外图像分析法和电气测量法.红外图像分析法利用红外摄像机拍摄光伏组件,分析温度特性诊断故障.文献[3]中通过邻近最慢嵌入法捕捉异常趋势变化信息,能够实时检测热斑,避免永久性损伤.此类方法适用于地形复杂的光伏设备,但检测易受外界环境干扰.电气测量法主要围绕测量I-V曲线,实测工作点与理论曲线对比判断是否发生故障^[4].文献[5]中利用数字孪生模型的工作电压电流作为参考,计算与实际系统最大功率点的残差向量识别故障.此外,还有基于回归、聚类、分类、集成学习等机器学习方法分析直流侧I-V特性识别故障类型^[6-8].

不同于集中式光伏所拥有的数据条件,分布式光伏没有高精度气象数据和完备的电气状态监测数据^[9],仅通过计量系统上传发电功率数据,现有基于直流侧I-V故障诊断方法在分布式光伏场景难以应用^[10].分布式光伏一般无人运维,即便在整县光伏模式下也只能做到以较长时间间隔定期巡视^[11],容易长期带病运行.在状态监测数据资源匮乏的分布式光伏系统中,运维检修的主要矛盾是如何识别出需要进行现场运维的故障系统,提高运检的靶向性,降低发电量损失和人工运维成本;而诊断故障原因和定位故障点则退化为次要矛盾,可由运维人员携带工器具现场采集状态量指标后诊断识别.因此,如何根据仅有的量测数据远程感知分布式光伏系统状态,是当前亟待解决的重要问题.

组件故障、杂物遮挡和违规扩容等异常运行状态均会导致发电功率偏离正常区间,设备异常状态识别可通过异常发电数据检测.文献[12]中用聚类划分相似日,随后分别用同时段对比和四分位法识别连续性和离散型异常数据.为了防止单一模型过拟合导致的误差,文献[13]中采取3层分类器递进式训练的集成框架,提高了不平衡的新能源发电数据的异常检测准确率.此类方法都是通过研究辐照度与发电功率的概率分布模型来检测异常数据,为仅有量测数据的分布式光伏异常状态识别奠定了理论基础.

针对光伏异常运行状态,文献[14]中研究了遮挡状态下的光伏输出特性,利用马尔可夫链模型计算遮挡概率,通过概率波动判断是否遮挡.文献[15]中针对不同安装角度的光伏面板,选取环境条件和产品规格构建特征量,通过对比特征量检测出故障的光伏阵列.文献[16]中提出了一种无需高地理精度辐照度的晴空检测方法,可消除辐照度与集中式光伏不完全匹配在性能评估中导致的噪声.文献[17]中使用空间反距离加权预测区域内光伏出力,并对比回归值与真实值应用在分布式光伏异常检测场景,可有效检测出异常设备.气象条件的随机波动性导致光伏发电在时间空间维度上更为复杂^[18],如何用有限量测数据排除气象和安装环境的干扰识别分布式光伏发电功率异常尚需进一步探索.

综上所述,国内外关于光伏异常检测的研究主要是集中式光伏的故障诊断,分布式光伏由于数据条件不满足无法直接照搬此类成熟方案.分布式光伏系统点多面广的特点导致人工巡检成本高,也无法作为分布式光伏主要运维方式,因而需要一种远程感知设备异常的方法.异常状态均会导致异常发电功率,因此提出一种基于神经网络分位数回归的光伏发电功率异常识别方法,利用晴天光伏发电功率特点来检测设备异常状态.首先分析光伏系统发电功率异常的原因和检测时的干扰因素,提出了排除气象因素干扰的晴天判别方法;然后利用相关性强的电站互为参考排除永久性故障等干扰,选用神经网络分位数回归模型(quantile regression neural network,QRNN)检测超出正常区间的异常光伏发电功率;最后,结合光伏电站现场数据及其仿真分析,验证了所提方法的有效性.

1 光伏发电功率异常的影响因素

光伏运维中的异常指导致发电效率降低或设备损坏的系统运行状态.异常状态主要包括故障、老化、遮挡、扩容和限电^[19],表现为发电功率的异常,其数据特征如表1所示.光伏发电系统广布于室外,易出现机械损伤和元件故障,比如组件开裂、接线老化、阵列间短路开路等.光伏面板也会被长期遮挡,可能发展为热斑,影响使用寿命^[20].随着运行时长增加,线路老化导致发电效率降低、发电量衰减.扩容是指私自加装光伏设备以骗取光伏发电补贴,体现为出力增加^[21].电网对光伏的消纳能力有限,因此对光伏限电时也会产生异常的上网电量数据.

表1 光伏系统异常数据类型

Tab.1 Types of abnormal data of photovoltaic system

异常状态	具体原因	出力数据表征
故障	接线错误,阵列间短路开路	等比例或随机下降
老化	组件和线路电阻老化	等比例下降
遮挡	灰尘、树叶、建筑、树木等	等比例或随机下降
扩容	用户私自扩容骗取发电补贴	增加
限电	对新能源上网消纳能力有限	降低

新窗口打开| 下载CSV

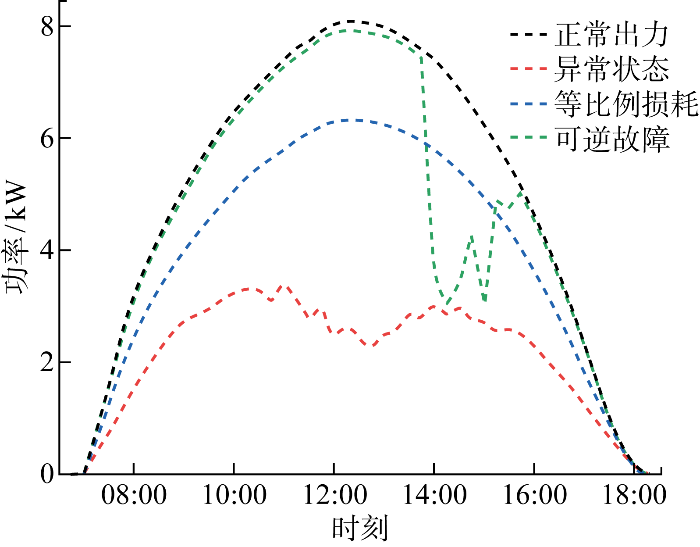
光伏阵列晴天发电状态如图1所示,设备正常时功率如黑色曲线所示;硬遮挡、老化和部分阵列故障时,系统功率略微下降,表示为蓝色曲线,其中硬遮挡指灰尘、树叶、鸟粪等附着在面板上的长期覆盖物;可逆故障的功率变化为下降后恢复的绿色曲线;随机遮挡指环境中树木建筑物等导致的遮挡,功率变化不规则,如红色曲线所示.其中,随机遮挡和可逆故障不会造成多时段功率损失和设备损坏,在检测中视为正常状态.因此,运维异常状态常表现为计量点发电功率等比例下降.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 晴天时光伏阵列不同状态功率

Fig.1 Output of photovoltaic array in different sates

如上讨论的影响光伏发电的干扰因素在功率异常检测时易造成误判.阴雨天气导致光伏发电出力波动,很难通过光伏有功功率直观判断设备状态.晴朗天气下无云层遮蔽,光伏出力曲线平滑无明显波动,日出力曲线呈拱门形.因此,选择光伏晴朗天气的出力状态可排除云层干扰.在光伏阵列仰角相同情况下,气温和纬度影响光伏发电出力.选择同一地区的光伏利用地理位置接近的特点,可消除气温和纬度因素影响.光伏阵列转换效率、仰角和朝向对发电出力有突出影响.但此类因素在投产后大致保持不变,在光伏发电出力的横向对比中不影响检测结果.光伏系统投产后可能出现部分元件故障,此后发电出力会持续降额运行,可通过同一地区内横向对比识别异常的光伏系统.限电会导致上网电量发生异常,采用光伏系统计量点数据,即实际发电功率,排除限电干扰.

综上所述,选择同一地区光伏系统在晴朗天气下的计量发电出力数据进行横向对比,可排除气象因素及光伏系统自身对异常检测的干扰.

2 晴朗日判别方法

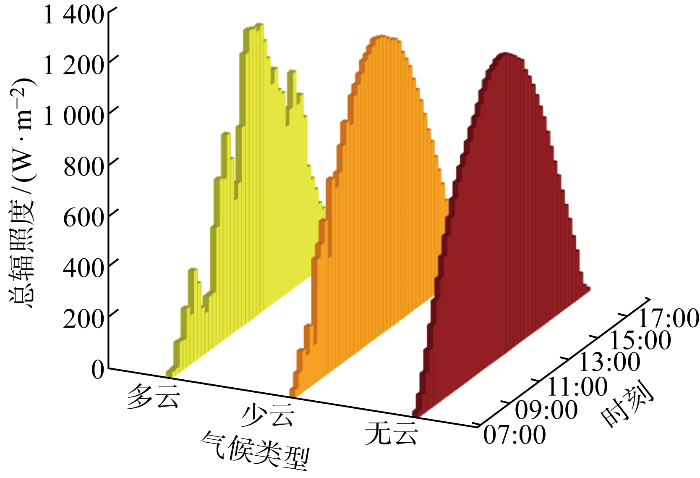
云层遮蔽造成太阳辐照度下降,使得光伏发电出力下降^[22].图2所示为1 d内晴朗无云、少云和多云时的辐照度曲线.云层使辐照度具有明显的波动性,根据辐照度的波动性判别是否为晴朗日.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 不同云量时的总辐照度

Fig.2 Total irradiance at different cloud cover levels

典型晴朗日的太阳辐照度分为递增和递减两个区间,晴朗日筛选方法如下:

(1) 灰霾天气时太阳辐照度可能相似于晴朗天气.从历史太阳辐照度数据计算一个季度中每天的最大辐照度数值,按数值大小排序并取1/4处位数值,即取上四分位数作为阈值.当最大辐照度小于该阈值时,天气存在雾霾等干扰,不能作为异常检测的晴朗日.

(2) 将筛除出的晴朗日日区间辐照度数据归一化,获得第j天15 min时间间隔的标幺化太阳辐照度数据序列A'_j={a'_1,_j, a'_2,_j, …, a'_96,_j},且

(1)a'=a/max A

式中:a'为太阳辐照度标幺值;a为太阳辐照度;A为当日太阳辐照度数据序列.

(3) 计算日区间数据单位时段的差分值,可称为单位时段波动量,得到单位时段波动量序列B_i={b_1,_j, b_2,_j, …, b_95,_j},且

(2)$b_{i, j}=a_{i, j}-a_{i-1, j}$

(4) 将单位时段波动量序列从第一时段开始逐次递推1个时段,与0比较定义不同的波动区间,前后两时段波动量正负相反时刻为一个波动点.由于绝对晴朗无云的天气有限,为丰富异常检测模型可利用样本数对波动点的波动量取绝对值,若小于阈值β,则没有新的波动区间生成;否则有新的波动区间生成,把该点的前一时段波动量作为前一个波动区间的结束,该点后一时段波动量作为后一个波动区间的开始.记录每日的波动区间数,晴朗日分为连续递增和连续递减两个波动区间,即晴朗日的辐照度波动区间数为2.

(5) 若波动区间数大于2,认为该日为非晴朗日;若波动区间等于2,则将每个波动区间的波动量进行二次差分;若二次差分绝对值小于阈值γ,则该日为晴朗日.

该方法筛选晴朗日依赖于阈值β和γ.阈值越小筛选出的辐照度曲线越光滑,但能用于异常检测的天数也越少.为满足实际应用,需结合当地实际情况和专家经验合理设置阈值.

3 光伏发电的出力相关性

以某省甲乙两地区的40个光伏系统为例,其中甲地34个,乙地6个,两地相隔202 km,区间气候条件存在一定差异.各地区涵盖多类型和不同倾角的光伏阵列,投产时间和发电效率不同,两地区之间及地区内部的光伏系统出力曲线存在差异,需根据不同电站出力曲线的相关系数定量评估光伏电站之间的关联性.不同光伏电站之间出力相关性高说明安装的地理位置相近、气候环境相似,互相作为横向参考可排除电站的永久性故障和气候对异常检测的干扰.

3.1 不同光伏电站出力相关性

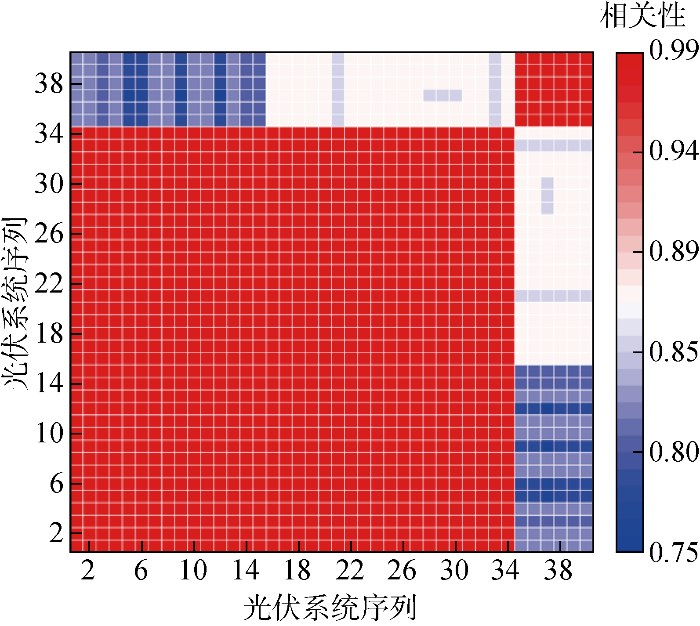
对上述40个光伏系统分别在同一个月中每 15 min 时间间隔的有功数据进行相关性分析,计算两地区不同光伏系统出力皮尔逊相关系数,计算结果的热力图如图3所示.由图3可见,同在甲地区的34个光伏电站之间相关性大于0.97,而乙地区的6个光伏电站间相关性也在0.95以上,但两地区之间的相关性都小于0.86,明显低于地区内部的相关性.因此同一地区光伏电站出力相似,可相互校验进行异常检测.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 光伏电站相关性分析

Fig.3 Correlation analysis of photovoltaic array

3.2 同一光伏电站不同晴朗日出力相关性分析

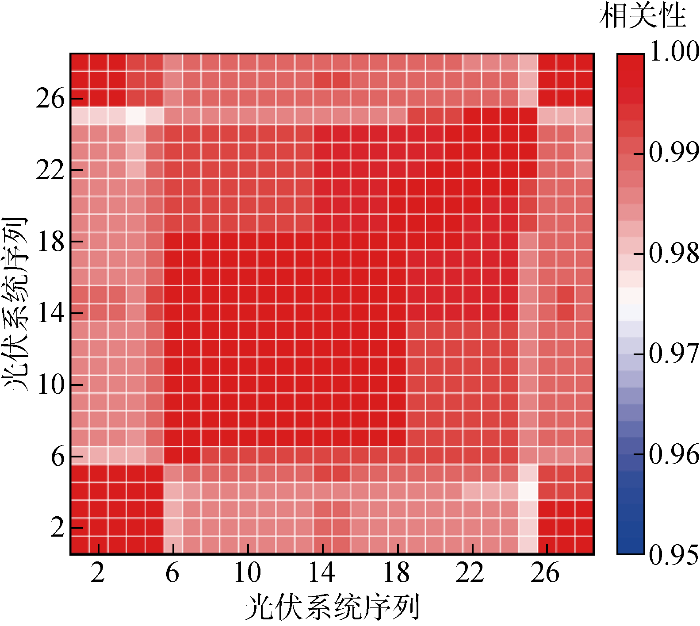
分析不同晴朗日下同一光伏系统的出力相关性,可排除如交直流电缆损耗及触点损耗、线路老化和设备陈旧等带来的固有损耗以及季节性日照角度变化的干扰.选取某光伏系统2020年全年的28个晴朗日数据,将各天光伏有功数据的相关性分析结果绘制如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同日期出力相关性结果

Fig.4 Photovoltaic output correlation across different dates

由图4可知,所有晴朗日的相关系数都大于0.96,说明一年中光伏设备未见明显损耗.另外,相近月份辐照度和气温相近,相关性也会更强;尽管不同月份气象条件变化较大,但晴朗日下光伏出力相关性都大于0.96,保持了很高的相似性水平.因此,同一光伏系统在纵向不同季节晴朗日的发电功率数据可用于异常检测.

综上,选择在横向上气候环境相似、纵向不同季节晴朗日的光伏发电出力相关性都大于0.95作为参考标准,对待测系统进行异常检测.

4 基于QRNN的异常检测原理

4.1 线性分位数回归模型

求解回归问题时,若样本Y=[Y₁Y₂ … Y_n] 是解释变量X=[X₁X₂ … X_n]的响应变量,则可求解目标函数获得线性回归的模型参数:

(3)min

\sum_{i = 1}^{n}

(Y_i-X_iξ)

式中:n为样本量;X_i代表真实值;Y_i代表拟合值;ξ为回归系数^[23].

式(3)中估计参数向量ξ可转化为如下的优化问题:

(4)$\begin{aligned} \min _{\xi} & \sum_{i=1}^{n} \rho_{\tau}\left(Y_{i}-X_{i}^{\prime} \xi\right)= \\ & \min _{\xi}\left[\sum_{i \mid Y_{i} \geqslant X_{i}^{\prime} \xi} \tau\left|Y_{i}-X_{i}^{\prime} \xi\right|+\right. \\ & \left.\sum_{i \mid Y_{i}<X_{i}^{\prime} \xi}(1-\tau)\left|Y_{i}-X_{i}^{\prime} \xi\right|\right] \end{aligned}$

式中:X'_i(i=1, 2, …, n)为分位数条件下的解释变量;i|Y_i≥X'_iξ为第i个响应变量实际值大于等于线性回归估计值;分位数τ∈(0,1);ρ_τ(u)=u[τ-I(u)],I(·)为示性函数,表示为

(5)I(u)=

\{\begin{array}{l} 1, & u < 0 \\ 0, & u \geq 0 \end{array}

由式(4)得出,在不同分位数τ可得到不同的参数估计ξ(τ),就能测算出在不同分位数τ处解释变量对响应变量条件分位数的影响.τ在(0, 1)连续取值时,即可得到响应变量的条件分位数.

4.2 QRNN模型

在式(3)所示线性回归模型中,限定了解释变量和响应变量之间只能是线性关系,但现实中变量之间多为非线性关系.Taylor^[24]提出一种QRNN模型,利用神经网络的非线性结构不依赖于明确函数形式设定即可取得准确的结果,在电力负荷时间序列拟合上应用效果好.实现过程如下:

(6)Q_Y(τ|X)=f(X, V(τ))

式中:Q_Y(τ|X)是对光伏发电功率拟合值Y的条件分位数估计,当τ在(0,1)上连续时为条件分布; V(τ)=(v_kl(τ))_k_{=1, 2, …}_K_;_l_{=1, 2, …,}_L为隐含层与输出层之间的连接权重,其中K和L分别为隐含层和输出层节点数.

神经网络分位数回归参考式(6),令 W(τ)=(w_jk(τ))_j_{=1, 2, …}_J_;_k_{=1, 2, …,}_K 为输入层与隐含层之间的连接权重,J为输入层节点数.将对参数矩阵W(τ)、V(τ)的估计转化为求下式的优化问题:

(7)$\begin{array}{l} \min _{\boldsymbol{W}, \boldsymbol{V}}\left(\sum_{i=1}^{N} \rho_{\tau}\left(Y_{i}-f\left(X_{i}, \boldsymbol{W}, \boldsymbol{V}\right)\right)+\right. \\ \left.\quad \lambda_{1} \sum_{j, k} w_{j k}^{2}+\lambda_{2} \sum_{j} v_{j}^{2}\right)= \\ \quad \min _{\boldsymbol{W}, \boldsymbol{V}}\left(\sum_{i \mid Y_{i} \geqslant f\left(X_{i}, \boldsymbol{W}, \boldsymbol{V}\right)} \tau\left|Y_{i}-f\left(X_{i}, \boldsymbol{W}, \boldsymbol{V}\right)\right|+\right. \\ \left.\quad \sum_{i \mid Y_{i}<f\left(X_{i}, \boldsymbol{W}, \boldsymbol{V}\right)}(1-\tau)\left|Y_{i}-f\left(X_{i}, \boldsymbol{W}, \boldsymbol{V}\right)\right|\right]+ \\ \quad \lambda_{1} \sum_{j, k} w_{j k}^{2}+\lambda_{2} \sum_{j} v_{j}^{2} \end{array} $

式中:λ₁、λ₂为惩罚参数;N为样本Y的数量.

式(7)中λ₁、λ₂可防止训练过程过拟合现象;可使用Adam随机梯度下降法求解式(7),估计得到W(τ)、V(τ),代入式(6)中并计算τ在(0, 1)的连续取值,得到不同分位点下的回归值Y.

QRNN模型对非线性时间序列拟合能力较强,具有一定的鲁棒性,可将分位数回归与神经网络有机结合起来,通过选取不同分位点即可得到响应变量的不同条件分位数,选择不同置信度下的拟合结果确定正常区间.

4.3 异常检测流程

前文提出的方法可降低不同电站间差异性对检测的影响:晴朗日筛选机制可排除阴雨天气和空气质量的干扰;对不同电站的时空关联分析,检测电站永久性故障的同时排除气温等因素的干扰;采用不同日期的纵向对比可排除同一电站阵列倾角不同和设备随时间产生固有损耗的干扰.

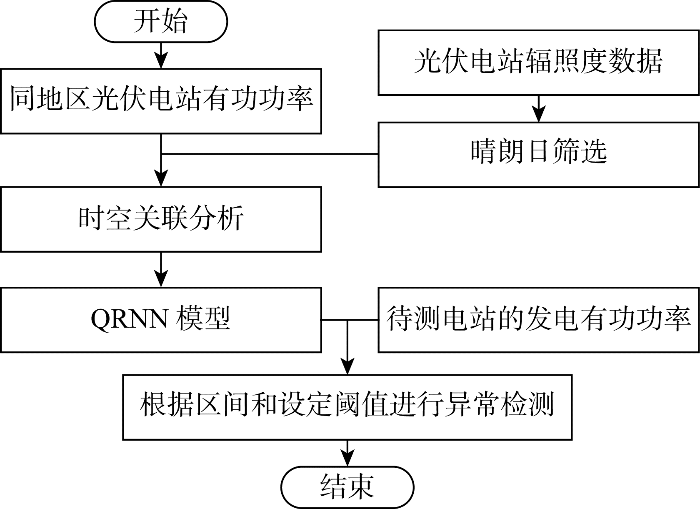
功率异常检测流程如图5所示,选择能够包含真实光伏出力曲线的分位数作为正常区间,将待检测序列与光伏有功功率拟合区间对比判别光伏系统是否异常,具体检测步骤如下.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 功率异常检测流程

Fig.5 Flow chart of outlier detection

(1) 数据预处理:获取光伏发电有功功率及太阳辐照度数据,根据相似日数据对缺失值插值.

(2) 确定待分析的电站以及晴朗日:根据第2章步骤获取晴朗日期,再通过时空关联分析对电站进行横、纵向对比.

(3) 获取光伏电站正常有功功率区间:将晴朗条件下且有功功率数据横纵相关性高的参考电站输入QRNN模型,训练获得光伏电站正常出力区间,选择能包含真实值的分位数区间并将区间上下限时间序列数据作为判断阈值.

(4) 异常用户识别:将得到的有功功率区间最小值构成的时序数据作为阈值,若待检测序列值小于对应时刻阈值,则认为存在异常,可能是随机遮挡和可逆故障;而持续低于阈值时则发出异常预警,需进行现场巡视;若大于阈值范围,说明存在违规扩容.

5 仿真验证及结果分析

将甲地34个新建光伏电站2020年全年15 min间隔采样功率数据分为训练集和验证集,训练集输入模型进行仿真分析.

5.1 多场景下拟合精度分析

为验证QRNN模型拟合的准确性,首先将QRNN与长短期记忆网络分位数回归(quantile regression long short term memory network, QRLSTM)模型在晴朗日和非晴朗日对比作为异常识别场景.仿真实验计算机配置为CPU酷睿i7-10700、内存16 GB、GPU2070 8 GB.通过Keras深度学习框架将每个分位数下的神经网络迭代100个轮次.

选取可靠性和敏锐性作为概率区间拟合评价指标,可靠性指标 (Reliability Index,RI)衡量真实值落在拟合区间的性能:

(8)I_R=

\sum_{n_{s} = 1}^{N_{s}} \frac{U_{n_{s}}}{N_{s}}

式中:N_s为区间采样点的数量; $U_{n_{s}}$ 取值为0或1,即光伏系统输出功率落在拟合区间之内则取1,反之取0.

敏锐性指标(acuity index,AI)是在置信度1-α条件下衡量拟合区间平均宽度的性能指标:

(9)I_A=

\sum_{n_{s} = 1}^{N_{s}} \frac{H_{n_{s}} - L_{n_{s}}}{N_{s}}

式中: $H_{n_{s}}$ 为光伏系统拟合区间的功率上限; $I_{n_{s}}$ 为光伏系统功率拟合区间的下限.

更高的可靠性和更低的敏锐性表明拟合结果更贴近真实值,将尽可能多的真实值包含在内,并使拟合区间平均宽度尽可能小.各算法在不同场景的可靠性和敏锐性指标如表2所示.可知,不同置信度表示不同的区间宽度,通过均衡可靠性和敏锐性两个指标选取最合适的置信度,达到在检测准确情况下的最窄曲线.置信度为80%时,各拟合模型的可靠性都有所下降,敏锐性能有所提升,但QRLSTM可靠性下降幅度大于QRNN模型.置信度为90%时,晴朗日的QRNN模型可靠性为99.90%,敏锐性为67.3 W,性能远超QRLSTM,此时可靠性足以完成后续异常检测,增加曲线宽度只会降低敏锐性.

表2 不同算法在不同气候环境下的拟合可靠性和敏锐性

Tab.2 Fitting reliability and sensitivity of different algorithms in different conditions

置信度/%	气候	算法	可靠性/%	敏锐性/W
90	晴朗日	QRNN	99.90	67.3
	晴朗日	QRLSTM	74.40	184.9
	未筛选晴朗日	QRNN	73.78	204.5
	未筛选晴朗日	QRLSTM	80.36	315.8
80	晴朗日	QRNN	92.36	24.7
	晴朗日	QRLSTM	51.60	121.1
	未筛选晴朗日	QRNN	63.31	85.0
	未筛选晴朗日	QRLSTM	57.73	161.6

新窗口打开| 下载CSV

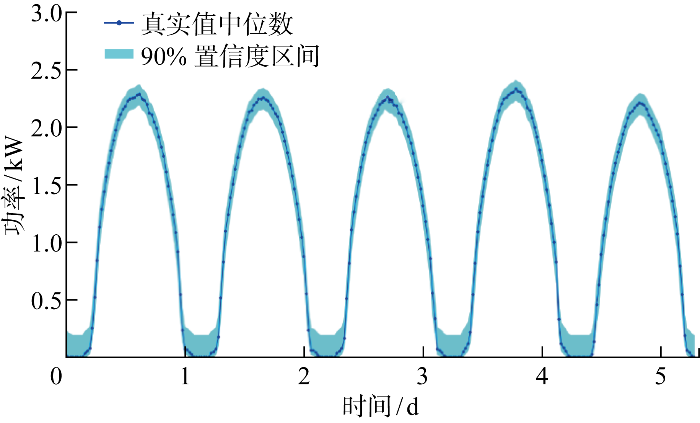
图6为5 d晴朗日的90%置信度下QRNN模型区间拟合结果.可知,真实值全部落在拟合区间内,且接近于区间中部,90%置信度拟合能为异常识别提供可靠且敏锐的参考区间.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 晴朗日下90%置信度的QRNN区间拟合的结果

Fig.6 Results of fitting QRNN intervals with 90% confidence under sunny day conditions

5.2 功率等比例下降场景实验

由于实际数据中异常状态较少,在仿真分析中无法验证有效性,所以将验证集光伏出力正常数据中随机抽选部分样本按8%的比例降低出力作为异常样本.分别获取晴朗日与未筛选晴朗日下QRNN模型90%置信度拟合的正常区间上下限作为阈值,将待检测的光伏电站数据按照是否筛选晴朗日分别与阈值对比进行异常检测.

孤立森林(isolation forest,iForest)算法和局部离群因子(local outlier factor,LOF)算法在异常检测领域中有广泛应用^[25-26].将5.1节得出的90%置信度区间异常检测与iForest和LOF算法对比分析,以检测率R_D和误报率R_FP作为检测指标,表达式为

(10)R_FP=

\frac{N_{F P}}{N_{F P} + N_{T N}}

(11)R_D=

\frac{N_{T P}}{N_{T P} + N_{F N}}

式中:N_FP、N_TN、N_TP和N_FN分别为假正例、真反例、真正例和假反例数量.计算结果如表3所示.

表3 不同气候环境下iForest、QRNN和LOF算法检测结果

Tab.3 Detection results of iForest, QRNN, and LOF algorithms in different climatic environments

气候	算法	R_FP/%	R_D/%
晴朗日	QRNN	2.25	95.15
未筛选晴朗日	QRNN	10.26	89.31
晴朗日	iForest	39.60	91.42
未筛选晴朗日	iForest	44.34	85.13
晴朗日	LOF	15.79	92.53
未筛选晴朗日	LOF	7.62	45.63

新窗口打开| 下载CSV

由表3可见,晴朗日下QRNN检测率为95.15%,误报率仅2.25%,效果最好;iForest异常检测的误报率偏高,检测率也明显低于本文方法.可能是由于iForest算法要求异常点特征明显,而且在96点高维数据处理上存在局限性,对光伏功率异常检测适用性较弱.而LOF算法在晴天时样本点集中,检测率较高,但边界处局部可达密度差异性较小,容易误判.未筛选晴朗日时,受天气波动性干扰,误报率和检测率均劣于晴朗日.

5.3 工程验证

集中式光伏电站可由专人根据较详尽的监测数据进行巡检,及时检出和修复故障设备.其故障主要为阵列故障不发电导致的有功功率等比例下降;而分布式光伏电站缺乏及时运维,难以确定异常检测结果的准确度.为验证本文异常检测方法的有效性,以集中式光伏电站支路为例,对各支路发电有功功率数据进行测试实验.

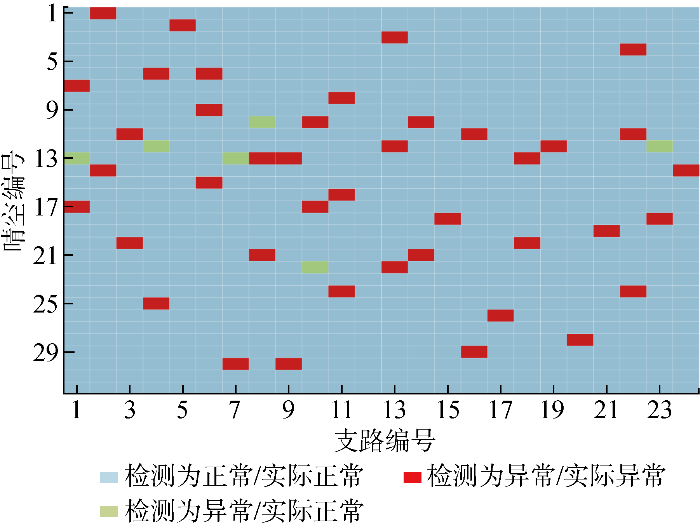
选择某实际50 MW装机光伏电站,共有24条支路及对应的集中式逆变器24台,将每条支路作为子系统进行检测.从集控中心获取2021年下半年共32个晴天的辐照度和不同支路光伏出力计量数据,应用本文方法进行异常检测,与现场实际巡视对比的检测结果如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 24条支路进行时长180 d的测试结果

Fig.7 Results of a 180-day test of 24 branches

由图7可以看出,基于各支路发电功率数据共检出支路异常47次,与现场检修记录对比,实际系统对应支路异常的为41次,说明此方法能够有效检测系统异常,降低运维周期.

5.4 异常处理措施

可逆故障和随机遮挡能自行恢复,可通过调整检测阈值设置为非异常提醒.检测出发电功率等比例下降的异常后,根据现场巡检结果可分为两类,分别采用不同的处理方案:若人工发现光伏面板存在灰尘、鸟粪等硬遮挡,则清洗光伏面板;若人工测量设备电气特性后确定为老化或组件故障,则更换相应的组件.

6 结论

分布式光伏发电系统点多面广、异常状态频发,针对功率异常检测易受气象和环境等因素干扰,提出基于神经网络分位数回归模型的光伏发电功率异常识别方法,结论如下:

(1) 分析了异常功率的产生原因和数据特征,提出晴朗日筛选和QRNN模型拟合出力区间的异常检测方法,进而识别光伏设备运行状态,提高分布式光伏运维靶向性.

(2) 通过晴朗日筛选机制和光伏发电出力时空关联分析,降低了气象环境、地理位置和安装角度对检测结果的干扰.

(3) 实际系统数据的工程验证表明,针对发电等比例下降的异常状态检测,采用QRNN算法比较正常区间阈值的检测方法降低了误报率,提高了检测可靠性.

由于依赖晴朗日筛选来提高检测效果,所以存在晴朗日数据不充分的情况,阈值选择对功率异常检测的影响及其修正方法有待进一步研究.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

L J

, LIU

H X

, YAN

, et al.

A virtual data collection model of distributed PVs considering spatio-temporal coupling and affine optimization reference

[J]. IEEE Transactions on Power Systems, 2023, 38(4): 3939-3951.