基于频域模态法的新能源电力系统振荡稳定性评估

doi:10.16183/j.cnki.jsjtu.2023.358

基于频域模态法的新能源电力系统振荡稳定性评估

高磊¹, 马骏超², 吕敬^,¹, 刘佳宁², 王晨旭², 蔡旭¹

1.上海交通大学电力传输与功率变换控制教育部重点实验室,上海 200240

2.国网浙江省电力有限公司电力科学研究院,杭州 310014

Oscillatory Stability Assessment of Renewable Power Systems Based on Frequency-Domain Modal Analysis

GAO Lei¹, MA Junchao², LÜ Jing^,¹, LIU Jianing², WANG Chenxu², CAI Xu¹

1. Key Laboratory of Control of Power Transmission and Conversion of the Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China

2. State Grid Zhejiang Electric Power Co., Ltd. Research Institute, Hangzhou 310014, China

通讯作者: 吕敬,副教授,博士生导师,电话(Tel.):021-34207001;E-mail:lvjing@sjtu.edu.cn.

责任编辑: 王历历

收稿日期: 2023-07-31 接受日期: 2023-10-26

基金资助:

国网浙江省电力有限公司科技项目(B311DS22000K)

Received: 2023-07-31 Accepted: 2023-10-26

作者简介 About authors

高磊(1997—),博士生,从事新能源柔直并网稳定分析与控制研究.

摘要

随着新能源接入比例的不断提高,电力系统的次/超同步振荡风险加剧,准确评估新能源电力系统的振荡稳定性是保障系统安全稳定运行的关键.首先,研究了一种基于频域模态分析的新能源电力系统振荡稳定性评估方法,该方法通过建立新能源机组和场站、传输线、同步机、变压器等关键设备和场站的频域阻抗或导纳模型,根据实际系统拓扑构建系统级频域网络模型.然后,通过求解回路阻抗矩阵或节点导纳矩阵行列式的零点来评估新能源电力系统的振荡稳定性,通过计算弱阻尼振荡模式的节点参与因子矩阵定位系统薄弱点,为振荡抑制措施的实施提供依据.以国内华东地区某实际新能源电力系统为例,利用频域模态分析法评估新能源接入容量和电网运行工况变化下系统的振荡稳定性.最后,利用PSCAD/EMTDC软件搭建该系统的时域仿真模型,验证了理论分析的正确性.

关键词： 新能源电力系统; 振荡稳定性; 频域网络; 频域模态分析; 稳定性评估; 薄弱点定位

Abstract

The increasing penetration of the renewable energy has increased the risks of sub/super synchronous oscillations in power systems. Therefore, it is critical to accurately evaluate the oscillatory stability of renewable power systems ensuring the safe and stable operation of the systems. In this paper, a method for evaluating the oscillatory stability of renewable power systems based on frequency-domain modal analysis is investigated. First, the frequency-domain impedance or admittance models of key equipment and stations are established, including the renewable power generators and stations, transmission lines, synchronous generators, transformers, etc. Next, a system-level frequency-domain network model is constructed based on the actual system topology. Then, the oscillatory stability of the renewable power system is evaluated by solving the zeros of the determinant of the loop impedance matrix or the node admittance matrix of the system. The weak points of the system are identified using the participated matrix of the weak oscillation mode, which provides reference for implementation of oscillation suppression measures. Taking the practical renewable power system in East China as an example, the oscillatory stability of the system considering the varying access capacity of renewables under different grid operating conditions is assessed using the frequency-domain modal analysis method. Finally, the time-domain simulation model of the actual renewable power system is built in PSCAD/EMTDC to verify the theoretical analysis.

Keywords： renewable power system; oscillatory stability; frequency-domain network; frequency-domain modal analysis; stability assessment; weak point location

PDF (4521KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

高磊, 马骏超, 吕敬, 刘佳宁, 王晨旭, 蔡旭. 基于频域模态法的新能源电力系统振荡稳定性评估[J]. 上海交通大学学报, 2025, 59(6): 821-835 doi:10.16183/j.cnki.jsjtu.2023.358

GAO Lei, MA Junchao, LÜ Jing, LIU Jianing, WANG Chenxu, CAI Xu. Oscillatory Stability Assessment of Renewable Power Systems Based on Frequency-Domain Modal Analysis[J]. Journal of Shanghai Jiaotong University, 2025, 59(6): 821-835 doi:10.16183/j.cnki.jsjtu.2023.358

在国家“3060”双碳目标的驱动下,构建以新能源为主体的新型电力系统已成为行业共识^[1].相较于传统电力系统,新型电力系统稳定性问题突出,大规模新能源接入导致的宽频振荡问题给电网稳定控制带来挑战^[2-3].2009年美国某风电场20 Hz的次同步振荡造成大量风力发电机脱网^[4];2011年以来我国华北某地区风电场发生多次3~10 Hz 的次同步振荡现象^[5];2020年张北新能源基地出现数十至数千赫兹的宽频振荡现象^[6];2021年如东工程相继出现2 kHz和320 Hz的中高频振荡^[7-8].新能源电力系统的宽频振荡问题给国民经济造成巨大损失,如何降低振荡发生的风险受到业界广泛关注.

在规划阶段,评估新能源电力系统的宽频振荡风险有助于避免宽频振荡的发生^[9].目前,针对宽频振荡的评估方法主要有特征值分析法、阻抗分析法等.特征值分析法也称模态分析法,通过求解时域状态空间模型的特征根来判断系统的稳定性,并利用参与因子获取影响系统稳定性的主要因素^[10-11],但该方法需要预先获知系统的详细信息,且应用在大规模复杂新能源电力系统时存在“维数灾”问题,在实际应用时具有局限性.阻抗分析法通过将系统划分为源-荷子系统,利用端口电压和电流的关系获取各子系统的阻抗模型,进而基于阻抗稳定性判据评估系统的宽频振荡稳定性.由于端口阻抗可以通过测量获得,所以该方法适用于“黑/灰箱”系统^[12-13].然而,传统基于源-荷子系统的阻抗分析法面临分割点难以确定、无法定位薄弱点等问题,因此在实际复杂系统应用时受到限制.

随着人工智能技术的快速发展,基于数据驱动的系统振荡稳定性评估和振荡源定位方法在新型电力系统中具有一定的应用前景^[14-15].文献[14]中提出一种基于等效系统和数据驱动的多风电场并网系统振荡稳定性评估方法,利用深度学习和联合分布适配算法,离线建立等效系统的振荡稳定性评估模型,并泛化到实际系统中实现次同步振荡在线评估.文献[15]中提出一种基于深度迁移学习的风电场次同步振荡源定位方法,该方法首先在仿真系统中获取训练数据样本,然后运用卷积神经网络进行振荡源特征提取并训练定位模型,最后通过迁移学习将训练模型迁移到实际系统.文献[16]中提出一种基于数据-模型融合驱动的新能源场站宽频阻抗或导纳辨识方法,并对新能源并网系统的振荡稳定性进行在线评估.然而需要指出的是,上述文献的研究算例均是基于含少量风电机组的新能源系统,该类方法在大规模复杂新能源电力系统中的表现有待进一步研究.此外,获取足够可靠的数据样本也是目前数据驱动方法普遍面临的关键问题之一.

频域模态分析法^[17](frequency-domain modal analysis,FDMA)结合了特征值法在分析上的优势和阻抗法在建模上的优势,建立各设备和场站的阻抗或导纳模型,根据实际系统拓扑构建系统的频域网络模型;通过求解回路阻抗矩阵或节点导纳矩阵行列式的零点来评估系统的振荡稳定性,并基于参与因子等信息定位系统的薄弱环节、振荡源及振荡传播路径等.该方法不对系统做任何划分或等效,能够保留系统的全部元件和拓扑信息,从而可以获得系统全部振荡模式,既适用于点对点或集中汇集拓扑,也适用于环状拓扑.文献[18-19]中利用FDMA分析多双馈风电场经串补并网系统的次同步谐振稳定性,基于节点或支路的参与因子和可观度获取了振荡路径和扰动源信息.文献[20]中针对交直流混联系统,提出一种结合FDMA和对角占优理论的振荡分析与评估方法,能够准确刻画广域或局域振荡特性,并以风电场经四端柔直送出系统为例验证了所提方法的有效性.文献[21]中将系统划分为有源节点和无源网络,采用基于环路增益矩阵的奈奎斯特稳定性判据进行振荡稳定性评估,并利用参与因子分析定位振荡源,最后以单个风电场接入戴维南等值电网为例对所提方法的有效性进行验证.上述文献中,交流电网采用戴维南等值电源,未考虑常规同步机电源、输电线路N-1运行等因素.随着新能源并网比例增加,系统振荡风险加剧,因此新能源接入前有必要充分评估新能源接入容量以及电网运行方式变化对系统振荡稳定性的影响.

本文利用频域模态分析法研究典型新能源电力系统的宽频振荡稳定性.首先,建立同步发电机(synchronizing generator, SG)、风电场、光伏电站、静止无功发生器(static var generator, SVG)、储能、输电线等的宽频阻抗模型,基于关键设备或场站的阻抗模型和系统拓扑结构,构建新能源电力系统的频域网络模型.然后,利用节点导纳矩阵模型评估系统振荡稳定性,并基于节点参与因子定位系统的薄弱环节.最后,基于PSCAD/EMTDC软件搭建该实际系统的时域仿真模型,仿真验证理论分析的正确性.

1 新能源电力系统振荡稳定性评估

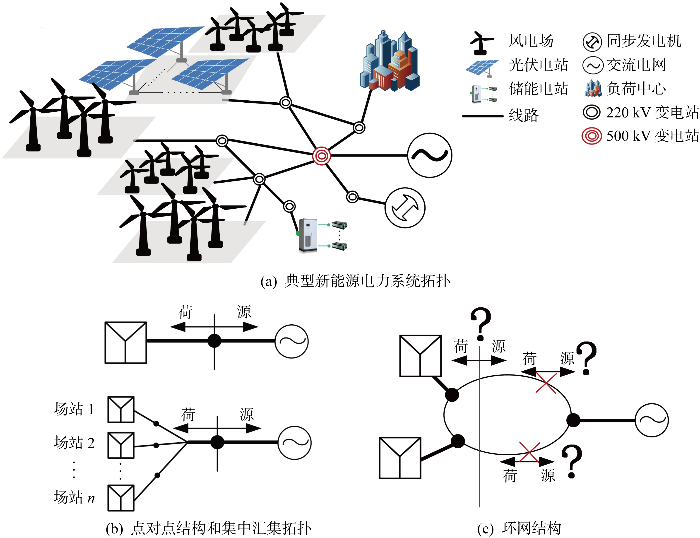
典型的新能源电力系统如图1(a)所示,主要包括同步发电机、风电场、光伏电站、SVG、储能、输电线路、负荷等关键设备.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 新能源电力系统拓扑

Fig.1 Topology of new energy system

对于一个点对点或者集中汇集并网的新能源电力系统,如图1(b)所示,可以利用奈奎斯特稳定性判据评估系统稳定性并获取系统潜在的振荡频率;在潜在振荡频率处,根据无源性理论^[22],获取各个场站的阻抗实部,根据电阻的大小进行薄弱点定位.对于图1(c)所示的呈现环状拓扑特性的新能源电力系统,各个场站之间的连接对稳定性的影响不可忽略,很难划分为两个独立的源/荷子系统,面临分割点难以确定的问题.对于这类拓扑结构,可以采用频域模态分析法进行振荡稳定性评估,具体步骤如下:①建立新能源电力系统中各关键装备和场站的频域阻抗或导纳模型;②根据新能源电力系统的实际拓扑,构建系统的频域网络模型,进而获取系统的节点导纳矩阵模型或回路阻抗矩阵模型;③求解节点导纳矩阵模型或回路阻抗矩阵模型行列式的零点,评估系统是否存在弱或负阻尼模态;④若不存在弱或负阻尼模态,则间隔时间t后,再次进行振荡稳定性评估;如果存在弱或负阻尼模态,则计算弱/负阻尼模态的节点参与因子矩阵;⑤根据参与因子矩阵定位系统的薄弱点或振荡源.

另外,对于图1(b)所示的多场站集中汇集拓扑,同样可以建立其回路阻抗或节点导纳矩阵模型,利用频域模态分析法评估系统稳定性并定位薄弱点或振荡源.频域模态分析法的基本原理^[20]如下.

若已知系统的节点导纳矩阵Y_node(s),则系统的振荡稳定性可由节点导纳矩阵Y_node(s)行列式的零点进行评估,即

(1)det(Y_node(s))=0

式中:s为拉普拉斯算子.当零点位于左半平面时,阻尼比较弱的模态称为弱阻尼模态;当出现右半平面零点时,表明系统失稳,对应的模态λ=σ±jω称为振荡模态,其中λ为特征值,σ为特征值实部,ω为特征值虚部,该振荡模态的阻尼比和振荡频率计算方式分别为

(2)$\xi=-\frac{\sigma}{\sqrt{\sigma^{2}+\omega^{2}}}, \quad f=\frac{\omega}{2 \pi}$

将弱阻尼或振荡模态代入节点导纳矩阵Y_node(s),并将该矩阵进行对角化,如下:

(3)Y_node(s)=LΛR

式中:L=[L₁L₂ … L_n]^T为左特征向量矩阵;Λ=[diag(λ₁, λ₂, …, λ_i)]为特征值构成的对角矩阵;R=[R₁R₂ … R_n]为右特征向量矩阵.

参与因子由状态空间矩阵的左和右特征向量相乘得到,量度了状态量与模态量的关联程度,用来衡量各节点或支路与振荡模式的关联程度^[19].频域网络的参与因子矩阵如下:

(4)P_m=L_i·R_i

式中:L_i为左特征向量矩阵的第i个列向量;R_i为右特征向量矩阵第i个行向量;P_m的每个对角元素刻画了节点对模式的参与程度,代表某节点注入的电流对该节点电压的激励,反映节点对振荡模式的参与度,激励出的节点电压反映振荡模式对节点的影响.因此,节点i的参与因子C_y(i)便可由P_m的每个对角元素归一化后进行表示,即

(5)C_y(i)=

\frac{|P_{m} (i, i)|}{\sum_{j = 1}^{n} |P_{m} (j, j)|}

式中:j为其余节点.

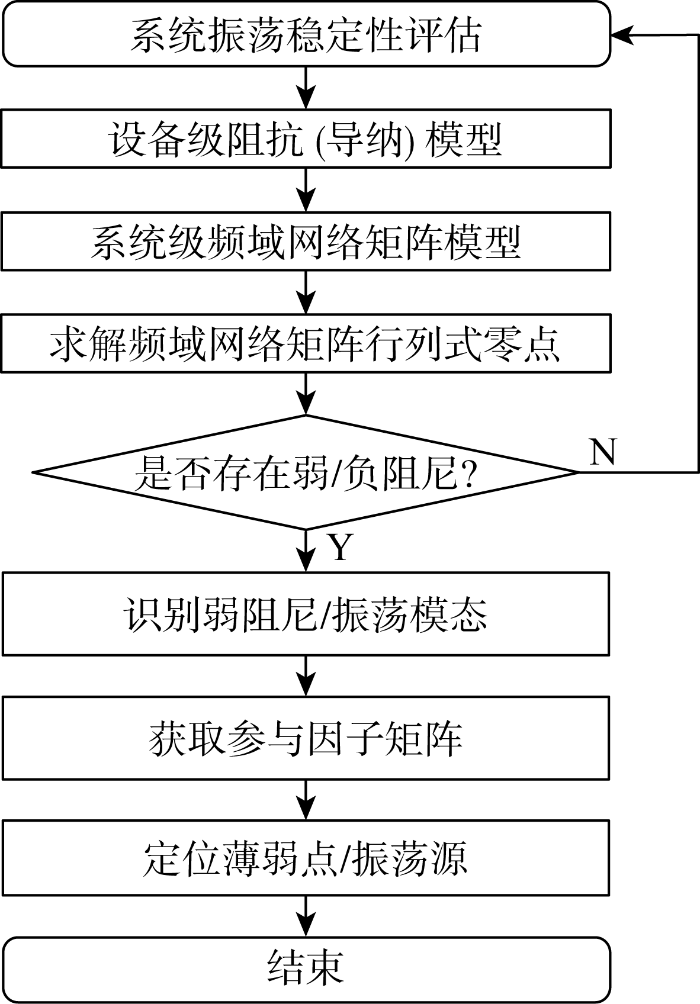
利用频域模态分析法评估新能源电力系统振荡稳定性的具体步骤如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 频域模态分析法流程图

Fig.2 Flow chart of frequency domain modal analysis method

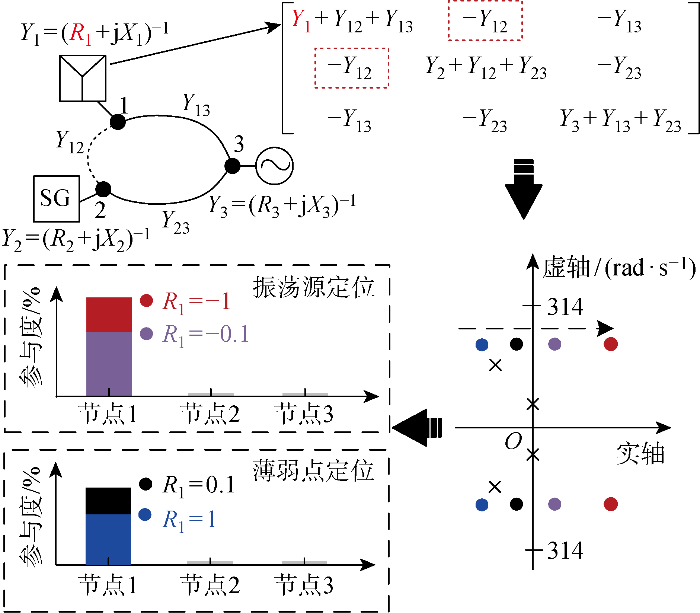
以图3所示的三节点互联系统为例,图中:节点1(Y₁)为一个存在振荡失稳风险的风电场,其导纳实部由负电阻R₁代替;节点2(Y₂)为同步发电机,失稳风险较低;Y₃为交流电网导纳;R₂、R₃分别为节点2、3电阻;X₁~X₃分别为3个节点电抗;Y₁₃表示风电场1与交流电网间的传输线或变压器导纳;Y₂₃表示同步发电机与交流电网间的传输线或变压器导纳;Y₁₂代表风电场与同步发电机间的线路导纳.通过构建三节点互联系统的节点导纳矩阵并求解其行列式零点,可以发现系统存在一对右半平面零点,无论Y₁₂是否等于0,该零点与风电场Y₁强相关.风电场Y₁的负电阻减小,系统右半平面零点左移,Y₁的实部变为正后,系统不存在右半平面零点,Y₁的实部增加,零点继续向左移动.若Y₁₂=0,则系统为集中汇集拓扑,结合奈奎斯特稳定性判据和无源性理论^[23],风电场1的阻抗实部较小或者为负,为系统的薄弱点或振荡源,与频域模态分析法得到的结果相同.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 三节点互联系统振荡稳定性评估

Fig.3 Evaluation of oscillatory stability of three-node interconnection system

2 关键设备的阻抗或导纳建模

通过获取每个节点的阻抗或导纳模型,根据系统实际拓扑构建系统的频域网络模型,采用频域模态分析法可以对不同拓扑的新能源电力系统进行振荡稳定性评估.因此,准确建立关键设备或场站的阻抗或导纳模型是实施频域模态分析法的关键,下面给出新能源电力系统中各关键设备和场站宽频阻抗或导纳的建模过程.

2.1 同步机的阻抗或导纳建模

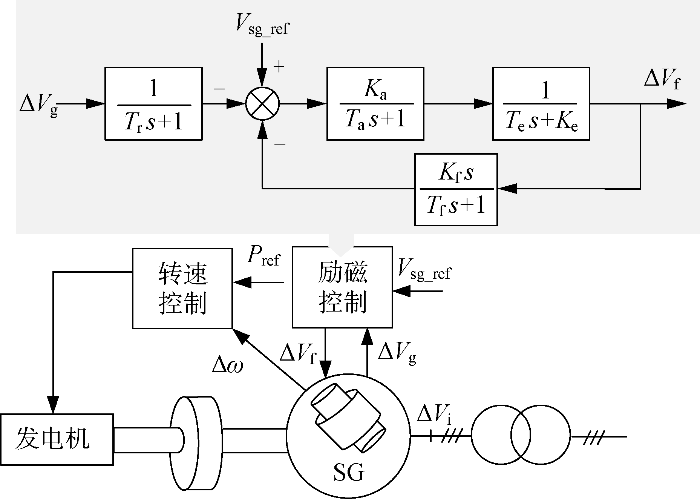
同步发电机是新能源电力系统的常规电源,用于给电网提供电压支撑.本文的火电、水电和核电机组均采用一对极的同步发电机等效,采用励磁控制器调节同步发电机端电压,采用恒转速控制调节输出功率,拓扑与控制结构如图4所示.图中:ΔV_g、ΔV_f分别为同步发电机的机端电压与励磁电压;T_r为滤波时间常数;K_a为放大器增益;T_a为放大器时间常数;T_e为延迟时间常数;K_e为延迟环节系数;K_f为阻尼系数;T_f为阻尼时间常数; Δω为转子角频率;V_{sg_ref}为电压参考值;P_ref为功率参考值;ΔV_i为发电机出口侧电压.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 同步发电机拓扑与励磁控制

Fig.4 Topology and excitation control of SG

同步发电机的机端电压ΔV_i_dq与空载电动势ΔE_dq之间关系如下:

(6)$\begin{array}{l} \Delta E_{d q}-\Delta V_{\mathrm{i} d q}=\Delta I_{\mathrm{i} d q} \boldsymbol{G}_{\mathrm{L}}+\Delta \omega \boldsymbol{G}_{\omega} \\ \boldsymbol{G}_{\mathrm{L}}=\left[\begin{array}{cc} R_{\mathrm{sg}}+s L_{\mathrm{sg}} & -\omega_{0} L_{\mathrm{sg}} \\ \omega_{0} L_{\mathrm{sg}} & R_{\mathrm{sg}}+s L_{\mathrm{sg}} \end{array}\right] \\ \boldsymbol{G}_{\omega}=\left[\begin{array}{c} -L_{\mathrm{sg}} I_{q 0} \\ L_{\mathrm{sg}} I_{d 0} \end{array}\right] \end{array}$

式中:R_sg为定子电枢回路等效电阻;L_sg为定子电枢电感;ω₀为基频角频率;ΔI_i_dq为定子电流;I_d₀和I_q₀为定子电流稳态值;下标dq表示dq轴分量.

由励磁控制可知,同步发电机的励磁电压ΔV_f与机端电压ΔV_g关系如下:

(7)$\begin{aligned} \Delta V_{\mathrm{f}}= & G_{\mathrm{e}} \Delta V_{\mathrm{g}} \\ G_{\mathrm{e}}= & -\frac{1}{T_{\mathrm{r}} s+1} \times \\ & \frac{K_{\mathrm{a}}\left(T_{\mathrm{f}} s+1\right)}{\left(T_{\mathrm{a}} s+1\right)\left(T_{\mathrm{e}} s+K_{\mathrm{e}}\right)\left(T_{\mathrm{f}} s+1\right)+K_{\mathrm{a}} K_{\mathrm{f}} s} \end{aligned}$

由ΔV_g=V_i_d₀ΔV_i_d+V_i_q₀ΔV_i_q可得,ΔV_f与同步发电机的端电压ΔV_i_d、ΔV_i_q的关系如下:

(8)ΔV_f=G_eV_i_d₀ΔV_i_d+G_eV_i_q₀ΔV_i_q

式中:V_i_d₀、V_i_q₀为机端电压稳态值.

根据励磁电压与空载电动势成正比,设比例系数为1,可得励磁电压与空载电动势的关系如下式所示:

(9)

\begin{array}{l} Δ E_{d} = Δ V_{f} = G_{e} V_{i d 0} Δ V_{i d} + G_{e} V_{i q 0} Δ V_{i q} \\ Δ E_{q} = 0 \end{array}\}

(10)ΔP_e=-ω₀(Js+D)Δω

式中:ΔP_e为发电机输出的有功功率,且

ΔP_e=[I_i_d₀I_i_q₀][ΔV_i_d ΔV_i_q]^T+ [V_i_d₀V_i_q₀] [ΔI_i_d ΔI_i_q]^T

J为转动惯量;D为阻尼系数.根据式(10)所示的同步发电机转子运动方程,线性化后可得转子角频率为

(11)$ \begin{array}{c} \Delta \omega=\boldsymbol{G}_{\omega \mathrm{u}}\left[\begin{array}{c} \Delta V_{\mathrm{i} d} \\ \Delta V_{\mathrm{i} q} \end{array}\right]+\boldsymbol{G}_{\omega \mathrm{i}}\left[\begin{array}{c} \Delta I_{\mathrm{i} d} \\ \Delta I_{\mathrm{i} q} \end{array}\right] \\ \boldsymbol{G}_{\omega \mathrm{u}}=-\frac{\left[\begin{array}{ll} I_{\mathrm{i} d 0} & I_{\mathrm{i} q 0} \end{array}\right]}{\omega_{0}(J s+D)}, \boldsymbol{G}_{\omega \mathrm{i}}=-\frac{\left[\begin{array}{ll} V_{\mathrm{i} d 0} & V_{\mathrm{i} q 0} \end{array}\right]}{\omega_{0}(J s+D)} \end{array} $

联立式(6)、(9)、(11)可得同步发电机的导纳模型如下:

(12)$\begin{array}{l} \boldsymbol{Y}_{d q \mathrm{SG}}= \left[\left(\boldsymbol{G}_{\mathrm{ev}}-\boldsymbol{I}-\boldsymbol{G}_{\omega} \boldsymbol{G}_{\omega \mathrm{u}}\right)^{-1}\left(\boldsymbol{G}_{\mathrm{L}}+\boldsymbol{G}_{\omega} \boldsymbol{G}_{\omega \mathrm{i}}\right)\right]^{-1} \\ \boldsymbol{G}_{\mathrm{ev}}=\left[\begin{array}{cc} G_{\mathrm{e}} V_{\mathrm{i} d 0} & G_{\mathrm{e}} V_{\mathrm{i} q 0} \\ 0 & 0 \end{array}\right] \end{array}$

式中:I为单位矩阵.

2.2 新能源机组/场站的宽频阻抗建模

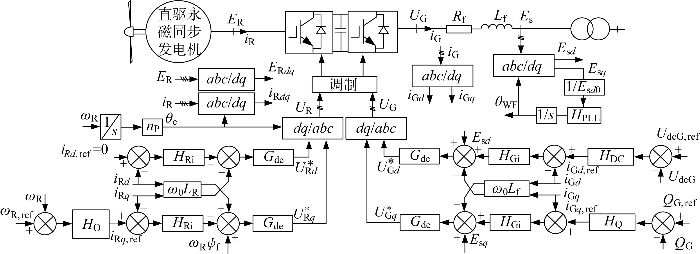
新能源场站主要包括风电场、光伏电站、SVG、储能设备.其中风电场主要由直驱全功率风电机组构成,具体主电路以及控制结构如图5所示.直驱风电机组由风力机(wind turbine generator, WTG)、直驱永磁同步发电机(directly driven permanent magnet synchronous generator, DDPMSG)、机侧变流器和网侧变流器等组成^[22],其中网侧逆变器采用定直流电压和无功控制,机侧变流器采用转速控制.图中:E_R、i_R分别为直驱永磁同步发电机交流侧电压与电流;L_R为绕组电感;ψ_f为磁链;ω_R为转子角速度;n_p为极对数;G_de为控制延时;H_O、H_Ri分别为机侧换流器外环与内环的比例-积分(PI)控制; $U_{R d}^{*}$ 、 $U_{R q}^{*}$ 为机侧变流器调制电压;U_G、i_G分别为网侧换流器出口侧电压与电流;E_s为网侧换流器公共连接点电压;R_f、L_f分别为网侧换流器交流侧电阻与滤波电感;U_dcG为网侧换流器定直流电压控制;Q_G为网侧换流器定无功功率控制;H_DC、H_Q、H_Gi为网侧换流器的PI控制, 其中H_DC为定直流电压控制的PI参数,

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 风电机组控制结构

Fig.5 Topology and control of DDPMSG-based WTG

H_Q为无功功率控制的PI参数,H_Gi为电流内环的PI参数;H_PLL为锁相环PI参数; $U_{G d}^{*}$ 、 $U_{G q}^{*}$ 为网侧换流器调制电压;U_R为机侧变流器调制电压;θ_WF为网侧变流器锁相环输出的角度;E_s_d₀为公共连接点电压在d轴的分量;θ_e为机侧park变化的角度;下标ref表示相应变量参考值;abc表示abc三相.

光伏发电单元和SVG的主电路和控制结构与直驱全功率风电机组的网侧逆变器类似,采用定直流电压和无功控制,具体主电路以及控制结构如附录图A1所示.储能设备外环采用有功和无功功率控制,具体主电路和控制结构如附录图A2所示.为简化分析,每个新能源场站采用单机聚合模型表示.

如图6所示,由于锁相环的作用,在所研究的变流器子系统中存在电气系统和控制系统坐标系,分别以c和s为上标,相角差的表达式如下:

(13)$\begin{array}{l} \Delta \theta_{\mathrm{WF}}=G_{\mathrm{PLL}}(s) \Delta E_{\mathrm{s} q}^{\mathrm{s}} \\ G_{\mathrm{PLL}}(s)=\frac{1}{E_{\mathrm{s} d 0}^{\mathrm{s}}} \frac{H_{\mathrm{PLL}}}{H_{\mathrm{PLL}}+s}, H_{\mathrm{PLL}}=k_{\mathrm{pPLL}}+\frac{k_{\mathrm{PLL}}}{s} \end{array} $

式中:G_PLL(s)为锁相环的闭环传递函数;k_pPLL为锁相环比例系数;k_iPLL为锁相环积分系数.两个坐标系下电气量的关系为

(14)

[\begin{array}{l} Δ E_{s d}^{c} \\ Δ E_{s q}^{c} \end{array}]

[\begin{array}{l} Δ E_{s d}^{s} + E_{s q 0}^{s} Δ θ_{W F} \\ - E_{s d 0}^{s} Δ θ_{W F} + Δ E_{s q}^{s} \end{array}]

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 控制和电气坐标系示意图

Fig.6 Coordinates of control system and electrical system

将式(13)代入式(14)可得锁相环影响下的电压表达式,即

(15)

[\begin{array}{l} Δ E_{s d}^{c} \\ Δ E_{s q}^{c} \end{array}]

[\begin{array}{l} Δ E_{s d}^{s} \\ Δ E_{s q}^{s} \end{array}]

[\begin{array}{l} 0 & i_{G q 0}^{s} G_{P L L} (s) \\ 0 & - i_{G d 0}^{s} G_{P L L} (s) \end{array}] [\begin{array}{l} Δ E_{s d}^{s} \\ Δ E_{s q}^{s} \end{array}]

式中: $i_{G q 0}^{s}$ 、 $i_{G d 0}^{s}$ 为网侧换流器出口侧电流稳态值.

同理,电流表达式为

(16)

[\begin{array}{l} Δ i_{G d}^{c} \\ Δ i_{G q}^{c} \end{array}]

[\begin{array}{l} Δ i_{G d}^{s} \\ Δ i_{G q}^{s} \end{array}]

[\begin{array}{l} 0 & i_{G q 0}^{s} G_{P L L} (s) \\ 0 & - i_{G d 0}^{s} G_{P L L} (s) \end{array}] [\begin{array}{l} Δ i_{G d}^{s} \\ Δ i_{G q}^{s} \end{array}]

交流侧并网点电压E_s_dq与逆变器出口侧电压U_G_dq的关系如下:

(17)$\begin{array}{l} {\left[\begin{array}{c} \Delta U_{\mathrm{G} d}^{\mathrm{s}} \\ \Delta U_{\mathrm{G} q}^{\mathrm{s}} \end{array}\right]=\left[\begin{array}{c} \Delta E_{\mathrm{s} d}^{\mathrm{s}} \\ \Delta E_{\mathrm{sq}}^{\mathrm{s}} \end{array}\right]+\boldsymbol{Z}_{d q \mathrm{f}}\left[\begin{array}{c} \Delta i_{\mathrm{G} d}^{\mathrm{s}} \\ \Delta i_{\mathrm{G} q}^{\mathrm{s}} \end{array}\right]} \\ \boldsymbol{Z}_{d q \mathrm{f}}=\left[\begin{array}{cc} R_{\mathrm{f}}+s L_{\mathrm{f}} & -\omega_{0} L_{\mathrm{f}} \\ \omega_{0} L_{\mathrm{f}} & R_{\mathrm{f}}+s L_{\mathrm{f}} \end{array}\right] \end{array} $

图5中仅考虑电流内环控制与锁相环的数学模型,即

(18)$\begin{array}{l} H_{\mathrm{Gi}}\left[\begin{array}{cc} I_{d}^{*}-\Delta i_{\mathrm{G} d}^{\mathrm{c}} \\ I_{q}^{*}-\Delta i_{\mathrm{G} q}^{\mathrm{c}} \end{array}\right]+k_{\mathrm{vf}} \mathrm{e}^{-s T_{\mathrm{d}}}\left[\begin{array}{c} \Delta E_{\mathrm{s} d}^{\mathrm{c}} \\ \Delta E_{\mathrm{s} q}^{\mathrm{c}} \end{array}\right]+ \\ k_{\mathrm{dec}}\left[\begin{array}{cc} 0 & -\omega_{0} L_{\mathrm{f}} \mathrm{e}^{-s T_{\mathrm{d}}} \\ \omega_{0} L_{\mathrm{f}} \mathrm{e}^{-s T_{\mathrm{d}}} & 0 \end{array}\right]\left[\begin{array}{c} \Delta i_{\mathrm{G} d}^{\mathrm{s}} \\ \Delta i_{\mathrm{G} q}^{\mathrm{s}} \end{array}\right]= \\ +\left[\begin{array}{c} \Delta U_{\mathrm{G} d}^{\mathrm{c}} \\ \Delta U_{\mathrm{G} q}^{\mathrm{c}} \end{array}\right] \end{array} $

式中:k_vf代表是否考虑电压前馈;k_dec代表是否考虑解耦项系数; $e^{- s T_{d}}$ 为控制延时函数,T_d为控制延时; $I_{d}^{*}$ 、 $I_{q}^{*}$ 为电流在dq轴的参考值.

对式(18)进行小信号线性化,并代入式(15)~(17),可得电压与电流的关系如下:

(19)$\begin{aligned} -\boldsymbol{A} & {\left[\begin{array}{c} \Delta i_{\mathrm{G} d}^{\mathrm{s}} \\ \Delta i_{\mathrm{G} q}^{\mathrm{s}} \end{array}\right]=\boldsymbol{B}\left[\begin{array}{c} \Delta E_{\mathrm{s} d}^{\mathrm{s}} \\ \Delta E_{\mathrm{sq}}^{\mathrm{s}} \end{array}\right] } \\ \boldsymbol{A}= & {\left[\boldsymbol{H}_{\mathrm{I}}+\boldsymbol{Z}_{d q \mathrm{f}}-k_{\mathrm{dec}} \boldsymbol{D}_{\mathrm{dec}}\right] } \\ \boldsymbol{B}= & {\left[\boldsymbol{I}+\boldsymbol{H}_{\mathrm{I}} \boldsymbol{G}_{\mathrm{IPLL}}+\boldsymbol{G}_{\mathrm{VPLL}}-\right.} \\ & \left.k_{\mathrm{dec}} \boldsymbol{G}_{\mathrm{IPLL}}-k_{\mathrm{vf}}\left(\boldsymbol{I}+\boldsymbol{G}_{\mathrm{VPLLx}}\right)\right] \end{aligned}$

由此可得仅含电流内环控制和锁相环的逆变器交流侧阻抗或导纳如下:

(20)

\begin{array}{l} Y_{d q (2 \times 2)} = A^{- 1} B \\ Z_{d q (2 \times 2)} = B^{- 1} A \end{array}\}

(21)

\begin{array}{l} H_{I} = [\begin{array}{l} (K_{p i} + \frac{K_{i i}}{s}) e^{- s T_{d}} & 0 \\ 0 & (K_{p i} + \frac{K_{i i}}{s}) e^{- s T_{d}} \end{array}] \\ G_{I P L L} = [\begin{array}{l} 0 & i_{G q 0}^{s} G_{P L L} (s) \\ 0 & - i_{G d 0}^{s} G_{P L L} (s) \end{array}] \\ G_{V P L L} = [\begin{array}{l} 0 & U_{G q 0}^{s} G_{P L L} (s) \\ 0 & - U_{G d 0}^{s} G_{P L L} (s) \end{array}] \\ G_{V P L L x} = [\begin{array}{l} 0 & E_{s q 0}^{s} G_{P L L} (s) \\ 0 & - E_{s d 0}^{s} G_{P L L} (s) \end{array}] \\ D_{d e c} = [\begin{array}{l} 0 & - ω_{0} L_{f} \\ ω_{0} L_{f} & 0 \end{array}] \end{array}\}

式中:K_pi、K_ii分别为电流内环控制的比例与积分系数;下标“0”表示电压电流的稳态值.

对于直驱风电机组,忽略机侧动态的影响,网侧逆变器直流电压外环及无功功率外环的数学模型为

(22)

[\begin{array}{l} I_{d}^{*} \\ I_{q}^{*} \end{array}]

[\begin{array}{l} H_{D C} Δ V_{d c} \\ H_{Q} Δ Q \end{array}]

=H_DCΔV_dc+V_iQ

[\begin{array}{l} Δ {i^{s}}_{d} \\ Δ {i^{s}}_{q} \end{array}]

+I_Q

[\begin{array}{l} Δ E_{s d}^{s} \\ Δ E_{s q}^{s} \end{array}]

(23)

\begin{array}{l} H_{D C} = [\begin{array}{l} H_{D C} \\ 0 \end{array}] \\ V_{i Q} = \frac{3}{2} H_{Q} [\begin{array}{l} - 1 & 0 \\ 0 & 1 \end{array}] [\begin{array}{l} E_{s d 0}^{s} & E_{s q 0}^{s} \\ E_{s q 0}^{s} & - E_{s d 0}^{s} \end{array}] \\ I_{Q} = \frac{3}{2} H_{Q} [\begin{array}{l} - 1 & 0 \\ 0 & 1 \end{array}] [\begin{array}{l} i_{G d 0}^{s} & i_{G q 0}^{s} \\ - i_{G q 0}^{s} & i_{G d 0}^{s} \end{array}] \end{array}\}

式中:ΔV_dc为直流电压的小信号分量;ΔQ为无功功率的小信号分量.

将式(22)代入式(18)并联立式(19)即可得到直驱风电机组网侧逆变器的交流侧阻抗模型Z_dq_WF或导纳模型Y_dq_WF.光伏发电单元和SVG的交流侧阻抗或导纳建模与直驱风电机组类似,光伏发电单元的交流侧阻抗为Z_dq_PV,导纳为Y_dq_PV,SVG的交流侧阻抗为Z_dq_SVG,导纳为Y_dq_SVG.

储能设备外环采用有功和无功功率控制,如下:

(24)

[\begin{array}{l} I_{d, r e f} \\ I_{q, r e f} \end{array}]

[\begin{array}{l} k_{P p} + \frac{k_{P i}}{s} \\ k_{Q p} + \frac{k_{Q i}}{s} \end{array}] [\begin{array}{l} P_{r e f} - P \\ Q_{r e f} - Q \end{array}]

(25)

[\begin{array}{l} I_{d, r e f} \\ I_{q, r e f} \end{array}]

=-1.5

[\begin{array}{l} k_{P p} + \frac{k_{P i}}{s} \\ k_{Q p} + \frac{k_{Q i}}{s} \end{array}]

([\begin{array}{l} V_{d 0} & V_{q 0} \\ V_{q 0} & - V_{d 0} \end{array}] [\begin{array}{l} Δ {i^{s}}_{d} \\ Δ {i^{s}}_{q} \end{array}] + [\begin{array}{l} I_{d 0} & I_{q 0} \\ - I_{q 0} & I_{d 0} \end{array}] [\begin{array}{l} Δ {u^{s}}_{d} \\ Δ {u^{s}}_{q} \end{array}])

式中:有功功率P和无功功率Q可以根据式(10)得到;k_Pp、k_Pi分别为有功外环PI控制的比例和积分参数;k_Qp、k_Qi分别为无功外环PI控制的比例和积分参数.

将式(25)代入式(18)并联立式(19)即可得到交流侧阻抗Z_dq_ES或导纳为Y_dq_ES.

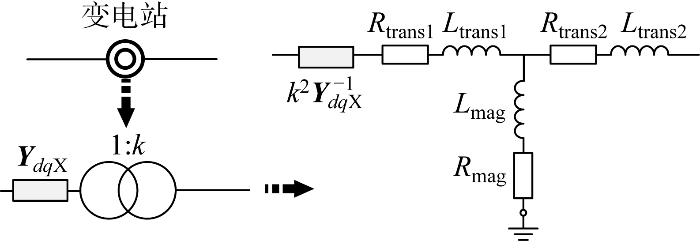
2.3 变电站阻抗建模

变电站主要用于连接不同节点以及传输线,其结构如图7所示.将变电站低压侧阻抗 $Y_{d q X}^{- 1}$ 等效至高压侧,变电站中的变压器采用T型等效电路代替,等效后的导纳或阻抗如下:

(26)$ \begin{aligned} \boldsymbol{Y}_{d q t}= & {\left[\left[\left(k^{2}\left(\boldsymbol{Y}_{d q \mathrm{X}}^{-1}+\boldsymbol{Z}_{\text {trans1 }}\right)\right)^{-1}+\boldsymbol{Z}_{\text {mag }}^{-1}\right]^{-1}+\right.} \\ & \left.\boldsymbol{Z}_{\text {trans2 }}\right]^{-1} \\ \boldsymbol{Z}_{\text {trans1 }}= & {\left[\begin{array}{ccc} R_{\text {trans1 }}+s L_{\text {trans1 }} & -\omega_{0} L_{\text {trans1 }} & \\ \omega_{0} L_{\text {trans1 }} & R_{\text {trans1 }}+s L_{\text {trans1 }} & \end{array}\right] } \\ \boldsymbol{Z}_{\text {trans2 }}= & {\left[\begin{array}{ccc} R_{\text {trans2 }}+s L_{\text {trans2 }} & -\omega_{0} L_{\text {trans2 }} & \\ \omega_{0} L_{\text {trans2 }} & R_{\text {trans } 2}+s L_{\text {trans2 }} & \end{array}\right] } \\ \boldsymbol{Z}_{\text {mag }}= & {\left[\begin{array}{ccc} R_{\text {mag }}+s L_{\text {mag }} & -\omega_{0} L_{\text {mag }} & \\ \omega_{0} L_{\text {mag }} & R_{\text {mag }}+s L_{\text {mag }} & \end{array}\right] } \end{aligned}$

式中:k为变压器的变比;R_trans1、L_trans1分别为低压侧电阻、电感值;R_trans2、L_trans2分别为高压侧电阻、电感值;R_mag、L_mag分别为变压器互感支路电阻及电感值.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 变电站拓扑

Fig.7 Topology of transformer

2.4 传输线的阻抗建模

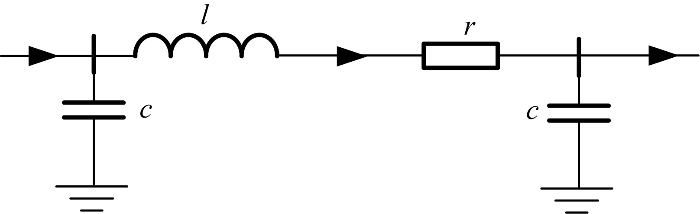
输电线路采用若干个 II 型电路等效,单个 II 型等效电路结构及数学模型如图8,公式如下:

(27)

\begin{array}{l} Z_{d q l} (s) = [\begin{array}{l} r + s l & - ω_{0} l \\ ω_{0} l & r + s l \end{array}] \\ Y_{d q c} (s) = [\begin{array}{l} s c & - ω_{0} c \\ ω_{0} c & s c \end{array}] \end{array}\}

式中:Z_dql、Y_dqc、r、l、c分别为单个II型电路的阻抗、导纳、电阻、电感及对地电容.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 II型等效电路

Fig.8 II-Type equivalent circuit

根据图8可得输电线路的频域阻抗或导纳模型:

(28)Z_dq_,0(s)=

{(\frac{1}{2} Y_{d q c} (s))}^{- 1}

+Z_dql(s)

(29)Y_dq_,_m_-1(s)=

Z_{d q, m - 1}^{- 1}

(s)+

\frac{1}{2}

Y_dqc(s)

(30)Y_dq_,_m(s)=[(Y_dq_,_m_-1(s))^-1+Z_dql(s)]^-1

(31)

\begin{array}{l} Y_{d q, n} (s) = (Y_{d q, n - 1} (s) + \frac{1}{2} Y_{d q c} (s)) \\ Z_{d q, n} (s) = (Y_{d q, n} {(s))}^{- 1} \end{array}\}

式中:Y_dq_,_n、Z_dq_,_n分别为第n个II型电路等效后的传输线阻抗或导纳模型;1≤m≤n-1.

3 案例分析

3.1 系统描述

以国内某局域新能源电力系统为例,其拓扑结构示意图如图9所示.其中3个500 kV汇集站分别命名为ZNY、ZCB、ZXG,两个风电场220 kV汇集站分别命名为ZQC和ZQJ,ZQJ连接的3个风电场分别命名为ZC1、ZC2、ZC4,ZXG连接的两个风电场分别命名为ZC3和ZC5,核电厂、火电厂和水电厂分别命名为ZCH、ZCN、ZSX,光伏电站命名为ZPV.该系统实际拓扑结构非常复杂,为简化理论分析,将该系统进行适当处理:①保留所有新能源场站及其所接入电网的三级断面;②保留所有500 kV变电站;③保留火电、核电和水电机组;④与新能源场站距离较远的220 kV变电站等效为阻抗或导纳;⑤220变电站下的负荷节点等效为阻抗或导纳;⑥将外部电网在500 kV连接点处进行单点等值.该系统含有6座新能源场站,其中1座500 MW光伏电站(ZPV)接入220 kV变电站ZQC,3座总容量 1 100 MW 的海上风电场(offshore wind Farm, OWF) #ZC1/2/4通过1级变电站接入220 kV变电站ZQJ,2座总容量 1 600 MW 的海上风电场#ZC3/5接入500 kV变电站ZXG.风电场含有6.25和10 MW直驱风电机组,每个风电场都配有一定容量的SVG或储能设备.常规电源由核电厂、水电厂和火电厂组成,额定容量分别为 1 200、200、4 000 MV·A,所有常规电源全部采用大开机方式运行,系统参数如附录B所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 国内某局域新能源电力系统拓扑结构

Fig.9 Topology of the new energy power system in China

3.2 系统建模

为了评估图9所示新能源电力系统的振荡稳定性,根据第2章关键设备的阻抗建模方法,首先建立关键装备和场站的频域阻抗模型;其次,进行大规模多互联系统频域模态分析时,利用旋转变换矩阵将各场站的参考坐标系转换至公共参考坐标系下进行频域建模^[24-25].定义公共参考坐标系d_s、q_s,d轴分量与交流电网电压V_s矢量重合,各个场站与外部电网电压的夹角Δθ_i如图10所示,转换关系如下:

(32)$\begin{array}{l} {\left[\begin{array}{c} f_{d}^{s i} \\ f_{q}^{s i} \end{array}\right]=\boldsymbol{T}_{\text {rot }}\left[\begin{array}{c} f_{d}^{i} \\ f_{q}^{i} \end{array}\right]} \\ \boldsymbol{T}_{\text {rot }}=\left[\begin{array}{cc} \cos \Delta \theta_{i} & -\sin \Delta \theta_{i} \\ \sin \Delta \theta_{i} & \cos \Delta \theta_{i} \end{array}\right] \end{array}$

式中:T_rot为旋转矩阵;矩阵 $[\begin{array}{l} f_{d}^{i} \\ f_{q}^{i} \end{array}]$ 代表各场站的参考坐标系下的变量;矩阵 $[\begin{array}{l} f_{d}^{s i} \\ f_{q}^{s i} \end{array}]$ 代表公共参考坐标系下的变量.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 各场站坐标系与公共坐标系的关系

Fig.10 Relationship between coordinate system of each station and PCC

某场站阻抗( $Z_{n}^{x}$ )或导纳( $Y_{n}^{x}$ )转换至公共参考坐标系后如下式所示:

(33)

{Z^{s}}_{y}

=T_rot

Z_{y}^{x} T_{r o t}^{- 1}

{Y^{s}}_{n}

=T_rot

Y_{y}^{x} T_{r o t}^{- 1}

式中:x代表某新能源场站,x=1, 2, …, y.最后,根据图9的拓扑构建系统的频域网络模型如图11所示,图中数字代表节点.根据图11的频域网络模型,建立系统的节点导纳矩阵模型,如下:

(34)Y_node=

A_{S}^{T}

Y_ZA_S

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 新能源电力系统频域网络模型

Fig.11 Frequency-domain network model of new energy power system

矩阵A_S代表实际拓扑之间的关联关系,具体为

(35)A_S=

[\begin{array}{l} I_{N (32 \times 32)} & 0_{32 \times 32} \\ A_{Z L (36 \times 32)} \end{array}]

式中:I_N(32×32)代表32阶单位矩阵;0_32×32代表零矩阵;A_ZL(36×32)代表各变电站之间的关联关系,即

(36)$\boldsymbol{A}_{\mathrm{ZL}(36 \times 32)}=\begin{vmatrix} I_{2\times 2} & & & & & & & & & & & & & -I_{2\times 2} & & \\ & I_{2\times 2}& & & & & & & & & & & & & -I_{2\times 2}& \\ & & I_{2\times 2}& & & & & & & & & -I_{2\times 2} & & & & \\ & & & I_{2\times 2}& & & & & & & & & & & -I_{2\times 2}& \\ & & & & I_{2\times 2}& & & & & & & & -I_{2\times 2}& & & \\ & & & & & I_{2\times 2}& & & & & & & -I_{2\times 2}& & & \\ & & & & & & I_{2\times 2} & -I_{2\times 2}& & & & & & & & \\ & & & & & & I_{2\times 2}& & & -I_{2\times 2}& & & & & & \\ & & & & & & I_{2\times 2}& & & & -I_{2\times 2}& & & & & \\ & & & & & & I_{2\times 2}& & & & & -I_{2\times 2}& & & & \\ & & & & & & I_{2\times 2}& & & & & & -I_{2\times 2}& & & \\ & & & & & & I_{2\times 2}& & & & & & & & & -I_{2\times 2}\\ & & & & & & & I_{2\times 2} & -I_{2\times 2}& & & & & & & \\ & & & & & & & I_{2\times 2}& & -I_{2\times 2}& & & & & & \\ & & & & & & & I_{2\times 2}& & & & & & & & -I_{2\times 2}\\ & & & & & & & & & & & & & & & \\ & & & & & & & & & & & & I_{2\times 2} & -I_{2\times 2}& & \\ & & & & & & & & & & & & & I_{2\times 2}& -I_{2\times 2}& \end{vmatrix}$

式(34)中矩阵Y_Z代表各节点的导纳模型,即

(37)Y_Z=

{[Y_{N} (s) Y_{Z L} (s)]}_{68 \times 68}

(38)

\begin{array}{l} \begin{array}{l} Y_{N} (s) = & d i a g (Y_{11 (2 \times 2)}, Y_{22 (2 \times 2)}, \dots, \\ Y_{15 - 15 (2 \times 2)}, Y_{16 - 16 (2 \times 2)})_{32 \times 32} \end{array} \\ \begin{array}{l} Y_{Z L} (s) = & d i a g (Y_{1 - 14 (2 \times 2)}, Y_{2 - 15 (2 \times 2)}, Y_{3 - 12 (2 \times 2)}, \\ Y_{4 - 15 (2 \times 2)}, Y_{5 - 13 (2 \times 2)}, Y_{6 - 13 (2 \times 2)}, \\ Y_{7 - 8 (2 \times 2)}, Y_{8 - 9 (2 \times 2)}, Y_{8 - 11 (2 \times 2)}, \\ Y_{8 - 12 (2 \times 2)}, Y_{8 - 13 (2 \times 2)}, Y_{8 - 14 (2 \times 2)}, \\ Y_{8 - 16 (2 \times 2)}, Y_{9 - 10 (2 \times 2)}, Y_{9 - 11 (2 \times 2)}, \\ Y_{9 - 16 (2 \times 2)}, Y_{13 - 14 (2 \times 2)}, Y_{14 - 15 (2 \times 2)})_{36 \times 36} \end{array} \end{array}\}

式中:Y_N(s)为每个场站构成的节点导纳矩阵;Y_ZL为各个节点之间线路的导纳.矩阵Y_N中,Y_11(2×2)代表汇集站ZQJ的1#风电场ZC1的节点导纳模型,Y_22(2×2)代表汇集站ZQJ的2#风电场ZC2的节点导纳模型,Y_33(2×2)代表汇集站ZXG的3#风电场ZC3的节点导纳模型,Y_44(2×2)代表汇集站ZQJ的4#风电场ZC4的节点导纳模型,Y_55(2×2)代表汇集站ZXG的5#风电场ZC5的节点导纳模型,Y_66(2×2)代表光伏电站的节点导纳模型,Y_77(2×2)代表火电厂的节点导纳模型,Y_10-10(2×2)代表水电厂的节点导纳模型,Y_11-11(2×2)代表核电厂的节点导纳模型,Y_N中其余元素代表汇集站下的节点导纳模型.由于系统阶数较大,Y_node的具体形式不再给出.

3.3 振荡稳定性评估

(1) 风电场接入容量变化下系统振荡稳定性评估.变电站ZQJ所接入风电场1#、2#和4#的额定容量分别为400、300和400 MW,变电站ZXG所接入风电场3#和5#是规划中的两个海上风电场,额定容量均为800 MW.下文小开机方式运行表示变电站接入风电场额定容量的10%,半容量方式运行表示变电站接入风电场额定容量的50%,大开机方式运行表示风电场按照额定容量接入.本节设置光伏电站以小开机方式运行.

ZQJ所接入的风电场以小开机方式运行时,变电站ZXG所接入风电场的容量不同时系统特征值分布如图12所示.图中:工况一至三分别设置为ZXG风场小开机接入、半容量接入、大开机接入.由图可见,随着变电站ZXG接入风电场的容量增大,振荡模式由左半平面向右半平面移动,系统稳定裕度较低,变电站ZXG所接入风电场容量的临界值标幺值(p.u.)约为0.9,超过临界值系统会出现40 Hz的次同步和60 Hz的超同步振荡.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 变电站ZXG所接入风电场容量变化对系统振荡稳定性的影响

Fig.12 Oscillation stability with variation of OWF capacity in ZXG

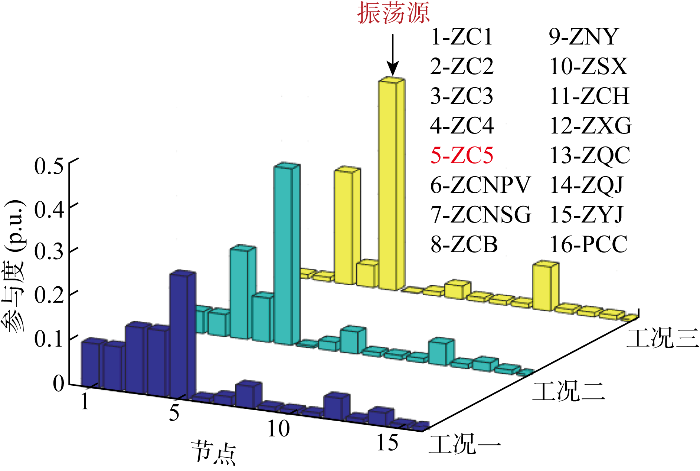
ZXG风电场接入容量变化时,系统振荡稳定性的评估结果如表1所示,各节点对该振荡模式的参与度如图13所示;PV、SG代表该节点的光伏和同步发电机.可以看出,ZQJ接入风资源较小时,ZXG-5#风电场对系统振荡稳定性影响较大,ZXG风电场以大开机方式运行时,系统出现负阻尼,如表1中红色数据所示.ZQJ风电场以半容量方式运行时,ZXG风电场接入容量变化对系统振荡稳定性影响如表2所示,ZXG风电场以大开机方式运行时,系统出现负阻尼,如表2中红色数据所示,此时ZXG能接入的风电场容量临界值的标幺值约为0.6. ZQJ风电场以大开机方式运行时,ZXG风电场接入容量变化对系统稳定性影响如表3所示,此时ZXG能接入的风电场容量临界值的标幺值约为0.3,ZXG风电场以半容量和大开机方式运行时,系统都出现负阻尼,如表3中红色数据所示.由表1~3中不同工况下每个模态的主导风电场结果可知,ZQJ风电场接入容量较大时,4#风电场对系统稳定性影响较大;ZXG风电场接入容量较大时,5#风电场对系统稳定性影响较大.

表1 ZQJ小开机方式运行时系统稳定性评估

Tab.1 System stability assessment of ZQJ with small capacity

工况	ZXG 风电场运行方式	振荡模态	阻尼比	振荡频率/ Hz	主导风电场
一	小开机	-2.9±j60.2	0.0420	9.58	ZXG-ZC5
二	半容量	-1.8±j59.4	0.0310	9.45	ZXG-ZC5
三	大开机	0.4±j60.4	-0.0066	9.61	ZXG-ZC5

新窗口打开| 下载CSV

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 ZXG风电场接入容量变化时主导节点

Fig.13 Dominant nodes with variation of operating mode of ZXG-OWFs

表2 ZQJ半容量方式运行时系统稳定评估

Tab.2 System stability assessment of ZQJ with half capacity

工况	ZXG 风电场运行方式	振荡模态	阻尼比	振荡频率/ Hz	主导风电场
一	小开机	-1.8±j59.6	0.0320	9.48	ZQJ-ZC4
二	半容量	-0.3±j58.4	0.0050	9.29	ZXG-ZC5
三	大开机	1.8±j57.4	-0.0320	9.14	ZXG-ZC5

新窗口打开| 下载CSV

表3 ZQJ大开机方式运行时系统稳定性评估

Tab.3 System stability assessment of ZQJ with full capacity

工况	ZXG 风电场运行方式	振荡模态	阻尼比	振荡频率/ Hz	主导风电场
一	小开机	-0.5±j58.4	0.0086	9.29	ZQJ-ZC4
二	半容量	2.1±j57.5	-0.0360	9.14	ZQJ-ZC4
三	大开机	6.5±j61.2	-0.1000	9.74	ZXG-ZC5

新窗口打开| 下载CSV

(2) N-1运行方式下系统振荡稳定性评估.如图14和表4所示,在ZQJ和ZXG所接入风电场半容量方式运行时,线路正常情况下,系统处于稳定状态,此时ZXG-5#风电场对稳定性影响较大;如果ZQJ与ZCB间的两回线路同时断线停电检修,ZQJ风电场所连线路的等效阻抗增加导致短路比降低,风电场运行状态不变的情况下振荡模式会从左半平面进入右半平面,存在振荡风险,如表4红色数据所示,此时ZQJ的4#风电场对系统稳定性影响较大.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 线路停电检修时系统特征根分布

Fig.14 System eigenvalue with maintenance of transmission line

表4 线路停电检修时系统稳定性评估

Tab.4 System stability assessment at maintenance of transmission lines

工况	线路状态	振荡模态	阻尼比	振荡频率/Hz	主导风电场
一	线路正常	-0.3±j58.4	0.00500	9.29	ZXG-ZC5
二	ZQJ-ZCB停电检修	0.19±j59.4	-0.00320	9.45	ZQJ-ZC4
三	ZQJ-ZCB停电检修ZQJ-ZQC单回线停电检修	0.53±j58.6	-0.00904	9.32	ZQJ-ZC4

新窗口打开| 下载CSV

进一步地,如果ZQJ与ZQC单回线路也停电检修,ZQJ的4#风电场会进一步削弱系统稳定性,风电场接入容量的临界值进一步降低,负阻尼进一步恶化,如表4红色数据所示,振荡风险持续增加.ZQJ和ZXG风电场采用半容量方式,线路停电检修情况下,对系统振荡稳定性影响较大的风电场如图15所示.

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 线路停电检修时主导节点

Fig.15 Dominant nodes with maintenance of transmission line

3.4 仿真验证及分析

为了验证理论分析的正确性,利用PSCAD/EMTDC软件搭建图9所示系统的详细电磁暂态仿真模型,系统参数如附录B所示.

(1) 风电场接入容量对系统振荡稳定性的影响.为了验证风电场接入容量对系统振荡稳定性的影响,设置ZQJ风电场以小开机方式运行,ZXG风电场接入容量标幺值从0.4增加到0.8,系统稳定.ZXG风电场大方式接入后,系统出现40/60 Hz的次/超同步振荡,ZXG的500 kV端口交流电流及频谱分析如图16(a)所示.ZQJ风电场以半容量方式运行,ZXG风电场接入容量标幺值从0.4增加到0.8,系统失稳,ZXG的500 kV端口交流电流和功率如图16(b)所示.ZQJ风电场以大开机方式运行时,ZXG风电场接入容量标幺值为0.4时系统便失稳,ZXG的500 kV端口交流电流和功率如图16(c)所示,此时功率波形的振荡频率约为9.8 Hz,与前文频域模态分析结果一致.图16中:有功功率单位为MW,无功功率单位为Mvar.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 ZXG风电场运行方式变化对振荡的影响

Fig.16 Effect of operation of OWT on oscillation stability in ZXG

(2) N-1运行方式对系统振荡稳定性的影响. 当ZXG和ZQJ风电场同时半容量方式运行时,ZQJ的#ZC4风电场和系统火电厂的仿真波形如图17所示.为了验证N-1运行方式对系统振荡稳定性的影响,10.3 s设置ZQJ和ZCB的两回线路停电检修断开,#ZC4风电场端口交流电流出现40.4/59.6 Hz的次/超同步振荡,功率出现9.6 Hz的次同步振荡,如图17(a)和17(b)所示.10.3 s后火电厂输出的功率也出现了9.4 Hz的次同步振荡,如图17(c)所示.与前文N-1运行方式下系统振荡稳定性分析结果一致.

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 线路停电检修时ZC4端口波形和火电厂功率波形

Fig.17 Waveforms of ZC4 and power waveforms of thermal station with maintenance of trans mission line

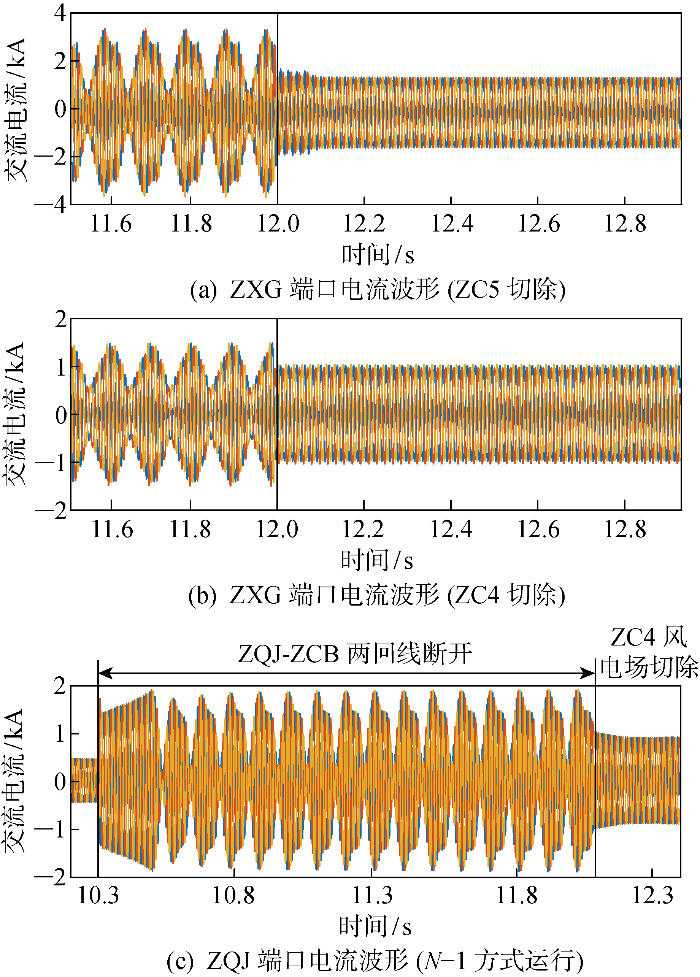
(3) 主导风电场对系统振荡稳定性的影响.根据图13的主导节点分析结果可知,ZQJ小开机、ZXG大开机方式运行,风电场ZC5对系统的振荡稳定性影响最大,是系统的薄弱点或振荡源.仿真工况与图13中的工况三一致,此时ZXG的500 kV端口交流电流波形如图18(a)所示,系统存在次/超同步振荡,在12.0 s将风电场ZC5切除,可以看出,切除对振荡影响最大的风电场ZC5后,振荡被抑制,系统恢复稳定.

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 主导风电场对振荡的影响

Fig.18 Effect of operation of dominant OWF on oscillation stability

根据表3的振荡稳定性评估结果可知,ZQJ大开机、ZXG半容量方式运行,风电场ZC4是系统的薄弱点或振荡源.仿真工况与表3中的工况二一致,ZXG的500 kV端口交流电流波形如图18(b)所示,系统存在次/超同步振荡,在12.0 s将风电场ZC4切除,振荡被抑制,系统恢复稳定.

根据图15的主导节点分析结果可知,ZQJ和ZXG以半容量方式接入,N-1运行方式下风电场ZC4是系统的薄弱点或振荡源.仿真工况与图15中的工况二一致,ZQJ的220 kV端口交流电流波形如图18(c)所示,10.3 s后ZQJ-ZCB线路断开,交流电流快速增加并出现次/超同步振荡,在12.0 s将风电场ZC4切除,振荡被抑制,系统恢复稳定.

4 结语

基于频域模态分析法评估新能源电力系统的振荡稳定性,建立关键设备和场站的阻抗模型,根据系统拓扑构建新能源电力系统的频域网络模型.以国内某局域新能源电力系统为案例,利用频域模态分析法对该系统在不同运行工况下的振荡稳定性及主导节点进行评估,包括不同风电场接入容量、线路N-1等运行工况,研究结论可为实际系统的规划设计和运行调度提供参考.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2025/1006-2467/1006-2467-59-06-0821.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

魏娟, 黎灿兵, 黄晟, 等.

大规模风电场高电压穿越控制方法研究综述

[J]. 上海交通大学学报, 2024, 58(6): 783-797.

DOI:10.16183/j.cnki.jsjtu.2022.416 [本文引用: 1]

大规模发展风电是新能源开发和利用的重大需求,是实现我国“碳达峰、碳中和”战略目标的关键支撑.由外部电网故障造成的风电场电压安全稳定运行问题成为制约风电大规模、集群化、智能化发展的关键瓶颈之一.主要针对电网电压骤升工况,首先从电磁关系和能量流动角度分析常见的双馈风电机组、永磁直驱风电机组以及风电场的高电压穿越(HVRT)暂态特性;然后,基于风电机组不同控制区域归纳总结风电机组HVRT控制策略和风电场HVRT及故障后电压恢复协调优化控制方法,梳理和比较现有各种控制策略的工作原理和优缺点,并从控制结构的角度归纳分析现有大规模风电场的HVRT控制方法的原理、优缺点和效果,总结风电机组和风电场在HVRT控制上的不同点;最后,探讨和预测未来风电场电压智能安全控制的发展趋势和潜在研究热点,为提升我国风电大规模应用和电网安全运行提供借鉴指导作用.

WEI

Juan

, LI

Canbing

, HUANG

Sheng

, et al.

Review on high voltage ride-through control method of large-scale wind farm

[J]. Journal of Shanghai Jiao Tong University, 2024, 58(6): 783-797.