小样本数据驱动模式下的新建微电网优化调度策略

doi:10.16183/j.cnki.jsjtu.2023.394

小样本数据驱动模式下的新建微电网优化调度策略

陈实, 杨林森, 刘艺洪, 罗欢^,, 臧天磊, 周步祥

四川大学电气工程学院, 成都 610065

Optimal Scheduling Strategy of Newly-Built Microgrid in Small Sample Data-Driven Mode

CHEN Shi, YANG Linsen, LIU Yihong, LUO Huan^,, ZANG Tianlei, ZHOU Buxiang

College of Electrical Engineering, Sichuan University, Chengdu 610065, China

通讯作者: 罗欢,博士,副研究员;E-mail:luohuan2378@163.com.

责任编辑: 王历历

收稿日期: 2023-08-14 接受日期: 2023-09-28

基金资助:

国家自然科学基金(51907097)
国家重点研发计划(2021YFB4000500)

Received: 2023-08-14 Accepted: 2023-09-28

作者简介 About authors

陈实(1977—),副教授,博士生导师,从事电力系统信息化及智能化、优化控制运行研究.

摘要

新建微电网缺少历史运行数据,常规数据驱动的方法难以精确预测可再生能源出力,进而影响调度计划制定的准确性.为此,提出一种适用于新建微电网小样本数据场景的微电网优化调度方法.首先,设计融合域对抗神经网络和长短期记忆网络的改进网络结构,将域对抗思想和梯度反转机制引入迁移学习中,提高模型泛化能力,减小数据的域分布差异,使用出力特征相似电站的丰富运行数据对目标电站出力进行预测,克服小样本条件下出力预测精度不高的问题.进一步,将优化调度模型转化为马尔可夫决策过程,使用双延迟深度确定性策略梯度算法求解.最后,以改进CIGRE 14节点微电网为例验证了所提方法的有效性.

关键词： 小样本; 可再生能源出力; 对抗迁移学习; 深度强化学习; 微电网优化调度

Abstract

Newly built microgrids lack historical operation data, making it challenging to predict renewable power output accurately using conventional data-driven methods, which in turn affects the accuracy of scheduling plans. To address this problem, an optimal scheduling method for newly built microgrids in scenarios with limited sample data is proposed. First, an improved network structure integrating a domain adversarial neural network with a long-short-term memory network is designed. The domain adversarial approach and gradient inversion mechanism are incorporated into transfer learning to improve the generalization ability of the model. This reduces the domain distribution discrepancy in the data, and uses the rich operation data of power stations with similar output characteristics to predict the output of the target station, which overcomes the challenge of poor accuracy under the conditions of small samples. Additionally, the optimal scheduling model is transformed into a Markov decision process and solved using double-delay deep deterministic policy gradient algorithm. Finally, the effectiveness of the proposed method is validated through a case study involving an improved CIGRE 14-node microgrid.

Keywords： small sample; renewable energy contribution; adversarial transfer learning; deep reinforcement learning; optimal scheduling of microgrid

PDF (4880KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈实, 杨林森, 刘艺洪, 罗欢, 臧天磊, 周步祥. 小样本数据驱动模式下的新建微电网优化调度策略[J]. 上海交通大学学报, 2025, 59(6): 732-745 doi:10.16183/j.cnki.jsjtu.2023.394

CHEN Shi, YANG Linsen, LIU Yihong, LUO Huan, ZANG Tianlei, ZHOU Buxiang. Optimal Scheduling Strategy of Newly-Built Microgrid in Small Sample Data-Driven Mode[J]. Journal of Shanghai Jiaotong University, 2025, 59(6): 732-745 doi:10.16183/j.cnki.jsjtu.2023.394

“双碳”背景下风光等可再生能源在传统电网中的渗透率不断提高.微电网能够解决分布式电源的灵活高效应用问题,实现对负荷多种能源形式的高可靠供给,近年来发展迅速^[1].但微电网中可再生能源出力波动性和不确定性严重影响能源供需平衡^[2]、储能系统能量管理^[3]、需求响应管理^[4],对其出力进行精确预测能够有效提高微电网日前调度计划制定科学性^[5].大量新建的微电网投入运行时间短,其中可再生能源缺少历史数据而更难以建立高精度的出力预测模型,因此在小样本数据条件下实现新建微电网的日前优化调度运行成为一个亟待解决的问题.

针对小样本条件下可再生能源出力预测问题研究方法可归纳为以下两类,一是利用数据增强的方法对少量历史数据进行扩充^[6-8]来增加参与预测任务的数据量,进而提高预测精度.然而基于数据增强的方法从相似域抽取样本时存在人为随机性,难以表现出可再生能源发电的时序特性.二是基于模型迁移的方法利用公共知识进行泛化,该方法首先在大数据集上训练得到一个具有强泛化能力的模型,然后使用少量目标可再生能源出力数据对该模型进行参数微调,避免数据扩充方法中人为抽取样本的过程,提升预测精度同时减少计算时间.文献[9-10]中分别对出力数据丰富的光伏电站和水电站出力进行建模并将该模型外推至目标电站的出力预测任务.文献[11]中将带物理约束性的长短期记忆网络(long short-term memory,LSTM)作为预训练网络,在多种天气条件下验证了新建光伏(photovoltaic,PV)电站的功率预测效果.文献[12]中提出目标风电(wind turbine,WT)出力的多层级迁移学习模型,验证了迁移层数对出力预测精度的影响.文献[13]在文献[9]的基础上提出针对广域范围分布式光伏电站的功率预测方法,引入误差修正环节构建双迁移模型提高预测精度.考虑到真实环境中每个电站具有自身独特的特点和运行环境,基于模型迁移的方法提取到的公共知识可能无法充分适应目标任务,模型可能出现过拟合,在特定时间尺度上预测精度较低.

在可再生能源出力预测基础上制定的微电网日前调度策略包括基于数学模型的经典优化算法^[14-16]和基于人工智能的数据驱动算法^[17-21].经典的优化方法依赖明确的目标函数,需要对微电网中发电组件和调度过程建立精确的数学模型.由于可再生能源出力具有不确定性,最初建立的模型和选定的参数必须随时间的改变而重新建立,增加计算成本的同时削弱了模型的鲁棒性.以深度强化学习(deep reinforcement learning,DRL)为代表的新一代人工智能算法是求解的另一个有效途径,其用奖惩函数对调度指令好坏作出评价来代替数学模型;同时,因其在处理大规模数据时表现出优良性能而广泛用于微电网的优化调度策略.文献[22]中采用微电网实时运行数据,使用双重深度Q学习算法降低微电网的日运行成本.文献[23]中提出基于改进竞争深度Q网络算法来优化神经网络结构,提高了微电网最优调度策略的稳定性.文献[24]中引入贝叶斯神经网络预测光伏出力,提出双深度期望Q网络算法解决含高比例光伏发电的微电网能量管理问题.上述文献适用于求解离散动作空间的优化问题,但微电网调度控制对象种类繁多,既有离散动作也有连续动作,基于Q学习的算法在连续动作场景下会出现维数灾^[25],无法求解最优调度策略.深度确定性策略梯度(deep deterministic policy gradient,DDPG)算法^[26]可用于动作空间连续的场景,然而该算法存在对可控单元动作Q值过估计的现象,过度依赖当前策略选择动作,导致全局寻优能力较弱.双延迟深度确定性策略梯度(twin delayed deep deterministic policy gradient,TD3)算法是目前深度强化学习中的优秀算法,其通过构建双评判器网络结构,使用目标策略平滑和策略更新延迟技术提高Q值估计能力,适用于连续动作的同时可以有效扩大调度策略寻优空间,因此可用于求解微电网的日前最优调度策略以提高经济性.

综上,针对当前小样本条件下微电网调度策略中存在的可再生能源出力预测精度较差、调度决策空间探索不充分的不足,提出一种基于小样本数据驱动模式的新建微电网优化调度方法.该方法将域对抗学习和梯度反转机制的思想融入迁移学习框架中,设计出域对抗神经网络(domain adversarial neural network,DANN)融合LSTM的迁移学习网络结构DANN-LSTM,增强了模型在目标域小样本条件下可再生能源出力预测任务上的泛化能力.在此基础上,首先,使用DANN-LSTM预测新建微电网中小样本条件下可再生能源出力;然后,进一步建立日前微电网优化调度的马尔可夫决策模型,使用TD3算法求解模型得到最优经济性调控策略;最后,进行仿真验证所提方法的有效性.

1 基于域对抗迁移学习的小样本条件下可再生能源出力预测

迁移学习(transfer learning,TL)与传统机器学习预测可再生能源出力方法不同,其放宽了训练数据与测试数据必须满足独立同分布这一基本假设,旨在利用源域丰富易获得的可再生能源出力数据和模型来帮助完成目标域上少量可再生能源出力的建模预测任务.基于迁移学习的小样本条件下可再生能源出力预测问题可以被定义为一个五元组:<D_s,T_s,D_t,T_t,f_τ(·)>,其中D_s和D_t分别为源域和目标域的数据集.已建成并投入运行时间较长的可再生能源电站数据充足,其出力随气象特征变化的模型容易训练且拟合效果良好,因此设定为源域;新建微电网中可再生能源出力数据匮乏,需要借助源域模型对其出力进行建模,因此设定为目标域.源域和目标域中的数据集包括气象数据、源域丰富风光出力数据和目标域少量风光出力数据及其标签空间,T_s和T_t为源域和目标域的任务,即需要分别建立的可再生能源出力随气象特征变化的模型;f_τ(·)为源域和目标域任务之间的迁移策略.

为了提高模型迁移的方法在目标域小样本条件下可再生能源出力数据上的泛化性能进而降低预测误差,文献[27]中基于生成对抗网络(generative adversarial network,GAN)的思想提出一种较为新颖的DANN,该网络可以有效提高目标域可再生能源出力数据在小样本条件下的学习效果进而提升预测精度.

常规基于模型迁移的小样本条件下可再生能源出力预测方法通常仅在源域电站出力数据上进行训练,这种做法忽略了目标域上可再生能源电站独特的运行环境,从而不能有效地将源域电站上训练所得模型迁移至目标域电站出力建模任务中.而DANN引入域对抗的方式,在源域和目标域之间同时进行域适应训练,增强了可再生能源出力数据的“域不变性”,具有降低过拟合风险,提升目标域小样本条件下可再生能源出力数据利用效率的独特优势,因此将DANN引入小样本条件下可再生出力预测可提高预测精度.

可再生能源出力通常表现出较强的时序特性,而传统DANN模型使用少量神经元构造的特征提取器由于结构单一,难以处理时序数据间的长期依赖关系.LSTM通过引入门机制^[9],能够有效捕捉到长时序可再生能源数据随时间变化的特征,因此将其用作特征提取器来对长期的源域和目标域少量数据进行特征提取.综上,本文将LSTM引入DANN中,设计出改进的DANN-LSTM网络结构,其能够适用于小样本条件下可再生能源长时序数据出力预测任务.

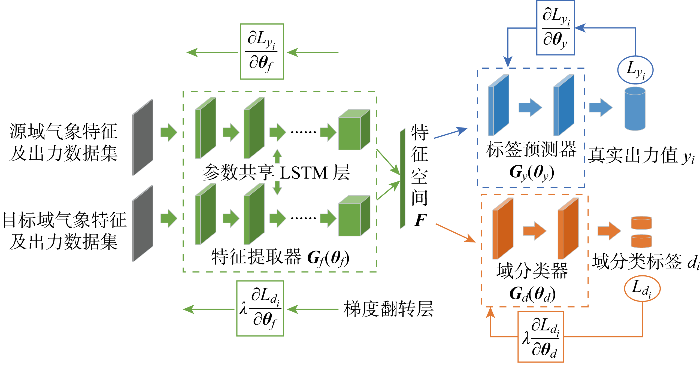
网络结构如图1所示,包括特征提取器G_f(θ_f)、标签预测器G_y(θ_y)、域分类器G_d(θ_d) 3个部分,θ_f、θ_y、θ_d分别为其参数,模型输入数据为包括出力和气象数据的源域电站数据集与仅有气象数据的目标域数据集.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 所提改进DANN-LSTM网络结构

Fig.1 Improved DANN-LSTM network structure proposed

基于DANN-LSTM的小样本条件下可再生能源出力预测方法的基本原理包括数据正向映射和误差反向传播两个过程,这两个过程按先后顺序进行.正向映射是将数据输入特征提取器G_f(θ_f)映射到一个共同的特征空间F;特征空间中源域电站数据集的特征向量则会经过预测器G_y(θ_y)的映射获得对应出力的预测结果;同时,源域电站和目标域电站的特征向量共同经过域分类器G_d(θ_d)得到每个输入的域分类结果.

正向映射过程实现两个目标:第一是实现源域电站出力的准确预测以及预测误差的最小化,因此构造其损失函数为

(1)$L_{y_{i}}\left(\boldsymbol{G}_{y}\left(\boldsymbol{G}_{f}\left(\boldsymbol{x}_{i}\right)\right), y_{i}\right)=\lg \frac{1}{\boldsymbol{G}_{y}\left(\boldsymbol{G}_{f}\left(\boldsymbol{x}_{i}\right)\right)_{y_{i}}}$

式中: $L_{y_{i}}$ 为第i个输入数据的出力预测损失;x_i、y_i分别表示第i个源域输入样本的气象数据和对应的功率.第二是对特征空间的数据进行域分类,使域分类器能够分辨出特征空间中的数据属于源域或目标域,实现域分类误差的最大化,构造其损失函数为

(2)

L_{d_{i}}

(G_d(G_f(x_i)),d_i)=d_ilg

\frac{1}{G_{d} (G_{f} (x_{i}))}

+
(1-d_i)lg

\frac{1}{1 - G_{d} (G_{f} (x_{i}))}

式中: $L_{d_{i}}$ 为第i个输入数据的域分类损失;d_i为第i个输入数据的域分类标签,d_i∈{0,1}. 若d_i=0,则该输入数据属于源域电站出力数据集;若d_i=1,则该输入数据属于目标域电站出力数据集.

在数据正向映射完成后,DANN-LSTM进行误差反向传播过程.误差反向传播是进行网络参数优化的过程.由式(1)和式(2)可知预测器和域分类器的输入都来自特征提取器,然而域分类器和预测器的损失函数寻优方向相反,导致特征提取器进行参数更新时,域分类损失的梯度与预测损失梯度更新方向相反.常规GAN的做法是以分别固定生成器与鉴别器参数的方式进行分阶段训练^[28],这会削弱两个网络间的耦合效果,限制信息交互能力,进而影响生成高质量出力预测数据的能力.DANN在特征提取器和域分类器之间加入梯度翻转层增强各个网络之间的协调性和一致性,将特征提取器、域分类器和预测器作为一个整体实现“端对端”训练,从而可以在目标域上获得更好的性能.具体做法是在域分类损失反向传播过程中加入梯度反转层使梯度方向自动取反并乘以平衡系数λ,提升模型的域适应能力.DANN-LSTM的总优化函数为

(3)$\begin{array}{l} W\left(\boldsymbol{\theta}_{f}, \boldsymbol{\theta}_{y}, \boldsymbol{\theta}_{d}\right)=\frac{1}{n_{\mathrm{s}}} \sum_{i=1}^{n_{\mathrm{s}}} L_{y_{i}}\left(\boldsymbol{\theta}_{f}, \boldsymbol{\theta}_{y}\right)- \\ \quad \lambda\left(\frac{1}{n_{\mathrm{s}}} \sum_{i=1}^{n_{\mathrm{s}}} L_{d_{i}}\left(\boldsymbol{\theta}_{f}, \boldsymbol{\theta}_{d}\right)+\frac{1}{n_{\mathrm{t}}} \sum_{i=n_{\mathrm{s}}+1}^{n_{\mathrm{s}}+n_{\mathrm{t}}} L_{d_{i}}\left(\boldsymbol{\theta}_{f}, \boldsymbol{\theta}_{d}\right)\right) \end{array}$

式中:n_s、n_t分别为源域数据数量和目标域数据数量.考虑到模型在训练初期更加注重提高域分类器性能,应避免域分类器过于敏感地响应噪声信号,确保在域自适应任务中能够得到一个合理的域判别边界来提升域对抗训练的稳定性;在训练后期更侧重预测器,提高目标域小样本条件下可再生能源出力的预测精度.因此,平衡系数λ∈ $[0,1]$ ,反映在不同训练阶段域分类器和预测器的重要程度,其计算公式如下:

(4)λ=

\frac{2}{1 + e x p (- χ p)}

-1

式中:χ为常系数,通常取值为10;p为当前训练次数与总训练次数的比值.在网络进行对抗训练过程中λ会自适应地由0变为1,体现出训练过程中重点任务的动态变化.

反向传播更新网络参数的过程体现了域对抗的思想,即训练过程中通过最小化目标函数来更新预测器的参数,最大化目标函数来更新域判别器的参数:

(5)

\begin{array}{l} (θ_{f}, θ_{y}) = \underset{θ_{f}, θ_{y}}{a r g m i n} W (θ_{f}, θ_{y}, θ_{d}) \\ θ_{d} = \underset{θ_{d}}{a r g m a x} W (θ_{f}, θ_{y}, θ_{d}) \end{array}\}

使用随机梯度下降算法^[29]优化DANN-LSTM的模型参数,梯度更新公式为

(6)

\begin{array}{l} θ_{f} \leftarrow θ_{f} - μ (\frac{\partial L_{y_{i}}}{\partial θ_{f}} - λ \frac{\partial L_{d_{i}}}{\partial θ_{f}}) \\ θ_{y} \leftarrow θ_{y} - μ \frac{\partial L_{y_{i}}}{\partial θ_{f}} \\ θ_{d} \leftarrow θ_{d} - μ \frac{\partial L_{d_{i}}}{\partial θ_{d}} \end{array}\}

μ为模型参数更新的学习率,计算公式为

(7)μ=

\frac{μ_{0}}{{(1 + α p)}^{β}}

式中:μ₀为初始学习率,取为0.01;α、β为超参数,分别取为10和0.75.使用风光出力均方根误差(root mean square error,RMSE)作为验证集上的性能指标,并设定其阈值为0.001,如果该指标在连续的若干轮迭代后不再显著变化或趋于平稳,则可以认为模型已经收敛或无法进一步改善,训练可以停止.

2 基于深度强化学习的微电网优化调度策略

2.1 微电网优化调度目标函数

微电网优化调度通过对储能充放电动作进行控制来获得日内最小运行成本,不同于以往微电网模型中单一储能形式所带来的能量密度和功率输出的限制,本文采用由蓄电池和超级电容器进行配合所组成的复合储能系统来灵活地调整和优化能量存储和释放.微电网优化调度目标函数由微电网与主网交易成本和复合储能系统度电成本组成:

(8)C=min

\sum_{t = 1}^{24}

(c_tp_grid,_t+L_bat

|Δ p_{b a t, t}|

+L_cap

|Δ p_{c a p, t}|

)

式中:c_t为t时段的实时电价;p_grid,_t为t时段微电网与主网之间的交互功率;L_bat、L_cap分别为蓄电池和电容器的度电成本,取值参考文献[30];p_bat,_t、p_cap,_t分别为t时段蓄电池和超级电容的有功功率.

同时微电网优化调度问题应满足以下约束:

(1) 功率平衡约束

(9)p_wt,_t+p_pv,_t+p_bat,_t+p_cap,_t+p_grid,_t-p_load,_t=0

式中:p_wt,_t、p_pv,_t分别表示t时段风电和光伏的总有功功率;p_load,_t为t时段负荷总有功功率.

(2) 储能系统约束.本文中微电网采用由锂蓄电池和超级电容器组成的复合储能系统来同时满足对能量的高效转换和长期储存,考虑建造成本问题和使用寿命损耗,应同时满足以下容量约束和充放电功率约束:

(10)

\begin{array}{l} s_{b a t, m i n} \leq s_{b a t, t} \leq s_{b a t, m a x} \\ p_{b a t, m i n} \leq p_{b a t, t} \leq p_{b a t, m a x} \\ s_{c a p, m i n} \leq s_{c a p, t} \leq s_{c a p, m a x} \\ p_{c a p, m i n} \leq p_{c a p, t} \leq p_{c a p, m a x} \end{array}\}

(11)s_bat,_t₊₁=

\{\begin{array}{l} s_{b a t, t} + p_{b a t, t} Δ t η_{b a t, c h}, p_{b a t, t} > 0 \\ s_{b a t, t} - p_{b a t, t} Δ t η_{b a t, d i s c h}, p_{b a t, t} \leq 0 \end{array}

(12)s_cap,_t₊₁=

\{\begin{array}{l} s_{c a p, t} + p_{c a p, t} Δ t η_{c a p, c h}, p_{c a p, t} > 0 \\ s_{c a p, t} - p_{c a p, t} Δ t η_{c a p, d i s c h}, p_{c a p, t} \leq 0 \end{array}

式中:s_bat,_t、s_cap,_t分别为蓄电池和超级电容器在时段t的容量比例,s_bat,max、s_cap,max和s_bat,min、s_cap,min分别为其上下限,分别取0.8、0.8、0.2和0.2;p_bat,max、p_bat,min分别为蓄电池充放电上下限,分别取±60 kW;p_cap,max、p_cap,min分别为超级电容器充放电上下限,分别取 ±200 kW;η_bat,ch、η_bat,disch和η_cap,ch、η_cap,disch分别为蓄电池和超级电容器充放电效率,取0.9;Δt为调度时段间隔,取1 h.

2.2 微电网优化调度的马尔可夫决策建模及求解方法

在微电网运行过程中,每个调度时段各电力组件的状态仅由上一调度时段和外部环境的变化所决定,因此可用马尔可夫决策过程(markov decision process,MDP)对其建模.一个MDP可由五元组表示:<S,A,P,R,γ>,S为系统的状态变量,A为系统的动作空间,P 为状态转移概率矩阵,R为奖励函数,γ∈(0,1]为折扣因子.

(1) 状态变量S.每个时段t内微电网系统的状态变量s_t∈S可表示为

(13)s_t=

[p_{p v - p r e, t} p_{w t - p r e, t} p_{l o a d, t} s_{b a t, t} s_{c a p, t} c_{t}]

式中:p_pv-pre,_t、p_wt-pre,_t分别为光伏和风电功率在t时段的预测值,由前文提出的DANN-LSTM模型预测得到.

(2) 动作变量A.每个时段t内微电网控制复合储能系统连续充放电动作来进行调度,系统的动作变量a_t可表示为

(14)a_t=

[p_{b a t, t} p_{c a p, t}]

(3) 奖励R.设微电网在状态s_t下选取动作a_t后得到的奖励为R_t,将目标成本函数转化为奖励的最大化形式:

(15)R_t=-C

(4) 状态转移概率:

(16)P(S_t₊₁|S_t=s_t, A_t=a_t)

状态转移概率描述了在给定状态和采取特定动作后,微电网系统从当前时段的状态S_t转移到下一时段状态S_t₊₁的概率分布.由于每一时段可再生能源及负荷具有不确定性,所以很难对其精确建模表示,本文采用深度强化学习算法通过不断尝试不同的动作并观察系统的奖励来逐步学习得到.

(5) 折扣因子γ.用于平衡当前和未来回报的重要性,表示系统对未来奖励的重视程度,本文取0.99.

深度强化学习能够有效地处理复杂的输入和输出空间并从大量的数据中进行学习,使智能体能够做出高质量的决策^[31].TD3是DRL当前较为优秀的算法,将其应用于上述微电网优化调度的马尔可夫决策过程求解,通过对微电网储能系统充放电动作寻优来降低微电网日运行成本.

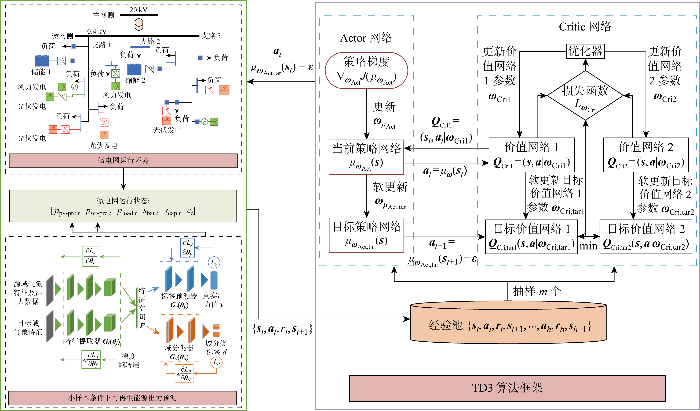
TD3是一种基于执行器-评判器(Actor-Critic)结构的算法^[32],具体结构见图2右侧TD3算法框架.Critic网络以微电网环境在t时段的可再生能源出力、负荷、复合储能系统和实时电价等状态s_t以及储能系统动作a_t作为输入,输出Q值函数 $Q_{ω_{C r i}}$ (s_t,a_t),该函数表示微电网在状态下s_t储能系统采取动作a_t所获得的预期累积奖励,用来评估储能系统在该状态下采取充放电动作a_t的优劣程度,其中ω_Cri为Critic网络参数.Actor网络将t时段的微电网环境状态s_t作为输入,输出储能系统动作策略 $μ_{ω_{A c t}}$ ,微电网获得储能系统动作策略后,根据策略信息对潮流分布结果进行更新并将更新后的状态s_t₊₁发送给储能系统以确保储能系统获得最新的状态信息,根据Q值函数对储能系统动作策略进行更新,其中ω_Act为Actor网络参数.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基于小样本数据驱动模式下的新建微电网优化调度策略求解框架

Fig.2 Solution framework of optimal scheduling strategies for newly built microgrids based on a small-sample data-driven model

TD3使用神经网络实现Critic网络和Actor网络的参数化,使用Critic网络输出Q值对每一调度时段储能系统动作a进行评估,并根据估计值与目标值的差异进行参数更新来优化估计值,使智能体能够更准确地评估动作策略的好坏.采用蒙特卡罗采样来近似Q值损失函数,该函数表示为

(17)

L_{ω_{C r i}}

[(y_{t} - Q_{ω_{C r i}} (s_{t}, a_{t} {))}^{2}]

式中:y_t=r_t+γQ(s_t₊₁, $μ_{ω_{A c t}}$ (s_t₊₁))表示时段t的目标Q值,其中r_t为当前调度时段的奖励;E(·)表示期望函数.

Critic网络应用时序差分学习的思想计算出Q值后,Actor网络使用策略梯度方法来更新参数,以使其在下一时间步生成的储能系统动作策略能够获得更高的累计奖励,计算方法如下:

(18)

Δ_{ω_{A c t}}

J(μ

'_{ω_{A c t}}

E_{S ~ ρ_{μ'}}

(

{Δ_{a} Q_{ω_{C r i}} (s, a)|}_{a = μ'_{ω_{A c t}} (s)} Δ_{ω_{A c t}}

'_{ω_{A c t}}

(s))

式中:s~ρ_μ'为当前微电网状态s在策略μ'下的分布; $Q_{ω_{C r i}}$ (s,a) $|_{a = μ'_{ω_{A c t}} (s)}$ 为在微电网状态s下按照策略储能系统进行动作a=μ $'_{ω_{A c t}}$ (s)得到的Q值;J(μ $'_{ω_{A c t}}$ )为能够获取的期望回报.

TD3通过构建双评判器网络结构、目标策略平滑和策略更新延迟技术使Q值估计更加准确,具体做法详见文献[32].微电网智能体通过反复与环境进行交互获得动作策略的同时,利用算法更新Critic网络和Actor网络参数直至奖励值收敛,得到微电网最优日前调度策略.

2.3 求解步骤

所提基于DANN-LSTM和TD3算法的小样本条件下微电网的优化调度策略求解框架如图2所示,具体流程如下:

(1) 利用地理位置相近电站的丰富历史出力数据作为源域,使用设计的DANN-LSTM网络预测目标微电网中可再生能源出力,为微电网调度过程提供数据支撑,提高决策能力.

(2) 初始化Critic网络和Actor网络的参数和经验池;在每个调度时段将微电网中运行状态和步骤(1)中预测得到的风光出力数据、复合储能系统容量、负荷和实时电价作为Actor网络的状态输入s_t;Actor网络根据当前状态分别给出蓄电池和超级电容的初始动作并加入噪声ε,微电网环境执行当前的控制策略进行状态转移生成下一时刻的状态s_t₊₁,同时智能体给出当前调度时段的奖励r_t并将经验样本{s_t, a_t, r_t, s_t₊₁}添加至经验池中.

(3) 从经验池中随机采样一批经验样本,对于每个样本,在Actor网络中根据式(13)计算下一调度时段的储能系统动作a_t₊₁,并在两个目标Critic网络中分别计算样本的目标值Q_Cri,tar1(s, a| $ω_{Q_{C r i, t a r 1}}$ )和Q_Cri,tar2(s, a| $ω_{Q_{C r i, t a r 2}}$ ),取较小者作为y_t防止过估计问题.根据式(10)更新两个价值Critic网络参数 $ω_{Q_{C r i, t a r 2}}$ 和 $ω_{Q_{C r i 2}}$ ,选取合适的延迟更新步长,根据式(14)更新Actor网络参数ω_Act.重复以上步骤直至奖励值达到最大且收敛,得到最优调度策略.图中: $μ_{ω_{A c t, t a r}}$ 为ω_Act,tar的策略.

3 算例分析

选择欧洲CIGRE 14节点低压微电网系统作为实验对象,并做相应调整,如图3所示.微电网系统包括一个蓄电池和一个超级电容器的2个储能单元、4个光伏电站、3个风电机组以及若干负荷.每个可再生能源电站装机容量均为1 MW,微网中其他元件和线路阻值参考文献[33].

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 CIGRE 14节点低压微电网系统

Fig.3 CIGRE 14-node low-voltage microgrid system

3.1 数据描述和仿真设置

采用编程语言版本Python 3.8,深度学习框架为 PyTorch 1.8.1.数据来自renewables.ninja,该开源网站所提供的数据包括辐射强度、温度、降水量、空气密度、风速以及对应的光伏输出功率和风光输出功率.为了能够捕捉到能源产出的细微变化和波动,从而更准确地评估微网系统的性能和经济效益,将数据的采样间隔设置为1 h.特征提取器由4层LSTM层和1层Dense层组成,4层LSTM层单元数分别选为(200,100,100,50),所选源域、目标域风电场和光伏电站地理位置如表1所示.

表1 源域和目标域电站地理位置

Tab.1 Geographic location of power plants in source and target domains

电站编号	经度/(°)	纬度/(°)
1号源域	-86.9124	36.8796
2号源域	-87.0241	37.1012
3号源域	-86.8248	36.4638
4号源域	-86.7568	36.5879
1号光伏	-86.9442	36.9118
2号光伏	-86.9365	36.9158
1号风电站	-86.9432	36.9089
2号风电站	-86.9412	36.9093

新窗口打开| 下载CSV

3.2 域相似度评估与气象特征筛选

在进行风光出力预测前,首先将得到的数据进行预处理,包括相似度评估和气象特征筛选.以1号光伏为例,采用最大均值差异函数来评估源域数据和目标域数据之间的相似度,避免了预测过程中可能产生负迁移造成预测精度降低,得到以下结果:1号电站与目标域之间的相似度最高,相似度为 0.1248;其次是2号电站,相似度为 0.3184;而3号和4号电站之间的相似度最低,分别为 0.3258 和 0.4752.因此,可以合理地假设1号电站数据更加贴近目标域的特征分布,该源域选择策略有助于减少负迁移现象,确保模型在目标域小样本条件下能够具备较高的出力预测能力.

对于源域风电场和光伏电站,历史数据包括2019年1月1日到2019年12月31日一年间的风光出力数据和对应的气象数据,对于目标域仅有2019年1月1日到1月10日共10 d的历史数据.将包括风光出力数据及对应的气象特征的源域和目标域可再生能源电站数据合并,构造融合数据集,从融合数据集中抽取前70%的数据作为训练集,将余下的30%数据作为测试集.

为了选取与可再生能源出力之间相关性最强的特征并且加快计算速度,使用皮尔逊相关系数来计算各气象特征与可再生能源出力之间的相关性,相关性计算的结果如表2所示.由表可见,在光伏出力方面,辐射强度与光伏出力之间显示出强相关性,并且远高于其他气候因素.因此,可以仅选取辐射强度作为光伏出力的特征.类似地,在风电出力方面选取风速作为风电出力的特征.

表2 风光出力和各气象特征相关性分析结果

Tab.2 Correlation analysis results of wind power and various air image characteristics

出力类型	相关系数
出力类型	温度	空气密度	辐射强度	风速	降水量
WT	-0.22	0.16	-0.23	0.97	0.04
PV	0.39	0.22	0.95	-0.21	-0.06

新窗口打开| 下载CSV

3.3 风光出力预测结果与误差分析

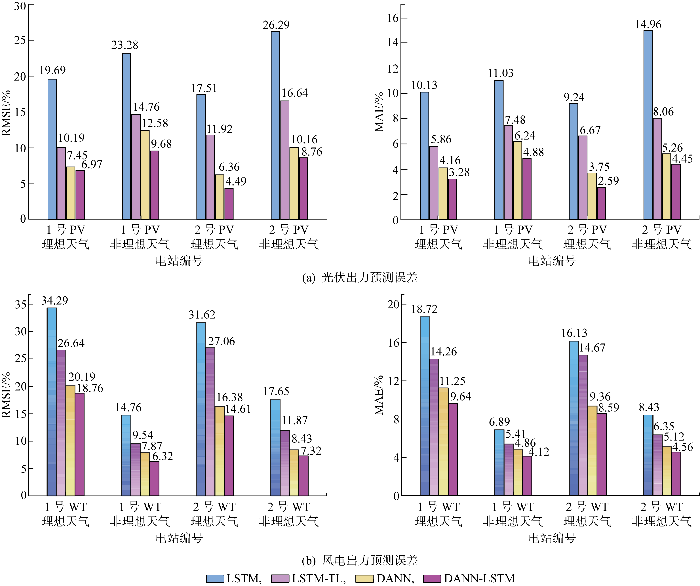
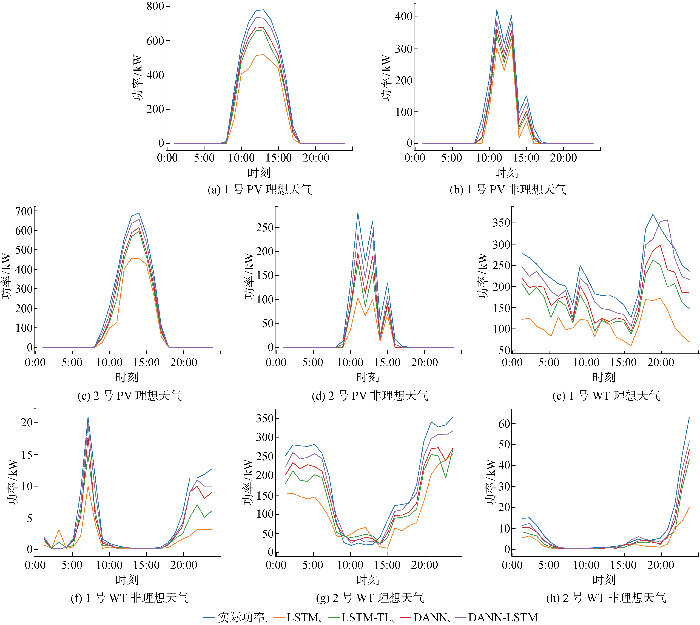
使用均方根误差和平均绝对误差(mean absolute error,MAE)作为评估预测精度的指标.图4展示了相关精度指标,目标域中风电和光伏电站的预测结果与实际值对比如图5所示.由图4和图5可知,新建微电网历史出力数据严重缺失,传统深度学习用于训练集的数据量过少易发生欠拟合,导致预测精度较差.在理想天气条件下1号和2号PV光伏出力预测结果的平均RMSE和MAE分别高达18.60%、9.68%,非理想天气条件下分别为24.78%、13.00%;在风电出力数据集上理想天气条件下的1号和2号PV平均RMSE和MAE分别为32.96%、17.42%,非理想天气条件下分别为16.20%、7.66%;当风光出力发生突变时,误差更加显著.而使用原深度学习网络模型中加入预训练-微调环节后(即图4中LSTM-TL对应数据),能使数据量较少的目标域电站学习到相似源域电站的出力特性,在光伏出力预测和风电出力预测的平均精度上分别得到较大提升:理想天气条件下光伏出力数据集平均RMSE降低至11.06%,非理想天气条件下出力预测结果平均RMSE降低至15.70%,相应的平均MAE分别降低至6.26%和7.77%;风电预测任务上理想天气条件下平均RMSE、MAE分别降低至26.85%、14.46%,非理想天气条件下平均RMSE、MAE分别降低至10.70%、5.88%.然而,依赖公共知识的预训练网络在目标域上精确时间尺度上的预测效果仍然不高.DANN通过引入域对抗的方法同时训练源域和目标领域的任务,增强公共特征在目标领域上的映射效果进而提高出力预测精度,与基于模型迁移的方法相比,光伏出力预测结果在理想天气条件下平均RMSE和MAE分别降低4.15百分点、2.31百分点,在非理想天气条件下平均RMSE和MAE分别降低4.33百分点、2.02百分点;风电出力预测结果在理想条件下平均RMSE和MAE分别降低8.56百分点、4.16百分点,在非理想天气下平均RMSE和MAE分别降低2.56百分点和0.89百分点.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 可再生能源预测误差指标

Fig.4 Prediction errors of renewable energy output

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 可再生能源出力预测结果

Fig.5 Prediction results of renewable energy output

与传统的DANN相比,所提网络在DANN的基础上加入LSTM用于特征提取任务,能够更好地捕捉风光出力数据的时序特性,在理想天气条件下光伏出力预测结果平均RMSE和MAE仅有5.73%和2.94%,非理想天气条件下光伏出力预测结果平均RMSE和MAE分别为9.22%和4.66%;同时,理想天气条件下风电预测结果平均RMSE和MAE分别降低至16.68%和9.12%,非理想条件下风电预测结果平均RMSE和MAE分别降低至6.82%和4.34%.证明所提的网络结构能够有效提高小样本条件下可再生能源出力预测的精度.

基于模型迁移的方法预测精度受迁移层数的精度的影响.图6和图7展示了不同迁移层数下的预测精度与所提方法的对比.图中:TL-fixed-n表示固定的前n层LSTM层数.由图可知,在理想天气条件下,光伏和风电的出力预测精度随着固定的网络层数增加先升后降,且选择固定前两层网络参数时精度最高:光伏出力预测结果RMSE分别为8.26%、7.89%,风电出力预测结果RMSE分别为23.12%和24.15%.固定前4层参数时误差最高,其原因可能在于:理想天气情况下,光伏和风电的出力随相应气象特征间的知识较易提取,只需要两层LSTM层便可充分知识提取;当固定的层数增加时,预训练模型更加关注提高源域电站上的出力预测精度,忽略了目标域电站上的特定出力特征,同时,随着固定的层数增加,模型的参数量也随之增加.过多参数可能导致模型在小数据集上过拟合,进而造成目标域上小样本条件下可再生能源出力预测精度下降,这是迁移学习中的一个常见问题,称为“迁移性能不匹配”^[34].而在非理想天气条件下,由于可再生能源的出力随相应气象特征之间的关系较为复杂,所以需要保留更高的LSTM层数进行充分的知识提取.因此,选取固定前4层LSTM层,只对全连接层进行参数微调时预测精度最高.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 基于模型迁移的可再生能源出力预测结果随迁移层数变化情况

Fig.6 Prediction results of model transfer-based renewable energy output versus numbers of migrated layers

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 基于模型迁移的可再生能源出力预测精度随迁移层数变化情况

Fig.7 Prediction accuracy of model transfer-based renewable energy output versus numbers of migrated layers

3.4 微电网优化调度结果

微电网的风光出力数据由DANN-LSTM预测得到,负荷和实时电价来自美国加州电力系统CASIO^[35]真实的运行数据.实验中仿真步长取为1 h,每次参与训练样本数设置为128,其他参数设置及仿真环境详见附录表A1.

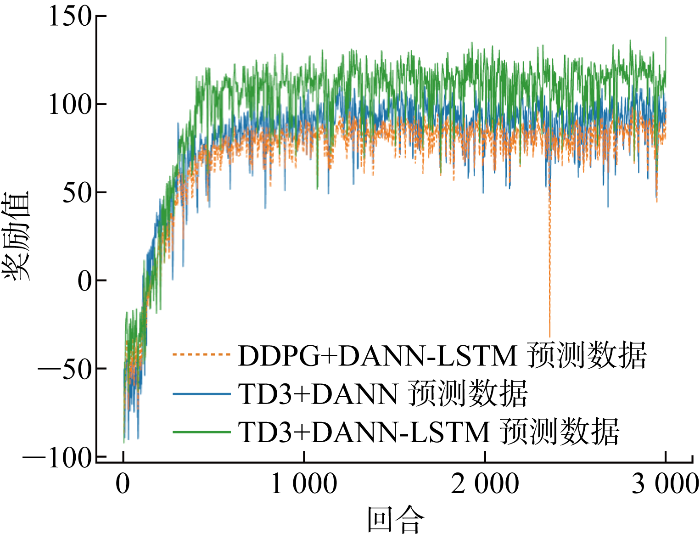
为了展现所提方法的最优动作空间探索能力,分别将LSTM、LSTM-TL和传统DANN这3种方法与所提方法DANN-LSTM预测所得可再生能源出力作为状态空间进行训练,并将TD3算法与DDPG算法在4种状态空间下所得奖励值进行对比,选取在TD3算法中奖励值最高的两种结果和DDPG算法训练结果中奖励值最高的结果及对应的日运行成本进行展示.图8和图9分别给出智能体训练过程中的奖励值和日运行成本变化.由图可见,在初始阶段,由于训练不充分,所以智能体抽取到低奖励值经验的概率较高;随着智能体不断与环境交互并使用高奖励值经验改进策略,在后续训练过程中能够做出更优秀的调度决策并获得更高奖励值,最终学习到日运行成本最低的调度策略.DDPG算法在 2 400 回合奖励函数出现异常值,其原因是神经网络发生“网络退化”现象^[32].DDPG算法使用确定性策略,倾向于根据当前的最优动作选择策略.在初始训练阶段,随机性较大的探索有助于探索更多状态-动作对,并发现更好的储能系统充放电策略.但随着训练进行,随机性减少,模型趋向于利用已知的最优充放电动作,可能导致陷入局部最优解.在某些情况下,模型可能会重新探索先前被认为是次优的动作,即输出的策略朝着奖励值较低的轨迹上前进而导致奖励值骤降,随着经验回放缓冲区的更新和样本的变化,模型将有机会学习到更多高奖励的样本,从而使奖励值回到原来的收敛值.与DDPG算法相比,TD3通过在动作策略中加入噪声避免储能动作陷入局部最优,增大最优动作被探索到的概率,并通过值函数的双重更新减小值函数的估计误差,提高智能体控制储能系统在每一调度时段内做出最优充放电动作的决策能力.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 奖励值随训练轮数变化结果

Fig.8 Reward value versus numbers of training rounds

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 日运行成本随训练轮数变化

Fig.9 Daily running cost versus numbers of training rounds

经过约 1 000 回合后,奖励值趋于收敛,DDPG算法训练所得的奖励值约为70,而使用不同预测数据作为状态空间的TD3算法所得的奖励值均高于DDPG.同时,可以看出在同时选用TD3作为优化算法的前提下,使用不同预测精度的可再生能源出力数据作为状态空间的智能体的学习效果也有所差异:使用传统DANN出力预测数据作为状态空间得到的奖励值约为80;使用所提DANN-LSTM方法所得出力预测数据作为状态空间得到的奖励值最高,约为110,同时得到的日运行成本最低,约为910美元,比DDPG算法训练得到的日运行成本降低约90美元,证明所提方法下所得最优调度策略的科学性和经济性.

图10展示了基于DANN-LSTM预测数据和TD3算法的储能系统充放电动作.通过该调度策略,在确保电力需求得到满足的同时,尽可能降低成本.由图可知,8:00—13:00 系统内光伏出力波动较大,蓄电池无法进行快速调节以应对系统内突变产生的波动.因系统储能形式多样,故超级电容可在光伏与负突变时段快速做出调整,抑制光伏出力波动,降低光伏出力特性对系统的影响.与此同时,储能系统选择在 9:00—13:00 电价较低时进行充电,在 16:00—21:00 电价较高时放电,通过低买高卖的套利策略提高经济效益.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 储能充放电动作

Fig.10 Storage charge and discharge

4 结论

提出一种基于小样本数据驱动模式下的新建微电网优化调度策略.设计了一种DANN-LSTM网络结构,通过域对抗的思想训练网络,提高了小样本条件下可再生能源出力预测精度.以最小化运行成本为目标,将优化调度问题转化为马尔可夫决策过程,应用深度强化学习TD3算法进行求解.仿真结果表明:

(1) 与模型迁移方法和传统的DANN相比,所提DANN-LSTM网络结构能有效减小风光出力的预测误差,为小样本条件下新建微电网调度策略的寻优提供有效的数据支撑.

(2) 所使用的TD3算法相较于DDPG能够寻找到更优的储能充放电动作,从而得到更低的系统运行成本.

所提方法在新建单微网中的应用效果良好,但未考虑多微网场景下的协调优化调度等更复杂的场景,这将是下一步的重点研究工作.

附录见本刊网络版(xuebao.sjtu.edu.cn/article/2025/1006-2467/1006-2467-59-06-0732.shtml)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王文彬, 郑蜀江, 范瑞祥, 等.

“双碳” 背景下微网分布式电能交易绩效评价指标与方法

[J]. 上海交通大学学报, 2022, 56(3): 312-324.

DOI:10.16183/j.cnki.jsjtu.2021.391 [本文引用: 1]

随着分布式发电研究与应用的迅速发展,分布式交易市场作为一种新型的电力交易模式,能够有效提升可再生能源消纳率,是推动实现“碳达峰、碳中和”目标的重要手段.将市场评价机制引入用户的竞拍交易机制中,将促使用户考虑市场评价机制对其交易策略的影响,推动分布式交易市场的良性发展.针对微网用户间的分布式电能交易市场展开研究,首先,以市场参与主体及交易支撑软硬件为研究对象,分别从电能供应能力、用户满意度、平台安全性等方面建立多维度绩效评价指标体系.然后,对分布式电能交易市场评价方法研究现状进行总结与梳理,并从指标体系建立、指标计算方法及综合评价方法三方面分析了分布式电能交易绩效评价的关键技术.最后,结合当前发展现状,对未来分布式电能交易绩效评价的研究方向进行了展望.

WANG

Wenbin

, ZHENG

Shujiang

, FAN

Ruixiang

, et al.

Performance evaluation index and method of micro-grid distributed electricity trading under the background of “carbon peaking and carbon neutrality”

[J]. Journal of Shanghai Jiao Tong University, 2022, 56(3): 312-324.